First-principles calculations and high thermoelectric performance of La–Nb doped SrTiO3 ceramics
Received
19th October 2018
, Accepted 20th November 2018
First published on 20th November 2018
Abstract
SrTiO3 is a promising thermoelectric material for high temperature application of waste heat electrical generation. However, its dimensionless figure of merit (zT) is restricted by its high thermal conductivity, which results from the simple perovskite structure and light elements of SrTiO3. In this paper, we successfully obtained complex structured bulk SrTiO3 with a TiO2 second phase and a porous structure by tuning the doping ratios of the heavy elements La and Nb, resulting in a low thermal conductivity of 1.97 W m−1 K−1 and a high zT value of 0.31 at 1050 K. The first-principles calculation was utilized to calculate the formation energy, effective mass and electron band structure of La–Nb co-doped SrTiO3, and the effects of the parameters on the thermoelectric properties were also discussed. We found that the doping ratio of La to Nb changed the electron band structure and controlled the formation of the TiO2 second phase, which affected the electrical transport and thermal transport properties, respectively. The formation of the in situ TiO2 second phase was related to the high formation energy derived from the high Nb concentration. These results offer an approach for the design of other thermoelectric materials with low thermal conductivity and a high power factor.
1. Introduction
In recent years, clean and efficient usage of energy sources has attracted increasing public attention. It is urgent to develop renewable energy resources to compensate for environmental pollution resulting from conventional fossil fuels and increasing energy demands, especially industrial waste heat.1 Thermoelectric materials have been regarded as a potential energy conversion material, which can be used to directly convert waste heat into electrical energy. In addition, such thermoelectric energy conversion has the advantages of being nontoxic, environmentally friendly, low cost, without the introduction of moving parts, and so on. The energy conversion efficiency of a thermoelectric material is primarily evaluated by the dimensionless figure of merit zT = σS2T/κtotal, where σ, S, κtotal, and T represent the electrical conductivity, Seebeck coefficient, thermal conductivity and absolute temperature, respectively. A high zT can be obtained using a large σ and S as well as a small κtotal. However, these interdependent parameters need independent control.
Previous researchers have made efforts to improve the zT value by several ways. One successful strategy is to reduce the lattice thermal conductivity by structural modification and defect engineering, such as the introduction of nanostructures,2 complex structures,3 point defects,4 dislocations,5 pores,6 and grain boundaries. Another route to improve the zT value is the enhancement of the power factor PF = S2σ, which can usually be realized by doping, band engineering and use of a heterojunction.7–9 By using the above approaches, significant improvement in the zT values of many thermoelectric materials10–15 has been achieved. Among classical oxides, SrTiO3 is a potential thermoelectric material for high temperature applications due to its high Seebeck coefficient and good stability. However, its applications are limited by its low efficiency resulting from its high thermal conductivity. Table 1 summarizes the reported properties of several doped SrTiO3 thermoelectric materials in previous studies, showing that almost all relatively large zTs were obtained in La or Nb single-doped SrTiO3 materials, which are usually prepared by hot pressing, spark plasma sintering (SPS) or solid state reaction. The improvement of zT in SrTiO3, however, is not significant due to its relatively high thermal conductivity. Although the introduction of structural modifications such as nanostructures,16 point defects17 and second phases18 into SrTiO3 can decrease the thermal conductivity to some extent, it is hard to significantly decrease the thermal conductivity of SrTiO3 using a single approach, where the simple perovskite structure and light elements of SrTiO3 are the main reasons for the high thermal conductivity. Differing from the single-doping approach, the combination of heavy La and Nb co-doping, a second phase and pores can significantly change the microstructures and compositions of SrTiO3 simultaneously, which is expected to decrease its thermal conductivity.
Table 1 Thermoelectric properties of doped SrTiO3 materials obtained by different preparation methods
| Composition |
Processing conditions |
zT
|
κ
total (W m−1 K−1) |
| Sr2Ti1.6Nb0.4O7, Sr2.85Gd0.15Ti2O7, Sr2.85Sm0.15Ti2O7, Sr2.85La0.15Ti2O7 (ref. 19) |
Hot pressing, Ar flow, 1723 K, 2 h |
0.14, 0.24, 0.22, 0.15, 1000K |
2.3 |
| Sr0.94Y0.06TiO3 (ref. 20) |
Hot pressing, Ar, 1627 K, 1 h, 31.2 MPa |
0.14, 659 K |
4.3 |
| Sr0.9Y0.1TiO3 (ref. 21) |
Hot pressing, Ar, 1673 K, 2 h, 25 MPa |
0.14, 870K |
5.3 |
| Sr2.7Ga0.3Ti1.9Nb0.1O7 (ref. 22) |
Hot pressing, Ar flow, 1673–1748 K, 1 h, 34 MPa |
0.15, 1000 K |
2.2 |
| Sr0.8La0.08Dy0.12TiO3 (ref. 23) |
Ar/5% H2, 1733 K, 4 h |
0.36, 1076 K |
2.3 |
| Sr0.92La0.08TiO3 (ref. 24) |
SPS, vacuum, 1573 K, 5 min, 34 MPa |
0.37, 1045 K |
2.2 |
| SrTi0.8Nb0.2O3 epitaxial film25 |
Pulsed laser deposition, 973 K |
0.37, 1000 K |
— |
| Sr0.1La0.6TiO3−δ (ref. 26) |
N2/5% H2, 1773 K, 6 h, cold isostatic pressing at 200 MPa |
0.4, 973 K |
2.4 |
It is known that the first-principles calculation has been extensively used to calculate the formation energy, effective mass and electron band structure.27 The formation energy can be used to characterize the stability of a compound. And then, the stability of a compound, the effective mass and electron structure are useful to determine the electron transport properties of thermoelectric materials. To the best of our knowledge, however, there has been no report so far focusing on first-principles calculations of the formation energy, effective mass and electron band structure of La and Nb co-doped SrTiO3 materials.
In this paper, we first calculate the formation energy, effective mass and electron band structure of La–Nb doped SrTiO3 using the first principles approach and then discuss the effects of the parameters on the thermoelectric properties. Based on the results of the calculation, we design desired n-type bulk SrTiO3 with a reduced lattice thermal conductivity of 1.97 W m−1 K−1 by introducing La and Nb dopants, a second phase and pores, resulting in a high zT value of 0.31 at 1050 K.
2. Experimental procedure
2.1 Model and calculation method
The ideal SrTiO3 has a cubic perovskite structure with a space group of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The ground state atomic and electronic structures of La and Nb co-doped SrTiO3 were calculated by first-principles density functional theory using CASTEP.28 These calculations are based on density functional theory (DFT) with the generalized-gradient approximation (GGA) and the plane-wave pseudo potentials as implemented in CASTEP.29 The exchange–correlation energy can be described by the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function. The valence atomic configurations are 4s24p65s2 for Sr, 2s22p4 for O, 3s23p63d24s2 for Ti, 4s24p64d45s1 for Nb, and 5s25p65d16s2 for La, respectively. The plane-wave cutoff energy is 340 eV, and the Monkhorst–Pack k-mesh is 3 × 3 × 3. The calculation precision was converged to be 1.0 × 10−5 eV per atom. All atoms are allowed to relax until the force on each atom is below 0.3 eV nm−1, the internal stress is below 0.05 GPa, and the displacement of each atom is below 0.0001 nm simultaneously.
m. The ground state atomic and electronic structures of La and Nb co-doped SrTiO3 were calculated by first-principles density functional theory using CASTEP.28 These calculations are based on density functional theory (DFT) with the generalized-gradient approximation (GGA) and the plane-wave pseudo potentials as implemented in CASTEP.29 The exchange–correlation energy can be described by the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function. The valence atomic configurations are 4s24p65s2 for Sr, 2s22p4 for O, 3s23p63d24s2 for Ti, 4s24p64d45s1 for Nb, and 5s25p65d16s2 for La, respectively. The plane-wave cutoff energy is 340 eV, and the Monkhorst–Pack k-mesh is 3 × 3 × 3. The calculation precision was converged to be 1.0 × 10−5 eV per atom. All atoms are allowed to relax until the force on each atom is below 0.3 eV nm−1, the internal stress is below 0.05 GPa, and the displacement of each atom is below 0.0001 nm simultaneously.
The total energy and formation energy of all samples were calculated using the following equation:30,31
| | | EF = ESrTiO3:La2m–Nb2n − ESrTiO3 − μELa2O3 − νENb2O5 + 2μESrO + 2νETiO2 | (1) |
where
ESrTiO3:La2m–Nb2n and
ESrTiO3 are the total energies of La–Nb co-doped and un-doped SrTiO
3, respectively.
ELa2O3,
ENb2O5,
ESrO,
ETiO2 are the ground state energies of the La
2O
3, Nb
2O
5, SrO and TiO
2, respectively;
μ and
ν are the number of La
2O
3 and Nb
2O
5 molecules in the reactants, respectively.
2.2 Materials preparation
The Sr1−xLaxTi1−yNbyO3 (0.03 ≤ x ≤ 0.1 and 0.03 ≤ y ≤ 0.2) powders were fabricated via a hydrothermal method. Table 1 lists the raw materials and their purity used in the experiments. First, Sr(NO3)2 (purity: 99.5%) and La(NO3)3·6H2O (purity: 99%) were dissolved in deionized water. Then, Ti[OCH(CH3)2]4 (purity: 98%) and NbCl5 (purity: 99%) were dissolved in ethylene glycol to form uniform solutions and NaOH (purity: 96%) was dissolved in deionized water. Eventually, three solutions were mixed and slowly stirred with an electromagnetic agitator in a beaker, ensuring that the pH value of the mixed solution was adjusted to 13. After 5 minutes, the solution was decanted into a Teflon autoclave and reacted at 180 °C for 24 h. After the autoclave was cooled down to room temperature, the obtained precipitate was washed several times with deionized water and glacial acetic acid before being dried at 80 °C. The obtained solid blocks were pulverized into powders by using an agate mortar and pestle.
The obtained powders were sintered using a hot pressing sintering furnace (ZT-60-20Y, Chenhua, China). The preceding powders were filled in a cylindrical graphite die and pressed into a disk of 18 mm in diameter under a uniaxial pressure of 20 MPa using a graphite punch, followed by hot pressing sintering at 1573 K for 2 hours in a vacuum. Graphite foil (with a thickness of 0.15 mm) was placed into graphite mold gaskets before filling with the powders so that the disk can be easily taken out. All samples were polished down each side to ensure complete removal of the graphite foil. The prepared samples are Sr0.97La0.03Ti0.97Nb0.03O3, Sr0.95La0.05Ti0.95Nb0.05O3, Sr0.93La0.07Ti0.93Nb0.07O3, Sr0.9La0.1Ti0.9Nb0.1O3, Sr0.95La0.05Ti0.9Nb0.1O3, Sr0.9La0.1Ti0.95Nb0.05O3, and Sr0.9La0.1Ti0.8Nb0.2O3, which are hereinafter referred to as La3Nb3, La5Nb5, La7Nb7, La10Nb10, La5Nb10, La10Nb5, and La10Nb20, respectively. The densities (ρ) of the sintered samples are higher than 93% of the theoretical density value except for the La10Nb20 sample with a density of 82%, as determined by the Archimedes method, which is 8% lower than the others.
2.3 Sample characterization
The phase composition was identified by X-ray diffraction (XRD, D/MAX 2500 PC, Rigaku) with Cu Kα doublet radiation. Rietveld refinements of the XRD patterns for the doped SrTiO3 bulk were carried out using General Structure Analysis System (GSAS) software.32 The refinements were executed with the ICSD 27045 (cubic crystal structure with the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as a reference for the structural model. The microstructures in the SrTiO3 bulk were characterized by field-emission scanning electron microscopy (SEM, JSM7000F, JEOL), with the SrTiO3 powders being characterized by transmission electron microscopy (TEM, JEM2010, JEOL Ltd.). The chemical composition of the bulk samples was acquired using an energy dispersive spectrometer (EDS). X-ray photoelectron spectroscopy (XPS, ESCALAB 250Xi, Thermo Fisher Scientific) was used to analyze the surface elemental compositions and valence states of the elements. The thermal diffusivity coefficient (D) was determined using a laser flash apparatus (LFA 427, Netzsch, Germany). The specific heat capacity (Cp) was measured using a differential scanning calorimeter (DSC 200 F3, Netzsch, Germany) under a flow of argon. The thermal conductivity was calculated by using the equation κ = DρCp. The Seebeck coefficient and electrical conductivity were measured simultaneously using a Seebeck coefficient and electric resistance measuring system (LRS-3, Linseis, Germany). The test temperature range was between 300 and 1050 K, and the sealed sample chamber was filled with helium gas. The carrier concentration (n) and Hall mobility (μH) were measured using a Hall measurement system from 300 to 800 K. As for the La10Nb20 sample, the extremely high carrier concentrations lead to a Hall voltage too small to be measured accurately, so we do not show values of n and μH in this paper.
m) as a reference for the structural model. The microstructures in the SrTiO3 bulk were characterized by field-emission scanning electron microscopy (SEM, JSM7000F, JEOL), with the SrTiO3 powders being characterized by transmission electron microscopy (TEM, JEM2010, JEOL Ltd.). The chemical composition of the bulk samples was acquired using an energy dispersive spectrometer (EDS). X-ray photoelectron spectroscopy (XPS, ESCALAB 250Xi, Thermo Fisher Scientific) was used to analyze the surface elemental compositions and valence states of the elements. The thermal diffusivity coefficient (D) was determined using a laser flash apparatus (LFA 427, Netzsch, Germany). The specific heat capacity (Cp) was measured using a differential scanning calorimeter (DSC 200 F3, Netzsch, Germany) under a flow of argon. The thermal conductivity was calculated by using the equation κ = DρCp. The Seebeck coefficient and electrical conductivity were measured simultaneously using a Seebeck coefficient and electric resistance measuring system (LRS-3, Linseis, Germany). The test temperature range was between 300 and 1050 K, and the sealed sample chamber was filled with helium gas. The carrier concentration (n) and Hall mobility (μH) were measured using a Hall measurement system from 300 to 800 K. As for the La10Nb20 sample, the extremely high carrier concentrations lead to a Hall voltage too small to be measured accurately, so we do not show values of n and μH in this paper.
3. Results and discussion
3.1 Geometry optimization results
The lattice parameters, total energy, formation energy, electron effective mass and carrier concentrations for Sr1−xLaxTi1−yNbyO3 calculated from first principles are presented in Table 2.
Table 2 Lattice parameter, total energy, formation energy, electron effective mass and carrier concentration of SrTiO3 with varying doping concentration calculated from first principles
| Sample |
a/Å |
E/eV |
E
F/eV |
m*/m0 |
n/1021 cm−3 |
| SrTiO3 |
3.946 |
−3758.94 |
— |
4.49 |
— |
| SrTi0.9Nb0.1O3 |
3.959 |
−3753.69 |
−2.34 |
6.13 |
1.60 |
| Sr0.9La0.1TiO3 |
3.950 |
−3761.33 |
−5.48 |
4.28 |
1.62 |
| Sr0.95La0.05Ti0.95Nb0.05O3 |
3.955 |
−3757.66 |
7.17 |
7.40 |
1.61 |
| Sr0.95La0.05Ti0.9Nb0.1O3 |
3.961 |
−3755.03 |
7.09 |
5.42 |
2.41 |
| Sr0.9La0.1Ti0.95Nb0.05O3 |
3.957 |
−3758.99 |
−6.23 |
6.32 |
2.42 |
| Sr0.9La0.1Ti0.9Nb0.1O3 |
3.963 |
−3756.35 |
−6.76 |
5.20 |
3.21 |
| Sr0.9La0.1Ti0.8Nb0.2O3 |
3.973 |
−3751.05 |
21.34 |
4.91 |
4.77 |
The calculated lattice parameter for pure SrTiO3 is a = 3.946 Å, in good agreement with the experimental value of a = 3.905 Å.33 Although the ionic radius of La3+ (1.36 Å) is smaller than that of Sr2+ (1.44 Å) and Nb5+ (0.64 Å), it is larger than that of Ti4+ (0.605 Å);34 the lattice parameters for all La–Nb-doped SrTiO3 samples are larger than that for the pure sample, which may be related to the increasing ionic repulsive force arising from the excess positive charge of La3+ and Nb5+. The effect of Nb on the increase in lattice parameter is larger than that of La because the ionic radius of Nb5+ is larger than that of Ti4+, which further results in a large formation energy. The doping ratio of La to Nb affects the formation energy. Except for the formation energies of Sr0.9La0.1Ti0.8Nb0.2O3, Sr0.95La0.05Ti0.95Nb0.05O3 and Sr0.95La0.05Ti0.9Nb0.1O3, the formation energies of the other samples are smaller than that of SrTi0.9Nb0.1O3, indicating that these samples are more easily obtained by experiment, which is also confirmed by the fact that the SrTi0.9Nb0.1O3 has been previously successfully synthesized by several experimental methods.35,36
The critical carrier concentration in the degenerate SrTiO3 semiconductor is nc = 7.95 × 1010 cm−3, which can be calculated by the following equation:37
where
aH and
nc are the Bohr radius and critical concentration for the degenerate semiconductor, respectively. All carrier concentrations (
n) in the present study are > 10
21 cm
−3 (
Table 2), which is far larger than the critical value of
nc = 7.95 × 10
10 cm
−3, suggesting that all the samples in the present study are a degenerate semiconductor. This is also confirmed by energy band structure analysis, as shown in
Fig. 1. The Fermi level of pure SrTiO
3 lies on the top of the valance band, while the Fermi level of La and Nb co-doped SrTiO
3 shifts into the conduction band when
nc ≥7.95 × 10
10 cm
−3, following which the sample changes into a degenerate semiconductor. The degree of the shift in the Fermi level depends on the ratio of La to Nb, indicating that the La and Nb dopants play different roles in the electron transport properties.
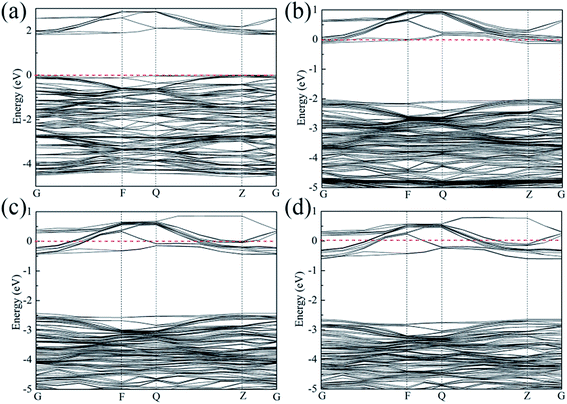 |
| | Fig. 1 Energy band structure for (a) SrTiO3, (b) Sr0.95La0.05Ti0.95Nb0.05O3, (c) Sr0.9La0.1Ti0.9Nb0.1O3 and (d) Sr0.9La0.1Ti0.8Nb0.2O3. | |
The conduction band minimum (CBM) shows a flat band, which may be induced by the large electron effective mass. The electron effective mass m* can be calculated by the following equation:38
| | 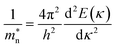 | (3) |
where
h is the Planck constant,
κ is the wave vector, and the energy
E(
κ) can be estimated from the second-order derivatives in the
G direction of the curves at the CBM. The electron effective mass also depends on the ratio of the dopants.
Fig. 2 shows the total density of states (DOS) and contribution of each component of the unit cell for pure and doped SrTiO3, respectively. The valance band maximum (VBM) of either pure or doped SrTiO3 is composed of O 2p states, with its CBM mainly composed of Ti 3d states, in good agreement with a previous report.39 On the other hand, the Nb 4d and La 5d of doped SrTiO3 show some contributions to the conduction band, with the contribution of the former being larger than that of the latter. This result indicates that the electrical transport properties can be optimized by the ratio of La to Nb.
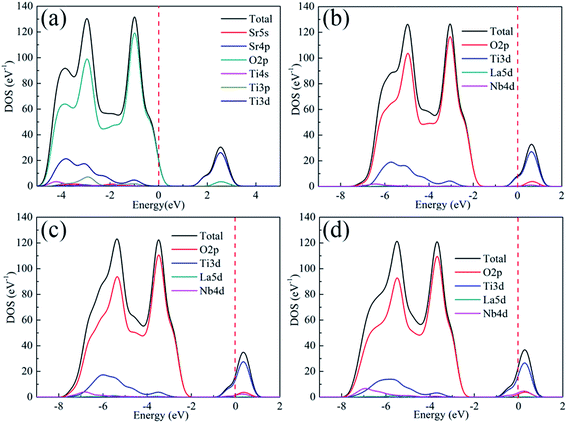 |
| | Fig. 2 Total density of states (DOS) and contribution of each component of the unit cell for (a) SrTiO3, (b) Sr0.95La0.05Ti0.95Nb0.05O3, (c) Sr0.9La0.1Ti0.9Nb0.1O3 and (d) Sr0.9La0.1Ti0.8Nb0.2O3. | |
3.2 Characterization of SrTiO3 powder and bulk samples
Fig. 3(a) shows the XRD patterns of hydrothermally synthesized SrTiO3 powders and pure SrTiO3 from the Powder Patterns Database (PDF# 84-0444). All the powder diffraction peaks of the La and Nb co-doped powders conformed to the cubic perovskite SrTiO3 structure with the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and no impurity phase was observed within the detection limit of XRD. However, after hot pressing, a TiO2 impurity phase appears for all doped SrTiO3 bulks, as shown in Fig. 3(b). A shift to lower angles is also observed for all the SrTiO3 and TiO2 peaks. The relative amount of TiO2 can be estimated using the following equation:40
m and no impurity phase was observed within the detection limit of XRD. However, after hot pressing, a TiO2 impurity phase appears for all doped SrTiO3 bulks, as shown in Fig. 3(b). A shift to lower angles is also observed for all the SrTiO3 and TiO2 peaks. The relative amount of TiO2 can be estimated using the following equation:40| | 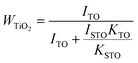 | (4) |
where ISTO and ITO are the intensities of the strongest XRD peak for SrTiO3 and TiO2; KSTO and KTO are the reference intensities for SrTiO3 and TiO2, respectively. As shown in Table 3, the content of the TiO2 second phase is related to the doping concentration, which can be explained from the formation energy. The La10Nb20 sample contains the maximum amount of the TiO2 second phase due to its large formation energy, as shown in Table 2.
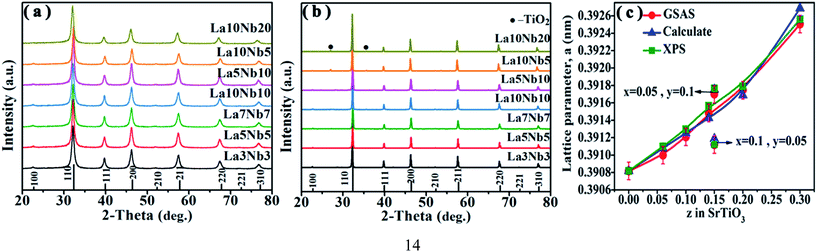 |
| | Fig. 3 (a) XRD patterns for powders and (b) XRD patterns for bulk samples. (c) Doping concentration dependence of the lattice parameter of SrTiO3 bulk samples; the red circle shows the data obtained from Rietveld refinement using GSAS software, and the blue triangle and green square show the data calculated from the ion ratio using eqn (6) based on the assumption of the formation of equal amounts of Ti3+ with total doped elements and analytic content of Ti3+ from XPS, respectively. | |
Table 3 The effective mass m*/m at room temperature, density, ratio of Ti3+/Ti4+ and relative content of TiO2 calculated from the XRD data measured for bulk samples
| Sample |
m*/m0 |
ρ (g cm−3) |
[Ti3+]/[Ti4+] |
TiO2 content |
| La3Nb3 |
4.7258 |
4.85 |
0.067 |
— |
| La5Nb5 |
5.5203 |
5.00 |
0.120 |
— |
| La7Nb7 |
6.2033 |
5.03 |
0.193 |
3.81% |
| La5Nb10 |
6.0434 |
4.78 |
0.179 |
— |
| La10Nb5 |
5.8432 |
5.03 |
0.163 |
— |
| La10Nb10 |
5.3524 |
5.05 |
0.276 |
1.86% |
| La10Nb20 |
5.4982 |
4.50 |
0.351 |
7.76% |
Fig. 3(c) shows the lattice parameters of the La and Nb co-doped SrTiO3 samples derived from the Rietveld refinement (red circle), which increase proportionally with doping concentration (z, z = x + y). This variation tendency is in agreement with the result obtained from the first principles calculation (Table 2). This increase in the lattice parameter can be attributed to the interaction of two primary factors. First, the larger-sized Nb5+ ions (0.64 Å) substitute for the smaller Ti4+ ion (0.605 Å), and the smaller-sized La3+ ions (1.36 Å) substitute for the larger Sr2+ (1.44 Å) ions in the perovskite structure. Second, to compensate the excess electrons introduced by La and Nb co-donor doping, a partial conversion of the smaller Ti4+ ions to larger Ti3+ ions (0.67 Å) occurs.34 The coexistence of a mixed valence state couple of Ti4+/Ti3+ can be confirmed by the Ti 2p XPS spectra in Fig. 4. All the binding energies were corrected using the C 1s peak (binding energy = 284.8 eV) as a reference and a Shirley background was used in the peak fitting. The fitting results show two broad peaks, which can be fitted using the two valence states Ti4+ and Ti3+. Table 3 lists the Ti3+ content calculated from the relative peak area ratio of Ti4+ and Ti3+, which depended on the doping concentration. The Ti3+ content in our samples presents an increasing tendency with the increasing total doping concentration. To validate the correctness of the above conjecture, an empirical equation is used to estimate the lattice parameters of cubic SrTiO3 perovskites as follows:41
| | 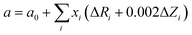 | (5) |
where
a and
a0 are the lattice parameters of the doped and pure SrTiO
3,
xi is the mole fraction of the cation
i substituting for the host cation; Δ
Ri and Δ
Zi are the difference in the ionic radius and in the charge between the substituting cation
i and the host cation, respectively. For our samples, the equation becomes
| | | a = a0 + 0.063xTi3+ − 0.076xLa3+ + 0.037xNb5+ | (6) |
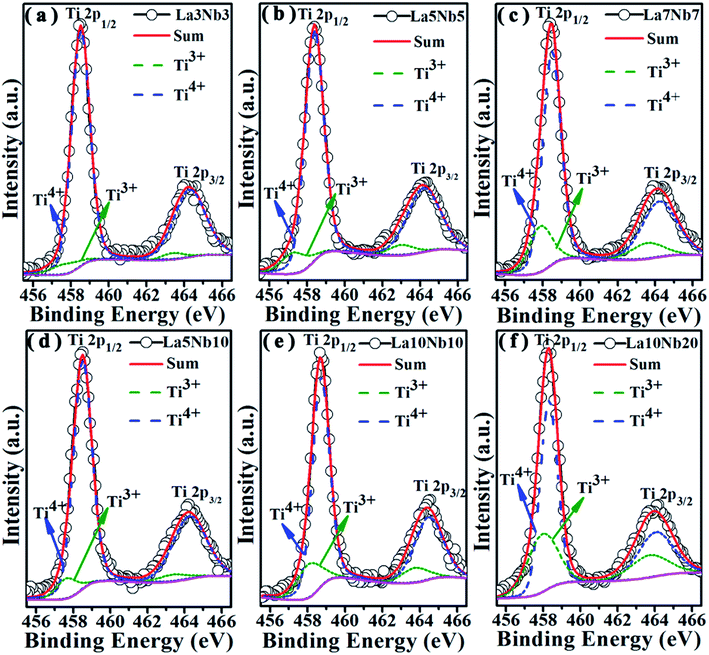 |
| | Fig. 4 The XPS spectra of Ti 2p of samples with varying doping concentration. (a) La3Nb3, (b) La5Nb5, (c) La7Nb7, (d) La5Nb10, (e) La10Nb10 and (f) La10Nb20. | |
The theoretically calculated value (blue triangle in Fig. 3(c)) is based on the assumption of the formation of equal amounts of Ti3+ with total doped elements and ignoring the effect of oxygen vacancies. The analytically calculated value (green square in Fig. 3(c)) based on the analytic content of Ti3+ from XPS is extremely close to the experimental value (red circle), as shown in Fig. 3(c). This suggests that the above conjecture is correct. The calculated value is a little bit larger than the experimental value because a part of Ti3+ coming from TiO2 is not subtracted during the calculation.
Fig. 5(a) shows a low magnification TEM image for the La10Nb20 powder. The individual grains show an irregular laminate shape with a size of 25 nm. The high-resolution TEM lattice fringe image shows the lattice fringes to be 0.27 nm, which corresponds to the typical (110) facets of cubic perovskite SrTiO3 in Fig. 5(b). The inset in Fig. 5(b) shows the fast Fourier transformation (FFT) image of the square region in Fig. 5(b) along the [110] axis. The SEM images of La–Nb co-doped SrTiO3 bulk samples are shown in Fig. 6. After sintering, the SrTiO3 crystals present irregular polyhedral morphologies with an average grain size of 2–10 μm. It is clear that nano-crystallites grow during the sintering process.
 |
| | Fig. 5 TEM images of the La10Nb20 powder sample. (a) Low magnification TEM image and (b) HRTEM image; the inset shows the FFT image of the red square region. | |
 |
| | Fig. 6 SEM images of the La–Nb doped SrTiO3 bulk samples. (a) La3Nb3, (b) La5Nb5, (c) La7Nb7, (d) La5Nb10, (e) La10Nb10 and (f) La10Nb20. | |
The grain size of the bulk sample increases with increasing doping concentration. Fig. 7 shows the TEM-EDS mapping and SAED pattern of the La10Nb20 sample. The precipitated TiO2 is observed clearly from the TEM-EDS mapping image (Fig. 7(a)), which is consistent with the XRD results discussed above. The electron diffraction patterns verify that the grain marked with the red circle is the perovskite SrTiO3 (Fig. 7(b)) and that the grain marked with the black square is rutile TiO2 (Fig. 7(c)). Moreover, a typical structure of small TiO2 grains surrounded by SrTiO3 grains is observed using a combination of TEM-EDS analysis and electron diffraction patterns (Fig. 8). Pores are formed near the interfaces between TiO2 and SrTiO3 grains, indicating that the precipitation of TiO2 promotes the formation of the pores.
 |
| | Fig. 7 Microstructure of the La10Nb20 bulk sample: (a) HAADF-STEM image and elemental mapping for Sr, Ti, O, Nb and La; SAED patterns for the (b) red circle and (c) black square in (a). | |
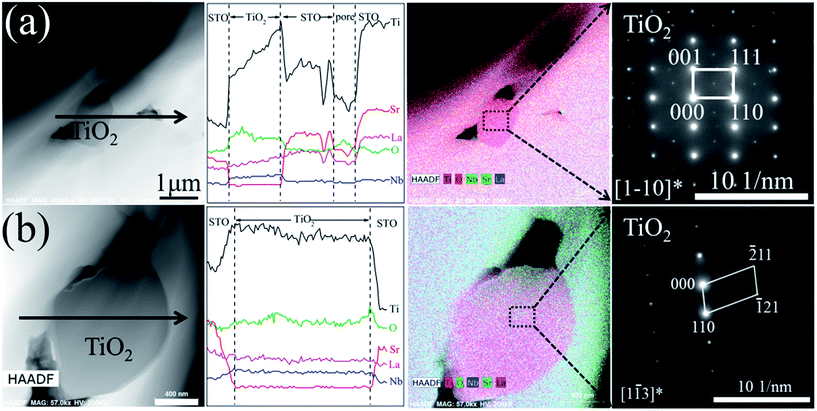 |
| | Fig. 8 TEM image, TEM-EDS line-scan analyses, TEM-EDS mapping and electron diffraction pattern for the (a) La10Nb10 and (b) La10Nb20 bulk samples. | |
3.3 Thermoelectric properties of SrTiO3 bulk samples
As shown in Fig. 9(a), the Seebeck coefficients (S) of all the samples are negative, indicating that electrons are the predominant charge carriers. With increasing temperature, the absolute values of the Seebeck coefficient (|S|) increase monotonously from 300 to 1000 K. Moreover, when the doping concentration ≤ 20 mol%, with increasing doping level, the |S| decreases, which is consistent with the result obtained for the Nb-doped SrTiO3 epitaxial film,25 as shown in Fig. 9(b). This can be attributed to the impurity ionization of donor impurities La3+ and Nb5+, leading to an increment in the electron concentration. However, the La10Nb10 and La10Nb20 samples show similar S, which may be related to the large amount of the second phase in La10Nb20, resulting in a decrease of its carrier concentration. The electron concentration obtained from Hall measurements (Fig. 9(c)) exceeds 1020 cm−3 and does not significantly depend on the temperature in all the samples, showing a typical trait of degenerate semiconductors. On the other hand, the carrier concentration almost tends to increase with increasing doping level of La and Nb. The measured carrier concentrations are smaller than that obtained from the corresponding first-principles calculation, which may be closely related to the presence of second phases and Ti3+ and Nb4+ ions. At such high electron concentrations (≥1020 cm−3), all the samples become an n-type degenerate semiconductor, as discussed in Section 3.1, with a Seebeck coefficient that can be demonstrated by the following equation:3| | 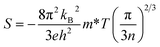 | (7) |
where kB,e, h, m* and n are the Boltzmann constant, electron charge, Planck constant, effective mass, and carrier concentration, respectively. The value of |S| decreases with increasing carrier concentrations. Although |S| in the present study is lower than that reported by Ohta et al.,42 it is larger than that of other oxide thermoelectric materials, such as Na2CoO4,43 due to its relatively large electron effective mass m*/m0 (m0 is the free electron mass).44m*/m0 for all the samples is estimated from the experimental n and S values, as displayed in Table 3. The experimentally estimated m*/m0 also varies with the doping ratio of La and Nb. The effective mass also satisfies the following equation:where e, τ, and μH are the electron charge, relaxation time and Hall mobility, respectively. Thus, the relaxation time is also affected by the dopant ratio of La and Nb.
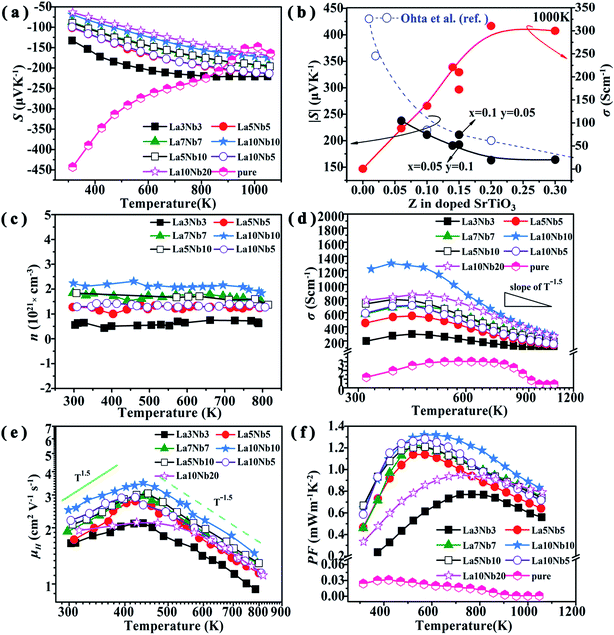 |
| | Fig. 9 (a) Temperature dependence of Seebeck coefficient for double-doped SrTiO3 samples. (b) Seebeck coefficient and electrical conductivity as a function of La and Nb concentrations at a temperature of 1000 K. (c) Temperature dependence of electrical conductivity, (d) carrier concentration, (e) Hall mobility and (f) power factor. | |
Fig. 9(d) reveals that the electrical conductivity (σ) of the samples increases with increasing the temperature up to 450 K, indicating a semiconductor property. At high temperatures above 450 K, the electrical conductivity decreases with increasing temperature and indicates a metallic behavior. As shown in the inset of Fig. 9(d), the electrical conductivity of all the samples decreases with a slope of T−1.5 at a high temperature above 750 K, indicating that phonon scattering is the dominant mechanism. Similar variation trends for the electrical conductivity have also been reported for bulk Nd-doped SrTiO3 and rare earth doped SrTiO3.45,46 To better understand the variation mechanism, we introduce the electrical conductivity formula σ = neμH, where n is the carrier concentration, e is the electron charge and μH is the carrier mobility. As shown in Fig. 9(e), μH gradually increases with increasing temperature at low temperature (T < 450 K) to allow the slope to be close to T1.5, indicating that it is dominated by an impurity scattering mechanism. As the temperature increases above 450 K, μH decreases with a slope of T−1.5, which shows a scattering mechanism dominated by acoustic phonons, e.g., the conduction electrons are scattered by phonons.47 These variation trends are similar to those observed for the electrical conductivities, suggesting that the temperature dependence of the electrical conductivity is dominated by the carrier mobility. The electrical conductivity increases with increasing doping concentration (Fig. 9(b)), expect for the La10Nb20 sample. The electrical conductivity of the La10Nb20 sample is smaller than that of La10Nb10 at low temperature, owing to its high porosity and large amount of second phases, while the electrical conductivity of the La10Nb20 is close to that of La10Nb10 when the temperatures exceed 600 K, which is because the scattering mechanism is dominated by acoustic phonons at high temperature. Consequently, the large electrical conductivity, together with the large Seebeck coefficient, results in a large power factor at high temperature.
Fig. 9(f) shows the power factor PF (=S2σ) of all the samples as a function of temperature. The PFs for all the samples show a similar variation tendency to σ, which shows an initial increase, followed by a gradual decrease with increasing temperature. At temperatures above 600 K, the PF increases with increasing doping concentration before reaching the peak value for La10Nb10 and then starts to fall for the La10Nb20 sample. It is noted that the PF exhibits peak values above 1 mW m−1 K−2 in the temperature range of 450 to 650 K for several samples, with the La10Nb10 sample showing a maximum power factor as high as PF ∼ 1.32 mW m−1 K−2 at 600 K.
The temperature dependence of the thermal diffusivity and total thermal conductivity (κtotal) is shown in Fig. 10(a) and (b). The total thermal conductivity decreases proportionally with T−1 with increasing temperature in the whole measurement temperature range, indicating a dominant phonon scattering due to the Umklapp process.48 According to the theoretical formula for the total thermal conductivity, κtotal is composed of the lattice thermal conductivity (κL) and electric thermal conductivity (κe), κtotal = κL + κe. The value of κe is obtained from the Wiedemann–Franz law as κe = LTσ, where L is the Lorentz factor (L = 2.44 × 10−8 V2 K−2, Fig. 10(c)). Therefore, the lattice thermal conductivity is determined by subtracting the electric thermal conductivity from the total thermal conductivity. As shown in Fig. 10(c), κL is similar to κtotal, indicating that κL plays a major role in the total thermal conductivity. The La10Nb20 sample shows the lowest value of κL ∼ 3.7 W m−1 K−1 at 300 K, which decreases to a minimum value of 2.67 W m−1 K−1 at 1050 K. There is no significant difference among the other samples, indicating that the impurity atoms are not the main reason for the low total thermal conductivity of the La10Nb20 sample. Contributions from the secondary phase TiO2 and high porosity are beneficial to reduce the lattice thermal conductivity. This is because the increased phonon scattering can reduce the phonon mean free path and, thus, lead to a further decrease in the lattice thermal conductivity, as observed in previous studies.15,36,49 Furthermore, plenty of inhomogeneous mesoscale (∼0.1–1.0 μm) pores, due to the lower density (Table 3) of the La10Nb20 sample, 82.8%, compared with the other samples, effectively enhance the scattering of phonons with long mean free paths, resulting in a decrease in the lattice thermal conductivity.50–52
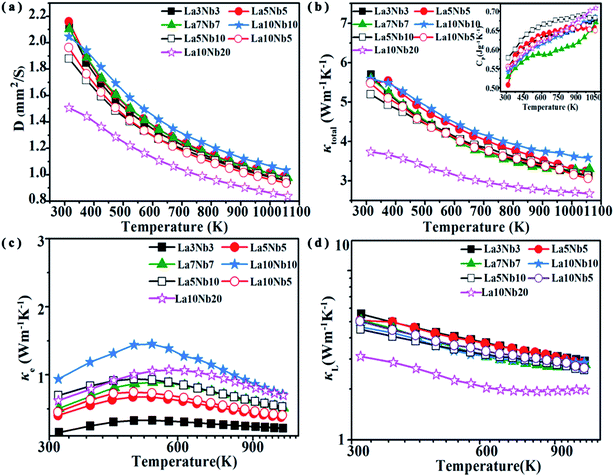 |
| | Fig. 10 Temperature dependence of the (a) thermal diffusivity, (b) total thermal conductivity and heat capacity (inset), (c) electrical thermal conductivity and (d) lattice thermal conductivity for Nb–La doped SrTiO3. | |
Fig. 11 shows the zT value for La–Nb doped SrTiO3 bulk samples with varying doping concentrations. When the doping contents of Nb and La are equal, the zTs for the samples increase with increasing temperature and stabilize above a high temperature of 800 K. If the zT value can be further improved, this excellent high-temperature stability is particularly suitable for the application of thermoelectric devices at high temperature. The zT value of the samples with La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nb ≠1 presents an increasing tendency with increasing temperature, with the La10Nb20 sample showing a maximum zT value of 0.31 at approximately 1050 K due to its lower thermal conductivity together with large PF. The maximum zT obtained is one of the highest values reported for the electron-doped SrTiO3 prepared by hot pressing.
Nb ≠1 presents an increasing tendency with increasing temperature, with the La10Nb20 sample showing a maximum zT value of 0.31 at approximately 1050 K due to its lower thermal conductivity together with large PF. The maximum zT obtained is one of the highest values reported for the electron-doped SrTiO3 prepared by hot pressing.
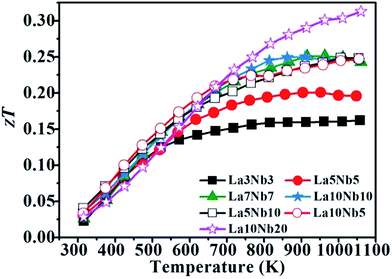 |
| | Fig. 11 Temperature dependence of zT for SrTiO3 samples with different Nb and La doping concentrations. | |
4. Conclusion
In conclusion, first-principles calculations and measurements of the thermoelectric properties of La–Nb co-doped SrTiO3 were carried out in this study, which show that the doping ratio of La to Nb affects the formation energy, effective mass and electron band structure of La–Nb doped SrTiO3, leading to an improvement in the thermoelectric properties. The heavily Nb-doped sample shows a large formation energy; the larger formation energy promotes the precipitation of the second phase and increases the porosities of the samples, which can significantly reduce the thermal conductivity. By controlling the doping ratio, a lower lattice thermal conductivity of 1.97 W m−1 K−1 and a maximum zT value of 0.31 are achieved at 1050 K in La–Nb co-doped SrTiO3 bulk materials. The low thermal conductivity is related to the introduction of La and Nb dopants, a second phase and porosity. The obtained maximum zT is one of the highest values reported for electron-doped SrTiO3 prepared by hot pressing. The SrTiO3 bulk samples doped with La and Nb elements (a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) show a relatively stable zT value in a broad range of high temperatures, which is promising for high-temperature thermoelectric applications.
1) show a relatively stable zT value in a broad range of high temperatures, which is promising for high-temperature thermoelectric applications.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This project was supported by the National Natural Science Foundation of China under the No. 61751404, 51702168, 51774065, 51525401, 51772056, 61366008 and 61664007; the State Key Laboratory of New Ceramic and Fine Processing (Tsinghua University) under the No. KF201608; the Opening Project of State Key Laboratory of High Performance Ceramics and Superfine Microstructure under the NO. SKL201705SIC; the Guangxi Key Laboratory of Information Materials, Guilin University of Electronic Technology, under the No. 151004-K; the Natural Science Foundation of Inner Mongolia under the No. 2016BS0507; the Guangxi Natural Science Foundation of China under Grant No. 2015GXNSFFA139002 and the Science and Technology Major Project of Inner Mongolia Autonomous Region (2018-810). J. W. thanks Yanzhong Pei and Hongxia Liu from Tongji University for valuable discussion and support provided for the Hall effect measurements. J. W. thanks Xue Jiang from Dalian University of Technology for valuable discussion on the calculations of formation energy.
References
- H. Lu, L. Price and Q. Zhang, Appl. Energy, 2016, 161, 497–511 CrossRef.
- M. S. Dresselhaus, G. Chen, M. Y. Tang, R. G. Yang, H. Lee, D. Z. Wang, Z. F. Ren, J. P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043–1053 CrossRef CAS.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105 CrossRef CAS PubMed.
- Y. Pei, L. Zheng, W. Li, S. Lin, Z. Chen, Y. Wang, X. Xu, H. Yu, Y. Chen and B. Ge, Adv. Electron. Mater., 2016, 2, 1600019 CrossRef.
- Z. Chen, Z. Jian, W. Li, Y. Chang, B. Ge, R. Hanus, J. Yang, Y. Chen, M. Huang, G. J. Snyder and Y. Pei, Adv. Mater., 2017, 29, 1606768 CrossRef PubMed.
- K. Zhao, H. Duan, N. Raghavendra, P. Qiu, Y. Zeng, W. Zhang, J. Yang, X. Shi and L. Chen, Adv. Mater., 2017, 29, 1701148 CrossRef PubMed.
- L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144 CrossRef CAS PubMed.
- G. Tan, L. D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- H. Ohta, T. Mizuno, S. Zheng, T. Kato, Y. Ikuhara, K. Abe, H. Kumomi, K. Nomura and H. Hosono, Adv. Mater., 2012, 24, 740–744 CrossRef CAS PubMed.
- B. Poudel, Q. Hao, Y. Ma, Y. C. Lan, A. Minnich, B. Yu, X. A. Yan, D. Z. Wang, A. Muto, D. Vashaee, X. Y. Chen, J. M. Liu, M. S. Dresselhaus, G. Chen and Z. F. Ren, Science, 2008, 320, 634–638 CrossRef CAS PubMed.
- K. Biswas, J. Q. He, I. D. Blum, C. I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- H. Ohta, S. Kim, Y. Mune, T. Mizoguchi, K. Nomura, S. Ohta, T. Nomura, Y. Nakanishi, Y. Ikuhara, M. Hirano, H. Hosono and K. Koumoto, Nat. Mater., 2007, 6, 129–134 CrossRef CAS PubMed.
- S. A. Yamini, D. R. G. Mitchell, Z. M. Gibbs, R. Santos, V. Patterson, S. Li, Y. Z. Pei, S. X. Dou and G. J. Snyder, Adv. Energy Mater., 2015, 5, 1501047 CrossRef.
- H. Zhao, J. Sui, Z. Tang, Y. Lan, Q. Jie, D. Kraemer, K. McEnaney, A. Guloy, G. Chen and Z. Ren, Nano Energy, 2014, 7, 97–103 CrossRef CAS.
- L. D. Zhao, S. H. Lo, J. He, H. Li, K. Biswas, J. Androulakis, C. I. Wu, T. P. Hogan, D. Y. Chung, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2011, 133, 20476–20487 CrossRef CAS PubMed.
- K. Park, J. S. Son, S. I. Woo, K. Shin, M.-W. Oh, S.-D. Park and T. Hyeon, J. Mater. Chem. A, 2014, 2, 4217–4224 RSC.
- A. V. Kovalevsky, M. H. Aguirre, S. Populoh, S. G. Patrício, N. M. Ferreira, S. M. Mikhalev, D. P. Fagg, A. Weidenkaff and J. R. Frade, J. Mater. Chem. A, 2017, 5, 3909–3922 RSC.
- N. Wang, L. Han, H. He, Y. Ba and K. Koumoto, J. Alloys Compd., 2010, 497, 308–311 CrossRef CAS.
- Y. Wang, K. H. Lee, H. Ohta and K. Koumoto, J. Appl. Phys., 2009, 105, 103701 CrossRef.
- H. Takenouchi, T. Imai, H. Mae, M. Fujimoto, T. Kineri, T. Iida, N. Hamada, T. Watanabe and K. Nishio, MRS Proceedings, 2007, 1044, 1044-U06-11 CrossRef.
- M. Ito and T. Matsuda, J. Alloys Compd., 2009, 477, 473–477 CrossRef CAS.
- K. H. Lee, S. W. Kim, H. Ohta and K. Koumoto, J. Appl. Phys., 2007, 101, 083707 CrossRef.
- H. C. Wang, C. L. Wang, W. B. Su, J. Liu, Y. Sun, H. Peng and L. M. Mei, J. Am. Ceram. Soc., 2011, 94, 838–842 CrossRef CAS.
- A. Kikuchi, N. Okinaka and T. Akiyama, Scr. Mater., 2010, 63, 407–410 CrossRef CAS.
- S. Ohta, T. Nomura, H. Ohta, M. Hirano, H. Hosono and K. Koumoto, Appl. Phys. Lett., 2005, 87, 092108 CrossRef.
- Z. Lu, H. Zhang, W. Lei, D. C. Sinclair and I. M. Reaney, Chem. Mater., 2016, 28, 925–935 CrossRef CAS.
- Q. Hou, J. Li, C. W. Zhao, C. Ying and Y. Zhang, Phys. B Condens. Matter, 2011, 406, 1956–1960 CrossRef CAS.
- M. D. Segall, J. D. L. Philip, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717 CrossRef CAS.
- J. Clark Stewart, D. Segall Matthew, J. Pickard Chris, J. Hasnip Phil, I. J. Probert Matt, K. Refson and C. Payne Mike, Z. Kristallogr. - Cryst. Mater., 2005, 567 Search PubMed.
- H. Shiiba, N. Zettsu, M. Nakayama, S. Oishi and K. Teshima, J. Phys. Chem. C, 2015, 119, 9117–9124 CrossRef CAS.
- H. Y. Xiao and W. J. Weber, J. Phys. Chem. B, 2011, 115, 6524–6533 CrossRef CAS PubMed.
-
A. C. Larson and R. B. v. Dreele, National Laboratory Report, LAUR 86-748, 2004 Search PubMed.
- T. Tomio, H. Miki, H. Tabata, T. Kawai and S. Kawai, J. Appl. Phys., 1994, 76, 5886–5890 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- S. Ohta, T. Nomura, H. Ohta, M. Hirano, H. Hosono and K. Koumoto, Appl. Phys. Lett., 2005, 87, 092108 CrossRef.
- N. Wang, H. Chen, H. He, W. Norimatsu, M. Kusunoki and K. Koumoto, Sci. Rep., 2013, 3, 3449 CrossRef PubMed.
- P. P. Edwards and M. J. Sienko, Phys. Rev. B: Solid State, 1978, 17, 2575–2581 CrossRef CAS.
- I. Vurgaftman, J. R. Meyer and L. R. Ram-Mohan, J. Appl. Phys., 2001, 89, 5815–5875 CrossRef CAS.
- T. Okuda, K. Nakanishi, S. Miyasaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 113104 CrossRef.
- F. H. Chung, J. Appl. Crystallogr., 1974, 7, 519–525 CrossRef.
- D. Neagu and J. T. S. Irvine, Chem. Mater., 2010, 22, 5042–5053 CrossRef CAS.
- S. Ohta, H. Ohta and K. Koumoto, J. Ceram. Soc. Jpn., 2006, 114, 102–105 CrossRef CAS.
- K. Fujita, T. Mochida and K. Nakamura, Jpn. J. Appl. Phys., 2001, 40, 4644 CrossRef CAS.
- S. Ohta, T. Nomura, H. Ohta and K. Koumoto, J. Appl. Phys., 2005, 97, 034106 CrossRef.
- J. Liu, C. L. Wang, W. B. Su, H. C. Wang, J. C. Li, J. L. Zhang and L. M. Mei, J. Alloys Compd., 2010, 492, L54–L56 CrossRef CAS.
- H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2003, 350, 292–295 CrossRef CAS.
- J. Shen, X. Zhang, S. Lin, J. Li, Z. Chen, W. Li and Y. Pei, J. Mater. Chem. A, 2016, 4, 15464–15470 RSC.
- W. Li, S. Lin, X. Zhang, Z. Chen, X. Xu and Y. Pei, Chem. Mater., 2016, 28, 6227–6232 CrossRef CAS.
- Y.-L. Pei, J. He, J.-F. Li, F. Li, Q. Liu, W. Pan, C. Barreteau, D. Berardan, N. Dragoe and L.-D. Zhao, NPG Asia Mater., 2013, 5, e47 CrossRef CAS.
- R. H. Tarkhanyan and D. G. Niarchos, Int. J. Therm. Sci., 2013, 67, 107–112 CrossRef.
- D. Mei, Y. Li, Z. Yao, H. Wang, T. Zhu and S. Chen, J. Alloys Compd., 2014, 609, 201–205 CrossRef CAS.
- R. H. Tarkhanyan and D. G. Niarchos, J. Electron. Mater., 2014, 43, 3808–3811 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Xiao-Huan
Wang
ae,
Hui-Jun
Kang
*c,
Xinba
Yaer
ae,
Jian-Bo
Li
a,
Tong-Min
Wang
*a,
Xiao-Huan
Wang
ae,
Hui-Jun
Kang
*c,
Xinba
Yaer
ae,
Jian-Bo
Li
a,
Tong-Min
Wang
 c,
Lei
Miao
c,
Lei
Miao
 d and
Jun
Wang
d and
Jun
Wang
 *ae
*ae
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The ground state atomic and electronic structures of La and Nb co-doped SrTiO3 were calculated by first-principles density functional theory using CASTEP.28 These calculations are based on density functional theory (DFT) with the generalized-gradient approximation (GGA) and the plane-wave pseudo potentials as implemented in CASTEP.29 The exchange–correlation energy can be described by the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function. The valence atomic configurations are 4s24p65s2 for Sr, 2s22p4 for O, 3s23p63d24s2 for Ti, 4s24p64d45s1 for Nb, and 5s25p65d16s2 for La, respectively. The plane-wave cutoff energy is 340 eV, and the Monkhorst–Pack k-mesh is 3 × 3 × 3. The calculation precision was converged to be 1.0 × 10−5 eV per atom. All atoms are allowed to relax until the force on each atom is below 0.3 eV nm−1, the internal stress is below 0.05 GPa, and the displacement of each atom is below 0.0001 nm simultaneously.
m. The ground state atomic and electronic structures of La and Nb co-doped SrTiO3 were calculated by first-principles density functional theory using CASTEP.28 These calculations are based on density functional theory (DFT) with the generalized-gradient approximation (GGA) and the plane-wave pseudo potentials as implemented in CASTEP.29 The exchange–correlation energy can be described by the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function. The valence atomic configurations are 4s24p65s2 for Sr, 2s22p4 for O, 3s23p63d24s2 for Ti, 4s24p64d45s1 for Nb, and 5s25p65d16s2 for La, respectively. The plane-wave cutoff energy is 340 eV, and the Monkhorst–Pack k-mesh is 3 × 3 × 3. The calculation precision was converged to be 1.0 × 10−5 eV per atom. All atoms are allowed to relax until the force on each atom is below 0.3 eV nm−1, the internal stress is below 0.05 GPa, and the displacement of each atom is below 0.0001 nm simultaneously.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as a reference for the structural model. The microstructures in the SrTiO3 bulk were characterized by field-emission scanning electron microscopy (SEM, JSM7000F, JEOL), with the SrTiO3 powders being characterized by transmission electron microscopy (TEM, JEM2010, JEOL Ltd.). The chemical composition of the bulk samples was acquired using an energy dispersive spectrometer (EDS). X-ray photoelectron spectroscopy (XPS, ESCALAB 250Xi, Thermo Fisher Scientific) was used to analyze the surface elemental compositions and valence states of the elements. The thermal diffusivity coefficient (D) was determined using a laser flash apparatus (LFA 427, Netzsch, Germany). The specific heat capacity (Cp) was measured using a differential scanning calorimeter (DSC 200 F3, Netzsch, Germany) under a flow of argon. The thermal conductivity was calculated by using the equation κ = DρCp. The Seebeck coefficient and electrical conductivity were measured simultaneously using a Seebeck coefficient and electric resistance measuring system (LRS-3, Linseis, Germany). The test temperature range was between 300 and 1050 K, and the sealed sample chamber was filled with helium gas. The carrier concentration (n) and Hall mobility (μH) were measured using a Hall measurement system from 300 to 800 K. As for the La10Nb20 sample, the extremely high carrier concentrations lead to a Hall voltage too small to be measured accurately, so we do not show values of n and μH in this paper.
m) as a reference for the structural model. The microstructures in the SrTiO3 bulk were characterized by field-emission scanning electron microscopy (SEM, JSM7000F, JEOL), with the SrTiO3 powders being characterized by transmission electron microscopy (TEM, JEM2010, JEOL Ltd.). The chemical composition of the bulk samples was acquired using an energy dispersive spectrometer (EDS). X-ray photoelectron spectroscopy (XPS, ESCALAB 250Xi, Thermo Fisher Scientific) was used to analyze the surface elemental compositions and valence states of the elements. The thermal diffusivity coefficient (D) was determined using a laser flash apparatus (LFA 427, Netzsch, Germany). The specific heat capacity (Cp) was measured using a differential scanning calorimeter (DSC 200 F3, Netzsch, Germany) under a flow of argon. The thermal conductivity was calculated by using the equation κ = DρCp. The Seebeck coefficient and electrical conductivity were measured simultaneously using a Seebeck coefficient and electric resistance measuring system (LRS-3, Linseis, Germany). The test temperature range was between 300 and 1050 K, and the sealed sample chamber was filled with helium gas. The carrier concentration (n) and Hall mobility (μH) were measured using a Hall measurement system from 300 to 800 K. As for the La10Nb20 sample, the extremely high carrier concentrations lead to a Hall voltage too small to be measured accurately, so we do not show values of n and μH in this paper.

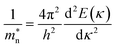

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and no impurity phase was observed within the detection limit of XRD. However, after hot pressing, a TiO2 impurity phase appears for all doped SrTiO3 bulks, as shown in Fig. 3(b). A shift to lower angles is also observed for all the SrTiO3 and TiO2 peaks. The relative amount of TiO2 can be estimated using the following equation:40
m and no impurity phase was observed within the detection limit of XRD. However, after hot pressing, a TiO2 impurity phase appears for all doped SrTiO3 bulks, as shown in Fig. 3(b). A shift to lower angles is also observed for all the SrTiO3 and TiO2 peaks. The relative amount of TiO2 can be estimated using the following equation:40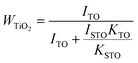

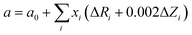





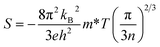
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nb ≠1 presents an increasing tendency with increasing temperature, with the La10Nb20 sample showing a maximum zT value of 0.31 at approximately 1050 K due to its lower thermal conductivity together with large PF. The maximum zT obtained is one of the highest values reported for the electron-doped SrTiO3 prepared by hot pressing.
Nb ≠1 presents an increasing tendency with increasing temperature, with the La10Nb20 sample showing a maximum zT value of 0.31 at approximately 1050 K due to its lower thermal conductivity together with large PF. The maximum zT obtained is one of the highest values reported for the electron-doped SrTiO3 prepared by hot pressing.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) show a relatively stable zT value in a broad range of high temperatures, which is promising for high-temperature thermoelectric applications.
1) show a relatively stable zT value in a broad range of high temperatures, which is promising for high-temperature thermoelectric applications.


