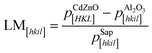Induced crystallographic changes in Cd1−xZnxO films grown on r-sapphire by AP-MOCVD: the effects of the Zn content when x ≤ 0.5
Maria del Carmen
Martínez-Tomás
 *,
Adelaida
Huerta-Barberà
*,
Adelaida
Huerta-Barberà
 ,
Saïd
Agouram
,
Saïd
Agouram
 and
Vicente
Muñoz-Sanjosé
and
Vicente
Muñoz-Sanjosé

Departament de Física Aplicada i Electromagnetisme, Universitat de València, C/Dr. Moliner 50, 46100 Burjassot, Spain. E-mail: Carmen.Martinez-tomas@uv.es
First published on 12th November 2019
Abstract
High-resolution X-ray diffraction, scanning electron microscopy and transmission electron microscopy techniques were used to investigate, as a function of the nominal Zn content in the range of 0–50%, the out-of-plane and in-plane crystallographic characteristics of Cd1−xZnxO films grown on r-plane sapphire substrates via atmospheric pressure metal–organic chemical vapor deposition. The study is conducted to search for knowledge relating to the structural details during the transition process from a rock-salt to a wurtzite structure as the Zn content increases in this CdO–ZnO system. It has been found that it is possible to obtain films exhibiting a single (001) cubic orientation with good crystalline quality up to a Zn content of about 10%. For zinc content values higher than 15%, the films become polycrystalline, with two main domains inclined with respect to the plane perpendicular to the surface that contains the c-axis of sapphire. The domains have a tilt that tends asymptotically to ±15° with the Zn content, and the cubic cell presents strong orthorhombic distortion. These two crystallographic domains (orientations) cannot be observed via conventional XRD measurements and are supposed to form part of an intermediate orthorhombic phase in the transition from a rock-salt structure towards a wurtzite structure, which finally appears at higher Zn content values.
1. Introduction
The development of ZnO-based devices can be advanced through achieving ZnO-based alloy semiconductors with different bandgaps.1,2 The bandgap of ZnO can be modulated to a lower level via alloying it with CdO. This band-gap modulation should lead to ZnO-based optoelectronic materials utilizing the whole visible-ultraviolet emission region, from 1.8 to 3.3 eV.3The growth of CdO–ZnO ternary oxides highlights the difficulty of combining materials with different crystalline structures, that is, hexagonal ZnO and cubic CdO. Thus, the achievement of good quality ternary alloys represents a challenge for crystal growers, since the coexistence of different structures is expected to occur at some transition composition, related to the solubility of the atoms that act as the solute in the solvent binary matrix.
With respect to the parent binary compounds, oxidized Cd adopts octahedral coordination in a cubic rock-salt structure, while ZnO favours tetrahedral coordination in a hexagonal wurtzite structure. When a ternary compound is pursued, the amount of solute in the solvent can be different depending on the chosen experimental conditions, which can favour one or the other binary compound becoming the host crystallographic structure. Most solubility studies deal with wurtzite Zn1−xCdxO ternary alloys. However, a few studies have been made on cubic structures of this alloy. For the wurtzite Zn1−xCdxO alloy, Fan et al.4 carried out a first principles analysis of the phase stabilities, chemical bonds and band gaps. These authors concluded that the transition region towards a cubic structure was located at 0.75 < x < 0.875, in accordance with experimental work conducted by Ishihara et al.5 on sapphire substrates. Likewise, A. Fouzri et al.6 studied the growth of Zn1−xCdxO alloys, also on sapphire substrates, and they determined that the maximum cadmium incorporation into the ZnO lattice was 11.2%. Venkatachalapathy et al.7 also investigated phase separation in wurtzite Zn1−xCdxO films, studying a wide Cd content range from 0–60%. In their first approach, a wurtzite matrix at low Cd content (<17%) was found, but more detailed analysis of the X-ray diffraction measurements revealed that the wurtzite single-phase stability range was as narrow as 0–2% Cd, while samples containing 7–17% Cd exhibited a mixture of wurtzite and zinc-blende phases. High Cd content (32–60%) in Zn1−xCdxO samples resulted in a mixture of wurtzite, zinc-blende and rock-salt phases. These results highlight the significance of accurate structural characterization to really assess the complex crystalline structures that can arise in ternary compounds that present different crystallographic structures in binary hosted compounds.
Among the few studies on the rock-salt Cd1−xZnxO alloy, Yu et al.8 grew layers via a radio-frequency magnetron co-sputtering system. They observed, through using X-ray conventional diffraction measurements, that polycrystalline films have a single-phase cubic structure at x ≤ 0.21 and mixed phases at x = 0.29. On the other hand, Han et al.9 obtained Cd1−xZnxO thin films with a rock-salt structure through the thermal decomposition of Cd1−xZnxO2 at room temperature; these films were polycrystalline with nanoparticles in the range of 11–15 nm. Likewise, Zhang et al.10 synthesized single-phase rock-salt Cd1−xZnxO films on r-plane sapphire substrates via MOCVD in the Zn content range of 0 < x < 59%. They found that the film growth orientation depended on the Zn/Cd stoichiometric ratio, as well as on the film thickness. Specifically, they determined that the (100)-orientation dominated below a critical Zn content, estimated as 7%; otherwise, the development of (111)-oriented grains took place on top of the (100) planes.
As can be concluded from the literature, the incorporation of Cd or Zn into the parent binary compound affects the structure of the solvent compound differently (hexagonal ZnO or cubic CdO, respectively) depending on the growth conditions. The coexistence of several phases and the spontaneous misorientation of films cannot be well determined via conventional XRD, and some misleading conclusions could be introduced in the analysis of results. Thus, changes and evolution of the crystallographic structure as a consequence of the solute content are open subjects that need accurate structural studies in order to clarify what happens over the solute content interval in which the transition from a cubic rock-salt structure to a wurtzite structure takes place. As said before, conventional XRD characterization provides limited structural information; thus, the only way to completely assess the crystalline structure of a film is analysis not only in the out-of-plane direction, but also in other directions. High resolution X-ray diffraction (HRXRD) can be a way to achieve this information.
In this paper, we analyze the structural and morphological properties of Cd1−xZnxO alloys grown via atmospheric pressure metal organic chemical vapour deposition (AP-MOCVD) on r-plane sapphire substrates as a function of the nominal Zn content in the range of 0–50%. The main experimental technique used to determine the unit cell structures of films is high-resolution X-ray diffraction (HRXRD), although other methods as scanning electron microscopy (SEM) and transmission electron microscopy (TEM) have also been used in order to assess the observed structures. Results obtained from this study reveal that outstanding features arise as the Zn content increases.
2. Experimental
Cd1−xZnxO films were grown via AP-MOCVD on r-sapphire substrates using tertiary butanol (TBA), dimethylcadmium (DMCd), and diethylzinc (DEZn) as oxygen, cadmium and zinc sources, respectively, in a horizontal vent-run type reactor. The growth temperature of the films was fixed at 330 °C. The DEZn/(DEZn + DMCd) nominal content was adjusted from x = 0 (pure CdO) to 0.5 with TBA flux values in the range of 282–46 μmol min−1, maintaining the VI/II precursor ratio near to 5 in all experiments. Cd1−xZnxO films ca. 200 nm thick were obtained over the entire studied composition range. The atomic Zn content values of the films were determined via EDX using an acceleration voltage of 10 kV. The nominal content values were found to be nearly the same as the molar ratios (as shown in the tables below). Hereafter, we will refer to the different samples using the nominal Zn content. More details can be found elsewhere.11 Al2O3 with r-plane orientation was chosen as the substrate due to the fact that high quality CdO films can be obtained on r-plane substrates,12 suggesting that the growth of cubic CdZnO at low Zn content values would be favoured.HRXRD measurements were performed using a Philips X'Pert MRD X-ray diffractometer with monochromatic Cu Kα1 radiation (λ = 1.54056 Å), which impinged on the sample after having traversed a parabolic graded multilayer mirror and a 4-bounce Ge (220) monochromator. For structural characterization of the samples, 2θ–ω scan, rocking curve and pole figure analyses were carried out.
The morphologies of the samples were studied using a Hitachi S-4800 field emission electron microscope with an acceleration voltage of 20 kV. Gold–palladium thin conductive film (≈2 nm) was deposited over the Cd1−xZnxO films using DC sputtering prior to scanning electron microscopy (SEM) analysis. Energy dispersive X-ray spectroscopy (EDX) measurements were carried out in order to estimate the different element content values in the films using an acceleration voltage of 10 kV. HRTEM micrographs and selected area electron diffraction (SAED) data were recorded using a Tecnai G2F20 field emission gun transmission electron microscope under an acceleration voltage of 200 kV.
3. Crystalline orientations and phases
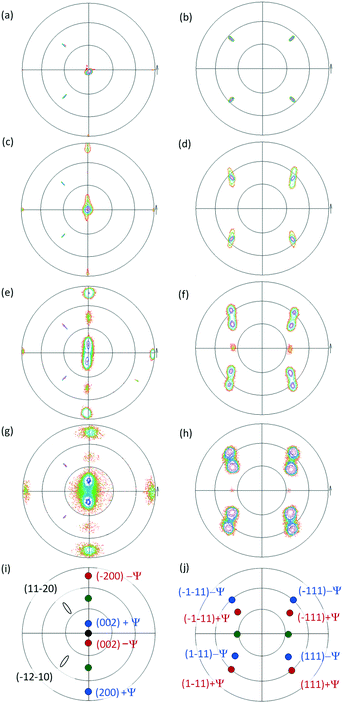
The out-of-plane orientations of Cd1−xZnxO films grown on r-sapphire have already been determined by means of 2θ–ω measurements, as can be seen in ref. 11, corresponding to samples with different Zn content values. In these XRD measurements, two main diffraction peaks can be seen, which are near the positions of cubic CdO(002) and CdO(004) reflections.13 A shift, in the sense of larger 2θ values, happens as the Zn content increases; this is a consequence of a decrease in the CdO lattice parameter, which is coherent with the replacement of Cd atoms by Zn atoms with a smaller atomic radius (0.97 Å and 0.74 Å, respectively).14 That is, all the films present a preferred orientation that corresponds to a cubic Cd1−xZnxO(001) crystal. Films with a Zn content equal to or higher than 15% are polycrystalline, since additional cubic CdO(022) and CdO(111) peaks appear. Additionally, the 50% sample exhibits a shifted wurtzite ZnO(0002) peak,15 showing that a coexistence of phases is present. In this case, the shift is in the sense of smaller 2θ values, which can be understood as resulting from an increase in the wurtzite ZnO cell volume as a consequence of the replacement of Zn atoms with Cd atoms.With the aim of determining the existence of possible in-plane film orientations and their evolution with Zn content, pole figure measurements were made. Pole figures were obtained by fixing the 2θ angle for the observation of CdO(002) reflections (2θ = 38.286°).13 An open detector was used for observing the expected shifts of the CdO peaks. In addition, Al2O3(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) peaks (2θ = 37.785°)16 could be observed, allowing for the determination of the epitaxial relationships between the crystalline films and the substrate. We describe first the findings from films with low Zn content values (≤10%) with well-defined Cd1−xZnxO(001) out-of-plane orientations, and then films with high Zn content values (15% ≤ x ≤ 50%).
0) peaks (2θ = 37.785°)16 could be observed, allowing for the determination of the epitaxial relationships between the crystalline films and the substrate. We describe first the findings from films with low Zn content values (≤10%) with well-defined Cd1−xZnxO(001) out-of-plane orientations, and then films with high Zn content values (15% ≤ x ≤ 50%).
4. CdZnO films with low Zn content values
4.1. Epitaxial relationships
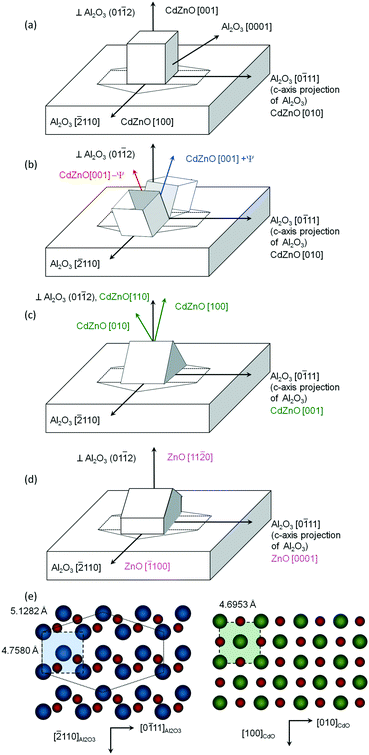
Fig. 1(a) and (b) show measured pole figures based on the Cd1−xZnxO(002) and Cd1−xZnxO(111) reflections for the film with 5% Zn content.The presence in Fig. 1(a) of a single CdO(002) pole confirms the preferred cubic orientation Cd1−xZnxO(001). From the relative positions in the pole figures of the substrate and film peaks, we determine that a lateral face of the cubic unit cell is parallel to the in-plane projection of the c-axis of sapphire (the Al2O3[0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11] direction). Using the axis definition given in Fig. 2(a), we give the following epitaxial relationships for the out-of-plane Cd1−xZnxO(001) oriented films
11] direction). Using the axis definition given in Fig. 2(a), we give the following epitaxial relationships for the out-of-plane Cd1−xZnxO(001) oriented films
Cd1−xZnxO(001)∥Al2O3(01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2) 2) |
Cd1−xZnxO[100]∥Al2O3[![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 110] 110] |
Cd1−xZnxO[010]∥Al2O3[0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11] 11] |
These epitaxial relationships are coherent with those previously obtained for CdO films grown on r-sapphire substrates,12,17 as evidence that the epitaxial coupling with the substrate is not altered as a result of zinc incorporation at this stage. Fig. 1(c) and (d) show pole figures obtained from films with a Zn content of 10%.
The pole of the CdO(002) reflection is observed to widen in a direction perpendicular to the projection of the c-axis of sapphire. This indicates a dispersion in the out-of-plane orientation of the Cd1−xZnxO(001) crystallites along this direction. That is, the film is monocrystalline, but with a small number of crystallites tilted with respect to the perpendicular to the surface, having as a rotation axis the sapphire c-axis projection. The same behaviour is observed in the CdO(111) pole figures.
In order to assess this behaviour in a more accurate manner, rocking curves of the Cd1−xZnxO(002) reflection were obtained in both in-plane directions. It can be seen in Fig. 3(a) and (b) that the rocking curves show different trends depending on the direction: parallel or perpendicular to the c-axis projection of sapphire. In the sample with 5% Zn content, the FWHM has a similar value in both directions; while in the sample with 10% Zn content, the curve exhibits a larger FWHM in the direction perpendicular to the c-axis projection of sapphire compared to the parallel direction, revealing marked anisotropy.
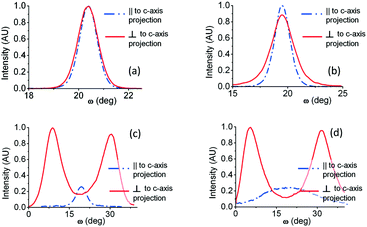 | ||
| Fig. 3 Rocking curves of the Cd1−xZnxO(002) reflection at different azimuth angles for different Zn nominal content values: (a) 5%, (b) 10%, (c) 20%, and (d) 50%. | ||
4.2. Lattice parameters
In ternary alloys, a way to estimate the x content is through using Vegard's law.18 This law is an approximate empirical rule stating that, at constant temperature, an alloy cell is isotropically shortened/enlarged, with the lattice constants obtainable using a linear function from the lattice constants of the constituents.In Cd1−xZnxO films a drawback appears as a consequence of the different crystal structures of the constituents: ZnO (wurtzite) and CdO (cubic), in its more stable configuration. Fan et al.,4 within a study of the phase stabilities and structural and electronic properties of three zinc-based oxide alloy systems (CaZnO, CdZnO and MgZnO), used the lattice parameters of the dominant structure, obtaining agreement of 2% between the calculated and experimental values for the rock-salt structures. As we are working with Cd-rich alloys, we will use the rock-salt lattice constants of the constituents. For CdO, we will use the value given by the crystallographic card (a(CdO)rock-salt = 4.6953 Å,13) and for ZnO, we use the value proposed in Fan's study (a(ZnO)rock-salt = 4.211 Å).
In addition, we need to consider another obstacle that arises when the unit cell is distorted, blurring the effects of foreign atoms in the host lattice. As a consequence of anisotropy in the lattice and thermal mismatch between the CdZnO alloy and the substrate, anisotropic strain is found in both the out-of-plane and in-plane directions. Such anisotropic strain results in the distortion of the unit cell and modifies the lattice parameters with respect to the relaxed values. To overcome this obstacle, we have assumed that the distorted cubic cell keeps the same volume as the undistorted one.
Then, we have taken the mean of the experimentally determined distorted parameters along the three axes of the lattice cell and used this as the undistorted lattice parameter of the cubic ternary cell a(x). Thus, an estimation of the Zn content (x) in Cd1−xZnxO films has been made through Vegard's law:
| a(x) = (1−x)a(CdO) + xa(ZnO) |
To obtain the lattice parameters along the three axes of the cubic cell, 2θ–ω scans were made in symmetric and skew-symmetric configurations. For in-plane measurements, the projection of the c-axis of sapphire was taken as a reference, measuring the lattice constants in both perpendicular and parallel directions (denominated as a⊥ and a‖, respectively). The out-of-plane lattice constant is named a0.
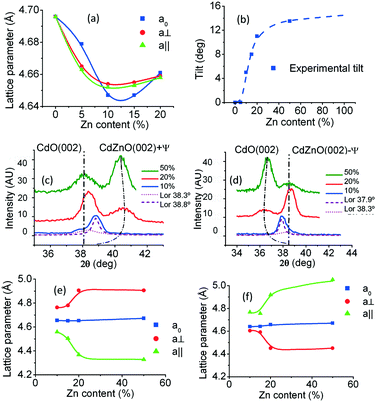
The calculated values of the lattice constants are reflected in Table 1. Fig. 4(a) exhibits their behaviour as the Zn content increases. It can be seen that these parameters first decrease as the Zn content increases, as is expected in accordance with the ionic radii, with the out-of-plane parameter larger than the in-plane parameters. That is, the unit cell exhibits slight orthorhombic distortion. Then, at a content of about 10%, there is a crossing of the curves, with the in-plane lattice constants becoming larger than the out-of-plane one. It can be seen in Table 1 that the calculated values of the Zn content using Vegard's law match quite well with the nominal content values and those measured via EDX.
| % Zn nominal | Crystalline domains with CdZnO(001) orientation | |||||||
|---|---|---|---|---|---|---|---|---|
| % Zn EDX (±0.2) | a 0 (±0.003 Å) | a⊥ (±0.003 Å) | a‖ (±0.003 Å) | Mean (±0.003 Å) | % Zn Vegard's (±0.2) | % mismatch ⊥ (±0.1) | % mismatch || (±0.1) | |
| 0 | 0 | 4.696 | 4.696 | 4.696 | 4.696 | 0 | −1.3 | −8.4 |
| 5 | 5.3 | 4.679 | 4.665 | 4.663 | 4.669 | 5.6 | −2.0 | −9.1 |
| 10 | 10.4 | 4.647 | 4.654 | 4.652 | 4.651 | 9.3 | −2.2 | −9.3 |
| 15 | 15.0 | 4.647 | 4.655 | 4.653 | 4.652 | 9.1 | −2.2 | −9.3 |
4.3. Mismatch
In epitaxial films, the atomic arrangement at the interface is intrinsically responsible for the orientation relationship between a film and its substrate. It is also the origin of the epitaxial mismatch and strain state of the film.
Fig. 2(e) shows a schematic diagram of the atomic arrangement of the (01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2) sapphire plane and (001) Cd1−xZnxO plane at the interface, deduced from the observed epitaxial relationships. The squares represent the coincident lattice points. The indicated distances correspond to the case of x = 0 (pure CdO). From these coincident lattice points, the lattice mismatch (LM) of the film along the [hkil] direction of sapphire can be defined as
2) sapphire plane and (001) Cd1−xZnxO plane at the interface, deduced from the observed epitaxial relationships. The squares represent the coincident lattice points. The indicated distances correspond to the case of x = 0 (pure CdO). From these coincident lattice points, the lattice mismatch (LM) of the film along the [hkil] direction of sapphire can be defined as
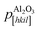 are the periodicities of the Cd1−xZnxO film and sapphire substrate along the Cd1−xZnxO[HKL] and Al2O3[hkil] directions, respectively.6,17 With this definition, the lattice mismatches along both in-plane directions have been calculated and are shown in Table 1, assuming the formation of a coincidence lattice with two pCdZnO[100] per
are the periodicities of the Cd1−xZnxO film and sapphire substrate along the Cd1−xZnxO[HKL] and Al2O3[hkil] directions, respectively.6,17 With this definition, the lattice mismatches along both in-plane directions have been calculated and are shown in Table 1, assuming the formation of a coincidence lattice with two pCdZnO[100] per 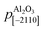 , and three pCdZnO[010] per
, and three pCdZnO[010] per 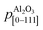 . According to the values shown in Table 1, both Cd1−xZnxO in-plane directions suffer from tensile stress, with the absolute value of lattice mismatch along the direction perpendicular to the c-axis projection of sapphire being lower than in the other in-plane direction.
. According to the values shown in Table 1, both Cd1−xZnxO in-plane directions suffer from tensile stress, with the absolute value of lattice mismatch along the direction perpendicular to the c-axis projection of sapphire being lower than in the other in-plane direction.
5. CdZnO films with high Zn content
5.1. Epitaxial relationships
Pole figures of samples with higher Zn content values (20%: Fig. 1(e) and (f); 50%: Fig. 1(g) and (h)) reveal additional poles with respect to the ones seen for Cd1−xZnxO films with low Zn content values, confirming the polycrystalline character of the films. Pole figures for samples with 15% Zn were similar to those at 20% and are not shown.The most outstanding feature is the presence of two symmetrically tilted Cd1−xZnxO(001) orientations. Fig. 2(b) shows the proposed relative orientation of the unit cells of these two crystalline orientations suggested by the pole figures. Fig. 1(i) and (j) show the index ascriptions of the poles. These two symmetrically tilted domains cannot be observed in 2θ–ω measurements because they don't have a low index plane parallel to the surface of the sample. This is one of the reasons for the suitability of using HRXRD in addition to conventional XRD measurements.
For each Zn content value, the two symmetrically tilted Cd1−xZnxO(001) orientations have an inclination angle, ±ψ, with respect to the surface normal, having as a rotation axis the edge of the cubic cell that is parallel to the sapphire c-axis projection. The dependence on the Zn content of this angle is shown in Fig. 4(b). It can be seen that the absolute value of tilt increases with the Zn content, reaching an angle ψ = ±13.0° in samples with 50% nominal Zn content. An asymptotic value of 15° can also be deduced (see Fig. 4(b)).
Rocking curves obtained from high Zn content samples are shown in Fig. 3(c) and (d). Due to the presence of the two tilted orientations, rocking curves obtained with the diffraction plane perpendicular to the c-axis projection of sapphire exhibit two peaks, each of them related to the two symmetrically tilted Cd1−xZnxO(001) orientations. On the contrary, rocking curves obtained with the diffraction plane parallel to the c-axis projection of sapphire exhibit one peak, in this case related to the remaining out-of-plane Cd1−xZnxO(001) orientation previously described.
The derived epitaxial relationships for the two Cd1−xZnxO(001) orientations symmetrically tilted at an angle ±ψ are
Cd1−xZnxO(001) ± ψ apart from Al2O3(01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2) 2) |
Cd1−xZnxO[010]∥Al2O3[0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11] 11] |
As discussed before, an additional cubic orientation, Cd1−xZnxO(110), is also observed in samples with 20% and 50% Zn. The presence of this orientation is confirmed from low intensity (111) poles, as can be seen in Fig. 1(f) and (h). From these figures, we can give the following relationships for the Cd1−xZnxO(110) orientation:
Cd1−xZnxO(110)∥Al2O3(01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2) 2) |
Cd1−xZnxO[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10]∥Al2O3[ 10]∥Al2O3[![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 110] 110] |
Cd1−xZnxO[001]∥Al2O3[0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11] 11] |
That is, crystals with Cd1−xZnxO(110) orientation also have an edge of the cubic cell parallel to the sapphire c-axis projection, as shown in Fig. 2(c). Poles from these samples have very low intensity; below, we will focus only on crystals with the lattice cells described in Fig. 2(a) and (b).
In regard to the c-oriented zinc oxide phase, no pole figures related to this phase have been found, pointing to a low amount of this crystalline phase. We will look later into the existence of a zinc oxide phase that could explain where the Zn atoms have gone.
5.2. Lattice parameters
Out-of-plane parameters of symmetrically tilted Cd1−xZnxO(001) crystals were obtained from 2θ–ω scans as described in previous sections, but bearing in mind that each cubic cell is tilted with respect to the plane that contains the surface normal and the c-axis of sapphire. For these crystals, the lattice constant named a0 will be the one in the nearly out-of-plane direction, that is, inclined at an angle ±ψ with respect to this direction. Similarly, the lattice constant named a⊥ will be the one in a direction perpendicular to the same axis, but inclined with respect to the surface by an angle ψ; a‖ will be the lattice constant parallel to the projection of the c-axis (see Fig. 2(b)).Interestingly, 2θ–ω scans for determining a0 present a single peak, while those for obtaining a⊥ exhibit two peaks, one near the position of the CdO(002) peak and the other clearly shifted; this is an indication of the shift being of different sign for each tilted domain. Fig. 4(c) and (d) show this behaviour. It can be seen that the shifts of the peaks increase with Zn content and that the direction depends on the sign of the ψ tilting angle. For a negative tilt, the shift is towards lower angles, reaching a value as low as 2θ = 35.5° for 50% Zn content. For a positive tilt, the shift is towards higher angles, reaching a value as high as 2θ = 40.5° for the same Zn content.
Also, 2θ–ω scans in the direction parallel to the projection of the c-axis of sapphire exhibited three peaks, one near the position of the CdO(002) peak and the other two shifted towards lower and higher angles, giving rise to three values of a‖. The peaks were not individually well defined in all cases. That is, in addition to the tilted cubic cells, there are also two orthorhombic cells with the same tilt but different lattice constants.
Due to the tilt around the c-axis projection of sapphire, perpendicular lattice parameters (a⊥) can be easily assigned to each tilted domain, but this is not the case for lattice constants parallel to this axis (a‖). We have assumed that the two tilted domains have cells with opposite orthorhombic distortion. That is, the short lattice constant in the parallel direction has been assigned to the domain with the larger lattice constant in the perpendicular direction, and vice versa.
Table 2 shows the calculated lattice parameters from the 2θ–ω scan peak positions. Fig. 4(e) and (f) exhibit their behaviour as a function of the Zn content. It can be seen that at first these parameters correspond to a slightly distorted cubic cell, but for 15% Zn content and higher, the distortion is highly increased. The out-of-plane parameter maintains its value near that of the CdO cubic cell. The distortion is opposite for each tilted crystal; that is, for Cd1−xZnxO(001) with a negative ψ tilt, then a⊥ > a0 > a‖, while for Cd1−xZnxO(001) with a positive ψ tilt, then a⊥ < a0 < a‖.
| % Zn nominal | % Zn EDX (± 0.2) | Crystalline domain CdZnO(001) with inclination −ψ | Crystalline domain CdZnO(001) with inclination +ψ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a 0 (±0.003 Å) | a⊥ (±0.003 Å) | a‖ (±0.003 Å) | Mean (±0.003 Å) | % Zn Vegard's (±0.2) | a 0 (±0.003 Å) | a⊥ (±0.003 Å) | a‖ (±0.003 Å) | Mean (±0.003 Å) | % Zn Vegard's (±0.2) | ||
| 15 | 15.0 | 4.651 | 4.780 | 4.504 | 4.645 | 10.5 | 4.641 | 4.592 | 4.756 | 4.663 | 6.8 |
| 20 | 24.0 | 4.652 | 4.906 | 4.368 | 4.642 | 11.1 | 4.658 | 4.451 | 4.919 | 4.676 | 4.1 |
| 50 | 59.4 | 4.672 | 4.906 | 4.328 | 4.635 | 12.5 | 4.670 | 4.451 | 5.053 | 4.725 | — |
6. SEM and TEM analysis
6.1. SEM characterization
For morphological analysis, tilted cross-section and top-view SEM images were taken. As seen for samples with 5% and 50% Zn content values (Fig. 5(a) and (b), respectively), a change in morphology can be observed when the Zn content is high, in the form of a rougher surface with more contrast.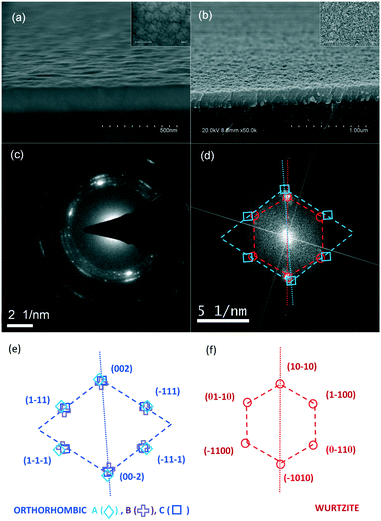 | ||
| Fig. 5 Tilted cross-section SEM images for Cd1−xZnxO sample with (a) 5% Zn content and (b) 50% Zn content (top views are given in the upper right insets). (c) The electron diffraction pattern of the Cd1−xZnxO 50% sample and (d) FFT of the same sample. (e) The calculated orthorhombic pattern for A, B, and C combinations (see Table 4) and (f) the calculated hexagonal pattern. | ||
On one hand, the electron contrast among different grains in SEM images can be explained in terms of secondary electron emission, which is mostly limited to the top few tens of nanometers of the surface. Secondary electron flux is expected to be greater in CdO then in ZnO due to the relatively high conductivity and carrier concentration of CdO. For this reason, we can assume that the crystals with lighter contrast are rock-salt CdZnO crystals and the dark crystals are wurtzite ZnCdO crystals.
On the other hand, the rougher surface can be attributed to a pyramid-like morphology as a result of the additional orientations that progressively occur as the Zn nominal content increases. As previously seen at low Zn content values, the preferred orientation is (001); for greater Zn content values, other orientations emerge, for example, inclined domains or even a wurtzite phase.
Nevertheless, the reduction in the smoothness of samples with high Zn content values is a consequence of several factors, such as the different volume of the wurtzite cell and the different orientation of ZnCdO and ZnO crystalline structures, amongst others.
6.2. TEM characterization
Electron diffraction measurements and HRTEM imaging were performed to complement the SEM and HRXRD analysis, in order to capture some intermediate phases appearing during the transformation from rock-salt to a wurtzite phase. A small amount of film from the sample with 50% Zn content was scratched off the substrate surface using a blade, and the particles were deposited directly on a copper grid. Fig. 5(c) shows the selected area electron diffraction (SAED) pattern obtained from this sample.Concentric rings in the zero-order Laue zone (ZOLZ) of the SAED pattern of Fig. 5(c) reflect the polycrystalline nature of the scratched particles, thus giving a nearly continuous angular distribution of (hkl) spots. Interplanar lattice spacings (dhkl) are calculated from the radii of the rings in reciprocal space, revealing a mixture of several phases. If only cubic and wurtzite phases are considered, the experimental dhkl values can be assigned to the ZnO(1000), CdO(111), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1), CdO(002), ZnO(11
1), CdO(002), ZnO(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and ZnO(20
0) and ZnO(20![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) planes, from inside to outside (see Table 3). dhkl distances for cubic spots are lower than the distances indicated in the crystallographic card of CdO,13 which is coherent with the shrinking of the CdO cell due to the incorporation of Zn. On the contrary, dhkl distances from the wurtzite spots are higher than the card values,15 in this case a consequence of the enlargement of the ZnO lattice when Cd was introduced. However, this approach is also compatible with the previously described orthorhombic structure. The non-negligible widths of the observed rings give the corresponding radii incertitude. This incertitude provides interplanar spacing values that include the corresponding values of the orthorhombic structure.
1) planes, from inside to outside (see Table 3). dhkl distances for cubic spots are lower than the distances indicated in the crystallographic card of CdO,13 which is coherent with the shrinking of the CdO cell due to the incorporation of Zn. On the contrary, dhkl distances from the wurtzite spots are higher than the card values,15 in this case a consequence of the enlargement of the ZnO lattice when Cd was introduced. However, this approach is also compatible with the previously described orthorhombic structure. The non-negligible widths of the observed rings give the corresponding radii incertitude. This incertitude provides interplanar spacing values that include the corresponding values of the orthorhombic structure.
| Planes (hkil)/(hkl) | d hkl (SAED)(±0.02 Å) | d hkl (crystallographic card) (Å) |
|---|---|---|
ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) 0) |
2.86 | 2.815 |
| CdO(111) | 2.68 | 2.710 |
ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) 1) |
2.50 | 2.336 |
| CdO(002) | 2.31 | 2.347 |
ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2) 2) |
1.91 | 1.923 |
ZnO(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) 0) |
1.66 | 1.625 |
| CdO(113) | 1.40 | 1.415 |
| % Zn nom | % Zn EDX | CdZnO(001) inclination −ψ | |||
|---|---|---|---|---|---|
| Name of combination | Lattice parameter a (Å) | Lattice parameter b (Å) | Lattice parameter c (Å) | ||
| 50 | 59.4 | A | 4.672 | 4.906 | 4.328 |
| 50 | 59.4 | B | 4.328 | 4.672 | 4.906 |
| 50 | 59.4 | C | 4.906 | 4.328 | 4.672 |
HRTEM images helped also to confirm this conclusion. Fig. 5(d) shows the fast Fourier transform (FFT) of the corresponding HRTEM micrograph obtained from a selected region of the 50% Zn content sample. It exhibits a superposition of blurred spots that can be assigned to an orthorhombic structure (squares) and to a hexagonal structure (circles). Fig. 5(e) and (f) exhibit the index identifications for each structure. As the previously calculated lattice parameters of the orthorhombic structure can be assigned in different orders to the three cubic axes, a, b and c, different combinations have been considered. Table 4 shows, as an example, the names of the combinations and the corresponding lattice constants in each case for the orthorhombic −ψ tilted Cd1−xZnxO(001) crystalline orientation given in Table 2. Fig. 5(e) shows the calculated reciprocal space points for these combinations and it can be seen that, in spite of the great differences between the lattice parameters, at this scale, the theoretical reciprocal space points are very close, as seen in FFT images. That is, we can say that the obtained HRTEM measurements are compatible with the presence of an orthorhombic phase.
The relative orientations of the orthorhombic and wurtzite structures are approximately the same as expected in the rock-salt-to-wurtzite transition (see below), and are characterized by the face of the orthorhombic cell parallel to the prismatic face (m-plane) of the wurtzite cell. However, some spots ((002) for cubic and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) for wurtzite) are not exactly aligned along the same direction, having an angular separation of about 4°. That is, the face of the orthorhombic cell is not exactly parallel to the m-plane of the wurtzite structure, but they are separated by 4° from each other.
0) for wurtzite) are not exactly aligned along the same direction, having an angular separation of about 4°. That is, the face of the orthorhombic cell is not exactly parallel to the m-plane of the wurtzite structure, but they are separated by 4° from each other.
7. Discussion
As mentioned, differences in the ionic radii of Zn and Cd and in the different stable crystal structures of the binary compounds limit the growth of single-phase films of ternary Cd1−xZnxO alloys over a broad compositional range. Above, we have experimentally shown that an increase in the Zn content produces a reduction of the lattice constants and the coexistence of several cubic orientations and phases. Next, we will analyze the different stages of growth that can be recognized in these ZnCdO films as the Zn content increases.In the first stage (x ≤ 10%), Cd1−xZnxO films have been found to preserve a single-phase cubic structure. As expected, lattice constants are shortened due to the substitution of Cd atoms by Zn ones but there is slight orthorhombic distortion, with the out-of-plane lattice constant being larger than the in-plane ones. By applying Vegard's law using the mean lattice constant, calculations of the Zn content introduced into the CdO lattice cell agree well with nominal values and EDX measurements. That is, the Zn content in Cd1−xZnxO films with a cubic structure has a direct dependence on the nominal Zn content and the molar ratio up to a maximum value of about 10% (see Table 1). Above this value, the introduction of Zn into the CdO matrix is less effective. We can say therefore that under our non-energy-assisted and atmospheric pressure growth conditions, the maximum efficient incorporation of Zn into the CdO lattice maintaining a (001) single orientation is about 10%. This relatively low value is explained by the small stable region of cubic Cd1−xZnxO. Otherwise, it is in accordance with the first principles analysis made by Fan et al.4 and measurements made by Yu et al.,8 who observed single-phase cubic structures in Cd-rich CdZnO films until x ≤ 0.2. In the same sense, stacking faults also contribute, since they can become seeds for hexagonal structures, mainly in the case of the dense accommodation of this type of defect, as demonstrated in ref. 19. It has to be noted that, in our samples, we would suppose that a larger range for the single cubic phase existed (x ≤ 0.2) if only conventional XRD measurements were considered. Nevertheless, strictly speaking and considering both out-of-plane and in-plane measurements, a more restricted value (≤10%) should be concluded.
A second stage, when the Zn content is 10% ≤ x ≤ 15%, can be considered as a transition stage, because strong changes take place. A reversal in the relative lengths of the lattice constants happens, with the out-of-plane parameter becoming shorter than the in-plane ones (Fig. 4(a)). This behaviour can be explained as resulting from an expansion of the in-plane lattice parameters of the layer, looking for a reduction in the mismatch. That is, as the Zn content increases, there is competition between the mismatch stress and the shrinking of the lattice. For Zn content higher than 10%, the mismatch dominates over the shrinking of the lattice, producing an inversion on the deformation of the lattice cell, which becomes enlarged in-plane and shortened out-of-plane. In addition, rotation of the cubic cell begins, with two cubic inclined orientations appearing on both sides of the plane that is perpendicular to the surface and contains the c-axis of sapphire. This behaviour was previously announced at a Zn content of 5% with a slight difference in the FWHM values of the rocking curves in the perpendicular and parallel directions (Fig. 3(a)). At a Zn content of 10%, the width is enlarged along the direction perpendicular to the projection of the c-axis of sapphire, indicating a larger tilt of the crystallographic domains in this direction rather than in the direction parallel to the same axis (Fig. 3(b)). Crystallographic tilts in epitaxial growth with large lattice mismatches prevent pseudomorphic growth and are usually caused by stacking faults. These defects are generated near the atomic steps of the growing surface and/or dislocations with anisotropic distributions, typically those generated during island coalescence.20 In this sense, we have found in previous work21 that the growth of CdO films begins with island-shaped structures, leading to the existence of a threshold thickness. Then, such anisotropic structural defects, being largely promoted by the strong anisotropic in-plane lattice mismatches, could be responsible for the significant anisotropic broadening of rocking curves. This explanation is reinforced by the fact that CdO has a low stacking fault energy compared to other materials in the II-O family. Concretely, the dislocation formation energy in CdO material is 3 times lower compared to ZnO and MgO materials.22
We can consider that a third stage takes place for x ≥ 15%, when the inclination of the rotated domains is strongly increased, with an angle that asymptotically tends to 15°. Within this process, the tilt sign and value can be explained as being a consequence of the strong mismatch, stacking faults and rock-salt-to-wurtzite transition. Vashaei et al.23 also observed 10° misoriented cubic Mg0.41Zn0.59O films grown on MgO/c-sapphire via P-MBE. Searching for a possible cause, they found the existence of stacking faults at the interface using TEM measurements. Defects of this type were present only over a range of Mg compositions that gave rise to films with cubic structures, with no evidence from films with hexagonal structures. Saha et al.,24 in a study on the rock-salt-to-wurtzite phase transformation of Sc1−xAlxN films, found crystals that exhibited twin relationships with each other. They observed two different wurtzite grain orientations, 30° apart but with each one rotated 15° about opposite sides of their common ZnO c-axis. Our case could be similar, with two differently oriented crystals with a rotation angle that tends to 15° at each side of the sapphire c-axis projection on the substrate surface, that is, 30° apart from each other. We must bear in mind that twin formation is a form of lowering the surface free energy of the film and stabilizing the crystal.25
Within this third stage, strong orthorhombic distortion of the cubic cell is also observed. This distortion can be interpreted as being a part of the rock-salt-to-wurtzite transformation through an orthorhombic and subsequent hexagonal stage. Microstructural and morphological evolution during the rock-salt-to-wurtzite structural phase transition has been described in studies of different types of materials, such as ab initio simulations carried out by Limpijumnong et al. on GaN and ZnO,26,27 metadynamics analysis performed by Duan et al.28 on AlN and InN, and detailed investigations made by Saha et al.24 on AlN and ScN. All of them analysed the transition from rock-salt to wurtzite in different compounds. The general trend in this phase transition involves a hexagonal intermediate state transformation path driven by homogeneous orthorhombic shear strain. According to this modelling analysis, the transition path is expected to be a two-step process. In the first step, opposite edges of the cubic cell should bend and the atom at the centre of the square will move horizontally at the centre of a triangle, thus leading to a hexagonal intermediate state.26,27 In the second step, the (c/a) ratio should increase, leading to the final wurtzite structure. After both these steps, it is expected that the relative crystallographic orientations between the initial rock-salt phase and final wurtzite phase should be as shown in Fig. 2(d). This behaviour is supported by the way in which ZnO grows on r-sapphire substrates with a preferred (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) ZnO orientation.29,30
0) ZnO orientation.29,30
Fig. 6 shows a proposed scheme to explain the rotated and distorted domains that have been found in the present study, assuming that they form part of the transition from a rock-salt phase to a wurtzite phase. The proposed scheme not only explains the symmetric ±15° inclination of the lattice cells, but also the different types of orthorhombic distortion for each tilted cell.
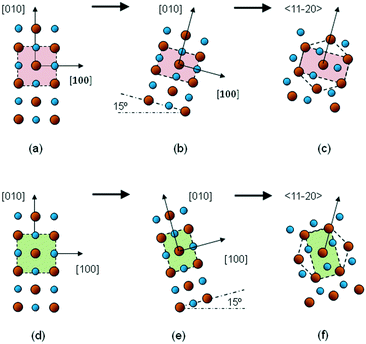 | ||
| Fig. 6 Schematic diagrams of the basal planes of the Zn1−xCdxO structure during the rock-salt-to-wurtzite transition: (a) in the early stages; (b) when tilt and orthorhombic distortion have taken place; (c) after transformation to a hexagonal structure; and (d)–(f) the same process but with tilt in the opposite direction. Small spheres: O; large spheres: Cd or Zn. The image is inspired by that shown in ref. 27. | ||
One type of orthorhombic distortion presents the longest lattice constant perpendicular to the sapphire c-axis projection (as in Fig. 6(b) and (c)), while the other one exhibits this parameter being shorter (as in Fig. 6(e) and (f)). That is, each distorted crystal could be interpreted as a different way to achieve the intermediate hexagonal state. These crystallographic domains would be rich in Zn, explaining both the high Zn content measured via EDX and the low Zn content determined from the application of Vegard's law to the Cd1−xZnxO layers.
8. Summary and conclusions
The growth of good quality films of the ternary alloy Cd1−xZnxO represents a challenge for crystal growers because the coexistence of phases will occur in some interval of solute concentration, depending on many factors. Few studies have dealt with films of cubic Cd-rich alloys, and the structural changes produced by the incorporation of Zn into the CdO parent lattice have not been clearly determined. These structural changes are key factors for better understanding the rock-salt to wurtzite transition in the CdO–ZnO system.In this work, Cd1−xZnxO films have been grown on r-sapphire substrates via MOCVD in the nominal Zn content range of 0 ≤ x ≤ 50%. HRXRD measurements have allowed a complete study, from analysis made using rocking curves, pole figures, and symmetric and skew-symmetric scans. We have found that Cd1−xZnxO films maintain a rock-salt structure with a (001) orientation until a Zn content of about 10% is reached. In the 10–15% range of Zn content, two differently oriented crystals appear with a tilt at both sides of the plane that contains the surface normal and the c-axis of sapphire, which asymptotically tends to ±15°. These inclined domains cannot be observed from conventional XRD measurements, as they don't have a low-index plane parallel to the surface. For Zn content values higher than 15%, the films are polycrystalline and a separation of phases (ZnO) happens at a Zn content of about 50%. These structural changes suggest that the transition from a rock-salt phase to a wurtzite phase takes place as follows: first, with an inclination of the (001) orientation of the cubic cell around the lattice edge parallel to the sapphire c-axis projection; and next with strong orthorhombic distortion of the cubic cell, which can be interpreted as an intermediate state in the transformation path, driven by inhomogeneous shear strain. These inclined crystallographic domains would be rich in Zn, explaining both the high Zn content measured via EDX and the low Zn content determined from XRD measurements using Vegard's law. The anisotropic strong mismatch and stacking faults generated during island coalescence seem to be the origin of the two tilted domains, and their orthorhombic distortion.
Specifically, the occurrence of inclined domains seems to be a consequence of the conjunction of two characteristics: on the one hand, the tensile type of mismatch between CdO and the r-plane of sapphire; and on the other hand, the shrinking of the Cd1−xZnxO cell with an increase in the Zn content. As the Zn content increases, the Cd1−xZnxO cell is shortened, making the mismatch larger. This leads to the Cd1−xZnxO cell becoming inclined in order to present larger surface dimension values and reduce the mismatch.
This study has revealed some unreported structural details related to the rock-salt-to-wurtzite transition in the CdO–ZnO system as the Zn content increases. Concretely, intermediate mixed phases having both stable rock-salt and orthorhombic structures are seen in the ternary alloy. HRXRD results are essential in order to analyze the microstructural characteristics during this phase transition in the Cd1−xZnxO alloy, because some information remains hidden if only conventional out-of-plane XRD measurements are used.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the Spanish Ministry of Economy, Industry and Competitiveness (MINECO) and the EU (FEDER) under project TEC2017-85912-C2-2, and by the Generalitat Valenciana under project Prometeo II 2015/004. The authors are also grateful to the SCSIE-University of Valencia for providing microscopy and HRXRD facilities.References
- K. Li, Y. Li and D. Xue, Funct. Mater. Lett., 2011, 4, 217–219 CrossRef CAS.
- M. Wei, R. C. Boutwell, J. W. Mares, A. Scheurer and W. V. Schoenfeld, Appl. Phys. Lett., 2011, 98, 261913 CrossRef.
- D. W. Ma, Z. Z. Ye, H. M. Lu, J. Y. Huang, B. H. Zhao, L. P. Zhu, H. J. Zhang and P. M. He, Thin Solid Films, 2004, 461, 250–255 CrossRef CAS.
- X. F. Fan, H. D. Sun, Z. X. Shen, J. L. Kuo and Y. M. Lu, J. Phys.: Condens. Matter, 2008, 20, 235221 CrossRef CAS PubMed.
- J. Ishihara, A. Nakamura, S. Shigemori, T. Aoki and J. Temmyo, Appl. Phys. Lett., 2006, 89, 091914 CrossRef.
- A. Fouzri, M. A. Boukadhaba, A. H. Taure, N. Sakly, A. Bchetnia and V. Sallet, J. Cryst. Process Technol., 2013, 3, 36–48 CrossRef CAS.
- V. Venkatachalapathy, A. Galeckas, M. Trunk, T. Zhang, A. Azarov and A. Y. Kuznetso, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 125315 CrossRef.
- J. H. Yu, J. H. Kim, T. S. Jeong, M. Shaheer Akhtar, C. J. Youn and K. J. Hong, Electron. Mater. Lett., 2011, 7, 215–220 CrossRef CAS.
- X. Han, R. Liu and Z. Xu, Thin Solid Films, 2009, 517, 5653–5657 CrossRef CAS.
- T. C. Zhang and A. Y. Kuznetsov, J. Appl. Phys., 2011, 110, 053512 CrossRef.
- A. Huerta-Barbera, E. de Prado, M. C. Martinez-Tomas, S. Agouram, E. Muñoz and V. Muñoz-Sanjose, Thin Solid Films, 2019, 683, 128–134 CrossRef CAS.
- J. Zúñiga-Pérez, C. Martínez-Tomás and V. Muñoz-Sanjosé, Phys. Status Solidi C, 2005, 2, 1233–1238 CrossRef.
- CdO ICDD card N° 05-0640.
- K. W. Böer, Handbook of the Physics of Thin-Film Solar Cells, Springer Science & Business, Berlin, Germany, 2014 Search PubMed.
- ZnO ICDD card No. 36-1451.
- Al2O3 ICDD card No. 10-0173.
- J. Zuñiga-Pérez, C. Munuera, C. Ocal and V. Muñoz-Sanjosé, J. Cryst. Growth, 2004, 271, 223–228 CrossRef.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- S. Suandon, S. Sanorpim, K. Yoodee and K. Onabe, Thin Solid Films, 2007, 515, 4393–4396 CrossRef CAS.
- H. F. Liu, W. Liu, S. Guo and D. Z. Chi, J. Phys. D: Appl. Phys., 2016, 49, 085103 CrossRef.
- A. Huerta-Barberà, L. M. Guia, O. Klymov, V. Marín-Borrás, C. Martínez-Tomás, J. Tamayo-Arriola, A. Kurtz, M. Montes-Bajo, E. Muñoz, A. Hierro and V. Muñoz-Sanjosé, Appl. Surf. Sci., 2016, 385, 209–215 CrossRef.
- V. P. Zhukov, N. I. Medvedeva and V. N. Krasilnikov, Int. J. Mod. Phys. B, 2018, 32, 1850059 CrossRef CAS.
- Z. Vashaei, T. Minegishi and T. Yao, J. Cryst. Growth, 2007, 306, 269–275 CrossRef CAS.
- B. Saha, S. Saber, E. A. Stach, E. P. Kvam and T. D. Sands, Appl. Phys. Lett., 2016, 109, 172102 CrossRef.
- R. Zhang and L. L. Kerr, J. Solid State Chem., 2007, 180, 988–994 CrossRef CAS.
- S. Limpijumnong and W. R. L. Lambrecht, Phys. Rev. Lett., 2001, 86, 91–94 CrossRef CAS PubMed.
- S. Limpijumnong and S. Jungthawan, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 054104 CrossRef.
- Y. Duan, L. Qin and H. Liu, J. Phys.: Condens. Matter, 2016, 28, 205403 CrossRef.
- P. Vennegues, J. M. Chauveau, M. Korytov, C. Deparis, J. Zuniga-Perez and C. Morhain, J. Appl. Phys., 2008, 103, 083525 CrossRef.
- J. M. Chauveau, P. Vennegues, M. Laügt, C. Deparis, J. Zuniga-Perez and C. Morhain, J. Appl. Phys., 2008, 104, 073535 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |