DOI:
10.1039/D0MA00518E
(Paper)
Mater. Adv., 2020,
1, 2492-2500
Morphology and crystal structure dependent pseudocapacitor performance of hydrated WO3 nanostructures†
Received
18th July 2020
, Accepted 11th August 2020
First published on 11th August 2020
Abstract
The strategic morphology tuning of hydrated WO3 nanostructures from two-dimensional (2D) nanosheets to three-dimensional (3D) slabs with enhanced in-plane crystalline nature and multilayered construction is realized via tailoring the synthesis temperature. The increasing synthesis temperature expands the degree of crystallinity, specific surface area and thickness of layered WO3·H2O sheets which results in slab like 3D morphology as characterized by X-ray diffraction spectra (XRD), Raman spectra and scanning electron microscopy (SEM). The electrochemical study reveals the higher specific capacitance (386 F g−1) of 3D slabs compared to that of 2D nanosheets (254 F g−1) at a scan rate of 2 mV s−1. Moreover, 3D slabs demonstrate an excellent capacitance retention of 96% compared to 2D nanosheets (86%) after 3000 cycles. The enhanced performance of supercapacitors in 3D slabs is attributed to three significant aspects: first, confined coordinated hydrate in the crystalline layer provides a significant surface area and allows fast electrochemical proton insertion via the Eigen–Zundel–Eigen mechanism; second, the enhanced crystalline nature offers improved in-plane conductivity; and finally the structural defects and disorders due to the layered structure promote faradaic redox reactions.
1. Introduction
The energy scenario at the global level is insisting on efficient efforts towards green and clean energy to fulfill the enormous demand of future generations. In this context, different energy harvesting related activities are initiated and implemented through renewable energy resources; however, the energy storage at a large scale is still challenging. Highly efficient and next-generation energy storage devices are required to fulfill the desire of the smart civilization, for example long-lasting portable electronic devices, ecofriendly e-vehicles and so on.1–4 Both batteries and supercapacitors are promising electrochemical energy storage devices. Remarkably, supercapacitors exhibit fascinating properties such as a fast charging–discharging rate, millions of life cycles and high power density compared to batteries.5,6 Nevertheless, supercapacitors have limitations in practical application because of their low energy density.7,8 The charge storage mechanisms distinguish supercapacitors into two categories: electrical double layer capacitors (EDLCs) and pseudocapacitors.9,10 The carbon electrodes are commonly used in EDLCs as they provide a greater surface area to absorb the charges without faradaic reaction at the interface between the electrode and the electrolyte.11,12 B. E. Conway has classified pseudocapacitors based on charge storage mechanisms: (1) capacitors involving underpotential deposition, where metal ions or protons adsorb on a metal surface above their redox potential, (2) redox capacitors, involving faradaic redox reactions on the surface or near the surface of electrode materials and (3) intercalated pseudocapacitors, involving fast faradaic insertion of ions into the tunnel or inter-layers of the electrode material.13,14 The pseudocapacitor type electrodes are highly demanded as a consequence of their ability to boost the energy density of supercapacitors with marginally compromised power density and cyclic life.15
Usually, the transition metal oxides (TMOs) such as RuO2, MnO2, NiO, and Co3O4 show the pseudocapacitive charge storage mechanism and are prominently employed as cathode materials in supercapacitors.16–20 However, these cathode materials suffer from high cost, toxicity, low density and low conductivity for practical application.21,22 Recently, more attention has been devoted to the WO3 structure owing to the three-dimensional (3D) lattice network similar to the perovskite unit, which consists of corner and edge sharing octahedra (WO6).23,24 It is cost-effective and has excellent physical and chemical properties such as an n-type wide band gap, high density (7.13 g cm−3), various oxidation states (W2+–W6+), and variable electrical conductivity (10–10−6 S cm−1).25,26 Also, WO3 exists in various crystalline phases which makes WO3 an extraordinary material amongst other TMOs for electrochromic, photocatalytic, gas sensing and electrochemical energy storage application.27–31 Moreover, the various crystal phases including trigonal tunnels and cavities are highly favorable for tuning its physical properties and electrochemical ion intercalation.32–35 Interestingly, the hydrated form of WO3 such as WO3·nH2O (n = 2, 1, 0.5, 0.33) exhibits a two-dimensional (2D) infinite layered crystal structure as a result of confined water in the crystalline structure.36 The crystal structure can be tuned by confined hydrate; for example, the monohydrate WO3·H2O is a distorted structure composed of two-dimensional crystal structures with appropriate van der Waals gaps between the stacks.37,38 The layer of octahedra (WO6) is composed of four equatorial oxygen atoms to form a bridging O–W–O bond along the ab-plane. One of the axial positions is occupied by the coordinate hydrate (W–OH2) bonds and the opposite axial position is bounded by a terminal oxygen atom (W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) perpendicular to the sheets (along the c-axis). It is impossible to build W bonds with adjacent layers by structural hydrate arrangement and therefore these structures possess an infinite 2D layered structure.39 These coordinated water molecules maintain the Eigen–Zundel–Eigen mechanism of rapid proton conduction as in the bulk water and improve the ion storage accessibility owing to the 2D layered structure.40 Kumagai et al. demonstrated that hydrated H2WO4 has a capacity of 450 A h kg−1 which is much higher than that of anhydrous WO3 (180 A h kg−1), but did not report the energy storage kinetics.41 Recently, Mitchell et al. have confirmed structural water within the crystalline layers that provided the rapid proton transfer kinetics.42 On the other hand, the surface redox chemistry via the terminal oxygen atom and diffusion of a proton within the hydrogen bond network of confined water layers in MXene hydrate has offered suitable faradaic reactions.43 Accordingly, the electrochemical charge storage mechanisms of electrode materials are highly subjective to their morphology, electrical conductivity and crystalline nature.44,45 The 2D layered crystalline MoO3, Nb2O5, V2O5, anatase TiO2, and δ-MnO2 with porous nature have demonstrated a high-rate charge storage capability via the intercalation pseudocapacitor mechanism.46–51
O) perpendicular to the sheets (along the c-axis). It is impossible to build W bonds with adjacent layers by structural hydrate arrangement and therefore these structures possess an infinite 2D layered structure.39 These coordinated water molecules maintain the Eigen–Zundel–Eigen mechanism of rapid proton conduction as in the bulk water and improve the ion storage accessibility owing to the 2D layered structure.40 Kumagai et al. demonstrated that hydrated H2WO4 has a capacity of 450 A h kg−1 which is much higher than that of anhydrous WO3 (180 A h kg−1), but did not report the energy storage kinetics.41 Recently, Mitchell et al. have confirmed structural water within the crystalline layers that provided the rapid proton transfer kinetics.42 On the other hand, the surface redox chemistry via the terminal oxygen atom and diffusion of a proton within the hydrogen bond network of confined water layers in MXene hydrate has offered suitable faradaic reactions.43 Accordingly, the electrochemical charge storage mechanisms of electrode materials are highly subjective to their morphology, electrical conductivity and crystalline nature.44,45 The 2D layered crystalline MoO3, Nb2O5, V2O5, anatase TiO2, and δ-MnO2 with porous nature have demonstrated a high-rate charge storage capability via the intercalation pseudocapacitor mechanism.46–51
In this study, we have proposed a facile strategy for the synthesis of single crystalline 2D layered crystal structures of WO3 nanostructures containing confined hydrates for supercapacitor applications. The obtained 3D WO3 slabs at a synthesis temperature of 110 °C have the highest degree of crystallinity and strong bond strength compared to 2D WO3 sheets prepared at 70 °C and 90 °C. The morphology and crystal structure dependent electrochemical charge storage performance of 3D slabs and 2D nanosheets were investigated. Further, the proton insertion into the layered crystalline structure, i.e. a signal of intercalated pseudocapacitance, was confirmed.
2. Materials and methods
2.1. Materials and reagents
Sodium tungstate dihydrate (Na2WO4·2H2O), concentrated sulfuric acid (H2SO4) and ethanol were purchased from SD Fine Chemicals, and Whatman paper was purchased from Sigma Aldrich. All aqueous solutions were prepared using double distilled water (DDW).
2.2. Synthesis of hydrated WO3 nanosheets
The hydrated WO3·H2O nanosheets were prepared by a one step wet chemical method without the addition of surfactant and varying the pH of the solution. Sodium tungstate (500 mg) was slowly added into 100 ml of aqueous 1 M H2SO4 solution, followed by stirring at room temperature for 30 min. After stirring at room temperature, the above solution was further heated at a temperature of 70 °C for 1 h. After this, the solution was naturally cooled down to room temperature and washed continuously with DDW and ethanol. The obtained product was dried at 80 °C for 12 h.
For the synthesis of hydrated WO3·H2O slabs, the reaction was carried out at higher temperatures (90 °C and 110 °C), keeping the other synthesis parameters the same. The obtained final products at the synthesis temperature of 70 °C, 90 °C and 110 °C were named W70, W90 and W110 respectively.
2.3. Material characterization
The crystal structure, phase purity and microstructure were characterized by X-ray diffraction (XRD) at λ = 1.54056 Å with CuKα radiation (Bruker D2 phaser) and Raman spectra (Raman microscope, (Renishaw inVia). The weight loss in a sample was measured by thermogravimetric analysis using a TA 2000 thermoanalyzer. The morphological investigation was done by field emission scanning electron microscopy (FESEM) (FEG Inspect 50, FEI) and high-resolution transmission electron microscopy (HR-TEM) with selected area electron diffraction (SAED; Tecnai G2-20-TWIN TEM) operating at 300 kV. The chemical composition and various oxidation states were investigated by XPS (Al-Kα source, PHI 5000 Versa probe scanning ESCA microprobe).
2.4. Electrochemical measurements
The electrochemical measurements were carried out in an Autolab PGSTAT 302N system using a three-electrode assembly. The glassy carbon was used as the working electrode, a platinum wire was used as the counter electrode and a Hg/HgCl electrode was used as the reference electrode. An active mass of 5 mg of the sample was dispersed in 2 ml of water–ethanol solvent of ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20 μl of Nafion was used as a binder and the mixture was further sonicated for 5 min. 10 μl of homogeneous ink was loaded on a polished working electrode and dried under an IR lamp for 30 min. Aqueous 1 M H2SO4 solutions were used as an electrolyte for all electrochemical measurements. The following equations were used to calculate the specific capacitance from the CV and GCD curves:
1 and 20 μl of Nafion was used as a binder and the mixture was further sonicated for 5 min. 10 μl of homogeneous ink was loaded on a polished working electrode and dried under an IR lamp for 30 min. Aqueous 1 M H2SO4 solutions were used as an electrolyte for all electrochemical measurements. The following equations were used to calculate the specific capacitance from the CV and GCD curves:| | 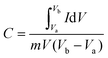 | (1) |
| | 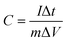 | (2) |
where C is the specific capacitance, I/m is the current density, and Δt and ΔV are the discharge time and the operating voltage window respectively.
3. Results and discussion
3.1. Structural and morphological investigations of hydrated WO3 nanoslabs
The three hydrated WO3 nanostructures namely W70, W90 and W110 were synthesized at three different temperatures of 70 °C, 90 °C and 110 °C respectively. The crystal structure and purity of hydrated WO3 nanostructures (W70, W90 and W110) were examined by XRD and Raman spectra (Fig. 1). The XRD pattern (Fig. 1(a)) clearly shows the monohydrate orthorhombic crystal structure of tungsten oxide (o-WO3·H2O) (JCPDS: 01:084:0886) with lattice parameters a = 5.24, b = 10.71, c = 5.133 of space group Pmnb (62) at all temperatures.52 However, the sample W110 depicts the most intense diffraction (111) plane (inset of Fig. 1(a)) reflecting the higher crystalline structure compared to that of the samples W70 and W90. Furthermore, the crystalline size (D) of W70, W90 and W110 was investigated by the Scherrer equation as follows:| | 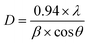 | (3) |
where λ is 1.54056 Å and 0.94 is constant for CuKα radiation, β is the line broadening in radians (FWHM). The estimated crystalline sizes along the (111) plane are 35 nm, 42 nm and 51 nm for samples W70, W90 and W110 respectively. Fig. 1(b) represents the schematic of the crystal structure of o-WO3·H2O. This structure clearly emphasizes the layer structure of the octahedra (WO6) along the ab-plane. The four oxygen atoms are coordinated to the central W atoms forming a number of O–W–O bridges along the ab-plane and the other open axial positions, in the c-axis perpendicular to the ab-plane, are bound by terminal oxygen atoms (W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and hydroxyl groups (W–OH2). Therefore it is difficult to create bonding between adjacent layers to form a 2D infinite layered crystalline structure. The Raman spectra (Fig. 1(c)) were investigated to further evaluate the various crystalline symmetry and microstructures of samples W70, W90 and W110. The Raman spectra of the sample W110 illustrate highly intense bands at 645 cm−1 and 946 cm−1 compared to samples W90 and W70 which reveals the characteristic feature of a strong bond in sample W110. The band at 946 cm−1 corresponds to the terminal W
O) and hydroxyl groups (W–OH2). Therefore it is difficult to create bonding between adjacent layers to form a 2D infinite layered crystalline structure. The Raman spectra (Fig. 1(c)) were investigated to further evaluate the various crystalline symmetry and microstructures of samples W70, W90 and W110. The Raman spectra of the sample W110 illustrate highly intense bands at 645 cm−1 and 946 cm−1 compared to samples W90 and W70 which reveals the characteristic feature of a strong bond in sample W110. The band at 946 cm−1 corresponds to the terminal W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond that arises due to the confined hydrate in the layered structure. The broad peak in the range of 500–700 cm−1 illustrates the stretching mode of the bridging O–W–O bond in the ab-plane, as expected from the 2D structure of the WO3·H2O network. The translational motion of the hydrogen atom in octahedral WO5–OH2 was assigned to a band at 370 cm−1. The band below 200 cm−1 corresponds to the lattice mode.53 The TGA curve (Fig. 1(d)) confirms the weight loss of coordinated water molecules around a temperature of 200 °C in agreement with previously reported temperature and approving the monohydrate WO3 structure.54
O bond that arises due to the confined hydrate in the layered structure. The broad peak in the range of 500–700 cm−1 illustrates the stretching mode of the bridging O–W–O bond in the ab-plane, as expected from the 2D structure of the WO3·H2O network. The translational motion of the hydrogen atom in octahedral WO5–OH2 was assigned to a band at 370 cm−1. The band below 200 cm−1 corresponds to the lattice mode.53 The TGA curve (Fig. 1(d)) confirms the weight loss of coordinated water molecules around a temperature of 200 °C in agreement with previously reported temperature and approving the monohydrate WO3 structure.54
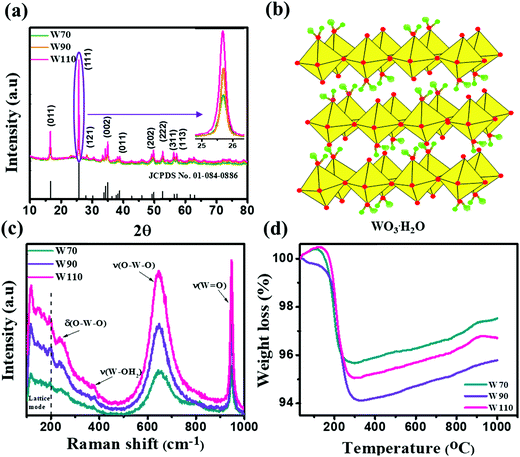 |
| | Fig. 1 (a) XRD spectra of W70, W90 and W110 and the inset shows the zoom area of plane (111), (b) schematic of the crystal structure of hydrate WO3·H2O, (c) Raman spectra of W70, W90 and W110, (d) TGA plots of W70, W90 and W110. | |
The synthesis temperature has a tremendous impact on morphological and structural change owing to the growth kinetics without alteration of pH and the addition of surfactant. The morphological analysis of samples W70, W90 and W110 was performed by FESEM (Fig. 2). The low-resolution image of W70 (Fig. 2(a)) shows a bunch of nanosheets like architecture. Furthermore, the high-resolution FESEM images (Fig. 2(b)) show the average thickness of a sheet to be in the range of 30–40 nm. Further, on increasing the synthesis temperature to 90 °C (W90) the thickness of the nanosheets increases to 60–100 nm as shown in Fig. 2(c) and (d). Moreover, at a high synthesis temperature of 110 °C, a densely packed 3D slab like morphology is created (Fig. 2(e)) and the high resolution FESEM image (Fig. 2(f)) displays that the thickness of the slabs increases to 200–250 nm. These slabs are made up of an attachment of 4–5 nanosheets together along the surface side with exposed top edges. Furthermore, the low-magnification TEM image of the sample W110 (Fig. 3(a)) illustrates the fragmented sheets affected by sonication. The HRTEM image (Fig. 3(b)) shows an interplanar spacing of 0.345 nm which corresponds to the d spacing of the (111) plane. The inverse fast Fourier transform (IFFT) images (Fig. 3(c)) of the selected region of Fig. 3(b) signify the various defects such as frank disorder and stacking fault. These defects have a strong impact on the stress and electrostatic repulsion between the layers, which can directly alter the migration energy or diffusion barriers that a proton or alkali ion must overcome during intercalation. Fig. 3(d) represents the intensity profile of Fig. 3(c). The SAED pattern (Fig. 3(e)) illustrates the set of bright diffraction spots indicating the single crystalline nature of sample W110 and the SAED pattern can be an index of the (001) zone axis of orthorhombic WO3·H2O. It is also observed that, along with the strong electron diffraction spot such as (111), weak diffraction spots can also be noted at those forbidden sites which are indicated by a white arrow. These weak spots are assigned to diffraction from the higher order Laue zone due to the combination of elongation of the diffraction spot along the normal of slabs and the larger (001) atomic spacing.
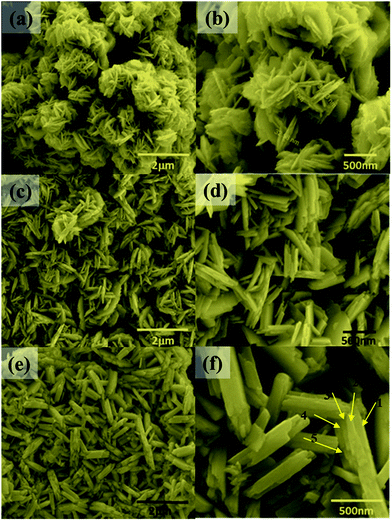 |
| | Fig. 2 (a and b) Low and high magnification FESEM images of nanosheets (W70), (c and d) low and high magnification images of nanosheets (W90), (e and f) low and high magnification images of the slab (W110). | |
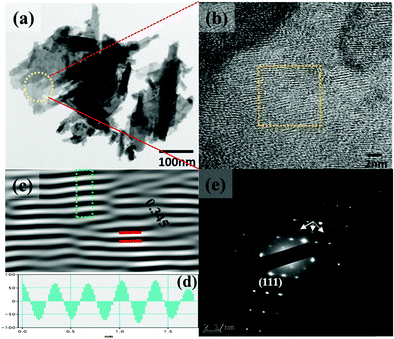 |
| | Fig. 3 (a and b) Low and high magnification TEM images of the slab (W110), (c) IFFT images, (d) intensity profile of the selected region of figure (c), (e) SAED pattern of W110. | |
The chemical composition and various oxidation states of WO3 nanoslabs (W110) were examined by XPS as shown in Fig. 4. The wide range survey scans of WO3 (Fig. S1, ESI†) show the presence of W and O. Moreover, the deconvoluted XPS spectra of doublet W (4f) comprising of W 4f7/2 and W 4f5/2 at a binding energy of 35.6 eV and 37.63 eV show spin–orbit splitting of the W (4f) level and correspond to the W6+ state (Fig. 4(a)). Nevertheless, the low-intensity peaks at 33.92 eV and 37.21 eV demonstrate the presence of W5+ state, which illustrates the existence of oxygen vacancy in the WO3 matrix. Furthermore, the deconvoluted spectra of O 1s (Fig. 4(b)) show two peaks at 531.1 eV and 531.9 eV which are assigned to the presence of lattice oxygen (O2−) and adsorbed oxygen (O− and O2−). These multi-oxidation states of W and surface oxygen attributed to the enhanced electrochemical properties of WO3 slabs.55 The porosity and surface area of W70, W90 and W110 were examined by Brunauer–Emmett–Teller (BET) analysis (Fig. 5). The samples W110, W90 and W70 exhibit the same Langmuir(III) nitrogen adsorption–desorption isotherm with a surface area of 68.8 m2 g−1, 49.3 m2 g−1 and 34.8 m2 g−1 respectively. The pore size distribution of the same sample was investigated by the Barrett–Joyner–Halenda (BJH) method as shown in the inset of Fig. 5. This illustrates the micro-porous nature with the pore size in the range of 1–3 nm. Thus, the high surface area of sample W110 ensures active sites for an effective electrochemical process and enhanced rate performance with storage capability.56
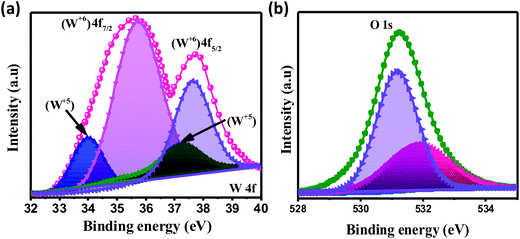 |
| | Fig. 4 XPS spectra of WO3 nanoslabs (W110): deconvoluted spectra of W 4f (a) and O 1s (b). | |
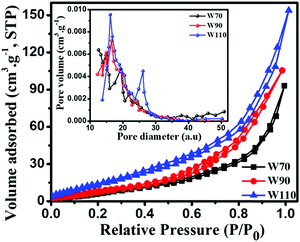 |
| | Fig. 5 Nitrogen adsorption–desorption isotherm and the inset shows the pore size distribution of W70, W90 and W110; the pore diameter unit is (a.u.) = Å (Angstrom). | |
3.2. Electrochemical performance of hydrated WO3 nanoslabs
The electrochemical performance measurement of electrodes W70, W90 and W110 was carried out on a three-electrode system in a 1 M H2SO4 electrolyte between potential windows −0.6 and 0 V. Fig. 6(a) shows the superimposed cyclic voltammetry (CV) curve of electrodes W70, W90 and W110 at a low scan rate of 2 mV s−1. It displays the higher current contribution of W110 with greater area under the curve indicating the better electrochemical charge storage performance compared to electrodes W70 and W90. However, the electrodes W110 and W90 are more faradaic in nature than electrode W70, revealing the high pseudocapacitive charge storage mechanism. The resulting anodic and cathodic waves at a low scan rate of 2 mV s−1 in the potential range of −0.45 V to −0.35 V and −0.35 V to −0.5 V of W90 and W110 indicate the more active surface sites and the reversible redox reaction W5+/W6+ accompanied with a dominant proton (H+) insertion/de-insertion pseudocapacitive process.57–59 Fig. S2 (ESI†) shows the CV curves at various scan rates from 2 to 100 mV s−1 of electrodes W70, W90 and W110. It demonstrates that at a high scan rate of 100 mV s−1 the cathodic and anodic redox waves fade out due to the fast movement of protons under the high scan rate ensuing less interaction time at the electrode surface and/or low intercalation into WO3 crystalline layers.55 The comparison of specific capacitance of W70, W90 and W110 samples at various scan rates is shown in Fig. 6(b). At a lower scan rate of 2 mV s−1, the specific capacitance of electrode W110 reached 386 F g−1, which is higher than the specific capacitance of 315 F g−1 and 254 F g−1 of W90 and W70 respectively. This highest specific capacitance of the electrode W110 is compared with the various structures of WO3 as listed in Table 1. Similarly, the galvanostatic charge–discharge (GCD) curves were recorded at various current densities from 1 A g−1 to 10 A g−1 as shown in Fig. S3 (ESI†). These GCD curves demonstrated the deviation from the triangular line in the potential range −0.3 V to −0.5 V, implying that the capacity mainly arises by faradaic redox reactions confirming the CV findings. Fig. 6(c) shows the discharge profile at a current density of 2 A g−1, which presents the highest discharge time of electrode W110 signifying the highest storage capacity compared to W70 and W90. In comparison, the electrode W110 shows the highest specific capacitance of 367 F g−1 compared to W90 (310 F g−1) and W70 (241 F g−1) at a high current density of 1 A g−1 (Fig. 6(d) and Fig. S3(d), ESI†). Interestingly, the capacitance values estimated from CV and GCD do not show any significant change in specific capacitance.
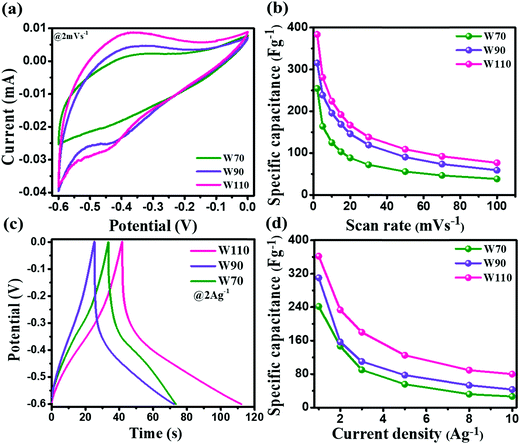 |
| | Fig. 6 (a) Comparison of the CV curve of W70, W90 and W110 at a scan rate of 2 mV s−1, (b) specific capacitance at various scan rates, (c) galvanostatic discharge curves of W70, W90 and W110 at a current density of 2 A g−1, (d) specific capacitance at various current densities. | |
Table 1 Performance comparison of various nanostructure and crystal structure of WO3
| Material |
Method |
Morphology |
Crystal structure |
Specific capacitance |
Stability |
Ref. |
| WO3 |
Hydrothermal |
Cube |
Hexagonal |
377.5 F g−1 |
90% after 4000 cycles |
35
|
| WO3 NRs/rGO |
Hydrothermal |
Nanorod |
Hexagonal |
343 F g−1 |
92% after 1000 cycles |
54
|
| WO3 |
Hydrothermal |
Nanoplate |
Monoclinic |
334 F g−1 |
91% after 5000 cycles |
61
|
| WO3 |
Hydrothermal |
Nanorod |
Hexagonal |
385 F g−1 |
89% after 1000 cycles |
65
|
| WO3–WO3·0.5H2O |
Microwave-assisted hydrothermal |
Disordered nanorods |
Hexagonal + cubic |
293 F g−1 |
NA |
66
|
| Bi2WO6 |
Sonochemical |
Nanoparticle |
Amorphous |
304 F g−1 |
200 cycles |
67
|
| m-WO3 |
Template-assisted synthesis |
Mesoporous |
Cubic |
199 F g−1 |
1000 cycles |
68
|
| m-WO3−x-C-s |
Block-polymer-assisted synthesis |
Hexagonal porous |
Triclinic |
103 F g−1 |
NA |
69
|
| WO3/rGO |
Hydrothermal |
Nanosheets |
Hexagonal |
244 F g−1 |
97% after 900 cycles |
70
|
| WO3 |
Hydrothermal |
Nanoparticle |
NA |
113 |
68.5% after 2000 cycles |
71
|
| WO3 |
Hydrothermal |
Nanorod |
Hexagonal |
155.5 |
84.9% after 5000 cycles |
72
|
|
3D WO
3
slab
|
Wet chemical
|
Nanoslab
|
Orthorhombic
|
386 F g
−1
|
96% after 3000 cycles
|
This work
|
3.3. Charge storage kinematics
The current contribution in the CV curve is related to the respective scan rate according to eqn (4):where I is the current, a is a constant, ν is the scan rate and b is a constant value which can be 0.5 or 1. The b-value is evaluated by the slope of linear fitting of log(current, I) vs. log(scan rate, ν). The dependency of current in the CV curve could be varied as either ν0.5 or ν, which represents the semi-infinite diffusion process or the dominant capacitive charge storage kinetics respectively.60 The electrode W110 shows the lowest anodic b-value (Fig. 7(a)) of 0.84 compared to electrodes W70 and W90 (1.2 and 1.1 respectively). Moreover, the electrode W110 clearly demonstrates the lowest b-value at various potential ranges of −0.1 V to −0.6 V (Fig. 7(b)) compared to electrodes W70 and W90. It confirms the significant proton insertion into the 2D structure of the slab (W110). Therefore, the highest specific capacitance of the slab (W110) compared to the nanosheets (W70 and W90) originating from the dominant proton insertion/deinsertion into the crystalline layer has been realized. Furthermore, the Trasatti procedure has been utilized to derive the current contributions by EDLC and proton insertion from the total capacitance using eqn (5):61,62where Qc is the capacitance contribution from EDLC, k is a constant, ν is the scan rate and Q(ν) is the charge storage at scan rate ν. The charge storage due to EDLC across the interface of electrode and electrolyte (Qc) was evaluated by the intercept of the plot of Q(ν) vs. ν−1/2 (Fig. S4, ESI†), and is almost 25 C g−1, 55 C g−1 and 74 C g−1 for electrodes W70, W90 and W110 (Fig. 7(c)) respectively. The highest value of Qc for electrode W110 correlated to its high surface area compared to W70 and W90. Moreover, the proton insertion contribution of electrodes with respect to the scan rate can be evaluated by subtracting the surface stored charge values from the total stored charges at various scan rates as shown in Fig. 7(d). Based on this, the capacity due to proton insertion into the crystalline layer is found to be 230 C g−1 which is four times higher than EDLC contribution (75 C g−1) at a low scan rate of 2 mV s−1. However, at a high scan rate of 50 mV s−1 the proton insertion capacity is found to be 54 C g−1 which highlights that the proton insertion pseudocapacitance is promising at a low scan rate than at a high scan rate.63,64
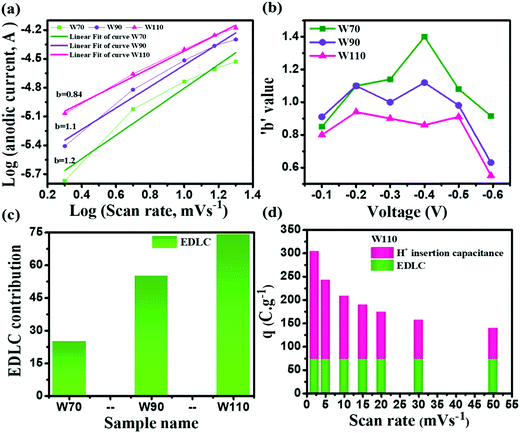 |
| | Fig. 7 Charge storage kinematics: (a) anodic peak potential b-values, (b) b-values calculated at various potentials, (c) EDLC contribution by W70, W90 and W110, (d) EDLC and H+ ion insertion contributions of electrode W110 at various scan rates. | |
Additionally, the cyclic stability test of electrodes W70, W90 and W110 was carried out using galvanostatic charge discharge (GCD) at a high current density of 5 A g−1 as shown in Fig. 8(a). The electrode W110 shows comparatively a high capacitance retention of 96% than W90 (89%) and W70 (86%) after 3000 cycles. It is noted that no significant variation in cyclic stability was observed in electrodes W70, W90 and W110 due to the advantage of the morphology and role of the confined hydrate in the crystalline-layered structure which enables the rapid movement of a proton. Furthermore, to better understand the charge transfer mechanism across the interface of electrode–electrolyte of all samples, electrochemical impedance spectroscopy (EIS) was carried out (Fig. S5, ESI†). The obtained electrochemical series resistance (RESR) in the high frequency region is 3.2 Ω, 2.4 Ω, and 1.09 Ω for W70, W90 and W110 respectively. On the other hand, the electrodes W70 and W90 exhibit a semi-circle (Fig. 8(b)) representing charge transfer resistance (Rct) across the interface of electrode–electrolyte, which is 54 Ω and 36 Ω respectively. The inset of Fig. 8(b) shows the equivalence circuit diagram with the impedance and resistance contributions to the electrochemical system. Interestingly, the slab (electrode W110) inhibits Rct with lower RESR demonstrating the smaller internal resistance and resulting in the faster kinetics of the redox reaction with high conductivity compared to electrodes W70 and W90.
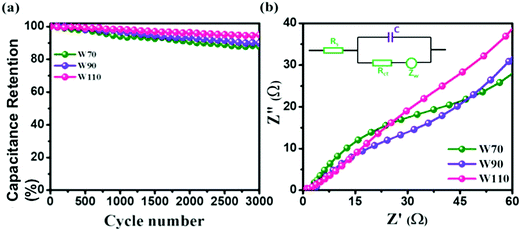 |
| | Fig. 8 (a) Cyclic stability, (b) impedance plot in the high frequency region and the inset is an equivalence circuit diagram of W70, W90 and W110. | |
4. Conclusion
In summary, tuning the morphology and crystallinity from hydrated WO3 nanosheets to high crystalline hydrated WO3 slabs via increasing the synthesis temperature from 70 to 110 °C is successfully achieved. The obtained 3D hydrated WO3 slabs exhibit an enhanced specific capacitance of 386 F g−1 than 2D hydrated WO3 nanosheets (254 F g−1) at a scan rate of 2 mV s−1. This improved performance of hydrated WO3 slabs is attributed to the enriched crystalline structure, increased surface area, enhanced active surface sides and effective proton insertion into the layered structure, resulting in the high redox pseudocapacitive mechanism. Therefore, the 3D highly crystalline WO3 with confined hydrate in the layered structure is a potential candidate for high-rate intercalated pseudocapacitors.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
The authors would like to thank the Director, National Centre for Nanosciences and Nanotechnology, and the Vice-Chancellor, Amity University, Mumbai, for their support and help.
References
- S. Sorrell, Renewable Sustainable Energy Rev., 2015, 47, 74–82 CrossRef
 .
.
- S. Chu and A. Majumdar, Nature, 2012, 488, 294 CrossRef CAS
 .
.
- J. R. Miller and P. Simon, Science, 2012, 321, 651 CrossRef
 .
.
- Q. Zhu, D. Zhao, M. Cheng, J. Zhou, K. A. Owusu, L. Mai and Y. Yu, Adv. Energy Mater., 2019, 9, 1901081 CrossRef
 .
.
- B. Li, F. Dai, Q. Xiao, L. Yang, J. Shen, C. Zhang and M. Cai, Energy Environ. Sci., 2016, 9, 102–106 RSC
 .
.
- Q. Wang, J. Yan and Z. Fan, Energy Environ. Sci., 2016, 9, 729–762, 10.1039/C5EE03109E
 .
.
- H. Liang, C. Xia, A. Emwas, D. H. Anjum, X. Miao and N. Husam, Nano Energy, 2018, 49, 155–162 CrossRef CAS
 .
.
- X. Li, C. Zhang, S. Xin, Z. Yang, Y. Li, D. Zhang and P. Yao, ACS Appl. Mater. Interfaces, 2016, 8, 21373–21380 CrossRef CAS
 .
.
- S. R. Suryawanshi, V. Kaware, D. Chakravarty, P. S. Walke, M. A. More, K. Joshi, C. S. Rout and D. J. Late, RSC Adv., 2015, 5, 80990–80997 RSC
 .
.
- B. D. Patrice Simon and Y. Gogotsi, Science, 2014, 343, 1210–1211 CrossRef
 .
.
- F. Yao, T. Pham and Y. Hee, ChemSusChem, 2015, 8, 2284–2311 CrossRef CAS
 .
.
- Y. Hao, F. Xu, M. Qian, J. Xu, W. Zhao and F. Huang, RSC Adv., 2017, 7, 10901–10905 RSC
 .
.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 RSC
 .
.
- Y. Wang, Y. Song and Y. Xia, Chem. Soc. Rev., 2016, 45, 5925–5950 RSC
 .
.
- J. Shen, C. Yang, X. Li and G. Wang, ACS Appl. Mater. Interfaces, 2013, 5, 8467–8476 CrossRef CAS
 .
.
- V. K. A. Muniraj, C. K. Kamaja and M. V. Shelke, ACS Sustainable Chem. Eng., 2016, 4, 2528–2534 CrossRef CAS
 .
.
- Y. Song, T. Liu, B. Yao, M. Li, Z. Huang, D. Feng, F. Wang, Y. Tong, X. Liu and Y. Li, ACS Energy Lett., 2017, 2(17), 1752–1759, DOI:10.1021/acsenergylett.7b00405
 .
.
- X. L. Guo, J. M. Zhang, W. N. Xu, C. G. Hu and L. Sun, J. Mater. Chem. A, 2017, 5, 20579–20587 RSC
 .
.
- X. Xia, J. Tu, Y. Zhang, Y. Mai, X. Wang, C. Gu and X. Zhao, RSC Adv., 2012, 2, 1835–1841 RSC
 .
.
- Y. Zeng, M. Yu, Y. Meng, P. Fang, X. Lu and Y. Tong, Adv. Energy Mater., 2016, 6, 1601053 CrossRef
 .
.
- Z. Xu, S. Sun, W. Cui, J. Lv, Y. Geng, H. Li and J. Deng, Electrochim. Acta, 2018, 268, 340–346 CrossRef CAS
 .
.
- M. V. K. Azhagan, M. V. Vaishampayan and M. V. Shelke, J. Mater. Chem. A, 2014, 2, 2152–2159 RSC
 .
.
- H. Zheng, J. Z. Ou, M. S. Strano, R. B. Kaner, A. Mitchell and K. Kalantar-Zadeh, Adv. Funct. Mater., 2011, 21, 2175–2196 CrossRef CAS
 .
.
- L. M. Kuti, S. S. Bhella and V. Thangadurai, Inorg. Chem., 2009, 48, 6804–6811 CrossRef CAS
 .
.
- R. Samal, B. Chakraborty, M. Saxena, D. J. Late and C. S. Rout, ACS Sustainable Chem. Eng., 2019, 7, 2350–2359 CrossRef CAS
 .
.
- P. A. Shinde and S. C. Jun, ChemSusChem, 2020, 13, 11–38 CrossRef CAS
 .
.
- Y. M. Shirke and S. P. Mukherjee, CrystEngComm, 2017, 19, 2096–2105 RSC
 .
.
- A. K. Nayak, S. Lee, Y. I. Choi, H. J. Yoon, Y. Sohn and D. Pradhan, ACS Sustainable Chem. Eng., 2017, 5, 2741–2750 CrossRef CAS
 .
.
- J. Besnardiere, B. Ma, A. Torres-pardo, G. Wallez, H. Kabbour, J. M. González-calbet, H. J. Von Bardeleben, B. Fleury, V. Buissette, C. Sanchez, T. Le Mercier, S. Cassaignon and D. Portehault, Nat. Commun., 2019, 10, 327 CrossRef
 .
.
- S. S. Kalanur, Y. J. Hwang, S. Y. Chae and O. S. Joo, J. Mater. Chem. A, 2013, 1, 3479–3488 RSC
 .
.
- Z. Chen, Y. Peng, F. Liu, Z. Le, J. Zhu, G. Shen, D. Zhang, M. Wen, S. Xiao, C. P. Liu, Y. Lu and H. Li, Nano Lett., 2015, 15, 6802–6808 CrossRef CAS
 .
.
- M. Zhu, W. Meng, Y. Huang, Y. Huang and C. Zhi, ACS Appl. Mater. Interfaces, 2014, 6, 18901–18910 CrossRef CAS
 .
.
- J. Cao, B. Luo, H. Lin, B. Xu and S. Chen, Appl. Catal., B, 2012, 111–112, 288–296 CrossRef CAS
 .
.
- W. Sun, M. T. Yeung, A. T. Lech, C. Lin, C. Lee, T. Li, X. Duan, J. Zhou and R. B. Kaner, Nano Lett., 2015, 15, 4834–4838 CrossRef CAS
 .
.
- V. Lokhande, A. Lokhande, G. Namkoong, J. H. Kim and T. Ji, Results Phys., 2019, 12, 2012–2020 CrossRef
 .
.
- Y. M. Li, M. Hibino, M. Miyayania and T. Kudo, Solid State Ionics, 2000, 134, 271–279 CrossRef CAS
 .
.
- J. Zheng, Z. Haider, T. K. Van, A. U. Pawar, C. Kang and Y. Kang, CrystEngComm, 2015, 17, 6070–6093, 10.1039/C5CE00900F
 .
.
- B. Kattouf, G. L. Frey, A. Siegmann and Y. Ein-Eli, Chem. Commun., 2009, 7396–7398 RSC
 .
.
- L. Liang, J. Zhang, Y. Zhou, J. Xie, X. Zhang, M. Guan, B. Pan and Y. Xie, Sci. Rep., 2013, 3, 1936 CrossRef
 .
.
- J. B. Mitchell, W. C. Lo, A. Genc, J. Lebeau and V. Augustyn, Chem. Mater., 2017, 29, 3928–3937 CrossRef CAS
 .
.
- N. Kumagai, N. Kumagai and K. Tanno, Appl. Phys. A: Mater. Sci. Process., 1989, 89, 83–89 CrossRef
 .
.
- J. B. Mitchell, N. R. Geise, A. R. Paterson, N. C. Osti, Y. Sun, S. Fleischmann, R. Zhang, L. A. Madsen, M. F. Toney, D. E. Jiang, A. I. Kolesnikov, E. Mamontov and V. Augustyn, ACS Energy Lett., 2019, 4, 2805–2812 CrossRef CAS
 .
.
- Y. Sun, C. Zhan, P. R. C. Kent, M. Naguib, Y. Gogotsi and D. Jiang, ACS Appl. Mater. Interfaces, 2019, 12, 763–770 CrossRef
 .
.
- T. Brousse, M. Toupin, R. Dugas, L. Athouël, O. Crosnier, T. Brousse, M. Toupin, R. Dugas, L. Athouël, O. Crosnier and D. Bélanger, J. Electrochem. Soc., 2006, 153, A2171–A2180 CrossRef CAS
 .
.
- H. Kim, J. B. Cook, H. Lin, J. S. Ko, S. H. Tolbert, V. Ozolins and B. Dunn, Nat. Mater., 2016, 16, 454–460 CrossRef
 .
.
- T. Brezesinski, J. Wang, S. H. Tolbert and B. Dunn, Nat. Mater., 2010, 9, 146–151 CrossRef CAS
 .
.
- V. Augustyn, J. Come, M. A. Lowe, J. W. Kim, P. Taberna, S. H. Tolbert, H. D. Abruña, P. Simon and B. Dunn, Nat. Mater., 2013, 12, 518 CrossRef CAS
 .
.
- Y. L. Zheng Chen, V. Augustyn, X. Jia, Q. Xiao and B. Dunn, ACS Nano, 2012, 6, 4319–4327 CrossRef
 .
.
- S. Devaraj and N. Munichandraiah, J. Mater. Chem. C, 2008, 112, 4406–4417 CAS
 .
.
- V. A. Online, G. Binitha, M. S. Soumya, A. A. Madhavan, P. Praveen, A. Balakrishnan, K. R. V. Subramanian, M. V. Reddy, S. V. Nair, A. S. Nair and N. Sivakumar, J. Mater. Chem. A, 2013, 1, 11698–11704 RSC
 .
.
- X. Zhang, L. Hou, A. Ciesielski and P. Samorì, Adv. Energy Mater., 2016, 6, 1600671 CrossRef
 .
.
- L. Ma, X. Zhou, L. Xu, X. Xu, L. Zhang, C. Ye, J. Luo and W. Chen, Colloids Surf., A, 2015, 481, 609–615 CrossRef CAS
 .
.
- B. Desbat and J. C. Lassegues, J. Solid State Chem., 1987, 67, 235–247 CrossRef
 .
.
- X. H. Guan, Z. W. Zhang, L. Yang and G. S. Wang, ChemPlusChem, 2017, 82, 1174–1181 CrossRef CAS
 .
.
- S. P. Gupta, V. B. Patil, N. L. Tarwal, S. D. Bhame, S. W. Gosavi, I. S. Mulla, D. J. Late, S. S. Suryavanshi and P. S. Walke, Mater. Chem. Phys., 2019, 225, 192–199 CrossRef CAS
 .
.
- M. Han, Y. Mu and J. Yu, Mater. Adv., 2020, 1, 421–429 RSC
 .
.
- Y. Zhu, C. Xia, Y. Lei, N. Singh, U. Schwingenschlögl and H. N. Alshareef, Nano Energy, 2019, 56, 357–364 CrossRef CAS
 .
.
- H. Kanoh, W. Tang, Y. Makita and K. Ooi, Langmuir, 1997, 7463, 6845–6849 CrossRef
 .
.
- K. S. Kumar, N. Choudhary, Y. Jung and J. Thomas, ACS Energy Lett., 2018, 3, 482–495 CrossRef CAS
 .
.
- A. Vlad, N. Singh, J. Rolland, S. Melinte and P. M. Ajayan, Sci. Rep., 2014, 4, 4315 CrossRef CAS
 .
.
- H. Vogh, Electrochim. Acta, 1994, 39, 1981–1983 CrossRef
 .
.
- S. P. Gupta, S. W. Gosavi, D. J. Late, Q. Qiao and P. S. Walke, Electrochim. Acta, 2020, 354, 136626 CrossRef CAS
 .
.
- J. Jia, X. D. Liu, X. Li, L. Cao, M. Zhang, B. Wu, X. D. Liu, X. Li, L. Cao, M. Zhang, B. Wu and X. Zhou, J. Alloys Compd., 2020, 823, 153715 CrossRef CAS
 .
.
- X. Xu, R. Zhao, B. Chen, L. Wu, C. Zou, W. Ai, H. Zhang, W. Huang and T. Yu, Adv. Mater., 2019, 31, 1900526 CrossRef
 .
.
- H. Peng, G. Ma, K. Sun, J. Mu, M. Luo and Z. Li, Electrochim. Acta, 2014, 147, 54–61 CrossRef CAS
 .
.
- K. H. Chang, C. C. Hu, C. M. Huang, Y. L. Liu and C. I. Chang, J. Power Sources, 2011, 196, 2387–2392 CrossRef CAS
 .
.
- V. D. Nithya, R. K. Selvan, D. Kalpan, L. Vasylechko and C. Sanjeeviraj, Electrochim. Acta, 2013, 109, 720–731 CrossRef CAS
 .
.
- S. H. Park, Y. H. Kim, T. G. Lee, H. K. Shon, H. M. Park and J. Y. Song, Mater. Res. Bull., 2012, 47, 3612–3618 CrossRef CAS
 .
.
- W. Xiao, W. Liu, X. Mao, H. Zhu and D. Wang, J. Mater. Chem. A, 2013, 1, 1261–1269 RSC
 .
.
- L. Ma, X. Zhou, L. Xu, X. Xu, L. Zhang, C. Ye, J. Luo and W. Chen, Colloids Surf., A, 2015, 481, 609–615 CrossRef CAS
 .
.
- C. Peng, Y. Yang, C. Li, Y. Lin, R. Zheng, Z. Kuai, S. Chen, R. Li and L. Li, Nanotechnology, 2020, 31, 27 CrossRef
 .
.
- P. A. Shinde, Y. Seo, C. Ray and S. C. Jun, Electrochim. Acta, 2019, 308, 231–242 CrossRef CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00518e |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Vandana B.
Patil
b,
Sanjay D.
Chakane
c,
Mahendra A.
More
d,
Dattatray J.
Late
a,
Vandana B.
Patil
b,
Sanjay D.
Chakane
c,
Mahendra A.
More
d,
Dattatray J.
Late
 e and
Pravin S.
Walke
e and
Pravin S.
Walke
 *a
*a
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) perpendicular to the sheets (along the c-axis). It is impossible to build W bonds with adjacent layers by structural hydrate arrangement and therefore these structures possess an infinite 2D layered structure.39 These coordinated water molecules maintain the Eigen–Zundel–Eigen mechanism of rapid proton conduction as in the bulk water and improve the ion storage accessibility owing to the 2D layered structure.40 Kumagai et al. demonstrated that hydrated H2WO4 has a capacity of 450 A h kg−1 which is much higher than that of anhydrous WO3 (180 A h kg−1), but did not report the energy storage kinetics.41 Recently, Mitchell et al. have confirmed structural water within the crystalline layers that provided the rapid proton transfer kinetics.42 On the other hand, the surface redox chemistry via the terminal oxygen atom and diffusion of a proton within the hydrogen bond network of confined water layers in MXene hydrate has offered suitable faradaic reactions.43 Accordingly, the electrochemical charge storage mechanisms of electrode materials are highly subjective to their morphology, electrical conductivity and crystalline nature.44,45 The 2D layered crystalline MoO3, Nb2O5, V2O5, anatase TiO2, and δ-MnO2 with porous nature have demonstrated a high-rate charge storage capability via the intercalation pseudocapacitor mechanism.46–51
O) perpendicular to the sheets (along the c-axis). It is impossible to build W bonds with adjacent layers by structural hydrate arrangement and therefore these structures possess an infinite 2D layered structure.39 These coordinated water molecules maintain the Eigen–Zundel–Eigen mechanism of rapid proton conduction as in the bulk water and improve the ion storage accessibility owing to the 2D layered structure.40 Kumagai et al. demonstrated that hydrated H2WO4 has a capacity of 450 A h kg−1 which is much higher than that of anhydrous WO3 (180 A h kg−1), but did not report the energy storage kinetics.41 Recently, Mitchell et al. have confirmed structural water within the crystalline layers that provided the rapid proton transfer kinetics.42 On the other hand, the surface redox chemistry via the terminal oxygen atom and diffusion of a proton within the hydrogen bond network of confined water layers in MXene hydrate has offered suitable faradaic reactions.43 Accordingly, the electrochemical charge storage mechanisms of electrode materials are highly subjective to their morphology, electrical conductivity and crystalline nature.44,45 The 2D layered crystalline MoO3, Nb2O5, V2O5, anatase TiO2, and δ-MnO2 with porous nature have demonstrated a high-rate charge storage capability via the intercalation pseudocapacitor mechanism.46–51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20 μl of Nafion was used as a binder and the mixture was further sonicated for 5 min. 10 μl of homogeneous ink was loaded on a polished working electrode and dried under an IR lamp for 30 min. Aqueous 1 M H2SO4 solutions were used as an electrolyte for all electrochemical measurements. The following equations were used to calculate the specific capacitance from the CV and GCD curves:
1 and 20 μl of Nafion was used as a binder and the mixture was further sonicated for 5 min. 10 μl of homogeneous ink was loaded on a polished working electrode and dried under an IR lamp for 30 min. Aqueous 1 M H2SO4 solutions were used as an electrolyte for all electrochemical measurements. The following equations were used to calculate the specific capacitance from the CV and GCD curves: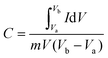
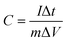
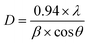
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and hydroxyl groups (W–OH2). Therefore it is difficult to create bonding between adjacent layers to form a 2D infinite layered crystalline structure. The Raman spectra (Fig. 1(c)) were investigated to further evaluate the various crystalline symmetry and microstructures of samples W70, W90 and W110. The Raman spectra of the sample W110 illustrate highly intense bands at 645 cm−1 and 946 cm−1 compared to samples W90 and W70 which reveals the characteristic feature of a strong bond in sample W110. The band at 946 cm−1 corresponds to the terminal W
O) and hydroxyl groups (W–OH2). Therefore it is difficult to create bonding between adjacent layers to form a 2D infinite layered crystalline structure. The Raman spectra (Fig. 1(c)) were investigated to further evaluate the various crystalline symmetry and microstructures of samples W70, W90 and W110. The Raman spectra of the sample W110 illustrate highly intense bands at 645 cm−1 and 946 cm−1 compared to samples W90 and W70 which reveals the characteristic feature of a strong bond in sample W110. The band at 946 cm−1 corresponds to the terminal W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond that arises due to the confined hydrate in the layered structure. The broad peak in the range of 500–700 cm−1 illustrates the stretching mode of the bridging O–W–O bond in the ab-plane, as expected from the 2D structure of the WO3·H2O network. The translational motion of the hydrogen atom in octahedral WO5–OH2 was assigned to a band at 370 cm−1. The band below 200 cm−1 corresponds to the lattice mode.53 The TGA curve (Fig. 1(d)) confirms the weight loss of coordinated water molecules around a temperature of 200 °C in agreement with previously reported temperature and approving the monohydrate WO3 structure.54
O bond that arises due to the confined hydrate in the layered structure. The broad peak in the range of 500–700 cm−1 illustrates the stretching mode of the bridging O–W–O bond in the ab-plane, as expected from the 2D structure of the WO3·H2O network. The translational motion of the hydrogen atom in octahedral WO5–OH2 was assigned to a band at 370 cm−1. The band below 200 cm−1 corresponds to the lattice mode.53 The TGA curve (Fig. 1(d)) confirms the weight loss of coordinated water molecules around a temperature of 200 °C in agreement with previously reported temperature and approving the monohydrate WO3 structure.54



.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





