Open Access Article
Open Access ArticleNonlinear elastic aspects of multi-component iron oxide core–shell nanowires by means of atom probe tomography, analytical microscopy, and nonlinear mechanics†
Gábor
Csiszár
 *a,
Helena
Solodenko
a,
Robert
Lawitzki
*a,
Helena
Solodenko
a,
Robert
Lawitzki
 a,
Wenhao
Ma
a,
Christopher
Everett
a and
Orsolya
Csiszár
bc
a,
Wenhao
Ma
a,
Christopher
Everett
a and
Orsolya
Csiszár
bc
aChair of Materials Physics, Department of Materials Science, University of Stuttgart, Heisenbergstraße 3, 70569 Stuttgart, Germany. E-mail: Gabor.Csiszar@mp.imw.uni-stuttgart.de; Helena.Solodenko@mp.imw.uni-stuttgart.de; Robert.Lawitzki@mp.imw.uni-stuttgart.de; st154509@stud.uni-stuttgart.de; Christopher.Everett@mp.imw.uni-stuttgart.de
bFaculty of Basic Sciences, University of Applied Sciences Esslingen, Kanalstraße 33, 73728 Esslingen, Germany. E-mail: Orsolya.Csiszar@hs-esslingen.de
cInstitute of Applied Mathematics, Óbuda University, Budapest, Hungary
First published on 26th November 2020
Abstract
One-dimensional objects as nanowires have been proven to be building blocks in novel applications due to their unique functionalities. In the realm of magnetic materials, iron-oxides form an important class by providing potential solutions in catalysis, magnetic devices, drug delivery, or in the field of sensors. The accurate composition and spatial structure analysis are crucial to describe the mechanical aspects and optimize strategies for the design of multi-component NWs. Atom probe tomography offers a unique analytic characterization tool to map the (re-)distribution of the constituents leading to a deeper insight into NW growth, thermally-assisted kinetics, and related mechanisms. As NW-based devices critically rely on the mechanical properties of NWs, the appropriate mechanical modeling with the resulting material constants is also highly demanded and can open novel ways to potential applications. Here, we report a compositional and structural study of quasi-ceramic one-dimensional objects: α-Fe ⊕ α-FeOOH(goethite) ⊕ Pt and α-Fe ⊕ α-Fe3O4(magnetite) ⊕ Pt core–shell NWs. We provide a theoretical model for the elastic behavior with terms accounting for the geometrical and mechanical nonlinearity, prior and subsequent to thermal treatment. The as-deposited system with a homogeneous distribution of the constituents demonstrates strikingly different structural and elastic features than that of after annealing, as observed by applying atom probe tomography, energy-dispersive spectroscopy, analytic electron microscopy, and a micromanipulator nanoprobe system. During annealing at a temperature of 350 °C for 20 h, (i) compositional partitioning between phases (α-Fe, α-Fe3O4 and in a minority of α-Fe2O3) in diffusional solid–solid phase transformations takes place, (ii) a distinct newly-formed shell formation develops, (iii) the degree of crystallinity increases and (iv) nanosized precipitation of evolving phases is detected leading to a considerable change in the description of the elastic material properties. The as-deposited nanowires already exhibit a significantly large maximum strain (1–8%) and stress (3–13 GPa) in moderately large bending tests, which become even more enhanced after the annealing treatment resulting at a maximum of about 2.5–10.5% and 6–18 GPa, respectively. As a constitutive parameter, the strain-dependent stretch modulus undoubtedly represents changes in the material properties as the deformation progresses.
1 Introduction
One-dimensional nanowires (NWs) have gained considerable attention in the last decades due to their outstanding optical, electrical, magnetic, chemical and mechanical properties in order to be used as building blocks in novel nanotechnological applications such as photocatalysis, energy conversion applications, micro/nano electromechanical systems and sensing.1–5 Magnetic materials with special nanostructural configurations are also of great scientific interest and technologically essential in future applications.6 As a well-known example, iron oxides as an important class of magnetic materials have been widely used in catalysis,7 magnetic devices,8 environment protection,9 sensors,10 drug delivery,11 and water splitting12 due to their promising physical properties. Many iron oxide particles fabricated in a wide variety of zero-to-three-dimensional nanostructures have already been synthesized with great success. As a remarkable example, magnetic media with perpendicular anisotropy allow smaller bit size, and as a result, greater recording density.13–16In the field of one-dimensional objects, from a microstructural perspective, morphology and porosity determine a variety of properties such as efficiency and stability of functional NWs. Another critical aspect is the spatial distributed structural defects such as vacancies or unintentional elements that can affect the functionality of materials by modifying the catalytic property, corrosion behaviour, or conductivity. The accurate composition of an individual nanowire, is also of significant importance to NW electronic, magnetic, mechanical properties, and consequently device performance. However, their detection on a local scale remains a challenge and is crucial to describe the mechanical aspects for the sake of optimizing strategies for the design of nanomaterials. A couple of the major challenges in nanowire synthesis are elementally related to the challenge of analyzing nanowire composition and morphology in order to, at least qualitatively, control the concentration of (un)intentional constituents, and to accurately map defect structure such as grain boundary structure in multiple dimensions. To fully characterize the potentially useful heterostructures fabricated by various growth techniques, three-dimensional visualization of nanoscale composition is also highly demanded. This need in recent examples was highlighted including modulation-doped core–shell nanowires17 and a quantum dot embedded within a nanowire capped by a co-axial shell.18
Many factors determine the suitability of characterization tools for composition analysis in terms of spatial resolution, detectability for all elements, detection limit, and analysis volume. In this regard, atom probe tomography (APT) is a unique analytical characterization tool displaying several advantages such as subnanometer-scale resolution, single-atom sensitivity, and in an ideal case, equal detectability for all elements.19 Furthermore, a statistical analysis of composition variations is also manageable with sufficient volume analysis or a sufficient number of atoms detected, and the 3D nature of reconstruction data allows a rigorous investigation of various features. Moreover, quantitative mapping of the constituents' distributions has led to important insights into NW growth kinetics and possible related mechanisms.17 As found in earlier studies, APT elemental studies naturally contribute to a greater understanding of the electrical, mechanical, and magnetic properties of NWs.20–22 Even if there is an insignificant difference in the atomic numbers between the precipitates and the matrix to identify elements by scattering alone, a successful combination with spectroscopies by electron microscopy such as EDS (energy-dispersive X-ray spectroscopy)23 or EELS (electron energy loss spectroscopy)24 can also be used complementarily together with APT. However, the detection limit of EDS is not sufficient for single atomic detection, and therefore quantitative analysis only for larger clusters with relatively high atomic fractions can be conducted with higher accuracy.
The sensitivity, resolution, and 3D nature of APT facilitate the quantitative analysis of clustering and alloy fluctuations on the nanoscale. It is particularly well suited to determine whether composition fluctuations exceed those of a random alloy and is appropriate to characterize the distribution of nanoscale clusters in terms of size, shape, and composition. As an example, GaAs–AlGaAs core–shell nanowires remarkably highlight numerous of the unique aspects of APT.22,25 The 2D nature of projected TEM images, the limited volume of analysis in cross-sectional samples, or the complexity of alloy segregation in radial heterostructures can restrict a rigorous quantitative analysis of an alloy distribution in a restricted shell region by using exclusively scanning/transmission electron microscopy (S/TEM),26–28 whereas the nature of the alloy composition fluctuations can clearly be identified by APT.22,25 Moreover, by utilizing isosurfaces, proxigrams, and 2D composition maps, enriched regions can also be identified, and their size distribution, shape, and composition can be statistically studied.25
APT is also especially beneficial for understanding the compositional partitioning between phases in thermally activated diffusional solid–solid phase transformations in metallic alloys. Within the wide variety of diffusional phase transformations, growth, and precipitate nucleation has been widely studied in many different metallic alloys using APT.29,30 A cluster in context of APT data can either be a solid-state concentration fluctuation or a well-developed precipitate. Methods, such as the maximum separation distance method31 and the proximity histogram method,32 are used depending on the nature of the solute cluster. To identify the precipitates and clusters, the iso-concentration surface method has also been utilized with significant accuracy for multi-component Fe–Cu steel.33 Additionally, APT has been used extensively to study the correlation of microstructure with various mechanical and magnetic properties of Fe–Cr-based alloys.34 In this regard, APT has also been essential for investigating solute segregation to material defects like grain boundaries in alloys.35,36
Despite the great success, in operation, NWs are subjected to mechanical and electrical stresses which impact significantly their mechanical properties.37 Moreover, the fabrication of NW-based devices has been found to be critically connected with the mechanical properties of NWs.38 Consequently, the reliability, and functionality of these devices strongly depend on several physical properties of their constituents. From a mechanical perspective, in the last two decades, the development of experimental methods such as atomic force microscopy (AFM), electron microscopy (EM),39 and nano-manipulation techniques based on focus ion beam technology (FIB-SEM),40 has given mechanical characterization of NWs an advanced potential.41,42 Furthermore, mechanical properties and behaviour in terms of uniaxial, biaxial, shear, and torsional loading through computational simulations have also extensively been investigated.43–45 As a consequence, probably due to their extremely small physical size and the high surface-to-volume ratio, the unique physical properties of the NWs have always indicated a significant difference from that of their 2D (thin film), or 3D (bulk) counterparts irrespective to the applied experimental methods or computational simulation.46–58 In many modern applications that involve larger strains, the deformation becomes inherently nonlinear (geometrical and/or mechanical).59–61 Therefore, to describe complex physical aspects of these materials, appropriate mechanical models are needed while they can open novel pathways to potential applications.62–64
Here, we report a compositional and structural investigation of core–shell NWs performed by using APT, EDS, and TEM techniques synthesized via template-assisted electrodeposition from an aqueous solution. Furthermore, via scanning electron microscopy (SEM), a mesoscale technique is employed to determine the mechanical properties using a micromanipulator nanoprobe system installed within the SEM chamber, where bending tests are conducted on individual, focused-ion-beam (FIB) fabricated NWs. Finally, through this direct approach to determine the deflection curves as a function of the applied forces, stress, strain, and also higher-order elastic tensor components are determined by utilizing an appropriate theoretical model of the nonlinear elastic response of α-Fe ⊕ α-FeOOH(goethite) ⊕ Pt and α-Fe ⊕ α-Fe3O4(magnetite) ⊕ Pt core–shell NWs as quasi-ceramic, nano-crystalline materials.
2 Theoretical considerations for mechanics
With moderately large (≤12%) deformation, strain and stress must be defined in the reference and the deformed configurations leading to an Eulerian (current) and Lagrangian (reference) frame of approach. For nonlinear elasticity theory, we have to confront the difficulty that the balance of stresses is performed in the deformed state, while the constitutive relation refers to the reference configuration. For more details, the readers may refer to Secs. 3.1–3.3 in ref. 61, and in Sec. 1 in ESI† and for more fundamentals, to Ogden65 on non-linear elasticity theory. In this study, we use the total Lagrangian formulation, where the nominal stress P (1st Piola-Kirchhoff stress) and the material stress S (2nd Piola-Kirchhoff stress) relate forces in the reference frame and the current frame to areas in the reference configuration. Additionally, for the sake of simplicity, we restrict to the material's homogeneous isotropic elastic property that is consistent implicitly with derivatives of a strain-energy density function depending only on the deformation gradient F.66For a complete description of deformation, the chosen material stress, S, and the Green–Lagrange strain (as a function of the deformation gradient, F), E(F), must be expressed for the particular sample geometry and the deformation involved in the deformation process. In this study, the concentrated load acts at the free end of the one-dimensional, cylindrical beam (NW) with a typical aspect ratio at or above 18, while the other end can be considered clamped. For the bending experiment, schematically shown in Fig. 1, the following assumptions are established: (i) all material points on a given plane align on a plane after deformation; with an aspect ratio of about 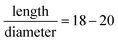 , the relative amplitude of warping is on the order of 10−3, therefore the warped cross-section can be neglected (εxz ≅ 0), (ii) anticlastic deformation is negligible; with realistic values of about ν = 1/3 and σyield/E = 10−3 to 10−2, the width or height of the beam changes up to 0.1–1% (εyy = εzz = −ν/Eσxx) causing a negligible change in the cross-sectional dimension, and thus, it has no effect on the deflection curve solution and the major strains/stresses (εyy = εzz ≅ 0), (iii) cross-sectional shape and size of the beam are assumed to be almost constant resulting in a displacement vector as being a function of the x-coordinate (w = w(x)) only, and (iv) planar deformation is considered exclusively meaning that the y-component of the displacement vector vanishes (v = 0).
, the relative amplitude of warping is on the order of 10−3, therefore the warped cross-section can be neglected (εxz ≅ 0), (ii) anticlastic deformation is negligible; with realistic values of about ν = 1/3 and σyield/E = 10−3 to 10−2, the width or height of the beam changes up to 0.1–1% (εyy = εzz = −ν/Eσxx) causing a negligible change in the cross-sectional dimension, and thus, it has no effect on the deflection curve solution and the major strains/stresses (εyy = εzz ≅ 0), (iii) cross-sectional shape and size of the beam are assumed to be almost constant resulting in a displacement vector as being a function of the x-coordinate (w = w(x)) only, and (iv) planar deformation is considered exclusively meaning that the y-component of the displacement vector vanishes (v = 0).
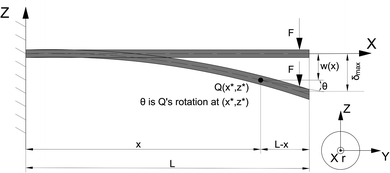 | ||
| Fig. 1 Schematic of the arrangement of the non-deformed-, and deflected nanowire in terms of the reference frame. | ||
According to the assumptions made for the bending, the satisfying u-component (in the x-direction) of the displacement vector (u = u(x,z)i + νj + w(x)k using the i, j and k unit vector notation; νj = 0) can be defined as a linear function of z as
| u(x,z) = u° − θ(x)z at any x, | (1) |
As a result of geometrical non-linearity (see details in Sec. 3.2 in ref. 61, and Sec. 1.1 in ESI†), the remaining non-zero Exx component of the strain tensor can be formulated as a function of the displacement vector component, w(x) and its derivatives as
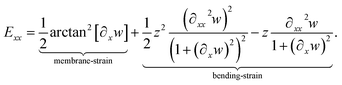 | (2) |
As an additional feature compared to the classical elementary beam theory (Euler–Bernoulli, E–B), the beam axis also extends due to the rotation of the deformed cross-section as the gradient of the axial component of the displacement vector (membrane-strain). Eqn (2) represents the Exx – Green–Lagrange tensor component equipped by the full-nonlinearity of the curvature with a quadratic approximation in u of the displacement field.
The 1st Piola-Kirchhoff stress tensor, P, describes the stress in the reference configuration, and the non-physical 2nd Piola-Kirchhoff stress tensor, S, is energy-conjugate to the Green–Lagrange strain tensor, E. The S tensor can be given by the product of the inverse deformation gradient tensor, F−1, and the 1st Piola-Kirchhoff tensor, P. To be exact, shown in eqn (6) and (9) in ref. 61, the relevant components of the corresponding tensors are determined. Thus, a general constitutive law
| Sxx = ϕ(Exx, Exz, Ezx, Ezz) | (3) |
As a result, the tensor component Pxx (see details in Sec. 1.2 in ESI†) yields
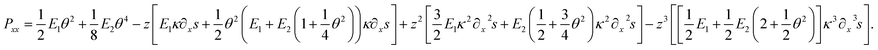 | (4) |
Consequently, one of the most descriptive part of bending, the bending moment becomes as
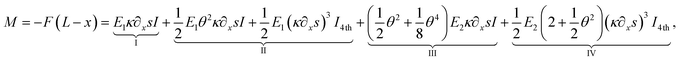 | (5) |
In eqn (5), the four distinguishable terms not only play a decisive role to the moment, M, but they also have different meanings with respect to elasticity. The first term (I) as a quasi-linear term contributes to the moment similar to E1∂2xxwI as if full linearity would be utilized (E–B theory). In this study, on the contrary, the curvature is utilized with its full-nonlinear form (quasi-linear). The second term (II) contributes to M additionally in terms of a quadratic geometrical non-linearity (a quadratic approximation of the displacement field). The third term (III) contributes in a mechanical sense to M with respect to a quadratic approximation of mechanics, whereas the fourth term represents a mixed term related to a quadratic geometric and mechanical approximation.
Eqn (5) can also be expressed in terms of the deflection curve using the formula given in eqn (10) in ref. 61. This provides an equation for the calculated moment that consists of linear and quadratic functions of the first and second derivatives of the deflection curve with respect to x. Thus the proposed theoretical approach can approximate directly the constants E1 and E2 by employing the appropriate numerical method. In this study, via the applied shooting method, one must solve a boundary value problem by reducing it to a system of initial value problems.
To expand the proposed description, another important quantifier similar to Young's modulus in isotropic linear elasticity can be introduced. For this purpose, the incremental stretch modulus can be introduced to study the nonlinear elastic response of an isotropic material under bending conditions. The gradient of P with respect to the displacement gradient, F − I, provides the incremental stretch modulus, Ỹincr, as
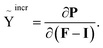 | (6) |
Applying eqn (S5) in ESI,† the incremental stretch modulus yields its final closed form in terms of derivatives of the deflection function as given in eqn (S11) in ESI.†
To bring the theoretical considerations to a conclusion, with the assistance of the determined Exx, Pxx and Ỹincr, an appropriate non-linear quadratic order description of bending can be conducted along with experimental deflection curves.
2.1 Effective bending modulus in case of a composite structure
In case of a core–shell structure, the different contribution of the core and the shell to the moment must be taken into account separately. The moment–curvature relationship for a composite beam may be determined from the condition that the moment resultant of the bending stresses is equal to the bending moment M acting at the cross section. Following similar steps as for a beam of one type of material and utilizing the result given in eqn (5), we can yield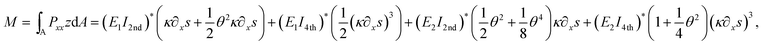 | (7) |
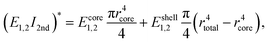 | (8) |
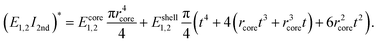 | (9) |
Similar to the derivation of the effective bending modulus in terms of the second moment of inertia, the effective bending modulus consisting of the fourth moment of inertia can be given as
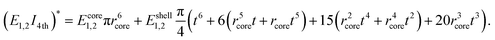 | (10) |
Note here that in the case of a multiple shell formation, the final effective bending modulus consists of more additive terms in eqn (8) generated by applying multiple times the same routine. To conclude, in composite structures, as an additional feature, the bending moment of the core and the shell can be described appropriately as given in eqn (8)–(10).
3 Experimental
3.1 Sample preparation
For the electrodeposition, a 200 nm thick gold layer on one side of the membrane is sputtered by ion beam (10−8 mbar; sputtering rate of 1.3 ± 0.2 Å s−1) to be served as a working electrode. A pure iron bar was chosen playing the role of a counter electrode. The electrodeposition was realized in a two-electrode electrochemical cell system. Chronopotentiometry (CP) mode was used to conduct a deposition with a fixed deposition rate. In order to ascertain the required composition and morphology, constant currents in the range of 200 μA to 3 mA were applied. Considering that the pore density is 6 × 108 cm−2, the effective deposition area is calculated as 0.925 mm2. This corresponds to an applied current density in the range of 216 A m−2 to 3242 A m−2. Furthermore, during the deposition, a constantly generated electrolyte flow facilitated the crucial H2 gas bubbles to be removed from the pores.
After deposition, the membrane was put into a 10 mL tube and dissolved in 0.7 mL dichloromethane (CH2Cl2) at a temperature of 38 °C for 40 minutes. In order to proceed to the FIB lift-outs (preparation for the bending test and TEM, APT investigations), NWs from the gold-sputtered layer were carefully scratched onto a TEM copper grid with a mesh size of 6.5 μm. A dual-beam FEI SCIOS FIBSEM was used to transfer isolated single NWs lying on the edge of the grid onto pre-fabricated tungsten posts and get them fixed by Pt-deposition. The average length of the NWs is found to be about 7 μm and between 100 and 200 nm in diameter grown on the sputtered gold layer.
3.2 Characterization
4 Results
4.1 Morphology and composition by using APT
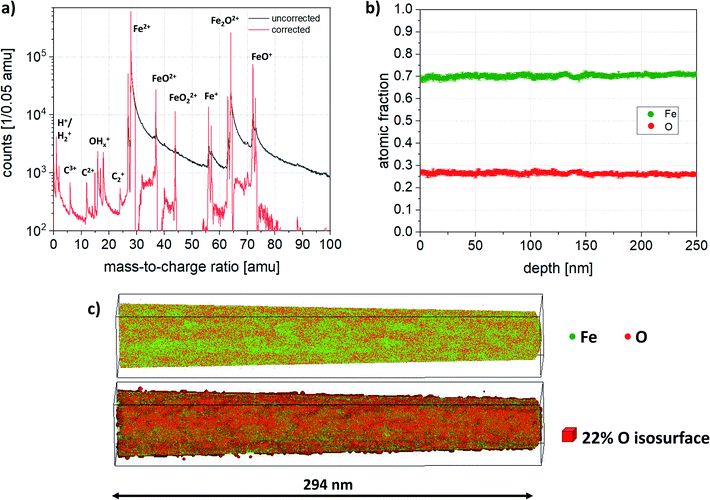
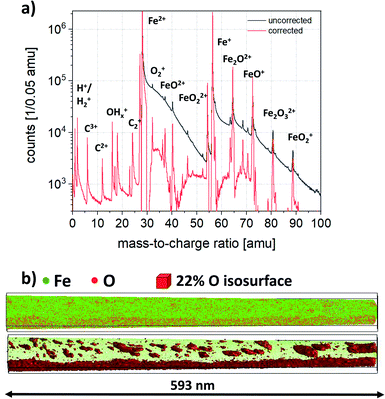
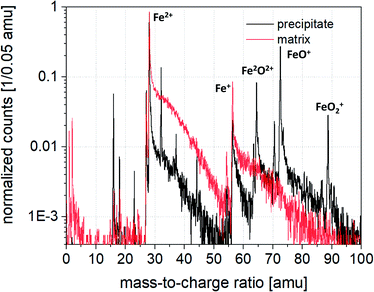
In contrast to the as-deposited state, where the NW contains oxygen homogeneously distributed in the entire volume, in the annealed state the surrounding matrix is depleted of oxygen and consists of pure iron. To compare the composition of matrix and precipitates, a local mass spectrum was extracted from both regions. Two box filters were placed inside and outside of the O isosurface, which are shown in Fig. 4. This confirms furthermore that the detected ions in the matrix are exclusively Fe, while the precipitate shows additional peaks of O, O2 and iron oxides. The corrected composition of the precipitates has been determined to be 71.4 at% Fe and 28.6 at% O, while the oxygen content outside the precipitates is less than 3 at%.
4.2 Morphology, crystalline structure and composition by using TEM and EDS
The morphology, grain, and crystal structure of the NWs before and after annealing has been analyzed by TEM and is presented in Fig. 5. Both nanowires are of polycrystalline nature which can be clearly seen in the diffraction patterns in Fig. 5a and g. In the as-deposited NW, the grains are significantly smaller since single reflections are barely visible in Fig. 5a; whereas in the annealed NW, several strong reflections are visible. The crystal structure in the as-deposited wire matches well with body-centered cubic α-Fe. A rather weak additional ring is also visible closest to the primary beam which would match to the intensity of the (113) reflection of a negligible amount of Fe3O4 (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with a = 0.8396 nm) structure. Moreover, it can be excluded that it stems from a Pt crystalline phase. After annealing (Fig. 5g), the DP consists of significantly more rings. Besides the reflections from bcc α-Fe (red), there are additional reflections from iron oxides. These reflections were indexed by comparison to simulated diffraction patterns with the software package JEMS.69 The majority of the additional reflections stems from the spinel phase magnetite Fe3O4 (Fd
m with a = 0.8396 nm) structure. Moreover, it can be excluded that it stems from a Pt crystalline phase. After annealing (Fig. 5g), the DP consists of significantly more rings. Besides the reflections from bcc α-Fe (red), there are additional reflections from iron oxides. These reflections were indexed by comparison to simulated diffraction patterns with the software package JEMS.69 The majority of the additional reflections stems from the spinel phase magnetite Fe3O4 (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with a = 0.8396 nm) illustrated by green rings. All remaining reflections (less than 5% in total) match well to the structure of bixbyite Fe2O3 (Ia
m with a = 0.8396 nm) illustrated by green rings. All remaining reflections (less than 5% in total) match well to the structure of bixbyite Fe2O3 (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) with a = 0.94 nm) illustrated by blue rings.
with a = 0.94 nm) illustrated by blue rings.
The grain structure is significantly different before and after annealing, which can be seen in the colored DF-grain maps in Fig. 5b and h. In the as-deposited state (b), the grains are very small (2.7 ± 0.9 nm) and align in domains of many grains with similar orientation in growth/length direction of the wire. After the annealing (h), the grains have a size of (14 ± 8 nm) and preferred orientations are not visible anymore. Both nanowires are covered by a 23 ± 3 nm thick shell consisting of Pt particles embedded in a carbon precursor. This shell is an unavoidable left-over from the preparation of the wires when using the FIB and fixing them on the tungsten posts with the gas injection system using this precursor. To expand on this issue, also discussed later in Fig. 9, it is demonstrated, that the shell was not measured on either side of the NW by APT. The atom probe has a limited field of view and therefore measures only the center part of the specimen. Due to slight misalignment of sample to detector center, the edge of the NW is measured only.
Chemical information of the NWs were obtained by EDS and are presented in the elemental maps in Fig. 5c–e and i–k. In the as-deposited NW, Fe and O are homogeneously distributed within the wire, whereas after annealing, iron and oxygen-rich regions exist. This can be clearly seen, when comparing the separate EDS maps measured for Fe and O in the as-deposited state (Fig. 5c and d), and the overlay of the net intensity map of Fe and O for the annealed NW (Fig. 5l), where each pixel is colorized by the element with the highest net intensity. Additionally, the overall oxygen content is quantified to be almost the same for both nanowires (as-deposited: ∼22.4 at% vs. annealed: ∼24.6 at%), meaning there was no additional oxidation during the annealing.
As tabulated in Table 1, the quantitative EDS analysis for the 20 h-long annealed sample reveals a strongly fluctuating oxygen concentration along the NW. The evaluated figures indicate that there are several regions with a 2.8 times higher normalized net intensity of oxygen content (approximately 2.3 times higher oxygen concentration) as oxygen-rich regions compared to those having a lack of the oxygen. Note here, since the determination of atomic concentration via EDS is influenced by numerous factors, the accuracy is rather limited.
| Region with lack of O | Region in abundance of O | |||
|---|---|---|---|---|
| Conc. [at%] | Net int. [%] | Conc. [at%] | Net int. [%] | |
| NW #1 | 20.3 | 5.9 | 43.7 | 16.3 |
| 16.7 | 4.7 | 40.4 | 14.6 | |
| NW #2 | 12.8 | 3.5 | 34.2 | 11.3 |
| — | — | 33.0 | 10.9 | |
| Average | 16.6 ± 3.8 | 4.7 ± 1.2 | 37.8 ± 5.1 | 13.3 ± 2.6 |
4.3 Mechanical bending tests
To determine the deflection curve w(x) of the synthesized individual Fe-based NW, concentrated lateral forces were exerted by the micromanipulator at the free end. While the clamped end connected to the W-post was stable, a force measurement tip detected the applied lateral forces during loadings. The force measurement tip (M-tip, see Fig. 6) was moved in a direction perpendicular to the NWs to apply gradually increasing lateral force to it. Furthermore, the position of the applied lateral force on the surface of the NW remained constant during measurement. Fig. 6 (a–c for the as-deposited-, d–f for the annealed case) illustrates a series of snapshots of SEM images that display the process of bending of two typical individual NWs with an effective length‡ of 2.39 ± 0.06 μm (2.89 ± 0.07-annealed) and a radius of 62 ± 6 nm (aspect ratio = 20, (AR); 82 ± 7-annealed; AR = 18). As shown in Fig. 6b, the initial point of the deflection is defined as the point where the nanowire connected to the W post by using Pt glue. In Fig. 6a–c (d–f-annealed), the increasing deflection indicates the gradually increased lateral force up to about a maximum force of 336 (624-annealed) nN. At higher applied forces, residual deformation was detected, therefore, further bending tests were not conducted since the elastic response of the NWs is of interest. After each bending test demonstrated in Fig. 6a–f, the tip was unloaded, and the free end of NW moved back to its initial position and restored completely its original shape without any residual plastic deformation.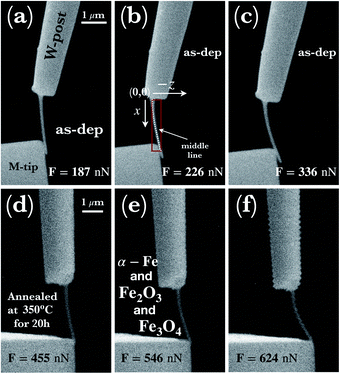 | ||
| Fig. 6 (a–c) A series of SEM snapshots of a typical synthesized (as-dep.) and (d–f) later annealed Fe-based NWs exerted by the applying concentrated lateral force perpendicular to it. The corresponding applied forces are also given in the images. NWs shown in (a–f) are under gradually increased concentrated forces with concomitantly recorded pronounced deflection characteristics. Schematics of a coordinate system visualized in (b) assists to demonstrate the applied method used to determine the deflection curves denoted as the middle line. As a preprocessing operation, skeletonization algorithm was applied using the distance transformation procedure implemented in ImageJ software.70 The dotted line represents experimental data points with errors of about 5 nm in the entire range. Note here that the deflection curves only represent the effective length of the wires. The scale bar given in (a) and (d) holds also for images shown in (b, c) and (e, f), respectively. | ||
The investigated deflections in the load-controlled bending were conducted for the as-deposited state under the forces of 187 ± 22 nN, 226 ± 23 nN, 336 ± 33 nN, whereas in the annealed state, the applied forces were 455 ± 42 nN, 546 ± 48 nN and 624 ± 57 nN. The deflection curves are determined by using the middle line shown schematically in Fig. 6b in a Cartesian coordinate system. As shown in Fig. 7, with increasing applied force, the effective maximum displacement (see δmax in Fig. 1) of the wire at the free end reaches about 220 nm, 375 nm, 555 nm, and in the case of after annealing, 425 nm, 600 nm, and 790 nm respectively, all in the elastic regime. At smaller applied forces, initially, the deformation indicates a constant gradient of the curvature along the wire, while at larger applied forces, a stronger variation of the gradient is demonstrated with respect to strain. Approaching to the free end, the curvature seemingly converges to infinity. Consistently, the curvature of deflections indicates that in the closer region to the clamped end, the highest bending contribution occurs, however, with increasing distance, the bending effect vanishes. Note here that such a phenomenon is not a unique feature of the employed nonlinear model, since from a linear mechanical perspective one would expect similar effect. From a different perspective, the proposed model is able to indicate consistency with its linear counterpart.
As verified in Fig. 7 by the fitted blue-colored deflection curves, in case of the smallest applied force, only the quadratic geometrical approximation is needed, while at higher forces (gray-, red curves), both the quadratic geometrical-, and mechanical approximation are found to be sufficient in the small-to-moderate regime.
5 Discussion
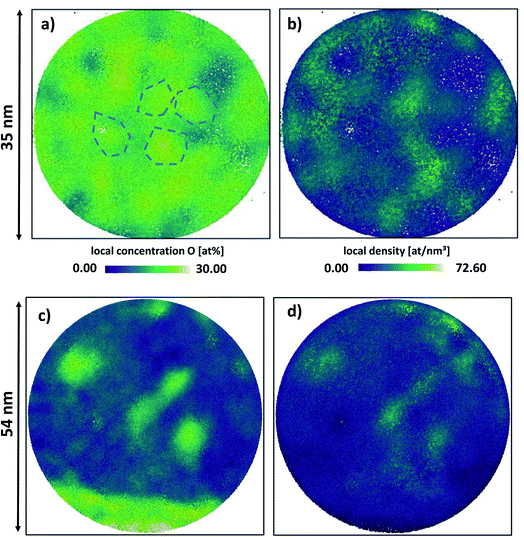
5.1 Composition and morphology
Fig. 8 is a top view on a slice from the center of the reconstruction via APT, where a local concentration (a and c) and a local atomic density analysis (b and d) was performed. The structure of the as-deposited NW displays slight fluctuations of oxygen and the atomic densities. The TEM investigations of the as-prepared NW indicated a very small grain size and a highly α-Fe polycrystalline diffraction pattern. The observation of the composition and density fluctuations in Fig. 8a and b might be due to the very small grain found within the NW. Furthermore, grain boundaries are usually only detectable by changes of the chemical contrast, i.e. segregation of solute atoms to the interface and/or differences in atomic densities.71 For pure crystalline materials, poles and zone lines are distinctive features and a break in the symmetry corresponds to a grain boundary. These imply always a lower atomic density. In this study, higher oxygen content corresponds to denser regions and vice versa. The size of the oxygen depleted regions has been determined to be (3.3 ± 1.7) nm, which would correspond to a very small grain size and which is very close to the grain size evaluated by TEM (2.7 ± 0.9) nm. Moreover, it has also been verified that the NWs in the as-prepared state contain oxygen and the overall oxygen content amounts to 20–27.5 at% (see Sec. 4.1.1), which agrees well with the content determined by TEM-EDS (approximately 22.4 at%).In the annealed case, the results of the APT and TEM analysis partially differ. While the TEM analysis indicates crystalline α-Fe, Fe3O4 and in minority of Fe2O3 phases, the APT analysis measures an oxygen content of 28.6 at% for the precipitates, while the measured oxygen content in the matrix is found to be less than 3 at% (see also Sec. 4.1.2). This oxygen content (28.6 at%) is still far off from the content that can be expected from the crystal structure of Fe2O3 or Fe3O4 (60 at% and 57 at% respectively), while the matrix consists of almost pure Fe (see Fig. 4).
It is difficult to quantify the actual content of gaseous species like oxygen and nitrogen in the atom probe since measurement artifacts can lead to loss of these species. This loss depends on many factors, for example, the laser wavelength, the laser energy, and the sample temperature.72 To avoid premature fracturing of the specimen, base temperature and laser energy were increased. Furthermore, the geometry of the wire is rather unfavorable for the removal of heat leading to an increase of the base temperature73–75 and thus evaporation in between the laser pulses, which results in the measured thermal tails. To expand on this issue, analyzing the density distribution of the annealed NW (see Fig. 8c and d), the precipitates display regions of increased density in comparison to the matrix. As a possible, but a not exclusive explanation of the loss in oxygen and the corresponding high density regions may be derived from the fact that iron oxides may have a lower evaporation threshold than the surrounding matrix. Therefore, iron oxides evaporate readily and mostly undetected, resulting in a concave curvature at the surface of the particle during field evaporation. As a consequence, trajectory aberrations lead to regions of increased atomic densities in the reconstructed volume.76,77 To conclude, even though the exact oxygen content could not be determined accurately for the evolved precipitates by using APT, it is obvious that the annealed NW consists of oxygen rich phases implying a strongly inhomogeneous structure.
5.2 Structural considerations for the initial- and annealed state
Based on the results given in Secs. 4.1 and 4.2, it could be said that the investigated NWs, irrespective to the thermal treatment, consists of α-Fe and iron-oxide phases with different morphologies and as a result of the fabrication, an additional outer shell formation. The TEM analysis given in Sec. 4.2 confirmed that NWs are fabricated together with a shell formation consisting of Pt nanoparticles embedded in a carbon precursor. However, this shell has not been measured by the atom probe due to the fact that the field of view in the atom probe is smaller than the wire diameter, therefore, only a part of this shell might have been measured.As a result of the annealing, a large elongated grain on the outer edge of the core of the wire indicated an additionally developed iron-oxide shell without any Pt content detected via APT. The measured thickness of this shell corresponds to about 13 nm at the widest point in the reconstruction. In reality, the shell thickness may additionally fluctuate, since the density (see Fig. 8d) fluctuates as well. Furthermore, the existence of the thin oxide shell is further supported qualitatively by the analysis of TEM-EDS (see Fig. 5l), however, quantitative analysis on the thickness of the oxide shell cannot be conducted accurately. Additionally, APT results also demonstrated precipitates inside the core region, which precipitates are also confirmed by the inhomogeneities in the oxygen EDS signal in the TEM analysis and have most probably an Fe3O4 structure, similar to the thin oxide shell, as concluded from the measured diffraction patterns (see Fig. 5g). To bring this summary to a conclusion, the initial homogeneous core–shell structure in the as-deposited state evolves to a double-shelled structure with a precipitated core region as illustrated by the schematic in Fig. 9.
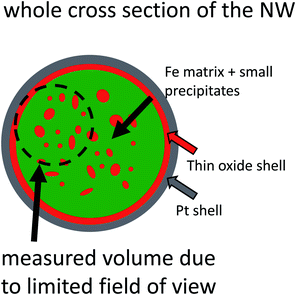 | ||
| Fig. 9 Schematic cross-section of the annealed NW and the probed volume due to limited field of view in APT analysis. | ||
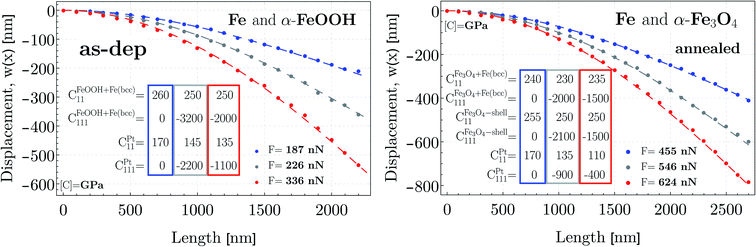
Consequently, based on our findings in terms of the results by using TEM, EDS, APT and the employed electrodeposition method, the actual structure of the NW can be determined in order to apply the most appropriate elastic constants used as initial parameters in the fitting procedure (see plotted results in Sec. 4.3). In the as-deposited state, shown in Fig. 2b, the homogeneous distribution of Fe with a slight fluctuation of O amounts to about 24 ± 4% – O and 76 ± 4% – Fe content in average throughout the whole NW. During the electrodeposition, the most likely phase to be formed beside the bcc iron is iron hydroxide.78–83 This phenomenon can also be confirmed that α-Fe cannot take up 24% of oxygen. Furthermore, since no further crystalline structure than the bcc Fe is detected (see Fig. 5), an amorphous FeOOH phase is most likely present and distributed finely, since it could not be resolved by APT either (cf.Fig. 2). Therefore, to calculate the volume fraction of a pure Fe and a pure FeOOH hydroxide region, we take into account the mass densities of ρFe = 7.87 g cm−3, ρFeOOH = 4.25 g cm−3 and the atomic weights of AFer = 55.85 g mol−1, AOr = 16 g mol−1. Assuming that only theses two constituents build the structure initially and the oxygen content in average equals to 24% (Fe-76%), the calculated volume fractions are about 60% and 40% for the Fe and the FeOOH hydroxide, respectively. Consequently, the applied Young's modulus can be approximated to Ecore = 243 ± 25 GPa by using the Voigt–Reuss model with respect to the average of the upper-, and lower bound case employing moduli as Eα-Fe = 230 ± 20 GPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 and Eα-FeOOH = 265 ± 30 GPa.78 Regarding the platinum shell, the measured thickness, as a general production feature, is taken as of 23 ± 3 nm as determined from Fig. 5. The corresponding Young's modulus is 174 ± 10 GPa.84
78 and Eα-FeOOH = 265 ± 30 GPa.78 Regarding the platinum shell, the measured thickness, as a general production feature, is taken as of 23 ± 3 nm as determined from Fig. 5. The corresponding Young's modulus is 174 ± 10 GPa.84
After annealing, the structure of the NW is significantly changed by forming an additional shell in the previously defined core region and developed by additional precipitates. The precipitates have most probably a stoichiometry close to Fe3O4 similar to the newly formed inner shell. The chemical composition of the shell and precipitates is also confirmed indirectly via TEM shown in Fig. 5. Based on the findings of the APT measurement demonstrated in Fig. 3, the shell formation can be characterized with an average thickness of about 10 ± 3 nm. In previous studies, authors presented that the annealing of a region consisting of FeOOH hydroxide at 500 °C for 2 hours in the presence of carbon, resulted in the transformation of the FeOOH into Fe3O4.85 Investigating the results performed via APT (see Fig. 3a) and additionally taking into account the ingredients of the bath used for the electrodeposition listed in Sec. 3.1.1, the measured carbon content partially originates from the applied acidic environment through the electrodeposition. Consequently, the presence of carbon facilitates the Fe3O4 to be formed with different morphologies (shell + precipitates) in the core region. As a result of the temperature test, not only the grain structure changed in both the core and the shell region, but the previously defined core has become a new core–shell formation. Furthermore, the Fe–Fe3O4 core–shell structure is further equipped with the outer platinum shell (thickness is about 21 ± 3 nm; see Fig. 5) forming finally a double-shelled NW. To expand on this, as mentioned earlier in Sec. 4.1.2, the measured concentrations determine an almost pure Fe prevalence around the precipitates. Moreover, in order to calculate the volume fractions of the newly formed precipitates, we used the results from the EDS measurements conducted prior to and after the annealing treatment which revealed constant overall atomic fractions. As a consequence, the volume fractions of the different formations (pure Fe – matrix; Fe3O4 – precipitate and shell) can be determined. Assuming an average 10 nm thickness of the newly formed Fe3O4 shell, 51 nm (see Sec. 4.3) as the radius of the newly defined core of the NW, and using the mass density of ρFe3O4 =5.17 g cm−3 together with the aforementioned atomic weights of Fe and O, the constant 24 ± 4% O overall content implies volume fractions of a pure Fe matrix and a total volume of Fe3O4 precipitates to be about 74% and 26% respectively determined exclusively for the newly formed core. This relative fractions can then be used for employing it in the Voigt–Reuss model with respect to the average of the upper-, and lower bound case with moduli as Eα-Fe = 230 ± 20 GPa (ref. 78) and Eα-Fe3O4 = 262 ± 12 GPa.78,86 Finally, the applied effective Young's modulus is approximated to Eanncore = 240 ± 22 GPa. Finally, all the calculated physical parameters together with the geometrical features of the NWs are tabulated in Table 2.
5.3 Nonlinear deflection
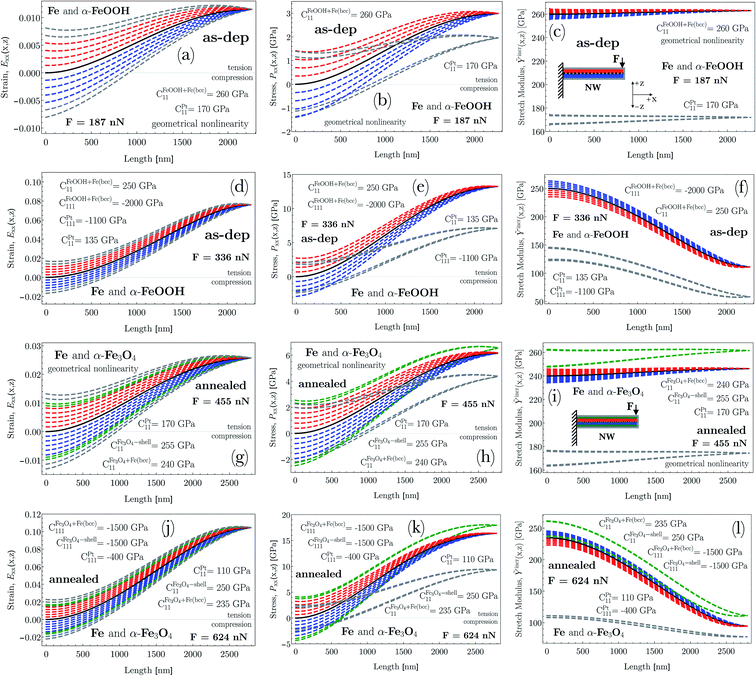
As shown in Fig. 7, the increasing applied force for a NW with an aspect ratio of about 18–20 resulted in specific experimental deflection curves (filled circle). Before annealing, from a force of F = 187 nN to 336 nN, whereas after annealing, from a force of F = 455 nN to 624 nN, the deflection does indicate a nonlinear behavior featured by an effective maximum displacement at the free end ranging from about 220 nm to 555 nm, and about 425 nm to 790 nm, respectively. By solving the differential equation given in eqn (5) in Sec. 2 equipped additionally with the effective bending modulus given in eqn (8), theoretical deflection curves in the case of F = 187 nN and F = 455 nN were determined by applying quadratic geometrical-, while in the other applied forces, both quadratic geometrical and mechanical approximation (the former case can be identified as Linear–NonLinear problem in which the deformation is relatively large, with a Hookean material response). By utilizing the least-squares method with the boundary conditions of w(0) = 0 and ∂xw(0) = 0, the determined shape of w(x) suggests for E1 and E2 as being positive and negative, respectively. It is worth noting here that in cases of F = 336 nN (as-dep.) and F = 624 nN (annealed), the numerically determined deflection curves deviate slightly from the measured data points. As a consequence, at higher exerted forces, the non-diagonal components of the G–L strain tensor may not be excluded for an appropriate description of the nonlinear deflection.As indicated by Fig. 5a and d, the as-deposited state implies an α-Fe- and an Fe-oxide dominated material property where the significant amount of oxygen can only be situated in a disordered manner (see Secs. 4.1 and 4.2). Eα-Fe+α-FeOOH1 is found to be almost constant in the range of 250 to 260 GPa in the course of the increasing applied force, while EPt1 fitting parameter decreased significantly from 170 to 135 GPa (E1 = C11, Eα-Fe+α-FeOOHbulk,RT = 243 GPa, EPtbulk,RT GPa; see Sec. 5.2). After annealing, 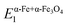 and
and 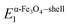 has remained in the range of 230 to 240 GPa and 250 to 255 GPa (Eanncore = 240 GPa,
has remained in the range of 230 to 240 GPa and 250 to 255 GPa (Eanncore = 240 GPa, 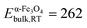 GPa; see Sec. 5.2), respectively, with increasing force suggesting, similarly to the initial state, that the proposed volume fractions of the prevailing phases may describe a realistic structure consisting of an α-Fe type- and an Fe3O4 oxide phase. After the thermal treatment, the EPt–ann1 fitting parameter also decreases drastically from 170 to 110 GPa as the NW is exerted with higher forces. To develop this point further, the approximated third-order elastic constants (E2 = C111) in the as-deposited state, at higher forces, also indicate that the elastic behavior changes moderately with increasing force, while in the annealed state, this feature is captured only at the outer platinum shell. As one of the major results, the magnitude of the third (III) and fourth term (IV) in eqn (5) in Sec. 2 considerably contributes to the calculated moment, M. We note here that the magnitudes of the fitting parameter E1 and E2 may depend on the effect of the aspect ratio on which the strength and deformation mechanism may depend (cf.Ref. 87).
GPa; see Sec. 5.2), respectively, with increasing force suggesting, similarly to the initial state, that the proposed volume fractions of the prevailing phases may describe a realistic structure consisting of an α-Fe type- and an Fe3O4 oxide phase. After the thermal treatment, the EPt–ann1 fitting parameter also decreases drastically from 170 to 110 GPa as the NW is exerted with higher forces. To develop this point further, the approximated third-order elastic constants (E2 = C111) in the as-deposited state, at higher forces, also indicate that the elastic behavior changes moderately with increasing force, while in the annealed state, this feature is captured only at the outer platinum shell. As one of the major results, the magnitude of the third (III) and fourth term (IV) in eqn (5) in Sec. 2 considerably contributes to the calculated moment, M. We note here that the magnitudes of the fitting parameter E1 and E2 may depend on the effect of the aspect ratio on which the strength and deformation mechanism may depend (cf.Ref. 87).
5.4 Non-linear strain analysis in terms of Exx
In Fig. 10a and d, the G–L strain in the as-deposited state is demonstrated for the applied forces of F = 187 nN and F = 336 nN, while for the annealed case shown in Fig. 10g and j, the G–L strain plotted for the forces of F = 455 nN and F = 624 nN. Middle line of the NW shown in the inset of Fig. 10c and i that separates the upper (red) and bottom (blue) parts is to help emphasize the evolving strain behavior with respect to the x and z coordinates. As an exception, the z-values regarding the platinum shell, and in the case of after annealing, the inner shell is visualized by gray (Pt–shell) and green (inner shell) colors irrespective of the sign of z. In Fig. 10a, d, g and j, strains referring to the upper part of NW as a function of z is plotted in such a manner to be envisaged at discrete values of z with an increment of 10 nm. At the bottom region, the plot goes in a similar manner. At z = 0, where only the membrane strain is taken into account (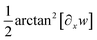 , cf. eqn (S2) in Sec. 1.1 in ESI†), the strain is illustrated by a black solid line. It is noteworthy to mention that at F = 187 nN and F = 455 nN, the NW deflects nonlinearly in terms of geometry up to ε = 1.2% (2.65%) without any mechanical nonlinearity. Strain at the highest applied force, Fas-dep. = 336 nN (Fannealed = 624 nN), however, exhibits an enormous relative displacement with an amount of 7.9% (10.5%) meaning that the elastic regime is more than an order of magnitude broader compared to that of the bulk ferritic counterpart (e.g. Δεferriteelastic ≈ 0.2%). On the other hand, the result for the as-deposited NW may consistent with earlier findings on single-crystal Fe3Pt NWs, where the elastic limit turned out to be about 6.8% due to second-order-like structural transformation.88 This structural transformation may occur during the deflection via a stress-driven redistribution of the carbon atoms. Furthermore, if dislocations are less present initially in the material, a considerably larger elastic strain is achievable as has been demonstrated in nanosized specimens89 and some whiskers (≈4%).90,91 Moreover, the FeOOH phase as a result of the relative fast electrodeposition, and the carbon-rich platinum shell by nature may take up an amorphous state facilitating a deformation mechanism through short-range order (SRO) structures in a sense of evolving different packing densities during deformation.92 In case of the annealed structure, the prevailing mayor ordered structure of Fe3O4 and the minor Fe2O3 may also play a role in inhibiting the movement of dislocations because the Burgers vector is large in the ordered structure.
, cf. eqn (S2) in Sec. 1.1 in ESI†), the strain is illustrated by a black solid line. It is noteworthy to mention that at F = 187 nN and F = 455 nN, the NW deflects nonlinearly in terms of geometry up to ε = 1.2% (2.65%) without any mechanical nonlinearity. Strain at the highest applied force, Fas-dep. = 336 nN (Fannealed = 624 nN), however, exhibits an enormous relative displacement with an amount of 7.9% (10.5%) meaning that the elastic regime is more than an order of magnitude broader compared to that of the bulk ferritic counterpart (e.g. Δεferriteelastic ≈ 0.2%). On the other hand, the result for the as-deposited NW may consistent with earlier findings on single-crystal Fe3Pt NWs, where the elastic limit turned out to be about 6.8% due to second-order-like structural transformation.88 This structural transformation may occur during the deflection via a stress-driven redistribution of the carbon atoms. Furthermore, if dislocations are less present initially in the material, a considerably larger elastic strain is achievable as has been demonstrated in nanosized specimens89 and some whiskers (≈4%).90,91 Moreover, the FeOOH phase as a result of the relative fast electrodeposition, and the carbon-rich platinum shell by nature may take up an amorphous state facilitating a deformation mechanism through short-range order (SRO) structures in a sense of evolving different packing densities during deformation.92 In case of the annealed structure, the prevailing mayor ordered structure of Fe3O4 and the minor Fe2O3 may also play a role in inhibiting the movement of dislocations because the Burgers vector is large in the ordered structure.
In a bending test, the bending- and membrane strain usually compete. Irrespective to the applied force, at x = 0, the G–L strain, Exx ranges symmetrically in the range of (i) −0.008 to +0.008 (F = 187 nN) and −0.0185 to +0.0185 (F = 336 nN), (ii) −0.012 to +0.012 (F = 455 nN) and −0.023 to +0.023 (F = 624 nN) with increasing/decreasing z. At the highest applied force, the broad range may be treated as being already non-linear. At x = 0, as a result of annealing, the generated strain falls into a somewhat broader range than that of the corresponding initial state. This contribution is purely bending strain, significantly large at higher force at the clamped end. To expand on this point, at small, increasing x values, the overall strain is characterized by a strongly convex regime, which relates to the membrane strain added to the diminishing bending strain (e.g. narrowing red/blue bands in Fig. 10). After the convex regime, the strictly increasing membrane strain becomes decreasing inducing a strongly concave regime and it develops with a concomitant reduction of the prevailing bending strain. As a result, when x approaches the free end, the drastically escalating membrane strain governs the overall strain. Consequently, the regions under the middle line closer to the clamped end is still characterized by compression, however, further from this end, the overall strain becomes tensile as a function of z. At larger applied forces, this phenomenon becomes even more striking. On the contrary, the upper region above the middle line is always characterized by tension. To sum up, the asymmetry originating from the competing strain contributions represents a considerable sensitivity to the signed ratios of the local membrane- and bending strains.
The applied method may be an underestimation of the real deformation at higher strains. However, in respect of the applied assumptions, the overall strain is found to be appropriately described by the applied model confirmed by the accuracy of the shape of the generated deflection curves, shown in Fig. 7 by fitting them to the experimental data. As a possible, but a more cumbersome description of the strain behavior, the Green–Lagrange strain (see eqn (S2) in ESI†) could be approximated by taking higher-order terms in the Taylor expansion of the displacement field. This is, however, out of the scope of the present study.
5.5 Non-linear stress analysis in terms of Pxx
As a general feature, the stresses at x = 0 as a function of z ranges in a symmetric way, for example, between (i) Pxx = −3 GPa and +3 GPa (F = 336 nN; as-dep. – core) whereas the corresponding range broadens to that of Pxx = −4.15 GPa and +4.18 GPa (F = 624 nN; annealed – core ⊕ inner shell). Regarding the platinum shell, the corresponding range is somewhat lower than that of the core. Additionally, the determined nonlinear stress (see Fig. 10e and k), in the case of the core (as-dep.)/core ⊕ inner-shell reaches a considerably high magnitude of Pxx ≈ +13 GPa and Pxx ≈ +16 − +17.5 GPa at F = 336 nN and F = 624 nN, respectively, still in the elastic regime. Similarly, the Pt shell can be characterized by a maximum stress of about Pxx ≈ +7 GPa and Pxx ≈ +9 GPa at F = 336 nN and F = 624 nN, respectively. It is worth noting that the yield strength of e.g. an iron-based superalloy strengthened by nanotwins and nanoprecipitates is in the range of 1130–1420 MPa.93 Furthermore, these results are in the range of that related to perfect single-crystalline Cu NWs, where the elastic limit was found to be about 5.8 GPa.94 The slightly higher results may be attributed to the fact that the prevailing grain size can vary in the range of the NWs' diameter (demonstrated in Sec. 4.2) and their morphology also determines the mechanical property.The different contributions of both membrane and bending strain (cf. eqn (S2) in Sec. 1.1 in ESI†) to the stress distribution as a function of z causes the zero stress axis to be shifted along the x axis. This implies an initial bending-, then later a tension-dominated response developed along the NW. At z = 0, the membrane stress plays a role exclusively (black solid line). This aspect is consistent with the diminishing contribution of bending strain with a concomitant evolving strain of the beam axis due to rotation (cf.Fig. 10a, d, g and j).
Another surprising phenomenon, shown in Fig. 10a, b, d, e, g, h, j and k pairwise, is that for all four given force levels, the strain vanishes completely at a certain position of x with a concomitant reducing stress even though the beam undergoes moderately large deformation. As shown in eqn (S9) in ESI,† the Pxx stress function contains additional terms, for example, 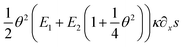 , as compared to a stress function determined by applying a linear approximation both in geometry and mechanics. As a consequence, these terms do account for the nonlinear stress and strain phenomena.
, as compared to a stress function determined by applying a linear approximation both in geometry and mechanics. As a consequence, these terms do account for the nonlinear stress and strain phenomena.
5.6 Stretch modulus, second- and third-order elastic constants
In the case of a study of nonlinear elastic response of an isotropic material, Ỹincr plays a crucial role in order to reflect softening (or stiffening) in a material as a function of a varying elastic nonlinear strain. As shown in Fig. 10c, f, i and l, the incremental stretch modulus reflects a varying elastic response along the NW. As a general feature, at lower exerted forces (Fig. 10c and i), the stretch modulus deviates slightly from the determined Young's modulus, however, it does vary along the NW. On the contrary, at larger applied forces (Fig. 10f and l), Ỹincr decreases drastically with increasing strain. The drastic reduction in stretch modulus is the consequence of the third-order polynomial approximation of the strain energy density function.The strain energy density, U, limiting the nonlinear features to the third order, and revisiting the aforementioned relation for Sxx mentioned in Sec. 1.2 in ESI,† it gives rise to the equation and relations as
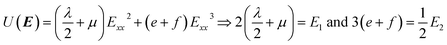 | (11) |
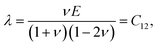 | (12) |
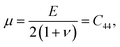 | (13) |
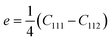 | (14) |
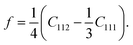 | (15) |
Since the system is assumed to be isotropic, the Cauchy relation 2C44 = C11 − C12 is always fulfilled. Revisiting the given assumptions in Sec. 2, the negligible change of the cross-sectional dimensions implies that the Poisson's ratio can be assumed to be about or slightly below than one third, ν < 1/3. Therefore, the parameters E1 and E2 can finally be approximated to E1 = C11 = E and E2 = C111.
The determined coefficients of the linear and quadratic term in the stress–strain relation are found to be decreasing in the as-deposited state as CFeOOH+Fe(bcc)11 = 260 ⇒ 250 GPa, CPt11 = 170 ⇒ 135 GPa and CFeOOH+Fe(bcc)111 = 3200 ⇒ −2000 GPa, CPt111 = 2200 ⇒ −1100 GPa. As a result of the thermal treatment, the linear coefficients of the newly-formed core and inner-shell slightly vary in the range of 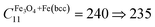 GPa,
GPa, 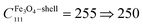 GPa, while the linear term of Pt and the quadratic terms of each phase indicate a considerable reduction as CPt11 = 170 ⇒ 110 GPa,
GPa, while the linear term of Pt and the quadratic terms of each phase indicate a considerable reduction as CPt11 = 170 ⇒ 110 GPa, 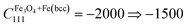 GPa,
GPa, 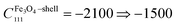 GPa and CPt111 = 900 ⇒ −400 GPa as a function of the applied force. Additionally, the determined moduli and effective moduli are in the range of that of the bulk counterparts or of that calculated from them. This strongly indicates that the existence of the different types of oxides and their relative volume fractions can determine an effective Young's modulus derived from the individual bulk Young's moduli. To elaborate further, based on the fitted elastic constants, two, mechanically different groups of material can be distinguished. The first group belonged to the newly formed core and inner-shell, consists of a more ordered, crystalline α-Fe and Fe3O4 with a small amount of Fe2O3 phase transformed from the so-called mixture of an α-Fe and FeOOH phases. This group possesses a constant mechanical behavior in a linear sense, but from a quadratic point of view, they indicate some sensitivity to a softer aspect. The slightly softer feature may be attributed to the still prevailing amorphous content derived from the initial FeOOH phase (fast electrodeposition). To expand on this issue, the linear and the quadratic elastic constants of the mixture of the α-Fe and FeOOH phase in the as-deposited state shows a slightly varying elastic property. Similarly, the carbon-enriched Pt shell behaves consistently in both the as-deposited- and annealed case, where the elastic constants are significantly reduced as the applied force gradually increases.
GPa and CPt111 = 900 ⇒ −400 GPa as a function of the applied force. Additionally, the determined moduli and effective moduli are in the range of that of the bulk counterparts or of that calculated from them. This strongly indicates that the existence of the different types of oxides and their relative volume fractions can determine an effective Young's modulus derived from the individual bulk Young's moduli. To elaborate further, based on the fitted elastic constants, two, mechanically different groups of material can be distinguished. The first group belonged to the newly formed core and inner-shell, consists of a more ordered, crystalline α-Fe and Fe3O4 with a small amount of Fe2O3 phase transformed from the so-called mixture of an α-Fe and FeOOH phases. This group possesses a constant mechanical behavior in a linear sense, but from a quadratic point of view, they indicate some sensitivity to a softer aspect. The slightly softer feature may be attributed to the still prevailing amorphous content derived from the initial FeOOH phase (fast electrodeposition). To expand on this issue, the linear and the quadratic elastic constants of the mixture of the α-Fe and FeOOH phase in the as-deposited state shows a slightly varying elastic property. Similarly, the carbon-enriched Pt shell behaves consistently in both the as-deposited- and annealed case, where the elastic constants are significantly reduced as the applied force gradually increases.
The reduction of the elastic constants of the initial core and outer shell formation may tie in with the amorphous nature of their constitutive FeOOH and Pt phases, respectively. Even after annealing at 350 °C for 20 hours, the majority of the Pt phase is still amorphous, since the recrystallization temperature of Pt is above 500 °C. The mechanical properties and their evolution during elastostatic bending of amorphous alloys are closely related to the degree of disorder which can be related to the atomic packing density in terms of short-range order atomic clusters.96–98 In an elastostatic deformation process, as a general principle, the fractions of the densely packed polyhedra, such as (0,0,12,0) and (0,1,10,2), decrease with increasing strain, while the fractions of the loosely packed polyhedra, such as (0,3,6,4), increase.92 Therefore, the enhancement of the deformation is considered to happen with a concomitant development of the increased degree of disorder, i.e., excess free volume, which is associated with an increase in the average interatomic spacing, resulting in a lowering of the atomic bonding force. Consequently, the lowering Young's modulus of the bent NWs arise due to this increase in interatomic spacing.
The beneficial higher-order approximation of the strain energy function clearly confirms that the material possesses a relatively stiffer response to the external force compared to that of the as-deposited state. This relatively stiffer aspect e.g. in the case of the core region, is well-visualized in Fig. 10f and l as the stretch modulus decreases in both cases to approximately the same extent (≈140 GPa), but in the case of the annealed state with larger evolved strain (≈11%) determined along the NW. At z = 0, illustrated by a black solid line, the stretch modulus is based on only the membrane stress and strain. Consequently, at higher applied loads (F = 336/624 nN) close to the free end of NW, the approximated 7.9%/10.5% strain gives rise to a drop of the stretch modulus from about Ỹincr =250/235 GPa to Ỹincr = 110/95 GPa, respectively. Furthermore, the almost purely axial strain with its evolving magnitude to 7.9%/10.5% implies that the nonlinear mechanical contribution to the elastic response develops drastically causing a significant reduction in the stretch modulus.
Additionally, it is worth mentioning that the elastic modulus is sensitive to the geometric shape, size, morphology, crystal orientation, point defects, or different oxygen/hydrogen concentration. These factors significantly influence the bonding strength and the periodicity of the lattice and hence the elastic moduli. Moreover, relating to what was mentioned earlier, the relative fast deposition compared to epitaxial growth, may cause an initially high defect density in the NWs. In most cases, the factor of surface enlargement impacts also the mechanical properties leading to an improvement in adhesive strength. Therefore, the mechanical characteristics of the surface of a nanowire influences its overall mechanical properties. Beside the numerous qualitative factors, the proposed model is also sensitive to the determined cross-sectional dimension of the NWs. Based on the terms in eqn (5) consisting of moments of inertia, the determined radius impacts the final results of the second and third elastic moduli. Consequently, the determined elastic constants, the incremental stretch modulus and the nonlinear stress quantify to a maximum of 15% experimental error.
6 Conclusions
In this study, we provide explicitly a bending moment function with terms accounting for the linear, quasi-linear, geometrical, and finally mechanical non-linearity as a global feature of moderately large elastic deformation. We apply the method to experimental data generated by NWs with multiple Fe-oxide substances under different concentrated loadings. The major findings can now be summarized as the followings:(1) The experimental results do indicate the robustness and relevance of APT analysis in the field of 1D objects by revealing a significant change from a homogeneous to an inhomogeneous structure inside the NWs and a concomitant existence of a thin oxide shell which would not be apparent by means of TEM analysis.
(2) During the thermal test, compositional partitioning between phases as α-Fe, α-Fe3O4 and Fe2O3 in diffusional solid–solid phase transformations may take place with a concomitant distinct grain growth in the NWs. Additionally, a nanoscale ordering of the evolving phases is also confirmed by TEM-EDS analysis, and together with the results supported by APT led to a considerable change in the description of the elastic material properties.
(3) Confirming the necessity of nonlinear elasticity, no fitting parameters were found to be appropriate to characterize the deflection curves at higher applied forces except when higher-order approximation in both geometry and mechanics are utilized.
(4) The existence of the amorphous phase of the Pt shell and the FeOOH constituent of the core can be characterized by a reduction of the second- and third-order elastic constants with increasing force. This implies a significant increase in the degree of disorder through the relative increase of the fractions of loosely packed polyhedra to the densely packed ones.
(5) Strains at higher applied forces (F = 336/624 nN) at the free end exhibit an enormous relative displacement with an amount of 7.9%/10.5% meaning that the elastic regime, more than an order of magnitude broader compared to that of the bulk counterpart.
(6) The determined non-linear stress can gain a considerably high magnitude of Pxx = +17.5 GPa at F = 624 nN still in the elastic regime.
(7) The incremental stretch modulus, Ỹincr, at higher applied loads (F = 336/624 nN), reflect a considerable softening in the core region as a function of a varying elastic nonlinear strain. Close to the free end of NW, the approximated 7.9%/10.5% strain gives rise to a drop of the stretch modulus from about Ỹincr = 250/235 GPa to Ỹincr = 110/95 GPa, respectively. Additionally, the Pt shell possesses a similar behavior with increasing strain. This indicates a strong dependence of the stretch modulus on the varying Green–Lagrange strain along the NW.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors are grateful for Prof. Dr Guido Schmitz for the fruitful scientific discussions about both the theoretical and experimental considerations. The authors gratefully acknowledge funding by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) within the collaborative research center (CRC) 1333 (project number 358283783) and within a further dedicated project (DFG-SCHM 1182/19-2). The used FIB instrument was jointly funded by DFG and the Baden-Württemberg-Stiftung (INST41/982-1 FUGG).References
- A. Heidelberg, L. Ngo, B. Wu, M. Phillips, S. Sharma, T. Kamins, J. Sader and J. Boland, Nano Lett., 2006, 6, 1101–1106 CrossRef CAS.
- Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, H. Yan, F. Kim and H. Yan, Adv. Mater., 2003, 15, 353–389 CrossRef CAS.
- M. Chang, C. Chung, J. Deka, C. Lin and T. Chung, Nanotechnology, 2008, 19, 025710 CrossRef CAS.
- S. Lee, C. Tekmen and W. Sigmund, Mater. Sci. Eng., A, 2005, 398, 77–81 CrossRef.
- Z. Ye, H. Zhu, Y. Zheng, W. Dong and B. Chen, Mater. Sci. Eng., A, 2015, 641, 281–289 CrossRef CAS.
- Y. Sui, R. Skomski, K. Sorge and D. Sellmyer, Appl. Phys. Lett., 2004, 84, 1525–1527 CrossRef CAS.
- J. Zhang, Y. Wang, H. Ji, Y. Wei, N. Wu and B. Zuo, J. Catal., 2005, 229, 114–118 CrossRef CAS.
- H. Zeng, J. Li, J. Liu, Z. Wang and S. Sun, Nature, 2002, 420, 395–398 CrossRef CAS.
- R. Wu, J. Qu and Y. Chen, Water Res., 2005, 39, 630–638 CrossRef CAS.
- Z. Sun, H. Yuan, Z. Liu, B. Han and X. Zhang, Adv. Mater., 2005, 17, 2993–2997 CrossRef CAS.
- P. Wu, W. Wang, Y. Huang, H. Sheu, Y. Lo and T. Tsai, Chem.–Eur. J., 2007, 13, 3878–3885 CrossRef CAS.
- I. Cesar, A. Kay, J. Gonzalez Martinez and M. Grätzel, J. Am. Chem. Soc., 2006, 128, 4582–4583 CrossRef CAS.
- G. Ji, S. Tang, B. Xu, B. Gu and Y. Du, Chem. Phys. Lett., 2003, 379, 484 CrossRef CAS.
- Y. W. Yang, G. W. Meng, C. H. Liang, G. Z. Wang and L. D. Zhang, Chem. Phys. Lett., 2001, 339, 174 CrossRef.
- H. R. Khan and K. Petrikowski, J. Magn. Magn. Mater., 2002, 249, 458 CrossRef CAS.
- R. Skomski, H. Zeng and D. J. Sellmyer, J. Magn. Magn. Mater., 2002, 249, 175 CrossRef CAS.
- D. E. Perea, J. E. Allen, S. J. May, B. W. Wessels, D. N. Seidman and L. J. Lauhon, Nano Lett., 2006, 6, 181–185 CrossRef CAS.
- N. Panev, A. Persson, N. Sköld and L. Samuelson, Appl. Phys. Lett., 2003, 83, 2238 CrossRef CAS.
- M. Miller, Atom Probe Tomography: Analysis at the Atomic Level, Kluwer Academic/Plenum, New York, 2000 Search PubMed.
- K. Yoon, J. Hyun, J. Connell, I. Amit, Y. Rosenwaks and L. Lauhon, Nano Lett., 2013, 13, 6183–6188 CrossRef CAS.
- C. Zeiner, A. Lugstein, T. Burchhart, P. Pongratz, J. Connell, L. Lauhon and E. Bertagnolli, Nano Lett., 2011, 11, 3108–3112 CrossRef CAS.
- S. Zhang, E. Hemesath, D. Perea, E. Wijaya, J. Lensch-Falk and L. Lauhon, Nano Lett., 2009, 9, 3268–3274 CrossRef CAS.
- T. Cohen-Karni, D. Casanova, J. Cahoon, Q. Qing, D. Bell and C. Lieber, Nano Lett., 2012, 12, 2639–2644 CrossRef CAS.
- C.-Y. Wang, C.-L. Kuo, C.-P. Liu, T.-Y. Wang, R.-K. Zheng and S. Ringer, J. Nanosci. Nanotechnol., 2011, 11, 10182–10186 CrossRef CAS.
- L. Mancini, Y. Fontana, S. Conesa-Boj, I. Blum, F. Vurpillot, L. Francaviglia, E. Russo-Averchi, M. Heiss, J. Arbiol, A. Fontcuberta, I. Morral and L. Rigutti, Appl. Phys. Lett., 2014, 105, 243106 CrossRef.
- M. Heiss, Y. Fontana, A. Gustafsson, G. Wust, C. Magen, D. Oregan, J. Luo, B. Ketterer, S. Conesa-Boj, A. Kuhlmann, J. Houel, E. Russo-Averchi, J. Morante, M. Cantoni, N. Marzari, J. Arbiol, A. Zunger, R. Warburton, I. Fontcuberta and A. Morral, Nat. Mater., 2013, 12, 439–444 CrossRef CAS.
- D. Rudolph, S. Funk, M. Döblinger, S. Morkötter, L. Hertenberger, S. nad Schweickert, S. Becker, J. Matich, M. Bichler, D. Spirkoska, I. Zardo, J. Finley, G. Abstreiter and G. Koblmüller, Nano Lett., 2013, 13, 1522–1527 CrossRef CAS.
- C. Zheng, J. Wong-Leung, Q. Gao, H. Tan, C. Jagadish and J. Etheridge, Nano Lett., 2013, 13, 3742–3748 CrossRef CAS.
- R. Lawitzki, S. Hassan, L. Karge, J. Wagner, D. Wang, J. von Kobylinski, M. Krempaszky, C. Hofmann, R. Gilles and G. Schmitz, Acta Mater., 2019, 163, 28–39 CrossRef CAS.
- R. Kolli, R. Wojes, S. Zaucha and D. Seidman, Int. J. Mater. Res., 2008, 99, 513–527 CrossRef CAS.
- A. Heinrich, T. Al-Kassab and R. Kirchheim, Mater. Sci. Eng., A, 2003, 353, 92–98 CrossRef.
- O. Hellman, J. Vandenbroucke, J. Rüsing, D. Isheim and D. Seidman, Microsc. Microanal., 2000, 6, 437–444 CrossRef CAS.
- R. Kolli and D. Seidman, Microsc. Microanal., 2007, 13, 272–284 CrossRef CAS.
- F. Danoix and P. Auger, Mater. Charact., 2000, 44, 177–201 CrossRef CAS.
- M. Kuzmina, M. Herbig, D. Ponge, S. Sandlöbes and D. Raabe, Science, 2015, 349, 1080–1083 CrossRef CAS.
- M. Miller, Microsc. Res. Tech., 2006, 69, 359–365 CrossRef CAS.
- C. Wang, Y. Hu, C. Lieber and S. Sun, J. Am. Chem. Soc., 2008, 130, 8902–8903 CrossRef CAS.
- E. Gil-Santos, D. Ramos, J. Martinez, M. Fernandez-Regulez, R. Garcia, A. San Paulo, M. Calleja and J. Tamayo, Nat. Nanotechnol., 2010, 5, 641 CrossRef CAS.
- G. Stan, S. Krylyuk, A. V. Davydov, I. Levin and R. Cook, Nano Lett., 2012, 12, 2599 CrossRef CAS.
- R. J. Young, M. V. Moore, Dual-Beam (FIB-SEM) Systems in, Introduction to Focused Ion Beams: Instrumentation, Theory, Techniques and Practice, ed. L. A. Giannuzzi and F. A. Stevie, Springer, US, Boston, MA, 2005, p. 247. Search PubMed.
- G. Jing, H. Duan, X. Sun, Z. Zhang, J. Xu, Y. Li, J. Wang and D. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235409 CrossRef.
- Y. Kim, K. Son, I. Choi, I. Choi, W. Park and J. Jang, Adv. Funct. Mater., 2011, 21, 279 CrossRef CAS.
- H. Zhan and Y. Gu, Comput. Mater. Sci., 2012, 55, 73–80 CrossRef CAS.
- Y. Gao, F. Wang, T. Zhu and J. Zhao, Comput. Mater. Sci., 2010, 49, 826–830 CrossRef CAS.
- W. Liang and M. Zhou, Proc. Inst. Mech. Eng., Part C, 2004, 218, 599–606 CrossRef CAS.
- G. Csiszár, L. Balogh, A. Misra, X. Zhang and T. Ungár, J. Appl. Phys., 2011, 110, 043502 CrossRef.
- G. Csiszár, Mater. Sci. Eng., A, 2014, 609, 185–194 CrossRef.
- Y. Chen, G. Csiszár, J. Cizek, X. Shi, C. Borchers, Y. Li, F. Liu and R. Kirchheim, Metall. Mater. Trans. A, 2016, 47, 726–738 CrossRef CAS.
- E. Huang, G. Csiszár, Y. Lo, B. Clausen, Y. Huang, W. Lee, T. Ungár and P. Liaw, Adv. Eng. Mater., 2012, 14, 902–908 CrossRef CAS.
- B. Jóni, T. Al-Samman, S. Chowdhury, G. Csiszár and T. Ungár, J. Appl. Crystallogr., 2013, 46, 55–62 CrossRef.
- M. Máthis, G. Csiszár, J. Capek, J. Gubicza, B. Clausen, P. Lukás, A. Vinogradov and S. Agnew, Int. J. Plast., 2015, 72, 127–150 CrossRef.
- M. Máthis, J. Gubicza, G. Csiszár, J. Capek, B. Clausen, V. Sima and P. Lukás, Acta Phys. Pol., A, 2015, 128, 700–703 CrossRef.
- G. Csiszár, A. Misra and T. Ungár, Mater. Sci. Eng., A, 2011, 528, 6887–6895 CrossRef.
- G. Csiszár, K. Pantleon, H. Alimadadi, G. Ribárik and T. Ungár, J. Appl. Crystallogr., 2012, 45, 61–70 CrossRef.
- J. Gubicza, L. Farbaniec, G. Csiszár, T. Sadat, H. Couque and G. Dirras, Mater. Sci. Eng., A, 2016, 662, 9–15 CrossRef CAS.
- G. Dirras, D. Tingaud, G. Csiszár, J. Gubicza, H. Couque and F. Mompiou, Mater. Sci. Eng., A, 2014, 601, 48–57 CrossRef CAS.
- Y. Chen, G. Csiszár, J. Cizek, S. Westerkamp, C. Borchers, T. Ungár, S. Goto, F. Liu and R. Kirchheim, Metall. Mater. Trans. A, 2013, 44, 3882–3889 CrossRef CAS.
- Y. Chen, G. Csiszár, J. Cizek, C. Borchers, T. Ungár, S. Goto and R. Kirchheim, Scr. Mater., 2011, 64, 390–393 CrossRef CAS.
- W.-H. Xu, L. Wang, Z. Guo, X. Chen, J. Liu and X.-J. Huang, ACS Nano, 2014, 9, 241–250 CrossRef.
- G. Csiszár, M. Schellenberger and G. Schmitz, Nanoscale, 2020, 12, 731 RSC.
- M. Jacob, R. Lawitzki, W. Ma, C. Everett, G. Schmitz and G. Csiszár, Nanoscale Adv., 2020, 2, 3002–3016 RSC.
- P.-O. Chen, J. McKittrick and M. Meyers, Prog. Mater. Sci., 2012, 57, 1492–1704 CrossRef CAS.
- M. Destrade, M. Gilchrist and G. Saccomandi, J. Acoust. Soc. Am., 2010, 127, 2759–2763 CrossRef.
- L. Dorfmann and R. Ogden, Proc. R. Soc. A, 2017, 473, 20170311 CrossRef.
- R. Ogden, Non-Linear Elastic Deformation, Dover Publication, New York, 1997 Search PubMed.
- L. Mihai and A. Goriely, Proc. R. Soc. A, 2017, 473, 20170607 CrossRef.
- R. Schlesiger, C. Oberdorfer, R. Würz, G. Greiwe, P. Stender, M. Artmeier and G. Schmitz, Rev. Sci. Instrum., 2010, 81, 043703 CrossRef.
- P. Stender and I. Balla, Inspico High Resolution Analysis, Scito V1.40, http://inspico.de, accessed, 27-November-2019 Search PubMed.
- P. Stadelmann, Microsc. Microanal., 2003, 9, 60–61 CrossRef.
- C. Rueden, J. Schindelin, M. Hiner, B. DeZonia, A. Walter, E. Arena and K. Eliceiri, BMC Bioinf., 2017, 18, 529 CrossRef.
- B. Gault, M. P. Moody, J. M. Cairney and S. P. Ringer, Atom probe microscopy, Springer Science & Business Media, 2012, p. 160 Search PubMed.
- M. Bachhav, R. Danoix, F. Danoix, B. Hannoyer, S. Ogale and F. Vurpillot, Ultramicroscopy, 2011, 111, 584–588 CrossRef CAS.
- J. H. Bunton, J. D. Olson, D. R. Lenz and T. F. Kelly, Microsc. Microanal., 2007, 13, 418–427 CrossRef CAS.
- L. Arnoldi, A. Vella, J. Houard and B. Deconihout, Appl. Phys. Lett., 2012, 101, 153101 CrossRef.
- T. F. Kelly, A. Vella, J. H. Bunton, J. Houard, E. P. Silaeva, J. Bogdanowicz and W. Vandervorst, Curr. Opin. Solid State Mater. Sci., 2014, 18, 81–89 CrossRef CAS.
- M. Miller and M. Hetherington, Surf. Sci., 1991, 246, 442–449 CrossRef CAS.
- F. Vurpillot, A. Bostel and D. Blavette, Appl. Phys. Lett., 2000, 76, 3127–3129 CrossRef CAS.
- H. Guo and A. Barnard, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094112 CrossRef.
- K. Chung, K. Kim, S. Han and H. Lee, J. Electrochem. Soc., 2005, 152, C560 CrossRef CAS.
- H. Antony, S. Peulon, L. Legrand and A. Chaussé, Electrochim. Acta, 2004, 50, 1015 CrossRef CAS.
- P. Refait and J.-M. Génin, Corros. Sci., 1993, 34, 797 CrossRef CAS.
- S. Drissi, P. Refait, M. Abdelmoula and J.-M. Génin, Corros. Sci., 1995, 37, 2025 CrossRef CAS.
- J.-M. Génin, A. Olowe, P. Refait and L. Simon, Corros. Sci., 1996, 38, 1751 CrossRef.
- A. Darling, Platinum Met. Rev., 1966, 10, 14–19 CAS.
- J. Wang, L. Li, C. Wong, L. Sun, Z. Shen and S. Madhavi, RSC Adv., 2013, 3, 15316 RSC.
- H. Reichmann and S. Jacobsen, Am. Mineral., 2004, 89, 1061–1066 CrossRef CAS.
- P. Peng, H. Sun, A. Gerlich, W. Gou, Y. Zhu, L. Liu, G. Zou, C. Singh and N. Zhou, Acta Mater., 2019, 173, 163–173 CrossRef CAS.
- T. Fukuda and T. Kakeshita, Scr. Mater., 2013, 69, 89–91 CrossRef CAS.
- J. Greer and J. De Hosson, Prog. Mater. Sci., 2011, 56, 654–724 CrossRef CAS.
- S. Brenner, J. Appl. Phys., 1959, 27, 1484 CrossRef.
- S. Brenner, Science, 1958, 128, 569 CrossRef CAS.
- K.-W. Park, C.-M. Lee, M. Wakeda, Y. Shibutani, M. Falk and J.-C. Lee, Acta Mater., 2008, 56, 5440–5450 CrossRef CAS.
- B. Zhang, F. Yan, M. Zhao, N. Tao and K. Lu, Acta Mater., 2018, 151, 310–320 CrossRef CAS.
- Y. Yue, P. Liu, Z. Zhang, X. Han and E. Ma, Nano Lett., 2011, 11, 3151–3155 CrossRef CAS.
- L. Landau and E. Lifschitz, Theory of Elasticity, Butterworth Heinemann, Oxford, 1986 Search PubMed.
- F. Albano and M.-L. Falk, J. Chem. Phys., 2005, 122, 154508 CrossRef.
- K.-W. Park, J.-I. Jang, M. Wakeda, Y. Shibutani and J.-C. Lee, Scr. Mater., 2007, 57, 805–808 CrossRef CAS.
- J. C. Lee, K. W. Park, K. K. Kim, E. Fleury, B. J. Lee, M. Wakeda and Y. Shibutani, J. Mater. Res., 2007, 22, 3087 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed theoretical consideration in terms of nonlinear elasticity. See DOI: 10.1039/d0na00919a |
| ‡ Effective length is defined as the length between the clamped end point and the point at the NW where the force measurement tip touched it. |
| This journal is © The Royal Society of Chemistry 2020 |