Two-dimensional polar metal of a PbTe monolayer by electrostatic doping†
Tao
Xu
 *a,
Jingtong
Zhang
b,
Yuquan
Zhu
a,
Jie
Wang
*a,
Jingtong
Zhang
b,
Yuquan
Zhu
a,
Jie
Wang
 *b,
Takahiro
Shimada
*b,
Takahiro
Shimada
 c,
Takayuki
Kitamura
c and
Tong-Yi
Zhang
c,
Takayuki
Kitamura
c and
Tong-Yi
Zhang
 *a
*a
aMaterials Genome Institute, Shanghai University, Shanghai 200444, China. E-mail: xutao6313@shu.edu.cn; zhangty@shu.edu.cn
bDepartment of Engineering Mechanics, School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China. E-mail: jw@zju.edu.cn
cDepartment of Mechanical Engineering and Science, Kyoto University, Nishikyo-ku, Kyoto 615-8540, Japan
First published on 15th August 2020
Abstract
Polar metals characterized by the simultaneous coexistence of a polar structure and metallicity have been a long-sought goal due to the promise of novel electronic devices. Developing such materials at low dimensions remains challenging since both conducting electrons and reduced dimensions are supposed to quench the polar state. Here, based on first-principles calculations, we report the discovery of a non-centrosymmetric polar structure in two-dimensional (2D) metallic materials with electrostatic doping, even though ferroelectricity is unconventional at the atomic scale. We revealed that the PbTe monolayer is intrinsically ferroelectric with pronounced out-of-plane electric polarization originating from its non-centrosymmetric buckled structure. Moreover, the polar distortions can be preserved with carrier doping in the monolayer, which further enables the doped PbTe monolayer to act as a 2D polar metal. With an effective Hamiltonian extracted from the parametrized energy space, we found that the special elastic-polar mode interaction is of great importance for the existence of robust polar instability (i.e., soft phonon mode associated with polar distortion) in the doped system. The application of this doping strategy is not specific to the present crystal, but is rather general to other 2D ferroelectrics to bring about the fascinating non-centrosymmetric metallic state. Our findings thus change the conventional knowledge in 2D materials and will facilitate the development of multifunctional materials in low dimensions.
New conceptsAtomic-scale polar metals characterized by the coexistence of ferroelectric distortions and metallicity hold promise for novel technological paradigms. However, such materials have not yet been realized since both conducting electrons and reduced dimensions are supposed to quench ferroelectricity. Here, we successfully achieved a breakthrough of these two physical limits for ferroelectricity, and demonstrated a new strategy for ultimately thin polar metals by carrier doping in two-dimensional materials. Combined with first-principles calculations and an effective Hamiltonian model, we revealed that the PbTe monolayer has intrinsic ferroelectricity whose ferroelectric distortions exhibit great compatibility with mobile carriers due to the special elastic-polar mode interaction. We also found that this doping strategy can be applied to a class of similar 2D ferroelectric materials to bring about the fascinating metallic ferroelectricity. The present work not only uncovers a new mechanism for the coexistence of normally incompatible states of matter but also presents an easy and general approach to develop 2D polar metals. |
Introduction
Polar metals with the coexistence of metallicity and polar structure are of significant interest in both fundamental science and application fields.1–3 From the conventional point of view, a polar state can only exist in insulating or semiconducting materials because the static internal fields arising from dipolar orders are fully screened out by conduction electrons in metals. This common belief was challenged by the first experimental observation of a centrosymmetric-to-noncentrosymmetric structural transition in metallic LiOsO3,4 which suggests the possibility of coexisting ferroelectric-like structure and metallicity. Since then, enormous efforts have been devoted to identifying and designing new systems with these seemingly contra-indicated characteristics. For instance, polar metals were achieved by interface engineering in oxide heterostructures.5,6 Some other polar metals were also proposed by doping well-established ferroelectric materials, such as BaTiO37 and PbTiO3.8,9With the fast-growing development of next-generation nanoelectronic devices, two-dimensional (2D) layered materials including graphene, silicene, phosphorene, and transition metal dichalcogenides have stimulated tremendous attention and research efforts.10–16 They are endowed with a plethora of novel properties and physical phenomena, and show promising potential in applications of nanoscale electronic and optoelectronic devices, and energy storage and conversion technologies.17–20 Very recently, a few 2D materials have been experimentally demonstrated or theoretically proposed to have non-trivial intrinsic ferroelectricity,21–29 although the depolarization field is significantly enhanced at the nanoscale and is believed to suppress electric polarization in common ferroelectrics. Despite the tremendous progress, however, polar metal in atomistic 2D materials is rarely explored, since both conducting electrons and reduced dimensions are supposed to quench ferroelectricity. The discovery of new 2D polar metals and the underlying mechanism will not only unveil novel physics associated with them, but also promote the development of nanodevices.
Here, we predict that the PbTe monolayer with electrostatic doping is a polar metal based on first-principles calculations. Although the PbTe monolayer has not been synthesized yet, a few atomic layer PbTe has been successfully grown in experiments.21 Monolayer PbTe and its analogues have attracted a lot of theoretical attention for their fascinating physical properties.30–34 We will demonstrate that the monolayer exhibits spontaneous polarization owing to its non-centrosymmetric buckled geometry. Moreover, the polar distortion shows a great compatibility with excess electrons, which can be introduced either intentionally or unintentionally in practice.35–38 This leads to non-centrosymmetric metallicity in the carrier-doped PbTe monolayer.
The theoretical calculations were performed within density functional theory (DFT) using the VASP package.39,40 The Perdue–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA) was adopted as the exchange–correlation functional. The projected augmented wave (PAW) method was used for the electron–ion interactions with a plane wave cutoff energy of 400 eV. The Brillouin zone was sampled using a 15 × 15 × 1 Monkhorst–Pack k-point mesh for the unit cell. A vacuum region of 30 Å normal to the monolayer was set to avoid any undesirable interactions between the neighboring monolayers due the periodic boundary conditions. The structures were fully relaxed until the energy change was less than 10−6 eV and the forces on each atom were less than 0.001 eV Å−1. The finite displacement method as implemented in the Phonopy package41 was used to calculate the phonon spectrum of the PbTe monolayer. In addition, Ab initio molecular dynamics (AIMD) simulation with the NVT ensemble and Nosé–Hoover thermostat were employed to assess the thermal stability of the PbTe monolayer. Carrier doping was modeled by adding or removing electrons in the system compensated with uniform background charges. An effective Hamiltonian model was built to elucidate the energy contributions from different interactions that stabilize the ferroelectric phase. The details of the effective Hamiltonian can be found in the ESI.†
Results and discussion
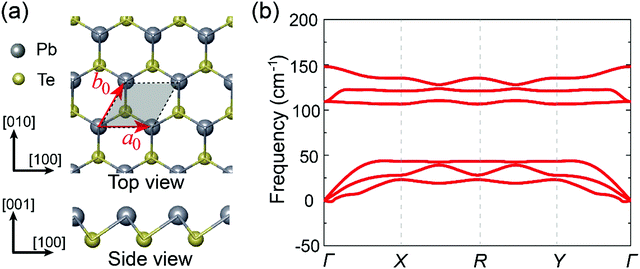
The crystal structure of bulk PbTe is characterized by rocksalt-type structure with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. In its monolayer form, existing reports indicate that PbTe is in a square shape with (space group P4mm)33 or without (space group Pmmm) buckling,32 while recent high-throughput calculations42 suggest that the buckled trigonal geometry (space group P3m1) is the stable structure. Here, our phonon dispersion calculations reveal that the buckled square and flat square structures are dynamically unstable because of the existence of a soft mode in the Brillouin zones (see Fig. S1, ESI†). Energetics of the buckled square and flat square structures are 0.25 eV f.u.−1 and 0.41 eV f.u.−1 higher than that of the P3m1 trigonal structure, respectively, which also indicates the P3m1 trigonal structure to be the ground state structure. A schematic view of the trigonal structure after full relaxation is presented in Fig. 1a. In this geometry, the PbTe monolayer consists of two atoms in a primitive unit cell and each Pb (Te) atom has a three-fold coordination with Te (Pb) atoms. The equilibrium in-plane lattice constants are a0 = b0 = 4.33 Å and the buckling value u, i.e., the displacement between the Pb and Te atoms along the (001) direction, is 1.69 Å, which is consistent with the previous calculations.42
m space group. In its monolayer form, existing reports indicate that PbTe is in a square shape with (space group P4mm)33 or without (space group Pmmm) buckling,32 while recent high-throughput calculations42 suggest that the buckled trigonal geometry (space group P3m1) is the stable structure. Here, our phonon dispersion calculations reveal that the buckled square and flat square structures are dynamically unstable because of the existence of a soft mode in the Brillouin zones (see Fig. S1, ESI†). Energetics of the buckled square and flat square structures are 0.25 eV f.u.−1 and 0.41 eV f.u.−1 higher than that of the P3m1 trigonal structure, respectively, which also indicates the P3m1 trigonal structure to be the ground state structure. A schematic view of the trigonal structure after full relaxation is presented in Fig. 1a. In this geometry, the PbTe monolayer consists of two atoms in a primitive unit cell and each Pb (Te) atom has a three-fold coordination with Te (Pb) atoms. The equilibrium in-plane lattice constants are a0 = b0 = 4.33 Å and the buckling value u, i.e., the displacement between the Pb and Te atoms along the (001) direction, is 1.69 Å, which is consistent with the previous calculations.42
The phonon spectrum of this structure is presented in Fig. 1b. It is evident that the studied monolayer is free from any imaginary-frequency modes within the entire Brillouin zone, which is a clear signature of its dynamic stability. We also calculated the cohesive energy of the PbTe monolayer Ec = EPbTe − EPb − ETe, with EPbTe, EPb and ETe being the total energies of the unit cell of the PbTe monolayer, isolated Pb atom and Te atom, respectively. The obtained cohesive energy is −5.60 eV, indicating the energetic favorability of the formation of the monolayer configuration. In addition, the mechanical stability of the monolayer is assessed by calculating the elastic constants of the crystal. The derived independent elastic constants are: C11 = 5.8 GPa, C22 = 5.8 GPa, C12 = 0.2 GPa, and C44 = 2.1 GPa. Obviously, the monolayer structure satisfies the mechanical stability of Born criteria of 2D materials,45i.e., C11C22 − C122 > 0 and C11, C22, C44 > 0. It is also necessary to check whether the monolayer can retain a stable structure at finite temperature. To this end, we performed AIMD simulations at a temperature of 300 K. As illustrated in Fig. S2 (ESI†), the total energy of the studied crystal shows slight fluctuation around a certain constant value and a snapshot of the crystalline structure after 5 ps simulation shows that the monolayer remains intact. This further indicates the thermal stability of the PbTe monolayer. These results demonstrate the stability and plausibility of the PbTe monolayer.
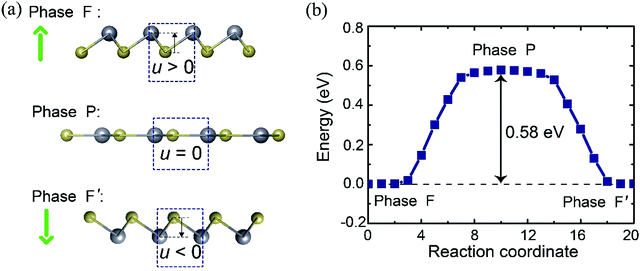
Having assessed the stability of the PbTe monolayer, we proceeded to analyze the ferroelectricity of the 2D crystal. As the PbTe monolayer consists of two kinds of atoms with different electronegativity, the atomic buckling of the monolayer breaks the spatial inversion symmetry. The lattice distortion that quantifies the symmetry breaking can be defined by the buckling parameter u, as denoted in Fig. 2a. This non-centrosymmetric structure (denoted as F phase) hints at the existence of out-of-plane electric polarization since ferroelectricity is derived from the separation of negative and positive charges. We also note that the buckled F phase can transform into an energy degenerate configuration F′ with opposite buckling value via a spatial inversion operation. As a result, F and F′ belong to the same ferroelectric phase. In comparison, when the buckling value is u = 0, we have a centrosymmetric structure (P phase) as illustrated in the middle of Fig. 2a, which forbids spontaneous polarization. This flat state with optimized in-plane lattice parameters of a′ = b′ = 5.31 Å is considered as the intermediate configuration between F and F′ phase transformation.
Our Berry phase analysis indeed confirms the existence of ferroelectricity in the buckled monolayer. The calculated spontaneous polarization is equivalent to 29.2 × 10−10 C m−1 along the [001] direction, while the in-plane components cancel out. This value is one order of magnitude larger than that in ultrathin ferroelectric SnTe (≈ 10−10 C m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21) as has been detected in the experiment. Polarization switching in this ferroelectric monolayer can be achieved by folding the direction of Pb–Te bonds. We further employed the solid-state nudge elastic band (SSNEB) method22,23 to estimate the minimum energy pathway for polarization conversion. The results are presented in Fig. 2b, in which the initial and final states are set as F and F′ phases, respectively. One can see that the energies of the buckled structures are gradually increased with increasing buckling height and the energy barrier for the transition is estimated to be about 0.58 eV. This value is the same order as those in conventional FE oxides (e.g., 0.1 to 0.2 eV f.u.−1 for PbTiO3) and other 2D ferroelectric materials.46,47 Furthermore, we applied a vertical electric field to the monolayer to directly inspect the feasibility of polarization reversal. With increasing applied electric field, the Pb atoms with positive charge gradually move down whereas the Te atoms with negative charge move up, leading to the decrease of electric polarization. The polarization direction is reverted suddenly when the electric field is larger than 30 V nm−1, which is very close to that predicted in other 2D ferroelectrics.48 All these results demonstrate that the PbTe monolayer is intrinsically ferroelectric with switchable polarization. Similar ferroelectric monolayers with out-of-plane spontaneous polarization have also been proposed very recently.46–49
21) as has been detected in the experiment. Polarization switching in this ferroelectric monolayer can be achieved by folding the direction of Pb–Te bonds. We further employed the solid-state nudge elastic band (SSNEB) method22,23 to estimate the minimum energy pathway for polarization conversion. The results are presented in Fig. 2b, in which the initial and final states are set as F and F′ phases, respectively. One can see that the energies of the buckled structures are gradually increased with increasing buckling height and the energy barrier for the transition is estimated to be about 0.58 eV. This value is the same order as those in conventional FE oxides (e.g., 0.1 to 0.2 eV f.u.−1 for PbTiO3) and other 2D ferroelectric materials.46,47 Furthermore, we applied a vertical electric field to the monolayer to directly inspect the feasibility of polarization reversal. With increasing applied electric field, the Pb atoms with positive charge gradually move down whereas the Te atoms with negative charge move up, leading to the decrease of electric polarization. The polarization direction is reverted suddenly when the electric field is larger than 30 V nm−1, which is very close to that predicted in other 2D ferroelectrics.48 All these results demonstrate that the PbTe monolayer is intrinsically ferroelectric with switchable polarization. Similar ferroelectric monolayers with out-of-plane spontaneous polarization have also been proposed very recently.46–49
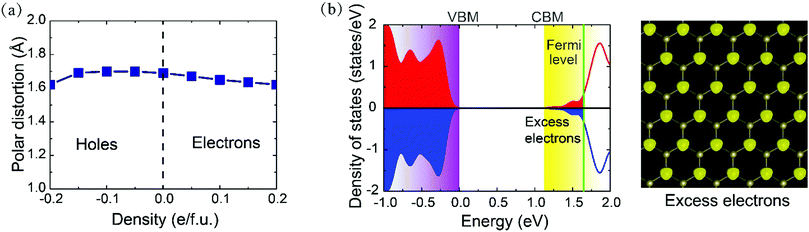
We now turn to examine the effect of electrostatic doping on its polar structure by adding or removing electrons. The range of doping density investigated in the present study is up to 0.2 e f.u.−1, corresponding to the carrier density of 1.24 × 1014 cm−2. Such kind of electron modulation for 2D materials is experimentally accessible by utilizing an electrolytic gate.43,44 The stability of the electron/hole doped PbTe monolayer has also been verified by performing the same AIMD simulations, as illustrated in Fig. S3 (ESI†) for the case of n = 0.10 e f.u.−1 as an example. Since ferroelectric polarization is ill defined in the metallic system and the Berry phase approach cannot be applied to a metal,50 we focus on the polar distortions to characterize the non-centrosymmetric phase. The variation of polar distortion in response to carrier doping density is depicted in Fig. 3a, in which positive and negative carrier densities indicate the electron and hole doping, respectively. In conventional ferroelectrics, the excess electrons are believed to be detrimental to the electric polarization due to the screening effect, thus leading to the disappearance of polar distortion for electron density beyond a certain critical value. Surprisingly, the polar distortion here in the PbTe monolayer is seen to only be marginally affected by electron doping. Although the distortion slightly decreases with electron doping, as large as d = 1.62 Å still remains when the injected electron concentration is raised to a large density of 0.20 e f.u.−1. On the other hand, the polar distortion is slightly increased with increasing hole density within a moderate doping level and then hardly changes at high doping density. Our results thus reveal that there is no critical carrier concentration for the disappearance of polar distortion in the PbTe monolayer, and the carriers do not suppress but coexist with the non-centrosymmetric state within practical doping density.
The electronic properties of the doped crystal are also analyzed to clarify the characteristics of the doped carriers. Fig. 3b presents the spin-resolved total density of states (DOS) of the electron doped PbTe monolayer at a concentration of n = 0.10 e f.u.−1, in which the spin-up and spin-down states are completely degenerate. The pristine PbTe monolayer without carrier doping is a semiconductor with a band gap of about 1.5 eV (see Fig. S4, ESI†). Nevertheless, the doping electrons introduce new occupied states and lead to the valence and conduction bands overlapping, which highlights a marked metallic character in the system. The projected DOS demonstrates that the weight at the Fermi level, i.e., the excess electrons, are primarily contributed by the s and pz orbital of Pb atoms. This can also be visualized from their squared wave functions. These delocalized free electrons contribute to electrical conduction in the system. Note that this kind of semiconductor–metal transition by electron/hole doping has also been reported in ferroelectric perovskite oxides with oxygen vacancies51 and other 2D materials utilizing an electrolytic gate.38 Similar metallic properties are also observed in the PbTe monolayer with hole doping. Thus, in sharp contrast to conventional ferroelectrics such as BaTiO3, where polar distortions and metallic conductivity are distinctly incompatible with each other, the polar instability unexpectedly persists with free carriers in the atomic PbTe layer.
This unusual interaction between polar distortion and excess electrons can be understood from the energy contributions of different interactions in the stabilization of the polar phase. We constructed an effective Hamiltonian that represents the energy change during paraelectric to polar phase transition. The parameterized Hamiltonian Etotal consists of the energy contributions from local mode self-energy Eself, short range interactions Eshort, dipole–dipole interactions Edpl, elastic-local mode interactions Eint and elastic energy Eelas, i.e.,
| Etot({u},η) = Eself({u}) + Eshort({u}) + Edpl({u}) + Eint({u},η) + Eelas(η), | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52). On the other hand, the screening effect of doping carriers for the dipole–dipole interactions and short-range interactions is reduced in the PbTe monolayer. However, they contribute to a positive energy gain in the polar structure and thus the weakening of the screening effect is not the main cause of polar instability in the PbTe monolayer. In contrast, we can find that the coupling between the elastic deformations and the local modes contributes greatly for lowering the total energy in the ferroelectric phase of the PbTe monolayer (see Fig. 4a). This strain-local mode interaction drives large compressive strain and buckling atomic structure, and thus stabilizes its ferroelectric buckled phase. Remarkably, this energy contribution is insensitive to the doping effect and is not screened by doping as illustrated in Fig. 4b for the electron doping density of n = 0.1 e f.u.−1. As a result, the polar distortions persist in the doped PbTe monolayer.
52). On the other hand, the screening effect of doping carriers for the dipole–dipole interactions and short-range interactions is reduced in the PbTe monolayer. However, they contribute to a positive energy gain in the polar structure and thus the weakening of the screening effect is not the main cause of polar instability in the PbTe monolayer. In contrast, we can find that the coupling between the elastic deformations and the local modes contributes greatly for lowering the total energy in the ferroelectric phase of the PbTe monolayer (see Fig. 4a). This strain-local mode interaction drives large compressive strain and buckling atomic structure, and thus stabilizes its ferroelectric buckled phase. Remarkably, this energy contribution is insensitive to the doping effect and is not screened by doping as illustrated in Fig. 4b for the electron doping density of n = 0.1 e f.u.−1. As a result, the polar distortions persist in the doped PbTe monolayer.
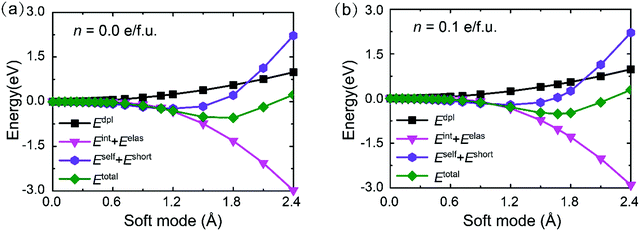 | ||
| Fig. 4 Energy contributions in the Hamiltonian during the phase transition in the PbTe monolayer at densities of (a) n = 0 and (b) n = 0.10 e f.u.−1. | ||
The above results thus demonstrate the coexistence of polar instability and excess electrons in the PbTe monolayer due to the strong elastic-local mode interactions. Although the doped monolayer PbTe structure complies with the symmetry requirements for switchable polar distortion, the polar distortion cannot be switched by a directly applied electric field due to the screening of the itinerant electrons. Note that the original concept of ferroelectric metal proposed by Anderson and Blount53 refers to a metal that possesses a polar axis, or involves the loss of a center of symmetry. However, for a material to be a truly ferroelectric, it needs to be both polar and to show a switchable electric polarization with an applied electric field. Any “ferroelectric metal” without switchable polarization, as in the case of a free carrier doped PbTe monolayer, should better be referred to as a polar metal or non-centrosymmetric metal.
Our design strategy based on the free carrier doping of the PbTe monolayer simultaneously overcomes the well-known physical limit for a polar structure imposed by the intrinsic size effect as well as the screening effects of free carriers, providing a possibility in the search of new 2D polar metals. Similar results can be anticipated for other 2D ferroelectric monolayers. A recent theoretical study predicted several 2D ferroelectric AB binary monolayers with out-of-plane polarization, including SiGe, GeSn and so forth.49 We analyzed the effect of electrostatic doping on polar distortions in these ferroelectric monolayers and found that polar distortions also resist metallization. Although different mechanisms (e.g., the lone-pair mechanism)54 or strategies (e.g., geometric design6) have also been proposed to realize bulk polar metals, the present strategy extends the concept of a polar metal to ultimately thin monolayers, which also have significant implications for the exploration of other unusual coexisting phenomena in low dimensions. Besides the conceptual significance, polar metals have the potential to exhibit and explore unique physical phenomena such as superconductivity,1,55 multiferroics,2,56 unusual optical properties,57,58 and large thermopower anisotropy,59 which provide possibilities for a plethora of innovative applications in electronics and spintronics. Our results thus also have significant technical implications for nanoscale materials or ultrahigh density integration of electronic devices owing to the ultrathin size of the proposed monolayers.
Conclusions
In summary, we predict that the carrier-doped PbTe monolayer is a 2D polar metal by using first-principles calculations. The dynamical, thermal, and mechanical stabilities of the PbTe monolayer are confirmed theoretically. The monolayer exhibits pronounced out-of-plane spontaneous polarization due to its non-centrosymmetric buckled structure. Remarkably, the polar distortions exhibit great compatibility with mobile carriers in such kind of ferroelectric monolayer attributed to the strong elastic-mode interaction. Our findings broaden the family of polar metals and lead to new types of multifunctional materials in low dimensions.Author contributions
T. X. conceived the project, designed and directed computational experiments, and wrote the entire manuscript. J. T. Z. built the effective Hamiltonian model and discussed the results. Y. Q. Z. supported the calculations. T. S. and T. K. discussed the results. J. W. and T. Y. Z. supervised the work and provided critical feedback on the manuscript. All authors read and commented on the manuscript. T. X. and J. T. Z. contributed equally to this work.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 11802169).References
- E. Bauer and M. Sigrist, Non-Centrosymmetric Superconductors: Introduction and Overview, Springer-Verlag, Heidelberg, 2012 Search PubMed.
- D. Puggioni, G. Giovannetti, M. Capone and J. M. Rondinelli, Phys. Rev. Lett., 2015, 115, 087202 CrossRef PubMed.
- N. A. Benedek and T. Birol, J. Mater. Chem. C, 2016, 4, 4000 RSC.
- Y. Shi, et al. , Nat. Mater., 2013, 12, 1024 CrossRef CAS PubMed.
- X. Z. Lu and J. M. Rondinelli, Nat. Mater., 2016, 15, 951 CrossRef CAS PubMed.
- T. H. Kim, D. Puggioni, Y. Yuan, L. Xie, H. Zhou, N. Campbell, P. J. Ryan, Y. Choi, J. W. Kim and J. Patzner, et al. , Nature, 2016, 533, 68 CrossRef CAS PubMed.
- J. Fujioka, et al. , Sci. Rep., 2015, 5, 13207 CrossRef CAS PubMed.
- T. Shimada, T. Xu, Y. Araki, J. Wang and T. Kitamura, Adv. Electron. Mater., 2017, 3, 1700134 CrossRef.
- J. X. Gu, K. J. Jin, C. Ma, Q. H. Zhang, L. Gu, C. Ge, J. S. Wang, C. Wang, H. Z. Guo and G. Z. Yang, Phys. Rev. B, 2017, 96, 165206 CrossRef.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183 CrossRef CAS PubMed.
- J. Liu, X. Qian and L. Fu, Nano Lett., 2015, 15, 2657 CrossRef CAS PubMed.
- G. R. Bhimanapati, Z. Lin and V. Meunier, et al. , ACS Nano, 2015, 9, 11509 CrossRef CAS PubMed.
- M. Wu and X. C. Zeng, Nano Lett., 2016, 16, 3236 CrossRef CAS PubMed.
- Y. Zhao, L. Lin, Q. Zhou, Y. Li, S. Yuan, Q. Chen, S. Dong and J. L. Wang, Nano Lett., 2018, 18, 2943 CrossRef CAS PubMed.
- B. Wang, Q. Wu, Y. Zhang, Y. Guo, X. Zhang, Q. Zhou, S. Dong and J. L. Wang, Nanoscale Horiz., 2019, 4, 1113–1123 RSC.
- Y. Jia, M. Zhao, G. Gou, X. C. Zeng and J. Li, Nanoscale Horiz., 2018, 3, 551–555 RSC.
- J. Pang, et al. , Chem. Soc. Rev., 2019, 48, 72 RSC.
- D. Pang, M. Alhabeb and X. Mu, et al. , Nano Lett., 2019, 19, 7443 CrossRef CAS PubMed.
- G. Xie, Z. Ju, K. Zhou, X. Wei, Z. Guo, Y. Cai and G. Zhang, npj Comput. Mater., 2018, 4, 21 CrossRef.
- Q. Zeng and Z. Liu, Adv. Electron. Mater., 2018, 4, 1700335 CrossRef.
- K. Chang, J. Liu, H. Lin, N. Wang, K. Zhao, A. Zhang, F. Jin, Y. Zhong, X. Hu, W. Duan, Q. Zhang, L. Fu, Q.-K. Xue, X. Chen and S. H. Ji, Science, 2016, 353, 274 CrossRef CAS PubMed.
- D. Sheppard, P. H. Xiao, W. Chemelewski, D. D. Johnson and G. Henkelman, J. Chem. Phys., 2012, 136, 074103 CrossRef PubMed.
- N. A. Zarkevich and D. D. Johnson, J. Chem. Phys., 2015, 143, 064707 CrossRef CAS PubMed.
- G. B. Bhandari, K. Subedi, Y. He, Z. Jiang, M. Leopold, N. Reilly, H. P. Lu, A. T. Zayak and L. Sun, Chem. Mater., 2014, 26, 5433 CrossRef CAS.
- S. Khan, Z. Jiang, S. M. Premathilka, A. Antu, J. Hu, A. A. Voevodin, P. J. Roland, R. J. Ellingson and L. Sun, Chem. Mater., 2016, 28, 5342 CrossRef CAS.
- H. Wang and X. Qian, 2D Mater., 2017, 4, 015042 CrossRef.
- S. Shen, C. Liu, Y. Ma, B. Huang and Y. Dai, Nanoscale, 2019, 11, 11864 RSC.
- C. C. Xiao, F. Wang, S. A. Yang, Y. H. Lu, Y. P. Feng and S. B. Zhang, Adv. Funct. Mater., 2018, 28, 1707383 CrossRef.
- Y. Wang, C. Xiao, M. Chen, C. Hua, J. Zou and C. Wu, et al. , Mater. Horiz., 2018, 5, 521 RSC.
- P. Z. Hanakata, A. S. Rodin, A. Carvalho, H. S. Park, D. K. Campbell and A. H. Castro Neto, Phys. Rev. B, 2017, 96, 161401(R) CrossRef.
- W. Wan, Y. Yao, L. Sun, C. C. Liu and F. Zhang, Adv. Mater., 2017, 29, 1604788 CrossRef PubMed.
- E. O. Wrasse and T. M. Schmidt, Nano Lett., 2014, 14, 5717 CrossRef CAS PubMed.
- P. Z. Hanakata, A. S. Rodin, H. S. Park, D. K. Campbell and A. H. Castro Neto, Phys. Rev. B, 2018, 97, 235312 CrossRef CAS.
- K. Kobayashi, Surf. Sci., 2015, 639, 54 CrossRef CAS.
- J. Martin, et al. , Nat. Phys., 2008, 4, 144 Search PubMed.
- I. Gierz, et al. , Nano Lett., 2008, 8, 4603 CrossRef CAS PubMed.
- X. Wang, X. Li, L. Zhang, Y. Yoon, P. K. Weber, H. Wang, J. Guo and H. Dai, Science, 2010, 324, 768 CrossRef PubMed.
- D. K. Efetov and P. Kim, Phys. Rev. Lett., 2010, 105, 256805 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246 CrossRef CAS PubMed.
- X. Xi, H. Berger, L. Forró, J. Shan and K. F. Mak, Phys. Rev. Lett., 2016, 117, 106801 CrossRef PubMed.
- Z. Chen, H. Yuan, Y. Xie, D. Lu, H. Inoue, Y. Hikita, C. Bell and H. Y. Hwang, Nano Lett., 2016, 16, 6130 CrossRef CAS PubMed.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1954 Search PubMed.
- A. Samad, H. J. Kim and Y. H. Shin, J. Phys.: Condens. Matter, 2018, 31, 045301 CrossRef PubMed.
- Z. Liu, Y. Sun and D. J. Singh, et al. , Adv. Electron. Mater., 2019, 5, 1900089 CrossRef.
- A. Chanana and U. V. Waghmare, Phys. Rev. Lett., 2019, 123, 037601 CrossRef CAS PubMed.
- D. Di Sante, A. Stroppa, P. Barone, M.-H. Whangbo and S. Picozzi, Phys. Rev. B, 2015, 91, 161401(R) CrossRef.
- R. Resta, J. Phys.: Condens. Matter, 2002, 14, R625 CrossRef CAS.
- T. Kolodiazhnyi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045107 CrossRef.
- Y. Iwazaki, T. Suzuki, Y. Mizuno and S. Tsuneyuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 214103 CrossRef.
- P. W. Anderson and E. I. Blount, Phys. Rev. Lett., 1965, 14, 217 CrossRef CAS.
- X. He and K. J. Jin, Phys. Rev. B, 2016, 94, 224107 CrossRef.
- E. Bauer, G. Rogl, X.-Q. Chen, R. T. Khan and H. Michor, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 064511 CrossRef.
- T. Xu, T. Shimada, Y. Araki, M. Mori and G. Fujimoto, et al. , npj Comput. Mater., 2019, 5, 23 CrossRef.
- V. P. Mineev and Y. Yoshioka, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 094525 CrossRef.
- V. M. Edelstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 113109 CrossRef.
- D. Puggioni and J. M. Rondinelli, Nat. Commun., 2014, 5, 3432 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00188k |
| This journal is © The Royal Society of Chemistry 2020 |