Ultra stable superatomic structure of doubly magic Ga13 and Ga13Li electrolyte†
Krista G.
Steenbergen
 *a and
Nicola
Gaston
*a and
Nicola
Gaston
 b
b
aThe MacDiarmid Institute for Advanced Materials and Nanotechnology, School of Chemical and Physical Sciences, Victoria University of Wellington, P.O. Box 600, Wellington, New Zealand. E-mail: kgsteen@gmail.com
bThe MacDiarmid Institute for Advanced Materials and Nanotechnology, Department of Physics, The University of Auckland, Private Bag 92019, Auckland, New Zealand
First published on 3rd December 2019
Abstract
We report the extreme thermal stability of the superatomic electronic structure for 13-atom gallium clusters and the Ga13Li electrolyte. Using previously-validated first-principles simulations, [K. G. Steenbergen and N. Gaston, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 161402–161405] we show that the superatomic shell progression of doubly-magic Ga13− remains stable up to 1000 K, making this cluster an ideal candidate for high-temperature applications requiring an exceptionally stable electronic structure. Using the neutral and cationic clusters for comparison, we quantify the extent to which cluster stability (geometric and electronic) is modified through addition or subtraction of a single electron. Finally, combining 13-atom gallium with lithium, we illustrate that superatomic closed-shell Ga13Li exhibits the same exceptionally high thermal stability as naked Ga13−. For technological use as a superatomic electrolyte, we demonstrate that Ga13Li has a low affinity to water as well as a low Li+ binding energy.
1. Introduction
Atomic nanoclusters, once regarded as contaminants in mass spectra experiments, now hold great promise for materials engineering. Whether in the gas phase, or as ligand or substrate-stabilized clusters, they exhibit promising size, shape and composition-tunable properties1–3 which have led to major breakthroughs in the fields of materials science, physics, chemistry, medicine and biology. The very recent addition of materials assembled from superatomic nanocluster building blocks (superatomic or cluster-assembled materials), where superatoms replace atoms or molecules, further expands the range of cluster-based technologies by allowing for fine-tuning of material properties.4–18 Two recent promising examples are: the experimentally engineered band gaps of As73− cluster-assembled materials;13 and the first two-dimensional (2D) semiconductor (1.48 eV optical band gap) composed of covalently bonded superatomic Re6Se8 clusters created last year by experimentalists at Columbia University.14 Outside of the realm of solid-state superatomic materials, other groups have been working towards creating halogen-free electrolytes composed of superatomic clusters.15–18One integral property for superatomic materials engineering is the ‘survivability’ of the superatomic state in real-world environments – i.e., far from the vacuum under which many superatoms are discovered and studied.5 For use as catalysts or electrolytes, for example, the superatomic electronic structure must remain intact even when subjected to harsh chemical and thermodynamic conditions. However, even focusing solely on the thermodynamic regime, the interplay of finite-size and finite-temperature effects remains intricate and puzzling. As discovered experimentally by Haberland et al. ∼30 years ago, finite size clusters exhibit strongly non-monotonic properties at finite temperature, whereby changing the cluster size by a single atom can dramatically change the thermodynamic response.19–23
Further complicating the problem of cluster thermodynamics, the Jarrold group discovered that small gallium clusters (∼20–93 atoms) remain solid at temperatures vastly exceeding the bulk melting temperature.26–28 Their ground-breaking work flips the normal paradigm – that small things melt at lower temperatures – completely on its head.24,25 Since melting causes a complete change in the structural and electronic properties of a cluster, their discovery held great promise if the effect could be understood and exploited for nanomaterial technologies. Recent theoretical work on these gallium clusters29–34 revealed that the greater-than-bulk melting phenomenon is driven by a unique quasi-two-dimensional (2D) structural preference in the cluster liquid phase.34 The premelted solid clusters are semiconducting and have an overall spherical shape, but they transition to a metallic liquid phase with three close-packed atomic layers.32,34 Interestingly, this liquid phase is strikingly similar to trilayer gallenene (2D metallic gallium), which we have recently discovered is thermodynamically stable up to 100 K above the bulk melting temperature.35
Despite the fact that both high temperatures and phase transitions often dramatically alter the electronic structure – and, in particular, the superatomic character – of nanoclusters, the vast majority of theoretical work on superatomic materials focuses solely on the global minimum. In order to properly investigate superatoms for technological use in non-ideal environments, it is integral to overcome this limitation. In this work, we go far beyond the ground state, focusing on the finite temperature persistence of the superatomic electronic structure of 13-atom gallium clusters. The 13-atom cluster has the potential to adopt a perfect icosahedral packing, associated with high-stability due to symmetry. Additionally, within the jellium model, the Ga13− anion has a closed superatomic 2P shell (1S21P61D102S21F142P6), meaning this cluster size has the potential to exhibit the exceptional stability endowed by both a geometric and electronic shell closing (leading to the descriptor ‘doubly-magic’).
Using density functional theory molecular dynamics (DFT-MD) simulation methods that have previously yielded excellent results29,30,32 in comparison to experimental data on gallium cluster thermodynamics,26,27 we model the three charge states, Ga13−, Ga13 and Ga13+, exploring the stability of their electronic properties, particularly their superatomic character, at high temperatures. The incremental changes in electronic structure between the charge states allow us to clearly observe the interplay of geometric and electronic structure that contributes to the extraordinary thermal stability of these small gallium nanoclusters. We also extend the simulations to the superatomic Ga13Li electrolyte, showing that the superatomic character of this ultra-stable closed-shell cluster remains unperturbed even at very high temperatures. With low lithium and water binding energies, we demonstrate that the Ga13Li superatomic cluster makes an ideal halogen-free electrolyte candidate for technologies requiring exceptional thermal stability.
2. Method
Using density functional theory (DFT) calculations, we complete cluster optimisations and molecular dynamics simulations for the three charge states of the 13-atom gallium clusters as well as the Ga13Li electrolyte. In brief overview, all calculations are performed using DFT at the Γ-point only with VASP 5.4,36–39 the GGA-PW91 exchange–correlation functional40,41 and the projector-augmented wave (PAW) method42,43 with the 4s24p1-valence gallium dataset. For all anionic and cationic simulations, we include corrections for the full dipole moment in all directions.We perform density functional theory (DFT) relaxations for each charge state of the 13-atom cluster in order to determine a low-energy starting structure for subsequent Born-Oppenheimer DFT-MD simulations. Using DFT-MD, we model the effect of temperature. The lowest-energy isomer of each charge state is used to seed 10 ps canonical (NVT) DFT-MD simulations. These canonical MD simulations are used only to equilibrate the cluster at a range of finite temperatures, including: 37 temperatures spanning 200–1540 K for Ga13−; 33 temperatures from 200–1460 K for Ga13; and 33 temperatures from 200–1620 K for Ga13+. The thermalised clusters from each canonical trajectory are then used as the initial structures in subsequent microcanonical (NVE) simulations. The average temperature of the microcanonical trajectories match those of the canonical simulations to within 20 K.
For the microcanonical simulations, we employ a parallel tempering algorithm29,44 to enhance the ergodicity of the simulations, and calculate specific heat curves by the multiple histogram (MH) method.29,45,46 Using a specific heat convergence criteria described in our previous work,29 the microcanonical simulations include 200 ps per temperature for Ga13− and Ga13, and 300 ps per temperature for Ga13+. Additional details of the parallel tempering and MH mathematical development are given in our previous works.29–34
This method has been benchmarked for gallium clusters by direct comparison to experimental results,26–28 for both the clusters29–34 and bulk gallium.34 The remarkable similarity between the detailed features of the simulated and experimental specific heat curves demonstrates the accuracy of our methods.30 Compared to experiment, we observe a consistent shift −90 K shift in the simulated melting temperatures for both the clusters30 and bulk,34 which we attribute to an energetic shift of the PW91 functional for gallium nanoclusters and bulk.
For Ga13Li, we focused solely on the thermal stability of the cluster at only 1000 K. Following 10 ps of canonical DFT-MD equilibration, we completed 200 ps of microcanonical simulation where the average temperature was 1000 K.
3. Results and discussion
3.1. 13-atom gallium
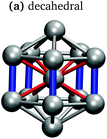
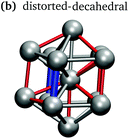
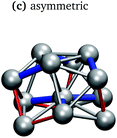
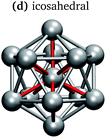
In keeping with previous simulations of small gallium clusters,29–34,47–49 the 13-atom clusters have a rich potential energy landscape with many low-lying isomers. Table 1 gives a visual summary of the 3 lowest-energy structures for each charge state. Similar to results of previous global minimum studies,48,49 we find the lowest energy of the anion and neutral clusters to be decahedral and Jahn–Teller distorted decahedral (Table 1a and b), respectively. The lowest-energy Ga13+ structure is flattened and asymmetric (Table 1c), where the overall shape is similar to the lowest energy Ga12 structure.31,48 We also include two other predominant low-lying isomers: the icosahedral and Jahn–Teller-distorted icosahedral structures (Table 1d and e). For context, ESI Fig. S1† gives a graphic summary of the cohesive energy (Ecoh) of the lowest energy 13-atom clusters compared with other gallium cluster sizes and charge states studied by our group.29–34We have also calculated the ionisation potential (IP) and electron affinities (EA), which show the expected electronic stability of a 40 electron system. Both the IP and EA increase steadily (anion to neutral to cation). Unsurprisingly, the EA for the anion is negative, while the neutral and cation are stabilised by the extra electron, which moves the neutral to a filled superatomic 2P shell and the cation closer to this shell filling. There are small variations for both the IP and EA between the different isomers of each charge state, with an apparent trend for higher symmetries leading to higher values.
It is curious that the decahedral packing schemes are preferred to icosahedral motifs, in marked difference to gallium's group-13 neighbour aluminium. Al13− adopts a perfect icosahedral structure with bonds of 2.8 Å while the neutral Al13 cluster takes on a distorted icosahedral structure.50–52 The Ga13− decahedron exhibits anisotropic bond lengths, with the rectangular-face vertical bonds shortened to 2.55 Å, centre-vertex bonds at 2.70–2.75 Å and rectangular-face horizontal bonds of 2.85 Å (Table 1a). This bonding pattern is similar to bulk α-gallium structure (optimised with the same computational parameters). However, an analysis of the electron localisation function (ELF)53 for Ga13− shows little covalency, whereas the ELF for bulk α-gallium indicates strong covalency in the short dimer bonds.31
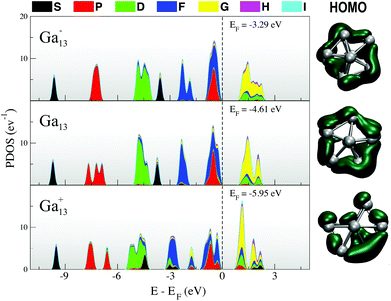
In Fig. 1, we include a visualisation of the highest occupied molecular orbital (HOMO) for each of the lowest-energy isomers, as well as an analysis of the projected density of states (PDOS), where the Kohn–Sham orbitals are projected onto the set of spherical harmonics in order to decompose the electronic structure into the different angular momentum contributions.54,55 Both the anion and neutral clusters demonstrate the classic superatomic shell progression 1S21P61D102S21F142Px (x = 5 for Ga13, x = 6 for Ga13−).56 Both have a lowest unoccupied molecular orbital (LUMO) of g angular momentum character. The P and D superatomic orbitals are clearly seen to split in response to the lowered symmetry of the neutral and cationic clusters. The neutral PDOS (Fig. 1, middle) clearly illustrates the Jahn–Teller effect, with the breaking of the 1D degeneracy observed for the anion (Fig. 1, top). The HOMO for all three charge states has a mixed f and p character. Intriguingly, the qualitative nature of the HOMO (right column, Fig. 1) for the neutral cluster is more similar to that of the cation than the anion. The layered nature of the cation HOMO illustrates that this cluster can be seen as a further-distorted, flattened version of the neutral decahedron.
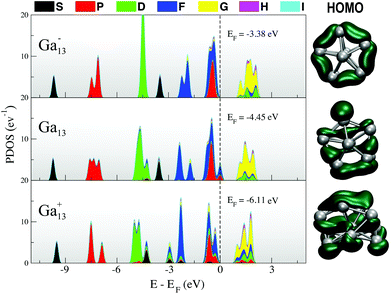 | ||
| Fig. 1 (left) Projected density of states and (right) HOMO for each of the lowest-energy 13-atom clusters. | ||
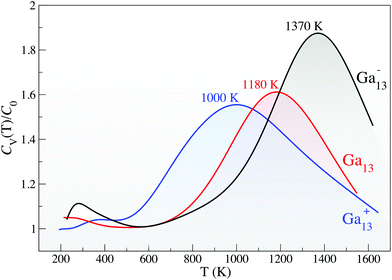
Using Born-Oppenheimer DFT molecular dynamics (DFT-MD),29,30 we investigate the finite temperature response of the 13-atom clusters. Fig. 2 gives the canonical specific heat curves, where the solid-to-liquid transition tells only part of the story. All three clusters have a remarkable greater than 1000 K melting temperature, defined by the peak in the specific heat curve (Fig. 2) and verified by an analysis of the root-mean square bond length variance (δrms, ESI Fig. S6†); however, the curious structural response of these small clusters at very high temperatures makes them even more extraordinary.
At the lowest temperatures, we consistently observe a vibrating central atom surrounded by either icosahedral or decahedral packing schemes. However, at temperatures exceeding ∼500 K, the structures manifest as a vibrating central atom (that remains central, and does not diffuse to the surface) surrounded by a shell of atoms that vibrationally reconfigure between the icosahedral and decahedral structural configurations. We note that a similar effect has been described for bi-metallic Ga19Al+ nanoparticles,57 where the central Al atom did not diffuse to the surface even at very high solid phase temperatures; however, the phenomenon is not directly comparable given the different atomic species, as well as the lack of well-defined packing for the surrounding “surface” atoms of the cluster. Here, we utilise an angular distribution function to study the packing schemes of the thermalised cluster, which show that the surface atoms maintain the pentagonal arrangements of decahedral and/or quasi-icosahedral. We note that the relative positions of the atoms remains constant – i.e., each atom's nearest-neighbour shell does not change, meaning there is no “surface diffusion” that would indicate surface melting.
Fig. 3a and b give the average structure of the Ga13− anion at both the lowest temperature and ∼1000 K, respectively. The decahedral double-pentagonal structure only vibrates at the lowest simulated temperature (Fig. 3a). For the higher-temperature structure shown in Fig. 3b, the double pentagons blur into a spherical shell of atoms, clearly illustrating that even at very high temperatures, the core–shell effect is strongly maintained. Remarkably, the radius of the shell remains nearly unaffected even at temperatures of 1000 K (Fig. 3c). Even for very high temperature solid clusters, the overall structure remains spherical. The central atom does not diffuse to the surface; however, the surface atoms reconfigure between icosahedral and decahedral positions on a sphere surrounding the central atom. The neutral cluster exhibits exactly the same structural patterns as the anion. Despite the flattened nature of the cation, it also has a similar surface degeneracy around a central atom, as demonstrated in ESI Fig. S2;† however, in that case, the pattern becomes more semi-spherical.
 | ||
| Fig. 3 The average structure (projected onto a plane) for Ga13− at (a) ∼200 K (the lowest simulated temperature) and (b) 1000 K. Panel (c) gives an overlay of the two structures, illustrating that the spherical geometry (including the radius) remains incredibly similar even at very high pre-melting temperatures. Note: In order to aid visual clarity, we utilise a simple 3D coordinate rotation prior to calculating the average projected structure shown here. This is done because the cluster structure undergoes rotations during the course of an MD trajectory, which would blur the structural features in the cumulative average structure. More details of the rotation are provided in section S1 of the ESI.† | ||
As illustrated in Fig. 4, the superatomic electronic structure is maintained even at these very high temperatures. At temperatures nearing Tm −300 K (1000 K for the anion), the orbital degeneracies begin to break; however, the clear superatomic progression of the electronic structure remains. The superatomic character of these clusters persists even to remarkably high temperatures, making them uniquely well-suited for any high-temperature technologies or reactions.
We posit that the spherical geometric shape of the clusters is dictated by the HOMO of pxyz character. This highly-symmetric orbital shape makes every atomic position degenerate. In this way, the atoms become indistinguishable so long as they occupy a pentagonal arrangement on the sphere surrounding the central atom. This “surface degeneracy” will significantly increase the configurational entropy of the solid with respect to the liquid, lowering the solid–liquid entropic difference (ΔSsl) and raising the melting temperature as
| Tm = ΔHsl/ΔSsl, | (1) |
There remain two outstanding questions regarding the interesting thermal response of these gallium clusters: (1) What phenomenon drives the melting temperature of a surface-dominated material so exceptionally high?; and (2) What is the origin of the large differences in Tm that accompanies a single-electron change in the electronic configuration?
To answer the first question, we look to the liquid state of the clusters. In addition to an increased configurational entropy in the solid state arising from the surface degeneracy, we also observe a decreased configurational entropy in the liquid state arising from a liquid configurational preference for flattened, quasi-2-dimensional (2D) liquid structure. The peak in the specific heat curve (Fig. 2) defines the temperature at which the cluster transitions from a spherical geometry with a well-defined superatomic shell progression to an elongated structure which loses its superatomic character. ESI Fig. S3, S4 and S5† give more detail to this 2D liquid, demonstrating that the average long-axis cluster dimension rises to ∼8 Å while the short-axis dimension drops to 4 Å. This result is reminiscent of the liquid structures of larger gallium cluster cations (n = 32–36), where the experimentally-measured greater-than-bulk melting temperature26–28 is driven by a liquid configurational preference for these same quasi-2-dimensional (2D) structures.34 This preference lowers the configurational entropy of the liquid in comparison to the solid, elevating the melting temperature in accordance with eqn (1).34 These 2D structures are similar to the very stable buckled-plane (010)-surface of gallium which has recently been experimentally shown to exfoliate on certain substrates from the solid–melt interface.58 Very recent work by our group demonstrates that a 2D gallenene trilayer is anomalously thermally stable, remaining solid up to 100 K above the bulk melting temperature.35 Surface layering several atomic layers thick has also been observed in experimental studies of liquid gallium.59
With the increased structural degeneracy in the solid state and decreased configurational states accessible to the liquid clusters, we have clarified how the melting temperature can exceed 1000 K for all three charge states. We look now to the second point of interest: the origin of the 180 K and 190 K differences in Tm between charge states (Fig. 2).
Comparing the electronic and geometric structure of the solid state clusters at finite temperature, we find that Ga13− and Ga13 respond nearly identically to finite temperature, while the cation is an outlier. For Ga13− and Ga13, the thermal fluctuations at finite temperature mask the small Jahn–Teller distortion observed at zero-temperature, as illustrated in Fig. 4 by the nearly identical PDOS and HOMO from finite temperature clusters. Both clusters maintain a clear superatomic orbital progression throughout the solid phase. The analysis of average cluster dimension (ESI Fig. S3†) shows that the anion and neutral clusters remain nearly spherical, with three approximately equal cluster dimensions, up to 200 K below Tm. Additional correlation analyses are included in the ESI,† illustrating that by all structural measures, the neutral and anionic clusters respond nearly identically to temperature. We can therefore be certain that the origin of the 190 K difference in Tm arises solely from the singly-occupied HOMO of the neutral in comparison to the filled HOMO of the anion, making the neutral cluster more susceptible to finite temperature destabilisation.
The cation is again an outlier, with a geometric structure that remains flattened and asymmetric throughout the solid phase. The average cation structure at a high solid-state temperature is shown in the ESI Fig. S2,† where we observe the clear core–shell flattened nature of the cluster. This structural geometry strongly mimics a pxy electronic shell configuration, where the lack of the pz lobe allows for the structural flattening. The pxy nature of the HOMO dictates the geometric properties of the cation even at very high temperatures, and the lack of the symmetrising pz orbital further destabilises the cation in comparison to the neutral cluster.
We note, however, that despite this destabilisation, the cation still exhibits exceptional thermal stability, maintaining a clear superatomic shell structure up to ∼800 K. These results doubly highlight the dominant influence of the electronic shell structure within these small metallic clusters: firstly, through the ∼190 K thermal destabilisation arising from single electron changes; secondly, by the fact that the superatomic electronic shell structure is still maintained even at very high temperatures for the 13-atom clusters, despite the geometric asymmetries introduced by the changing nature of the HOMO.
3.2. Ga13Li electrolyte
The extreme thermal stability of the 13-atom gallium cluster makes it a perfect candidate as a superatomic material for technological use. With one atom shy of a superatomic shell closing in its neutral state, a natural role for Ga13 would be as the anionic component in a salt, coupled with alkali elements such as lithium.Optimisations for the Ga13Li cluster show that the preferred binding site for the lithium atom is centred on the Ga13 decahedral's rectangular face, with little geometric distortion arising from the addition of Li. DFT calculations for the ground state energies reveal that this superatomic salt will be an ideal candidate as a halogen-free electrolyte:17 the binding between Ga13Li and H2O is only 0.79 eV; the binding between Ga13− and Li+ is only 4.16 eV (considerably lower than 4.94 eV for Al13−Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60). The dissociation energy between Ga13− and Li+ is lowest energy, with the next lowest dissociation being the division to Ga12Li and a neutral gallium atom (−4.62 eV). Previous DFT calculations for the electron affinity of Ga13 give a value of 3.35 eV.61
60). The dissociation energy between Ga13− and Li+ is lowest energy, with the next lowest dissociation being the division to Ga12Li and a neutral gallium atom (−4.62 eV). Previous DFT calculations for the electron affinity of Ga13 give a value of 3.35 eV.61
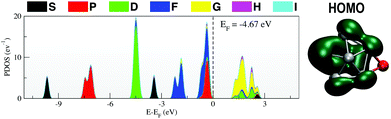
The PDOS for Ga13Li, given in Fig. 5, shows that the superatomic electronic shell structure is stabilised by the addition of the lithium atom. In fact, the PDOS matches Ga13− (Fig. 1) nearly exactly. The nature of the HOMO changes slightly from that of the naked anion.
Given the increasing interest in superatomic materials for real-world technological applications,4–6,8–11,13–18 we have also investigated the finite temperature response of Ga13Li. The 13-atom gallium core remains nearly unperturbed by the lithium atom, even at an average temperature of 1000 K (200 ps MD simulation). The 13-gallium atom core maintains a spherical shape and exhibits the same surface degeneracy as was noted for Ga13−. The lithium atom remains an adatom to the gallium sphere throughout the simulation. The superatomic electronic shell progression stays structured, even up to 1000 K. Even combined with an adatom, this cluster exhibits extraordinary thermal stability, making it an ideal halogen-free candidate for any high-temperature electrolytic applications.
4. Conclusions
Using previously-validated first-principles simulations, we demonstrate that the 13-atom gallium anion and Ga13Li salt maintain their superatomic electronic shell structure even at extreme temperatures up to 1000 K. This high thermal stability makes these clusters ideal candidates for any high-temperature applications. In particular, with low water and lithium binding energies, we show that Ga13Li is an ideal halogen-free electrolyte candidate.Ga13+, Ga13, Ga13− and Ga13Li all have exceptionally high thermal stabilities, which is endowed by a highly-degenerate solid state coupled with a quasi-2D liquid state. Using the different charge states of the 13-atom clusters, we are able to show that the structural instability introduced by changing a single-electron reduces the thermal stability of the clusters by ∼190 K. This incredible result clearly demonstrates the powerful effect of electronic structure, and has given us the unprecedented opportunity to quantify thermodynamic effect of electronic shell structure.
Finally, our results emphasise the importance of investigating cluster stability in non-idealised environments. Previous studies of superatomic shell structure have focused solely on the global minimum manifestation. By raising the temperature through first-principles MD, we have discovered that the 13-atom gallium clusters and Ga13Li electrolyte maintain their clear superatomic shell structure even at extremely high temperatures. Based on the exceptional stability of their electronic structures, we expect that these clusters will remain stable in other non-idealised environments – i.e., as building blocks within superatomic solids, in solution if protected by suitable ligands, as ad-superatoms on surfaces for catalytic applications – each of which make very interesting topics for future study.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the New Zealand eScience Infrastructure (NeSI, nesi224 and uoa49) for computational time and exceptional support. KGS gratefully acknowledges the funding and support of The MacDiarmid Institute for Advanced Materials and Nanotechnology.References
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2008, 48, 60–103 CrossRef PubMed.
- A. Cuko, A. Macià Escatllar, M. Calatayud and S. T. Bromley, Nanoscale, 2018, 10, 21518–21532 RSC.
- F. Priolo, T. Gregorkiewicz, M. Galli and T. F. Krauss, Nature, 2014, 9, 19–32 CAS.
- S. A. Claridge, A. W. Castleman Jr., S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, ACS Nano, 2009, 3, 244–255 CrossRef CAS PubMed.
- P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870 CrossRef CAS PubMed.
- J. R. Olson, K. A. Topp and R. O. Pohl, Science, 1993, 259, 1145–1148 CrossRef CAS PubMed.
- O. Lopez-Acevedo, P. A. Clayborne and H. Häkkinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035434 CrossRef.
- X. Roy, C. H. Lee, A. C. Crowther, C. L. Schenck, T. Besara, R. A. Lalancette, T. Siegrist, P. W. Stephen, L. E. Brus, P. Kim, M. L. Steigerwald and C. Nuckolls, Science, 2013, 341, 157–160 CrossRef CAS PubMed.
- A. Lebon, A. Aguado and A. Vega, Phys. Chem. Chem. Phys., 2015, 17, 28033–28043 RSC.
- Y. Song, F. Fu, J. Zhang, J. Chai, X. Kang, P. Li, S. Li, H. Zhou and M. Zhu, Angew. Chem., Int. Ed., 2015, 54, 8430–8434 CrossRef CAS PubMed.
- B. Choi, J. Yu, D. W. Paley, M. T. Trinh, M. V. Paley, J. M. Karch, A. C. Crowther, C.-H. Lee, R. A. Lalancette, X. Zhu, P. Kim, M. L. Steigerwald, C. Nuckolls and X. Roy, Nano Lett., 2016, 16, 1445–1449 CrossRef CAS PubMed.
- L. Hammerschmidt, J. Schacht and N. Gaston, Phys. Chem. Chem. Phys., 2016, 18, 32541–32550 RSC.
- M. Qian, A. C. Reber, A. Ugrinov, N. K. Chaki, S. Mandal, H. M. Saavedra, S. N. Khanna, A. Sen and P. S. Weiss, ACS Nano, 2010, 4, 235–240 CrossRef CAS PubMed.
- X. Zhong, K. Lee, B. Choi, D. Meggiolaro, F. Liu, C. Nuckolls, A. Pasupathy, F. De Angelis, P. Batail, X. Roy and X. Zhu, Nano Lett., 2018, 18, 1483–1488 CrossRef CAS PubMed.
- D. Aurbach, Z. Lu, A. Schechter, Y. Gofer, H. Gizbar, R. Turgeman, Y. Cohen, M. Moshkovich and E. Levi, Nature, 2000, 407, 724–727 CrossRef CAS PubMed.
- W. S. Tang, A. Unemoto, W. Zhou, V. Stavila, M. Matsuo, H. Wu, S.-I. Orimo and T. J. Udovic, Energy Environ. Sci., 2015, 8, 3637–3645 RSC.
- S. Giri, S. Behera and P. Jena, Angew. Chem., Int. Ed., 2014, 33, 13916–13919 CrossRef PubMed.
- O. Tutusaus, R. Mohtadi, T. S. Arthur, F. Mizuno, E. G. Nelson and Y. V. Sevryugina, Angew. Chem., 2015, 127, 8011–8015 CrossRef.
- M. Schmidt, R. Kusche, B. von Issendorff and H. Haberland, Nature, 1998, 393, 238–240 CrossRef CAS.
- M. Schmidt, R. Kusche, W. Kronmüller, B. von Issendorff and H. Haberland, Phys. Rev., 1997, 79, 99–102 CAS.
- M. Schmidt, J. Donges, T. Hippler and H. Haberland, Phys. Rev. Lett., 2003, 90, 103401 CrossRef CAS PubMed.
- H. Haberland, T. Hippler, J. Donges, O. Kostko, M. Schmidt and B. von Issendorff, Phys. Rev. Lett., 2005, 94, 035701 CrossRef PubMed.
- C. Hock, C. Bartels, S. Straßburg, M. Schmidt, H. Haberland, B. von Issendorff and A. Aguado, Phys. Rev. Lett., 2009, 102, 043401 CrossRef PubMed.
- P. Pawlow, Z. Phys. Chem., 1909, 65, 1–35 CAS.
- P. Buffat and J. P. Borel, Phys. Rev. A, 1976, 13, 2287–2298 CrossRef CAS.
- G. A. Breaux, D. A. Hillman, C. M. Neal, R. C. Benirschke and M. F. Jarrold, J. Am. Chem. Soc., 2004, 126, 8628–8629 CrossRef CAS PubMed.
- G. A. Breaux, B. Cao and M. F. Jarrold, J. Phys. Chem. B, 2005, 109, 16575–16578 CrossRef CAS PubMed.
- K. L. Pyfer, J. O. Kafader, A. Yalamanchali and M. F. Jarrold, J. Phys. Chem. A, 2014, 118, 4900–4906 CrossRef CAS PubMed.
- K. G. Steenbergen, D. Schebarchov and N. Gaston, J. Chem. Phys., 2012, 137, 144307–144312 CrossRef CAS PubMed.
- K. G. Steenbergen and N. Gaston, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 161402–161405 CrossRef.
- K. G. Steenbergen and N. Gaston, Phys. Chem. Chem. Phys., 2013, 15, 15325–15329 RSC.
- K. G. Steenbergen and N. Gaston, Chem. – Eur. J., 2014, 21, 2862–2869 CrossRef PubMed.
- K. G. Steenbergen and N. Gaston, J. Chem. Phys., 2014, 140, 064102–064107 CrossRef CAS PubMed.
- K. G. Steenbergen and N. Gaston, Nano Lett., 2016, 16, 21–26 CrossRef CAS PubMed.
- K. G. Steenbergen and N. Gaston, Chem. Commun., 2019, 55, 8872 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko and K. A. Jackson, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- F. Calvo, J. P. Neirotti and D. L. Freeman, J. Chem. Phys., 2000, 112, 10350–10357 CrossRef CAS.
- N. Metropolis and A. W. Rosenbluth, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- F. Calvo and P. Labastie, Chem. Phys. Lett., 1995, 247, 395–400 CrossRef CAS.
- U. Ojha, K. G. Steenbergen and N. Gaston, Phys. Chem. Chem. Phys., 2015, 17, 3741–3748 RSC.
- N. Drebov, F. Weigend and R. Ahlrichs, J. Chem. Phys., 2011, 135, 044314 CrossRef PubMed.
- S. Núñez, J. M. López and A. Aguado, Nanoscale, 2012, 4, 6481 RSC.
- R. Ahlrichs and S. D. Elliott, Phys. Chem. Chem. Phys., 1999, 1, 13–21 RSC.
- D. E. Bergeron, A. W. Castleman, T. Morisato and S. N. Khanna, J. Chem. Phys., 2004, 121, 10456 CrossRef CAS PubMed.
- D. E. Bergeron, A. W. Castleman, T. Morisato and S. N. Khanna, Science, 2004, 304, 84–87 CrossRef CAS PubMed.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- D. Schebarchov and N. Gaston, Phys. Chem. Chem. Phys., 2011, 13, 21109 RSC.
- D. Schebarchov and N. Gaston, Phys. Chem. Chem. Phys., 2012, 14, 9912 RSC.
- M. L. Cohen, M. Y. Chou and W. D. Knight, J. Phys. Chem., 1987, 91, 3141–3149 CrossRef CAS.
- U. Ojha, K. G. Steenbergen and N. Gaston, J. Chem. Phys., 2013, 139, 094309–094309 CrossRef PubMed.
- V. Kochat, A. Samanta, Y. Zhang, S. Bhowmick, P. Manimunda, S. A. S. Asif, A. S. Stender, R. Vajtai, A. K. Singh, C. S. Tiwary and P. M. Ajayan, Sci. Adv., 2018, 4, e1701373 CrossRef PubMed.
- M. J. Regan, E. H. Kawamoto, S. Lee, P. S. Pershan, N. Maskil, M. Deutsch, O. M. Magnussen, B. M. Ocko and L. E. Berman, Phys. Rev. Lett., 1995, 75, 2498–2501 CrossRef CAS PubMed.
- Y. J. Ko, A. Shakya, H. Wang, A. Grubisic, W. Zheng, M. Götz, G. Ganteför, K. H. Bowen, P. Jena and B. Kiran, J. Chem. Phys., 2010, 133, 124308–124307 CrossRef PubMed.
- K. Weiß, R. Köppe and H. Schnoeckel, Int. J. Mass Spectrom., 2002, 214, 383–395 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C9NR06959C |
| This journal is © The Royal Society of Chemistry 2020 |