Supramolecular cyclization of semiflexible cylindrical micelles assembled from rod-coil graft copolymers†
Liang
Gao
,
Rui
Hu
,
Pengfei
Xu
,
Jiaping
Lin
 *,
Liangshun
Zhang
*,
Liangshun
Zhang
 and
Liquan
Wang
and
Liquan
Wang
 *
*
Shanghai Key Laboratory of Advanced Polymeric Materials, Key Laboratory for Ultrafine Materials of Ministry of Education, School of Materials Science and Engineering, East China University of Science and Technology, Shanghai 200237, China. E-mail: jlin@ecust.edu.cn; lq_wang@ecust.edu.cn
First published on 12th November 2019
Abstract
Uniform toroidal micelles can be constructed via the supramolecular cyclization of semiflexible cylindrical micelles, but revealing the conditions under which the cyclization occurs and the mechanism underlying the cyclization remains a challenge. In this study, we performed Brownian dynamics simulations of the supramolecular cyclization of semiflexible cylindrical micelles formed by rod-coil graft copolymers to obtain the cyclization conditions and understand the cyclization mechanism. It was found that the balance of the bending energy of the polymer backbones with the self-attraction energy between the pendant groups on the polymer backbones plays an important role in the cyclization process. A theoretical model based on this balance is developed to explain the cyclization mechanism, and the conditions required for realizing the supramolecular cyclization are obtained. The proposed mechanism is supported by our experimental findings regarding the supramolecular cyclization of polypeptide cylindrical micelles. The cyclization conditions and the revealed mechanism can guide further preparation of uniform toroidal micelles from semiflexible cylindrical micelles in an end-to-end closure manner.
Introduction
Block copolymers are able to spontaneously self-assemble in selective solvents into aggregates with a variety of morphologies, such as spherical micelles, cylindrical micelles, and vesicles.1–3 Among these aggregates, toroidal micelles with a central internal pore have attracted considerable attention due to their unique annular geometry and potential applications, such as gene delivery and biomimetic model.4–13 Toroidal micelles are usually considered to have potential in mimicking biological systems because many transmembrane proteins, such as β-barrels and α-helical bundles, have ring-like shapes and because DNA in most bacterial phages and vertebrate sperm cells is condensed into toroidal structures with an outer diameter of approximately 100 nm.13–16Practically, the toroidal micelles reported to date can be created via two different mechanisms. In the first mechanism, toroidal micelles are spontaneously self-assembled from homogeneous solutions via nucleation and growth mechanisms, that is, spherical micelles are first formed, then grow into small disks, and finally evolve into toroids through the perforation of the disks.5,6,17–19 The more general mechanism is the end-to-end closure of rod-like or cylindrical micelles, as the toroidal micelles are essentially looped rod-like or cylindrical micelles.4,10,11,20–26 The evolution from rod-like or cylindrical micelles to toroid structures, resembling the cyclization reactions of small molecules, can be regarded as supramolecular cyclization.11 Pochan et al. revealed the origin of toroidal micelle formation and suggested that three requirements should be met to construct toroids from cylindrical micelles: high flexibility of cylinders, self-attraction of charged polymers in the corona of the cylinders, and extra end-capping energy originating from chain packing frustration.4,9 Our recent experimental observations, however, seem beyond the scope of these requirements. We found that semiflexible (not highly flexible) cylindrical micelles with rigid polymer backbones arranged parallel to the long axis of the micelle can also be bent into toroids via end-to-end closure.11 More interestingly, the immediate states of crescents can be stabilized in solution. The question then arises as to what are the requirements and mechanisms for the cyclization of semiflexible cylindrical micelles.
Theory and simulation, which are able to capture the essential features of experimental systems, can be applied to reveal the mechanism behind self-assembling systems.18,19,27–32 To this end, dissipative particle dynamics simulation,18,27 self-consistent field theory,28 and mesoscopic field-based simulation19 have been employed to investigate the formation of toroidal micelles. For example, He and Schmid conducted a mesoscopic field-based simulation on the formation of toroidal micelles in copolymer solutions and proposed a mechanism in which toroidal micelles form by a pathway that proceeds via nucleation, growth, and subsequent breakup of disk-like micelles.19 The proposed mechanism was proven by the experiments carried out by Chang et al.6 and by Pochan et al.,9 indicating the power of theoretical simulations.
In this work, we applied Brownian dynamics (BD) simulations to reveal the mechanism behind the cylinder-to-toroid transformation of semiflexible cylindrical micelles. Cylindrical micelles, curved cylinders, and toroidal micelles were observed during the cyclization (i.e., end-to-end closure) process. The effects of the rigidity of the polymer backbones and the interaction strength between the pendant groups joined at the polymer backbones on this cyclization process were examined. Furthermore, a theoretical model based on the balance of the bending energy of the backbone with the interaction energy between pendant groups was developed to clarify the cyclization conditions. The theory can well account for the simulation results. Finally, the theory and simulation studies were compared with our experimental observations. The good agreement between them further supports the proposed cyclization mechanism and conditions.
Results and discussion
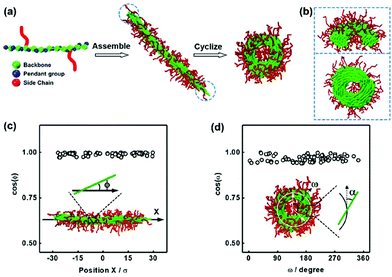
This section presents a study on the cyclization conditions and the mechanism of toroid formation from semiflexible cylindrical micelles. The cylindrical micelles are self-assembled from rod-coil graft copolymers comprising a rigid backbone with pendant groups and two flexible side chains (Fig. 1a). The architecture of the graft copolymer was chosen as Rm-g-(Cn)2, where R, C, and the subscript denote the backbone, side chain, and bead number of each block, respectively. The model of the rod-coil copolymer corresponds to the molecular structure of the polypeptide-based graft copolymers used in the experiments. The amphiphilicity of the graft copolymers was realized by setting the interaction potentials as follows: the interactions between R and R beads were modeled with an attractive Lennard-Jones (LJ) potential to describe the hydrophobicity of the backbones, and the C–C interaction and R–C interaction were modeled with a purely repulsive LJ potential to describe the hydrophilicity of the side chain and the incompatibility between the backbone and the side chain, respectively. Since the pendant groups P represent the phenyl groups of the polypeptide backbones and exhibit strong nonbonding interactions such as π–π interactions, we modeled the P–P interaction as an attractive LJ potential. The selected interaction strengths are shown in section 1 of the ESI.†The cyclization of cylindrical micelles into toroidal micelles was simulated using the following procedure (Fig. 1a). The cylindrical micelles of the R12-g-(C6)2 rod-coil graft copolymers are first formed by setting the interaction strengths εRR = 3.5ε and εPP = 1.0ε and the angle spring constant k = 20ε (a higher k corresponds to a stronger rigidity of the polymer backbone; the other parameter settings are given in section 1 of the ESI†). In our previous work, the toroidal micelles were formed through the end-to-end closure of the cylindrical micelles of poly(γ-benzyl-L-glutamate)-g-poly(ethylene glycol) (PBLG-g-PEG) graft copolymers after adding THF into the micelle solution. THF can lead to the constriction of the phenyl groups according to the circular dichroism (CD) spectra.11 To simulate this situation, we changed the parameter conditions, for example, increasing εPP to 5.0ε, to mimic the constriction of pendant groups. The change of interaction strength εPP can induce the bending and end-to-end closure of the cylindrical micelles into toroidal micelles (see Fig. 1a). We name such an end-to-end closure process a supramolecular cyclization of cylindrical micelles, which is akin to the cyclization of small molecules. The simulation results are consistent with our experimental observations.11
The structural details of the cylindrical micelles and the toroidal micelles were first examined prior to the detailed analysis of the cyclization mechanism. As shown in Fig. 1a, the cylindrical micelles consist of a core formed by the rigid backbones and a corona formed by the side chains. The rigid backbones take an ordered parallel packing in the micellar cores, while the micelle ends cannot be well covered by the side chains, resulting in the two partially exposed ends (see the marked region in Fig. 1a). The exposure of the micelle cores to the solution environment leads to extra end-capping energy. This end-capping energy can be eliminated through the end-to-end closure of the cylindrical micelles to form toroids11 or polymerization to form nanowires in an end-to-end connection manner.33 Due to the short-range interaction between the two end-caps, the elimination of extra end-capping energy only occurs as the two end-cap approach, for example, at the moment of end-to-end closure during cyclization.11Fig. 1b shows the cross-sectional views along the diameter and the circumference of the toroidal micelle. Clearly, the rigid backbones in the core of the toroid micelles were bent. The orientations of the rigid backbones in the cores of cylindrical micelles are characterized by orientation angles ϕ of the rigid backbones (the definition of orientation angles is given in section 1.3 of the ESI†). As shown in Fig. 1c, the values of cos(ϕ) are close to 1.0, which means that the rigid backbones are approximately parallel to the long axis of the cylindrical micelles. For the toroidal micelles, the orientation angle α is defined as the angle between the direction vector of the backbones and the tangent vector of the toroids. The values of cos(α) shown in Fig. 1d suggest that the rigid backbones are parallel to each other along the contour of the toroidal micelles.
Thermodynamic conditions for supramolecular cyclization
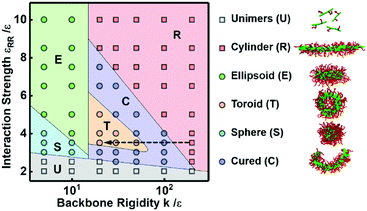
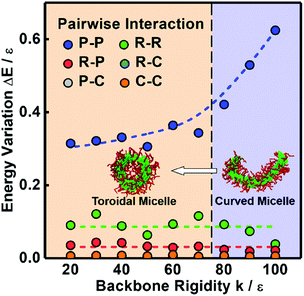
We designed an in silico experiment to understand the conditions under which toroidal micelles are formed. The preassembled cylindrical micelles are formed by R12-g-(C6)2 under the conditions of εPP = 1.0ε, εRR = 3.5ε, and k = 20ε. Then, we fixed εPP at 5.0ε and varied the values of εRR and k to examine the effects of the hydrophobicity and rigidity of the polymer backbones on the cyclization of preassembled cylindrical micelles, respectively (the other simulation parameters remain unchanged, see section 1.2 of the ESI†). We mapped out a morphology diagram in the space of εRRversus k to show how they influence the stability of the micelle morphologies. As shown in Fig. 2, six kinds of aggregates, namely, unimers (U) and cylindrical (R), spherical (S), ellipsoidal (E), toroidal (T), and curved (C) micelles, were observed under various parameter conditions. At lower εRR values (see the bottom region), the backbones are not very hydrophobic, and so the cylindrical micelles disassemble into unimers (U). At lower k values (see the left regions), spherical (S) and ellipsoidal (E) micelles are formed from the collapse of cylindrical micelles. The toroidal (T) micelles are formed at only intermediate values of εRR and k, and their morphology region is surrounded by the region of curved (C) micelles. Higher values of εRR and k favor the stability of the cylindrical micelles.We learn from Fig. 2 that the decrease of k (a higher k value corresponds to a more rigid backbone) can lead to the morphological transformation from cylindrical micelles to toroidal micelles for appropriate choices of interaction strength conditions (see the arrow in Fig. 2). This implies that the more rigid polymer backbones are able to resist the bending of the cylinders. According to our previous work, the interfacial energy gradually decreases during the cyclization process.11 The interfacial energy between the micellar core and corona includes all the pairwise interaction energy among the various types of beads in the simulations, that is, P–P, R–R, R–P, R–C, P–C, and C–C interactions. To gain insights into which type of interaction is the main contributor to the bending behavior, we calculated the variations in the average energy of the various types of interactions during the cyclization process. The energy variations were calculated from the initial cylinder to the curved micelle and toroidal micelle as the backbone rigidity k decreases (see the arrow in Fig. 2). All the interaction strengths are fixed, for example, εPP and εRR are fixed at 5.0ε and 3.5ε, respectively. Fig. 3 shows the energy variations ΔE for various types of interactions. As shown in Fig. 3, with increasing k, ΔE for the P–P interaction gradually increases, while the ΔE for the other interactions remains nearly unchanged. Moreover, the ΔE for the P–P interaction is much larger than those for the other interactions, especially for more rigid backbones. This result reveals that the variation in the P–P interaction is the main contributor to the variation of the interfacial energy and thereby the cyclization process.
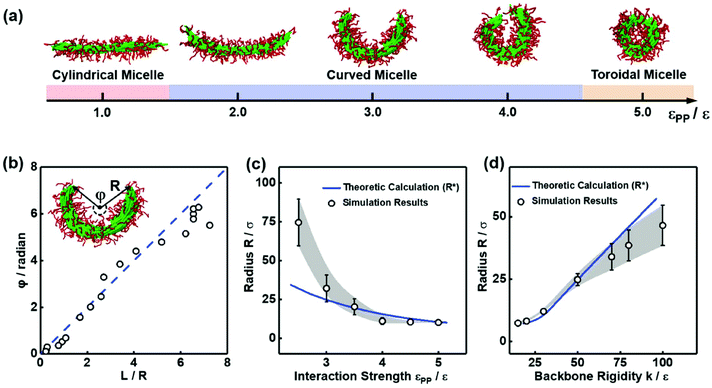
Because the P–P interaction plays the dominant role in determining the structural transformation from cylinders to toroids, we investigated the morphological transformation at various values of εPP between pendant groups. Representative structures are shown in Fig. 4a. With increasing εPP values, cylindrical micelles, curved cylinders, and toroidal micelles were sequentially observed. During this transformation, the cylinders are increasingly bending, and the central angle φ gradually increases (the definition of φ is illustrated in the inset of Fig. 4b). We plotted the central angle φ as a function of the ratio L/R of the arc length to the radius for the micelles, which is shown in Fig. 4b. As shown in the figure, the central angle φ is proportional to L/R, indicating that the arc lengths and structures of the micelles are nearly unchanged during the cyclization process. This inference is also demonstrated by the evidence that the circumference (63σ) of the formed toroids is very close to the initial length (69σ) of the cylindrical micelles.
To gain insights into the bending behavior, the variation in the radius R as a function of the interaction strength εPP was examined, which is shown in Fig. 4c. As the interaction strength εPP between pendant groups increases, R gradually decreases, and the central angle φ increases (according to the relation shown in Fig. 4b). This result implies that the enhancement in εPP promotes the bending of cylindrical micelles and the formation of toroids. In contrast to εPP, the rigidity of the polymer backbones can resist the bending of the cylinders. We, therefore, plotted the variation in the radius R as a function of the value of k. As shown in Fig. 4d, as the value of k increases, R increases, and thus, φ decreases, which indicates that the cylinders bend harder as they become more rigid. In addition to the impact on the bending behavior, the rigidity of the backbone also influences the morphologies of the closed structures. The inner hole of the toroids decreases as the value of k decreases (see Fig. S6a and S6b†). This result implies that the toroids shrink as the backbones become flexible. Further decreasing the backbone rigidity (k = 5.0ε) leads to the collapse of toroidal micelles into spherical micelles (see Fig. S6c†).
From Fig. 3, 4c and d, we learn that the cyclization of cylindrical micelles into toroidal micelles is mainly a balance of the self-attraction between pendant groups with the rigidity of the backbone. We then develop a theoretical model to check whether these effects dominate the supramolecular cyclization. Note that the total energy Ecylinder of the cylindrical micelle comprises the interfacial energy Einter, the bending energy Ebend and the end-capping energy Eend.11,34,35 Then, the total energy Ecurved of the curved micelles can be written as (for the details of the theory, see section 3.1 of the ESI†)
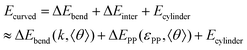 | (1) |
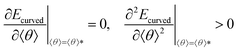 | (2) |
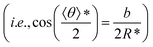 satisfies
satisfies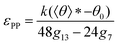 | (3) |
Here, gn is an exponential function with an exponent n, 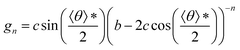 , where b = 1.5σ is the bond length of the backbone; c = 0.75σ is the length of the bond connecting the backbone bead and pendant group; and * denotes the extreme value. The variation in R* as a function of εPP and k can be theoretically calculated using eqn (3). The calculated values are presented as blue solid lines in Fig. 4c and d. As shown in the figures, the theoretical values approach the simulation results. Although a deviation in the R* value is found at a smaller εPP value, the difference in the central angle φ, for example, at εPP = 2.5ε, does not exceed 1 degree. The slight deviation between the theoretical prediction and simulation results could be attributed to the fact that the theory neglects the fluctuations of bond lengths and bond angles. Nevertheless, the good agreement between the theory and simulation results supports our proposed mechanism that the balance of the self-attraction energy between pendant groups and the bending energy of the copolymer backbones plays the dominant role in the cyclization process. Note that the formation of toroids is not to eliminate the end-cap energy only. Due to the balance of the interfacial energy to the bending energy, the curved micelles are more favorable than the straight cylinders as the solvent condition changes.
, where b = 1.5σ is the bond length of the backbone; c = 0.75σ is the length of the bond connecting the backbone bead and pendant group; and * denotes the extreme value. The variation in R* as a function of εPP and k can be theoretically calculated using eqn (3). The calculated values are presented as blue solid lines in Fig. 4c and d. As shown in the figures, the theoretical values approach the simulation results. Although a deviation in the R* value is found at a smaller εPP value, the difference in the central angle φ, for example, at εPP = 2.5ε, does not exceed 1 degree. The slight deviation between the theoretical prediction and simulation results could be attributed to the fact that the theory neglects the fluctuations of bond lengths and bond angles. Nevertheless, the good agreement between the theory and simulation results supports our proposed mechanism that the balance of the self-attraction energy between pendant groups and the bending energy of the copolymer backbones plays the dominant role in the cyclization process. Note that the formation of toroids is not to eliminate the end-cap energy only. Due to the balance of the interfacial energy to the bending energy, the curved micelles are more favorable than the straight cylinders as the solvent condition changes.
Geometric conditions for supramolecular cyclization
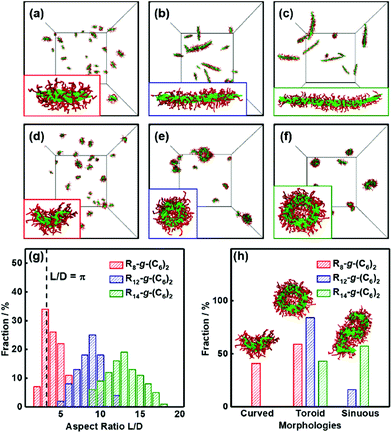
Apart from the above thermodynamic conditions, the cylindrical micelles must satisfy a geometric requirement for forming toroids. When the end-to-end closure of the cylinder occurs, the circumference of toroidal micelles is equal to the length L of the initial cylinder, and the diameter of the toroidal cylinder is close to the diameter D of the initial cylinder. Because the hole in the center of the toroid is a necessary geometric feature, the diameter of the toroid should be larger than the diameter of the toroidal cylinder. Thus, we can obtain geometric conditions for the end-to-end closure to form toroidal micelles, that is, the aspect ratio L/D of the cylindrical micelles has to be larger than π (L/D > π) (for details, see section 3.2 of the ESI†).Herein, to verify the proposed geometric conditions, the effect of the micelle size on the supramolecular cyclization of the cylindrical micelles was examined. We first obtained cylindrical micelles of various lengths from the self-assembly of three types of rod-coil graft copolymers, that is, R8-g-(C6)2, R12-g-(C6)2, and R14-g-(C6)2, as shown in Fig. 5a–c. The interaction strength εRR and the backbone rigidity k were set as 3.5ε and 20ε, respectively. The simulation results indicate that the aspect ratio of the cylindrical micelles increases with the length of the polymer backbones (see the insets of Fig. 5a–c). Fig. 5g shows the distribution of the aspect ratio L/D of the preassembled cylindrical micelles assembled from various kinds of graft copolymers. The statistical results were obtained from more than 200 micelles from 10 groups of independent simulations. As shown in the figure, the cylindrical micelles exhibit polydisperse distributions. As the length of the rigid backbones increases, the aspect ratio L/D gradually increases, and its distribution becomes wider. For the preassembled micelles formed by R8-g-(C6)2 graft copolymers, the value of L/D for approximately 56% of the micelles is larger than π (as shown by the dashed line in Fig. 5g), while the values of L/D are always larger than π for all the preassembled micelles formed by R12-g-(C6)2 and R14-g-(C6)2 graft copolymers.
We then changed the conditions, i.e., increased εPP to 5.0ε, to realize the cyclization of three kinds of preassembled cylindrical micelles. Fig. 5d–f display the corresponding simulation snapshots of the obtained aggregates. Curved micelles with partially open ends are formed via the bending of the short cylindrical micelles, while the cylindrical micelles with intermediate lengths are mainly end-to-end closed into toroidal micelles (Fig. 5d and e). Moreover, the toroids with larger holes and the sinuous micelles are formed by longer cylindrical micelles (Fig. 5f). The morphologies of aggregates including toroidal, curved, and sinuous micelles coexist as shown in Fig. 5d–f due to the polydispersity of the aspect ratio of initial cylinders. Then, we analyzed the fractions of various morphologies transformed from the three groups of preassembled cylindrical micelles, respectively. The statistical results are shown in Fig. 5h. For the preassembled micelles of R8-g-(C6)2 graft copolymers, 59% of the cylindrical micelles can cyclize to form toroidal micelles, while the remainders are bent into curved micelles (see the red columns). The fraction (59%) of toroids is close to the fraction (56%) of the preassembled cylinders that satisfy the geometric conditions of L/D > π. In addition, the graft copolymers R6-g-(C6)2 with shorter backbones can assemble into micelles with lower L/D (L/D < π for 95% micelles), and these micelles cannot cyclize into toroids or even bend into curved micelles (see Fig. S7†). Even if we further enhance εPP to 7.0ε, curved or toroidal micelles still cannot be observed. In contrast, 84% of the preassembled micelles formed by R12-g-(C6)2 graft copolymers are cyclized into toroidal micelles (see the blue column). The fraction decreases to 43% for the cylindrical micelles of R14-g-(C6)2 graft copolymers (see the green column) because the sinuous micelles are formed at significantly larger aspect ratios (see the inset in Fig. 5h). This phenomenon may be ascribed to the decreased probability of the end-to-end collision and closure for the ends of longer cylindrical micelles. The results reveal that an appropriate aspect ratio L/D is necessary to form toroidal micelles, which is in good agreement with the geometric conditions proposed based on the cyclization theory.
Comparison with experiments
In our previous work, we discovered the supramolecular cyclization of cylindrical micelles self-assembled from polypeptide-based graft copolymers PBLG-g-PEG.11 The PBLG backbones, which take a α-helix conformation, are semiflexible, while the PEG side chains are flexible. PBLG-g-PEG can thus be modeled as a rod-coil graft copolymer. We first prepared cylindrical micelles through the self-assembly of PBLG-g-PEG and then added THF to the solution. The addition of THF results in the constriction of the phenyl groups of PBLG, which leads to the end-to-end closure of the cylindrical micelles into toroidal micelles. In this work, we analyzed previous experimental results and carried out some additional experiments. Then, we compared these experimental observations with simulation results and explained the supramolecular cyclization behaviors of the polypeptide micelles with the proposed theory.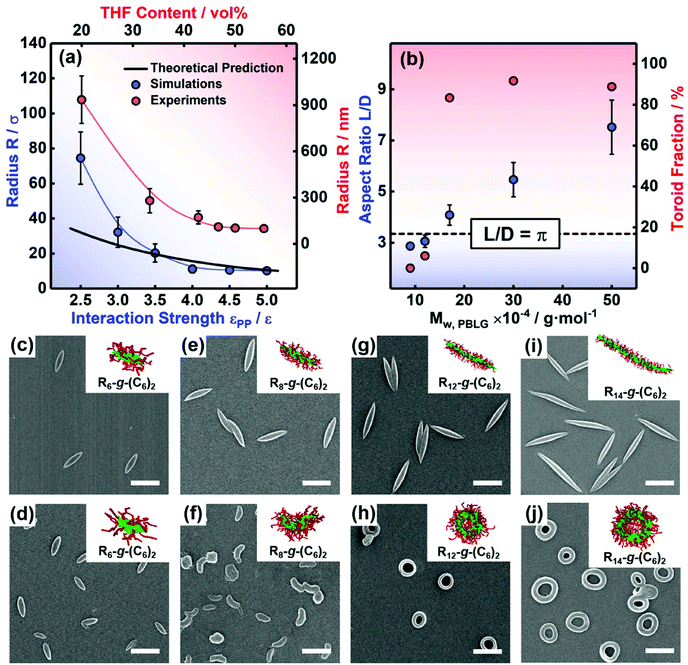 | ||
Fig. 6 Supramolecular cyclization of semiflexible cylindrical micelles assembled from PBLG-g-PEG graft copolymers. (a) Dependence of the curvature radius R on εPP and the variation in R as a function of THF content according to ref. 11. (b) The aspect ratio L/D of cylinders and the fraction of toroids for the graft copolymers with various weight-average molecular weights Mw,PBLG of PBLG backbones. SEM images of (c, e, g and i) the cylindrical micelles obtained in the first-step assembly and (d, f, h and j) the cyclized structures from the cylindrical micelles assembled from (c and d) PBLG90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG, (e and f) PBLG120 000-g-PEG, (e and f) PBLG120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG, (g and h) PBLG170 000-g-PEG, (g and h) PBLG170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG, and (i and j) PBLG500 000-g-PEG, and (i and j) PBLG500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG, where (i) and (j) are reproduced with permission from ref. 11. Insets show the simulated structures of rod-coil graft copolymers with various lengths of backbones. Scale bar: 500 nm. 000-g-PEG, where (i) and (j) are reproduced with permission from ref. 11. Insets show the simulated structures of rod-coil graft copolymers with various lengths of backbones. Scale bar: 500 nm. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG750, PBLG120
000-g-PEG750, PBLG120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG750, and PBLG170
000-g-PEG750, and PBLG170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG750, to examine the effect of the aspect ratio on the toroid formation (the details of the synthesis and characterization of the graft copolymers are given in section 2 of the ESI†). The subscripts denote the weight-average molecular weights Mw of PBLG backbones and PEG chains, respectively. A two-step self-assembly experiment was carried out as follows. In the first step of self-assembly, 0.3 mL of deionized water (a selective solvent for PEG) was added to 2.0 mL of PBLG-g-PEG solution (THF/DMF, 1
000-g-PEG750, to examine the effect of the aspect ratio on the toroid formation (the details of the synthesis and characterization of the graft copolymers are given in section 2 of the ESI†). The subscripts denote the weight-average molecular weights Mw of PBLG backbones and PEG chains, respectively. A two-step self-assembly experiment was carried out as follows. In the first step of self-assembly, 0.3 mL of deionized water (a selective solvent for PEG) was added to 2.0 mL of PBLG-g-PEG solution (THF/DMF, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v), and then the mixture solution was dialyzed against deionized water for 3 days. The cylindrical micelles can be formed by PBLG90
1, v/v), and then the mixture solution was dialyzed against deionized water for 3 days. The cylindrical micelles can be formed by PBLG90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG750, PBLG120
000-g-PEG750, PBLG120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG750, and PBLG170
000-g-PEG750, and PBLG170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG750 in the first-step assembly. As shown in Fig. 6c, e and g, the micelle lengths for the three groups of samples are ca. 390 nm (aspect ratio L/D = 0.92π), ca. 445 nm (L/D = 0.97π), and ca. 550 nm (L/D = 1.30π), respectively. The aqueous solution of cylindrical micelles is stable and can be used for further cyclization. Synchrotron radiation small-angle X-ray scattering (SAXS) and wide-angle X-ray scattering (WAXS) results suggest that the PBLG backbones take an ordered packing manner in the micellar core (Fig. S11†), which is consistent with the theoretical simulations (Fig. 1).
000-g-PEG750 in the first-step assembly. As shown in Fig. 6c, e and g, the micelle lengths for the three groups of samples are ca. 390 nm (aspect ratio L/D = 0.92π), ca. 445 nm (L/D = 0.97π), and ca. 550 nm (L/D = 1.30π), respectively. The aqueous solution of cylindrical micelles is stable and can be used for further cyclization. Synchrotron radiation small-angle X-ray scattering (SAXS) and wide-angle X-ray scattering (WAXS) results suggest that the PBLG backbones take an ordered packing manner in the micellar core (Fig. S11†), which is consistent with the theoretical simulations (Fig. 1).
Then, 1.2 mL of THF was added to 1.0 mL of the cylindrical micelle solutions (the resulting THF content is 54.5 vol%) to induce the cyclization reaction. Fig. 6d, f and h show the SEM images of the aggregates prepared from the three groups of cylindrical micelle samples. The toroidal morphologies are also confirmed by TEM and AFM measurements (Fig. S9†). Note that the parallel packing of PBLG backbones can be maintained in the core of toroidal micelles, suggested by the synchrotron radiation SAXS and WAXS measurements (Fig. S11†). For the micelle with a lower aspect ratio (L/D = 0.92π), the cylindrical micelles cannot be bent into curved or toroidal micelles, but ellipsoidal structures are observed (see Fig. 6d). Even if we further increase the THF content to 75.0 vol%, (i.e. 3.0 mL of THF was added), curved or toroidal structures still cannot be observed (see Fig. S8†). The cylinders with a medium aspect ratio (L/D = 0.97π) transform into the mixture of curved micelles and ellipsoidal micelles (Fig. 6f), with only a small fraction (6%) of cylinders forming toroids, while 83% of the longer cylinders (L/D = 1.30π) finally cyclize into toroids (Fig. 6h). By further increasing the Mw of PBLG backbones, cylindrical micelles with larger aspect ratios were formed, and these longer cylinders can transform into larger toroids after adding THF.11 By further analyzing the SEM images, we found that 89% of PBLG500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-g-PEG750 cylindrical micelles with an aspect ratio L/D of 2.39π can cyclize into toroids (see Fig. 6i and j; the SEM image is reproduced from ref. 11). To verify the critical value of L/D for supramolecular cyclization, the value of L/D and the fraction of toroids after adding THF are plotted as a function of the Mw of PBLG backbones in Fig. 6b. With the increasing Mw of PBLG backbones, the L/D value gradually increases, and the fraction of toroids significantly increases as the L/D value is larger than π (above the dashed line in Fig. 6b). In addition, the suitable molecular weight of PEG is necessary to guarantee that the aspect ratio of micelles can satisfy the geometric condition for cyclization (Fig. S10†). The results indicate that toroidal structures can be formed from cylinders when the geometric condition of L/D > π is satisfactory. These experimental observations are consistent with the proposed geometric condition and simulation results (see the insets of Fig. 6c–j).
000-g-PEG750 cylindrical micelles with an aspect ratio L/D of 2.39π can cyclize into toroids (see Fig. 6i and j; the SEM image is reproduced from ref. 11). To verify the critical value of L/D for supramolecular cyclization, the value of L/D and the fraction of toroids after adding THF are plotted as a function of the Mw of PBLG backbones in Fig. 6b. With the increasing Mw of PBLG backbones, the L/D value gradually increases, and the fraction of toroids significantly increases as the L/D value is larger than π (above the dashed line in Fig. 6b). In addition, the suitable molecular weight of PEG is necessary to guarantee that the aspect ratio of micelles can satisfy the geometric condition for cyclization (Fig. S10†). The results indicate that toroidal structures can be formed from cylinders when the geometric condition of L/D > π is satisfactory. These experimental observations are consistent with the proposed geometric condition and simulation results (see the insets of Fig. 6c–j).
In the present work, we proposed the thermodynamic and geometric conditions for the supramolecular cyclization of semiflexible cylindrical micelles, which is far beyond our preliminary work.11 Compared to the other toroidal micelle systems,4,9,20–26 the contribution of the bending energy to thermodynamic equilibrium is an important feature of the supramolecular cyclization of semiflexible cylindrical micelles. We noted that the high flexibility is unnecessary, and the toroidal micelles can be formed by balancing the bending energy and the interfacial energy. Therefore, our findings could deepen the understanding of cyclization of semiflexible nanoparticles and guide the precise preparation of uniform nanotoroids.
We also note that the bending behavior of cylindrical micelles is spontaneous and symmetry breaking. The symmetry breaking in our system can be attributed to the α-helix conformation of PBLG backbones. When the phenyl groups are constricted, the twist and bend of PBLG backbones can lead to the symmetry breaking in the bending of cylindrical micelles. Similar symmetry breaking can be observed in the supramolecular helical system and Mobius strips formed by chiral block copolymers.36–38 Additionally, although the theory neglects the fluctuations of bond lengths and bond angles and simplifies the assemblies as cylinders with a uniform diameter, the proposed theory can be applicable to describe the cyclization process of semiflexible micelles and could guide us to explore the winding and cyclization behaviors of longer fibrous structures. With an improvement of the simulation model, we will try to develop a theoretical model to self-assemble the system of different copolymers in future work.16,39,40
Conclusions
We applied BD simulations to investigate the supramolecular cyclization of cylindrical micelles self-assembled from rod-coil graft copolymers. The self-attraction of pendant groups is able to induce the cyclization of the cylindrical micelles. However, the rigidity of the polymer backbone has to be tuned to meet the conditions of forming toroidal micelles. When the backbone is too rigid, the self-attraction energy cannot overcome the bending energy to realize the cyclization of cylindrical micelles. In contrast, when the backbone is not rigid enough, the backbones cannot sustain the toroidal structures, and collapsed aggregates are formed. A theory based on the balance of the interfacial energy to the bending energy is developed, and the corresponding thermodynamic condition is proposed. The effect of the aspect ratio L/D of the cylindrical micelles was examined, and it was found that the geometric condition of L/D > π is required to form toroidal micelles. The simulation results and cyclization conditions were further verified by experiments regarding the stepwise self-assembly of PBLG-g-PEG graft copolymers. The proposed cyclization conditions and the mechanism can guide future preparation of toroids from rigid cylinders in the manner of end-to-end closure and can deepen our understanding of supramolecular cyclization.Methods
Simulation method
Brownian dynamics (BD) is a coarse-grained mesoscopic simulation method and has been successfully used to investigate the self-assembly of copolymers.41–45 The simulations were performed by applying the simulator, a coarse-grained molecular dynamics program based on LAMMPS. We considered the simulation system consisting of rod-coil graft copolymers in implicit solvents. In the simulation, each bead represents a cluster of atoms and is connected by the harmonic spring potential. The graft copolymer comprises a rigid backbone, multiple pendant groups, and two side chains, as shown in Fig. 1a. The junction points on the backbone were chosen randomly for grafting the coil chains. The rigidity of the backbone and the pairwise interaction were given by the angle bending potential and the Lennard-Jones (LJ) potential, respectively. The simulations were conducted in a cubic box with periodic boundary conditions, and the NVT ensemble was adopted. The temporal evolution of the beads obeys the Langevin equation, including all the potentials, the friction term, and the noise term. More than 10 micelles are formed in each simulation box, and the polydisperse distribution from 10 independent groups of simulations is shown in Fig. 5. The detailed simulation method is available in section 1.1 of the ESI.†Parameter setting
In the first step of assembly, for the purely repulsive interactions, the interaction strengths were set as εCC = εRC = εPC = 1.0ε. For the short-range attractive interaction, the interaction strengths were set as εRR = 3.5ε, εPP = εRP = 1.0ε. In the cyclization stage, the addition of THF can lead to the constriction of phenyl groups.11 To simulate this situation, we increased the attractive interaction strength εPP from 1.0ε to 5.0ε. The detailed parameter settings are given in section 1.2 of the ESI.†Polymer synthesis
PBLG was synthesized using ring-opening polymerization of BLG-NCA initiated by anhydrous trimethylamine. PBLG-g-PEG was prepared by the ester exchange reaction of PBLG with mPEG-OH. At the end of two polymerizations, the reaction mixture was precipitated into a large volume of anhydrous methanol. The product was purified twice by repeated precipitation from a chloroform solution into a large volume of anhydrous methanol and dried under vacuum.3,11,33 The polymer synthesis is described in detail in section 2.1 of the ESI.†Preparation of cylindrical and toroidal micelles
In the first-step assembly, the cylindrical micelles were prepared using a dialysis method. A total of 0.3 mL of deionized water, a selective solvent for PEG, was added to 2.0 mL of polymer solution (THF/DMF, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v; the initial polymer concentration was 0.5 g L−1). The solution was dialyzed against deionized water for 3 days to remove the organic solvents. In the second-step assembly, 1.2 mL of THF was added to 1.0 mL of the cylindrical micelle solution in water at 30 °C (the resulting THF content in the THF/water mixed solvent is 54.5 vol%). The solution was allowed to stir for 24 hours and then dialyzed against water to remove THF.
1, v/v; the initial polymer concentration was 0.5 g L−1). The solution was dialyzed against deionized water for 3 days to remove the organic solvents. In the second-step assembly, 1.2 mL of THF was added to 1.0 mL of the cylindrical micelle solution in water at 30 °C (the resulting THF content in the THF/water mixed solvent is 54.5 vol%). The solution was allowed to stir for 24 hours and then dialyzed against water to remove THF.
Characterization of assemblies
The morphologies of the aggregates were obtained using a field-emission SEM (S4800, Hitachi) operating at an accelerating voltage of 15 kV. The detailed experimental information including TEM, AFM, synchrotron radiation SAXS, and WAXS measurements is available in section 2.3 of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21774032, 51833003, and 21474029). The support from the Project of Shanghai Municipality (16520721900) and the Fundamental Research Funds for the Central Universities (222201714042) is also appreciated. This work was also supported by Chunming Yang, beamline BL16B, Shanghai Synchrotron Radiation Facility.Notes and references
- Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969–5985 RSC.
- A. H. Gröschel and A. H. Müller, Nanoscale, 2015, 7, 11841–11876 RSC.
- C. Cai, J. Lin, Y. Lu, Q. Zhang and L. Wang, Chem. Soc. Rev., 2016, 45, 5985–6012 RSC.
- D. J. Pochan, Z. Chen, H. Cui, K. Hales, K. Qi and K. L. Wooley, Science, 2004, 306, 94–97 CrossRef CAS PubMed.
- D. Presa-Soto, G. A. Carriedo, R. de la Campa and A. Presa Soto, Angew. Chem., Int. Ed., 2016, 55, 10102–10107 CrossRef CAS PubMed.
- H. Huang, B. Chung, J. Jung, H. W. Park and T. Chang, Angew. Chem., Int. Ed., 2009, 48, 4594–4597 CrossRef CAS PubMed.
- S. Al-Rehili, K. Fhayli, M. A. Hammami, B. Moosa, S. Patil, D. Zhang, O. Alharbi, M. N. Hedhili, H. Mohwald and N. M. Khashab, J. Am. Chem. Soc., 2017, 139, 10232–10238 CrossRef CAS PubMed.
- C. Liu, G. Chen, H. Sun, J. Xu, Y. Feng, Z. Zhang, T. Wu and H. Chen, Small, 2011, 7, 2721–2726 CrossRef CAS PubMed.
- H. G. Cui, Z. Y. Chen, K. L. Wooley and D. J. Pochan, Soft Matter, 2009, 5, 1269–1278 RSC.
- J. Zhu, Y. Liao and W. Jiang, Langmuir, 2004, 20, 3809–3812 CrossRef CAS PubMed.
- C. Yang, L. Gao, J. Lin, L. Wang, C. Cai, Y. Wei and Z. Li, Angew. Chem., Int. Ed., 2017, 56, 5546–5550 CrossRef CAS PubMed.
- K. Zhang, H. Miao and D. Chen, J. Am. Chem. Soc., 2014, 136, 15933–15941 CrossRef CAS PubMed.
- N. V. Hud and I. D. Vilfan, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 295–318 CrossRef CAS PubMed.
- R. Golan, L. I. Pietrasanta, W. Hsieh and H. G. Hansma, Biochemistry, 1999, 38, 14069–14076 CrossRef CAS PubMed.
- A. P. Rolland, Crit. Rev. Ther. Drug Carrier Syst., 1998, 15, 143–198 CrossRef CAS PubMed.
- Y. Li, K. Osada, Q. Chen, T. A. Tockary, A. Dirisala, K. M. Takeda, S. Uchida, K. Nagata, K. Itaka and K. Kataoka, Biomacromolecules, 2015, 16, 2664–2671 CrossRef CAS PubMed.
- S. J. Holder and N. A. J. M. Sommerdijk, Polym. Chem., 2011, 2, 1018–1028 RSC.
- L. Chen, T. Jiang, J. Lin and C. Cai, Langmuir, 2013, 29, 8417–8426 CrossRef CAS PubMed.
- X. He and F. Schmid, Phys. Rev. Lett., 2008, 100, 137802 CrossRef PubMed.
- H. Yu and W. Jiang, Macromolecules, 2009, 42, 3399–3404 CrossRef CAS.
- Z. Wang, F. Sun, S. Huang and C. Yan, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1450–1457 CrossRef CAS.
- X. Li, Y. Gao, X. Xing and G. Liu, Macromolecules, 2013, 46, 7436–7442 CrossRef CAS.
- D. Podder, S. Bera, M. Debnath, T. Das and D. Haldar, J. Mater. Chem. B, 2017, 5, 7583–7590 RSC.
- J. K. Kim, E. Lee, Z. Huang and M. Lee, J. Am. Chem. Soc., 2006, 128, 14022–14023 CrossRef CAS PubMed.
- I. C. Reynhout, J. J. Cornelissen and R. J. Nolte, J. Am. Chem. Soc., 2007, 129, 2327–2332 CrossRef CAS PubMed.
- S. Yagai, Y. Goto, X. Lin, T. Karatsu, A. Kitamura, D. Kuzuhara, H. Yamada, Y. Kikkawa, A. Saeki and S. Seki, Angew. Chem., Int. Ed., 2012, 51, 6643–6647 CrossRef CAS PubMed.
- X. Li, M. Deng, Y. Liu and H. Liang, J. Phys. Chem. B, 2008, 112, 14762–14765 CrossRef CAS PubMed.
- Y. Jiang, J. Zhu, W. Jiang and H. Liang, J. Phys. Chem. B, 2005, 109, 21549–21555 CrossRef CAS PubMed.
- T. Skrbic, T. X. Hoang and A. Giacometti, J. Chem. Phys., 2016, 145, 084904 CrossRef PubMed.
- Z. Ou and M. Muthukumar, J. Chem. Phys., 2005, 123, 074905 CrossRef PubMed.
- T. X. Hoang, A. Giacometti, R. Podgornik, N. T. Nguyen, J. R. Banavar and A. Maritan, J. Chem. Phys., 2014, 140, 064902 CrossRef PubMed.
- R. Cortini, B. R. Care, J. M. Victor and M. Barbi, J. Chem. Phys., 2015, 142, 105102 CrossRef PubMed.
- Z. Zhuang, T. Jiang, J. Lin, L. Gao, C. Yang, L. Wang and C. Cai, Angew. Chem., Int. Ed., 2016, 55, 12522–12527 CrossRef CAS PubMed.
- S. May, Y. Bohbot and A. Ben-Shaul, J. Phys. Chem. B, 1997, 101, 8648–8657 CrossRef CAS.
- M. Asgari, Eur. Phys. J. E, 2015, 38, 98 CrossRef PubMed.
- Z. Geng, B. Xiong, L. Wang, K. Wang, M. Ren, L. Zhang, J. Zhu and Z. Yang, Nat. Commun., 2019, 10, 4090 CrossRef PubMed.
- C. Tschierske, Angew. Chem., Int. Ed., 2013, 52, 8828–8878 CrossRef CAS PubMed.
- Z. Shen, Y. Jiang, R. Wang and M. Liu, J. Am. Chem. Soc., 2015, 137, 16109–16115 CrossRef CAS PubMed.
- H. Cabral, K. Miyata, K. Osada and K. Kataoka, Chem. Rev., 2018, 118, 6844–6892 CrossRef CAS PubMed.
- P. G. Millili, J. A. Selekman, K. M. Blocker, D. A. Johnson, U. P. Naik and M. O. Sullivan, Microsc. Res. Tech., 2010, 73, 866–877 CrossRef CAS PubMed.
- G. S. Grest and K. Kremer, Phys. Rev. A, 1986, 33, 3628–3631 CrossRef CAS PubMed.
- Q. Zhang, J. Lin, L. Wang and Z. Xu, Prog. Polym. Sci., 2017, 75, 1–30 CrossRef CAS.
- S. Lin, N. Numasawa, T. Nose and J. Lin, Macromolecules, 2007, 40, 1684–1692 CrossRef CAS.
- M. A. Horsch, Z. Zhang and S. C. Glotzer, Phys. Rev. Lett., 2005, 95, 056105 CrossRef PubMed.
- L. Gao, J. Lin, L. Zhang and L. Wang, Nano Lett., 2019, 19, 2032–2036 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation method, theoretical model, and experimental details. See DOI: 10.1039/c9nr07930k |
| This journal is © The Royal Society of Chemistry 2020 |