Transport properties of polycrystalline SnTe prepared by saturation annealing

Abstract

Because the binary chalcogenide SnTe is an interesting Pb-free alternative to the state-of-the-art thermoelectric material PbTe, significant efforts were devoted to the optimization of its thermoelectric properties over the last few years. Here, we show that saturation-annealing treatments performed at 823, 873 or 973 K under Sn-rich conditions provide a successful strategy to prepare polycrystalline samples with a controlled concentration of Sn vacancies. Both scanning transmission electron microscopy and Mössbauer spectroscopy demonstrate the absence of Sn-rich areas at the grain boundaries in the saturation-annealed samples. Transport property measurements, performed over a wide range of temperatures (5–800 K), show that this technique enables achieving thermoelectric performances at 800 K similar to those obtained using Sn self-compensation. The three saturation annealing temperatures result in comparable transport properties across the entire temperature range due to similar hole concentrations ranging between 1.0 and 1.5 × 10²⁰ cm⁻³ at 300 K. As equally observed in samples prepared by other synthetic routes, the temperature dependence of the Hall mobility evidences that charge transport is strongly affected by point-defect scattering caused by the random distribution of Sn vacancies.

---

Introduction

Devices based on thermoelectric effects enable solid-state conversion of heat into electricity and vice versa.^1,2 The conversion efficiency is mostly governed by the dimensionless thermoelectric figure of merit ZT = α²T/ρκ.^1,2 Achieving high efficiency at an operating absolute temperature T thus requires materials that simultaneously possess a high thermopower or Seebeck coefficient α, low electrical resistivity ρ and low total thermal conductivity κ. Chalcogenide semiconductors are an historically important class of thermoelectric materials for which, high ZT values have been obtained and optimized through band structure engineering or reduction of the heat transport by nanostructuration.^2–10 Among them, PbTe has been continuously investigated over the last few decades and remains one of the best thermoelectric materials for mid-temperature thermoelectric applications in power generation.

As a Pb-free analogue to PbTe, SnTe has been for a long time overlooked due to its inherent off-stoichiometry associated with Sn vacancies that result in highly-degenerate transport properties and poor thermoelectric performances.^11–33 As in most chalcogenide semiconductors, this defect chemistry depends sensitively on the conditions employed during the growth process and post-treatments, should the samples be in single-crystalline or polycrystalline form.^34–37 A careful control of the defect concentration is pivotal in ensuring good reproducibility and meaningful comparison of the transport data between different series of samples.

Saturation annealing is the experimental tool of choice to control deviations from the ideal stoichiometry in semiconductors and to systematically probe the maximum deviation at a given temperature. In addition, this technique allows avoiding the presence of secondary phases which may have a detrimental impact on the transport properties. While this strategy has been widely applied on most state-of-the-art thermoelectric materials in single-crystalline form such as Bi₂Te₃ or PbTe,^2,38–41 this approach has been only scarcely considered on polycrystalline compounds for which the presence of grain boundaries can prevent diffusion of the elements. Here, we demonstrate that this technique can be successfully applied on polycrystalline SnTe. Varying the saturation annealing temperature from 973 down to 823 K under Sn-rich conditions enables controlling the Sn vacancy concentration and hence, the transport properties. In particular, samples with hole concentrations equivalent to those achieved by intentionally introducing Sn excess can be obtained, but without the presence of elemental Sn at the grain boundaries, as demonstrated by scanning transmission electron microscopy and Mössbauer spectroscopy.

Experimental section

Synthesis

Polycrystalline samples of SnTe were first prepared by powder metallurgy. Prior to use, Sn (shots, 99.999%, Alfa Aesar) and Te (powder, 99.999%, 5N⁺) elements were purified to eliminate oxides. Sn was washed in successive baths of diluted hydrochloric acid and a distilled water–ethanol mixture. Te was purified at 773 K under inert atmosphere in a sealed silica tube. Stoichiometric quantities of these purified elements were loaded into silica tubes sealed under secondary vacuum, heated at 1133 K in 10 h in a rocking furnace and dwelt at this temperature for 5 h. The tubes were then quenched in room-temperature water.

The obtained ingots were ground into fine powders before being consolidated by spark plasma sintering in graphite dies at 773 K for 5 min under a pressure of 65 MPa. The experimental density of the cylindrical pellets was determined by weight and dimensions to be higher than 95% of the theoretical density from X-ray diffraction data. Subsequently, the cylindrical pellets were cut with a diamond wire saw into cylinders (10 mm in diameter and 1 mm thickness) and parallelepiped-shaped samples (1.5 × 2 × 7 mm³).

The saturation annealing process was carried out by placing these cut samples in a silica sample holder of 5 cm long on one end while a powdered source was placed on the other end. This sample holder was then placed in a silica tube sealed under secondary vacuum (Fig. 1). The composition of the source used here (Sn₅₅Te₄₅) was chosen to probe the Sn-rich solidus line according to the Sn–Te binary phase diagram. The source was synthesized by a direct reaction of the elements at high temperature in sealed silica tubes. During the saturation-annealing process, the solid, liquid and gaseous phases are all present. According to the Gibbs phase rule under constant temperature and pressure, the variance or degree of freedom of this system F = C − P + 2, where C is the number of components and P is the number of phases, is equal to 1 (C = 2 and P = 3 in the present case). Subjecting the samples to this annealing process at a fixed temperature thus determines their final chemical composition which will correspond to the composition of the solidus on the Sn-rich side of the phase diagram. This technique allows mass exchange between the source and the samples in the vapor phase and can be used to fix the defect concentration which remains constant and homogeneous within the samples. This annealing procedure was performed at 823, 873 and 973 K in a horizontal furnace. The duration of this process has been estimated by considering the self-diffusion profile of Sn in SnTe,^42,43 yielding saturation times of 21, 10 and 7 days at 823, 873 and 973 K, respectively.

Fig. 1 View of the sealed silica tube showing the dense samples cut from the consolidated ingots separated from the powdered source (a) prior to saturation-annealing and (b) after completion of the process. Mass exchange that occurred between the source and the samples can be seen by the small shiny crystals that grew up on the surface of the dense samples and by the change of the appearance of the source indicating that the solid, liquid and gas phases were in equilibrium in the tube. After this process, the surfaces of the saturation-annealed samples are slightly polished.

Structural and chemical characterizations

Power X-ray diffraction was performed at 300 K on a Bruker D8 Advance diffractometer. Lattice parameters were inferred from Rietveld refinements against the PXRD data using Fullprof (Fig. S1–S3 in the ESI†).⁴⁴

High-resolution transmission electron microscopy (HRTEM) and scanning transmission electron microscopy (STEM) experiments were carried out using a JEOL ARM 200F – cold FEG TEM/STEM microscope with an accelerating voltage of 200 keV equipped with double Cs-correctors. The observed thin slice of a sample saturation-annealed at 973 K was prepared by the dual ion beam (FIB) – scanning electron microscope system using the in situ lift-out technique. STEM images were taken in high-angle annular dark-field (HAADF) and annular bright-field (ABF) modes.

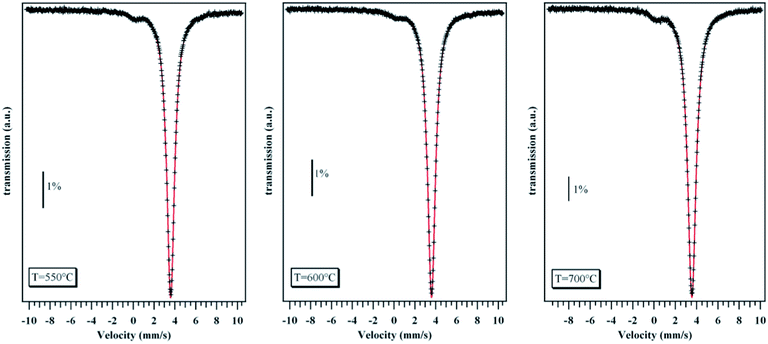
¹¹⁹Sn Mössbauer spectra were recorded at 4.2 K for the three saturation-annealed samples, in order to exalt the response of a possible Sn⁰ occurrence, in transmission geometry with a spectrometer operating in the constant-acceleration mode. The polycrystalline absorber with natural abundance of ¹¹⁹Sn used for these experiments had a thickness of 10 mg cm⁻². The source Ba¹¹⁹SnO₃ with a nominal strength of 10 mCi was kept at 300 K to collect the Mössbauer spectra. A palladium foil of 0.5 mm in thickness was used as a critical absorber for Sn X-rays. The velocity was calibrated at 300 K against a 12 μm thick Fe foil. The ¹¹⁹Sn isomer shifts IS reported herein are referred to BaSnO₃ at 300 K. The Mössbauer spectra were fitted by a least-squares method assuming Lorentzian-like peak shapes.

Transport properties measurements

Prior to measurements, the surfaces of the samples were slightly polished to remove the shiny crystals that appear during the saturation-annealed process. Hall effect measurements were performed between 5 and 300 K on the saturation-annealed, bar-shaped samples using a five-probe configuration and the AC transport option of a physical property measurement system (PPMS, Quantum Design). Five copper wires were attached onto the samples using silver paint. The transverse electrical resistivity ρ_xy was measured under magnetic fields μ₀H ranging between −1 and +1 T. The Hall resistivity ρ_H was derived via the expression ρ_H = [ρ_xy(+μ₀H) − ρ_xy(−μ₀H)]/2 used to dismiss magnetoresistive contributions by taking the antisymmetric part of ρ_xy under magnetic field reversal. The Hall hole concentrations p_H and Hall mobilities μ_H were inferred from the Hall coefficient R_H, determined as the slope of the magnetic field dependence of the Hall resistivity, using the single-band formulas p_H = 1/R_He and μ_H = R_H/ρ where e is the elementary charge. Electrical resistivity, thermopower and thermal conductivity were simultaneously measured in the same temperature range and on the same bar-shaped samples using the thermal transport option of the PPMS. Ohmic and thermal contacts were realized by gluing copper bars with conducting silver epoxy.

High-temperature measurements (300–800 K) of the electrical resistivity and thermopower were performed using a ZEM-3 apparatus (Ulvac-Riko) on other bar-shaped samples. The thermal diffusivity a was measured on the circular annealed pellets (∼10 mm diameter, ∼1 mm thickness) up to the same temperature with a Netzsch laser flash instrument (LFA 467) under continuous argon flow. The measured thermal diffusivity was used to calculate the total thermal conductivity κ via the formula κ = aC_pd where C_p is the specific heat and d is the experimental density. C_p was estimated using the Dulong–Petit law 3NR where N is the number of atoms per formula unit and R is the gas constant. The temperature-dependence of the density was not taken into account in the present case.

Results and discussion

Phase purity of saturation-annealed samples

In polycrystalline SnTe samples prepared by conventional melt-quenching or slow cooling, STEM experiments clearly evidenced the presence of excess Sn located at the grain boundaries, the presence of which is undetectable by scanning electron microscopy.⁴⁵ Unlike these samples, STEM images taken on a thin slice of the sample saturation-annealed at 973 K demonstrate that both Sn and Te are homogeneously distributed with no obvious traces of elemental Sn at the grain boundaries (Fig. 2).

Fig. 2 STEM images taken (a) on the melt-quenched sample and (d) on the saturation-annealed sample treated at 973 K. The elemental maps of Sn and Te are shown in red and green for the melt-quenched sample in panels (b) and (c), respectively, and in pink and yellow for the saturation-annealed sample in panels (e) and (f), respectively.

Because HRTEM experiments were conducted on one thin slice, we further tried to unveil the possible presence of elemental Sn by ¹¹⁹Sn Mössbauer spectroscopy which is a bulk-sensitive probe. As shown in Fig. 3, the Mössbauer spectra measured at 4.2 K on the three saturation-annealed samples do not show any evident signal of elemental Sn⁰, in contrast to the spectrum collected on a Sn_1.03Te sample prepared by melt-quenching where a slight but detectable asymmetry of the main peak was a clear indication of the presence of a Sn⁰ phase.⁴⁵ This absence is a strong evidence that mass exchange between the samples and the source has occurred during the saturation annealing process. These results demonstrate that this method is equally applicable to control the stoichiometry of polycrystalline SnTe without resorting to additional Sn in the nominal composition, the excess of which is located at the grain boundaries.

Fig. 3 ¹¹⁹Sn Mössbauer spectra measured at 4.2 K of the saturation-annealed samples treated at 823, 873 and 973 K. The experimental data points are marked by the black crosses while the red curves represent the least-squares fit. The peak observed with an isomer shift close to zero is due to a small amount of SnO₂ (≈2%). According to the point symmetry (m3̄m) of the Sn site, the main peak is a singlet with full width at half maximum of Γ = 0.90 mm s⁻¹. The isomer shift (IS = 3.56 mm s⁻¹) is consistent with a Sn²⁺ oxidation state.

Transport properties

Fig. 4a and b show the temperature dependence of the electrical resistivity and thermopower of the three samples saturation-annealed at 823, 873 and 973 K. For comparison purposes, the data measured on a SnTe sample prepared by melt-quenching (MQ) have been added.⁴⁵ While all the samples show similar ρ(T) data characteristic of degenerate p-type semiconductors below 300 K, significant differences emerge at higher temperatures. Above 500 K, the ρ values of the three annealed samples exhibit a steeper rise in temperature compared to the MQ sample. In prior studies, this high-temperature behavior has been attributed to the second, heavy-hole valence band that starts contributing to the transport.^11–15 Because this behavior appears in samples with the lowest hole concentrations, these results suggest that the annealing process led to a decrease in the hole concentration, regardless of the annealing temperature. The different annealing temperatures are, however, not equivalent as revealed by the data of the sample annealed at 973 K that are slightly below those of the two other samples which do not show any differences to within experimental uncertainty. This slight but noticeable difference indicates that the concentration of Sn vacancies depends on the annealing temperature, in agreement with the boundaries of the single-phase region determined in prior studies (see below).^{34,35,46–49}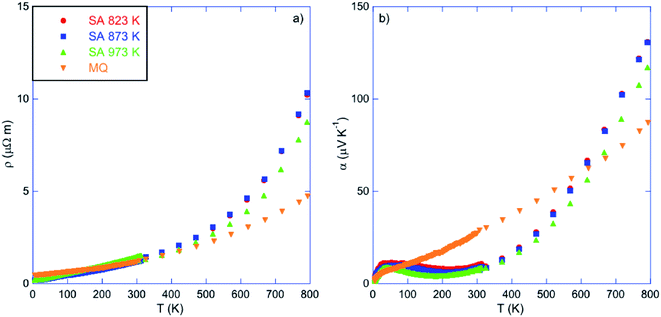

Fig. 4 Temperature dependence of (a) the electrical resistivity ρ and (b) thermopower α of the samples annealed at 823, 873 and 973 K. For comparison purposes, data collected on a sample prepared by melt-quenching (MQ) have been added (ref. 45). The color-coded symbols are similar in both panels.

These conclusions hold true when considering the evolution of the thermopower in Fig. 4b. While the MQ sample shows a quasi-linear temperature dependence consistent with a diffusive regime in a strongly degenerate system, the α(T) curves of the annealed samples display more complex variations with temperature. Our prior study has shown that this complex evolution of α(T) is strongly sensitive to the synthesis conditions used, or equivalently, to the hole concentration.⁴⁵ In particular, the maximum in α that exists in all samples near 35 K has been attributed to a phonon-drag contribution, similarly to what has been observed in PbTe.^50,51 Interestingly, the behavior of α(T) below 300 K in the saturation annealed samples differs from that observed in polycrystalline SnTe prepared by conventional synthesis routes.⁴⁵ The phonon-drag peak near 35 K is followed by a decrease in the α values upon further heating up to about 200–250 K where α(T) starts increasing again with temperature. The strong superlinear variation observed above 250 K likely reflects the temperature-dependent density-of-states effective mass of holes which varies with temperature up to 800 K.¹⁶ Both the low-temperature peak α value and the temperature at which α(T) reaches its minimum are sensitive to the annealing temperature, as evidenced by clear differences between the samples annealed at 873 and 973 K.

The marked differences in the electronic transport between the MQ and the annealed samples suggests that the concentration of Sn vacancies is drastically reduced by annealing under Sn-rich conditions. This is confirmed by Hall effect measurements indicating that the hole concentration p_H decreases from 1.4 to 1.1 × 10²⁰ cm⁻³ at 300 K with decreasing the annealing temperature (Table 1 and Fig. 5a). These values are one order of magnitude lower than that measured in the MQ sample (1.1 × 10²¹ cm⁻³ at 300 K), confirming the strong reduction in the Sn vacancy concentration. Thus, the saturation annealing process provides a reliable method to control precisely the chemical potential in SnTe through the Sn vacancy concentration, achieved over a large temperature window ranging from 823 up to 973 K.

Table 1 Theoretical Sn vacancy concentration δ in the Sn_1−δTe samples prepared by saturation annealing (SA). The corresponding Te content in at% and the theoretical lattice parameters a_th determined by the relation of Brebrick (ref. 52) are also given. The experimental lattice parameters a_exp have been inferred from Rietveld refinements against the PXRD data (Fig. S1–S3 in the ESI). Note that for the MQ sample, we used the a_exp value which provides a more consistent estimate of δ of 0.0176 due to strong deviations of the Hall factor r_H from unity at high p_H concentrations

Sample	pH (cm^−3)	δ (Sn1−δTe)	Composition	at% Te	ath (Å)	aexp (Å)
SnTe MQ	1.10 × 10^21	0.0176	Sn0.9824Te	50.88	—	6.3120
SA 823 K	1.09 × 10^20	0.0034	Sn0.9966Te	50.16	6.3221	6.3262
SA 873 K	1.12 × 10^20	0.0035	Sn0.9965Te	50.17	6.3218	6.3258
SA 973 K	1.38 × 10^20	0.0044	Sn0.9956Te	50.22	6.3200	6.3247

---

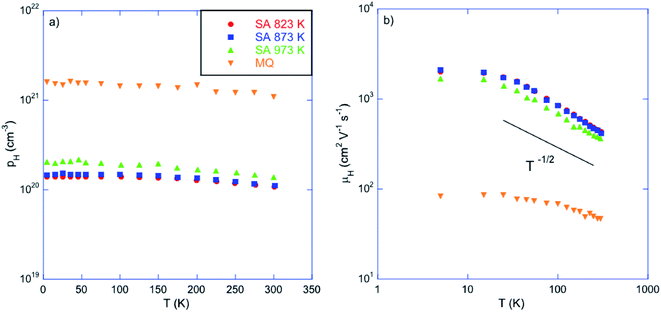Fig. 5 (a) Hall hole concentration p_H and (b) Hall mobility μ_H as a function of temperature for the samples annealed at 823, 873 and 973 K. For comparison purposes, data collected on a sample prepared by melt-quenching (MQ) have been added (ref. 45). The color-coded symbols are similar in both panels.

The temperature dependence of the hole mobility μ_H, shown in Fig. 5b, confirms the physical picture that emerged from data collected on samples prepared by various synthesis techniques.⁴⁵ The μ_H data vary with temperature above 15 K following a T^−1/2 law indicating that hole transport is limited by alloy scattering as a result of the random distribution of Sn vacancies within the samples. The absence of elemental Sn in the annealed samples demonstrates that this behavior is not affected by impurities and thus, is an intrinsic characteristic of SnTe. The smoother variation observed in the MQ sample has been attributed to the possible influence of electron–electron scattering shown to play a role in heavily-doped PbTe compounds.⁵⁰

If we make the reasonable assumption that each Sn vacancy provides two holes and that the Hall factor r_H is close to unity in the range of hole concentrations measured in the present case,^34,35,45 the p_H values can be used to estimate the deviations from the ideal 1 : 1 stoichiometry by applying successively the two relations 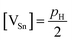and [V_Sn] = Sδ. In these relations, [V_Sn] is the concentration of Sn vacancies, S = 1.58 × 10²² cm⁻³ is the number of Sn sites in the crystal structure and δ represents the deviation from the ideal stoichiometry when considering the chemical formula Sn_1−δTe. The results, gathered in Table 1, are in agreement with the relation proposed by Brebrick (ref. 51) that relates the percentage of Te, y, in the chemical formula to the lattice parameter a = 6.3278 Å − 3.54(y − 0.5) where y = 1/(2 − δ). Moreover, the very good agreement with the deviations in the phase diagram determined by various authors (ref. 47–49; Fig. 6) shows that saturation annealing provides a direct access to the maximum deviation at the annealing temperature considered. Furthermore, the p_H values are also consistent with the literature data obtained on similarly post-treated single crystals (Fig. 7).⁵² This further demonstrates that saturation annealing is also effective in polycrystalline SnTe despite the presence of grain boundaries that may have prevented diffusion of the elements from the surface towards the core of the bulk samples.

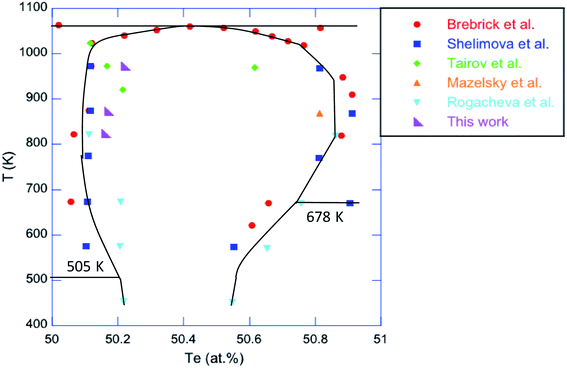Fig. 6 Portion of the Sn–Te phase diagram showing the deviations from the ideal stoichiometry in SnTe determined by various authors (ref. 47–49) and in this work.

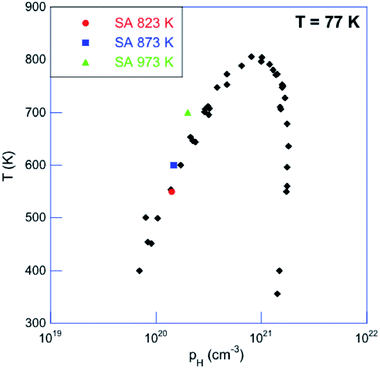Fig. 7 Saturation-annealing temperature as a function of the Hall hole concentration p_H measured at 77 K. The literature data obtained on single crystals treated by saturation annealing on both the Sn-rich and Te-rich sides of the solidus line are shown in black (ref. 52).

Fig. 8 shows the temperature dependence of the total thermal conductivity of all the samples. The monotonic increase in the κ values observed in the MQ sample is significantly influenced by saturation annealing. In the three annealed samples, a well-defined Umklapp peak dominates the low-temperature data near 30 K. The magnitude of this peak trends with the Sn vacancy concentration estimated from p_H, the lowest p_H values being synonymous with the highest peak value. The sensitivity of the Umklapp peak to the vacancy concentration is not restricted to the annealed samples and has been also observed in other SnTe samples irrespective of the synthesis technique employed.⁴⁵ These variations are due to the Sn vacancies that act as efficient point-defect scattering centers which directly affects the phonon transport at low temperatures. This is confirmed by a fit of the low-temperature κ_L(T) data to the Debye–Callaway model (Fig. 9; the equations used can be found in the ESI†) which shows that the parameter A describing point-defect scattering scales as δ(1 − δ) (see Table 2 for the values of the fitting parameters).

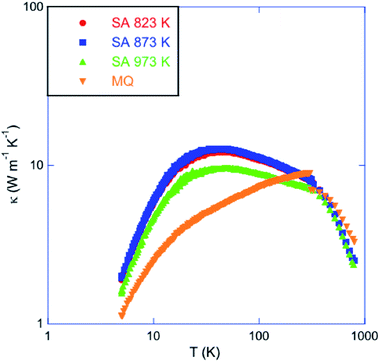Fig. 8 Temperature dependence of the total thermal conductivity κ of the samples treated at 823, 873 and 973 K. For comparison purposes, data collected on a sample prepared by melt-quenching (MQ) have been added (ref. 45).

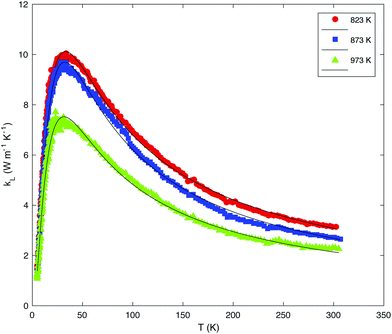Fig. 9 Fit of the lattice thermal conductivity κ_L of the saturation-annealed samples to the Debye–Callaway model represented as a solid black curve. κ_L has been obtained by subtracting the electronic contribution κ_e estimated using the Wiedemann–Franz law κ_e = LT/ρ. The temperature-dependence of the Lorenz number has been calculated assuming a single-parabolic band model which provides a reasonable approximation below 300 K for these compounds (see ref. 45).

Table 2 Values of the fitting parameters L (grain size), A (point-defect scattering) and B (phonon–phonon scattering via Umklapp processes) inferred from fits of the lattice thermal conductivity of the melt-quenched (MQ) and saturation-annealed (SA) samples

Sample	L (μm)	A (10^−42 s^3)	B (10^−18 s K^−1)
SnTe (MQ)	1.5	42	1.3
SA 823 K	1.8	7.3	5.8
SA 873 K	1.5	6.8	7.0
SA 973 K	1.5	10	8.5

---

Fig. 10 shows the evolution of the ZT values as a function of temperature. The peak ZT value achieved in this series (0.55 at 800 K) is similar for the three annealed samples to within experimental uncertainty and slightly higher than that obtained in the MQ sample for which a maximum value of 0.4 is obtained at 800 K. The saturation annealing method thus yields samples with thermoelectric performances comparable to those achieved by introducing excess Sn in the nominal composition (maximum ZT of 0.65 at 800 K),^11,33 but without the presence of elemental Sn at the grain boundaries.

Fig. 10 Dimensionless thermoelectric figure of merit ZT as a function of temperature of the samples annealed at 823, 873 and 973 K. For comparison purposes, data collected on a sample prepared by melt-quenching (MQ) have been added (ref. 45).

Conclusion

We reported on the successful control of the hole concentration in polycrystalline SnTe by subjecting samples to saturation-annealing treatments at 823, 873 and 973 K. The absence of elemental Sn in the annealed samples, evidenced by a combination of STEM and Mössbauer spectroscopy, demonstrates the effectiveness of the saturation-annealing method in polycrystalline samples to carefully control the stoichiometry of the material without introducing excess Sn during the synthesis process. Transport properties measurements performed on the three annealed samples are consistent with a significant reduction in the Sn vacancy concentration that directly controls the hole concentration. The absence of elemental Sn in these samples further confirm that several important traits observed in samples prepared by conventional methods such as the phonon-drag contribution to the thermopower below 100 K or the transport limited by alloy scattering are not side effects of impurities but are intrinsic to polycrystalline SnTe. Of note, the peak ZT values achieved in the annealed samples are comparable to those obtained by intentionally introducing excess Sn in the nominal composition. Although this last strategy appears as more straightforward than saturation annealing to produce SnTe samples with optimum thermoelectric properties, the careful control of the defect concentration offered by this technique enables probing the phase boundaries at a given temperature. This technique, widely employed in the past decades to control and optimize the thermoelectric properties of state-of-the-art thermoelectric materials, should be applicable in SnTe samples substituted by various elements and more generally, is an essential tool to obtain reliable and reproducible results on chalcogenide semiconductors.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors thank the financial support of the European Space Agency under NPI contract no. 40001134346/15/NL/RA and of the Région Lorraine under the contract DPR-NT No. 2015-9337.

References

1. H. J. Goldsmid, in Thermoelectric Refrigeration, Springer, New York, 1964.
2. Thermoelectrics and its Energy Harvesting, ed. D. M. Rowe, CRC Press, 2012.
3. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554.
4. J.-S. Rhyee, K. H. Lee, S. M. Lee, E. Cho, S. I. Kim, E. Lee, Y. S. Kwon, J. H. Shim and G. Kotliar, Nature, 2009, 459, 965.
5. J.-B. Vaney, J. Carreaud, G. Delaizir, A. Pradel, A. Piarristeguy, C. Morin, E. Alleno, J. Monnier, A. P. Gonçalves, C. Candolfi, A. Dauscher and B. Lenoir, Adv. Electron. Mater., 2015, 1, 1400008.
6. J.-B. Vaney, J. Carreaud, G. Delaizir, A. Piarristeguy, A. Pradel, E. Alleno, J. Monnier, E. B. Lopes, A. P. Gonçalves, A. Dauscher, C. Candolfi and B. Lenoir, J. Mater. Chem. C, 2016, 4, 2329.
7. B. Wiendlocha, J.-B. Vaney, C. Candolfi, A. Dauscher, B. Lenoir and J. Tobola, Phys. Chem. Chem. Phys., 2018, 20, 12948.
8. T.-R. Wei, G. Tan, X. Zhang, C.-F. Wu, J.-F. Li, V. P. Dravid, G. J. Snyder and M. G. Kanatzidis, J. Am. Chem. Soc., 2016, 138, 8875.
9. G. Dennler, R. Chmielowski, S. Jacob, F. Capet, P. Roussel, S. Zastrow, K. Nielsch, I. Opahle and G. K. H. Madsen, Adv. Energy Mater., 2014, 4, 1301581.
10. J. Shen, Z. Chen, S. Lin, L. Zheng, W. Li and Y. Pei, J. Mater. Chem. C, 2016, 4, 209.
11. G. Tan, L.-D. Zhao, F. Shi, J. W. Doak, S.-H. Lo, H. Sun, P. Wang, C. Wolverton, V. P. Dravid, C. Uher and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 7006.
12. G. Tan, F. Shi, S. Hao, H. Chi, L.-D. Zhao, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 5100.
13. G. Tan, F. Shi, S. Hao, H. Chi, T. P. Bailey, L.-D. Zhao, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 11507.
14. G. Tan, F. Shi, J. W. Doak, H. Sun, L.-D. Zhao, P. Wang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2015, 8, 267.
15. G. Tan, W. G. Zeier, F. Shi, P. Wang, G. J. Snyder, V. P. Dravid and M. G. Kanatzidis, Chem. Mater., 2015, 27, 7801.
16. M. Zhou, Z. M. Gibbs, H. Wang, Y. Han, C. Xin, L. Li and G. J. Snyder, Phys. Chem. Chem. Phys., 2014, 16, 20741.
17. J. He, X. Tan, J. Xu, G.-Q. Liu, H. Shao, Y. Fu, X. Wang, Z. Liu, J. Xu, H. Jiang and J. Jiang, J. Mater. Chem. A, 2015, 3, 19974.
18. A. Banik, U. S. Shenoy, S. Anand, U. W. Waghmare and K. Biswas, Chem. Mater., 2015, 27, 581.
19. Q. Zhang, B. Liao, Y. Lan, K. Lukas, W. Liu, K. Esfarjani, C. Opeil, D. Broido, G. Chen and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13261.
20. Z. Zhou, J. Yang, Q. Jiang, Y. Luo, D. Zhang, Y. Ren, X. He and J. Xin, J. Mater. Chem. A, 2016, 4, 13171.
21. L.-D. Zhao, X. Zhang, H. Wu, G. Tan, Y. Pei, Y. Xiao, C. Chang, D. Wu, H. Chi, L. Zheng, S. Gong, C. Uher, J. He and M. G. Kanatzidis, J. Am. Chem. Soc., 2016, 138, 2366.
22. R. Al Rahal Al Orabi, J. Hwang, C.-C. Lin, R. Gautier, B. Fontaine, W. Kim, J.-S. Rhyee, D. Wee and M. Fornari, Chem. Mater., 2017, 29, 612.
23. L. Zhang, J. Wang, Z. Cheng, Q. Sun, Z. Li and S. Dou, J. Mater. Chem. A, 2016, 4, 7936.
24. A. Banik, B. Vishal, S. Perumal, R. Datta and K. Biswas, Energy Environ. Sci., 2016, 9, 2011.
25. R. Al Rahal Al Orabi, N. A. Mecholsky, J. Hwang, W. Kim, J.-S. Rhyee, D. Wee and M. Fornari, Chem. Mater., 2016, 28, 376.
26. L. Wang, X. Tan, G. Liu, J. Xu, H. Shao, B. Yu, H. Jiang, S. Yue and J. Jiang, ACS Energy Lett., 2017, 2, 1203.
27. W. Li, L. Zheng, B. Ge, S. Lin, X. Zhang, Z. Chen, Y. Chang and Y. Pei, Adv. Mater., 2017, 29, 1605887.
28. N. Wang, D. West, J. Liu, J. Li, Q. Yan, B.-L. Gu, S. B. Zhang and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 045142.
29. L. Zheng, W. Li, S. Lin, J. Li, Z. Chen and Y. Pei, ACS Energy Lett., 2017, 2, 563.
30. L. Hu, Y. Zhang, H. Wu, J. Li, Y. Li, M. McKenna, J. He, F. Liu, S. J. Pennycook and X. Zeng, Adv. Energy Mater., 2018, 8, 1802116.
31. J. Q. Li, S. Huang, Z. P. Chen, Y. Li, S. H. Song, F. S. Liu and W. Q. Ao, Phys. Chem. Chem. Phys., 2017, 19, 28749.
32. S. Roychowdhury, U. S. Shenoy, U. V. Waghmare and K. Biswas, J. Mater. Chem. C, 2017, 5, 5737.
33. D. Ibrahim, V. Ohorodniichuk, C. Candolfi, C. Semprimoschnig, A. Dauscher and B. Lenoir, ACS Omega, 2017, 2, 7106.
34. R. F. Brebrick and A. J. Strauss, Phys. Rev., 1963, 131, 104.
35. R. F. Brebrick, J. Phys. Chem. Solids, 1963, 24, 27.
36. J. A. Kafalas, R. F. Brebrick and A. J. Strauss, Appl. Phys. Lett., 1964, 4, 93.
37. D. M. Chigikov and V. P. Schastliviy, in Tellure and Tellurides, Nauka, Moscow, 1966.
38. J. P. Fleurial, L. Gailliard, R. Triboulet, H. Scherrer and S. Scherrer, J. Phys. Chem. Solids, 1988, 49, 1237.
39. R. F. Brebrick, J. Phys. Chem. Solids, 1969, 30, 719.
40. R. F. Brebrick and E. Gubner, J. Chem. Phys., 1962, 36, 1283.
41. C. Hewes, M. S. Adler and S. D. Senturia, J. Appl. Phys., 1973, 44, 1327.
42. H. Scherrer, G. Pineau and S. Scherrer, Phys. Lett., 1979, 75, 118.
43. H. Scherrer, S. Weber and S. Scherrer, Phys. Lett., 1980, 77, 189.
44. J. Rodriguez-Carjaval, Phys. B, 1993, 192, 55.
45. D. Ibrahim, C. Candolfi, S. Migot, J. Ghanbaja, A. Dauscher, B. Malaman, C. Semprimoschnig and B. Lenoir, Phys. Rev. Mater., 2019, 3, 085404.
46. S. M. Tairov, B. F. Ormont and N. O. Sostak, Bulletin of the Academy of Sciences of the USSR, Inorganic Materials series, 1970, 6, 1584.
47. R. Maselsky and M. S. Lubell, Adv. Chem. Ser., 1963, 39, 210.
48. E. I. Rogacheva, G. V. Gorne, N. K. Zhigareva and A. B. Ivanova, Inorg. Mater., 1991, 27, 194.
49. Y. I. Ravich, Semiconducting Lead Chalcogenides, Plenum Press, New York, NY, 1979, and references therein.
50. C. M. Jaworski, M. D. Nielsen, H. Wang, S. N. Girard, W. Cai, W. D. Porter, M. G. Kanatzidis and J. P. Heremans, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 045203.
51. R. F. Brebrick, J. Phys. Chem. Solids, 1971, 32, 551.
52. Y. G. Sha and R. F. Brebrick, J. Electron. Mater., 1989, 18, 421.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10841f

---