Open Access Article
Open Access ArticleHighly spin-polarized electronic structure and magnetic properties of Mn2.25Co0.75Al1−xGex Heusler alloys: first-principles calculations†
Yue Wanga,
Liying Wang *ab and
Wenbo Mi
*ab and
Wenbo Mi a
a
aTianjin Key Laboratory of Low Dimensional Materials Physics and Preparation Technology, School of Science, Tianjin University, Tianjin 300354, China. E-mail: liying.wang@tju.edu.cn
bTianjin Demonstration Center for Experimental Physics Education, School of Science, Tianjin University, Tianjin 300354, China
First published on 12th June 2020
Abstract
Highly spin-polarized half-metals (HMs) and spin-gapless semiconductors (SGSs) are the promising candidates in spintronic devices. However, the HM and SGS Heusler materials are very sensitive to the stoichiometric defects and lattice distortion, which will be not beneficial to the practical applications. Here, the electronic structure and magnetic properties of Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) Heusler alloys were investigated by first-principles calculations. Large negative formation energy, cohesive energy and phonon spectra confirm that the Mn2.25Co0.75Al1−xGex alloys are stable. It is found that Mn2.25Co0.75Al1−xGex with x = 0, 0.25, 0.75 and 1.00 show robust ferrimagnetic HM characteristics, while Mn2.25Co0.75Al0.5Ge0.5 shows robust SGS characteristic. Under the hydrostatic and uniaxial strains, Mn2.25Co0.75Al1−xGex exhibit a series of rich electronic transitions. The magnetic anisotropy of Mn2.25Co0.75Al1−xGex turns from the in-plane [100] direction to the out-of-plane [001] one by applying the uniaxial strains. The results suggest that the complete spin polarizations of Mn2.25Co0.75Al1−xGex alloys are robust against the stoichiometric defects and lattice distortion, which have potential applications in spintronic devices.
1 Introduction
The half-metals (HMs)1 and spin-gapless semiconductors (SGSs)2 with high spin polarization have been paid much attention as the promising candidates in spintronic devices. HM was firstly predicted in NiMnSb by de Groot et al.,3 where one spin channel is metallic and the other spin channel is semiconducting. Thus, HM can provide 100% spin polarized current. Up to now, HMs have been found in Heusler alloys,4–7 diluted magnetic semiconductors,8,9 perovskite compounds,10,11 two dimensional materials,12–14 zinc blende compounds,15,16 nanowires,17 nanoribbons18,19 and nanotubes,20 etc. SGS was firstly theoretically proposed and experimentally verified in Co-doped PbPdO2,21 where one spin channel is semiconducting and the other has an almost vanishing zero-width band gap at Fermi level. SGSs have been widely observed in Heusler alloys,22–24 nanoribbons,25 two-dimensional materials26,27 and perovskite compounds,28,29 etc. Both the electrons and holes in SGS and HM are 100% spin polarized, where no threshold energy needs to excite them from occupied states to empty ones. The special band structure of SGS leads to some unique properties, such as (i) high carrier mobility, (ii) tunable physical properties by external influences, (iii) the coexistence of high resistance and high Curie temperature, (iv) new spin injection source to overcome the conductivity mismatch. HM can provide the completely spin-polarized current, which is an ideal candidate in spintronic devices with high speed and low power consumption. Therefore, HMs and SGSs are attractive in spintronic devices, such as spin valves, spin diodes and spin filters.30–32Heusler alloy is a remarkable class of intermetallic materials,33 which has attracted much attention due to highly ordered atomic occupation and abundant atomic arrangement. The general formula of full Heusler alloy is the L21 ordered X2YZ (Cu2MnAl-type) with a space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, like Co2MnAl,34 where X and Y are the transition metal elements, and Z are s–p elements. The full Heusler structure has four formula units per cubic unit cell with the atomic sequence X–Y–X–Z, two X occupy the Wyckoff-positions namely A (0, 0, 0) and C (1/2, 1/2, 1/2) sites, Y occupies B (1/4, 1/4, 1/4) sites and Z occupies D (3/4, 3/4, 3/4) sites, respectively. Generally, when X is less electronegative than Y, the atomic sequence changes to X–X–Y–Z27,35 as Hg2CuTi-type, which is also known as the inverse Heusler alloy with a space group of F
m, like Co2MnAl,34 where X and Y are the transition metal elements, and Z are s–p elements. The full Heusler structure has four formula units per cubic unit cell with the atomic sequence X–Y–X–Z, two X occupy the Wyckoff-positions namely A (0, 0, 0) and C (1/2, 1/2, 1/2) sites, Y occupies B (1/4, 1/4, 1/4) sites and Z occupies D (3/4, 3/4, 3/4) sites, respectively. Generally, when X is less electronegative than Y, the atomic sequence changes to X–X–Y–Z27,35 as Hg2CuTi-type, which is also known as the inverse Heusler alloy with a space group of F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, like Mn2CoAl.36,37 When one of the X atoms is removed, a C1b-ordered half-Heusler structure XYZ (MgAgAs-type) with a space group of F
3m, like Mn2CoAl.36,37 When one of the X atoms is removed, a C1b-ordered half-Heusler structure XYZ (MgAgAs-type) with a space group of F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m can be derived. Further, when one of X atoms is replaced by another transition metal element M, a quaternary Heusler alloys X–M–Y–Z (LiMgPdSb-type) with a space group F
3m can be derived. Further, when one of X atoms is replaced by another transition metal element M, a quaternary Heusler alloys X–M–Y–Z (LiMgPdSb-type) with a space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m is obtained.
3m is obtained.
Lots of HMs and SGSs have been found in experiment and theory.38–45 HMs and SGSs in Heusler alloys attract much attention due to the tunable electronic structures, high Curie temperature,46–52 simple preparation procedure53,54 and tunable magnetic anisotropy energy (MAE),55,56 etc. However, the stoichiometric defect in Heusler alloys can destroy the HM and SGS characteristics, which usually happens during the preparation of bulk materials and thin films. Meanwhile, the HM and SGS characteristics can also be destroyed by lattice distortion due to the temperature or pressure changes.57 Thus, the HMs and SGSs verified in experiments are much less than that predicted theoretically. Therefore, it is important to find the completely spin-polarized HM and SGS which are robust against the stoichiometric defects and lattice distortion. Additionally, the substitution is an effective way to tailor the electronic structure,58–64 where the first SGS was obtained by substituting Co atom for Pd in PbPdO2.21,22 Ayuela et al. firstly reported that Co2MnGa has a large spin-up density of states (DOS) at the Fermi level, while spin-down density of states at the Fermi level nearly vanishes, which results a high spin polarization despite it's not completely spin-polarized.65 In the further exploration work, Varaprasad proved that the spin-polarization can be definitely increased in Co2MnGa0.5Sn0.5 by substituting Sn atom for Ga in Co2MnGa.66 Feng et al. found that Mn2Co0.75Cr0.25Al can maintain the half-metallicity even though the lattice structure is disordered.67 Li et al. found that the magnetic properties of Fe4N can be tailored by doping rare-earth elements.68
Mn2CoAl Heusler alloy has attracted great attention since its SGS behavior has been confirmed experimentally by Felser et al.22 The complete spin polarization of SGS makes Mn2CoAl a promising candidate in spintronic devices. However, the SGS characteristics of Mn2CoAl were sensitive to the external strains, dopants and atomic disorder. Jamer et al. reported that the tetragonal distortion and atomic disorder which were introduced in epitaxial growth destroyed the SGS characteristics of Mn2CoAl film on GaAs substrate.69 It is necessary to address the issues of stoichiometry and chemical ordering of the sublattices. Galanakis et al. and Chen et al. pointed that the atomic swaps and Co-surplus during growth can destroy the SGS characteristics of Mn2CoAl.70,71 Mn2CoGe is another HM with complete spin polarization.37 It was reported that the high spin-polarized characteristics of Mn2CoAl and Mn2CoGe are robust and insensitive to Mn–Co disorder.72 In this work, the electronic structure and magnetic properties of Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys are investigated by first-principles calculations. It is found that Mn2.25Co0.75Al1−xGex alloys are stable, where the complete spin polarization is robust against the stoichiometric defects and lattice distortion. Meanwhile, the electronic structure and MAE of Mn2.25Co0.75Al1−xGex can be tailored by applying hydrostatic and uniaxial strains. These results indicate that Mn2.25Co0.75Al1−xGex alloys have the potential applications in spintronic devices for spin filter, high-density magnetic recording media etc.
2 Calculation details
The calculations are performed by Vienna Ab initio Simulation Package based on density functional theory.73,74 The exchange correlation functional selects the Perdew–Burke–Ernzerhof75 under generalized gradient approximation.76 The projector augmented wave77 method is used to describe the interaction between electrons and ions. The energy cutoff for plane-wave basis set is 500 eV. The valence electrons of Al, Mn, Co and Ge are 3s23p1, 3d64s1, 3d84s1 and 4s24p2, respectively. The Brillouin zone integration is performed using Monkhorst–Pack of 13 × 13 × 13. The convergence criteria of the energy and atomic force are set to 1 × 10−6 eV per atom and 1 × 10−3 eV Å−1, respectively. Phonon spectrum is calculated by PHONOPY code78 for Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00). Electronic structure and magnetic properties are calculated by considering the hydrostatic and uniaxial strains. The hydrostatic strain is defined as| εu = (a − a0)/a0 × 100%. | (1) |
The uniaxial strain is defined as
| εt = a/c × 100% | (2) |
The MAE is obtained based on the magnetic force theorem method.79 In order to get the reliable results, we have improved the accuracy of the MAE calculations with a much denser Monkhorst–Pack 32 × 32 × 32 k point meshes in the Brillouin zone.80 Firstly, the accurate collinear calculation in the ground state is performed with 32 × 32 × 32 Monkhorst–Pack k point meshes. Then, the spin–orbital coupling is taken into account non-self-consistently to calculated the energy for [001] and [100] directions of the magnetic moment. Finally, MAE is calculated from the energy difference between the magnetic moment aligning along [001] and [100] directions,81 which can be written as
| MAE = E[001] − E[100] | (3) |
| MAEiλ = E[001]iλ − E[100]iλ | (4) |
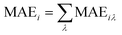 | (5) |
The sum of MAEi over all of the atoms in the same atomic layer is the layer-resolved MAE.
3 Results and discussion
3.1 Lattice structure
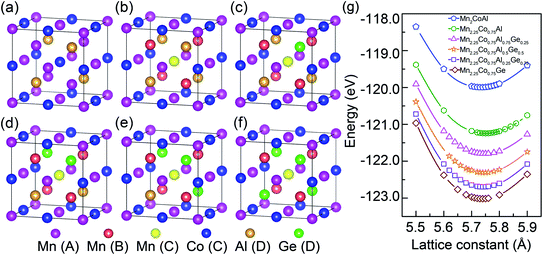
In inverse Heusler alloy Mn2CoAl, Mn atoms occupy the Wyckoff-positions A (0, 0, 0) and B (1/4, 1/4, 1/4), which are labeled as Mn(A) and Mn(B), respectively. Co and Al atoms occupy C (1/2, 1/2, 1/2) and D (3/4, 3/4, 3/4), which are labeled as Co(C) and Al(D), respectively. So, the atomic sequence of Mn2CoAl is Mn–Mn–Co–Al, as shown in Fig. 1(a). In order to construct Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys, Co and Al atoms in Mn2CoAl are consecutively replaced by Mn and Ge. In a supercell with 4 formula units, 1 Co atom is substituted randomly by Mn and 0–4 Al atoms are substituted randomly by Ge. Fig. 1(b)–(f) show the atomic structure of Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys.Fig. 1(g) shows the dependence of calculated total energy on lattice constant of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys. The optimized equilibrium lattice constants are summarized in Table 1. In Fig. 1(g) and Table 1, the equilibrium lattice constant of Mn2CoAl is 5.73 Å, which is consistent with the previous results.84,85 The equilibrium lattice constants are 5.75 Å and 5.74 Å for Mn2.25Co0.75Al1−xGex (x = 0 and 0.25) and Mn2.25Co0.75Al1−xGex (x = 0.50, 0.75 and 1.00), respectively. The small variation of the equilibrium lattice constants can be ascribed to the similar atomic radius of Co and Mn atoms, as well as Al and Ge atoms.
| Alloys | a0 | Mtot | MMn(A) | MMn(B) | MMn(C) | MCo(C) | MAl(D) | MGe(D) | Efor | Ecoh |
|---|---|---|---|---|---|---|---|---|---|---|
| Mn2CoAl | 5.73 | 2.00 | −1.54 | 2.63 | — | 0.95 | −0.01 | — | −1.59 | −15.77 |
| Mn2.25Co0.75Al | 5.75 | 1.50 | −1.59 | 2.67 | −1.15 | 0.94 | 0 | — | −1.44 | −15.24 |
| Mn2.25Co0.75Al0.75Ge0.25 | 5.75 | 1.75 | −1.43 | 2.71 | −0.93 | 0.93 | 0 | 0.03 | −1.45 | −14.01 |
| Mn2.25Co0.75Al0.5Ge0.5 | 5.74 | 2.00 | −1.23 | 2.73 | −0.69 | 0.89 | 0 | 0.02 | −1.44 | −12.78 |
| Mn2.25Co0.75Al0.25Ge0.75 | 5.74 | 2.25 | −1.01 | 2.75 | −0.59 | 0.88 | 0 | 0.02 | −1.41 | −11.51 |
| Mn2.25Co0.75Ge | 5.74 | 2.50 | −0.82 | 2.78 | −0.69 | 0.87 | — | 0.02 | −1.36 | −10.22 |
3.2 Electronic structure and magnetic properties
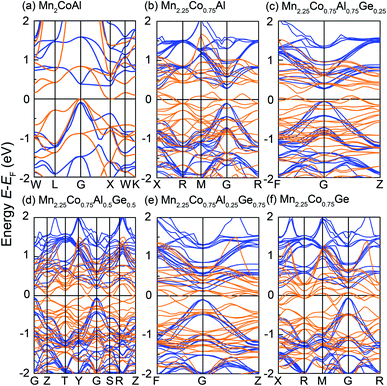
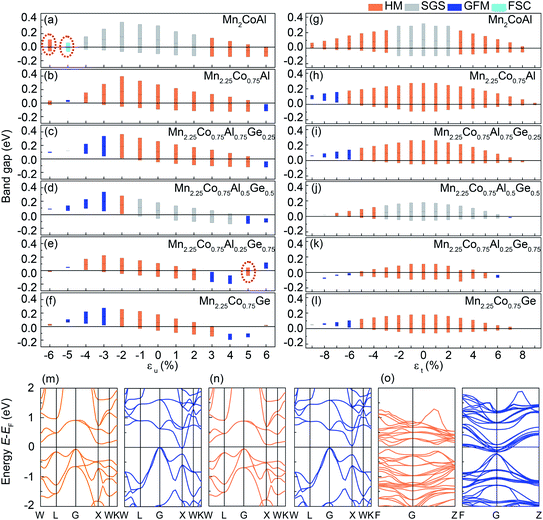
Fig. 2 shows the spin-resolved band structure of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys at the equilibrium lattice constant. It is found that the Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys show a semiconducting characteristic with a distinct energy gap in the spin-down channel (Fig. 2). The gap between the valence band maximum (VBM) and conduction band minimum (CBM) appears at G point of Brillouin zone (BZ), which is 0.384, 0.366, 0.308, 0.234, 0.201 and 0.238 eV for Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00), respectively. However, the spin-up band structure of Mn2.25Co0.75Al1−xGex is different from Mn2CoAl. In Mn2CoAl, the VBM at G exactly touches the bottom of the CBM at X, which is a typical indirect zero-width gap at Fermi level in spin-up channel. So, Mn2CoAl shows the SGS characteristics, which is in well agreement with the previous results.22,85 In Fig. 2(d), the band structure of Mn2.25Co0.75Al0.5Ge0.5 shows the similar characteristics to Mn2CoAl, which is also a SGS candidate at its ground state. However, in Mn2.25Co0.75Al, Mn2.25Co0.75Al0.75Ge0.25, Mn2.25Co0.75Al0.25Ge0.75 and Mn2.25Co0.75Ge, Ge substitution leads to continuous bands across EF in spin-up channel, so all of them are HMs. Thus, the Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys are completely spin-polarized. A new kind of materials with complete spin polarization is predicted, which are robust against the stoichiometric defects.Next, the effects of doped Mn and Ge on the band structure will be discussed in details. In Fig. 2(b), the partial Mn doping in Mn2.25Co0.75Al creates a dense energy level around Fermi level and pushes the zero energy gap in spin-up channel to higher energy direction, resulting in a metallic characteristic in spin-up channel. So, the SGS characteristics disappear. However, the zero-width energy gap in the spin-up channel still exists in a higher energy region above EF in Mn2.25Co0.75Al. It was expected that, with further doping of Ge, EF should gradually shift towards to the conduction band edge. At x = 0.5, EF exactly locates at the zero-width gap in Mn2.25Co0.75Al0.5Ge0.5, showing a SGS characteristic. With further Ge substitution, EF continuously shifts to a higher energy. Finally, the energy gap shifts below EF in Mn2.25Co0.75Al0.25Ge0.75 and Mn2.25Co0.75Ge, which results in the HM characteristics.
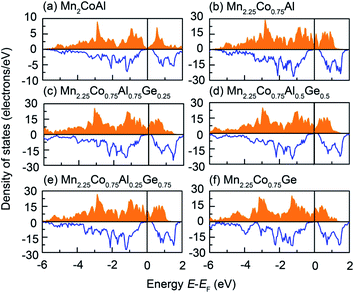
The total DOS of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) have been shown in Fig. 3. In Fig. 3, one can clearly see that the semiconducting band gaps appear in spin-down channels of the Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys. However, the spin-up electronic states go across Fermi level for all alloys, showing the HM characteristics with 100% spin polarization. In Mn2CoAl and Mn2.25Co0.75Al0.5Ge0.5, EF just falls into a zero-width energy gap, yielding a SGS nature. By comparing Fig. 3(a) with Fig. 3(b), it can be seen that the dense states appear around EF in spin-up channel, which can attribute to the doped Mn. The slight EF shift along the energy axis can be ascribed to the contribution of the doped Ge.
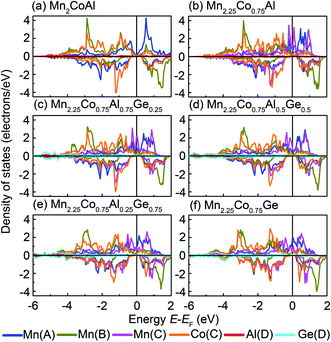
Fig. 4 shows the partial DOS of d components for Mn(A), Mn(B), Mn(C) and Co(C), as well as s/p states of Al(D) and Ge(D). It is found that a strong hybridization appears between the transition-metal atoms. In Fig. 3 and 4, three peaks occur in the spin-up channel. Two peaks of them locate in a lower energy region, which can be ascribed to the bonding states of Mn(B) and Co(C) sites. The peak at a higher energy region is mainly composed of the antibonding states of Mn(A) and Mn(C) atoms. In Mn2.25Co0.75Al1−xGex, two sharp peaks appear around Fermi level, where is a zero gap in Mn2CoAl. These two peaks mainly come from the doped Mn(C) atom and move to a lower energy by doping Ge atoms. In the spin-down channel, the large band gap near EF is kept for the Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00). A strong covalent hybridization happens between the d states of Mn(A), Mn(B), Mn(C) and Co(C) atoms, resulting in the formation of the bonding and antibonding bands separated by the gap. Similar to Mn2CoAl, in the Mn2.25Co0.75Al1−xGex, the situations of Mn(A), Mn(C) and Co(C) atoms are different from Mn(B) atom. The partial DOS of Mn(A), Mn(C) and Co(C) have a similar gap width, while the Mn(B) atom has a larger gap width. Hence, the actual gap width in Mn2.25Co0.75Al1−xGex alloys is mainly determined by Mn(A), Mn(C) and Co(C) atoms. The occupied bonding states at a lower energy region and unoccupied antibonding bands at 0.5–1.0 eV can be mainly attributed to Mn(A), Mn(C) and Co(C). The peak around 1.3 eV mainly arises from the antibonding nature of Mn(B) atom. Thus, the doped Mn(C) atom has a strong covalent hybridization with the other transition-metals in Mn2.25Co0.75Al1−xGex, which has an evident influence on the electronic states around EF. Whereas, the doped Ge atoms mainly contribute more valence electrons in a lower energy region and push the EF to a higher energy direction.
The total and atomic resolved magnetic moments of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) are listed in Table 1. The total magnetic moment of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) per unit formula is 2.00, 1.50, 1.75, 2.00, 2.25 and 2.50 μB, respectively. The change of magnetic moments obeys the Slater-Pauling rule of Mt = Zt − 24, where Mt is the total magnetic moment and Zt is the number of valence electrons. Fig. 5 shows the variation of magnetic moments of Mn(A), Mn(B), Mn(C), Co(C) and total magnetic moments per formula unit of Mn2.25Co0.75Al1−xGex at different x. In Fig. 5, it is found that the total magnetic moment of Mn2.25Co0.75Al1−xGex almost increases linearly with Ge concentration, which can be ascribed to the decrease of the negative magnetic moments of Mn(A) and Mn(C) atoms. The magnetic moment of Mn(A) is antiparallel to that of Mn(B) and Co(C) atoms, but is parallel to Mn(C) atom. Mn(A) and Mn(C) atoms contribute the negative magnetic moments, while Mn(B) and Co(C) atoms contribute the positive values. Mn(B) is the main contributor to the total positive magnetic moments. At different Ge concentrations, the positive magnetic moments of Mn(B) and Co(C) almost remain unchanged. However, the negative moments of Mn(A) and Mn(C) decrease with the increase of Ge concentration. Combined with Table 1, it can be found that the variations of all the Mn and Co atomic magnetic moments are negligible when Al concentration was fixed as 100% (Mn2CoAl and Mn2.25Co0.75Al). However, the substitution of nonmagnetic Ge atom affects the magnetic moments of Mn(A) and Mn(C) appreciably. As discussed in Fig. 3 and 4, the doped Ge atoms mainly contribute more valence electrons in a lower energy region, which leads to an increasement of the occupied states and pushes the EF to the higher energy direction. From Fig. 4, it can be seen that there is a clearly unoccupied antibonding peak above the EF in the spin-up channel for Mn2.25Co0.75Al1−xGex, which is mainly composed of the antibonding states of Mn(A) and Mn(C) atoms. Therefore, with the increasing Ge concentration in Mn2.25Co0.75Al1−xGex, the antibonding states of Mn(A) and Mn(C) move to lower energy region and the spin-splitting of Mn(A) and Mn(C) atoms will be reduced, which leads to the obviously reduction of Mn(A) and Mn(C) magnetic moments. In addition, the magnetic moments of Al and Ge atoms are comparatively negligible. So, Mn2CoAl and Mn2.25Co0.75Al1−xGex are ferrimagnetic HM/SGS materials with complete spin polarization.
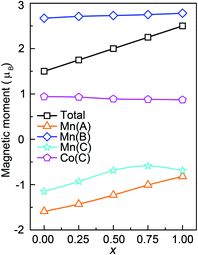 | ||
| Fig. 5 Calculated total (per formula unit) and atomic magnetic moments of Mn2.25Co0.75Al1−xGex at different x. | ||
In order to investigate the effects of spin–orbit coupling (SOC), the electronic structure of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) is also calculated by considering SOC, as shown in Fig. S1.† It is found that SOC does not affect the HM/SGS characteristics of Mn2CoAl and Mn2.25Co0.75Al1−xGex. Only some degenerated states are split into several singlet states at the high symmetry points. Thus, in the next sections (except for the MAE results), SOC also has not been considered.
Owing to the special band structures, the HM and SGS characteristics are sensitive to the stoichiometric defects, which usually happen during the preparation of Heusler bulk materials and thin films. Jamer et al. found that the atomic disorder which was introduced in epitaxial growth destroyed the SGS characteristics of Mn2CoAl films.69 Galanakis et al. and Chen et al. reported that Co-surplus and atomic swaps during growth also lead to the vanishing of the SGS characteristics in Mn2CoAl.70,71 Zhou et al. found that the substitution of Al by Si in Ti2NiAl Heusler alloy destroyed its HM characteristics.86 However, the present results clearly show that the Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys are new ferrimagnetic HM or SGS materials with 100% spin polarization, which is stable against the stoichiometric defects. The robust complete spin-polarization of Mn2.25Co0.75Al1−xGex alloys makes them series promising candidates for the practical applications in spintronics devices.
3.3 Structure stability
It is necessary to check the structure stability of the alloys. Firstly, the formation energies (Efor) of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) have been calculated based on the following formula| Efor = Etotal − 2EbulkMn − EbulkCo − EbulkAl | (6) |
| Efor = Etotal − 2.25EbulkMn − 0.75EbulkCo − (1 − x)EbulkAl − xEbulkGe | (7) |
| Ecoh = Etotal − 2EisoMn − EisoCo − EisoAl | (8) |
| Ecoh = Etotal − 2.25EisoMn − 0.75EisoCo − (1 − x)EisoAl − xEisoGe | (9) |
Furthermore, the phonon spectra of Mn2CoAl and Mn2.25Co0.75Al1−xGex at equilibrium lattice are shown in Fig. 6. Evidently, the spectra of all the alloys have no imaginary frequencies, which means that Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) are dynamical stable. The structure stability indicates that Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.5, 0.75 and 1.00) may be realized in experiments. Fortunately, the Mn2CoAl bulk and thin films have been successfully fabricated in experiments and proved to be SGS in previous reports.67,68,83
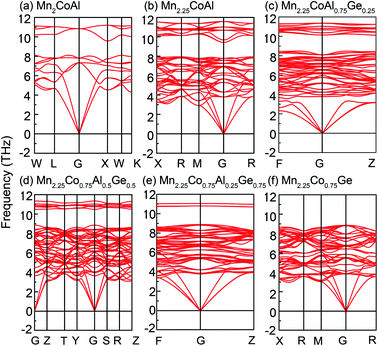 | ||
| Fig. 6 Phonon spectrum of (a) Mn2CoAl, (b) Mn2.25Co0.75Al, (c) Mn2.25Co0.75Al0.75Ge0.25, (d) Mn2.25Co0.75Al0.5Ge0.5, (e) Mn2.25Co0.75Al0.25Ge0.75 and (f) Mn2.25Co0.75Ge. | ||
3.4 Effects of hydrostatic and uniaxial strains
It was known that the lattice deformation usually occurs during the film growth on different substrates. According to the previous theoretical and experimental results,87 the electronic structure and magnetic properties of Heusler alloys are tunable under the hydrostatic (εu) and uniaxial (εt) strains. Owing to the varying of the lattice constant, the inter-atomic hybridization interaction and intra-atomic exchange interaction between transitional metal elements will be affected, which will influence the energy dispersion of the valence and conduction bands in the two spin directions. Here, the hydrostatic and uniaxial strains effects on Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) are considered in the calculations. Fig. 7(a)–(i) show the location and width of the band gaps in spin-down channel of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) under hydrostatic and uniaxial strains, where the top of the bar represents the CBM location, the bottom of the bar represents the VBM location and the height of the bar indicates the bandwidth. In Fig. 7(a)–(f), the hydrostatic strain (εu) is considered from −6% to 6% in Mn2CoAl and Mn2.25Co0.75Al1−xGex, where the positive and negative εu represent the tensile and compressive strains, respectively. In Fig. 7(a)–(f), the HM or SGS characteristics of Mn2CoAl and Mn2.25Co0.75Al1−xGex are quite robust against the varying εu. The half–metallic properties of Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.75 and 1.00) can be maintained in the εu range of −4–5%, −2–5%, −4–2% and −2–3%, respectively. The SGS properties of Mn2CoAl and Mn2.25Co0.75Al0.5Ge0.5 can be kept in the εu range of −5–2% and −1–4%, respectively. The wide εu ranges where Mn2CoAl and Mn2.25Co0.75Al1−xGex can keep the HM and SGS characteristics indicate the robust stabilities of their HM and SGS properties. In Fig. 7(a)–(f), one can see that not only the gap width changes with the hydrostatic strains, but also the location of the gaps shift to lower or higher energy region. As a result, the rich electronic structure can be derived in Mn2CoAl and Mn2.25Co0.75Al1−xGex alloys. It should be noted that, for Mn2CoAl, the spin direction of the conducting channel also changes with the hydrostatic strains. In Fig. 7(a), one can see that Mn2CoAl undergoes HM with spin-up as conducting channel (εu = −6%, as shown in Fig. 7(m)) → ferromagnetic semidoncuctor (FSC, εu = −5%, as shown in Fig. 7(n)) → SGS with spin-down as conducting channel (in the εu range of −4–2%) → HM with spin-down as conducting channel (in the εu range of 3–6%) transitions with the varying hydrostatic strains, which is consistent with the previous result.88 For Mn2.25Co0.75Al1−xGex alloys, Mn2.25Co0.75Al undergoes HM → general ferrimagnetic metal (GFM) → HM → GFM transitions (Fig. 7(b)). In Fig. 7(c), Mn2.25Co0.75Al0.75Ge0.25 undergoes GFM → HM → GFM transitions. In Fig. 7(d), Mn2.25Co0.75Al0.5Ge0.5 undergoes GFM → HM → SGS → GFM transitions. In Fig. 7(f), Mn2.25Co0.75Ge undergoes HM → GFM → HM → GFM transitions. Particularly, Mn2.25Co0.75Al0.25Ge0.75 alloy can transfer from a HM to another HM with band gaps in opposite spin channels, which is similar to that of Mn2CoAl. Namely, in Fig. 7(e), Mn2.25Co0.75Al0.25Ge0.75 undergoes HM with spin-up as conducting channel (εu = −6%) → GFM (εu = −5%) → HM with spin-up as conducting channel (in the εu range of −4–2%) → GFM (in the εu range of 3–4%) → HM with spin-down as conducting channel (εu = 5%, as shown in Fig. 7(o)) → GFM (εu = 6%) transitions, which can be derived from the different responses of the spin-up and spin-down electrons under strains. This rich electronic structures transition indicates that the spin polarization can be manipulated via applying external pressure and the polarized current direction of the spintronic devices may be inversed under extra influence, which will be good spintronics candidates used in pressure involved fields. The diverse and tunable electronic structures of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) make them quite promising to realize the relative spintronic applications in the future.The effects of uniaxial strains (εt) on the electronic structure of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) are also investigated. In Fig. 7(g)–(l), the HM or SGS characteristics of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) are robust to the uniaxial strains. The HM properties of Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.75 and 1.00) can be preserved in the εt ranges of −6–9%, −5–8%, −5–5% and −5–7%, respectively. The SGS properties of Mn2CoAl just can be kept in a relative narrow εt range of −2–2%, but it turns into HM at other εt. It has been found that the SGS characteristic of Mn2CoAl films on GaAs was destroyed when a tetragonal distortion was introduced during the epitaxial growth.68 However, the SGS characteristic of Mn2.25Co0.75Al0.5Ge0.5 can be kept in a wide εt range of −3–6%, which is better than Mn2CoAl for practical applications. All of the alloys exhibit the electronic transitions under the uniaxial strains, as shown in Fig. 7(g)–(l). Namely, Mn2CoAl undergoes the transition of HM → SGS → HM under the uniaxial strains, as shown in Fig. 7(g). Mn2.25Co0.75Al undergoes a GFM → HM transition, as shown in Fig. 7(h). Mn2.25Co0.75Al0.75Ge0.25 undergoes the GFM → HM transition as shown in Fig. 7(i). Mn2.25Co0.75Al0.5Ge0.5 undergoes the transition of HM → SGS → GFM (Fig. 7(j)). Mn2.25Co0.75Al0.25Ge0.75 undergoes the transition of GFM → HM → GFM (Fig. 7(k)). Mn2.25Co0.75Ge undergoes a GFM → HM transition (Fig. 7(l)). In Fig. 7(g)–(l), both the CBM and VBM shift towards Fermi level under the uniaxial strains, which results in the decrease of the bandwidth. The maximum bandwidth of Mn2CoAl and Mn2.25Co0.75Al1−xGex appears at the ground state (εt = 0%).
The lattice deformation usually occurs during the film growth on different substrates, which may serve to destroy the HM and SGS properties. As reported by Jamer et al., the SGS characteristics of Mn2CoAl film on GaAs substrate were destroyed because the tetragonal distortion was introduced during epitaxial growth.69 However, the HM and SGS characteristics of Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) alloys are quite robust against the lattice distortions. Furthermore, the electronic structures of them can be tailored by the hydrostatic and uniaxial strains, which are beneficial to design the novel flexible spintronic devices.
3.5 Magnetic anisotropy
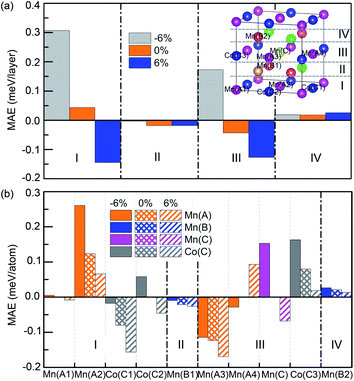
Ferromagnetic materials with the high magnetic anisotropy have attracted much attention for application in high-density magnetic recording media and nonvolatile magnetoresistive random access memory. The MAE of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) at the ground state is calculated. However, the calculated results show that the MAEs of all these alloys are nearly zero due to the cubic structure. Generally, the anisotropy of the ferromagnet is a combined effect of SOC and electrostatic crystal-field interactions. However, in cubic environments, cubic crystal-field states of 3d wave function are nearly quenched, which will lead to a zero MAE. Under the uniaxial strain, the cubic symmetry of Mn2CoAl and Mn2.25Co0.75Al1−xGex turns into the tetragonal symmetry, which can result in asymmetrical crystal field to enhance the magnetic anisotropy. Fig. 8 shows the MAEs of Mn2CoAl and Mn2.25Co0.75Al1−xGex at different uniaxial strains. Here, the negative MAE represents the magnetic easy axis along [001] direction (out of plane direction), and the positive one means the magnetic easy axis along [100] direction (in-plane direction). In Fig. 8, the similar trend appears in all the alloys at different uniaxial strains. By applying the uniaxial strain, the positive MAE turns into negative one, where MAE is positive at compressive strains and negative at tensile strains. Therefore, the magnetic anisotropy of the alloys can be tailored from in-plane direction to perpendicular one by applying the uniaxial strains. Meanwhile, the MAE value almost linearly increases with the increased compressive or tensile strain. Mn2.25Co0.75Al0.25Ge0.75 shows the biggest MAE at the uniaxial strain of −9% and 9%, which are 0.92 meV per unit cell and −0.88 meV per unit cell, respectively.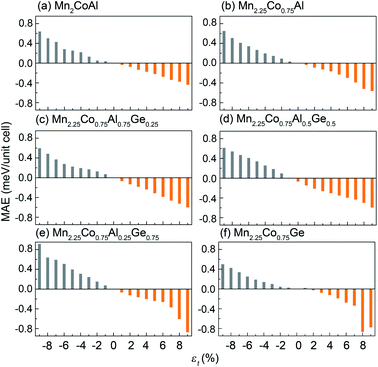 | ||
| Fig. 8 MAE for (a) Mn2CoAl, (b) Mn2.25Co0.75Al, (c) Mn2.25Co0.75Al0.75Ge0.25, (d) Mn2.25Co0.75Al0.5Ge0.5, (e) Mn2.25Co0.75Al0.25Ge0.75 and (f) Mn2.25Co0.75Ge at different uniaxial strains. | ||
In order to further analyze the origin of the strain-dependent MAEs of Mn2.25Co0.75Al1−xGex, the layer and atom-resolved MAEs are calculated. Since the alloys show the similar MAE profiles (Fig. 8), only the layer and atom-resolved MAE of Mn2.25Co0.75Al0.25Ge0.75 is shown to discuss the MAE's origin, as shown in Fig. 9. The atom-resolved MAEs of Mn2CoAl and Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.5, 1.00) have been shown in the ESI Fig. S2.† Owing to the element substitution and lattice distortion, the lattice symmetry is reduced, which results in different kinds of Mn(A), Mn(B) and Co(C) atoms, as shown in the inset of Fig. 9(a). The contribution of different Mn(A), Mn(B) and Co(C) atoms to MAE is different from each other. In Fig. 9(a), I/IV and II/III layers of the cubic Mn2.25Co0.75Al0.25Ge0.75 (εt = 0%) exhibit a minor opposite MAE, which leads to a nearly zero MAE. The zero MAE mainly comes from the minor opposite MAE of Mn(A2) atom in I-layer and Mn(A3) atom in III-layer, as shown in Fig. 9(b). However, at εt = −6%, MAE of each layer becomes positive, where the MAE of I- and III-layers significantly increases. The positive MAE can mainly be attributed to Mn(A2) and Co(C2) atom in I-layer, Mn(C) and Co(C3) atoms in III-layer. Mn(A3) atom in III-layer contributes a relatively small negative MAE. So Mn2.25Co0.75Si0.25Ge0.75 exhibits the in-plane magnetic anisotropy at εt = −6%. At εt = 6%, every layer contributes a negative MAE, where Co(C1), Co(C2), Mn(A3), Mn(C) in I-, III-layers gives much contribution. Thus, the magnetic easy axis turns from the in-plane direction into the out-of-plane one.
Based on the second-order perturbation theory,81,89 MAE can be defined as
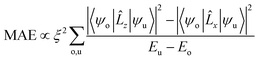 | (10) |
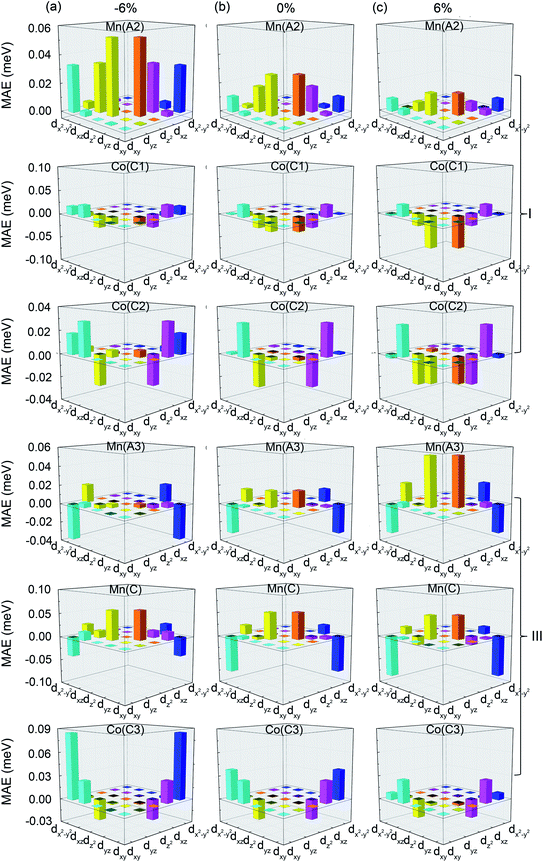 | ||
| Fig. 10 Orbital-resolved MAE of Mn(A2), Co(C1), Co(C2) atoms in I-layer and Mn(A3), Mn(C), Co(C3) atoms in III-layer of Mn2.25Co0.75Al0.25Ge0.75 at (a) εt = −6%, (b) εt = 0%, and (c) εt = 6%. | ||
The MAE results show that the magnetic anisotropy of the series Mn2.25Co0.75Al1−xGex can be tailored from in-plane direction to perpendicular one under the uniaxial strains. Furthermore, the MAE values exhibit a linear dependence on uniaxial strains. It has been demonstrated experimentally that the easy axis of magnetization in the inverse spinels CoFe2O4 and NiFe2O4 can be tuned from perpendicular direction to in-plane one under tensile and compressive strains, respectively.90,91 Thus, it may be an effective way to manipulate the magnetic anisotropy of Mn2.25Co0.75Al1−xGex by applying uniaxial strain. In addition, all the PMA values of Mn2.25Co0.75Al1−xGex can be up to more than −0.51 MJ m−3 (−0.6 meV per unit cell) at εt = 9% which is much larger than that of the reported Co-based Heusler films whose PMA values range from −0.09 MJ m−3 to −0.31 MJ m−3.55
4 Conclusions
In summary, the electronic structure, stability and magnetic properties of Mn2.25Co0.75Al1−xGex (x = 0, 0.25, 0.50, 0.75 and 1.00) are investigated by first-principles calculations. Our results reveal that the partial Mn doping in Mn2CoAl creates a dense energy level around Fermi level and pushes the zero energy gap in Mn2CoAl to higher energy direction, resulting in a metallic characteristic in Mn2.25Co0.75Al. The additional Ge atoms mainly contribute more valence electrons in a lower energy region and push the EF to a higher energy direction, resulting in half-metallic behaviors for Mn2.25Co0.75Al1−xGex with x = 0, 0.25, 0.75 and 1.00. However, at x = 0.5, EF exactly locates at the zero energy gap in Mn2.25Co0.75Al0.5Ge0.5, showing a SGS characteristic again. The series of the Mn2.25Co0.75Al1−xGex are confirmed that they are promising to be fabricated in experiment based on the stability calculational results. The HM or SGS characteristics of Mn2.25Co0.75Al1−xGex can be kept in wide ranges of hydrostatic and uniaxial strains. For example, the SGS characteristics of Mn2.25Co0.75Al0.5Ge0.5 can be kept in the wide εu and εt range of −1–4% and −3–6%, respectively, which is even better than that of Mn2CoAl for practical applications. The magnetic anisotropy energy of Mn2CoAl and Mn2.25Co0.75Al1−xGex are nearly zero due to the cubic structure. However, we show that the magnetic anisotropy energy in these alloys almost linearly improves with varying uniaxial strains, while showing an opposite response to compressive and tensile strain. As a result, the magnetic anisotropy of Mn2CoAl and Mn2.25Co0.75Al1−xGex can be manipulated from the in-plane [100] direction to the out-of-plane [001] one under uniaxial strains. The results suggest that Mn2.25Co0.75Al1−xGex alloys are very promising for spintronics applications such as spin injection and spin valves.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Nature Science Foundations of China (Grant No. 51701138) and Natural Science Foundation of Tianjin City (Grant No. 17JCQNJC02800, 16JCYBJC17200).Notes and references
- C. Lidig, J. Minár, J. Braun, H. Ebert, A. Gloskovskii, J. A. Krieger, V. Strocov, M. Kläui and M. Jourdan, Surface resonance of thin films of the Heusler half-metal Co2MnSi probed by soft X-ray angular resolved photoemission spectroscopy, Phys. Rev. B, 2019, 99(17), 174432 CrossRef CAS.
- X. L. Wang, Dirac spin-gapless semiconductors: promising platforms for massless and dissipationless spintronics and new (quantum) anomalous spin Hall effects, Natl. Sci. Rev., 2017, 4(2), 252–257 CrossRef CAS.
- R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024–2027 CrossRef CAS.
- M. Moradi, N. Taheri and M. Rostami, Structural, electronic, magnetic and vibrational properties of half-Heusler NaZrZ (Z = P, As, Sb) compounds discussion, Phys. Lett. A, 2018, 382(41), 3004–3011 CrossRef CAS.
- M. Ram, A. Saxena, A. E. Aly and A. Shankar, Half-metallicity in new Heusler alloys Mn2ScZ (Z = Si, Ge, Sn), RSC Adv., 2020, 10(13), 7661–7670 RSC.
- L. Fan, F. Chen and Z. Q. Chen, First-principles calculations of magnetism and half-metallic properties of CsYO2 (Y = V, Cr, Mn, Fe, Co, Ni) Heusler alloys, J. Magn. Magn. Mater., 2019, 478, 264–273 CrossRef CAS.
- S. Bahramian and F. Ahmadian, Half-metallicity and magnetism of quaternary Heusler compounds CoRuTiZ (Z = Si, Ge, and Sn), J. Magn. Magn. Mater., 2017, 424, 122–129 CrossRef CAS.
- W. Y. Yu, Z. L. Zhu, C. Y. Niu, C. Li, J. H. Cho and Y. Jia, Dilute magnetic semiconductor and half-metal behaviors in 3d transition-metal doped black and blue phosphorenes: a first-principles study, Nanoscale Res. Lett., 2016, 11, 1–9 CrossRef CAS PubMed.
- F. Ahmadian, Electronic and magnetic properties of diluted magnetic semiconductors Zn1−xVxSe in zincblende structure, Solid State Commun., 2011, 151(21), 1622–1626 CrossRef CAS.
- N. N. Zu, R. Li, Q. N. Li and J. Wang, Electronic and magnetic properties of Sr2MoBO6 (B = W, Re, Os): investigation of possible half metal, J. Magn. Magn. Mater., 2016, 399, 72–76 CrossRef CAS.
- L. Ding, D. D. Khalyavin, P. Manuel, J. Blake, F. Orlandi, W. Yi and A. A. Belik, Colossal magnetoresistance in the insulating ferromagnetic double perovskites Tl2NiMnO6: a neutron diffraction study, Acta Mater., 2019, 173, 20–26 CrossRef CAS.
- J. Y. Liu, Z. F. Liu, T. L. Song and X. Cui, Computational search for two-dimensional intrinsic half-metals in transition-metal dinitrides, J. Mater. Chem. C, 2017, 5(3), 727–732 RSC.
- F. Aguilera-Granja and A. Ayuela, Magnetism and distortions in two-dimensional transition-metal dioxides: on the quest for intrinsic magnetic semiconductor layers, J. Phys. Chem. C, 2020, 124(4), 2634–2643 CrossRef.
- J. M. Zheng, R. J. He, Y. Wan, P. J. Zhao, P. Guo and Z. Y. Jiang, Half-metal state of a Ti2C monolayer by asymmetric surface decoration, Phys. Chem. Chem. Phys., 2019, 21(6), 3318–3326 RSC.
- J. E. Pask, L. H. Yang, C. Y. Fong, W. E. Pickett and S. Dag, Six low-strain zinc-blende half metals: an ab initio investigation, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(22), 224420 CrossRef.
- M. Moradi, M. Rostami and M. Afshari, Half-metallic ferromagnetism in wurtzite and rocksalt TiTe: a density functional theory study, Comput. Mater. Sci., 2013, 69, 278–283 CrossRef CAS.
- P. Lou and J. Y. Lee, Singular nonmagnetic semiconductor SCH3 molecular nanowire: a new type of room-temperature spintronic material, J. Phys. Chem. C, 2019, 123(27), 16994–17001 CrossRef CAS.
- Y. W. Son, M. L. Cohen and S. G. Louie, Half-metallic graphene nanoribbons, Nature, 2006, 444(7117), 347–349 CrossRef CAS PubMed.
- S. C. Zhu, C. T. Yip, S. J. Peng, K. M. Wu, K. L. Yao, C. L. Mak and C. H. Lam, Half-metallic and magnetic semiconducting behaviors of metal-doped blue phosphorus nanoribbons from first-principles calculations, Phys. Chem. Chem. Phys., 2018, 20(11), 7635–7642 RSC.
- K. W. Lee and C. E. Lee, Half-Metallic Carbon Nanotubes, Adv. Mater., 2012, 24(15), 2019–2023 CrossRef CAS PubMed.
- X. L. Wang, Proposal for a new class of materials: spin gapless semiconductors, Phys. Rev. Lett., 2008, 100(15), 156404 CrossRef CAS PubMed.
- S. Ouardi, G. H. Fecher and C. Felser, Realization of spin gapless semiconductors: the Heusler compound Mn2CoAl, Phys. Rev. Lett., 2013, 110(10), 100401 CrossRef PubMed.
- G. Y. Gao and K. L. Yao, Antiferromagnetic half-metals, gapless half-metals, and spin gapless semiconductors: The D03-type Heusler alloys, Appl. Phys. Lett., 2013, 103(23), 232409 CrossRef.
- X. T. Wang, Z. X. Cheng, J. L. Wang, X. L. Wang and G. D. Liu, Recent advances in the Heusler based spin-gapless semiconductors, J. Mater. Chem. C, 2016, 4(30), 7176–7192 RSC.
- Y. Ding and Y. L. Wang, Electronic structures of zigzag silicene nanoribbons with asymmetric sp2–sp3 edges, Appl. Phys. Lett., 2013, 102(14), 143115 CrossRef.
- J. Lei, M. C. Xu and S. J. Hu, Anchoring transition metal elements on graphene-like ZnO monolayer by CO molecule to obtain spin gapless semiconductor, Appl. Surf. Sci., 2017, 416, 681–685 CrossRef CAS.
- A. Z. Wang, X. M. Zhang, Y. P. Feng and M. W. Zhao, Chern insulator and Chern half-metal states in the two-dimensional spin-gapless semiconductor Mn2C6S12, J. Phys. Chem. Lett., 2017, 8(16), 3770–3775 CrossRef CAS PubMed.
- H. M. Huang, Z. Y. Jiang, Y. M. Lin, B. Z. Zhou and C. K. Zhang, Design of half-metal and spin gapless semiconductor for spintronics application via cation substitution in methylammonium lead iodide, Appl. Phys. Express, 2017, 10(12), 123002 CrossRef.
- H. P. Wu, Y. Qian, W. S. Tan, E. J. Kan, R. F. Lu and K. M. Deng, Vacancy-induced insulator-direct spin gapless semiconductor-half-metal transition in double perovskite La2CrFeO6: a first-principles study, Phys. Lett. A, 2015, 379(43–44), 2897–2901 CrossRef CAS.
- V. Varade, T. Markus, K. Vankayala, N. Friedman, M. Sheves, D. H. Waldeck and R. Naaman, Bacteriorhodopsin based non-magnetic spin filters for biomolecular spintronics, Phys. Chem. Chem. Phys., 2018, 20(2), 1091–1097 RSC.
- Z. H. Xiong, D. Wu, Z. V. Vardeny and J. Shi, Giant magnetoresistance in organic spin-valves, Nature, 2004, 427(6977), 821–824 CrossRef CAS PubMed.
- F. J. Jedema, M. S. Nijboer, A. T. Filip and B. J. van Wees, Spin injection and spin accumulation in all-metal mesoscopic spin valves, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(8), 085319 CrossRef.
- F. Heusler, W. Starck and E. Haupt, Magnetisch-chemische studien, Verh. Dtsch. Phys. Ges., 1903, 5, 219–232 CAS.
- I. Di Marco, A. Held, S. Keshavarz, Y. O. Kvashnin and L. Chioncel, Half-metallicity and magnetism in the Co2MnAl/CoMnVAl heterostructure, Phys. Rev. B, 2018, 97(3), 035105 CrossRef CAS.
- I. Galanakis, P. Mavropoulos and P. H. Dederichs, Electronic structure and Slater-Pauling behaviour in half-metallic Heusler alloys calculated from first principles, J. Phys. D: Appl. Phys., 2006, 39(5), 765–775 CrossRef CAS.
- H. Z. Luo, H. W. Zhang, Z. Y. Zhu, L. Ma, S. F. Xu, G. H. Wu, X. X. Zhu, C. B. Jiang and H. B. Xu, Half-metallic properties for the Mn2FeZ (Z = Al, Ga, Si, Ge, Sb) Heusler alloys: a first-principles study, J. Appl. Phys., 2008, 103(8), 083908 CrossRef.
- G. D. Liu, X. F. Dai, H. Y. Liu, J. L. Chen, Y. X. Li, G. Xiao and G. H. Wu, Mn2CoZ (Z = Al, Ga, In, Si, Ge, Sn, Sb) compounds: structural, electronic, and magnetic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(1), 014424 CrossRef.
- P. Wang, J. B. Xia and H. B. Wu, Electronic structures, magnetic properties and strain effects of quaternary Heusler alloys FeMnCrZ (Z = P, As, Sb, Bi, Se, Te), J. Magn. Magn. Mater., 2019, 490, 165490 CrossRef CAS.
- S. A. Khandy and J. D. Chai, Novel half-metallic L21 structured full-Heusler compound for promising spintronic applications: a DFT-based computer simulation, J. Magn. Magn. Mater., 2019, 487, 165289 CrossRef CAS.
- L. Fan, F. Chen and Z. Q. Chen, First-principles calculations of magnetism and half-metallic properties of CsYO2 (Y = V, Cr, Mn, Fe, Co, Ni) Heusler alloys, J. Magn. Magn. Mater., 2019, 478, 264–273 CrossRef CAS.
- M. Baral and A. Chakrabarti, Half-metallicity versus symmetry in half-Heusler alloys based on Pt, Ni, and Co: an ab initio study, Phys. Rev. B, 2019, 99(20), 205136 CrossRef CAS.
- L. Fan, F. Chen, C. M. Li, X. Hou, X. Zhu, J. L. Luo and Z. Q. Chen, Promising spintronics: Mn-based Heusler alloys Mn3Ga, Mn2YGa (Y = V, Nb, Ta), ScMnVGa, J. Magn. Magn. Mater., 2020, 497, 166060 CrossRef.
- M. I. Khan, H. Arshad, M. Rizwan, S. S. A. Gillani, M. Zafar, S. Ahmed and M. Shakil, Investigation of structural, electronic, magnetic and mechanical properties of a new series of equiatomic quaternary Heusler alloys CoYCrZ (Z = Si, Ge, Ga, Al): a DFT study, J. Alloys Compd., 2019, 819, 152964 CrossRef.
- G. Z. Xu, Y. Du, X. M. Zhang, H. G. Zhang, E. K. Liu, W. H. Wang and G. H. Wu, Magneto-transport properties of oriented Mn2CoAl films sputtered on thermally oxidized Si substrates, Appl. Phys. Lett., 2014, 104(24), 242408 CrossRef.
- P. Chen, C. X. Gao, G. L. Chen, K. Mi, M. Liu, P. Zhang and D. S. Xue, The low-temperature transport properties of Heusler alloy Mn2CoAl, Appl. Phys. Lett., 2018, 113(12), 122402 CrossRef.
- S. Picozzi, A. Continenza and A. J. Freeman, Co2MnX (X = Si, Ge, Sn) Heusler compounds: an ab initio study of their structural, electronic, and magnetic properties at zero and elevated pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(9), 094421 CrossRef.
- S. Ishida, S. Fujii, S. Kashiwagi and S. Asano, Search for half-metallic compounds in Co2MnZ (Z = IIIb, IVb, Vb element), J. Phys. Soc. Jpn., 1995, 64(6), 2152–2157 CrossRef CAS.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(17), 174429 CrossRef.
- M. Yamamoto, T. Ishikawa, T. Taira, G. Li, K. Matsuda and T. Uemura, Effect of defects in Heusler alloy thin films on spin-dependent tunnelling characteristics of Co2MnSi/MgO/Co2MnSi and Co2MnGe/MgO/Co2MnGe magnetic tunnel junctions, J. Phys.: Condens. Matter, 2010, 22(16), 164212 CrossRef PubMed.
- S. Tsunegi, Y. Sakuraba, M. Oogane, K. Takanashi and Y. Ando, Large tunnel magnetoresistance in magnetic tunnel junctions using a Co2MnSi Heusler alloy electrode and a MgO barrier, Appl. Phys. Lett., 2008, 93(11), 112506 CrossRef.
- T. Ishikawa, T. Marukame, H. Kijima, K.-I. Matsuda, T. Uemura, M. Arita and M. Yamamoto, Spin-dependent tunneling characteristics of fully epitaxial magnetic tunneling junctions with a full-Heusler alloy Co2MnSi thin film and a MgO tunnel barrier, Appl. Phys. Lett., 2006, 89(19), 192505 CrossRef.
- X. H. Zhu, E. H. Jiang, Y. F. Dai and C. L. Luo, Stability, magnetic, and electronic properties of L21 and B2 phases in Co2MnAl Heusler alloy, J. Alloys Compd., 2015, 632, 528–532 CrossRef CAS.
- L. Bainsla, A. I. Mallick, M. M. Raja, A. K. Nigam, B. S. D. C. S. Varaprasad, Y. K. Takahashi, A. Alam, K. G. Suresh and K. Hono, Spin gapless semiconducting behavior in equiatomic quaternary CoFeMnSi Heusler alloy, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(10), 104408 CrossRef.
- M. E. Jamer, B. A. Assaf, G. E. Sterbinsky, D. Arena, L. H. Lewis, A. A. Saúl, G. Radtke and D. Heiman, Antiferromagnetic phase of the gapless semiconductor V3Al, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(9), 094409 CrossRef.
- Y. Wu, X. G. Xu, J. Miao and Y. Jiang, Perpendicular magnetic anisotropy in Co-based full heusler alloy thin films, Spin, 2015, 5(4), 1540012 CrossRef CAS.
- W. H. Wang, M. Przybylski, W. Kuch, L. I. Chelaru, J. Wang, Y. F. Lu, J. Barthel, H. L. Meyerheim and J. Kirschner, Magnetic properties and spin polarization of Co2MnSi Heusler alloy thin films epitaxially grown on GaAs(001), Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(14), 144416 CrossRef.
- G. Y. Gao, G. Q. Ding, J. Li, K. L. Yao, M. H. Wu and M. C. Qian, Monolayer MXenes: promising half-metals and spin gapless semiconductors, Nanoscale, 2016, 8(16), 8986–8994 RSC.
- H. Z. Luo, F. B. Meng, Z. Q. Feng, Y. X. Li, W. Zhu, G. H. Wu, X. X. Zhu, C. B. Jiang and H. B. Xu, The structural and magnetic properties of Mn2−xFexNiGa Heusler alloys, J. Appl. Phys., 2010, 107(1), 013905 CrossRef.
- M. Meinert, J. M. Schmalhorst, G. Reiss and E. Arenholz, Ferrimagnetism and disorder of epitaxial Mn2−xCoxVAl Heusler compound thin films, J. Phys. D: Appl. Phys., 2011, 44(21), 215003 CrossRef.
- M. Y. Jiang, M. G. Samant, C. Felser and S. S. P. Parkin, Strong dependence of the tetragonal Mn2.1Ga thin film crystallization temperature window on seed layer, Appl. Phys. Lett., 2013, 103(3), 032410 CrossRef.
- Z. W. Du, X. L. Han, T. Li, E. K. Liu, X. D. Ma, J. C. Xiong and G. H. Wu, Microstructures and phase transformations in as-aged Mn2.04NiGa Heusler alloy, J. Alloys Compd., 2016, 657, 443–449 CrossRef CAS.
- R. Gavrea, C. Leostean, M. Coldea, O. Isnard, V. Pop and D. Benea, Effects of Co for Mn substitution on the electronic properties of Mn2−xCoxVAl as probed by XPS, Intermetallics, 2018, 93, 155–161 CrossRef CAS.
- A. Kalache, A. Markou, S. Selle, T. Höche, R. Sahoo, G. H. Fecher and C. Felser, Heteroepitaxial growth of tetragonal Mn2.7−xFexGa1.3 (0 ≤ x ≤ 1.2) Heusler films with perpendicular magnetic anisotropy, APL Mater., 2017, 5, 096102 CrossRef.
- M. Ram, A. Saxena, A. E. Aly and A. Shankar, Study of half metallicity, structural and mechanical properties in inverse Heusler alloy Mn2ZnSi(1−x)Gex and a superlattice, RSC Adv., 2019, 9(63), 36680–36689 RSC.
- A. Ayuela, J. Enkovaara, K. Ullakko and R. M. Nieminen, Structural properties of magnetic Heusler alloys, J. Phys.: Condens. Matter, 1999, 11, 2017–2026 CrossRef CAS.
- B. S. D. C. S. Varaprasad, A. Srinivasan, Y. K. Takahashi and K. Hono, Highly spin-polarized Co2MnGa0.5Sn0.5 Heusler compound, Acta Mater., 2009, 57(9), 2702–2709 CrossRef CAS.
- X. Feng, L. Feng, C. C. Guo and W. X. Zhang, First-principles investigation of half-metallicity of Mn2Co1−xCrxAl, Comput. Mater. Sci., 2017, 127, 15–21 CrossRef CAS.
- Z. R. Li, W. B. Mi and H. L. Bai, The role of rare-earth dopants in tailoring the magnetism and magnetic anisotropy in Fe4N, J. Phys. Chem. Solids, 2018, 116, 7–14 CrossRef CAS.
- M. E. Jamer, B. A. Assaf, T. Devakul and D. Heiman, Magnetic and transport properties of Mn2CoAl oriented films, Appl. Phys. Lett., 2013, 103(14), 142403 CrossRef.
- I. Galanakis, K. Özdoğan, E. Şaşıoğlu and S. Blügel, Conditions for spin-gapless semiconducting behavior in Mn2CoAl inverse Heusler compound, J. Appl. Phys., 2014, 115(9), 093908 CrossRef.
- X. R. Chen, M. M. Zhong, Y. Feng, Y. Zhou, H. K. Yuan and H. Chen, Structural, electronic, elastic, and thermodynamic properties of the spin-gapless semiconducting Mn2CoAl inverse Heusler alloy under pressure, Phys. Status Solidi B, 2015, 252(12), 2830–2839 CrossRef CAS.
- Y. P. Xin, H. Y. Hao, Y. X. Ma, H. Z. Luo, F. B. Meng, H. Y. Liu, E. K. Liu and G. H. Wu, Competition of XA and L21B ordering in Heusler alloys Mn2CoZ (Z = Al, Ga, Si, Ge and Sb) and its influence on electronic structure, Intermetallics, 2017, 80, 10–15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- M. Marlo and V. Milman, Density-functional study of bulk and surface properties of titanium nitride using different exchange-correlation functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(4), 2899–2907 CrossRef CAS.
- X. Blanc, É. Cancès and M. S. Dupuy, Variational projector augmented-wave method, Comptes Rendus Mathematique, 2017, 355(6), 665–670 CrossRef.
- A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(13), 134106 CrossRef.
- X. D. Wang, D. S. Wang, R. Q. Wu and A. J. Freeman, Validity of the force theorem for magnetocrystalline anisotropy, J. Magn. Magn. Mater., 1996, 159, 337–341 CrossRef CAS.
- J. Enkovaara and A. Ayuela, Magnetic anisotropy in Ni2MnGa, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 134422 CrossRef.
- B. S. Yang, J. Zhang, L. N. Jiang, W. Z. Chen, P. Tang, X. G. Zhang, Y. Yan and X. F. Han, Strain induced enhancement of perpendicular magnetic anisotropy in Co/graphene and Co/BN heterostructures, Phys. Rev. B, 2017, 95(17), 174424 CrossRef.
- A. Hallal, H. X. Yang, B. Dieny and M. Chshiev, Anatomy of perpendicular magnetic anisotropy in Fe/MgO magnetic tunnel junctions: first-principles insight, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(18), 184423 CrossRef.
- D. Z. Li, C. Barreteau, M. R. Castell, F. Silly and A. Smogunov, Out-versus in-plane magnetic anisotropy of free Fe and Co nanocrystals: tight-binding and first-principles studies, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(20), 205409 CrossRef.
- X. D. Xu, Z. X. Chen, Y. Sakuraba, A. Perumal, K. Masuda, L. S. R. Kumara, H. Tajiri, T. Nakatani, J. Wang, W. Zhou, Y. Miura, T. Ohkubo and K. Hono, Microstructure, magnetic and transport properties of a Mn2CoAl Heusler compound, Acta Mater., 2019, 176, 33–42 CrossRef CAS.
- X. R. Chen, M. M. Zhong, Y. Feng, Y. Zhou, H. K. Yuan and H. Chen, Structural, electronic, elastic, and thermodynamic properties of the spin-gapless semiconducting Mn2CoAl inverse Heusler alloy under pressure, Phys. Status Solidi B, 2015, 252(12), 2830–2839 CrossRef CAS.
- T. Zhou, Y. Feng, X. Chen, H. Yuan and H. Chen, Half-metallicity and magnetism of Ti2Ni1−xCoxAl1−ySiy inverse Heusler alloys, J. Magn. Magn. Mater., 2017, 423, 306–313 CrossRef CAS.
- T. Yang, L. Y. Hao, R. Khenata and X. T. Wang, Investigation of the structural competing and atomic ordering in Heusler compounds Fe2NiSi and Ni2FeSi under strain condition, R. Soc. Open Sci., 2019, 6(9), 191007 CrossRef PubMed.
- J. Zhou, B. S. Sa, Z. M. Sun, C. Si and R. Ahujia, Manipulating carriers' spin polarization in the Heusler alloy Mn2CoAl, RSC Adv., 2015, 5(90), 73814–73819 RSC.
- P. V. Ong, N. Kioussis, P. K. Amiri, J. G. Alzate, K. L. Wang, G. P. Carman, J. Hu and R. Q. Wu, Electric field control and effect of Pd capping on magnetocrystalline anisotropy in FePd thin films: a first-principles study, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(9), 094422 CrossRef.
- D. Fritsch and C. Ederer, Epitaxial strain effects in the spinel ferrites CoFe2O4 and NiFe2O4 from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(10), 104117 CrossRef.
- J. A. Heuver, A. Scaramucci, Y. Blickenstorfer, S. Matzen, N. A. Spaldin, C. Ederer and B. Noheda, Strain-induced magnetic anisotropy in epitaxial thin films of the spinel CoCr2O4, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(21), 214429 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra03413d |
| This journal is © The Royal Society of Chemistry 2020 |