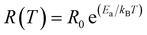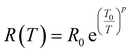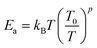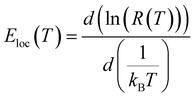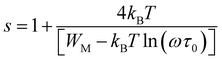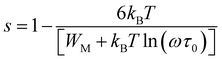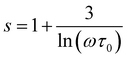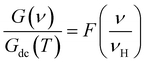Open Access Article
Open Access ArticlePossibility of controlling the conduction mechanism by choosing a specific doping element in a praseodymium manganite system
Y.
Moualhi
a,
R.
M'nassri
a,
H.
Rahmouni
 *a,
M.
Gassoumi
ab and
K.
Khirouni
c
*a,
M.
Gassoumi
ab and
K.
Khirouni
c
aUnité de Recherche Matériaux Avancés et Nanotechnologies (URMAN), Institut Supérieur des Sciences Appliquées et de Technologie de Kasserine, Université de Kairouan, BP 471, 1200 Kasserine, Tunisia. E-mail: rahmounihedi@yahoo.fr
bDepartement of Physics, College of Sciences, Qassim University, Saudi Arabia
cLaboratoire de Physique des Matériaux et des Nanomatériaux appliquée à l'Environnement, Faculté des Sciences de Gabes cite Erriadh, Université de Gabes, 6079 Gabes, Tunisia
First published on 11th September 2020
Abstract
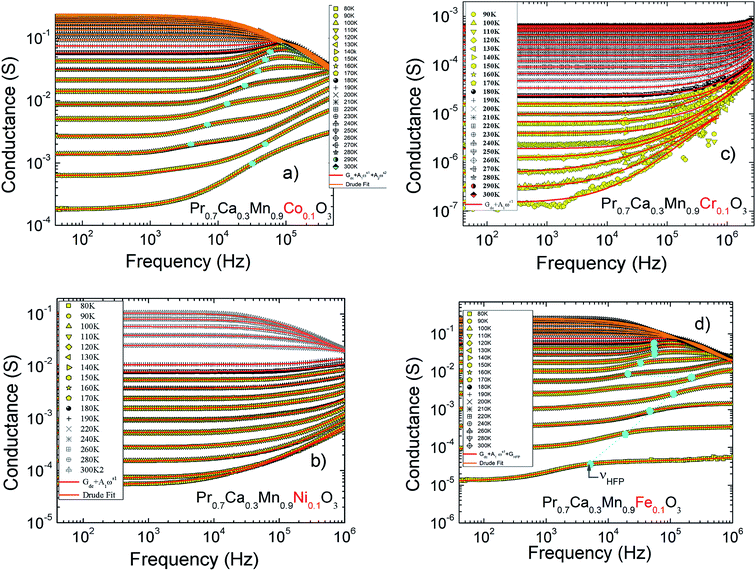
Electrical properties of Pr0.7Ca0.3Mn0.9X0.1O3 (X = Co, Ni, Cr and Fe) systems have been investigated using impedance spectroscopy measurements. The reported results confirmed the role of cationic disorder on the transport properties of the doped Pr0.7Ca0.3MnO3 system. For the case of the substitution by Co and Ni and Fe transition metals, the lower temperature side has been marked by the activation of the hopping conductivity over the nearest sites. Moreover, the Shklovskii–Efros-variable range hopping conductivity mechanism has been observed in the case of the substitution by Cr element. In the high temperature range, the evolution of the resistance with temperature confirmed the activation of a hopping process. In such a temperature range, the conduction process of all the studied compounds is dominated by a thermally activated small polaron hopping mechanism. For the Pr0.7Ca0.3Mn0.9Cr0.1O3 compound, AC studies have confirmed that the electrical conductance should be investigated in terms of an activated quantum mechanical tunneling process. At higher frequencies, the Pr0.7Ca0.3Mn0.9Fe0.1O3 compound is characterized by the existence of a high frequency plateau. For the Pr0.7Ca0.3Mn0.9Fe0.1O3 ceramic, the dispersive region of the spectrum has confirmed the activation of the correlated barrier hopping mechanism. Thus, the conductance is found to follow the double Jonscher power law only for the temperature range of [80 K, 200 K]. For the Pr0.7Ca0.3Mn0.9Ni0.1O3 compound, the evolution of the frequency exponent has confirmed the activation of two conduction mechanisms. The non small polaron tunneling mechanism was activated at lower temperatures. Accordingly, the activation of the correlated barrier hopping mechanism was detected for the high temperature range. For Pr0.7Ca0.3Mn0.9Co0.1O3 manganite, the coexistence of two conduction mechanisms (correlated barrier hopping and the non small polaron tunneling) is noticed. The latter's were activated in the whole of the explored temperature range. Using the scaling model, the spectra of both Pr0.7Ca0.3Mn0.9Cr0.1O3 and Pr0.7Ca0.3Mn0.9Ni0.1O3 compounds merge into a single master curve, which confirms the validity of the time temperature superposition principle.
1. Introduction
Recent investigations on physical properties of perovskite oxides confirm that rare earth manganites having general formula AMnO3 (A = rare earth of alkaline earth ions) are good candidates for fundamental physical research.1–5 It has been shown that manganites present a strong correlation between their structural, transport, optical and magnetic properties.6–13 Thanks to the multifunctional behavior of manganites, they can be considered as well-qualified for several applications.14–20 The enhancement of the mentioned properties is usually possible via several factors such as the annealing temperature and the nature of the doping element. The examined properties can also be modified by the creation of A/Mn site deficiency. It has been reported that the manganite system Pr0.7Ca0.3MnO3 is a good candidate for theoretical analyses and experimental investigations.21–30 The interesting physical properties of such an oxide family are based principally on the mixed valence character (Mn3+, Mn4+) of Pr0.7Ca0.3MnO3 manganite. This character is imposed by the coexistence of a trivalent praseodymium ion (70% of Pr3+) and a bivalent alkaline earth metal ion (30% of Ca2+) in the A-site. Previous studies have verified that the Pr0.7Ca0.3MnO3 system exhibits ferromagnetic metallic behavior.22–30 In this context, the substitution by transition metal elements modifies the mixed valence leading to strengthen the interactions between the double and the super-exchange mechanisms. It had shown that the substitution of the manganese affects mainly the Mn3+/Mn4+ ratio, leads to modify the relative cooling power (RCP), the magnetoresistance effects and the transport properties of manganites.22–32 Also, the substitution by a transition metal like iron element can block the electron transfer between Mn3+ and Mn4+ ions. Numerous electrical studies had shown that the substitution of the manganese affect strongly the electrical properties.32,33 Accordingly, it improves the transport properties of manganites via the creation of new conduction sites.32,33 It also affects the electrical properties by the activation of new conduction processes.33Numerous researches on physical properties of manganites had confirmed that the substitution by iron reduces the Mn3+/Mn4+ ratio.22–30 It affects strongly the Mn–O–Mn network, the double exchange (DE) (Mn3+–Mn4+) and the super exchange (Mn3+–Mn3+) interactions. As a result, it implies a change of the transport and the magnetic properties of several mixed manganites. Different conduction processes can appear when introducing the Fe in manganites (the hopping and the tunneling mechanisms).34–36 The main benefits of the substitution by cobalt transition metal are the enhancement of the magnetic entropy change, the distortion of the charge order state of Pr0.7Ca0.3MnO3 compound.23,27–29 Also, it permits the appearance of a ferromagnetic phase at the lower temperature side.29 At lower temperatures, the substitution of manganite system by Co induces a change of both super-exchange and the double–exchange interactions. Then, it affects the mobile carrier concentration. For La0.7Ca0.3MnO3, Srivastava et al.37 had demonstrated that the substitution of such system by 10% of Co concentration decreased considerably the DE interaction.38–40
Nickel transition metal had been considered as an important doping element in perovskite materials. It affects strongly the physical properties of manganites.31,41,42 Thus, it modifies the Mn3+–Mn4+ ratio and weakens the double exchange interaction.31,41,42 It reduces the Curie temperature, the magnetization and leads to the modification of the resistivity.41 Recent investigations have confirmed that the chrome is one of great substitutions element for manganites.22,23,26,28 Introducing Cr permits the appearance of a ferromagnetic phase at low temperatures.26,28 Manganite materials substituted by Cr are characterized by a large RCP. Introducing Cr in praseodymium-manganite system strongly modifies the magnetic entropy change. Also, it increases the resistance.23,26,28 Taking advantage of the interested physical properties of the manganite Pr0.7Ca0.3MnO3 and the fascinating effects of introducing transition metal elements in manganite materials, we have interested on the electrical properties of Pr0.7Ca0.3Mn0.9X0.1O3 (X-PCMO) (X = Co, Ni, Cr and Fe) system. The principal idea of this work is to investigate the effect of substituting manganese by several dopant elements on transport properties of X-PCMO (X = Co, Ni, Cr and Fe) systems. Also, we focus in the analysis of the controlling conduction process for each doping element. This study allows to plannify in future, mixed substitutions to optimize the properties of this compound.
2. Experimental details
Bulk polycrystalline X-PCMO (X = Co, Ni, Cr and Fe) compounds were prepared by the conventional solid state reaction method.28 High purity precursors: Pr6O11, CaCO3, Mn2O3, Co2O3, Cr2O3, Ni2O3 and Fe2O3 are used to prepare the samples X-PCMO (X = Co, Ni, Cr and Fe). The samples were prepared according to the chemical reaction:| 0.11Pr6O11 + 0.3CaCO3 + 0.9MnO2 + 0.05X2O3 ⇒ Pr0.7Ca0.3Mn0.9X0.1O3 + δCO2 + δ′O2 |
Preparation steps are well presented in our previous work.28 Also, at room temperature, structural properties are studied.28 Such investigations show that the prepared compounds are single phase perovskite manganites with no detectible secondary phases. Conductivity measurements of the prepared samples were conducted with plane capacitor configuration. For this reason, thin silver disk of approximately 20 nm thick and 6 mm of diameter was deposited on the both sides of the pellet by thermal evaporation under vacuum. To vary the temperature from 77 K to 300 K, each compound was mounted in a cryostat. It was connected through silver wire to the electrodes of an Agilent 4294A analyzer to measure the conductance and the capacitance. We used a signal test of 20 mV of amplitude and measurements were conducted in dark under primary vacuum.
3. Results and discussion
Table 1 shows the structural parameters of Pr0.7Ca0.3Mn0.9X0.1O3 (X = Co, Cr, Ni and Fe) system. The factors (a(Å), b(Å), c(Å) and V(Å3)) have been obtained using a Rietveld refinement of X-ray diffraction patterns.28 In our previous study,28 we found that all the studied samples were indexed in the orthorhombic perovskite structure by Pnma space group. It is observed that the change in the nature of the dopant element affects the unit cell parameters. Subsequently, the unit cell volume changes. In similar systems,27–32 the change in the unit cell volume has been explained in terms of difference between the ionic radius of the doped element and the ionic radius of Mn3+ and Mn4+ ions.28 The variation in the ionic radius of the substituted element affects equally the bond distance and the bond angles. As reported in our previous work,24 the parent sample Pr0.7Ca0.3MnO3 presents a unit cell volume V = 227.52(3) Å3 and a bond angle 〈Mn–O–Mn〉 = 157.55(4). Comparing such parameters by the obtained results in Table 1, we found that the substitution of Mn3+ by 10% Co3+ induces a reduction in Mn3+ ions which changes the unit cell volume (V = 226.96 Å3). Also, it modifies both the average bond length 〈Mn–O〉 and the bond angle 〈Mn–O–Mn〉. Such effects have a direct impact on the double exchange (DE) interactions. As a result, the transport properties of Co-PCMO manganite will be changed. Moreover, introducing 10% of Ni3+ ions in Pr0.7Ca0.3MnO3 manganite structure slightly weakens the double exchange interactions of Mn3+–O–Mn4+. The partial substitution of Mn3+ by Ni element induces a changes in the unit cell parameters (a = 5.432(8) Å, b = 7.689(2) Å and c = 5.419(5) Å) which leads to vary the unit cell volume (V = 226.39(38) Å3). In the case of Cr-PCMO compound, the partial replacement of Mn3+ ions by Cr3+ ions causes a decrease in the number of hopping electrons and a decline in the available hopping sites between Mn3+ and Mn4+ ions which significantly weakens the double exchange interaction mechanism. Introducing 10% of Cr in Pr0.7Ca0.3MnO3 has caused an increase the bond angle 〈Mn–O–Mn〉 =160.63(1). It causes a changes in the unit cell parameters which leads to a slight decrease in the unit cell volume (V = 227.14(3) Å3). For Fe-PCMO compound, the strong anti-ferromagnetic Mn–Fe interaction can simultaneously coupled the Mn ions with neighboring Mn and Fe ions which leads to changes in structural parameters. So, the replacement of Mn3+ ions by Fe3+ ions leads to modify the unit cell parameters. Such variation is usually accompanied by variations in the unit cell volume, the average bond length 〈Mn–O〉 and the bond angle 〈Mn–O–Mn〉.| Elements | Co | Ni | Cr | Fe |
|---|---|---|---|---|
| a(Å) | 5.430(6) | 5.432(8) | 5.429(3) | 5.431(9) |
| b(Å) | 7.670(5) | 7.689(2) | 7.669(1) | 7.675(3) |
| c(Å) | 5.448(4) | 5.419(5) | 5.455(2) | 5.464(6) |
| V(Å3) | 226.956(4) | 226.39(38) | 227.143(4) | 227.82(6) |
The Fig. 1(a–d) illustrate the evolution of the resistance with temperature for X-PCMO (X = Co, Ni, Cr and Fe) system. According to the reported results, the temperature dependence of the resistance confirms the semiconductor behavior of all prepared samples. The higher resistance was observed for the case of the substitution by Cr transition metal. A theoretical fit confirms that the evolution of the resistance with temperature obeys to the Arrhenius-like expression:43
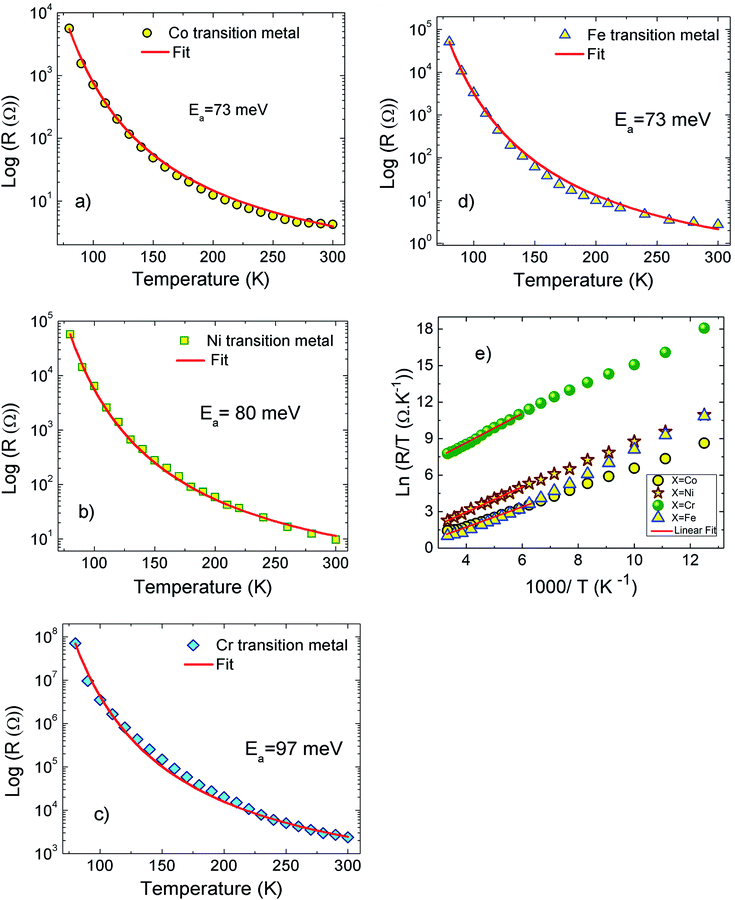 | ||
| Fig. 1 (a–d) Temperature dependence of the resistance for X-PCMO (X = Co, Ni, Cr and Fe) ceramics. (e) Variation of ln(R/T) as a function of 1000/T for X-PCMO (X = Co, Ni, Cr and Fe) samples. | ||
R
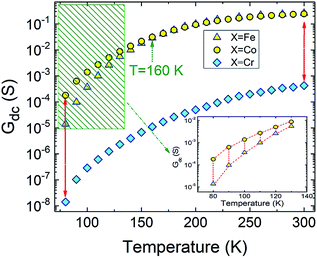
0 is pre-factor, kB is the Boltzmann constant and Ea is the activation energy. Fig. 1(e) presents the evolution of log(R/T) versus 1000/T for all the studied compounds. The linear fits could confirm that the conduction of charge carriers is occurred via hopping phenomena.43 Therefore, a thermally activated small polaron hopping (SPH) conduction process governs the transport properties at high temperatures. Based on Mott investigations,44–49 the high temperature range is characterized by the strong electron–phonon interaction. The thermally activated SPH conduction mechanism needs activation energy Ea. The latter is the result of polaron formation via the bonding energy (WP) and the disorder energy (WD) due to the variation in the local arrangements of ions. Experimentally, the activation energies (Ea) are obtained from the Arrhenius resistance fits (Fig. 1(a–d)). Same activation energy of 73 meV was obtained for the cobalt and iron doping elements. For the case of Ni-PCMO and Cr-PCMO compounds, the activation energies Ea = 80 meV and Ea = 97 meV were obtained respectively. According to our previous work in ref. 22, we found that the activation energy of the parent compound (Pr0.7Ca0.3MnO3) is Ea = 26 meV. Then, in our work, the activation energy of Cr doped PCMO system attain a value of Ea = 97 meV. This value confirms the strong effect of introducing Cr element on the activation energy. At low temperature range, the reported results in ref. 22 confirm that the parent sample present a resistance R (80 K) ≈106 Ω. The effect of introducing Cr element is strongly observed, accordingly, R (80 K) ≈108 Ω. The observed changes in the resistance variation and the activation energy values can be explained variations in the unit cell structural parameters. Fig. 2 presents the evolution of the conductance with temperature for Co-PCMO, Cr-PCMO and Fe-PCMO compounds. In this figure we examine the effect of the cationic disorder on the variation of DC conductance. The present result demonstrates the existence of two principal regions. The lower temperature side is characterized by the dominance of the cationic disorder effects on the transport properties. For the case of Co-PCMO and Fe-PCMO compounds, such effect becomes less significant when approaching to T = 160 K. The observed phenomenon is the result of the difference between the ionic radius of manganese and the radius of the substituted elements (Fe, Co)). As clearly shown in Fig. 2, the cationic disorder affects the evolution of the conductance at lower temperature range. In this part, the charge carrier transport is an acoustical one-phonon assisted the variable range hopping mechanism (VRH). According to Mott theories,44–49 the lower temperature range is generally characterized by the negligible hopping energy (WH) (small bonding energy (WP)). The activation of the VRH conduction mechanism is usually dominated by the disorder energy (Ea = WD). The higher disorder effect where observed for case of the substitution by the Co transition metal (σCo2 = 9.12 10−3 Å2). Else, for the case of the substitution by Fe, Ni and Cr, the obtained values of the disorder parameter are respectively σFe2 = 7.46 10−3 Å2, σNi2 = 3.85 10−3 Å2 and σCr2 = 10−3 Å2. According to the obtained result from the DC conductance analysis, it can be noticed that increasing the disorder ameliorates the conductance at lower temperature region. The obtained experimental results are in good agreement with Mott investigations.44–49 According to these studies,44–49 the evolution of the resistance with temperature follows the universal expression:43
In the literature,33,43 three principle regimes are reported and used to more detail the transport properties of polycrystalline materials at low temperatures. In the case of the nearest site hopping (NSH) regime, p is equal to 1 and thus Ea = kBT0. The Mott–VRH regime is characterized by the absence of the electron–electron coupling, p = 1/4 and 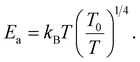 For the case of the Shklovskii–Efros regime p = 1/2 and
For the case of the Shklovskii–Efros regime p = 1/2 and 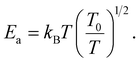 33,50–52
33,50–52
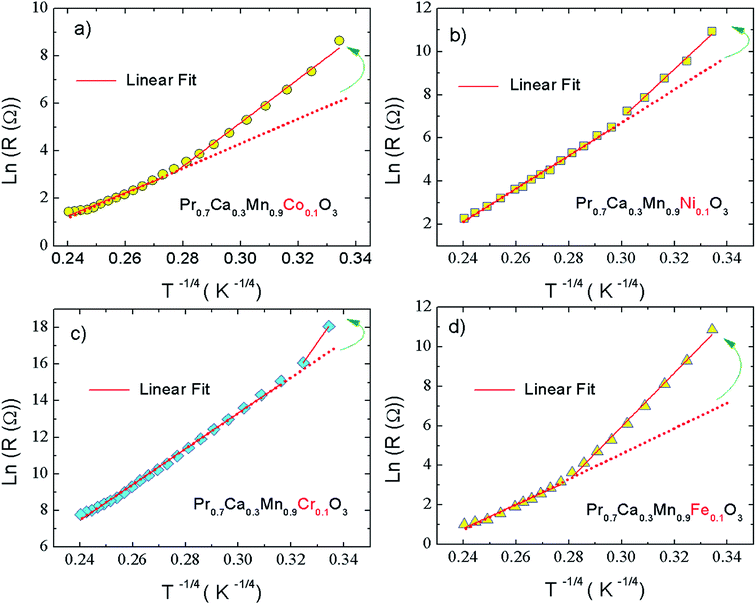
In our present work, the type of the activated VRH conduction mechanism can be estimated from the evolution of ln(R) with T−1/4 (Fig. 3(a–d)) and the variation of ln(RT−1/2) as a function of T−1/2 (Fig. 4(a–d)). At lower temperatures, a linear variation was observed for all studied compounds. Such linearity proves the activation of a hopping process. In Fig. 4(b), the plot of ln(RT−1/2) as a function of T−1/2 presents the best linear variation which confirms that the Shklovskii–Efros regime is more valid to describe the hopping of charge carriers for the case of Cr-PCMO sample. However, for the case of Co-PCMO, Ni-PCMO and Fe-PCMO compounds, the plots of ln(R) against T−1/4 (Fig. 3(a, c and d)) and ln(RT−1/2) against T−1/2 (Fig. 4(a, c and d)) present a straight line with identical quality. In this case, it is obvious to evaluate the evolution of the local energy with the temperature by the following relation:43
For all investigated samples, the variation of ln(Eloc(T)/(kBT)) as a function of ln(T) is shown in Fig. 5(a–d). For Co-PCMO sample, the reported result confirms that the curve reveals a linear variation with a slope p = 1 and error of 6%. Such result proves the evidence of the NSH conductivity in such compound.43 Also, for the Ni-PCMO sample, a linear variation with p = 1 and an error of 10% is obtained and confirm the presence of the same conduction regime (NSH conductivity).43 However, for Cr-PCMO compound, it is found that p = 0.5 with error of 7%. Such value proved the evidence of the Shklovskii–Efros regime and confirms the result of Fig. 4(b).33,43 The same result is reported recently in Fe-PCMO compound33 and in LCMO system.43 In the case of Fe-PCMO sample, p = 1 with error of 7% confirming the dominance of the NSH conductivity.43 As can be noticed from the obtained results, the change in the nature of the dopant element can strongly affect the conduction mechanism.
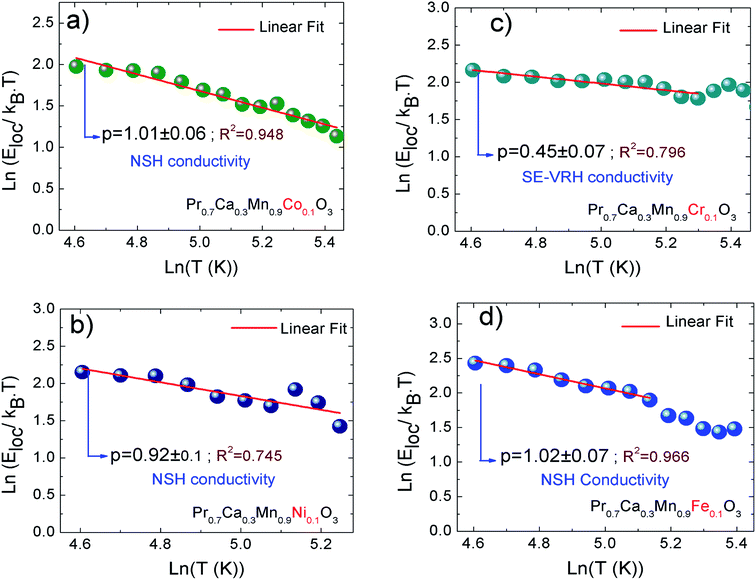 | ||
| Fig. 5 (a–d) Temperature dependence of the local activation energy for X-PCMO (X = Co, Ni, Cr and Fe) ceramics. | ||
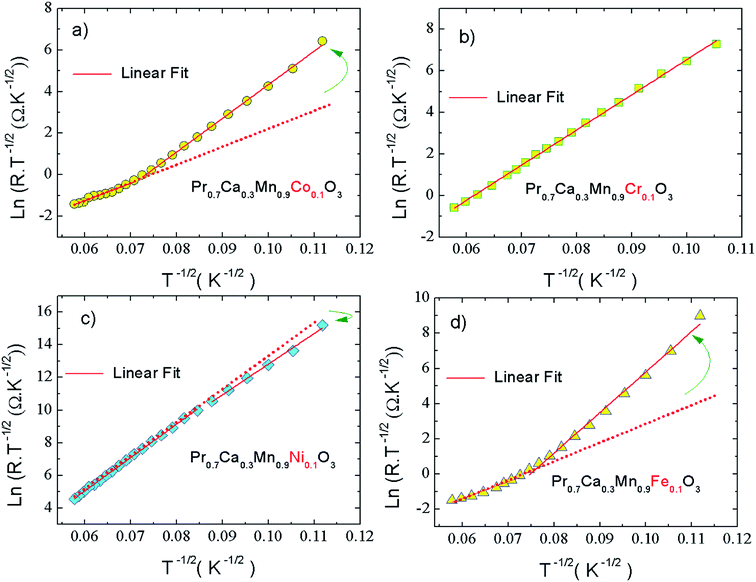
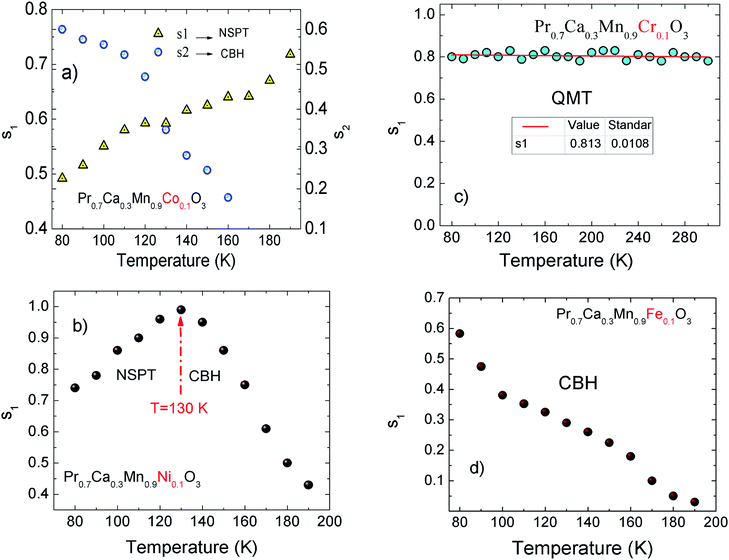
The evolution of the conductance with frequency is shown in Fig. 6(a–d). For all the investigated samples, a theoretical fits demonstrate that the conductance spectra obey to the double or the single Jonscher power laws at low temperatures.33,53,61,62 In such temperature side, we can infer the evolution of the frequency exponent with temperature which could be used to identify the activated conduction processes in each frequency and temperature ranges. For Co-PCMO sample, the evolution of the conductance with frequency (Fig. 6(a)) presents a double Jonscher variation. Indeed, each conductance spectrum is characterized by a low frequency DC plateau and two dispersive regions. In this case the conductance could be fitted according to Bruce equation:53
| Gac = G0 + A1ωs1 + A2ωs2 |
A
1, A2 and G0 are constants. Then, s1 and s2 are the frequency exponents obtained respectively from the fits of the conductance in the intermediate and the high frequency ranges. To identify the type of the conduction mechanism in the alternative regime, it is interesting to follow the thermally evolution of such frequency exponent (Fig. 7(a–d)). Various conduction mechanisms have been used in manganites to understand the dynamics of charge carriers in each frequency interval based on the evolution of the frequency exponent with temperature.33 For Co-PCMO compound, the exponent “s1” increases with increasing temperature confirming the activation of the non-small polaron tunneling (NSPT) mechanism46,48,54–60 in the intermediate frequency region. However, for the higher frequency range, the obtained frequency exponent “s2” confirms the activation of the correlated barrier hopping (CBH) mechanism.46,48,54–60 In the case of the conduction by the NSPT mechanism, the frequency exponent is given by:
 | ||
| Fig. 7 (a–d) Temperature dependence of the frequency exponent for the doped X-PCMO (X = Co, Ni, Cr and Fe) system. | ||
In such equation τ0 is a relaxation time and WM is the polaron hopping energy. The same result has been reported and investigated recently in Pr0.7Ca0.3Mn0.95Fe0.05O3 compound.33 Then, the authors are explained the double Jonscher variation by the coexistence of two conduction process at low temperature.
In the present study, the double Jonscher law has been also used to investigate the conductance spectra and the transport properties in Fe-PCMO compound. At high frequencies, it is noticed that each conductance spectrum presents a constant conductance plateau. In such frequency range the conductance is almost frequency independent. In the dispersive region of the spectra, the obtained frequency exponent “s1” decreases with increasing temperature. Such evolution is observed mainly in manganites.33,54–60 It confirms the activation of the CBH mechanism. For such model, the exponent “s” is expressed as follow:
The double Jonscher variation of the conductance is observed by Nandi et al.63 in a wide variety of materials like the manganite oxide LaMn1−xFexO3 and the nanocrystalline La2NiMnO6.64 In ref. 63 and 64, the authors explain such behaviour by the fact that the hopping phenomenon has been occurred among more than two localized states during an electric field period.
For Cr-PCMO and Ni-PCMO compounds, the universal Jonscher power law is used to identify the evolution of the conductance with frequency at low temperatures. In such case, each spectrum has been fitted by the following relation:61,62
| Gac = G0 + A1ωs1 |
The reported results (Fig. 7(a–d)) confirm that the conduction mechanism is strongly sensitive to the nature of the substituted element. However, for the case of the Ni-PCMO system, the frequency exponent increases with temperature until s ∼ 1 (130 K), confirming the activation of the NSPT conduction mechanism. Beyond T = 130 K, the exponent “s1” decreases rapidly (Fig. 7(b)) which confirms the activation of the CBH mechanism.
For the case of the quantum mechanical tunneling (QMT) mechanism, it is known that the frequency exponent is temperature independent.33,54–60 It takes a value of 0.81. A similar result was confirmed in the case Cr-PCMO sample. In this limit frequency parameter takes the form:54–60
The obtained results from the evolution of the frequency exponent confirm that the change in the nature of the substitution element can be used to control the type of the activated conduction mechanisms.
At elevated temperatures, Fig. 6(a, b and d) shows that X-PCMO (X = Co, Ni and Fe) compounds exhibit a metallic behaviour. Thus, it is observed that the spectra were fitted and investigated using the Drude model.33 At high frequencies, it is observed that the conductance of Ni-PCMO and Fe-PCMO compounds varies with the frequency. It decreases against the increases in the frequency. For such samples, the observed metallic behaviour can be explained by the changes in the dynamics of charge carriers. In addition, the increase in the temperature strengthens the charge density. As a result, a colloid phenomenon contributes in decreasing the electrical conductance. Also, the decrease in the conductance can be due to the drop of charge efficiency on following the signal of excitation. Such variation can be also explained by variations in the double exchange interaction mechanism. So, it is observed28 that introducing 10% of Ni slightly weakens the double exchange interaction of Mn3+–O–Mn4+. The same effect is observed for the case of Fe-PCMO compound, the Mn ions can couple simultaneously with neighboring Mn and Fe ions. In such case the replacement of Mn3+ with Fe3+ can greatly weaken the double exchange interrelation of Mn3+–O–Mn4+. Due to the correlation between crystallographic, magnetic, and the electrical properties of manganites, the changes in the double exchange interaction affect the conductance of manganites practically at high frequencies.
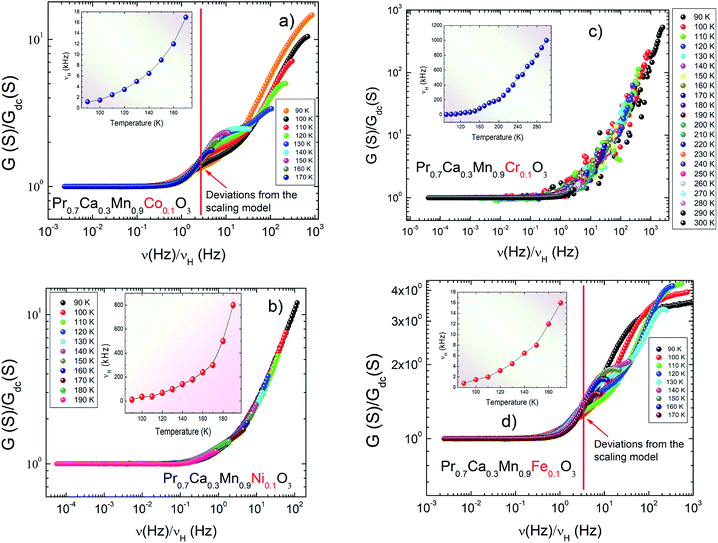
To get an idea about the charge transport properties and with a view to examine the validity of the time temperature superposition principle, we interest on the application of scaling model.63–65 In such approach, the frequency and the conductance axis must be scaled with respect to the hooping frequency (νH) and the DC conductance (Gdc) parameters, respectively. The curves of the conductance spectra are scaled using the following relation:
Fig. 8(a–d) presents the scaled conductance spectra of X-PCMO (X = Co, Ni, Cr and Fe) compounds. For the sample Ni-PCMO, it is noticed that the spectra collapse perfectly into a single master curve. Such result proves that the curve shape becomes temperature independent. The same result is observed in the scaled spectra of Cr-PCMO compound. Obviously, the merges of the AC conductance confirms that the single power law is valid to fits the conductance spectra. Also, such result has confirmed the validity of the time temperature superposition principle (TTSP) over wide frequency range. What's more, the single master curve variation indicates the existence of general formalism for the AC conductance in perovskite materials.63,64 For Co-PCMO compound, the obtained result confirms the existence of two dissimilar variations. Below ν/νH ≈ 2, the spectra are perfectly collapsed to a single master curve. The universal behaviour of the conductance spectra must verifies the validity of the TTSP below variation ν/νH ≈ 2. Beyond the frequency ν = 2νH, the application of the scaling approach does not leads to the superposition of the spectra. A strong deviation is observed. Such deviations are due to the double Jonscher variation of the conductance. It may be due to the migration of the conduction process from NSPT process to CBH process. The same result is observed for the case of Fe-PCMO compound. Accordingly, the application of the scaling approach has leads to the superposition of the spectra only below ν/νH ≈ 2. In this case, the deviations from the single master curve behaviour should be due to the existence of a constant conductance values at high frequencies. In this limit, the single power law cannot fit the spectra over the investigated frequency range.
 | ||
| Fig. 8 (a–d) Scaling of the conductance spectra of Pr0.7Ca0.3Mn0.9X0.1O3 (X = Co, Ni, Cr and Fe) system. | ||
4. Conclusion
The present work highlights the possibility of controlling the conduction mechanisms in manganite system by using specific dopant element. For each dopant element, the electrical transport can be dominated by one or several conduction mechanisms. It is found that the type of the activated conduction mechanism is very sensitive to the nature of the substitution element. At high temperatures, the conduction phenomenon is governed by the thermally activated small polaron hopping process. The same activation energy was observed for the case of the substitution by Fe and Co elements (Ea = 73 meV). The alternative current regime indicates that the conductance spectra of Co-PCMO and Fe-PCMO samples follow a double power law. In Co-PCMO compound, it is observed that the conductance spectra are characterized by the coexistence of the CBH and the NSPT conduction mechanisms respectively at high and for the intermediate frequency ranges. In Fe-PCMO sample, the conduction mechanism can be described by the CBH model. Over the studied temperature range, the conductance spectra of Cr-PCMO sample follow the Jonscher power law. For such compound, the deduced frequency exponent confirms that the conduction process is governed by the activation of the QMT mechanism. At lower temperature range, the Ni-PCMO sample is characterized by the activation of the NSPT conduction mechanism. Beyond a specific temperature, the conduction process in Ni-PCMO ceramic has been explained by the CBH model. Using the scaling approach, it is concluded that the spectra of Cr-PCMO and Ni-PCMO samples have merged into a single master curve. Such variation has confirmed that the time temperature superposition principle is more valid for the case of the substitution by Ni and Cr elements.Conflicts of interest
There are no conflicts to declare.References
- A. Gómez, E. Chavarriaga, J. L. Izquierdo, J. Prado-Gonjal, F. Mompean, N. Rojas and O. Morán, J. Magn. Magn. Mater., 2019, 469, 558 CrossRef
.
- P. T. Phong, L. T. T. Ngan, L. V. Bau, N. X. Phuc, P. H. Nam, L. T. H. Phong, N. V. Dang and In-Ja Lee, J. Magn. Magn. Mater., 2019, 475, 374 CrossRef CAS
.
- A. Tozri and E. Dhahri, J. Alloys Compd., 2019, 718–783 CrossRef CAS
.
- R. E. A. Ngida, M. F. Zawrah, R. M. Khattab and E. Heikal, Ceram. Int., 2019, 45(4), 4894 CrossRef CAS
.
- K. Cherif, A. Belkahla and J. Dhahri, J. Alloys Compd., 2019, 777, 358 CrossRef CAS
.
- J. Fan, Y. Xie, Y.-E. Yang, C. Kan, L. Ling, W. Tong, C. Wang, C. Ma, W. Sun, Y. Zhu and H. Yang, Ceram. Int., 2019, 45(7), 9179 CrossRef CAS
.
- P. Meshram, B. D. Pandey and Abhilash, Resour. Policy, 2019, 60, 9 CrossRef
.
- Q. Yang, J. Yao, K. Zhang, W. Wang, X. Zuo, H. Tang, M. Wu and G. Li, J. Electroanal. Chem., 2019, 833, 1 CrossRef CAS
.
- B. Lucio, M. Romero and J. G. Aguilar, Solid State Ionics, 2019, 338, 47 CrossRef CAS
.
- A. Ben Jazia Kharrat, M. Bourouina, N. Chniba-Boudjada and W. Boujelben, Solid State Sci., 2019, 87, 27 CrossRef CAS
.
- H. E. Sekrafi, A. Ben Jazia Kharrat, M. A. Wederni, K. Khirouni, N. Chniba-Boudjada and W. Boujelben, Mater. Res. Bull., 2019, 111, 329 CrossRef CAS
.
- P. D. H. Yen, N. T. Dung, T. D. Thanh and S.-C. Yu, Curr. Appl. Phys., 2018, 18(11), 1280 CrossRef
.
- V. Lahteenlahti, A. Schulman, H. Huhtinen and P. Paturi, J. Alloys Compd., 2019, 786, 84 CrossRef CAS
.
- N. Assoudi, I. Walha and E. Dhahri, Chem. Phys. Lett., 2019, 731, 136609 CrossRef CAS
.
- A. R. Shelke, K. P. Shinde, N. Patra, S. N. Jha, D. Bhattacharyya, K. C. Chung, Y. P. Lee, D. M. Phase, S. D. Kaushik and N. G. Deshpande, J. Magn. Magn. Mater., 2019, 480, 22 CrossRef CAS
.
- E. Dogdibegovic, R. Wang, G. Y. Lau and M. C. Tucker, J. Power Sources, 2019, 410–411, 91 CrossRef CAS
.
- L. Dhal, S. Rayaprol, A. V. Morozkin, N. Shukla, T. Geetha Kumary, S. K. Malik, P. N. Santhosh and R. Nirmala, Solid State Commun., 2019, 294, 55 CrossRef CAS
.
- O. Siddiqui and I. Dincer, Energy, 2019, 169, 914 CrossRef CAS
.
- J. Xu and Z. Zou, Phys. B, 2019, 557, 52 CrossRef CAS
.
- M. Pękała, K. Pękała, J. Szydłowska and V. Drozd, J. Magn. Magn. Mater., 2019, 475, 189 CrossRef
.
- R. Zhang, J. Miao, F. Shao, W. T. Huang, C. Dong, X. G. Xu and Y. Jiang, J. Non-Cryst. Solids, 2014, 406, 102 CrossRef CAS
.
- A. Selmi, A. Bettaibi, H. Rahmouni, R. M’nassri, N. Chniba Boudjada, A. Cheikhrouhou and K. Khirouni, Ceram. Int., 2015, 41(9), 11221 CrossRef CAS
.
- A. Selmi, R. M’nassri, W. Cheikhrouhou-Koubaa, N. Chniba Boudjada and A. Cheikhrouhou, J. Alloys Compd., 2015, 619, 627 CrossRef CAS
.
- A. Selmi, W. Cheikhrouhou-Koubaa, M. Koubaa and A. Cheikhrouhou, J. Supercond. Novel Magn., 2012, 26(5), 1421 CrossRef
.
- R. M’nassri, N. Chniba-Boudjada and A. Cheikhrouhou, J. Alloys Compd., 2015, 640, 183 CrossRef
.
- A. Selmi, W. Cheikhrouhou-Koubaa, M. Koubaa and A. Cheikhrouhou, IOP Conf. Ser.: Mater. Sci. Eng., 2012, 28, 012052 Search PubMed
.
- R. M’nassri, M. Khelifi, H. Rahmouni, A. Selmi, K. Khirouni, N. Chniba-Boudjada and A. Cheikhrouhou, Ceram. Int., 2016, 42(5), 6145 CrossRef
.
- A. Selmi, R. M’nassri, W. Cheikhrouhou-Koubaa, N. Chniba Boudjada and A. Cheikhrouhou, Ceram. Int., 2015, 41(8), 10177 CrossRef CAS
.
- M. Khelifi, R. M’nassri, A. Selmi, H. Rahmouni, K. Khirouni, N. C. Boudjada and A. Cheikhrouhou, J. Magn. Magn. Mater., 2017, 423, 20 CrossRef CAS
.
- R. Jemai, R. M’nassri, A. Selmi, H. Rahmouni, K. Khirouni, N. Chniba Boudjada and A. Cheikhrouhou, J. Alloys Compd., 2017, 693, 631 CrossRef CAS
.
- R. Rozilah, N. Ibrahim and A. K. Yahya, Solid State Sci., 2019, 87, 64 CrossRef CAS
.
- H. Rahmouni, B. Cherif, K. Khirouni, M. Baazaoui and S. Zemni, J. Phys. Chem. Solids, 2016, 88, 35 CrossRef CAS
.
- Y. Moualhi, M. M. Nofal, R. M'nassri, H. Rahmouni, A. Selmi, M. Gassoumi, K. Khirouni and A. Cheikrouhou, Ceram. Int., 2020, 46, 1601 CrossRef CAS
.
- H. Rahmouni, B. Cherif, M. Baazaoui and K. Khirouni, J. Alloys Compd., 2013, 575, 5–9 CrossRef CAS
.
- N. T. Dang, V. S. Zakhvalinskii, D. P. Kozlenko, T.-L. Phan, S. E. Kichanov, S. V. Trukhanov, A. V. Trukhanov, Y. S. Nekrasova, S. V. Taran, S. V. Ovsyannikov, S. G. Jabarov and E. L. Trukhanova, Ceram. Int., 2018, 44, 14974 CrossRef CAS
.
- M. Baazaoui, S. Zemni, M. Boudard, H. Rahmouni, M. Oumezzine and A. Selmi, Phys. B, 2010, 405, 1470 CrossRef CAS
.
- C. M. Srivastava, S. Banerjee, T. K. GunduRao, A. K. Nigam and D. Bahadur, J. Phys.: Condens. Matter, 2003, 15, 2375 CrossRef CAS
.
- V. Y. Mitrofanov, S. K. Estemirova and G. A. Kozhina, J. Magn. Magn. Mater., 2019, 476, 199 CrossRef CAS
.
- M. A. Gdaiem, S. Ghodhbane, A. Dhahri, J. Dhahri and E. K. Hlil, J. Alloys Compd., 2016, 681, 547 CrossRef CAS
.
- J. Kuo and G. Sheng-Kai, Chin. Phys. B, 2009, 18(7), 3035 CrossRef
.
- A. Gómez, J. L. Izquierdo, I. Supelano, C. A. Parra, E. Chavarriaga and O. Morán, J. Magn. Magn. Mater., 2019, 475, 524 CrossRef
.
- S. Y. Lee, J. Yun and W. P. Tai, Adv. Powder Technol., 2018, 29(10), 2423 CrossRef CAS
.
- R. Laiho, K. G. Lisunov, E. Lähderanta, V. N. Stamov and V. S. Zakhvalinskii, J. Phys.: Condens. Matter, 2001, 13(6), 1233 CrossRef CAS
.
- N. F. Mott, Mater. Res. Bull., 1978, 13(12), 1389 CrossRef CAS
.
- N. F. Mott, J. Non-Cryst. Solids, 1978, 28(2), 147 CrossRef CAS
.
- N. F. Mott, J. Non-Cryst. Solids, 1968, 1(1), 1 CrossRef CAS
.
- N. F. Mott, Philos. Mag., 1969, 19(160), 835 CrossRef CAS
.
- N. F. Mott, J. Non-Cryst. Solids, 1980, 35–36, 1321 CrossRef
.
- I. G. Austin and N. F. Mott, Adv. Phys., 1969, 18(71), 41 CrossRef CAS
.
- B. Xie, P. Mao, M. Chen, Z. Li, C. Liu, Y. Qin, L. Yang, M. Wei, M. Liu, X. Wang, D. Han, S. Li, F. Sang, M. Han, J.-M. Liu and G. Wang, Sens. Actuators, A, 2018, 272, 161 CrossRef CAS
.
-
A. L. Efros and B. I. Shklovskii, Modern Problems in Condensed Matter Sciences, 1985, vol. 10, p. 409 Search PubMed
.
- S. M. Wasim, L. Essaleh, G. Marín, C. Rincón, S. Amhil and J. Galibert, Superlattices Microstruct., 2017, 107, 285 CrossRef CAS
.
- P. Bruce, Solid State Ionics, 1985, 15(3), 247 CrossRef CAS
.
- A. Ghosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(3), 1479 CrossRef CAS PubMed
.
- A. A. Khan, M. U. Fayaz, M. N. Khan, M. Iqbal, A. Majeed, R. Bilkees, S. Mukhtar and M. Javed, J. Mater. Sci.: Mater. Electron., 2018, 29(16), 13577 CrossRef CAS
.
- G. E. Pike, Phys. Rev. B: Solid State, 1972, 6(4), 1572 CrossRef CAS
.
- A. Ghosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42(9), 5665 CrossRef CAS PubMed
.
- A. K. Jonscher, Nature, 1977, 267(5613), 673 CrossRef CAS
.
- K. Park, J. Eur. Ceram. Soc., 2006, 26(6), 909 CrossRef CAS
.
- S. Das and A. Ghosh, J. Non-Cryst. Solids, 2017, 458, 28 CrossRef CAS
.
- S. R. Elliott and F. E. G. Henn, J. Non-Cryst. Solids, 1990, 116(2–3), 179 CrossRef CAS
.
- A. K. Jonscher and M. S. Frost, Thin Solid Films, 1976, 37(2), 267 CrossRef CAS
.
- U. N. Nandi, S. Sircar, A. Karmakar and S. Giri, J. Phys.: Condens. Matter, 2012, 24, 26560 CrossRef PubMed
.
- D. Chakraborty, U. N. Nandi, D. Jana, M. G. Masud and S. Giri, J. Appl. Phys., 2015, 118, 035103 CrossRef
.
- Y. Moualhi, H. Rahmouni, M. Gassoumi and K. Khirouni, Ceram. Int., 2020, 46, 24710 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2020 |