Open Access Article
Open Access ArticleSensitivity enhancement via multiple contacts in the {1H–29Si}–1H cross polarization experiment: a case study of modified silica nanoparticle surfaces†
Chuanyu Yanab,
François Kayserc and
Reiner Dieden *a
*a
aLuxembourg Institute of Science and Technology, Department of “Materials Research and Technology”, Avenue des Hauts-Fourneaux, L-4362 Esch-sur-Alzette, Luxembourg. E-mail: reiner.dieden@list.lu; Fax: (+352) 275 885; Tel: (+352) 275 888 4576
bUniversity of Luxembourg, Faculty of Science, Technology and Communication, Avenue des Hauts-Fourneaux, L-4365 Esch-sur-Alzette, Luxembourg
cGoodyear Innovation Center Luxembourg, Avenue Gordon Smith, L-7750 Colmar-Berg, Luxembourg
First published on 17th June 2020
Abstract
{1H–29Si}–1H double cross polarization inverse detection (DCPi) solid-state NMR, has recently been shown to be a powerful tool for studying molecules adsorbed on the silica surface. In this contribution, we develop an improved version (MCPi) which incorporates a block of multiple contact pulses, and quantitatively compare the sensitivities of MCPi and DCPi over a typical range of experimental parameters. The MCPi pulse sequence aims at higher sensitivity and robustness for studying samples with various relaxation characteristics. In the case of dimethyl sulfoxide (DMSO) molecules adsorbed on the silica surface, MCPi performs equally well or up to 2.5 times better than DCPi over a wide range of parameters. The applicability to and performance of MCPi on composite materials was demonstrated using a sample of polymer–silica composite, where significantly higher sensitivity could be achieved at very long total mixing times. The results also showed that both techniques are surface specific in the sense that only the groups close to the surface can be detected.
1. Introduction
Understanding the chemistry occurring on surfaces and at interfaces plays a critical role in materials science. For example, it helps to rationalize the mechanism of catalytic reactions,1–4 to improve the performance of anode/cathode materials in energy devices,5–7 to increase the separation efficiency of chromatography8,9 and to compatibilize different phases in composite materials.10–12 Silica, e.g., in addition to serving as a support material in materials science,4,13,14 has also been used for drug-delivery systems through either inclusion16 or adsorption17 of the active ingredient. However, while many of the spectroscopic techniques available today are very powerful for analysing bulk properties, it is still non-trivial to obtain surface-specific chemical information.1.1 Study of silica by 29Si solid-state NMR
Silica and its surface have been studied extensively using a wide array of solid-state NMR (ssNMR) techniques that have revealed the presence of water and several hydroxy (silanol) species, involved to different degrees in hydrogen bonding.15,18–20For the characterization of silica and silicate surfaces, 29Si cross polarisation under magic angle spinning solid-state nuclear magnetic resonance spectroscopy (29Si CP/MAS ssNMR) has proven to be a valuable tool.15,20–24 Although direct polarisation (DP) can also provide valuable information its use is hampered by very long spin–lattice (T1) relaxation times.25,26
If the Hartmann–Hahn matching condition ωI = ωS is met, the polarisations of two nuclear species can equilibrate through dipolar coupling. If the polarisations are different, this cross-polarisation (CP) can lead to an enhancement of the lowest population by a factor of γI/γS (γ is the gyromagnetic ratio of the isotope).
The efficiency of CP depends essentially on two parameters, the rotating frame relaxation (TI1ρ) of the reservoir species (e.g. 1H), and the cross-polarisation constant, TIS. Since TIS can be very different for different I–S pair in the same sample, a single setting of CP parameters is not optimal for all S nuclei of the sample in most cases.
As improvements on the simple CP experiment, schemes involving multiple CP contacts have been proposed, mostly aiming at generating a more even signal enhancement and quantitative response.27–29
While the theoretical maximum enhancement (i.e. γ1H/γ29Si) is rarely achieved by one single CP step, it has been shown that multiple-step CP (multiCP) can significantly enhance the magnetisation for species with unequal cross-relaxation characteristics.28
In multiCP, the X nucleus magnetization can be pushed closer and closer to the maximum enhancement with increasing number of contacts, eventually achieving a homogeneous enhancement for all X-nuclei via multiple CP steps. The multiCP experiment was initially designed to obtain quantitative X nucleus response.28–30 Nevertheless, there are recent reports of using a multiCP block for the purpose of sensitivity enhancement.31,32
1.2 Surface specific techniques
Approaches to achieve surface specific detection in solid state NMR encompass the use of relaxation agents,26 29Si DNP,33,34 and 17O DNP.35,36 Nevertheless, regular CP can be considered to be a surface selective technique, provided that the protons are occurring exclusively at the surface of the silica particle.20,37This is because magnetization transfer via CP relies on through-space dipolar couplings, the strength of which is proportional to 1/r3 (r is the distance between the dipolar coupled spin pair). Hence, the information derived from CP ssNMR is usually limited to a region of a few nanometers.38 The dipolar coupled protons and silicon atoms have been investigated by 2D 1H–29Si heteronuclear correlation (HETCOR) on the silicon39 and silica19,38,40–42 surfaces.
Similarly, X-filtered double-cross polarisation experiments have been reported to specifically record spectra of X-nuclei of small molecules in the indirect dimension of a 2D experiment. This technique consists of two distinct CP periods during the first of which magnetisation is transferred from 1H to the X nucleus, from where it is then back-transferred to proton via the second CP block.43–48
A 1D version of this experiment, {1H–29Si}–1H double cross polarization inverse detection (DCPi), has recently been applied to the study of molecules adsorbed on the silica and silicate surfaces.38,49–52 The {1H–29Si}–1H DCPi experiment38 consists of three steps. First, a 1H → 29Si CP period (tcp1) ensures the surface 29Si magnetization is established. Second, a train of 90° excitation pulses is used to saturate the 1H magnetization so that no transverse magnetization, due to direct excitation during the second spin lock period (tcp2), could be detected in the final spectrum. During the proton saturation period, the 29Si magnetization is stored on the longitudinal axis. In the third step, the 29Si magnetisation is rotated back onto the transverse plane by a 90° pulse and then, during the second cross-polarization period (tcp2), transferred back only to those 1H spins that are within reach, i.e. close to the surface. Because of its dependence on the 1H–29Si dipolar couplings, the intensity of the 1H signal depends on the inter-nuclear distance, although proton–proton spin diffusion can also interfere, which can be minimized by using short contact times (tcp2). By applying this approach one can tell whether a molecule/functional group is on (or close to) the silica surface.
This {1H–29Si}–1H DCPi technique could provide information complementary to other sensitivity-enhanced techniques (X-nucleus detected) such as the Carr–Purcell–Meiboom–Gill (CPMG)34,40,41,53,54 and dynamic nuclear polarization techniques (DNP).33,34,55–57 In terms of silica/silicate materials, the former can reveal the local proton environments on the surface, while the latter can provide information about the silicon groups of silica and silicates.
In addition to the applications reported so far, the {1H–29Si}–1H DCPi technique also has the potential to study competitive adsorption phenomena on the surface of silica and silicate, which is an important and challenging topic.58 These ubiquitous phenomena can occur, for example, among small molecules,59–62 among polymers63,64 and between polymer and surfactant.65,66
In order to further improve the sensitivity of this surface-specific technique for composite materials with a rather low silica content or nanoparticles with a relatively low surface loading,17,56,67,68 where even slight sensitivity improvement could reduce experiment time significantly, we report here a modified version of DCPi. This new version, multiple contact cross polarization inverse detection ssNMR (MCPi), uses a multiCP block to enhance the polarisation build-up during the initial CP period. Its sensitivity is quantitatively compared to that of DCPi over a typical range of conditions.
One of the reasons for replacing the first CP step of DCPi with a block of multiple CP steps is because it is expected to further push the 29Si magnetization towards the maximum level (γ1H/γ29Si).
Another reason for inserting the multiCP block is its robustness, i.e. its capability of achieving strong enhancements for spins with different cross-polarisation kinetics.28 Although it has always been assumed that TI1ρ > TIS, the situation can be the opposite in some cases, i.e. TI1ρ < TIS.69 To cover a wide range of relaxation characteristics, e.g. as for the different types of hydroxyl groups at the silica surface, without the need of putting too much effort on measuring the TI1ρ and TIS for every sample, multiCP can safely enhance the magnetization without losing it due to TI1ρ.
2. Experimental
2.1 Materials
The materials used in this work were obtained from the following sources with given specifications. Silica nanoparticle (SiNP) (Sigma-Aldrich, product no. 637246, 99.5% particle size 5–15 nm (TEM), surface area 590–690 m2 g−1 (TEM)); Pure water (resistance 18.2 MΩ, purified by Simplicity® water purification system, Millipore S.A.S, France); dimethyl sulfoxide (DMSO-h6, from ACROS Organics, >99.7%); deuterated dimethyl sulfoxide (DMSO-d6, from ACROS Organics, 99.8% deuterium); deuterated chloroform (CDCl3, Aldrich, >99.8%D).2.2 Preparation of DMSO-adsorbed SiNP
Individual chemicals were used as received. In addition, the DMSO-adsorbed SiNP was prepared in the following way. (1) 0.20 gram of silica was mixed with 0.11 gram of DMSO-h6 or DMSO-d6 in the suspension of 5 mL of CDCl3 under magnetic stirring overnight at a speed of 300 rpm at room temperature. (2) The mixture was then subjected to high speed centrifuging at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. (3) Afterwards, the DMSO-adsorbed SiNPs were dried in a warm air-circulating oven at 50 °C for 1 hour.
000 rpm for 10 minutes. (3) Afterwards, the DMSO-adsorbed SiNPs were dried in a warm air-circulating oven at 50 °C for 1 hour.
2.3 Preparation of polymer–silica composite
1 gram of silica (Zeosil® Premium 200MP, Solvay) was reacted overnight with 20 mL of trimethylchlorosilane (≥98.0%, Sigma Aldrich) in a round bottom flask on a magnetic stirrer at room temperature. Then, the flask was opened to air to let the unreacted silane, formed hydrochloric acid and silane dimer evaporate at room temperature in a fume hood for about one day. The silanized silica was then mixed with polyisoprene (LIR-10, Kuraray) – (mass ratio ∼ 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80) in deuterated chloroform and the chloroform removed by oven-drying at 50 °C.
80) in deuterated chloroform and the chloroform removed by oven-drying at 50 °C.
2.4 ssNMR experiments
The details about the pulse sequences of {1H–29Si}–1H DCPi/MCPi, {1H}–29Si multiCP and 1H–1H RFDR are provided in Fig. S1.† In addition, routine experiments such as 29Si direct polarization (DP) under high power decoupling and 1H one-pulse were also performed.The solid samples were loaded into a 4 mm zirconium oxide (ZrO2) rotor with a Kel-F cap, while the liquid samples were loaded in a Kel-F HR-MAS insert, which was then inserted into the ZrO2 rotor. The rotors were spun at a MAS speed of 14 kHz (unless noted otherwise) at 303 K in a double resonance probe of a Bruker Avance III HD 600 MHz spectrometer, controlled by TopSpin 3.5pl7 software. The chemical shifts reported here were externally referenced vs. pure TMS by setting the methylene carbon of adamantane to 38.48 ppm. The 1H and 29Si 90° pulse lengths were 2.9 and 5.0 microseconds, respectively. In cross polarization experiments, the spin locking strength of 29Si was set to 50 kHz while that of 1H was a shaped ramp from 34 to 66 kHz. The number of scans (NS) for the {1H–29Si}–1H DCPi/MCPi and {1H}–29Si multiCP were 2048, the recycle delay (RD) was 4.0 seconds and acquisition time was 50 ms, unless noted otherwise. For the saturation train in DCPi and MCPi, we used 64 saturation pulses separated by a delay (τsat) of 1 ms, unless noted otherwise. In the MCPi experiments of the polymer–silica compound, the saturation scheme of Fig. 1B was replaced with two long low-power pulses (pulse length = 500 ms at a power level of 1 watts) with a 90°-phase shift, because even a train of 512 saturation pulses (inter-pulse delay τsat = 1 ms) was found to be insufficient for obtaining a clean background. For 1H–1H RFDR, the following acquisition parameters were used: RD = 4.0 seconds, mixing time = 18 ms, 128 increments on the indirect dimension and NS = 16. For the 29Si DP experiment at natural abundance, note that the T1 of 29Si is so long that our attempt to measure it in a practical timeframe was not successful. Thus, a RD of 120 s that is quite common in literature,16 was used here.
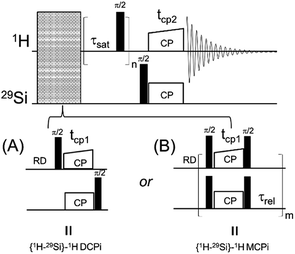 | ||
| Fig. 1 The diagrams of two solid-state NMR pulse sequences. (A) {1H–29Si}–1H double cross polarization inverse detection (DCPi). (B) {1H–29Si}–1H multiple cross polarization inverse detection (MCPi). | ||
The signal-to-noise ratio (S/N) was calculated in TopSpin using the Bruker command “SINO” with the signal and noise ranges defined in Tables S1 and S2.† To make fair comparisons, the {1H –29Si}–1H DCPi and MCPi spectra were processed using the same processing parameters (512 time domain points, without apodization and fixed regions for calculating S/N ratio).
3. Results and discussion
3.1 A case study of DMSO adsorption
In order to compare the sensitivities of the two sequences, {1H–29Si}–1H DCPi (Fig. 1A) and {1H–29Si}–1H MCPi (Fig. 1B), we used a surface modified silica nanoparticle. In this model sample, dimethyl sulfoxide (DMSO, a strong hydrogen bonding acceptor known to displace other molecules on the silica63) was used to displace the ubiquitous physically adsorbed water on the surface of silica nanoparticles (SiNP) (Fig. 2A). DMSO has a single methyl proton resonance far away from the silanol and water peaks, which allows to make unambiguous assignments. In order to be able to assign the 1H chemical shifts to each surface molecule/group (Fig. 2B), the 1H one-pulse experiments were compared with those of the individual materials as well as the mixtures (Fig. S3†). The 1H peak at 3.16 ppm was assigned to the protons of DMSO because this peak vanished when using deuterated DMSO. The broad 1H peaks at 7.5 ppm and at 5.0 ppm were assigned to hydrogen-bonded (HB)-silanols and physically adsorbed water, respectively, which is consistent with the values reported in most previous reports.18,70,71 In addition, further distinction between HB-water (4.63 ppm) and free-water (5.08 ppm) could also be made because this peak vanished in the “SiNP-as received” after being mixed with DMSO and dried at 50 °C for 1 hour. The 1H peak at 4.63 ppm still appeared in the {1H–29Si}–1H DCPi spectrum, suggesting this water is tightly bound to the SiNP surface. The 1H–1H RFDR spectrum (Fig. 2C) showed that the three aforementioned groups are in close proximity in space, probably bound by strong hydrogen bonds.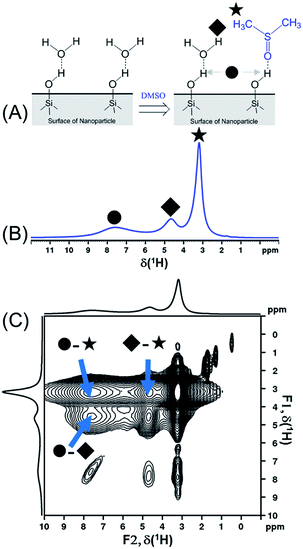 | ||
| Fig. 2 (A) Schematic presentation of displacement of physically adsorbed water by dimethyl sulfoxide molecules on the silica nanoparticle surface. (B) 1H one-pulse spectrum of DMSO-adsorbed SiNP (0.20 g SiNP + 0.11 g DMSO-h6) obtained by 1H one-pulse experiment (recycle delay = 4 seconds). The assignment of chemical shifts is as follow: ● δ(HB-silanol) = 7.50 ppm; ◆ δ(HB-water) = 4.63 ppm; ★ δ(HB-DMSO) = 3.16 ppm. (C) The 1H–1H radio-frequency-driven-recoupling (RFDR) correlation spectrum of DMSO-adsorbed SiNP (same sample as shown in (B)), using the pulse sequence of Fig. S1D† (mixing time = 18 ms). Note: three diagonal peaks in the region of 2 to 0 ppm might be assigned to isolated silanols and a very weak peak at 0.47 ppm that cannot be assigned.15 | ||
Determination of the proton spin–lattice relaxation constant (TH1, Fig. S2†) showed that the slowest relaxing group is the DMSO protons (TH1 = 0.35 seconds). Based on the finding in Schmidt-Rohr's report,28 τrel (Fig. 1B) in the multiCP block was therefore set to 0.7 seconds (2 × TH1) in order to allow 1H to repolarize to 95% of the thermal equilibrium. For obtaining optimal sensitivity, a relaxation delay of RD = 0.44 s (i.e. 1.26 × TH1) was initially chosen. However, in order to ensure that all protons have fully relaxed in cases where the T1 (s) could not be clearly determined due to heavily overlapped 1H peaks, we chose RD = 4.0 (the second to last points of the T1 relaxation curves in Fig. S2†).
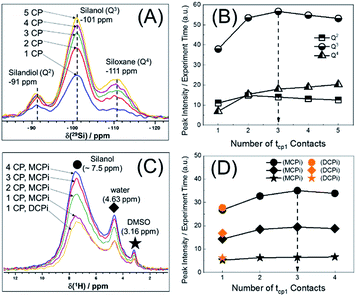
Another important parameter for running the {1H–29Si}–1H experiment is the number of CP contacts (m of Fig. 1B). To figure out the optimal m value, 29Si detected and 1H detected experiments (Fig. S1B and C†) were performed on the same sample used in Fig. 2. The optimization process is shown in Fig. 3. There are pros and cons for higher values of m. Theoretically, more contacts (higher m values) result in more magnetization transfer from 1H to 29Si and therefore more backward magnetization transfer, as was experimentally confirmed (see Fig. 3A and C). However, for qualitative analysis (as in this case), higher values of m result in longer experiment time. In addition, the closer the 29Si magnetization approaches the theoretical enhancement, the less efficient per time unit is each individual multiple CP step (Fig. 3B). Therefore, there is an optimal value for m, beyond which, there is no further marginal sensitivity gain per time unit (Fig. 3D). For the sample used in this case, the optimum was found to be m = 3, based on the maximum marginal gain of sensitivity of the silanol, water and DMSO signals (Fig. 3D).
With the key parameters being known (RD, τrel and m of Fig. 1), the sensitivities of the {1H–29Si}–1H DCPi and MCPi techniques were compared. The two experiments were performed on the same sample (Fig. S4 and S5†) and the S/N ratios were calculated (Tables S1 and S2†). As expected, one immediately noticeable difference with the 1H one-pulse is the relative intensities of the silanol, water and DMSO signals. In the one-pulse experiment (Fig. 2B), the relative peak intensities from highest to lowest is DMSO, water and silanol, whereas it is the opposite in the inverse detection experiments (Fig. 4A), which makes sense because the peak intensity of the one-pulse experiment are solely determined by concentration whereas it is modulated by inter-nuclear distance.
 | ||
| Fig. 4 The sensitivity comparison between {1H–29Si}–1H MCPi and DCPi. Same sample as used in Fig. 2B. (A) 1H spectra obtained using the following parameters: RD = 0.44 s, tcp1 = 1 ms, tcp2 = 5 ms for both MCPi and DCPi, and m = 3 for MCPi. (B) Sensitivity ratio of MCPi over DCPi (kMCPi/kDCPi) when RD = 0.44 s (i.e. 1.26 × TH1), tcp1 = variable and tcp2 = 5 ms, and m = 3 for MCPi. (C) Same experiments as performed for (B), except RD = 4.0 s. | ||
The overall sensitivity of each technique depends on the signal intensity, which was gained from one or multiple CP steps. Under three different conditions, the signals in the {1H–29Si}–1H MCPi spectra were all stronger than in DCPi spectra. Overall, {1H–29Si}–1H MCPi yields higher signal to noise ratio (S/N) than DCPi (Table S1 and Fig. S4†).
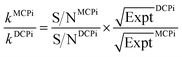
By normalizing the S/N ratios to experiment time per scan (i.e. the recycle delay + tcp1 × m + τsat × n + τrel × m + tcp2 + acquisition time), we could compare the intrinsic sensitivities of {1H–29Si}–1H MCPi and DCPi (Table S1†) using eqn (1)–(6). In a fully relaxed spin system, the S/N is proportional to the square root of the number of scans (NS) (eqn (1)), which is proportional to the total experimental time (Expt, eqn (2)). Therefore, the S/N is proportional to the square root of the total experimental time (eqn (3)). Thus, the sensitivity of a given pulse sequence can be expressed as a sensitivity factor (k) times the square root of total experimental time (eqn (4)). Under the same experimental conditions (i.e. identical sample, temperature, receiver gain, number of scans, processing parameters, etc.), the k value can be determined by normalizing the S/N to total experimental time (eqn (5)). Hence, the time-efficiency of two sequences can be compared by comparing their k values (eqn (6)).
 | (1) |
| NS ∝ Expt | (2) |
 | (3) |
 | (4) |
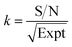 | (5) |
 | (6) |
The tcp1 dependence of the k ratios between {1H–29Si}–1H MCPi and DCPi under variable tcp1 are shown in Fig. 4B and C. In NMR experiments, the sensitivity per time unit can be maximized by setting the recycle delay to 1.26 times the longest T1 in a sample.72–74 As shown in Fig. 4B, when a short relaxation delay of RD = 0.44 s was used, the overall sensitivity of MCPi for the molecule of interest, DMSO, was better or equivalent than that of DCPi over the tcp1 range. For silanol and water peaks, the sensitivity of MCPi is similar to that of DCPi, which makes sense because these groups are located closely to the surface silicon atoms so that magnetization transfer via CP is fast and a single CP contact is probably sufficient for transferring most of the proton magnetization to silicon. However, the optimum of 1.26 × T1 is derived from an idealized situation where all the 1H T1 values in a sample can be clearly determined. Although this choice of recycle delay was applicable to the DMSO-adsorbed SiNP, that may be different in the case of composite materials where the 1H peaks are heavily overlapped and some of the peaks might be so overwhelming that the T1 of 1H of other surface groups cannot be clearly determined. In that case, one needs to resort to using a long recycle delay in order to avoid saturating the surface groups (see the next section of a polymer–silica composite).
As shown in Fig. 4C, the results of RD = 4.0 s showed that the sensitivity improvement of {1H–29Si}–1H MCPi compared to DCPi, was nearly three-fold at tcp1 = 1 ms (meaning that it would take about 9 times longer time for DCPi to achieve the same S/N level as MCPi). At longer tcp1, the improvement factor is around 1.5. Theoretically speaking, {1H–29Si}–1H MCPi would be even more efficient over the DCPi in situations where the proton spin–lattice relaxation in the rotating frame is much faster (shorter T1ρ) (i.e. long spin locking pulse is inapplicable). In fact, a contact pulse of 1 ms is quite common.28,38,50
Moreover, we further explored the dependence of signal intensity on tcp2 in the experiments of {1H–29Si}–1H MCPi (Fig. S6†). The rates of S/N evolution with tcp2 differ between DMSO, silanol and water due to the difference in the distance relative to the silica surface. This behaviour is analogous to the one reported previously for the regular DCPi.38
3.2 Modified silica in a polymer matrix
In order to demonstrate the applicability of both MCPi and DCPi and their truly unique surface specificity in practical applications, we applied it to a polymer–silica composite (Fig. 5). In order to illustrate the surface specificity of our approach, silica was silanized by trimethylchlorosilane. The grafted trimethylsilyl groups increase the surface's hydrophobicity compared to non-silanized silica, but no bonding between the silane and the polymer chains is created. The use of this mono-functional silane also prevents the occurrence of self-condensed polysiloxane chains, which might extend deeper into the polymer phase and entangle with the polymer chains, and achieve compatibility on those grounds.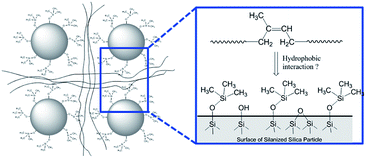 | ||
| Fig. 5 Schematic representation of the silica surface in a polymer–silica composite, where the silica has been silanized by trimethylchlorosilane and the polymer is polyisoprene (see Experimental). | ||
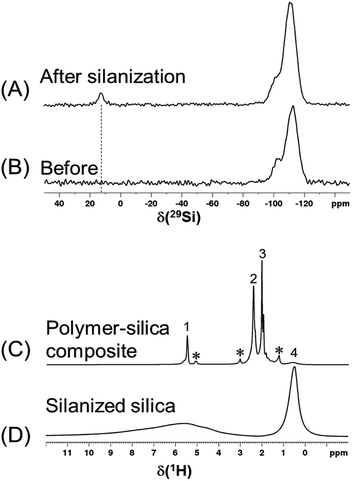
The 29Si spectra in Fig. 6A and B show that after the reaction with an excessive amount of silane, there is a significant amount of trimethylsilyl group grafted onto the silica surface and a noticeable decrease of the silanol peak (at −102 ppm). The 1H spectra in Fig. 6C and D show that once the silanized silica was mixed with polymer, the 1H peaks of polymer are so dominant that not all of the silanized silica 1H peaks (3 to 10 ppm) can be distinguished. Thus, instead of performing a regular 1H T1 measurement, the recycle delay needed for reaching the thermal equilibrium was estimated to be >3.5 s in a set of 1H one-pulse spectra with variable recycle delays (Fig. S7†). As a result, a recycle delay of 4.0 s and therefore an estimated inter-CP block delay τrel = 0.7 s were used for the following MCPi experiments. These two key parameters were confirmed to be efficient for building up the 29Si magnetization rapidly (Fig. S8†).
The 1H spectra in Fig. 7A were obtained by MCPi at various m values. As mentioned earlier, the MCPi pulse sequence of Fig. 1B actually can also achieve the function of DCPi simply by setting the multiCP loop number, m = 1 and inter-CP delay τrel = 0, because the contribution of the first 90° pulse on 29Si is negligible due to the long T1 relaxation of 29Si (Fig. 3C).
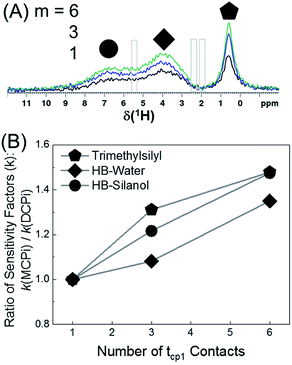 | ||
| Fig. 7 (A) 1H MCPi spectra of polymer–silica composite obtained by a slightly modified pulse sequence (Fig. S9†): RD = 4.0 s, tcp1 = tcp2 = 5 ms, τrel = 0.7 s and m = 1 (black), 3 (blue) and 6 (green). For m = 1, τrel = 0 s, this is effectively a DCPi experiment. Grey boxes are the regions where the polyisoprene signals would be expected. (B) The ratio of sensitivity factors k, between MCPi and DCPi calculated by eqn (6) using the S/N and experiment duration (Expt) values from Table S3.† | ||
The sensitivity factor, k (see eqn (5)), for each m value was calculated plugging in the S/N ratios and the experiment duration (Expt) of Table S3.† As can be seen in Fig. 7B, the MCPi pulse sequence achieves a higher sensitivity by increasing the number of multiCP loops, m, with total mixing times that could not normally be achieved with a single contact. This result was overall in agreement with the results of the DMSO-adsorbed silica case. As mentioned in the Introduction, the observable inter-nuclear distance has an upper limit of a few nanometers. Even though a wide range of tcp2 values have been used (i.e. tcp2 = 5 ms in Fig. 7A and tcp2 = 1, 10 & 15 ms in Fig. S10†), none of the polyisoprene 1H peaks was observed, which is probably due to the weak dipolar coupling between the polyisoprene and silica surface.
4. Conclusions
In this work, we report a new solid-state NMR technique for characterizing the silica surface, {1H–29Si}–1H multiple cross polarization inverse detection (MCPi). This new technique combines the principle of multiple cross polarization and the recently reported {1H–29Si}–1H double cross polarization inverse detection (DCPi) technique. It was demonstrated in a model system composed of dimethyl sulfoxide adsorbed on silica nanoparticles that the sensitivity of MCPi was better or equivalent to DCPi under a wide range of experimental conditions. In a preliminary study of a polymer–silica composite sample, MCPi achieved a higher sensitivity than DCPi at long total mixing times, not attainable with a single contact.Overall, MCPi is expected to perform better than DCPi in three situations: (1) the sample (e.g. composite materials) has multiple relatively fast 1H spin–lattice relaxations in the rotating frame TH1ρ, (2) the silica surface is not (or only slightly) protonated, and (3) the overall silica content in the sample is very low. In the first situation, the built-up 29Si magnetization will be constantly drained away due to TH1ρ. This will be attenuated using multiple, but short, cross polarisation steps, which will also be better suited for a variety of TH1ρs. In the second scenario, i.e. when there are only few protons near the silica surface (e.g. in pyrogenic silica or modified silicas with few grafted or adsorbed groups), the proton–silicon dipolar coupling is weaker and the CP kinetics is slower. Therefore, the total contact time has to be very long, which can be safely achieved by a multiCP block. In the third case, when the total amount of silica in sample, e.g. a composite material, is low, therefore requiring long experimental time in order to achieve signal-to-noise ratios suitable for analysis, even a small sensitivity enhancement means significant saving of experiment time.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work is funded by the Luxembourg National Research Fund (FNR) under the project number IPBG16/11514551/TireMat-Tech. Support for implementing the {1H}–29Si multiCP sequence by Dr Gerhard Althoff-Ospelt is also gratefully acknowledged. The authors would like to thank Mr Enzo Moretto for helpful discussion on the synthesis of silane-modified silicas.Notes and references
- J. K. Norskov and C. H. Christensen, Science, 2006, 312, 1322 CrossRef CAS PubMed.
- J. Gong, H. Yue, Y. Zhao, S. Zhao, L. Zhao, J. Lv, S. Wang and X. Ma, J. Am. Chem. Soc., 2012, 134, 13922–13925 CrossRef CAS PubMed.
- S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296 CrossRef CAS PubMed.
- A. Wong, Q. Liu, S. Griffin, A. Nicholls and J. R. Regalbuto, Science, 2017, 358, 1427 CrossRef CAS PubMed.
- D. Strmcnik, K. Kodama, D. van der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Marković, Nat. Chem., 2009, 1, 466–472 CrossRef CAS PubMed.
- W. Li, A. Dolocan, P. Oh, H. Celio, S. Park, J. Cho and A. Manthiram, Nat. Commun., 2017, 8, 14589 CrossRef PubMed.
- H. Gao, L. Xue, S. Xin and J. B. Goodenough, Angew. Chem., Int. Ed., 2018, 57, 5449–5453 CrossRef CAS PubMed.
- J. Nawrocki, M. Rigney, A. McCormick and P. W. Carr, J. Chromatogr. A, 1993, 657, 229–282 CrossRef CAS PubMed.
- J. Nawrocki, J. Chromatogr. A, 1997, 779, 29–71 CrossRef CAS.
- Y. Song, Y. Shen, H. Liu, Y. Lin, M. Li and C.-W. Nan, J. Mater. Chem., 2012, 22, 16491–16498 RSC.
- B. P. Kapgate, C. Das, D. Basu, A. Das and G. Heinrich, J. Elastomers Plast., 2013, 47, 248–261 CrossRef.
- R. Semino, N. A. Ramsahye, A. Ghoufi and G. Maurin, ACS Appl. Mater. Interfaces, 2016, 8, 809–819 CrossRef CAS PubMed.
- A. K. Clarke, M. J. James, P. O'Brien, R. J. K. Taylor and W. P. Unsworth, Angew. Chem., Int. Ed., 2016, 55, 13798–13802 CrossRef CAS PubMed.
- C. M. Crudden, M. Sateesh and R. Lewis, J. Am. Chem. Soc., 2005, 127, 10045–10050 CrossRef CAS PubMed.
- J. Brus and J. Dybal, Polymer, 2000, 41, 5269–5282 CrossRef CAS.
- Z. Teng, C. Wang, Y. Tang, W. Li, L. Bao, X. Zhang, X. Su, F. Zhang, J. Zhang, S. Wang, D. Zhao and G. Lu, J. Am. Chem. Soc., 2018, 140, 1385–1393 CrossRef CAS PubMed.
- J. Brus, W. Albrecht, F. Lehmann, J. Geier, J. Czernek, M. Urbanova, L. Kobera and A. Jegorov, Mol. Pharm., 2017, 14, 2070–2078 CrossRef CAS PubMed.
- C. E. Bronnimann, R. C. Zeigler and G. E. Maciel, J. Am. Chem. Soc., 1988, 110, 2023–2026 CrossRef CAS.
- J. Brus and J. Dybal, Macromolecules, 2002, 35, 10038–10047 CrossRef CAS.
- G. E. Maciel, Silica Surfaces: Characterization, in eMagRes ed. R. K. Harris and R. L. Wasylishen, 2007, DOI:10.1002/9780470034590.emrstm0504.
- G. E. Maciel and D. W. Sindorf, J. Am. Chem. Soc., 1980, 102, 7606–7607 CrossRef CAS.
- G. E. Michael, D. W. Sindorf and V. J. Bartuska, J. Chromatogr. A, 1981, 205, 438–443 CrossRef.
- D. W. Sindorf and G. E. Maciel, J. Am. Chem. Soc., 1981, 103, 4263–4265 CrossRef CAS.
- B. Pfleiderer, K. Albert, E. Bayer, L. van de Ven, J. de Haan and C. Cramers, J. Phys. Chem., 1990, 94, 4189–4194 CrossRef CAS.
- D. R. Spearing, I. Farnan and J. F. Stebbins, Phys. Chem. Minerals, 1992, 19, 307–321 CrossRef CAS.
- S. Inagaki, I. Kawamura, Y. Sasaki, K. Yoshida, Y. Kubota and A. Naito, Phys. Chem. Chem. Phys., 2013, 15, 13523–13531 RSC.
- S. Zhang, X. Wu and M. Mehring, Chem. Phys. Lett., 1990, 166, 92–94 CrossRef CAS.
- R. L. Johnson and K. Schmidt-Rohr, J. Magn. Reson., 2014, 239, 44–49 CrossRef CAS PubMed.
- H. Liu, X. Zhou, Q. Chen and S. Zhang, Chem. Phys. Lett., 2017, 679, 233–236 CrossRef CAS.
- P. Duan and K. Schmidt-Rohr, J. Magn. Reson., 2017, 285, 68–78 CrossRef CAS PubMed.
- J. Raya and J. Hirschinger, J. Magn. Reson., 2017, 281, 253–271 CrossRef CAS PubMed.
- S. Smet, P. Verlooy, F. Saïdi, F. Taulelle, J. A. Martens and C. Martineau-Corcos, Magn. Reson. Chem., 2019, 57, 224–229 CrossRef CAS PubMed.
- M. Lelli, D. Gajan, A. Lesage, M. A. Caporini, V. Vitzthum, P. Miéville, F. Héroguel, F. Rascón, A. Roussey, C. Thieuleux, M. Boualleg, L. Veyre, G. Bodenhausen, C. Coperet and L. Emsley, J. Am. Chem. Soc., 2011, 133, 2104–2107 CrossRef CAS PubMed.
- A. J. Rossini, A. Zagdoun, M. Lelli, D. Gajan, F. Rascón, M. Rosay, W. E. Maas, C. Copéret, A. Lesage and L. Emsley, Chem. Sci., 2012, 3, 108–115 RSC.
- T. H. Walter, G. L. Turner and E. Oldfield, J. Magn. Reson., 1969, 76, 106–120 Search PubMed.
- F. A. Perras, Z. Wang, P. Naik, I. I. Slowing and M. Pruski, Angew. Chem., Int. Ed., 2017, 56, 9165–9169 CrossRef CAS PubMed.
- H. D. Morris and P. D. Ellis, J. Am. Chem. Soc., 1989, 111, 6045–6049 CrossRef CAS.
- N. Baccile, G. Laurent, C. Bonhomme, P. Innocenzi and F. Babonneau, Chem. Mater., 2007, 19, 1343–1354 CrossRef CAS.
- M. P. Hanrahan, E. L. Fought, T. L. Windus, L. M. Wheeler, N. C. Anderson, N. R. Neale and A. J. Rossini, Chem. Mater., 2017, 29, 10339–10351 CrossRef CAS.
- J. Trebosc, J. W. Wiench, S. Huh, V. S. Lin and M. Pruski, J. Am. Chem. Soc., 2005, 127, 3057–3068 CrossRef CAS PubMed.
- J. W. Wiench, V. S. Lin and M. Pruski, J. Magn. Reson., 2008, 193, 233–242 CrossRef CAS PubMed.
- W. J. Malfait, S. Zhao, R. Verel, S. Iswar, D. Rentsch, R. Fener, Y. Zhang, B. Milow and M. M. Koebel, Chem. Mater., 2015, 27, 6737–6745 CrossRef CAS.
- P. Brunner, M. Reinhold and R. R. Ernst, J. Chem. Phys., 1980, 73, 1086–1094 CrossRef CAS.
- Y. Ishii and R. Tycko, J. Magn. Reson., 2000, 142, 199–204 CrossRef CAS PubMed.
- Y. Ishii, J. P. Yesinowski and R. Tycko, J. Am. Chem. Soc., 2001, 123, 2921–2922 CrossRef CAS.
- A. K. Khitrin and B. M. Fung, J. Magn. Reson., 2001, 152, 185–188 CrossRef CAS.
- J. W. Wiench, C. E. Bronnimann, V. S. Y. Lin and M. Pruski, J. Am. Chem. Soc., 2007, 129, 12076–12077 CrossRef CAS PubMed.
- D. Carnevale, X. Ji and G. Bodenhausen, J. Chem. Phys., 2017, 147, 184201 CrossRef PubMed.
- J. S. Bridel, T. Azaïs, M. Morcrette, J. M. Tarascon and D. Larcher, Chem. Mater., 2010, 22, 1229–1241 CrossRef CAS.
- N. Folliet, C. Roiland, S. Bégu, A. Aubert, T. Mineva, A. Goursot, K. Selvaraj, L. Duma, F. Tielens, F. Mauri, G. Laurent, C. Bonhomme, C. Gervais, F. Babonneau and T. Azaïs, J. Am. Chem. Soc., 2011, 133, 16815–16827 CrossRef CAS PubMed.
- S. Cadars, R. Guégan, M. N. Garaga, X. Bourrat, L. Le Forestier, F. Fayon, T. V. Huynh, T. Allier, Z. Nour and D. Massiot, Chem. Mater., 2012, 24, 4376–4389 CrossRef CAS.
- B. Thomas, T. Coradin, G. Laurent, R. Valentin, Z. Mouloungui, F. Babonneau and N. Baccile, RSC Adv., 2012, 2, 426–435 RSC.
- K. Mao, T. Kobayashi, J. W. Wiench, H. T. Chen, C. H. Tsai, V. S. Lin and M. Pruski, J. Am. Chem. Soc., 2010, 132, 12452–12457 CrossRef CAS PubMed.
- K. Hara, S. Akahane, J. W. Wiench, B. R. Burgin, N. Ishito, V. S. Y. Lin, A. Fukuoka and M. Pruski, J. Phys. Chem. C, 2012, 116, 7083–7090 CrossRef CAS.
- A. R. Mouat, T. Kobayashi, M. Pruski, T. J. Marks and P. C. Stair, J. Phys. Chem. C, 2017, 121, 6060–6064 CrossRef CAS.
- T. Kobayashi and M. Pruski, ACS Catal., 2019, 9, 7238–7249 CrossRef CAS.
- A. G. M. Rankin, P. B. Webb, D. M. Dawson, J. Viger-Gravel, B. J. Walder, L. Emsley and S. E. Ashbrook, J. Phys. Chem. C, 2017, 121, 22977–22984 CrossRef CAS PubMed.
- S. K. Parida, S. Dash, S. Patel and B. K. Mishra, Adv. Colloid Interface Sci., 2006, 121, 77–110 CrossRef CAS PubMed.
- J. K. Moon, D. K. Keum and W. K. Lee, Korean J. Chem. Eng., 1989, 6, 172–178 CrossRef CAS.
- Z. Yang, Q. Li, R. Hua, M. R. Gray and K. C. Chou, J. Phys. Chem. C, 2009, 113, 20355–20359 CrossRef CAS.
- Y. Wu, M. Zhang, H. Zhao, S. Yang and A. Arkin, RSC Adv., 2014, 4, 61256–61267 RSC.
- J. Shi, L. Gong, S. Sun, Z. Huang, B. Ding and J. Yao, RSC Adv., 2019, 9, 25326–25335 RSC.
- A. M. Bodratti, B. Sarkar, D. Song, M. Tsianou and P. Alexandridis, J. Dispersion Sci. Technol., 2015, 36, 1–9 CrossRef CAS.
- H. Bessaies-Bey, J. Fusier, M. Hanafi, S. Zhang, M. Destarac, S. Jouenne, N. Passade-Boupat, F. Lequeux, J. B. d'Espinose de Lacaillerie and N. Sanson, Colloids Surf., A, 2019, 579, 123673 CrossRef CAS.
- J. Ghodbane and R. Denoyel, Colloids Surf., A, 1997, 127, 97–104 CrossRef CAS.
- B. R. Postmus, F. A. M. Leermakers, L. K. Koopal and M. A. Cohen Stuart, Langmuir, 2007, 23, 5532–5540 CrossRef CAS PubMed.
- R. Simonutti, A. Comotti, F. Negroni and P. Sozzani, Chem. Mater., 1999, 11, 822–828 CrossRef CAS.
- H. Dohi and S. Horiuchi, Langmuir, 2007, 23, 12344–12349 CrossRef CAS PubMed.
- I. Klur, J. F. Jacquinot, F. Brunet, T. Charpentier, J. Virlet, C. Schneider and P. Tekely, J. Phys. Chem. B, 2000, 104, 10162–10167 CrossRef CAS.
- A. J. Vega and G. W. Scherer, J. Non-Cryst. Solids, 1989, 111, 153–166 CrossRef CAS.
- J.-B. d'Espinose de la Caillerie, M. R. Aimeur, Y. E. Kortobi and A. P. Legrand, J. Colloid Interface Sci., 1997, 194, 434–439 CrossRef PubMed.
- Y. Q. Ye, M. Malon, C. Martineau, F. Taulelle and Y. Nishiyama, J. Magn. Reson., 2014, 239, 75–80 CrossRef CAS PubMed.
- Y. Q. Ye, C. Martineau-Corcos, F. Taulelle and Y. Nishiyama, J. Magn. Reson., 2018, 294, 122–127 CrossRef CAS PubMed.
- Y. Nishiyama, Experimental Approaches of NMR Spectroscopy: Methodology and Application to Life Science and Materials Science, Springer Nature, Singapore, 2018, pp. 180–181 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra04995f |
| This journal is © The Royal Society of Chemistry 2020 |