Open Access Article
Open Access ArticleJustification of crystal stability and origin of transport properties in ternary half-Heusler ScPtBi
R. Majumder a and
S. K. Mitro
a and
S. K. Mitro *b
*b
aPhysics Discipline, Khulna University, Khulna-9208, Bangladesh
bBangamata Sheikh Fojilatunnesa Mujib Science and Technology University, Jamalpur-2012, Bangladesh. E-mail: sujonmitrophysics@gmail.com
First published on 12th October 2020
Abstract
In this study, the mechanical stability, machinability, flexibility, ductility, hardness and crystal stability have been analysed for the justification of suitability of ScPtBi for practical applications and device fabrication. We observed that ScPtBi satisfies the Born stability criterion nicely as well as possessing a negative value of formation enthalpy which suggests that ScPtBi is a mechanically stable compound and can be synthesized by chemical synthesis techniques. We have investigated the nature of the bonding in ScPtBi via Mulliken bond population analysis and charge density mapping which suggest that both ionic and covalent bonding exist in the ScPtBi with bonding and anti-bonding features. We have correlated band structure (BS), density of states (DOS), Fermi surface (FS) and charge density mapping to explain the origin of transport properties in ScPtBi by exploring the electronic behavior in detail with the help of first principles calculation. We have observed an octahedral hole like sheet due to a heavy hole pocket at the Γ point whose flat surfaces enhance transport properties in the direction parallel to the edges. The electron and hole like multi sheets achieved in the same topology are favorable for skipping of carriers and Fermi surface nesting. We have also calculated the electronic specific heat coefficient successfully using the density of states at the Fermi level.
1. Introduction
The research on topological insulators (TIs) is attracting the increased attention of the research community for their broad range of applications and exposure of interesting physics.1–4 Their novel quantum state in which the interior insulating feature coexists with the conducting states on the edges or surfaces, has made them reliable for several purposes.5,6 Considering their scientific significance, the search for TIs has been extended in different directions ranging from early binary to ternary compounds. Among these ternary compounds, some ternary half-Heusler (THH) compounds with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry together with a MgAgAs-type crystal structure can be treated as TIs by alloying, applying strain and probing the band topology.6,7 These THHs have been reported extensively over the past few decades for their outstanding physical properties.6–12 Their flexible band gap tuning capability ranging from wide band gap semiconductors to zero band gap insulators introduce them as “properties on request”.7–12 The ScPtBi is one of the members of such THHs, possesses non-trivial band inversion topology (the difference between Γ8 and Γ6 is positive) which is one of the key features for the large magnetoresistance and high mobility characters.13 Despite its potential application sides, this compound was not investigated extensively for a long time in contrast to the other ternary half-Heuslers belong to the same family (28 members reported by W. Al-Sawai et al.6) due to its unsuccessful synthesis attempts for thermal instability (no matter polycrystal or single crystal).13 But recently, Z. Hou et al.13 have synthesized high quality ScPtBi single crystal successfully and demonstrated some interesting properties of this material ranging from large low-field magnetoresistance effect to a high mobility over a wide range of temperature even up to room temperature. They have proposed that ScPtBi is a potential candidate for applications in high-sensitivity magnetic sensors and one of the ideal systems for a comprehensive understanding of the rare-earth based half-Heusler compounds. After their successful synthesis, some research on this promising system has been already initiated with a new view and all of them are based on the investigation on transport and thermoelectric behaviors.14,15 Though Z. Hou et al.13 successfully synthesized the ScPtBi single crystal but they didn't discuss its mechanical and crystal stability which is very important for the consideration of practical applications and device fabrication. However, ScPtBi possesses thermal instability but information on crystal formation enthalpy, mechanical stability, machinability, elastic moduli can be helpful to overcome the limitations associated with thermal instability by choosing appropriate synthesis techniques. Therefore, the primary objective of this research is to discuss the crystal and mechanical stability with the help of elastic constants and formation enthalpy. At the same time, in view of materials science, elastic constants are a very significant factor because using these some vital information such as ductility, Poisson ratio, hardness, bonding nature, inter-atomic potential can be figured out nicely.16–18 We have also focused on investigating the Milliken bond population analysis and charge density mapping because bonding analysis can give the information about the bonding strength, bonding nature as well as bonding length which is also important for understanding the material nature properly.
1 stoichiometry together with a MgAgAs-type crystal structure can be treated as TIs by alloying, applying strain and probing the band topology.6,7 These THHs have been reported extensively over the past few decades for their outstanding physical properties.6–12 Their flexible band gap tuning capability ranging from wide band gap semiconductors to zero band gap insulators introduce them as “properties on request”.7–12 The ScPtBi is one of the members of such THHs, possesses non-trivial band inversion topology (the difference between Γ8 and Γ6 is positive) which is one of the key features for the large magnetoresistance and high mobility characters.13 Despite its potential application sides, this compound was not investigated extensively for a long time in contrast to the other ternary half-Heuslers belong to the same family (28 members reported by W. Al-Sawai et al.6) due to its unsuccessful synthesis attempts for thermal instability (no matter polycrystal or single crystal).13 But recently, Z. Hou et al.13 have synthesized high quality ScPtBi single crystal successfully and demonstrated some interesting properties of this material ranging from large low-field magnetoresistance effect to a high mobility over a wide range of temperature even up to room temperature. They have proposed that ScPtBi is a potential candidate for applications in high-sensitivity magnetic sensors and one of the ideal systems for a comprehensive understanding of the rare-earth based half-Heusler compounds. After their successful synthesis, some research on this promising system has been already initiated with a new view and all of them are based on the investigation on transport and thermoelectric behaviors.14,15 Though Z. Hou et al.13 successfully synthesized the ScPtBi single crystal but they didn't discuss its mechanical and crystal stability which is very important for the consideration of practical applications and device fabrication. However, ScPtBi possesses thermal instability but information on crystal formation enthalpy, mechanical stability, machinability, elastic moduli can be helpful to overcome the limitations associated with thermal instability by choosing appropriate synthesis techniques. Therefore, the primary objective of this research is to discuss the crystal and mechanical stability with the help of elastic constants and formation enthalpy. At the same time, in view of materials science, elastic constants are a very significant factor because using these some vital information such as ductility, Poisson ratio, hardness, bonding nature, inter-atomic potential can be figured out nicely.16–18 We have also focused on investigating the Milliken bond population analysis and charge density mapping because bonding analysis can give the information about the bonding strength, bonding nature as well as bonding length which is also important for understanding the material nature properly.
On the other hand, all the reported literature on ScPtBi have focused on the thermoelectric and transport properties due the potentiality of this material in this new window. Therefore, the secondary purposes of this study is to find and discuss the origin of transport properties reported in previous literature via exploring the electronic properties with the help of Fermi surface (FS), band structure (BS), density of state (DOS) and charge density mapping. We hope that the findings of this research will help to improve the transport properties for ScPtBi as well as for these types of platinum–bismuthides in future by understanding the origin of transport behaviors of ScPtBi. For example, the addition of suitable doping, tuning BS by applying hydrostatic pressure, magnetic fields, temperature etc. will be possible to tune FS as well as electronic behaviors for upgrading transport properties well as other properties.
2. Method of calculations
The first-principles calculations have been performed on CASTEP (Cambridge Serial Total Energy Package) code19 in the frame of density functional theory (DFT).20,21 The generalized gradient approximation (GGA) exchange correlation function along with Perdew–Burke–Ernzerhof (PBE)22 scheme have been treated for this investigation employing the well-known Vanderbilt type ultrasoft pseudopotential23 according to the ref. 17, 18 and 24, which were used to analyze similar type of THHs. Since, the constituents of this material involve mass number greater than 50, therefore, for all types of calculations, we have included spin orbital interaction.25 To confirm the well convergence of the geometrical optimization and the elastic constant, cut-off energy of plane wave has been used 550 eV. The k-point mesh of 8 × 8 × 8 grids has been chosen to sample Monkhorst–Pack scheme26 for our ScPtBi system. Since, dense mesh of uniformly distributed k-points is necessary for BS and FS calculations. Therefore, the sampling of Brillouin zone has been performed using a k-point mesh of 20 × 20 × 20 grid of Monkhorst–Pack points for these investigations.27 The stress–strain method has been employed to calculate the elastic stiffness constants of ScPtBi at normal condition.28 The structure has been optimized with the help of Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.29 The unit cell and atomic relaxation are executed considering the total energy 5 × 10−6 eV per atom, maximum force 0.01 eV Å−1, maximum stress 0.02 GPa and maximum ionic displacement 5 × 10−4 Å.3. Result and discussions
3.1. Structural analysis
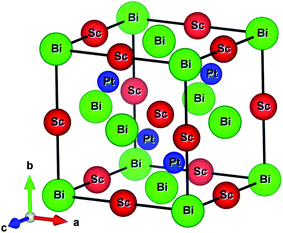
The ScPtBi possesses MgAgAs-type crystal structure belong to the F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group (216), has been built by considering the Bi at Wyckoff position 4a corresponding to the coordinate (0, 0, 0) while Sc and Pt atom at the Wyckoff position 4b (1/2, 1/2, 1/2) and 4c (1/4, 1/4, 1/4), respectively.16–18 The optimized conventional unit cell for ScPtBi has been shown in Fig. 1. The equilibrium lattice parameters and unit cell volume obtained in this study have been enlisted in Table 1. We have compared our results with experimental and theoretical data available for ScPtBi.14,15 It can be observed that lattice constant obtained from Vanderbilt type ultrasoft method is very much consistent with the available data. Therefore for further analysis we have used this pseudopotential to predict our results.
3m space group (216), has been built by considering the Bi at Wyckoff position 4a corresponding to the coordinate (0, 0, 0) while Sc and Pt atom at the Wyckoff position 4b (1/2, 1/2, 1/2) and 4c (1/4, 1/4, 1/4), respectively.16–18 The optimized conventional unit cell for ScPtBi has been shown in Fig. 1. The equilibrium lattice parameters and unit cell volume obtained in this study have been enlisted in Table 1. We have compared our results with experimental and theoretical data available for ScPtBi.14,15 It can be observed that lattice constant obtained from Vanderbilt type ultrasoft method is very much consistent with the available data. Therefore for further analysis we have used this pseudopotential to predict our results.
3.2. Elastic properties and crystal stability
The information about the elastic and mechanical behaviors of a crystal is very much essential in the view of materials science. Because several limiting factors are associated with the practical applications of a material although has a successful synthesis history. The tolerance ability of external stress under different environment, flexibility, regaining ability to its original state after the withdrawal of external deforming force, bonding nature, ductility/brittleness and hardness of a solid substance can be figure out by inquiring the elastic and mechanical properties of a material. To understand the elastic and mechanical properties nicely only three self sufficient elastic constants for a cubic crystal are sufficient. Because in the case of cubical symmetry C11 = C22 = C33, C12 = C23 = C13 and C44 = C55 = C66.18 On the other hand, the elastic and mechanical stability can also be confirmed from these independent elastic constants applying Born stability criterion. Since there is no evidence of investigation of these parameters for ScPtBi. Therefore, various elastic and mechanical properties such as the bulk modulus (B), shear modulus (G), Young's modulus (Y), Poisson's ratio (ν), Pugh's indicator (B/G), machinability index (μM), Vickers hardness (Hv) and Peierls stress (σp) have been calculated for the first time for ScPtBi and summarized in Table 2. We have found that ScPtBi is a mechanically stable compound as the Born stability criteria is well satisfied by the elastic constants (see Table 2): C11 − C12 > 0, C44 > 0 and C11 + 2C12 > 0.30 Since, the material under study has several unsuccessful synthesis attempts due to its thermal instability although high class single crystal has been reported by Z. Hou et al.13 Therefore, it's very much important to justify its formation enthalpy, crystal formation stability which could be a guide line and clue for the next chemical synthesis attempts to be successful in future applying a less expensive and easier synthesis techniques. The chemical stability or crystal stability of solid materials can be ensured via formation enthalpy.31,32 In order to inspect the phase stability of the studied THH ScPtBi, we have evaluated the formation energy for ScPtBi. The formation energy (ΔEf) is defined as the subtraction of the total energies of pure obligate atoms in their stable crystal structures from the total energy of the solid material system. Here, the formation energy (ΔEf) is calculated at zero temperature and zero pressure, therefore, the energy of formation is equal to the enthalpy of formation i.e., ΔEf = ΔHf. The ΔEf of ScPtBi is obtained from the expression:31,32
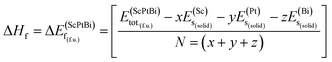 | (1) |
| Compound | C11 | C12 | C44 | B | G | Y | B/G | μM | ν | Hv | σp | Remarks |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ScPtBi | 165.0 | 76.1 | 61.3 | 105.7 | 53.9 | 138.2 | 1.96 | 1.72 | 0.282 | 7.83 | 1.89 | [Our cal.] |
| ScPdBi | 113.1 | 53.5 | 39.2 | 79.3 | 29.8 | 79.0 | 2.67 | 2.02 | 0.333 | 3.31 | — | [Our cal.] |
| ScNiBi | 170.4 | 71.5 | 59.0 | 81.8 | 40.7 | 104.7 | 2.00 | 1.38 | 0.286 | 5.81 | — | [Our cal.] |
| LuPtBi | 143.6 | 67.8 | 15.6 | 93.0 | 37.9 | 100.1 | 2.45 | — | 0.320 | 2.86 | — | 16 |
| LuPdBi | 125.8 | 63.2 | 51.9 | 87.0 | 30.5 | 81.9 | 2.85 | — | 0.340 | 1.33 | — | 17 |
| LuPdSb | 151.3 | 76.6 | 59.6 | 101.5 | 49.4 | 127.6 | 2.05 | 1.70 | 0.290 | 6.91 | — | 18 |
In eqn (1), here, 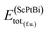 represents the total energy per formula unit, whereas,
represents the total energy per formula unit, whereas, 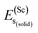 ,
, 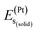 , and
, and 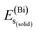 represent the total energies per atom of the pure elements Sc, Pt and Bi, respectively, in their stable structures and N is the number of formula units per unit cell. The calculated value of formation enthalpy for the ScPtBi system is negative value (−7.326 eV per atom) confirming THH ScPtBi stable phase. The observed value of formation enthalpy suggest from the knowledge of thermodynamic, the ScPtBi is energetically favorable and this structure is achievable to be formed experimentally by chemical synthesis. The elastic constant C11 gives the hints of the elasticity along the length wise direction and thus can be useful to measure the response to the stiffness of materials against the uniaxial strain. With a large value of C11, ScPtBi is stiffer than the other half-Heuslers belong to the same family (see Table 2).16–18 For details investigation of elastic and mechanical behavior of ScPtBi, we have calculated above-mentioned parameters (B, G, Y, and ν) using flowing expressions which have been enlisted in Table 2:18
represent the total energies per atom of the pure elements Sc, Pt and Bi, respectively, in their stable structures and N is the number of formula units per unit cell. The calculated value of formation enthalpy for the ScPtBi system is negative value (−7.326 eV per atom) confirming THH ScPtBi stable phase. The observed value of formation enthalpy suggest from the knowledge of thermodynamic, the ScPtBi is energetically favorable and this structure is achievable to be formed experimentally by chemical synthesis. The elastic constant C11 gives the hints of the elasticity along the length wise direction and thus can be useful to measure the response to the stiffness of materials against the uniaxial strain. With a large value of C11, ScPtBi is stiffer than the other half-Heuslers belong to the same family (see Table 2).16–18 For details investigation of elastic and mechanical behavior of ScPtBi, we have calculated above-mentioned parameters (B, G, Y, and ν) using flowing expressions which have been enlisted in Table 2:18
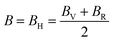 | (2) |
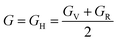 | (3) |
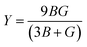 | (4) |
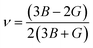 | (5) |
We have compared our results with some Bi-based half-Heuslers (ScPdBi, ScNiBi, LuPtBi, and LuPdBi) and our results are in good agreement with the available data for other half-Heusler compounds. The high value of B for the half-Heusler ScPtBi indicates its high incompressibility character compared to the isostructural half-Heuslers ScPdBi, ScNiBi, LuPtBi, LuPdBi and LuPdSb.16–18 The resistance to plastic deformation can be measured by the Shear modulus, G and is associated with a crucial relationship with the hardness of solids. The values of shear modulus, G of the material under study reflects the higher resistance against plastic deformation as well as show the high level of micro hardness of ScPtBi in comparison to the recently reported isostructural half-Heusler compounds.16–18 We know that materials can be classified as either brittle or ductile in a practical situation. The Pugh and Poisson's ratios are powerful tools for the prediction of brittle and ductile nature of solid materials. One can easily predict the nature of ScPtBi (whether it is ductile or brittle in nature) according to the limiting values reported in ref. 33 and 34. On the other hand, Cauchy pressure, (C12–C44) also can be used as a useful tool for the measurement of ductility/brittleness.35 In addition, the interatomic force here is basically central as the value of Poisson's ratio is within the range 0.25 to 0.50.36 The value of machinability index 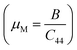 37,38 of ScPtBi half-Heusler is larger (see Table 2) than LuPdBi (∼1.67, calculated by using given expression) and LuPdSb (∼1.70) indicating that ScPtBi is more machinable than the other two half-Heuslers.17,18 Thus, this study introduces a new half-Heusler which is fairly machinable or better mechanical manipulation nature. An empirical model
37,38 of ScPtBi half-Heusler is larger (see Table 2) than LuPdBi (∼1.67, calculated by using given expression) and LuPdSb (∼1.70) indicating that ScPtBi is more machinable than the other two half-Heuslers.17,18 Thus, this study introduces a new half-Heusler which is fairly machinable or better mechanical manipulation nature. An empirical model 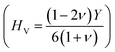 39,40 correlating the elastic moduli and Vicker's hardness to evaluate the hardness of materials and using this correlation the observed value of Vicker's hardness ∼7.83 GPa (see Table 2) is fairly good for conventional applications. The Peierls stress, σp can assess the progress of dislocation of a crystal in a glide plane and details explanation can be found in literature in ref. 36. The estimated Peierls stress, σp of ScPtBi has been enlisted in Table 2 which is high in comparison with several MAX phases (Ti2AlC, V2AlC, Cr2AlC, Nb2AlC and Ta2AlC for which the values lie within the range 0.7–0.98 GPa) and superconductor ((K1.00)(Ba1.00)3(Bi0.89Na0.11)4O12 gives the σp value is 1.1 GPa).41–43 To conclude, the movements of dislocation in ScPtBi compound may be more difficult in contrast to the above mentioned superconductor and MAX phases.
39,40 correlating the elastic moduli and Vicker's hardness to evaluate the hardness of materials and using this correlation the observed value of Vicker's hardness ∼7.83 GPa (see Table 2) is fairly good for conventional applications. The Peierls stress, σp can assess the progress of dislocation of a crystal in a glide plane and details explanation can be found in literature in ref. 36. The estimated Peierls stress, σp of ScPtBi has been enlisted in Table 2 which is high in comparison with several MAX phases (Ti2AlC, V2AlC, Cr2AlC, Nb2AlC and Ta2AlC for which the values lie within the range 0.7–0.98 GPa) and superconductor ((K1.00)(Ba1.00)3(Bi0.89Na0.11)4O12 gives the σp value is 1.1 GPa).41–43 To conclude, the movements of dislocation in ScPtBi compound may be more difficult in contrast to the above mentioned superconductor and MAX phases.
3.3. Bonding analysis and charge density mapping
To choose a suitable synthesis process of a material it's very important to know about the bonding nature and strength among the constituent atoms. For example, ionic compounds can be grown by the solid state reaction, solvent evaporation, precipitation, or the electron transfer reaction incorporating reactive and non reactive metals and nonmetals like halogen gases or inert gases. As solids they can be electrically insulating, but when melted or dissolved they become highly conductive, because the ions are mobilized. Therefore, to get a deep insight into the bonding strength among the atoms in the ScPtBi, we have investigated the Mulliken bond population which is particularly important for the measurement of bonding nature and choosing proper synthesis techniques. The calculated atomic Mulliken bond populations for ScPtBi have been enlisted in Table 3. The Table 3 reveals that the ScPtBi can be considered as the valance state of Sc0.39Pt−1.33Bi0.31 and the charge (∼1.33e) is transferred from Sc and Bi to Pt. Since, the negative and positive values of the population are representative to ionic and covalent bonding, respectively and for zero value of the population the bonding is perfectly ionic.18 Therefore, from the observed values of the population for ScPtBi, it can be concluded that the bonding exists between Sc–Pt is ionic whereas for Pt–Bi it's covalent. The value of bonding length is about 2.809 which are very much consistent with the reported bonding length for other species of half-Heusler compounds.16–18 At the same time, bonding and anti-bonding features among atoms can also be calculated using this bond population analysis in which positive and negative values are representative of bonding and anti-bonding nature, respectively.18 Therefore, from Table 3 it can be concluded that the bonding nature exists between Pt–Bi whereas for Sc–Pt it's anti-bonding.| Species | s | p | d | f | Total | Charge | Bond | Population | Length |
|---|---|---|---|---|---|---|---|---|---|
| Sc | 2.47 | 6.44 | 1.56 | 0.00 | 10.47 | 0.39 | Pt–Bi | 0.11 | 2.809 |
| Pt | 1.02 | 1.31 | 8.99 | 0.00 | 11.33 | −1.33 | Sc–Pt | −1.39 | 2.809 |
| Bi | 1.09 | 3.11 | 0.00 | 0.00 | 4.20 | 0.31 | — | — | — |
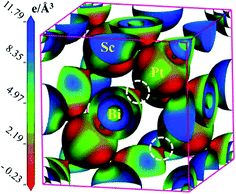
To justify the Mulliken bond population analysis, we have investigated the charge density difference mapping along the (100) crystallographic plane with the help of a charge density scale interns of light intensity. In the scale, the higher electron density is indicated by blue colour and lower electron density is represented by red colour. It's clear from the Fig. 2 that electron density is very high for Sc and low for Pt. At the same time, there is no overlapping between the electron density of Sc and Pt. On the other hand, a clear overlapping can be observed between Pt and Bi. Therefore, we can conclude that the bonding between Sc and Pt is ionic and covalent bonding exists between Pt–Bi. These bonding nature obtained from the charge density mapping confirms Mulliken bond population analysis perfectly.
3.4. Electronic properties and origin of transport behaviors
To understand the optical, optoelectronic, photonic as well as the electromagnetic response of materials preciously, the band structure (BS) can be an effective tool. Therefore, a detailed analysis of BS along with the density of states (DOS) has been performed in this study to explore the electronic behaviors. Fig. 3(a) (left panel) and Fig. 3(b) (right panel) represent the BS and DOS for ScPtBi, respectively. The bands below the Fermi level (in the energy range from 0 eV to −6 eV) are mainly manifested by the 4d state of Pt whereas just above the Fermi level (from the Fermi level to 4 eV) bands are mainly contributed by 3d state of Sc. It can be clearly observed that the overlapping of conduction bands (CB) and valance bands (VB) are only at the Γ symmetry line of the Brillouin zone and in other symmetry points there is no overlapping of CB and VB. This nature of BS (zero band gaps at Γ point) clearly reflects the semi-metallic nature of ScPtBi just like non-trivial semi-metallic nature of HgTe.44 The Γ8 states at the Fermi level have p-like symmetry, while the valence level Γ6 has s-like symmetry. The quantity, Δ (=Γ8 − Γ6) should be positive for non-trivial topology and negative for topological trivial system according to band inversion symmetry. It can be clearly seen from the calculated BS in this work, the quantity Δ is positive for ScPtBi. This confirms the non-trivial band inversion of ScPtBi which is very significant and convenient characteristic for this type of THHs.6,45 These non-trivial bands inversion are mainly responsible for attributing outstanding transport properties for these THHs.46–48 The flat bands located at the lower portion around −6 eV of the BS are manifest by the 4s state of the Sc. It should be noted that the hybridization of 4s state of Sc with Pt and Bi is hardly possible and this, in turn, reveals that the 4s states of Sc are irrelevant near the Fermi level and can be treated as core electronic states. On the other hand, bands lie just below the Fermi level are contributed mainly due to the Bi-6p states. There is a strong hybridization between 6p orbital of Bi and 4d orbital of Pt below the Fermi level (can be confirmed from charge density mapping marked by the white circles in Fig. 2) and which also can be noticeable for between 6p-Bi and 3d-Sc above the Fermi level. Therefore, p–d mixing of states has a vital contribution throughout the all over BS of ScPtBi. Our study on BS is very much consistent with the reported literature on different half-Heusler compounds.6,15–18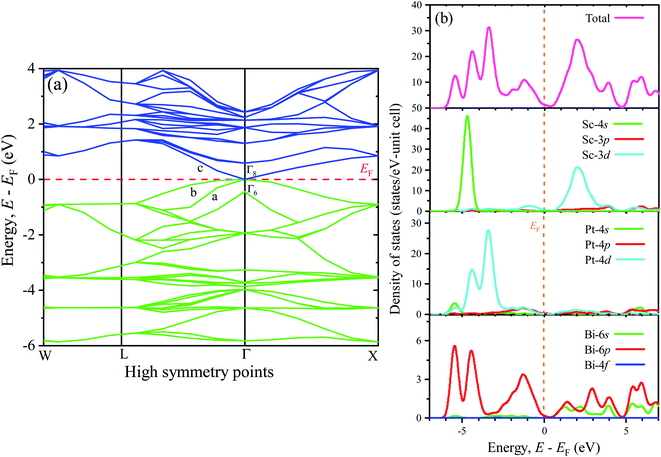 | ||
| Fig. 3 Electronic (a) band structure of ScPtBi (left panel) and the right panel shows the (b) density of states (total and partial). | ||
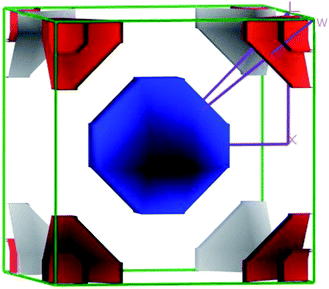
The closer inspection of Γ point on the Fermi level reveals that only three significant bands crossing through the Fermi level, namely a, b and c. Actually, these three bands manifest all the electronic characteristics for ScPtBi along with the transport behavior. The Fermi surface which is an important tool for the visualization of electronic behavior depends much on these significant crossing bands. Fig. 4 shows the Fermi surface topology for the ScPtBi mainly originated due to the bands crossing through the Fermi level. The Fermi sheet within the octahedral shape originated due to the existence of a heavy hole pocket at the Γ point. At the same time, electron like curved Fermi sheets with nesting features along the Γ–W direction and at the corners of the topology is manifested by electron pocket. The heavy hole pocket at the Γ point is mainly contributed by the bands ‘a’ and ‘b’ crossing from the valance band to the conduction band. Equally important, comparatively lighter electron pockets are manifested by the band ‘c’ crossing from the conduction to the valance band (see Fig. 3(a)). Shrivastava et al. have demonstrated the similar contributions of bands for LuPtBi.49
The flatness of the octahedral surfaces is conducive to enhance the transport properties of ScPtBi.50 The origin of observed outstanding transport properties including high mobility at nearly room temperature investigated by Z. Hou et al. is the flatness of the hole pocket at Γ point.13 Which suggests that to attain better transport properties in these type of THHs hole like sheet with hole pocket should be flat reasonably. These multi sheets Fermi surfaces with flat faces are the favorable condition for skipping of carriers and Fermi surface nesting51 (can be seen in Γ–W direction as well as in the corners of the topology). The existence of multi like sheets (electron and hole like sheets) in the same topology is also an important character to obtain the multi-band nature.36 It's worth mentioning that the presence of a heavy hole pocket at Γ point together with a lighter electron pocket in the same topology is very convenient for this type of half-Heusler compounds.14 Therefore, it can be easily concluded that ScPtBi exhibit all the necessary properties to show important properties ranging from emerging thermoelectric transport to ultra-high mobility of carriers. The electronic specific heat coefficient (γ) is very important parameters to discuss the electronic behaviors of materials. The electronic specific heat coefficient is defined as the fraction of heat used by the electron to raise up the energy of itself and a much important factor for attributing thermoelectric transport properties because the specific heat of electrons varies with absolute temperature in all the states of materials. To evaluate electronic specific heat coefficient, density of states at Fermi level, N(EF) is very essential. One can easily find out the electron phonon coupling constant by comparing theoretical electronic specific heat coefficient with experimental electronic specific heat coefficient via the relationship mentioned in ref. 52 and the theoretical electronic specific heat coefficient can be calculated using the following expression:53
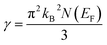 | (6) |
The calculated value of electronic specific heat coefficient is ∼4.08 mJ K−2 mol−1 which is comparable to the observed theoretical value for Co2FeGa Heusler compound (∼4.9 mJ K−2 mol−1).54
4. Conclusion
In summary, in the present study, we have justified the crystal stability of THH ScPtBi by incorporating the elastic constants and formation enthalpy measurement techniques. At the same time, we have discussed about the origin of transport properties in ScPtBi by exploring electronic behaviors with the help of BS, DOS and FS analysis. The calculated formation enthalpy and the Born stability criteria show that ScPtBi has the good alloying ability as well as structural stability. Bonding analysis confirms a valance state of Sc0.39Pt−1.33Bi0.31 where charge (1.33e) is transferred from Sc and Bi to Pt. Both the ionic and covalent bonding with bonding and anti bonding features is available in ScPtBi with a bonding length of ∼2.809. To discuss the origin of transport properties in ScPtBi, we have observed a hole like sheet at the Γ point which is manifested by heavy hole pocket and electron like sheets on the corners of the topology with nesting features. The flatness of the planes of hole like sheet at Γ point is the main origin of the transport behaviors of ScPtBi. The electronic specific heat coefficient has been also calculated successfully using the density of states at the Fermi level, EF.Author contributions
R. Majumder: Conceptualization, supervision, formal analysis, validation, writing-original draft, writing-review & editing. S. K. Mitro: Methodology, data curation, formal analysis, writing-original draft, writing-review & editing.Data availability
All data needed to evaluate the conclusion of this study are presented in the paper. Additional data are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors are highly acknowledged Khulna University, Khulna, Bangladesh and Bangamata Sheikh Fojilatunnesa Mujib Science and Technology University, Jamalpur, Bangladesh for the computer support.References
- Z. K. Liu, L. X. Yang, S.-C. Wu, C. Shekhar, J. Jiang, H. F. Yang, Y. Zhang, S.-K. Mo, Z. Hussain, B. Yan, C. Felser and Y. L. Chen, Nat. Commun., 2016, 7, 1–7 Search PubMed.
- X. L. Qi and S. C. Zhang, Rev. Mod. Phys., 2011, 83, 1057–1110 CrossRef CAS.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045–3067 CrossRef CAS.
- S. D. Sarma and Q. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 081404–081405 CrossRef.
- S. Deepika and S. P. Sanyal, Solid State Commun., 2018, 273, 1–4 CrossRef.
- W. Al-Sawai, L. Hsin, R. S. Markiewicz, L. A. Wray, Y. Xia, S.-Y. Xu, M. Z. Hasan and A. Bansil, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(12), 125208 CrossRef.
- A. Mukhopadhyay, S. Mahana, S. Chowki, D. Topwal, and N. Mohapatra, AIP Conference Proceedings, AIP Publishing LLC, 2017, vol. 1832, iss. 1, p. 110024 Search PubMed.
- S. K. Dhar, N. Nambudripad and R. Vijayaraghavan, J. Phys., 1988, 18, L41–L44 CrossRef CAS.
- J. Pierre and I. Karla, J. Magn. Magn. Mater., 2000, 217, 74–82 CrossRef CAS.
- T. V. Bay, et al., Solid State Commun., 2014, 183, 13–17 CrossRef CAS.
- M. H. Jung, T. Yoshino, S. Kawasaki, T. Pietrus, Y. Bando, T. Suemitsu, M. Sera and T. Takabatake, J. Appl. Phys., 2001, 89, 7631–7633 CrossRef CAS.
- S. Bhattacharya, A. L. Pope, R. T. Littleton IV, T. M. Tritt, V. Ponnambalam, Y. Xia and S. J. Poon, Appl. Phys. Lett., 2000, 77, 16 CrossRef.
- Z. Hou, Y. Wang, E. Liu, H. Zhang, W. Wang and G. Wu, Appl. Phys. Lett., 2015, 107(20), 202103 CrossRef.
- K. A. Gschneidner, J. C. G. B€unzli, and V. K. Pecharsky, Handbook on the Physics and Chemistry of Rare Earths, Elsevier, New York, 2007, vol. 36 Search PubMed.
- G. Ding, G. Y. Gao, L. Yu, Y. Ni and K. Yao, J. Appl. Phys., 2016, 119(2), 025105 CrossRef.
- R. Majumder and M. M. Hossain, Comput. Condens. Matter, 2019, 21, e00402 CrossRef.
- R. Majumder, M. M. Hossain and D. Shen, Mod. Phys. Lett. B, 2019, 33(30), 1950378, DOI:10.1142/S0217984919503780.
- R. Majumder, S. K. Mitro and B. Bairagi, J. Alloys Compd., 2020, 836, 155395 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567 CAS.
- P. Hohenberg and W. Kohn, Phys. Rev. [Sect.] B, 1964, 136, 864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev. [Sect.] A, 1965, 140, 1133 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- N. Korozlu, K. Colakoglu, E. Deligoz and G. Surucu, Europhys. Lett., 2010, 18, 181040 Search PubMed.
- G. Tse and D. Yu, Comput. Condens. Matter, 2015, 4, 59–63 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- B. Ghebouli, M. A. Ghebouli and M. Fatmi, Solid State Sci., 2010, 12, 587 CrossRef CAS.
- J. Kang, E. C. Lee and K. J. Chang, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 054106 CrossRef.
- T. H. Fischer and J. Almlof, J. Phys. Chem., 1992, 96, 9768 CrossRef CAS.
- C. Shekhar, S. Ouardi, A. K. Nayak, G. H. Fecher, W. Schnelle and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155314 CrossRef.
- M. H. K. Rubel, K. M. Hossain, S. K. Mitro, M. M. Rahman, M. A. Hadi and A. K. M. A. Islam, Mater. Today Commun., 2020, 24, 100935, DOI:10.1016/j.mtcomm.2020.100935.
- H. Mebtouche, O. Baraka, A. Yakoubi, R. Khenata, S. A. Tahir, R. Ahmed, S. H. Naqib, A. Bouhemadou, S. Bin Omran and X. Wang, Mater. Today Commun., 2020, 101420 CrossRef CAS.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823 CrossRef CAS.
- H. Fu, D. Li, F. Peng, T. Gao and X. Cheng, Comput. Mater. Sci., 2008, 44, 774 CrossRef CAS.
- D. G. Pettifor, Mater. Sci. Technol., 1992, 8, 345–349 CrossRef CAS.
- M. H. K. Rubel, S. K. Mitro, B. K. Mondal, M. M. Rahaman, M. Saiduzzaman, J. Hossain and N. Kumada, Phys. C, 2020, 574, 1353669 CrossRef CAS.
- X. Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- S. K. Mitro, K. M. Hossain, R. Majumder and M. Z. Hasan, J. Alloys Compd., 2020, 157088, DOI:10.1016/j.jallcom.2020.157088.
- M. Mattesini, R. Ahuja and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 184108 Search PubMed.
- S. K. Mitro, R. Majumder, K. M. Hossain, M. Z. Hasan, M. E. Hossain and M. A. Hadi, Chin. Phys. B, 2020 DOI:10.1088/1674-1056/abaf9d.
- D. Music and J. M. Schneider, J. Phys.: Condens. Matter, 2008, 20, 05522 Search PubMed.
- M. A. Hossain, M. S. Ali, F. Parvin and A. K. M. A. Islam, Comput. Mater. Sci., 2013, 73, 1–8 CrossRef CAS.
- M. H. K. Rubel, M. A. Hadi, M. M. Rahaman, M. S. Ali, M. Aftabuzzaman, R. Parvin, A. K. M. A. Islam and N. Kumada, Comput. Mater. Sci., 2017, 138, 160–165 CrossRef CAS.
- P. W. Hawkes, Advances in Electronics and Electron Physics, Academic Press, New York, 1988, vol. 72 Search PubMed.
- S. Chadov, X. Qi, J. Kübler, G. H. Fecher, C. Felser and S. C. Zhang, Nat. Mater., 2010, 9, 541 CrossRef CAS.
- G. Xu, W. Wang, X. Zhang, Y. Du, E. Liu, S. Wang, G. Wu, Z. Liu and X. X. Zhang, Sci. Rep., 2014, 4, 5709 CrossRef.
- O. Pavlosiuk, D. Kaczorowski and P. Wi_sniewski, Sci. Rep., 2015, 5, 9158 CrossRef.
- F. F. Tafti, T. Fujii, A. J. Fecteau, S. R. De Cotret, N. D. Leyyaud, A. Asamitsu and L. Taillefer, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184504–184505 CrossRef.
- D. Shrivastava and S. P. Sanyal, Phys. C, 2018, 544, 22–26 CrossRef CAS.
- M. H. Rubel, M. M. Ali, M. S. Ali, R. Parvin, M. M. Rahaman, K. M. Hossain and N. Kumada, Solid State Commun., 2019, 288, 22–27 CrossRef CAS.
- W. E. Pickett and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, R8642 CrossRef CAS.
- R. Swetarekha, V. Kanchana, G. Vaitheeswaran, A. Svane, S. B. Dugdale and N. E. Christensen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174531 CrossRef.
- M. Z. Rahaman and M. A. Rahman, J. Alloys Compd., 2017, 695, 2827–2834 CrossRef CAS.
- R. Y. Umetsu, N. Endo, A. Fujita, R. Kainuma, A. Sakuma, K. Fukamichi and K. Ishida, J. Phys.: Conf. Ser., 2010, 200, 6 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |