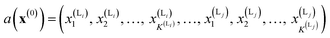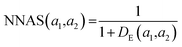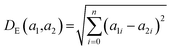Open Access Article
Open Access ArticleNeural network activation similarity: a new measure to assist decision making in chemical toxicology†
Timothy E. H.
Allen
 *ab,
Andrew J.
Wedlake
b,
Elena
Gelžinytė
*ab,
Andrew J.
Wedlake
b,
Elena
Gelžinytė
 b,
Charles
Gong
b,
Jonathan M.
Goodman
b,
Charles
Gong
b,
Jonathan M.
Goodman
 b,
Steve
Gutsell
c and
Paul J.
Russell
c
b,
Steve
Gutsell
c and
Paul J.
Russell
c
aMRC Toxicology Unit, University of Cambridge, Hodgkin Building, Lancaster Road, Leicester, LE1 7HB, UK
bCentre for Molecular Informatics, Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK
cUnilever Safety and Environmental Assurance Centre, Colworth Science Park, Sharnbrook, Bedfordshire, MK44 1LQ, UK. E-mail: teha2@cam.ac.uk
First published on 24th June 2020
Abstract
Deep learning neural networks, constructed for the prediction of chemical binding at 79 pharmacologically important human biological targets, show extremely high performance on test data (accuracy 92.2 ± 4.2%, MCC 0.814 ± 0.093 and ROC-AUC 0.96 ± 0.04). A new molecular similarity measure, Neural Network Activation Similarity, has been developed, based on signal propagation through the network. This is complementary to standard Tanimoto similarity, and the combined use increases confidence in the computer's prediction of activity for new chemicals by providing a greater understanding of the underlying justification. The in silico prediction of these human molecular initiating events is central to the future of chemical safety risk assessment and improves the efficiency of safety decision making.
Introduction
Machine learning algorithms are mathematical models able to learn from data without explicit programming from a human expert. The algorithms have gained much attention as high-quality predictors and classifiers. Classification tasks in toxicology are often explored using a variety of machine learning algorithms. Some examples of this include a support vector machine for predicting liver injury,1 genotoxicity prediction using random forests (RFs),2 carcinogenicity predicted using nearest neighbour calculations,3 and using a naive Bayes classifier,4 and ensemble methods, combining several classifiers into a single decision-making model for hepatotoxicity.5 Deep learning or deep neural networks (DNNs) are a machine learning approach that has been gaining attention. These algorithms are extremely powerful but require a large amount of data, and high-powered computers for training.6 The power of DNNs has been illustrated in drug discovery, where the Merck Molecular Activity Challenge in 2012 was won by an approach using neural networks to make molecular activity predictions.7 In toxicology these networks can be used to aid in risk assessment and safety science in predictive toxicology.8 An example of this approach won the Toxicity in the 21st Century (Tox21) prediction challenge in 2015,9,10 and deep learning has also been applied to predict drug-induced liver injury11 and cardiac toxicity.12 A number of studies have shown that DNNs outperform other machine learning algorithms on identical prediction tasks7,9,10,13 including direct comparisons to RFs in regression14 and classification.15In toxicology, computational methods need to be transparent to be accepted by toxicologists, risk assessors and regulators.16 Several attempts have been made to do this in the past,17 including by assigning importance values to features in the test data by removing features of the test set and observing changes in DNN output,18 or by calculating the gradient of DNN output with respect to features in the test set.19,20 Making the machine learning methodology more akin to a read-across, in which experimental data on one chemical is used in the evaluation of a similar chemical, is a good strategy to increase confidence in the prediction.21 We aim to extend these methodologies, in a way appropriate to toxicity prediction, using chemical inputs.
Human molecular initiating events (MIEs) make good targets for prediction using DNNs. MIEs are initial chemical–biological interactions which start adverse outcome pathways (AOPs).22–24 In the past, a wide variety of computational methods have been used to predict MIEs. Some of these methods rely on the use of chemical substructures as alerts or to define chemical categories for the prediction of molecular activity.25–30 Some compare chemical similarity and reactivity31 or use decision trees to classify reactivity.32 Some use more complex calculations including quantum chemistry to identify reactivity barriers.33 There are also a wide variety of mathematical quantitative structure–activity relationships (QSARs) appropriate for this task.16,34 While machine learning algorithms such as DNNs,13 shallow NNs and decision trees,35 and convolutional neural networks36 have been used in ligand–receptor binding binary classification tasks in the past, this is the first time DNNs have been applied to predicting MIEs. A wide variety of diverse and important human targets were chosen for DNN classifier construction, including the well-known Bowes targets37 and an extended list identified in our previous work38 including targets published by Sipes et al.39 Many of the previously published papers on machine learning only provide models for a single biological target or endpoint.1–5,11,12,15 This limits their usefulness and coverage of human toxicology, which we aim to overcome by constructing models for a large number of MIEs. Generating models for this extended list of targets provides a wider screen of potential molecular toxicity.
By constructing binary classification DNNs for these targets we can establish their importance in the prediction of MIEs, investigate their working and better understand their predictions, and both compare them to other methods of prediction and consider how these approaches can work together to improve their predictive power and confidence.
Methods
Data set
Data for 79 pharmacologically important biological targets were extracted from the publicly available databases ChEMBL40 and ToxCast41 (Table 1). These targets are a subset of those used in our previous work38 including targets published by Bowes et al.37 and Sipes et al.39 These targets were chosen as they provide valuable toxicological information for risk assessment. ChEMBL and ToxCast were combined to provide a relatively balanced dataset with more than 1000 chemicals per target for model construction and evaluation, an amount that was found to be required for DNN training. In total 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 active and 141
109 active and 141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 inactive unique compound–target relationships were obtained, for a total of 285
796 inactive unique compound–target relationships were obtained, for a total of 285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 and a positive data percentage of 50.4%. On average this equates to 3530 data points per target. Imbalanced datasets cause difficulties for machine learning algorithms,4,12,13,15 and developing a balanced dataset is a key advantage when constructing models.
905 and a positive data percentage of 50.4%. On average this equates to 3530 data points per target. Imbalanced datasets cause difficulties for machine learning algorithms,4,12,13,15 and developing a balanced dataset is a key advantage when constructing models.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 actives and 141
109 actives and 141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 inactives for a total of 285
796 inactives for a total of 285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 compounds
905 compounds
| Target | Target gene | Actives | Inactives | Total |
|---|---|---|---|---|
| Acetylcholinesterase | AChE | 2611 | 1964 | 4575 |
| Adenosine A2a receptor | ADORA2A | 3943 | 2082 | 6025 |
| Alpha-2a adrenergic receptor | ADRA2A | 842 | 1013 | 1855 |
| Androgen receptor | AR | 2637 | 7283 | 9920 |
| Beta-1 adrenergic receptor | ADRB1 | 1260 | 1080 | 2340 |
| Beta-2 adrenergic receptor | ADRB2 | 1943 | 2012 | 3955 |
| Delta opioid receptor | OPRD1 | 3006 | 1219 | 4225 |
| Dopamine D1 receptor | DRD1 | 1350 | 1990 | 3340 |
| Dopamine D2 receptor | DRD2 | 5694 | 1136 | 6830 |
| Dopamine transporter | SLC6A3 | 2509 | 1916 | 4425 |
| Endothelin receptor ET-A | EDNRA | 1285 | 1150 | 2435 |
| Glucocorticoid receptor | NR3C1 | 3018 | 6972 | 9990 |
| hERG | KCNH2 | 4895 | 3245 | 8140 |
| Histamine H1 receptor | HRH1 | 1275 | 1105 | 2380 |
| Mu opioid receptor | OPRM1 | 3610 | 2305 | 5915 |
| Muscarinic acetylcholine receptor M1 | CHRM1 | 2014 | 1241 | 3255 |
| Muscarinic acetylcholine receptor M2 | CHRM2 | 1633 | 2032 | 3665 |
| Muscarinic acetylcholine receptor M3 | CHRM3 | 1537 | 1113 | 2650 |
| Norepinephrine transporter | SLC6A2 | 2910 | 1940 | 4850 |
| Serotonin 2a (5-HT2a) receptor | HTR2A | 3757 | 1033 | 4790 |
| Serotonin 3a (5-HT3a) receptor | HTR3A | 451 | 1054 | 1505 |
| Serotonin transporter | SLC6A4 | 4041 | 1134 | 5175 |
| Tyrosine-protein kinase LCK | LCK | 1732 | 523 | 2255 |
| Vasopressin V1a receptor | AVPR1A | 619 | 1056 | 1675 |
| Type-1 angiotensin II receptor | AGTR1 | 806 | 1179 | 1985 |
| RAC-alpha serine/threonine-protein kinase | AKT1 | 2765 | 1220 | 3985 |
| Beta-secretase 1 | BACE1 | 6016 | 2604 | 8620 |
| Cholinesterase | BCHE | 1400 | 2145 | 3545 |
| Caspase-1 | CASP1 | 1369 | 3196 | 4565 |
| Caspase-3 | CASP3 | 1177 | 1828 | 3005 |
| Caspase-8 | CASP8 | 330 | 1130 | 1460 |
| Muscarinic acetylcholine receptor M5 | CHRM5 | 679 | 1081 | 1760 |
| Inhibitor of nuclear factor kappa-B kinase subunit alpha | CHUK | 316 | 1069 | 1385 |
| Macrophage colony-stimulating factor 1 receptor | CSF1R | 1336 | 1049 | 2385 |
| Casein kinase I isoform delta | CSNK1D | 708 | 1027 | 1735 |
| Endothelin B receptor | EDNRB | 809 | 1236 | 2045 |
| Neutrophil elastase | ELANE | 2134 | 1371 | 3505 |
| Ephrin type-A receptor 2 | EPHA2 | 528 | 1102 | 1630 |
| Fibroblast growth factor receptor 1 | FGFR1 | 2163 | 1207 | 3370 |
| Peptidyl-prolyl cis–trans isomerase | FKBP1A | 354 | 1006 | 1360 |
| Vascular endothelial growth factor receptor 1 | FLT1 | 1088 | 2077 | 3165 |
| Vascular endothelial growth factor receptor 3 | FLT4 | 674 | 1081 | 1755 |
| Tyrosine-protein kinase FYN | FYN | 420 | 1075 | 1495 |
| Glycogen synthase kinase-3 beta | GSK3B | 2549 | 1256 | 3805 |
| Histone deacetylase 3 | HDAC3 | 1051 | 1139 | 2190 |
| Insulin-like growth factor 1 receptor | IGF1R | 2483 | 1132 | 3615 |
| Insulin receptor | INSR | 887 | 1093 | 1980 |
| Vascular endothelial growth factor receptor 2 | KDR | 7816 | 1579 | 9395 |
| Leukotriene B4 receptor 1 | LTB4R | 350 | 1030 | 1380 |
| Tyrosine-protein kinase Lyn | LYN | 454 | 1046 | 1500 |
| Mitogen-activated protein kinase 1 | MAPK1 | 6209 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285 285 |
| Mitogen-activated protein kinase 9 | MAPK9 | 1227 | 1088 | 2315 |
| MAP kinase-activated protein kinase 2 | MAPKAPK2 | 829 | 1156 | 1985 |
| Hepatocyte growth factor receptor | MET | 2871 | 1144 | 4015 |
| Matrix metalloproteinase-13 | MMP13 | 2388 | 1112 | 3500 |
| Matrix metalloproteinase-2 | MMP2 | 2938 | 1677 | 4615 |
| Matrix metalloproteinase-3 | MMP3 | 1759 | 1036 | 2795 |
| Matrix metalloproteinase-9 | MMP9 | 2582 | 1848 | 4430 |
| Serine/threonine-protein kinase NEK2 | NEK2 | 298 | 1057 | 1355 |
| P2Y purinoceptor 1 | P2RY1 | 560 | 1100 | 1660 |
| Serine/threonine-protein kinase PAK 4 | PAK4 | 380 | 1100 | 1480 |
| Phosphodiesterase 4A | PDE4A | 653 | 1017 | 1670 |
| Phosphodiesterase 5A | PDE5A | 1551 | 1174 | 2725 |
| Phosphatidylinositol 4,5-bisphosphate 3-kinase catalytic subunit alpha | PIK3CA | 4724 | 2086 | 6810 |
| Peroxisome proliferator-activated receptor gamma | PPARG | 4362 | 7283 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 645 |
| Protein tyrosine phosphatase non-receptor type 1 | PTPN1 | 1471 | 2179 | 3650 |
| Protein tyrosine phosphatase non-receptor type 11 | PTPN11 | 354 | 1211 | 1565 |
| Protein tyrosine phosphatase non-receptor type 2 | PTPN2 | 339 | 1206 | 1545 |
| RAF proto-oncogene serine/threonine-protein kinase | RAF1 | 1351 | 1084 | 2435 |
| Retinoic acid receptor alpha | RARA | 356 | 3249 | 3605 |
| Retinoic acid receptor beta | RARB | 298 | 3347 | 3645 |
| Rho-associated coiled-coil-containing protein kinase I | ROCK1 | 1293 | 1117 | 2410 |
| Ribosomal protein S6 kinase alpha-5 | RPS6KA5 | 224 | 1036 | 1260 |
| NAD-dependent protein deacetylase sirtuin-2 | SIRT2 | 361 | 1284 | 1645 |
| NAD-dependent protein deacetylase sirtuin-3 | SIRT3 | 151 | 1074 | 1225 |
| Proto-oncogene tyrosine-protein kinase Src | SRC | 2704 | 1531 | 4235 |
| Substance-K receptor | TACR2 | 876 | 1914 | 2790 |
| Thromboxane A2 receptor | TBXA2R | 978 | 1922 | 2900 |
| Tyrosine-protein kinase receptor TEK | TEK | 788 | 1132 | 1920 |
ChEMBL (https://www.ebi.ac.uk/chembl/, version 23, data collected April 2018),40 contains more than a million annotated compounds comprising over twelve million bioactivities covering in excess of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 targets, all abstracted from the primary scientific literature.42 Compounds with a confidence score of 8 or 9 and with reported activities (Ki/Kd/IC50/EC50) less than, or equal to, 10 μM against human protein targets were treated as binders and those with activity greater than 10 μM treated as non-binders. These cutoffs were chosen to provide chemicals with a pharmacologically relevant activity at a specific, well-defined, human target. A cut-off of 10 μM ensures that the compounds have a good degree of biological activity and represents a trade-off between activity and dataset size. A confidence score of 8 represents the assignment of homologous single proteins, and 9 direct single protein interactions.40
000 targets, all abstracted from the primary scientific literature.42 Compounds with a confidence score of 8 or 9 and with reported activities (Ki/Kd/IC50/EC50) less than, or equal to, 10 μM against human protein targets were treated as binders and those with activity greater than 10 μM treated as non-binders. These cutoffs were chosen to provide chemicals with a pharmacologically relevant activity at a specific, well-defined, human target. A cut-off of 10 μM ensures that the compounds have a good degree of biological activity and represents a trade-off between activity and dataset size. A confidence score of 8 represents the assignment of homologous single proteins, and 9 direct single protein interactions.40
ToxCast is a high throughput screening library of over nine thousand compounds tested across a thousand assays (https://www.epa.gov/chemical-research/toxicity-forecasting, data collected April 2018).41 Data were extracted using ToxCast's in-built binary activity assignments43 and combined with the ChEMBL data.
Duplicate data points were removed. This was performed on the molecular structure of each chemical based on its atomic connectivity once salt counterions have been stripped, resulting in different tautomers and enantiomers being treated as different data points. Where chemicals have contrasting experimental datapoints from ChEMBL and ToxCast, the ChEMBL data value was used. All experimental positive compounds are binders irrespective of agonistic and antagonistic activity.
Molecular representation
Chemical fingerprints were generated using RDKit (version 2019.09) for Python.44 To obtain a good balance between model performance and computational complexity, the type, radius and length of fingerprints must be chosen appropriately. Extended Connectivity Fingerprints (ECFPs) at radius 4 and 6 and several lengths, and MACCS keys were investigated using data for five biological targets and several network architectures. The results of this study are shown in the ESI (Tables S1 and S2†), and the best models were produced using ECFP4 fingerprints at length 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
Cross-validation strategy
The statistical performance of these networks as molecular activity predictors was evaluated using clustered five-fold cross-validation.13 This should help to alleviate bias in the ChEMBL and ToxCast data where in some cases several molecules are from a structural series, with only small structural differences between them. These molecules can then be easy to predict in the test set if others are placed in the training set, overestimating model performance.Chemical clustering was performed based on chemical fingerprints of the type used as DNN input (ECFP4, length 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) using a maximum distance between any 2 clusters of 0.3. This produces a large number of clusters based on the input data. Recombination was then performed to form five clusters of equal size. In each case, one cluster was withheld as a test set and a model trained and validated on the remaining four clusters, with the training and validation sets shuffled and split randomly into 75% training and 25% validation sets.
000) using a maximum distance between any 2 clusters of 0.3. This produces a large number of clusters based on the input data. Recombination was then performed to form five clusters of equal size. In each case, one cluster was withheld as a test set and a model trained and validated on the remaining four clusters, with the training and validation sets shuffled and split randomly into 75% training and 25% validation sets.
DNN architecture
Binary classification DNNs were constructed and trained using TensorFlow in Python 3. For five initial biological targets (AChE. ADORA2A, AR, KCNH2 and SLC6A4) the number of hidden layers was varied as either one or two, and the number of neurons in each hidden layer was also varied (10, 100 or 1000) to establish the best architectures for further biological targets. ReLU (rectified linear unit) activation functions were used to provide non-linearity based on an initial investigation into model performance comparing Sigmoid, ReLU and combinations of both. The results of this study can be found in the ESI (Tables S3 and S4†). Chemical features were input as discussed above and a binary prediction of biological activity at a target was provided as an output.In these initial cases (Table 2), networks with two hidden layers of either 100 or 1000 neurons were found to perform best, judged based on having (i) the highest test set MCC, (ii) the highest test set ROC-AUC, (iii) the highest validation set MCC. For the remaining biological targets, the networks were trained and compared to establish the best models. These models were then compared to structural alert (SA) and RF models using identical training and test sets to establish which predictors worked best. Further details on the neural networks and validation statistics are given in the ESI.†
| Training | Validation | Test | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | SP | ACC | MCC | ROC-AUC | SE | SP | ACC | MCC | ROC-AUC | SE | SP | ACC | MCC | ROC-AUC | |
| a SE = sensitivity, SP = specificity, ACC = accuracy, MCC = Matthews correlation coefficient, ROC-AUC = area under receiver operating characteristic curve. | |||||||||||||||
| AChE | |||||||||||||||
| [10] | 88.7 | 83.9 | 86.6 | 0.726 | 0.93 | 84.9 | 80.7 | 83.1 | 0.655 | 0.90 | 84.2 | 78.9 | 81.9 | 0.631 | 0.89 |
| [100] | 90.7 | 88.4 | 89.7 | 0.791 | 0.96 | 87.4 | 83.2 | 85.6 | 0.706 | 0.92 | 86.2 | 80.7 | 83.8 | 0.670 | 0.90 |
| [1000] | 88.0 | 83.7 | 86.2 | 0.718 | 0.93 | 85.5 | 78.0 | 82.3 | 0.637 | 0.89 | 84.4 | 78.8 | 82.0 | 0.632 | 0.88 |
| [10,10] | 90.7 | 89.7 | 90.3 | 0.802 | 0.96 | 86.1 | 82.9 | 84.7 | 0.688 | 0.92 | 84.3 | 82.4 | 83.5 | 0.664 | 0.90 |
| [100,100] | 91.5 | 91.3 | 91.4 | 0.826 | 0.97 | 87.1 | 85.2 | 86.3 | 0.721 | 0.92 | 85.0 | 84.2 | 84.7 | 0.689 | 0.91 |
| [1000,1000] | 95.2 | 96.6 | 95.8 | 0.915 | 0.99 | 88.0 | 86.7 | 87.4 | 0.744 | 0.93 | 84.7 | 84.0 | 84.4 | 0.684 | 0.92 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||
| ADORA2A | |||||||||||||||
| [10] | 97.6 | 89.9 | 95.0 | 0.888 | 0.98 | 97.2 | 90.2 | 94.7 | 0.884 | 0.98 | 97.2 | 88.5 | 94.2 | 0.871 | 0.97 |
| [100] | 97.8 | 92.9 | 96.1 | 0.913 | 0.99 | 96.9 | 90.9 | 94.8 | 0.886 | 0.98 | 97.2 | 90.2 | 94.8 | 0.884 | 0.98 |
| [1000] | 97.5 | 90.7 | 95.2 | 0.893 | 0.98 | 97.2 | 89.5 | 94.6 | 0.879 | 0.98 | 97.0 | 89.1 | 94.3 | 0.872 | 0.97 |
| [10,10] | 97.8 | 92.7 | 96.0 | 0.911 | 0.99 | 97.6 | 90.6 | 95.3 | 0.893 | 0.98 | 97.0 | 90.0 | 94.6 | 0.880 | 0.98 |
| [100,100] | 98.1 | 93.7 | 96.6 | 0.924 | 0.99 | 96.8 | 90.8 | 94.8 | 0.883 | 0.98 | 96.9 | 90.5 | 94.7 | 0.881 | 0.98 |
| [1000,1000] | 99.0 | 77.8 | 91.7 | 0.817 | 1.00 | 97.3 | 92.4 | 95.6 | 0.903 | 0.98 | 96.7 | 91.2 | 94.8 | 0.884 | 0.98 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||
| AR | |||||||||||||||
| [10] | 58.0 | 99.3 | 88.3 | 0.691 | 0.88 | 59.1 | 98.9 | 88.3 | 0.691 | 0.87 | 55.8 | 99.0 | 87.5 | 0.667 | 0.86 |
| [100] | 69.1 | 98.7 | 90.9 | 0.759 | 0.91 | 64.4 | 98.1 | 89.1 | 0.711 | 0.87 | 64.5 | 98.3 | 89.3 | 0.715 | 0.86 |
| [1000] | 65.0 | 98.6 | 89.7 | 0.727 | 0.89 | 61.6 | 98.2 | 88.5 | 0.693 | 0.86 | 61.5 | 98.3 | 88.6 | 0.695 | 0.86 |
| [10,10] | 67.1 | 99.0 | 90.5 | 0.750 | 0.90 | 62.7 | 98.5 | 89.0 | 0.708 | 0.86 | 61.6 | 98.6 | 88.8 | 0.701 | 0.87 |
| [100,100] | 76.1 | 99.4 | 93.2 | 0.823 | 0.95 | 69.2 | 97.8 | 90.2 | 0.740 | 0.87 | 68.0 | 98.1 | 90.1 | 0.737 | 0.87 |
| [1000,1000] | 73.3 | 99.4 | 92.5 | 0.804 | 0.94 | 65.8 | 97.9 | 89.3 | 0.717 | 0.87 | 64.4 | 98.2 | 89.2 | 0.713 | 0.87 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||
| hERG | |||||||||||||||
| [10] | 93.5 | 53.5 | 77.5 | 0.529 | 0.87 | 91.6 | 48.2 | 74.3 | 0.454 | 0.82 | 92.0 | 46.1 | 73.7 | 0.441 | 0.81 |
| [100] | 94.1 | 49.9 | 76.4 | 0.508 | 0.86 | 92.2 | 45.8 | 74.2 | 0.443 | 0.81 | 92.9 | 44.1 | 73.4 | 0.438 | 0.80 |
| [1000] | 89.7 | 64.3 | 79.7 | 0.568 | 0.87 | 84.6 | 59.5 | 72.7 | 0.458 | 0.82 | 87.0 | 55.0 | 74.2 | 0.450 | 0.81 |
| [10,10] | 94.1 | 85.0 | 90.5 | 0.800 | 0.97 | 86.1 | 67.0 | 78.4 | 0.545 | 0.86 | 86.3 | 63.8 | 77.3 | 0.519 | 0.85 |
| [100,100] | 96.2 | 90.5 | 93.9 | 0.873 | 0.98 | 84.9 | 69.8 | 78.8 | 0.555 | 0.86 | 85.1 | 65.5 | 77.3 | 0.519 | 0.84 |
| [1000,1000] | 95.0 | 87.5 | 92.0 | 0.833 | 0.98 | 84.2 | 66.8 | 77.2 | 0.520 | 0.86 | 83.4 | 65.5 | 76.2 | 0.498 | 0.84 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||
| SERT | |||||||||||||||
| [10] | 99.2 | 72.4 | 93.4 | 0.799 | 0.98 | 99.1 | 66.1 | 91.7 | 0.752 | 0.97 | 99.0 | 67.6 | 92.1 | 0.760 | 0.97 |
| [100] | 99.0 | 89.2 | 96.9 | 0.906 | 0.99 | 98.4 | 83.8 | 95.1 | 0.856 | 0.98 | 98.6 | 83.1 | 95.2 | 0.857 | 0.98 |
| [1000] | 99.2 | 77.2 | 94.4 | 0.831 | 0.98 | 98.8 | 73.8 | 93.3 | 0.797 | 0.97 | 99.1 | 73.9 | 93.5 | 0.805 | 0.97 |
| [10,10] | 99.0 | 89.7 | 97.0 | 0.909 | 0.99 | 98.9 | 82.1 | 95.1 | 0.857 | 0.98 | 98.7 | 83.1 | 95.3 | 0.858 | 0.98 |
| [100,100] | 99.4 | 95.8 | 98.6 | 0.959 | 1.00 | 98.2 | 86.1 | 95.6 | 0.867 | 0.98 | 98.6 | 86.8 | 96.0 | 0.882 | 0.99 |
| [1000,1000] | 99.4 | 98.2 | 99.1 | 0.975 | 1.00 | 98.1 | 91.1 | 96.5 | 0.897 | 0.99 | 98.4 | 90.5 | 96.6 | 0.901 | 0.99 |
Neural network activation similarity
We calculate the neural network activation similarity (NNAS) from the properties of each of the nodes of a trained neural network reacting to the fingerprint of a molecule. For a trained DNN a network activation vector, a, is induced by an input fingerprint, x(0), which can be defined as a vector:
K(L) is the total number of nodes in layer L and different layers can be combined. The similarity between two compound's network activation vectors, a1 and a2 is measured by Euclidean similarity, which relates to Euclidean distance DE via the following equations:
where 0 ≤ NNAS ≤ 1 and n is the total number of nodes considered in the calculation. The NNAS provides a measure of the similarity of molecules which is different to traditional Tanimoto similarity. As an additional comparison point, RF similarity (RFS), was calculated using the Euclidean distance between normalized vectors consisting of the 50 most important physicochemical descriptors identified in RF model construction.38 This gives an appropriate comparison point based on trained machine learning models, and Tanimoto similarity gives a comparison based on chemical similarity and the DNN model inputs.
All datasets and code used in this project are provided via GitHub (https://github.com/teha2/chemical_toxicology). These and generated models are available in the University of Cambridge repository (https://doi.org/10.17863/CAM.50429).
Results and discussion
Statistical performance for the DNNs constructed is included in the ESI.† A summary of the results is shown in Table 3. On average the models show high levels of predictivity, with test accuracy of 92.2 ± 4.2%, test MCC of 0.814 ± 0.093 and test ROC-AUC 0.96 ± 0.04. This is a high level of performance considering several machine learning algorithms struggle to achieve accuracy values above 90% in binary classification tasks,1–5 although the difficulty of the task must be considered when comparing model performance. The models also do not show excessive levels of overfitting, as can be a problem with DNNs. This can be assessed by considering the differences between model performance on the training set and the validation/test sets. In this case, the differences are 3.3%, 0.079 and 0.03 for the validation set and 3.6%, 0.087 and 0.03 for the test set for the accuracy, MCC and ROC-AUC respectively, which can be considered modest.| Training data | Validation data | Test data | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | SP | ACC | MCC | ROC-AUC | SE | SP | ACC | MCC | ROC-AUC | SE | SP | ACC | MCC | ROC-AUC | |
| a SE = sensitivity, SP = specificity, ACC = accuracy, MCC = Matthews correlation coefficient, ROC-AUC = area under receiver operating characteristic curve. | |||||||||||||||
| AVERAGE | 92.1 | 96.5 | 95.8 | 0.901 | 0.99 | 86.9 | 93.2 | 92.5 | 0.822 | 0.96 | 86.2 | 92.9 | 92.2 | 0.814 | 0.96 |
| SD | 8.8 | 4.2 | 3.1 | 0.069 | 0.02 | 11.7 | 5.9 | 4.1 | 0.091 | 0.04 | 12.1 | 6.5 | 4.2 | 0.093 | 0.04 |
Individual model performance was also considered in relation to the dataset size (Fig. 1). Test MCC does not appear to increase as dataset size increase, as one might expect, but the standard deviation across the five-fold clustered cross-validation, shown by the error bars, does appear to decrease. This does suggest that larger datasets will provide more consistent models, even if their performance is similar to datasets of around 2000–4000 data points. Notable in Fig. 1 are the labelled data points which appear to show low model MCC for quite large datasets. These are the targets KCNH2 and MAPK1, which were identified in our previous publication as challenging classifications in this dataset.38
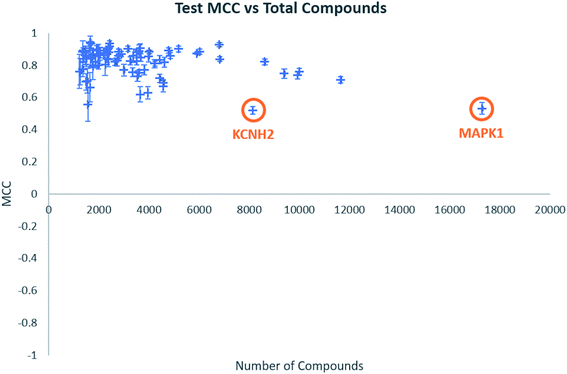 | ||
| Fig. 1 Test MCC vs. total number of compounds for all biological targets. Error bars shown are standard deviations across the five-fold clustered cross-validation. | ||
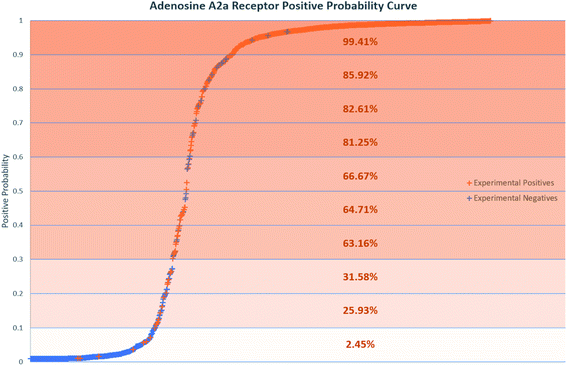
Positive probability values were also calculated for AR binders using the Softmax function on an optimal trained DNN (Fig. 2). This functionality allows a prediction made by the DNN to be accompanied by a percentage indicating how confident the method is that the chemical is an experimental positive. This provides an estimation of the quality of a given binary prediction, with higher probabilities indicating higher confidence in a prediction. For example, the confidence in a positive prediction with positive probability greater than 0.9 at the AR increases greatly, with almost 99.5% of validation set compounds in this area being experimental positives in Fig. 2. This helps to increase confidence in the method for a safety science decision. Positive probability predictions around 0.5 can be considered untrustworthy and followed up with further calculations or experimental testing, and the threshold for model positive prediction assignment can also be adjusted depending on the model's purpose. Table 4 shows a summary of two such example cases, where the threshold during model recall is changed to 0.1 and 0.9 to provide better predictivity of active or inactive chemicals respectively. The 0.1 threshold may be of more use in a screening process when you are considering which chemicals to advance during product development where no pharmacological effects are desired, as any negative predictions made are more likely to be correct. If you are prioritizing chemicals for experimental testing and want to increase the likelihood of finding an active at a particular MIE, the 0.9 threshold may be more useful for the inverse reason. More extensive results in this study are included in the ESI.†
| 0.1 | 0.9 | |||||||
|---|---|---|---|---|---|---|---|---|
| SE | SP | ACC | MCC | SE | SP | ACC | MCC | |
| a SE = sensitivity, SP = specificity, ACC = accuracy, MCC = Matthews correlation coefficient. | ||||||||
| AVERAGE | 97.0 | 59.9 | 79.9 | 0.619 | 53.5 | 98.8 | 81.3 | 0.610 |
| SD | 4.2 | 21.3 | 10.2 | 0.137 | 22.8 | 1.6 | 6.6 | 0.125 |
The best performing DNN for each biological target was compared to models previously generated using SAs and RFs.38 In our previous study, the SAs were constructed using structures obtained from a maximal common substructure algorithm and selected using Bayesian statistics to iteratively select the best alerts. The RF models were based on 200 physicochemical descriptors calculated in RDKit and modelled in sklearn. To ensure fairest possible comparison the DNNs were retrained using the same training and test data as the other two methods. Average results across the three methods are compared in Table 5, with the distributions of these comparisons shown in Fig. 3. Further comparisons are available in Table S13 and Fig. S1 and S2 in the ESI.† Overall, the DNNs show a statistically significant increase in MCC over the SAs and RFs in a P-value test (α = 0.05). On average the accuracy of models increases by 1.7% compared to SAs and 0.67% compared to RFs. The MCC increases by 0.042 and 0.018 respectively. This represents a notable improvement, as the number of inaccurate predictions decreases from 8.9% in the SA model to 7.2% in the DNN model, a percentage decrease of 19%. For the RF models, the decrease is 9%, from 7.8% incorrect predictions to 7.2%. Fig. 5 shows that the distributions of model accuracies and MCCs do show overlap between the methods with DNN predictions being the highest performing overall. Despite this overlap the DNNs do well in direct model comparisons, with 69 DNN models showing higher test accuracies and 71 higher test MCC values compared to SAs, and 59 higher test accuracies and 62 higher test MCC values compared to RFs. Of the 632 comparisons in model performance shown in Table S13,† the DNNs perform better 459 times (73%).
| Training set | Test set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SE | SP | ACC | MCC | SE | SP | ACC | MCC | ||
| a SE = sensitivity, SP = specificity, ACC = accuracy, MCC = Matthews correlation coefficient. | |||||||||
| SA | Average | 91.0 | 95.8 | 95.0 | 0.882 | 84.1 | 93.5 | 91.1 | 0.790 |
| SD | 7.4 | 3.5 | 2.3 | 0.050 | 11.6 | 4.6 | 4.2 | 0.096 | |
| RF | Average | 94.9 | 94.7 | 96.4 | 0.915 | 89.0 | 90.4 | 92.2 | 0.815 |
| SD | 9.9 | 5.7 | 3.1 | 0.072 | 11.6 | 8.1 | 4.0 | 0.091 | |
| DNN | Average | 92.3 | 96.8 | 95.9 | 0.904 | 87.9 | 93.6 | 92.8 | 0.832 |
| SD | 8.8 | 3.0 | 3.1 | 0.066 | 10.4 | 5.9 | 4.0 | 0.089 | |
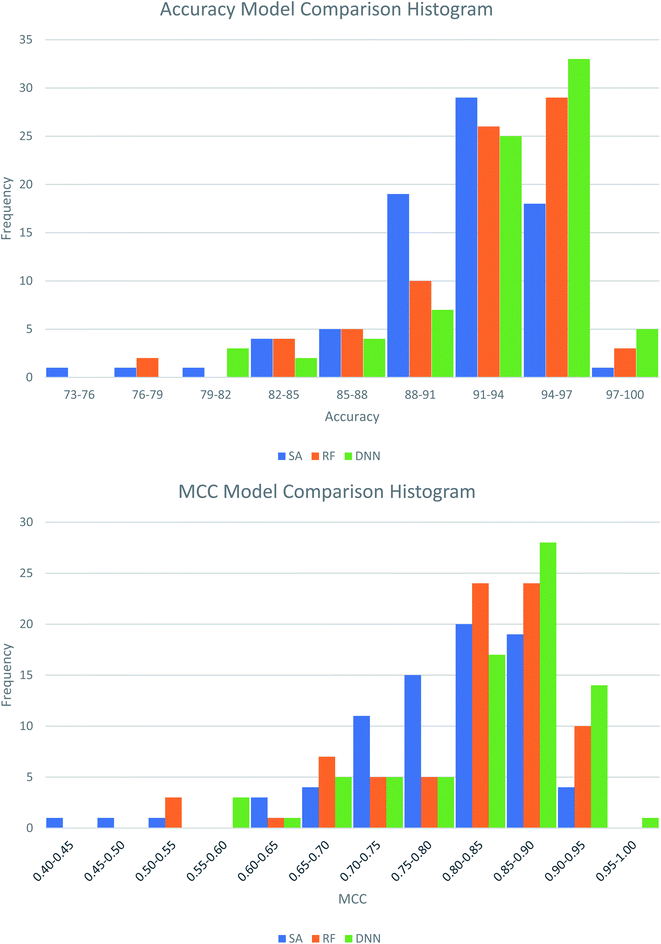 | ||
| Fig. 3 Histograms showing the distribution of test set model performance across the three modelling approaches, structural alerts (SAs), random forests (RFs) and deep neural networks (DNNs). | ||
The average test set results for these models can also be considered as a comparison between cross-validating using a clustered test set and a randomly assigned test set. These differences are shown in Table 6 and show a small decrease in statistical performance when clustering is used, as is to be expected. The first two decimal places of the ROC-AUC values do not change.
| ACC | MCC | ROC-AUC | |
|---|---|---|---|
| a ACC = accuracy, MCC = Matthews correlation coefficient, ROC-AUC = area under receiver operating characteristic curve. | |||
| Clustered test set | 92.2 | 0.814 | 0.96 |
| Random test set | 92.8 | 0.832 | 0.96 |
| Difference | −0.6 | −0.018 | 0 |
Finally, NNAS calculations were made, considering how signals propagate through the hidden layers of a DNN when different chemical fingerprints are introduced. This approach is analogous to the use of feature-space distance or latent-space distance which has been used to quantitatively assess DNN uncertainty.45 These neural network activation similarities between chemicals are considered as potential guidance for read-across in toxicity risk assessment. NNAS calculations were carried out on the highest performing trained DNNs we compared to the SA and RF models using all nodes in all hidden layers of those networks. Typical binders from the literature that were not in the model training sets were identified and use for this task. Andarine, a typical AR binder,46 amiodarone, a typical KCNH2 binder,47 and 3-amino-4-(2-dimethylaminomethylphenylsulfanyl)-benzonitrile (DASB), a typical SLC6A4 binder,48 had their activities predicted by the networks and the highest NNAS, Tanimoto similarity49 and RFS compounds from the training set were identified. In all three cases, the DNN and the RF correctly predicted the activity of the typical binder. Generally, NNAS values are higher than Tanimoto or RF similarities and have a narrower range. Both Tanimoto and RF similarities typically range from zero to a high between 0.2 and 0.6. Network similarities typically range between 0.8 and 1. In most cases, the compounds with the highest similarities, measured by one metric, are different from the compounds with the others. This is reflected throughout the dataset if the compounds are ranked based on their network and Tanimoto similarity the RMSE between these ranks is always found to be greater than 1000 places. The relationship between Tanimoto and NNAS values is shown for all three case studies in Fig. 4. These plots show a difference between the similarity values as a lack of strong correlation between them. The lack of clear correlation here shows that the networks are not simply memorizing the fingerprint bit strings, they are learning which bits and combinations of bits are important for chemical activity.
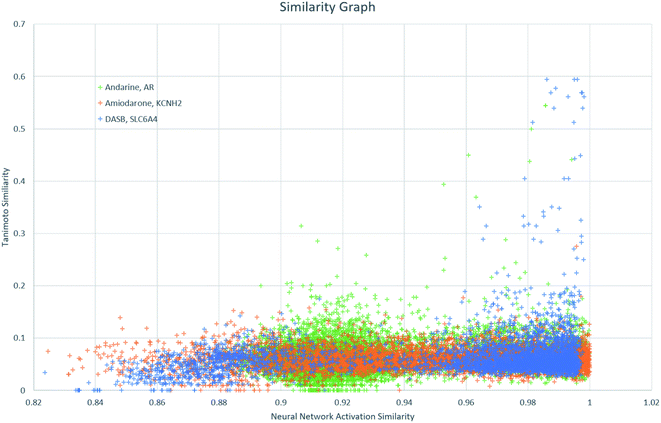 | ||
| Fig. 4 A graph showing the relationship between Tanimoto similarity and NNAS values for the three typical binders andarine, amiodarone and DASB. | ||
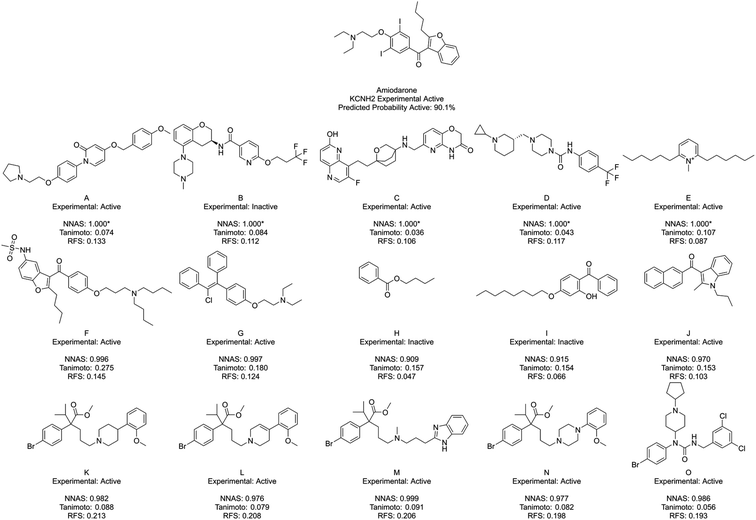
Fig. 5 shows amiodarone, an experimentally active KCNH2 binder, and its five most similar chemicals as measured by NNAS (A–E), Tanimoto similarity (F–J) and RFS (K–O). In this case, the Tanimoto similar compounds all show relatively low similarity (<0.3) and only F appears similar enough to consider making a read-across. The NNAS calculation may be more useful in this case, identifying more experimentally active compounds (4 vs. 3) and more compounds with basic nitrogen atoms attached by linkers to aromatic rings (4 vs. 2), a structural feature associated with biological activity at the KCNH2 target.50 The RFS calculation identified 5 experimental positive compounds which all contain the basic nitrogen attached to aromatic ring motif, but they all appear to come from a single chemical series – perhaps biasing this result. This example suggests the DNN classifier is learning the right kind of features in this difficult classification task.
Fig. 6 shows DASB, an SLC6A4 active chemical, and its similar compounds using the same lettering system. All identified chemicals are active in this case. The Tanimoto and RFS most similar chemicals show a high level of structural similarity to DASB, making them appear as good read-across candidates. They do miss a chemical feature picked up by the NNAS chemicals in a pi-bonding group in the lower left-hand corner, which is present in A. D also shows a similar feature attached to an aromatic ring. Features such as these can be critical to biological activity, and, interestingly, the most network similar compounds pick up these features over the arguably more similar features in F–O.
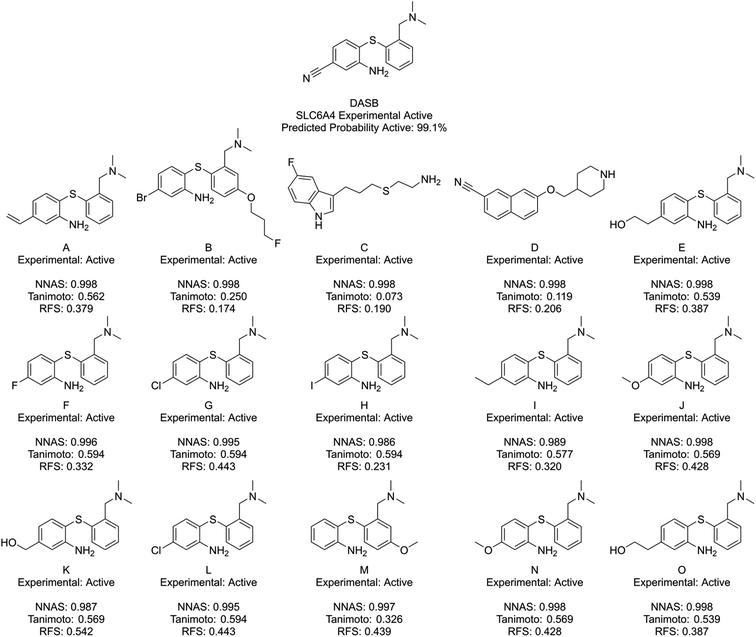 | ||
| Fig. 6 DASB, a typical SLC6A4 binder, and its five most similar neighbours as measured by NNAS (A–E), Tanimoto similarity (F–J) and RFS (K–O). | ||
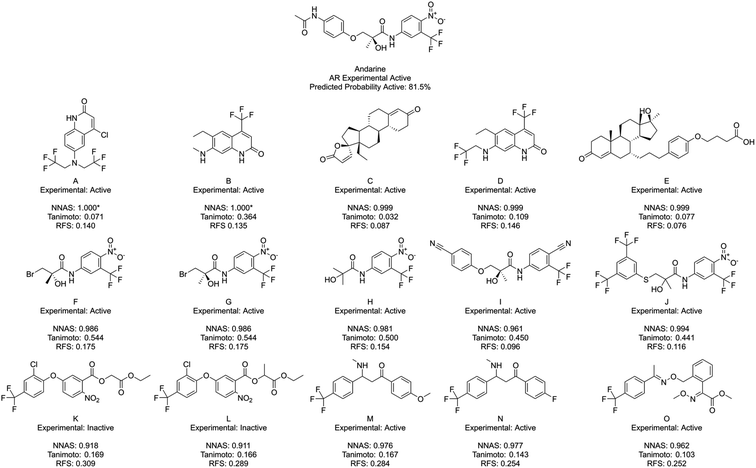
Finally, Fig. 7 shows Andarine, an experimentally active chemical at the AR, and its most similar compounds. The top five in both the NNAS and Tanimoto lists are all experimentally active, while only two of the most similar RFS compounds are. No chemical is in the top five for two of the similarity measures showing how they are able to measure different types of similarity. Chemicals F, G and H are highly similar to the right-hand side of Andarine, while I and J appear to have more overall similarity with Andarine's shape. The RFS compounds show flexibly attached aromatic rings trifluoromethyl groups and nitro groups. NNAS compounds show trifluoromethyl groups in A, B and D and steroidal structures in C and D. Chemical B, in particular, is an interesting case as it shows relatively high Tanimoto similarity (0.364) while appearing quite different. In this case, the highest Tanimoto similar chemicals are probably the most useful for identifying a read-across relationship.
Across the three case studies, the concordance between reference chemical experimental activity and analogue activities was calculated. When considering the five most similar analogues, network, Tanimoto and RF similarities show similar concordances (93%, 87% and 80% respectively). When additional most similar cases are considered the NNAS show a steadily more impressive concordance (98%, 72% and 60% for twenty, and 98%, 65% and 76% for fifty most similar chemicals). The RFS particularly struggled in the Andarine task – identifying only 17 experimental actives in its top 50 most similar compounds, and otherwise should also be considered a potentially useful metric when RF classifiers are used. While the most Tanimoto similar chemicals can be useful for read-across in a more traditional sense when more cases are considered NNAS is far more useful and does provide insight into the otherwise “black box” NN predictions. All three similarity measures provide potentially useful molecular candidates for read-across, and it is useful that they each provide different molecules giving more options for toxicologists using NNs and RFs in decision making. It is certainly the case that all three similarities should be used together to gain confidence in in silico predictions in predictive safety assessment.
Conclusions
In this work, we have constructed DNNs to predict binary activity at human MIEs and developed a new similarity measure, NNAS, which increases confidence in the predictions. Key advantages of this work include the development of a large number of models covering many human MIEs allowing for predictions across a wide expanse of human toxicology, the use of a balanced dataset with an almost equal number of active and inactive chemicals, high-quality predictions with a high level of statistical performance which outperforms SAs and RF on identical prediction tasks and the introduction of NNAS for use in toxicity safety evaluation to increase confidence in the predictions made. The developed networks use chemical fingerprint inputs to learn and correctly classify molecules as binders or non-binders. The classifiers show high performance, with an average ROC-AUC value of 0.96 ± 0.04 in clustered five-fold cross-validation. The DNNs can also be used to provide positive probability values associated with each prediction, and these values can provide additional information and confidence values a risk assessor can use in a safety evaluation, including the ability to adjust the threshold for activity depending on the prediction task. These DNNs have been considered against SA and RF models and show a statistically significant (α = 0.05) improvement in MCC. We introduce a new measure of similarity, NNAS which can be used as read-across in a safety evaluation decision. These values provide information on how the DNN evaluates the test compound, providing information that Tanimoto similarity alone does not and considerably improving our ability to predict adverse outcomes using computational methods.The NNAS improves our understanding of these highly predictive DNNs, and so can contribute to the safety evaluation of new chemicals. These powerful machine learning approaches can be used alongside other computational methods, such as QSARs, SAs or expert systems to provide additional confidence when a consensus is reached among predictions. More impact for these in silico methods will assist in reducing the reliance on animal experiments, in line with 3Rs objectives.51,52 These methods can also be considered in other predictive tasks using DNNs, particularly those using chemical inputs. Neural networks have the potential to assist in a number of chemical-based tasks, including biological activity prediction, choice of chemical reactants or solvents, and spectra interpretation. As such, understanding gained through methods such as this can assist in the discovery of new chemical reactions, the streamlining of chemical synthesis, and reduction in cost associated with experimental discovery.
Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Funding sources
The authors acknowledge the financial support of Unilever.Data statement
According to the University of Cambridge data management policy, all the data used in this paper are available either in the paper or in the SI. A copy of the data is also available in the University of Cambridge repository at: https://doi.org/10.17863/CAM.50429.Conflicts of interest
There are no conflicts to declare.Abbreviations
| ACC | Accuracy |
| AOP | Adverse outcome pathways |
| DASB | 3-Amino-4-(2-dimethylaminomethylphenylsulfanyl)-benzonitrile |
| DNN | Deep neural network |
| ECFP | Extended connectivity fingerprint |
| FN | False negative |
| FP | False positive |
| MCC | Matthews correlation coefficient |
| MIE | Molecular initiating event |
| NNAS | Neural network activation similarity |
| QSAR | Quantitative structure–activity relationship |
| ReLU | Rectified linear unit |
| RF | Random forest |
| RFS | Random forest similarity |
| ROC-AUC | Area under receiver operating curve |
| SA | Structural alert |
| SE | Sensitivity |
| SERT | Serotonin transporter |
| SP | Specificity |
| TN | True negative |
| TP | True positive |
References
- X. Li, et al., The development and application of: in silico models for drug induced liver injury, RSC Adv., 2018, 8, 8101–8111 RSC.
- D. Fan, et al., In silico prediction of chemical genotoxicity using machine learning methods and structural alerts, Toxicol. Res., 2018, 7, 211–220 CrossRef CAS PubMed.
- X. Li, et al., In silico estimation of chemical carcinogenicity with binary and ternary classification methods, Mol. Inform., 2015, 34, 228–235 CrossRef CAS PubMed.
- H. Zhang, et al., Development of novel in silico model for developmental toxicity assessment by using naïve Bayes classifier method, Reprod. Toxicol., 2017, 71, 8–15 CrossRef CAS PubMed.
- S. He, et al., An in silico model for predicting drug-induced hepatotoxicity, Int. J. Mol. Sci., 2019, 20, 1–17 Search PubMed.
- E. Gawehn, J. A. Hiss and G. Schneider, Deep Learning in Drug Discovery, Mol. Inform., 2016, 35, 3–14 CrossRef CAS PubMed.
- G. E. Dahl, N. Jaitly and R. Salakhutdinov, Multi-task Neural Networks for QSAR Predictions, arXiv, 2014, 1–21.
- Y. Wu and G. Wang, Machine learning based toxicity prediction: from chemical structural description to transcriptome analysis, Int. J. Mol. Sci., 2018, 19, 2358–2378 CrossRef PubMed.
- T. Unterthiner, A. Mayr, G. Klambauer and S. Hochreiter, Toxicity Prediction using Deep Learning, 2015 Search PubMed.
- A. Mayr, G. Klambauer, T. Unterthiner and S. Hochreiter, DeepTox: Toxicity Prediction using Deep Learning, Front. Environ. Sci., 2016, 3, 1–15 Search PubMed.
- Y. Xu, et al., Deep Learning for Drug-Induced Liver Injury, J. Chem. Inf. Model., 2015, 55, 2085–2093 CrossRef CAS PubMed.
- C. Cai, et al., Deep Learning-Based Prediction of Drug-Induced Cardiotoxicity, J. Chem. Inf. Model., 2019, 59, 1073–1084 CrossRef CAS PubMed.
- A. Mayr, et al., Large-scale comparison of machine learning methods for drug target prediction on ChEMBL, Chem. Sci., 2018, 9, 5441–5451 RSC.
- K. Wu and G. Wei, Quantitative Toxicity Prediction Using Topology Based Multitask Deep Neural Networks, J. od Chem. Inf. Model., 2018, 58, 520–531 CrossRef CAS PubMed.
- G. Idakwo, S. Thangapandian, J. L. Iv and Z. Zhou, Deep Learning-Based Structure-Activity Relationship Modeling for Multi-Category Toxicity Classification: A Case Study of 10K Tox21 Chemicals With Androgen Receptor Bioassay Data, Front. Physiol., 2019, 10, 1–13 Search PubMed.
- A. Cherkasov, et al., QSAR Modeling: Where Have You Been? Where Are You Going To?, J. Med. Chem., 2014, 57, 4977–5010 CrossRef CAS PubMed.
- K. Preuer, G. Klambauer, F. Rippmann, S. Hochreiter and T. UnterthinerInterpretable Deep Learning in Drug Discovery, in Explainable AI: Interpreting, Explaining and Visualizing Deep Learning, ed. W. Samek, G. Montavon, A. Vedaldi, L. K. Hansen and K.-R. Müller, Springer International Publishing, 2019, pp. 331–345, DOI:10.1007/978-3-030-28954-6_18.
- L. M. Zintgraf, T. S. Cohen, T. Adel and M. Welling, Visualizing Deep Neural Network Decisions: Prediction Difference Analysis, arXiv, 2017, 1–12.
- S. Bach, et al., On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation, PLoS One, 2015, 10, 1–46 Search PubMed.
- M. Ancona, E. Ceolini, C. Öztireli and M. Gross, Towards better understanding of gradient-based attribution methods for Deep Neural Networks, arXiv, 2017, 1–16.
- T. Luechtefeld, D. Marsh, C. Rowlands and T. Hartung, Machine Learning of Toxicological Big Data Enables Read-Across Structure Activity Relationships (RASAR) Outperforming Animal Test Reproducibility, Toxicol. Sci., 2018, 165, 198–212 CrossRef CAS PubMed.
- G. T. Ankley, et al., Adverse outcome pathways: a conceptual framework to support ecotoxicology research and risk assessment, Environ. Toxicol. Chem., 2010, 29, 730–741 CrossRef CAS PubMed.
- T. E. H. Allen, J. M. Goodman, S. Gutsell and P. J. Russell, Defining Molecular Initiating Events in the Adverse Outcome Pathway Framework for Risk Assessment, Chem. Res. Toxicol., 2014, 27, 2100–2112 Search PubMed.
- T. E. H. Allen, J. M. Goodman, S. Gutsell and P. J. Russell, A History of the Molecular Initiating Event, Chem. Res. Toxicol., 2016, 29, 2060–2070 Search PubMed.
- T. E. H. Allen, S. Liggi, J. M. Goodman, S. Gutsell and P. J. Russell, Using Molecular Initiating Events to Generate 2D Structure Activity Relationships for Toxicity Screening, Chem. Res. Toxicol., 2016, 29, 2060–2070 Search PubMed.
- T. E. H. Allen, J. M. Goodman, S. Gutsell and P. J. Russell, Using 2D structural alerts to define chemical categories for molecular initiating events, Toxicol. Sci., 2018, 165, 213–223 CrossRef CAS PubMed.
- S. J. Enoch, M. T. D. Cronin and C. M. Ellison, The use of a chemistry-based profiler for covalent DNA binding in the development of chemical categories for read-across for genotoxicity, ATLA, 2011, 39, 131–145 CAS.
- C. L. Mellor, F. P. Steinmetz and M. T. D. Cronin, Using Molecular Initiating Events to Develop a Structural Alert Based Screening Workflow for Nuclear Receptor Ligands Associated with Hepatic Steatosis, Chem. Res. Toxicol., 2016, 29, 203–212 Search PubMed.
- M. D. Nelms, et al., Proposal of an in silico profiler for categorisation of repeat dose toxicity data of hair dyes, Arch. Toxicol., 2014, 89, 733–741 CrossRef PubMed.
- M. D. Nelms, C. L. Mellor, M. T. D. Cronin, J. C. Madden and S. J. Enoch, Development of an in silico profiler for mitochondrial toxicity, Chem. Res. Toxicol., 2015, 28, 1891–1902 Search PubMed.
- M. Casalegno and G. Sello, Determination of toxicant mode of action by augmented top priority fragment class, J. Chem. Inf. Model., 2013, 53, 1113–1126 CrossRef CAS PubMed.
- G. F. Gerberick, et al., Quantification of chemical peptide reactivity for screening contact allergens: a classification tree model approach, Toxicol. Sci., 2007, 97, 417–427 CrossRef CAS PubMed.
- T. E. H. Allen, M. N. Grayson, J. M. Goodman, S. Gutsell and P. J. Russell, Using Transition State Modeling To Predict Mutagenicity for Michael Acceptors, J. Chem. Inf. Model., 2018, 58, 1266–1271 CrossRef CAS PubMed.
- G. Patlewicz, A. O. Aptula, D. W. Roberts and E. Uriarte, A minireview of available skin sensitization (Q)SARs/expert systems, QSAR Comb. Sci., 2008, 27, 60–76 CrossRef CAS.
- A. Karim, A. Mishra, M. A. H. Newton and A. Sattar, Efficient Toxicity Prediction via Simple Features Using Shallow Neural Networks and Decision Trees, ACS Omega, 2019, 4, 1874–1888 CrossRef CAS.
- H. Altae-Tran, B. Ramsundar, A. S. Pappu and V. Pande, Low Data Drug Discovery with One-Shot Learning, ACS Cent. Sci., 2017, 3, 283–293 CrossRef CAS PubMed.
- J. Bowes, et al., Reducing safety-related drug attrition: the use of in vitro pharmacological profiling, Nat. Rev. Drug Discov., 2012, 11, 909–922 CrossRef CAS PubMed.
- A. J. Wedlake, et al., Structural Alerts and Random Forest Models in a Consensus Approach for Receptor Binding Molecular Initiating Events, Chem. Res. Toxicol., 2020, 33(2), 388–401 Search PubMed.
- N. S. Sipes, et al., Profiling 976 ToxCast chemicals across 331 enzymatic and receptor signaling assays, Chem. Res. Toxicol., 2013, 26, 878–895 Search PubMed.
- ChEMBL Database, http://www.ebi.ac.uk/chembl/ Search PubMed.
- ToxCast Database, https://www.epa.gov/chemical-research/toxicity-forecasting Search PubMed.
- A. P. Bento, et al., The ChEMBL bioactivity database: an update, Nucleic Acids Res., 2014, 42, 1083–1090 CrossRef PubMed.
- D. L. Filer, P. Kothiya, W. R. Setzer, R. S. Judson and M. T. Martin, The ToxCast Analysis Pipeline: An R Package for Processing and Modeling Chemical Screening Data, 2015 Search PubMed.
- D. Rogers and M. Hahn, Extended-Connectivity Fingerprints, J. Chem. Inf. Model., 2010, 742 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A quantitative uncertainty metric controls error in neural network-driven chemical discovery, Chem. Sci., 2019, 10, 7913–7922 RSC.
- J. Chen, J. Kim and J. T. Dalton, Discovery and therapeutic promise of selective androgen receptor modulators, Mol. Interv., 2005, 5, 173–188 CrossRef CAS PubMed.
- S. P. Wang, J. A. Wang, R. H. Luo, W. Y. Cui and H. Wang, Potassium channel currents in rat mesenchymal stem cells and their possible roles in cell proliferation, Clin. Exp. Pharmacol. Physiol., 2008, 35, 1077–1084 CrossRef CAS PubMed.
- S. Houle, N. Ginovart, D. Hussey, J. H. Meyer and A. A. Wilson, Imaging the serotonin transporter with positron emission tomography: initial human studies with [11C]DAPP and [11C]DASB, Eur. J. Nucl. Med., 2000, 27, 1719–1722 CrossRef CAS PubMed.
- D. J. Rogers and T. T. Tanimoto, A Computer Program for Classifying Plants, Science, 1960, 132, 1115–1118 CrossRef CAS PubMed.
- K. M. Waldhauser, et al., Interaction with the hERG channel and cytotoxicity of amiodarone and amiodarone analogues, Br. J. Pharmacol., 2008, 155, 585–595 CrossRef CAS PubMed.
- H. Kandárová and S. Letaáiová, Alternative methods in toxicology: pre-validated and validated methods, Interdiscip. Toxicol., 2011, 4, 107–113 Search PubMed.
- N. Burden, et al., Adverse Outcome Pathways can drive non-animal approaches for safety assessment, J. Appl. Toxicol., 2015, 35, 971–975 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Links to models generated and source code in GitHub and the University of Cambridge repository, model performance using various chemical fingerprints and activation functions, full model performance at all biological targets, full model performance at predicted activity thresholds 0.1 and 0.9, DNN model performance comparison to SAs and RFs, and p-value analysis of model performance. See DOI: 10.1039/d0sc01637c |
| This journal is © The Royal Society of Chemistry 2020 |