Open Access Article
Open Access ArticleThermodynamic rules for zeolite formation from machine learning based global optimization†
Sicong
Ma
 a,
Cheng
Shang
a,
Cheng
Shang
 a,
Chuan-Ming
Wang
a,
Chuan-Ming
Wang
 *b and
Zhi-Pan
Liu
*b and
Zhi-Pan
Liu
 *a
*a
aCollaborative Innovation Center of Chemistry for Energy Material, Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Key Laboratory of Computational Physical Science, Department of Chemistry, Fudan University, Shanghai 200433, China. E-mail: zpliu@fudan.edu.cn
bState Key Laboratory of Green Chemical Engineering and Industrial Catalysis, Sinopec Shanghai Research Institute of Petrochemical Technology, Shanghai, 201208, China. E-mail: wangcm.sshy@sinopec.com
First published on 2nd September 2020
Abstract
While the [TO4] tetrahedron packing rule leads to millions of likely zeolite structures, there are currently only 252 types of zeolite frameworks reported after decades of synthetic efforts. The subtle synthetic conditions, e.g. the structure-directing agents, pH and the feed ratio, were often blamed for the limited zeolite types due to the complex kinetics. Here by developing machine learning global optimization techniques, we are now able to establish the global potential energy surface of a typical zeolite system, SixAlyPzO2Hy−z with 12 T atoms (T: Si, Al and P) that is the general formula shared by CHA, ATS, ATO and ATV zeolite frameworks. After analyzing more than 106 minima data, we identify thermodynamic rules on energetics and local bonding patterns for stable zeolites. These rules provide general guidelines to classify zeolite types and correlate them with synthesis conditions. The machine learning based atomistic simulation thus paves a new way towards rational design and synthesis of stable zeolite frameworks with desirable compositions.
1. Introduction
Zeolites, a class of crystalline microporous materials with well-defined channels and cages packed with corner-sharing [TO4] tetrahedral units (T: Si, Al, P etc.), are widely used in chemical industries, e.g. as catalysts for converting petrochemicals.1–7 While millions of hypothetical zeolite structures have been proposed by theory8–11 and a number of synthetic approaches were innovated for zeolite synthesis, only 252 distinct zeolite structures (IZC-SC database)12 have been successfully synthesized in the past century. The trial-and-error method prevails in zeolite synthesis via the testing of many conditions, including the feed Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios, pH and structure-directing agents (SDAs), besides the crystallization temperature and the time conventional to chemical synthesis.13–16 The physical laws governing the structures of zeolites remain largely a mystery to chemists.
P ratios, pH and structure-directing agents (SDAs), besides the crystallization temperature and the time conventional to chemical synthesis.13–16 The physical laws governing the structures of zeolites remain largely a mystery to chemists.
Direct crystallization from an alkaline solution mixture containing silicon, aluminum and alkali metals is the most traditional way to synthesize zeolites, which only leads to aluminosilicate zeolites with a low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio (e.g. <10).17 The kinetics was suggested to control the liquid-to-solid condensation due to the metastable nature of the product, where the strong alkali (OH−) acts as the key mineralizer to dissolve Si and Al ions.4,18 However, the replacement of inorganic alkalis by tetramethylammonium found by Barrer et al. in 1961
Al ratio (e.g. <10).17 The kinetics was suggested to control the liquid-to-solid condensation due to the metastable nature of the product, where the strong alkali (OH−) acts as the key mineralizer to dissolve Si and Al ions.4,18 However, the replacement of inorganic alkalis by tetramethylammonium found by Barrer et al. in 1961![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 breaks the Si
19 breaks the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio limitation to obtain even pure SiO2 zeolites (e.g. silicalite-1), which can also be produced using a recently reported solvent-free calcination synthetic route.5,20 The aluminophosphate zeolite (AlPO) that entered the zeolite family in the 1980s21 utilizes boehmite, phosphoric acid and organic amine as reagents. All these new findings question the essentiality of strong alkalis and the kinetics-controlled mechanism. Recent decades have witnessed an increasing variety of zeolites owing to the introduction of different SDAs. Some rules of thumb gleaned from synthesis are: (i) the SDA can define the pore size and thus is critical to the zeolite type and shape;2,3,22 (ii) pH environment affects zeolite formation that aluminosilicate zeolites prefer alkaline condition but phosphate-containing zeolites like weak acidic or near neutral condition;17,23 and (iii) the compositions of feed Si
Al ratio limitation to obtain even pure SiO2 zeolites (e.g. silicalite-1), which can also be produced using a recently reported solvent-free calcination synthetic route.5,20 The aluminophosphate zeolite (AlPO) that entered the zeolite family in the 1980s21 utilizes boehmite, phosphoric acid and organic amine as reagents. All these new findings question the essentiality of strong alkalis and the kinetics-controlled mechanism. Recent decades have witnessed an increasing variety of zeolites owing to the introduction of different SDAs. Some rules of thumb gleaned from synthesis are: (i) the SDA can define the pore size and thus is critical to the zeolite type and shape;2,3,22 (ii) pH environment affects zeolite formation that aluminosilicate zeolites prefer alkaline condition but phosphate-containing zeolites like weak acidic or near neutral condition;17,23 and (iii) the compositions of feed Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios are limited to few choices, such as the silicoaluminophosphate (SAPO) zeolite that has nAl
P ratios are limited to few choices, such as the silicoaluminophosphate (SAPO) zeolite that has nAl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSi+P ∼ 1
nSi+P ∼ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and nP > nSi (nT: the number of element T atoms in the crystal). Many underlying questions on zeolites thus arise and three of them must rank top:
1 and nP > nSi (nT: the number of element T atoms in the crystal). Many underlying questions on zeolites thus arise and three of them must rank top:
(Q1) Is zeolite formation thermodynamically controlled?
(Q2) Why are the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios not freely tunable in synthesis?
P ratios not freely tunable in synthesis?
(Q3) How does pH control the zeolite formation?
To date, few theories are available to answer these questions. The most accepted rule is perhaps the exclusion of the Al–O–Al (known as Löwenstein's rule), P–O–P and Si–O–P patterns in zeolites, which were summarized from a reported zeolite structure.17 Here by developing a machine learning based global optimization technique, we are able to, for the first time, establish the global potential energy surface (PES) of zeolites as represented by SixAlyPzO2Hy−z using a 12 T system as an example. This leads to quantitative solutions to the key puzzles associated with zeolite structures, compositions and energetics.
2. Methods
We have utilized a new technique, as implemented in our LASP code,24 to solve the complex PES problem as encountered in zeolites. A five-element Si–Al–P–O–H global neural network (G-NN) potential is constructed via self-learning global PES data,25,26 which can fast and accurately evaluate the PES and facilitate exploring the huge dimensionality of the zeolite global PES, in both the element and the configuration space, where the current quantum mechanics and empirical force field calculations fail either in speed or in accuracy. The global PES exploration is achieved via an enhanced stochastic surface walking (E-SSW) method designed for zeolite structures to cope with variable-size micropores in the framework. We note that traditional PES methods, such as molecular dynamics and evolution algorithms,27 are generally frustrated in the global search for zeolite structures.2.1 E-SSW method
The E-SSW method extends SSW global optimization by implementing explicitly virtual rigid bodies to enhance the PES search towards structures with open space. The SSW algorithm28 is an unbiased global optimization method that can explore both minima and saddle points on the PES. SSW implements an automated climbing mechanism to manipulate a structural configuration moving smoothly from a local minimum to a high-energy configuration along one random mode direction. The method was initially developed for aperiodic systems,29 such as molecules and clusters, and has been extended to periodic crystals.30In the E-SSW method, the real PES is transformed after the addition of a tunable external potential U(ri), where i is the index of the rigid body, as shown in eqn (1). We utilize a power-type repulsive potential to create a repulsive sphere with a variable radius, see ESI Fig. S1.†30
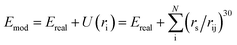 | (1) |
2.2 E-SSW-NN simulation
Our approach to resolve complex zeolite (Si–Al–P–O–H elements) structures is based on the E-SSW-NN method where the E-SSW-NN combines E-SSW global PES exploration with fast G-NN potential calculations. The G-NN potential31,32 is generated by iterative self-learning of the plane wave DFT global PES dataset generated from E-SSW search. The E-SSW-NN simulation to explore the PES can be divided into three steps: global dataset generation based on DFT calculations using selected structures from E-SSW simulation, G-NN potential fitting and E-SSW global optimization using G-NN potential. These steps are iteratively performed until the G-NN potential is transferable and robust enough to describe the global PES. The procedure is briefly summarized below.At first, a global dataset is built iteratively during the iterative self-learning of G-NN potential. The initial data come from the density functional theory (DFT) based E-SSW simulation and the data in the subsequent cycles are from E-SSW-NN PES exploration. In order to maximally cover the likely configurations from all elements, extensive SSW simulations have been carried out for as many as possible structures, compositions and supercell sizes. Overall, these SSW simulations generate more than 107 structures on the PES. The final global dataset that is computed by high accuracy DFT calculation contains 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 structures, and is detailed in ESI Table S1.†
135 structures, and is detailed in ESI Table S1.†
Then, the G-NN potential is generated using the method as introduced in our previous work.31,33 To pursue a high accuracy for the PES, we have adopted a large set of power-type structure descriptors, which contains 343 descriptors for every element, including 129 2-body, 208 3-body, and 6 4-body descriptors, and compatibly, the network involves two-hidden layers (343-50-50-1 net), equivalent to 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 network parameters in total. The min–max scaling is utilized to normalization the training data sets. Hyperbolic tangent activation functions are used for the hidden layers, while a linear transformation is applied to the output layer of all networks. The limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method is used to minimize the loss function to match DFT energy, force and stress. The final energy and force criteria of the root mean square errors are around 2.73 meV per atom and 0.103 eV Å−1 respectively. The benchmark between G-NN and DFT results can be found in ESI Tables S2–S4,† which is accurate enough for searching for stable structure candidates.
005 network parameters in total. The min–max scaling is utilized to normalization the training data sets. Hyperbolic tangent activation functions are used for the hidden layers, while a linear transformation is applied to the output layer of all networks. The limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method is used to minimize the loss function to match DFT energy, force and stress. The final energy and force criteria of the root mean square errors are around 2.73 meV per atom and 0.103 eV Å−1 respectively. The benchmark between G-NN and DFT results can be found in ESI Tables S2–S4,† which is accurate enough for searching for stable structure candidates.
Finally, E-SSW-NN simulation is performed over a wide range of compositions and structures, both for the global dataset generation and for the final production of the ternary phase diagram. For the E-SSW-NN simulation, each composition is simulated in the unit cells of 36–42 and explored to cover more than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 minima on the PES by E-SSW. Thus, a large variety of structures ranging from crystalline to amorphous structures have been obtained from E-SSW-NN simulation.
000 minima on the PES by E-SSW. Thus, a large variety of structures ranging from crystalline to amorphous structures have been obtained from E-SSW-NN simulation.
2.3 DFT calculation
All DFT calculations are performed by using the plane wave VASP code, where electron–ion interaction is represented by the projector augmented wave pseudopotential.34,35 The exchange–correlation functional utilized is the BEEF-vdw functional36 because of its accurate estimation of adsorption energies37 and its explicit inclusion of van der Waals interactions. The kinetic energy cutoff is set as 450 eV. The first Brillouin zone k-point sampling utilizes the Monkhorst–Pack scheme with an automated mesh determined by 25 times the reciprocal lattice vectors. The energy and force criteria for the convergence of the electron density and structure optimization are set at 10−6 eV and 0.02 eV Å−1, respectively. To determine the Gibbs formation energy (Gf) of SixAlyPzO2Hy−z and SixAlyPzO2Nay−z, ab initio thermodynamics analyses have been performed with respect to quartz–SiO2, quartz–AlPO, α-Al2O3, NaOH solution and H2O at 200 °C and 15.53 bar (saturated vapor). The free energy of H2O is computed by the standard thermodynamics approach by incorporating zero-point energy and entropy contribution to the total energy (see the ESI†).3. Results and discussion
Using the G-NN based E-SSW search, we have explored the global PES for every likely zeolite composition in the ternary (Si–Al–P) phase diagram from Al0.5P0.5O2 to SiO2 and to Si0.5Al0.5O2H0.5. For each composition, five different radii were examined, namely rs = 0, 3, 4, 5 and 6 Å, and each simulation with a fixed rs was set to explore 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 minima structures starting from known configurations (e.g. quartz and CHA-type zeolite). The minima were confirmed via full structure relaxation after the removal of the external potential and the low energy structures identified were finally verified by using DFT calculations.
000 minima structures starting from known configurations (e.g. quartz and CHA-type zeolite). The minima were confirmed via full structure relaxation after the removal of the external potential and the low energy structures identified were finally verified by using DFT calculations.
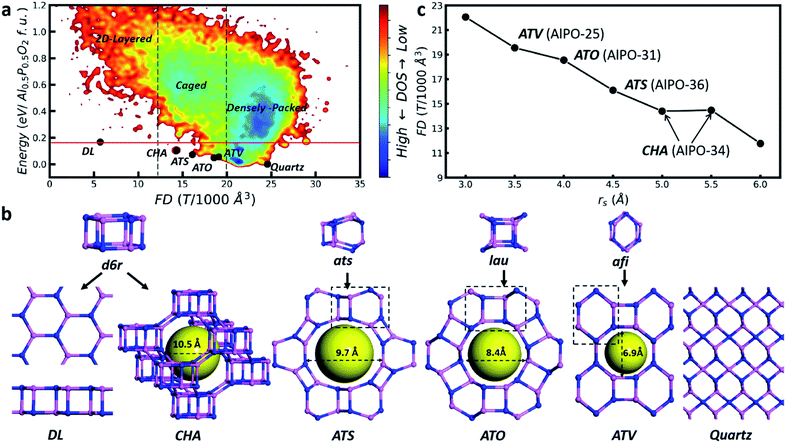
Fig. 1a illustrates a representative global PES of AlPO (Al6P6O24), where the framework density (FD, the number of tetrahedral T atoms per 1000 Å3), the key structural feature of the zeolite, is plotted against the total energy of minima. Similar plots for other compositions can be found in ESI Fig. S2.† As denoted in the figure, the global PES can be divided roughly into three regions according to the FD value, i.e. densely packed, caged and layered regions from right to left. The densely packed region, as represented by the quartz structure (P3121) with FD = 24.6 which is the global minimum (GM), has FD values above 20. The zeolite belongs to the caged region with FD values of 12–20. Importantly, four known zeolites, i.e. with the topology of CHA, ATS, ATO and ATV, appear at the bottom of this region. They can be visualized as the three-dimensional (3D) crystalline assembly of the basic structural units, so-called d6r, ats, lau and afi, respectively (Fig. 1b). The energies of these four zeolites are 0.07–0.10 eV per TO2 (Al0.5P0.5O2) formula unit (f.u., i.e. per TO2) relative to the quartz GM, confirming the metastable nature of the caged structures. The layered region represents the most open structure with the FD values of 2–12, where a special 2D layer AlPO phase, denoted as the DL phase, is located at the bottom of this region, 0.17 eV per f.u. above the GM. The DL phase can be visualized as a 2D assembly of the d6r structural unit (Fig. 1b), similar to the CHA zeolite.
The global PES defines clearly the energy criterion for zeolite formation. Being the crystalline form of the caged structures, the energy of the zeolite has to be lower than that of the DL phase, but higher than that of the densely packed quartz phase, e.g. in between 0 and 0.17 eV per f.u., as indicated by the red lines in Fig. 1a. The universality of the energy criterion is supported by analyzing the zeolite bank. Among 252 known zeolite structures, there are 29 as-synthesized AlPO zeolites and their energies are in between 0.05 and 0.14 eV per f.u. (ESI Table S5†). The structure classification from the global PES and the energy criterion of the zeolite are not limited to AlPO. For SiO2 zeolites, similarly, the presence of the DL phase (0.18 eV per f.u. above quartz) dictates the upper energy bound: 60 as-synthesized SiO2 zeolites are indeed in the energy window from 0.04 to 0.18 eV per f.u. (ESI Table S6†). This finding suggests that the type of stable zeolite structure is strongly restrained by the presence of the corresponding DL phase, which provides the key cause for the fact that the types of known zeolites are far fewer than the theoretical prediction based on the TO4 packing rule.
Since the zeolite is located only in a small region of the global PES, being metastable in nature, it would be interesting to determine how they are formed under experimental conditions. Fig. 1c (data in ESI Table S7†) provides the clue, which illustrates the identified GMs of AlPO in the presence of an external rigid body (a rigid body per Al6P6O24). It shows that the increase of rs rapidly decreases the FD value: too large or too small rs fails to identify the zeolite, not surprisingly, leading to either a layered or a densely packed structure. The zeolite only turns out to be the GM under the suitable rs being applied, i.e. in between 3.5 and 5.5 Å. The four known zeolites, i.e. ATV-, ATO-, ATS- and CHA-types, do emerge as the GM at rs = 3.5, 4, 4.5 and 5–5.5 Å, respectively. Their cage size matches well with the rs value of the rigid body (see Fig. 1b). Indeed, in the experiment these zeolites are synthesized by using selected-size molecular SDAs: for example, the synthesis of ATO-type AlPO utilizes dipropylamine (8 Å diameter, see ESI Fig. S3†).38Fig. 1c thus supports that the zeolite may well be the thermodynamically favored product under the synthetic conditions. In particular, the choice of SDAs with suitable sizes can be the key way to condense [TO4] towards the zeolite, instead of the quartz or DL phase.
Now for each sensible rs, we can further examine the composition effect of the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
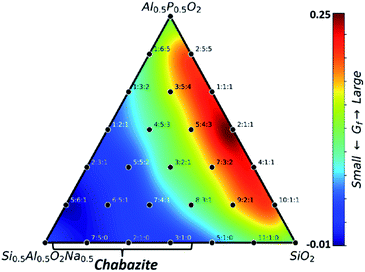
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio on the zeolite stability. By using the formation free energy (Gf) of the obtained GM structure, Fig. 2a illustrates the ternary phase diagram at rs = 5 Å for different SAPO compositions. Gf is the free energy of the zeolite (without the rigid body) relative to the free energies of quartz–SiO2, quartz–AlPO, α-Al2O3 and H2O at 200 °C and 15.53 bar (saturated vapor), corresponding to the neutral pH in normally used hydrothermal synthesis (in ESI Fig. S4† we discuss the effect of hydrothermal conditions on zeolite thermodynamics). Not surprisingly, due to the presence of the rigid body (rs = 5 Å) in our global PES search, all GMs in Fig. 2a are in the CHA-type framework, but they differ significantly in Gf: it has the minima nearby two vertexes, Al0.5P0.5O2 and SiO2 (∼0.11 eV per f.u.), but yields the maximum (∼0.30 eV per f.u.) at the left-bottom corner (Si0.5Al0.5O2H0.5). Most phases in the map are higher than their corresponding layer structure (0.17–0.18 eV per f.u., dotted lines), only the phases nearby two vertices (Al0.5P0.5O2 and SiO2), i.e. nAl
P ratio on the zeolite stability. By using the formation free energy (Gf) of the obtained GM structure, Fig. 2a illustrates the ternary phase diagram at rs = 5 Å for different SAPO compositions. Gf is the free energy of the zeolite (without the rigid body) relative to the free energies of quartz–SiO2, quartz–AlPO, α-Al2O3 and H2O at 200 °C and 15.53 bar (saturated vapor), corresponding to the neutral pH in normally used hydrothermal synthesis (in ESI Fig. S4† we discuss the effect of hydrothermal conditions on zeolite thermodynamics). Not surprisingly, due to the presence of the rigid body (rs = 5 Å) in our global PES search, all GMs in Fig. 2a are in the CHA-type framework, but they differ significantly in Gf: it has the minima nearby two vertexes, Al0.5P0.5O2 and SiO2 (∼0.11 eV per f.u.), but yields the maximum (∼0.30 eV per f.u.) at the left-bottom corner (Si0.5Al0.5O2H0.5). Most phases in the map are higher than their corresponding layer structure (0.17–0.18 eV per f.u., dotted lines), only the phases nearby two vertices (Al0.5P0.5O2 and SiO2), i.e. nAl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nSi+P ∼ 1
nSi+P ∼ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and nP > nSi (SAPO) and nSi
1 and nP > nSi (SAPO) and nSi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nAl > 5
nAl > 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, survive in thermodynamics. As indicated by the brackets in the figure, these Si
1, survive in thermodynamics. As indicated by the brackets in the figure, these Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios correspond to two CHA-type SAPO-34 and SSZ-13 materials, which are normally synthesized with the aid of SDAs (N,N,N-trimethyladamantammonium) in near neutral pH (pH < 8).39,40 We note that SSZ-13 can be synthesized not only under neutral but also under alkaline conditions, and under both conditions the SDAs have to be supplied, suggesting the critical role of SDAs.40–42 Overall, even in the presence of suitable rigid bodies, the Si
P ratios correspond to two CHA-type SAPO-34 and SSZ-13 materials, which are normally synthesized with the aid of SDAs (N,N,N-trimethyladamantammonium) in near neutral pH (pH < 8).39,40 We note that SSZ-13 can be synthesized not only under neutral but also under alkaline conditions, and under both conditions the SDAs have to be supplied, suggesting the critical role of SDAs.40–42 Overall, even in the presence of suitable rigid bodies, the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P composition is still critical to the stability of zeolites, causing a non-freely tunable Si
P composition is still critical to the stability of zeolites, causing a non-freely tunable Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio in experiments (ESI Table S8†).
P ratio in experiments (ESI Table S8†).
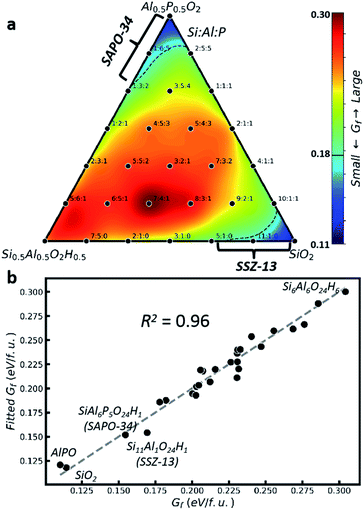 | ||
Fig. 2 Thermodynamics of zeolite formation with different Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios at acidic or neutral pH. (a) Gibbs formation free energy (Gf) contour plot in the ternary phase diagram using the GM identified by E-SSW with rs = 5 Å for each composition (black point). The Si P ratios at acidic or neutral pH. (a) Gibbs formation free energy (Gf) contour plot in the ternary phase diagram using the GM identified by E-SSW with rs = 5 Å for each composition (black point). The Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio is indicated for each composition; (b) correlation between Gf and the linear fitting of Gf (eqn (2)) for all GM data in (a). P ratio is indicated for each composition; (b) correlation between Gf and the linear fitting of Gf (eqn (2)) for all GM data in (a). | ||
Fig. 2b correlates the stability (Gf) with the structure using the GM data in Fig. 2a. By approximating Gf as a function of the proportions of TO4 (monomer, PT) and their linkages (T–O–T′, PTT′), see ESI Table S9,† we can obtain eqn (2) by linear fitting with R2 = 0.96. As Gf is positive in nature, it is no wonder that most terms, including monomers terms, Si–O–P, Al–O–Al, and Si–O–Al terms, have positive energy contributions. But it is important to reveal that Si–O–Si and Al–O–P terms yield negative contributions, suggesting that they are the major driving forces to stabilize the zeolite. The empirical rule in zeolite chemistry, namely, no Si–O–P and Al–O–Al patterns, is clearly manifested by their large positive prefactors, 0.35 and 0.16. In addition, our results identify the positive prefactor for the Si–O–Al term and thus explain the difficulty to incorporate Si element in AlPO and the special Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio of nSi < nP in SAPO synthesized under neutral pH conditions. This finding on the bonding patterns is general and well confirmed in other zeolite frameworks (ESI Fig. S5†).
P ratio of nSi < nP in SAPO synthesized under neutral pH conditions. This finding on the bonding patterns is general and well confirmed in other zeolite frameworks (ESI Fig. S5†).
| Gf ≈ (0.18 × PSi + 0.20 × PAl + 0.15 × PP) + (0.35 × PSiP + 0.16 × PAlAl + 0.13 × PSiAl − 0.06 × PSiSi − 0.05 × PAlP) | (2) |
We would like to point out that low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio zeolites, while not favorable under acidic and neutral conditions, are known to form under strongly alkali conditions in the experiment (ESI Table S10†).17 This is not surprising from thermodynamics as the replacement of H by an alkali metal, i.e. Na, changes the energy reference from H2O to NaOH solution. Fig. 3 illustrates the thermodynamic ternary phase diagram for different SAPO compositions under alkaline conditions (in the presence of Na ions for charge balance: the system is charge neutral) and all these calculations were performed by DFT. The structures of each composition are determined by Metropolis Monte Carlo sampling in the same CHA-type framework where the skeleton positions of T (T: Si, Al and P) and the likely positions of Na atoms (at the centers of 6- and 8-membered rings, see ESI Fig. S6† for details) are utilized as the pool of sites for random selection. The final Gibbs formation free energy Gf turns out to be completely different from that under acidic and neutral environments. A high Gf occurs at the compositions without Na, e.g. Si0.5Al0.25P0.25O2 (0.25 eV per f.u.) and the increase of the Na content can significantly stabilize the zeolite, leading to low Gf appearing at the left-bottom corner with a low Si
Al ratio zeolites, while not favorable under acidic and neutral conditions, are known to form under strongly alkali conditions in the experiment (ESI Table S10†).17 This is not surprising from thermodynamics as the replacement of H by an alkali metal, i.e. Na, changes the energy reference from H2O to NaOH solution. Fig. 3 illustrates the thermodynamic ternary phase diagram for different SAPO compositions under alkaline conditions (in the presence of Na ions for charge balance: the system is charge neutral) and all these calculations were performed by DFT. The structures of each composition are determined by Metropolis Monte Carlo sampling in the same CHA-type framework where the skeleton positions of T (T: Si, Al and P) and the likely positions of Na atoms (at the centers of 6- and 8-membered rings, see ESI Fig. S6† for details) are utilized as the pool of sites for random selection. The final Gibbs formation free energy Gf turns out to be completely different from that under acidic and neutral environments. A high Gf occurs at the compositions without Na, e.g. Si0.5Al0.25P0.25O2 (0.25 eV per f.u.) and the increase of the Na content can significantly stabilize the zeolite, leading to low Gf appearing at the left-bottom corner with a low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio. In particular, the Gf of Si7/12Al5/12O2Na5/12 is −0.01 eV per f.u., which is the most stable composition. As indicated by the brackets in the figure, these low Si
Al ratio. In particular, the Gf of Si7/12Al5/12O2Na5/12 is −0.01 eV per f.u., which is the most stable composition. As indicated by the brackets in the figure, these low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio zeolites happen to be chabazite materials, which were synthesized in strongly alkaline NaOH solution (pH > 13). Moreover, further considering the presence of water molecules to coordinate with Na ions in the zeolite framework, the zeolite containing Na can further be stabilized to reach even larger exothermic Gf (see, e.g. a hydrated SiAlO4Na zeolite in ESI Fig. S7†). This finding also proves that the zeolite formed under alkaline conditions is again the thermodynamically preferred product, which, unlike that under neural/acidic conditions, occurs even without the introduction of external SDA molecules. The Si–O–Al bonding pattern is thus only favored under alkaline conditions.
Al ratio zeolites happen to be chabazite materials, which were synthesized in strongly alkaline NaOH solution (pH > 13). Moreover, further considering the presence of water molecules to coordinate with Na ions in the zeolite framework, the zeolite containing Na can further be stabilized to reach even larger exothermic Gf (see, e.g. a hydrated SiAlO4Na zeolite in ESI Fig. S7†). This finding also proves that the zeolite formed under alkaline conditions is again the thermodynamically preferred product, which, unlike that under neural/acidic conditions, occurs even without the introduction of external SDA molecules. The Si–O–Al bonding pattern is thus only favored under alkaline conditions.
Both the energy bound and the pH-dependent bonding pattern rule indicate that thermodynamics dictates largely zeolite formation. This knowledge from the global PES leads to the classification of synthetic conditions for zeolites into three types:
• AlPO (and SAPO): SDAs + water + Al2O3 + H3PO4 + (SiO2);
• Pure silica (and aluminosilicates with high Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios): SDAs + water + SiO2 + (Al2O3);
Al ratios): SDAs + water + SiO2 + (Al2O3);
• Aluminosilicates with low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios: NaOH + water + SiO2 + Al2O3.
Al ratios: NaOH + water + SiO2 + Al2O3.
The first two types of zeolites rely on appropriate SDAs to enforce thermodynamics towards microporous structures, while a strong alkali leads to the third type zeolite, although SDAs may not be required.
With this knowledge, we have examined 252 known zeolite frameworks from the IZC-SC database12 and we can quickly select 63 and 233 of the 252 frameworks that satisfy the energy criterion (<0.17 (0.18) eV per f.u.) for AlPO and SiO2 zeolites, respectively (as listed in ESI Tables S5 and S6†). The same approach is applicable to millions of conceived zeolite topologies in the DEEM PCOD database,43 which shows that 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900, only ∼4.5%, hypothetical zeolite structures satisfy the energy criterion. In the experiment, we note that there are 29 AlPO and 60 SiO2 zeolites synthesized, where only five (AST, ATS, AFI, CHA, and ANA) have both AlPO and SiO2 forms. Obviously, from our work there is ample room to synthesize new zeolites, particularly for AlPO (SAPO) and pure silica (high Si
900, only ∼4.5%, hypothetical zeolite structures satisfy the energy criterion. In the experiment, we note that there are 29 AlPO and 60 SiO2 zeolites synthesized, where only five (AST, ATS, AFI, CHA, and ANA) have both AlPO and SiO2 forms. Obviously, from our work there is ample room to synthesize new zeolites, particularly for AlPO (SAPO) and pure silica (high Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio aluminosilicates).
Al ratio aluminosilicates).
4. Conclusions
By developing machine-learning based atomic simulation techniques, this work explores the global PES of zeolites which reveals the roles of SDAs, Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratios and pH values on the zeolite stability. We find that (i) zeolites, while being metastable in energy, become the thermodynamically stable products under synthetic conditions; (ii) the energy of zeolites is limited by an upper bound determined by the 2D layered phase, which is 0.17–0.18 eV per f.u.; and (iii) the preferred bonding patterns are pH sensitive: the Si–O–P, Al–O–Al and Si–O–Al bonding patterns are not favored under acidic and neutral pH environments, but the Si–O–Al pattern becomes desirable under basic conditions. With these rules, we answer the long-standing questions on zeolite formation, in particular on the Si
P ratios and pH values on the zeolite stability. We find that (i) zeolites, while being metastable in energy, become the thermodynamically stable products under synthetic conditions; (ii) the energy of zeolites is limited by an upper bound determined by the 2D layered phase, which is 0.17–0.18 eV per f.u.; and (iii) the preferred bonding patterns are pH sensitive: the Si–O–P, Al–O–Al and Si–O–Al bonding patterns are not favored under acidic and neutral pH environments, but the Si–O–Al pattern becomes desirable under basic conditions. With these rules, we answer the long-standing questions on zeolite formation, in particular on the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio, the choice of SDA molecules and the pH conditions in synthesis. Besides these thermodynamic rules, the advent of machine learning based atomic simulation enables the fast and reliable analyses of unknown zeolite structures and thus opens new avenues towards the rational design of zeolites.
P ratio, the choice of SDA molecules and the pH conditions in synthesis. Besides these thermodynamic rules, the advent of machine learning based atomic simulation enables the fast and reliable analyses of unknown zeolite structures and thus opens new avenues towards the rational design of zeolites.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (2018YFA0208600), National Science Foundation of China (91945301, 21533001, 91745201 and 21673295) and China Postdoctoral Science Foundation (2019M661340).References
- K. Na, C. Jo, J. Kim, K. Cho, J. Jung, Y. Seo, R. J. Messinger, B. F. Chmelka and R. Ryoo, Science, 2011, 333, 328–332 CrossRef CAS.
- J. Y. Li, J. H. Yu, W. F. Yan, Y. H. Xu, W. G. Xu, S. L. Qiu and R. R. Xu, Chem. Mater., 1999, 11, 2600–2606 CrossRef CAS.
- J. H. Yu, J. Y. Li, K. X. Wang, R. R. Xu, K. Sugiyama and O. Terasaki, Chem. Mater., 2000, 12, 3783–3787 CrossRef CAS.
- J. Yu and R. Xu, Acc. Chem. Res., 2010, 43, 1195–1204 CrossRef CAS.
- Y. Jin, Q. Sun, G. Qi, C. Yang, J. Xu, F. Chen, X. Meng, F. Deng and F.-S. Xiao, Angew. Chem., Int. Ed., 2013, 52, 9172–9175 CrossRef CAS.
- S. S. Arora, D. L. S. N. Ieskens, A. Malek and A. Bhan, Nat. Catal., 2018, 1, 666–672 CrossRef CAS.
- I. Yarulina, K. De Wispelaere, S. Bailleul, J. Goetze, M. Radersma, E. Abou-Hamad, I. Vollmer, M. Goesten, B. Mezari, E. J. M. Hensen, J. S. Martinez-Espin, M. Morten, S. Mitchell, J. Perez-Ramirez, U. Olsbye, B. M. Weckhuysen, V. Van Speybroeck, F. Kapteijn and J. Gascon, Nat. Chem., 2018, 10, 897 CrossRef CAS.
- M. Treacy, I. Rivin, E. Balkovsky, K. Randall and M. Foster, Microporous Mesoporous Mater., 2004, 74, 121–132 CrossRef CAS.
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef CAS.
- R. Pophale, P. A. Cheeseman and M. W. Deem, Phys. Chem. Chem. Phys., 2011, 13, 12407–12412 RSC.
- M. Moliner, Y. Roman-Leshkov and A. Corma, Acc. Chem. Res., 2019, 52, 2971–2980 CrossRef CAS.
- IZC-SC database, http://www.iza-structure.org/databases Search PubMed.
- S. L. Burkett and M. E. Davis, Chem. Mater., 1995, 7, 920–928 CrossRef CAS.
- J. Li, A. Corma and J. Yu, Chem. Soc. Rev., 2015, 44, 7112–7127 RSC.
- M. Dusselier and M. E. Davis, Chem. Rev., 2018, 118, 5265–5329 CrossRef CAS.
- E. M. Gallego, M. T. Portilla, C. Paris, A. León-Escamilla, M. Boronat, M. Moliner and A. Corma, Science, 2017, 355, 1051–1054 CrossRef CAS.
- R. Xu, W. Pang, J. Yu, Q. Huo and J. Chen, Chemistry of Zeolites and Related porous Materials: Synthesis and Structure, Wiley Online Books, 2007, p. 17 Search PubMed.
- C. S. Cundy and P. A. Cox, Microporous Mesoporous Mater., 2005, 82, 1–78 CrossRef CAS.
- R. Barrer and P. Denny, J. Chem. Soc., 1961, 971–982 RSC.
- L. M. Ren, Q. M. Wu, C. G. Yang, L. F. Zhu, C. J. Li, P. L. Zhang, H. Y. Zhang, X. J. Meng and F. S. Xiao, J. Am. Chem. Soc., 2012, 134, 15173–15176 CrossRef CAS.
- S. T. Wilson, B. M. Lok, C. A. Messina, T. R. Cannan and E. M. Flanigen, J. Am. Chem. Soc., 1982, 104, 1146–1147 CrossRef CAS.
- A. Jackowski, S. I. Zones, S. J. Hwang and A. W. Burton, J. Am. Chem. Soc., 2009, 131, 1092–1100 CrossRef CAS.
- M. Moliner, F. Rey and A. Corma, Angew. Chem., Int. Ed., 2013, 52, 13880–13889 CrossRef CAS.
- S. D. Huang, C. Shang, P. L. Kang, X. J. Zhang and Z. P. Liu, Wires Comput. Mol. Sci., 2019, e1415 CAS.
- S. Ma, C. Shang and Z.-P. Liu, J. Chem. Phys., 2019, 151, 050901 CrossRef.
- S. Ma, S.-D. Huang and Z.-P. Liu, Nat. Catal., 2019, 2, 671–677 CrossRef CAS.
- R. Martoňák, D. Donadio, A. R. Oganov and M. Parrinello, Nat. Mater., 2006, 5, 623 CrossRef.
- C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845 CrossRef CAS.
- X.-J. Zhang, C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 3252–3260 CrossRef CAS.
- C. Shang, X.-J. Zhang and Z.-P. Liu, Phys. Chem. Chem. Phys., 2014, 16, 17845–17856 RSC.
- S.-D. Huang, C. Shang, X.-J. Zhang and Z.-P. Liu, Chem. Sci., 2017, 8, 6327–6337 RSC.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef.
- S.-D. Huang, C. Shang, P.-L. Kang and Z.-P. Liu, Chem. Sci., 2018, 9, 8644–8655 RSC.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- J. M. Bennett and R. M. Kirchner, Zeolites, 1992, 12, 338–342 CrossRef CAS.
- J. Zhong, J. Han, Y. Wei, P. Tian, X. Guo, C. Song and Z. Liu, Catal. Sci. Technol., 2017, 7, 4905–4923 RSC.
- M. J. Diaz-Cabanas, P. A. Barrett and M. A. Camblor, Chem. Commun., 1998, 1881–1882 RSC.
- L. M. Ren, L. F. Zhu, C. G. Yang, Y. M. Chen, Q. Sun, H. Y. Zhang, C. J. Li, F. Nawaz, X. J. Meng and F. S. Xiao, Chem. Commun., 2011, 47, 9789–9791 RSC.
- B. H. Chen, R. N. Xu, R. D. Zhang and N. Liu, Environ. Sci. Technol., 2014, 48, 13909–13916 CrossRef CAS.
- 14900 hypothetical zeolites are obtained from DEEM PCOD database with the quartz phase as the energy zero and 0.17 eV per f.u. as the upper energy boundary, http://www.hypotheticalzeolites.net/DATABASE/DEEM/DEEM_PCOD/index.php.
Footnote |
† Electronic supplementary information (ESI) available. Supplementary methods; IZC-SC bank data of SiO2, AlPO, SAPO and low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio aluminosilicate zeolites; global PESs; SDAs; thermodynamic analysis of zeolites. See DOI: 10.1039/d0sc03918g Al ratio aluminosilicate zeolites; global PESs; SDAs; thermodynamic analysis of zeolites. See DOI: 10.1039/d0sc03918g |
| This journal is © The Royal Society of Chemistry 2020 |