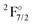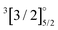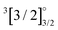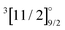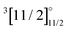Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic spectra of ytterbium fluoride from relativistic electronic structure calculations†
Johann V.
Pototschnig
 *ab,
Kenneth G.
Dyall
*ab,
Kenneth G.
Dyall
 c,
Lucas
Visscher
c,
Lucas
Visscher
 b and
André Severo Pereira
Gomes
b and
André Severo Pereira
Gomes
 d
d
aInstitut für Experimentalphysik, Technische Universität Graz, Petersgasse 16, 8010 Graz, Austria. E-mail: johann.pototschnig@tugraz.at
bDepartment of Chemistry and Pharmaceutical Sciences, Faculty of Sciences, Vrije Universiteit Amsterdam, De Boelelaan 1083, NL-1081 HV Amsterdam, The Netherlands. E-mail: visscher@chem.vu.nl
cDirac Solutions, 10527 NW Lost Park Drive, Portland, OR 97229, USA. E-mail: diracsolutions@gmail.com
dUniversité de Lille, CNRS, UMR 8523 - PhLAM - Physique des Lasers, Atomes et Molécules, F-59000 Lille, France. E-mail: andre.gomes@univ-lille.fr
First published on 1st October 2021
Abstract
We report an investigation of the low-lying excited states of the YbF molecule-a candidate molecule for experimental measurements of the electron electric dipole moment-with 2-component based multi-reference configuration interaction (MRCI), equation of motion coupled cluster (EOM-CCSD) and the extrapolated intermediate Hamiltonian Fock-space coupled cluster (XIHFS-CCSD). Specifically, we address the question of the nature of these low-lying states in terms of configurations containing filled or partially-filled Yb 4f shells. We show that while it does not appear possible to carry out calculations with both kinds of configurations contained in the same active space, reliable information can be extracted from different sectors of Fock space-that is, by performing electron attachment and detachment IHFS-CCSD and EOM-CCSD calculation on the closed-shell YbF+ and YbF− species, respectively. From these calculations we predict Ω = 1/2, 3/2 states, arising from the 4f13σ26s, 4f145d1/6p1, and 4f135d1σ16s configurations to be able to interact as they appear in the same energy range around the ground-state equilibrium geometry. As these states are generated from different sectors of Fock space, they are almost orthogonal and provide complementary descriptions of parts of the excited state manifold. To obtain a comprehensive picture, we introduce a simple adiabatization model to extract energies of interacting Ω = 1/2, 3/2 states that can be compared to experimental observations.
1 Introduction
In a previous paper,1 we introduced all-electron relativistic basis sets for the lanthanides (La–Lu) and discussed their performance for the determination of spectroscopic constants for the ground state of ytterbium fluoride (YbF), an open-shell molecule with a 2Σ+ ground state. This molecule has received a fair amount of experimental and theoretical attention because of its potential application in the observation of parity-violating interactions2–4via determination of the electric dipole moment of the electron (eEDM)-see, for instance ref. 4–11 and references therein). There is also some interest in the Yb atom, cation and dimer in connection to ultracold physics.12–14 An example15 is the parity violation observed in the Yb atom.A noteworthy finding in our previous work was the sensitivity of coupled cluster calculations to the basis set in use and, indirectly, to the amount of electron correlation recovered in the calculations. We observed a spike in the values of the T1 diagnostic around the ground state equilibrium geometry, so it appears that the perturbative treatment of triple excitations in the CCSD(T) calculations breaks down in this region of the potential energy curves unless there is enough flexibility in the correlation treatment. The same was recently observed by Pasteka et al.16 for the nuclear quadruple coupling constant. This suggests the existence of a low lying perturbing state, which we want to investigate further in the current work.
Experimental17,18 and previous theoretical19–21 investigations suggest that in the ground state the unpaired electron is located in a σs orbital with dominant contributions from the 6s orbital of Yb, corresponding to a Yb(4f14σ16s)F configuration. This 2Σ1/2 state ground state was studied in greater detail by combining microwave and optical spectroscopy for the odd 171Yb isotope.22
Experimentally,18 the lowest excited state observed is assigned as 2Π1/2, with an energy of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 cm−1, while the 2Π3/2 component is found at 19
106 cm−1, while the 2Π3/2 component is found at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 cm−1, yielding a spin–orbit splitting of 1365 cm−1 of this spin–orbit split A 2Π state. The lower component will be denoted 31/2 in the current work. Experiments indicate a perturbation of its vibrational levels,18,23–25 which was attributed to the presence of a perturbing state (denoted by 41/2 here) found at 18
471 cm−1, yielding a spin–orbit splitting of 1365 cm−1 of this spin–orbit split A 2Π state. The lower component will be denoted 31/2 in the current work. Experiments indicate a perturbation of its vibrational levels,18,23–25 which was attributed to the presence of a perturbing state (denoted by 41/2 here) found at 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 cm−1.18 This perturbing 41/2 state is sometimes referred to as [18.6]1/2 by experimentalists18,23 (energy in cm−1 divided by 103 in the square brackets, and Ω-value as subscript). The mixing of these two Ω = 1/2 states gives rise to states designated as [557] and [561] (the values in square brackets referring to transition energies in Thz from the vibronic ground state) with transition energies of 18
705 cm−1.18 This perturbing 41/2 state is sometimes referred to as [18.6]1/2 by experimentalists18,23 (energy in cm−1 divided by 103 in the square brackets, and Ω-value as subscript). The mixing of these two Ω = 1/2 states gives rise to states designated as [557] and [561] (the values in square brackets referring to transition energies in Thz from the vibronic ground state) with transition energies of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 574 and 18
574 and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 699 cm−1, respectively.24,25 These two states are of importance for laser cooling schemes that have been investigated26 and tested25 with the purpose of realizing high-accuracy measurements of YbF at very low temperatures. Besides these first excited states, Smallman26 investigated also two not yet fully characterized mixed states, [574](≈19
699 cm−1, respectively.24,25 These two states are of importance for laser cooling schemes that have been investigated26 and tested25 with the purpose of realizing high-accuracy measurements of YbF at very low temperatures. Besides these first excited states, Smallman26 investigated also two not yet fully characterized mixed states, [574](≈19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 cm−1) and [578](≈19
150 cm−1) and [578](≈19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 cm−1) at higher energies. These can be compared with the Ω = 3/2 state at 19
280 cm−1) at higher energies. These can be compared with the Ω = 3/2 state at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 cm−1 found earlier by Dunfield,18 which will be denoted 23/2 in the current work. Uttam et al.27,28 furthermore measured additional unidentified higher bands at about 23
471 cm−1 found earlier by Dunfield,18 which will be denoted 23/2 in the current work. Uttam et al.27,28 furthermore measured additional unidentified higher bands at about 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035, 23
035, 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 256 and 26
256 and 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 cm−1, which they denoted as C1, C2 and D, respectively.
015 cm−1, which they denoted as C1, C2 and D, respectively.
Theoretically, excited states arising from the Yb(4f146p1)F and Yb(4f145d1)F configurations were considered by Nayak and Chaudhuri6 with RAS-CI based on 4-component spinors, yielding the A2Π1/2 (31/2), A2Π3/2 (23/2), and a 2Σ1/2 state. Earlier multireference CI calculations by Dolg et al.19 furthermore indicate the possibility of low-lying Ω = 1/2 states arising from the 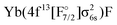 or
or 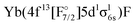 configurations, to be lying below or close to the Yb(4f146p1)F states. This was also found in the DFT calculations of Liu et al.20 who place excited states arising from the
configurations, to be lying below or close to the Yb(4f146p1)F states. This was also found in the DFT calculations of Liu et al.20 who place excited states arising from the 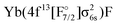 configuration in the range from 9000 to 15
configuration in the range from 9000 to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 relative to the Yb(4f14σ16s)F ground state. These findings make it of interest to explicitly consider the configuration interaction between the f13 and f14 configurations in the Yb atom.29
000 cm−1 relative to the Yb(4f14σ16s)F ground state. These findings make it of interest to explicitly consider the configuration interaction between the f13 and f14 configurations in the Yb atom.29
The vibronic states are additionally split due to hyperfine interactions. In atomic experiments they were measured for the ground and excited states9,22,30–33 also using Zeeman spectroscopy.34 The hyperfine interaction of the atom35–37 and molecule38 were studied theoretically, and should have similar uncertainties to the contribution of the eEDM to the spectrum due to the similarity of the matrix elements. Recently, uncertainties of the hyperfine constants arising in relativistic coupled cluster computations have been studied.39
It is clear from the above that a proper description of the Yb atom and the YbF molecule requires an accurate treatment of both spin–orbit coupling and electron correlation, for ground as well as excited states. A popular approach is the so-called two-step approach to spin–orbit coupling (SOC), in which electron correlation methods based on non-relativistic or scalar relativistic Hamiltonians are used to obtain excited state energies, that are in turn used to dress a spin–orbit configuration interaction (SOCI) matrix. This approach can yield quite accurate spin–orbit coupled states, but results are particularly sensitive to the number of spin-free states serving as a basis for the SOCI step.40–46 An alternative is to include SOC already at the mean-field level, and use fully SO-coupled molecular spinors to construct the correlated wave functions.47 This can be done with four-component Hamiltonians, as done for the ground1 and excited states6,37,48,49 of YbF, or with more computationally efficient two-component Hamiltonians based on the eXact 2-Component (X2C) approach,50–57 in which a transformation to decouple the positive and negative energy states of the Dirac Hamiltonian can be carried out in matrix form, yielding the same positive energy spectrum as the original 4-component Hamiltonian. More details can be found in the recent review by Liu.47 Among the different X2C flavors, we can distinguish two main strategies for the decoupling, which is performed based on: (i) the one-electron Dirac Hamiltonian prior to the mean-field step,54,57 and for which two-electron spin–orbit contributions due to the untransformed two-electron potential are included via atomic mean-field contributions calculated with the AMFI code41,58,59 (X2C-AMFI); (ii) after a converged 4-component mean-field calculation on atoms52,53,56 or molecules55 (2DCM). Recent benchmarks show that 2DCM calculations closely reproduce equivalent 4-component ones for valence60 or core61 states.
Moreover, the aforementioned calculations for the excited states of YbF have mostly employed multireference CI (MRCI) approaches. While these can provide great flexibility in capturing static correlation, it remains the case that dynamical correlation is better accounted for with coupled cluster approaches. Among the coupled cluster singles and doubles (CCSD) approaches for excited states, we have the equation of motion (EOM-CCSD) method as well as Fock-space (IHFS-CCSD) methods,62 of which the single electron attachment, detachment, and singly excited states variants are the most commonly used. The two approaches have been found to yield very accurate results in general and in particular for calculations with relativistic Hamiltonians as discussed elsewhere (see ref. 60 and references therein).
The first goal of this work is therefore to go beyond the investigations performed to date in the literature, and apply the relativistic EOM-CCSD and IHFS-CCSD approaches to describe the low-lying excited states of YbF. For such states, where the most important excited state configurations appear have a single open-shell character (4f14σ16s, 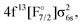 4f145d1,
4f145d1, 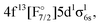 4f146p1), these coupled cluster approaches are in principle applicable, provided one starts from closed shell configurations such as Yb(4f14σ26s)F− or Yb(4f14)F+. Additionally, we assess the performance of relativistic MRCI with respect to the coupled cluster methods. Our second goal is to confirm whether any low-lying state is close enough to the ground state to perturb the latter, and explain the anomalous behavior observed in the open-shell ground-state calculations in the literature.
4f146p1), these coupled cluster approaches are in principle applicable, provided one starts from closed shell configurations such as Yb(4f14σ26s)F− or Yb(4f14)F+. Additionally, we assess the performance of relativistic MRCI with respect to the coupled cluster methods. Our second goal is to confirm whether any low-lying state is close enough to the ground state to perturb the latter, and explain the anomalous behavior observed in the open-shell ground-state calculations in the literature.
2 Computational details
All relativistic electronic structure calculations were performed with a development version of the Dirac program suite63 (revision 6e10c5d3), employing for Yb the valence double-zeta (24s19p13d9f2g), triple-zeta (30s24p18d14f4g2h) and quadruple-zeta (35s30p19d16f6g4h2i) basis sets from the previous work,1 along with the matching augmented correlation-consistent (aug-cc-pVnZ, n = 2, 3, 4) basis sets of Dunning64 for F. All basis sets were kept uncontracted, with the small component basis generated by restricted kinetic balance. In addition to these individual basis sets, we have used the calculations with triple- and quadruple-zeta sets to construct extrapolations to the complete basis set limit (E∞) for the underlying potential energy curves, using the relation65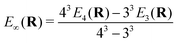 | (1) |
In the coupled cluster computations the 2DCM Hamiltonian54,55 was applied, all two-electron integrals over small component (S) basis sets (i.e. the so-called (SS|SS)-type integrals) appearing in the SCF step have been replaced by a simple correction.66 In order to account for spin–orbit coupling and other relativistic effects the X2C-AMFI Hamiltonian was employed for the Kramers-restricted configuration interaction (KRCI) method.
Spectroscopic constants (re, De, ωe and ωeχe) were determined from a Morse potential fit in the vicinity of the potential energy minima. The potential energy curves were determined for bond lengths between 1.6 Å and 2.3 Å spaced by 0.02 Å and additional points with larger spacing up to 3.5 Å. In the calculation of De the asymptotic dissociation limit is calculated from the energies of the isolated neutral atoms, F in the 2P3/2 state and Yb in the 1S0 state.
The dataset associated with this manuscript (outputs from calculations, codes to extract and process information from these, and code to obtain the spectroscopic constants) is provided in ref. 67.
2.1 Kramers-restricted configuration interaction
For YbF we first consider Kramers-restricted configuration interaction (KRCI) based on an average-of-configuration Hartree–Fock approach (AOC-SCF).68 This method was employed in order to treat the open shells, where one or two valence electrons were distributed over the s- and d-orbitals and the f-shell was either completely filled or contained one hole, depending on the states of interest. The AOC-SCF reference wave function in the KRCI computation is occupied according to a definition given by a generalized active space (GAS).69 In this approach the Hamiltonian is computed for all allowed configurations and then diagonalized. The GAS space was defined by a f-shell which was completely filled or contained one hole and one or two electrons distributed over 29 orbitals.2.2 Equation-of-motion coupled cluster
The first approach we use to describe the dynamical correlation that is largely missing in KRCI is EOM-CCSD, which can give access to electronic states of different kinds, depending on the single determinant wave function that is chosen as the starting point. In it, the CCSD amplitudes are determined for the chosen ground state in the first step, and subsequently the similarity transformed Hamiltonian is constructed using these amplitudes and the desired states are generated by an operator that either removes or adds an electron.The first set of states was obtained by electron attachment on Yb(4f14F+ ion, where the HOMO (σ6s,1/2) of YbF was initially empty. This computation on the (0h,1p) sector of Fock space yielded states with 4f14 and a valence electron in the σ6s, d or p orbital. This means that, in the process of obtaining the potentials for the ground and excited states of YbF, we immediately obtain energies of CCSD quality for YbF+, and therefore vertical ionization potentials (IP) at each geometry.
Another set of states was obtained by ionizing the Yb(4f14σ26s)F− anion, where the HOMO (σ6s,1/2) of YbF was initially doubly occupied. States arising from the Yb(4f14σ16s)F, 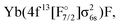
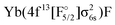 and Yb(4f14σ26s)F(2p5) configurations were obtained by considering the (1h,0p) sector of Fock space. This means that, in the process of obtaining the potentials for the ground and excited states of YbF, we immediately obtain energies of CCSD quality for YbF−, and therefore vertical electron affinities (EA) at each geometry. We note that states arising from the (2h,1p) and (1h,2p) manifolds are also accessible from EOM-IP and EOM-EA calculations, though the energy of electronic states determined by such configurations will be less accurate than states dominated by single detachment or attachment configurations.
and Yb(4f14σ26s)F(2p5) configurations were obtained by considering the (1h,0p) sector of Fock space. This means that, in the process of obtaining the potentials for the ground and excited states of YbF, we immediately obtain energies of CCSD quality for YbF−, and therefore vertical electron affinities (EA) at each geometry. We note that states arising from the (2h,1p) and (1h,2p) manifolds are also accessible from EOM-IP and EOM-EA calculations, though the energy of electronic states determined by such configurations will be less accurate than states dominated by single detachment or attachment configurations.
The EOM-CCSD electronic states are obtained by an iterative diagonalization (Davidson) procedure in which only the energies of a certain number of the lowest states are determined. For the IP-EOM-CCSD we obtained 16 Ω = 1/2, 8 Ω = 3/2, 6 Ω = 5/2 and 2 Ω = 7/2 states, whereas for EA-EOM-CCSD we obtained 8 Ω = 1/2, 6 Ω = 3/2, 4 Ω = 5/2 and 2 Ω = 7/2 states.
As transition moments are not yet available for the EOM-CCSD implementation in Dirac, we have only obtained the potential energy curves. These are nevertheless useful since, by not requiring the definition of model spaces or the use of an extrapolation procedure, they serve as a cross validation of the IHFS-CCSD calculations below.
2.3 Fock-space coupled cluster
Fock-space coupled cluster70 (FS-CCSD) is our second approach to include dynamical correlation in the electronically excited states. Here it was employed in a similar fashion to EOM-CCSD, starting from YbF+ or YbF− and proceeding to the (0h,1p) and (1h,0p) sectors of Fock space, respectively. For FS-CCSD a model space is defined by selecting a number of occupied and virtual orbitals and how many electrons are added and removed. The matrix for this subspace is constructed and subsequently diagonalized, thus yielding all states within the chosen model space, in this case states arising from single electron attachment (EA) or single electron detachment (IP). This method requires solving first for the underlying sectors, starting with (0h,0p), which corresponds to CCSD. Due to computational constraints, we have truncated the virtual space so that 117, 230 and 296 orbitals were used in the double-, triple- and quadruple-zeta CCSD calculations, respectively.The separation into a model and external space leads to the appearance of the so-called intruder states, a well-known difficulty with Fock-space coupled cluster and other effective Hamiltonian approaches, that can be dealt with in many cases by the intermediate Hamiltonian (IH) Fock-space coupled cluster (IHFS-CCSD) method.71,72
The IH approach was employed to compute Yb(4f14{σ6s,6p,5d…}1)F states starting from YbF+. The active P space in such calculations contained about 50 spinors varying slightly with bond distance and basis set. Of these 26 spinors are always present in the model (Pm) space, whereas the remaining active spinors are placed in the intermediate (PI) space. Due to using the (0h,1p) sector for the cation, states arising from configurations where the Yb 4f shell is partially filled (such as 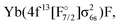
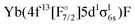 or
or 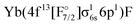 ) are not accessible in this calculation.
) are not accessible in this calculation.
The approach outlined above was, however, not enough to avoid divergence in the computation of the (1h,0p) sector using the anion as a reference. Therefore, the extrapolated intermediate Hamiltonian (XIH) Fock-space coupled-cluster approach73 (XIHFS-CCSD) was applied using the same shifts as in ref. 73. Values of 0.1 and 0.2 Hartree were selected if one of the holes is not in the model space. These shifts were doubled for two holes outside the model space. Using the determined energies an extrapolation to the system without shifts was performed. The model (Pm) space in these computations contained 22 spinors, the intermediate (PI) space about 24 spinors depending on the bond distance and basis set. Since we start out from the anion and only allow holes, only Yb(4f14σ16s)F, 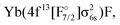
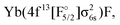 and Yb(4f14σ26s)F(2p5) configurations are accessible in this computation.
and Yb(4f14σ26s)F(2p5) configurations are accessible in this computation.
Combining the two sectors allows us to get different excited states of YbF, although there are limitations. Firstly, the interactions between configurations with open f-shell and the ones with an electron in the p- or d-shell are not included, since they will be obtained for different sectors of Fock space. This interaction will nevertheless be treated with a simple adiabatization approach, described in Sections 2.4 and 3.6. Secondly, configurations such as 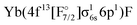 or
or 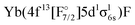 are not included in the current treatment. This limitations is not as significant because these states have higher energies than the ones we are interested in. Both of these problems could be dealt with by using the (1h,1p) sector, but this goes beyond the current work as convergence is very unstable for this sector and it requires the use of an open-shell reference.
are not included in the current treatment. This limitations is not as significant because these states have higher energies than the ones we are interested in. Both of these problems could be dealt with by using the (1h,1p) sector, but this goes beyond the current work as convergence is very unstable for this sector and it requires the use of an open-shell reference.
2.4 Adiabatization of electronic states
As we separated the computations of states with 4f13 and 4f14 character, these states cannot interact with each other, and states with the same Ω value cross although they should have an avoided crossing. In order to correct this deficiency we considered a simple adiabatization model, in which we set up and diagonalize the following matrix for each Ω value: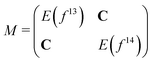 | (2) |
3 Results and discussion
We start our discussion with the electronic transitions of the atomic Yb+ cation, before moving on to the YbF molecule. This is because the cation's electronic structure is similar to the Yb in YbF since, due to the large electronegativity of fluorine, one electron is almost completely removed from the Yb atom.Subsequently, the potential energy curves for Kramers-restricted configuration interaction are presented. A discussion of the coupled cluster approaches follows, with a focus on the comparison of the coupled cluster results for the Fock space and equation-of-motion approach. This section is followed by a presentation of the spectroscopic data for the ground and excited states. In the last part we take a closer look at the mixing of states at around 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and apply the adiabatization procedure.
000 cm−1 and apply the adiabatization procedure.
3.1 Ytterbium cation
As discussed in the introduction, states from both the 4f13 and the 4f14 configurations are of importance. This is difficult to realize in a balanced manner when using one set of orbitals to describe all states. Any change in the occupation of the 4f-shell will alter the screening of the 5s and 5p orbitals of Yb, resulting in differences between orbital sets optimized for a 4f13 or a 4f14 configuration. Additionally, the 4f orbitals are very compact and since they are the first f-shell there are no orthogonality conditions limiting the radial expansion or contraction of the orbital. Depictions of the orbitals for both configurations can be found in Table S1 in the ESI.†These observations help to understand why it turned out to be very difficult to treat both sets of states in the same calculation, which we attempted to do from AOC-SCF on the Yb+. We started out by performing AOC-SCF computations on the atom, based on the 4f closed shell configuration. While we obtained the correct ground state configuration, the 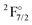 has an energy of about 46
has an energy of about 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (over two times higher than the experimental value), and the wrong order for the hole states is observed. If the wave function is optimized for a 4f13 configuration, one obtains the
000 cm−1 (over two times higher than the experimental value), and the wrong order for the hole states is observed. If the wave function is optimized for a 4f13 configuration, one obtains the 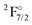 as the lowest state and finds the true ground state more than 20
as the lowest state and finds the true ground state more than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 higher. Because of these difficulties, the KRCI calculations discussed below all follow the strategy of different orbital sets that is also employed in the subsequent coupled cluster calculations.
000 cm−1 higher. Because of these difficulties, the KRCI calculations discussed below all follow the strategy of different orbital sets that is also employed in the subsequent coupled cluster calculations.
Table 1 contains KRCI values of electronic transitions for the cation. The transition energies show deviations of about 10% and the spin–orbit splitting is underestimated for states with a 4f14 configuration. The squared transition dipole moment (TDM2) of the 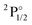 state is underestimated by about 13%, the one for the
state is underestimated by about 13%, the one for the 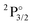 state overestimated by about 47%. The second set of states with a hole in the f-shell and different distributions of the 2 valence electrons are given in the lower part of Table 1, the energies are relative to the
state overestimated by about 47%. The second set of states with a hole in the f-shell and different distributions of the 2 valence electrons are given in the lower part of Table 1, the energies are relative to the 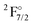 state. In this case the two valence electrons are distributed over the s- and d-shell. The lowest state with a
state. In this case the two valence electrons are distributed over the s- and d-shell. The lowest state with a 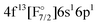 configuration has a transition energy of 47912.31 cm−1 and was not included in the current treatment.
configuration has a transition energy of 47912.31 cm−1 and was not included in the current treatment.
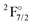 state are also given. 2z, 3z, 4z, and extr. indicate double, triple, quadruple zeta and extrapolated results, respectively
state are also given. 2z, 3z, 4z, and extr. indicate double, triple, quadruple zeta and extrapolated results, respectively
| State | Conf. | NIST74 | 2z | 3z | 4z | extr. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| E | S | E | TDM2 | E | TDM2 | E | TDM2 | E | ||
| 2S1/2 | 4f146s1 | 0 | 0 | 0 | 0 | 0 | ||||
| 2D3/2 | 4f145d1 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 322 322 |
0.0 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 802 802 |
0.0 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 606 606 |
0.0 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192 192 |
|
| 2D5/2 | 4f145d1 | 24333 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882 882 |
0.0 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321 321 |
0.0 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117 117 |
0.0 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698 698 |
|
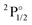
|
4f146p1 | 27062 | 6.1 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 210 |
3.5 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 533 533 |
3.8 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 331 331 |
3.6 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914 914 |
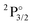
|
4f146p1 | 30392 | 11.4 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 104 104 |
16.9 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 385 |
18.9 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
17.4 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
The excited states of the Yb atom for the 4f14 configuration have already been investigated by relativistic Fock-space coupled cluster36,37,75,76 as well as for the cation,75 including the transition moment of magnetic transitions.76 With our current calculations we can go beyond these studies and investigate the f13 configurations as well. Before discussing our IHFS-CCSD calculations for Yb+, we focus on the EOM-CCSD excitation energies, shown in Table 2. The EOM-IP-CCSD energies of 4f13 states obtained from the extrapolation to the complete basis set limit underestimate the experimental transition energies by around 3000 cm−1, whereas the values for 4f14 states, obtained with EOM-EA-CCSD are within 1000 cm−1 of the experimental values, which yields a quantitative improvement over the KRCI ones for both configurations, even though qualitatively the two methods provide a similar picture. From that and the preceeding discussion, we attribute the relatively lower accuracy for the 4f13 to arise from the incomplete account of the relaxation of the wave function upon the creation of the hole in the f shell. Beyond the states presented in Table 2, which are dominated by single electron attachment and detachment, we are able to access states with significant (1h,2p) and (2h,1p) character with EOM-CCSD. These states, available in Table S14 in the ESI,† are about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 higher in energy than the experimental ones.
000 cm−1 higher in energy than the experimental ones.
| State | Conf. | NIST74 | 2z | 3z | 4z | Extr. |
|---|---|---|---|---|---|---|
| 2S1/2 | 4f146s1 | 0 | 0 | 0 | 0 | 0 |
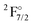
|
4f136s2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 419 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 054 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524 524 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 092 092 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966 966 |
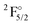
|
4f136s2 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568 568 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 139 139 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 655 655 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491 491 |
| 2D3/2 | 4f145d1 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 073 073 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209 209 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060 060 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951 951 |
| 2D5/2 | 4f145d1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 333 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 351 351 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 341 341 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 257 257 |
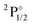
|
4f146p1 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062 062 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 539 539 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 780 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 857 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913 913 |
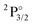
|
4f146p1 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 392 392 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 954 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 323 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380 380 |
Finally, our IHFS-CCSD results are presented in Table 3. The transition energies for 4f14 configuration reproduce well the experimental ones, with errors below 6%, and only show a small dependence on the basis set. The states arising from the 4f13 configuration (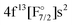 etc.), in contrast, show a significant dependence on the basis and a rather slow convergence and underestimate the value by about 30%, which makes them less accurate than the EOM-CCSD ones. This lower accuracy is a consequence of the reduced flexibility in the model spaces, due to the need of adding the 5p-shell just below the 4f-shell to the intermediate space, in order to achieve convergence. These results are in line with the observations of Shee et al.,60 in that the formal equivalence between EOM-CCSD and IHFS-CCSD for the sectors of Fock space considered depends, in fact, on the flexibility of the main model space.
etc.), in contrast, show a significant dependence on the basis and a rather slow convergence and underestimate the value by about 30%, which makes them less accurate than the EOM-CCSD ones. This lower accuracy is a consequence of the reduced flexibility in the model spaces, due to the need of adding the 5p-shell just below the 4f-shell to the intermediate space, in order to achieve convergence. These results are in line with the observations of Shee et al.,60 in that the formal equivalence between EOM-CCSD and IHFS-CCSD for the sectors of Fock space considered depends, in fact, on the flexibility of the main model space.
| State | Conf. | NIST74 | 2z | 3z | 4z | Extr. | DCB75 |
|---|---|---|---|---|---|---|---|
| 2S1/2 | 4f146s1 | 0 | 0 | 0 | 0 | 0 | 0 |
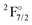
|
4f136s2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 419 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087 087 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 390 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618 618 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514 514 |
|
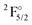
|
4f136s2 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568 568 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 631 631 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 976 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042 042 |
|
| 2D3/2 | 4f145d1 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058 058 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 223 223 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 059 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 720 |
| 2D5/2 | 4f145d1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 333 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 336 336 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 469 469 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 998 |
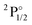
|
4f146p1 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062 062 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 518 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 851 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 870 |
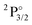
|
4f146p1 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 392 392 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934 934 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 316 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312 312 |
Furthermore, the removal of the 5p spinors from the main model space underscores the importance of the 5p for the energetics of the states with a hole in the 4f shell, since by doing so, we undress the contributions from the 5p configurations, and thus prevent them from interacting effectively with 4f13 determinants.
3.2 Kramers-restricted configuration interaction potential energy curves
In Fig. 1 the potential energy curves obtained by an approach corresponding to the one used for Yb+ are shown for f14 and f13 configurations. For separate potential energy curves and transition dipole moments we refer the interested reader to the ESI† (Fig. S2–S7).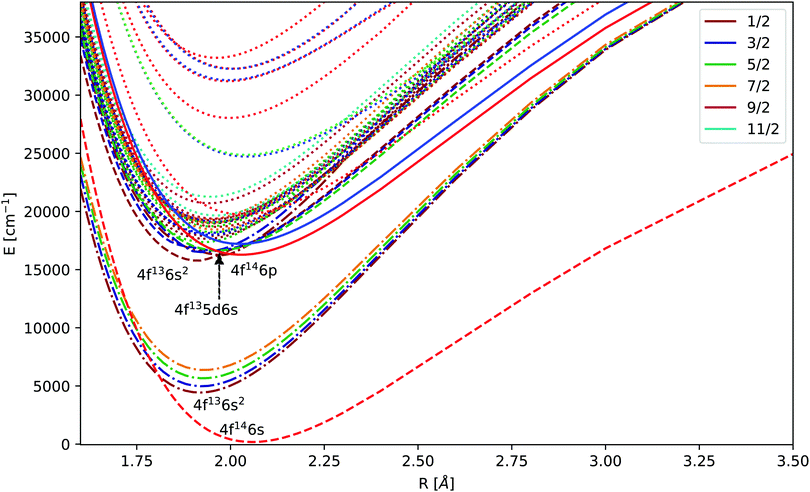 | ||
| Fig. 1 Combination of the sets of KRCI potentials obtained by extrapolating triple and quadruple zeta basis sets. The lowest Ω = 1/2 states are denoted by their dominant configuration. | ||
The potential energy curves have been determined up to 15 Å for the closed and open f-shells. The energy difference in the atom between these states is 21418.75 cm−1. Accordingly, the PECs for the hole states were shifted to obtain this separation at this distance. There is still some interaction between ytterbium and fluorine at 15 Å, but the long range behaviour can be expected to be similar for the two configurations (this assumption was checked, see Fig. S8 in the ESI,† for further details). Taking into account the position of the minima, the curvatures, spin–orbit splitting, the avoided crossings and asymptotes the states can be assigned to a dominant configuration, shown in Fig. 1.
Regarding the 4f14 manifold, the lowest two excited states in the figure belong to the Yb(4f146p1)F configuration, but approach asymptotically the 2D3/2 state. The asymptote of the next three states is 2D5/2 corresponding to the Yb(4f145d1)F configuration for smaller internuclear separations. For Ω = 5/2 the transition dipole moment with the ground state is zero, for the other four the values are shown in Fig. S3 in the ESI.† The first Ω = 3/2 and the third Ω = 1/2 state have a larger transition dipole moment close to equilibrium, but get close to each other at the largest internuclear separations.
Regarding states of the 4f13 manifold, the lowest four states belonging to the 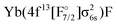 configuration are well separated from a dense region with a lot of states about 12
configuration are well separated from a dense region with a lot of states about 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 higher. Most of these states are of the
000 cm−1 higher. Most of these states are of the 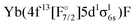 configuration, with the
configuration, with the 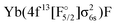 state slightly higher in energy asymptotically and more strongly bound, resulting in several avoided crossings. For each of the four
state slightly higher in energy asymptotically and more strongly bound, resulting in several avoided crossings. For each of the four 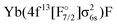 states the transition dipole moments with higher excited states of varying Ω are plotted in Fig. S6 in the ESI.† The transition dipole moments are substantially smaller than the ones for the closed 4f-shells but some of them are non-zero.
states the transition dipole moments with higher excited states of varying Ω are plotted in Fig. S6 in the ESI.† The transition dipole moments are substantially smaller than the ones for the closed 4f-shells but some of them are non-zero.
An alternative to AOC-SCF for obtaining orbitals for several configurations is multiconfigurational SCF, but similar difficulties as for AOC-SCF in obtaining a balanced description of the 4f14 and 4f13 states are observed: either the wrong ground state is obtained (if only the hole states are optimized in MCSCF), or the hole states are too high in energy by about 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (if the ground state is optimized). We also made attempts using state-averaged MCSCF in a non-relativistic quantum chemistry code and observed the same difficulties (see dataset67). If the 4f13 configurations are excluded one obtains meaningful results, but at the expense of obtaining a
000 cm−1 (if the ground state is optimized). We also made attempts using state-averaged MCSCF in a non-relativistic quantum chemistry code and observed the same difficulties (see dataset67). If the 4f13 configurations are excluded one obtains meaningful results, but at the expense of obtaining a 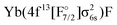 states too high in energy. If all the states are included, the wrong ground state is obtained.
states too high in energy. If all the states are included, the wrong ground state is obtained.
3.3 Coupled cluster potential energy curves
The potential energy curves of excited states obtained by the equation-of-motion and Fock space methods are displayed in Fig. 2, the values for the complete basis set limit are shown. The basis set dependence in the molecule is similar to the one observed for Yb+: energies for 4f14 states depend only weakly on the basis set, while the gap between the ground state and the excited states corresponding to the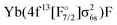 configuration increases upon improving the basis sets.
configuration increases upon improving the basis sets.
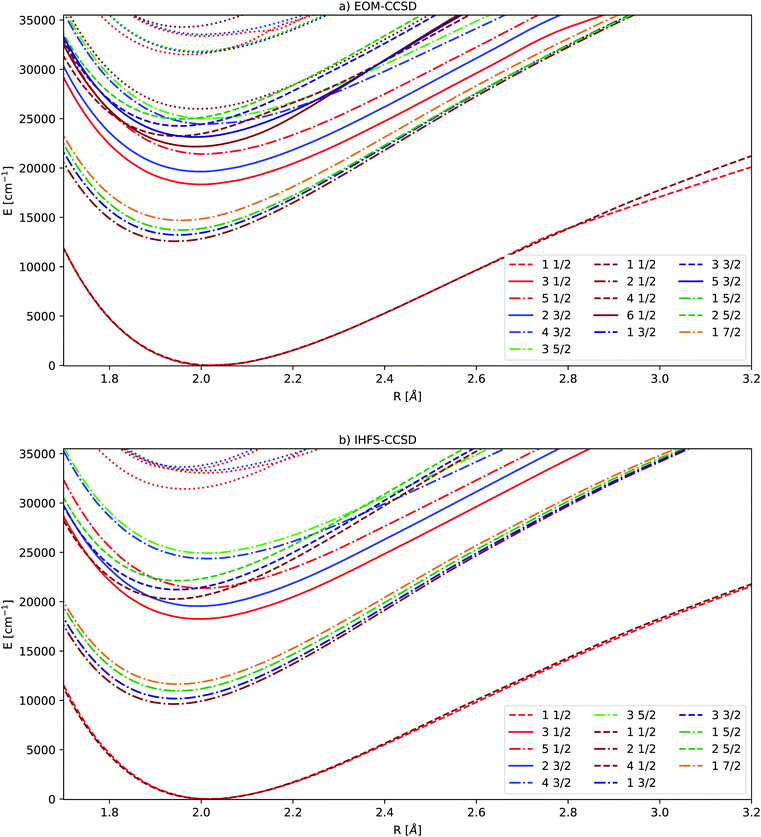 | ||
Fig. 2 Potential energy curves obtained by extrapolating triple and quadruple zeta basis sets. EOM-CCSD results in the upper part, IHFS-CCSD in the lower part. The Ω values of 1/2, 3/2, 5/2 and 7/2 are indicated by the colors red, blue, green and orange. The light colors are used for the (0h,1p) sector, dark ones for (1h,0p). For the states below 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 we employ the same color coding and state notation as in Fig. 1. 000 cm−1 we employ the same color coding and state notation as in Fig. 1. | ||
While the EOM-CCSD excitations energies of Yb+ are closer to the experimental ones, the 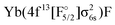 states are too high to perturb the Yb(4f146p1/5d1)F PECs. From the extended potential energy curves provided in the ESI† (Fig. S15 and S16), we can observe that the ground state of the non-interacting system (Yb(4f14σ26s)F(2p5)) is repulsive and has a high energy at the equilibrium distance. This results in several avoided crossings being observed at 3, 3.5, and 5 Å.
states are too high to perturb the Yb(4f146p1/5d1)F PECs. From the extended potential energy curves provided in the ESI† (Fig. S15 and S16), we can observe that the ground state of the non-interacting system (Yb(4f14σ26s)F(2p5)) is repulsive and has a high energy at the equilibrium distance. This results in several avoided crossings being observed at 3, 3.5, and 5 Å.
Since the Yb(4f14σ16s)F ground state is accessible for both sectors employed in the coupled cluster calculations (Fock space as well as EOM), we can assess the compatibility of the two separate sets of calculations (in the sense of having comparable accuracies) by looking more closely at the differences between the ground states in Fig. 2. From that, we can see that the EOM-CCSD and IHFS-CCSD approaches the curves are on top of each other from the smallest considered internuclear separation up to about 2.8 Å. This assures us that there should not be artifacts in putting together and comparing the calculations on the two sectors.
3.4 Dissociation and ionization energies
Since the (1h,0p) and (0h,1p) sectors have been considered in our EOM-CCSD and IHFS-CCSD calculations, we have as a by-product of our calculations the ionization potentials (IP) and electron affinities (EA) for YbF for all computed distances. Therefore these quantities are presented first in Table 4, before proceeding to the spectroscopic constants.| Quant. | System | KRCI | EOM-CCSD | IHFS-CCSD | Experiment | |||
|---|---|---|---|---|---|---|---|---|
| 4z | Extr. | 4z | Extr. | 4z | Extr. | |||
| IP | Yb | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406 406 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 128 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822 822 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837 837 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44374 44374 |
| IP2 | Yb | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 581 |
90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 926 926 |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 919 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 035 |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 918 918 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23274 23274 |
| IP | F | 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 131 131 |
126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617 617 |
144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
143![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321 321 |
144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703 703 |
140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52574 52574 |
| EA | F | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326 326 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 978 978 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 279 279 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 759 759 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43277 43277 |
| IP | YbF | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 478 478 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884 884 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 471 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578 578 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 426 426 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901 901 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70078 70078 |
| EA | YbF | 7423 | 7326 | 9713 | 9876 | 9579 | 8197 | |
| D e(IP) | YbF | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 059 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 887 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 824 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782 782 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 591 591 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931 931 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26079 26079 |
| D e(EA) | YbF | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 394 394 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534 534 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430 430 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26079 26079 |
Unlike coupled cluster calculations, for KRCI a consistent definition of active spaces is difficult, and its lack of size-consistency results in large deviations from experiment and from the coupled cluster values. For adiabatic electron affinities, for which to the best of our knowledge there are no experimental values, the extrapolated values are 8393 and 8197 cm−1 for EOM-CCSD and IHFS-CCSD, respectively. For a distance of 6.5 Å a value of 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651 cm−1 was obtained, which is reasonably close to the electron affinity of fluorine (27
651 cm−1 was obtained, which is reasonably close to the electron affinity of fluorine (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 432 cm−1).77 Corresponding results for the atoms are listed in the table, which allow to calculate the dissociation energies (De). They deviate from the experimental values of 43
432 cm−1).77 Corresponding results for the atoms are listed in the table, which allow to calculate the dissociation energies (De). They deviate from the experimental values of 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ± 800 cm−1 by Kaledin et al.78 and 43
600 ± 800 cm−1 by Kaledin et al.78 and 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 ± 800 cm−1 by Yokozeki and Menzinger.79 The ionization potentials in Table 4 show acceptable agreement with experimental values.
260 ± 800 cm−1 by Yokozeki and Menzinger.79 The ionization potentials in Table 4 show acceptable agreement with experimental values.
3.5 Spectroscopic constants
The spectroscopic constants for the ground state are now considered. In Table 5 our results are summarized, along those from the literature.| Method | Ref. | r e | ω e | ω e χ e | D e |
|---|---|---|---|---|---|
| KRCI | YbF | 2.0829 | 465 | 2.40 | 39 660 |
| EOM-CCSD | YbF+ | 2.0230 | 511 | 2.80 | 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
| YbF− | 2.0250 | 508 | 2.53 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782 782 |
|
| IHFS-CCSD | YbF+ | 2.0176 | 515 | 2.82 | 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
| YbF− | 2.0159 | 513 | 2.42 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931 931 |
|
| CCSD1 | YbF | 2.0174 | 507.6 | 2.357 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904 904 |
| CCSD(T)1 | YbF | 2.0289 | 528.2 | 1.939 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 156 |
| CCSD21 | 2.0127 | 566.8 | 3.7885 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 650 |
|
| RASCI6 | 2.051 | 529 | |||
| CCSD(T)80 | 2.03 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
|||
| CISD81 | 2.034 | 502 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
||
| DFT20 | 1.987 | 532 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||
| Exp.79 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
||||
| Exp.18 | 2.0158 | 506.6674 | 2.2452 | ||
| Exp.27 | 505.5 | 1.9 | |||
| Exp.78 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
||||
| Exp.30 | 2.016514 | ||||
| Exp.24 | 2.0195 | 506.616 | 2.235 | ||
We observe that the extrapolated KRCI bond distances, at about 2.058 Å, are significantly longer (by around 0.04 Å) than experiment,30 whereas the coupled cluster calculations show differences from experiment smaller than 0.01 Å, with EOM-CCSD showing slightly larger discrepancies than IHFS-CCSD. Between the extrapolated EOM-CCSD and IHFS-CCSD, we also see small differences between the 4f14 and 4f13 for EOM-CCSD these differ by around 0.001 Å whereas for IHFS-CCSD the difference is slightly under 0.002 Å, with the 4f13 configuration yielding a slightly underestimated value, compared to experiment, something that can be traced back to the differences in model spaces for this configuration.
Our results for harmonic frequencies further indicate that KRCI seems to underestimate the bonding strength in YbF, as the harmonic vibrational frequency is smaller (491 cm−1) than experiment (between 505.5 and 506.7 cm−1 depending on the experiment). The coupled cluster results, on the other hand, show the typical 5–6 cm−1 overestimation of the harmonic frequencies with respect to experiment (something also seen for the anharmonic constants), which can be attributed to lack of triples in the EOM or FS treatment, that would introduce further orbital relaxation. This can be seen in comparison to the unrestricted coupled cluster calculations of Gomes et al.,1 which in spite of the large value of the T1 diagnostic, reproduce well the experimental bond lengths, harmonic frequencies and anharmonic constants.
Taken together, our 2-component CCSD-based calculations and the 4-component ones of Gomes et al.1 compare consistently better to experiment than the other theoretical works for bond lengths, vibrational frequencies and anharmonic constants. For the dissociation energies, on the other hand, the extrapolated calculations presented here do not provide a significant improvement over the results of prior theoretical investigations (quadruple zeta values are closer to the experimental ones for this quantity, see Table 4). Especially, electron attachment values are off, which might be related to the absence of the configuration with a hole in the p orbitals of fluorine.
Moving now to excited states, we start by considering the four lowest excited states, which belong to the 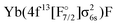 configuration. These states are well separated from the ground state (the lowest excited state is about 10
configuration. These states are well separated from the ground state (the lowest excited state is about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the ground state) and higher excited states. That such states are quite well separated from the ground state would, in our view, tend to exclude the interaction with a low-lying excited state as an explanation for the appearance of the large T1 diagnostic values observed by Gomes et al.1 From their spectroscopic constants, presented in Table 6, we see that with the exception of DFT all methods yield similar level splittings of about 500, 1200, and 2000 cm−1. To the best of the authors knowledge there is no experimental data available for these states, due to their negligible transition dipole moments for dipole excitations (see for instance Fig. S6 in the ESI†) and small Franck–Condon factors due to the difference in bond distances between these states and the ground state, see Section 3.6.
000 cm−1 above the ground state) and higher excited states. That such states are quite well separated from the ground state would, in our view, tend to exclude the interaction with a low-lying excited state as an explanation for the appearance of the large T1 diagnostic values observed by Gomes et al.1 From their spectroscopic constants, presented in Table 6, we see that with the exception of DFT all methods yield similar level splittings of about 500, 1200, and 2000 cm−1. To the best of the authors knowledge there is no experimental data available for these states, due to their negligible transition dipole moments for dipole excitations (see for instance Fig. S6 in the ESI†) and small Franck–Condon factors due to the difference in bond distances between these states and the ground state, see Section 3.6.
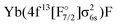 for different wave function methods using the potential energy curves extrapolated to the basis set limit. In the case of KRCI and MRCI19 the ground state is not included in the computation and absolute transition energies are not available. The transition energy (Te), level splitting (Trel, energy relative to 21/2), harmonic frequencies (ωe) and anharmonicity constants (ωeχe) are given in cm−1, the equilibrium bond distances (re) in Å
for different wave function methods using the potential energy curves extrapolated to the basis set limit. In the case of KRCI and MRCI19 the ground state is not included in the computation and absolute transition energies are not available. The transition energy (Te), level splitting (Trel, energy relative to 21/2), harmonic frequencies (ωe) and anharmonicity constants (ωeχe) are given in cm−1, the equilibrium bond distances (re) in Å
| State | Method | T e | r e | ω e | ω e χ e | T rel |
|---|---|---|---|---|---|---|
| 21/2 | KRCI | 1.9200 | 631 | 2.51 | ||
| EOM-CCSD | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568 568 |
1.9432 | 591 | 2.59 | ||
| IHFS-CCSD | 9627 | 1.9396 | 599 | 2.79 | ||
| DFT20 | 3790 | 1.9570 | 561 | |||
| MRCI19 | 1.9480 | 600 | ||||
| 13/2 | KRCI | 1.9253 | 628 | 2.50 | 540 | |
| EOM-CCSD | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211 211 |
1.9494 | 588 | 2.61 | 643 | |
| IHFS-CCSD | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
1.9438 | 595 | 2.79 | 553 | |
| DFT20 | 9520 | 1.9440 | 597 | 5730 | ||
| MRCI19 | 1.951 0 | 598 | 428 | |||
| 15/2 | KRCI | 1.9296 | 622 | 2.45 | 1223 | |
| EOM-CCSD | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703 703 |
1.9553 | 582 | 2.61 | 1135 | |
| IHFS-CCSD | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 968 968 |
1.9493 | 589 | 2.78 | 1341 | |
| DFT20 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970 970 |
1.9360 | 598 | 7180 | ||
| MRCI19 | 1.9540 | 594 | 1021 | |||
| 17/2 | KRCI | 1.9315 | 616 | 2.43 | 1933 | |
| EOM-CCSD | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 685 |
1.9556 | 577 | 2.62 | 2117 | |
| IHFS-CCSD | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 645 |
1.9496 | 583 | 2.77 | 2018 | |
| DFT20 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 530 |
1.936 | 592 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
||
| MRCI19 | 1.954 | 589 | 1709 |
The smallest equilibrium distance was obtained for the 21/2 state with 1.94 Å for the coupled cluster methods and 0.02 Å less for KRCI. The vibrational frequencies are between 570 and 600 cm−1 for the coupled cluster methods and about 30 cm−1 higher for KRCI.
For higher excited states, as apparent from the figures in the previous section, the identification and assignment of states gets more difficult and there are differences between the methods. We have nevertheless provided in Table 7 the spectroscopic constants for excited with Ω values of 1/2, 3/2, and 5/2, respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for different methods using the values after extrapolation to the basis set limit. Transition energy (Te), vibrational constant (ωe), and anharmonicty constant (ωeχe) are given in cm−1, the equilibrium bond distance (re) in Å. Experimental transitions that were not assigned (n.a.) are also listed. Labels of experimental results are defined in the introduction
000 cm−1 for different methods using the values after extrapolation to the basis set limit. Transition energy (Te), vibrational constant (ωe), and anharmonicty constant (ωeχe) are given in cm−1, the equilibrium bond distance (re) in Å. Experimental transitions that were not assigned (n.a.) are also listed. Labels of experimental results are defined in the introduction
| Ω | Method | State | Configuration | T e | r e | ω e | ω e χ e |
|---|---|---|---|---|---|---|---|
| a KRCI transition energies for the 4f13 sector were obtained by adding 4144 cm−1, an estimate for the energy of the lowest state in this manifold. | |||||||
| 1/2 | KRCIa | 3 | 4f13σ26s | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 572 |
1.9038 | 655 | 13.57 |
| 5 | 4f146p1 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 189 189 |
2.0504 | 496 | 2.38 | ||
| 10 | 4f145d1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 631 631 |
2.0552 | 490 | 2.49 | ||
| EOM-CCSD | 3 | 4f146p1 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 373 373 |
2.0004 | 536 | 2.72 | |
| 4 | 4f145d1 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 448 |
2.0079 | 532 | 2.78 | ||
| 6 | 4f13σ26s | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
1.9432 | 582 | 4.06 | ||
| IHFS-CCSD | 3 | 4f146p1 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249 249 |
1.9953 | 539 | 2.63 | |
| 4 | 4f13σ26s | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267 267 |
1.9397 | 597 | 2.78 | ||
| 5 | 4f145d1 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 375 |
2.0032 | 533 | 2.73 | ||
| MRCI19 | 4f13σ26s | 1.948 | 600 | ||||
Exp.18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
3 | 18106.20 | 537 | 3 | |||
| Exp.18 | 4 | [18.6]1/2 | 18705.06 | ||||
| Exp.24 | [557] | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 574 574 |
1.9656 | 502.15 | |||
| Exp.24 | [561] | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 699 699 |
1.9571 | ||||
| 3/2 | KRCIa | 2 | 4f13σ26s | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 206 206 |
1.9331 | 711 | 8.45 |
| 4 | 4f146p1 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 123 |
2.0473 | 499 | 2.37 | ||
| >7 | 4f145d1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583 583 |
2.0669 | 470 | 2.50 | ||
| EOM-CCSD | 2 | 4f146p1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 672 |
1.9971 | 540 | 2.72 | |
| 4 | 4f13σ26s | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 251 251 |
1.9537 | 584 | 2.64 | ||
| 5 | 4f145d1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 468 468 |
2.0177 | 509 | 2.78 | ||
| IHFS-CCSD | 2 | 4f146p1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543 543 |
1.9920 | 542 | 2.63 | |
| 3 | 4f13σ26s | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222 |
1.9480 | 591 | 2.80 | ||
| 4 | 4f145d1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 363 363 |
2.0120 | 512 | 2.73 | ||
| MRCI19 | 4f13σ26s | 1.953 | 596 | ||||
| Exp.18 | 2 | 19471.49 | |||||
| 5/2 | KRCIa | 3 | 4f13σ26s | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 063 |
1.9302 | 635 | 1.41 |
| >6 | 4f145d1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 744 744 |
2.0639 | 474 | 2.48 | ||
| EOM-CCSD | 2 | 4f13σ26s | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957 957 |
1.9536 | 577 | 2.62 | |
| 3 | 4f145d1 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023 023 |
2.0146 | 513 | 2.80 | ||
| IHFS-CCSD | 2 | 4f13σ26s | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 127 |
1.9499 | 584 | 2.77 | |
| 3 | 4f145d1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 919 |
2.0089 | 515 | 2.77 | ||
| MRCI19 | 4f13σ26s | 1.954 | 590 | ||||
| n.a. | Exp.26 | [574] | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150 |
||||
| Exp.26 | [578] | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280 |
|||||
| Exp.27 | C1 | 23035.3 | 523 | 2 | |||
| Exp.27 | C2 | 23256.0 | 507 | 2 | |||
| Exp.27 | D | 26014.8 | 574.6 | 2.8 | |||
The comparison with experimental results allows assignment of the lowest excited state reported in experiments and give some indications for higher states. The lowest Ω = 1/2 state observed in experiment can be identified as the 31/2 state (51/2 for KRCI). Spectroscopic parameters agree well with the ones obtained by fitting to the A2Π1/2 in experiments. A bond distance of 1.9935 Å obtained by fitting to the same states in ref. 34 agrees well with the coupled cluster values for the 31/2 state, the vibrational constant of about 540 cm−1 is close to the experimental value of ref. 18. Similarly, the lowest Ω = 3/2 state reported by Dunfield et al.18 can be identified as the 23/2 state (43/2 for KRCI), see Table 7.
The lowest states with Ω = 1/2 and Ω = 3/2 for this energy range approach asymptotically a state with a Yb(4f145d1)F configuration, but if one analyses the EOM-CCSD and IHFS-CCSD orbital composition, significant contributions of the atomic 6p are identified. The Ω = 3/2 state is dominated (97%) by a single configuration, corresponding to a HOMO(σ6s,1/2) → LUMO+1 where the latter is made up of a mixture of 6pπ and 5dπ orbitals (the 6pπ contributions being the dominant − ≃80% – in the reference YbF+ orbitals). The few other significant configurations arise from excitations to higher-lying orbitals with increasingly large (≥50% 5dπ) contributions. The Π1/2 state is also dominated by a single configuration, now corresponding to a HOMO(σ1/2) → LUMO transition, and shows a rather similar picture in terms of the relative weights of the 6pπ and 5dπ orbitals, with very small contributions from the ground-state mixing due to spin–orbit coupling. The splitting in Yb+ of 2D3/2 and 2D5/2 is 1372 cm−1, for 2P1/2 and 2P3/2 it is 3330 cm−1. The separation between the lowest excited Ω = 1/2 states in the closed shell computation is 3779 and 3126 cm−1 for EOM-CCSD and IHFS-CCSD, respectively. This is an indication that the two states must be regarded as a fairly strong admixture of 6p and 5d orbitals of j = 1/2 or 3/2, as one can expect a much smaller spin–orbit splitting in the axial field of the molecule (about 1/3 of the atomic spin–orbit splitting for the P state). This picture also finds experimental support in recent measurements of hyperfine constants (d and eq0Q) for the ground and Π1/2 excited state of YbF9, where a simple ligand-field model disregarding the contributions from 5dπ orbitals predicted values of d a factor of 2 larger than the measurements. For bond distances much larger that the equilibrium one the system gets closer to the configurations in Yb+ with a dominating 5d contribution.
As already mentioned this energy range above 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 is dense with a large number of excited states that can mix with each other and result in new mixed states, like the [557] and [561] ones.24 These will be addressed in Section 3.6.
000 cm−1 is dense with a large number of excited states that can mix with each other and result in new mixed states, like the [557] and [561] ones.24 These will be addressed in Section 3.6.
Uttam et al.27 reported three unidentified states with energies above 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 which are listed in Table 7 and cannot uniquely be identified with the current results. The one at 26014.8 cm−1 has a larger vibrational constant indicating a more strongly bound state, possibly of the 4f13σ26s configuration. The vibrational spacing of the two states at 23
000 cm−1 which are listed in Table 7 and cannot uniquely be identified with the current results. The one at 26014.8 cm−1 has a larger vibrational constant indicating a more strongly bound state, possibly of the 4f13σ26s configuration. The vibrational spacing of the two states at 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 rather points to states with a closed f shell.
000 cm−1 rather points to states with a closed f shell.
3.6 Perturbation of the 31/2 excited state
Due to the use of different sectors of Fock space to obtain the 4f14 and 4f13 configurations, the excited states with the same Ω values cannot interact among themselves, as is the case within each sector. However, from the discussion above, it is clear that dealing with states which are artificially prevented from interaction makes it difficult to establish a comparison to experiment, for states from about 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to about 26
000 cm−1 to about 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which is where these configurations should be the most entangled. In order to remedy that, in the following we introduce a simple adiabatization model (eqn (2)) that allows us to investigate how coupling such states would affect the overall spectra in the aforementioned energy region.
000 cm−1, which is where these configurations should be the most entangled. In order to remedy that, in the following we introduce a simple adiabatization model (eqn (2)) that allows us to investigate how coupling such states would affect the overall spectra in the aforementioned energy region.
In the following we only consider the IHFS-CCSD potential energy curves, as the spectroscopic parameters are more reliable for CCSD than for KRCI. The coupled cluster results for the two methods are quite similar, and FS-CCSD was selected (because it does not include the (2h,1p) and (1h,2p) transitions with rather large uncertainties). Fig. 3 contains the original FS-CCSD curves as well as the ones obtained after adiabatzation with three different coupling constants. Looking at the potential energy curves for this energetic region, there are two Ω = 1/2 and two Ω = 3/2 states of Yb(4f146p1)F and Yb(4f145d1)F configurations originating from the (0h,1p) sector. For both Ω values there is an additional state with a 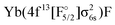 configuration stemming from the (1h,0p) sector. By looking at the KRCI results one expects additional states belonging to the
configuration stemming from the (1h,0p) sector. By looking at the KRCI results one expects additional states belonging to the 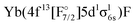 configuration for this energy range, which will not be included in the current considerations.
configuration for this energy range, which will not be included in the current considerations.
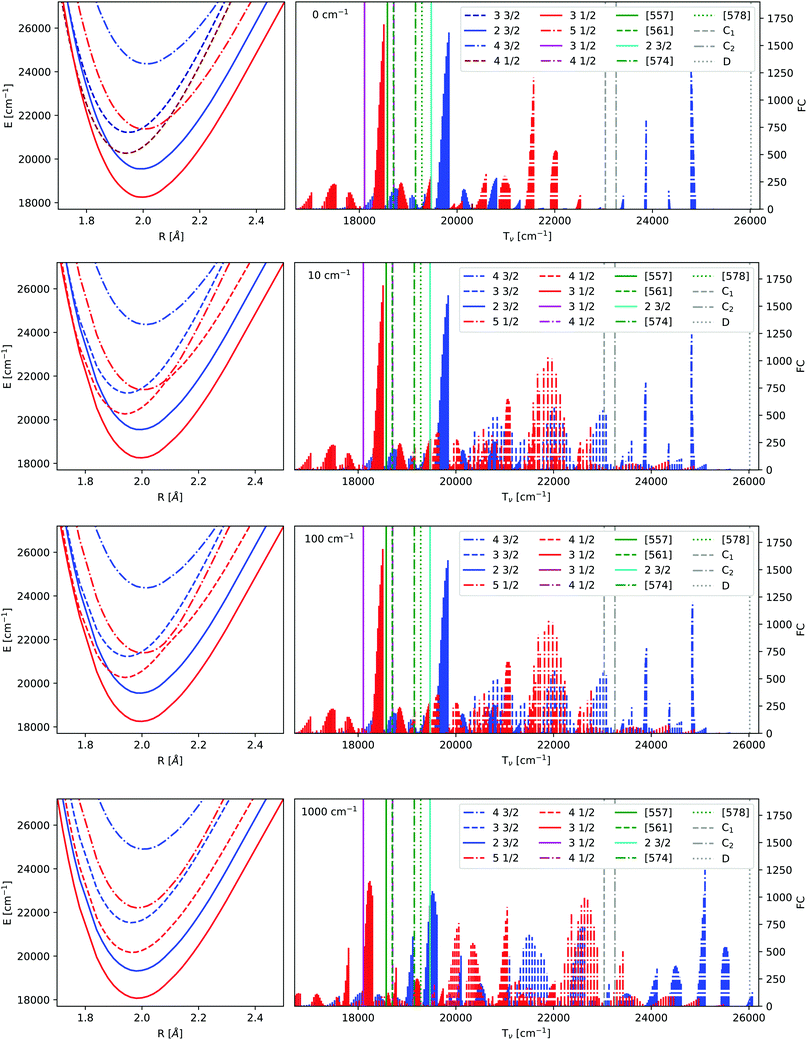 | ||
| Fig. 3 Frank-Condon factors before and after adiabatization for the IHFS-CCSD potential energy curves. C is the coupling strength in Hartree. The lowest 10 vibrational levels of the ground state as well as the lowest 60 vibrational levels of the excited state were computed using the LEVEL program.82 The experimental values18,24,26 have been added as straight lines, the labels are defined in the introduction and Table 7. | ||
As already mentioned earlier the lowest Ω = 1/2 and Ω = 3/2 states can be identified clearly and assigned to experimental observations. There are several experimental states in this energy region attributed to the mixing of states. The [557] and [561] ones24 are assumed to arise from a mixing of the 31/2 and 41/2. The vibrational constant of the perturbing state (41/2) was estimated to be 605 cm−1 in ref. 18. This agrees with the 41/2 state in Fig. 3 with a 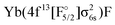 configuration, see also Table 7. [574] and [578]26 have not been identified and since their Ω value is unknown, we were not able to assign them to a configuration.
configuration, see also Table 7. [574] and [578]26 have not been identified and since their Ω value is unknown, we were not able to assign them to a configuration.
Next we take a look at the changes introduced by adiabatization. For small and intermediate coupling strengths there are no major differences in the potential energy curves, although close to the crossing points the potentials are deformed. Intermediate coupling strengths with slightly deformed potentials close to the avoided crossings will be the most realistic description. For very large coupling strengths one obtains parallel potential energy curves due to the strong repulsion. This also results in a major change of the spectra above 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. One of the differences between the adiabatic spectrum and the upermost one in Fig. 3 is that the Frank-Condon factors of the 41/2 state, which is of the Yb(4f13σ26s)F configuration, are now noticeable and the spacing of the energy levels of the 51/2 is changed. Similarly, transitions belonging to the 51/2 appear.
000 cm−1. One of the differences between the adiabatic spectrum and the upermost one in Fig. 3 is that the Frank-Condon factors of the 41/2 state, which is of the Yb(4f13σ26s)F configuration, are now noticeable and the spacing of the energy levels of the 51/2 is changed. Similarly, transitions belonging to the 51/2 appear.
The influence of adiabatization on spectroscopic parameters can be investigated by comparing spectroscopic constants calculated for the IHFS-CCSD curves without and with a coupling of 100 cm−1 (Table 8). We observe that for this coupling strength, there are small but non-negligible changes for the excitation energies, harmonic frequencies and anharmonicity constants, for all but the fourth and fifth Ω = 1/2 states; there, the coupling does seem to significantly change the anharmonicity constants. Equilibrium distances, on the other hand, are largely unperturbed in all cases. Furthermore, as expected from the preceding discussion, no changes are observed for the ground-state, since it is too separated in energy from the other electronic states.
| Ω | CBS | C = 100 cm−1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| State | r e | ω e | ω e χ e | T e | State | r e | ω e | ω e χ e | T e | |
| 1/2 | f14 – 1 | 2.018 | 515 | 2.9 | 0 | 1 | 2.018 | 515 | 2.8 | 0 |
| f13 – 2 | 1.940 | 599 | 2.8 | 9627 | 2 | 1.940 | 599 | 2.8 | 9617 | |
| f14 – 2 | 1.995 | 539 | 2.6 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249 249 |
3 | 1.995 | 538 | 2.6 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 247 247 |
|
| f13 – 3 | 1.940 | 597 | 2.8 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267 267 |
4 | 1.935 | 603 | 8.6 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258 258 |
|
| f14 – 3 | 2.003 | 533 | 2.7 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 375 |
5 | 2.002 | 586 | 0.4 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 359 359 |
|
| f14 – 4 | 1.964 | 581 | 1.8 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416 416 |
6 | 1.964 | 581 | 1.8 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 419 |
|
| 3/2 | f13 – 1 | 1.944 | 595 | 2.8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
1 | 1.944 | 594 | 2.8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
| f14 – 1 | 1.992 | 542 | 2.6 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543 543 |
2 | 1.992 | 542 | 2.6 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540 540 |
|
| f13 – 2 | 1.948 | 591 | 2.8 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222 |
3 | 1.948 | 591 | 2.8 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 217 |
|
| f14 – 2 | 2.012 | 512 | 2.7 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 363 363 |
4 | 2.012 | 512 | 2.7 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369 369 |
|
| 5/2 | f13 – 1 | 1.949 | 589 | 2.8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
1 | 1.949 | 589 | 2.8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
| f13 – 2 | 1.950 | 584 | 2.8 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 127 |
2 | 1.950 | 583 | 2.8 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117 117 |
|
| f14 – 1 | 2.009 | 515 | 2.8 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 919 |
3 | 2.009 | 516 | 2.7 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 926 926 |
|
4 Conclusion
In this manuscript we have presented a study of the ground and excited states of the YbF molecule, with 2-component multireference CI, equation-of-motion and Fock space coupled cluster approaches (in all cases, performing extrapolations to the complete basis set limit). In particular, we have focused on obtaining electronic states up to around 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 arising from configurations which differ in the occupation of the 4f shell (4f14 and 4f13), which are very difficult to treat on the same footing due to a number of subtle correlation and relaxation effects.
000 cm−1 arising from configurations which differ in the occupation of the 4f shell (4f14 and 4f13), which are very difficult to treat on the same footing due to a number of subtle correlation and relaxation effects.
In order to achieve such a balanced description, our strategy consisted of starting from YbF+ and YbF−, in order to arrive at the wavefunctions for YbF through the (1h,0p) and (0h,1p) sectors of Fock space. Once obtained, electronic states with same Ω values coming from these different sectors are further coupled through a simple adiabatization model in which the coupling strength is taken as a constant.
As a general rule we find that the CI calculations do capture the essential physics of the system, though they are not as reliable as the coupled cluster approaches for excitation energies, bond lengths, harmonic vibrational frequencies and anharmonic constants. In effect, the coupled cluster calculations for the (1h,0p) and (0h,1p) sectors yield the same potential energy curves for the ground state, for internuclear distances up to around 2.8 Å, which is sufficient to capture the bound regions of all states under consideration,
We have determined that the lowest lying excited states arise from the 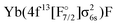 configuration, with transition energies of around 10
configuration, with transition energies of around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, and a splitting about 2000 cm−1. These states are, however, not generally accessible in experiment due to their low dipolar intensity and significantly shifted minima of the potential energy curve resulting in small Frank-Condon factors.
000 cm−1, and a splitting about 2000 cm−1. These states are, however, not generally accessible in experiment due to their low dipolar intensity and significantly shifted minima of the potential energy curve resulting in small Frank-Condon factors.
The next set of states, coming above 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, arise from the Yb(4f146p1)F, Yb(4f145d1)F,
000 cm−1, arise from the Yb(4f146p1)F, Yb(4f145d1)F,  and
and 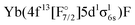 configurations. Among these, the
configurations. Among these, the 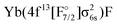 configurations generally display the shortest equilibrium distances and deepest potential well, while the Yb(4f145d1)F and Yb(4f146p1)F configurations exhibits the largest bond distances and smallest harmonic frequencies, with the other configurations falling somewhere in between. The lowest Ω = 1/2 and Ω = 3/2 states of this group show a Yb(4f146p1)F orbital composition around the ground-state equilibrium structure, though for longer bond lengths they asymptotically approach the Yb(4f145d1)F configuration.
configurations generally display the shortest equilibrium distances and deepest potential well, while the Yb(4f145d1)F and Yb(4f146p1)F configurations exhibits the largest bond distances and smallest harmonic frequencies, with the other configurations falling somewhere in between. The lowest Ω = 1/2 and Ω = 3/2 states of this group show a Yb(4f146p1)F orbital composition around the ground-state equilibrium structure, though for longer bond lengths they asymptotically approach the Yb(4f145d1)F configuration.
We note that configurations with three unpaired electrons, such as 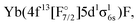 were only considered with the KRCI method, which has larger uncertainties. This only allows us to make some qualitative statements, e.g. that their bond distances and vibrational constant should be between the values for the other configurations and that they should be higher in energy than the lowes excited Yb(4f146p1)F and
were only considered with the KRCI method, which has larger uncertainties. This only allows us to make some qualitative statements, e.g. that their bond distances and vibrational constant should be between the values for the other configurations and that they should be higher in energy than the lowes excited Yb(4f146p1)F and 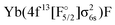 states.
states.
A simple method was applied in order to adiabatize the curves obtained for different sectors and reference wave functions. It was applied to potential energy curves between 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 26
000 and 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and small changes of the Franck–Condon factors were observed. The influence on spectroscopic constant was minor, with the exception of the asymmetry constant for two states. However, the approximation introduced (same coupling strength for all states and all geometries) is perhaps not flexible enough, and more sophisticated models should be investigated.
000 cm−1 and small changes of the Franck–Condon factors were observed. The influence on spectroscopic constant was minor, with the exception of the asymmetry constant for two states. However, the approximation introduced (same coupling strength for all states and all geometries) is perhaps not flexible enough, and more sophisticated models should be investigated.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. V. and J. V. P. wish to thank The Netherlands Organization for Scientific Research (NWO) for financial support via the ECHO and computer time. J. V. P. acknowledges funding by the Austrian Science Fund (FWF):J 4177-N36. ASPG acknowledges support from PIA ANR project CaPPA (ANR-11-LABX-0005-01), the Franco-German project CompRIXS (Agence nationale de la recherche ANR-19-CE29-0019, Deutsche Forschungsgemeinschaft JA 2329/6-1), I-SITE ULNE projects OVERSEE, the French Ministry of Higher Education and Research, region Hauts de France council and European Regional Development Fund (ERDF) project CPER CLIMIBIO, and the French national supercomputing facilities (grants DARI A0070801859 and A0090801859). A. S. P. G., L. H., J. P. and L. V. acknowledge support from MESONM International Associated Laboratory (LAI) (ANR-16-IDEX-0004).References
- A. S. P. Gomes, K. G. Dyall and L. Visscher, Theor. Chem. Acc., 2010, 127, 369–381 Search PubMed.
- J. Sapirstein, in Theoretical and Computational Chemistry, ed. P. Schwerdtfeger, Elsevier, 2002, vol. 11, pp. 468–522 Search PubMed.
- R. Berger, in Theoretical and Computational Chemistry, ed. P. Schwerdtfeger, Elsevier, 2004, vol. 14, pp. 188–288 Search PubMed.
- A. Sunaga, M. Abe, M. Hada and B. P. Das, Phys. Rev. A, 2016, 93, 042507 CrossRef.
- F. A. Parpia, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, 1409–1430 CrossRef CAS.
- M. K. Nayak and R. K. Chaudhuri, Chem. Phys. Lett., 2006, 419, 191–194 CrossRef CAS.
- A. V. Titov, N. S. Mosyagin, A. N. Petrov and T. A. Isaev, Int. J. Quantum Chem., 2005, 104, 223–239 CrossRef CAS.
- J. J. Hudson, B. E. Sauer, M. R. Tarbutt and E. A. Hinds, Phys. Rev. Lett., 2002, 89, 023003 CrossRef CAS PubMed.
- T. C. Steimle, T. M. Ma and C. Linton, J. Chem. Phys., 2007, 127, 234316 CrossRef PubMed.
- M. Fukuda, K. Soga, M. Senami and A. Tachibana, Phys. Rev. A, 2016, 93, 012518 CrossRef.
- N. J. Fitch, J. Lim, E. A. Hinds, B. E. Sauer and M. R. Tarbutt, Quantum Sci. Technol., 2020, 6, 014006 CrossRef.
- Y. Takasu, K. Maki, K. Komori, T. Takano, K. Honda, M. Kumakura, T. Yabuzaki and Y. Takahashi, PRL, 2003, 91, 040404 CrossRef PubMed.
- T. Fukuhara, S. Sugawa, Y. Takasu and Y. Takahashi, PRA, 2009, 79, 021601 CrossRef.
- P. Tecmer, K. Boguslawski, M. Borkowski, P. S. Żuchowski and D. Kedziera, Int. J. Quantum Chem., 2019, 119, e25983 CrossRef.
- K. Tsigutkin, D. Dounas-Frazer, A. Family, J. E. Stalnaker, V. V. Yashchuk and D. Budker, PRL, 2009, 103, 071601 CrossRef CAS PubMed.
- L. F. Pasteka, R. J. Mawhorter and P. Schwerdtfeger, Mol. Phys., 2016, 114, 1110–1117 CrossRef CAS.
- K. Huber and G. Herzberg, in Constants of Diatomic Molecules, National Institute of Standards and Technology, ed. P. J. Linstrom and W. G. Mallard, Gaithersburg MD, 20899, 2005, (data prepared by J.W. Gallagher and R.D. Johnson, III) in NIST Chemistry WebBook, NIST Standard Reference Database, Number 69 Search PubMed.
- K. L. Dunfield, C. Linton, T. E. Clarke, J. McBride, A. G. Adam and J. R. D. Peers, J. Mol. Spectrosc., 1995, 174, 433–445 CrossRef CAS.
- M. Dolg, H. Stoll and H. Preuss, Chem. Phys., 1992, 165, 21–30 CrossRef CAS.
- W. Liu, M. Dolg and L. Li, J. Chem. Phys., 1998, 108, 2886–2895 CrossRef CAS.
- T. Su, C. L. Yang, X. Q. Wang, F. J. Bai and M. S. Wang, Chem. Phys. Lett., 2009, 467, 265–269 CrossRef CAS.
- Z. Glassman, R. Mawhorter, J. U. Grabow, A. Le and T. C. Steimle, J. Mol. Spectrosc., 2014, 300, 7–11 CrossRef CAS.
- B. E. Sauer, S. B. Cahn, M. G. Kozlov, G. D. Redgrave and E. A. Hinds, J. Chem. Phys., 1999, 110, 8424–8428 CrossRef CAS.
- J. Lim, J. R. Almond, M. R. Tarbutt, D. T. Nguyen and T. C. Steimle, J. Mol. Spectrosc., 2017, 338, 81–90 CrossRef CAS.
- J. Lim, J. R. Almond, M. A. Trigatzis, J. A. Devlin, N. J. Fitch, B. E. Sauer, M. R. Tarbutt and E. A. Hinds, Phys. Rev. Lett., 2018, 120, 123201 CrossRef CAS PubMed.
- I. J. Smallman, F. Wang, T. C. Steimle, M. R. Tarbutt and E. A. Hinds, Spectroscopic Tests of Fundamental Physics, 2014, 300, 3–6 CAS.
- K. N. Uttam and M. M. Joshi, J. Mol. Spectrosc., 1995, 174, 290–296 CrossRef CAS.
- H. U. Lee and R. N. Zare, J. Mol. Spectrosc., 1977, 64, 233–243 CrossRef.
- V. A. Dzuba and A. Derevianko, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 074011 CrossRef.
- C. S. Dickinson, J. A. Coxon, N. R. Walker and M. C. L. Gerry, J. Chem. Phys., 2001, 115, 6979–6989 CrossRef CAS.
- T. C. Steimle, T. M. Ma and C. Linton, J. Chem. Phys., 2008, 128, 209903 CrossRef.
- T. C. Steimle, T. M. Ma and C. Linton, J. Chem. Phys., 2012, 137, 109901 CrossRef.
- H. Wang, A. T. Le, T. C. Steimle, E. A. C. Koskelo, G. Aufderheide, R. Mawhorter and J.-U. Grabow, Phys. Rev. A, 2019, 100, 022516 CrossRef CAS.
- T. Ma, C. Butler, J. M. Brown, C. Linton and T. C. Steimle, J. Phys. Chem. A, 2009, 113, 8038–8044 CrossRef CAS PubMed.
- S. G. Porsev, Y. G. Rakhlina and M. G. Kozlov, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 1113–1120 CrossRef CAS.
- B. K. Mani and D. Angom, PRA, 2011, 83, 012501 CrossRef.
- M. K. Nayak and R. K. Chaudhuri, Eur. Phys. J. D, 2006, 37, 171–176 CrossRef CAS.
- D. Naik, M. Sikarwar, M. K. Nayak and S. K. Ghosh, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 225103 CrossRef.
- P. A. B. Haase, E. Eliav, M. Iliaš and A. Borschevsky, J. Phys. Chem. A, 2020, 124, 3157–3169 CrossRef CAS PubMed.
- V. Vallet, L. Maron, C. Teichteil and J.-P. Flament, J. Chem. Phys., 2000, 113, 1391–1402 CrossRef CAS.
- C. M. Marian, Spin-Orbit Coupling in Molecules, John Wiley & Sons, Ltd, 2001, ch. 3, pp. 99–204 Search PubMed.
- C. Danilo, V. Vallet, J.-P. Flament and U. Wahlgren, Phys. Chem. Chem. Phys., 2010, 12, 1116–1130 RSC.
- A. Farhat and S. N. Abdul-Al, J. Comput. Chem., 2015, 36, 1252–1258 CrossRef CAS PubMed.
- W. Chmaisani and M. Korek, J. Quant. Spectrosc. Radiat. Transfer, 2018, 217, 63–72 CrossRef CAS.
- W. Chmaisani, N. El-Kork, S. Elmoussaoui and M. Korek, ACS Omega, 2019, 4, 14987–14995 CrossRef CAS PubMed.
- S. Kervazo, F. Réal, F. Virot, A. Severo Pereira Gomes and V. Vallet, Inorg. Chem., 2019, 58, 14507–14521 CrossRef CAS PubMed.
- W. Liu, J. Chem. Phys., 2020, 152, 180901 CrossRef CAS PubMed.
- M. K. Nayak and R. K. Chaudhuri, Pramana J. Phys., 2009, 73, 581–586 CrossRef CAS.
- M. K. Nayak and R. K. Chaudhuri, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 022504 CrossRef.
- H. J. A. Jensen, 2005, Douglas-Kroll the Easy Way, Talk at Conference on Relativistic Effects in Heavy Elements - REHE, Mülheim, Germany, April, 2005. Available at DOI:10.6084/m9.figshare.12046158.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- W. Liu and D. Peng, J. Chem. Phys., 2006, 125, 044102 CrossRef PubMed.
- D. Peng, W. Liu, Y. Xiao and L. Cheng, J. Chem. Phys., 2007, 127, 104106 CrossRef PubMed.
- M. Ilias and T. Saue, J. Chem. Phys., 2007, 126, 064102 CrossRef PubMed.
- J. Sikkema, L. Visscher, T. Saue and M. Iliaš, J. Chem. Phys., 2009, 131, 124116 CrossRef PubMed.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104 CrossRef PubMed.
- L. Konecny, M. Kadek, S. Komorovsky, O. L. Malkina, K. Ruud and M. Repisky, J. Chem. Theory Comput., 2016, 12, 5823–5833 CrossRef CAS PubMed.
- B. A. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef CAS.
- B. Schimmelpfennig, AMFI, an atomic mean-field spin–orbit integral program, University of Stockholm, Stockholm, Sweden, 1999 Search PubMed.
- A. Shee, T. Saue, L. Visscher and A. Severo Pereira Gomes, J. Chem. Phys., 2018, 149, 174113 CrossRef PubMed.
- L. Halbert, M. Lopez Vidal, A. Shee, S. Coriani and A. S. P. Gomes, J. Chem. Theory Comput., 2021, 17, 3583–3598 CrossRef CAS PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- T. Saue, L. Visscher, H. J. A. Jensen, R. Bast and A. S. P. Gomes, DIRAC, a relativistic ab initio electronic structure program, 2019, with new contributions from R. Bast, S. Dubillard, K. G. Dyall, U. Ekström, E. Eliav, T. Fleig, A. S. P. Gomes, T. U. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, P. Norman, J. Olsen, M. Pernpointner, K. Ruud, P. Sałek and J. Sikkema; see http://www.diracprogram.org.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- T. Helgaker, P. Joergensen and J. Olsen, Molecular Electronic-Structure Theory, John Wiley & Sons, 2000 Search PubMed.
- L. Visscher, Theor. Chem. Acc., 1997, 98, 68–70 Search PubMed.
- J. V. Pototschnig, K. G. Dyall, L. Visscher and A. Severo Pereira Gomes, Dataset: Electronic Spectra of Ytterbium Fluoride from Relativistic Electronic Structure Calculations, 2021 DOI:10.5281/zenodo.5121372.
- J. Thyssen, PhD thesis, University of Southern Denmark, 2001.
- T. Fleig, H. J. A. Jensen, J. Olsen and L. Visscher, J. Chem. Phys., 2006, 124, 104106 CrossRef PubMed.
- L. Visscher, E. Eliav and U. Kaldor, J. Chem. Phys., 2001, 115, 9720–9726 CrossRef CAS.
- A. Landau, E. Eliav, Y. Ishikawa and U. Kaldor, J. Chem. Phys., 2000, 113, 9905–9910 CrossRef CAS.
- A. Landau, E. Eliav, Y. Ishikawa and U. Kaldor, J. Chem. Phys., 2001, 115, 6862–6865 CrossRef CAS.
- E. Eliav, M. J. Vilkas, Y. Ishikawa and U. Kaldor, J. Chem. Phys., 2005, 122, 224113 CrossRef PubMed.
- A. Kramida, Yu Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.8), [Online]. Available: https://physics.nist.gov/asd [2017, April 9]. National Institute of Standards and Technology, Gaithersburg, MD, 2020.
- E. Eliav, U. Kaldor and Y. Ishikawa, PRA, 1995, 52, 291–296 CrossRef CAS PubMed.
- C. Sur and R. K. Chaudhuri, PRA, 2007, 76, 012509 CrossRef.
- C. Blondel, C. Delsart and F. Goldfarb, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, L281–L288 CrossRef CAS.
- L. A. Kaledin, M. C. Heaven and R. W. Field, J. Mol. Spectrosc., 1999, 193, 285–292 CrossRef CAS PubMed.
- A. Yokozeki and M. Menzinger, Chem. Phys., 1976, 14, 427–439 CrossRef CAS.
- H. Heiberg, O. Gropen, J. K. Laerdahl, O. Swang and U. Wahlgren, Theor. Chem. Acc., 2003, 110, 118–125 Search PubMed.
- X. Y. Cao, W. J. Liu and M. Dolg, Sci. China, Ser. B: Chem., 2002, 45, 91–96 CrossRef CAS.
- R. J. Le Roy, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 167–178 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A supplementary pdf file is available containing orbitals, additional information about dipole moments and additional Franck–Condon factors. See DOI: 10.1039/d1cp03701c |
| This journal is © the Owner Societies 2021 |