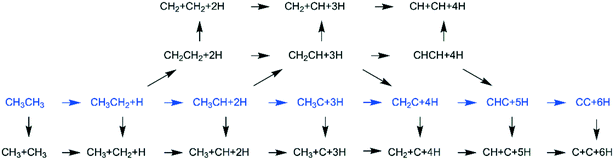
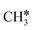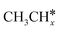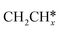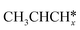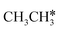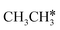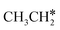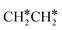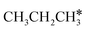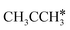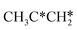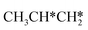Interactive network of the dehydrogenation of alkanes, alkenes and alkynes – surface carbon hydrogenative coupling on Ru(111)†
Yueyue
Jiao
 abc,
Huan
Ma
abc,
Huan
Ma
 abc,
Hui
Wang
abc,
Yong-Wang
Li
abcd,
Xiao-Dong
Wen
abc,
Hui
Wang
abc,
Yong-Wang
Li
abcd,
Xiao-Dong
Wen
 *abcd and
Haijun
Jiao
*abcd and
Haijun
Jiao
 *e
*e
aState Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan 030001, P.R. China. E-mail: wxd@sxicc.ac.cn
bThe University of Chinese Academy of Sciences, Beijing 100049, P.R. China
cNational Energy Center for Coal to Liquids, Synfuels China Co., Ltd., Beijing 101400, P.R. China
dBeijing Advanced Innovation Center for Materials Genome Engineering, Industry-University Cooperation Base between Beijing Information S&T University and Synfuels China Co. Ltd, Beijing, China
eLeibniz-Institut für Katalyse e.V. an der Universität Rostock, Albert-Einstein Strasse 29a, 18059 Rostock, Germany. E-mail: Haijun.jiao@catalysis.de
First published on 3rd November 2020
Abstract
To understand the reaction mechanisms of the dehydrogenation and retrosynthesis of alkanes, the consecutive dissociation of methane, ethane, ethene and ethyne, as well as propane, propene and propyne, on the fcc Ru(111) surface has been investigated using periodic density functional theory computations (rPBE). Methane dissociation has the energy minimum path of 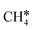 →
→ 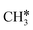 →
→ 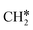 → CH* → C*. Although ethane dissociation does not have ethene and ethyne as intermediates, they have the same final surface species with the minimum energy paths for ethane [
→ CH* → C*. Although ethane dissociation does not have ethene and ethyne as intermediates, they have the same final surface species with the minimum energy paths for ethane [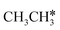 →
→ 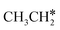 → CH3CH* → CH3C* →
→ CH3CH* → CH3C* → 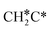 → HC*C* → HC* + C*], ethene [
→ HC*C* → HC* + C*], ethene [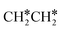 →
→ 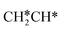 →
→ 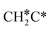 → HC*C* → HC* + C*] and ethyne [CH*CH* → HC*C* → HC* + C*]. Propane dissociation has the competitive routes of n-propyl [
→ HC*C* → HC* + C*] and ethyne [CH*CH* → HC*C* → HC* + C*]. Propane dissociation has the competitive routes of n-propyl [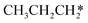 → CH3CH2CH* → CH3CH2C* → CH3CH*C* → CH3C*C* → CH3C* + C* →→ HC* + C*] and isopropyl with propyne as an intermediate [CH3CH*CH3 → CH3C*CH3 →
→ CH3CH2CH* → CH3CH2C* → CH3CH*C* → CH3C*C* → CH3C* + C* →→ HC* + C*] and isopropyl with propyne as an intermediate [CH3CH*CH3 → CH3C*CH3 → 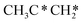 → CH3C*CH* → CH3C*C* →→ HC* + C*], and the n-propyl route has propene as an intermediate for dissociation [
→ CH3C*CH* → CH3C*C* →→ HC* + C*], and the n-propyl route has propene as an intermediate for dissociation [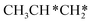 → CH3C*CH2*/CH3CH*CH* → CH3CH*C*/CH3C*CH* → CH3C*C* →→ HC* + C*]. In these reactions, the most stable surface intermediates are HC*, CH3C* and CH3CH2C* as homologs, as found experimentally on other metal surfaces. Our results rationalized the experimentally observed interconversion between
→ CH3C*CH2*/CH3CH*CH* → CH3CH*C*/CH3C*CH* → CH3C*C* →→ HC* + C*]. In these reactions, the most stable surface intermediates are HC*, CH3C* and CH3CH2C* as homologs, as found experimentally on other metal surfaces. Our results rationalized the experimentally observed interconversion between 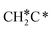 + H* and CH3C* as well as surface HC*C* and CH3C*C* as key intermediates for the first C–C bond dissociation [HC*C* → HC* + C*; CH3C*C* → CH3C* + C*]. On the basis of surface C* and H2 gas, the retrosynthesis of methane, ethane and propane has increasing apparent barriers of 1.08, 1.51 and 1.66 eV, respectively, at 490 K and 1 atm H2 and 0.83, 1.14 and 1.15 eV, respectively, at 19.7 atm H2. Surface carbon coverage changes the formation of alkanes from endergonic to exergonic. This pressure- and coverage-dependency is very important for understanding the reaction mechanism and selectivity. Surface alkynyl groups should be the intermediates for C–C coupling. The computed vibrational frequencies of CH*, CH3C*, CH2C*, HC*C* and
+ H* and CH3C* as well as surface HC*C* and CH3C*C* as key intermediates for the first C–C bond dissociation [HC*C* → HC* + C*; CH3C*C* → CH3C* + C*]. On the basis of surface C* and H2 gas, the retrosynthesis of methane, ethane and propane has increasing apparent barriers of 1.08, 1.51 and 1.66 eV, respectively, at 490 K and 1 atm H2 and 0.83, 1.14 and 1.15 eV, respectively, at 19.7 atm H2. Surface carbon coverage changes the formation of alkanes from endergonic to exergonic. This pressure- and coverage-dependency is very important for understanding the reaction mechanism and selectivity. Surface alkynyl groups should be the intermediates for C–C coupling. The computed vibrational frequencies of CH*, CH3C*, CH2C*, HC*C* and 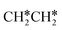 agree with the experiments. The comparison in adsorption energies and reaction barriers and energies shows that the fcc Ru(111) surface is more active than the hcp Ru(0001) surface despite their very similar surface structures.
agree with the experiments. The comparison in adsorption energies and reaction barriers and energies shows that the fcc Ru(111) surface is more active than the hcp Ru(0001) surface despite their very similar surface structures.
1. Introduction
Activation of alkanes is of great importance for many industrial processes, such as direct dehydrogenation,1,2 steam reforming, dry reforming3 and partial oxidation. In particular, light alkane dehydrogenation, which produces light olefins such as ethene and propene as very important basic chemicals and materials in industry, has attracted steadily increasing attention.4–6 As reverse processes of alkane dehydrogenation, hydrogenation and hydrogenative C–C coupling represent also important reactions in academic research and industrial applications, i.e., methanation reaction,7 methanol synthesis, synthesis of lower alcohols8 and Fischer–Tropsch synthesis (FTS),9 where CO (also CO2) is hydrogenated. Therefore, understanding the mechanisms of the dehydrogenation of alkanes can provide insights into the hydrogenation and hydrogenative C–C coupling from the retrosynthetic point of view.Commercially, CrxOy- and Pt-based catalysts have excellent performance in propane dehydrogenation to propylene.10–12 However, CrxOy-based catalysts have significant risk to health from Cr6+ leakage or exposure during catalytic processes and are not environmentally friendly.13 In addition, the low melting point of Cr2O3 (196 °C) has a negative impact on the catalyst life. Platinum and Pt alloy catalysts need high temperature for the dehydrogenation of lower alkanes and have the disadvantage of rupture of C–C bonds leading to coking and sintering, which can deactivate the catalyst.12 On the Pt(111) surface, density functional theory (PBE) computation showed that ethane dehydrogenation has the minimum energy path of 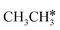 →
→ 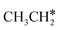 →
→ 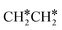 →
→ 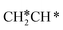 → CH2C* → HC*C* → CH* + C* with the lowest C–C bond breaking barrier of 0.90 eV,14 and the dehydrogenation of propane has propylene and propyne as intermediates and ends up with the formation of CH3C* + CH* by a fracture of the C–C bond in propyne.15 Low price nickel catalysts show excellent catalytic performance for methane, ethane, propane and butane activation,7,16–18 but has the disadvantage of methanation and coke formation.19 On the Ni(111) surface, Mueller et al.16 computed ethane dissociation and found a minimum energy path leading to ethyne at low surface coverage and ethylidyne at high surface coverage. For propane dehydrogenation on the Ni(111) surface, Saelee et al.20 found 1-propyl as the key intermediate.
→ CH2C* → HC*C* → CH* + C* with the lowest C–C bond breaking barrier of 0.90 eV,14 and the dehydrogenation of propane has propylene and propyne as intermediates and ends up with the formation of CH3C* + CH* by a fracture of the C–C bond in propyne.15 Low price nickel catalysts show excellent catalytic performance for methane, ethane, propane and butane activation,7,16–18 but has the disadvantage of methanation and coke formation.19 On the Ni(111) surface, Mueller et al.16 computed ethane dissociation and found a minimum energy path leading to ethyne at low surface coverage and ethylidyne at high surface coverage. For propane dehydrogenation on the Ni(111) surface, Saelee et al.20 found 1-propyl as the key intermediate.
Ruthenium and ruthenium-supported catalysts show moderate reactivity in ethane hydrogenolysis.21,22 However, metallic ruthenium is an excellent catalyst for FTS and has the advantage of low reaction temperature, high catalytic activity, high product selectivity and rare carbon accumulation.23–25 There are theoretical studies on the Ru(0001) surface26,27 about the dehydrogenation of light alkanes. For CH4 dissociation on the Ru(0001) surface, Ciobîcă et al.26 found that the consecutive barrier for the first, second, third and final C–H dissociation is 0.88, 0.51, 0.17 and 1.12 eV (PW91), respectively, and the first step is rate-determining and surface CH* represents the most stable species as the resting state, and the same result was also found by Ande et al.27 (0.86, 0.65, 0.16 and 1.06 eV, respectively, PBE). For ethane consecutive dissociation on the Ru(0001) surface, Ande et al.27 identified the minimum energy path of 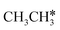 →
→ 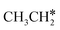 → CH3CH* → CH3C* → CH2C* → HC*C*; however, their results lack the important information on the rupture of C–C bonds.
→ CH3CH* → CH3C* → CH2C* → HC*C*; however, their results lack the important information on the rupture of C–C bonds.
Using high resolution electron energy loss spectroscopy (HREELS) and temperature programmed desorption (TPD) techniques, Barteau et al.28 studied the dissociative adsorption of ethene on the Ru(001) surface under ultra-high vacuum conditions (UHV) and found chemisorbed ethene at 180 K and surface ethylidene CH3C* upon heating to 280 K, which further recomposites in a series of steps between 300 and 600 K to liberate H2 and deposit surface carbon atoms. Using the ultraviolet photoelectron technique, Egawa et al.29 studied the dissociation of ethene and ethyne on the Ru(001) surface and observed their molecular adsorption at 120 K, the formation of ethylidene CH3C* at 280 K, the formation of H2 and HC*C* by heating at 450 K, and the formation of CH* at 550 K and C* above 650 K, and the CO presence delayed CH3C* decomposition. Using HREELS and thermal desorption mass spectroscopy, Hills et al.30 studied ethene dissociative adsorption on the Ru(001) surface and found di-σ-bonded molecular ethene on the surface after desorption of an ethene multilayer at 110 K. They further observed the competing desorption of molecular ethene and ethene dehydrogenation to form adsorbed CH3C* and HC*C* as well as H* occurring between approximately 150 and 260 K. Surface CH3C* is stable to approximately 330 K and begins to decompose to carbon and hydrogen adatoms. The desorption of H2 gives rise to a sharp peak centered at 355 K, resulting from the simultaneous CH3C* decomposition and desorption of surface H*. Further annealing of the overlayer to 380 K causes cleavage of the C–C bond of acetylide, creating carbon adatoms and adsorbed methylidyne (CH*), which decomposes above 500 K accompanied by hydrogen desorption, leaving only carbon adatoms (C*) at 700 K. On the Rh(111) surface, ethene has molecular adsorption at low temperatures and dissociative adsorption with CH3C* as an intermediate at high temperatures.31,32 Using HREELS and TPD techniques, Wu et al.33 studied methane decomposition on the flat Ru(0001) surface and found the formation of surface CH* and CH2C*. Similar results are found for CO hydrogenation on the Ru(0001) and Ru(1120) surfaces.34 On the Ru(0001) surface, Kirsch et al.35 first reported the existence of HC*C* during methane decomposition (400–550 K) and the existence of HC*C* and CH2C* (250–350 K) during ethene decomposition using vibrational sum frequency generation spectroscopy. On the Ru(0001) surface under UHV conditions, Ransley et al.36 observed the formation of propylidyne (CH3CH2C*) at 150–260 K and CH3C* at 300–330 K from consecutive propene dissociation using reflection-absorption infrared spectroscopy. They also proved the formation of CH3C* from ethene dissociation.
Surface CH* as the important intermediate was also identified in the hydrogenation of surface carbon on the Ru(001) surface using HREELS under UHV conditions37 and there was no evidence of surface 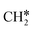 and
and 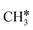 as well as no CH4 formation under UHV conditions. It is very interesting to note that the reaction of surface carbon prepared with electron beam-stimulated CO dissociation, thermal decomposition of ethene or by ethene hydrogenolysis showed the same results. Furthermore, it is found that the maximum intensity of CH* stretching was observed at a surface temperature of 370 K; the CH* species decomposed completely to H2 and C* upon heating the surface to 500 K.37 Shan et al.38 computed the conversion of ethene to ethylidyne on the Rh(111) surface (PW91) and found the minimum energy path of
as well as no CH4 formation under UHV conditions. It is very interesting to note that the reaction of surface carbon prepared with electron beam-stimulated CO dissociation, thermal decomposition of ethene or by ethene hydrogenolysis showed the same results. Furthermore, it is found that the maximum intensity of CH* stretching was observed at a surface temperature of 370 K; the CH* species decomposed completely to H2 and C* upon heating the surface to 500 K.37 Shan et al.38 computed the conversion of ethene to ethylidyne on the Rh(111) surface (PW91) and found the minimum energy path of 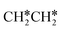 →
→ 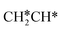 →
→ 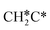 → CH3C*, and
→ CH3C*, and 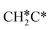 hydrogenation as the rate-limiting step.
hydrogenation as the rate-limiting step.
Most of the previous theoretical studies focused on the hexagonal-close-packed (hcp) ruthenium metal, which is a stable phase in bulk. However, it is also found experimentally that the face-centered-cubic (fcc) ruthenium phase can be stable to 400 °C39 and has higher catalytic activity in FTS,40 CO oxidation,41p-nitrophenol reduction by NaBH4, ammonia borane dehydrogenation,42 N2 reduction for ammonia synthesis43 and oxygen evolution reactions.39 There is a lack of systematic studies on the activation of light alkanes on the fcc ruthenium metal. On the basis of systematic DFT computation, we studied the adsorption of 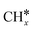 (x = 4–0),
(x = 4–0), 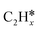 (x = 6–0) and
(x = 6–0) and 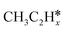 (x = 5–0) on the fcc Ru(111) surface. Our goal is the complete reaction networks of methane, ethane and propane consecutive dehydrogenation. Inversely, our results can also be used for understanding the retrosynthetic process of hydrogenative coupling of surface carbon species in FTS and the synthesis of lower alcohols.
(x = 5–0) on the fcc Ru(111) surface. Our goal is the complete reaction networks of methane, ethane and propane consecutive dehydrogenation. Inversely, our results can also be used for understanding the retrosynthetic process of hydrogenative coupling of surface carbon species in FTS and the synthesis of lower alcohols.
2. Methods and models
All calculations were performed using the Vienna ab initio simulation package code (VASP).44,45 The interaction of electrons and ions was described by the projector augmented wave (PAW)46,47 potential, and the revised Perdew–Burke–Ernzerhof (rPBE)48,49 functional of generalized gradient approximation (GGA) was used to obtain the electron exchange and correlation energies. In our study we used the computed CO adsorption energy as the benchmark for the choice of functional (Table S1†), and the best agreement with the experiment (−1.66 eV50) is found for rPBE + ZPE (−1.77 eV), while including dispersion correction (rPBE + ZPE + D3) gives a much stronger adsorption energy (−2.06 eV). Stronger adsorption energies are also found for PBE + ZPE and PBE + ZPE + D3 (−2.00 and −2.40 eV, respectively). The same trend is also found for the adsorption of alkanes and alkyls with the largest difference of 0.76 eV for rBPE + ZPE + D3 and 0.89 eV for PBE + ZPE + D3. Thus, rPBE was used. The cut-off energy of the plane-wave basis was set to 400 eV to make sure that the energy difference is less than 10−4 eV and the force per atom is less than 0.05 eV Å−1, respectively. Electron smearing was employed via the first order Methfessel–Paxton technique with the width of the smearing consistent to 0.1 eV.51 For sampling at the Brillouin zone, a k point of 3 × 3 × 1 in the Monkhorst Pack grid52 was adopted. The vacuum layer between the periodically repeated slabs was set as 15 Å. The determined equilibrium lattice constants based on density functional theory calculation for the fcc ruthenium phase are a = b = c = 3.832 Å, in agreement with the references 3.82 Å43 and 3.83 Å.53In our computation, a p(4 × 4) Ru(111) model with four ruthenium layers was used, with the bottom two layers fixed and the top two layers with adsorbates relaxed. Fig. 1 shows the top and side views of the p(4 × 4) Ru(111) surface with possible adsorption sites, i.e.; bridge, fcc hollow, hcp hollow and top sites (Fig. 1).
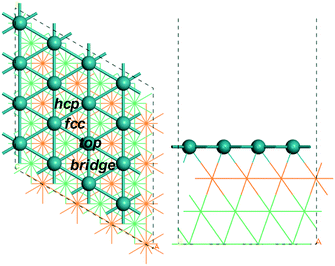 | ||
| Fig. 1 Top and side views of (4 × 4) Ru(111) (first layer Ru in green, second layer Ru in orange; two bottom layers Ru in light green lines). | ||
The adsorption energy (Eads) of the adsorbate (X*) is obtained from the equation Eads = EX*/slab − Eslab − Ex, where EX*/slab is the total energy of the slab with X* in its equilibrium geometry, Eslab is the total energy of the clean slab, and EX is the total energy of the free adsorbate (X) in the gas phase (isolated species in a 20 Å × 20 Å × 20 Å cell). The more negative the Eads, the stronger the adsorption. The climbing-image nudged elastic band method (CI-NEB)54 was adopted to search the transition state (TS) and the vibrational frequency analysis was processed to verify the authentic transition state with only one imaginary frequency. The barrier (Ea) and the reaction energy (Er) are calculated according to Ea = ETS − EIS and Er = EFS − EIS, where EIS, ETS and EFS are the total energies of the corresponding initial state (IS), transition state (TS) and final state (FS), respectively. All reported energetic data include the corrections of zero-point energies (ZPEs). To discuss the reaction under realistic conditions, we computed the Gibbs free energy at 490 K and 1 atm H2 partial pressure using the VASPKIT code;55 and this is because that CH* was detected from 260 K to above 600 K during methane decomposition on the Ru(0001) surface under UHV,35 and the maximum peaking temperature of methane formation from surface carbon on the Ru/Al2O3 catalyst at 1 atm H2 partial pressure was 490 K.56 In addition, the Gibbs free energies at 490 K at 19.7 atm H2 partial pressure (H2 partial pressure in FTS)40 are given in the ESI.†
3. Results
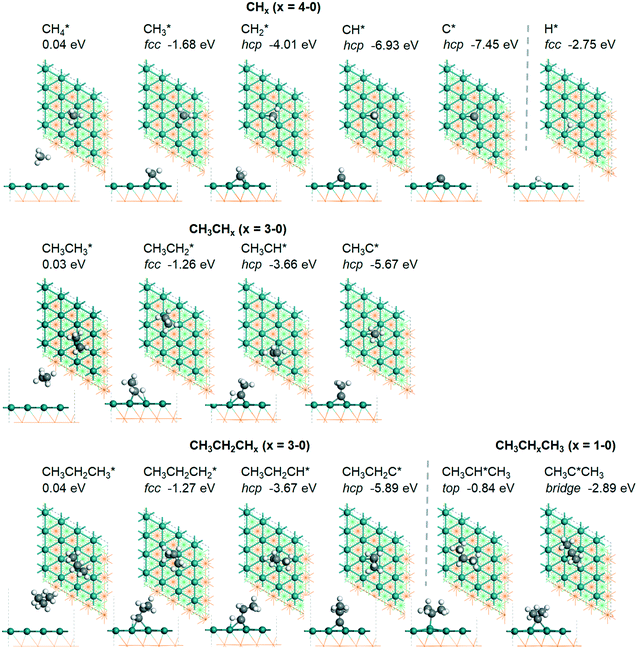
3.1. Adsorption of surface intermediates
For understanding the full dehydrogenation of methane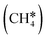 , ethane
, ethane 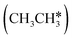 , and propane (
, and propane (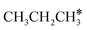 ), we calculated the adsorption of all
), we calculated the adsorption of all 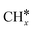 , (x = 4–0),
, (x = 4–0), 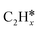 (x = 5–0),
(x = 5–0), 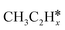 (x = 5–0) species. The adsorption structures and energies of the most stable sites are presented in Table 1. Table 1 lists the adsorption sites and energies, the C–C distances, and the nearest distances of C and H to surface Ru atoms as well as C–H distances with agostic interaction.
(x = 5–0) species. The adsorption structures and energies of the most stable sites are presented in Table 1. Table 1 lists the adsorption sites and energies, the C–C distances, and the nearest distances of C and H to surface Ru atoms as well as C–H distances with agostic interaction.
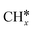 ,
, 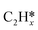 and
and 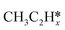 on the Ru(111) surface, dC–C for the length of the nearest C–C bond from the surface, dRu-C and dRu-H respectively for the distance between the top layer Ru atoms and the closest C atom and H atom (the values of dRu–C and dRu–H greater than 2.5 Å are not listed), dC–H for the length of the longest C–H bond in adsorbed C atoms, as well as f for fcc, h for hcp, b for bridge and t for top sites
on the Ru(111) surface, dC–C for the length of the nearest C–C bond from the surface, dRu-C and dRu-H respectively for the distance between the top layer Ru atoms and the closest C atom and H atom (the values of dRu–C and dRu–H greater than 2.5 Å are not listed), dC–H for the length of the longest C–H bond in adsorbed C atoms, as well as f for fcc, h for hcp, b for bridge and t for top sites
| Species | Site | E ads (eV) | d C–C (Å) | d Ru–C (Å) | d Ru–H (Å) | d C–H (Å) |
|---|---|---|---|---|---|---|
| a PBE p(2×2) Ru(0001) results from ref. 27 are given in square brackets. | ||||||
| CH4 | 0.04 [−0.02] | 1.096 | ||||
| CH3 | f | −1.68 [−2.05] | 2.307; 2.317; 2.320 | 2.201; 2.226; 2.211 | 1.121 | |
| CH2 | h | −4.01 [−4.33] | 2.080; 2.082; 2.152 | 1.819 | 1.216 | |
| CH | h | −6.93 [−6.83] | 2.019; 2.022; 2.022 | 1.103 | ||
| C | h | −7.45 [−7.54] | 1.945; 1.944; 1.944 | |||
| H | f | −2.75 [−2.87] | 1.904; 1.905; 1.909 | |||
| CH3CH3 | 0.03 [−0.03] | 1.529 | 1.098 | |||
| CH3CH2 | f | −1.26 [−1.58] | 1.544 | 2.190; 2.399; 2.436 | 1.974; 2.008 | 1.153; 1.148 |
| CH3CH | h | −3.66 [−3.96] | 1.531 | 2.095; 2.097; 2.184 | 1.754 | 1.252 |
| CH3C | h | −5.67 [−5.91] | 1.512 | 2.039; 2.041; 2.041 | 1.100 | |
| CH3CH2CH3 | 0.04 | 1.530 | 1.099 | |||
| CH3CH2CH2 | f | −1.27 | 1.556 | 2.176; 2.423; 2.451 | 1.951; 1.956 | 1.159 |
| CH3CH2CH | h | −3.67 | 1.541 | 2.093; 2.103; 2.178 | 1.719 | 1.274 |
| CH3CH2C | h | −5.89 | 1.519 | 2.036; 2.038; 2.040 | 1.102 | |
| CH3CHCH3 | t | −0.84 | 1.528 | 2.165 | 1.104 | |
| CH3CCH3 | b | −2.89 | 1.530 | 2.124; 2.125 | 1.993 | 1.135 |
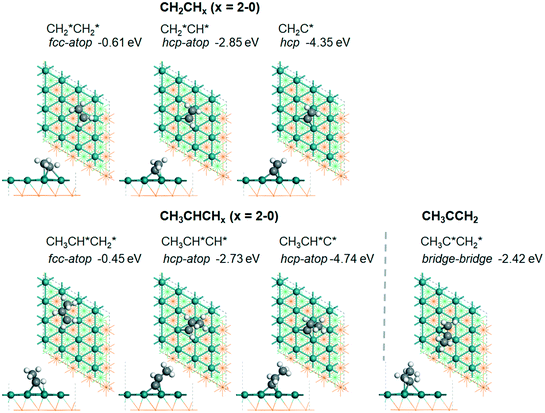
| CH2CH2 | f + t | −0.61 [−0.87] | 1.452 | 2.158 (t); 2.225 (f); 2.503 (f); 2.503 (f) | 2.199; 2.205 | 1.118 |
| CH2CH | h + t | −2.85 [−3.20] | 1.434 | 2.231 (t); 2.066 (h); 2.142 (h); 2.183 (h) | 1.871 | 1.193 |
| CH2C | h + t | −4.35 [−4.70] | 1.415 | 2.075 (t); 2.024 (h); 2.205 (h); 2.075 (h) | 1.092 | |
| CH3CHCH2 | f + t | −0.45 | 1.460 | 2.171 (t); 2.215 (f); 2.426 (f); 2.482 (f) | 2.107; 2.207 | 1.129 |
| CH3CHCH | h + t | −2.73 | 1.433 | 2.275 (t); 2.064 (h); 2.140 (h); 2.170 (h) | 1.855 | 1.199 |
| CH3CHC | h + t | −4.74 | 1.412 | 2.354 (t); 2.028 (h); 2.030 (h); 2.354 (h) | 1.097 | |
| CH3CCH2 | b + b | −2.42 | 1.442 | 2.073 (b); 2.182 (b); 2.191 (b); 2.324 (b) | 1.902 | 1.165 |
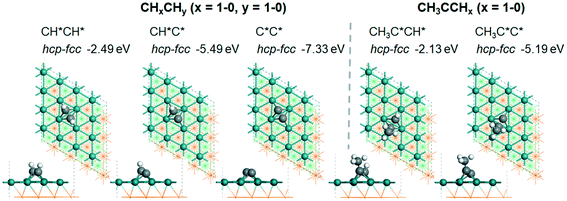
| CHCH | h + f | −2.49 [−2.67] | 1.444 | 2.147 (f); 2.152 (f); 2.181 (f); 2.162 (h); 2.176 (h); 2.180 (h) | 1.098 | |
| CHC | h + f | −5.49 [−5.76] | 1.408 | 1.987 (f); 2.067 (f); 2.068 (f); 2.207 (h); 2.209 (h); 2.269 (h) | 1.094 | |
| CC | h + f | −7.33 [−7.65] | 1.393 | 2.035 (f); 2.123 (f); 2.123 (f); 2.040 (h); 2.142 (h); 2.142 (h) | ||
| CH3CCH | h + f | −2.13 | 1.448 | 2.135 (f); 2.139 (f); 2.177 (f); 2.181 (h); 2.209 (h); 2.231 (h) | 1.102 | |
| CH3CC | h + f | −5.19 | 1.400 | 1.983 (f); 2.072 (f); 2.073 (f), 2.224 (h); 2.239 (h); 2.366 (h) | 1.100 | |
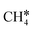 ,
, 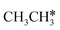 and
and 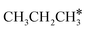 , as well as the consecutive C–H dissociation of the terminal methyl groups. It shows that
, as well as the consecutive C–H dissociation of the terminal methyl groups. It shows that 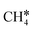 ,
, 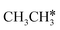 and
and 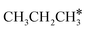 molecules have negligible positive adsorption energies, indicating a physisorption nature. The adsorption energies of
molecules have negligible positive adsorption energies, indicating a physisorption nature. The adsorption energies of 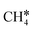 (0.04 eV) and
(0.04 eV) and 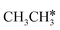 (0.03 eV) are close to those (−0.02 and −0.03 eV, respectively) on the Ru(0001) surface.27
(0.03 eV) are close to those (−0.02 and −0.03 eV, respectively) on the Ru(0001) surface.27
The alkyl fragments, methyl 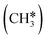 , ethyl
, ethyl 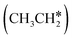 and n-propyl (
and n-propyl (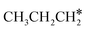 ), have the same adsorption configuration over the fcc hollow site. The adsorption energy of
), have the same adsorption configuration over the fcc hollow site. The adsorption energy of 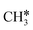 is higher than those of
is higher than those of 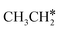 and
and 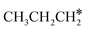 (−1.68 vs. −1.26 and −1.27 eV, respectively), despite that fact that the C–Ru distance of
(−1.68 vs. −1.26 and −1.27 eV, respectively), despite that fact that the C–Ru distance of 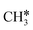 is longer than those of
is longer than those of 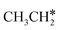 and
and 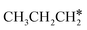 (2.307 vs. 2.190 and 2.176 Å). It is in particular interesting to note their eclipsed adsorption configuration of the surface C–H bond to the surface Ru atoms, and the C–H bonds at the C atom to the surface are longer (1.121, 1.153 and 1.159 Å) in comparison with the terminal C–H bond in the molecules, indicating their additional interaction with surface Ru atoms, and the three surface C–H bonds in
(2.307 vs. 2.190 and 2.176 Å). It is in particular interesting to note their eclipsed adsorption configuration of the surface C–H bond to the surface Ru atoms, and the C–H bonds at the C atom to the surface are longer (1.121, 1.153 and 1.159 Å) in comparison with the terminal C–H bond in the molecules, indicating their additional interaction with surface Ru atoms, and the three surface C–H bonds in 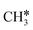 are longer than those of
are longer than those of 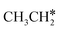 and
and 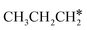 . In addition, such similar adsorption configurations and structural parameters of
. In addition, such similar adsorption configurations and structural parameters of 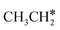 and
and 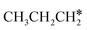 also explain their close adsorption energies.
also explain their close adsorption energies.
As in the case of the alkyl fragments, the alkylidene fragments, HCH*, CH3CH* and CH3CH2CH*, have the same adsorption configuration over the hcp hollow site. The adsorption energy of HCH* is stronger than those of CH3CH* and CH3CH2CH* (−4.01 vs. −3.66 and −3.67 eV, respectively), although the end-up C–Ru distance of HCH* is longer than those of CH3CH* and CH3CH2CH* (2.152 vs. 2.095 and 2.093 Å). It is noted that one of the C–H bonds has strong agostic interaction with the surface Ru atoms resulting in a rather long C–H distance of 1.216, 1.252 and 1.274 Å, respectively, and the corresponding Ru–H distance is 1.819, 1.753 and 1.719 Å, respectively. These results for HCH* are consistent with other calculations26,57,58 on the Ru(0001) surface.
A high similarity in energy and structure has also been found for alkylidyne fragments, HC*, CH3C* and CH3CH2C*, over the hcp hollow site. The preferred hcp hollow site of CH3C* adsorption, the computed C–C distance (1.512 Å) and the Ru–C distance (2.040 Å) are in reasonable agreement with the experimental values (1.45 ± 0.10 and 2.03 ± 0.07 Å) on the Rh(111) surface.31 The preferred hollow sites of HC* and CH3C* are the same as those found on the Ru(0001) surface.26,27 For example, HC* has stronger adsorption energy than CH3C* and CH3CH2C* (−6.93 vs. −5.67 and −5.89 eV, respectively), and the end-up C–Ru distance of HC* is shorter than those of CH3C* and CH3CH2C* (2.019 vs. 2.039 and 2.036 Å). In addition, surface carbon (C*) prefers the hcp hollow site (−7.45 eV) and surface hydrogen (H*) prefers the fcc hollow site (−2.75 eV). Surface C* and H* on Ru(0001) have the same adsorption sites and their adsorption energies are −7.54 and −2.87 eV.27
In contrast to the alkyl fragments, the adsorption of isopropyl (CH3)2CH* prefers the top site and has a much lower adsorption energy (−0.84 eV). In addition, isopropylidene (CH3)2C* prefers the adsorption at the bridge site instead of the hcp hollow site for other alkylidene fragments and also has a much lower adsorption energy (−2.89 eV). This can be ascribed to the repulsive interaction of the two terminal CH3 groups with the surface and the lower coordination number to surface Ru atoms.
A comparison among these homolog fragments shows that each type of fragment has similar adsorption configurations and the adsorption energy increases in the order alkyl, alkylidene and alkylidyne, due to the formal change of the hybridization from sp3, sp2 and sp1. In addition, the 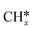 fragments have stronger adsorption energy than the higher homolog fragments of
fragments have stronger adsorption energy than the higher homolog fragments of 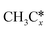 and
and 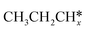 . The adsorption configurations and energies of
. The adsorption configurations and energies of 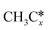 as well as
as well as 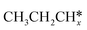 and (CH3)2CH* can also be used for the adsorption of higher alkanes, since the terminal alkyl groups point away from the surface.
and (CH3)2CH* can also be used for the adsorption of higher alkanes, since the terminal alkyl groups point away from the surface.
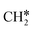 groups. As expected, ethene and propene have a flat adsorption configuration, in which the surface
groups. As expected, ethene and propene have a flat adsorption configuration, in which the surface 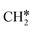 group is at the fcc hollow site and the second surface
group is at the fcc hollow site and the second surface 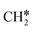 of ethene and the central CH* of propane are at the top site. Compared with free ethene and propene in the gas phase (1.333 and 1.336 Å, respectively), the C
of ethene and the central CH* of propane are at the top site. Compared with free ethene and propene in the gas phase (1.333 and 1.336 Å, respectively), the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond is elongated to 1.452 and 1.460 Å, respectively, due to the bonding and back-bonding interaction between the C
C double bond is elongated to 1.452 and 1.460 Å, respectively, due to the bonding and back-bonding interaction between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond and surface Ru atoms, and accordingly the adsorbed ethene and propene can be considered to have a typical di-σ configuration.28 In addition, ethene has a somewhat stronger adsorption energy than propene due to the methyl substitution (−0.61 vs. −0.45 eV).
C double bond and surface Ru atoms, and accordingly the adsorbed ethene and propene can be considered to have a typical di-σ configuration.28 In addition, ethene has a somewhat stronger adsorption energy than propene due to the methyl substitution (−0.61 vs. −0.45 eV).
For the adsorption of ethenyl 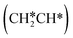 and propenyl propen-1-yl (CH3CH*CH*), the terminal CH* groups are at the hcp hollow site and the
and propenyl propen-1-yl (CH3CH*CH*), the terminal CH* groups are at the hcp hollow site and the 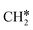 group of ethenyl and the central CH* group of propen-1-yl are at the top sites, and
group of ethenyl and the central CH* group of propen-1-yl are at the top sites, and 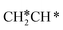 and CH3CH*CH* have close adsorption energies (−2.85 and −2.73 eV, respectively). In ethenyl
and CH3CH*CH* have close adsorption energies (−2.85 and −2.73 eV, respectively). In ethenyl 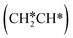 , the C–H bond of
, the C–H bond of 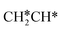 has agostic interaction with one surface Ru atom (1.871 Å), and the C–C distance is 1.434 Å. The same is also found for CH3CH*CH*, where the terminal C–H bond has agostic interaction with one surface Ru atom (1.855 Å) and the C–C distance is 1.433 Å. For propen-2-yl (
has agostic interaction with one surface Ru atom (1.871 Å), and the C–C distance is 1.434 Å. The same is also found for CH3CH*CH*, where the terminal C–H bond has agostic interaction with one surface Ru atom (1.855 Å) and the C–C distance is 1.433 Å. For propen-2-yl (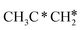 ), both central C* and terminal
), both central C* and terminal 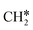 adsorb at the bridge sites, and one of the C–H bonds of the terminal
adsorb at the bridge sites, and one of the C–H bonds of the terminal 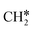 has agostic interaction with one surface Ru atom (1.902 Å); and the adsorption energy (−2.42 eV) is somewhat lower than those of
has agostic interaction with one surface Ru atom (1.902 Å); and the adsorption energy (−2.42 eV) is somewhat lower than those of 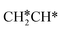 and CH3CH*CH*.
and CH3CH*CH*.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond is elongated to 1.444 and 1.448 Å, as compared with those of free ethyne and propyne in the gas phase (1.206 and 1.210 Å, respectively). The same adsorption configurations have also been found for both alkynyl groups, and the adsorption energy is −5.49 and −5.19 eV, respectively.
C triple bond is elongated to 1.444 and 1.448 Å, as compared with those of free ethyne and propyne in the gas phase (1.206 and 1.210 Å, respectively). The same adsorption configurations have also been found for both alkynyl groups, and the adsorption energy is −5.49 and −5.19 eV, respectively.
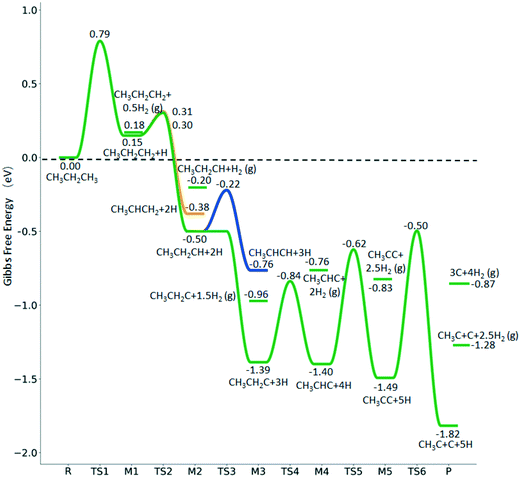
3.2. Methane dehydrogenation
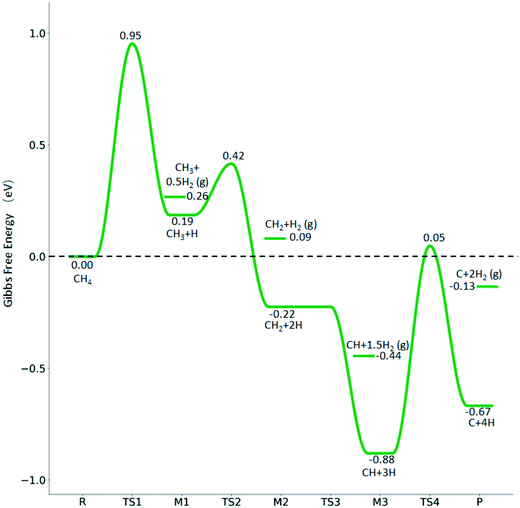
The consecutive CH4 dehydrogenation process is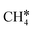 →
→ 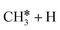 →
→ 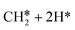 → CH* + 3H* → C* + 4H*. Fig. 5 shows the whole profile of Gibbs free energy at 490 K and 1 atm H2 partial pressure and the reaction Gibbs free energy of each elementary step is computed after the diffusion of H atoms to the most stable sites. Detailed structural and energetic information calculated by DFT are given in the ESI† (Table S2). It is found that both pressure and temperature hardly affect the energetics on the surface, while strongly for reactions involving gas molecules. The energy profiles from DFT and the Gibbs free energy profiles at a higher H2 partial pressure (19.7 atm) are given in the ESI† (Fig. S1 and S2).
→ CH* + 3H* → C* + 4H*. Fig. 5 shows the whole profile of Gibbs free energy at 490 K and 1 atm H2 partial pressure and the reaction Gibbs free energy of each elementary step is computed after the diffusion of H atoms to the most stable sites. Detailed structural and energetic information calculated by DFT are given in the ESI† (Table S2). It is found that both pressure and temperature hardly affect the energetics on the surface, while strongly for reactions involving gas molecules. The energy profiles from DFT and the Gibbs free energy profiles at a higher H2 partial pressure (19.7 atm) are given in the ESI† (Fig. S1 and S2).
It is found that the Gibbs free energy barrier (0.95 eV) of the first C–H bond dissociation is much higher than that of the adsorbed 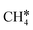 as the reference. In the transition state, the breaking C–H bond is over a surface Ru atom and has a distance of 1.606 Å, and the distance of the forming Ru–C and Ru–H bonds is 2.284 and 1.678 Å, respectively. From
as the reference. In the transition state, the breaking C–H bond is over a surface Ru atom and has a distance of 1.606 Å, and the distance of the forming Ru–C and Ru–H bonds is 2.284 and 1.678 Å, respectively. From 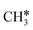 to
to 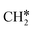 + H*, the second C–H dissociation has a Gibbs free energy barrier of 0.23 eV and a reaction Gibbs free energy of −0.41 eV. In the transition state, the breaking C–H distance is 1.571 Å, and the Ru–C distances are 2.102, 2.129 and 2.229 Å and the Ru–H distance is 1.672 Å, respectively. From
+ H*, the second C–H dissociation has a Gibbs free energy barrier of 0.23 eV and a reaction Gibbs free energy of −0.41 eV. In the transition state, the breaking C–H distance is 1.571 Å, and the Ru–C distances are 2.102, 2.129 and 2.229 Å and the Ru–H distance is 1.672 Å, respectively. From 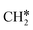 to CH* + H*, the third C–H dissociation is in fact barrier-less and has a reaction Gibbs free energy of −0.66 eV, the barrier-less property is due to the very strong C–H agostic interaction of one C–H bond with a surface Ru atom of
to CH* + H*, the third C–H dissociation is in fact barrier-less and has a reaction Gibbs free energy of −0.66 eV, the barrier-less property is due to the very strong C–H agostic interaction of one C–H bond with a surface Ru atom of 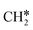 (1.216 Å, Table 1). In the transition state, the breaking C–H distance is 1.491 Å, the Ru–C distances are 2.057, 2.057 and 2.062 Å, and the Ru–H distance is 1.675 Å. From CH* to C* + H*, the last C–H dissociation has a Gibbs free energy barrier of 0.93 eV and a reaction Gibbs free energy of 0.21 eV. In the transition state, the breaking C–H distance is 1.654 Å, and the Ru–C distances are 1.947, 1.950 and 1.974 Å, and the Ru–H distance is 1.676 Å.
(1.216 Å, Table 1). In the transition state, the breaking C–H distance is 1.491 Å, the Ru–C distances are 2.057, 2.057 and 2.062 Å, and the Ru–H distance is 1.675 Å. From CH* to C* + H*, the last C–H dissociation has a Gibbs free energy barrier of 0.93 eV and a reaction Gibbs free energy of 0.21 eV. In the transition state, the breaking C–H distance is 1.654 Å, and the Ru–C distances are 1.947, 1.950 and 1.974 Å, and the Ru–H distance is 1.676 Å.
The overall potential energy surface of CH4 consecutive dissociation on the Ru(111) surface is similar to that on the Ru(0001) surface,27 where the first C–H dissociation determines the reaction. However, differences are found for the second step, which has a low barrier (0.20 eV) and is exothermic (−0.45 eV) on p(4 × 4) Ru(111) (Table S2†), while having a higher barrier (0.65 eV) and being endothermic (0.08 eV) on p(2 × 2) Ru(0001). This could be due to the surface area, adsorption site, or functional, or Ru (111) is more active than Ru (0001), as discussed in the next section of ethane dissociation.
The Gibbs free energy profile in Fig. 5 shows that surface CH* is the resting intermediate, and surface carbon, once formed in the presence of hydrogen, will be hydrogenated to surface CH* with a Gibbs free energy barrier of 0.72 eV and a reaction Gibbs free energy of −0.21 eV. It also shows that the adsorbed H* atoms will remain on the surface, since H2 adsorption is exergonic by −0.07, −0.31, −0.44, and −0.54 eV for surface 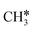 + 0.5H2,
+ 0.5H2, 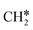 + H2, CH* + 1.5H2 and C* + 2H2. Considering the effect of pressure and temperature, the surface H coverage may increase and keep balance with the gas phase H2 to attain chemical potential equilibrium. Thus, the formation of methane has a Gibbs free energy of 0.13, 0.44, −0.09, and −0.26 eV based on C*, CH*,
+ H2, CH* + 1.5H2 and C* + 2H2. Considering the effect of pressure and temperature, the surface H coverage may increase and keep balance with the gas phase H2 to attain chemical potential equilibrium. Thus, the formation of methane has a Gibbs free energy of 0.13, 0.44, −0.09, and −0.26 eV based on C*, CH*, 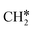 , and
, and 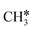 , respectively. At a higher H2 partial pressure (19.7 atm, Fig. S2†), H2 adsorption is exergonic by 0.13, 0.43, 0.63, and 0.79 eV for surface
, respectively. At a higher H2 partial pressure (19.7 atm, Fig. S2†), H2 adsorption is exergonic by 0.13, 0.43, 0.63, and 0.79 eV for surface 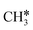 + 0.5H2,
+ 0.5H2, 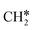 + H2, CH* + 1.5H2 and C* + 2H2, respectively, and methane formation has a Gibbs free energy of −0.12, 0.25, −0.21, and −0.32 eV based on C*, CH*,
+ H2, CH* + 1.5H2 and C* + 2H2, respectively, and methane formation has a Gibbs free energy of −0.12, 0.25, −0.21, and −0.32 eV based on C*, CH*, 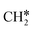 , and
, and 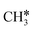 , respectively, and becomes thermodynamically possible.
, respectively, and becomes thermodynamically possible.
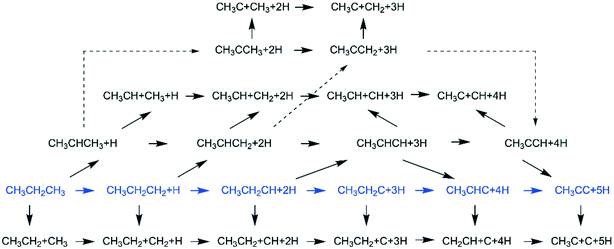
3.3. Dissociation of ethane, ethene and ethyne
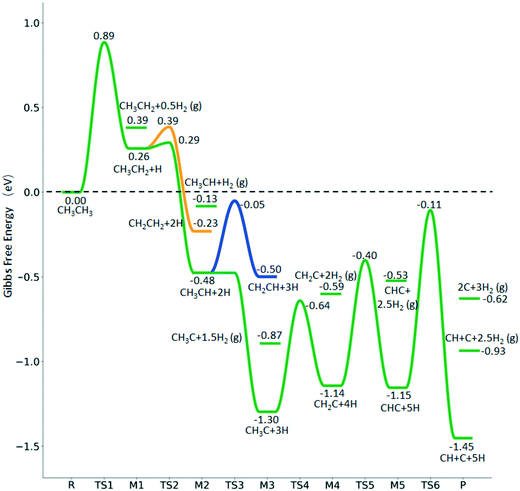
In addition to CH4 consecutive dissociation, we computed full ethane dissociation and the complete reaction network is shown in Fig. 6, where not only C–H but also C–C dissociations were considered. As shown in Fig. 6, we firstly computed the consecutive C–H dissociation of CH3CH3, and then the corresponding C–C and C–H dissociations of the intermediates leading to complete dissociation.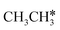 consecutive dehydrogenation are shown in Fig. 7 and the specific values are summarized in the ESI† (Table S3). The energetic and geometric data of the less favored elementary steps are given in the ESI† (Table S6). Energies of
consecutive dehydrogenation are shown in Fig. 7 and the specific values are summarized in the ESI† (Table S3). The energetic and geometric data of the less favored elementary steps are given in the ESI† (Table S6). Energies of 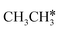 dehydrogenation calculated by DFT and the Gibbs free energy profiles at a higher H2 partial pressure (19.7 atm) are given in the ESI† (Fig. S3–S6). It is noted that the reported final dissociation energy is calculated after considering the diffusion of the dissociated surface H* atoms to the most stable sites.
dehydrogenation calculated by DFT and the Gibbs free energy profiles at a higher H2 partial pressure (19.7 atm) are given in the ESI† (Fig. S3–S6). It is noted that the reported final dissociation energy is calculated after considering the diffusion of the dissociated surface H* atoms to the most stable sites.
The breaking of the first C–H bond has a Gibbs free energy barrier of 0.89 eV and a reaction Gibbs free energy of 0.26 eV. As shown in Table 2, this endothermic property (0.25 eV from DFT, Table S3†) is consistent with that on the Ni(111),16 Ru(0001),27 Rh(111),38 Pd(111),59 and Ir(111)60 surfaces, while in contrast to the exothermic property on the Fe(100),61 Fe(110),62 Rh(211),63 Pt(111) and Pt(211)14 surfaces. In the transition state, the breaking C–H bond stands over one Ru atom and has a distance of 1.619 Å, and the distance of the forming Ru–C and Ru–H bonds is 2.314 and 1.656 Å, respectively. In contrast, the C–C bond breaking of 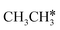 leading to
leading to 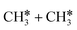 has a Gibbs free energy barrier of 2.25 eV and a positive reaction Gibbs free energy of 0.09 eV, and is much less competitive kinetically with the C–H bond dissociation.
has a Gibbs free energy barrier of 2.25 eV and a positive reaction Gibbs free energy of 0.09 eV, and is much less competitive kinetically with the C–H bond dissociation.
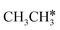 to
to 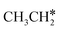 and H* on transition metal surfaces. The models and methods in their computation are listed
and H* on transition metal surfaces. The models and methods in their computation are listed
| Surface | Model/method | E a | ΔEr |
|---|---|---|---|
| Fe(100)61 | p(2 × 2); 4L1R/PW91 | 0.80 | −0.23 |
| Fe(110)62 | p(5 × 5); 5L4R/PBE | 0.65 | −0.48 |
| Ni(111)16 |
p(2 ×  ); 4L1R/PBE ); 4L1R/PBE |
— | 0.04 |
| Ru(0001)27 | p(2 × 2), p(3 × 3); 6L3R/PBE | 0.86 | 0.09 |
| Rh(111)38 | p(2 × 2); 3L2R/PW91 | 0.66 | 0.24 |
| Rh(211)63 | p(3 × 2); 8L8R/PBE | 0.34 | −0.57 |
| Pd(111)59 | p(2 × 2); 3L2R/PW91 | 1.06 | 0.05 |
| Ir(111)60 |
p(3 × 3); 4L1R/PW91 (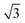 × × 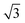 )R30°; 4L1R/PW91 )R30°; 4L1R/PW91 |
0.45 | 0.28 |
| 0.45 | 0.51 | ||
| Pt(111)14 | p(2 × 2); 4L2R/PBE | 0.54 | −0.48 |
| Pt(211)14 | p(2 × 1); 12L6R/PBE | 0.08 | −0.81 |
Starting from 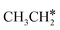 , it is possible to break the α-C–H bond to CH3CH*, the β-C–H bond to
, it is possible to break the α-C–H bond to CH3CH*, the β-C–H bond to 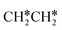 and the C–C bond to
and the C–C bond to 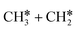 . It is found that breaking the α-C–H bond to CH3CH* has a Gibbs free energy barrier of 0.03 eV and a reaction Gibbs free energy of −0.74 eV, due to the strong agostic interaction of the adsorbed
. It is found that breaking the α-C–H bond to CH3CH* has a Gibbs free energy barrier of 0.03 eV and a reaction Gibbs free energy of −0.74 eV, due to the strong agostic interaction of the adsorbed 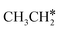 . In the transition state, the breaking C–H bond is 1.516 Å, the Ru–C distance is 2.137 Å and the Ru–H distance is 1.669 Å. Next, breaking the β-C–H bond to
. In the transition state, the breaking C–H bond is 1.516 Å, the Ru–C distance is 2.137 Å and the Ru–H distance is 1.669 Å. Next, breaking the β-C–H bond to 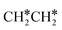 has a very low Gibbs free energy barrier of 0.13 eV and a reaction Gibbs free energy of −0.49 eV. In contrast, breaking the C–C bond to
has a very low Gibbs free energy barrier of 0.13 eV and a reaction Gibbs free energy of −0.49 eV. In contrast, breaking the C–C bond to 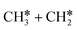 has a Gibbs free energy barrier of 0.77 eV and a reaction Gibbs free energy of −0.51 eV. Therefore, breaking both α- and β-C–H bonds is competitive and favored kinetically, while C–C bond cleavage is not favored kinetically.
has a Gibbs free energy barrier of 0.77 eV and a reaction Gibbs free energy of −0.51 eV. Therefore, breaking both α- and β-C–H bonds is competitive and favored kinetically, while C–C bond cleavage is not favored kinetically.
Starting from CH3CH*, it is very easy for CH3CH* to lose the α-H atom and the reaction has a reaction Gibbs free energy of −0.82 eV and is barrier-less, due to the very strong C–H agostic interaction with a surface Ru atom (1.252 Å, Table 1), similar to that of HCH* dissociation. In the transition state, the breaking C–H distance is 1.421 Å, the Ru–C distance is 2.101 Å and the Ru–H distance is 1.673 Å. Alternatively, losing a H atom of CH3 in CH3CH* to form 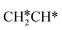 has a Gibbs free energy barrier of 0.43 eV and a slight reaction Gibbs free energy of −0.02 eV. In contrast, the C–C bond dissociation of
has a Gibbs free energy barrier of 0.43 eV and a slight reaction Gibbs free energy of −0.02 eV. In contrast, the C–C bond dissociation of 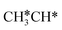 to
to 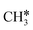 + CH* has a Gibbs free energy barrier of 0.98 eV and a reaction Gibbs free energy of −0.41 eV. Therefore, the dissociation of CH3CH* to CH3C* + H* is the most favored kinetically and thermodynamically.
+ CH* has a Gibbs free energy barrier of 0.98 eV and a reaction Gibbs free energy of −0.41 eV. Therefore, the dissociation of CH3CH* to CH3C* + H* is the most favored kinetically and thermodynamically.
There are two possible routes to dissociate CH3C*, C–H and C–C, and both routes need to bend the C–C bond due to the upright adsorption configuration. The C–H bond dissociation of CH3C* to 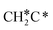 + H* has a Gibbs free energy barrier of 0.66 eV and a reaction Gibbs free energy of 0.16 eV. In the transition state, the breaking C–H distance is 1.637 Å, and the distance of the forming Ru–C and Ru–H bonds is 2.292 Å and 1.680 Å, respectively. Alternatively, the C–C bond dissociation of CH3C* to
+ H* has a Gibbs free energy barrier of 0.66 eV and a reaction Gibbs free energy of 0.16 eV. In the transition state, the breaking C–H distance is 1.637 Å, and the distance of the forming Ru–C and Ru–H bonds is 2.292 Å and 1.680 Å, respectively. Alternatively, the C–C bond dissociation of CH3C* to 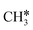 + C* has a Gibbs free energy barrier of 1.54 eV and a reaction Gibbs free energy of 0.64 eV. Therefore, it is easier to break the C–H bond both kinetically and thermodynamically.
+ C* has a Gibbs free energy barrier of 1.54 eV and a reaction Gibbs free energy of 0.64 eV. Therefore, it is easier to break the C–H bond both kinetically and thermodynamically.
Next, the formed 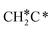 can break either one C–H bond to HC*C* or the C–C bond to
can break either one C–H bond to HC*C* or the C–C bond to 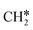 + C*. The C–H bond dissociation has a Gibbs free energy barrier of 0.74 eV and a slight reaction Gibbs free energy of −0.01 eV, and in the transition state the breaking C–H distance is 1.467 Å and the forming Ru–H distance is 1.728 Å. In contrast, the C–C bond dissociation needs the migration of the CH2 group to the top site at first and then breaks the C–C bond with a Gibbs free energy barrier of 1.60 eV and a reaction Gibbs free energy of 0.29 eV, and the breaking C–C distance in the transition state is 2.068 Å. For
+ C*. The C–H bond dissociation has a Gibbs free energy barrier of 0.74 eV and a slight reaction Gibbs free energy of −0.01 eV, and in the transition state the breaking C–H distance is 1.467 Å and the forming Ru–H distance is 1.728 Å. In contrast, the C–C bond dissociation needs the migration of the CH2 group to the top site at first and then breaks the C–C bond with a Gibbs free energy barrier of 1.60 eV and a reaction Gibbs free energy of 0.29 eV, and the breaking C–C distance in the transition state is 2.068 Å. For 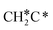 , it is easier to break the C–H bond both kinetically and thermodynamically.
, it is easier to break the C–H bond both kinetically and thermodynamically.
In the flat adsorption configuration of HC*C*, both carbon atoms are at the 3-fold sites. In the transition state of the C–C bond dissociation, the HC group changes to the bridge site and the breaking C–C distance is 2.080 Å, and the Ru–C distances are 1.938 and 2.001 Å. It is found that the C–C bond dissociation has a lower Gibbs free energy barrier than the C–H bond dissociation (1.04 vs. 1.33 eV) and the former has a reaction Gibbs free energy of −0.30 eV, while the latter has a reaction Gibbs free energy of 0.43 eV.
In the Gibbs free energy profiles in Fig. 7, 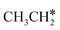 , once formed, will dissociate directly to CH3C* and the formation of surface CH3C* has a reaction Gibbs free energy of −1.30 eV. In addition, the co-adsorbed CH3C* + 3H*, CH2C* + 4H* and HC*C* + 5H* states are close in energy. Although CH* + C* + 5H* is more stable, the corresponding step needs a Gibbs free energy barrier of 1.04 eV. For the full decomposition, surface CH* is the most stable species. Considering the back reaction of C* + H* to CH, which has a reaction Gibbs free energy of −0.29 and has a Gibbs free energy barrier of 0.68 eV (Table S3†), the final surface species should be CH* + CH*. On Ru(111), ethane dissociation has the minimum energy path of
, once formed, will dissociate directly to CH3C* and the formation of surface CH3C* has a reaction Gibbs free energy of −1.30 eV. In addition, the co-adsorbed CH3C* + 3H*, CH2C* + 4H* and HC*C* + 5H* states are close in energy. Although CH* + C* + 5H* is more stable, the corresponding step needs a Gibbs free energy barrier of 1.04 eV. For the full decomposition, surface CH* is the most stable species. Considering the back reaction of C* + H* to CH, which has a reaction Gibbs free energy of −0.29 and has a Gibbs free energy barrier of 0.68 eV (Table S3†), the final surface species should be CH* + CH*. On Ru(111), ethane dissociation has the minimum energy path of 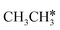 →
→ 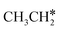 → CH3CH* → CH3C* → CH2C* → HC*C* → HC* + C* → C* + C*, and the final surface species should be CH* by considering the favored surface C* hydrogenation (Table S3†). Fig. 7 also shows that the adsorbed H* atoms will remain on the surface, since H2 adsorption is exergonic for all stable surface species. On the basis of 2C* + 3H2(g), ethane formation has a Gibbs free energy of 0.62 eV at 490 K and 1 atm H2 and 0.25 eV at 490 K and 19.7 atm H2 (Fig. S4†).
→ CH3CH* → CH3C* → CH2C* → HC*C* → HC* + C* → C* + C*, and the final surface species should be CH* by considering the favored surface C* hydrogenation (Table S3†). Fig. 7 also shows that the adsorbed H* atoms will remain on the surface, since H2 adsorption is exergonic for all stable surface species. On the basis of 2C* + 3H2(g), ethane formation has a Gibbs free energy of 0.62 eV at 490 K and 1 atm H2 and 0.25 eV at 490 K and 19.7 atm H2 (Fig. S4†).
This minimum energy path is roughly the same as that found by Ande et al. on the Ru(0001) surface,27 although they did not consider the last step of the C–C bond dissociation and the differences in the barriers and reaction energies might be due to the use of different methods and surface sizes. Nevertheless, we computed the dissociation of 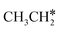 + H* to CH3CH* + 2H* and
+ H* to CH3CH* + 2H* and 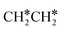 + 2H* on the p(4 × 4) Ru(0001) surface using the same method and surface size for comparison and the detailed results are given in the ESI† (Table S4). At first, we found that the Ru–Ru distance is shorter on the Ru(111) surface than on the Ru(0001) surface (2.698 vs. 2.732 Å), while the interlayer Ru–Ru distance of Ru(111) is longer than that of Ru(0001) (2.636 vs. 2.615 Å). This shows that the surface Ru atoms of Ru(111) are denser than those of Ru(0001).
+ 2H* on the p(4 × 4) Ru(0001) surface using the same method and surface size for comparison and the detailed results are given in the ESI† (Table S4). At first, we found that the Ru–Ru distance is shorter on the Ru(111) surface than on the Ru(0001) surface (2.698 vs. 2.732 Å), while the interlayer Ru–Ru distance of Ru(111) is longer than that of Ru(0001) (2.636 vs. 2.615 Å). This shows that the surface Ru atoms of Ru(111) are denser than those of Ru(0001).
Next, we compared the adsorption of H*, 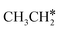 , CH3CH* and
, CH3CH* and 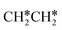 on Ru(0001) (Table S5†) and Ru(111) (Table 1). The most preferred site of adsorbed H* is the fcc site on Ru (111) and Ru (0001) with close adsorption energies (−2.75 vs. −2.78 eV). It is found that
on Ru(0001) (Table S5†) and Ru(111) (Table 1). The most preferred site of adsorbed H* is the fcc site on Ru (111) and Ru (0001) with close adsorption energies (−2.75 vs. −2.78 eV). It is found that 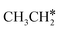 adsorption prefers the hcp site on Ru(0001) and the fcc site (−1.26 eV) on Ru(111), and both surfaces have close adsorption energies (−1.23 vs. −1.26 eV). A small difference (0.05 eV) is found for the adsorption energy of
adsorption prefers the hcp site on Ru(0001) and the fcc site (−1.26 eV) on Ru(111), and both surfaces have close adsorption energies (−1.23 vs. −1.26 eV). A small difference (0.05 eV) is found for the adsorption energy of 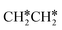 (−0.56 vs. −0.61 eV) on Ru(0001) and Ru(111). However, a larger difference (0.23 eV) is found for the adsorption of CH3CH* (−3.43 vs. −3.66 eV) on Ru(0001) and Ru(111) and further analysis shows that CH3CH* has a stronger C–H agostic interaction (1.254 vs. 1.206 Å) on Ru(111) than on Ru(0001).
(−0.56 vs. −0.61 eV) on Ru(0001) and Ru(111). However, a larger difference (0.23 eV) is found for the adsorption of CH3CH* (−3.43 vs. −3.66 eV) on Ru(0001) and Ru(111) and further analysis shows that CH3CH* has a stronger C–H agostic interaction (1.254 vs. 1.206 Å) on Ru(111) than on Ru(0001).
For 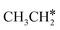 + H* dissociation to
+ H* dissociation to 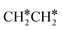 + 2H*, the barrier is 0.24 eV and the reaction is exothermic by 0.35 eV on Ru(0001) (Table S4†), and on Ru(111) the barrier is lower (0.10 eV) and the reaction is more exothermic (−0.50 eV). For
+ 2H*, the barrier is 0.24 eV and the reaction is exothermic by 0.35 eV on Ru(0001) (Table S4†), and on Ru(111) the barrier is lower (0.10 eV) and the reaction is more exothermic (−0.50 eV). For 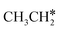 + H* dissociation to
+ H* dissociation to 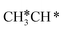 + 2H* on Ru(0001), the barrier is 0.23 eV and the reaction is exothermic by 0.35 eV, while on Ru(111) this reaction is barrier-less (0.00 eV) and much more exothermic (−0.75 eV). These demonstrate clearly that Ru(111) has a stronger adsorption ability than Ru(0001) despite their similar surface structures on the one hand, and the fcc Ru(111) surface is more active than the hcp Ru(0001) surface on the other hand. In addition to the above results for the dissociation of
+ 2H* on Ru(0001), the barrier is 0.23 eV and the reaction is exothermic by 0.35 eV, while on Ru(111) this reaction is barrier-less (0.00 eV) and much more exothermic (−0.75 eV). These demonstrate clearly that Ru(111) has a stronger adsorption ability than Ru(0001) despite their similar surface structures on the one hand, and the fcc Ru(111) surface is more active than the hcp Ru(0001) surface on the other hand. In addition to the above results for the dissociation of 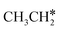 , distinct differences between hcp Ru and fcc were also reported,40 which include denser active sites of fcc Ru than hcp Ru, i.e., more facets of fcc Ru for CO* dissociation in the barrier range from 1.12 to 1.20 eV than hcp Ru as well as decreasing methane selectivity of fcc Ru compared to that of hcp Ru with increasing temperature in FTS.
, distinct differences between hcp Ru and fcc were also reported,40 which include denser active sites of fcc Ru than hcp Ru, i.e., more facets of fcc Ru for CO* dissociation in the barrier range from 1.12 to 1.20 eV than hcp Ru as well as decreasing methane selectivity of fcc Ru compared to that of hcp Ru with increasing temperature in FTS.
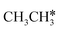 consecutive dissociation can also form adsorbed ethene
consecutive dissociation can also form adsorbed ethene 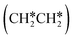 , we therefore computed their dissociation to complete the potential energy surface. To keep these species comparable on the potential energy surface, we used the same reference as in Fig. 7.
, we therefore computed their dissociation to complete the potential energy surface. To keep these species comparable on the potential energy surface, we used the same reference as in Fig. 7.
For 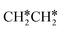 dissociation, there are two possibilities, C–H dissociation to
dissociation, there are two possibilities, C–H dissociation to 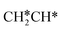 + H* and C–C dissociation to
+ H* and C–C dissociation to 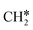 +
+ 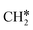 . Alternatively, the adsorbed ethene can also desorb from the surface in the gas phase. As shown in Fig. 8, C–H dissociation has a much lower Gibbs free energy barrier than C–C dissociation (0.20 vs. 1.20 eV), and the reaction Gibbs free energy of C–H dissociation is also more negative than that of C–C dissociation (−0.34 vs. −0.29 eV). Due to the uncertainty of ethene partial pressure, we computed its desorption by DFT (Fig. S5†), and found that the desorption energy of ethene is higher than the C–H dissociation barrier (0.58 vs. 0.13 eV). Thus, surface
. Alternatively, the adsorbed ethene can also desorb from the surface in the gas phase. As shown in Fig. 8, C–H dissociation has a much lower Gibbs free energy barrier than C–C dissociation (0.20 vs. 1.20 eV), and the reaction Gibbs free energy of C–H dissociation is also more negative than that of C–C dissociation (−0.34 vs. −0.29 eV). Due to the uncertainty of ethene partial pressure, we computed its desorption by DFT (Fig. S5†), and found that the desorption energy of ethene is higher than the C–H dissociation barrier (0.58 vs. 0.13 eV). Thus, surface 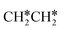 will dissociate preferably into surface
will dissociate preferably into surface 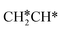 + H*. Although surface
+ H*. Although surface 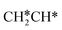 will dissociate spontaneously into CH2C* (Fig. 7), we computed surface CH*CH* formation from
will dissociate spontaneously into CH2C* (Fig. 7), we computed surface CH*CH* formation from 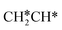 dissociation, which has a very low Gibbs free energy barrier of 0.24 eV and a very strong reaction Gibbs free energy of −0.61 eV. For the adsorbed CH*CH* on the surface (Fig. 8), it also has the possibilities for C–H dissociation to form HC*C* + H* and C–C dissociation to form CH* + CH*. It is found that the C–H dissociation has a lower Gibbs free energy barrier than the C–C dissociation (0.63 vs. 0.86 eV), and the former is nearly thermally neutral (0.03 eV) and the latter is negative by −0.56 eV. In addition, the desorption energy of ethyne (2.43 eV, Fig. S5†) is much higher than the C–H dissociation barrier. Therefore, surface CH*CH* will dissociate preferably into surface HC*C* + H*. Combining Fig. 7 and 8 shows that the dissociation of
dissociation, which has a very low Gibbs free energy barrier of 0.24 eV and a very strong reaction Gibbs free energy of −0.61 eV. For the adsorbed CH*CH* on the surface (Fig. 8), it also has the possibilities for C–H dissociation to form HC*C* + H* and C–C dissociation to form CH* + CH*. It is found that the C–H dissociation has a lower Gibbs free energy barrier than the C–C dissociation (0.63 vs. 0.86 eV), and the former is nearly thermally neutral (0.03 eV) and the latter is negative by −0.56 eV. In addition, the desorption energy of ethyne (2.43 eV, Fig. S5†) is much higher than the C–H dissociation barrier. Therefore, surface CH*CH* will dissociate preferably into surface HC*C* + H*. Combining Fig. 7 and 8 shows that the dissociation of 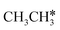 ,
, 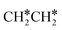 and CH*CH* will end up with the same surface intermediate HC*C*, which will first dissociate into CH* + C* and then become CH* + CH* with the presence of surface H*.
and CH*CH* will end up with the same surface intermediate HC*C*, which will first dissociate into CH* + C* and then become CH* + CH* with the presence of surface H*.
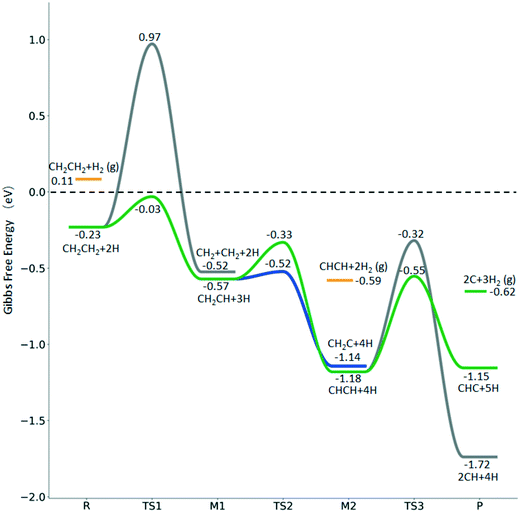 | ||
Fig. 8 Gibbs free energy profiles of 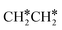 consecutive dissociation at 490 K and 1 atm H2 (energy level on the basis of adsorbed consecutive dissociation at 490 K and 1 atm H2 (energy level on the basis of adsorbed 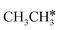 ); combined with Fig. 7, a complete potential energy surface of ); combined with Fig. 7, a complete potential energy surface of 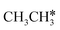 dissociation is presented; the path of ethene dissociation through the ethyne intermediate is in green; the desorption of surface H* and the breaking of the C–C bond for dissociation is presented; the path of ethene dissociation through the ethyne intermediate is in green; the desorption of surface H* and the breaking of the C–C bond for 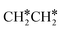 + 2H* and CH*CH* + 4H* are given in orange and grey, respectively. + 2H* and CH*CH* + 4H* are given in orange and grey, respectively. | ||
The Gibbs free energy profile shows that the minimum energy path of 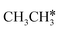 full dissociation on Ru(111) does not have surface ethene and ethyne as intermediates (Fig. 7), and ethene dissociation does not have ethyne as an intermediate (Fig. 8); however ethane, ethene and ethyne dissociations end up with the same surface intermediates (HC* and H*). Without considering the isomerization steps, the minimum energy path for ethene dissociative adsorption has the order
full dissociation on Ru(111) does not have surface ethene and ethyne as intermediates (Fig. 7), and ethene dissociation does not have ethyne as an intermediate (Fig. 8); however ethane, ethene and ethyne dissociations end up with the same surface intermediates (HC* and H*). Without considering the isomerization steps, the minimum energy path for ethene dissociative adsorption has the order 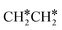 →
→ 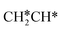 →
→ 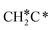 → HC*C* → CH* + C* → C* + C*, and the minimum energy path of ethyne dissociative adsorption has the order CH*CH* → HC*C* → CH* + C* → C* + C*. Experimentally, ethene dissociative adsorption has surface intermediates of
→ HC*C* → CH* + C* → C* + C*, and the minimum energy path of ethyne dissociative adsorption has the order CH*CH* → HC*C* → CH* + C* → C* + C*. Experimentally, ethene dissociative adsorption has surface intermediates of 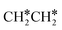 at 120 K, CH3C* at 280 K, HC*C* at 450 K, HC* at 550 K and C* above 650 K,29 and therefore, there must be an arrangement or isomerization for CH3C* formation during ethene dissociative adsorption. Since
at 120 K, CH3C* at 280 K, HC*C* at 450 K, HC* at 550 K and C* above 650 K,29 and therefore, there must be an arrangement or isomerization for CH3C* formation during ethene dissociative adsorption. Since 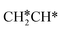 dissociation to CH2C* has a very low Gibbs free energy barrier of 0.05 eV and a very strong reaction Gibbs free energy of −0.57 eV (Fig. 8),
dissociation to CH2C* has a very low Gibbs free energy barrier of 0.05 eV and a very strong reaction Gibbs free energy of −0.57 eV (Fig. 8), 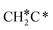 should be formed first. Next,
should be formed first. Next, 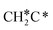 can react with surface H* to form CH3C* with a Gibbs free energy barrier of 0.50 eV and a reaction Gibbs free energy of −0.16 eV (Fig. 7), while
can react with surface H* to form CH3C* with a Gibbs free energy barrier of 0.50 eV and a reaction Gibbs free energy of −0.16 eV (Fig. 7), while 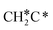 dissociation to HC*C* has a higher Gibbs free energy barrier of 0.74 eV and is not competitive kinetically. With the increase of temperature, surface CH3C* can sequentially dissociate to surface
dissociation to HC*C* has a higher Gibbs free energy barrier of 0.74 eV and is not competitive kinetically. With the increase of temperature, surface CH3C* can sequentially dissociate to surface 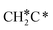 , HC*C*, CH* + C* and C* + C*. In general, our computed results agree with those of Shan et al.38 for ethene dissociative adsorption on the Rh(111) surface despite the higher adsorption energy of ethene (−0.97 vs. −0.61 eV), the higher barrier and lower exothermicity of the formation of
, HC*C*, CH* + C* and C* + C*. In general, our computed results agree with those of Shan et al.38 for ethene dissociative adsorption on the Rh(111) surface despite the higher adsorption energy of ethene (−0.97 vs. −0.61 eV), the higher barrier and lower exothermicity of the formation of 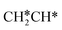 (0.52 and 0.02 eV) and
(0.52 and 0.02 eV) and 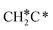 (0.21 and −0.26 eV), and the higher barrier and higher exothermicity for
(0.21 and −0.26 eV), and the higher barrier and higher exothermicity for 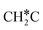 hydrogenation to CH3C* (0.66 and −0.30 eV).
hydrogenation to CH3C* (0.66 and −0.30 eV).
Although the hydrogen co-adsorbed species of CH3C* + 3H*, CH2C* + 4H* and HC*C* + 5H* are close in terms of free energy (−1.30, −1.14 and −1.15 eV, respectively, Fig. 7), surface CH3C*, CH2C* and HC*C* differ strongly in stability on the basis of gaseous H2 (−0.87, −0.59, and −0.53 eV, respectively). Considering the associative desorption of H2, the formation barriers of CH2C*, HC*C*, HC* + C* and C* + C* will be located at −0.21, 0.15, 0.51 and 0.00 eV in free energy profiles, and this is in line with the temperature change observed in the experiment. On the basis of 2C* + 3H2(g), ethene formation has a Gibbs free energy of 0.73 eV at 490 K and 1 atm H2 and 0.48 eV at 490 K and 19.7 atm H2 (Fig. S6†).
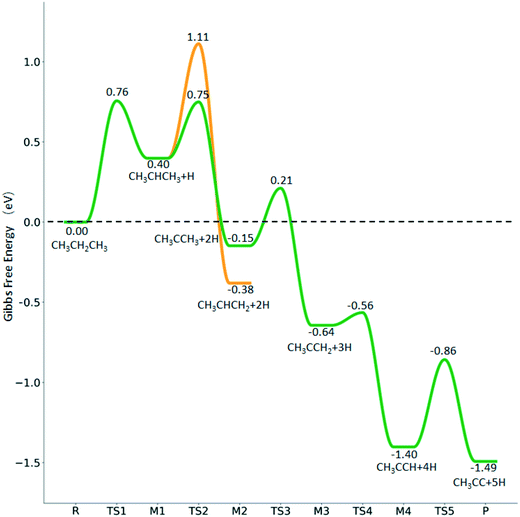
3.4. Dehydrogenation of propane, propene, and Propyne
In addition to the dehydrogenation of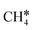 and
and 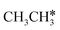 , we further computed the complete dissociation of propane and this is particularly interesting for understanding the formation of propene and the intrinsic nature of FTS. Compared with
, we further computed the complete dissociation of propane and this is particularly interesting for understanding the formation of propene and the intrinsic nature of FTS. Compared with 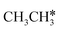 ,
, 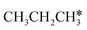 dissociation is more complex with the cleavage of 17 C–H bonds and 14 C–C bonds (Fig. 9).
dissociation is more complex with the cleavage of 17 C–H bonds and 14 C–C bonds (Fig. 9).
In contrast to 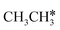 ,
, 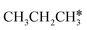 has two types of C–H bonds, the terminal and central C–H bonds. The formation of n-propyl and isopropyl from terminal and central C–H bond dissociation has Gibbs free energy barriers of 0.79 and 0.76 eV, respectively, and positive reaction Gibbs free energies of 0.15 and 0.40 eV, respectively, revealing their kinetic competitivity. In the transition state of n-propyl formation, the breaking C–H bond is captured by a Ru atom and has a distance of 1.642 Å; the Ru–C distance is 2.323 Å, and the Ru–H distance is 1.684 Å. In the transition state of isopropyl formation, the breaking C–H bond is also captured by a Ru atom and has a distance of 1.672 Å; the Ru–C distance is 2.356 Å, and the Ru–H distance is 1.664 Å.
has two types of C–H bonds, the terminal and central C–H bonds. The formation of n-propyl and isopropyl from terminal and central C–H bond dissociation has Gibbs free energy barriers of 0.79 and 0.76 eV, respectively, and positive reaction Gibbs free energies of 0.15 and 0.40 eV, respectively, revealing their kinetic competitivity. In the transition state of n-propyl formation, the breaking C–H bond is captured by a Ru atom and has a distance of 1.642 Å; the Ru–C distance is 2.323 Å, and the Ru–H distance is 1.684 Å. In the transition state of isopropyl formation, the breaking C–H bond is also captured by a Ru atom and has a distance of 1.672 Å; the Ru–C distance is 2.356 Å, and the Ru–H distance is 1.664 Å.
Since 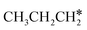 and
and 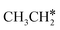 are homologs, we computed the consecutive C–H dissociation of
are homologs, we computed the consecutive C–H dissociation of 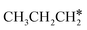 + H* → CH3CH2CH* + 2H*,
+ H* → CH3CH2CH* + 2H*, 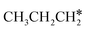 + H* →
+ H* → 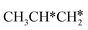 + 2H* and
+ 2H* and 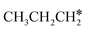 + H* →
+ H* → 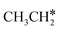 +
+ 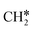 + H* for direct comparison (Fig. 10). Since the terminal CH3 group of
+ H* for direct comparison (Fig. 10). Since the terminal CH3 group of 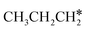 hardly interacts with the surface, the corresponding C–H and C–C dissociation should not be dominant. Our results show that
hardly interacts with the surface, the corresponding C–H and C–C dissociation should not be dominant. Our results show that 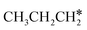 dehydrogenation into CH3CH2CH* and
dehydrogenation into CH3CH2CH* and 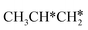 via α- and β-C–H bonds has close Gibbs free energy barriers of 0.15 and 0.16 eV and reaction Gibbs free energies of −0.65 and −0.53 eV, respectively. Thus, both α- and β-C–H dissociations are favored and competitive, and they are similar to those of the C–H dissociation of
via α- and β-C–H bonds has close Gibbs free energy barriers of 0.15 and 0.16 eV and reaction Gibbs free energies of −0.65 and −0.53 eV, respectively. Thus, both α- and β-C–H dissociations are favored and competitive, and they are similar to those of the C–H dissociation of 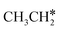 . In the transition state of α-C–H dissociation, the breaking C–H distance is 1.568 Å and the forming Ru–H distance is 1.671 Å. In the transition state of β-C–H dissociation, the breaking C–H distance is 1.552 Å and the forming Ru–H distance is 1.701 Å.
. In the transition state of α-C–H dissociation, the breaking C–H distance is 1.568 Å and the forming Ru–H distance is 1.671 Å. In the transition state of β-C–H dissociation, the breaking C–H distance is 1.552 Å and the forming Ru–H distance is 1.701 Å.
For the dissociation of the isopropyl group (Fig. 11), the dissociation of the central C–H bond leading to (CH3)2C* + H* has a Gibbs free energy barrier of 0.33 eV and a reaction Gibbs free energy of −0.55 eV, while one terminal C–H bond dissociation resulting in adsorbed propene 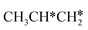 + H* has a Gibbs free energy barrier of 0.71 and a reaction Gibbs free energy of −0.78 eV, and the former is more favored kinetically and the latter is more preferred thermodynamically. Comparing Fig. 10 and 11 shows that the formation of propylidene (CH3CH2CH*) is more favored thermodynamically than that of isopropylidene, (CH3)2C*, by 0.35 eV.
+ H* has a Gibbs free energy barrier of 0.71 and a reaction Gibbs free energy of −0.78 eV, and the former is more favored kinetically and the latter is more preferred thermodynamically. Comparing Fig. 10 and 11 shows that the formation of propylidene (CH3CH2CH*) is more favored thermodynamically than that of isopropylidene, (CH3)2C*, by 0.35 eV.
As in the case of HCH* and CH3CH*, the adsorbed CH3CH2CH* also has a very strong α-C–H agostic interaction (1.278 Å, Table 1). As expected, the surface CH3CH2C* formation is barrier-less and has a reaction Gibbs free energy of −0.89 eV. In the transition state, the breaking C–H distance is 1.406 Å and the forming Ru–H distance is 1.673 Å. In contrast, the reactions of CH3CH2CH* → CH3CH*CH* + H* and CH3CH2CH* → 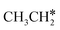 + CH* have higher Gibbs free energy barriers (0.28 and 0.86 eV, respectively) and much less negative reaction Gibbs free energies (−0.26 and −0.18 eV, respectively). It is noted that CH3CH2C* is a higher homolog of CH3C* and HC*. Starting from CH3CH2C*, the β-C–H dissociation of CH3CH2C* → CH3CH*C* + H* has a lower Gibbs free energy barrier (0.55 eV) and is nearly thermally neutral (−0.01 eV), while the C–C dissociation of CH3CH2C* →
+ CH* have higher Gibbs free energy barriers (0.28 and 0.86 eV, respectively) and much less negative reaction Gibbs free energies (−0.26 and −0.18 eV, respectively). It is noted that CH3CH2C* is a higher homolog of CH3C* and HC*. Starting from CH3CH2C*, the β-C–H dissociation of CH3CH2C* → CH3CH*C* + H* has a lower Gibbs free energy barrier (0.55 eV) and is nearly thermally neutral (−0.01 eV), while the C–C dissociation of CH3CH2C* → 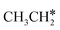 + C* has a higher Gibbs free energy barrier (1.71 eV) and a very positive reaction Gibbs free energy (0.88 eV). In the transition state of β-C–H dissociation, the breaking C–H distance is 1.686 Å and the forming Ru–H distance is 1.680 Å.
+ C* has a higher Gibbs free energy barrier (1.71 eV) and a very positive reaction Gibbs free energy (0.88 eV). In the transition state of β-C–H dissociation, the breaking C–H distance is 1.686 Å and the forming Ru–H distance is 1.680 Å.
Based on the most stable co-adsorption configuration of CH3CH*C* + 4H* atoms, we compared the β-C–H bond dissociation of CH3CH*C* to CH3C*C* + H* and the C–C bond dissociation of CH3CH*C* to CH3CH* + C*. It is found that the former has a Gibbs free energy barrier of 0.78 eV and is nearly thermally neutral (−0.09 eV), while the latter has a Gibbs free energy barrier of 1.78 eV and a positive reaction Gibbs free energy of 0.33 eV. Thus, the β-C–H bond dissociation is more favored kinetically and thermodynamically, and in the transition state the breaking C–H distance is 1.483 Å and the forming Ru–H distance is 1.737 Å.
For the consecutive C–H dissociation of isopropylidene (Fig. 11), (CH3)2C* → 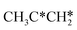 → CH3C*CH* → CH3C*C*, all steps have low Gibbs free energy barriers (0.36, 0.08 and 0.54 eV, respectively) and negative reaction Gibbs free energies (−0.49, −0.76 and −0.09, respectively). Both the n-propyl and isopropyl routes end up with the formation of CH3C*C*. On the basis of their similar barriers and reaction energies of intermediates, both routes are possible once n-propyl and isopropyl are formed simultaneously.
→ CH3C*CH* → CH3C*C*, all steps have low Gibbs free energy barriers (0.36, 0.08 and 0.54 eV, respectively) and negative reaction Gibbs free energies (−0.49, −0.76 and −0.09, respectively). Both the n-propyl and isopropyl routes end up with the formation of CH3C*C*. On the basis of their similar barriers and reaction energies of intermediates, both routes are possible once n-propyl and isopropyl are formed simultaneously.
Different from the previous HC*C*, we computed the breaking of the two C–C bonds in CH3C*C* by considering CH3C*C* as the higher homolog of HC*C*. It is found that the surface C–C bond dissociation resulting in CH3C* + C* has a Gibbs free energy barrier of 0.99 eV and a reaction Gibbs free energy of −0.33 eV, while the terminal C–C bond dissociation leading to 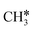 + C*C* has a much higher Gibbs free energy barrier (2.08 eV) and a very endothermic reaction Gibbs free energy (1.27 eV). Therefore, the surface C–C bond dissociation is more favored kinetically and thermodynamically; in the transition state the breaking C–C distance is 2.059 Å. Thus, the formation of CH3C* + C* is favored than that of
+ C*C* has a much higher Gibbs free energy barrier (2.08 eV) and a very endothermic reaction Gibbs free energy (1.27 eV). Therefore, the surface C–C bond dissociation is more favored kinetically and thermodynamically; in the transition state the breaking C–C distance is 2.059 Å. Thus, the formation of CH3C* + C* is favored than that of 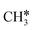 + C*C* on the Ru(111) surface.
+ C*C* on the Ru(111) surface.
Fig. 10 shows some very interesting points. After the first C–H dissociation, CH3CH2C*, the higher homolog of CH3C* and HC*, is also a stable surface intermediate. As in the case of CH3C* dissociation to HC* (Fig. 7), which has an increasing barrier and is endothermic till the last step, CH3CH2C* dissociation to CH3C* has also an increasing barrier and is exothermic in all steps. Considering the CH3C* dissociation in Fig. 7 and the CH3CH2C* dissociation in Fig. 10 as well as the favored surface carbon hydrogenation (Tables S3 and S7†), one can expect that 3CH* + 5H* should be the dominant surface species for CH3CH2CH3 full dissociation. Fig. 10 also shows that the adsorbed H* atoms will remain on the surface, since H2 adsorption is exergonic for all stable surface species. On the basis of C* + C* + C* + 4H2(g), propane formation has a Gibbs free energy of 0.87 eV at 490 K and 1 atm H2 as well as 0.36 eV at 490 K and 19.7 atm H2 (Fig. S8†).
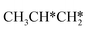 and CH3C*CH* can be formed from the n-propyl and isopropyl routes, respectively, and their consecutive C–H bond dissociations end up with the formation of CH3C*C* + 5H*, which further dissociates into CH3C* + C* + 5H*. Nevertheless, we computed their consecutive dissociation for comparison on the basis of the same reference line (Fig. 12).
and CH3C*CH* can be formed from the n-propyl and isopropyl routes, respectively, and their consecutive C–H bond dissociations end up with the formation of CH3C*C* + 5H*, which further dissociates into CH3C* + C* + 5H*. Nevertheless, we computed their consecutive dissociation for comparison on the basis of the same reference line (Fig. 12).
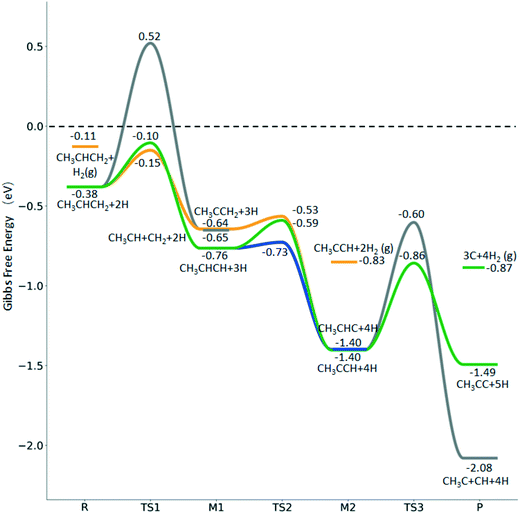 | ||
Fig. 12 Gibbs free energy profiles of 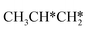 consecutive dissociation at 490 K and 1 atm H2 (energy level on the basis of adsorbed consecutive dissociation at 490 K and 1 atm H2 (energy level on the basis of adsorbed 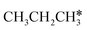 ); combined with Fig. 10 and 11, a complete potential energy surface of ); combined with Fig. 10 and 11, a complete potential energy surface of 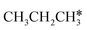 dissociation is presented; the path of propene dissociation through the propyne intermediate is in green; the path of dissociation is presented; the path of propene dissociation through the propyne intermediate is in green; the path of 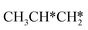 +2H* → +2H* → 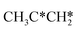 + 3H* → CH3C*CH* + 4H* is in orange; the path of CH3CH*CH* + 3H* → CH3CH*C* + 4H* is in blue; the desorption of surface H* and the breaking of the C–C bond for + 3H* → CH3C*CH* + 4H* is in orange; the path of CH3CH*CH* + 3H* → CH3CH*C* + 4H* is in blue; the desorption of surface H* and the breaking of the C–C bond for 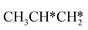 + 2H* and CH3C*CH* + 4H* are respectively in orange and grey. + 2H* and CH3C*CH* + 4H* are respectively in orange and grey. | ||
Starting from surface 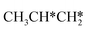 , the dissociation of the central surface and terminal C–H bonds leading to CH3CH*CH* and
, the dissociation of the central surface and terminal C–H bonds leading to CH3CH*CH* and 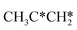 has close Gibbs free energy barriers (0.28 and 0.23 eV, respectively) and reaction Gibbs free energies (−0.38 and −0.26 eV, respectively). In contrast, the surface C–C bond dissociation has a higher Gibbs free energy barrier (0.90 eV) and a reaction Gibbs free energy of −0.24 eV. The further C–H dissociation from CH3CH*CH* and
has close Gibbs free energy barriers (0.28 and 0.23 eV, respectively) and reaction Gibbs free energies (−0.38 and −0.26 eV, respectively). In contrast, the surface C–C bond dissociation has a higher Gibbs free energy barrier (0.90 eV) and a reaction Gibbs free energy of −0.24 eV. The further C–H dissociation from CH3CH*CH* and 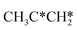 forming CH3C*CH* has very low Gibbs free energy barriers (0.17 and 0.08 eV, respectively) and very strong reaction free energies (−0.64 and −0.76 eV, respectively). The formation of CH3CH*C* from CH3CH*CH* has a reaction Gibbs free energy of −0.64 eV and has a negligible Gibbs free energy barrier of 0.03 eV. Starting from CH3C*CH*, the surface C–H bond dissociation leading to CH3C*C* + H* has a Gibbs free energy barrier of 0.54 eV and a reaction Gibbs free energy of −0.09 eV, and the surface C–C bond dissociation has a Gibbs free energy barrier of 0.80 eV and a reaction Gibbs free energy of −0.68 eV. From the surface carbon and gaseous H2, the formation of propene has a Gibbs free energy of 0.76 eV at 490 K and 1 atm H2 and 0.37 eV at 490 K and 19.7 atm H2 (Fig. S12†). Furthermore, both propene and propyne have very strong adsorption energies and prefer dissociation rather than desorption. Such properties should affect the selectivity in FTS.
forming CH3C*CH* has very low Gibbs free energy barriers (0.17 and 0.08 eV, respectively) and very strong reaction free energies (−0.64 and −0.76 eV, respectively). The formation of CH3CH*C* from CH3CH*CH* has a reaction Gibbs free energy of −0.64 eV and has a negligible Gibbs free energy barrier of 0.03 eV. Starting from CH3C*CH*, the surface C–H bond dissociation leading to CH3C*C* + H* has a Gibbs free energy barrier of 0.54 eV and a reaction Gibbs free energy of −0.09 eV, and the surface C–C bond dissociation has a Gibbs free energy barrier of 0.80 eV and a reaction Gibbs free energy of −0.68 eV. From the surface carbon and gaseous H2, the formation of propene has a Gibbs free energy of 0.76 eV at 490 K and 1 atm H2 and 0.37 eV at 490 K and 19.7 atm H2 (Fig. S12†). Furthermore, both propene and propyne have very strong adsorption energies and prefer dissociation rather than desorption. Such properties should affect the selectivity in FTS.
In contrast to ethene dissociation with surface CH2C* as the first stable intermediate, which can isomerize to CH3C*, propene dissociation resulting in surface CH3CH*C is the first stable intermediate, which can further dissociate to CH3C*C* as the second stable intermediate, which can further dissociate to CH3C* + C* and HC* + 2C*. On the basis of the agreement in ethene dissociation between theory and experiments, similar dissociation activity of propene is expected.
4. Discussion
Having our results and the computed vibrational frequencies of all surface intermediates (Tables S7–S14†) in hand, it is interesting to do comparison with the experiments. A direct comparison for the experimentally detected surface species is listed in Table 3.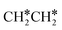 ,
, 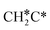 , and HC*C*. (ν, δ, ρ, ω, and τ represent the stretching, scissoring, rocking, wagging and twisting modes, respectively, the subscripts a and s represent the asymmetric and symmetric modes, respectively)
, and HC*C*. (ν, δ, ρ, ω, and τ represent the stretching, scissoring, rocking, wagging and twisting modes, respectively, the subscripts a and s represent the asymmetric and symmetric modes, respectively)
| Mode | Ru(111) | Ru(001) | Ru(0001) | Rh(111) | Pd(111) | Ir(111) | Pt(111) |
|---|---|---|---|---|---|---|---|
| HC* | |||||||
| ν(CH) | 2985 | 295037 | 300264 | ||||
| CH3C* | |||||||
| ν(CH3) | 3039 | 3000;28 294530 | 292065 | 290064 | 294066 | 295067 | |
| ν(CH3) | 3013 | 2910;28 304530 | 298065 | 289067 | |||
| ν(CH3) | 2978 | ||||||
| δ a(CH3) | 1432 | 1450;28 145030 | 142065 | 142067 | |||
| δ s(CH3) | 1324 | 1340;28 137030 | 133765 | 1332;64 133464 | 140066 | 135067 | |
| ν(CC) | 1036 | 1120;28 114030 | 112165 | 1080;64 109864 | 116566 | 113067 | |
| ρ(CH3) | 971 | 980;28 100030 | 97265 | 91464 | 98666 | 98067 | |
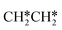
|
|||||||
| ν a(CH2) | 3141 | 3110;28 305030 | |||||
| ν s(CH2) | 3094 | 2910;28 294030 | |||||
| δ(CH2) | 1433 | 1400;28 145030 | |||||
| ν(CC) | 1311; 1109 | 1330;28 104030 | |||||
| ω(CH2) | 1030 | 1110;28 114530 | |||||
| τ(CH2) | 903 | 90030 | |||||
| ρ(CH2) | 752 | 77530 | |||||
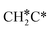
|
|||||||
| δ(CH2) | 1417 | 139533 | |||||
| ν(CC) | 1247 | 116033 | |||||
| HC*C* | |||||||
| ν(CH) | 3102 | 296030 | 295935 | ||||
| ν(CC) | 1207 | 129030 | |||||
| δ(CH) | 753 | 75030 | |||||
In the hydrogenation of pre-deposited carbon on the Ru(001) surface,37 surface CH* was detected and identified using high-resolution electron energy-loss spectroscopy at 2950 cm−1 for the C–H stretching mode as the only intermediate, while neither 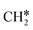 nor
nor 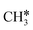 was found. Our computed C–H stretching frequency of CH* is 2985 cm−1, in close agreement with the experiment, while those of
was found. Our computed C–H stretching frequency of CH* is 2985 cm−1, in close agreement with the experiment, while those of 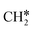 (2982 and 1938 cm−1) and those of
(2982 and 1938 cm−1) and those of 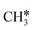 (2862, 2824 and 2811 cm−1) are very different. This finding indeed supports our result of CH* as a stable and key intermediate in CH4 dehydrogenation, where surface C* can be easily hydrogenated to CH* with a low Gibbs free energy barrier (0.72 eV) and a negative reaction Gibbs free energy (−0.21 eV) at 490 K and 1 atm H2 partial pressure. With respect to surface C* and gaseous H2 (Fig. 5), CH* is the most stable, and
(2862, 2824 and 2811 cm−1) are very different. This finding indeed supports our result of CH* as a stable and key intermediate in CH4 dehydrogenation, where surface C* can be easily hydrogenated to CH* with a low Gibbs free energy barrier (0.72 eV) and a negative reaction Gibbs free energy (−0.21 eV) at 490 K and 1 atm H2 partial pressure. With respect to surface C* and gaseous H2 (Fig. 5), CH* is the most stable, and 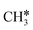 and
and 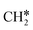 are higher in Gibbs free energy by 0.70 and 0.53 eV. On a Ru catalyst, Brady et al.68 compared the reaction of CH2N2 and H2 with that of synthesis gas, and found that both reactions gave the same products. This is probably because CH2N2 can easily produce
are higher in Gibbs free energy by 0.70 and 0.53 eV. On a Ru catalyst, Brady et al.68 compared the reaction of CH2N2 and H2 with that of synthesis gas, and found that both reactions gave the same products. This is probably because CH2N2 can easily produce 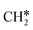 , which can dissociate easily to CH* as the key intermediate for the reaction starting from synthesis gas. This is indeed shown by the barrier-less and exothermic dissociation of
, which can dissociate easily to CH* as the key intermediate for the reaction starting from synthesis gas. This is indeed shown by the barrier-less and exothermic dissociation of 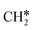 (Fig. 5). This is also true for CH4 dissociation on the Ru(0001) surface,27 where
(Fig. 5). This is also true for CH4 dissociation on the Ru(0001) surface,27 where 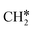 dissociation has a very low barrier (0.16 eV) and is exothermic (−0.46 eV).
dissociation has a very low barrier (0.16 eV) and is exothermic (−0.46 eV).
By using high-resolution electron energy-loss spectroscopy, Barteau et al.28 proved that ethene decomposition leads to a rearrangement of surface H* to CH3C* on the Ru(001) surface, and listed the vibrational spectra of 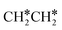 and CH3C*. At 170 K, surface
and CH3C*. At 170 K, surface 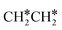 in di-σ configuration is characterized by a reduction of the C–C bond with a stretching mode of the C–C bond at 1330 cm−1, and the computed value is 1311 cm−1. At 310 K, ethylidyne (CH3C*) is characterized by a stretching mode of the C–C bond at 1120 cm−1 and an umbrella mode of CH3 (symmetric bending) at 1340 cm−1. However, the computed C–C stretching frequency is 1036 cm−1, and the symmetric C–H bending mode of CH3 is 1324 cm−1.
in di-σ configuration is characterized by a reduction of the C–C bond with a stretching mode of the C–C bond at 1330 cm−1, and the computed value is 1311 cm−1. At 310 K, ethylidyne (CH3C*) is characterized by a stretching mode of the C–C bond at 1120 cm−1 and an umbrella mode of CH3 (symmetric bending) at 1340 cm−1. However, the computed C–C stretching frequency is 1036 cm−1, and the symmetric C–H bending mode of CH3 is 1324 cm−1.
For ethene adsorption on the Ru(001) surface by using HREELS, Hills et al.30 observed the formation of CH3C* and HC*C* as well as the breaking of the C–C bond occurring in the HC*C* intermediate, which is characterized by a C–H bending mode at 750 cm−1, a C–H stretching mode at 2960 cm−1 and a C–C stretching mode at 1290 cm−1 at 360 K. For HC*C*, the computed C–H bending and stretching modes are 753 and 3012 cm−1, while the C–C stretching mode is 1207 cm−1. The same products (CH3C* and HC*C*) can also be acquired from the co-adsorption of ethene and hydrogen and that of ethene and carbon monoxide.69 This also supports our results for ethene dissociation with 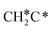 as a key intermediate (Fig. 8), which can become CH3C* in the presence of H* with a low Gibbs free barrier (0.50 eV) and a negative reaction Gibbs free energy (−0.16 eV) (Fig. 7). Indeed,
as a key intermediate (Fig. 8), which can become CH3C* in the presence of H* with a low Gibbs free barrier (0.50 eV) and a negative reaction Gibbs free energy (−0.16 eV) (Fig. 7). Indeed, 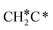 was detected and characterized at 350 K with an overlapping at 1350 cm−1 of a C–C stretching mode and a CH2 scissoring mode in the annealing process of the adsorbed CH3C* on the Ru(001) p(2 × 2)O surface.70 For
was detected and characterized at 350 K with an overlapping at 1350 cm−1 of a C–C stretching mode and a CH2 scissoring mode in the annealing process of the adsorbed CH3C* on the Ru(001) p(2 × 2)O surface.70 For 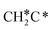 , the computed C–C stretching mode is 1247 cm−1 and 1417 cm−1 for the scissoring mode. Jakob et al.71 presented a thermal desorption spectrum of ethyne, which is similar to that of ethene on the Ru(001) surface (>450 K), and proved the formation of
, the computed C–C stretching mode is 1247 cm−1 and 1417 cm−1 for the scissoring mode. Jakob et al.71 presented a thermal desorption spectrum of ethyne, which is similar to that of ethene on the Ru(001) surface (>450 K), and proved the formation of 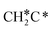 with the appearance of the 1420 cm−1 loss, in addition to CH3C* and HC*C*. This also supports our results for ethene dissociation with CH2C* as a key intermediate (Fig. 8).
with the appearance of the 1420 cm−1 loss, in addition to CH3C* and HC*C*. This also supports our results for ethene dissociation with CH2C* as a key intermediate (Fig. 8).
In the process of methane adsorption on the Ru(0001) and Ru(11–21) surfaces, HC* and 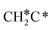 were found on both surfaces, but only CH3C* was observed on the Ru(11–21) surface at low temperature (<400 K), which can be dehydrogenated to
were found on both surfaces, but only CH3C* was observed on the Ru(11–21) surface at low temperature (<400 K), which can be dehydrogenated to 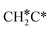 upon heating to above 500 K, while ≥C3+ species were not observed due to the lower concentration compared with the HREELS detection limit.33 They further revealed that the carbonaceous species formed on Ru surfaces at temperatures exceeding 800 K was graphitic on the Ru(0001) surface.72 In addition, surface HC*C* as the intermediate for C–C bond dissociation (Fig. 7) agrees also with the experiment. They also proved the identical HREELS spectra of CO hydrogenation and methane decomposition, and found two peaks at 1160 and 1395 cm−1 attributed to C–C stretching and CH2 scissoring from
upon heating to above 500 K, while ≥C3+ species were not observed due to the lower concentration compared with the HREELS detection limit.33 They further revealed that the carbonaceous species formed on Ru surfaces at temperatures exceeding 800 K was graphitic on the Ru(0001) surface.72 In addition, surface HC*C* as the intermediate for C–C bond dissociation (Fig. 7) agrees also with the experiment. They also proved the identical HREELS spectra of CO hydrogenation and methane decomposition, and found two peaks at 1160 and 1395 cm−1 attributed to C–C stretching and CH2 scissoring from 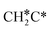 (500–550 K).34 Similar results occur on the Ru(1120) surface. Kirsch et al.35 first reported the formation of HC*C* from methane decomposition on the Ru(0001) surface (400–550 K), due to an undefined C–H stretching mode at 2959 cm−1 by vibrational sum frequency (VSF) generation spectroscopy. This is also consistent with our results that CH4 dissociation forms surface C* and CH*(Fig. 5), which would couple with each other with a Gibbs free energy barrier of 1.34 eV and a reaction Gibbs free energy of 0.30 eV (Fig. 7). On the Ru(0001) surface, there was propylidene (CH3CH2C*) during propene decomposition (150–260 K), which can further be converted into CH3C* (300–330 K).36 From reflection-absorption infrared spectroscopy (RAIRS), CH3CH2C* was characterized by an asymmetric CH3 stretching mode at 2963 cm−1, a symmetric CH3 stretching mode at 2863 cm−1 and a symmetric CH2 stretching mode at 2928 cm−1. Our computed values are 3055, 3031 and 3009 cm−1, respectively. The existence of CH3CH2C* during propene dissociation can be interpreted by a similar mechanism of ethene decomposition to ethylidyne:
(500–550 K).34 Similar results occur on the Ru(1120) surface. Kirsch et al.35 first reported the formation of HC*C* from methane decomposition on the Ru(0001) surface (400–550 K), due to an undefined C–H stretching mode at 2959 cm−1 by vibrational sum frequency (VSF) generation spectroscopy. This is also consistent with our results that CH4 dissociation forms surface C* and CH*(Fig. 5), which would couple with each other with a Gibbs free energy barrier of 1.34 eV and a reaction Gibbs free energy of 0.30 eV (Fig. 7). On the Ru(0001) surface, there was propylidene (CH3CH2C*) during propene decomposition (150–260 K), which can further be converted into CH3C* (300–330 K).36 From reflection-absorption infrared spectroscopy (RAIRS), CH3CH2C* was characterized by an asymmetric CH3 stretching mode at 2963 cm−1, a symmetric CH3 stretching mode at 2863 cm−1 and a symmetric CH2 stretching mode at 2928 cm−1. Our computed values are 3055, 3031 and 3009 cm−1, respectively. The existence of CH3CH2C* during propene dissociation can be interpreted by a similar mechanism of ethene decomposition to ethylidyne: 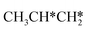 → CH3CH*CH* → CH3CH*C* → CH3CH2C*, which has stepwise Gibbs free energy barriers of 0.28, 0.03, and 0.56 eV and stepwise reaction Gibbs free energies of −0.38, −0.64 and 0.01 eV (Fig. 10).
→ CH3CH*CH* → CH3CH*C* → CH3CH2C*, which has stepwise Gibbs free energy barriers of 0.28, 0.03, and 0.56 eV and stepwise reaction Gibbs free energies of −0.38, −0.64 and 0.01 eV (Fig. 10).
As the reverse reaction of the dissociative adsorption of hydrocarbons on the surfaces of transition metals as catalysts, surface carbon hydrogenation has been used to study the reaction mechanisms of FTS.62 For the possible mechanism of carbon chain growth on the Ru(111) surface from a retrosynthetic perspective, we analyzed surface carbon hydrogenation and hydrogenative coupling for the formation of methane, ethane and propane on the basis of microscopic reversibility, which states that the chemical elementary reaction and its reverse reaction will go through the same intermediates with the latter in the opposite order.73 These results are interesting for the selectivity and distribution of the products of FTS; in particular, methane is used to evaluate the catalysts.
For surface carbon hydrogenation with molecular H2 to methane (Fig. 5), surface CH* formation has a reaction Gibbs free energy of −0.31 eV and it also represents the most stable surface species, while 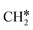 and
and 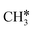 are less stable by 0.53 and 0.70 eV. On the basis of the co-adsorbed C* + 4H*, only the formation of CH* is exergonic and favored thermodynamically, while that of
are less stable by 0.53 and 0.70 eV. On the basis of the co-adsorbed C* + 4H*, only the formation of CH* is exergonic and favored thermodynamically, while that of 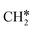 ,
, 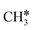 and
and 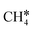 is endergonic and not accessible thermodynamically. This agrees perfectly with the experimentally reported surface carbon hydrogenation on Ru(0001) under UHV,28 where surface CH* was the observed intermediate and no formation of methane was found. According to our result (Fig. 5), the hydrogen desorption energy for C* + 4H* is 0.54 eV, slightly lower than the barrier of surface carbon hydrogenation (0.72 eV), thus H2 desorption rather than hydrogenation is more favored, and therefore, no methane formation should be due to the lack of surface hydrogen. On the basis of C* + 2H2(g) at a higher H2 chemical potential (1 atm), CH4 formation has a positive reaction Gibbs free energy of 0.13 eV and needs an apparent Gibbs free energy barrier of 1.08 eV, indicating that methane formation is neither kinetically nor thermodynamically favorable at the lowest carbon coverage, and this is in contrast to the experimental results.56 To understand this difference, we considered the carbon coverage effect, which is found to affect the activation barriers and reaction energies.74 As shown in Table 4, the reaction Gibbs free energy of methane formation changes from endergonic to exergonic (nC = 1–4; from 0.13 to −0.14 eV). This change with the increase of surface carbon coverage explains the experimentally observed methane formation,56 and the reaction mechanisms depend on conditions, such as temperature, pressure and coverage.
is endergonic and not accessible thermodynamically. This agrees perfectly with the experimentally reported surface carbon hydrogenation on Ru(0001) under UHV,28 where surface CH* was the observed intermediate and no formation of methane was found. According to our result (Fig. 5), the hydrogen desorption energy for C* + 4H* is 0.54 eV, slightly lower than the barrier of surface carbon hydrogenation (0.72 eV), thus H2 desorption rather than hydrogenation is more favored, and therefore, no methane formation should be due to the lack of surface hydrogen. On the basis of C* + 2H2(g) at a higher H2 chemical potential (1 atm), CH4 formation has a positive reaction Gibbs free energy of 0.13 eV and needs an apparent Gibbs free energy barrier of 1.08 eV, indicating that methane formation is neither kinetically nor thermodynamically favorable at the lowest carbon coverage, and this is in contrast to the experimental results.56 To understand this difference, we considered the carbon coverage effect, which is found to affect the activation barriers and reaction energies.74 As shown in Table 4, the reaction Gibbs free energy of methane formation changes from endergonic to exergonic (nC = 1–4; from 0.13 to −0.14 eV). This change with the increase of surface carbon coverage explains the experimentally observed methane formation,56 and the reaction mechanisms depend on conditions, such as temperature, pressure and coverage.
| Reactions | ΔG |
|---|---|
| C + 2H2(g) → CH4(a) | 0.13 |
| 2C + 2H2(g) → C + CH4(a) | 0.18 |
| 3C + 2H2(g) → 2C + CH4(a) | −0.01 |
| 4C + 2H2(g) → 3C + CH4(a) | −0.14 |
| 2C + 3H2(g) → CH3CH3(a) | 0.62 |
| 3C + 3H2(g) → C + CH3CH3(a) | 0.59 |
| 4C + 3H2(g) → 2C + CH3CH3(a) | 0.27 |
| 5C + 3H2(g) → 3C + CH3CH3(a) | −0.60 |
| 6C + 3H2(g) → 4C + CH3CH3(a) | −1.35 |
| 3C + 4H2(g) → CH3CH2CH3(a) | 0.87 |
| 4C + 4H2(g) → C + CH3CH2CH3(a) | 0.59 |
| 5C + 4H2(g) → 3C + CH3CH2CH3(a) | −0.57 |
| 6C + 4H2(g) → 4C + CH3CH2CH3(a) | −1.42 |
For the formation of ethane which forms the first C–C bond from hydrogenative coupling of surface C* + C* and gaseous H2 (Fig. 7), surface methylidyne HC* and CH3C* are the most stable surface C1 and C2, respectively. In addition, surface HC*C* and 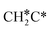 are higher in Gibbs free energy than CH3C* by 0.28 and 0.34 eV. This might explain the observed rapid formation of CH3C* from
are higher in Gibbs free energy than CH3C* by 0.28 and 0.34 eV. This might explain the observed rapid formation of CH3C* from 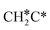 in the presence of hydrogen. In addition, surface CH3CH* and
in the presence of hydrogen. In addition, surface CH3CH* and 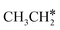 are also higher in Gibbs free energy than CH3C* by 0.74 and 1.26 eV. Starting from C* + C* + 3H2(g) and on the basis of the barriers of the reverse steps, CH3CH3 formation has a reaction Gibbs free energy of 0.62 eV but needs an apparent Gibbs free energy barrier of 1.51 eV. With the increase of surface carbon coverage, the formation of ethane changes also from endergonic to exergonic (nC = 2–6; from 0.62 to −1.35 eV; Table 4). Fig. 7 and 8 show that gaseous H2 evolution from the surface is exothermic for CH3C* (−0.87 eV).
are also higher in Gibbs free energy than CH3C* by 0.74 and 1.26 eV. Starting from C* + C* + 3H2(g) and on the basis of the barriers of the reverse steps, CH3CH3 formation has a reaction Gibbs free energy of 0.62 eV but needs an apparent Gibbs free energy barrier of 1.51 eV. With the increase of surface carbon coverage, the formation of ethane changes also from endergonic to exergonic (nC = 2–6; from 0.62 to −1.35 eV; Table 4). Fig. 7 and 8 show that gaseous H2 evolution from the surface is exothermic for CH3C* (−0.87 eV).
For the hydrogenative coupling of surface C* + C* + C* to 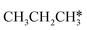 from gaseous H2, surface HC*, CH3C* and CH3CH2C* are the most stable C1, C2 and C3 intermediates as homologs. Starting from C* + C* + C* + 4H2(g) and on the basis of the barriers of the reverse steps, CH3CH2CH3 formation has a reaction Gibbs free energy of 0.87 eV and needs an apparent Gibbs free energy barrier of 1.66 eV, and the reaction changes form endergonic to exergonic with the increase of surface carbon coverage (nC = 3–6; from 0.87 to −1.42 eV; Table 4).
from gaseous H2, surface HC*, CH3C* and CH3CH2C* are the most stable C1, C2 and C3 intermediates as homologs. Starting from C* + C* + C* + 4H2(g) and on the basis of the barriers of the reverse steps, CH3CH2CH3 formation has a reaction Gibbs free energy of 0.87 eV and needs an apparent Gibbs free energy barrier of 1.66 eV, and the reaction changes form endergonic to exergonic with the increase of surface carbon coverage (nC = 3–6; from 0.87 to −1.42 eV; Table 4).
In addition to the coverage dependent reaction Gibbs free energies, we also estimated the pressure dependent apparent barriers of the formation of alkanes and alkenes. From 1 to 19.7 H2 partial pressure, the apparent barrier of the formation of methane, ethane and propane reduces from 1.08, 1.51 and 1.66 eV to 0.83, 1.14 and 1.15 eV, respectively. The same trend is also found for the formation of ethene and propene, i.e., from 0.93 and 1.04 eV to 0.68 and 0.65 eV, respectively. These coverage-dependent barriers are very interesting, since coverage can change the apparent barriers and also accordingly the selectivity and distribution of products in FTS. That alkylidynes (CH*, CH3C* and CH3CH2C* or RCH2C*) are the important intermediates is indeed found experimentally on Ru(001),28–30,37 Ru(0001),33–36 Fe(110),75,76 Rh(111),65 Pd(111),64 Ir(111),66 Pt(111),67 and Co(0001).77
5. Conclusion
In this study, complete reaction networks of consecutive dissociative adsorption of methane, ethane, ethene and ethyne, as well as propane, propene and propyne, on the face-centered cubic Ru(111) surface have been outlined on the basis of systematic periodic density functional theory computations. Our goal is the understanding of the dehydrogenation mechanism of alkanes, alkenes and alkynes on the one hand, and on the other hand the retrosynthetic pathways of surface carbon hydrogenation and hydrogenative C–C coupling, which are related to the mechanisms of FTS and synthesis of lower alcohols. We further considered the effects of temperature and pressure (490 K, 1 atm H2 and 490 K, 19.7 atm H2) on the reactions by Gibbs free energy analysis. In our study we compared fcc Ru(111) and hcp Ru(0001) in adsorption and dissociation of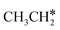 into
into 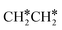 and CH3CH* and found that fcc Ru(111) has stronger adsorption energies and is more active than hcp Ru(0001) despite their very similar surface structures, and these agree with the experimentally observed differences in FTS.
and CH3CH* and found that fcc Ru(111) has stronger adsorption energies and is more active than hcp Ru(0001) despite their very similar surface structures, and these agree with the experimentally observed differences in FTS.
First of all, it is noted that the same types of surface fragments have the same adsorption configuration and comparable adsorption energies. As expected, alkanes have physisorption on the surface with negligible adsorption energy. The adsorption of alkyls, 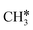 ,
, 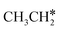 and
and 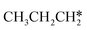 , prefers the fcc hollow site with additional interaction of the C–H bonds of the surface carbon atoms with surface Ru atoms. The adsorption of alkylidenes, HCH*, CH3CH* and CH3CH2CH*, prefers the surface hcp hollow site with the surface C–H bonds interacting with surface Ru atoms in an agostic way, and this enables the easy and exothermic dissociation. The adsorption of alkylidynes, HC*, CH3C* and CH3CH2C*, prefers the surface hcp hollow site in a perpendicular configuration, and this makes them the most stable and important surface intermediates in the dissociation reaction of alkanes, alkenes and alkynes, as well as surface carbon hydrogenation. In contrast to n-propyl and n-propylidene, the adsorption of isopropyl (CH3)2CH* and isopropylidene (CH3)2C* prefers the top and bridge sites, respectively, due to the repulsive interaction between the CH3 groups and the surface metal atoms, and has lower adsorption energies. In addition, surface C* prefers the hcp site and surface H* prefers the fcc site. In contrast to alkyls, alkylidenes and alkylidynes, the adsorption of alkenes, alkenyls and alkenylidenes, as well as alkynes and alkynyls, has a flat configuration with two carbon atoms interacting with surface Ru atoms.
, prefers the fcc hollow site with additional interaction of the C–H bonds of the surface carbon atoms with surface Ru atoms. The adsorption of alkylidenes, HCH*, CH3CH* and CH3CH2CH*, prefers the surface hcp hollow site with the surface C–H bonds interacting with surface Ru atoms in an agostic way, and this enables the easy and exothermic dissociation. The adsorption of alkylidynes, HC*, CH3C* and CH3CH2C*, prefers the surface hcp hollow site in a perpendicular configuration, and this makes them the most stable and important surface intermediates in the dissociation reaction of alkanes, alkenes and alkynes, as well as surface carbon hydrogenation. In contrast to n-propyl and n-propylidene, the adsorption of isopropyl (CH3)2CH* and isopropylidene (CH3)2C* prefers the top and bridge sites, respectively, due to the repulsive interaction between the CH3 groups and the surface metal atoms, and has lower adsorption energies. In addition, surface C* prefers the hcp site and surface H* prefers the fcc site. In contrast to alkyls, alkylidenes and alkylidynes, the adsorption of alkenes, alkenyls and alkenylidenes, as well as alkynes and alkynyls, has a flat configuration with two carbon atoms interacting with surface Ru atoms.
Methane consecutive dissociation follows the minimum energy path of 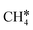 →
→ 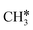 →
→ 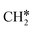 → CH* → C*, and the first C–H dissociation has a Gibbs free energy barrier of 0.95 eV and has a reaction Gibbs free energy of 0.19 eV, while the second and third C–H dissociations are exothermic and have very low barriers, and the last C–H dissociation has a high barrier and is endothermic. In the presence of hydrogen, surface C* will be hydrogenated to CH*, which is the most stable surface intermediate as found experimentally.
→ CH* → C*, and the first C–H dissociation has a Gibbs free energy barrier of 0.95 eV and has a reaction Gibbs free energy of 0.19 eV, while the second and third C–H dissociations are exothermic and have very low barriers, and the last C–H dissociation has a high barrier and is endothermic. In the presence of hydrogen, surface C* will be hydrogenated to CH*, which is the most stable surface intermediate as found experimentally.
Ethane consecutive dissociation follows the minimum energy path of 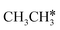 →
→ 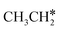 → CH3CH* → CH3C* →
→ CH3CH* → CH3C* → 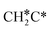 → HC*C* → HC* + C* without ethene and ethyne as intermediates. In addition, ethene consecutive dissociation follows the minimum energy path of
→ HC*C* → HC* + C* without ethene and ethyne as intermediates. In addition, ethene consecutive dissociation follows the minimum energy path of 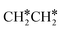 →
→ 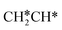 →
→ 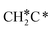 → HC*C* → HC* + C* without ethyne as an intermediate, and ethyne consecutive dissociation has the minimum energy path of CH*CH* → HC*C* → HC* + C*. All these results have the same final surface species of HC* + C*, and surface HC*C* dissociation into HC* + C* represents the most kinetically favored step of C–C bond rupture. It is also noted that the experimentally observed formation of surface CH3C* from ethene dissociative adsorption comes from surface
→ HC*C* → HC* + C* without ethyne as an intermediate, and ethyne consecutive dissociation has the minimum energy path of CH*CH* → HC*C* → HC* + C*. All these results have the same final surface species of HC* + C*, and surface HC*C* dissociation into HC* + C* represents the most kinetically favored step of C–C bond rupture. It is also noted that the experimentally observed formation of surface CH3C* from ethene dissociative adsorption comes from surface 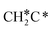 hydrogenation and this step is reversible at high temperature. Our computed kinetic and thermodynamic parameters rationalized the experimental observations.
hydrogenation and this step is reversible at high temperature. Our computed kinetic and thermodynamic parameters rationalized the experimental observations.
Propane consecutive dissociation can have the kinetically competitive n-propyl and isopropyl routes: 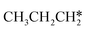 → CH3CH2CH* → CH3CH2C* → CH3CH*C* → CH3C*C* → CH3C* + C* →→ HC* + C* and CH3CH*CH3 → CH3C*CH3 →
→ CH3CH2CH* → CH3CH2C* → CH3CH*C* → CH3C*C* → CH3C* + C* →→ HC* + C* and CH3CH*CH3 → CH3C*CH3 → 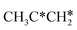 → CH3C*CH* → CH3C*C* →→ HC* + C*, and both routes cross at surface CH3C*C*. The n-propyl route can also have propene and/or propyne as intermediates for dissociation in the order
→ CH3C*CH* → CH3C*C* →→ HC* + C*, and both routes cross at surface CH3C*C*. The n-propyl route can also have propene and/or propyne as intermediates for dissociation in the order 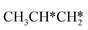 →
→ 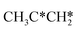 /CH3CH*CH*→ CH3CH*C*/CH3C*CH* → CH3C*C* →→ HC* + C*. In these reactions, the most stable surface intermediates are the HC*, CH3C* and CH3CH2C* homologs, and this is the same as those found experimentally on the Ru(001) and Ru(0001) surfaces. In addition, our results also rationalized the role of surface HC*C* and CH3C*C* as the key intermediates for the first C–C bond dissociation (HC*C* → HC* + C* and CH3C*C* → CH3C* + C*).
/CH3CH*CH*→ CH3CH*C*/CH3C*CH* → CH3C*C* →→ HC* + C*. In these reactions, the most stable surface intermediates are the HC*, CH3C* and CH3CH2C* homologs, and this is the same as those found experimentally on the Ru(001) and Ru(0001) surfaces. In addition, our results also rationalized the role of surface HC*C* and CH3C*C* as the key intermediates for the first C–C bond dissociation (HC*C* → HC* + C* and CH3C*C* → CH3C* + C*).
On the basis of surface carbon and gaseous H2 as references, the retrosynthesis of methane, ethane and propane has increasing apparent Gibbs free energy barriers (1.08, 1.51 and 1.66 eV, respectively) at 490 K and 1 atm H2, and the corresponding values are 0.83, 1.14 and 1.15 eV at 19.7 atm H2, respectively. In addition, the increase of surface carbon coverage changes the formation of alkanes from endergonic to exergonic. Thus, such pressure- and coverage-dependency is very important for understanding the selectivity and distribution of products in FTS. In addition, surface alkylidynes, CH*, CH3C* and CH3CH2C*, are the most stable C1, C2 and C3 intermediates, which are responsible for the chain growth in FTS, which is our current interest.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 21473229, No. 91545121, No. 21703272), the Key R&D Plan of Beijing Municipal Science and Technology Commission (Z181100005118014), funding support from the Beijing Advanced Innovation Center for Materials Genome Engineering, Synfuels China, Co. Ltd and “Transformational Technologies for Clean Energy and Demonstration”, Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDA 21000000). We are also grateful to the Innovation Foundation of Institute of Coal Chemistry, Chinese Academy of Sciences, the Hundred-Talent Program of Chinese Academy of Sciences, the Shanxi Hundred-Talent Program and the National Thousand Young Talents Program of China as well as general financial support from the BMBF and the state of Mecklenburg-Vorpommern, Germany.References
- H. Seo, J. K. Lee, U. G. Hong, G. Park, Y. Yoo, J. Lee, H. Chang and I. K. Song, Catal. Commun., 2014, 47, 22–27 CrossRef CAS.
- J. Sattler, J. Ruiz-Martinez, E. Santillan-Jimenez and B. M. Weckhuysen, Chem. Rev., 2014, 114, 10613–10653 CrossRef CAS PubMed.
- Y. A. Zhu, D. Chen, X. G. Zhou and W. K. Yuan, Catal. Today, 2009, 148, 260–267 CrossRef CAS.
- J. C. Li, J. M. Li, Z. Zhao, X. Q. Fan, J. Liu, Y. C. Wei, A. J. Duan, Z. Xie and Q. L. Liu, J. Catal., 2017, 352, 361–370 CrossRef CAS.
- P. C. Bruijnincx and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2013, 52, 11980–11987 CrossRef CAS PubMed.
- B. V. Vora, Top. Catal., 2012, 55, 1297–1308 CrossRef CAS.
- J. G. Xu and G. F. Froment, AIChE J., 1989, 35, 88–96 CrossRef CAS.
- G. A. Vedage, P. B. Himelfarb, G. W. Simmons and K. Klier, ACS Symp. Ser., 1985, 279, 295–312 CrossRef CAS.
- Q. H. Zhang, J. C. Kang and Y. Wang, ChemCatChem, 2010, 2, 1030–1058 CrossRef CAS.
- O. O. James, S. Mandal, N. Alele, B. Chowdhury and S. Maity, Fuel Process. Technol., 2016, 149, 239–255 CrossRef CAS.
- M. M. Bhasin, J. H. McCain, B. V. Vora, T. Imai and P. R. Pujado, Appl. Catal., A, 2001, 221, 397–419 CrossRef CAS.
- Z. J. Zhao, C. C. Chiu and J. L. Gong, Chem. Sci., 2015, 6, 4403–4425 RSC.
- Z. Nawaz, Rev. Chem. Eng., 2015, 31, 413–436 CAS.
- Y. Chen and D. G. Vlachos, J. Phys. Chem. C, 2010, 114, 4973–4982 CrossRef CAS.
- S. Saerens, M. K. Sabbe, V. V. Galvita, E. A. Redekop, M. F. Reyniers and G. B. Marin, ACS Catal., 2017, 7, 7495–7508 CrossRef CAS.
- J. E. Mueller, A. C. T. van Duin and W. A. Goddard, J. Phys. Chem. C, 2010, 114, 20028–20041 CrossRef CAS.
- K. Lee, E. Lee, C. S. Song and M. J. Janik, J. Catal., 2014, 309, 248–259 CrossRef CAS.
- C. Wu, L. Wang, Z. R. Xiao, G. Z. Li and L. C. Wang, Phys. Chem. Chem. Phys., 2020, 22, 724–733 RSC.
- G. W. Wang, S. Zhang, X. L. Zhu, C. Y. Li and H. H. Shan, J. Ind. Eng. Chem., 2020, 86, 1–12 CrossRef CAS.
- T. Saelee, S. Namuangruk, N. Kungwan and A. Junkaew, J. Phys. Chem. C, 2018, 122, 14678–14690 CrossRef CAS.
- A. V. Zeigarnik, R. E. Valdés-Pérez and O. N. Myatkovskaya, J. Phys. Chem. B, 2000, 104, 10578–10587 CrossRef CAS.
- A. Almithn and D. Hibbitts, J. Phys. Chem. C, 2019, 123, 5421–5432 CrossRef CAS.
- G. J. Lan, Y. Yao, X. M. Zhang, M. Guo, H. D. Tang, Y. Li and Q. H. Yang, Catal. Sci. Technol., 2016, 6, 2181–2187 RSC.
- X. Y. Quek, Y. J. Guan, R. A. van Santen and E. J. M. Hensen, ChemCatChem, 2011, 3, 1735–1738 CrossRef CAS.
- C. X. Xiao, Z. P. Cai, T. Wang, Y. Kou and N. Yan, Angew. Chem., Int. Ed., 2008, 47, 746–749 CrossRef CAS.
- I. M. Ciobîcă, F. Frechard, R. A. van Santen, A. W. Kleyn and J. Hafner, J. Phys. Chem. B, 2000, 104, 3364–3369 CrossRef.
- C. K. Ande, S. D. Elliott and W. M. M. Kessels, J. Phys. Chem. C, 2014, 118, 26683–26694 CrossRef CAS.
- M. A. Barteau, J. Q. Broughton and D. Menzel, Appl. Surf. Sci., 1984, 19, 92–115 CrossRef CAS.
- C. Egawa, S. Naito and K. Tamaru, J. Chem. Soc., Faraday Trans. 1, 1986, 82, 3197–3204 RSC.
- M. M. Hills, J. E. Parmeter, C. B. Mullins and W. H. Weinberg, J. Am. Chem. Soc., 1986, 108, 3554–3562 CrossRef CAS.
- R. J. Koestner, M. A. Van Hove and G. A. Somorjai, Surf. Sci., 1982, 121, 321–337 CrossRef CAS.
- A. Wander, M. A. Van Hove and G. A. Somorjai, Phys. Rev. Lett., 1991, 67, 626–628 CrossRef CAS PubMed.
- M. C. Wu and D. W. Goodman, J. Am. Chem. Soc., 1994, 116, 1364–1371 CrossRef CAS.
- M. C. Wu, D. W. Goodman and G. W. Zajac, Catal. Lett., 1994, 24, 23–30 CrossRef CAS.
- H. Kirsch, Y. J. Tong and R. K. Campen, ChemCatChem, 2016, 8, 728–735 CrossRef CAS.
- I. A. Ransley, L. M. Ilharco, J. E. Bateman, B. H. Sakakini, J. C. Vickerman and M. A. Chesters, Surf. Sci., 1993, 298, 187–194 CrossRef CAS.
- M. A. Barteau, P. Feulner, R. Stengl, J. Q. Broughton and D. Menzel, J. Catal., 1985, 94, 51–59 CrossRef CAS.
- M. Li, W. Y. Guo, R. B. Jiang, L. M. Zhao, X. Q. Lu, H. Y. Zhu, D. L. Fu and H. H. Shan, J. Phys. Chem. C, 2010, 114, 8440–8448 CrossRef CAS.
- M. Zhao, Z. Chen, Z. Lyu, Z. D. Hood, M. Xie, M. Vara, M. Chi and Y. Xia, J. Am. Chem. Soc., 2019, 141, 7028–7036 CrossRef CAS PubMed.
- W. Z. Li, et al. , J. Am. Chem. Soc., 2017, 139, 2267–2276 CrossRef CAS PubMed.
- K. Kusada, H. Kobayashi, T. Yamamoto, S. Matsumura, S. Naoya, K. Sato, K. Nagaoka, Y. Kubota and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 5493–5496 CrossRef CAS PubMed.
- H. H. Ye, Q. X. Wang, M. Catalano, N. Lu, J. Vermeylen, M. J. Kim, Y. Z. Liu, Y. G. Sun and X. H. Xia, Nano Lett., 2016, 16, 2812–2817 CrossRef CAS PubMed.
- M. Zhao, L. Figueroa-Cosme, A. O. Elnabawy, M. Vara, X. Yang, L. T. Roling, M. F. Chi, M. Mavrikakis and Y. N. Xia, Nano Lett., 2016, 16, 5310–5317 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- H. Pfnür, P. Feulner and D. Menzel, J. Chem. Phys., 1983, 79, 4613–4623 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. Haglund, A. Fernandez Guillermet, G. Grimvall and M. Korling, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11685–11691 CrossRef PubMed.
- H. Jónsson, G. Mills and K. W. Jacobsen, in Classical and Quantum Dynamics Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, Hackensack, 1998, pp. 385–404, DOI:10.1142/9789812839664_0016.
- V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, VASPKIT: A Pre- and Post-Processing Program for VASP Code, 2019, arXiv:1908.08269 Search PubMed.
- H. Wise and J. G. McCarty, Surf. Sci., 1983, 133, 311–320 CrossRef CAS.
- I. M. Ciobîcă, F. Frechard, R. A. van Santen, A. W. Kleyn and J. Hafner, Chem. Phys. Lett., 1999, 311, 185–192 CrossRef.
- J. A. Herron, S. Tonelli and M. Mavrikakis, Surf. Sci., 2013, 614, 64–74 CrossRef CAS.
- M. Neurock and R. A. van Santen, J. Phys. Chem. B, 2000, 104, 11127–11145 CrossRef CAS.
- X. R. Shi, H. J. Kong, S. G. Wang, H. Wang, Z. F. Qin and J. G. Wang, ChemPhysChem, 2017, 18, 906–916 CrossRef CAS PubMed.
- A. Govender, D. Curulla-Ferre, M. Perez-Jigato and H. Niemantsverdriet, Molecules, 2013, 18, 3806–3824 CrossRef CAS PubMed.
- T. Li, X. D. Wen, Y. W. Li and H. J. Jiao, J. Phys. Chem. C, 2018, 122, 28846–28855 CrossRef CAS.
- I. A. W. Filot, R. J. P. Broos, J. P. M. van Rijn, G. van Heugten, R. A. van Santen and E. J. M. Hensen, ACS Catal., 2015, 5, 5453–5467 CrossRef CAS.
- J. A. Gates and L. L. Kesmodel, Surf. Sci., 1983, 124, 68–86 CrossRef CAS.
- B. E. Koel, B. E. Bent and G. A. Somorjai, Surf. Sci., 1984, 146, 211–228 CrossRef CAS.
- T. S. Marinova and K. L. Kostov, Surf. Sci., 1987, 181, 573–585 CrossRef CAS.
- H. Steininger, H. Ibach and S. Lehwald, Surf. Sci., 1982, 117, 685–698 CrossRef CAS.
- R. C. Brady and R. Pettit, J. Am. Chem. Soc., 1980, 102, 6181–6182 CrossRef CAS.
- M. M. Hills, J. E. Parmeter and W. H. Weinberg, J. Am. Chem. Soc., 1986, 108, 7215–7221 CrossRef CAS.
- M. M. Hills, J. E. Parmeter and W. H. Weinberg, J. Am. Chem. Soc., 1987, 109, 597–599 CrossRef CAS.
- P. Jakob, A. Cassuto and D. Menzel, Surf. Sci., 1987, 187, 407–433 CrossRef CAS.
- M.-C. Wu, Q. Xu and D. W. Goodman, J. Phys. Chem., 1994, 98, 5104–5110 CrossRef CAS.
- P. Stoltze, Prog. Surf. Sci., 2000, 65, 65–150 CrossRef CAS.
- T. Li, X. D. Wen, Y. W. Li and H. J. Jiao, J. Phys. Chem. C, 2019, 123, 25657–25667 CrossRef CAS.
- W. Erley, P. H. Mcbreen and H. Ibach, J. Catal., 1983, 84, 229–234 CrossRef CAS.
- H. P. Bonzel and H. J. Krebs, Surf. Sci., 1980, 91, 499–513 CrossRef CAS.
- C. J. Weststrate, I. M. Ciobîcă, J. van de Loosdrecht and J. W. Niemantsverdriet, J. Phys. Chem. C, 2016, 120, 29210–29224 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Comparison of reaction barriers and energies with and without ZPE; transition state structures of each elementary reaction (Tables S2–S8); the computed vibrational frequencies and their assignments (Tables S9–S16); and DFT energy profiles and Gibbs free energy profiles (490 K and 19.7 atm H2) of the alkane dissociations (Fig. S1–S12). See DOI: 10.1039/d0cy02055a |
| This journal is © The Royal Society of Chemistry 2021 |