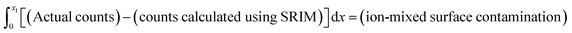Open Access Article
Open Access ArticleQuantifying low fluence ion implants in diamond-like carbon film by secondary ion mass spectrometry by understanding matrix effects†
Amy J. G.
Jurewicz
 *a,
Chad T.
Olinger
*a,
Chad T.
Olinger
 b,
Donald S.
Burnett
b,
Donald S.
Burnett
 c,
Yunbin
Guan
d,
Richard
Hervig
c,
Yunbin
Guan
d,
Richard
Hervig
 e,
Karen D.
Rieck
e,
Karen D.
Rieck
 f and
Dorothy S.
Woolum
f and
Dorothy S.
Woolum
 g
g
aArizona State University, Center for Meteorite Studies, Tempe AZ 85287-6004, USA. E-mail: Amy.Jurewicz@asu.edu
bGET, Inc., AU-62, 19901 Germantown Rd, Germantown, MD 20875, USA
cCalifornia Institute of Technology, Dept. of Geology and Planetary Sciences, m/c 100-23, Pasadena, CA 91125, USA
dCalifornia Institute of Technology, Dept. of Geology and Planetary Sciences, m/c 100-10, Pasadena, CA 91125, USA
eArizona State University, School of Earth and Space Exploration, Tempe AZ 85287-1404, USA
fNew Mexico Consortium, 4200 West Jemez Rd. #200, Los Alamos, NM 87544, USA
gCalifornia State University Fullerton, Department of Physics, 800 N. State College Blvd, Fullerton CA 92834-6866, USA
First published on 7th December 2020
Abstract
Minor and trace elements in diamond-like carbon (DLC) are difficult to quantify using SIMS analysis because minor elemental and structural variations can result in major matrix effects even across individual, cm-sized samples. While this material is most commonly used for tribological coatings where minor element composition is not of critical importance, it is being increasingly used in electronic devices. However, it is a unique application that spurred this work: anhydrous, tetrahedrally-coordinated DLC (ta-C) was used as a solar wind (SW) collector material in the Genesis solar-wind sample return mission (NASA Discovery 5). So, for ∼15 years, we have been working on attaining accurate and precise measurement of minor and trace elements in the Genesis DLC using SIMS to achieve our mission goals. Specifically, we have learned to deal with relevant matrix effects in our samples, ion implants into ta-C. Our unknown element for quantification is SW Mg, a low-dose (1.67 × 1012 at cm−2; ∼6 μg g−1 24Mg), low-energy (∼24 keV average energy) implant; our standard is a high-dose (∼1 × 1014 at cm−2 of both 25Mg, 26Mg) 75 keV laboratory implant for which the absolute 26Mg/25Mg ratio had been measured to account for variable instrumental mass fractionation. Analyses were performed using O2+ primary ions having both a low impact energy and a current density of ∼2 × 1014 ions per cm2. Although our unknown was solar wind, the method is applicable to many situations where minor elements in DLC need to be quantified. Recommendations are presented for modifying this data-reduction technique for other SIMS conditions.
1. Introduction
Diamond-like carbon (DLC) is a common commercial coating most often used to mitigate friction and wear, but versions of this material are being developed for electronic applications (e.g.,ref. 1 and 2). For friction and wear applications, knowing the concentration profile of minor ions such as H can be useful;3 knowing minor element chemistry is often important in electronic applications. The method of trace-element quantification presented here has been developed for a novel, non-commercial use of DLC: its use as a solar wind (SW) collector on the Genesis spacecraft.4,5 This use has driven a number of investigations into the analysis of minor and trace elements in DLC that required a level of effort that would probably not have been feasible in the private sector, but the techniques are accessible to the public.The DLC used for Genesis, an anhydrous tetrahedrally-coordinated carbon film (ta-C) developed by Sandia National Laboratories, was deposited on 4′′ hexagonal silicon wafers (for physical strength and support), and mounted in approximately 1 meter-diameter arrays with a variety of other films and commercial semiconductor materials. These “Collector Arrays” comprised one of the instruments aboard the spacecraft5 that was launched into orbit around the L1 point (outside the lunar orbit). In this orbit, these arrays faced the Sun for about two years and passively collected the ions emitted as solar wind (SW). The spacecraft then returned the collectors containing the solar wind sample to Earth for analysis. Pre-flight, DLC collectors were designated for analyses by successive oxidation or laser ablation;4 however, the hard landing of the Genesis sample-return capsule in 2004 reduced the area of individual collectors available for analysis and added terrestrial contamination to their surfaces.6,7 Therefore, it became imperative to develop all possible small-area techniques capable of depth resolution (in order to exclude surface contamination) for measuring the solar wind, including secondary ion mass spectrometry (SIMS).
The first attempts to measure SW by SIMS after the Genesis return focused on silicon collectors, primarily because of the long history of SIMS analyses of silicon in the semiconductor literature. However, (1) silicon scratches easily, is reactive, and is especially difficult to clean without removing many nanometers of the surface, and (2) there are indications of radiation-induced segregation of solar wind ions in the silicon collectors,8‡.
Radiation-induced segregation in silicon is a diffusive process in which implanted ions adjust their distribution to a radiation-induced gradient of internal energy within the crystal. In the solar wind collectors the highest internal energy (i.e., the most intense disruption of the crystal lattice) is radiation damage from SW H and He because H is ∼95% of the SW and He is ∼3% of the solar wind. The rest of the lattice disruption is caused by the combined effects from the implantation of the rest of the periodic table. These heavier ions are initially planted deeper than the SW H or He but tend to diffuse towards the surface of the SW collectors. By moving into sites within the most damaged portion of the silicon, the larger ions can lower the energy of both their own bonds and those of the disrupted lattice. Similarly, some vacancies and other defects from the radiation damage (including H and He) will move down their concentration gradient into the depths of the silicon crystal, enabling heavier ions to move down their concentration gradient as well. So, radiation-induced segregation does not indicate the gain or loss of ions; rather, it is just a means to establish a lower total energy state inside the damaged crystal lattice: i.e., diffusion can simply re-distribute the impurities and their related vacancies. Still, because the SW implant is shallow, there may be an exchange of SW ions with contamination from the free surface of the silicon collector. Therefore, it is important that a second collector type be analyzed to confirm retention of SW species in the silicon. This need to confirm analytical results of this unique SW sample using multiple collector-types drove this research into using SIMS to accurately and precisely quantify minor ions in ta-C films.
1.1. Issues encountered analysing DLC by SIMS
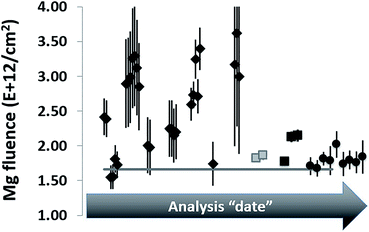
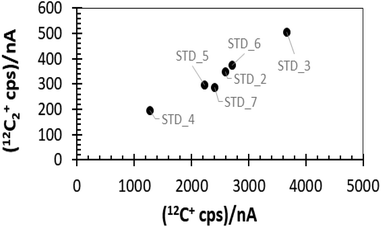
Our first SIMS analyses of SW 24Mg in DLC treated the collector as a homogeneous material and, in addition, used implants of minor ions (25Mg, 26Mg) for calibration. This method was exactly the same as that used for silicon. However, the results were – mostly – disastrous. Initial results were not reproducible within a factor of 2 (see Fig. 1). The only way to achieve a consistently reproducible number was to put the implant used as a standard directly into the collector itself (an “internal standard” – two grey squares in Fig. 1). The reproducibility attained using internal standards implied that the non-reproducibility observed initially was due to matrix affects within the DLC. To track differences in ta-C matrix properties, we developed a parametrization using two ions from the matrix: 12C+ and 12C2+ (circles in Fig. 1). Then, the reproducibility achieved using an “external” implant standard (i.e., an implant into a piece of flight-spare wafer not exposed to the SW) began to approach that of the internal standards. Still, the results for SW Mg from DLC tended to be ∼8% higher than that from silicon,10 and, until this work, it was unclear why.1.2. Sources and examples of observed matrix effects in DLC
Although the Genesis diamond-like carbon on silicon (DoS) flight wafers look beautifully uniform when studied by eye, post-analysis inspections flagged inhomogeneity that affected SIMS analyses.9,10 Occasional macroscopic features that indicate variations in structure and composition have been observed in the analytical pits in the DLC. These features include diamond crystals, exsolved clusters of SiC crystallites, and embedded particulates (probably either common dust and/or silicon powder present from cleaving wafers in the lab). Raman spectroscopy gave results consistent with inferred variations in composition (e.g., the presence/absence of silicon or silicon carbide domains) and bonding (e.g., variable ratios and distributions of sp3vs. sp2 carbon bonds) among analysed areas. SIMS analysis confirmed a non-uniform distribution of minor silicon – likely inherited from the sputtering target used for the fabrication – and the presence of occasional embedded particulates. SIMS also revealed periodic contaminant layers in some wafers. This monolayer-scale contamination, when present, likely decorates surfaces exposed to the vacuum chamber during annealing steps. These annealing steps are necessary to mitigate the extremely high internal stresses of the un-annealed DLC film.11,12 The Genesis DLC was annealed after each ∼120–200 nm layer of the DLC film was deposited. The annealing process was also shown to change the texture of the DLC noticeably with depth12,13 although no effect on our SIMS analyses was observed (short discussion in ESI, Section B†). Finally, Monte Carlo models of implants into the DLC calculated using SRIM indicated a striking variation in density across the wafers. For example, model densities calculated for our standard ranged from ∼2.8 g cm−3 to ∼3.4 g cm−3. Diamond crystals were observed in the analysis crater having the highest calculated density. Density, although not usually included as a “matrix effect”, has a direct effect on both quantifying the implant and understanding ion yields for SIMS analysis of DLC.For example, imagine two substrates that are otherwise identical but have strikingly-different densities. If these two substrates are co-implanted with the same ion implant, then, the substrate having the higher density matrix will exhibit a more compact implant profile. Because the number of implanted atoms is the same in both matrices, a compact profile also means that the implanted ions are present in higher concentrations. Therefore, if identical SIMS conditions are used to analyse each of the substrates and if the sputtering rates happen to be identical:
(1) Then the dense substrate should have a higher peak intensity. If that is not the case, then the ion yields for the implant in the two substrates are different.
(2) Then more of the higher density matrix is being removed per unit time and the depth profile into the lower density matrix will show implanted ions at greater depths.
Thus, in DLC, which is inhomogeneous in density, sequential depth profiles through a uniform implant should be expected to have different intensities and shapes, even if all else is constant.
A corollary for analysts is that double-checking for uniformity of analyses during collection of data is nearly impossible. The intensities and shapes of the raw implant depth profiles will not be consistent and, therefore, differences do not reflect the reliability of analyses. Even summing the total counts (normalized to beam current or matrix species) collected during each depth profile are of little use, because the sum of the normalized counts per second of the implanted ion relative to with their integral over the depth profile will differ for each analysis (further discussion in the ESI, Section A†).
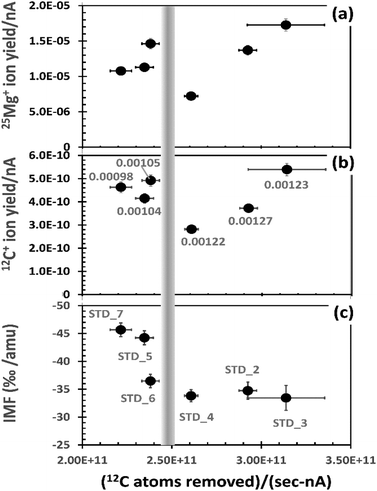
The effects of the matrix variability on SIMS analysis is significant. For example, sputtering rates for multiple analyses on a single ∼2.5 × 3 cm sample were observed to be non-linear with beam current, even when changes in beam current were small; e.g., those standard analyses in ref. 9 and 10 having average beam currents of 21–24 nA had per nA sputtering rates that ranged from 0.00098 to 0.00127 nm per (s per nA), almost a ∼30% variation. Moreover, for analyses from that SIMS session, after correcting data for instantaneous count rate and dead time, peak counting rates for the implanted 25Mg of the standard varied between 9.5 × 103 cps and 3.7 × 104 cps. Fig. 2 plots results from the standard showing significant matrix effects on ion yields and instrumental mass fractionation (IMF)
To mitigate the influence of density variations, Fig. 2 uses the average number of matrix carbon atoms (in the analysed area) sputtered per second per nA for the x-axis. The number of matrix carbon atoms sputtered is calculated for each analysis by first using SRIM to model the density, assuming an all carbon matrix. Then, the beam current is assumed to be constant (i.e., the average of the initial and final readings) – a necessary assumption because beam-current measurements for each duty cycle were not recorded by the depth-profiling routine.
The 25Mg+ and 12C+ ion yields per nA (y-axis in Fig. 2(a) and (b), respectively) are also given in relation to the atoms sputtered. In Fig. 2(a), 25Mg+ ion yield per nA is calculated as follows. The integral ∫(25Mg+dx) for each depth profile is corrected for the measured IMF (Fig. 2(c)) and then divided by the total number of 25Mg implanted per analysed area (for our standard, ∼1.97E+10 atoms per 150 × 150 μm2; i.e., the analysed area for Cameca's 60% DTOS function for a 250 × 250 μm2 raster). The quotient is then divided by the average beam current. In Fig. 2(b), 12C+ ion yield per nA is calculated by taking the 12C+ cps and dividing by the average number of matrix carbon atoms sputtered per second in the analysed area (i.e., the x-axis value multiplied by average beam current).
For a homogeneous material, each plot in Fig. 2 would plot to a single point within error. Clearly, this is not the case (see Section A in the ESI† for illustrations of depth profiles). Note: even the patterns for 12C+ and 25Mg+ ion yields are not identical; thus, even the integrals for each analysis (∫(25Mg+/12C+)dx) will not give a constant value! Still, the analyses having the fewest carbon atoms removed per (s per nA) sputter more slowly than the analyses in which the primary beam removes the most carbon atoms per (s per nA). This observation is illustrated by the labels in (b), the calculated sputtering rate in nm nA−1. However, the slowly sputtering DLC also has a consistently high yield of 25Mg+ and 12C+ ions – higher than two of three analyses that sputtered more quickly. This seemingly contradictory observation is a function of minor the variability of both the silicon concentration and the structure of the DLC, as outlined below.
The comparatively high ion yields and slow sputtering rates to the left of the vertical bar in Fig. 2 are probably due to the presence of minor silicon in the DLC matrix. Oxides of carbon are volatile compounds and, thus, easily removed from the area being sputtered; in contrast, oxides of silicon are refractory solids which are less easily removed from the area being sputtered. Since the SiOx compounds do not form a stable gas, they will build-up relative to the more easily removed carbon in the zone of sputtering. Because this silicon “residue” contains O, the SiOx will stabilize a higher, steady state oxygen concentration in the matrix and a higher oxygen content in the zone of sputtering increases ion yield.14 Raman results were consistent with this interpretation, showing that sputtering rate depended on the presence (or absence) of minor silicon, as well as how it was bonded in the DLC (e.g., silicon metal or silicon carbide; see example 1 of ref. 13).
Using similar logic, the data to the right of the vertical bar in Fig. 2 are inferred to be from matrices low in silicon. Sputtering rates per nA are significantly higher, indicating that reactive ion etching (volatilization) of carbon by the O of the primary beam plays a dominant role during sputtering. In addition, there are strong variations in ion yields; we surmise that these variations are a function of an inconsistent electrical conductivity on the sample. This inference is based in part on the work by Sullivan et al. (1998),12 who showed that 2.5 μm2 columns of DLC can vary in conductivity by more than 10× as the concentration of sp3 bonds and the relative size, orientation and connectivity of their domains vary with respect to the sp2 domains within the DLC. Assuming that these variations exist in our similar DLC, the effect of these domains on SIMS analyses can be imagined as analogous to analysing a wafer which has a matrix of an electrically conducting material that contains ∼70% by volume embedded, unevenly distributed, micron-sized particles of an insulator.
Note the variability of the IMF (Fig. 2(c)). IMF is a function of the target matrix and its influence on the ambient electrical fields within the SIMS. Therefore, the variability in the measured IMF seen in Fig. 2(c) is consistent with the observed deviations in ion yield and sputtering as functions of minor variations in the matrix properties. The two analyses with the slowest matrix atom removal rate (LHS) and high 25Mg ion yield in Fig. 2(a) also have the highest measured IMF (∼−4.5%); the three analyses with the fastest matrix atom removal rates (LHS) due, in part, to O-etching have a lower, nearly constant IMF (∼−3.3%). The final analysis (STD_6, closest to the bar on the LHS), has high ion yields but an “intermediate” IMF of 3.6%.
The matrix effects described above can also differentially change the intensities of the secondary ions derived from the C matrix. For example, Fig. 3 plots the intensity of 12C2+vs.12C+ as the average of the raw cps per duty cycle for each analysis. Both species vary from analysis to analysis and their magnitude correlates linearly (R2 = ∼0.96); however, the slope is not 1 (i.e., doubling the 12C+ counts does not double the 12C2+ counts). So, simple explanations (such as unaccounted for variations in beam current) are not applicable. Nor is this observed variation in intensity dependent upon the rate of carbon atoms sputtered per nA (Fig. 2(b)). The changing 12C2+/12C2+ ratio is almost certainly due to minor voltage differences across the sample caused by inconsistencies in the composition and structure of the matrix. These voltage differences skew the energy spectrum of each ion independently. This interpretation will be detailed fully in the Discussion (Section 4.1) and the ESI (Section D†). However, the important point here is that – under the conditions used in this study – the two ions behave differently in response to each DLC matrix type and, therefore, can be used for tracking the properties of the matrix in order to compensate for matrix effects.
 | ||
| Fig. 3 Comparison of average cps of two matrix ions. Labels are the implant designation. Note the linear correlation (R2 = 0.96). The slope is ∼0.13 and position on the trend does not depend on the atoms removed per (s per nA) shown in Fig. 2. | ||
2. Experimental
This work uses six depth profiles on one implant standard and ten SW depth profiles from Genesis collector (#20732,2) taken during a single (1 week) analysis session. The standard was ∼2.5 × 3 cm in size, and was uniformly implanted by Kroko, Inc. of Tustin, CA with 25Mg and 26Mg (as well as with a small “accidental” implant of 24Mg). ICPMS at ASU's Isotope Chronology and Geochronology Laboratory was used to calibrate the 25Mg/26Mg ratio; SIMS analysis using the Cameca IMS 7f at the Center for Microanalysis at The California Institute of Technology was used to calibrate the 25Mg fluence. Both the SIMS and ICPMS calibrations measured silicon positioned adjacent to the DLC during the implant. The Genesis ta-C on silicon (AKA “DoS” in Genesis literature for DLC on silicon or for “diamond” on silicon) bulk solar wind collector was ∼5 × 7 mm in size.Collection of SIMS data used the ASU Cameca IMS 6f with a 12.5 keV accelerating voltage (5 keV nominal sample voltage) 20 nA O2+ primary beam raftered over a 250 × 250 μm area. To increase total counts, the Cameca Dynamic Transfer Optical System (DTOS) was used, along with both 60% electronic gating and a field aperture that circumscribed the spot to which the secondary ions were focused in the image plane. The field aperture did not change the nominal field of view; however, it reduced the collection of scattered of secondary ions originating from the sample's surface and the walls of the analysis pit. For the standard, signals from all three Mg isotopes and both 12C+ and 12C2+ were collected through the depth profile. For the SW collectors, signals from all three Mg isotopes were collected throughout the depth profile, but the matrix species 12C+ and 12C2+ were only collected for two short durations: once before the Mg profiles began and once after the Mg depth profiles were completed. For SW analyses, only data collected at the end of the depth profiles (12Cfinal+ and 12C2 final+) were used to reduce the fluence data, both because the initial counts were from the zone of transient sputtering and because the SW H (implanted shallowly relative to SW Mg) may change the relative ion yield of 12C+ to 12C2+ as the H concentration changes [e.g., ref. 15]. The variable effect of SW H on Mg ion yields from DLC will be detailed in the Discussion. The reader is referred to ref. 9, 10 and 16 for further details concerning the analyses and calibrations.
2.1. The SIMS data reduction
The typical data reduction procedure for depth profiles of implants is to:(1) Subtract the background;
(2) Correct for surface contamination;
(3) Integrate over the entire depth profile to find the total (counts/matrix counts) for both the standard and the unknown, and then,
(4) Quantify the unknown by assuming that the total (counts/matrix counts) in both standard and unknown are proportional to their respective implant fluence, F. That is, for 24Mg in a carbon matrix,
| (FUNK)/(FSTD) = (∫24Mg/12C)UNKdx)/(∫24Mg/12C)STDdx) | (1) |
An overview of the modified data-reduction procedure is given below in four sections: (i) the standard, (ii) the solar wind, (iii) matching solar wind analyses to matrix-appropriate standard analyses, and (iv) how SRIM-fits were calculated. Each section points out relevant similarities and differences from the “typical” data reduction technique outlined above.
2.2. The DLC standard
Depth profiles of the standard implant ran overnight (7 to 12 hours) to achieve total depths well past the end of the implant. Therefore, subtraction of the background was well defined and step (1) was straightforward. In all of the profiles conducted on the standard, the constant background at mass 24 was <0.6 cps. On occasion, because of inhomogeneity in the DLC, the profiles included excursions of the matrix ion signal we associate with the presence of particulates or structural irregularities that briefly influence sputtering rate (and thus the O content of the sputtered matrix). Anomalous secondary ion signals near the surface were eliminated incidentally by the surface correction (step 2) and any other clearly anomalous sections of the depth profile (e.g., signal likely indicating embedded particulates) were manually eliminated.Step (2), the surface contamination correction, was also relatively straightforward. Because the calibrated implants were minor ions (25Mg and 26Mg), the 24Mg depth profile could be used to indicate ion-mixed surface contamination. To correct the 25Mg and 26Mg depth profiles, first the counts originating from the small accidental 24Mg implant were subtracted (note: where the accidental implant overlapped surface contamination, the near-surface portion of the accidental implant was defined using SRIM as detailed later). Any remaining 24Mg was treated as ion-mixed contamination. This remaining 24Mg depth profile was integrated [i.e., (∫24Mg/12C)STDdx] to calculate the ion-mixed surface contamination. Then the integrand was multiplied by the terrestrial 25Mg/24Mg and 26Mg/24Mg ratios18 to give the 25Mg and 26Mg contamination, respectively. The 25Mg and 26Mg contamination was then subtracted from the integrals of the 25Mg and 26Mg implants. In theory, the terrestrial ratio should have been modified to include the IMF of each depth profile because, for these analyses, the IMF was surprisingly large (3–5%; i.e., 30–50‰). But the correction for contamination was small relative to the total counts of the implant (≤1%), so the IMF correction to the contamination was considered negligible.
Step (3) for the standard was a simple integration of the surface-corrected 25Mg curve, (∫25Mg/12C)STDdx. To evaluate FSTD/(∫25Mg/12C)STDdx, the 25Mg fluence had already been measured in co-implanted silicon by SIMS. However, the SW measurement was for 24Mg, not 25Mg. So, to compare the integral in the standard with the solar wind integral in step (4), an effective (∫24Mg*/12C)STDdx value was needed; i.e., the 25Mg integral of the standard had to be corrected for IMF. In these DLC measurements, IMF was calculated for each standard analysis using the difference between the measured 25Mg/26Mg vs. the (ICPMS-derived) actual 25Mg/26Mg. These IMFs ranged from 3–5% (∼30‰ to 50‰) per amu. Once corrected for IMF so that the absolute counts represented a 24Mg counting rate, the (∫25Mg/12C)dx became (∫24Mg*/12C)STDdx and could be used for SW 24Mg in eqn (1).
2.3. The DLC solar wind collector
SW is a low-fluence, low energy implant. Accordingly, analyses of SW are more sensitive to small spatial variations in DLC properties, as well as small errors from the data reduction, than analyses of the high-energy, high fluence standard. Step (1), the background correction, would, ideally, be the same for the DLC SW collector as for a uniform substrate like silicon; however, for reasons of expediency, SW analyses were limited to ∼2.5 hours. Although the shorter analysis time measured ≥99% of the SW 24Mg, it was also problematic because the bulk solar wind sample has a long, deep, low-intensity tail comprised of ions from high-velocity coronal mass ejections (e.g., ref. 17 and 18). These high-energy SW ions were implanted beyond the total analysis depth so the background could not be measured directly. Luckily, by using the velocity distribution of the SW Mg ions collected in situ by spacecraft in our models, the intensity of the counts in this long SW tail can be estimated using SRIM. Thus, the background can be calculated as one part of our iterative data reduction; i.e., (actual counts near end of analysis) − (tail of SRIM-model counts) = background counts.Removing ion-mixed surface contamination, step (2), also could not use the method applied to the standard. Unlike the commercial two-isotope implant, the 25Mg/24Mg and 26Mg/24Mg ratios differed less than 5% from the terrestrial value.10 The situation was exacerbated because all SW depth profiles started within 1 nm of the collection surface and so were always partially overlapped by ion-mixed surface contamination. Therefore, there was no way to a priori calculate the terrestrial contamination from any of the three isotopes without knowing the distribution of the SW ions.
This work used SRIM to calculate the likely distribution of the implanted SW ions to enable the surface correction. To avoid skewing the calculated SW distribution by including surface contamination, the SRIM model was fit to the data that was both (1) deeper than the peak and (2) distinguishable from the background. To avoid including background in the SRIM model, the depth profile was plotted on a log scale and the deepest point chosen for the fit had to be from a section of profile where the counts were still decreasing. Counts from surface contamination were defined as the counts greater than predicted by SRIM-fit at depths adjacent the surface of the sample. That is,
When quantifying a SW fluence, step (3) of the basic method (the integration of the depth profiles) was unchanged. Since the 24Mg of the solar wind was directly measured and since the integrated depth of the 25Mg in the (IMF) standard had been corrected to the counts per atomic mass unit for a 24Mg standard, no IMF correction to the integrated SW 24Mg was necessary.
The fluence calculation (step 4) given in eqn (1) assumes that the standard has the same matrix properties as the unknown. Because the matrix properties of the DLC under SIMS are spatially variable, (∫24Mg/12C)STD in eqn (1) becomes (∫24Mg/12C)STD*; i.e., the integral of a specific standard analysis with the appropriate matrix properties.
2.4. Matching SW data with a matrix-appropriate standard analysis
In this study the ratio C2+/C+ was used to track the properties of the analysed DLC, after the method used in ref. 9 and 10. The C2+/C+ parameterization works extremely well for this data set. Most of the data collected from the DLC were inferred to have silicon present, and the ion yields of both standard and SW analyses were approximately linear with C2+/C+. The few analyses with sputtering that appeared to be controlled by reactive ion etching were offset from the dominant C2+/C+ trend. These other data also appeared to have a linear trend with C2+/C+, possibly controlled by density. The integrals of ion yield for standard and SW analyses could be overlaid and the transition between etching and no etching could be matched, as will be shown in the Results section, Fig. 4. This matching of each SW analyses to a matrix-appropriate standard analyses allowed eqn (1) to be solved accurately.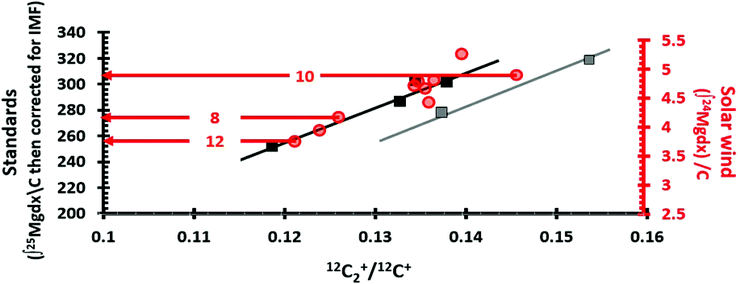 | ||
| Fig. 4 Matching SW analyses (circles) with matrix appropriate standards (squares) using the matrix parameter 12C2+/12C+. LHS axis = integral of 25Mg depth profiles from the standard after correction for IMF (squares); RHS axis = integral of 24Mg SW depth profiles (red circles); horizontal axis is (12C2+/12C+ final for SW; 12C2+/12C + average for standards). Lines (x = 12C2+/12C+, y = integral of IMF corrected 25Mg/C) are trends of depth profiles from standards in two matrix types: black for silicon-controlled sputtering; grey for etching-controlled sputtering. The equations are: y = 2716.697x − 70.2135 and y = 2716.697x − 97.0570 for black and grey trends, respectively. The black “silicon” trend is a fit to 4 points with R2 = 0.95. The grey “reactive etching” or “diamond” line has two points which, when the linear fit is forced to the slope of the black line, gives an R2 = 0.99. The “Direct Reading” method for matrix-matching is illustrated for SW_10, SW_8 and SW_12 by red arrows (circle to LHS). For the “Analytical” approach for matrix-matching SW_10, SW_8 and SW_12, the 12C2+/12C+ parameters for SW_8 and SW_12 would be x in the equation of the “black” trend, while SW_10 would use the equation for the “grey” trend. This is equivalent to drawing a vertical line from the SW marker to the nearest trendline and then reading the LHS-axis. See Table 1 for the results. | ||
2.5. Modelling implants using SRIM
For the standard implant, SRIM plays a relatively minor role: correcting the 24Mg depth profile for the (deep) 24Mg accidental implant so that surface corrections will be more accurate. In contrast, for the DLC collector, both the background correction and the surface correction depend strongly on how well the SRIM model matches the implanted SW ions. But, the SRIM model not only depends on the energy spectrum of the ion implant, but also matrix properties, especially composition (with respect to silicon or silicon carbide) and density, both of which are somewhat variable in DLC.To determine the appropriate density for the DLC and to ensure internal consistency in the choice of matrix, a parametrization was developed and used for both standard and sample as follows. The coordinates (Xpeak, Xhalf) were plotted for a set of SRIM models using the same matrix and varying densities, where Xpeak was the peak depth and Xhalf was the depth after the peak where the counts had dropped to half of the peak value. When both the matrix and densities were appropriately adjusted, the plots of the data overlapped that of the SRIM models. Then, the density of DLC at each analysis point could be estimated from its position with respect to the density of the SRIM models (see ref. 9 and ESI† of ref. 10 for more details). The estimated initial density was then iterated until the model achieved its best match to the data. At this point, the SRIM model for each standard analysis, which was only used for the surface correction, was complete. However, the SRIM model for each SW analysis had to be further refined because the background was also a variable. So, the tail of the SRIM model was subtracted from the actual counts near the end of the analysis, and that became the first estimate of the background. Then, the SRIM model was re-fit to the newly background corrected SW data, and both density and intensity were varied until the minimum deviation was reached.
The fit of the SW data to the SRIM model was quantified using the following equation:
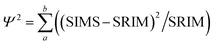 | (2) |
3. Results
Fig. 4 overlays separate plots for the 24Mg*/C integrals of the standard analyses (squares) and the 24Mg/C integrals for the SW depth profiles (circles) vs. the parameter 12C2+/12C+ as outlined previously in Section 2.4. The match of the SW overlay to the standard plot was done visually, making sure that the 12C2+/12C+ coordinates matched and that the main trend of the SW data overlaid the solid black line, the “silicon” trend for the standards. The second trend, plotted through STD_3 and STD_4 with a slope parallel to the solid black line, is present because these two analyses appeared to be DLC having an anomalously-high level of diamond (sp3 bonds). In the analysis pit for STD_3, diamond crystals (up to 600 nm in diameter) were observed. STD_4 had anomalously low matrix ion yields (Fig. 3), a low number of matrix removed per (s per nA) (Fig. 2(b)) despite having the lowest model density, and showed no sign of enhancement of Mg ions by silicon (Fig. 2(a)). In addition, STD_4 had a high 12C2+/12C+ which is indicative of low electrical conductivity (as discussed in Section 4.1 and in the ESI, Section D†).Table 1 gives two methods for matching the SW data with matrix-appropriate standards based on Fig. 4. Our preferred method is “Direct Reading”. Given the Fig. 4, direct reading entailed simply drawing an arrow from the center of the SW value to the corresponding standard value, whether or not it fell directly on one of the trend lines (e.g., the example horizontal red arrows Fig. 4). Because the SW value is not forced to fit a calculated trend, direct reading implicitly assumes that there may be matrix effects not accounted for by C2+/C+ ratio, but that their effect is small enough that the parametrization still gives the matrix-appropriate standard.
| Analytical | Direct Reading | |||||
|---|---|---|---|---|---|---|
| SRIM-corrected SW integral | STD integral | 24Mg fluence | STD integral | 24Mg fluence | Difference | |
| a Particulate precludes iterative SRIM fit. | ||||||
| SW_2 | 4.700 | 296 | 1.39 × 1012 | 299 | 1.38 × 1012 | 1.10% |
| SW_3 | 4.419 | 274 | 1.42 × 1012 | 286 | 1.35 × 1012 | 4.37% |
| SW_5 | 4.818 | 302 | 1.40 × 1012 | 304 | 1.39 × 1012 | 0.79% |
| SW_6 | 4.667 | 299 | 1.37 × 1012 | 297 | 1.38 × 1012 | −0.65% |
| SW_7 | 4.795 | 297 | 1.41 × 1012 | 304 | 1.38 × 1012 | 2.30% |
| SW_8 | 4.164 | 273 | 1.33 × 1012 | 276 | 1.32 × 1012 | 0.83% |
| SW_9 | 5.266 | 310 | 1.49 × 1012 | 325 | 1.42 × 1012 | 4.64% |
| SW_10 | 4.893 | 300 | 1.43 × 1012 | 308 | 1.39 × 1012 | 2.75% |
| SW_11 | 3.945 | 267 | 1.29 × 1012 | 265 | 1.30 × 1012 | −0.89% |
| SW_12a | 3.753 | 260 | 1.26 × 1012 | 257 | 1.28 × 1012 | −1.20% |
The second method, “Analytical”, takes the C2+/C+ ratio for each SW analysis and calculates the standard value using the equation of the closest trend; i.e., it assumes that the C2+/C+ ratios for the matrix matches are a perfect predictor of the minor ion yield. The difference for the calculated fluences in the two sets of results is <5%. However, fluences calculated using the analytical approach are more scattered than for direct reading (1σ of 4.9% vs. 1σ of 3.2%).
Fig. 5 shows the distribution of the calculated fluences from the “Direct Reading” as a function of the C2+/C+ ratio for each SW analysis and compares them to the preliminary SW results from silicon.19 The 24Mg fluences measured in DLC are about 6% higher than the 24Mg fluences in silicon at the higher C2+/C+ ratios; however, they are consistent with those from silicon at the lower C2+/C+ ratios. It is possible that this spread of 24Mg fluences is simply due to counting statistics, but the spread may also indicate that other issues exist for quantification of DLC characterized by a matrix that yields a lower C2+/C+ (Discussion in Section 4.4).
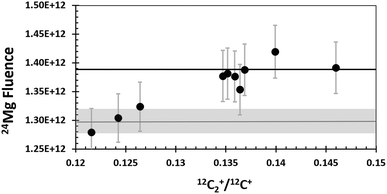 | ||
| Fig. 5 SW 24Mg from DLC (circles are “direct reading” of Table 1) and silicon19 (grey bar gives range of Si). Error bars are + 3.2%. The analysis with the lowest +C2+/+C+ is SW_12. SW_11 and SW_8, the next lowest, have isotopic ratios that show multiple interferences, likely H-related.11 SW_11 and SW_8 also plot between STD_7 and STD_5 on Fig. 4, the two standards that show increased ion yields due to minor Si in Fig. 2. The solid black line is the average from dlc without SW_8, 11 and 12, giving the maximum likely deviation of 24Mg fluences from DLC vs. Si. | ||
4. Discussion
SIMS analysis of diamond-like carbon is not yet a preferred method for the characterization of diamond-like carbon films because secondary ion yields often vary with position on the film, making the data difficult to quantify (e.g., Fig. 2). However, technique development on the quantitative analysis of solar wind in DLC for NASA's GENESIS solar wind sample return mission has shown that reproducible quantification of SIMS analyses of diamond-like carbon is not only possible10,15 but, in some situations, can provide incidental structural and chemical information.10 Below we discuss the reason this data reduction technique works, as well as its limitations.4.1. Relevance of the C2+/C+ parametrization
Previously, in Section 1.2, sources and examples of observed matrix effects in DLC, the use of the 12C2+/12C+ ratio for understanding matrix properties was justified empirically in Fig. 3. Specifically, Fig. 3 presented a strong linear correlation for the intensity of the 12C2+ dimers with those of the 12C+ ions. Then, since the slope of the correlation of 12C2+ with 12C+ was 0.13 (i.e., anything but ∼1, which might have indicated primary beam fluctuations, etc.), the 12C2+/12C+ ratio was deemed useful for matching analyses with matrix appropriate standards. Indeed, for this data set, the 12C2+/12C+ ratio appears to work remarkably well for that purpose (see Fig. 4 and Table 1). But, in Fig. 3 and in earlier studies10,11 there was no concrete evidence for why it worked. This lack of knowledge was an issue. Understanding why the parameter is effective is needed so that other researchers can: (1) evaluate whether or not this parameter is applicable to their data sets, and (2) understand how to develop another useful parametrizations if necessary.The explanation for why the 12C2+/12C+ ratio worked as a useful parameter for matching analyses with matrix appropriate standards in this study is as follows. Elemental and molecular species are both formed during sputtering, irrespective of whether the SIMS is configured for positive or negative secondary ions. Moreover, the range of energies of ions ejected from the matrix is different for elemental versus molecular species. An example of the energy spectra for 12C2+ and 12C+ that were recently (May 2020) measured under conditions similar to our original SIMS conditions is given in Fig. 6(b). The C2+ dimer has a narrow energy range compared with the C+ ion. For an O2+ primary beam, if the area selected for analysis is less conducting, then the sputtered crater will develop a slightly positive charge, the energy spectra (Fig. 6(b)) will be shifted to the right, and the 12C2+/12C+ ratio (measured at “0” volts) will become larger. If the area selected for sputtering has a more negative charge than the 0 V Offset in Fig. 6(b), then the energy spectra will slide to the left, and the 12C2+/12C+ ratio (measured at “0” volts) will become smaller. In addition, if the energy spectra slide in either direction from where they were initially centred, 0 V will no longer be positioned at the peak of the spectra and the individual intensities of 12C2+ and 12C+ will decrease with distance from the 0 V position.
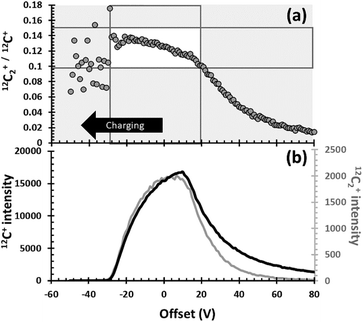 | ||
| Fig. 6 Illustration of why the 12C2+/12C+ parametrization works. (a) the intensity of the 12C2+/12C+ ratio vs. voltage offset from the matrix where the energy window was set. This voltage offset depends directly on the conductance of the matrix in this location (see eqn (3)). (b) the relative distribution of intensities for both the 12C2+ dimer (grey) and the 12C+ ions (black) as a function of the voltage offset. White box marks the range of 12C2+/12C+ values observed in this work with their corresponding voltage offsets. Further details in the SOM. | ||
For a homogeneous, conductive material, the energy spectra should be stable; i.e., there will be no imposed voltage offsets if good analytical practices are maintained. However, for DLC, the situation is different. Sullivan et al. (1998)12 showed that multiple measurements of electrical conductivity (Cmatrix) through 2.5 μm2 areas across his 2′′ test wafer of DLC varied by more than 10×. Our SIMS analyses sampled 250 μm2 columns of DLC. This sampling of a larger area likely averaged some of the variations seen by Sullivan et al. on the 2.5 μm2 scale, so the range of conductivity measured was likely less than 10×. Still, one factor in the matrix structure (which, in turn determines the electrical conductivity) is the stress state of the film. The intrinsic stresses at the edge of a film will have the opportunity to minimize (i.e., the free surface can move); therefore, internal stresses across a finite material are never uniform. Thus, spatial variations in the electrical conductivity of the matrix must certainly exist, even when areas measured are 250 μm2.
Strong variation of the electrical conductivity of the DLC matrix can have a direct effect on SIMS analyses in the following way. Although the voltage applied to the wafer fragment being analysed, V, is always a constant (here, 5000 V), the voltage that the matrix experiences while sputtering each profile varies as the conductivity of the matrix varies. Specifically,
| ΔVmatrix = (Vmatrix − Vo) = Ibeam/ΔCmatrix | (3) |
Normally, when the bandpass of ∼40 eV is set up for the SIMS conditions required, the energy window is centred at the point of highest conductivity. However, at the time of this study, it was thought that the DLC was uniformly conductive in 250 μm2 areas, so a spot was chosen at random. It is unlikely that an area having the highest conductivity was used to set the 0 V position of the energy window. Therefore, in this study, an area with a positive charge less than the area used for setting 0 V would slide the energy spectra to the left and give a smaller 12C2+/12C+ ratio; e.g., the range of voltage offsets from 5000 V from −30 V to +20 V in Fig. 6a probably all represent positive charging from the O2+ beam.
The white box in Fig. 6a gives 12C2+/12C+ ratios observed in this study as a function of a shifting ΔVmatrix. Note the roughly linear trend of 12C2+/12C+ ratios diagonally through the box; this variation explains the trend illustrated by Fig. 3. In Fig. 3, STD_4 was the analysis with the lowest intensity counts; it also had a 12C2+/12C+ ratio of 0.154 (the upper LH corner of the white box in 6a). Thus, it had a strong positive charge – so strong, in fact, that it was on the edge of signal loss. Diamond is a semiconductor, but the band gap is 5.5 eV, which is 5× that of silicon. That is, undoped, diamond is essentially electrically insulating. So, the extreme voltage offset (charging) during the STD_4 analysis is consistent with large areas of sp3 bonds whose electrical resistance is not mitigated by smaller areas of sp2 bonds, and that consistency supports the speculation that the matrix of STD_4 was an area consisting of nanodiamond. STD_7 also had low intensities of 12C2+ and 12C+; however, it's 12C2+/12C+ ratio was the lowest measured (0.119), which suggests that the analysis was in the most conductive DLC matrix measured in the standard. The low absolute 12C2+ and 12C+ ion yields in Fig. 3 confirm that the matrix of STD_7 was significantly more conductive than the DLC matrix on which the energy window was centred. Note that the 25Mg+ ion yield per C sputtered per nA was high (Fig. 2a). So, silicon (as silicon or silicon carbide) was probably present to boost the local oxidation state. This observation is consistent with the low 12C2+/12C+ ratio because both silicon and silicon carbide are more electrically conductive than diamond. Note that some of the change in the 12C2+/12C+ ratio could, in theory, also be caused by dilution of the C bonds present by silicon.9
Interestingly, the standard analysis with the highest intensity of matrix ions was STD_3, the analysis with the matrix that had the highest model density and residual diamond crystals in the SIMS crater. The 12C2+/12C+ ratio of STD_3 was 0.137. Clearly STD_3 was from a diamond-like area and must have been positively charged, certainly more so than STD_7, but less so than the matrix of STD_4. The offset from 0 V in Fig. 6 was about −17 V (vs. ∼ −30 V for STD_4 and +20 V for STD_7). Given that the large (∼600 nm) diamond crystal in the crater of STD_3 was able to remained euhedral after being sputtered overnight (∼9.5 hours),10 the matrix surrounding the crystals must have been sp2-rich, interconnected, and capable of dissipating a significant portion of the deflected charge. So, the high ion yield suggests that this voltage may be similar in conductivity to where the energy window was set.
One final comment on the above discussion of conductivity controlling the 12C2+/12C+ ratio. Matching analyses with matrix-appropriate standards using the 12C2+/12C+ ratio would – at best – be complicated if electrical conductivity changed with depth in the DLC. However, the measured 12C2+/12C+ ratio has been constant in our standard analyses, in even throughout our deepest crater, 992 nm. That the observed uniformity of the 12C2+/12C+ ratio with depth is a proxy for a uniform electrical conductivity of DLC in columns is consistent with the results of Sullivan et al. (1998).12 Their work showed that the conductivity depended on the local stresses and the temperature of annealing; however, conductivity was essentially constant with the time of annealing after a relatively short initial anneal. So, even with multiple deposition/annealing steps, the cumulative annealing time throughout the thickness of the Genesis DLC films should be short enough that conductivity remains constant.
More explanation on variations in electrical conductivity in DLC and its effects on SIMS analyses outlined above is included in Section B, Section C, and Section D of the ESI.†
Still, Table 1 does make it clear that the C2+/C+ parametrization is not perfect, as demonstrated by the occasional differences in the data given for “Analytical” vs. the “Direct Reading” techniques (Table 1). At this point, it is not clear why there are discrepancies between the two techniques. However, note that The multiple annealing steps may result in changes in the texture of the earliest deposited DLC layers.12 Such a change was detected in a Genesis sample by comparing Raman spectra taken from the surface (edge of the crater) and the floor of a single analysis crater and then calculating the change in the Raman D and G peaks.13 It is possible that variations in the DLC matrix with depth caused by adjustments in texture or bonding due to the numerous anneals occasionally cause matrix-related variations in secondary ion yields or conductivity. Other factors (e.g., an embedded particulate or other defect in the film) could also potentially change the C2+/C+ value.
4.2. SRIM surface and background corrections (and how they differ from the same implants into silicon)
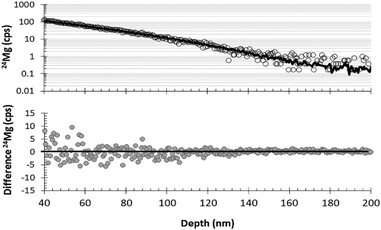
Although being able to match an analysis with a matrix appropriate standard is imperative for enabling the quantification of SIMS data from DLC, being able to separate ion mixed surface contamination from the shallow, trace-level implant profiles is the next most important step. The fundamental assumption behind using SRIM for these corrections is that the depth profiles calculated by the SRIM program accurately approximate the implant profile present in the collector. SRIM calculates the model depth profiles using a Monte Carlo method; so, although there is some error in the computation of the model, that particular error can be mitigated by increasing the number of ions in the model. The fundamental issues for using SRIM is to understand whether or not the implant to be modelled meets the assumptions of the program: (1) implanted ions do not diffuse after implantation, and (2) the implantation profile is not skewed by either localized variations in the matrix composition or the ions and defects that accumulate during the implantation.DLC is, in general, very retentive of implanted ions. For example, Vainonen et al.20 showed that H does not diffuse measurably in DLC films at temperatures under 700 °C, even when moderately radiation-damaged by He implantation. H is, in general, a fast diffuser relative to other elements. Moreover, ∼97% of the SW is SW H and SW He while the remaining 3% (the “minor ions”) consists of the rest of the periodic table; therefore, the other elements are present at concentrations orders of magnitude lower. The question is whether or not the implant profile of the minor ions can be modelled by SRIM into a C matrix, or if the damage from the concurrently implanted SW H and He allows them to move. To this end, Fig. 7 and 8 compare the raw, measured 24Mg data from SW_3 to a SRIM model, indicating an excellent fit. Other examples of SRIM fits to SW in DLC are available in the ESI† of ref. 10, and thus far, the profiles of “minor ions” in DLC appear to be accurately modelled using SRIM. SRIM modelling of implants into DLC for the purpose of the surface correction can be cumbersome and is not always necessary. An alternative is to draw a line from the break-in-slope of the SIMS data as illustrated by the dashed line in Fig. 8 (note: the break in slope is weak due to significant contamination up to the peak but, as a best guess, it is typical, with the line starting at 0 and intersecting the raw data ∼10–12 nm from the origin). For the bulk SW 24Mg data reported here (peak counting rate < 300 cps), linear surface corrections give fluences approximately 6% higher than those made using SRIM. (Note: the linear approximation to the SW was used for the data in Jurewicz et al. (2017)10 published before the method using a SRIM-fit was developed). In contrast, the linear correction for surface contamination made on data from the high-fluence standard implant (peak concentrations ∼ 1 × 104 and minor isotopes) gave results negligibly different from the SRIM correction.
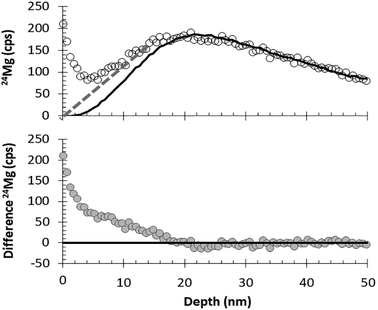 | ||
| Fig. 8 Illustration of DLC surface correction using measured data (circles, SW_3) vs. SRIM best fit (solid line) for the first 50 nm of the 24Mg depth profile. Top: comparison of raw data with the SRIM best–fit curve; dashed line gives an example of a (previously used10) visual correction based only on curve shape. Bottom: the difference between SRIM and the raw SIMS data. | ||
In practice, because of the ion-mixed surface contamination, Fig. 7 and 8 only demonstrate that the tail of the SRIM curve is consistent with the SIMS data. Other information is needed before the appropriateness of the SRIM-fit to the surface of the SW depth profile is validated. However, there are two observations that strongly suggest that the SRIM model accurately defines the front side of the SW implant into DLC. First, after surface corrections using SRIM, results for SW 24Mg become more internally consistent with other DLC analyses and closer to SW results from silicon. Second, there is an observation that was made in the special case where the surface contamination can be approximated as a thin film in both the SW collector and the standard (e.g., no large particulates at the surface). In that case, the surface contamination profile determined from the standard (and scaled to density and intensity) can be subtracted from the SW depth profile to match the SRIM correction (examples in ESI† of ref. 10).
The response of DLC to the SW radiation damage (modal bulk SW energy of ∼1 keV amu−1) is special: in many materials with similarly high concentration implants (such as the solar wind in the Genesis silicon collectors, Fig. 9), the ions move after the initial implantation in a process called radiation-enhanced segregation.8 The obvious disagreement between the measured profile in silicon and the SRIM model in Fig. 9 is that 24Mg appears to have migrated outward towards the SW H peak (vertical dashed line); some fraction has certainly moved towards the depths of the wafer as well. The extensive near-surface damage from SW H (∼95% of the SW and a compact profile because of its low energy) is an important control for the shape of the Mg implant. Moreover, H and related vacancies diffuse relatively quickly in silicon. Movement of both the implanted H ions and the defects created during implantation dissipates the energy input into the substrate by the capture of the high-velocity ions. As H and its defects move, they enable Mg diffusion. Mg mostly moves into the damaged portion of the lattice but can also follow point defects towards the undamaged lattice, forming its own metastable equilibrium concentration gradient.
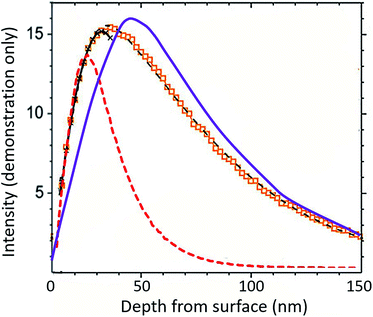 | ||
| Fig. 9 Back-side 24Mg depth profile into Genesis silicon (data as markers with geometric best fits superimposed as thin black lines: near surface = crossed; deep = dashed) modified from Heber et al. Fig. 10a.21 Bulk SW 24Mg SRIM into silicon is purple line; bulk SW H SRIM is dashed red line. Unlike the DLC data in Fig. 7 and 8, the bulk SW 24Mg SRIM clearly does not capture the shape of the actual SW 24Mg data. SRIM models of DLC suggest that the primary issue is not SRIM; rather, to achieve a lower energy state within the damaged silicon lattice, 24Mg diffuses in conjunction with vacancies and other defects to occupy lower energy positions. | ||
It is important to emphasize that movement of the SW ions does not mean that ions are lost or gained at the collection surface; only that the ions have adjusted to a lower energy (i.e., ΔG = ΔH + TΔS) configuration in the matrix.
Spreading of some ion implants in DLC relative to SRIM models has also been seen, but for different reasons. SRIM is a basic model and does not allow for previously implanted ions to effect the matrix composition and its stopping power. Our standard implants (75 keV of 25Mg and 26Mg at ∼9 × 1013 atoms per cm2) had a concentration of only ∼0.02% Mg atoms per carbon atom at the peak of the implant, so this was not a significant issue. Ion mixing during SIMS analysis can broaden the measured depth profiles. If recognized and accommodated, deviation of the depth profile of the implant from the ideal does not preclude using this data reduction technique to quantify SIMS measurements.
4.3. Relevance of results to DLC structure
Dynamic SIMS analysis is not anyones first choice for determining matrix properties, especially structure. By definition, during dynamic SIMS the ion beam pulverizes and mixes the matrix within the zone of sputtering before emitting the secondary ions. This process creates analytical artefacts (e.g., spreading of the depth profile from ion mixing) and the molecular secondary ions that form may or may not represent compounds present in the original matrix.Yet, using this data set, we have gleaned significant information about the properties of the DLC. The 12C2+/12C+ parametrization allowed inferences about the relative conductivity of specific columns of matrix. Similarly, sputtering rates, the apparent sputter yields, and measured IMF (Fig. 2) indicated the presence or absence of silicon within different portions of the DLC film – inferences which were later confirmed using Raman spectroscopy. Contamination was occasionally observed in the DLC at surfaces exposed to the vacuum during annealing steps, and in some depth profiles, variations in the intensity of individual matrix ions were also observed near these surfaces [e.g., ESI, Section B†]. The matrix ion fluctuations in the vicinity of annealing steps may indicate that the surface carbon is either a different density or bonding-structure; however, the 12C2+/12C+ ratio, which was primarily controlled by conductivity [e.g., ESI, Section D†], remained constant. SEM inspection of the sputtered craters revealed textures present at the sub-micron scale internal to the film. Perhaps most interesting of all is that the SRIM models used here – meant as estimates of the shape of the implant – gave densities for the DLC consistent with other modes of density determination (e.g., ref. 2). Our SRIM models were simple approximations: silicon (and H for SW models) was omitted from the calculations. The omission of both Si and H would tend to make our SRIM model densities slightly low when either of these elements are present in significant concentrations. Spreading from ion mixing was assumed minimal and ignored. Yet, a density of 3.4 gm cm−3 for an area of DLC dominated by the presence of diamond crystals (density of 3.54 gm cm−3) but also containing matrix cannot be far from correct.
On the other hand, STD_4, which had a matrix of extremely high 12C2+/12C+ ratio (0.153), also had very low ion yields suggestive of charging at the ∼30 eV level (refer to Fig. 6 and ESI, Section D†). This charging hinted at a region of nanodiamonds; i.e., a matrix of sp3 bonding with a electrical minimal conductivity because of the very few regions of sp2 bonding. But, the SRIM model density was low (2.85 gm cm−3). The density may indicate a region of poor compaction: i.e., if diamond nuclei formed an interconnected framework rapidly – before maximum densification – they would be unlikely to change their structure afterwards because of their high strength. This “imperfect sintering” scenario is plausible, but unlikely, because the internal stresses induced during fabrication are enormous.1,11,12 STD_4 also had the slowest sputtering rate per nanoampere of the matrices dominated by reactive ion etching (Fig. 2b), and that sputtering rate was close to that of STD_3, the matrix of density 3.4 gm cm−3 that contained euhedral diamonds. It is doubtful that the primary ion beam was deflected: in fact, there appeared to be much less scattering of the primary beam ions from surface 24Mg in the near-surface portion of the depth profile for STD_4 than for either STD_3 or STD_2 (see Section A3.2 of ESI of ref. 10 for examples†). In a discussion of this possibility in both oral and written communications, J. Ziegler (creator of SRIM) stated that the electrical properties of crystalline diamond meant that SRIM models were unreliable. So, if the matrix was effectively all sp3 bonding (diamond) for this particular analysis, the SRIM model density may incorrect (low) because the lattice parameters in the SRIM model are incorrect. Thus, although SRIM has given us what appear to be very reasonable densities, they are still model densities. Using our analysis conditions, the presence of diamond may result in a SRIM model density that is lower than the true density unless an experimentally-derived bonding correction is used for the SRIM input.
Additional, experimentally based bonding corrections for SRIM of DLC will be detailed later in this section; but, first, we note that ion mixing by the primary beam could also result in a SRIM model density that is too low. Specifically, if the peak and tail of the depth profile are extended by mixing of the measured ion with the matrix during sputtering, then the SRIM model needed to fit our depth profile will be stretched, thus giving a slightly lower density. However, the SIMS conditions in this study were designed to get the maximum depth-resolution from the ion implants: low impact energy and a 20 nA current rastered over a 250 μm2 area. The large raster was instituted to increase the analysed area and lower sputtering rate; however, it also lowered the number of impacting primary beam ions per unit area (4.2 × 1014 O ions per cm2). A smaller flux of charge per unit area probably made it easier for the DLC to dissipate the charge over a wide range of matrix conductivity, too. The effect of these SIMS conditions can be seen in the depth of the zone of transient sputtering which was negligible for 12C2+ and only ∼4 nm for 12C+ (see ref. 9). Since the depth of the zone of transient sputtering is proportional to the depth of mixing at steady state sputtering,14 there was very little ion mixing of the matrix during this SIMS session.
The quality of the depth resolution (or the amount of ion mixing) should not be estimated using previous experience with silicon, the standard material analysed by SIMS. DLC and silicon have exceedingly different stopping powers when hit by an ion beam. The differences in the stopping power of DLC vs. silicon are due to three factors: the stopping power of C vs. Si, the higher density of DLC, and the effect of the strong sp2 and sp3 C bonds. This fact can be illustrated using SRIM by running simulations of the primary beam impact. First, run simulations into plain carbon and silicon matrices of the same density (2.321 gm cm−3). Using O ions at 3.5 keV (i.e., 1/2 O2+ at a 7 kV impact energy) and a primary beam angle of 42°, the range for the depth of the implant peak into C calculated by SRIM is 6.3 nm, but 9.6 nm for Si. Moreover, the average density of the DLC calculated in this study was 3.0 gm cm−3 and 6.3 nm × (2.321 gm cm−3)/(3.0 gm cm−3) = 4.9 nm, only about 20% more than the observed transient into DLC of ∼4 nm. That 20% difference in the calculated vs. observed transient sputtering can be at least partially explained by the strong carbon bonds, as discussed below.
Although bonding is a second order effect on stopping power, according to the SRIM website's background information (see Stopping of Ions in Compounds under SRIM 2008), carbon bonds have a significant stopping power relative the atomic core (if C core = 1, then C–C bonds = 1, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (sp2) = 2.49, and C
C bonds (sp2) = 2.49, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (sp3) = 3.81). The Core and Bonding (CAB) model used in SRIM deals with contribution of the bonds using a linear addition of stopping powers through their “compound correction”. Note that SRIM 2008 has a catalogue material #906 nuclear grade graphite having a compound correction of 0.8684 (or 13%). Unfortunately, a description of #906 graphite could not be found in the literature, but since the phrase “nuclear grade” simply refers to purity, this was probably a pressed graphite containing both a minor amount of sp3 bonding (which would decrease the compound correction relative to 0.8684) as well as a small amount of void space (which would increase the compound correction relative to 0.8684). Assuming that this material is, nominally, 100% sp2 bonded carbon (i.e., sp3 bonds and voids cancel), then the compound correction for sp3 bonded carbon should be 0.7986 (20%). This result is the same as that calculated above using SRIM to determine the depth of the transient sputtering zone of the O from the primary beam into simple carbon, and then correcting 20%. Note that if a carbon SRIM model using a compound correction of 0.7986 is used to model STD_4, then the model density becomes 3.0 gm cm−3. This value is consistent with STD_2, 5, 6, and 7 which have SRIM model densities of 3.00–3.05 gm cm−3. Only STD_3 – which contained diamonds visible by SEM – is different, with a model density of 3.4 gm cm−3 [calculation in ESI Section E†].
C bonds (sp3) = 3.81). The Core and Bonding (CAB) model used in SRIM deals with contribution of the bonds using a linear addition of stopping powers through their “compound correction”. Note that SRIM 2008 has a catalogue material #906 nuclear grade graphite having a compound correction of 0.8684 (or 13%). Unfortunately, a description of #906 graphite could not be found in the literature, but since the phrase “nuclear grade” simply refers to purity, this was probably a pressed graphite containing both a minor amount of sp3 bonding (which would decrease the compound correction relative to 0.8684) as well as a small amount of void space (which would increase the compound correction relative to 0.8684). Assuming that this material is, nominally, 100% sp2 bonded carbon (i.e., sp3 bonds and voids cancel), then the compound correction for sp3 bonded carbon should be 0.7986 (20%). This result is the same as that calculated above using SRIM to determine the depth of the transient sputtering zone of the O from the primary beam into simple carbon, and then correcting 20%. Note that if a carbon SRIM model using a compound correction of 0.7986 is used to model STD_4, then the model density becomes 3.0 gm cm−3. This value is consistent with STD_2, 5, 6, and 7 which have SRIM model densities of 3.00–3.05 gm cm−3. Only STD_3 – which contained diamonds visible by SEM – is different, with a model density of 3.4 gm cm−3 [calculation in ESI Section E†].
In summary, the SRIM model densities calculated under the conditions of this study seem relatively consistent, especially if accommodations are made for matrix bonding and ion mixing by the primary beam. The accuracy of our calculated densities for this data also suggests that, unlike Mg in silicon, the implanted ions in DLC have been effectively immobile both during and after collection, and there is little mixing during sputtering by the SIMS ion beam. But, could we have improved our analytical conditions to give more accurate densities? That is, would our calculated SRIM densities have been higher if we had further lowered the impact energy for even less ion mixing and conducted an analysis session using the same raster and current? Although more research is needed, the first author thinks not, for the following reason. For the SRIM model mentioned above, the nominal depths of the O ions were 6.3 nm and 9.6 nm for C and Si, respectively, but the lateral ranges were 7.3 nm and 11.5 nm, respectively. Taking into account the 3.0 gm cm−3 density of the DLC and the estimated 20% additional stopping power from the concentration of sp3 bonds, the lateral damage radius for the incoming ions into DLC was 7.3 × 2.321/3.0/1.2 = 6.8 nm vs. 11.5 nm for silicon. Since the area damaged by each incoming ion is proportional to the square of the radius (after McPhail 2006 ref. 22) and the lower limit for dynamic SIMS in silicon is ∼5 × 1012, the lower limit for dynamic SIMS in DLC is ∼5 × 1012 × (11.52)/(6.82) = ∼1.4 × 1013 ions per cm2, whereas we were running about 2 × 1014. But, if you happened to hit an anomalous area where the voltage offset (Vmatrix) is high (e.g., STD_4) with a high density (e.g., STD_3) the 6.8 nm radius becomes a 4.2 nm radius, and the lower limit for dynamic SIMS becomes 3.9 × 1013. Therefore, further lowering the impact energy (which would decrease the lateral damage radius of each primary ion) could, in theory, mean that – on rare occasions – the DLC would hit the limit between dynamic and static SIMS and that analysis would not be quantifiable. Support for this concept comes from an experiment performed at the beginning of the analysis STD_4: for first ∼300 s, the matrix was purposely sputtered using a slightly defocused beam (i.e., finite round beam instead of a spot). The result was that it was not clear that there was any sputtering during the first ∼300 s (see the ESI of both9 and this work, Section F†).
4.4. The role of matrix effects due to SW H
The DLC used for solar wind collection in the Genesis spacecraft was anhydrous, but hydrogen was present after SW collection. Hydrogen is the primary component of the solar wind, with the Genesis bulk solar wind collectors implanted with 1H at a fluence of ∼1.6 × 1016 atoms per cm2 as measured by Huss et al.15 (there is no measurable deuterium23). In DLC the SW H implant peaks within the first 10–12 nm of the collection surface and the local concentration of H can reach as much as ∼2 atom%, which is still in the ta-C field of the phase diagram of Robertson.2 Although this study is concerned with ta-C throughout, hydrogen is an important component of many types of commercial DLC. Accordingly, we emphasize that clear “matrix effects” of SW H and other H implants into the Genesis ta-C were observed in both10 and in ref. 15. Below we discuss the contribution of H to matrix effects observed in SIMS data and how they may influence some calculated SW Mg fluences from Genesis DLC.First, near the surface of our Genesis collectors (also corresponding to depths where SW H was concentrated), the C2+/C+ ratio tended to be higher than the rest of the depth profile.9 The C2+ ion yield appeared to be nearly unaffected by the initial transient sputtering; in contrast, the C+ ion yield showed noticeable transient sputtering effects. One interpretation of this observation is that the surface has become “more diamond like” in that the SW H ions damage high-stress areas of DLC and allow strongly bonded, strained regions to restructure (e.g., an opportunity to increase the percentage of sp3 domains and perhaps grow crystallites such as nanodiamond or perhaps silicon carbide in a Si-rich areas). This first interpretation is consistent with observations of changes in amorphous carbon films such as ta-C when radiation damaged noted in multiple studies (e.g., ref. 24 and 25). An alternative interpretation is that low-energy sputtering during SW H bombardment winnowed the weaker C bonds from the DLC surface creating an increased C2+/C+ ratio at the surface as observed by Nakazawa et al. (2010);26 however, both the low current of SW ions and the low dose of SW H ions relative to atoms in the carbon matrix makes a major contribution from sputtering during the two-year exposure to the solar wind highly unlikely. A final option is chemical interactions of H with the C matrix; i.e., a matrix effect. During their study of SW H in Genesis DLC, Huss et al.15 noted that, as H peaked in their standard implants, C2− tended to increase and C− tended to decrease. Moreover, the measured CH−/C2− was more scattered than the measured H−/C− and did not give exactly the same fluence. They give a detailed discussion of possible instrumental and matrix effects that could contribute to the variations. Among the latter was the change in structure with depth, electrical transfers between the matrix and sputtered ions at depth, and variations in silicon content, which had been shown by Raman Spectroscopy to affect their sputtering rates13 in spite of the fact that the ion beam was Cs+ and not O2+.
Clearly, the H in the SW reacted with the DLC and lowered the carbon intensity during analysis of negative secondary ions in Huss et al.15 since the lower C intensity was observed in H implant standards. Although this observation was made for sputtering by Cs+, it is conceivable that something similar could happen under an O2+ beam. Positive secondary molecular ions could contain both C and H although, in practice, such molecular secondary ions would probably include O as well, since an O2+ primary beam makes the system so oxidizing. If H-bearing positive molecular secondary ions are abundant, then the SW H should also lower the intensity of carbon in areas of the DLC in areas where the SW H was concentrated. However, although this scenario seems plausible, we have yet to encounter an observable effect of a H implant on the carbon intensity during depth profiling.
Our tests for a direct effect of a H implant on carbon intensity included measurements on (1) a flight-like DLC film implanted with both H and 25Mg, and (2) a single SW sample that was sputtered past the end of the transient sputtering zone. Both tests resulted in a flat carbon intensity with depth. So, at least in the cases that we have investigated, sputtering using an O2+ primary beam likely makes the DLC too oxidizing for significant C(OH)+ or CH+ or related molecules to form (versus H2O or some molecule not carbon based).
There is a caveat to our tests. The occasional sp3 rich (i.e., diamond-like) areas that reactively etch during sputtering (i.e., the analyses to the right of the vertical bar in Fig. 2) were not encountered in our H-tests. These areas of DLC were shown to form a significant amount of (C3O)++ at mass 26, even though this molecule was not observed in the other analyses. Thus, it is plausible that these relatively unusual regions may have a lowered carbon intensity in the zones where H is concentrated due to, say, (CO2H)+. Accordingly, analysts who are normalizing their positive secondary ion data from DLC to carbon and who find that they have analysed an sp3 rich (i.e., diamond-like) zone, should plot the C intensity versus depth to check for a H-effect on the carbon intensity.
Of course, H interacting with C is not the only possible matrix effect. Indeed, Mg readily forms oxides and hydroxides under the right conditions. Three of the ten SW Mg fluences calculated from our DLC are lower (at 1σ or 2SE) than the other seven: 1.34 × 1012vs. 1.38 × 1012 with (±0.02 × 1012) = 1σ for both (plotted in Results, Fig. 5). Moreover, the low fluences were calculated from the analyses with the lowest C2+/C+ ratios. These were SW analyses whose parametrization (Results, Fig. 4) indicated that they were most similar to STD_5 and STD_7, the two standards that showed the most enhancement of Mg ion yield relative to the carbon sputtered; i.e., the two standard analyses plotting on the far LHS of Fig. 2.
The SW analysis from which the lowest SW Mg fluence was derived, SW_12, clearly contained a Mg-bearing near-surface particulate, probably dust. So, it is possible that some SW Mg was removed in the data reduction. However, the other two analysis, SW_8 and SW_11, not only had lower fluences, but the isotopes calculated from these analyses also had anomalous isotopic ratios (discussed in the text and ESI† of ref. 10). Accordingly, it is plausible that, under an O2+ ion beam, if enough oxygen is mixed into the DLC matrix, a different suite of molecular ions will be produced during sputtering, including hydride formation in the presence of H.
Table 2 gives a mass balance to test if the marginally lower 24Mg fluences of SW_8 and SW_11 could be due to hydride formation caused by the presence of SW H in the presence of enough silicon to slow the sputtering rate and mix additional O into the DLC matrix. Note that the estimated molecules are reasonably consistent, even though they would be expected to vary with the amount of overlap between the SW H and the embedded silicon. Although the isotopic data from ref. 10 and the calculation in Table 2 do not prove that H formed molecular ions with Mg when silicon was present, it does lend support to the likelihood of this matrix effect.
| Measured fractionationb | Total 24Mg reductiona | Total % of 24Mg diverted to molecular ionsa | ||||
|---|---|---|---|---|---|---|
| d25Mg | d26Mg | (%) | 24MgH | (24Mg28Si)++ | Other (Si, H)-related 24Mg molecules | |
| a From Table 1 – relative to 1.38 × 1012. b Corrected for IMF10. | ||||||
| SW_8 | −8.57‰ | 62.04‰ | 4.0% | 0.41% | 0.96% | 2.63% |
| SW_11 | −54.70‰ | −19.70‰ | 6.1% | 1.30% | 0.48% | 4.32% |
5. Conclusions
We present a new data-reduction technique which compensates for matrix effects in SIMS data when measuring low-dose implants into DLC. For the data set used herein, fluences calculated using relative sensitivity factors would have varied over a factor of ∼2×, while analyses quantified using our technique were consistent to <3.5%. Moreover, the <3.5% includes data suspected of being scattered by weak matrix effects caused by H which future research might be able to positively identify and mitigate. Use of a SIMS instrument having a higher transmission would have given fluences that were even more robust since the solar wind 24Mg being measured (a ∼ 1 keV amu−1 implant) was present at only at ∼1.4 × 1012 atoms per cm2. One of the 10 analyses contained a large (dust?) particulate embedded near the surface: if radiation-induced segregation had occurred in that near-surface particulate, then it is plausible that <∼6% of the SW Mg may have been mistaken for contamination by the SRIM fit and removed.The procedure used here is iterative: it simultaneously calculates surface contamination, background, and compensates for matrix effects using a parametrization. The parametrization employed here was the relative intensity of two matrix ions and it was successful because it sorted data by the compositional and structural differences that controlled the electrical conductivity of the matrix. The use of our matrix parameter, C2+/C+, can be checked at the beginning of an analysis session to verify its usefulness. This check only requires assessment of the energy spectra of two matrix ions at the same position on the DLC to ensure that the spectra have a sufficient spread of intensities over the energy offset of the window. Moreover, if the two ions we used (12C2+ and 12C+) do not have a sufficient spread of distinguishable relative intensities with the offset, it is possible to look for another pair of ions (or perhaps a double parametrization using two pairs of ions) in order to modify our procedure for different analysis conditions.
Matrix effects encountered varied spatially at both the 150 μm and larger (e.g., cm) scales. Changes in ion yield, sputtering rate, instrumental mass fractionation (e.g., ∼3% to ∼5%) and mode of sputtering were observed. A weak effect of H on the Mg ion yield in some of the analyses was strongly suspected. The effects of H are different for DLC sputtered with Cs+ rather than O2+ and for DLC containing silicon vs. effectively silicon-free DLC. These differences are likely due to differences in the oxidation state which stabilizes within the zone of sputtering.
Again, we encountered strong matrix effects during our analyses, and these matrix effects reflect the local electrical and/or compositional properties of the DLC film. Therefore, in addition to providing accurate and reproducible SIMS results, the technique presented here also allowed physical, compositional and electrical characteristics of the DLC film to be mapped at the 150 μm to 250 μm scale across the DLC fragment being analysed.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
SIMS analyses were performed at Arizona State University National SIMS facility, supported by EAR0622775. This work was initiated using Genesis mission funds, including JPL sub-contract #1354958. Subsequent work was supported by NASA LARS Grants # NNX14AF26G and 80NSSC17K0025 (DSB, AJ), NNH15AZ25I and NNH15AZ67I (KDR). G. Huss worked in parallel with this team on his H measurements and provided samples for Raman Spectroscopy and is greatly appreciated. Thanks to J. Ziegler, USNA Annapolis for advice on SRIM, L. Williams for oversight using the ASU Cameca IMS 6f. Tom Friedmann provided significant insight into the material properties of the DLC made at Sandia National Laboratory. Thanks also to the two anonymous reviewers for their suggestions and support for this work.Notes and references
- M. P. Siegal, T. A. Friedmann, J. P. Sullivan, J. Mikkalson, F. Dominguez, S. R. Kurtz, D. R. Tallant, R. L. Simpson, K. F. McCarty, L. Bernardez, D. Dibble, P. B. Mirkarimi, Diamond and Diamond-Like Carbon Films for Advanced Electronic Applications, Sandia Report #SAND 96-0516-UC-404, 1996, p. 42 Search PubMed.
- J. Robertson, Mater. Sci. Eng. R Rep., 2002, 37, 129–281 CrossRef.
- C. Schubert, V. Hoffmann, A. Kummel, J. Sinn, M. Härtel, A. Reuther, M. Thomalla, T. Gemming, J. Eckert and C. Leyens, J. Anal. At. Spectrom., 2016, 31, 2207–2212 RSC.
- A. J. G. Jurewicz, D. S. Burnett, R. C. Wiens, T. A. Friedmann, C. C. Hays, R. J. Hohlfelder, K. Nishiizumi, J. A. Stone, D. S. Woolum, R. Becker, A. L. Butterworth, A. J. Campbell, M. Ebihara, I. A. Franchi, V. Heber, C. M. Hohenberg, M. Humayun, K. D. McKeegan, K. McNamara, A. Meshik, R. O. Pepin, D. Schlutter and R. Wieler, Space Sci. Rev., 2003, 102, 27–52 Search PubMed.
- D. S. Burnett, B. L. Barraclough, R. Bennett, M. Neugebauer, L. P. Oldham, C. N. Sasaki, D. Sevilla, N. Smith, E. Stansbery, D. Sweetnam and R. C. Wiens, Space Sci. Rev., 2003, 105, 509–534 CrossRef CAS.
- J. H. Allton, E. K. Stansbery and K. M. McNamara, 36thLunar and Planetary Science Conference, Houston TX, March 2005, #2083 Online Search PubMed.
- D. S. Burnett, A. J. G. Jurewicz and D. S. Woolum, Meteorit. Planet. Sci., 2020, 54(5), 1092–1114 CrossRef , open access.
- J. H. Allton, L. P. Keller, Z. Rahman, C. P. Gonzalez, K. K. Allums, R. A. Synowicki, and A. J. G. Jurewicz, 50th Lunar and Planetary Science Conference, Houston TX, March 2019, #2083, Online Search PubMed.
- A. J. G. Jurewicz, D. S. Burnett, K. D. Rieck, R. Hervig, T. Friedmann, P. Williams, C. Daghlian and R. Wiens, J. Mater. Sci., 2017, 52(19), 11282–11305 CrossRef CAS , open access.
- A. J. G. Jurewicz, K. D. Rieck, R. Hervig, D. S. Burnett, M. Wadhwa, C. T. Olinger, R. C. Wiens, J. M. Laming, Y. Guan, G. R. Huss, D. B. Reisenfeld and P. Williams, Meteorit. Planet. Sci., 2020, 55(2), 352–375 CrossRef CAS , open access.
- T. A. Friedmann, M. P. Siegal, D. R. Tallant, R. L. Simpson, and F. Dominguez, Spring meeting of the Materials Research Society (MRS), San Francisco, CA (United States), 4-8 Apr 1994, online, www.osti.gov/scitech/biblio/10151495, accessed 22 Nov 2016 Search PubMed.
- J. P. Sullivan, T. A. Friedmann, R. G. Dunn, E. B. Stechel, P. A. Schultz, M. P. Siegal and N. Missert, Mater. Res. Soc. Symp. Proc., 1998, 498, 97–102 CrossRef CAS.
- A. J. G. Jurewicz, E. Koeman-Shields, G. Huss, and C. Daghlian, 49th Lunar and Planetary Science Conference, The Woodlands, Texas – March 19-23, 2018, #2058, online and e-poster online Search PubMed.
- P. Williams and J. Baker, Nucl. Instrum. Methods, 1981, 182/183, 15–24 CrossRef.
- G. R. Huss, E. Keoman-Shields, A. J. G. Jurewicz, D. S. Burnett, K. Nagashima, R. Ogliore and C. T. Olinger, Meteorit. Planet. Sci., 2020, 55(2), 326–351 CrossRef CAS.
- D. S. Burnett, A. J. G. Jurewicz, D. Woolum, J. Wang, J. Paque, L. Nittler, K. McKeegan, M. Humayun, R. Hervig, V. S. Heber and Y. Guan, Geostand. Geoanal. Res., 2015, 39(3), 265–276 CrossRef CAS . open access.
- D. B. Reisenfeld, R. C. Wiens, B. L. Barraclough, J. T. Steinberg, M. Neugebauer, J. Raines and T. H. Zurbuchen, Space Sci. Rev., 2013, 175, 125–164 CrossRef.
- H. Yurimoto, K. Bajo, I. Sakaguchi, T. T. Suzuki, A. J. G. Jurewicz, S. Itose, K. Uchinof and M. Ishihara, Surf. Interface Anal., 2016, 48, 1181–1184 CrossRef CAS , open access.
- D. S. Burnett written communication re: frontside depth profiling in silicon, March 2020.
- E. Vainonen, J. Likonen, T. Ahlgren, P. Haussalo and J. Keinonen, J. Appl. Phys., 1997, 82(8) CrossRef CAS.
- V. S. Heber, K. D. McKeegan, D. S. Burnett, J. Duprat, Y. Guan, A. J. G. Jurewicz, C. T. Olinger and S. P. Smith, Chem. Geol., 2014, 390, 61–73 CrossRef CAS.
- D. S. McPhail, J. Mater. Sci., 2006, 41, 873–903 CrossRef CAS.
- G. R. Huss, K. Nagashima, D. S. Burnett, A. J. G. Jurewicz, and C. T. Olinger, 43rd Lunar and Planetary Science Conference, The Woodlands TX, March 2012, #1709, online Search PubMed.
- P. Patsalas, S. Logothetidis, P. Douka, M. Gioti, G. Stergioudis, Ph Komninou, G. Nouet and Th. Karakostas, Carbon, 1999, 37, 865–869 CrossRef CAS.
- S. Logothetidis, Ch. B. Lioutas and M. Gioti, Diamond Relat. Mater., 1998, 7, 449–453 CrossRef CAS.
- H. Nakazawa, R. Osozawa, Y. Enta and M. Suemitsu, Diamond Relat. Mater., 2010, 19, 1387–1392 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Online appendix contents: (A) spatial variations in ion yields and density, (B) textural changes with depth and their lack of effect on electrical conductivity, (C) reason for spatial variations in electrical conductivity, (D) matrix effects due to electrical conductivity variations, (E) effect of changing the compound correction of the SRIM model: e.g., STD_4, and (F) effect of a lower ion beam density on a diamond-like matrix: e.g., STD_4 after ref. 4. See DOI: 10.1039/d0ja00375a |
| ‡ Credit for first reporting radiation-induced segregation (also called radiation-induced diffusion) based on SW Mg in the silicon Genesis collectors to the Genesis science team goes to B.V. King (U. Newcastle, Australia). Because of his observations, and those of his colleagues at Argonne National Lab, there is an attempt to measure each SW element in at least two collector materials.7 |
| This journal is © The Royal Society of Chemistry 2021 |