Ionic liquid decoration for the hole transport improvement of PEDOT

Abstract

Ionic liquids (ILs) play an important role in conducting polymer poly(3,4-ethylenedioxythiophene) (PEDOT) based electronics and thermoelectrics through regulating morphology and electronic properties. Herein, the hole transport and interface electronic coupling properties of three kinds of IL ([BMIM]:[BF₄], [BuPhIM]:[BF₄], and [BnPhIM]:[BF₄]) mediated PEDOT systems have been researched via multiscale molecular mechanics simulations and quantum mechanics calculations, where the cations of the ILs feature gradually extended π-conjugation. It is indicated that [BnPhIM]:[BF₄] induces PEDOT to show more ordered π–π stacking than its counterparts, where the chains are oriented with face-to-face alignment. This is attributed to the larger evenness of the net charge distribution at the [BnPhIM]:[BF₄]-PEDOT interface. Consequently, the average mobility in [BnPhIM]:[BF₄]-PEDOT is 4.01 cm² V⁻¹ s⁻¹ and the instantaneous maximum reaches 17 cm² V⁻¹ s⁻¹, far surpassing its counterparts. Although the predicted PEDOT single crystal presents a well-ordered lamellar structure, the one-dimensional orientation causes hole tunneling along the nanowire-like direction, leading to its mobility lagging behind the [BnPhIM]:[BF₄] decorated system by one order of magnitude. On the other hand, the interface electronic coupling and doping efficiency in [BnPhIM]:[BF₄]-PEDOT is strengthened, confirming that improving the π-conjugation of the cation of the IL can enhance the mobility of PEDOT and interface electronic coupling synergistically. To improve the mobility further, a novel series of cations containing [BnPhIM-oOMe]⁺, [BnPhIM-mOMe]⁺, and [BnPhIM-pOMe]⁺ has been designed based on the outstanding properties of [BnPhIM]⁺. Combining the novel designed cations with [BF₄]⁻ and [B(CN)₄]⁻, it is observed that [BnPhIM-pOMe]:[B(CN)₄] causes PEDOT to assemble with well-ordered π–π stacking. Assessments rationalize that it could serve as a potential candidate for application in PEDOT-based electronics, since it shows similar interface electronic coupling and has a 35–43% improvement in PEDOT mobility compared to the excellent reference [BnPhIM]:[BF₄].

---

Introduction

High conducting polymers are an essential component in the fields of organic electronics,¹ solar cells,² thermoelectrics,³ bioelectronics,⁴ and wearable devices.⁵ Conducting polymers can be classified as n-type or p-type based on the kind of charge carriers (the former via negative charge carriers and the latter via positive ones). Among the abundant p-type polymers, poly(3,4-ethylenedioxythiophene) (PEDOT, Fig. 1) has attracted considerable attention in these past decades owing to its excellent properties of easy accessibility, excellent mechanical flexibility, and high transparency in the visible and near-infrared regions.^1,6,7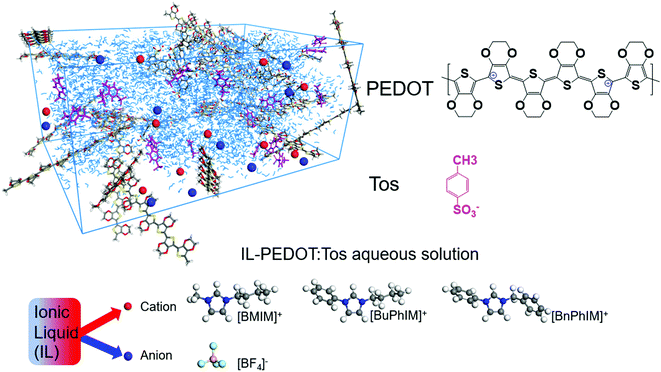

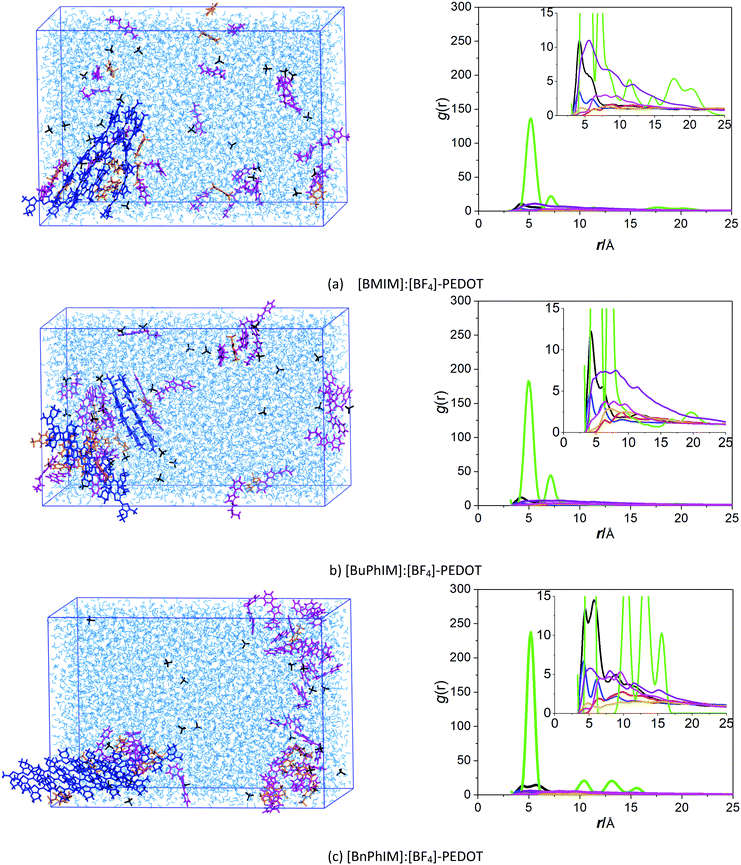
Fig. 1 A schematic illustration of IL-PEDOT:Tos aqueous solution and the chemical structures of oligomeric PEDOT, Tos, and the cations/anion of the ionic liquid additives.

Pristine PEDOT is heavily oxidized (p-doped), has poor solubility, generally shows low conductivity and is therefore unfeasible for use in practical applications.⁸ Prepared PEDOT for applications is commonly in an aqueous dispersion, where a counterion⁹ such as poly(styrenesulfonate) (PSS) or tosylate (Tos) is introduced to stabilize the doped PEDOT.¹⁰ The mechanism of conductivity for PEDOT:counterion blends is governed by hole transport within the PEDOT domain not only along the molecular backbone but also by passing through inter-crossing chains depending on the π–π interactions.¹¹ The anticipated properties of PEDOT in widespread electronic applications are basically identical and well-defined: (a) a high degree of molecular order and (b) a large hole mobility.¹² A structurally ordered alignment is one of the prerequisites for achieving prominent hole transport and acquiring critical microstructural information, including the average π–π packing distance and the orientation between the neighboring molecules (face-to-face, face-to-edge, dislocation etc.), is crucial in order to comprehend the macroscopic hole transport properties and subsequent electrical conductivity. Moreover, an excess of insulating counterions can act as a barrier for the order of π-stacked PEDOT and the hole transport in the conductive PEDOT-rich domain, therefore it is another important factor that should be considered.¹³

There are many treatments that can be either applied to PEDOT solution prior to film deposition or post-treatment using various additives,^8,14,15 ranging from strong acids/bases, such as H₂SO₄ and NaOH, and different boiling-point additives, including dimethyl sulfoxide (DMSO), ethylene glycol (EG), and ionic liquids (ILs). As green solvents consisting of positively and negatively charged binary ionic compounds, which show a high performance in ion transport, ILs have been used as additives in widespread electronic equipment and ion batteries.^16–21 Because of the same binary nature of PEDOT and the counterion, ILs are highly interesting as treating agents for separating the counterion from the PEDOT domain from the point of view of ion exchange.²² Meanwhile, recent explorations through both experiments^{16–18,23–25} and theoretical calculations^22,26 have affirmed the critical role of ILs in regulating the doping, hole mobility, and conductivity of PEDOT in large spanning orders of magnitude from the side of the electronic properties. Similarly, taking the advantage of the adjustable ion ratio of IL, it has been observed in our previous work that regulating [EMIM]:[TFSI] with an excess of cation produces a significant improvement of hole mobility by 1–3 orders of magnitude with respect to the pristine PEDOT:Tos solution, while increasing the content of anion damages the molecular order and leads to a dynamic mobility 10⁻² to 10⁰ cm² V⁻¹ s⁻¹ smaller than that of the pristine solution.²⁷ Despite recent efforts in the field of PEDOT organic electrics, the current understanding of the dependence of the hole transport of PEDOT on the structural and electronic properties of ILs is still insufficient. This lack of knowledge limits the pace of discovery of promising functional ILs and for this reason, systematic exploration of the structure–property relationship would be beneficial.

The commonly used cations of ILs are 1-ethyl-3-methylimidazolium ([EMIM]⁺) and 1-n-butyl-3-methylimidazolium ([BMIM]⁺), which differ only in the length of the attached alkyl chain but cause PEDOT to produce different hole mobility and conductivity values. In view of the obvious difference, we decided to specifically investigate the effect of aromatized imidazole derivatives on the interfacial electronic coupling of IL-PEDOT and the degree of molecular order and the hole mobility of PEDOT, extending the π-conjugation of the organic backbone typically tunes the frontier molecular orbitals (the highest occupied and the lowest unoccupied molecular orbitals, HOMO and LUMO) energy level as well as shrinks the energy gap, favoring the improvement of charge transport. The series of analogues are [BMIM]⁺, 1-butyl-3-phenylimidazole ([BuPhIM]⁺),^28,29 and 1-benzyl-3-phenylimidazolium ([BnPhIM]⁺),³⁰ the latter two were synthesized by substituting the imidazole ring and side chain of [BMIM]⁺ by benzene (Fig. 1, the orbital distribution and the energy gap of the frontier molecular orbitals can be seen in Fig. S1, ESI†) and they have not been used in PEDOT-based electrics before as far as we know. Each cation is coupled with the widely used tetrafluoroborate ([BF₄]⁻) anion to produce varied ion pairs. Our results demonstrate that extending the π-conjugation of the imidazole cation synergistically boosts the hole transport within the PEDOT domain and the electronic coupling of the IL-PEDOT interface. Along this line, three novel ILs have been designed and further enhancement of hole mobility has been observed. It emphasizes the active role of extending the π-conjugation of the imidazole cation in improving the hole transport and provides a guide for designing and optimizing efficient IL additives in PEDOT-based electrics.

Methodology

Molecular dynamics simulations

In this work, we considered the treatment of 0.1 mol L⁻¹ PEDOT:Tos solution by an IL prior to film deposition. Based on experimental detection, PEDOT is commonly constituted of 3–18 repeated monomer units,³¹ therefore, we selected oligomeric PEDOT containing 9 structural units to compromise between computational accuracy and time. Correspondingly, each of the four chains with an oxidation level of 33.3% doping (charge equals +3) combined with 12 negatively charged Tos and 6696 water molecules were put together in a sufficiently large 9 × 6 × 4 nm³ unit cell. Then, 24 cation and anion binary ion pairs were introduced to permit them to diffuse into the pristine solution. The amorphous solution model was generated by PACKMOL code³² as the starting point to perform molecular dynamic (MD) simulations. The MD simulations of the considered samples were carried out under periodic boundary conditions via LAMMPS code.³³ The parameters of bonded and van der Waals (vdW) nonbonded interactions were taken from the OPLS-AA force field,³⁴ the water solvent was described by the SPC/E model,³⁵ and the atomic charge used for coulombic nonbonded interactions was obtained by the restrained electrostatic potential (RESP) method,³⁶ which was calculated by Multiwfn code³⁷ on top of the structure optimized by the B3LYP/6-311G(d,p) level via the Gaussian 09 program.³⁸ Each system was firstly relaxed via a conjugate gradient algorithm, followed by a 5 ns NPT run (293 K, 1 bar) using the Parrinello–Rahman barostat, followed by equilibration in the NVT ensemble (293 K, 1 bar) using the Nose–Hoover thermostat until the density and total energy reached equilibrium (∼20 ns). The time step in all the simulations was 0.1 fs and the cutoff for the vdW interaction was 12 Å. Finally, a 5 ns production run for the radial distribution function (RDF) simulations was performed and 500 snapshots for the hole transport simulations by quantum mechanics calculations were abstracted every 10 ps.

Quantum mechanics calculations

After obtaining the stable configuration from the MD simulations, calculation of the hole transport property was carried out. To obtain the hole hopping rate and mobility, the critical items of transfer integral, reorganization energy, and hopping site energy were computed separately in different levels by the Gaussian program. The former was performed by M06-2X/6-311G(d,p) combined with the D3BJ-correction³⁹ for vdW interaction of dimeric molecules and the latter two were finished by B3LYP/6-311G(d,p) to perform the structure optimization and frequency calculation. Further normal mode analysis based on the frequency calculation was conducted by the Dushin program.⁴⁰ To compare the mobility in a solution model and crystallized solid, the structure of the PEDOT single crystal was predicted, and the mobility was implemented by the MOMAP code.⁴¹ The structure of the positively charged and negatively charged binary was firstly searched by Molclus code⁴² to locate the most stable conformer with the aim of calculating the binding energy and ion exchange Gibbs free energy. To identify the contribution of the electrostatic, induction, and dispersion items to the interaction, the symmetry adapted perturbation theory (SAPT)⁴³ was applied in terms of the SAPT0/6-311+G(d,p) level as implemented in the PSI4 program.⁴⁴ The electron excitation and heterogeneous electronic coupling was carried out by the time-dependent density functional theory (TDDFT)-CAM-B3LYP/6-311G(d,p) level in water solvent which is described by SMD⁴⁵ model.

Results and discussion

The mobility in the PEDOT domain

The spatial distribution. One of the critical parameters determining the hole transport in the PEDOT domain is the degree of molecular order of the π–π stacked chains. To explore its consequences on the resulting morphology at a larger length-scale, molecular dynamic (MD) simulations were firstly performed on periodic model systems representing a mixed aqueous solution. The last snapshot for each IL-PEDOT system is shown in the left of Fig. 2. Intuitively, [BMIM]:[BF₄] causes PEDOT to assemble into one cluster where the chains unmanifest regular orientation to each other. For [BuPhIM]:[BF₄], it triggers the chains to be oriented in the face-to-edge alignment. As for the [BnPhIM]:[BF₄] modulated system, it observes an ordered alignment where the chains are oriented in the mutually face-to-face π–π stacking. It can be found that more than two peaks of the radial distribution function (RDF) of the C atom on the backbone of PEDOT (RDF(C_π–C_π)) are distinguished in each system (the green lines in the right of Fig. 2), and the peak of RDF(C_π–C_π) is strengthened gradually in the order of [BMIM]:[BF₄], [BuPhIM]:[BF₄], and the [BnPhIM]:[BF₄] decorated system, revealing that extending the π-conjugation of [BMIM]⁺ leads to the interaction of PEDOT becoming stronger. On the other hand, [BnPhIM]:Tos is seemingly far away from the PEDOT domain more obviously in [BnPhIM]:[BF₄]-PEDOT than its counterparts, qualitatively suggesting that the ion exchange reaction is more efficient in the system. The RDF of S_Tos, C_Im, and B, which represent the S atom of Tos, the C atom on the C2 site of the imidazole ring of the cation (Fig. S2, ESI†), and the B atom of [BF₄]⁻ has been further analyzed and it is observed that RDF (S_Tos–C_Im) strengthens in the order of [BMIM]⁺, [BuPhIM]⁺, to [BnPhIM]⁺ (the black lines) and RDF (C_π–S_Tos) weakens in an identical order (the purple lines), supporting the hypothesis that extending the π-conjugation of [BMIM]⁺ weakens the binding between PEDOT and Tos, finally favoring the ion exchange of Tos from the PEDOT domain.

Fig. 2 (a–c) (Left) The last snapshots of the IL-PEDOT solution models (blue, orange, pink, and black represent PEDOT, Tos, the series of imidazole cations, and the [BF₄]⁻ anion, respectively). (Right) Specified site–site RDFs (the green, purple, black, blue, pink, orange, and red lines represent RDF(C_π–C_π), RDF(C_π–S_Tos), RDF(S_Tos–C_Im), RDF(C_Im–B), RDF(C_π–B), RDF(C_π–C_Im), and RDF(S_Tos–B), respectively).

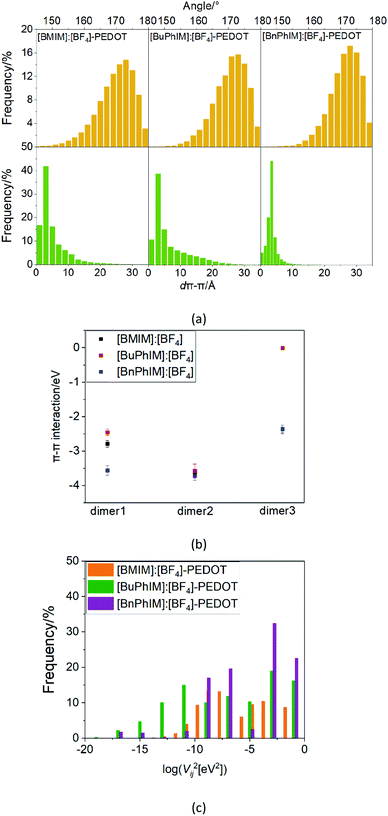
On the other hand, the molecular polarity index (MPI)⁴⁶ reflects the evenness of the net charge distribution, the larger the MPI, the smaller the evenness of the net charge distribution will be. It reflects that [BnPhIM]⁺ manifests the smallest molecular polarity (73.291 kcal mol⁻¹, Table 1) among all the cations, inducing [BnPhIM]:[BF₄]-PEDOT to display the smallest local polarity (the MPI is 104.266 kcal mol⁻¹). As a result, PEDOT is triggered to gather into an ordered orientation in its chains. The MPI qualitatively correlates well with the charge distribution and the π-stacked alignment of PEDOT (the electrostatic potential (ESP) is shown in Fig. S3 in the ESI†) and clarifies the reason for [BnPhIM]:[BF₄] doing better in regulating the high degree of molecular order.

Table 1 The molecular polarity index (MPI, in kcal mol⁻¹) values

Component	MPI
PEDOT	107.018
Tos	84.217
[BMIM]^+	85.745
[BuPhIM]^+	76.226
[BnPhIM]^+	73.291
[BF4]^−	128.182
[BMIM]:[BF4]-PEDOT	106.325
[BuPhIM]:[BF4]-PEDOT	107.019
[BnPhIM]:[BF4]-PEDOT	104.266

---

The π-stacked structure of PEDOT. To gain knowledge of the degree of molecular order of PEDOT quantitatively, the critical intramolecular angle between the neighboring thiophene rings (θ) and the π–π distance of the C_π–C_π on the neighboring monomer (d_π–π) were identified. With the aim of accessing the average structural information, 500 frames were abstracted from the last 5 ns of the dynamic trajectory. Apparently from the upper panel in Fig. 3(a), the distribution of θ falls in the region of 150–180° in all systems, and the slightly increased percentage centers in the 170–180° in [BnPhIM]:[BF₄]-PEDOT with respect to the counterparts, indicating the subtle increase of the co-planar for the PEDOT backbone after aromatization of [BMIM]⁺ by two benzenes. On the other hand, the distribution of d_π–π for dimeric PEDOT (the lower panel in Fig. 3(a)) in the bare and one benzene substituted cation added systems is similar in that the d_π–π is mainly within 10 Å combined with a small amount close to 30 Å. In contrast, the d_π–π of the double benzene substituted cation regulated system exhibits a more concentrated distribution, in which 45% d_π–π centers in 3.2 Å (the maximum value is observed near 15 Å), suggesting that a denser and more ordered cluster is produced after decoration by [BnPhIM]:[BF₄]. For the simulated amorphous 0.1 mol L⁻¹ solution, there are four monomers and the most interacted three dimeric PEDOT structures were in the well-ordered face-to-face alignment. Fig. 3(b) shows that the average π–π interaction of the most interacted three dimeric PEDOT in [BnPhIM]:[BF₄]-PEDOT fluctuates in the range of −2.4 to −3.7 eV, which is the most stable compared to its counterparts, further verifying the denser packing of PEDOT after assistance by [BnPhIM]:[BF₄].

Fig. 3 (a) Histograms of the angle (θ) between neighboring thiophene rings in each PEDOT chain and the π–π distance (d_π–π) between neighboring PEDOT chains for [BMIM]:[BF₄], [BuPhIM]:[BF₄], and [BnPhIM]:[BF₄] modified systems, respectively. (b) The π–π interactions of dimeric PEDOT. (c) The logarithmic distributions for the square of the transfer integral of PEDOT in different IL-PEDOT systems (all these statistics are based on the abstracted 500 frames).

The transfer integral and mobility. In the amorphous PEDOT domain, the hole transport is characterized by means of a hopping model, in which the intermolecular hole transport of neighboring molecules is assumed to be instantaneously localized on one hopping site.⁴⁷ Correspondingly, the transfer integral (V_ij) between the localized site and the neighboring site is calculated by the direct coupling method:^48,49

V_ij = 〈ψ^0,i_HOMO|F|ψ^0,j_HOMO〉

where ψ^0,i_HOMO and ψ^0,j_HOMO are the HOMOs of the sites i and j, and F is the Fock operator. The transfer integral reflects the electronic coupling between the neighboring molecules and needs to be maximized to improve the charge transport. The respective predominant orientation in the chains and average d_π–π can directly impact the transfer integral to a large extent and correlating these important structural parameters to V_ij is indispensable to acquire macroscopic hole transport. Fig. 3(c) shows that there is a significantly increased distribution of log(V²_ij) in the region larger than −5 in [BnPhIM]:[BF₄]-PEDOT, overwhelmingly larger than the counterparts in the region less than −10. Correlating the critical structural parameters and transfer integral, it can be found that a larger electronic coupling of PEDOT chains after modulation by [BnPhIM]:[BF₄] is ascribed to more planar and more compact stacking. It anticipates that the fastest hole mobility in the PEDOT domain could be achieved in [BnPhIM]:[BF₄]-PEDOT because of the high degree of molecule order.

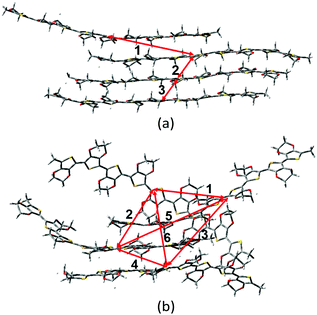
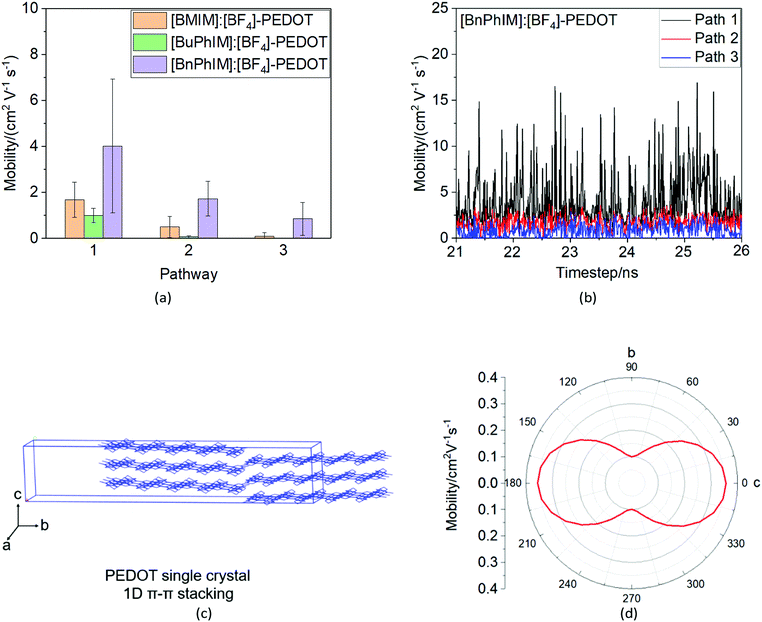
As mentioned above, there are four monomers in 0.1 M solution, hence, there are a maximum of three hole hopping pathways in the ordered π–π stacking, otherwise a maximum of six hopping pathways can be expected in the disordered packing (Fig. 4). Based on the non-adiabatic Marcus charge transfer theory,^50–52 the hole mobility (μ) can be obtained (the calculation details can be seen in the ESI†). Commonly, the order of magnitude of μ located in 10⁻² cm² V⁻¹ s⁻¹ is moderate among the abundant hole transport materials (<10⁻³ cm² V⁻¹ s⁻¹ for pristine spiro-linked organic small molecules utilized in the perovskite solar cell,⁵³ 10⁻⁷ cm² V⁻¹ s⁻¹ for P3HT typically in organic solar cells,⁵⁴ and a record high value of 92.64 cm² V⁻¹ s⁻¹ for single crystal PCDTPT nanowires⁵⁵). Hence, modulating the mobility to >10⁰ cm² V⁻¹ s⁻¹ for polymeric PEDOT is desirable. For [BMIM]:[BF₄]-PEDOT, four hopping pathways are measured where the maximum one (μ_max) fluctuates around 1.85 cm² V⁻¹ s⁻¹, followed by 0.51 and 0.10 cm² V⁻¹ s⁻¹ for the second and third pathways (Fig. 5(a)). As for the fourth pathway, it can be ignored with respect to the former three because of the average mobility around 10⁻⁴ cm² V⁻¹ s⁻¹ (not shown). For a single benzene substituted [BuPhIM]⁺ associated system, a comparable μ_max of 1.48 cm² V⁻¹ s⁻¹ was observed compared to the bare [BMIM]⁺ contained system, and the μ diminishes to 7.72 × 10⁻² and 8.34 × 10⁻⁴ cm² V⁻¹ s⁻¹ for the second and third pathway. Contrarily, further substituting [BuPhIM]⁺ causes the μ to maximize to an average of 4.01 cm² V⁻¹ s⁻¹, especially, the instantaneous maximum value reaches 17 cm² V⁻¹ s⁻¹, overwhelmingly surpassing its counterparts by 3 times (the evolution of hole mobility for the representative [BnPhIM]:[BF₄]-PEDOT has been plotted in Fig. 5(b), and Fig. S4 (ESI†) shows that for [BMIM]:[BF₄]-PEDOT and [BuPhIM]:[BF₄]-PEDOT). Meanwhile, the second and third pathways separately achieve a larger mobility by 1.73 and 0.86 cm² V⁻¹ s⁻¹, directly confirming a high degree of molecular order.

Fig. 4 The hopping pathways in the (a) ordered and (b) disordered π–π stacking structures.

Fig. 5 (a) The average mobility of the corresponding pathway for the three IL modulated systems, (b) the dynamic evolution of the hole mobility of PEDOT after modulation by [BnPhIM]:[BF₄], (c) the predicted crystal structure of PEDOT (the orthorhombic unit cell parameters are: a/b/c: 7.9708/73.7605/5.1762 Å; α/β/γ: 90.0000/69.0223/90.0000 degrees), and (d) the mobility anisotropy curve of the predicted single crystal.

A comparison of mobility between IL-PEDOT and PEDOT single crystals. As we expected, [BnPhIM]:[BF₄] modulated PEDOT shows the fastest hole transport due to the highly ordered face-to-face motif. Although it is typically difficult to form ordered crystalline structures for polymers because of the interpenetrating and entangled chains and there are very few publications on the single crystal of PEDOT, the crystallization of P3HT (an analogue of PEDOT which possesses an identical conjugated thiophene backbone) has been reported from a dilute solution of a poor solvent.⁵⁶ In view of the similar backbone of P3HT and PEDOT, we infer that they should adopt a similar lamellar structure. Hence, the single crystal of PEDOT has been predicted to distinguish the difference of the hole mobility in IL decorated solution and pristine bulk. As we expected, pristine PEDOT shares a similar one-dimensional (1D) π–π stacking in an orthorhombic unit cell with respect to P3HT (Fig. 5(c)), and this 1D orientation is attributed to the most positive and negative potential appearing in the 3,4-ethylene side and O atom (for the ESP distribution mapped onto a surface of total electrons see Fig. S3 in the ESI†), leading to the electrostatic attraction mainly in the manner of the dislocated molecular backbone of one molecule and the molecular backbone of its adjacent one. The anisotropy of holes is an intrinsic property to comprehend the transistor channel relative to the reference axis of the molecular crystal, and the dependence of mobility on angles has been plotted in Fig. 5(d). It shows remarkable anisotropic behavior in the crystal. The direction with the highest hole mobility of 3.55 × 10⁻¹ cm² V⁻¹ s⁻¹ is along axis c of the cell, and the smallest value of 1.85 × 10⁻² cm² V⁻¹ s⁻¹ is along axis a. Accordingly, the single crystal behaves as 1D nanowires and produces a total mobility by 1.58 × 10⁻¹ cm² V⁻¹ s⁻¹. Obviously, PEDOT in the assistance of [BnPhIM]:[BF₄] achieves outstanding hole transport, one order of magnitude larger than in the single crystal, which is essentially attributed to the dislocated lamellar 1D structure in the single crystal limiting the tunneling of hole transport, while the more compact stacking in the [BnPhIM]:[BF₄] decorated solution significantly speeds up the transport channel.

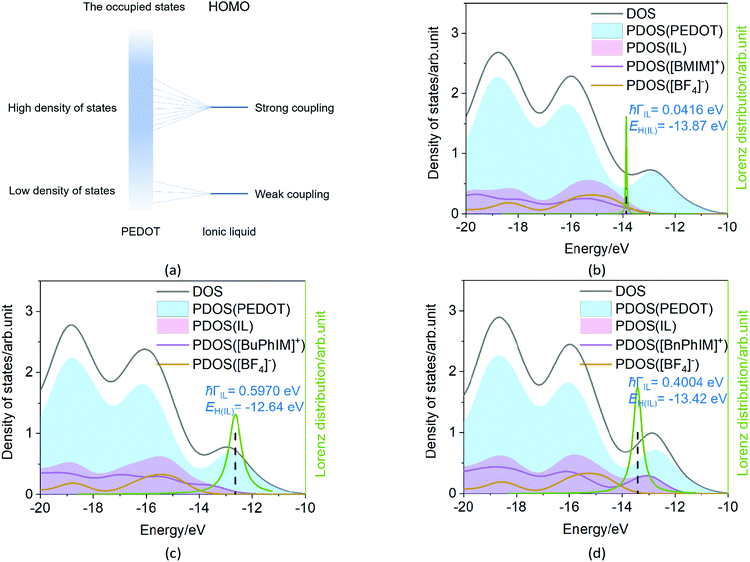
The electronic coupling of the IL-PEDOT interface

The Newns–Anderson model^57,58 can help to explain the electronic coupling of the discrete level of adsorbent and the manifold acceptor states of the substrate (the background can be seen in ESI†). It has been successfully applied in the IL-PEDOT interface in our previous work²⁷ to relate the hybridization between the HOMO of IL and the occupied states of PEDOT. In detail, when the HOMO of the IL lies within the energy region spanned by the occupied states of PEDOT, and if they are strongly coupled, the interaction can result in a splitting of the original HOMO into new hybrid orbitals. Contrarily, when this discrete HOMO lies outside the occupied states, even if coupled, the orbital is hardly hybridized with the manifold acceptor states of PEDOT (see the model in Fig. 6(a)).⁵⁹

Fig. 6 (a) The model of the electronic coupling of the HOMO of IL with the lower density and higher density of states in the occupied states of PEDOT. (b–d) Density of states (total, PEDOT, and IL), the HOMO level of the IL, the electronic coupling of the IL-PEDOT interface, and the Lorentzian distribution of the hybridization of the HOMO.

The density of states (DOS) and the Lorentzian distribution of the hybridization of the HOMO have been plotted in Fig. 6(b)–(d). Intuitively, the higher DOS region which is near the edge of the occupied states of IL (PDOS(IL)) gradually approaches the higher DOS region of PEDOT (PDOS(PEDOT)) from [BMIM]⁺, [BuPhIM]⁺, to [BnPhIM]⁺ constructed ILs, and the contribution of the cation to the whole IL (the purple lines) increases in the same sequence. Meanwhile, the HOMO (the dotted lines) level of [BMIM]:[BF₄] emerges in the lower energy region compared to the [BuPhIM]:[BF₄] and [BnPhIM]:[BF₄] (−12.64 and −13.42 eV). As a result, the HOMO of [BMIM]:[BF₄] interacts with the lower DOS region of PEDOT mostly and a pronounced weak coupling is detected (4.16 × 10⁻² eV). Contrarily, [BuPhIM]⁺ and [BnPhIM]⁺ can apparently improve the electron delocalization, promoting the HOMO upward and appropriately regulating the HOMO level lying in the region of PDOS(PEDOT) possessing denser states near the edge of the occupied states, therefore it shows stronger coupling with PEDOT than [BMIM]:[BF₄] by one order of magnitude (0.597 and 0.400 eV). The Lorentzian distribution of hybridization (the green lines) of the HOMO is higher and narrower in [BMIM]:[BF₄] while lower and wider in [BuPhIM]:[BF₄] and [BnPhIM]:[BF₄]. This means that the interfacial hole transport from the benzene modified ILs to PEDOT is only 1.10 and 1.64 fs based on the relationship of τ = 658/(1000 × ℏΓ (meV)),⁵⁸ while it is prolonged to 15.82 fs in the [BMIM][BF₄] associated interface. Obviously, extending the π-conjugation of the imidazole cation strengthens the electronic coupling between the IL and PEDOT in the occupied states, enhancing the heterogeneous hole transport by one order of magnitude.

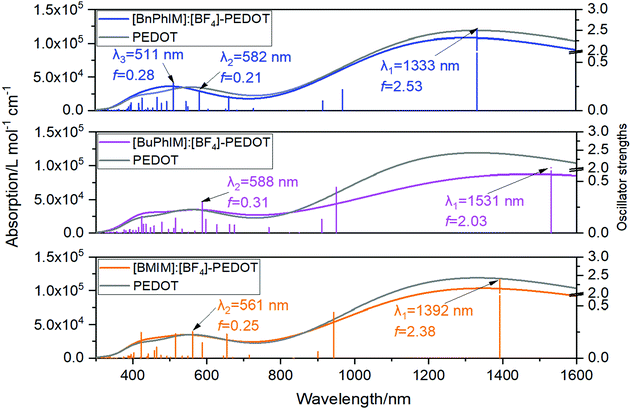
Electron excitation analysis further illustrates the essence of the increased coupling between IL and PEDOT. Each IL decorated PEDOT produces two strong absorption band at 1330–1530 and 580–650 nm (λ₁ and λ₂, the left of Fig. 7). The λ₁ of all the complexes is governed by the excitation from S0 → S1 state, and the main transition contribution is the electron promoted from the HOMO (H) to the LUMO (L), and all of the orbitals are localized on the PEDOT (the orbital distribution is collected in Fig. S5 in the ESI†). However, for the λ₂, the main transition character displays a distinct discrepancy in each system. We distinguish each transition state of λ₂ with oscillator strengths (f) larger than 0.1 and find that [BMIM]:[BF₄] participates in the transition from the S0 → S11 state (f = 0.25 in the right of Fig. 7), which is reflected by the hybrid orbitals of H−8, H−11, and H−12 delocalized on IL and PEDOT simultaneously (Fig. S5, ESI† and Table 2). For instance, it contributes 24.3% to the S0 → S11 transition from the H−8 to L, where 0.68% orbital distributes on [BMIM]⁺ and 0.07% on [BF₄]⁻. With extending the π-conjugation, the weight of the involved IL increases pronouncedly, and further resolution verifies that the contribution of the IL nearly all comes from the cation and that from the anion can be ignored.

Fig. 7 The absorption spectra and oscillator strengths for the IL-PEDOT complexes.

Table 2 The excitation energy (E_exc), oscillator strength (f), and transition contribution associated with the second absorption peak (λ₂) for different IL-PEDOT systems

Complex	E exc	f	Transition contribution
a The energy of the associated orbitals (eV). b Hyb represents heterogeneous IL/PEDOT. c Value is the transition contribution. d C represent the orbital contributions of the cation. e A represent the orbital contributions of the anion.
[BMIM][BF4]-PEDOT	2.21	0.25	S0 → S11	H−8 → L (−12.84, −8.51)^a	Hyb^b → PEDOT
					24.3%^c	C = 0.68%^d	A = 0.07%^e
				H−11 → L (−13.10, −8.51)^a	Hyb^b → PEDOT
					66%^c	C = 0.80%^d	A = 0.19%^e
				H−12 → L (−13.32, −8.51)^a	Hyb^b → PEDOT
					11.57%^c	C = 1.29%^d	A = 0.08%^e
[BuPhIM][BF4]-PEDOT	2.11	0.30	S0 → S11	H−12 → L (−13.31, −8.58)^a	Hyb^b → PEDOT
					5.81%^c	C = 6.16%^d	A = 0.01%^e
[BnPhIM][BF4]-PEDOT	2.13	0.21	S0 → S11	H−10 → L (−12.90, −8.30)^a	Hyb^b → PEDOT
					2.54%^c	C = 27.86%^d	A = 0.02%^e
	2.43	0.28	S0 → S14	H−5 → L (−12.60, −8.30)^a	Hyb^b → PEDOT
					4.01%^c	C = 4.03%^d	A = 0.03%^e
				H−6 → L (−12.63, −8.30)^a	Hyb^b → PEDOT
					4.57%^c	C = 1.62%^d	A = 0.01%^e
				H−11 → L (−12.92, −8.30)^a	Hyb^b → PEDOT
					3.69%^c	C = 34.75%^d	A = 0.04%^e
				H−14 → L (−13.07, −8.30)^a	Hyb^b → PEDOT
					4.85%^c	C = 40.61%^d	A = 0.06%^e

---

Moreover, ILs often play a role in the secondary doping⁶⁰ of molecular hole conducting. The offset (E_g) between the HOMO energy of the host (here it is the HOMO_PEDOT) and the LUMO energy of the dopant (here it is the LUMO_IL) is commonly viewed as an important factor in governing the doping extent of the host component.⁶¹ Effective doping usually needs the LUMO of the dopant approaching or lower than the HOMO of the host.^19,61,62 To distinguish the doping efficiency on the aromatized cation, the critical HOMO_PEDOT and LUMO_IL have been further resolved. The HOMO_PEDOT is upward subtly with bare, single, to double aromatized cations (the maximum difference is 0.07 eV, Table 3), while the LUMO_IL displays a downward gradient with the same sequence (−3.89, −4.10, and −4.56 eV), consequently the offset E_g shrinks obviously (7.38, 7.14, and 6.64 eV, respectively). As a result, [BnPhIM]:[BF₄] behaves as the prominent dopant with respect to its counterparts.

Table 3 The critical orbital energy values of the HOMO of PEDOT and the LUMO of the IL, as well as the offset (E_g) related to the doping of PEDOT (units of eV)

Complex	HOMOPEDOT	LUMOIL	E g
[BMIM]:[BF4]-PEDOT	−11.27	−3.89	7.38
[BuPhIM]:[BF4]-PEDOT	−11.24	−4.10	7.14
[BnPhIM]:[BF4]-PEDOT	−11.20	−4.56	6.64

---

In all, the MD simulations combined with DFT calculations prove that [BnPhIM]:[BF₄] is an excellent additive in PEDOT-based electronics, not only from its capacity in modulating well-ordered π–π stacking of PEDOT, but also from its strong electronic coupling and doping with PEDOT.

The design of a novel IL

Generally, utilizing various electron-donating/-withdrawing functional groups is an appropriate strategy to effectively modulate electronic properties. To further design a superior IL, the excellent [BnPhIM]:[BF₄] has been modified in terms of substituting the benzene of the cation and the F atom of the anion. For an IL applied in PEDOT-based electronics, fulfilling the large binding energy between the cation and Tos as well as the anion and PEDOT, guaranteeing efficient ion exchange, achieving large electronic coupling with the occupied states of PEDOT, possessing a strong doping ability, and regulating the high degree of molecular order of PEDOT simultaneously would be promising. Based on these criteria, a novel IL design has been proposed by: (1) tethering a methoxy (–OMe) on the benzene of [BnPhIM]⁺ because its electron-donating property is stronger than other typical electron-donating groups, such as –OH, –NH₂, halogen, alkyl groups etc., and it is bulky in size and hence interacts with anions less liable to electrostatic and hydrogen bonding, benefiting from ion exchange; (2) substituting the –F of [BF₄]⁻ for another stronger electron-withdrawing group –CN with the consideration that it favors the LUMO_IL moving downward, potentially strengthening the doping of PEDOT. Therefore, three [BnPhIM]⁺ derivatives with the ortho-/meta-/para-sites substituted on benzene relative to the N1 and N3 sites of imidazole by –OMe have been designed and combined with [BF₄]⁻ and commonly-used [B(CN)₄]⁻ to produce six novel ILs (Fig. 8).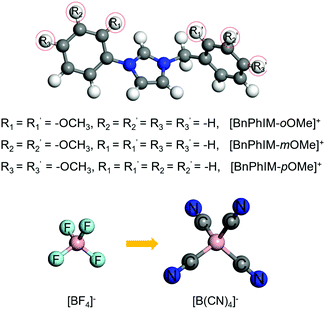

Fig. 8 The structures of the novel designed cations of [BnPhIM-oOMe]⁺, [BnPhIM-mOMe]⁺, and [BnPhIM-pOMe]⁺ for combination with [BF₄]⁻ and [B(CN)₄]⁻.

The stacking structure of PEDOT after decoration by these novel designed ILs shows that all –OMe substituted cations combined with [BF₄]⁻ produce apparent disordered packing (Fig. S6 in ESI†), while it likely manifests a high degree of molecular order with the assistance of [BnPhIM-pOMe]:[B(CN)₄] among the newly designed ILs, in which the distribution of d_π–π centers on 3.5 Å (Fig. S7, ESI†) similar to [BnPhIM]:[BF₄]-PEDOT. Therefore, we screened [BnPhIM-pOMe]:[B(CN)₄]-PEDOT and compared it to the performance of [BnPhIM]:[BF₄]-PEDOT in the following, the other systems were not further researched.

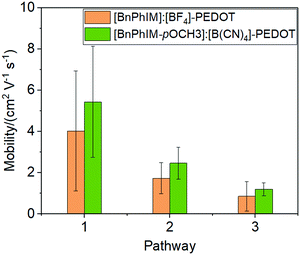
The electronic coupling between [BnPhIM-pOMe]:[B(CN)₄] and PEDOT is 0.3467 eV (Fig. S8 in ESI†), compared to [BnPhIM]:[BF₄], [BnPhIM-pOMe]:[B(CN)₄] realizes a considerable heterogeneous hole transport time (1.64 and 1.90 fs). On the other hand, the LUMO of [BnPhIM-pOMe]:[B(CN)₄] is downshifted to −5.07 eV (Fig. S8, ESI†) with respect to [BnPhIM]:[BF₄] (−4.55 eV). Compared to the obvious downshift of the LUMO of [BnPhIM-pOMe]:[B(CN)₄], the HOMO_PEDOT after the modulation varies subtly (−11.18 eV) with respect to that of [BnPhIM]:[BF₄], implying that [BnPhIM-pOMe]:[B(CN)₄] and [BnPhIM]:[BF₄] show comparable IL-PEDOT interfacial hole transport properties, while the former achieves more efficient doping. The mobility of PEDOT after introducing [BnPhIM-pOMe]:[B(CN)₄] fluctuates around 5.43, 2.47, and 1.20 cm⁻² V⁻¹ s⁻¹ for the three observed pathways (Fig. S9, ESI†), which is improved by 35%, 43%, and 40% for the corresponding pathway in [BnPhIM]:[BF₄]-PEDOT (Fig. 9). These suggest that the novel designed [BnPhIM-pOMe]⁺ combined with [B(CN)₄]⁻ can achieve considerable heterogeneous electronic coupling with PEDOT, stronger doping, and improved mobility with respect to [BnPhIM]:[BF₄]. Therefore, it is confirmed that [BnPhIM-pOMe]:[B(CN)₄] is a potential candidate for PEDOT-based electronics.

Fig. 9 A comparison of mobility in [BnPhIM]:[BF₄]-PEDOT and [BnPhIM-pOMe]:[B(CN)₄].

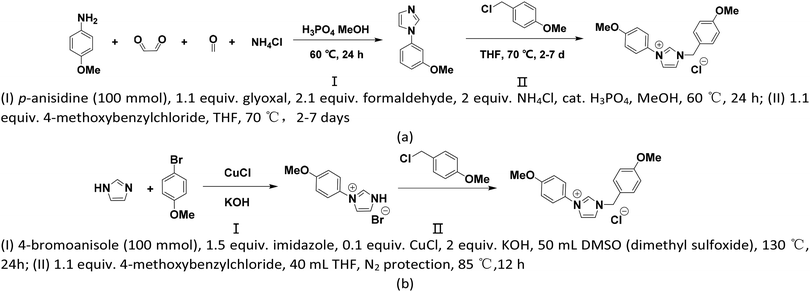
From a realistic perspective, the theoretically designed cation should be easily synthesized. As shown in Scheme 1, two synthetic pathways (a) and (b) are proposed where path (a) is accessible by a two-step synthesis starting from commercially available aniline derivates⁶³ and path (b) is completed via 4-bromoanisole based on the reported routines in ref. 64. Apart from easy availability, the low synthetic cost of the reaction reagents and moderate reaction conditions together support that our proposed [BnPhIM-pOMe]⁺ can be expected.

Scheme 1 Two proposed synthetic pathways (a) and (b) for the predicted [BnPhIM-pOMe]⁺ cation.

Conclusions

In summary, the hole transport properties of highly conducting PEDOT after mediation by IL additives have been researched using multiscale MD simulations and DFT calculations. The [BMIM]:[BF₄] IL and its aromatized derivatives [BuPhIM]:[BF₄] and [BnPhIM]:[BF₄] have been considered due to the π-conjugation extension of the [BMIM]⁺ backbone, favoring charge delocalization. With the increase in aromatization in the order [BMIM]⁺ to [BuPhIM]⁺ to [BnPhIM]⁺, these cation-constructed ILs show a significant increase in electronic coupling and doping efficiency compared to PEDOT. In particular, [BnPhIM]:[BF₄] causes PEDOT to approach the fastest hole transport properties in solution (an average of 4.01 cm² V⁻¹ s⁻¹ and an instantaneous maximum reaching 17 cm² V⁻¹ s⁻¹), far surpassing its counterparts. This reflects that PEDOT chains gather into a highly ordered cluster, triggered by the larger evenness of the net charge distribution at the [BnPhIM]:[BF₄]-PEDOT interface. On the other hand, the fastest transport pathway after introducing [BnPhIM]:[BF₄] into solution is larger by one order of magnitude than that of the quantity in the predicted PEDOT single crystal. These verify that extending the π-conjugation of [BMIM]⁺ benefits heterogeneous and homogeneous hole transport. Finally, the hole mobility of PEDOT after introducing the novel designed [BnPhIM-pOMe]:[B(CN)₄] is improved by 35–43% compared to that of [BnPhIM]:[BF₄], rationalizing that [BnPhIM-pOMe]:[B(CN)₄] could serve as a potential candidate for application in IL-PEDOT-based organic electronics. We believe that both our computational protocols and our analysis highlighted here will be useful for future work aiming to investigate structure-mobility relationships for PEDOT-based applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (22008238, 21922813, 21776278, and 21673175), the Fund of State Key Laboratory of Multiphase complex systems (No. MPCS-2019-A-08), and Youth Innovation Promotion Association CAS (2017066). We thank Mr Cheng Qian for the programming of transfer integrals.

Notes and references

1. L. V. Kayser and D. J. Lipomi, Adv. Mater., 2019, 31, 1806133.
2. L. Hu, J. Song, X. Yin, Z. Su and Z. Li, Polymers, 2020, 12, 145.
3. Z. Fan and J. Ouyang, Adv. Electron. Mater., 2019, 5, 1800769.
4. S. Zhang, Y. Chen, H. Liu, Z. Wang, H. Ling, C. Wang, J. Ni, B. C. Saltik, X. Wang, X. Meng, H. J. Kim, A. Baidya, S. Ahadian, N. Ashammakhi, M. R. Dokmeci, J. Travas-Sejdic and A. Khademhosseini, Adv. Mater., 2020, 32, 2070005.
5. Y. H. Jia, L. L. Shen, J. Liu, W. Q. Zhou, Y. K. Du, J. K. Xu, C. C. Liu, G. Zhang, Z. S. Zhang and F. X. Jiang, J. Mater. Chem. C, 2019, 7, 3496–3502.
6. M. N. Gueye, A. Carella, J. Faure-Vincent, R. Demadrille and J.-P. Simonato, Prog. Mater. Sci., 2020, 108, 100616.
7. B. C. K. Tee and J. Ouyang, Adv. Mater., 2018, 30, 1802560.
8. Y. Zheng, H. Zeng, Q. Zhu and J. Xu, J. Mater. Chem. C, 2018, 6, 8858–8873.
9. Z. A. King, C. M. Shaw, S. A. Spanninga and D. C. Martin, Polymer, 2011, 52, 1302–1308.
10. J. G. Ibanez, M. E. Rincon, S. Gutierrez-Granados, M. Chahma, O. A. Jaramillo-Quintero and B. A. Frontana-Uribe, Chem. Rev., 2018, 118, 4731–4816.
11. N. Rolland, J. F. Franco-Gonzalez, R. Volpi, M. Linares and I. V. Zozoulenko, Phys. Rev. Mater., 2018, 2, 045605.
12. Q. Wei, M. Mukaida, Y. Naitoh and T. Ishida, Adv. Mater., 2013, 25, 2831–2836.
13. J. Rivnay, S. Inal, B. A. Collins, M. Sessolo, E. Stavrinidou, X. Strakosas, C. Tassone, D. M. Delongchamp and G. G. Malliaras, Nat. Commun., 2016, 7, 11287.
14. E. Dauzon, A. E. Mansour, M. R. Niazi, R. Munir, D. M. Smilgies, X. Sallenave, C. Plesse, F. Goubard and A. Amassian, ACS Appl. Mater. Interfaces, 2019, 11, 17570–17582.
15. M. Y. Teo, N. RaviChandran, N. Kim, S. Kee, L. Stuart, K. C. Aw and J. Stringer, ACS Appl. Mater. Interfaces, 2019, 11, 37069–37076.
16. X. Wu, A. Surendran, J. Ko, O. Filonik, E. M. Herzig, P. Muller-Buschbaum and W. L. Leong, Adv. Mater., 2019, 31, 1805544.
17. Q. Li, M. Deng, S. Zhang, D. Zhao, Q. Jiang, C. Guo, Q. Zhou and W. Liu, J. Mater. Chem. C, 2019, 7, 4374–4381.
18. S. Kee, H. Kim, S. H. K. Paleti, A. El Labban, M. Neophytou, A.-H. Emwas, H. N. Alshareef and D. Baran, Chem. Mater., 2019, 31, 3519–3526.
19. A. Ispas, R. Peipmann, A. Bund and I. Efimov, Electrochim. Acta, 2009, 54, 4668–4675.
20. V. Armel, J. Rivnay, G. Malliaras and B. Winther-Jensen, J. Am. Chem. Soc., 2013, 135, 11309–11313.
21. Z. Ma, M. Forsyth, D. R. MacFarlane and M. Kar, Green Energy Environ., 2019, 4, 146–153.
22. A. de Izarra, S. Park, J. Lee, Y. Lansac and Y. H. Jang, J. Am. Chem. Soc., 2018, 140, 5375–5384.
23. A. Mazaheripour, S. Majumdar, D. Hanemann-Rawlings, E. M. Thomas, C. McGuiness, L. d’Alencon, M. L. Chabinyc and R. A. Segalman, Chem. Mater., 2018, 30, 4816–4822.
24. N. Saxena, B. Pretzl, X. Lamprecht, L. Biessmann, D. Yang, N. Li, C. Bilko, S. Bernstorff and P. Muller-Buschbaum, ACS Appl. Mater. Interfaces, 2019, 11, 8060–8071.
25. M. Culebras, C. M. Gómez and A. Cantarero, J. Mater. Chem. A, 2014, 2, 10109–10115.
26. R. Gangopadhyay, B. Das and M. R. Molla, RSC Adv., 2014, 4, 43912–43920.
27. W.-L. Ding, Z.-Z. Sun, X.-L. Peng, C.-L. Wang, Y.-Q. Zhang, H.-Y. He and S.-J. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 9796–9807.
28. S. Ahrens, A. Peritz and T. Strassner, Angew. Chem., Int. Ed., 2009, 121, 8048–8051.
29. D. Meyer and T. Strassner, J. Org. Chem., 2011, 76, 305–308.
30. P. Jiang, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o2177.
31. N. Kim, I. Petsagkourakis, S. Chen, M. Berggren, X. Crispin, M. P. Jonsson and I. Zozoulenko, Electric Transport Properties in PEDOT Thin Films, CRC Press Taylor & Francis Group, 2019.
32. L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164.
33. S. Plimpton, J. Chem. Phys., 1995, 117, 1–19.
34. W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
35. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960.
36. J. Zeng, L. Duan, J. Z. Zhang and Y. Mei, J. Comput. Chem., 2013, 34, 847–853.
37. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta Jr., F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Wallingford CT, Gaussian Inc., 2013.
39. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
40. J. R. Reimers, J. Chem. Phys., 2001, 115, 9103–9109.
41. Y. L. Niu, W. Q. Li, Q. Peng, H. Geng, Y. P. Yi, L. J. Wang, G. J. Nan, D. Wang and Z. G. Shuai, Mol. Phys., 2018, 116, 1078–1090.
42. T. Lu, Molclus Program, Version 1.9, http://www.keinsci.com/research/molclus.html.
43. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
44. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, 3rd, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, 3rd, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197.
45. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
46. Z. Liu, T. Lu and Q. Chen, Carbon, 2021, 171, 514–523.
47. Z. Shuai, L. Wang and C. Song, Theory of Charge Transport in Carbon Electronic Materials, Springer Science & Business Media, 2012.
48. Y. Geng, S. X. Wu, H. B. Li, X. D. Tang, Y. Wu, Z. M. Su and Y. Liao, J. Mater. Chem., 2011, 21, 15558–15566.
49. G. Nan, L. Wang, X. Yang, Z. Shuai and Y. Zhao, J. Chem. Phys., 2009, 130, 024704.
50. R. A. Marcus and S. Norman, Biochim. Biophys. Acta, Bioenerg., 1985, 811, 265–322.
51. R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599.
52. R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701.
53. S. Gangala and R. Misra, J. Mater. Chem. A, 2018, 6, 18750–18765.
54. A. J. Moulé, D. Neher and S. T. Turner, P3HT-Based Solar Cells: Structural Properties and Photovoltaic Performance, 2014, vol. 265, pp. 181–232.
55. Y. Park, J. W. Jung, H. Kang, J. Seth, Y. Kang and M. M. Sung, Nano Lett., 2019, 19, 1028–1032.
56. C. Poelking, K. Daoulas, A. Troisi and D. Andrienko, Adv. Polym. Sci., 2014, 265, 139–180.
57. J. P. Muscat and D. M. Newns, Prog. Surf. Sci., 1978, 9, 1–43.
58. P. Persson, M. J. Lundqvist, R. Ernstorfer, W. A. Goddard and F. Willig, J. Chem. Theory Comput., 2006, 2, 441–451.
59. W.-L. Ding, X.-L. Peng and Z.-S. Li, Org. Electron., 2016, 38, 384–395.
60. R. Lindblad, J. Oscarsson, K. Fredin, S. K. Eriksson, H. Siegbahn, E. M. J. Johansson and H. Rensmo, J. Electron Spectrosc. Relat. Phenom., 2018, 224, 100–106.
61. B. Nell, K. Ortstein, O. V. Boltalina and K. Vandewal, J. Phys. Chem. C, 2018, 122, 11730–11735.
62. G. Zuo, Z. Li, O. Andersson, H. Abdalla, E. Wang and M. Kemerink, J. Phys. Chem. C, 2017, 121, 7767–7775.
63. S. Lerch and T. Strassner, Chemistry, 2019, 25, 16251–16256.
64. Y.-Z. Huang, H. Miao, Q.-H. Zhang, C. Chen and J. Xu, Catal. Lett., 2008, 122, 344–348.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00040c

---