 Open Access Article
Open Access ArticleParticle formation mechanisms supported by in situ synchrotron XAFS and SAXS studies: a review of metal, metal-oxide, semiconductor and selected other nanoparticle formation reactions†
Christopher B.
Whitehead
 and
Richard G.
Finke
and
Richard G.
Finke
 *
*
Department of Chemistry, Colorado State University, Fort Collins, Colorado 80523, USA. E-mail: Richard.Finke@colostate.edu
First published on 27th September 2021
Abstract
Following a brief description of synchrotron X-ray absorption fine structure (XAFS) spectroscopy and small/wide angle X-ray scattering (SAXS/WAXS), the definition of and four primary criteria for attaining reliable, disproof-based chemical mechanisms of particle formation are given. A total of 74 papers using synchrotron techniques for mechanistic investigation are then analyzed in detail via the construction of four tables provided in the ESI that analyze each of the 74 papers. Six primary case studies are selected out of the 74 total papers for presentation in greater detail in the main text, specifically the illustrative case histories of: (i) palladium nanoparticles studied using SAXS, (ii) rhodium nanocubes examined using XAFS, (iii) iridium nanoparticles studied by XAFS and SAXS, (iv) gold nanoparticles studied by XAFS, SAXS, and XRD, (v) cadmium-selenide nanocrystals studied by XAFS, and (vi) zinc-oxide nanoparticles studied using SAXS/WAXS/UV-vis. Additionally, two shorter case studies are presented that address particle formation shapes: tungstite nanoplatelets and copper nanocrystals. Two summary tables are presented in the main text that present the current state of disproof-based, deliberately minimalistic particle formation mechanisms expressed in terms of generalized, pseudoelementary steps. Finally, a Conclusions section with nine takeaways and an Outlook section are also provided. The goal of the present review is to expedite the use of powerful synchrotron SAXS and XAFS studies to provide reliable, disproof-based chemical mechanisms and their associated quantitative differential equations that can then be employed to predict particle-size distributions via the recent development of Mechanism-Enabled Population Balance Modeling (ME-PBM).
1. Introduction
Knowledge and understanding of chemical reaction mechanisms are critical to accomplishing the long-sought goal of synthetic control of especially particle-size distributions in particle formation science.1–4 Complete understanding of the nucleation, growth, and agglomeration processes5–12 promises to provide the desired size and size-distribution control in particle synthesis,13–23 just as mechanistic insights into other chemical and industrial processes have resulted in improvements in the fields of renewable energy, semiconductor synthesis, nanocatalysis, and many others.24–29Due to the sub-nanoscale size (<1 nm) of just-formed nuclei, it is very difficult to observe directly in real time the smallest, kinetically first-formed cluster(s), termed the kinetically effective nucleus (KEN).30 Indeed, recent work shows that the KEN consists of just 2–3 atoms in at least some strong-bonding systems.31,32 Hence, there is a need to use synchrotron-based spectroscopic techniques to monitor the nucleation, growth and any agglomeration of particles, notably synchrotron X-ray absorption fine structure (XAFS) spectroscopy (that provides oxidation state, coordination number, and associated structural information) as a function of time, and synchrotron small-angle X-ray scattering (SAXS) (that allows monitoring of particle radius and, significantly, the number of particles) in real-time.33–38 These techniques can be used in tandem with each other or with other methods, and they can be used to monitor directly particle formation reactions in situ.
However, significant gaps remain in the nanoparticle formation literature en route to a deeper understanding of (i) first, what constitutes a reliable, disproof-based chemical reaction mechanism; (ii) the experimental data needed to be able to claim such a mechanism; (iii) how such mechanisms differ from non-disproof-based model(s); (iv) the preferred experimental methods for collecting the needed kinetics data; and then (v) what are the arguably best, prototype mechanistic case studies to date by synchrotron-based methods?
Hence herein we begin by discussing the requirements for a reliable, disproof-based chemical mechanism and then we present six case studies of particle formation monitored by synchrotron-based SAXS, XAFS or tandem SAXS/XAFS methods.39–44 We systemically assess the results and strengths of each case study and, where needed, suggest additional studies en route to a reliable reaction mechanism. The goal is to use these six case studies as pedagogically valuable examples of how to most efficiently achieve reliable, disproof-based reaction mechanisms of particle formation regardless of the exact type or composition of the resultant particles. Two summary tables that present the current state-of-the-art in terms of disproof-based, deliberately minimalistic (i.e., Ockham's razor obeying) particle formation mechanisms are provided as part of the summary and conclusions.
2. Background
2.1. Key requirements for a minimum chemical mechanism
From classical physical-organic chemistry, the definition of a mechanism is well understood dating back at least 50 years.45–47 Reliable chemical mechanisms typically result only if the following, minimum requirements are met:(1) If a complete mass- and charge-balanced reaction stoichiometry is experimentally determined, as that stoichiometry is what the proposed steps of the mechanism must add up to.48 Problems result if even a world class expert mechanistic chemist49 studies a much simpler reaction than nanoparticle formation in the absence of an experimentally established, full, balanced stoichiometry.50
(2) If kinetics data are obtained,51,52 ideally the full rate law, and ideally using multiple, direct physical methods and handles;
(3) If elementary, or if not possible pseudoelementary,53,54 step reactions are written that present the stepwise mechanism that also add up to the experimentally established reaction stoichiometry. Those mechanistic steps also define the rate constants and define the unambiguous words55,56 one can use to discuss the observed chemistry—the latter point being much more important than one might initially imagine for avoiding confusion in the description of the mechanism and associated chemistry;
(4) If, critically, disproof-based57–59 quantitative comparisons of the experimental data to competing, alternative mechanisms are made, specifically how well (or poorly) a given postulated mechanism is able to fit that data. Adherence to Ockham's razor is also important en route to deliberately minimalistic mechanisms that are the initial goal of mechanistic studies.60 Those minimum mechanisms are expected to be replaced—disproved if you like—by more complex mechanisms as more data, from better experiments or improved computational methods, become available over time.
Once one has the minimum, disproof-based chemical mechanism in hand, then one has a good start on a broader and more generalized understanding of the system. That mechanistic understanding of nucleation, growth, and agglomeration that are ubiquitous processes across nature can then be used to further control key properties of the system: average particle size, particle-size distribution, catalytic activity, photochemical properties (that are often size and size-dispersion dependent, e.g., in semiconductor quantum dot nanoparticles), and so on.
Unfortunately, experimental kinetics and rate-law-backed mechanisms for nucleation are rare at the molecular and atomic level, save for a small handful of studies.26,30–32,39,41 The precise mechanism of nucleation is critical as it starts off the particle-formation process; without the precise details of the nucleation process one cannot possibly claim to a complete nor reliable mechanism of particle formation. Growth and agglomeration are in a bit better shape,61–66 but still not well supported kinetically and mechanistically with, again, the required experimental rate law for growth or agglomeration. Hence, advances are needed there as well. Through the basic four requirements outlined above en route to a reliable mechanism illustrated via six case studies, we hope to demystify how one can perform reliable mechanistic investigations that allow elucidation of the most probable particle formation process. We also detail the importance of pseudoelementary steps53,54 in the construction, and attempted disproof, of more complex mechanisms in materials and other chemistries.
2.2. Why disproof-based, minimum, reliable reaction mechanisms are an important goal
Even if one obtains powerful synchrotron-based evidence on a well-designed, important particle formation process, the broader application and impact of that sophisticated effort and often impressive data will have been wasted if one just summarizes that hard-won data in a cartoon that just restates the observed particle sizes vs. time, for example and as too often done presently. The power of the observed kinetics data is lost until and unless one expresses that data in its most concise, most powerful form—a reaction mechanism in the form of charge and mass balanced reactions that, then, define the differential equations able to account quantitatively for the intermediate species as well as the net process over time. It is the more general application to other systems as well as quantitative predictability that is contained within generalized kinetics equations, expressed in terms of generalized A, B, C…N species, all with rate constants defined by ideally elementary, or at least pseudoelementary,53,54 steps. Again, each of those steps must be mass- and charge-balanced, and those proposed mechanistic steps must add up to the observed, experimentally determined reaction stoichiometry—otherwise one is proposing a mechanism for some reaction different than the one at hand. Note the power here of avoiding mistakes or proposing something foolish by making sure what one proposes obeys the Laws of Mass and Charge Balance. Additionally, if the rate constants are known—ideally as a function of temperature—then there is predictability from one set of starting conditions and temperature to another set of, for example, more optimized conditions. The use of balanced reactions for nanoparticle formation promises to be especially significant for understanding ligand effects that are key to particle formation and stabilization, but presently are little studied, in part because the reactions written typically do not even show those key ligands to be present.With the 2019 advent of Mechanism-Enabled Population Balance Modeling (ME-PBM),67,68 one can track every particle in a proposed particle-formation pathway consisting of even thousands of elementary steps. Disproof-based, deliberately minimum mechanisms are necessary and sufficient to be able to predict both average particle sizes and particle-size distributions (PSDs), including the PSD shape, with ME-PBM. The available evidence to date also illustrates the ability of disproof-based ME-PBM to confirm—or more often to date to refute67,68—a proposed mechanism67,68 en route to a refined mechanism. ME-PBM is also able to extract rate constants for the proposed, pseudoelementary step mechanism from PSD data.67,68 But, to exploit the full generality, predictability and for knowledge transfer to other systems or conditions, a reliable minimum reaction mechanism is required to start, as the name Mechanism-Enabled PBM indicates. Ligand effects are, once again, just now being taken into account as part of ME-PBM,31,32,39vide infra.
2.3. Literature search and paper selection
A total of 74 papers were collected through a search of the literature via SciFinder and the Web of Science. Series of searches were performed over a period of more than 3 years, where various combinations of terms were cross referenced including, but not limited to: “XAFS”, “SAXS”, “in situ”, “in operando”, “tandem”, “mechanism”, “kinetics”, “formation”, “nanoparticle”, and “nanocrystal”. The 74 papers collected and analyzed in this publication are tabulated into four tables in the ESI:† Table S1, 5 entries (instructional, review articles on the general use of XAFS and SAXS in scientific research); Table S2, 24 entries (SAXS studies of nanoparticle formation); Table S3, 24 entries (XAFS studies of nanoparticle formation); and Table S4, 21 entries (Tandem techniques, where at least one technique is synchrotron XAFS or SAXS). Not unsurprisingly, transition-metal nanoparticles comprise the majority of papers tabulated as they often represent systems with fewer components that have been studied more extensively over a longer period of time. We have also included promising, emerging examples of metal oxide, semiconductor, quantum dot, and perovskite materials.The interested reader is encouraged—actually strongly encouraged—to study and analyze for themselves these four tables to understand the variety of systems covered, the status of the approaches, and the overall efforts at nanoparticle reaction development and associated mechanistic investigation summarized in Tables S1–S4 of the ESI.† Indeed, if Tables S1–S4 of the ESI† covered anything smaller than their current 50 pages, we would have placed them upfront in this review to make them even more available and apparent. Self-study of Tables S2–S4 of the ESI† will generate the reader's own assessment and insights regarding the status of the field of particle formation synthesis, kinetics and mechanism using synchrotron methods. Papers that did not present, discuss, or claim a mechanism are not included even if they reported XAFS or SAXS data.
In what follows we have selected 6 case studies for a closer look and critical analysis based, overall, on how they illustrate together the state-of-the-art in the field as well as what else is needed to attain reliable chemical mechanisms for the particle formation reaction under study. Our apologies in advance to authors of the many other interesting studies summarized in ESI,† Tables S2–S4 that either space, or our approach and organization of this review, did not permit us to cover in detail in the main text that follows. Also not covered herein due to scope and space limitations are computational chemistry approaches and contributions that promise to be of increasing importance, perhaps especially to a deeper understanding of nucleation processes.69,70 That said, computations not carefully connected to experimental results can lead to erroneous conclusions, even for chemical systems much simpler than particle formation reactions.71
3. Selected, illustrative case studies of metal nanoparticles
The goal of the current review is to expedite the conversion of a growing body of powerful synchrotron-based spectroscopic studies and data now available (Tables S2–S4, ESI,† by the multiple expert investigators and studies), into the “causes” (the mechanisms) for those “effects” (the observables) as monitored by powerful, direct, in situ synchrotron-based spectroscopies. In this section of the review, four state-of-the-art kinetics case studies of metal nanoparticle formation that utilize synchrotron techniques are summarized. These four case studies have been chosen as illustrative, often arguably top examples in the field of nanoparticle formation kinetics and mechanistic studies or at least synchrotron-based studies. Each will have several of the required pieces of information necessary to be able to claim a reliable mechanism, although an interesting observation is that each prototype system is missing one or more aspects that, ideally, will be added in the future to that system and study.The four case studies are: (Section 3.1) palladium nanoparticle formation monitored by SAXS;39 (Section 3.2) rhodium nanocube formation monitored by XAFS;40 (Section 3.3) iridium nanoparticle formation monitored by XAFS and SAXS;41 and (Section 3.4) gold nanosphere and nanowire formation monitored by XAFS, SAXS, and XRD.42 Each case study is organized by: (i) a summary of the system and techniques used to study it; (ii) a review of the key kinetics data; (iii) the authors’ proposed formation model or mechanism; and (iv) an analysis of the case's results as compared to the four components required for establishing a minimum, disproof-based mechanism. Overall, our intent is to be supportive of the excellent synchrotron-based studies and encouraging to how those studies can be taken to the next level of mechanistic formulation, analysis, and use.
3.1. Case study #1: mechanistic investigation of palladium nanoparticle formation using small-angle X-ray scattering
Karim and coworkers, in 2017, published their detailed, disproof-based mechanistic investigation of palladium nanoparticle formation—a critical study because it details quantitatively with ligand effects.39 Spherical palladium nanoparticles were prepared from Pd(II) acetate, Pd(OAc)2, and trioctylphosphine (TOP) ligand in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 solvent mixture of toluene and 1-hexanol at 100 °C under nitrogen.39,72 The formation kinetics were monitored by in situ SAXS, where a syringe pump was used to draw a small sample into the beam and then inject it back into the reaction solution after each measurement. The reaction was studied at palladium concentrations from 0.5 to 25 mM, hence a relatively wide factor of 50. Importantly, the tri-octylphosphine ligand-to-metal molar ratios (TOP
50 solvent mixture of toluene and 1-hexanol at 100 °C under nitrogen.39,72 The formation kinetics were monitored by in situ SAXS, where a syringe pump was used to draw a small sample into the beam and then inject it back into the reaction solution after each measurement. The reaction was studied at palladium concentrations from 0.5 to 25 mM, hence a relatively wide factor of 50. Importantly, the tri-octylphosphine ligand-to-metal molar ratios (TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd) were studied at ratios of 1, 1.5, and 2. Finally, the end-time particle size and size distributions were collected ex situ using dark-field STEM. The generalized reaction stoichiometry as given in ref. 39, that does not include the specific ligand component, is reproduced below as eqn (1).
Pd) were studied at ratios of 1, 1.5, and 2. Finally, the end-time particle size and size distributions were collected ex situ using dark-field STEM. The generalized reaction stoichiometry as given in ref. 39, that does not include the specific ligand component, is reproduced below as eqn (1).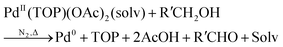 | (1) |
The authors directly monitored the Pd nanoparticle formation by in situ synchrotron SAXS experiments—while making the important point that SAXS counts as “two methods” if one monitors both the particle radius as well as the number of particles vs. time,39,72vide infra. By using a Schultz polydisperse spherical model, they were able to fit the SAXS data and simultaneously extract both the particle sizes and the total number of particles with respect to time.
The data display direct evidence of slow, continuous nucleation with fast (but slower than diffusion-controlled) growth, results in direct contradiction to the classical LaMer model of 1950 that postulates burst nucleation followed by diffusion-controlled growth.39,65,66 Furthermore, the continuous increase in particles suggests that agglomeration, which would reduce the number of particles, is not involved in the Pd(0)n-particle formation process under their conditions that include an excess of strongly coordinating tri-octylphosphine ligand. The authors hypothesized that, at a minimum, continuous nucleation, fast autocatalytic growth, and the incorporation of ligand effects will be needed for any kinetic model and associated minimum mechanism able to fit their SAXS data.
The authors proceeded by constructing a model relying on three assumptions: (i) that the fraction of surface versus core atoms can be ignored, which for particles smaller than 1.5 nm (as seen in Fig. 1) means that the percentage of surface atoms is >75% of the total atoms;39 (ii) that the growth and ligand binding to the particle surface is independent of particle size and ligand coverage, in this first model to be able to account for ligand effects. (“In the absence of experimental or theoretical information, the effects of size, polydispersity and ligand coverage on the rate constants are not included in the model.”39); and (iii) that the ligand–metal precursor binding ratio is assumed to be 1 because isothermal titration calorimetry73 shows, “the equilibrium binding constant for the second TOP binding (A·L + L ⇌ A·L2) is around two orders of magnitude lower than the first binding”,39 where A is the Pd precursor and L is TOP.
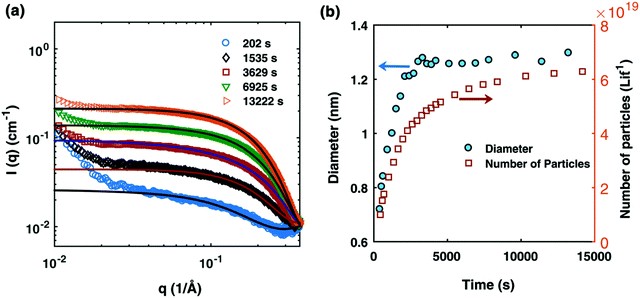 | ||
Fig. 1 (a) SAXS data at different reaction times after absolute scaling with fitting by Schultz polydisperse spherical model; (b) particle size evolution (blue circles) and number of particles (open orange squares) plotted as a function of time (in seconds). The Pd nanoparticles were prepared from a solution of 10 mM Pd(OAc)2, 20 mM TOP, in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 solution of toluene and 1-hexanol at 100 °C. Figure reproduced with permission from ref. 39. Copyright 2017 Royal Society of Chemistry. 50 solution of toluene and 1-hexanol at 100 °C. Figure reproduced with permission from ref. 39. Copyright 2017 Royal Society of Chemistry. | ||
By using their proposed mechanism under the above reasonable if not necessary assumptions for an initial, carefully constructed, not over-parameterized model, the authors developed a kinetic model and associated minimum mechanism able to fit quantitatively their experimentally determined number of particles as a function of time data. The proposed kinetics model for nucleation, autocatalytic growth, and accompanying ligand effects used to fit the experimental data in Fig. 2 is given in Scheme 1. The model was constructed using the minimum number of pseudoelementary steps necessary to describe the reaction, that is, by ensuring that Ockham's razor60 is obeyed in their proposed mechanism.
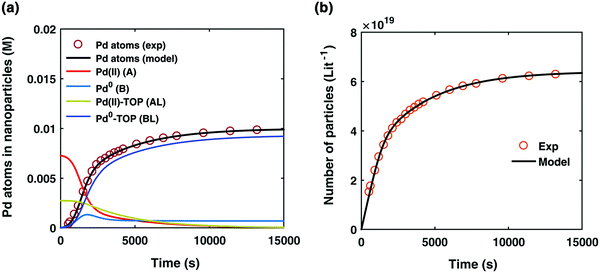 | ||
Fig. 2 (a) Experimentally determined concentration of Pd atoms in nanoparticles (molarity, M) as a function of time (seconds, s) is plotted (red open circles) and fit with the kinetic model (black line) accounting for Pd atoms as total nanoparticles (B + B·L). The resultant rate constants are: k1 = 2.45 × 10−5 s−1, k2 = 8.5 × 10−1 s−1 M−1, k3 = 7.9 × 10−3 s−1 M−1, k4 = 2.1 × 10−1 s−1 M−1, Keq,3 = 2.18 × 101 M−1, and Keq,4 = 1.27 × 103 M−1. Based on the kinetic model rate constants, concentrations of A (red line), B (light blue line), A·L (green line), and B·L (dark blue line) were simulated as a function of time. (b) Experimentally determined number of particles as a function of time fit with the kinetic model. The reaction conditions for the experimental data were 10 mM Pd(OAc)2, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 toluene 50 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexanol solvent, TOP hexanol solvent, TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd ratio of 2 Pd ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 100 °C reaction temperature. Figure reproduced with permission from ref. 39. Copyright 2017 Royal Society of Chemistry. 1, and 100 °C reaction temperature. Figure reproduced with permission from ref. 39. Copyright 2017 Royal Society of Chemistry. | ||
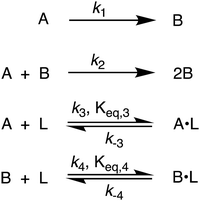 | ||
| Scheme 1 Karim and co-workers39 4-step model for particle formation, autocatalytic surface growth, ligand–precursor interactions (A·L), and ligand–particle interactions (B·L). | ||
The model contains four pseudoelementary steps that define the corresponding rate constants. The first step is nucleation including reduction (A → B, k1), where Pd(II) is reduced to Pd(0) and Pd(0)n nuclei are formed. Note, as discussed elsewhere,30 under constant initial [A]Total, higher-order nucleation nA → nB (= Bn) is kinetically hidden because (d[A0]/dt)/n = k1[A0]n, where [A]0 is often constant to a ≥99.9% level during the induction period.30 In the present case, unimolecular rate-determining Pd(II) → Pd(0) is arguably likely present given that the slow step is the release of A, that is A − L → A + L. The second step employed is autocatalytic surface growth (A + B → 2B, k2),54 where Pd(II) is reduced and added to the surface of the growing Pd(0)n particle. Next, the equilibrium between the Pd(II) precursor complex and the ligand, TOP, (A + L ⇌ A·L, k3 and Keq,3), and the equilibrium between the Pd(0)n particle and TOP (B + L ⇌ B·L, k4 and Keq,4) are included. The kinetic model's ability to account quantitatively for the experimental data in Fig. 2 demonstrates the value of obtaining simultaneous size and number of particles data by SAXS as Prof. Karim has insightfully emphasized.39,72 The quantitative fits presented Fig. 2 argue strongly that the ligand-based kinetics model, incorporating the species A, B, A·L, B·L, and L, is a satisfactory, quantitative kinetics model for describing this valuable Pd(0)n particle-formation system from the Karim laboratory.
The model can be further visualized using the pictorial representation provided by the authors shown in Fig. 3:
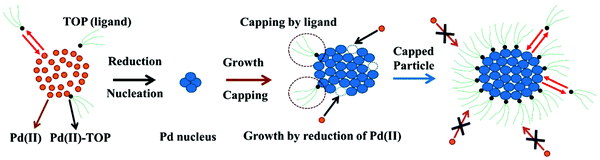 | ||
| Fig. 3 Schematic representation of the ligand-based model. The figure represents the 4 steps of the model: (1) reduction of Pd(II) to Pd(0) and the formation of the Pd nucleus (A → B); (2) autocatalytic growth of the Pd nucleus by further addition and reduction of Pd(II) (A + B → 2B); (3) reversible ligand binding with the precursor Pd(II) (A + L ⇌ A·L); and (4) reversible ligand binding to the particle surface (B + L ⇌ B·L). Orange circles are the unreduced Pd(II), small black circles with green tails are trioctylphosphine (TOP, ligand), and blue circles are reduced Pd(0)n particles. Figure reproduced with permission from ref. 39. Copyright 2017 Royal Society of Chemistry. | ||
Noteworthy here is that the Karim and co-authors’ contribution is ahead of most in that it provides a balanced reaction, the detailed kinetic scheme in Scheme 1, quantitative fitting of the SAXS data, and the resultant quantitative rate constants that can be used to quantitatively describe and predict particle size and size-distributions via Population-Balance Modeling. Furthermore, the Karim group tested alternative mechanisms as is needed en route to a reliable, disproof-based mechanism. In the ESI of ref. 39, five models were tested. Included in these models are mechanisms that did not include ligand steps (A → B and A + B → 2B), included only the A·L ligand step (A → B, A + B → 2B, and A + L ⇌ A·L), and included only the B·L ligand step (A → B, A + B → 2B, and B + L ⇌ B·L). These three models, the first of which is the classic 2-step mechanism of just A → B, A + B → 2B,54 were unable to fit the data. Out of the 5 models tested, the only model capable of accounting for the experimental data was the four-step model presented in Scheme 1. Here, the authors disproved four alternative mechanisms en route to the Ockham's Razor60 obeying mechanistic model in Scheme 1 that can quantitatively describe their Pd(0)n nanoparticle system.
Additionally, the authors demonstrated the applicability of their minimal ligand-based kinetic model to other literature systems that exhibit a particle-size dependence based on the ligand concentration employed. They found that their ligand-based kinetic model, that includes reversible ligand binding to the precursor (“A”) and the particle surface (“B”), fit literature data sets for Pd/PVP74 and Au/thiol75 systems as well—a valuable demonstration of the broader generality of their kinetics model.
The authors’ work highlights one of the most important pieces of this mechanistic investigation—the power of pseudoelementary steps.53,54 A pseudoelementary step is a composite of underlying elementary steps,53,54 even if those exact steps are not known to start. Nanoparticle formation consists of at least hundreds (for smaller particles) to often thousands of elementary steps—and millions of elementary steps once one reaches micron-sized particles. In the case of Karim's Pd system, the final particles contain 100s of atoms in a mechanism that must, therefore, correspond minimally to hundreds of elementary steps. Yet, Karim and coworkers were able to describe the Pd nanoparticle formation39 process, and the formation process of others systems,74,75 quantitatively using only 4 pseudoelementary steps as shown in Scheme 1—an instructive demonstration of the pseudoelementary step concept.53,54
Available elsewhere is the most illustrative example presently available where the pseudoelementary step concept has been used to elucidate the intimate, elementary-step catalytic mechanism.48 A review of the pseudoelementary step method for approaching the mechanism of complex reactions is in progress and will be published in due course. There is of course ambiguity in what especially “B” is in Scheme 1 and in general in use of the PEStep concept—B really being a sum of different nanoparticles en route to the final nanoparticles, also grouped under B. But the case illustrated elsewhere48 shows how one can deconvolute B in favorable cases to its precise specie(s)—and indeed in that case, that only by using the PEStep concept and an initial fit to a simple A → B, k1, A + B → 2B, k2, PEStep mechanism were the otherwise stumped authors able to deduce the true catalytic mechanism. That mechanism was then verified by following directly by 1H NMR four the five reaction reagents and products and showing they fit the kinetics predicted by the deduced, elementary step mechanism.48
In summary of this first important case study, the authors used SAXS to simultaneously monitor the total number of particles and the concentration of Pd nanoparticles as a function of time. Their mechanistic model satisfies three of the four criteria for a reliable mechanistic study and partially satisfies the first criteria. For criterion (i)—a complete, balanced reaction stoichiometry—“A” is a complex of the Pd starting material, Pd(OAc)2, the solvent (toluene or pyridine), and/or hexanol,39 so that the precise composition of “A” is not known unequivocally and will be needed for a more detailed understanding of the more intimate nucleation mechanism. The precise compositions of the products, PdnLm(solvent)a, are not known, but proved to not be a major hindrance to the study and its goals. The authors’ TEM studies show that an increase in solvent polarity results in an increase in particle size, yet other studies76,77 find the opposite trend, so that the exact composition of “A” and the resulting effect of the choice of solvent remain topics of interest and potential future study in this interesting system. Second, the authors fully satisfied criterion (ii)—collection of kinetics data—with their direct SAXS kinetics data that yields two observables, particle-size and concentration.39,72 Finally, the authors also satisfied criteria (iii) and (iv)—(pseudo)-elementary steps present the mechanism and disproof of multiple alternative hypotheses, respectively—leading to their development of a minimal, pseudoelementary 4-step kinetic model. The model accurately describes the physical processes, defines the rate constants, and importantly provides the correct words for describing, unambiguously, each pseudoelementary step. The final 4-step kinetics model proposed is the only mechanism out of several tested to account for the experimental data and is an Ockham's Razor-obeying model.
Overall, the excellent work39 by Karim and coworkers is an important case study of nanoparticle formation employing SAXS monitoring and proper mechanistic model building. It is a “must-read” in our opinion for anyone pursuing reliable particle-formation mechanisms and certainly a must read for researchers hoping to understand ligand-effects in their particle formation and stabilization reaction.
3.2. Case study #2: mechanistic analysis of rhodium nanoparticle formation using X-ray absorption fine structure spectroscopy
In 2012, Tanaka and coworkers published a noteworthy study on the formation of rhodium nanocubes.40 The authors prepared the nanocubes from RhCl3·3H2O (0.2 mmol) in ethylene glycol (10 mL) with the bromide source tetradecyltrimethylammonium bromide (TTAB, 3.0 mmol) and poly(vinylpyrrolidone) (PVP, 3.0 mmol) at 130 °C, eqn (2).40 The solution was stirred at room temperature under N2 for 20–30 minutes, and then it was heated to 130 °C within 3 minutes with vigorous stirring.40 The proposed reaction stoichiometry from the experimental of ref. 40 is given as eqn (2) below, but is incomplete as it doesn’t indicate the critical reductant, almost surely the ethylene glycol solvent, nor its oxidized products, initially glycolaldehyde one expects, then possibly higher oxidation to glycolic acid—depending in no small part on the (unspecified) amount of H2O present in the system as required for the oxidation of glycoaldehyde to glycolic acid.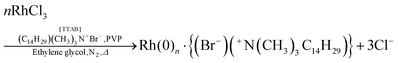 | (2) |
To begin, the authors directly monitored the EXAFS intensity as a function of time, Fig. 4.
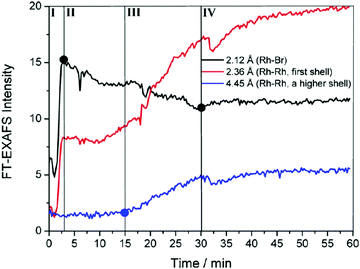 | ||
| Fig. 4 FT-EXAFS peak intensities as a function of time are shown for Rh–Br (black), Rh–Rh first coordination shell (red), and Rh–Rh higher-order coordination shells (blue). Overlain are four detectable stages for the formation of Rh nanocrystals for the RhCl3–TTAB–PVP–EG system labeled by the authors as: ligand exchange (stage I), Rh2–4 nuclei formation (stage II), nanocrystal growth (stage III), and transformation to high-quality nanocubes (stage IV). Figure reproduced with permission from ref. 40. Copyright 2012 American Chemical Society. | ||
The authors observed three points where the EXAFS data changed and thereby identified four “Stages” in the reaction. During the first stage (Stage I), they observed a sharp increase in Rh–Br bonds. The second stage (Stage II) was highlighted by a decrease in Rh–Br bonds, an increase in first shell Rh–Rh bonds, but no change in higher shell Rh–Rh interactions. In the third stage (Stage III), they saw a continued decrease in Rh–Br bonds, a sharp increase in first shell Rh–Rh bonds, and a steady increase in higher shell Rh–Rh interactions. The final stage (Stage IV) was characterized by a leveling off for all species. The EXAFS intensity versus time data is consistent with four kinetic stages of the Rh particle formation process. Whether or not it requires three, four (or more) kinetic steps is not clear from just the raw data.
Next, the authors observed the Rh XANES K-edge as it evolved over time (Fig. 5a–c) and separated it for the first three stages observed in Fig. 4. In Fig. 5a, they observed the signal of the reaction solution changes from being consistent with the RhCl3 reference to being consistent with the RhBr3 reference. The change suggests that in Stage I the Rh precursor undergoes a ligand exchange—note that determining if the balanced reaction stoichiometry involves ligands, as it seemingly must, would be useful here. In Fig. 5b, the signal begins to show features consistent with the Rh foil reference, and in Fig. 5c, significant changes are observed to suggest the formation of Rh nanoparticles.
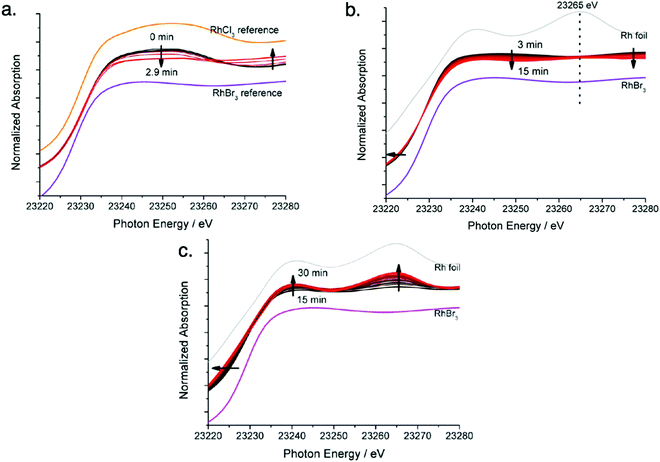 | ||
| Fig. 5 Rh K-edge XANES evolution for the RhCl3–TTAB–PVP–EG system. (a) Stage I: chloro ligands substituted by bromo ligands, time 0 min to 3 min, with RhCl3 and RhBr3 reference spectra given. (b) Stage II: formation of Rh2–4 nuclei, time 3 min to 15 min, with RhBr3 and Rh foil reference spectra given. (c) Stage III: growth of nuclei to nanoparticles of size 5.2 ± 0.8, time 15 min to 30 min, with RhBr3 and Rh foil reference spectra given. Arrows present in (a)–(c) indicate the direction of spectra change with time. Figure adapted with permission from ref. 40. Copyright 2012 American Chemical Society. | ||
The EXAFS and XANES data, from Fig. 4 and 5 respectively, are interpreted by the authors as suggesting a four-stage process for formation of their Rh nanoparticles. To investigate their hypothesis, the authors sought to fit their kinetics data, the loss of [Rh3+] as a function of time (Fig. 6). They used a known literature minimum mechanism, the 2-step mechanism of slow, continuous nucleation followed by autocatalytic surface growth,54 to fit their kinetics data (green triangles in Fig. 6).
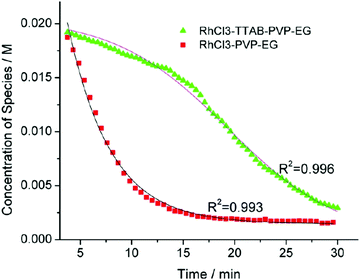 | ||
| Fig. 6 Loss of [Rh3+] as a function of time is plotted for RhCl3–PVP–EG with the bromide TTAB (green triangles) and without the bromide source TTAB (red squares). The system without TTAB (red) was fit using a pseudo-first-order rate law. The system with TTAB (green) was fit using the 2-step mechanism of slow continuous nucleation followed by autocatalytic surface growth (A → B with rate constant k1 and A + B → 2B, rate constant k2, where A = Rh3+ and B = Rh0). The fit yielded the following results: k1 = 0.005 min−1 and k2 = 8.77 min−1 M−1. Figure reproduced with permission from ref. 40. Copyright 2012 American Chemical Society. | ||
The authors demonstrated in Fig. 6 that bromide is critical kinetically to their reaction. The reaction without TTAB (red squares) was fit with an empirical power law79—and could not be fit (not shown) with a 2-step model.54 However, the reaction with TTAB (green triangles) was fit at least roughly by the 2-step mechanistic model of continuous nucleation, A → B with rate constant k1, and autocatalytic growth, A + B → 2B with rate constant k2, where A = Rh3+ and B = Rh(0).54 The data in Fig. 4–6, combined with mass spectrometry data in Fig. S1–S3 (ESI†), led the authors to proposal the pictorial four-stage model for Rh nanocrystal formation shown in Fig. 7.
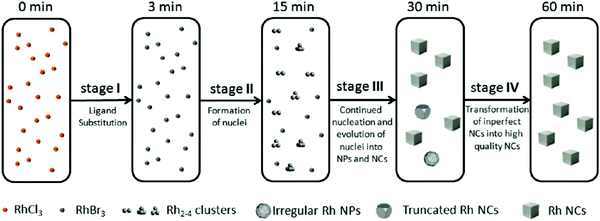 | ||
| Fig. 7 Schematic representation of the proposed four-stage formation process of Rh nanocrystals from RhCl3 deduced from XAFS and MALDI-TOF experiments. Stage I is ligand substitution from chloro to bromo ligands. Stage II is the formation of Rh2–4 nuclei. Stage III is proposed to be continued nucleation and growth of nuclei into nanoparticles and cubic nanocrystals. Finally, Stage IV is a final growth stage where imperfect nanoparticles and nanocrystals transform into more crystalline nanocrystals. The authors note, “the Rh species shown in the five boxes represent the predominant but not the exclusive Rh species present, and the chemical transformations illustrated under each arrow represent the major characteristic, but not necessarily the only process involved during each stage.”40 Figure reproduced with permission from ref. 40. Copyright 2012 American Chemical Society. | ||
Overall, the authors demonstrated the power of directly monitoring the loss of Rh3+ and the formation of Rh0 with DXAFS while also employing ex situ MS and TEM. Their 4-stage pictorial model—while not a chemical mechanism—does satisfy two of the criteria and partially satisfies the other two criteria underlying reliable mechanistic studies. For criterion (i), the authors monitored the transformation of Rh species throughout the reaction from Rh3+–Cl to Rh3+–Br and finally Rh0. They identified, through MS, low molecularity nucleation, where the kinetically effective nucleation (KEN)30 was observed to be Rh2–4—an important result in its own right.
However, the complete, balanced reaction stoichiometry was not reported and would at a minimum suggest the species that could be important in the rate law for particle formation. The true nature of the final product remains unspecified, nominally something like “RhnBra(PVP)b(glycolic acid)c(ethylene glycol)d”, where the unknown coefficients c and d might be small enough to be negligible. Additionally, the Stage I ligand substitution reaction merits additional study—as does the simplification of the system by starting with preformed RhBr3. The fully study of the exchange reaction and the proposed equilibrium constants are of interest as are controls of the effects of added H2O on this reaction, almost surely important as glycolaldehyde is expected to be a kinetically more facile oxidant than ethylene glycol when the H2O needed for the reaction converting glycolaldehyde plus H2O to glycolic acid (and 2e−/2H+) is present—additional reasons why getting the balanced reaction stoichiometry is needed as well as key for this system.
As for the second criterion (ii) of a reliable mechanistic study, the authors collected excellent, direct kinetics data (Fig. 4 and 5). The Rh species were monitored by in situ XANES and EXAFS throughout the entire reaction. (iii) The third criterion of pseudoelementary steps to describe the physical processes has been partially satisfied. Unfortunately, the authors then appear to skip the 2-step mechanism used in Fig. 6 to fit their kinetics data and jump to the proposed a 4-stage representation in Fig. 7 that is ultimately just a pictorial restatement of their hypothesis of a 4-stage process. Helping the community move beyond just such pictorial, qualitative representation of their otherwise powerful synchrotron-radiation-based studies is a primary goal of this review.
Finally, criterion (iv) has been accounted for as the authors disproved alternative hypotheses throughout their investigation. One example was the reaction without TTAB (red squares) in Fig. 6, where the control experiment produced different kinetics and further supported Stage I of the proposed 4-stage model. Additionally, the authors fit their kinetics data (in their ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) with an additional literature mechanism, a 4-step model80 of continuous nucleation, autocatalytic surface growth, bimolecular agglomeration, and autocatalytic agglomerative growth. They found that agglomerative growth is not a significant contributor to the growth of their nanocubes, evidence supportive of their proposed growth pathway (Stage III) and shape correction (Stage IV). Presumably, the 2-step mechanism used to fit their data corresponds to Stages II and III, but without writing out the precise pseudoelementary steps, one does not know what steps are being fit in Fig. 6.
40) with an additional literature mechanism, a 4-step model80 of continuous nucleation, autocatalytic surface growth, bimolecular agglomeration, and autocatalytic agglomerative growth. They found that agglomerative growth is not a significant contributor to the growth of their nanocubes, evidence supportive of their proposed growth pathway (Stage III) and shape correction (Stage IV). Presumably, the 2-step mechanism used to fit their data corresponds to Stages II and III, but without writing out the precise pseudoelementary steps, one does not know what steps are being fit in Fig. 6.
Noteworthy is that the authors are careful and do not claim that they know the mechanism. Rather, they have offered their evidence and conclusions while working towards a disproof-based mechanism, achieving a quite plausible model consistent with and supported by their data. Their study is a good example of acquiring high-quality, direct kinetics data from XAFS and corroborating it with other physical techniques.
Welcome on this valuable system would be additional XAFS as well as SAXS studies (i) starting with RhBr3 to avoid the ligand exchange, (ii) establishing the composition of the “RhnBra(PVP)b(glycolic acid)c(ethylene glycol)d” products, and (iii) establishing the balanced reaction including any role of water and the expected role of glycol as the reductant and the oxidized, glycolaldehyde/glycolic products. Writing plausible balanced reactions teaches that H+ are almost surely produced in the particle-formation process so that the effects of added, non-coordinating bases such as Proton Sponge™ may well significantly accelerate the reaction—and likely lead to better stabilized particles. Then (iv) measuring the full rate law for the nucleation and growth processes ([RhBr3], [Br−], [glycol], [Base], [PVP], Proton Sponge™ and any other dependencies will be needed, along critically with (v) expressing the results in pseudoelementary step mechanisms that can be subjected to further disproof until, ideally, a single proposed mechanism remains, are also needed. The results of those studies promises to be a reliable mechanism for Rh(0)n and by extension to other particle formations starting with the common precursor of the metal-halide and using alcohol as a common reductant in the presence of water.
3.3. Case study #3: a second-generation Ir(0)n system studied by XAFS, SAXS and four other methods, including mechanism-enabled population balance modeling
In 2019 and 2021, extensive work on a second-generation {[(1,5-COD)IrI·HPO4]2}2− precursor to Ir(0)n·(HPO42−)x nanoparticle system32,41 was reported, research that follows a series of papers since 1997 on a first-generation {(1,5-COD)IrI·POM}8− (POM = P2W15Nb3O629−, polyoxometalate) precursor to Ir(0)n·(POM9−)m nanoparticle system.31,54,80–82 Iridium nanoparticles in the 2nd-generation system were prepared by combining [(1,5-COD)IrI(solv)2]+ with 2–6 molar equivalents of (Bu4N)2HPO4 in acetone. The exact composition of the iridium precursor and its solution dimeric resting state, {[(1,5-COD)IrI·HPO4]2}2−, were established by using UV-vis, 1H NMR, ESI-MS, and a Signer solution molecular weight apparatus.32,83The experimentally determined, balanced reaction stoichiometry of the HPO42−-stabilized Ir(0)∼150 nanoparticles has been published,32 is given in eqn (3) in its more general form, and makes apparent that the HPO42− nanoparticle-stabilizing ligand is one key in the reaction that, therefore, needs investigation in the kinetics studies:
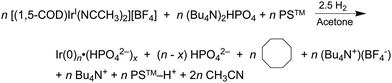 | (3) |
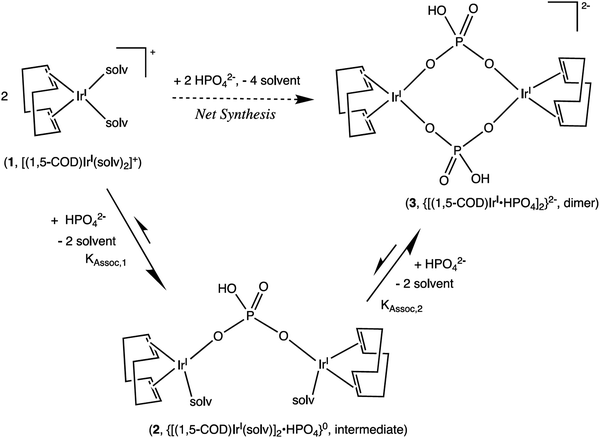 | ||
Scheme 2 Formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 HPO42−/IrI(1,5-COD)+ Intermediate, 2, and Then the final 1 2 HPO42−/IrI(1,5-COD)+ Intermediate, 2, and Then the final 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 diphosphate-bridged complex, 3, supported by the 1H NMR titration studies. Reproduced with permission from ref. 32. Copyright 2019 American Chemical Society. 1 diphosphate-bridged complex, 3, supported by the 1H NMR titration studies. Reproduced with permission from ref. 32. Copyright 2019 American Chemical Society. | ||
A convenient, albeit indirect, cyclohexene hydrogenation catalytic reporter reaction (CHCRR)54 was developed54 and used for in-house monitoring of the Ir(0)n particle formation. Another advantage of that method besides its convenience is that it generates thousands of precise, ±0.01 psig kinetics data points. (For a more extensive understanding of the CHCRR and its accompanying assumptions, please refer to ref. 32, 41, and Appendix A of ref. 54 that provides the original derivation for the use of the CHCRR.) In addition, in-house GLC of the cyclooctane product, 1H NMR, and UV-vis were used to monitor the reaction and check on the in-house CHCRR kinetics—the CHCRR proving to be the most indirect, but the quickest and overall quite useful, monitoring method to scout out optimized conditions for subsequent more direct methods of XAFS and SAXS monitoring of the particle formation reaction, vide infra.
The reproducible sigmoidal kinetics curves obtained prior to the XAFS and SAXS studies were fit by the literature 1997 2-step mechanism54 of slow, continuous nucleation (A → B, k1obs) and autocatalytic surface growth (A + B → 2B, k2obs). Reactions were run around a range of [Ir2]Initial from 1.5 mM to 6.0 mM and at five different amounts of HPO42− stabilizer, [HPO42−]Added. A total of 20 different combinations of [Ir2]Initial and [HPO42−]Added were studied and run in triplicate or more—multiple experiments any time they are desired being a significant advantage of in-house methods such as the CHCRR prior to more direct XAFS and SAXS studies. Additionally, the dependence of the nucleation rate constant, k1obs, on both the starting [Ir2]Initial and, importantly, on the amount of [HPO42−]Added (as suggested by the balanced reaction stoichiometry) were examined experimentally. The resultant data are reproduced below in Fig. 8a and b.32
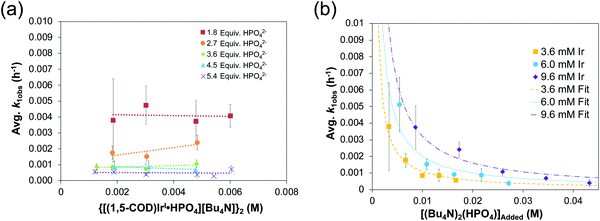 | ||
Fig. 8 (a) Plot of k1obs (h−1) vs. the initial {[(1,5-COD)IrI·HPO4][Bu4N]}2 precursor concentration (M). Nucleation rate constants (k1obs) were collected from 0.0015–0.006 M at five ratios of [(Bu4N)2HPO4]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Ir] (red squares = 1.8 [Ir] (red squares = 1.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, orange circles = 2.7 1, orange circles = 2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, green diamonds = 3.6 1, green diamonds = 3.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, blue triangles = 4.5 1, blue triangles = 4.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and purples X's = 5.4 1, and purples X's = 5.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). “The important result is the slope = 0 in each case within experimental error, indicating that there is no further dependence (i.e., beyond the observed, first-order dependence) of k1obs on the starting concentration of {[(1,5-COD)IrI·HPO4][Bu4N]}2.”32 (b) Plot of k1obs (h−1) vs. the added (Bu4N)2HPO4 beyond a 1 1). “The important result is the slope = 0 in each case within experimental error, indicating that there is no further dependence (i.e., beyond the observed, first-order dependence) of k1obs on the starting concentration of {[(1,5-COD)IrI·HPO4][Bu4N]}2.”32 (b) Plot of k1obs (h−1) vs. the added (Bu4N)2HPO4 beyond a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of [HPO42−] 1 ratio of [HPO42−]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Ir]. The starting iridium concentrations were 3.6 mM (yellow squares), 6.0 mM (blue circles), and 9.6 mM (purple diamonds). Data were fit based on a derivation for KDiss (see Scheme 3 below) that is given in ref. 32. Reproduced with permission from ref. 32. Copyright 2019 American Chemical Society. [Ir]. The starting iridium concentrations were 3.6 mM (yellow squares), 6.0 mM (blue circles), and 9.6 mM (purple diamonds). Data were fit based on a derivation for KDiss (see Scheme 3 below) that is given in ref. 32. Reproduced with permission from ref. 32. Copyright 2019 American Chemical Society. | ||
Fig. 8a demonstrates that, for this 2nd-generation iridium nanoparticle formation, nucleation is first-order in the well-characterized, dimeric precursor {[(1,5-COD)IrI·HPO4]2}2−, consistent with a small kinetically effective nucleus (KEN)30 of just two iridium atoms, Ir(0)2. Furthermore, the k1obs nucleation rate constants versus the added [(Bu4N)2(HPO4)] data led to the proposed nucleation mechanism32,41 given in Scheme 3 as the only mechanism of five nucleation mechanisms considered able to fit the data in Fig. 8b. The kinetics analysis also reveal that {[(1,5-COD)IrI·HPO4]2}2− is not the active species that nucleates to Ir(0)2, but instead suggests {[(COD)IrI(solv)]2·HPO4}0 as one top candidates for a kinetically competent intermediate involved in nucleation (eqn (5)) (and possibly also (1,5-COD)IrI(solvent)2+ based on prior precedent31 and studies in progress).Noteworthy here is that multiple attempts over many years to obtain XAFS and SAXS kinetics data for the first-generation {(1,5-COD)IrI·POM}8− system failed due to the large, W-containing POM9− stabilizer, the large ca. 1.5 nm by 1.2 nm “cigar-shaped” POM9− size obscuring SAXS monitoring of early time nucleation events and the W in the POM9− (= P2W15Nb3O629−) interfering with the Ir-XANES. Hence, the {[(1,5-COD)IrI·HPO4]2}2− second generation system was developed specifically with XAFS and SAXS monitoring in mind and in order to check on the convenient, precise-data-generating, but indirect, CHCRR kinetics method.
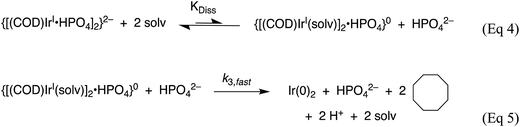 | ||
| Scheme 3 Proposed nucleation mechanism32 involving the dissociative equilibrium from {[(1,5-COD)IrI·HPO4][Bu4N]2} in acetone, based on the [HPO42−] dependence of the kinetics and 1H NMR evidence for the neutral, {[(COD)IrI(solv)]2·HPO4}0 Intermediate. Adapted and Reproduced with Permission from ref. 41. Copyright 2021 American Chemical Society. | ||
Synchrotron XAFS and SAXS experiments were conducted on the second-generation {[(1,5-COD)IrI·HPO4]2}2− precursor to Ir(0)n·(HPO42−)x nanoparticle formation system at initial Ir concentrations from 3.0 mM to 12.0 mM and at five Ir![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HPO42− stabilizer ratios of from 1
HPO42− stabilizer ratios of from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.8 to 1
1.8 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.4.41 The Ir(0)n nanoparticle formation reactions were run under the standard conditions of ∼40 psig H2 at 22 °C and with 1 molar equivalent of Proton Sponge base per Ir present to absorb the H+ produced in the balanced reaction, eqn (3)—the Proton Sponge also prevents hydrogenation of the acetone solvent to 2-propanol by the highly catalytically active Ir(0)n nanoparticles,84 experimental design that takes advantage of the deep knowledge of the two Ir(0)n nanoparticle formation systems.30–32,54,67,68,80–82,84
5.4.41 The Ir(0)n nanoparticle formation reactions were run under the standard conditions of ∼40 psig H2 at 22 °C and with 1 molar equivalent of Proton Sponge base per Ir present to absorb the H+ produced in the balanced reaction, eqn (3)—the Proton Sponge also prevents hydrogenation of the acetone solvent to 2-propanol by the highly catalytically active Ir(0)n nanoparticles,84 experimental design that takes advantage of the deep knowledge of the two Ir(0)n nanoparticle formation systems.30–32,54,67,68,80–82,84
Optimized conditions for the XANES ([Ir] = 0.005 M, 2.25 molar equiv. HPO42−) and SAXS ([Ir] = 0.009 M, 3.6 molar equiv. HPO42−) were worked out first with the in-house CHCRR. Those optimized conditions were then employed at the synchrotron along with Tandem CHCRR kinetics data collected simultaneously with (separate) XANES and SAXS studies done at different synchrotrons via separate collaborators.41 Also collected was additional in-house CHCRR data (i.e., under the XANES and SAXS conditions41) as was gas–liquid chromatography quantification of the cyclooctane (COA) product formation vs. time, again under the XANES and SAXS conditions. The composite data in terms of molar concentration of iridium (M) as a function of time (h) are given below in Fig. 9.
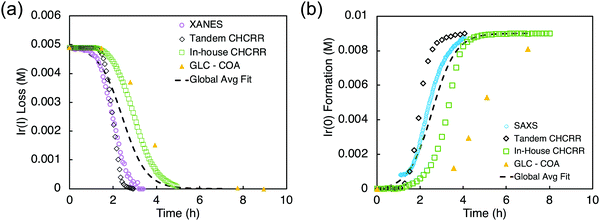 | ||
| Fig. 9 (a) XANES data (hollow purple circles), tandem CHCRR data collected at the synchrotron (hollow black diamonds), in-house CHCRR data collected under otherwise identical conditions (open green squares), and GLC of the cyclooctane product (solid yellow triangles) were fit with the 2-step mechanism54 to yield a global average fit (dashed black line). Resultant rate constants are k1obs(avg,XANES) = (2.2 ± 0.3) × 10−2 h−1 and k2obs(avg,XANES) = (3.7 ± 0.1) × 102 h−1 M−1. (b) SAXS data (hollow blue circles), tandem CHCRR data collected at the synchrotron (hollow black diamonds), in-house CHCRR data collected under otherwise identical conditions (open green squares), and GLC of the cyclooctane produced (solid yellow triangles) were fit with the 2-step mechanism54 to yield a global average fit (dashed black line). Resultant rate constants are k1obs(avg,SAXS) = (1.7 ± 0.2) × 10−2 h−1 and k2obs(avg,SAXS) = (2.0 ± 0.1) × 102 h−1 M−1. Reproduced with permission from ref. 41. Copyright 2021 American Chemical Society. | ||
The k1obs nucleation rate constants for the XANES, in-house CHCRR, and GLCcyclooctane datasets are equivalent within 1.6-fold. The Tandem CHCRR dataset to the XANES was determined to be an outlier statistically (>5σ) and experimentally (due, apparently, to small amounts of Ir(0) from X-ray radiolysis catalyzing and accelerating the CHCRR).41 The k1obs nucleation rate constants for the SAXS, Tandem CHCRR, in-house CHCRR, and GLCcyclooctane datasets all proved to be within a similar factor of 2. The Tandem CHCRR run simultaneously to the SAXS undercuts the synchrotron data some, but there was evidence of Ir(0) metal fouling found on the SAXS cell window,41 presumably due to actually well-precedented—but little discussed and certainly under recognized—X-ray radiolysis during such synchrotron studies.85–93
There is compelling precedent in the well-studied Ir(0)n nanoparticle system that even trace amounts of adventitious Ir(0) hugely increase the nucleation and subsequent growth rates, sometimes resulting in complete elimination of the induction period of the typically sigmoidal kinetics curve.54,82 A fundamental contribution from as well as these particular synchrotron XANES and SAXS studies is, then, to raise a red flag concerning the involvement in X-ray-based methods that are more often than not assumed to be completely direct without artifacts. Relevant here is that Frenkel and collaborators have shown85 that a photon flux of ∼3 × 1013 photons per second results in an estimated ∼1016 solvated electrons94 even when that radiolysis involves the otherwise improbable, highly energetic removal of an electron from divalent zinc, Zn2+ + hν → Zn3+ + e−. Highly relevant here is that in particle formation systems exhibiting autocatalytic, exponential growth as is commonly seen, any trace nucleation events due to X-ray radiation-induced radiolysis will then be quickly magnified, autocatalytically and, hence, exponentially.
The data from all the monitoring methods (XANES, SAXS, CHCRR, and GLC) were standardized, compiled, and analyzed as a single dataset containing 1178 total data points. These data and the global fit using the 2-step mechanism are reproduced as Fig. 10. The resultant, globally average, fit-determined rate constants yielded the relatively precise rate constants k1obs,global![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) avg = (1.5 ± 0.1) × 10−2 and k2obs,global
avg = (1.5 ± 0.1) × 10−2 and k2obs,global![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) avg = (2.4 ± 0.1) × 102 (±7% and ±4% error, respectively) that are believed to be reasonably accurate41k1obs and k2obs rate constants as well.
avg = (2.4 ± 0.1) × 102 (±7% and ±4% error, respectively) that are believed to be reasonably accurate41k1obs and k2obs rate constants as well.
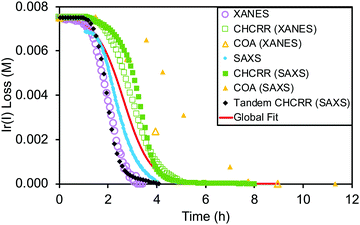 | ||
Fig. 10 “The seven datasets are given: XANES as hollow purple circles, in-house CHCRR (under XANES conditions) as hollow green squares, COA (under XANES conditions) as hollow yellow triangles, SAXS as solid blue circles, in-house CHCRR (under SAXS conditions) as solid green squares, COA (under SAXS conditions) as solid yellow triangles, and Tandem CHCRR (simultaneous with SAXS measurements) as solid black diamonds. The solid red line represents the global fit to all seven datasets.”41 The resultant, globally average, fit-determined rate constants with fitting error are k1obs,global![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) avg = (1.5 ± 0.1) × 10−2 and k2obs,global avg = (1.5 ± 0.1) × 10−2 and k2obs,global![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) avg = (2.4 ± 0.1) × 102. All datasets, as mentioned in ref. 41, were standardized to 7.5 mM in IrI. Reproduced with permission from ref. 41. Copyright 2021 American Chemical Society. avg = (2.4 ± 0.1) × 102. All datasets, as mentioned in ref. 41, were standardized to 7.5 mM in IrI. Reproduced with permission from ref. 41. Copyright 2021 American Chemical Society. | ||
Overall, the XANES, SAXS, in-house CHCRR, and GLC methods all reported equivalent rate constants within either 1.6 or 2.0 orders of magnitude for XANES and SAXS, respectively, a rare comparison of multiple in-house as well as synchrotron XANES plus SAXS particle formation monitoring methods. The composite kinetics data from all available experimental methods (XANES, SAXS, CHCRR, GLC, and 1H NMR), were fit by the 2-step mechanism of slow, continuous nucleation (A → B, k1obs) and autocatalytic surface growth (A + B → 2B, k2obs). Therefore, all experimental methods, including the synchrotron XANES and SAXS, presently support the 2-step mechanism as the minimum mechanism to describe quantitatively Ir(0)n formation.
What is interesting from the well-studied Ir(0)n nanoparticle systems is that, in both the first and second-generation systems now, even with the addition of synchrotron XANES and SAXS and XAFS, the sum of all of the kinetics methods are insufficient to determine the true particle formation mechanism as demonstrated by ME-PBM analysis, discussed next. In addition, even with all the effort that went into this32,41 Ir(0)n system, the exact role of the HPO42− ligand has been elucidated on only the nucleation step, so only partially—so that full incorporation of specific ligand effects into the pseudoelementary step mechanism is of interest and remains to be accomplished. Ligand effects of the POM9− polyoxometalate on the nucleation31 and growth95 steps of the first generation {(1,5-COD)IrI·POM}8− precursor to Ir(0)n·(POM9−)m nanoparticle system are available, however, to help guide the needed studies.
ME-PBM is also able to inform the inverse problem of going from “observations/effects” back to “cause/a mechanism” whereby one tests and thereby refutes—or supports—that minimum mechanism via ME-PBM analysis of the PSD data.67,68 As alluded to above, in both the first67,68 and now second generation Ir(0)n nanoparticle systems, the ME-PBM analysis of the wealth of kinetics data otherwise buried in the PSD has led to disproof of the minimum mechanisms that were previously able to account for all of the experimental data (i.e., other than the PSD). Significantly, ME-PBM analysis of the PSD in the first generation Ir(0)n system also provided a new paradigm for how narrow PSDs can be formed:67,68 smaller particles grow faster than larger particles, thereby catching up in size to them and resulting in near-monodisperse PSDs despite the inherently broadening effects of continuous nucleation.67,68
Hence, initial ME-PBM analysis of the TEM-determined PSDs in the second-generation Ir(0)n nanoparticle formation system was reported in the 2021 paper that reports the XANES and SAXS studies.41 Specifically, ME-PBM was used to analyze the end-time PSD at 10.0 h (shown as the black distribution in Fig. 11), using to start the 2-step mechanism while also including the experimentally determined prior equilibrium nucleation mechanism (given back as eqn (4) and (5)).
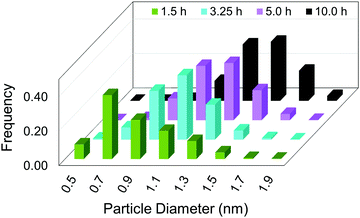 | ||
| Fig. 11 “Particle size distributions for the formation of Ir(0)n nanoparticles at 1.5 h (green), 3.25 h (teal), 5.0 h (purple), and 10.0 h (black) binned in 0.2 nm width bins. At each time point, a new reaction solution was prepared of 5.0 mM [(1,5-COD)IrI(NCCH3)2][BF4] in the presence of 2.25 molar equiv. of (Bu4N)2HPO4 in 3.33 mL acetone and 0.67 mL cyclohexene at 22.0 ± 0.1 °C. Each data point represents >450 measured particles; across the 4 samples >2700 particles were measured.”41 Reproduced with permission from ref. 41. Copyright 2021 American Chemical Society. | ||
The attempted fit using the 2-step mechanism consistent with the XANES, SAXS and all the other data to this point, along with the simulated [A]t loss curve from the resulting rate constants of that attempted fit, are reproduced as Fig. 12a and b, respectively. The fit is obvious poor—no fit at all, really—disproving the 2-step mechanism that was otherwise consistent with all of the XAFS, SAXS, and other kinetics data.41
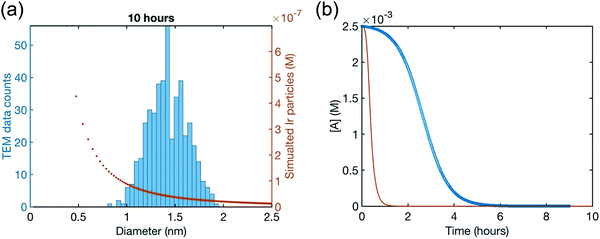 | ||
| Fig. 12 (a) Attempted fit to the end-time, 10.0 h histogram using ME-PBM built off of the 2-step mechanism with experimentally determined nucleation mechanism. The resultant fit-determined rate constants are as follows: k+Diss = 4.0 × 10−1 h−1 M−2, k−Diss = 3.7 × 104 h−1 M−1, k1 = 6.6 × 10−1 h−1, k2 = 9.2 × 103 h−1 M−1, unreliable rate constants given the poor fit. The Best Function Value (BFV)67,68 is 90.0, indicating a poor fit (as lower BFVs indicate67,68 better agreement between the experimental data and the attempted fit). However, the rate constants are provided here because they are used to generate the predicted precursor loss curve discussed next. (b) Calculated precursor loss, [A]t, using the “best-fit” rate constants parameters from the above attempted fit to the PSD, are co-plotted with the experimental global [A]t data from the simulated global fit of data from all the available methods. Reproduced with permission from ref. 41. Copyright 2021 American Chemical Society. | ||
Given the poor fit in Fig. 12a, the authors considered—that is, attempted to disprove—15 total minimal mechanisms, even if those are but a fraction of the 96 possible mechanisms summarized via Table S5 (ESI†) of the present review. The minimal mechanism the authors report as a current best-fit of the PSD is the 4-step mechanism given in Scheme 4 that contains slow, continuous nucleation (Asolv → B, k1obs), small particle growth (A + B → C, k2obs), bimolecular small particle agglomeration (B + B → C, k3obs), and large particle growth (A + C → 1.5C, k4obs), where A = {[(1,5-COD)IrI·HPO4]2}2−, Asolv = {[(COD)IrI(solv)]2·HPO4}0, B = small Ir(0)m, and C = large Ir(0)n.
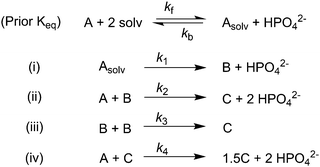 | ||
| Scheme 4 Experimentally determined prior equilibrium and the proposed 4-step mechanism of (i) slow, continuous nucleation, (ii) small particle growth, (iii) bimolecular small particle agglomeration, and (iv) large particle growth. Reproduced with permission from ref. 41. Copyright 2021 American Chemical Society. | ||
Although the authors demonstrate that the 4-step mechanism given in Scheme 4 can fit the PSD reasonably well, Fig. 13a, the authors note that the fit to the experimental [A]t loss curve in Fig. 12b “is poor” when compared to the simulated [A]t loss curve (i.e., the expected [A]t loss curve simulated using the rate constant parameters extracted from the PDS). This example illustrates both the mechanistic power, as well as the amount of work needed, when using ME-PBM as a now apparently “Gold-Standard Test” of ones proposed particle formation mechanism.41,67,68 As the authors note, they “still have more work to do to uncover the more detailed, even closer to correct particle formation mechanism.”41 Preliminary studies point towards the possibility that Ir(1,5-COD)(solv)2+ may function as a precedented,31 kinetically competent intermediate in the true nucleation mechanism and its associated elementary steps.
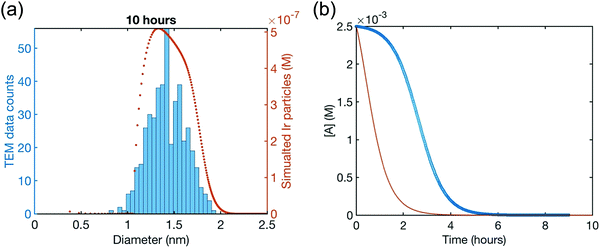 | ||
| Fig. 13 (a) Fit to the end-time, 10.0 h histogram using ME-PBM built off of the new 4-step mechanism with experimentally determined nucleation mechanism. The resultant fit-determined rate constants are as follows: k+Diss = 2.6 × 10−1 h−1 M−2, k−Diss = 2.2 × 104 h−1 M−1, k1 = 2.2 h−1, k2 = 5.4 × 104 h−1 M−1, k3 = 1.6 × 106 h−1 M−1, k4 = 1.0 × 103 h−1 M−1, and the B versus C cutoff value M = 23. The Best Function Value (BFV)67,68 is 25.4, indicating an improved fit over the 2-step shown in Fig. 12—as, again, a lower BFV indicate67,68 better agreement between the experimental data and the attempted fit. (b) Calculated precursor loss, [A]t, using the “best-fit” rate constants parameters from the above attempted fit to the PSD, are co-plotted with the experimental global [A]t data from the simulated global fit of data from all the available methods. Reproduced with permission from ref. 41. Copyright 2021 American Chemical Society. | ||
Evaluating the second-generation {[(1,5-COD)IrI·HPO4]2}2− precursor to Ir(0)n·(HPO42−)x nanoparticle system32,41 for how well it stacks up to the four criteria for establishing a minimum mechanism, the study provides: (i) an experimentally determined, balanced reaction stoichiometry that predicted the subsequently observed importance of the HPO42− nanoparticle-stabilizing ligand in the particle-formation kinetics; (ii) extensive kinetics data by 4 methods including XANES and SAXS; (iii) (pseudo)-elementary reaction steps for the proposed mechanism that add up to the experimental stoichiometry, define the rate constants, and provide defined, unambiguous words for describing the mechanism. Additionally, the authors provide (iv) disproof of 14 alternative (out of 15 total), possible hypothesized mechanisms.
Somewhat hidden behind the success of the Ir(0)n systems is the amount of synthesis and characterization of the first generation {(1,5-COD)IrI·POM}8− precursor81,82 and then the second-generation {[(1,5-COD)IrI·HPO4]2}2− precursor32,96,97 characterization of their nanoparticle products by as many applicable methods as possible,81,82,97 and the care in establishing the balanced reaction stoichiometry81,82,97 before beginning serious kinetics and mechanistic studies. Strict adherence to a disproof- and Ockham's razor-based approach, as rigorous mechanism demands, is another key underlying the Ir(0)n kinetics and mechanistic studies—as is a philosophical acceptance of the truism that all deliberately minimum mechanisms will eventually be upgraded (“disproved”) as new methods, experiments, or data analyses (such as ME-PBM) become available. At present, a 1-step upgrade, hence 3-step total, PEStep mechanism is what is really a minimum mechanism for particle formation67,68 and despite the (still recommended67,68) use of just the 2-step mechanism for the initial analysis of kinetics data before moving on to the examination and fitting of PSD data (the 2-step rate constants being, for example, useful starting guesses for 3-step mechanism analyses and fits of PSDs).67,68
Needed additional studies for even this relatively well studied, second-generation Ir(O)n nanoparticle formation system include: (i) resolution of the precise nucleation mechanism with the help of the additional ME-PBM; (ii) a better accounting of the reporter reaction kinetics in Fig. 12b (i.e., by an updated nucleation mechanism or some other, needed update of the mechanism); and (iii) elucidation of how ksurface growth varies with nanoparticle size in more detail−that is, elucidation of the more detailed, “growth kernel”, including the likely role of ligand capping effects in that growth kernel, better than the k2 > k4 step-function kernel66,67 used presently (Scheme 4 and Fig. 13).
3.4. Case study #4: investigation of pre-nucleation clusters en route to gold nanospheres and nanowires by XAFS, SAXS, and HE-XRD
In 2020 Ramamoorthy and co-workers reported their syntheses of gold nanospheres and nanowires by injecting the gold precursor and reductant into a T-micromixer and monitoring the formation by XAFS, SAXS, and HE-XRD.42 All experiments were performed at 20 mM HAuCl4·3H2O and 1 M triisopropylsilane (TIPS) in hexane. Three concentrations of ligand, oleylamine (OY), were used: 50 mM, 100 mM, and 400 mM. The reaction stoichiometry proposed by the authors is given as eqn (6) with R = isopropyl.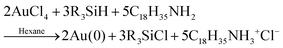 | (6) |
First, the formation of nanospheres from the reactions with 50 mM and 100 mM OY (i.e., and not the nanowires formed under different conditions, vide infra) were investigated by XAFS and SAXS. The XAFS data were interpreted using linear combination analysis (LCA) that allowed for simultaneous determination of precursor concentration (AuIII), intermediate concentration (AuI), and final product concentration (Au0) as a function of time. The XAFS formation data as a function of time and an example of the LCA result are given as Fig. 14a and b, respectively.
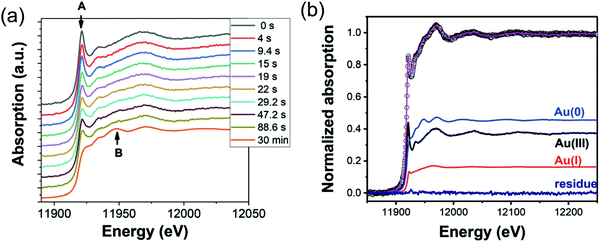 | ||
| Fig. 14 (a) In situ XAS spectra at the Au LIII-edge monitoring the formation of Au nanospheres from the gold precursor solution with [OY] = 50 mM. Spectra are given stepwise from 0–88.6 s and 30 min. The decrease in the intensity of the white line intensity at 11921.2 eV is denoted by “A”, and the increase in the signal corresponding to Au foil at 11948.5 eV is denoted by “B”. (b) The XAFS spectrum collected at 29.2 s, hollow circles, is given as a representative spectrum for linear combination analysis (LCA). The pink line is the LCA fit of the XAFS spectrum, which yields the three components: Au(III) precursor (black line), Au(I) intermediate species (red line), and resultant Au(0) nanospheres (blue line). Reproduced with permission from ref. 42. Copyright 2020 Royal Society of Chemistry. | ||
As CNT did not accurately describe the particle-formation data, a new kinetic model had to be devised in order to fit the data. The authors constructed a multistep kinetic model to account for the induction period, nucleation, and for growth. The proposed nanosphere formation kinetic model is given as Scheme 5 and includes equilibrium expressions between reactive and non-reactive Au(III) and Au(I) species.
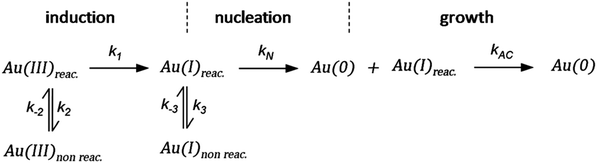 | ||
| Scheme 5 Kinetic model for the formation of Au nanospheres with [OY] = 50 mM. Reproduced with permission from ref. 42. Copyright 2020 Royal Society of Chemistry. | ||
The proposed kinetic model contains two reduction steps: Au(III)reac to Au(I)reac with rate constant k1 and Au(I)reac to Au(0) with rate constant kN. That second step with kN is the first step in the two-step nucleation/growth process. The final, autocatalytic process54 involves Au(0) and Au(I)reac to form additional Au(0) with rate constant kAC. The authors report that “a competition between reduction and complexation of the Au(III) and Au(I) by OY is described by two additional equilibria during the induction stage. The two ‘non-reactive’ complexes are not directly involved in the reduction steps but serve as a reservoir for the ‘reactive complexes’.”42
Using the mass-balance expressions of [Au(III)Total] = [Au(III)R] + [Au(III)NR], [Au(I)Total] = [Au(I)R] + [Au(I)NR], and [Au(0)] = 1 − [Au(III)Total] − [Au(I)Total], the authors input their model into MatLab as a series of ordinary differential equations (ODEs), eqn (7)–(10).
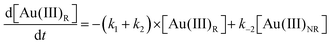 | (7) |
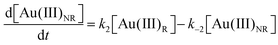 | (8) |
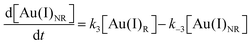 | (9) |
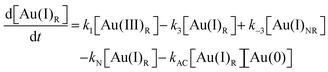 | (10) |
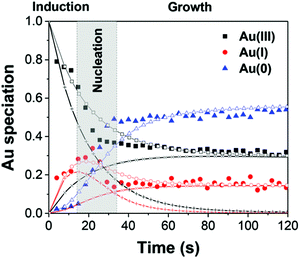 | ||
| Fig. 15 The Au(III), Au(I), and Au(0) concentrations determined by LCA analysis of the XAFS spectra (example given in Fig. 14b) are given here from 0–120 s as filled black squares, filled red circles, and filled blue triangles, respectively. The best-fit lines from each Au species are given using the corresponding connected hollow shape. The black (+) represents the reactive Au(III) species, while the black (×) represent the non-reactive Au(III) species. The red (+) represents the reactive Au(I) species, while the red (×) represent the non-reactive Au(I) species. Reproduced with permission from ref. 42. Copyright 2020 Royal Society of Chemistry. | ||
The data are well-fit from 0–20 s and then again from 45–120 s. For all species of Au, there is a discrepancy between the data and the fit lines between 20–45 s, somewhat surprising given the considerable flexibility of 7 variable rate-constant parameters, an indication that one or more of the assumed steps in the proposed model is incorrect (e.g., the assumed first-order nucleation?) or that needed additional steps are missing.
Next, the formation of nanowires from the reaction with 400 mM OY were also investigated by XAFS and SAXS. The XAFS data were interpreted using LCA to simultaneous determine precursor concentration (AuIII), intermediate concentration (AuI), and final product concentration (Au0) as a function of time. The XAFS formation data as a function of time is given as Fig. 16.
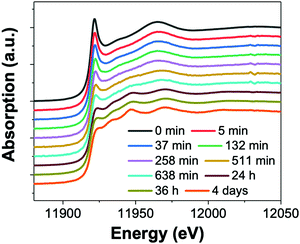 | ||
| Fig. 16 (a) In situ XAS spectra at the Au LIII-edge monitoring the formation of Au nanowires from the gold precursor solution with [OY] = 400 mM. Spectra are given from 0 min – 4 days. Reproduced with permission from ref. 42. Copyright 2020 Royal Society of Chemistry. | ||
Using the kinetics model presented in Scheme 6 and the mass-balance expressions from before, the authors derived ODEs, reproduced below as eqn (11)–(13), and associate 6 rate-constant parameters.
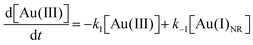 | (11) |
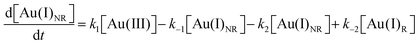 | (12) |
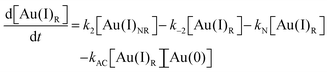 | (13) |
 | ||
| Scheme 6 Kinetics model for the formation of Au nanowires with [OY] = 400 mM. Reproduced with permission from ref. 42. Copyright Royal Society of Chemistry 2020. | ||
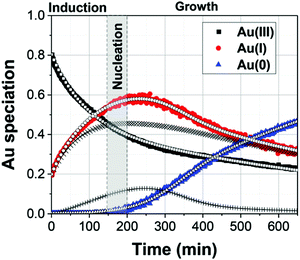 | ||
| Fig. 17 The Au(III), Au(I), and Au(0) concentrations determined by LCA analysis of the XAFS spectra are given here from 0–650 min as filled black squares, filled red circles, and filled blue triangles, respectively. The best-fit lines from each Au species are given using the corresponding hollow shape. The black (+) represents the reactive Au(I) species, while the black (×) represent the non-reactive Au(I) species. Reproduced with permission from ref. 42. Copyright 2020 Royal Society of Chemistry. | ||
Next, and returning to the case with [OY] = 50 mM that formed nanospheres, the in situ SAXS patterns were closely analyzed during the first 38 s when the authors hypothesize pre-nucleation clusters (PNCs) are formed. Prior to nucleation at 38 s, it was observed that the scattering pattern changed. The scattering pattern shifts again following the onset of nucleation during the primarily growth period from 48 s–30 min. These scattering patterns have been reproduced herein as Fig. 18.
 | ||
| Fig. 18 In situ SAXS patterns for the Au precursor system with [OY] = 50 mM from (a) 4–38 s, where it is believed that pre-nucleation clusters are formed and nucleation begins. Next, from (b) 48 s–30 min, primarily growth is believed to occur. Reproduced with permission from ref. 42. Copyright 2020 Royal Society of Chemistry. | ||
These scattering patterns were fit, and the particle diameter versus time plotted. These data are presented in Fig. 19 as diameter in nanometers versus time in seconds, where time is plotted on a log scale.
 | ||
| Fig. 19 Mean particle diameter (nm) is given as a function of log time (s) for the Au precursor system with [OY] = 50 mM, as shown in Fig. 18. In the induction period, the mean diameter was calculated “from the radius of gyration of the Au(III)–Au(I) pre-nucleation clusters”.42 In the growth period, the mean diameter was determined from the Au(0) nanospheres. The shaded region is believed to be the time period when primarily nucleation takes place. Reproduced with permission from ref. 42. Copyright 2020 Royal Society of Chemistry. | ||
Based on the data presented in Fig. 19, the authors believe during the induction period that the SAXS scattering is reporting “the radius of gyration of the Au(III)–Au(I) pre-nucleation clusters”42 and not of Au(0) nanospheres. Then, following what the authors have labeled as the nucleation period, the implication is that the SAXS is reporting the mean radius of the resultant Au(0) nanospheres.42 Hence, it follows that the true nucleation kinetics are obscured by the much larger PNC, so that only growth data are what is primarily observed in the SAXS measurements. The authors did not attempt to fit the SAXS data with their kinetic model.
Overall, Ramamoorthy and co-workers have reported a very valuable study on the formation of Au(0)n in which they directly monitor the formation of Au(0)n nanospheres or nanowires by in situ XAFS, SAXS, and HE-XRD, and also characterize the resultant particles with ex situ TEM.42 Of perhaps special interest is the observation of Pre Nucleation Clusters (PNCs) and even though those PNCs have not yet been shown by the needed kinetics studies to be on (vs. off) the kinetically dominant pathway to the nanoparticle product. In terms of satisfying the four criteria for a reliable mechanistic investigation, for criterion (i) the authors have proposed a balanced reaction stoichiometry that was reproduced herein as eqn (6). The exact composition of the pre-nucleation clusters would be a useful target for future studies. The authors discussed possible compositions of the Au-based PNCs, but the PNCs were not determined beyond aggregates of {(RNH3+)(AuCl4−)(OY)}n, where R = isopropyl.42 However, after nucleation has been initiated and growth has begun, the authors have been able to determine the Au speciation—a non-trivial task—and plot several Au species as a function of time, another non-trivial achievement. Criterion (ii) was also fully satisfied as the kinetics of Au(0)n were collected in situ by both EXAFS and SAXS over the entire reaction as Fig. 14–18 document for both the nanospheres and the nanowires.
Criterion (iii), namely the task of constructing a pseudoelementary step-based mechanism, has been partially satisfied. For the two cases—nanospheres and nanowires—the authors have presented proposed kinetic models reproduced herein as Schemes 5 and 6, respectively. They have used these kinetic models to write differential equations and then fit their kinetics data with those differential equations. In a future study, once the composition of the PNCs have been determined, then one will be able to write the exact pseudoelementary step reactions that sum to the overall net Au(0)n formation mechanism. Missing at present is an experimentally determined rate law for nucleation. As for criterion (iv), one alternative model was examined. The authors demonstrated that CNT was invalid for their Au(0)n formation system, but they did not report the disproof of any other alternative mechanisms en route to their proposed kinetic models. A greater amount of disproof will be required to provide higher confidence in the resultant, proposed mechanism.
In short, the valuable Ramamoorthy and co-workers Au(0)n system is an illustrative case history demonstrating state-of-the-art, in situ use of three separate synchrotron techniques: XAFS, SAXS, and HE-XRD, a study that also identifies PNCs. Additional studies of this interesting system the community would likely welcome include those hinted at above: (i) determination of the composition(s) of the pre-nucleation clusters; (ii) further work on the experimental rate law especially of nucleation and showing whether or not the observed PNCs are on the kinetically dominant nucleation pathway; and (iii) testing of additional reasonable alternative mechanistic models for formation of the gold nanosphere and nanowires. We look forward to seeing those important, likely exciting studies.
4. Semiconductor and metal-oxide case studies and systems
In this section of the review, two state-of-the-art case studies of semiconductor and metal-oxide nanoparticles that utilize synchrotron techniques are summarized. These two case studies have been chosen as illustrative examples of synchrotron-based studies. Each will have several of the required pieces of information necessary to be able to claim a reliable mechanism, although an interesting observation is that each prototype system is missing one or more aspects that, ideally, can and will be added in the future to that system and study.The two case studies are: (Section 4.1) cadmium-selenide nanocrystal formation monitored by XAFS43 and (Section 4.2) zinc-oxide nanoparticle formation monitored by SAXS/WAXS/UV-visible.44 Like before in Section 3, each case study is organized by: (i) a summary of the system and techniques used to study it; (ii) a review of the key kinetics data; (iii) the authors’ proposed formation model or mechanism; and (iv) an analysis of the case's results as compared to the four components required for establishing a minimum, disproof-based mechanism. Following these two main case studies of this section are two additional shorter sections: (Section 4.3) two studies on shape control (tungstite nanoplatelets and copper nanocrystals), and a listing of (Section 4.4) Additional systems of interest (perovskites, quaternary nanocrystals, amorphous nanoparticles, and carbon quantum dots). These latter sections serve to highlight newer systems of interest to the broader nano community even if of those systems are less well investigated at present— our intent being to be supportive and encouraging of those intriguing studies as they strive to achieve the next level of mechanistic analysis.
4.1. Case study #5: early-stage CdSe nanocrystal formation studied by in situ XAFS in a microfluidic cell
In 2011, Maeda and co-workers studied the early-time formation of (CdSe)n nanocrystals using XAFS and microfluidic cell.43 The three reactant solutions (Cd, Se, and ligand) were mixed and measurements were taken a different points along the microfluidic cell that correspond to different time points in the reaction between 0.0 s and 8.1 s.43 The cadmium reactant solution was prepared by heating Cd(CH3COO)2, oleic acid, and octadecene (ODE) at 453 K under Ar. The selenium reactant solution was prepared by dissolving selenium powder in trioctylphosphine (TOP or P(C8H17)3) and diluted by ODE. Ligand, dodecylamine (CH3(CH2)11NH2, DDA), solution was prepared by dissolving DDA in ODE. The solutions were combined, heated to 513 K, and monitored by XAFS. Fig. 20 provides the schematic of the microfluidic cell with its UV-vis and X-ray components. | ||
| Fig. 20 “Schematic principle of the in situ XAFS experimental set-up using a microfluidic cell. Fluorescence yield spectra record at positions (x,y) along a microreactor channel provide time-dependent XAFS spectra. In the present reaction, precursor flows (TOP-Se and Cd stock solution) are mixed before introducing to a heated microchannel.”43 Reproduced with permission from ref. 43. Copyright 2011 International Union of Crystallography. | ||
The proposed reaction stoichiometry, that is, as far as we can determine it from the data provided in ref. 43, is given in eqn (14).
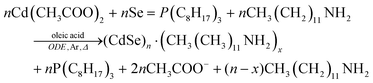 | (14) |
The authors analyzed their XANES, EXAFS, UV-vis and photoluminescence (PL) results to determine the early time (0.0–8.1 s) (CdSe)n formation behavior. The XANES results given in Fig. 21a indicate the author's direct observation of (CdSe)n particle formation. Simultaneously, the authors used UV-vis and PL spectroscopies (Fig. 21b and c) to monitor directly both (CdSe)n particle formation and crystallinity.
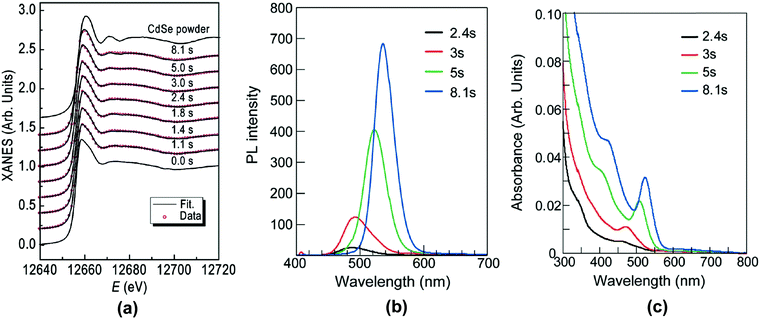 | ||
| Fig. 21 (a) Experimental XANES spectra collected from 0.0–8.1 s after “initiation of the reaction with the addition of 5 wt% DDA,” where again DDA is dodecylamine.43 Reference spectra of (CdSe)n were given for (CdSe)n powder crystals of 3 nm. “Open circles indicate simulated XANES spectra.”43 (b) Photoluminescence spectra of (CdSe)n nanoparticles in the presence of 5 wt% DDA.43 (c) UV-vis absorbance spectra of the (CdSe)n nanoparticles for the same solution as (b). Reproduced with permission from ref. 43. Copyright 2011 International Union of Crystallography. | ||
By XANES, one can see the increase at ca. 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 eV with time that is indicative of (CdSe)n particle formation, by comparison to authentic (CdSe)n powder. (CdSe)n particle formation is further monitored by the UV-vis absorbance at 350 nm, due to the well-studied cross section99, and the full-wide half-maximum of the PL peaks.43 Notably, prior to 2.4 s, there are no absorption or emission peaks present, indicating a lack of crystalline (CdSe)n. A closer observation of the PL spectra shows a red-shift with time, interpreted by the authors as the loss of deep-trap states due to increased crystallinity.43 The PL spectra also indicate that the particle shape is growing more symmetrical, the narrowing and increased symmetry of the peak supporting the interpretation of increased crystallinity.100 Hence, at the earlier times of 2.4 and 3 s, amorphous (CdSe)n nanoparticles are most likely formed, but by 8.1 s they have increased crystallinity.
670 eV with time that is indicative of (CdSe)n particle formation, by comparison to authentic (CdSe)n powder. (CdSe)n particle formation is further monitored by the UV-vis absorbance at 350 nm, due to the well-studied cross section99, and the full-wide half-maximum of the PL peaks.43 Notably, prior to 2.4 s, there are no absorption or emission peaks present, indicating a lack of crystalline (CdSe)n. A closer observation of the PL spectra shows a red-shift with time, interpreted by the authors as the loss of deep-trap states due to increased crystallinity.43 The PL spectra also indicate that the particle shape is growing more symmetrical, the narrowing and increased symmetry of the peak supporting the interpretation of increased crystallinity.100 Hence, at the earlier times of 2.4 and 3 s, amorphous (CdSe)n nanoparticles are most likely formed, but by 8.1 s they have increased crystallinity.
The synchrotron EXAFS and XANES results were compiled in Fig. 22, where the Se–Cd coordination number was independently determined three ways as a function of time. The two data sets collected by EXAFS are the same within error, which is consistent with “a two-component model” (i.e., “unreacted Se–TOP does not dissolve leaving Se2− ions”).43 The authors remark that the XANES results are lower in average Se–Cd coordination number due to the reference used in processing the data.43 Furthermore, the authors considered three possible alternative hypotheses for the difference between the EXAFS and XANES data en route to their final Se–Cd coordination numbers.43 The (CdSe)n study43 presented by Maeda and co-workers demonstrates an important approach to observing particle formation at early times. They have designed a direct, tandem UV-vis and XAFS microfluidic technique and used it to monitor the formation of (CdSe)n during the first 10 s of the reaction.
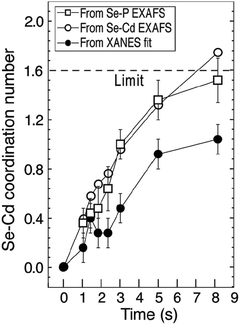 | ||
| Fig. 22 “Se–Cd coordination number as a function of elapsed time determined by EXAFS independently for the Se–P and Se–Cd pairs (open squares and open circles, respectively) compared with the value determined by the XANES fit (closed circles). The dashed line indicates the Se–Cd coordination limit. The reacted amount of Se and Cd during the reaction is assumed to be equal.”43 Reproduced with permission from ref. 43. Copyright 2011 International Union of Crystallography. | ||
In future studies the exact reaction stoichiometry would be desirable, thereby satisfying criterion (i) of a reliable mechanistic study. In that endeavor, the considerable literature in the semiconductor/quantum dot field, and the advances the field has made in the last decade, are likely to prove useful.25,101–104 For example, the authors claim43 that ODE was used because it is a non-coordinating solvent. However, a recent 2019 paper has demonstrated that ODE is not innocuous at temperatures greater than 393 K, where ODE will autopolymerize and coat the nanoparticle in a manner that cannot be removed with standard purification methods.105 Hence, at the temperature of the reaction43 (513 K), ODE polymers at least are likely to be coordinating.
Criterion (ii)—namely collecting kinetics data—was well satisfied by the use of XANES, EXAFS, UV-vis, and PL to address the kinetics of (CdSe)n nanoparticle formation. The use of a microfluidic device was effective in providing early time points. That said, future studies are needed to obtain the full rate law for particle formation. Criterion (iii) will also need to be addressed in future studies, that is, the need to write out the complete pseudoelementary steps to describe the (CdSe)n particle-formation mechanism. Finally, regarding criterion (iv), the authors did apply a disproof-based method to a number of their experiments. Importantly, they were careful to not overinterpreted their data, nor have they claimed to know more about the precise (CdSe)n formation mechanism than their data allows.
Overall, the authors provide a noteworthy initial study43 using in situ XAFS to produce Se–Cd bond formation kinetics data and garner insights into the early time of (CdSe)n nanoparticle formation. Future studies of (a) determination of a full rate law for particle formation, including nucleation, and (b) pseudoelementary step construction consistent with that experimental rate law would be most welcome on this valuable, interesting system building off the reported, valuable initial kinetics studies.
4.2. Case study #6: zinc-oxide nanoparticle formation investigated using in situ stopped-flow microfluidic SAXS/WAXS/UV-vis experiments
A 2019 study by Förster and co-workers monitored the formation kinetics of ZnO nanoparticles using a state-of-the-art in situ tandem SAXS/WAXS/UV-vis stopped-flow microfluidic set-up.44 The ZnO nanoparticles were prepared by mixing solutions of zinc oleate in THF and TBA+OH− (tetrabutylammonium hydroxide, 1 M in methanol) in THF using a Y-shaped Teflon mixer at high flow rates flowing into a quartz capillary. The proposed reaction stoichiometry is given as eqn (15), that is, in-so-far as we can construct the balanced reaction stoichiometry given the data provided in ref. 44.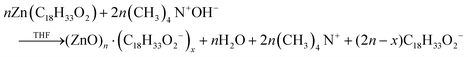 | (15) |
 | (16) |
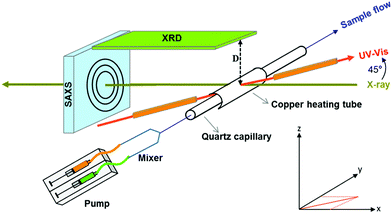 | ||
| Fig. 23 As noted by the authors,44 “Schematic presentation of the in situ setup employed for real-time SAXS/WAXS/UV-vis measurements during the formation of ZnO nanoparticles. The setup measures SAXS, WAXS, and the UV-vis spectra simultaneously in the same sample volume.”44 Reproduced with permission from ref. 44. Copyright 2019 American Chemical Society. | ||
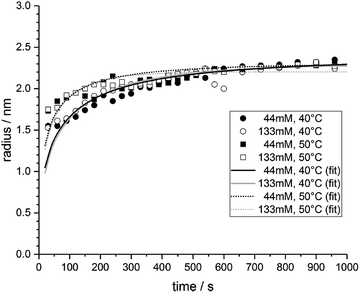 | ||
| Fig. 24 “Time evolution of the average ZnO nanoparticle radii determined from the fitted SAXS curves for two different concentrations and temperature during the first 1000 s of the nucleation and growth reaction. The solid lines are fits to a homogeneous nucleation and growth model.”44 Reproduced with permission from ref. 44. Copyright 2019 American Chemical Society. | ||
Based on the in situ SAXS data reported in Fig. 24 and eqn (16), a series of differential equations, eqn (17)–(21), were derived to describe the ZnO particle formation process, only eqn (17) of which looks like it is somewhat based on a pseudoelementary step, that is, on eqn (16), albeit with a second-order dependence on [OH−] being implied if eqn (16) were truly elementary.
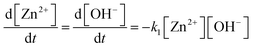 | (17) |
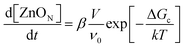 | (18) |
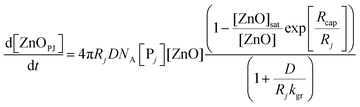 | (19) |
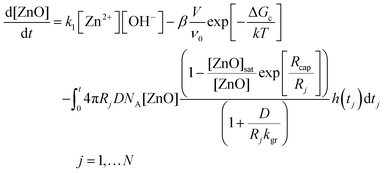 | (20) |
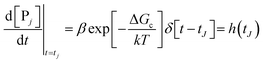 | (21) |
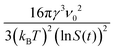 , where γ is the interfacial tension of the ZnO nanoparticles, kB is Boltzmann's constant, and S is the supersaturation =
, where γ is the interfacial tension of the ZnO nanoparticles, kB is Boltzmann's constant, and S is the supersaturation = 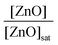 .
.
The authors report that solving the set of “coupled differential equations yields the concentration [PJ](t) and radii RJ(t) of all particles J that have been formed during the nucleation process.”44 They solved the set of differential equations for each data set in Fig. 24, which resulted in the fits given and values for the precursor rate constant (k1), the growth rate constant (kgr), the interfacial tension (γ), and the saturation concentration ([ZnO]sat). However, even with ≥4 adjustable parameters, the fits appear to match only ca. 50% of the experimental data. This suggests that something important is missing from the model, a point which will be discussed more in a moment.
Of interest is that the authors observe a change in the WAXS signal and UV-vis peaks after 1 h, where higher-order Bragg reflections are identified and a red-shift of the absorption edge is observed (Fig. 25).44 The overall particle-size by SAXS does not change significantly after 1 h, which suggests that a different type of growth process is occurring. The authors conclude that an increase in ZnO crystallinity is taking place during this “second growth phase”, where the ZnO is observed to “develop full crystallinity.”44 Overall, the authors present expertly collected, high-quality kinetics data on the formation of ZnO. They collected it by multiple direct techniques using three direct physical methods, SAXS/WAXS and UV-vis, reasons among others that this study was selected as an illustrative case study.
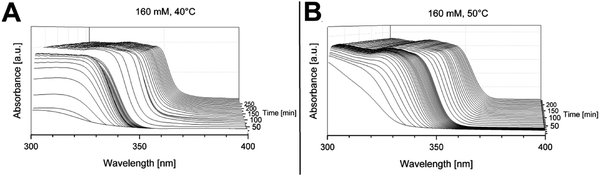 | ||
| Fig. 25 “UV-vis spectra as a function of time recorded in situ during the formation of the ZnO nanoparticles at a concentration [Zn2+]0 = 0.133 mol L−1 at temperatures of 40 °C (A) and 50 °C (B).”44 The red-shift of the absorption edge for both spectra is observed after 1 h, after which the primary nucleation and growth processes are hypothesized to have concluded as judged by the authors’ interpretation of their SAXS data. Reproduced with permission from ref. 44. Copyright 2019 American Chemical Society. | ||
The authors’ kinetics model partially satisfies two of the four minimum criteria for reliable mechanistic study. Unfortunately, the first criterion was not met in that a complete, balanced reaction stoichiometry was not provided.44 We presented a possible mass- and charge-balanced formation reaction back in eqn (15), but further characterization studies are warranted to elucidate the exact values for x and n in eqn (15). Note that even the stoichiometry written eqn (15), suggests a possible higher, perhaps second order in [OH−], rather than the assumed first-order dependence, [OH−]1, used in eqn (17). Next, criterion (ii) was satisfied: the authors collected high-quality size versus time SAXS data and absorbance versus time UV-vis data for the entire ZnO formation. The third criterion was partially satisfied as differential equations for the different processes were derived but, unfortunately, pseudoelementary steps for the reaction were not provided as required for a clearer chemical mechanism. Classical Nucleation Theory (CNT) was assumed over the needed experimental rate law. As a result, the d[ZnON]/dt term is equal to a compilation of CNT-based constants and not the desired concentration terms (i.e., functions of [Zn2+], [OH−], and [C18H33O2−]) and associated rate constants corresponding to a mechanism composed of (pseudo)-elementary step reactions.106 Lastly, criterion (iv) remains to be addressed in that other possible, if not probable, nucleation and growth models need to be tested to determine what model is best accounts for the formation of the observed “ZnO”—really more closer to (ZnO)n·(C18H33O2−)x—nanoparticles.
In short, the authors study zinc-oxide particle formation using state-of-the-art tandem in situ SAXS/WAXS and UV-vis techniques. A single, non-disproof-based physical–chemical model is provided with ≥4 adjustable parameters that doesn’t fully fit the observed kinetics data. Additional studies that would be welcome include: (i) writing out proposed pseudoelementary steps for the reaction; (ii) obtaining an experimental rate law in terms of [ZnII], [OH−], and [C18H33O2−] as a minimum; and then (iii) testing the proposes as well as alternative models to determine the best, disproof-based model for ZnO nanoparticle formation. Importantly, a more reliable, disproof-based mechanism for ZnO nanoparticle formation could result from just one set of additional studies based on this valuable, initial, once again interesting work.
4.3. Shape considerations: two mini-case studies on 2D tungstite platelets and copper nanocrystals
Controlling particle shape is an active area of interest to the nanoscience community. Nanoparticles with controlled shapes and sizes offer new, exciting opportunities in the fields of catalysis and energy conversion.102,107 Twenty-five years ago in 1996, El-Sayed and coworkers demonstrated shape control over platinum nanoparticles by modifying the concentration of stabilizer in a classic paper.108 In 1997 the mechanistic basis for shape control—namely that growth is often autocatalytic surface growth54—made apparent mechanistically that shape control via poisoning of certain facets, or faster growth of a given facet, could achieve shape control more generally—as well as rational syntheses and hence control over bi-metallic, tri-metallic and higher core–shell nanoparticles.109 So far in this review, we have covered primarily spherical particle systems. In what follows, we will consider two additional, mini-case studies. The first covers a multi-year study of 2D tungstite platelet formation by the Niederberger group using XRD, EXAFS, SAXS, GC, and HR-TEM.110,111 The second is a recent study of Cu nanocrystal formation by the Buonsanti group using EXAFS, NMR, MALDI-TOF-MS, and TEM.112 These two additional case studies offer an insight into the current state-of-the-art mechanistic studies, now towards understanding control of particle shape.| WCl6 + 8.7BnOH → WO3·H2O + 3.3BnCl + 2.7BnOBn + 2.7HCl + 2H2O | (22) |
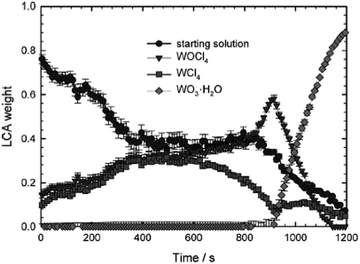 | ||
Fig. 26 EXAFS measurements were collected at the W L3-edge at around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 207 eV and then analyzed using LCA to product the relative amount of each species as a function of time in seconds for the tungstite formation reaction. Reproduced with permission from ref. 110. Copyright 2012 Wiley-VCH Verlag GmbH & Co. 207 eV and then analyzed using LCA to product the relative amount of each species as a function of time in seconds for the tungstite formation reaction. Reproduced with permission from ref. 110. Copyright 2012 Wiley-VCH Verlag GmbH & Co. | ||
Next, to investigate the morphological changes during the reaction, the authors used SAXS and TEM. Their reported TEM micrographs are shown in Fig. 27.
 | ||
| Fig. 27 “Time-dependent TEM and HRTEM images of the tungstite nanostructures after different reaction times (a) and (b) 10 min, (c) and (d) 20 min, (e) 60 min and (f) 240 min.”111 Figure reproduced with permission from ref. 111. Copyright 2013 Royal Society of Chemistry. | ||
From these studies, they observed the formation of spherical particles that assembled into cylinders, and then exfoliated into nanoplatelets. A proposed reaction scheme is provided as Scheme 7.
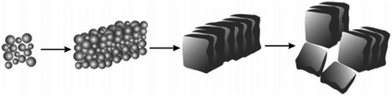 | ||
| Scheme 7 Proposed reaction scheme for the formation of tungstite nanoplatelets starting from WCl6 in benzyl alcohol. Reproduced with permission from ref. 111. Copyright 2013 Royal Society of Chemistry. | ||
Overall, Neiderberger and coworkers have demonstrated the applicability and usefulness of synchrotron XAFS and SAXS measurements to the synthesis of tungstite nanoplatelets. They were able to determine the reaction stoichiometry and then follow the reaction both directly and indirectly. Even with the multiple techniques and depth of analysis, the exact understanding of why, and by what mechanism, the cylinders exfoliate to nanoplatelets is presently unknown. The authors comment that “these two studies exemplarily show how elaborate the investigation of just one system can be and how many ex and in situ techniques have to be applied to monitor both the organic and inorganic processes,”111 sage advice for other workers. Also, “the study of the reaction mechanism over the course of the whole reaction from the dissolution of the precursor to the final nanomaterial is not straightforward and dedicated analytical tools still have to be developed,”110 more truths according to all the present review has uncovered or we know.
Hence, while these two papers uncover a number of insights into formation of non-spherical shapes, mechanistic work remains to be done on these systems. One could conceivably take their proposed reaction scheme, strive to write pseudoelementary step reactions, and see if it is possible to fit their hard-won kinetics data. Furthermore, as the authors state “it is worth the efforts to study as many systems as possible, because every mechanistic study contributes to the overall picture of nanoparticle formation and helps to systematically extend the crystallization models.”111 The value of this system and others like it,113 striving for mechanistic understanding of shape control, is high with a bright future for the needed additional studies.
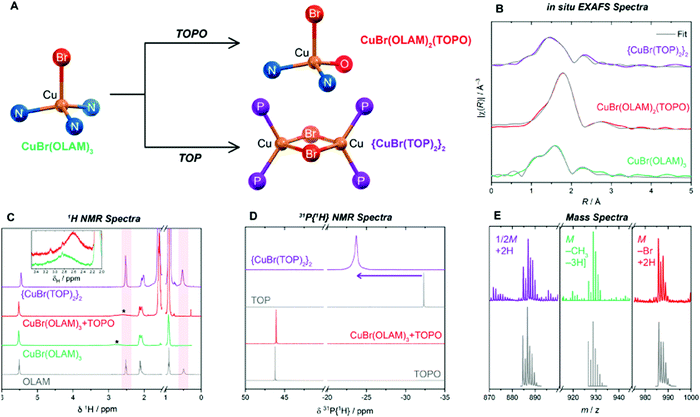 | ||
Fig. 28 (A) “Complexes formed at 80 °C from reaction of CuBr(OLAM)3 with TOPO and TOP, where TOP, TOPO and OLAM ligands are represented by their donor atoms P, O and N, respectively.”112 (B) In situ EXAFS spectra. (C) 1H NMR spectra at room temperature. “OLAM C![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2N 2N![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2 resonances are highlighted in red, the broadened C 2 resonances are highlighted in red, the broadened C![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2NH2 resonances are marked by * and shown separately in the inset plot.”112 (D) 31P{1H} NMR spectra. (E) “Mass spectra of reaction mixtures measured by MALDI-TOF for TOPO and TOP complexes and ESI-MS for the OLAM complex; M is the molecular ion, and the fragmentation or adduct formation required to give the simulated isotope patterns (gray) in indicated.”112 Reproduced with permission from ref. 112. Copyright 2019 American Chemical Society. 2NH2 resonances are marked by * and shown separately in the inset plot.”112 (D) 31P{1H} NMR spectra. (E) “Mass spectra of reaction mixtures measured by MALDI-TOF for TOPO and TOP complexes and ESI-MS for the OLAM complex; M is the molecular ion, and the fragmentation or adduct formation required to give the simulated isotope patterns (gray) in indicated.”112 Reproduced with permission from ref. 112. Copyright 2019 American Chemical Society. | ||
With the critical precursor speciation in hand, Buonsanti and coworkers conducted a series of kinetics experiments to try and elucidate the nucleation pathway. The authors propose two potential pathways for Cu(0) formation, but were not able to definitively support one over the other. However, they provide the community with a description of the needed, additional experiments. They state that “EXAFS combined with X-ray scattering and relative PDF analysis can help in catching the nucleation event and in identifying the actual monomer species.”112
The authors also use their understanding of the reaction kinetics and thermodynamics to access different final shapes. Specifically, they correlate “the conversion kinetics of the intermediates to the Cu(0) monomer flux and the final shape of the NC products… to explore the free energy landscape of the reaction.”112 Those experiments were conducted by varying two parameters: the temperature of the injection and the speed of the injection. Reactions were carried out at 260 °C and 335 °C and injections were done either rapid (all at once) or slow (dropwise). The resulting TEMs from these experiments are reproduced herein as Fig. 29.
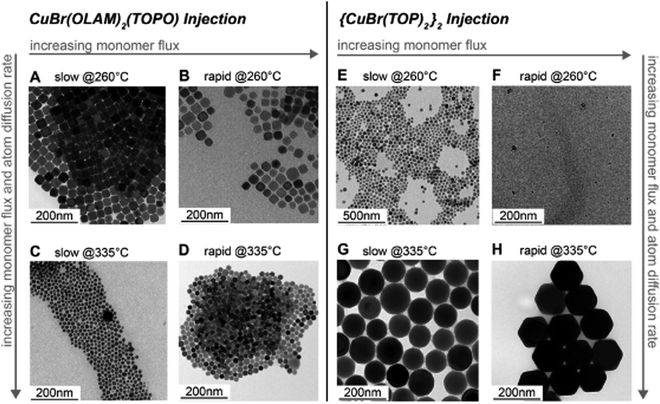 | ||
| Fig. 29 Representative TEM images of Cu NCs obtained after (A and B) dropwise and rapid injection of CuBr(OLAM)2(TOPO) at 260 °C, respectively; (C and D) dropwise and rapid injection of CuBr(OLAM)2(TOPO) at 335 °C, respectively; (E and F) dropwise and rapid injection of {CuBr(TOP)2}2; and (G and H) dropwise and rapid injection of {CuBr(TOP)2}2 at 335 °C, respectively.112 Reproduced with permission from ref. 112. Copyright 2019 American Chemical Society. | ||
Overall, Buonsanti and coworkers have compellingly demonstrated the value and power of elucidating the precursor speciation. By doing this, they are able to probe the kinetic and thermodynamic control of their reaction, which resulted in control over the final shape of the particles. The researchers were able to obtain particles with spherical, cubic, octahedral, truncated-octahedral, and tetrahedra morphologies. Access to these different shapes was due to their in-depth characterization of the reaction speciation using a multitude of techniques (EXAFS, NMR, and MS). They state that “as a general lesson on the synthesis of colloidal metal NCs, we have learned that the choice of the precursor and the identification of the reaction intermediates are crucial to enable a more rational approach to shape control.”112 Well said. Here, the authors have satisfied the first criterion for a mechanistic study of knowing their reaction—which includes knowing the precursor speciation. They also give attention to disproving potential alternative hypotheses during their experiments. In the future, it would be of great interest to try and fit their kinetics data by deriving the equations that correspond to their proposed nucleation pathways. Overall, the study by Buonsanti and coworkers is an exciting and cutting-edge advancement in elucidating shape control, a leading study in an exciting, still wide-open subfield of particle formation synthesis, kinetics and associated mechanism(s).
4.4. Additional systems of interest: perovskites, quaternary nanocrystals, amorphous nanoparticles, and carbon dots
The field of perovskite and quaternary nanocrystals has exploded in the last decade.114–116 These nanocrystal materials have enormous potential in photovoltaics and green energy due to their optical properties and, hence, are of considerable current interest.115,116 Given the young scientific age of these materials, an understanding of their formation processes is an area of active research around the world. The synthesis of these materials often requires furnaces at high temperatures or hot-injection of precursors into high temperature solutions that leads to rapid synthesis, often on the timescale of seconds.117 In order to follow the formation reaction, techniques like synchrotron XAFS and SAXS, among others, are needed118 and, as expected, have been used to characterize these materials. Understanding their phase stability and local structure or characterizing the material in situ as a photovoltaic device are the types of studies that have been reported.119–127Amorphous nanoparticles are of interest due to their applications in catalysis, optics, magnetism, bioactivity, electrochemistry, and nanocomposites.128–134 In particular, there are cases within the water oxidation catalysis literature where the amorphous materials have produced superior catalytic activity to their crystalline counterparts.135,136 For the formation of amorphous nanoparticles, there are a limited number of studies that use synchrotron XAFS or SAXS techniques to investigate the local structural changes of what are typically amorphous nanoparticles at least initially.137–140
A good example is a 2013 study on the synthesis of Ni2P, where the authors used to two similar syntheses to produce amorphous and crystalline Ni2P nanoparticles.141 They used EXAFS combined with XRD and TEM results to develop a method to “determine crystalline behavior based on standard deviations in interatomic distance offsets.”141 Then, when combined with XRD, one can determine the level of crystalline versus amorphous character in their sample.141 Overall, there is great potential for synchrotron XAFS in the formation of amorphous nanoparticles, particularly when paired with an addition technique like XRD or PDF.
A final field of particular interest in the past decade, that a referee asked we comment on, is carbon-based quantum dots (CQDs or C dots).142–144 These materials are of interest for their tunable photoluminescent (PL) properties and applications in energy, catalysis, and biomedical engineering.145–148 There are no current studies that we could find that utilize synchrotron XAFS or SAXS to study the formation of CQDs. A number of papers, including an excellent review by Shamsipur and coworkers,149 have detailed the various synthetic strategies to produce CQDs that fluorescence from blue to red.150–152 However, the field of CQDs remains wide open for investigation by synchrotron-based methods. As Shamsipur and coworkers wrote, “it should be noted that most of the reported [CQDs] with unique PL properties were obtained by chance and not by design.”149 In short, a bottom line regarding these additional systems of often high current interest is that each is wide open for kinetics and other studies aimed at a detailed understanding of their formation mechanism.
5. Current state of particle formation mechanisms
Prior to 1997,54 Classical Nucleation Theory (CNT), Avrami's equation, and the LaMer physical-chemistry models dominated the particle formation literature.65,66 However, modern techniques and advances indicate that each of these physical–chemical models have serious if not fatal weaknesses.25,26,31,32,39,41,55,56,65–68,153,154 CNT was developed155–157 in the late 1800s as a mathematical model for particle nucleation, but agrees with experiment within ca. 10±1only for gas-phase hydrocarbon or other weakly, reversibly associating systems at temperatures >300 K, as demonstrated by El-Shall and co-workers in their noteworthy studies.153,154 The Avrami model was developed in 1939158–160 and has been modified at least 13 times,161–164 but remains a semi-empirical treatment and equation that fails to yield physically relevant rate constants,55,56,165 nor other physically unambiguously interpretable parameters.165 The reader wishing to know more about these topics is urged to consult the references cited.The LaMer model166 postulating “burst” nucleation and “diffusion-controlled” growth was developed for sulfur sols and has since been used to try to explain hundreds of particle formation systems.65,66,167 Yet, in its 70 years of existence, the LaMer mathematical model and equation has never been used to successfully fit kinetics data save his original case on (S)n sols,166 a remarkable testament to its lack of quantitative utility. Moreover, the LaMer qualitative hypothesis of “burst” nucleation and “diffusion-controlled” growth has been compellingly disputed25,26,168–173 in three recent65,66,167 reviews of 1953 papers citing the LaMer model over the 70+ years since 1950. Relevant here are the wise words of B. Peters that “The classic theories work poorly or not at all when applied beyond the validity of their assumptions.”174
Little known is that Victor LaMer also published a stepwise mechanism for particle formation in 1952,175 but never tested it with nor used it to explain experimental kinetics data for particle formation. Turkevich's 1953 “organizer mechanism”176,177 merits mention in Table 1 as well, even though it lacks specific pseudoelementary steps, because it is the early example of what are now termed Pre-Nucleation Clusters as discussed in a 2021 review.66 Indeed, reading Turkevich's literature reveals he was often far ahead of his time in his intuition and understanding about particle synthesis, physical properties, and probable mechanisms.
| Year | Person(s) | Mechanism (A, B, and C formalism) | Mechanism (in words), and comments |
|---|---|---|---|
| 1952 | V. K. LaMer175 | mA1 ⇌ Bm Bm + A1 ⇌ Bm+1 B(i−1) + A1 ⇌ Bi | Stepwise bimolecular addition leading to “burst nucleation” (NB: “diffusion-controlled growth”166 was not included175 as part of the scheme provided) |
| [A1 = “kinetically independent unit of phase A”, Bi = “embryo of phase B containing i units”, and “m is usually 2, whereas i in the case of water vapor condensation is about 80—i.e., this reaction is of the 80th order”] | |||
| 1953 | Turkevich,176,177 Stevenson, Hillier | No pseudoelementary step mechanism was provided in ref. 176 and 177. | Nucleating agents build up a chemical complex, organize macromolecularly, then undergo a molecular rearrangement to produce the metal nucleus, Turkevich's “organizer” mechanism/hypothesis—what can now be seen to be an early version of the prenucleation clusters postulate. |
| 1997 | Finke, Watzky54 |
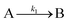
|
Slow, kinetically continuous nucleation followed by typically fast, explosive autocatalytic surface growth. Important to note is that higher order  nucleations are covered by (i.e., can be hidden in) the pseudoelementary first step, as the subsequent discovery of second-order and termolecular nucleations demonstrates.30,31 nucleations are covered by (i.e., can be hidden in) the pseudoelementary first step, as the subsequent discovery of second-order and termolecular nucleations demonstrates.30,31 |

|
|||
| [A = metal precursor, B = growing, metal(0) particle] | |||
| 2004 | Hornstein, et al.184 |
|
Evidence for bimolecular agglomeration as a 3rd step added to the 1997 2-step mechanism54 |

|
|||
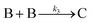
|
|||
| 2005 | Besson, Finney, et al.80,185,186 |
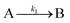
|
Evidence for a 4th step of autocatalytic agglomeration where the smaller particles, B, and larger particles, C, agglomerate with a separate, k4, rate constant |

|
|||
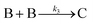
|
|||

|
|||
| [A = metal precursor, B = small particles, C = larger particles] | |||
| 2005 | Drew, Katsoulakis, Tsapatsis188 |
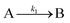
|
A proposed mechanism for crystal growth by aggregation of meta-stable nanoparticle precursors, one used with Population-Balance Modeling. Three alternative mechanisms were tested; shown is the author's preferred Mechanism II. |
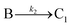
|
|||
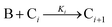
|
|||
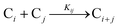
|
|||
| [A = primary colloidal particles; B = growing crystal; C1 = nucleated primary particles] | |||
[b = nAoKi/k2; c = nAoKij/k2; nAo = initial number of fresh primary particles; ni = particle density of crystal i; y = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) /nAo; τ = k2t] /nAo; τ = k2t] |
|||
| 2014 | Kent, Mondloch, et al.187 |
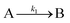
|
Evidence for a new 4th step of secondary autocatalytic growth where larger particles, C, growth with a separate, k4′, rate constant. |

|
|||
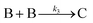
|
|||
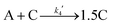
|
|||
| [A = metal precursor, B = smaller particles, C = larger particles] | |||
| 2017 | Karim, et al.39 | A·L ⇌ A + L | Proposed four step mechanism, including two ligand binding equilibria steps, for the formation of metal nanoparticles, the first A·L step having additional precedent.31,32 |
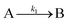
|
A set of 5 differential equations are reproduced in the ESI. | ||

|
|||
| B·L ⇌ B + L | |||
| [A = metal precursor, B = growing particle, A·L = precursor with ligand, B·L = growing particle with ligand; both ligand steps have associated Keq equilibrium constants] | |||
| 2019 | Handwerk, Shipman, Whitehead, Özkar, et al.67,68 |
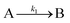
|
A new, 3-step mechanism, discovered by disproof-based Mechanism-Enabled Population-Balance Modeling, in which the  pseudoelementary step of the 1997 2-step mechanism was expanded into two growth steps (or, alternatively, and as actually discovered67,68 the 2nd and 3rd steps of the 2014 4-step mechanism are combined into a single, new 2nd step). Eleven alternative mechanisms were disproved. Quantitative fitting of Particle-Size Distributions (PSDs) was demonstrated, including the PSD shape. pseudoelementary step of the 1997 2-step mechanism was expanded into two growth steps (or, alternatively, and as actually discovered67,68 the 2nd and 3rd steps of the 2014 4-step mechanism are combined into a single, new 2nd step). Eleven alternative mechanisms were disproved. Quantitative fitting of Particle-Size Distributions (PSDs) was demonstrated, including the PSD shape. |
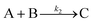
|
|||

|
|||
| [A = metal precursor, B = smaller particles, C = larger particles] | |||
The first, disproof-based minimum mechanism for particle formation mechanism composed of specific pseudoelementary steps (that also add up to an experimentally demonstrated balanced reaction to well-characterized products) did not appear until 1997,54 the 2-step mechanism of continuous nucleation and autocatalytic surface growth listed in Table 1. This simplest version of particle formation has since been used to successfully fit homogeneous nanoparticle formation,178 heterogeneous nanoparticle formation,179 solid state kinetics,180 dye aggregation,181 protein aggregation,182 and other “cooperative” autocatalytic phenomena in nature.183 Six upgraded, themselves deliberately minimum mechanisms for particle formation have since been reported39,54,67,68,80,184–187 as summarized in Table 1. Those specific upgrades to the 2-step mechanism occurred 5 times as additional evidence for more complex pathways became available (entries 2, 3, 5, 6, and 7 – Table 1)—and include disproof57–59 of at least 21 additional alternatively mechanisms en route to those 6 of the 7 mechanisms in Table 1.26,54,67,68,80,184–187 The 2005 crystal-growth model from Tsapatsis and co-workers188 is also included in Table 1 because their model has proposed pseudoelementary steps supported by Population Balance Modeling while disproving one alternative mechanism—and hence is an early example of a mechanistic model partially tested by what is denoted ME-PBM.67,68
An important point growing out of Table 1 is that the 1997 2-step mechanism was upgraded67,68—“disproved” if one likes—in favor of the 2019 3-step mechanism as needed to be able to quantitatively account for PSD data.67,68 Put in other terms, although the 2-step mechanism has been used in several studies in this review—and remains recommended67,68—for initial data analysis of sigmoidal particle-formation kinetics curves, a new 2019 3-step mechanism67,68 is now the minimal PEStep mechanism able to account for PSDs once programed into Mechanism-Enabled Population Balance Modeling.67,68
Of considerable interest is what results if one takes just the 5 basic classes of mechanistic models in Table 1 that have been subjected to extensive disproof and therefore deemed to be more reliable,54,67,68,80,184–187 and then combines them with 3 different precedented nucleation molecularities30–32,54 and up to 3 different types of ligand binding steps based on A. Karim's groundbreaking39 work on ligand-dependent PESteps and A·L and B·L species (plus other precedent for A·L to A + L dissociative steps31,32). Looking at the possible combinations, one now has 5 classes of ≥96 possible mechanisms that one can use to try to use in a disproof-based approach57–59 to fitting one's particle formation data while striving for a disproof-based minimum mechanism for one's particle formation reaction.
6. Conclusions
Synchrotron X-ray radiation-based methods of XAFS and SAXS are powerful, largely direct methods for observing particle formations across every area of nature and science where particles are formed. Often, one wants to be able to control size and size-dispersion to optimize properties and applications of those particles, and this is where a detailed, quantitative, experimentally based mechanism becomes important. Key takeaways, from the analysis of 74 synchrotron-based particle formation papers summarized in Tables S1–S4 of the ESI† and the 6 case studies examined in detail in this review, are as followed:• Employing synchrotron X-ray radiation-based experiments provides powerful, largely direct particle formation kinetics data. Indeed, Tables S1–S4 of the ESI† document the wealth of typically expert obtained, in situ, many times creative tandem-methods monitoring of particle formation reactions. One caveat here, that merits closer attention in the future, is that X-ray radiation induced radiolysis can initiate nucleation events that then quickly magnify the loss of precursor by exponential, autocatalytic growth54 in at least some cases.
• The value in completely characterizing ones’ precursors and the overall speciation in one's starting solutions cannot be overemphasized. This follows both from experience as well as the fact that kinetics generally gives one the composition of the activated complex of the rate-determining step, which in turn relies on knowing what species you are actually changing when you vary the concentrations of the starting materials—that is, relies on you being able to confidently write d[Product]/dt in terms of known species.
• Four minimum criteria one needs to satisfy in order to be able to claim a chemical mechanism of particle formation for a given system are the following,65 criteria well-known from physical-organic and physical-inorganic mechanistic chemistry: (i) a complete mass- and charge-balanced, experimentally determined reaction stoichiometry—because the proposed mechanistic steps must add up to that observed reaction, for example the presence of ligand-based steps such as particle capping; (ii) kinetics data, ideally the full rate law for nucleation, growth and any agglomeration that might be present—again in terms of known precursor species; (iii) postulation of pseudoelementary step-based mechanisms, such as those in Table 2, that are also able to add up to the observed reaction stoichiometry, followed by writing down the differential equations corresponding to each mechanism; and critically then also (iv) disproof of ideally all reasonable alternative mechanistic hypotheses by checking each mechanism against the observed kinetics data en route to an Ockham's razor obeying, experimentally supported, disproof-based proposed minimum mechanism of particle formation for the system at hand.
| Class | Mechanism | Unimolecular nucleation | Bimolecular nucleation | Termolecular nucleation | Ligand dependence |
|---|---|---|---|---|---|
| (I) | FW 2-step | A → B | 2A → 2B | 3A → 3B | (i) A·L ⇌ A + L |
| A + B → 2B | A + B → 2B | A + B → 2B | (ii) B·L ⇌ B + L | ||
| (iii) With A·L and B·L steps | |||||
| (II) | Classic 3-step with bimolecular agglomeration | A → B | 2A → 2B | 3A → 3B | (i) A·L ⇌ A + L |
| A + B → 2B | A + B → 2B | A + B → 2B | (ii) B·L ⇌ B + L | ||
| B + B → C | B + B → C | B + B → C | (iii) C·L ⇌ C + L | ||
| (iv) With A·L and B·L steps | |||||
| (v) With A·L and C·L steps | |||||
| (vi) With B·L and C·L steps | |||||
| (III) | New, Handwerk et al. 3-step | A → B | 2A → 2B | 3A → 3B | (i) A·L ⇌ A + L |
| A + B → C | A + B → C | A + B → C | (ii) B·L ⇌ B + L | ||
| A + C → 1.5C | A + C → 1.5C | A + C → 1.5C | (iii) C·L ⇌ C + L | ||
| (iv) With A·L and B·L steps | |||||
| (v) With A·L and C·L steps | |||||
| (vi) With B·L and C·L steps | |||||
| (IV) | 4-Step with B + C agglomerative growth | A → B | 2A → 2B | 2A → 2B | (i) A·L ⇌ A + L |
| A + B → 2B | A + B → 2B | A + B → 2B | (ii) B·L ⇌ B + L | ||
| B + B → C | B + B → C | B + B → C | (iii) C·L ⇌ C+ L | ||
| B + C → 1.5C | B + C → 1.5C | B + C → 1.5C | (iv) With A·L and B·L steps | ||
| (v) With A·L and C·L steps | |||||
| (vi) With B·L and C·L steps | |||||
| (V) | 4-Step with A + C secondary autocatalytic surface growth | A → B | 2A → 2B | 3A → 3B | (i) A·L ⇌ A + L |
| A + B → 2B | A + B → 2B | A + B → 2B | (ii) B·L ⇌ B + L | ||
| B + B → C | B + B → C | B + B → C | (iii) C·L ⇌ C + L | ||
| A + C → 1.5C | A + C → 1.5C | A + C → 1.5C | (iv) With A·L and B·L steps | ||
| (v) With A·L and C·L steps | |||||
| (vi) With B·L and C·L steps |
• Even a brief survey of Tables S2–S4 of the ESI,† that we hope the reader has done for themselves, teaches several other important points: (i) at least ∼94% of the time to date, the systems examined are not well defined, without for example even a complete, balanced reaction stoichiometry having been determined. In that sense, more in-house, more “synthetic” efforts before “synchrotron spectroscopic” efforts—actually, much, much more—would, in many cases, have provided better defined systems worthier of the sophisticated, expert, often creative synchrotron XAFS and SAXS efforts one finds listed in Tables S2–S4 of the ESI.† Put another way, one can view all 69 cases in Tables S2–S4 (ESI†) as using synchrotron radiation methods to examine particle formation systems directly and see what insights can be obtained. That is fine, but one should not claim that a mechanism has resulted from those largely survey studies. (ii) In 4 of the 69 cases in Tables S2–S4 of the ESI,† all four of the requirements (i)–(iv) for a reliable mechanism are missing; in 39 of the 69 cases (57% of the time) in Tables S2–S4 of the ESI,† three of the four requirements are missing; in 20 cases (29% of the time) two of (i)–(iv) are missing; and in only 4 cases (5.8% of the time) are just one of requirements (i)–(iv) for a reliable mechanism missing.
• Worth emphasizing is that the required but missing first component in ca. 94% of particle formation studies examined by this review is the balanced reaction stoichiometry. Without a balanced reaction stoichiometry, the pseudoelementary steps of the proposed mechanism—that must add up to that net reaction stoichiometry—cannot be reliably nor unequivocally determined. Even for the 6 studies in the main text, only one has (and only 2 more partially have) an experimentally determined, balanced reaction stoichiometry. The studies examined herein, as well as one's intuition, teach that a balanced reaction stoichiometry promises to be especially important for obtaining and understanding ligand effects in particle formation reactions, as A. Karim's valuable, telling example demonstrates.
• Also missing in 66 of 69 examples in Tables S2–S4 (ESI†) and in 3 of the 6 cases in the main text is a full, experimentally determined rate law for nucleation and growth. One cannot possibly have a reliable reaction mechanism without the full rate law. Rate laws for nucleation are especially rare,31 being present in arguably only 1 case32 of the 64 total studies covered in this review—and even then that proposed nucleation mechanism is currently under further scrutiny using ME-PBM.
• Too often presently mechanisms are claimed based on qualitative data or ‘snapshots’ and sometimes cartoons of what size particles are present at what times. These qualitative schematic models or just word-based pictorial models189–197 are of some use, but are not, and should not be confused with, disproof-based, minimum mechanisms expressed in balanced reactions as detailed in Tables 1 and 2.
• Presently, one can write 5 primary classes of pseudoelementary-step based, minimum mechanisms, that include 3 precedented types of nucleation and 3 precedented types of ligand binding, for a total of ≥96 possible mechanisms now available to test out on one's experimental data. Relevant here is that only two studies have elucidated the effects of ligands on the kinetics and mechanism of nucleation and growth.31,39,72,95 Hence, especially important for future studies is to include the specific effects of ligands on particle nucleation, growth, agglomeration and associated ligand-capping (of the particle) processes.
• Mechanism-Enabled Population Balance Modeling has recently emerged as a must-use tool to test one's mechanism, specifically to see if the proposed mechanism can quantitatively account for the proposed particle-size distribution, including its shape.
• One should expect, and indeed hope, that one's initial, minimum mechanism will one day be disproved, replaced by a more complex, experimentally further supported pathway. This is the expectation of minimal, disproof-based mechanisms, where, as time progresses and techniques improve, new insights and new details become possible as new methods, additional experimentation, or applicable computations become available. Relevant here are recommend articles by Platt,57 Chamberlain,58 Scott,59 and Weinfurt198 on employing a proper disproof-based scientific method and avoiding the >400-year-old problem in science of “idols and false notions”.198
7. Outlook
The future is bright—indeed “synchrotron bright”—for the use of synchrotron-based experimental methods en route to reliable, disproof-based chemical mechanisms for particle formation. Efforts that will enhance that bright future include a focus on the four requirements outlined herein for obtaining a reliable reaction mechanism, starting with establishment of a balanced reaction stoichiometry. The combination of complimentary, in-house physical methods with synchrotron-based methods will expedite and make more efficient the use of finite synchrotron beam time. A focus on establishing the full rate law for especially nucleation, but also growth as well as any agglomeration, is also needed—without a full rate law, unequivocal mechanism is impossible. Testing the known mechanisms in Table 2 against one's experimental data, before postulating additional mechanisms, and using ME-PBM in conjunction with PSD data—as the present, apparent “Gold standard/acid test” of any proposed mechanism—promise to aid rapid mechanistic progress. Computational chemistry69,70 employed skeptically71 as well as first-principles molecular dynamics simulations199 promise to play an important role, too. Furthermore, the number of systems of interest has grown well beyond industrially-relevant catalytically active and other metal nanoparticles. Systems highlighted in Section 4 continue to garner enormous attention with their applications to sustainable energy. With the advances being made in synchrotron methods, it is a golden time for researchers interested in elucidating the mechanisms of particle formation for these technologically and environmentally relevant materials. Indeed, it appears that the particle-formation community is on the cusp of significant mechanistic breakthroughs for a multitude of systems that produce particles throughout nature, in no small part to the continued creative, expert use of powerful synchrotron-radiation methods!Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The Finke Research Group members are thanked for their insightful comments and thoughtful recommendations. We would also like to thank two of the reviewers for their informed, helpful suggestions. The work at Colorado State University was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Catalysis Science Program, via Award SE-FG402-02ER15453.References
- A. H. L. Chow, H. H. Y. Tong, P. Chattopadhyay and B. Y. Shekunov, Particle engineering for pulmonary drug delivery, Pharm. Res., 2007, 24, 411–437 CrossRef CAS PubMed.
- R. Vehring, Pharmaceutical Particle Engineering via Spray Drying, Pharm. Res., 2008, 25, 999–1022 CrossRef CAS PubMed.
- A. Baldelli, M. A. Boraey, D. S. Nobes and R. Vehring, Analysis of the Particle Formation Process of Structured Microparticles, Mol. Pharmaceutics, 2015, 12, 2562–2573 CrossRef CAS PubMed.
- J. M. Koehler, N. Visaveliya and A. Knauer, Controlling formation and assembling of nanoparticles by control of electrical charging, polarization, and electrochemical potential, Nanotechnol. Rev., 2014, 3, 553–568 CAS.
- D. Kashchiev, Nucleation: Basic Theory with Applications, Butterworth-Heinemann, Oxford, UK, 2000 Search PubMed.
- D. W. Oxtoby, Homogeneous nucleation: theory and experiment, J. Phys.: Condens. Matter, 1992, 4, 7627–7650 CrossRef.
- Nucleation—a Transition State to the Directed Assembly of Materials. Faraday Discussions, Royal Society of Chemistry, UK, 2015, vol. 179, pp. 9–154 Search PubMed.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Nucleation for Crystals from Solution: Classical and Two-Step Models, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS PubMed . Note the “Two-Step Model” referred to in this work is distinct from and should not be confused with the FW 2-step mechanism.
- T. H. Zhang and X. Y. Liu, Nucleation: What Happens at the Initial Stage?, Angew. Chem., Int. Ed., 2009, 48, 1308–1312 CrossRef CAS PubMed.
- A. M. Morris, M. A. Watzky and R. G. Finke, Protein aggregation kinetics, mechanism, and curve-fitting: a review of the literature, Biochim. Biophys. Acta, Proteins Proteomics, 2009, 1794, 375–397 CrossRef CAS PubMed.
- R. Zhang, Getting to the Critical Nucleus of Aerosol Formation, Science, 2010, 328, 1366–1367 CrossRef CAS PubMed.
- E. E. Finney and R. G. Finke, Nanocluster nucleation and growth kinetic and mechanistic studies: A review emphasizing transition-metal nanoclusters, J. Colloid Interface Sci., 2008, 317, 351–374 CrossRef CAS PubMed.
- G. Schmid, Large Clusters and Colloids. Metals in the Embryonic State, Chem. Rev., 1992, 92, 1709–1727 CrossRef CAS.
- M. N. Vargaftik, V. P. Nagorodnikov, I. P. StoIarov, I. I. Moiseev, V. A. Likholobov, D. I. Kotchubey, A. L. Chuvilin, V. I. Zaikovsky, K. I. Zamaraev and G. I. Timofeeva, A novel giant palladium cluster, J. Chem. Soc., Chem. Commun., 1985, 937–939 RSC.
- T. S. Ahmadi, Z. L. Wang, T. C. Green, A. Henglein and M. A. El-Sayed, Shape-Controlled Synthesis of Colloidal Platinum Nanoparticles, Science, 1996, 272, 1924–1926 CrossRef CAS PubMed.
- J. D. Aiken and R. G. Finke, A review of modern transition-metal nanoclusters: their synthesis, characterization, and applications in catalysis, J. Mol. Catal. A: Chem., 1999, 145, 1–44 CrossRef CAS.
- O. Vidoni, K. Philippot, C. Amiens, B. Chaudret, O. Balmes, J. O. Malm, J. O. Bovin, F. Senocq and M. J. Casanove, Novel Spongelike Ruthenium Particles of Controllable Size Stabilized Only by Organic Solvents, Angew. Chem., Int. Ed., 1999, 38, 6736–6738 CrossRef.
- K. Pelzer, O. Vidoni, K. Philippot, B. Chaudret and V. Colliere, Organometallic Synthesis of Size-Controlled Polycrystalline Ruthenium Nanoparticles in the Presence of Alcohols, Adv. Funct. Mater., 2003, 13, 118–126 CrossRef CAS.
- L. S. Ott and R. G. Finke, Transition-metal nanocluster stabilization for catalysis: A critical review of ranking methods and putative stabilizers, Coord. Chem. Rev., 2007, 251, 1075–1100 CrossRef CAS.
- R. Jin, Quantum sized, thiolate-protected gold nanoclusters, Nanoscale, 2010, 2, 343–362 RSC.
- L. G. AbdulHalim, N. Kothalawala, L. Sinatra, A. Dass and O. M. Bakr, Neat and Complete: Thiolate-Ligand Exchange on a Silver Molecular Nanoparticle, J. Am. Chem. Soc., 2014, 136, 15865–15868 CrossRef CAS PubMed.
- N. Goswami, Q. Yao, T. Chen and J. Xie, Mechanistic exploration and controlled synthesis of precise thiolate-gold nanoclusters, Coord. Chem. Rev., 2016, 329, 1–15 CrossRef CAS.
- C. A. Hosier and C. J. Ackerson, Regiochemistry of Thiolate for Selenolate Ligand Exchange on Gold Clusters, J. Am. Chem. Soc., 2019, 141, 309–314 CrossRef CAS PubMed.
- J. M. Lee, L. A. Kraynak and A. L. Prieto, A Directed Route to Colloidal Nanoparticle Synthesis of the Copper Selenophosphate Cu3PSe4, Angew. Chem., Int. Ed., 2020, 59, 3038–3042 CrossRef CAS PubMed.
- B. M. McMurtry, K. Qian, J. K. Teglasi and A. K. Swarnakar, De Roo, J.; Owen, J. S. Continuous Nucleation and Size Dependent Growth Kinetics of Indium Phosphide Nanocrystals, Chem. Mater., 2020, 32, 4358–4368 CrossRef CAS.
- S. Mozaffari, W. Li, M. Dixit, S. Seifert, B. Lee, L. Kovarik, G. Mpourmpakis and A. M. Karim, The role of nanoparticle size and ligand coverage in size focusing of colloidal metal nanoparticles, Nanoscale Adv., 2019, 1, 4052–4066 RSC.
- L. M. Rossi, I. M. Nangoi and N. J. S. Costa, Ligand-Assisted Preparation of Palladium Supported nanoparticles: a Step toward Size Control, Inorg. Chem., 2009, 48, 4640–4642 CrossRef CAS PubMed.
- G. A. Somorjai and J. Y. Park, Colloid Science of Metal Nanoparticle Catalysts in 2D and 3D Structures. Challenges of Nucleation, Growth, Composition, Particle Shape, Size Control and Their Influence on Activity and Selectivity, Top. Catal., 2008, 49, 126–135 CrossRef CAS.
- R. Lai, C. Pu and X. Peng, On-Surface Reactions in the Growth of High-Quality CdSe Nanocrystals in Nonpolar Solutions, J. Am. Chem. Soc., 2018, 140, 9174–9183 CrossRef CAS PubMed.
- W. W. Laxson and R. G. Finke, Nucleation is Second Order: An Apparent Kinetically Effective Nucleus of Two for Ir(0)n Nanoparticle Formation from [(1,5-COD)IrI·P2W15Nb3O62]8− Plus Hydrogen, J. Am. Chem. Soc., 2014, 136, 17601–17615 CrossRef CAS PubMed.
- S. Özkar and R. G. Finke, Nanoparticle Nucleation Is Termolecular in Metal and Involves Hydrogen: Evidence for a Kinetically Effective Nucleus of Three {Ir3H2x·P2H15Nb3O62}6− in Ir(0)n Nanoparticle Formation From [(1,5-COD)IrI·P2W15Nb3O62]8− Plus Dihydrogen, J. Am. Chem. Soc., 2017, 139, 5444–5457 CrossRef PubMed.
- C. B. Whitehead and R. G. Finke, Nucleation Kinetics and Molecular Mechanism in Transition-Metal Nanoparticle Formation: The Intriguing, Informative Case of a Bimetallic Precursor, {[(1,5-COD)IrI·HPO4]2}2−, Chem. Mater., 2019, 31, 2848–2862 CrossRef CAS.
- T. Li, A. J. Senesi and B. Lee, Small Angle X-ray Scattering for Nanoparticle Research, Chem. Rev., 2016, 116, 11128–11180 CrossRef CAS PubMed.
- B. Chu and T. Liu, Characterization of nanoparticles by scattering techniques, J. Nanopart. Res., 2000, 2, 29–41 CrossRef CAS.
- P. S. Goyal and V. K. Aswal, Use of SANS and SAXS in study of nanoparticles, Int. J. Nanosci., 2005, 4, 987–994 CrossRef CAS.
- U. Bentrup, Combining in situ characterization methods in one set-up: looking with more eyes into the intricate chemistry of the synthesis and working of heterogeneous catalysts, Chem. Soc. Rev., 2010, 39, 4718–4730 RSC.
- Y. Sun and Y. Ren, In Situ Synchrotron X-Ray Techniques for Real-Time Probing of Colloidal Nanoparticles Synthesis, Part. Part. Syst. Charact., 2013, 30, 399–419 CrossRef CAS.
- D. Koziej, Revealing Complexity of Nanoparticle Synthesis in Solution by in Situ Hard X-ray Spectroscopy—Today and Beyond, Chem. Mater., 2016, 28, 2478–2490 CrossRef CAS.
- S. Mozaffari, W. Li, C. Thompson, S. Ivanov, S. Seifert, B. Lee, L. Kovarik and A. M. Karim, Colloidal nanoparticle size control: experimental and kinetic modeling investigation of the ligand–metal binding role in controlling the nucleation and growth kinetics, Nanoscale, 2017, 9, 13772–13785 RSC.
- S. Yao, Y. Yuan, C. Xiao, W. Li, Y. Kou, P. J. Dyson, N. Yan, H. Asakura, K. Teramura and T. Tanaka, Insights into the Formation Mechanism of Rhodium Nanocubes, J. Phys. Chem. C, 2012, 116, 15076–15086 CrossRef CAS.
- C. B. Whitehead, D. R. Handwerk, Y. Li, A. Frenkel, B. Ingham, N. M. Kirby and R. G. Finke, Nanoparticle Formation Kinetics, Mechanisms and Accurate Rate Constants: Examination of a Second-Generation Ir(0)n Particle Formation System by Five Monitoring Methods Plus Initial Mechanism-Enabled Population Balance Modeling, J. Phys. Chem. C, 2021, 125, 13449–13476 CrossRef CAS.
- R. K. Ramamoorthy, E. Yildirim, E. Barba, P. Roblin, J. A. Vargas, L.-M. Lacroix, I. Rodriguez-Ruiz, P. Decorse, V. Petkov, S. Teychené and G. Viau, The role of pre-nucleation clusters in the crystallization of gold nanoparticles, Nanoscale, 2020, 12, 16173–16188 RSC.
- H. Oyanagi, Z. H. Sun, Y. Jiang, M. Uehara, H. Nakamura, K. Yamashita, L. Zhang, C. Lee, A. Fukano and H. Maeda, In situ XAFS experiments using a microfluidic cell: application to initial growth of CdSe nanocrystals, J. Synchrotron Radiat., 2011, 18, 272–279 CrossRef CAS PubMed.
- M. Herbst, E. Hofmann and S. Förster, Nucleation and Growth Kinetics of ZnO Nanoparticles Studied by in Situ Microfluidic SAXS/WAXS/UV-Vis Experiments, Langmuir, 2019, 35, 11702–11709 CrossRef CAS PubMed.
- T. T. Tidwell, The First Century of Physical Organic Chemistry: A Prologue, Pure Appl. Chem., 1997, 69, 211–213 CAS.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Sausalito, CA, 2006 Search PubMed.
- T. H. Lowry and K. S. Richardson, Mechanism and Theory in Organic Chemistry, Harper & Row, New York, 3rd edn, 1987 Search PubMed.
- S. E. Smith, J. M. Sasaki, R. G. Bergman, J. E. Mondloch and R. G. Finke, Platinum-Catalyzed Phenyl and Methyl Group Transfer from Tin to Iridium: Evidence for an Autocatalytic Reaction Pathway with an Unusual Preference for Methyl Transfer, J. Am. Chem. Soc., 2008, 130, 1839–1841 CrossRef CAS PubMed.
- J. Halpern, S.-H. Kim and T. W. Leung, Cobalt–Carbon Bond Dissociation Energy of Coenzyme B12, J. Am. Chem. Soc., 1984, 106, 8317–8319 CrossRef CAS.
- B. P. Hay and R. G. Finke, Thermolysis of the Co–C Bond of the Adensylcobalamin. 2. Products, Kinetics, and Co–C Bond Dissociation Energy in Aqueous Solution, J. Am. Chem. Soc., 1986, 108, 4820–4829 CrossRef CAS.
- A. A. Frost and R. G. Pearson, Kinetics and Mechanism. A Study of Homogeneous Chemical Reactions, Wiley & Sons, New York, 2nd edn, 1961 Search PubMed.
- J. H. Espenson, Chemical Kinetics and Reactions Mechanisms, McGraw-Hill, New York, 2nd edn, 1995 Search PubMed.
- R. J. Field and R. M. Noyes, Oscillations in chemical systems. 19. Mechanisms of chemical oscillators: Conceptual bases, Acc. Chem. Res., 1977, 10, 214–221 CrossRef CAS . Please also see references cited therein.
- M. A. Watzky and R. G. Finke, Transition Metal Nanocluster Formation Kinetic and Mechanistic Studies. A New Mechanism When Hydrogen Is the Reductant: Slow, Continuous Nucleation and Fast Autocatalytic Surface Growth, J. Am. Chem. Soc., 1997, 119, 10382–10400 CrossRef CAS.
- E. E. Finney and R. G. Finke, Is There a Minimal Chemical Mechanism Underlying Classical Avrami-Erofe’ev Treatments of Phase Transformation Kinetic Data?, Chem. Mater., 2009, 21, 4692–4705 CrossRef CAS.
- E. E. Finney and R. G. Finke, Fitting and Interpreting Transition-Metal Nanocluster Formation and Other Sigmoidal Kinetic Data: A More Thorough Testing of Dispersive Kinetics vs. Chemical-Mechanism-Based Equations and Treatments for 4-Step Type Kinetic Data, Chem. Mater., 2009, 21, 4468–4479 CrossRef CAS.
- J. R. Platt, Strong Inference, Science, 1964, 146, 347–353 CrossRef CAS PubMed.
- T. C. Chamberlain, Studies for Students. The Method of Multiple Working Hypotheses, J. Geol., 1897, 5, 837–848 CrossRef.
- S. L. Scott, The Burden of Disproof, ACS Catal., 2019, 9, 4706–4708 CrossRef CAS.
- R. Hoffmann, V. I. Minkin and B. K. Carpenter, Ockham's Razor and chemistry, Bull. Soc. Chim. Fr., 1996, 133, 117–130 CAS.
- T. O. Drews, M. A. Katsoulakis and M. Tsapatsis, A Mathematical Model for Crystal Growth by Aggregation of Precursor Metastable Nanoparticles, J. Phys. Chem. B, 2005, 109, 23879–23887 CrossRef CAS PubMed.
- E. D. Dill, A. A. Josey, J. C. W. Folmer, F. Hou and J. D. Martin, Experimental Determination of the Crystallization Phase-Boundary Velocity in the Halozeotype CZX-1, Chem. Mater., 2013, 25, 3932–3940 CrossRef CAS.
- L. K. Plummer, B. M. Crockett, M. K. Pennel, A. W. Jansons, K. M. Kosela and J. E. Hutchison, Influence of Monomer Flux and Temperature on Morphology of Indium Oxide Nanocrystals during a Continuous Growth Synthesis, Chem. Mater., 2019, 31, 7638–7649 CrossRef CAS.
- T. J. Woehl, C. Park, J. E. Evans, I. Arslan, W. D. Ristenpart and N. D. Browning, Direct Observation of Aggregative Nanoparticle Growth: Kinetic Modeling of the Size Distribution and Growth Rate, Nano Lett., 2014, 14, 373–378 CrossRef CAS PubMed.
- C. B. Whitehead, S. Özkar and R. G. Finke, LaMer's 1950 Model for Particle Formation of Instantaneous Nucleation and Diffusion-Controlled Growth: A Historical Look at the Model's Origins, Assumptions, Equations, and Underlying Sulfur Sol Formation Kinetics Data, Chem. Mater., 2019, 31, 7116–7132 CrossRef CAS.
- C. B. Whitehead, S. Özkar and R. G. Finke, LaMer's 1950 Model of Particle Formation: A Review and Critical Analysis of Its Classical Nucleation and Fluctuation Theory Basis, of Competing Models and Mechanisms for Phase-Changes and Particle Formation, and then of Its Application to Silver Halide, Semiconductor, Metal, and Metal-Oxide Nanoparticles, Mater. Adv., 2021, 2, 186–235 RSC.
- D. R. Handwerk, P. D. Shipman, C. B. Whitehead, S. Özkar and R. G. Finke, Mechanism-Enabled Population Balance Modeling of Particle Formation en Route to Particle Average Size and Size Distribution Understanding and Control, J. Am. Chem. Soc., 2019, 141, 15827–15839 CrossRef CAS PubMed.
- D. R. Handwerk, P. D. Shipman, C. B. Whitehead, S. Özkar and R. G. Finke, Particle Size Distributions via Mechanism-Enabled Population Balance Modeling, J. Phys. Chem. C, 2020, 124, 4852–4880 CrossRef CAS.
- S. M. Kathmann, G. K. Schenter and B. C. Garrett, Understanding the Sensitivity of Nucleation Kinetics, J. Chem. Phys., 2002, 116, 5046–5057 CrossRef CAS.
- S. M. Kathmann, G. K. Schenter, B. C. Garrett, B. Chen and J. I. Siepmann, Thermodynamics and Kinetics of Nanoclusters Controlling Gas-to-Particle Nucleation, J. Phys. Chem. C, 2009, 113, 10354–10370 CrossRef CAS . See also the ref. 16 and 25-37 therein concerning DFT studies that strive to go beyond Classical Nucleation Theory.
- R. E. Plata and D. A. Singleton, A Case Study of the Mechanism of Alcohol-Mediated Morita Baylis Hillman Reactions. The Important of Experimental Observations, J. Am. Chem. Soc., 2015, 137, 3811–3826 CrossRef CAS PubMed.
- A. M. Karim, N. Al-Hasan, S. Ivanov, S. Siefert, R. T. Kelly, N. G. Hallfors, A. Benavidez, L. Kovarik, A. Jenkins, R. E. Winans and A. K. Datye, Synthesis of 1 nm Pd Nanoparticles in a Microfluidic Reactor: Insights from in Situ X-ray Absorption Fine Structure Spectroscopy and Small-Angle X-ray Scattering, J. Phys. Chem. C, 2015, 119, 13257–13267 CrossRef.
- E. G. Moschetta, K. M. Gans and R. M. Rioux, Characterization of sites of different thermodynamic affinities on the same metal center via isothermal titration calorimetry, J. Catal., 2013, 302, 1–9 CrossRef CAS.
- T. Teranishi and M. Miyake, Size Control of Palladium Nanoparticles and Their Crystal Structures, Chem. Mater., 1998, 10, 594–600 CrossRef CAS.
- M. J. Hostetler, J. E. Wingate, C.-J. Zhong, J. E. Harris, R. W. Vachet, M. R. Clark, J. D. Londono, S. J. Green, J. J. Stokes, G. D. Wignall, G. L. Glish, M. D. Porter, N. D. Evans and R. W. Murray, Alkanethiolate Gold Cluster Molecules with Core Diameters from 1.5 to 5.2 nm: Core and Monolayer Properties as a Function of Core Size, Langmuir, 1998, 14, 17–30 CrossRef CAS.
- B.-H. Wu, H.-Y. Yang, H.-Q. Huang, G.-X. Chen and N.-F. Zheng, Solvent effect on the synthesis of monodisperse amine-capped Au nanoparticles, Chin. Chem. Lett., 2013, 24, 457–462 CrossRef CAS.
- Y. Jiang, Y. Huang, H. Cheng, Q. Liu, Z. Xie, T. Yao, Z. Jiang, Y. Huang, Q. Bian, G. Pan, Z. Sun and S. Wei, Solvent Influence on the Role of Thiols in Growth of Thiols-Capped Au Nanocrystals, J. Phys. Chem. C, 2014, 118, 714–719 CrossRef CAS.
- C. Nayak, S. N. Jha and D. Bhattacharyya, In Situ X-Ray Absorption Spectroscopy to Study Growth of Nanoparticles, in In-Situ Characterization Techniques for Nanomaterials, ed. C. S. S. R. Kumar, Springer-Verlag GmbH, Berlin Heidelberg, 2018, pp. 189–222 Search PubMed.
- H. Asakura, K. Teramura, T. Shishido, T. Tanaka, N. Yan, C. Xiao, S. Yao and Y. Kou, In situ time-resolved DXAFS study of Rh nanoparticle formation mechanism in ethylene glycol at elevated temperature, Phys. Chem. Chem. Phys., 2012, 14, 2983–2990 RSC.
- C. Besson, E. E. Finney and R. G. Finke, Nanocluster Nucleation, Growth and Then Agglomeration Kinetic and Mechanistic Studies: A More General, Four-Step Mechanism Involving Double Autocatalysis, Chem. Mater., 2005, 17, 4925–4938 CrossRef CAS.
- Y. Lin and R. G. Finke, Novel Polyoxoanion and Bu4N+ Stabilized, Isolable, and Redissolvable, 20-30 Å Ir∼300-900 Nanoclusters: The Kinetically Controlled Synthesis, Characterization, and Mechanism of Formation of Organic Solvent-Soluble, Reproducible Size, and Reproducible Catalytic Activity Metal Nanoclusters, J. Am. Chem. Soc., 1994, 116, 8335–8353 CrossRef CAS.
- Y. Lin and R. G. Finke, A More General Approach to Distinguishing “Homogeneous” from “Heterogeneous” Catalysis: Discovery of Polyoxoanion- and Bu4N+-Stabilized, Isolable and Redissolvable, High Reactivity Ir∼190-450 Nanocluster Catalysts, Inorg. Chem., 1994, 33, 4891–4910 CrossRef CAS.
- E. P. Clark, Signer Method for Determining Molecular Weights, Ind. Eng. Chem., Anal. Ed., 1941, 13, 821 CrossRef.
- S. Özkar and R. G. Finke, Iridium(0) Nanocluster, Acid-Assisted Catalysis of Neat Acetone Hydrogenation at Room Temperature: Exceptional Activity, Catalyst Lifetime, and Selectivity at Complete Conversion, J. Am. Chem. Soc., 2005, 127, 4800–4808 CrossRef PubMed.
- E. T. Dias, S. K. Gill, Y. Liu, P. Halstenberg, S. Dai, J. Huang, J. Mausz, R. Gakhar, W. C. Phillips, S. Mahurin, S. M. Pimblott, J. F. Wishart and A. I. Frenkel, Radiation-Assisted Formation of Metal Nanoparticles in Molten Salts, J. Phys. Chem. Lett., 2021, 12, 157–164 CrossRef CAS PubMed.
- J. Ma, Y. Zou, Z. Jiang, W. Huang, J. Li, G. Wu, Y. Huang and H. Xu, An in situ XAFS study—the formation mechanism of gold nanoparticles from X-ray-irradiated ionic liquid, Phys. Chem. Chem. Phys., 2013, 15, 11904–11908 RSC.
- A. Bharti, R. Bhardwaj, A. K. Agrawal, N. Goyal and S. Gautam, Monochromatic X-Ray Induced Novel Synthesis of Plasmonic Nanostructure for Photovoltaic Application, Sci. Rep., 2016, 6, 22394 CrossRef CAS PubMed.
- J. Grand, S. R. Ferreira, V. de Waele, S. Mintova and T. M. Nenoff, Nanoparticle Alloy Formation by Radiolysis, J. Phys. Chem. C, 2018, 122, 12573–12588 CrossRef CAS.
- J. Quinson and K. M. Ø. Jensen, From platinum atoms in molecules to colloidal nanoparticles: A review on reduction, nucleation and growth mechanisms, Adv. Colloid Interface Sci., 2020, 286, 102300 CrossRef CAS PubMed.
- S. Remita, P. Fontaine, E. Lacaze, Y. Borensztein, H. Sellame, R. Farha, C. Rochas and M. Goldmann, X-ray radiolysis induced formation of silver nano-particles: A SAXS and UV-visible absorption spectroscopy study, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 263, 436–440 CrossRef CAS.
- L. Bondaz, P. Fontaine, F. Muller, N. Pantoustier, P. Perrin, I. Morfin, M. Goldmann and F. Cousin, Controlled Synthesis of Gold Nanoparticles in Copolymers Nanomolds by X-ray Radiolysis, Langmuir, 2020, 36, 6132–6144 CrossRef CAS PubMed.
- A. Yamaguchi, T. Fukuoka, I. Okada, M. Ishihara, I. Sakurai and Y. Utsumi, Caltrop Particles Synthesized by Photochemical Reaction Induced by X-Ray Radiolysis, J. Synchrotron Radiat., 2017, 24, 653–660 CrossRef CAS PubMed.
- T. R. Stachowski, M. E. Snell and E. H. Snell, SAXS studies of X-ray induced disulfide bond damge: Engineering high-resolution insight from a low-resolution technique, PLoS One, 2020, 15, 0239702, DOI:10.1371/journal.pone.0239702.
- The ∼1016 solvated electrons results from the rough estimation reported in the ESI of ref. 85. Therein, it is calculated that 1 photon of 8 keV energy results in the formation of ∼300 absorbed electrons. Hence, given the observed complete absorption of radiation in the system examined, it was calculated that (300 absorbed electrons/photon) × (∼3 × 1013 photons/second) = ∼1016 solvated electrons per second are produced.
- S. Özkar and R. G. Finke, Nanoparticle Formation Kinetics and Mechanistic Studies Important to Mechanism-Based Particle-Size Control: Evidence for Ligand-Based Slowing of the Autocatalytic Surface Growth Step Plus Postulated Mechanisms, J. Phys. Chem. C, 2019, 123, 14047–14057 CrossRef.
- S. Özkar and R. G. Finke, The hydrogenphosphate complex of (1,5-cyclooctadiene)iridium(I), {[Bu4N][(1,5-COD)Ir•HPO4]}n: synthesis, spectroscopic characterization, and ES-MS of a new, preferred precursor to HPO42− and Bu4N+ stabilized Ir(0)n nanoclusters, J. Organomet. Chem., 2004, 689, 493–501 CrossRef.
- S. Özkar and R. G. Finke, Transition-Metal Nanocluster Stabilization Fundamental Studies: Hydrogen Phosphate as a Simple, Effective, Readily Available, Robust, and Previously Unappreciated Stabilizer for Well-Formed, Isolable, and Redissolvable Ir(0) and Other Transition-Metal Nanoclusters, Langmuir, 2003, 19, 6247–6260 CrossRef.
- B. Ravel and M. Newville, ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- C. A. Leatherdale, W.-K. Woo, F. V. Mukulec and M. G. Bawendi, On the Absorption Cross Section of CdSe Nanocrystal Quantum Dots, J. Phys. Chem. B, 2002, 106, 7619–7622 CrossRef CAS.
- X. Jia, P. Zhang, Z. Lin, R. Anthony, U. Kortshagen, S. Huang, B. Puthen-Veettil, G. Conibeer and I. Perez-Wurfl, Accurate determination of the size distribution of Si nanocrystals from PL spectra, RSC Adv., 2015, 5, 55119–55125 RSC.
- A. J. Houtepen, Z. Hens, J. S. Owen and I. Infante, On the Origin of Surface Traps in Colloidal II–VI Semiconductor Nanocrystals, Chem. Mater., 2017, 29, 752–761 CrossRef CAS.
- M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnest, G. Konstantataos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, Prospects of nanoscience with nanocrystals, ACS Nano, 2015, 9, 1012–1057 CrossRef CAS PubMed.
- J. De Roo, K. De Keukeleere, Z. Hens and I. Van Driessche, From ligands to binding motifs and beyond; the enhanced versatility of nanocrystal surfaces, Dalton Trans., 2016, 45, 13277–13283 RSC.
- P. Reiss, M. Carrière, C. Lincheneau, L. Vaure and S. Tamang, Synthesis of Semiconductor Nanocrystals, Focusing on Nontoxic and Earth-Abundant Materials, Chem. Rev., 2016, 116, 10731–10819 CrossRef CAS PubMed.
- E. Dhaene, J. Billet, E. Bennett, I. Van Driessche and J. De Roo, The Trouble with ODE: Polymerization during Nanocrystal Synthesis, Nano Lett., 2019, 19, 7411–7417 CrossRef CAS PubMed.
- Further, given the discussion vide supra in the Background section concerning CNT's inapplicability to strong bonding systems, alternative mechanisms need to be tests and disproven en route to claiming an understanding of ZnO particle-formation mechanism.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Shape-Controlled Synthesis of Metal Nanocrystals: Simple Chemistry Meets Complex Physics?, Angew. Chem., Int. Ed., 2009, 48, 60–103 CrossRef CAS PubMed.
- T. S. Ahmadi, Z. L. Wang, T. C. Green, A. Henglein and M. A. El-Sayed, Shape-Controlled Synthesis of Colloidal Platinum Nanoparticles, Science, 1996, 272, 1924–1926 CrossRef CAS PubMed.
- M. A. Watzky and R. G. Finke, Nanocluster Size-Control and “Magic Number” Investigations. Experimental Tests of the “Living-Metal Polymer” Concept and of Mechanism-Based Size-Control Predictions Leading to the Syntheses of Iridium(0) Nanoclusters Centering About Four Sequential Magic Numbers, Chem. Mater., 1997, 9, 3083 CrossRef CAS.
- I. Olliges-Stadler, J. Stötzel, D. Koziej, M. D. Rossell, J.-D. Grunwaldt, M. Nachtegaal, R. Frahm and M. Niederberger, Study of the Chemical Mechanism Involved in the Formation of Tungstite in Benzyl Alcohol by the Advanced QEXAFS Technique, Chem. – Eur. J., 2012, 18, 2305–2312 CrossRef CAS PubMed.
- I. Olliges-Stadler, M. D. Rossell, M. J. Süess, B. Ludi, O. Bunk, J. S. Pedersen, H. Birkedal and M. Niederberger, A comprehensive study of the crystallization mechanism involved in the nonaqueous formation of tungstite, Nanoscale, 2013, 5, 8517–8525 RSC.
- M. Strach, V. Mantella, J. R. Pankhurst, P. Iyengar, A. Loiudice, S. Das, C. Corminboeuf, W. van Beek and R. Buonsanti, Insights into Reaction Intermediates to Predict Synthetic Pathways for Shape-Controlled Metal Nanocrystals, J. Am. Chem. Soc., 2019, 41, 16312–16322 CrossRef PubMed.
- M. Staniuk, O. Hirsch, N. Kránzlin, R. Böhlen, W. van Beek, P. M. Abdala and D. Koziej, Puzzling Mechanism behind a Simple Synthesis of Cobalt and Cobalt Oxide Nanoparticles: In Situ Synchrotron X-ray Absorption and Diffraction Studies, Chem. Mater., 2014, 26, 2086–2094 CrossRef CAS.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Movalenko, Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut, Nano Lett., 2015, 15, 2692–2696 CrossRef PubMed.
- D. W. Talapin, J.-S. Lee, M. V. Kovalenko and E. V. Shevchenko, Prospects of Colloidal Nanocrystals for Electronic and Optoelectronic Applications, Chem. Rev., 2010, 110, 389–458 CrossRef CAS PubMed.
- A. Dey, J. Ye, A. De, E. Debroye, S. K. Ha, E. Bladt, A. S. Kshiragar, Z. Wang, J. Yin, Y. Wang, L. N. Quan, F. Yan, M. Gao, Z. Li, J. Shamsi, T. Debnath, M. Cao, M. A. Scheel, S. Kumar, J. A. Steele, M. Gerhard, L. Chouhan, K. Xu, X. Wu, Y. Li, Y. Zhang, A. Dutta, C. Han, I. Vincon, A. L. Rogach, A. Nag, A. Samanta, B. A. Korgetl, C.-J. Shih, D. R. Gamelin, D. H. Son, H. Zeng, H. Zhong, H. Sun, H. V. Demir, I. G. Scheblykin, I. Mora-Seró, J. K. Stolarczyk, J. Z. Zhang, J. Feldmann, J. Hofkens, J. M. Luther, J. Pérez-Prieto, L. Li, L. Manna, M. I. Bodnarchuk, M. V. Kovalenko, M. B. J. Roeffaers, N. Pradhan, O. F. Mohammed, O. M. Bakr, P. Yang, P. Müller-Buschbaum, P. V. Kamat, Q. Bao, Q. Zhang, R. Krahne, R. E. Galian, S. D. Stranks, S. Bals, V. Biju, W. A. Tisdale, Y. Yan, R. L. Z. Hoye and L. Polavarapu, State of the Art and Prospects for Halide Perovskite Nanocrystals, ACS Nano, 2021, 15, 10775–10981 CrossRef CAS PubMed.
- Y. Zhang, T. D. Siegler, C. J. Thomas, M. K. Abney, T. Shah, A. De Gorostiza, R. M. Greene and B. A. Korgel, A “Tips and Tricks” Practical Guide to the Synthesis of Metal Halide Perovskite Nanocrystals, Chem. Mater., 2020, 32, 5410–5423 CrossRef CAS.
- J. Just, C. Coughlan, S. Singh, H. Ren, O. Müller, P. Becker, T. Unold and K. M. Ryan, Insights into Nucleation and Growth of Colloidal Quaternary Nanocrystals by Multimodal X-ray Analysis, ACS Nano, 2021, 15, 6439–6447 CrossRef CAS PubMed.
- M. J. Turnbull, D. Vaccarello, J. Wong, Y. M. Yiu, T.-K. Sham and Z. Ding, Probing the CZTS/CdS heterojunction utilizing photoelectrochemistry and X-ray absorption spectroscopy, J. Chem. Phys., 2018, 148, 134702 CrossRef PubMed.
- F. J. Espinosa-Faller, D. R. Conradson, S. C. Riha, M. B. Martucci, S. J. Fredrick, S. Vogel, A. L. Prieto and S. D. Conradson, Neutron Diffraction and X-ray Absorption Fine Structure Evidence for Local Lattice Distortions and Aperiodic Antisite Substitution in Cu2ZnSnS4 Nanoparticles, J. Phys. Chem. C, 2014, 118, 26292–26303 CrossRef CAS.
- A. E. Maughan, E. M. Mozur, A. M. Candia and J. R. Neilson, Ferroelastic Phase Transition in Formamidinium Tin(IV) Iodide Driven by Organic–Inorganic Coupling, Inorg. Chem., 2020, 59, 14399–14406 CrossRef CAS PubMed.
- E. M. Mozur, M. A. Hope, J. C. Trowbridge, D. M. Halat, L. L. Daemen, A. E. Maughan, T. R. Prisk, C. P. Grey and J. R. Neilson, Cesium Substitution Disrupts Concerted Cation Dynamics in Formamidinium Hybrid Perovskites, Chem. Mater., 2020, 32, 6266–6277 CrossRef CAS.
- B. Liu, R. Cui, H. Huang, X. Guo, S. Zuo, J. Dong, H. Yao, Y. Li, D. Zhao, J. Wang, J. Zhang, Y. Chen, J. Yang and B. Sun, Structure optimization of CH3NH3PbI3 by higher-valence Pb in perovskite solar cells with enhanced efficiency and stability, Sol. Energy, 2020, 205, 202–210 CrossRef CAS.
- K. Shen, J. Hu, Z. Liang, J. Hu, H. Sun, Z. Jiang and F. Song, Emerging Characterizing Techniques in the Fine Structure Observation of Metal Halide Perovskite Crystal, Crystals, 2018, 8, 232 CrossRef.
- H. Sun and W. Zhou, Progress on X-ray Absorption Spectroscopy for the Characterization of Perovskite-Type Oxide Electrocatalysts, Energy Fuels, 2021, 35, 5716–5737 CrossRef CAS.
- S. Song, J. Zhou, Y. Wang, J. Li, L. Zhang, G. Xiao, C. Guan, R. Liu, S. Chen, H.-J. Lin, S. Zhang and J.-Q. Wang, Operando X-ray spectroscopic tracking of self-reconstruction for anchored nanoparticles as high-performance electrocatalysts towards oxygen evolution, Energy Environ. Sci., 2018, 11, 2945–2953 RSC.
- H. Huang, M. W. Feil, S. Fuchs, T. Debnath, A. F. Richter, Y. Tong, L. Wu, Y. Wang, M. Döblinger and B. Nickel, Growth of Perovskite CsPbBr3 Nanocrystals and Their Formed Superstructures Revealed by In Situ Spectroscopy, Chem. Mater., 2020, 32, 8877–8884 CrossRef CAS.
- V. V. Hoang and D. Ganguli, Amorphous nanoparticles – Experiments and computer simulations, Phys. Rep., 2012, 518, 81–140 CrossRef CAS.
- J. B. Lee, O. H. Chae, S. Chae, J. H. Ryu and S. M. Oh, Amorphous Vanadium Titanates as a Negative Electrode for Lithium-ion Batteries, J. Electrochem. Sci. Technol., 2016, 7, 306–315 CrossRef CAS.
- R. Jog and D. J. Burgess, Pharmaceutical Amorphous Nanoparticles, J. Pharm. Sci., 2017, 106, 39–65 CrossRef CAS PubMed.
- Q. T. Phan, K. C. Poon and H. Sato, A review on amorphous noble-metal-based electrocatalysts for fuel cells: Synthesis, characterization, performance, and future perspective, Int. J. Hydrogen Energy, 2021, 46, 14190–14211 CrossRef CAS.
- J. Wang, M. Fan, X. Bian, M. Yu, T. Wang, S. Liu, Y. Yang, Y. Tian and R. Guan, Enhanced magnetic heating efficiency and thermal conductivity of magnetic nanofluids with FeZrB amorphous nanoparticles, J. Magn. Magn. Mater., 2018, 465, 480–488 CrossRef CAS.
- B. Cantaert, D. Kuo, S. Matsumura, T. Nishimura, T. Sakamoto and T. Kato, Use of Amorphous Calcium Carbonate for the Design of New Materials, ChemPlusChem, 2017, 82, 107–120 CrossRef CAS PubMed.
- S. Von Euw, T. Azaïs, W. Manichev, G. Laurent, G. Pehau-Arnaudet, M. Rivers, N. Murali, D. J. Kelly and P. G. Falkowski, Solid-State Phase Transformation and Self-Assembly of Amorphous Nanoparticles into Higher-Order Mineral Structures, J. Am. Chem. Soc., 2020, 142, 12811–12825 CrossRef CAS PubMed.
- A. Indra, P. W. Menezes, N. R. Sahraie, A. Bergmann, C. Das, M. Tallarida, D. Schmeißer, P. Strasser and M. Driess, Unification of Catalytic Water Oxidation and Oxygen Reduction Reactions: Amorphous Beat Crystalline Cobalt Iron Oxides, J. Am. Chem. Soc., 2014, 136, 17530–17536 CrossRef CAS PubMed.
- Z. Chen, Z. Duan, Z. Wang, X. Liu, L. Gu, F. Zhang, M. Dupuis and C. Li, Amorphous Cobalt Oxide Nanoparticles as Active Water Oxidation Catalysts, ChemCatChem, 2017, 9, 3641–3645 CrossRef CAS.
- Y. Tan, D. Sun, H. Yu, B. Yang, Y. Gong, S. Yan, Z. Chen, Q. Cai and Z. Wu, Crystallization mechanism analysis of noncrystalline Ni-P nanoparticles through XRD, HRTEM and XAFS, CrystEngComm, 2014, 16, 9657–9668 RSC.
- H. Yoshitake, T. Sugihara and T. Tatsumi, XAFS study on the local structure of Ti in amorphous mesoporous titania, Phys. Chem. Chem. Phys., 2003, 5, 767–772 RSC.
- L. Khouchaf, F. Boinski, M. H. Tuilier and A. M. Flank, Characterization of heterogeneous SiO2 materials by scanning electron microscope and micro fluorescence XAS techniques, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 252, 333–338 CrossRef CAS.
- D. Singh, S. Basu, R. K. Mandal, O. N. Srivastava and R. S. Tiwari, Formation of nano-amorphous domains in Ce75Al25-xGax alloys with delocalization of cerium 4f electrons, Intermetallics, 2015, 67, 87–93 CrossRef CAS.
- L. M. Moreau, D.-H. Ha, H. Zhang, R. Hovden, D. A. Muller and R. D. Robinson, Defining Crystalline/Amorphous Phases of Nanoparticles through X-ray Absorption Spectroscopy and X-ray Diffraction: The Case of Nickel Phosphide, Chem. Mater., 2013, 25, 2394–2403 CrossRef CAS.
- X. Xu, R. Ray, Y. Gu, H. J. Ploehn, L. Gearheart, K. Raker and W. A. Scrivens, Electrophoretic Analysis and Purification of Fluorescent Single-Walled Carbon Nanotube Fragments, J. Am. Chem. Soc., 2004, 126, 12736–12737 CrossRef CAS PubMed.
- L. Zhu, D. Shen, C. Wu and S. Gu, State-of-the-Art on the Preparation, Modification, and Application of Biomass-Derived Carbon Quantum Dots, Ind. Eng. Chem. Res., 2020, 59, 22017–22039 CrossRef CAS.
- Y. Wang and A. Hu, Carbon quantum dots: synthesis, properties and applications, J. Mater. Chem. C, 2014, 2, 6921–6939 RSC.
- R. Kumar, V. B. Kumar and A. Gedanken, Sonochemical synthesis of carbon dots, mechanism, effect of parameters, and catalytic, energy, biomedical and tissue engineering applications, Ultrason. Sonochem., 2020, 64, 105009 CrossRef CAS PubMed.
- V. C. Hoang, K. Dave and V. G. Gomes, Carbon quantum dot-based composites for energy storage and electrocatalysis: Mechanism, applications and future prospects, Nano Energy, 2019, 66, 104093 CrossRef CAS.
- M. Han, S. Zhu, S. Lu, Y. Song, T. Feng, S. Tao, J. Liu and B. Yang, Recent progress on the photocatalysis of carbon dots: Classification, mechanism and applications, Nano Today, 2018, 19, 201–218 CrossRef CAS.
- Z. Song, F. Quan, Y. Xu, M. Liu, L. Cui and J. Liu, Multifunctional N,S co-doped carbon quantum dots with pH- and thermo-dependent switchable fluorescent properties and highly selective detection of glutathione, Carbon, 2016, 104, 169–178 CrossRef CAS.
- M. Shamsipur, A. Barati and S. Karami, Long-wavelength, multicolor, and white-light emitting carbon-based dots: Achievements made, challenges remaining, and applications, Carbon, 2017, 124, 429–472 CrossRef CAS.
- G. He, M. Shu, Z. Yang, Y. Ma, D. Huang, S. Xu, Y. Wang, N. Hu, Y. Zhang and L. Xu, Microwave formation and photoluminescence mechanisms of multi-states nitrogen doped carbon dots, Appl. Surf. Sci., 2017, 422, 257–265 CrossRef CAS.
- D. Pu, J. Zhang, Z. Li and M. Wu, Hydrothermal Route for Cutting Graphene Sheets into Blue-Luminescent Graphene Quantum Dots, Adv. Mater., 2010, 22, 734–738 CrossRef PubMed.
- M. J. Krysmann, A. Kelarakis, P. Dallas and E. P. Giannelis, Formation Mechanism of Carbogenic Nanoparticles with Dual Photoluminescence Emission, J. Am. Chem. Soc., 2012, 134, 747–750 CrossRef CAS PubMed.
- M. Rusyniak, V. Abdelsayed, J. Campbell and M. S. El-Shall, Vapor Phase Homogeneous Nucleation of Higher Alkanes: Dodecane, Hexadecane, and Octadecane. 1. Critical Supersaturation and Nucleation Rate Measurements, J. Phys. Chem. B, 2011, 105, 11866–11872 CrossRef.
- M. Rusyniak and M. S. El-Shall, Vapor Phase Homogeneous Nucleation of Higher Alkanes: Dodecane, Hexadecane, and Octadecane. 2. Corresponding States and Scaling Law Analysis, J. Phys. Chem. B, 2001, 105, 11873–11879 CrossRef CAS.
- J. W. Gibbs, On the Equilibrium of Heterogeneous Substances, Trans. Conn. Acad. Arts Sci., 1874, III, 343–523 Search PubMed.
- M. Volmer, Kinetik der Phasenbildung, Verlag von Theordor Steinkopff, Leipzig, 1939 Search PubMed.
- R. Becker and W. Döring, Kinetische Behandlung der Keimbildung in übersättigten Dampfen, Ann. Phys., 1935, 24, 719–752 CrossRef CAS.
- M. Avrami, Kinetics of Phase Change. I. General Theory, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- M. Avrami, Kinetics of Phase Change. II. Transformation-Time Relations for Random Distribution of Nuclei, J. Chem. Phys., 1940, 8, 212–224 CrossRef CAS.
- M. Avrami, Kinetics of Phase Change. III. Granulation, Phase Change, and Microstructure, J. Chem. Phys., 1941, 9, 177–184 CrossRef CAS.
- A. N. Kolmogorov, On the Statistical Theory of Metal Crystallization, Bull. Acad. Sci. USSR, Phys. Ser., 1937, 3, 555–560 Search PubMed.
- W. A. Johnson and R. F. Mehl, Reaction Kinetics in Processes of Nucleation and Growth, Trans. AIME, 1939, 135, 416–458 Search PubMed.
- B. A. Erofe’ev, A Generalized Equation of Chemical Kinetics and its Application in Reactions Involving Solids, Dokl. Akad. Sci. USSR, 1946, 52, 511–514 Search PubMed.
- E. D. Dill, A. A. Josey, J. C. W. Folmer, F. Hou and J. D. Martin, Experimental Determination of the Crystallization Phase-Boundary Velocity in the Halozeotype CZX-1, Chem. Mater., 2013, 25, 3932–3940 CrossRef CAS.
- R. G. Finke, M. A. Watzky and C. B. Whitehead, Response to “Particle Size Is a Primary Determinant for Sigmoidal Kinetics of Nanoparticle Formation: A “Disproof” of the Finke–Watzky (F-W) Nanoparticle Nucleation and Growth Mechanism”, Chem. Mater., 2020, 32, 3657–3672 CrossRef CAS.
- V. K. LaMer and R. H. Dinegar, Theory, Production and Mechanism of Formation of Monodispersed Hydrosols, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- C. B. Whitehead, M. A. Watzky and R. G. Finke, “Burst Nucleation” vs. Autocatalytic, “Burst” Growth In Near-Monodisperse Particle Formation Reactions, J. Phys. Chem. C, 2020, 32, 3657–3672 Search PubMed.
- M. Harada and Y. Inada, In Situ Time-Resolved XAFS Studies of Metal Particle Formation by Photoreduction in Polymer Solutions, Langmuir, 2009, 25, 6049–6061 CrossRef CAS PubMed.
- A. P. LaGrow, B. Ingham, M. F. Toney and R. D. Tilley, Effect of Surfactant Concentration and Aggregation on the Growth Kinetics of Nickel Nanoparticles, J. Phys. Chem. C, 2013, 117, 16709–16718 CrossRef CAS.
- A. Kytsya, L. Hazylyak, Y. Hrynda, A. Horechyy and Y. Medvedevdkikh, The Kinetic Rate Law for the Autocatalytic Growth of Citrate-Stabilized Silver Nanoparticles, Int. J. Chem. Kinet., 2015, 47, 351–360 CrossRef CAS.
- A. P. Sergievskaya, V. V. Tatarchuk, E. V. Makotchenko and I. V. Mironov, Formation of gold nanoparticles during the reduction of HAuBr4 in reverse micelles of oxyethylated surfactant: Influence of gold precursor on the growth kinetics and properties of the particles, J. Mater. Res., 2015, 30, 1925–1933 CrossRef CAS.
- M. Harada and S. Kizaki, Formation Mechanism of Gold Nanoparticles Synthesized by Photoreduction in Aqueous Ethanol Solution of Polymers Using In Situ Quick Scanning X-ray Absorption Fine Structure and Small-Angle X-ray Scattering, Cryst. Growth Des., 2016, 16, 1200–1212 CrossRef CAS.
- T.-H. Yang, H.-C. Peng, S. Zhou, C.-T. Lee, S. Bao, Y.-H. Lee, J.-M. Wu and Y. Xia, Toward a Quantitative Understanding of the Reduction Pathways of a Salt Precursor in the Synthesis of Metal Nanocrystals, Nano Lett., 2017, 17, 334–340 CrossRef CAS PubMed.
- B. Peters, Common Features of Extraordinary Rate Theories, J. Phys. Chem. B, 2015, 119, 6349–6356 CrossRef CAS PubMed.
- V. K. La Mer, Nucleation in Phase Transitions, Ind. Eng. Chem., 1952, 44, 1270–1277 CrossRef CAS.
- J. Turkevich, P. C. Stevenson and J. Hillier, A Study of the Nucleation and Growth Processes in the Synthesis of Colloidal Gold, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- J. Turkevich, P. C. Stevenson and J. Hillier, The Formation of Colloid Gold, J. Phys. Chem., 1953, 57, 670–673 CrossRef CAS.
- E. Bayram, J. C. Linehan, J. L. Fulton, J. A. S. Roberts, N. K. Szymczak, T. D. Smurthwaite, S. Özkar, M. Balasubramanian and R. G. Finke, Is it Homogeneous or Heterogeneous Catalysis Derived from [RhCp*Cl2]2? In Operando XAFS, Kinetic, and Crucial Kinetic Poisoning Evidence for Subnanometer Rh4 Cluster-Based Benzene Hydrogenation Catalysis, J. Am. Chem. Soc., 2011, 133, 18889–18902 CrossRef CAS PubMed.
- J. E. Mondloch, Q. Wang, A. I. Frenkel and R. G. Finke, Development Plus Kinetic and Mechanistic Studies of a Prototype Supported-Nanoparticle Heterogeneous Catalyst Formation System in Contact with Solution: Ir(1,5-COD)Cl/γ-Al2O3 and Its Reduction by H2 to Ir(0)n/γ-Al2O3, J. Am. Chem. Soc., 2010, 132, 9701–9714 CrossRef CAS PubMed.
- F. Tong, M. P. Hanson and C. Bardeen, Analysis of reaction kinetics in the photochemical molecular crystal 9-methylanthracene using an extended Finke-Watzky model, Phys. Chem. Chem. Phys., 2016, 18, 31936–31945 RSC.
- M. B. Avinash, K. V. Sandeepa and T. Govindaraju, Emergent Behaviors in Kinetically Controlled Dynamic Self-Assembly of Synthetic Molecular Systems, ACS Omega, 2016, 1, 378–387 CrossRef CAS PubMed.
- A. M. Morris, M. A. Watzky, J. N. Agar and R. G. Finke, Fitting neurological protein aggregation kinetic data via a 2-step, minimal/”Ockham's razor” model: the Finke-Watzky mechanism of nucleation followed by autocatalytic surface growth, Biochemistry, 2008, 47, 2413–2427 CrossRef CAS PubMed.
- N. A. Oladoja, A critical review of the applicability of Avrami fractional kinetic equation in adsorption-based water treatment studies, Desalin. Water Treat., 2015, 57, 15813–15825 CrossRef.
- B. J. Hornstein and R. G. Finke, Transition-Metal Nanocluster Kinetic and Mechanistic Studies Emphasizing Nanocluster Agglomeration: Demonstration of a Kinetic Method That Allows Monitoring All Three Phases of Nanocluster Formation and Aging, Chem. Mater., 2004, 16, 139–150 CrossRef CAS . (See also the addition/correction: Chem. Mater., 2004, 16, 3972).
- C. Besson, E. E. Finney and R. G. Finke, A Mechanism for Transition-Metal Nanoparticle Self-Assembly, J. Am. Chem. Soc., 2005, 127, 8179–8184 CrossRef CAS PubMed.
- E. E. Finney and R. G. Finke, The Four-Step, Double-Autocatalytic Mechanism for Transition-Metal Nanocluster Nucleation, Growth and Then Agglomeration: Metal, Ligand, Concentration, Temperature, and Solvent Dependency Studies, Chem. Mater., 2008, 20, 1956–1970 CrossRef CAS.
- P. D. Kent, J. E. Mondloch and R. G. Finke, A Four-Step Mechanism for the Formation of Supported-Nanoparticle Heterogeneous Catalysts in Contact with Solution: The Conversion of Ir(1,5-COD)Cl/γ-Al2O3 to Ir(0)∼170/γ-Al2O3, J. Am. Chem. Soc., 2014, 136, 1930–1941 CrossRef CAS PubMed.
- T. O. Drews, M. A. Katsoulakis and M. Tsapatsis, A Mathematical Model for Crystal Growth by Aggregation of Precursor Metastable Nanoparticles, J. Phys. Chem. B, 2005, 109, 23879–23887 CrossRef CAS PubMed.
- H. Koerner, R. I. MacCuspie, K. Park and R. A. Vaia, In Situ UV/Vis, SAXS, and TEM Study of Single-Phase Gold Nanoparticle Growth, Chem. Mater., 2012, 24, 981–995 CrossRef CAS.
- T. Yao, Z. Sun, Y. Li, Z. Pan, H. Wei, Y. Xie, M. Nomura, Y. Niwa, W. Yan, Z. Wu, Y. Jiang, Q. Liu and S. Wei, Insights into Initial Kinetic Nucleation of Gold Nanocrystals, J. Am. Chem. Soc., 2010, 132, 7696–7701 CrossRef CAS PubMed.
- T. Tanaka, J. Ohyama, K. Teramura and Y. Hitomi, Formation mechanism of metal nanoparticles studied by XAFS spectroscopy and effective synthesis of small metal nanoparticles, Catal. Today, 2012, 183, 108–118 CrossRef CAS.
- Y. Liu, L. Qian, X. Zhao, J. Wang, L. Yao, X. Xing, G. Mo, Q. Cai, Z. Chen and Z. Wu, Synthesis and formation mechanism of self-assembled 3D flower-like Bi/γ-Fe2O3 composite particles, CrystEngComm, 2019, 21, 2799–2808 RSC.
- M. Saeki, D. Matsumura, T. Yomogida, T. Taguchi, T. Tsuji, H. Saitoh and H. Ohba, In Situ Time-Resolved XAFS Studies on Laser-Induced Particle Formation of Palladium Metal in an Aqueous/EtOH Solution, J. Phys. Chem. C, 2019, 123, 817–824 CrossRef CAS.
- J. Wang, R. E. Winans, S. L. Anderson, S. Seifert, B. Lee, P. J. Chupas, Y. Ren, S. Lee and Y. Liu, In Situ Small-Angle X-ray Scattering from Pd Nanoparticles Formed by Thermal Decomposition of Organo-Pd Catalyst Precursors Dissolved in Hydrocarbons, J. Phys. Chem. C, 2013, 117, 22627–22635 CrossRef CAS.
- H. Asakura, K. Teramura, T. Shishido, T. Tanaka, N. Yan, C. Xiao, S. Yao and Y. Kou, In situ time-resolved DXAFS study of Rh nanoparticle formation mechanism in ethylene glycol at elevated temperature, Phys. Chem. Chem. Phys., 2012, 14, 2983–2990 RSC.
- T. Yao, S. Liu, Z. Sun, Y. Li, S. He, H. Cheng, Y. Xie, Q. Liu, Y. Jiang, Z. Wu, W. Yan and S. Wei, Probing Nucleation Pathways for Morphological Manipulation of Platinum Nanocrystals, J. Am. Chem. Soc., 2012, 134, 9410–9416 CrossRef CAS PubMed.
- K. X. Bhattacharyya, C. Pradel, P. Lecante and N. Mézailles, Mechanistic Investigations of the Synthesis of Size-Tunable Ni Nanoparticles by Reduction of Simple NiII Diamide Precursors, Chem. – Eur. J., 2017, 23, 9352–9361 CrossRef CAS PubMed.
- K. P. Weinfurt, Vanquishing false idols, then and now, Science, 2020, 367, 1312 CrossRef CAS.
- L. C. Ciacchi, W. Pompe and A. De Vita, Initial Nucleation of Platinum Clusters after Reduction of K2PtCl4 in Aqueous Solution:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A First Principles Study, J. Am. Chem. Soc., 2001, 123, 7371–7380 CrossRef CAS PubMed.
A First Principles Study, J. Am. Chem. Soc., 2001, 123, 7371–7380 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Summary of supporting information; case study #6: additional figures and information; differential equations for the Karim 4-step mechanism; Table S1 Summary of reviews on synchrotron XAFS and/or SAXS; Table S2 Summary of papers using SAXS to collect kinetics data; Table S3 Summary of papers using XAFS to collect kinetics data; Table S4 Summary of papers using tandem techniques: use of synchrotron XAFS and/or SAXS in combination with another technique. See DOI: 10.1039/d1ma00222h |
| This journal is © The Royal Society of Chemistry 2021 |
