Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical ordering in Pt–Au, Pt–Ag and Pt–Cu nanoparticles from density functional calculations using a topological approach†
Lorena
Vega
a,
Hristiyan A.
Aleksandrov
 *b,
Riccardo
Farris
a,
Albert
Bruix
*b,
Riccardo
Farris
a,
Albert
Bruix
 a,
Francesc
Viñes
a,
Francesc
Viñes
 a and
Konstantin M.
Neyman
a and
Konstantin M.
Neyman
 *ac
*ac
aDepartament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, 08028 Barcelona, Spain
bFaculty of Chemistry and Pharmacy, University of Sofia, 1126 Sofia, Bulgaria. E-mail: haa@chem.uni-sofia.bg
cICREA (Institució Catalana de Recerca i Estudis Avançats), 08010 Barcelona, Spain. E-mail: konstantin.neyman@icrea.cat
First published on 6th August 2021
Abstract
Bimetallic alloys are actively investigated as promising new materials for catalytic and other energy-related applications. However, the stable arrangements of the two metals in prevailing nanostructured systems, which define their structure and surface reactivity, are seldom addressed. The equilibrium chemical orderings of bimetallic nanoparticles are usually different from those in the corresponding bulk phases and hard to control experimentally, which hampers assessment of the relations between composition, structure, and reactivity. Herewith, we study mixtures of platinum—an essential metal in catalysis—alloyed with coinage metals gold, silver, and copper. These systems are interesting, for instance, for reducing the costly Pt content and designing improved multifunctional catalysts, but the chemical orderings in such mixtures at the nanoscale are still debated. We therefore explore chemical orderings and properties of Pt-containing nanoalloys by means of a topological method based on density functional calculations. We determine the lowest-energy chemical orderings in 1.4 to 4.4 nm large Pt–Au, Pt–Ag and Pt–Cu particles with different contents of metals. Chemical ordering, bonding, and charge distribution in the nanoparticles are analyzed, identifying how peculiar structural motifs relevant for catalysis and sensing applications, such as monometallic skins and surface single-atom sites, emerge. We compare these results with previous data for the corresponding Pd-based particles, identifying trends in chemical ordering, deepening understanding of the behaviour of catalytically relevant bimetallic compositions, and establishing appropriate models for studying the bimetallic nanoalloys.
1. Introduction
Studies of materials containing bimetallic nanoparticles (NPs), often referred to as nanoalloys, is a dynamically developing research area. The latter is interrelated to diverse applications of nanoalloy particles ranging from optics and magnetism to medicine and catalysis.1,2 Properties of a bimetallic NP are defined, besides its geometric structure and size, by the relative amount (composition) of the two constituting metals. Tuning the composition extends the design variables of materials containing bimetallic NPs tailor-made for the desired applications to function better, often at reduced cost.The size, shape, and composition of bimetallic NPs can be quite well controlled by the preparation conditions. At variance, such elusive degree of complexity as chemical (or atomic) ordering, i.e. a distribution pattern of metal atoms of two types among lattice positions of an alloy NP, is hard to precisely control experimentally. The reactivity of metal NPs is directly related to their surface arrangement. The chemical ordering defines what types and how many surface sites are exposed by a bimetallic NP of a given size, shape, and composition. This is key information for catalysis, sensing, and many other applications. Yet, it remains barely accessible experimentally at the atom-by-atom level even for the most modern structure characterization techniques.
Computational modeling using Density Functional Theory (DFT) can provide detailed information about the structure and properties of bimetallic NPs, complementing experimental data. DFT calculations of bimetallic NPs with over a hundred atoms and sizes of ∼1.5 nm, which are required to realistically represent larger particles dealt with in catalysis,3–5 are feasible since two decades.6 However, the presence of more than one type of atoms in nanoalloys severely hinders their comprehensive DFT simulation, often restricting it to quite small particles and considering only several chemical orderings (homotops).7–12 In fact, a direct search for the equilibrium chemical ordering in a ∼2 nm large bimetallic crystallite comprising ∼200 atoms requires calculating energies of a colossal number of 1050 homotops (including symmetry-equivalent ones),13 which is excessive for any computational method.
This challenge can be dealt with by a Topological (TOP) approach,14,15 which enables determining equilibrium chemical orderings in bimetallic nanocrystallites containing 102–104 atoms of different metals across the Periodic Table from a small number of DFT calculations. Briefly, the TOP method divides all homotops of a bimetallic nanocrystallite with a given stoichiometry and shape into groups with the same topologies. Definition of the latter depends on how atomically detailed the resulting ordering needs to be. For instance, for studying the catalytic activity of a bimetallic 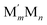 NP comprising m + n atoms it is essential to know how many active surface sites of each type the NP exposes. These data are related to the propensity of M′ and M atoms to segregate on the surface and define which atoms occupy surface positions of the NP with different coordination numbers, e.g. in corner, edge, and terrace sites. Since all homotops of the NP under scrutiny share the same crystal lattice and composition, it suffices to specify atomic positions for just one of the two metals. The types of the exposed surface sites and their abundance are also affected by the propensity of the metals M′ and M to mix, which is reflected by the number of heterometallic bonds (nearest-neighbor atom pairs) M′–M formed. For surface reactivity studies it is often sufficient to specify ordering patterns in bimetallic nanoalloys by the topology defined solely by the number of M′–M bonds
NP comprising m + n atoms it is essential to know how many active surface sites of each type the NP exposes. These data are related to the propensity of M′ and M atoms to segregate on the surface and define which atoms occupy surface positions of the NP with different coordination numbers, e.g. in corner, edge, and terrace sites. Since all homotops of the NP under scrutiny share the same crystal lattice and composition, it suffices to specify atomic positions for just one of the two metals. The types of the exposed surface sites and their abundance are also affected by the propensity of the metals M′ and M to mix, which is reflected by the number of heterometallic bonds (nearest-neighbor atom pairs) M′–M formed. For surface reactivity studies it is often sufficient to specify ordering patterns in bimetallic nanoalloys by the topology defined solely by the number of M′–M bonds 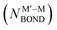 and surface M atoms in the corner/vertex (NMCORNER), edge (NMEDGE), and facet/terrace (NMFACET) positions. Hereafter, topologies of
and surface M atoms in the corner/vertex (NMCORNER), edge (NMEDGE), and facet/terrace (NMFACET) positions. Hereafter, topologies of  NPs are designated as
NPs are designated as 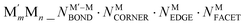 ; to specify a particular homotop of the considered topology, its EDFT value in eV is added to the above designation, resulting in the designation
; to specify a particular homotop of the considered topology, its EDFT value in eV is added to the above designation, resulting in the designation  . Energies of all homotops with a given topology are represented in the TOP method by the energy of just one of the homotops, chosen arbitrarily.14
. Energies of all homotops with a given topology are represented in the TOP method by the energy of just one of the homotops, chosen arbitrarily.14
Energy difference, ΔETOPij, between any two homotops i and j of a bimetallic NP reads:14,16
 | (1) |
Here, the energies ε are contributions of either a M′–M bond or an M atom located in a certain outer position of the NP to its topological energy ETOP. The terms ε quantify either the surface segregation energy of metal atoms M′ and M or the energy gained or lost upon metals mixing to form a pair M′–M of the nearest-neighbor atoms. These terms are calculated by fitting eqn (1) to DFT energies EDFT of a series of homotops of a bimetallic NP with diverse topologies. Using thus obtained TOP expressions a comprehensive ordering screening is performed by means of Monte Carlo (MC) simulations to find the topology—a set of the N values—of the most energetically stable homotops of the NP along with topologies of less stable homotops. Then, atomic positions in the selected low-energy homotops are optimized by DFT. This allows examining accuracy of the energies ε and eqn (1) overall. The resulting latter expressions can be used to simulate the chemical orderings in bimetallic NPs containing thousands atoms, not accessible for DFT calculations.
Successfully determined chemical orderings in NPs of various metal combinations, such as Pd–Au,13–17 Pd–Ag,14 Pd–Cu,14 Pd–Zn,14 Pd–Rh,16 Pt–Ag,18 Pt–Co,19,20 Pt–Ni,21 Pt–Sn,22 and Ni–Cu,23 revealed efficiency and broad applicability of the TOP method. This study deals with bimetallic nanoalloys of essential for catalysis metal Pt with quite inert coinage metals Au, Ag, and Cu. These combinations of metals are actively studied in the rapidly developing field of single-atom catalysis24,25 as single-atom alloy catalysts,26 where individual Pt atoms surrounded by coinage atoms can act as very selective catalytic centers.
Among the aims of the present study are:(i) quantifying by DFT calculations the chemical orderings and surface segregation in up to ∼2 nm large Pt–Au, Pt–Ag and Pt–Cu crystallites at different concentrations of the metals; (ii) analyzing the structure, bonding, and atomic charges in these nanoparticles compared to the analogous Pd-containing nanoalloys studied earlier; (iii) deepening the knowledge of the accuracy and applicability of the Topological approach; (iv) identifying equilibrium chemical orderings in Pt–Au, Pt–Ag and Pt–Cu particles at sizes over 4 nm commonly found in catalysts, also at elevated temperatures.
2. Computational methods
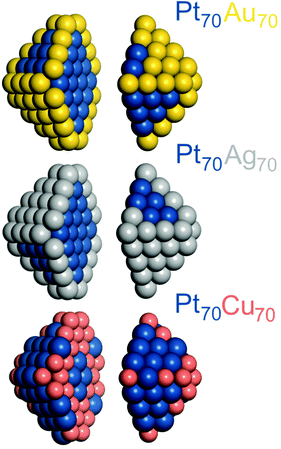
All DFT calculations were performed using the plane-wave code VASP.27,28 A gradient-corrected Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional29 was employed as one of the most reliable functionals for transition metals bulks and surfaces30–32 in combination with the projector augmented wave (PAW) representation of core electrons.33,34 Insignificant spin-polarization effects for the non-magnetic platinum and coinage metals were neglected. To moderate the computational cost, cutoff energies for the plane-wave functions were defined by the values of the PBE core-electrons PAW potentials:Cu – 273.2 eV, Ag – 249.85 eV, Au – 229.95 eV and Pt – 230.28 eV. According to our benchmarks, the total energy differences between distinct chemical orderings of a given NP computed using these cutoff energies are essentially as accurate as when using the cutoff energy 415 eV (typically used for describing adsorbate–metal interactions). The Brillouin zone was sampled only at the Γ-point. One-electron Kohn–Sham levels were smeared by 0.1 eV and the converged energies were finally extrapolated to zero smearing. All atoms were locally relaxed without any restrictions until forces acting on each atom decreased to 0.2 eV nm−1.In line with our DFT calculations of other nanoalloy particles,13,14,16,21 here the Pt–X (X = Au, Ag, Cu) NPs were also represented by truncated octahedrons with the fcc lattice. Ca. 1.4 nm large 140-atomic Pt70Au70, Pt70Ag70, and Pt70Cu70 NPs, see Fig. 1, were considered for comparison with the results for Pd-based Pd70Au70, Pd70Ag70, and Pd70Cu70 analogs.14 1.7–1.8 nm large 201-atomic NPs Pt–Au, Pt–Ag and Pt–Cu with Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X 1
X 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 3
1, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compositions, see Fig. 2, were modelled to study the size, shape, and composition effects. Placing these 140- and 201-atom NPs in periodically repeated cubic cells of 2.3 × 2.3 × 2.3 and 2.5 × 2.5 × 2.5 nm3 allowed separation >0.7 nm between them. At such distances interaction of metal particles with their periodic images is negligible for the purpose of this work.35,36
1 compositions, see Fig. 2, were modelled to study the size, shape, and composition effects. Placing these 140- and 201-atom NPs in periodically repeated cubic cells of 2.3 × 2.3 × 2.3 and 2.5 × 2.5 × 2.5 nm3 allowed separation >0.7 nm between them. At such distances interaction of metal particles with their periodic images is negligible for the purpose of this work.35,36
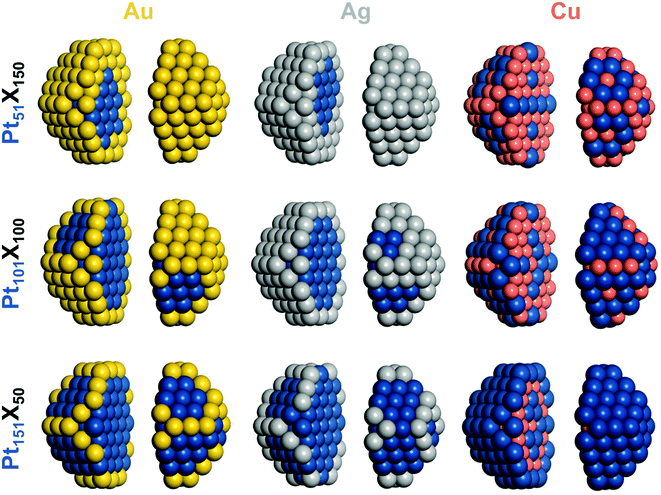 | ||
Fig. 2 Chemical orderings of 1.7–1.8 nm large 201-atomic truncated-octahedral fcc nanoparticles of the compositions Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X (X = Au, Ag, Cu):1 X (X = Au, Ag, Cu):1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 – Pt51X150, 1 3 – Pt51X150, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 – Pt101X100, 3 1 – Pt101X100, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 – Pt151X50 with the lowest DFT energies. Particles images are split in two parts for better visualization. Colors of atoms as in Fig. 1. 1 – Pt151X50 with the lowest DFT energies. Particles images are split in two parts for better visualization. Colors of atoms as in Fig. 1. | ||
3. Results and discussion
In the following we present and discuss results for model Pt–X (X = Au, Ag, Cu) NPs Pt51X150 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), Pt101X100 (1
3), Pt101X100 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), Pt151X50 (3
1), Pt151X50 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), and Pt70X70 (1
1), and Pt70X70 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). These fcc crystallites expose surface atoms with the coordination numbers (CN) 6 (corner/vertex), 7 (edge), and 9 ({111} facets). Besides, the 201-atomic particles contain one atom with CN = 8 in each of their six {100} facets. Table 1 shows the calculated energy terms ε in the topological expressions (eqn (1)). Details of the lowest-energy chemical orderings resulting from DFT calculations (EDFT) and from MC calculations using eqn (1) (ETOP) are specified in Table 2. These two kinds of chemical orderings are quite similar for each studied model NP. Thus, unless stated otherwise, herein we consider the chemical orderings corresponding to the ETOP values.
1). These fcc crystallites expose surface atoms with the coordination numbers (CN) 6 (corner/vertex), 7 (edge), and 9 ({111} facets). Besides, the 201-atomic particles contain one atom with CN = 8 in each of their six {100} facets. Table 1 shows the calculated energy terms ε in the topological expressions (eqn (1)). Details of the lowest-energy chemical orderings resulting from DFT calculations (EDFT) and from MC calculations using eqn (1) (ETOP) are specified in Table 2. These two kinds of chemical orderings are quite similar for each studied model NP. Thus, unless stated otherwise, herein we consider the chemical orderings corresponding to the ETOP values.
| Nanoparticle | ε Pt-XBOND | ε XCORNER | ε XEDGE | ε XFACET | δ | ΔE | N FIT |
|---|---|---|---|---|---|---|---|
| a 95% confidence interval of ε given as, e.g. 19+4−2 denotes a range from 17 meV to 23 meV. b When several homotops were optimized by DFT for one of the selected ≥10 low-energy topologies, see Section 3.6, all these EDFT values were also used in the calculations of δ. | |||||||
| Pt70Au70 | 19+4−2 | −619+62−48 | −377+44−44 | −256+88−69 | 470 | 0 | 35 |
| Pd70Au70 | −13+4−6 | −404+76−72 | −301+52−77 | −200+52−64 | 115 | 26 | 32 |
| Pt70Ag70 | 11+10−13 | −625+122−185 | −336+72−185 | −195+75−58 | 358 | 0 | 45 |
| Pd70Ag70 | −1+2−2 | −361+50−68 | −289+78−129 | −163+43−64 | 150 | 29 | 53 |
| Pt70Cu70 | −35+4−4 | −27+47−44 | 182+56−54 | 344+43−36 | 879 | 415 | 65 |
| Pd70Cu70 | −26+5−5 | 95+36−33 | 147+46−45 | 183+42−40 | 360 | 171 | 127 |
| Pt151Au50 | 21+1−1 | −507+51−62 | −543+16−18 | −431+30−43 | 114 | 354 | 101 |
| Pt101Au100 | 21+7−6 | −530+136−107 | −492+59−56 | −335+83−95 | 456 | 0 | 68 |
| Pt51Au150 | 15+14−15 | −558+49−34 | −547+53−84 | −259+47−92 | 279 | 198 | 44 |
| Pt151Ag50 | 32+11−12 | −396+108−135 | −380+95−90 | −237+103−95 | 461 | 176 | 90 |
| Pt101Ag100 | 16+9−10 | −499+95−112 | −466+87−83 | −308+77−91 | 493 | 65 | 68 |
| Pt51Ag150 | 7+5−5 | −408+118−158 | −511+79−68 | −240+49−65 | 169 | 43 | 99 |
| Pt151Cu50 | −25+9−13 | 267+30−22 | 342+14−14 | 372+42−44 | 784 | 204 | 165 |
| Pt101Cu100 | −43+6−5 | 15+60−72 | 208+55−68 | 325+34−41 | 576 | 284 | 87 |
| Pt51Cu150 | −54+14−15 | 134+73−78 | 184+151−93 | 259+65−59 | 239 | 0 | 40 |
| Particle | N Pt-XBOND | N XCORNER | N XEDGE | N XFACET | N X100 | E DFTDFTmin (eV) | E DFTTOPmin (eV) |
|---|---|---|---|---|---|---|---|
| a The overall topological numbers NBOND, NCORNER, NEDGE, NFACET, and NINSIDE are 636, 24, 24, 48, 44 (Pt70X70), and 948, 24, 36, 62, 79 (Pt201−nXn), respectively. | |||||||
| Pt70Au70 | 196/196 | 24/24 | 24/24 | 22/22 | −588.108 | −588.108 | |
| Pt70Ag70 | 196/196 | 24/24 | 24/24 | 22/22 | −561.294 | −561.294 | |
| Pt70Cu70 | 308/340 | 23/24 | 8/12 | 0/0 | −626.920 | −626.610 | |
| Pt151Au50 | 215/214 | 23/20 | 25/30 | 2/0 | 2/0 | −978.389 | −978.283 |
| Pt151Ag50 | 222/215 | 24/21 | 26/29 | 0/0 | 0/0 | −962.454 | −961.772 |
| Pt151Cu50 | 404/412 | 0/0 | 0/0 | 0/0 | 0/0 | −1015.683 | −1015.214 |
| Pt101Au100 | 267/267 | 24/24 | 36/36 | 40/40 | 5/5 | −859.505 | −859.505 |
| Pt101Ag100 | 274/270 | 24/24 | 36/36 | 40/40 | 6/4 | −822.032 | −821.660 |
| Pt101Cu100 | 525/560 | 24/24 | 10/8 | 3/8 | 0/0 | −914.377 | −913.767 |
| Pt51Au150 | 224/210 | 24/24 | 36/36 | 62/62 | 6/6 | −730.046 | −729.869 |
| Pt51Ag150 | 220/214 | 24/24 | 36/36 | 62/62 | 6/6 | −669.026 | −668.827 |
| Pt51Cu150 | 418/418 | 24/24 | 36/36 | 18/18 | 0/0 | −799.627 | −799.627 |
The following literature data are relevant for the present study of the Pt–X nanoalloys:(i) the surface energies calculated for close-packed surfaces of the pure metals are 1.03 (Pt), 0.72 (Au), 0.58 (Ag), and 0.77 eV per atom (Cu);37 (ii) calculated solutes/hosts surface segregation energies of monoatomic impurities (solutes) in fcc(111) metal hosts are −0.36 (Au/Pt), 0.34 (Pt/Au), −0.27 (Ag/Pt), 0.34 (Pt/Ag), 0.32 (Cu/Pt), and −0.04 eV (Pt/Cu), where the negative sign indicates stabilizing surface segregation of the solute;37 (iii) Pt atoms in the bulk alloys are immiscible with Au38–41 and Ag40 atoms, but miscible with Cu40,42–44 atoms; and (iv) relative sizes of metal atoms,45 139 (Pt), 144 (Au), 144 (Ag), and 128 pm (Cu), affect the propensity of smaller atoms to surface segregate in compressively strained bimetallic particles40,46–48 so that the surface segregation of Cu is suppressed in Pt–Cu nanoalloys despite Cu has a lower surface energy than Pt (see above).
3.1. DFT data for chemical orderings of Pt–Au nanoparticles
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au compositions 1
Au compositions 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 1
3, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 3
1, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, see Tables 1, 2 and Fig. 2, reveal that their chemical orderings are controlled, in agreement with the data for Pt–Au bulk, surface, and nanoalloys,37–40 by the following effects:first, the positive energies εPt-AuBOND = 15–21 meV (Table 1) indicate that the formation of Pt–Au bonds in the alloys is disfavored with respect to Pt–Pt and Au–Au bonds, suppressing mixing of Pt and Au atoms. Second, quite large in magnitude negative terms εAuCORNER = −507 to −558 meV, εAuEDGE = −492 to −547 meV and εAuFACET = −259 to −431 meV show that Au atoms are notably more stable on the surface of the NPs than inside them and thus segregate on the surface. More open corner and edge Au atoms are more stable than higher-coordinated facet Au atoms. Increase of εAuFACET in magnitude with increasing Pt
1, see Tables 1, 2 and Fig. 2, reveal that their chemical orderings are controlled, in agreement with the data for Pt–Au bulk, surface, and nanoalloys,37–40 by the following effects:first, the positive energies εPt-AuBOND = 15–21 meV (Table 1) indicate that the formation of Pt–Au bonds in the alloys is disfavored with respect to Pt–Pt and Au–Au bonds, suppressing mixing of Pt and Au atoms. Second, quite large in magnitude negative terms εAuCORNER = −507 to −558 meV, εAuEDGE = −492 to −547 meV and εAuFACET = −259 to −431 meV show that Au atoms are notably more stable on the surface of the NPs than inside them and thus segregate on the surface. More open corner and edge Au atoms are more stable than higher-coordinated facet Au atoms. Increase of εAuFACET in magnitude with increasing Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au content from 1
Au content from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 1
3 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and to 3
1, and to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 suggests that the location of Pt atoms in facets of Pt–Au NPs is less energetically penalized at lower Pt concentrations than at higher ones. The surface segregation of Au atoms in the 201-atomic Pt–Au NPs with the lowest-energy orderings is illustrated in Fig. 2 and additionally detailed in Table 2 by numbers of atoms in various sites. Au atoms of Pt51Au150 occupy all 24 corner, 36 edge, and 62 facet sites forming a complete monolayer Au skin. The remaining 28 Au atoms are located inside, tending to minimize the number of unfavorable Pt–Au nearest-neighbor contacts. Pt101Au100 NP has insufficient Au atoms to complete the Au skin. There, 100 Au atoms occupy all 24 corner and 36 edge surface sites plus 40 of 62 facet sites. Even fewer Au atoms in Pt151Au50 NP results in their competition to partly occupy only corner and edge sites.
1 suggests that the location of Pt atoms in facets of Pt–Au NPs is less energetically penalized at lower Pt concentrations than at higher ones. The surface segregation of Au atoms in the 201-atomic Pt–Au NPs with the lowest-energy orderings is illustrated in Fig. 2 and additionally detailed in Table 2 by numbers of atoms in various sites. Au atoms of Pt51Au150 occupy all 24 corner, 36 edge, and 62 facet sites forming a complete monolayer Au skin. The remaining 28 Au atoms are located inside, tending to minimize the number of unfavorable Pt–Au nearest-neighbor contacts. Pt101Au100 NP has insufficient Au atoms to complete the Au skin. There, 100 Au atoms occupy all 24 corner and 36 edge surface sites plus 40 of 62 facet sites. Even fewer Au atoms in Pt151Au50 NP results in their competition to partly occupy only corner and edge sites.
The usefulness of the TOP approach and the meaning of terms in eqn (1) can be illustrated by comparing the TOP and DFT segregation energies. A homotop of Pt51Au150 with almost lowest TOP energy, Pt51Au150_212.24.36.62–729.864 (see ESI†), is characterized by NPt-AuBOND = 212, NAuCORNER = 24, NAuEDGE = 36 and NAuFACET = 62 and EDFT = −729.864 eV (homotops are labeled in this way throughout the present article). Exchange of an atom Au from center of a {111} facet with a near-neighbor subsurface atom Pt (each of the exchanged atoms Au number 39 and Pt number 198 formed 3 Pt–Au bonds) results in the homotop Pt51Au150_223.24.36.61–729.507 (see ESI†), where, the surface Pt atom forms 7 Pt–Au bonds and the Au atom moved to the subsurface forms 10 Pt–Au bonds. Its energy increase with respect to the pristine homotop is 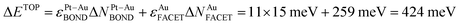 , using eqn (1) and energies ε in Table 1. The DFT energy increase 357 meV is close to the ΔETOP value in terms of the precision δ(EDFT − ETOP) = 279 meV (Table 1). δ(EDFT − ETOP) is twice the residual standard deviation between EDFT and ETOP energies for homotops of ≥10 test low-energy topologies, according to which the respective ΔETOP and ΔEDFT values differ by less than δ with the probability ≥95%.14 Exchange of an edge atom Au with a nearby subsurface atom Pt in the pristine homotop models even less favorable surface segregation of inner atoms Pt to edge sites. NPt-AuBOND after this exchange of atom Au number 132 with atom Pt number 176 (see ESI†) increases in the resulting homotop Pt51Au150_219.24.35.62–729.345 for the atom Au from 1 to 6 and for the atom Pt from 5 to 7. The energy increase vs. the pristine homotop,
, using eqn (1) and energies ε in Table 1. The DFT energy increase 357 meV is close to the ΔETOP value in terms of the precision δ(EDFT − ETOP) = 279 meV (Table 1). δ(EDFT − ETOP) is twice the residual standard deviation between EDFT and ETOP energies for homotops of ≥10 test low-energy topologies, according to which the respective ΔETOP and ΔEDFT values differ by less than δ with the probability ≥95%.14 Exchange of an edge atom Au with a nearby subsurface atom Pt in the pristine homotop models even less favorable surface segregation of inner atoms Pt to edge sites. NPt-AuBOND after this exchange of atom Au number 132 with atom Pt number 176 (see ESI†) increases in the resulting homotop Pt51Au150_219.24.35.62–729.345 for the atom Au from 1 to 6 and for the atom Pt from 5 to 7. The energy increase vs. the pristine homotop, 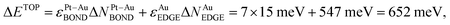 is indeed larger than for the displacement of the inner atom Pt to a {111} facet and reasonably well agrees with ΔEDFT = 519 meV.
is indeed larger than for the displacement of the inner atom Pt to a {111} facet and reasonably well agrees with ΔEDFT = 519 meV.
These two examples demonstrate that the TOP method, beyond providing adequate relative energies of different chemical orderings of a bimetallic NP, also allows rationalizing the energy differences in such important terms as propensities of their two types of metal atoms to form heterometallic bonds and to occupy differently coordinated surface sites.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Pt–Au particles than in smaller ones, where Au clearly prefers corners. The lowest-energy topology of the Pt70Au70 particle, see Table 2, corresponds to complete occupation of all 24 corner and 24 edge sites by Au atoms and location of all remaining 22 Au atoms on the facets. The percentage of 196 Pt–Au bonds in Pt70Au70, 31% of all metal–metal bonds, is comparable to 28% of 267 Pt–Au bonds in Pt101Au100. Some Pt70Au70 results will be further discussed in the sections dealing with the comparison of Pt–X NPs with their Pd–X analogs as well as with predicting chemical orderings in larger Pt–X NPs, where DFT calculations are unfeasible.
1 Pt–Au particles than in smaller ones, where Au clearly prefers corners. The lowest-energy topology of the Pt70Au70 particle, see Table 2, corresponds to complete occupation of all 24 corner and 24 edge sites by Au atoms and location of all remaining 22 Au atoms on the facets. The percentage of 196 Pt–Au bonds in Pt70Au70, 31% of all metal–metal bonds, is comparable to 28% of 267 Pt–Au bonds in Pt101Au100. Some Pt70Au70 results will be further discussed in the sections dealing with the comparison of Pt–X NPs with their Pd–X analogs as well as with predicting chemical orderings in larger Pt–X NPs, where DFT calculations are unfeasible.
| Particle | Pt | X | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 7 | 8 | 9 | 12 | 6 | 7 | 8 | 9 | 12 | |
| Pt70Au70 | — | — | — | −0.02 | 0.05 | −0.05 | −0.02 | 0.02 | — | |
| Pt151Au50 | −0.09 | −0.07 | −0.08 | −0.02 | 0.02 | −0.05 | −0.03 | — | — | — |
| Pt101Au100 | — | — | −0.09 | −0.04 | 0.03 | −0.05 | −0.03 | 0.01 | 0.02 | — |
| Pt51Au150 | — | — | — | — | 0.01 | −0.06 | −0.03 | −0.01 | 0.01 | 0.06 |
| Pt70Ag70 | −0.17 | −0.04 | 0.05 | 0.10 | 0.10 | — | ||||
| Pt151Ag50 | −0.13 | −0.13 | −0.24 | −0.11 | 0.02 | 0.12 | 0.15 | — | — | — |
| Pt101Ag100 | — | — | −0.30 | −0.16 | −0.05 | 0.05 | 0.08 | 0.13 | 0.09 | — |
| Pt51Ag150 | — | — | — | — | −0.11 | −0.02 | 0.01 | 0.04 | 0.04 | 0.12 |
| Pt70Cu70 | — | −0.25 | −0.23 | −0.33 | 0.18 | 0.27 | — | 0.30 | ||
| Pt151Cu50 | −0.14 | −0.11 | −0.08 | −0.07 | −0.23 | — | — | — | — | 0.37 |
| Pt101Cu100 | — | −0.29 | −0.12 | −0.27 | −0.39 | 0.27 | 0.22 | — | 0.32 | 0.31 |
| Pt51Cu150 | — | — | −0.57 | −0.46 | −0.60 | 0.11 | 0.15 | — | 0.19 | 0.19 |
| Pt201 | −0.09 | −0.06 | −0.03 | −0.01 | 0.07 | |||||
| Au201 | −0.07 | −0.04 | −0.02 | −0.01 | 0.04 | |||||
| Ag201 | −0.04 | −0.03 | 0.01 | −0.01 | 0.03 | |||||
| Cu201 | −0.05 | −0.02 | 0.02 | −0.01 | 0.03 | |||||
3.2. DFT data for chemical orderings of Pt–Ag nanoparticles
Ordering of the lowest-energy homotops of Pt101Ag100 NP is very similar to those of Pt101Au100 NP, see Fig. 2 and Table 2. All Ag atoms are located on the surface occupying all 24 corner and 36 edge sites and 40 of 62 terrace sites. Pt atoms occupy the remaining terrace sites and all 79 inner sites. This ordering exhibits incomplete Ag outer shell and monometallic Pt core. Qualitatively the same values of energies ε guiding the orderings in 201-atom NPs with other Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ag ratios, Pt51Ag150, and Pt151Ag50, as in the Pt101Ag100 NP, result in completing the Ag skin in the former case and depleting the skin (mainly by the facet atoms) in the latter case. Comparing equilibrium chemical orderings of the 201-atomic Pt–Ag NPs with their Pt–Au analogs, see Table 2, one notices very close similarities, especially at low Pt concentrations. Indeed, topologies of most corresponding Pt–Ag and Pt–Au pairs of NPs differ at most by just small amount of heterometallic bonds contributing up to a fraction of an eV to the NP energy. It is worth mentioning that a peculiar layered chemical ordering L11 was experimentally identified inside monolayer Ag skins of some relatively small Pt–Ag NPs.49 Small energetic preference calculated by DFT of such layering in Pt–Ag NPs18 becomes even smaller in the analogous Pd–Ag NPs and disappears in Pt–Au and Pd–Au NPs that feature monolayer Au skins.50 Thus, the elusive phenomenon of Pt and Pd layering inside the coinage metal skins appears to be uncommon.
Ag ratios, Pt51Ag150, and Pt151Ag50, as in the Pt101Ag100 NP, result in completing the Ag skin in the former case and depleting the skin (mainly by the facet atoms) in the latter case. Comparing equilibrium chemical orderings of the 201-atomic Pt–Ag NPs with their Pt–Au analogs, see Table 2, one notices very close similarities, especially at low Pt concentrations. Indeed, topologies of most corresponding Pt–Ag and Pt–Au pairs of NPs differ at most by just small amount of heterometallic bonds contributing up to a fraction of an eV to the NP energy. It is worth mentioning that a peculiar layered chemical ordering L11 was experimentally identified inside monolayer Ag skins of some relatively small Pt–Ag NPs.49 Small energetic preference calculated by DFT of such layering in Pt–Ag NPs18 becomes even smaller in the analogous Pd–Ag NPs and disappears in Pt–Au and Pd–Au NPs that feature monolayer Au skins.50 Thus, the elusive phenomenon of Pt and Pd layering inside the coinage metal skins appears to be uncommon.
3.3. DFT data for chemical orderings of Pt–Cu nanoparticles
At the lowest studied Cu content (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Pt
1 Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu), all 50 Cu atoms of Pt151Cu50 NP are energetically driven to be located inside the monolayer Pt skin and to form 412 bonds with inner and surface Pt atoms, see Table 2 and Fig. 2. At the 1
Cu), all 50 Cu atoms of Pt151Cu50 NP are energetically driven to be located inside the monolayer Pt skin and to form 412 bonds with inner and surface Pt atoms, see Table 2 and Fig. 2. At the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Cu
1 Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt content, 60 out of the 100 Cu atoms of Pt101Cu100 NP stay in the core, 24 Cu atoms occupy all corner positions and the remaining 16 Cu atoms are distributed over edge (8 atoms) and facet (8 atoms) positions. The number of Pt–Cu bonds increases to 560. At the lower 1
Pt content, 60 out of the 100 Cu atoms of Pt101Cu100 NP stay in the core, 24 Cu atoms occupy all corner positions and the remaining 16 Cu atoms are distributed over edge (8 atoms) and facet (8 atoms) positions. The number of Pt–Cu bonds increases to 560. At the lower 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Pt
3 Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu content, all corner and edge positions of Pt51Cu150 NP are occupied by Cu atoms. Cu atoms are also located in 18 of 62 facet positions and form most of the 79-atom core. Interestingly, see Fig. 2, most of surface Pt atoms are directly neighboring other Pt atoms instead of being completely surrounded by Cu atoms, which would enable maximizing the number of Pt–Cu bonds. This implies that low Pt contents are required to form stable single Pt atoms on the surface of Pt–Cu NPs.
Cu content, all corner and edge positions of Pt51Cu150 NP are occupied by Cu atoms. Cu atoms are also located in 18 of 62 facet positions and form most of the 79-atom core. Interestingly, see Fig. 2, most of surface Pt atoms are directly neighboring other Pt atoms instead of being completely surrounded by Cu atoms, which would enable maximizing the number of Pt–Cu bonds. This implies that low Pt contents are required to form stable single Pt atoms on the surface of Pt–Cu NPs.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 201-atom Pt–Au and Pt–Ag NPs only slightly changed vs that in 140-atom NPs, one notices essentially the same mixing propensity of Pt and Cu atoms in Pt101Cu100 and Pt70Cu70 NPs, with εPt-CuBOND equals to −31 and −39 meV, respectively. However, the unfavorable by 15 meV corner position for Cu atom in Pt101Cu100 NP becomes favorable by 27 meV in the smaller Pt70Cu70 NP, see Table 1. The destabilizing contributions of the edge and facet positions occupied by Cu atoms remain almost the same in the 201- and 140-atomic Pt–Cu NPs. The terms ε rationalize that 100% of the corner positions and 50% of the edge positions in the lowest-energy homotop of Pt70Cu70 NP are occupied by Cu, whereas no Cu atoms are located in terrace positions and 77% of the core sites are occupied by Cu. Importantly, more than a half of all metal–metal bonds in Pt70Cu70 NP are stabilizing heterometallic Pt–Cu bonds, in comparison with only less than one-third of Pt–Au and Pt–Ag bonds in the corresponding equilibrium structures of Pt70Au70 and Pt70Ag70 NPs.
1 201-atom Pt–Au and Pt–Ag NPs only slightly changed vs that in 140-atom NPs, one notices essentially the same mixing propensity of Pt and Cu atoms in Pt101Cu100 and Pt70Cu70 NPs, with εPt-CuBOND equals to −31 and −39 meV, respectively. However, the unfavorable by 15 meV corner position for Cu atom in Pt101Cu100 NP becomes favorable by 27 meV in the smaller Pt70Cu70 NP, see Table 1. The destabilizing contributions of the edge and facet positions occupied by Cu atoms remain almost the same in the 201- and 140-atomic Pt–Cu NPs. The terms ε rationalize that 100% of the corner positions and 50% of the edge positions in the lowest-energy homotop of Pt70Cu70 NP are occupied by Cu, whereas no Cu atoms are located in terrace positions and 77% of the core sites are occupied by Cu. Importantly, more than a half of all metal–metal bonds in Pt70Cu70 NP are stabilizing heterometallic Pt–Cu bonds, in comparison with only less than one-third of Pt–Au and Pt–Ag bonds in the corresponding equilibrium structures of Pt70Au70 and Pt70Ag70 NPs.
3.4. Miscibility of Pt atoms with Au, Ag, and Cu atoms at the nanoscale
As already mentioned, Pt atoms in bulk alloys are immiscible at common conditions with Au and Ag atoms, but they mix with Cu atoms. These miscibility relations in the bulk are properly reflected in the terms εPt-XBOND of the studied Pt–X NPs, see Table 1, manifesting relative energies of heterometallic bonds Pt–X. The energies εPt-XBOND are positive for Pt–Au and Pt–Ag NPs (unfavorable formation of the heterometallic bonds) and negative for Pt–Cu NPs (favorable formation of the Pt–Cu bonds). At the nanoscale, the bulk immiscibility of bimetallic alloys can be counterbalanced by significant propensity of one metal component to segregate on the surface. That is why the equilibrium chemical orderings of Pt–Au and Pt–Ag NPs do not feature separate, as compact as possible domains of the two metals, e.g. Janus-type ones,1,16 but feature core–shell arrangements with full or partially incomplete Au and Ag skins, see Fig. 1 and 2.The miscibility of metals M and M′ in a bimetallic 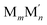 NP can be also evaluated by its excess energy vs the energies of the corresponding monometallic Mn+m and
NP can be also evaluated by its excess energy vs the energies of the corresponding monometallic Mn+m and 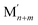 particles of the same size and structure.7,55 The excess energy (also known as mixing energy) per atom for a PtmXn particle is calculated as:
particles of the same size and structure.7,55 The excess energy (also known as mixing energy) per atom for a PtmXn particle is calculated as:
| Eexc(PtmXn) = {E(PtmXn) − [m/(m + n)]E(Ptm+n) − [n/(m + n)]E(Xm+n)}/(m + n), | (2) |
The DFT excess energies of 201-atom Pt–X NPs are plotted in Fig. 3. The energies for Pt–Au and Pt–Ag NPs with Pt and X atoms that are immiscible in the bulk are spread depending on the concentrations of atoms X from −38 to −65 meV and from −58 to −90 meV, respectively. The corresponding energies for Pt–Cu NPs ranging from −127 to −163 meV are notably more negative, as expected for the miscible Pt and Cu atoms. For all these 201-atomic Pt–X NPs the miscibility in terms of the excess energies reaches maximum close to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compositions. This mixing indicator remains nearly the same for the 1
1 compositions. This mixing indicator remains nearly the same for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 140-atomic NPs, see Fig. 3: −54, −80, and −165 meV for Pt70Au70, Pt70Ag70, and Pt70Cu70, respectively.
1 140-atomic NPs, see Fig. 3: −54, −80, and −165 meV for Pt70Au70, Pt70Ag70, and Pt70Cu70, respectively.
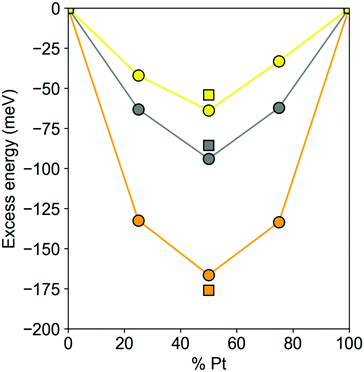 | ||
| Fig. 3 DFT excess energies Eexc per atom (see eqn (2)) circles – of Pt201−nXn (X = Au, Ag, Cu; n = 50, 100, 150) nanoparticles and squares – of Pt70X70 nanoparticles. Pt–Au – yellow, Pt–Ag – gray, Pt–Cu – orange. | ||
3.5. Comparison of Pt–X and Pd–X nanoparticles (X = Au, Ag, Cu)
To better understand differences and similarities in the catalytic behavior of Pt- and Pd-based nanomaterials we compare the chemical ordering and related properties of the Pt70X70 NPs with the previously calculated data for the Pd70X70 NPs.14The main qualitative difference of changing Pt to Pd in the nanoalloys with Au and Ag, see Table 1, is that, at variance with Pt, Pd becomes slightly miscible with these coinage metals, by −13 and −1 meV per Pd–X bond, respectively. On the other hand, the notable preference of Au and Ag atoms to occupy surface positions remains present in the Pd-based NPs, although the corresponding energies ε for them are significantly smaller than for the analogous Pt-based NPs. The stabilizing effect of the location of Au and Ag atoms in surface positions decreases in both Pt- and Pd-based NPs with increasing coordination number of the surface position. The most favorable are 6-coordinated corner sites, then 7-coordinated edge sites, and finally 9-coordinated sites in the {111} facets. Similarities of the energies ε for the corresponding Pt70X70 and Pd70X70 (X = Ag, Au) NPs result in similar orderings of their lowest-energy homotops. In all four NPs X atoms occupy all 48 corner plus edge sites, while the remaining 22 X atoms are located in the {111} facet sites. Pt and Pd atoms occupy the remaining 26 surface sites of the facets and all 44 positions in the interior of the NPs. The main difference in the orderings comes from the number of heterometallic bonds. The equilibrium Pt70X70 structures feature 196 Pt–X bonds, 31% of overall 636 bonds in the 140-atomic NP, to be compared with significantly larger number of heterometallic bonds in the Pd70X70 structures, 234–262 (37–41%). A consequence of the different numbers of the heterometallic bonds is that most of the {111} facets in the Pt70X70 structures are formed by either only X or only Pt atoms, whereas the individual facets in the Pd70X70 structures contain a mixture of X and Pd atoms, increasing the number of Pd–X bonds.
Miscibility of the coinage and platinum-group metal atoms is favorable in both Pt70Cu70 and Pd70Cu70 NPs, see Table 1. Each heterometallic bond stabilizes the former particle by 9 meV more than the latter. The occupation of surface positions by Cu destabilizes these two NPs, with one exception. Namely, the occupation of corner position of Pt70Cu70 NP by atom Cu instead of atom Pt has a slight stabilizing effect, by −27 meV. The destabilization due to the presence of surface Cu atoms increases with increasing their coordination numbers, though the destabilization values (energy differences between the most stable and the least stable surface positions) are quite different, 371 meV for Pt70Cu70 and 88 meV for Pd70Cu70. It is least favorable for Cu atoms to occupy terrace sites of Pt70Cu70 and Pd70Cu70 NPs. Cu atoms are differently distributed on the surface of Pt70Cu70 and Pd70Cu70 homotops with the lowest ETOP energy. In the Pt70Cu70 NP, 36 surface Cu atoms occupy all 24 corner positions and a half of 24 edge positions, leaving all 48 terrace positions to be occupied by Pt atoms, see Table 2. 32 surface Cu atoms of the Pd70Cu70 NP are quite evenly spread over three types of sites: corner – 12, edge – 14, and terrace – 814 as a result of relatively small energy difference of Cu in these sites. To maximize the number of stabilizing heterometallic bonds the equilibrium Pt70Cu70 and Pd70Cu70 structures are of quite common onion-like type,1,2,56,57 with Pt/Pd-rich core, Cu-rich subsurface shell and monatomic skin shared by Pt/Pd and Cu atoms. These chemical orderings allow formation of 340 Pt–Cu and 382 Pd–Cu bonds.
The present topological approach has been recently employed to analyze in detail the formation of single-atom Pd sites in Pd–Au NPs appealing for catalysis as a function of Pd concentration inside the particles.17 It was shown that no surface Pd atoms emerge at low Pd concentrations in the Au skin at equilibrium chemical orderings. Single-atom surface Pd sites become stable in 201-atom Pd–Au particles when Pd content inside the skin reaches ca. 60% (corresponding to 153 Au and 48 Pd atoms) and further increase of Pd content results in more surface Pd, first mostly as single atoms. Such emergence of surface Pd atoms is triggered by stabilizing Pd–Au bonds reflected in negative εPd-AuBOND energies for Pd–Au NPs.13–15,17 According to εPt-XBOND (Table 1), heterometallic bonds of Pt are stabilizing neither in Pt–Au, nor in Pt–Ag NPs. Thus, the location of Pt atoms is not favored on the surface of Pt–Au and Pt–Ag NPs at the equilibrium orderings, unless the number of Au and Ag atoms in these particles is smaller than the 122 required to form complete coinage-metal skins. However, single-atom Pt sites can be easily created on the surface of Pt–Au and Pt–Ag NPs in the course of catalytic reactions already at low Pt concentration due to energetically preferable interactions of Pt centers with reactants and intermediates compared to Au and Ag centers. This adsorbate-induced surface segregation phenomenon is well known for nanoalloy catalysts.13,16,21,23,25,26,51 In the cases of Pd–Cu and Pt–Cu NPs Pd and Pt atoms show a strong preference to be located in the surface skin and to form stabilizing heterometallic bonds, see Tables 1 and 2. Thus, the presence of Pd and Pt on the surface of these nanoalloys as unique single-atom catalytic sites is conceivable only at very low concentration of the platinum-group metals.
3.6. Performance of the topological method to describe chemical orderings
The present TOP method14,15 focuses on patterns of the equilibrium chemical orderings of bimetallic NPs, which determine the surface reactivity. The method employs a very simple topological equation (i.e. in the form of eqn (1)) to pre-screen a huge number of the chemical orderings (homotops) of a NP to find several best candidates in terms of their lowest ETOP energies for subsequent electronic-structure (DFT) calculations with locally relaxed positions of atoms. Among the method simplifications are: (i) accounting only for interactions between nearest-neighbor pairs of atoms and assuming all bond of the same type (e.g. all Pt–Pt bonds) to be equal; (ii) describing positions of atoms in the NP lattice solely by the coordination numbers, distinguishing between surface atoms with different coordination numbers but treating all atoms of each metal type inside the NP as equivalent; (iii) grouping homotops in so-called topologies of the same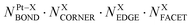 numbers in eqn (1), and assuming that an arbitrarily chosen homotop of a given topology represents reasonably well the DFT energy and the chemical ordering of all other numerous homotops of the same topology.
numbers in eqn (1), and assuming that an arbitrarily chosen homotop of a given topology represents reasonably well the DFT energy and the chemical ordering of all other numerous homotops of the same topology.
To evaluate the correctness of some of these assumptions we randomly generated ≥10 different homotops for several selected topologies of Pt–Au and Pt–Cu NPs and locally optimized those by DFT; see results in Table S1 (ESI†). The DFT energy splits for the homotops belonging to each of the considered low-energy topologies of 201-atomic Pt–Au NPs are very small, up to ca. 1 meV per atom. The splits slightly increase with growing content of Au atoms (preferably located on the surface), ranging from only 25 meV for the topology Pt151Au50_214.20.30.0 to 286 meV for the topology Pt51Au150_210.24.36.62. DFT energy splits for low-lying topologies of Pt–Cu NPs noticeably increased compared to the corresponding Pt–Au NPs. Noteworthy, the Pt–Cu energy splits also increase with growing content of Pt on the surface, from 153 meV for the topology Pt51Cu150_418.24.36.18 to 930 meV for the topology Pt151Cu50_412.0.0.0, the latter with solely Pt atoms on the surface. We note that the prediction error of ETOPvs. EDFT energies for such low-energy orderings range from 1.1 to 6.8 meV per atom (see Table S1, ESI†), although the errors for high-energy structures are significantly larger. For many practical applications, the up to ca. 7 meV per atom uncertainty in total energy of the Pt151Cu50_412.0.0.0 homotops provided by the present computational setup may be sufficient. If not, DFT calculations can be performed, as just discussed, for additional homotops of the putative lowest-energy topologies, to more precisely approach equilibrium DFT chemical orderings.
A similar procedure could be applied to go beyond the topology approach, when a more precise energetic representation of chemical orderings is required for assessing notably higher-lying homotops. One can see from Table S1 (ESI†) a substantial energy split in one of the higher-lying topologies of 201-atomic NPs, namely by 1501 meV in Pt101Au100_594.24.0.54, but this seems to be not very often the case.
Interestingly, the energy splitting for 10 random homotops with putative lowest-energy topologies Pt70Au70_196.24.24.22 and Pt70Cu70_340.24.12.0, 1027 and 1568 meV, respectively, see structures of the homotops with minimum and maximum DFT energies of these topologies in Fig. S1 (ESI†), are notably larger than those for the 201-atom Pt–Au and Pt–Cu NPs. Again, the Pt–Cu homotops split more than the Pt–Au homotops. Our detailed analysis of this splitting reveals that not all atoms of one type (Pt–Pt, Pt–X, or X–X bonds) are equivalent, i.e. that the energy of bonds formed by Pt or X atoms to each of their first neighbours is partially dependent on the identity (and quantity) of the rest of first neighbours. This challenges the convenient assumption that all bonds between a given pair of atoms are equally strong. In addition, certain structural motifs (such as {111} facets solely composed of Au) seem to become stable for some compositions due to elusive long-range interactions neglected by the employed topological description.
Although the δ values in Table 1 may seem large, they correspond to average prediction errors 1 to 6 meV per atom. The large size of the studied particles obviously increases the errors in total energies, but changes in energy caused by permuting atoms are, on average, rather well approximated. This means that irrespective of possible inaccuracies of the present TOP approach based on the DFT structure optimization, the equilibrium chemical orderings in bimetallic nanoalloys provided by this approach approximate reasonably well those obtained with the employed DFT exchange–correlation functional. The calculated atomic-level data, which are notably more detailed than those currently accessible experimentally, are very useful for rationalizing surface reactivity of bimetallic catalysts and related applications.
3.7. Larger Pt-based nanoparticles and temperature effects on the chemical ordering
Chemical orderings with the lowest-energy topology were also determined for ca. 4.4 nm large fcc truncated octahedral Pt732X731 NPs using the energies ε obtained for 140-atomic Pt70X70 and for 201-atomic Pt101X100 NPs, see Table 1. Orderings of these homotops at 0 K, denoted as Pt732X731(140) and Pt732X731(201), respectively, are shown in Fig. 4 and occupations of various atomic positions in them are quantified in Table 4. As the 1463-atomic particles are too large for DFT calculations, results for them were obtained only using the Monte Carlo simulation part of the Topological description approach,14,15vide supra.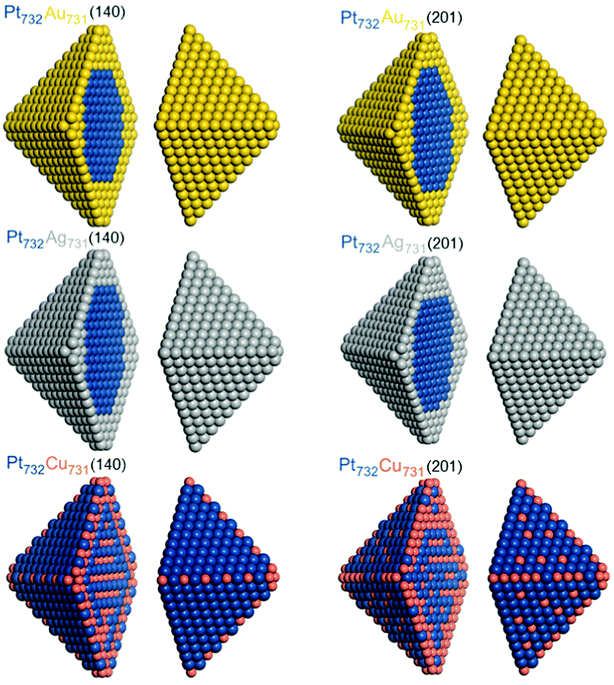 | ||
| Fig. 4 Equilibrium chemical orderings of ca. 4.4 nm large truncated-octahedral fcc Pt732Au731, Pt732Ag731, and Pt732Cu731 nanoparticles at 0 K with the lowest TOP energies calculated using eqn (1) for Pt70X70 particles (Pt732X731(140), left column) and Pt101X100 (particles Pt732X731(201), right column). Colors of atoms are as in Fig. 1. | ||
| Nanoparticle | T, K | N Pt-XBOND | N XCORNER | N XEDGE | N XFACET | N XINSIDE |
|---|---|---|---|---|---|---|
| The total topological numbers for the Pt732X731 particles are: NBOND = 7776, NCORNER = 24, NEDGE = 108, NFACET = 440, NINSIDE = 891. | ||||||
| Pt732Au731(140) | 0 | 1238 (16) | 24 (100) | 108 (100) | 440 (100) | 159 (18) |
| Pt732Au731(201) | 0 | 1238 (16) | 24 (100) | 108 (100) | 440 (100) | 159 (18) |
| 300 | 1309 (17) | 24 (100) | 108 (100) | 439 (100) | 160 (18) | |
| 600 | 1502 (19) | 24 (100) | 107 (99) | 439 (100) | 161 (18) | |
| 1000 | 1885 (24) | 23 (96) | 108 (100) | 433 (98) | 167 (19) | |
| Pt732Ag731(140) | 0 | 1238 (16) | 24 (100) | 108 (100) | 440 (100) | 159 (18) |
| Pt732Ag731(201) | 0 | 1238 (16) | 24 (100) | 108 (100) | 440 (100) | 159 (18) |
| 300 | 1354 (17) | 24 (100) | 108 (100) | 440 (100) | 159 (18) | |
| 600 | 1671 (21) | 24 (100) | 107 (99) | 440 (100) | 160 (18) | |
| 1000 | 2129 (27) | 24 (100) | 108 (100) | 429 (98) | 170 (19) | |
| Pt732Cu731(140) | 0 | 3868 (50) | 24 (100) | 48 (44) | 0 (0) | 659 (74) |
| Pt732Cu731(201) | 0 | 4543 (58) | 24 (100) | 86 (80) | 57 (13) | 564 (63) |
| 300 | 4343 (56) | 23 (96) | 63 (58) | 58 (13) | 587 (66) | |
| 600 | 4244 (55) | 21 (88) | 61 (56) | 73 (17) | 576 (65) | |
| 1000 | 4183 (54) | 19 (79) | 55 (51) | 98 (22) | 559 (63) | |
Usage of both the (140) and (201) sets of energies ε results in the same topologies of the lowest-energy orderings of Pt732Au731 and Pt732Ag731 NPs. These are core–shell orderings with Au and Ag atoms occupying all surface and a part of subsurface positions, while Pt atoms form compact cores inside the monolayer skins of coinage metals. Since Au and Ag atoms tend to surface segregate and Pt–Au and Pt–Ag bonds are destabilizing with respect to forming homometallic bonds, by 11–21 meV each, these 1238 bonds comprise only 16% of all 7776 bonds in the 1463-atom NPs, see Table 4.
The equilibrium ordering in Pt732Cu731 NP is more complex, reflecting that Pt–Cu bonds are stabilizing with respect to the corresponding homometallic bonds, and that smaller Cu atoms alloyed with Pt are less disfavored when located inside the particles compared to Au and Ag atoms. In Pt732Cu731(140) all 24 corner positions are occupied by Cu atoms, each of them stabilizing the system by −27 meV with respect to having Pt in the same positions. Occupation of almost a half of edge positions by Cu atoms alternating with Pt atoms to increase the number of favorable Pt–Cu bonds partially counterbalanced the preference, by 181 meV, of each edge Pt atom compared to having an edge Cu atom. A layered arrangement of inner Pt and Cu atoms seems to be also result from an increased number of favorable Pt–Cu bonds. No Cu atoms occupy terrace sites in line with the largest destabilization by 344 meV per terrace Cu atom with respect to having a Pt atom in those positions. Interestingly, the number of surface Cu atoms in the Pt732Cu731(201) NP, 167, is more than twice larger than in the Pt732Cu731(140) NP, 72. This finding seems counterintuitive based on the energies ε, which indicate stronger destabilization of surface Cu atoms in Pt101Cu100 NP than in Pt70Cu70 NP. It can be explained by the fact that Cu atoms in the Pt732Cu731(201) NP are scattered and mostly surrounded by Pt atoms forming more favorable Pt–Cu contacts. Indeed, there are more Pt–Cu bonds in the structure Pt732Cu731(201), 4543 (58%), than in Pt732Cu731(140), 3868 (50%), since the εPt-CuBOND values for the 201- and 140-atomic NPs are −43 and −35 meV, respectively. The energy gain due to an increased number of Pt–Cu contacts in Pt732Cu731(201) NP, −29.025 eV according to the energies ε, see Table 1, overcompensates the energy penalty caused by the presence of more surface Cu atoms, 26.429 eV. Thus, the equilibrium ordering Pt732Cu731(201) is estimated to be ca. 2.6 eV more stable than Pt732Cu731(140) one, which for such large particles translates in a difference of 1.8 meV per atom. Note that many adsorbates from the reacting media interact with Pt surface sites at least 1 eV stronger than with the corresponding Cu sites. Therefore, similar changes of the ordering patterns as those simulated for the structures Pt732Cu731(201) and Pt732Cu731(140), see Fig. 4, can be easily caused at experimental conditions in Pt–Cu NPs by adsorbing even a few reacting species from the environment.
The calculated results presented so far have corresponded to equilibrium structurers at temperature 0 K. Since the TOP method allows to approximately account for entropy effects associated with the chemical orderings (neglecting vibrational contributions), we employed a computational setup introduced elsewhere15 for estimating properties associated with Boltzmann population of different homotops. Specifically, we calculated the average topology in the Pt732X731 (X = Au, Ag, Cu) NPs in the temperature range 0–1000 K by means of the Metropolis Monte Carlo algorithm. In particular, the averaging was done over accepted configurations obtained during an MC run at a given temperature, which results in the probability of occupying of each site by either Pt or X atoms. The homotop with the most similar topology to the calculated average is then chosen as the representative model for each run. As expected, temperature increase noticeably increased the disorder in all modeled particles, see Table 4 and Fig. 5 for the results corresponding to 300, 600, and 1000 K.
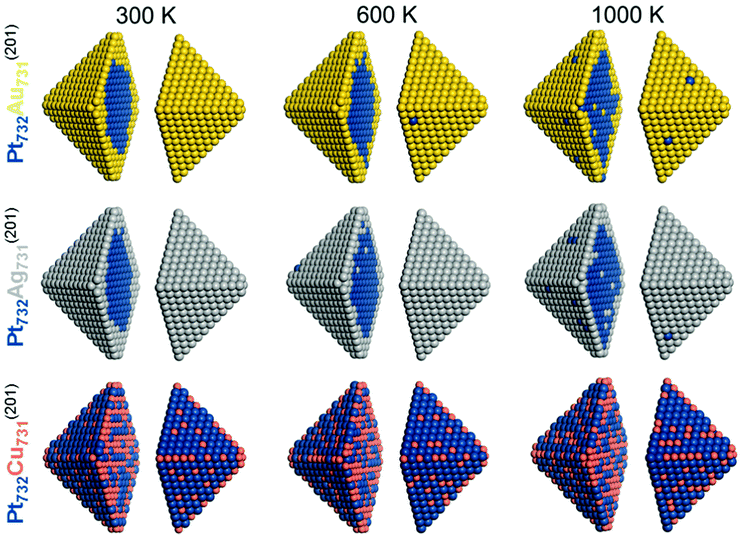 | ||
| Fig. 5 Equilibrium chemical orderings of Pt732Au731, Pt732Ag731, and Pt732Cu731 nanoparticles at temperatures 300 K, 600 K and 1000 K calculated using eqn (1) for the corresponding Pt101Au100, Pt101Ag100, and Pt101Cu100 particles. Colors of atoms are as in Fig. 1. | ||
For instance, several Pt atoms appeared at 600 and 1000 K on the surface of Pt732Au731 and Pt732Ag731 NPs that exhibited complete surface shells of Au and Ag atoms at 0 and 300 K. Concomitantly, single Au and Ag atoms migrated in the compact Pt cores. Also, the number of both Pt–Au and Pt–Ag bonds increased with the temperature increase. The fraction of Pt–Au bonds in Pt732Au731 NP increased from 16% (0 K) to 17% (300 K), 19% (600 K), and 24% (1000 K). The corresponding number of bonds in Pt732Ag731 NP increases somewhat more steep at elevated temperature, in line with less destabilizing character of Pt–Ag bonds compared with Pt–Au bonds.
In Pt732Cu731 NP the number of stabilizing Pt–Cu bonds slightly decreased at higher temperatures, from 58% at 0 K to 54% at 1000 K. Cu atoms migrate upon the temperature increase from corner and edge positions most populated at 0 K primarily to surface terrace positions.
4. Summary and conclusions
We determined equilibrium chemical orderings in truncated-octahedral Pt–Au, Pt–Ag, and Pt–Cu nanoparticles containing 140 and 201 atoms at metals concentrations 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1
1, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 by means of DFT calculations combined with the Topological approach.14,15
3 by means of DFT calculations combined with the Topological approach.14,15
The equilibrium chemical orderings in the Pt–Au and Pt–Ag particles with ≤201 atoms closely resemble each other: Au and Ag atoms are strongly energetically driven to be on the surface, whereas Pt atoms preferentially occupy inner positions. The immiscibility of Au and Ag atoms with Pt atoms prevents the appearance of Pt atoms on the surface of these nanoalloys as single-atom catalytic sites until the coinage metal content becomes low. Atoms in Pt–Au nanoparticles are essentially neutral, whereas in Pt–Ag nanoparticles Pt and Ag atoms are moderately charged negatively and positively, respectively. This suggests noticeably different reactivity of surface Pt sites on Pt–Ag than on single-metal Pt particles.
In Pt–Cu nanoparticles, Pt atoms are driven to the surface and most stabilized in the 9- and 8-coordinated positions of the {111} and {100} nanofacets. Pt–Cu bonds formed upon the favorable mixing of Pt and Cu atoms induce a strong Cu to Pt charge transfer. The up to half of an electron transferred to surface Pt atoms from nearby Cu atoms is expected to substantially affect the surface reactivity of both Pt and Cu sites.
Ordering trends in Pt–X nanoalloys are quite similar to the trends in previously characterized Pd–X nanoalloys, i.e. with the coinage metal atoms at the surface for X = Au or Ag, and rather well mixed orderings for X = Cu. The main difference is that heterometallic bonds slightly destabilize (with respect to homometallic bonds) Pt–Ag and Pt–Au particles, but stabilize Pd–Ag and Pd–Au ones, leading to more mixed terraces in the later two.
The most stable orderings in ca. 4.4 nm Pt732Au731 and Pt732Ag731 particles are of the Pt–core/Au(Ag)–shell type. The lowest-energy chemical ordering pattern of Pt732Cu731 particle is characterized by surface Cu atoms scattered over Pt atoms in the facets and quite randomly distributed inner atoms of both metals. Modelling the evolution of the orderings upon temperature increase revealed that heating leads to the appearance of single-atom or diatomic surface Pt sites on facets of Pt732Au731 and Pt732Ag731 particles and increases the disorder and number of surface Cu atoms on facets of Pt732Cu731 particle. New surface sites with correspondingly different chemical properties are formed upon heating.
The results presented in this work are relevant for studies in which structure and surface properties of a large number of bimetallic compositions are simulated using machine-learning and/or high-throughput approaches. Such studies often relied on models produced by directly cutting bulk structures,58,59 without considering that due to the stability of particular chemical orderings inherently different sites can be exposed on the surface.
Author contributions
L. Vega: calculations, conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft, review & editing; H. A. Aleksandrov: calculations, conceptualization, investigation, methodology, writing – original draft, review & editing; F. Viñes: investigation, supervision, validation, writing – review & editing; R. Farris: calculations, validation; A. Bruix: investigation, methodology, validation, writing – review & editing; K. M. Neyman: conceptualization, methodology, project administration, supervision, validation, writing – original draft, review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Authors acknowledge support by the grants PGC2018-093863-B-C22, RTI2018-095460-B-I00, and MDM-2017-0767 of the Spanish Ministerio de Ciencia y Universitades as well as by the grant 2017SGR13 of the Generalitat de Catalunya. HAA is grateful to the Operational Program “Science and Education for Smart Growth” under contract UNITe No. BG05M2OP001-1.001-0004-C01 (2018–2023). The Generalitat de Catalunya financed the work of LV (via pre-doctoral grant 2018FI-B-00384) and AB (via grant 2018BP00190). Research contribution of RF has been supported by a visiting grant HPC17YE51L of the HPC-Europa3 program. The study was also supported by Bulgarian Ministry of Education and Science via the contract D01-76/2021 and by European COST Action CA18234. Computer resources have been partly provided by the Red Española de Supercomputación (projects QS-2020-2-0020, QS-2019-3-0023, QSM-2018-1-0029).References
- R. Ferrando, J. Jellinek and R. L. Johnston, Nanoalloys:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) From Theory to Applications of Alloy Clusters and Nanoparticles, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
From Theory to Applications of Alloy Clusters and Nanoparticles, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed. - F. Calvo, Nanoalloys from Fundamentals to Emergent Applications, Elsevier, Amsterdam, 2013 Search PubMed.
- I. V. Yudanov, R. Sahnoun, K. M. Neyman and N. Rösch, Carbon Monoxide Adsorption on Palladium Nanoparticles: A Relativistic Density Functional Study, J. Chem. Phys., 2002, 117, 9887–9896 CrossRef CAS.
- I. V. Yudanov, R. Sahnoun, K. M. Neyman, N. Rösch, J. Hoffmann, S. Schauermann, V. Johánek, H. Unterhalt, G. Rupprechter, J. Libuda and H.-J. Freund, CO Adsorption on Pd Nanoparticles: Density Functional and Vibrational Spectroscopy Studies, J. Phys. Chem. B, 2003, 107, 255–264 CrossRef CAS.
- A. Roldán, F. Viñes, F. Illas, J. M. Ricart and K. M. Neyman, Density Functional Studies of Coinage Metal Nanoparticles: Scalability of Their Properties to Bulk, Theor. Chem. Acc., 2008, 120, 565–573 Search PubMed.
- K. M. Neyman, R. Sahnoun, C. Inntam, S. Hengrasmee and N. Rösch, Computational Study of Model Pd–Zn Nanoclusters and Their Adsorption Complexes with CO Molecules, J. Phys. Chem. B, 2004, 108, 5424–5430 CrossRef CAS.
- I. V. Yudanov and K. M. Neyman, Stabilization of Au at Edges of Bimetallic PdAu Nanocrystallites, Phys. Chem. Chem. Phys., 2010, 12, 5094–5100 RSC.
- J. Ryosuke, K. K. T. Suzuki and Y. Morimoto, DFT Calculations on Electro-Oxidations And Dissolutions of Pt and Pt–Au Nanoparticles, Catal. Today, 2016, 262, 100–109 CrossRef.
- L. Piccolo, Z. Y. Li, I. Demiroglu, F. Moyon, Z. Konuspayeva, G. Berhault, P. Afanasiev, W. Lefebvre, J. Yuan and R. L. Johnston, Understanding And Controlling The Structure And Segregation Behaviour of AuRh Nanocatalysts, Sci. Rep., 2016, 6, 35226 CrossRef CAS PubMed.
- M. Hu, D. P. Linder, M. B. Nardelli and A. Striolo, Hydrogen Adsorption on Platinum–Gold Bimetallic Nanoparticles: A Density Functional Theory Study, J. Phys. Chem. C, 2013, 117, 15050–15060 CrossRef CAS.
- X. Lei, H. Mu, S. Li, G. Liu, B. Xu and C. Ouyang, The Structural and Electronic Properties of Pt–Cu Alloy Clusters: Embedding Atom Method Combined with Density Functional Theory Study, J. Alloys Compd., 2018, 741, 604–609 CrossRef CAS.
- L.-L. Wang and D. D. Johnson, Predicted Trends of Core-Shell Preferences for 132 Late Transition-Metal Binary-Alloy Nanoparticles, J. Am. Chem. Soc., 2009, 131, 14023–14029 CrossRef CAS PubMed.
- M. Mamatkulov, I. V. Yudanov, A. V. Bukhtiyarov, I. P. Prosvirin, V. I. Bukhtiyarov and K. M. Neyman, Pd Segregation on the Surface of Bimetallic PdAu Nanoparticles Induced by Low Coverage of Adsorbed CO, J. Phys. Chem. C, 2019, 123, 8037–8046 CrossRef CAS.
- S. M. Kozlov, G. Kovács, R. Ferrando and K. M. Neyman, How to Determine Accurate Chemical Ordering in Several Nanometer Large Bimetallic Crystallites from Electronic Structure Calculations, Chem. Sci., 2015, 6, 3868–3880 RSC.
- G. Kovács, S. M. Kozlov and K. M. Neyman, Versatile Optimization of Chemical Ordering in Bimetallic Nanoparticles, J. Phys. Chem. C, 2017, 121, 10803–10808 CrossRef.
- L. Vega, H. A. Aleksandrov and K. M. Neyman, Using Density Functional Calculations to Elucidate Atomic Ordering of Pd-Rh Nanoparticles at Sizes Relevant for Catalytic Applications, Chin. J. Catal., 2019, 40, 1749–1757 CrossRef.
- M. Mamatkulov, I. V. Yudanov, A. V. Bukhtiyarov and K. M. Neyman, Pd Single-atom Sites on the Surface of PdAu Nanoparticles: A DFT-based Topological Search for Suitable Compositions, Nanomaterials, 2021, 11, 122 CrossRef CAS PubMed.
- S. Olobardi, L. Vega, A. Fortunelli, M. Stener, F. Viñes and K. M. Neyman, Optical Properties and Chemical Ordering of Ag–Pt Nanoalloys: A Computational Study, J. Phys. Chem. C, 2019, 123, 25482–25491 CrossRef CAS.
- G. Kovács, S. M. Kozlov, I. Matolínová, M. Vorokhta, V. Matolín and K. M. Neyman, Revealing Chemical Ordering in Pt–Co Nanoparticles Using Electronic Structure Calculations and X-ray Photoelectron Spectroscopy, Phys. Chem. Chem. Phys., 2015, 17, 28298–28310 RSC.
- M. Vorokhta, I. Khalakhan, M. Václavů, G. Kovács, S. M. Kozlov, P. Kúš, T. Skála, N. Tsud, J. Lavková, V. Potin, I. Matolínová, K. M. Neyman and V. Matolín, Surface Composition of Magnetron Sputtered Pt–Co Thin Film Catalyst for Proton Exchange Membrane Fuel Cells, Appl. Surf. Sci., 2016, 365, 245–251 CrossRef CAS.
- I. Khalakhan, L. Vega, M. Vorokhta, T. Skála, F. Viñes, Y. V. Yakovlev, K. M. Neyman and I. Matolínová, Irreversible Structural Dynamics on the Surface of Bimetallic PtNi Alloy Catalyst under Alternating Oxidizing And Reducing Environments, Appl. Catal., B, 2020, 264, 118476 CrossRef.
- A. Neitzel, G. Kovács, Y. Lykhach, S. M. Kozlov, N. Tsud, T. Skála, M. Vorokhta, V. Matolín, K. M. Neyman and J. Libuda, Atomic Ordering and Sn Segregation in Pt–Sn Nanoalloys Supported on CeO2 Thin Films, Top. Catal., 2017, 60, 522–532 CrossRef CAS.
- A. Wolfbeisser, G. Kovács, S. M. Kozlov, K. Föttinger, J. Bernardi, B. Klötzer, K. M. Neyman and G. Rupprechter, Surface Composition Changes of CuNi-ZrO2 During Methane Decomposition: An Operando NAP-XPS and Density Functional Study, Catal. Today, 2017, 283, 134–143 CrossRef CAS.
- L. Liu and A. Corma, Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- L. Li, X. Chang, X. Lin, Z.-J. Zhao and J. Gong, Theoretical Insights into Single-Atom Catalysts, Chem. Soc. Rev., 2020, 49, 8156–8178 RSC.
- R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Single-Atom Alloy Catalysis, Chem. Rev., 2020, 120, 12044–12088 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed ; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
- P. Janthon, S. M. Kozlov, F. Viñes, J. Limtrakul and F. Illas, Establishing the Accuracy of Broadly Used Density Functionals in Describing Bulk Properties of Transition Metals, J. Chem. Theory Comput., 2013, 9, 1631–1640 CrossRef CAS PubMed.
- P. Janthon, S. Luo, S. M. Kozlov, F. Viñes, J. Limtrakul, D. G. Truhlar and F. Illas, Bulk Properties of Transition Metals: A Challenge for the Design of Universal Density Functionals, J. Chem. Theory Comput., 2014, 10, 3832–3839 CrossRef CAS PubMed.
- L. Vega, J. Ruvireta, F. Viñes and F. Illas, Jacob's Ladder as Sketched by Escher: Assessing the Performance of Broadly Used Density Functionals on Transition Metal Surface Properties, J. Chem. Theory Comput., 2018, 14, 395–403 CrossRef CAS PubMed.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- F. Viñes, F. Illas and K. M. Neyman, On the Mechanism of Formation of Metal Nanowires by Self-Assembly, Angew. Chem., Int. Ed., 2007, 46, 7094–7097 CrossRef PubMed.
- S. M. Kozlov, H. A. Aleksandrov, J. Goniakowski and K. M. Neyman, Effect of MgO(100) Support on Structure and Properties of Pd and Pt Nanoparticles with 49–155 Atoms, J. Chem. Phys., 2013, 139, 084701 CrossRef PubMed.
- A. Ruban, H. L. Skriver and J. K. Nørskov, Surface Segregation Energies in Transition-Metal Alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15990–16000 CrossRef.
- V. Grolier and R. Schmid-Fetzer, Experimental Study of Au–Pt–Sn Phase Equilibria and Thermodynamic Assessment of the Au–Pt and Au–Pt–Sn Systems, J. Electron. Mater., 2008, 37, 264–278 CrossRef CAS.
- L. Deng, W. Hu, H. Deng and S. Xiao, Surface Segregation and Structural Features of Bimetallic Au–Pt Nanoparticles, J. Phys. Chem. C, 2010, 114, 11026–11032 CrossRef CAS.
- S. Takizawa, K. Terakura and T. Mohri, Electronic Theory for Phase Stability of Nine AB Binary Alloys, with A = Ni, Pd, or Pt and B = Cu, Ag, or Au, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5792–5797 CrossRef CAS PubMed.
- O. Kubaschewski, C. B. Alcock and P. J. Spencer, Materials Thermochemistry, Oxford, Pergamon, 6th edn, 1993 Search PubMed.
- J. Tang, L. Deng, S. Xiao, H. Deng, X. Zhang and W. Hu, Chemical Ordering and Surface Segregation in Cu–Pt Nanoalloys: The Synergetic Roles in the Formation of Multishell Structures, J. Phys. Chem. C, 2015, 119, 21515–21527 CrossRef CAS.
- T. Abe, B. Sundman and H. Onodera, Thermodynamic Assessment of the Cu–Pt System, J. Phase Equilibria Diffus., 2006, 27, 5–13 CrossRef CAS.
- Z. W. Lu, S.-H. Wei, A. Zunger, S. Frota-Pessoa and L. G. Ferreira, First-Principles Statistical Mechanics of Structural Stability of Intermetallic Compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 512–544 CrossRef CAS PubMed.
- A. F. Wells, Structural Inorganic Chemistry, Clarendon Press, Oxford, 5th edn, 1984 Search PubMed.
- J. Tang, L. Deng, H. Deng, S. Xiao, X. Zhang and W. Hu, Surface Segregation and Chemical Ordering Patterns of Ag–Pd Nanoalloys: Energetic Factors, Nanoscale Effects, and Catalytic Implication, J. Phys. Chem. C, 2014, 118, 27850–27860 CrossRef CAS.
- J. M. Rahm and P. Erhart, Understanding Chemical Ordering in Bimetallic Nanoparticles from Atomic-Scale Simulations: The Competition between Bulk, Surface, and Strain, J. Phys. Chem. C, 2018, 122, 28439–28445 CrossRef CAS.
- L. Deng, X. Liu, X. Zhang, L. Wang, W. Wei Li, M. Song, J. Tang, H. Deng, S. Xiao and W. Hu, Intrinsic Strain-Induced Segregation in Multiply Twinned Cu–Pt Icosahedra, Phys. Chem. Chem. Phys., 2019, 21, 4802–4809 RSC.
- J. Pirart, A. Front, D. Rapetti, C. Andreazza-Vignolle, P. Andreazza, C. Mottet and R. Ferrando, Reversed size-dependent stabilization of ordered nanophases, Nat. Commun., 2019, 10, 1982 CrossRef CAS PubMed.
- N. Danielis, L. Vega, G. Fronzoni, M. Stener, A. Bruix and K. M. Neyman, AgPd, AuPd, and AuPt Nanoalloys with Ag- or Au-rich Compositions: Modeling Chemical Ordering and Optical Properties, J. Phys. Chem. C, 2021, 125 DOI:10.1021/acs.jpcc.1c04222.
- S. Liu, Z.-J. Zhao, C. Yang, S. Zha, K. M. Neyman, F. Studt and J. Gong, Adsorption Preference Determines Segregation Direction: A Shortcut to More Realistic Surface Models of Alloy Catalysts, ACS Catal., 2019, 9, 5011–5018 CrossRef CAS.
- Y. Lykhach, S. M. Kozlov, T. Skála, A. Tovt, V. Stetsovych, N. Tsud, F. Dvořák, V. Johánek, A. Neitzel, J. Mysliveček, S. Fabris, V. Matolín, K. M. Neyman and J. Libuda, Counting Electrons on Supported Nanoparticles, Nat. Mater., 2016, 15, 284–288 CrossRef CAS PubMed.
- F. Viñes and A. Görling, Explaining Cu@Pt Bimetallic Nanoparticles Activity Based on NO Adsorption, Chem. – Eur. J., 2020, 26, 11478–11491 CrossRef PubMed.
- Y. Suchorski, S. M. Kozlov, I. Bespalov, M. Datler, D. Vogel, Z. Budinska, K. M. Neyman and G. Rupprechter, The Role of Metal/Oxide Interfaces for Long-Range Metal Particle Activation during CO Oxidation, Nat. Mater., 2018, 17, 519–522 CrossRef CAS PubMed.
- R. Ferrando, A. Fortunelli and G. Rossi, Quantum Effects on The Structure of Pure and Binary Metallic Nanoclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085449 CrossRef.
- D. Cheng, W. Wang and S. Huang, The Onion-Ring Structure for Pd–Pt Bimetallic Clusters, J. Phys. Chem. B, 2006, 110, 16193–16196 CrossRef CAS PubMed.
- D. Cheng, W. Wang, S. Huang and D. Cao, Atomistic Modeling of Multishell Onion-Ring Bimetallic Nanowires and Clusters, J. Phys. Chem. C, 2008, 112, 4855–4860 CrossRef CAS.
- C. D. Feldt, R. Moreira, E. Meyer, P. Clawin, W. Riedel, T. Risse, L. Moskaleva, W. Dononelli and T. Klüner, CO Adsorption on Au(332):Combined Infrared Spectroscopy and Density Functional Theory Study, J. Phys. Chem. C, 2019, 123, 8187–8197 CrossRef CAS.
- K. Tran and Z. W. Ulissi, Active Learning across Intermetallics to Guide Discovery of Electrocatalysts for CO2 Reduction and H2 Evolution, Nat. Catal., 2018, 1, 696–703 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Structural and energy data calculated by DFT of the discussed in the article Pt–Au, Pt–Ag and Pt–Cu nanoparticles (PDF). See DOI: 10.1039/d1ma00529d |
| This journal is © The Royal Society of Chemistry 2021 |