Open Access Article
Open Access ArticleFrom starphenes to non-benzenoid linear conjugated polymers by substrate templating†
Mohammed S. G.
Mohammed‡
ab,
James
Lawrence‡
*ab,
Fátima
García
 c,
Pedro
Brandimarte
a,
Alejandro
Berdonces-Layunta
ab,
Dolores
Pérez
c,
Pedro
Brandimarte
a,
Alejandro
Berdonces-Layunta
ab,
Dolores
Pérez
 c,
Daniel
Sánchez-Portal
ab,
Diego
Peña
c,
Daniel
Sánchez-Portal
ab,
Diego
Peña
 *c and
Dimas G.
de Oteyza
*c and
Dimas G.
de Oteyza
 *abd
*abd
aDonostia International Physics Center (DIPC), San Sebastián, Spain. E-mail: james.lawrence@dipc.org; d_g_oteyza@ehu.eus
bCentro de Física de Materiales (CSIC-UPV/EHU), San Sebastián, Spain
cCentro Singular de Investigación en Química Biolóxica e Materiais Moleculares (CiQUS), Departamento de Química Orgánica, Universidade de Santiago de Compostela, Santiago de Compostela, Spain. E-mail: diego.pena@usc.es
dIkerbasque, Basque Foundation for Science, Bilbao, Spain
First published on 8th March 2021
Abstract
Combining on-surface synthetic methods with the power of scanning tunneling microscopy to characterize novel materials at the single molecule level, we show how to steer the reactivity of one anthracene-based precursor towards different product nanostructures. Whereas using a Au(111) surface with three-fold symmetry results in the dominant formation of a starphene derivative, the two-fold symmetry of a reconstructed Au(110) surface allows the selective growth of non-benzenoid linear conjugated polymers. We further assess the electronic properties of each of the observed product structures via tunneling spectroscopy and DFT calculations, altogether advancing the synthesis and characterization of molecular structures of notable scientific interest that have been only scarcely investigated to date, as applies both to starphenes and to non-benzenoid conjugated polymers.
Introduction
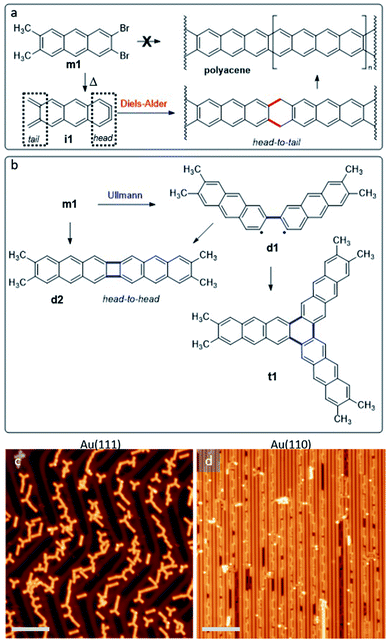
On-surface synthesis is becoming an increasingly popular approach for the synthesis of novel organic materials.1–3 Performed on well-defined surfaces and under ultra-high-vacuum conditions, it has been shown to allow for the synthesis of materials unachievable by conventional solution chemistry alone.4–6 One such example are higher acenes, whose open-shell character increases as the number of fused benzene rings grows.7,8 This compromises their stability and makes their synthesis challenging.9 One way to overcome this stability limitation is an inert environment such as an ultra-high-vacuum,10,11 which has indeed allowed the synthesis of the longest acenes to date.12 However, the synthesis of even longer acenes still remains an open challenge in spite of its notable interest from both fundamental and application oriented viewpoints, the limiting case being the narrowest possible zigzag-edge graphene nanoribbons.13,14In addition to the infinite polyacene, other linear acene-based polymers display similarly interesting properties, which can range e.g. from ultra-low band gaps15 to spin-polarized bands.16 In fact, also acene-based molecules attract great interest, as for example in the case of starphenes.17–21 All of the aforementioned structures may potentially be obtained by on-surface synthesis from the reactant m1 displayed in Fig. 1a (see ESI Notes 1.1, 1.2 and Fig. S1–S5† for synthesis details). It includes two halogen atoms and two methyl groups on either side of the anthracene backbone. Both types of functionalization are included among the first groups whose thermal activation was demonstrated to work in “on-surface synthesis” experiments, leading to the controlled and reproducible covalent coupling of reactants.22,23 On-surface, the ortho-dibromo moiety could afford an aryne (named as head, Fig. 1a), while the vicinal dimethyl groups could lead to an ortho-quinodimethane (named as tail, Fig. 1a), therefore forming intermediate i1. We expected that this intermediate could polymerize on surface to obtain polyacene by means of Diels–Alder cycloaddition (head-to-tail polymerization) followed by dehydrogenation.
We have performed on-surface synthesis experiments with compound m1 on two different substrates, namely Au(111) and Au(110). By using scanning tunneling microscopy and spectroscopy (STM and STS), in combination with density functional theory (DFT) calculations, we analyze the chemical structure and electronic properties of the reaction products (see ESI Note 1 and Fig. S6† for methods details). Because the C–Br bond is activated at lower temperatures than C–H, Ullmann coupling dominates the initial reaction steps independently of the substrate. That is, instead of the head-to-tail product described in Fig. 1a, head-to-head products like those outlined in Fig. 1b are obtained. The products can include reactant molecules that are either at an angle (e.g.d1 or t1) or collinearly oriented (e.g.d2). Compound d2 and t1 can be formally considered as [2 + 2] and [2 + 2 + 2] aryne cycloaddition products.17,24 Importantly, the substrate symmetry determines the reaction outcome:24 whereas on the hexagonal Au(111) surface the reaction products include both linear and non-linear (“two-dimensional”) molecules with a pronounced favoritism for molecular trimers (t1) with three-fold symmetry,17,24 on the 2 × 1 Au(110) reconstruction its linear trenches act as templates that limit the reaction products to collinearly fused reactants (e.g.d2). That is, as occurred also with closely related non-methylated reactants on Au(111) and Au(100),24 the substrate templating can be used to steer the reaction outcome and the product's alignment.
Results and discussion
The deposition of m1 has been performed onto Au(111) and Au(110) substrates held at RT. Under such conditions, the molecules remain intact on both surfaces and self-assemble into structures as shown in Fig. S7.† On Au(111), the molecules show a remarkable tendency to form three-fold symmetric self-assembled trimers (Fig. S7b†) in which the molecules are aligned along the1–10 and its two equivalent substrate directions, with the halogen-functionalized side facing towards the trimer's center (Fig. S7c†) and at a distance of about 3.2 Å from one another. The driving force for such self-assembly may thus be either the formation of halogen bonds,25,26 or the coordination through a gold atom. For the former to be attractive, C–Br bonds require a certain angular offset, whereas the latter requires a surface atom or adatom to be coordinated to the halogens. None of the two is clearly observed in the images. However, the offset required may be too low to be distinguished by STM, and also coordinating metal adatoms are often not easily distinguished in scanning probe microscopy. None of the two scenarios can thus be discarded at this point. The comparison between the experiment and the DFT relaxed structure of the free-standing non-covalent trimmers (see Fig. S7d†) seem to indicate that the substrate plays a crucial role. However, it is not clear whether this is due to a substrate-induced modification of the character of the Br–Br bonds or to the presence of a coordinating metal that does not produce a clear feature in the STM images. As occurs with many other molecules,27,28 including also the reaction products analyzed in more detail below, the molecules adsorb preferentially on the fcc regions of the Au(111) reconstruction.On Au(110) the molecules are uniaxially aligned parallel to the 2 × 1 surface reconstruction. The intact molecules adsorb preferentially on top of the reconstruction's Au rows, with the halogenated sides facing each other, although the opposite halogen-to-methyl alignment can also be observed occasionally (Fig. S7a†). Carbon–halogen bonds display a lower activation temperature than that corresponding to carbon–hydrogen bonds, causing the initial reactions to be dominated by Ullmann coupling, whose main products are depicted in Fig. 1b (completed with additional minority products shown in Fig. S8†). Only at higher temperatures in the range of 525 K do the methyl groups become activated, leading to the intermolecular coupling of the previously formed Ullmann coupling products (Fig. 1c and d). Interestingly, as shown in Fig. 1b–d the preferred molecules' relative alignment on either substrate is perpetuated as the intermolecular covalent coupling reactions are thermally activated. That is, the two- and three-fold symmetry of the Au(110) and Au(111) substrates, respectively, is preserved in the self-assembled non-covalent structures of the as-deposited reactants, as well as in the predominant reaction products.
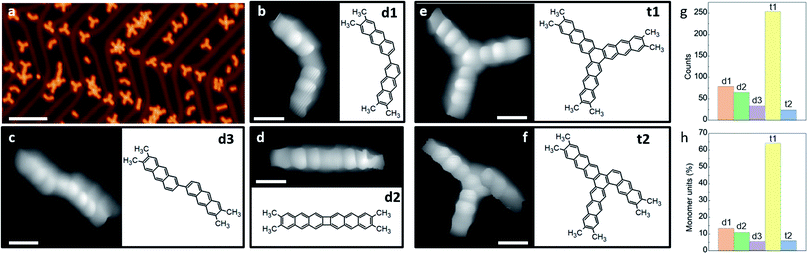
In the following, we analyze in detail the initial reactions observed after annealing to only 425 K. Only the C–Br bonds are activated at this temperature, restricting the generated products to a well-defined and limited set of structures. A representative large-scale image after a sub-monolayer deposition of m1 on Au(111) followed by an annealing treatment is shown in Fig. 2a. The compendium of all observed covalently coupled products is presented in Fig. 2b–f (some apparently more complex structures observed in Fig. 2a are just some of these products interacting non-covalently with additional unreacted monomers), and their relative abundance is shown in the histograms of Fig. 2g and h. Among the products we observe dimers linked by a single covalent bond that is either on the same molecular side, resulting in a structure with the two acene moieties at an angle of approximately 120 degrees (d1, Fig. 2c), or on opposite sides, resulting in a staggered structure of two collinearly oriented acene moieties (d3, Fig. 2b). The other observed dimer presents two bonds linking the two anthracene moieties, forming a four-membered ring (d2, Fig. 2d). This product may evolve from d1 by a second bond C–C bond formation that quenches its remaining radicals, or be the result of a concerted formation of two bonds from two activated m1 monomers.17,24
Whereas the two new bonds formed with d2 quench all the four radicals generated with the homolytic cleavage of the C–Br bonds of two reactant molecules, the single-bond formation of d1 and d3 quenches only two of them. Whether in the observed dimers the remaining radicals are passivated by H of unknown origin (e.g. residual H from the UHV chamber) or not remains unknown, but at least no obvious bonding of the σ-radical to the Au substrate is apparent from a molecular tilt that would in principle be associated with it. In any case, structures d1 and d3 with remaining radicals are very reactive species that presumably act as precursors for the formation of trimers. Taking the most common dimer d1 as starting point, the natural addition of a third activated m1 monomer quenching all radicals would form the three-fold symmetric hexamethyl [10]-starphene (t1, Fig. 2e). However, an alternative scenario including a hydrogen migration may result in an asymmetric triphenylene derivative (t2, Fig. 2f). The latter may also be obtained from d3 under the same conditions: the addition of an activated m1 monomer and an associated H migration (Fig. S8†). The product's relative abundance, however, shows that among the dimers the most common is d1, while in total numbers there is a dramatic preference for t1. The stepwise evolution of m1 to d1 and to t1 thus appears as the presumably most favorable pathway.
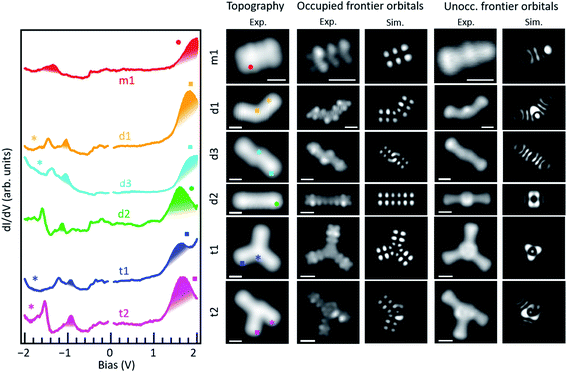
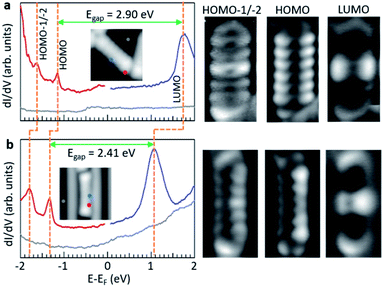
It is interesting to compare the electronic properties of the various structures, all consisting of different coupling motifs of the same precursor unit. As reference we thus take the precursor unit. Scanning tunneling spectroscopy measurements on the as-deposited molecules, however, are hindered by their limited stability. Whereas well-defined resonances associated with the occupied states can be observed (Fig. S9†), at positive bias values of around +2 V there is always a sudden jump in the conductance associated with a chemical transformation of the molecules; in particular, with their debromination. The unoccupied molecular orbitals of m1 are expected to be around those energies and the instability may be actually promoted by the population of the LUMO level upon tunneling. In any case, a proper characterization of the unoccupied orbitals is thus hindered. However, such instability is no longer present in debrominated monomer molecules. In this case we can also observe a clear resonance from the HOMO level, although shifted by about 0.29 eV towards the Fermi level to an energy of −1.34 eV (Fig. 3). Halogenation of molecules is a commonly applied method to increase their ionization potential and electron affinity.29,30 We thus associate the observed shift with the disappearance of the halogen's effect as its bond to the molecule is broken. An advantage of this is that the LUMO resonance can now be nicely resolved as well, with its maximum at an energy of 2.05 eV, resulting in a HOMO–LUMO gap of 3.39 eV (Fig. 3). The molecule under study consists of a conjugated anthracene backbone with two additional methyl groups. The sp3 conjugation of the latter severely limits their contribution to the low energy π-orbitals,10,31,32 making the molecule's electronic properties comparable to those of pristine anthracene. Anthracene's reported HOMO–LUMO gap is indeed only slightly larger (EG ≈ 3.6 eV),12 and the appearances of its frontier orbitals33 are very similar to those of the frontier orbitals of the hydrogen-passivated m1 (Fig. 3). The conductance measurements, however, show a stronger than expected contribution at the methyl positions if compared to the calculations. Here it needs to be noted that the DFT calculations are performed for gas-phase molecules, according to which the molecule presents a completely planar C backbone with the H atoms bound to each of the sp3 C atoms protruding to either side of the plane. Upon adsorption on Au(111) the symmetry is broken and the hydrogen atoms pointing towards the surface are repelled by steric repulsion. This causes the sp3 carbons atoms to lie higher up (farther from the surface), a distortion that is still noticeable at the nearest sp2 hybridized carbon atoms of the anthracene moiety and may even help in decoupling electronically the molecules from the substrate.32 This topographic effect translates into a larger STM signal at the higher C atoms and thus into the apparently stronger-than-expected contribution of the methyl groups to the frontier molecular orbitals.
As two such monomers are linked by a single bond into d1, both the HOMO and LUMO shift toward the Fermi level to −1.05 eV and 1.82 eV, respectively (Fig. 3). The HOMO–LUMO gap thus shrinks notably to 2.87 eV, as expected from a bonding motif that maintains the conjugation at the inter-monomer level and thus results in an overall extension of the electron conjugation and delocalization.34 A similar coupling with a single bond but with the monomers in a collinear and staggered position (d3) results in an only slightly larger gap of 2.97 eV (Fig. 3) with the HOMO and LUMO at −1.12 eV and 1.85 eV, respectively. As the two monomers become linked with two covalent bonds that form a new four membered ring at the junction (d2), the changes in the frontier orbital energies are not so pronounced either. The HOMO remains at −1.14 eV and the LUMO displays a downward shift to 1.66 eV, which results in a gap of 2.8 eV (Fig. 3). This implies a change of only 70 meV with respect to d1, which can be understood as both cases having a relatively similar amount of electron delocalization.
The overall appearance of the HOMO and LUMO molecular orbitals within each of the anthracene segments basically maintains that of the monomer, with a series of lobes at the sides of each hexagon and a nodal plane along the long axis at the HOMO energies, and banana-like intensities along the acene segment's short axis at the LUMO energies. For all the dimers, experiment and theory show a nice agreement in this respect, as well as in the varying junction-dependent signal that further confirms the assignment of their chemical structure. This is shown in Fig. 3, which compares the frontier orbitals as measured by constant height conductance maps, and in the extended Fig. S10,† which includes more molecular states and shows how their conductance maps measured with different STM scanning modes compare to theory for each of the products. It is important to note here that, in the theoretical simulation, dangling bonds created after the cleavage of C–Br bonds have been saturated by hydrogen. Therefore, the good agreement between the simulated STM images and the experiment indicates that, whether they are radicals or are indeed saturated by H, the molecules remain approximately planar and the observed molecular states are mostly derived from carbon π orbitals. In fact, given the π character of the frontier orbitals in these molecules, the appearance of the STM images and STS maps are not expected to depend critically on the details of the saturation of the sigma bonds left after Br cleavage.
As the molecules form trimers, the electron delocalization is expected to increase further and thus the gap to shrink accordingly. That is indeed the case. For the hexamethyl [10]-starphene t1, taking the dimer d2 as reference, the LUMO remains hardly unchanged at 1.64 eV. However, the HOMO level shifts upward to 0.94 eV and thus closes the semiconducting gap to 2.58 eV. Also here the conductance maps at the HOMO and LUMO energy agree nicely with density functional theory calculations (Fig. 3), keeping in mind that the main discrepancies relate, as in the case of the dimers, to the deviations from planarity as the molecules adsorb on the Au(111) surface. That is, the highest position of the methyl groups and the concomitant increase in height of the nearest sp2 carbon atoms cause the DOS lobes on the latter to appear strongest, as well as the appearance of additional unexpectedly strong lobes at the positions of the former (Fig. 3). The calculated wavefunctions of HOMO and LUMO on each of the arms of t1 look extremely similar to those of m1 (Fig. 3). However, the conjugation and electronic coupling between the arms becomes evident from the decreased gap, which implies a substantial electron delocalization over the whole structure. It is interesting to compare the symmetric t1 molecule with the asymmetric t2 molecule. Although both are closely related, in the case of t2, theory predicts the HOMO and HOMO−1 to be quasi-degenerate, and the same applies to the LUMO and LUMO+1. Indeed, their superposition provides a substantially better match to the experimentally measured conductance maps at the energies of the frontier orbitals (Fig. S10†) than if compared to HOMO and LUMO alone (Fig. S11†). Nevertheless, the experimentally observed gap of t2 is, within our experimental resolution, equal to that of t1.
As advanced in the beginning of this article, on Au(110) the situation is completely different. As occurs on Au(111), the initial reactions are dominated by Ullmann coupling. However, the action of the highly anisotropic Au(110) surface as a template limits the reaction products to structures composed of collinear reactant molecules, which in turn limits the possible Ullmann coupling products to d2 and d3. Out of these two structures d3 is much less common, amounting only to 17 ± 2%. Henceforth we will thus only focus on structures hierarchically built from d2. To covalently couple d2 molecules the methyl groups need first to be activated through the formation of the corresponding benzylic radicals. This requires higher temperatures than the Ullmann coupling, namely in the order of 525 K. Whereas on Au(111) such temperature treatment results in highly disordered polymers (Fig. 1b), the uniaxial monomer alignment on Au(110) drives a polymerization of d2 molecules into regular non-benzenoid one-dimensional polymers (Fig. 4).
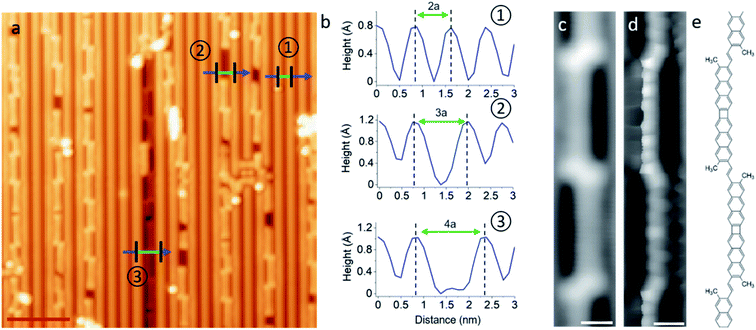
As a first observation, it becomes evident that the polymers always adsorb within trenches of the reconstructed substrate surface. As prepared, the Au(110) is characterized by a 2 × 1 reconstruction in which neighboring rows of Au atoms are separated by twice the Au lattice constant a = 4.07 Å.35 Such a reconstruction can be observed in the clean substrate regions of Fig. 4a, and its periodicity is shown in the top profile of Fig. 4b marked with a circled “1”. However, although the mere “as deposited” m1 reactants don't cause any changes to it (Fig. S7a†), the surface in the vicinity of the polymers changes into a 3 × 1 (circled “2” in Fig. 4a and b) or occasionally also a 4 × 1 (circled “3” in Fig. 4a and b) reconstruction as the sample is annealed, with the polymers always embedded within the widened trenches.
Fig. 4c shows a representative constant current image of the dominant reaction product. Its building unit is clearly recognized as head-to-headd2, but the inter-unit coupling through the tails (methyl groups) is not trivial to determine even from high-resolution images with CO-functionalized probes in the repulsive interaction regime (Fig. 4d), in part due to the non-planarity of the polymer carbon backbone within the reconstruction trenches. We have considered five different tail-to-tail linking motifs (Fig. S12†) and could determine the structure displayed in Fig. 4e as the actual product because it is the only one reproducing the electronic properties of the polymers that are described below. The two lobes of enhanced contrast at either side of the junction in constant current images (Fig. 4c) are thus assigned to the remaining sp3 methyl groups and their increased height, as occurred with the molecular structures on Au(111).
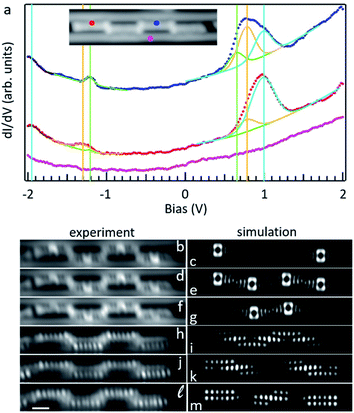
Fig. 5a displays differential conductance point spectra obtained on an oligomer composed of four d2 units shown in the inset. The spectra display a pronounced location-dependent signal, as presented with two examples (blue and red curves) obtained at the accordingly colored points in the inset (the pink curve is the reference spectrum on the substrate). In either case the spectra reveal broad resonances both for the occupied and unoccupied states. Conductance maps of occupied and unoccupied states are reminiscent of the HOMO and LUMO of d2 (Fig. 3), with a series of lobes along the molecular sides for the former and a large dominating signal at the position of the four-membered ring for the latter. The signal is additionally modulated by an asymmetry along the long molecular axis due to the alternating tilt of the different d2 units, whose sides nearest to the Au rows delimiting the trench are higher and thus appear with a stronger contrast.
Interestingly, conductance maps at different energies within the range of those broad resonances show a markedly different appearance. Focusing on the unoccupied states, as the energy is increased the maps show an increased signal first on the two central 4-membered rings (Fig. 5f), then homogeneously distributed over the four 4-membered rings of the tetramer (Fig. 5d), and finally on the 4-membered rings of the two outer units (Fig. 5b). In contrast, as we move away from the Fermi energy for the occupied states, the signal is first strongest on the two central units (Fig. 5h), then on the outer units (Fig. 5j) and then appears homogeneously distributed over the four units (Fig. 5l). The same findings, although with increased contrast, are obtained from constant current conductance maps (Fig. S13e†). DFT calculations on a free-standing tetramer reveal the DOS of the first three occupied and unoccupied states to have exactly the same distribution (the discrepancies between theory and experiment can be accounted for by the substrate-driven alternating tilt of the d2 units in the experiment and the planar structure in the calculations). We thus conclude that the broad resonances observed in the spectra correspond to a convolution of multiple orbitals. We have deconvoluted the various states fitting the spectra with a background and six Gaussian resonances, displayed with green, orange and light blue colored lines as their energy departs from the Fermi level for both occupied and unoccupied states (Fig. 5a). The fits of both spectra show the six resonances at the same energies (additionally marked by accordingly colored vertical lines) but with a varying intensity that follows the orbital's distribution measured experimentally and confirmed by theory (Fig. 5b–m). This overall nice agreement, along with the excellently matching DOS from experiment and calculations at the inter-unit junctions (Fig. S14†), proves our structural assignment for the linking motif. Besides, annealing to even higher temperatures (at which additional cyclodehydrogenation events can be triggered) rendered different types of junctions that have instead been assigned to some of the other coupling motifs that were considered (Fig. S12IV and V†) by a comparison of their measured and calculated low-energy orbitals (Fig. S15†).
Although with few specific exceptions,12,36 the HOMO–LUMO gap in conjugated oligomers and polymers is usually expected to scale inversely with the molecular size.37–40 We have analyzed that behavior comparing oligomers with lengths from one single d2 unit to six of them (Fig. S13†). The spectra indeed reveal the onset of the occupied and unoccupied frontier states to approach the Fermi level as the length increases, although with negligible changes for lengths above four units, for which the peak-to-peak of the fitted HOMO and LUMO resonances marked in green in Fig. 5a amounts to 1.85 eV. Regardless of the oligomer length the conductance maps of the low-energy orbitals (Fig. S13b–f†) show the same intensity distribution: the unoccupied orbitals are most intense first on the central units, then all over the structure and thereafter on the outer units, whereas the occupied orbitals are most intense first on the central unit, then on the outer units and then all over the structure.
It is also interesting to compare the measured electronic properties of adsorbates as a function of the underlying substrate. Within this work, the common product on which to perform such comparison is d2, and the associated data are displayed in Fig. 6. On both surfaces, the dI/dV spectra reveal clear resonances for the HOMO−1, HOMO and LUMO orbitals. However, there are substantial differences between the two gold surfaces. Taking the data on Au(111) as reference, we see a substantial downward shift in the energy of all molecular orbitals of molecules adsorbed on Au(110). This effect could in principle be ascribed to the different workfunction of the two gold surfaces, which is lower by about 170 meV for Au(110).41 In an ideal vacuum level pinning scenario, as expected for weakly interacting molecule–substrate interfaces,42,43 this would translate into a rigid downward shift of all molecular orbitals by that amount. However, whereas the HOMO and HOMO−1 indeed shift rigidly by that same amount, the LUMO shifts substantially more, resulting in a reduction of the HOMO–LUMO gap by nearly 0.5 eV. We hypothesize that, although maintaining a weak adsorbate–substrate electronic coupling and thus showing no obvious changes in the conductance maps of the orbitals, the larger shift of the LUMO may result from a slightly increased hybridization of the unoccupied molecular orbitals with the undercoordinated (and thus more reactive) Au atoms that form the rows of the Au(110) reconstruction and cause the molecule's tilting. Furthermore, the gap reduction is also compatible with a larger role of the electronic screening induced by the substrate, which is consistent with the position of the molecules inside the trenches of the surface reconstruction.
Conclusion
In conclusion, we have analyzed the reactivity of acene-based precursor molecules functionalized with halogen atoms and methyl groups on two substrates of different symmetry. The one- and three-fold symmetry of the Au(110) and Au(111) substrates, respectively, is transferred to the self-assembled non-covalent structures of the as-deposited reactants, as well as to the predominant reaction products. Whereas on the Au(111) surface the molecules show a marked preference for the formation of starphene, on Au(110) the one-dimensional trenches of its reconstruction limit the product structures to those conformed by collinearly fused precursors, which end up polymerizing into one-dimensional non-benzenoid conjugated polymers. We further provide a detailed characterization of the electronic properties of each of the observed products. This work thus constitutes a substantial advance in the controlled synthesis and the characterization of to date only scarcely investigated organic products of great scientific interest, as applies both to starphenes and to non-benzenoid conjugated polymers.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge funding from the European Union's Horizon 2020 programme (Grant Agreement No. 635919 and 863098), from the Spanish Agencia Estatal de Investigación (Grant No. MAT2016-78293-C6, PID2019-107338RB-C63, PID2019-107338RB-C66 and FIS2017-83780-P), Xunta de Galicia (Centro singular de investigación de Galicia, accreditation 2019–2022, ED431G 2009/03), Dep. Educación of the Basque Government and UPV/EHU (Grant No. IT-756-13), and the European Regional Development Fund (ERDF).References
- S. Clair and D. G. de Oteyza, Chem. Rev., 2019, 119, 4717–4776 CrossRef CAS PubMed.
- Q. Shen, H.-Y. Gao and H. Fuchs, Nano Today, 2017, 13, 77–96 CrossRef CAS.
- T. Wang and J. Zhu, Surf. Sci. Rep., 2019, 74, 97–140 CrossRef CAS.
- N. Pavliček, A. Mistry, Z. Majzik, N. Moll, G. Meyer, D. J. Fox and L. Gross, Nat. Nanotechnol., 2017, 12, 308–311 CrossRef PubMed.
- S. Mishra, D. Beyer, K. Eimre, S. Kezilebieke, R. Berger, O. Gröning, C. A. Pignedoli, K. Müllen, P. Liljeroth, P. Ruffieux, X. Feng and R. Fasel, Nat. Nanotechnol., 2020, 15, 22–28 CrossRef CAS PubMed.
- K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299–1301 CrossRef CAS PubMed.
- J. Hachmann, J. J. Dorando, M. Avilés and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309 CrossRef PubMed.
- M. Bendikov, H. M. Duong, K. Starkey, K. N. Houk, E. A. Carter and F. Wudl, J. Am. Chem. Soc., 2004, 126, 7416–7417 CrossRef CAS PubMed.
- R. Dorel and A. M. Echavarren, Eur. J. Org. Chem., 2017, 2017, 14–24 CrossRef CAS PubMed.
- R. Zuzak, R. Dorel, M. Krawiec, B. Such, M. Kolmer, M. Szymonski, A. M. Echavarren and S. Godlewski, ACS Nano, 2017, 11, 9321–9329 CrossRef CAS PubMed.
- J. Krüger, F. García, F. Eisenhut, D. Skidin, J. M. Alonso, E. Guitián, D. Pérez, G. Cuniberti, F. Moresco and D. Peña, Angew. Chem., Int. Ed., 2017, 56, 11945–11948 CrossRef PubMed.
- F. Eisenhut, T. Kühne, F. García, S. Fernández, E. Guitián, D. Pérez, G. Trinquier, G. Cuniberti, C. Joachim, D. Peña and F. Moresco, ACS Nano, 2020, 14, 1011–1017 CrossRef CAS PubMed.
- M. Corso, E. Carbonell-Sanromà and D. G. de Oteyza, in On-Surface Synthesis II, ed. D. G. de Oteyza and C. Rogero, Springer International Publishing, Cham, 2018, pp. 113–152 Search PubMed.
- P. Ruffieux, S. Wang, B. Yang, C. Sánchez-Sánchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli, D. Passerone, T. Dumslaff, X. Feng, K. Müllen and R. Fasel, Nature, 2016, 531, 489–492 CrossRef CAS PubMed.
- B. Cirera, A. Sánchez-Grande, B. de la Torre, J. Santos, S. Edalatmanesh, E. Rodríguez-Sánchez, K. Lauwaet, B. Mallada, R. Zbořil, R. Miranda, O. Gröning, P. Jelínek, N. Martín and D. Ecija, Nat. Nanotechnol., 2020, 15, 437–443 CrossRef CAS PubMed.
- C. Sánchez-Sánchez, T. Dienel, A. Nicolaï, N. Kharche, L. Liang, C. Daniels, V. Meunier, J. Liu, X. Feng, K. Müllen, J. R. Sánchez-Valencia, O. Gröning, P. Ruffieux and R. Fasel, Chem.–Eur. J., 2019, 25, 12074–12082 CrossRef PubMed.
- C. Sánchez-Sánchez, A. Nicolaï, F. Rossel, J. Cai, J. Liu, X. Feng, K. Müllen, P. Ruffieux, R. Fasel and V. Meunier, J. Am. Chem. Soc., 2017, 139, 17617–17623 CrossRef PubMed.
- I. Pozo, E. Guitián, D. Pérez and D. Peña, Acc. Chem. Res., 2019, 52, 2472–2481 CrossRef CAS PubMed.
- S. Godlewski, M. Kolmer, M. Engelund, H. Kawai, R. Zuzak, A. Garcia-Lekue, M. Saeys, A. M. Echavarren, C. Joachim, D. Sanchez-Portal and M. Szymonski, Phys. Chem. Chem. Phys., 2016, 18, 3854–3861 RSC.
- S. Godlewski, H. Kawai, M. Engelund, M. Kolmer, R. Zuzak, A. Garcia-Lekue, G. Novell-Leruth, A. M. Echavarren, D. Sanchez-Portal, C. Joachim and M. Saeys, Phys. Chem. Chem. Phys., 2016, 18, 16757–16765 RSC.
- J. Holec, B. Cogliati, J. Lawrence, A. Berdonces-Layunta, P. Herrero, Y. Nagata, M. Banasiewicz, B. Kozankiewicz, M. Corso, D. de Oteyza, A. Jancarik and A. Gourdon, Angew. Chem., Int. Ed., 2021 DOI:10.1002/anie.202016163.
- L. Grill, M. Dyer, L. Lafferentz, M. Persson, M. V. Peters and S. Hecht, Nat. Nanotechnol., 2007, 2, 687–691 CrossRef CAS PubMed.
- M. In't Veld, P. Iavicoli, S. Haq, D. B. Amabilino and R. Raval, Chem. Commun., 2008, 1536 RSC.
- M. Koch, M. Gille, S. Hecht and L. Grill, Surf. Sci., 2018, 678, 194–200 CrossRef CAS.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- J. Tschakert, Q. Zhong, D. Martin-Jimenez, J. Carracedo-Cosme, C. Romero-Muñiz, P. Henkel, T. Schlöder, S. Ahles, D. Mollenhauer, H. A. Wegner, P. Pou, R. Pérez, A. Schirmeisen and D. Ebeling, Nat. Commun., 2020, 11, 5630 CrossRef CAS PubMed.
- I. Fernandez-Torrente, S. Monturet, K. J. Franke, J. Fraxedas, N. Lorente and J. I. Pascual, Phys. Rev. Lett., 2007, 99, 176103 CrossRef CAS PubMed.
- M. S. G. Mohammed, L. Colazzo, A. Gallardo, J. A. Pomposo, P. Jelínek and D. G. de Oteyza, Chem. Commun., 2020, 56, 8659–8662 RSC.
- D. G. de Oteyza, A. El-Sayed, J. M. Garcia-Lastra, E. Goiri, T. N. Krauss, A. Turak, E. Barrena, H. Dosch, J. Zegenhagen, A. Rubio, Y. Wakayama and J. E. Ortega, J. Chem. Phys., 2010, 133, 214703 CrossRef CAS PubMed.
- F. Babudri, G. M. Farinola, F. Naso and R. Ragni, Chem. Commun., 2007, 1003–1022 RSC.
- L. Colazzo, M. S. G. Mohammed, R. Dorel, P. Nita, C. García Fernández, P. Abufager, N. Lorente, A. M. Echavarren and D. G. de Oteyza, Chem. Commun., 2018, 54, 10260–10263 RSC.
- M. S. G. Mohammed, L. Colazzo, R. Robles, R. Dorel, A. M. Echavarren, N. Lorente and D. G. de Oteyza, Commun. Phys., 2020, 3, 159 CrossRef CAS.
- A. V. Kukhta, I. N. Kukhta, N. A. Kukhta, O. L. Neyra and E. Meza, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 205701 CrossRef.
- C. Steiner, J. Gebhardt, M. Ammon, Z. Yang, A. Heidenreich, N. Hammer, A. Görling, M. Kivala and S. Maier, Nat. Commun., 2017, 8, 14765 CrossRef CAS PubMed.
- M. Copel, P. Fenter and T. Gustafsson, J. Vac. Sci. Technol., A, 1987, 5, 742–746 CrossRef CAS.
- S. Hemmatiyan and D. A. Mazziotti, J. Phys. Chem. C, 2019, 123, 14619–14624 CrossRef CAS.
- M. Kertesz, C. H. Choi and S. Yang, Chem. Rev., 2005, 105, 3448–3481 CrossRef CAS PubMed.
- J. Torras, J. Casanovas and C. Alemán, J. Phys. Chem. A, 2012, 116, 7571–7583 CrossRef CAS PubMed.
- R. Gutzler and D. F. Perepichka, J. Am. Chem. Soc., 2013, 135, 16585–16594 CrossRef CAS PubMed.
- J. Lawrence, P. Brandimarte, A. Berdonces-Layunta, M. S. G. Mohammed, A. Grewal, C. C. Leon, D. Sánchez-Portal and D. G. de Oteyza, ACS Nano, 2020, 14, 4499–4508 CrossRef CAS PubMed.
- G. N. Derry, M. E. Kern and E. H. Worth, J. Vac. Sci. Technol., A, 2015, 33, 060801 CrossRef.
- E. Goiri, P. Borghetti, A. El-Sayed, J. E. Ortega and D. G. de Oteyza, Adv. Mater., 2016, 28, 1340–1368 CrossRef CAS PubMed.
- A. El-Sayed, P. Borghetti, E. Goiri, C. Rogero, L. Floreano, G. Lovat, D. J. Mowbray, J. L. Cabellos, Y. Wakayama, A. Rubio, J. E. Ortega and D. G. de Oteyza, ACS Nano, 2013, 7, 6914–6920 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00126d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |