Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
NIR luminescence lifetime nanothermometry based on phonon assisted Yb3+–Nd3+ energy transfer†
K.
Maciejewska
,
A.
Bednarkiewicz
 and
L.
Marciniak
and
L.
Marciniak
 *
*
Institute of Low Temperature and Structure Research, Polish Academy of Sciences, Okólna 2, 50-422 Wroclaw, Poland. E-mail: l.marciniak@intibs.pl
First published on 14th June 2021
Abstract
Luminescence thermometry in biomedical sciences is a highly desirable, but also highly challenging and demanding technology. Numerous artifacts have been found during steady-state spectroscopy temperature quantification, such as ratiometric spectroscopy. Oppositely, the luminescence lifetime is considered as the most reliable indicator of temperature thermometry because this luminescent feature is not susceptible to sample properties or luminescence reabsorption by the nanothermometers themselves. Unfortunately, this type of thermometer is much less studied and known. Here, the thermometric properties of Yb3+ ions in Nd0.5RE0.4Yb0.1PO4 luminescent temperature probes were evaluated, aiming to design and optimize luminescence lifetime based nanothermometers. Temperature dependence of the luminescence lifetimes is induced by thermally activated phonon assisted energy transfer from the 2F5/2 state of Yb3+ ions to the 4F3/2 state of Nd3+ ions, which in turn is responsible for the significant quenching of the Yb3+:2F5/2 lifetime. It was also found that the thermal quenching and thus the relative sensitivity of the luminescent thermometer can be intentionally altered by the RE ions used (RE = Y, Lu, La, and Gd). The highest relative sensitivity was found to be SR = 1.22% K−1 at 355 K for Nd0.5Y0.4Yb0.1PO4 and it remains above 1% K−1 up to 500 K. The high sensitivity and reliable thermometric performance of Nd0.5La0.4Yb0.1PO4 were confirmed by the high reproducibility of the temperature readout and the temperature uncertainty being as low as δT = 0.05 K at 383 K.
1. Introduction
The consistent growth of scientific interest in luminescence thermometry (LT), a technique that exploits temperature-induced changes in the luminescence properties of phosphors for temperature readout, results from the capability of remote thermal imaging that it offers.1–7 One of the most sophisticated examples of such remote temperature readout is in vivo thermal imaging of biological systems, where, in a noninvasive and electrically passive manner, information about temperature distribution in the living cells and tissues can be visualized with a submicrometer spatial resolution.6,8–11 This may not only provide the information about the rate of the biological processes (e.g. thermogenesis) but may also enable feedback-controlled medical treatments (e.g. hyperthermal therapy).12–14The most commonly exploited spectroscopic feature of the thermometric phosphors that, after calibration, reports about temperature is the shape of luminescence spectra. Most commonly, the intensity ratio of two emission bands is used.15–24 However, because the shape of the emission band may be affected by the unknown and sample-to-sample variable absorption of the medium surrounding the phosphor or by interparticle interactions within the sample, the credibility of the ratiometric LT approach, especially in the in vivo applications, has been recently undermined.25,26 Although some strategies to mitigate, correct or circumvent these limitations have been recently proposed by involving a primary thermometry concept or multiparametric luminescent thermometers, these approaches require complicated correction and analysis of the obtained data.27
An important alternative temperature indicator utilizes temperature dependent kinetics of the excited states. Unlike short living fluorophores (e.g. organic dyes, fluorescent proteins, and most QDs), the luminescence lifetime of excited states of lanthanides is almost unaffected by the absorption or scattering by the medium, and when the surface of the phosphor is isolated from the surroundings by the optically passive shell, its kinetics is also independent of the local chemical environment. Despite this concept being promising, the relative sensitivity of lifetime-based LTs is usually considered lower with respect to the ratiometric counterpart.5,28–31 This is because the excited level kinetics is modified by quenching through temperature dependent multi-phonon processes. Therefore, to boost the sensitivity of luminescence lifetime based LTs, the other energy transfer processes susceptible to temperature should be involved.
As has been recently demonstrated, the energy transfer relying on the absorption of phonons could be an appropriate direction to follow.32 Therefore, in this manuscript, a comprehensive and detailed investigation on the temperature dependence of phonon mediated energy transfer between Yb3+ and Nd3+ ions is performed in order to develop a highly sensitive luminescent thermometer based on the kinetics of the Yb3+ ions. As the probability of phonon assisted energy transfer depends on many material parameters of the host, the performed studies have been conducted on a series of Nd0.5RE0.4Yb0.1PO4 (where RE = Y3+, Lu3+, La3+, and Gd3+) nanocrystals in order to select the most promising candidate. The proposed phosphate matrix is inherently biocompatible, resistant to strong oxidizing and reducing acids (nitric and hydrochloric acids) and enables easy fine tuning of spectral properties by intentional substitution of RE with numerous optically passive ions (e.g. RE: Y3+, Lu3+, La3+, and Gd3+ which differ in ionic radius, coordination number, etc.).33–35
2. Materials and methods
Materials
The monazite Nd1−xRExPO4:Yb3+ nanoparticles (NPs) (RE: Y3+, Lu3+, La3+, Gd3+) were synthesized via a precipitation method. All chemicals, ytterbium(III) oxide Yb2O3 (99.99%, Alfa Aesar), europium(III) oxide Nd2O3 (99.9%, Alfa Aesar), yttrium(III) oxide Y2O3 (99.99%, Alfa Aesar), lutetium(III) oxide Lu2O3 (99.99%, Alfa Aesar), lanthanum(III) oxide La2O3 (99.99%, Alfa Aesar), gadolinium(III) oxide Gd2O3 (99.99%, Alfa Aesar), ammonium hydrogen phosphate (NH4)2HPO4 (98.0%, Alfa Aesar) and polyethylene glycol (99.5%, Chempur) were used without further purification.Synthesis
Stoichiometric amounts of oxides (Y2O3, Lu2O3, La2O3, Gd2O3, Nd2O3 and Yb2O3) were diluted in ultrapure nitric acid to produce nitrates and placed in a Teflon-lined autoclave , followed by evaporation of the excess solution and drying over P2O5 in a vacuum desiccator for 1 day. The procedure for the synthesis of Nd0.5RE0.4Yb0.1PO4 (where RE: Y3+, Lu3+, La3+, and Gd3+) nanoparticles contains two steps. The first step consisted of the precipitation of orthophosphates in polyethylene glycol and water solution using (NH4)2HPO4 water solution (0.17 mol L−1) at 50 °C. In the second step, the slurry was centrifuged and washed three times in water and ethanol. The obtained orthophosphates were aged at 80 °C for 12 h and after that were annealed at 900 °C for 2 h to obtain the powders.Methods
Powder diffraction studies were carried out using a PANalytical X'Pert Pro diffractometer equipped with an Anton Paar TCU 1000 N temperature control unit using Ni-filtered Cu Kα radiation (V = 40 kV, I = 30 mA). Transmission electron microscopy images were obtained using an FEI Tecnai G2 20 X-TWIN microscope equipped with a CCD FEI Eagle 2K camera with a HAADF detector and electron gun with a LaB6 cathode. The pattern present on the left side of the TEM images is a microscope artifact.An FLS1000 spectrometer from Edinburgh Instruments equipped with a R928P side window photomultiplier tube and a Hamamatsu detector was used to carry out measurements of photoluminescence decay curves and excitation spectra utilizing a micro-flash lamp and a halogen lamp, respectively. The emission spectra were measured using a Silver-Nova Super Range TEC spectrometer from Stellarnet of 1 nm spectral resolution and 808 nm excitation lines from a laser diode. The excitation pulse duration was modulated using a simple electronic PWM system. The temperature dependencies of both emission spectra and luminescence decay profiles were measured using a THMS 600 heating–cooling stage from Linkam (0.1 °C temperature stability and 0.1 °C set point resolution) to control the temperature.
3. Results and discussion
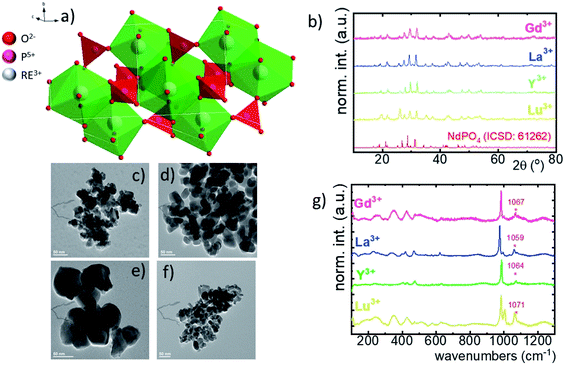
Although the RE orthophosphates crystalize in three different crystallographic structures (tetragonal, monoclinic and hexagonal) due to the ionic size of the Nd3+ ions, NdPO4 crystalizes in the monazite-type monoclinic structure of P21/c (ref. 14) symmetry with the following unit parameters: a = 6.4537 Å, b = 7.0425 Å, c = 8.2012 Å, and β = 125.8328°. In this case, the [PO4]–[REOx]–[PO4] chains are interlinked with 9 oxygen ions (Fig. 1a).36 The nine-fold coordinated site of the Nd3+ ions of C1 point symmetry can be successfully substituted by the RE ions because of the similarity in the ionic radii. The phase purity of the synthesized nanocrystals has been confirmed by the powder X-ray diffraction pattern measurements. All of the observed diffraction reflexes correspond to the reference pattern (ICSD 61262). However, due to the difference in the ionic radii between the substituting RE and Nd3+ ions, and in consequence a change of the unit cell parameters, the shift of the diffraction peaks can be observed. The values of the cell parameters obtained from the Rietveld refinement method are listed in Table 1. It can be clearly seen that for the Nd0.5RE0.4Yb0.1PO4 nanocrystals, the cell volume increases according to the following order: VY3+ < VLu3+ < VGd3+ < VLa3+. As was confirmed by the TEM studies, the synthesized powders consist of the aggregated nanocrystals (Fig. 1c–f, see also Fig. S1†). The diameter of the nanocrystals is affected by the type of the RE cation used, reaching d = 40 ± 12 nm for Y3+; d = 55 ± 10 nm for Lu3+; d = 60 ± 10 nm for La3+; d = 32 ± 12 nm for Gd3+ (Fig. S2†). In the case of Raman spectra, most of the recorded bands are characteristic of the vibrations of the phosphate groups (i.e. P–O symmetric stretching, P–O asymmetric stretching, and O–P–O symmetric/asymmetric bending vibrations). However, all the modes are shifted toward higher energies in a sequence La3+ < Y3+ < Lu3+ < Gd3+ (dashed area in the spectra).| RE3+ | Crystal structure | Point symmetry | Max phonon energy (cm−1) | a | b | c | Cell volume (Å3) | Ionic radius of RE (Å) [coordination number] |
|---|---|---|---|---|---|---|---|---|
| Lu | Monoclinic | C 1 | 1071 | 6.35179 | 6.85549 | 8.01249 | 348.90 | 1.019 [8] |
| Y | Monoclinic | C 1 | 1063 | 6.37804 | 6.87694 | 8.03117 | 352.26 | 0.977 [8] |
| La | Monoclinic | C 1 | 1060 | 6.44380 | 6.98207 | 8.17155 | 367.65 | 1.216 [9] |
| Gd | Monoclinic | C 1 | 1072 | 6.36476 | 6.88189 | 8.04216 | 352.26 | 1.107 [9] |
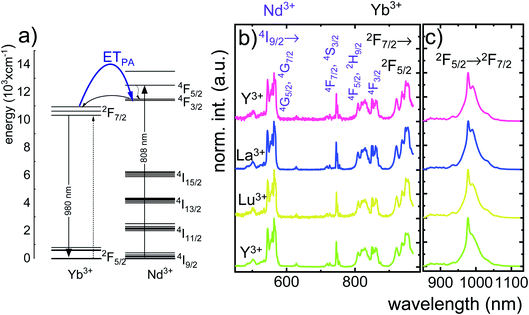
In order to explain the luminescence properties of the Nd0.5Lu0.5PO4:Yb3+ nanocrystals, simplified energy level diagrams of Nd3+ and Yb3+ ions are presented in Fig. 2a. As can be found, the Yb3+ energy level scheme is relatively simple and consists only of two energy levels –the 2F7/2 ground state and 2F5/2 excited state. Therefore, upon λexc = 940 nm photoexcitation, which corresponds to the energy difference between these two states, only a single emission band of Yb3+ at λexc = 980 nm can be observed. The relatively large energy gap between these two states leads to the low probability of the nonradiative 2F5/2 state depopulation via multiphonon processes. On the other hand, the Nd3+ ions are characterized by the more abundant energy state configuration. The radiative depopulation of the excited metastable 4F3/2 state leads to the occurrence of three emission bands usually localized at around 880 nm, 1060 nm and 1350 nm attributed to 4F3/2 → 4I9/2, 4F3/2 → 4I11/2 and 4F3/2 → 4I13/2, respectively. The fact that the 4F3/2 energy level is localized roughly 900 cm−1 above that of the 2F5/2 state of Yb3+ ions allows for energy transfer between these ions which however must be accompanied by the absorption of the host phonon. According to the Miyakava–Dexter theorem, the probability of the interionic energy transfer WET(T) is expressed using the following formula:37–40
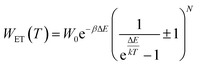 | (1) |
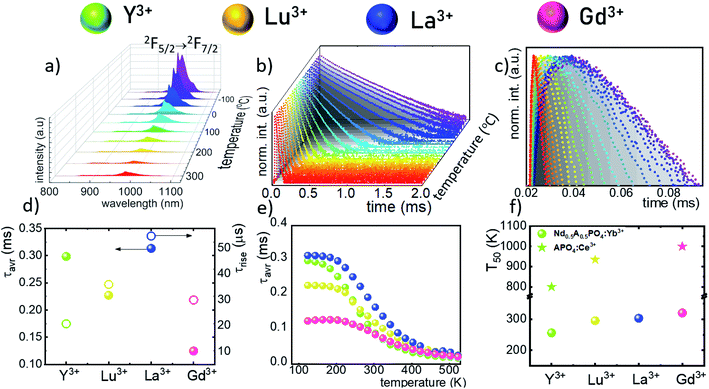
The technical feasibility and accuracy of lifetime-based remote temperature determination can be improved when the lifetime of the emitting center is relatively long and strongly temperature dependent, respectively. The feasibility of this method is improved from efficient phosphors, which can be easily photoexcited with cheap, powerful and all-electronically controlled laser diodes, while the detection of long (μs–ms) kinetics can be easily performed with current Si based photosensors equipped with simple (opposite to digitizers of sub ns–ns lifetimes) digital oscilloscope based fluorescence acquisition. Moreover, in the case of some specific applications, such as thermal bioimaging, longer luminescence decay enables temporal separation of the luminescence of the thermal probe from the background emission (i.e. autofluorescence) of the tissue. Additionally, boosting the sensitivity of the thermal probe to temperature changes is possible, because the probability of the energy transfer with the absorption of the phonon (eqn (1)) is strongly dependent on temperature. Therefore, a luminescent thermometer that involves this process is expected to possess favorable thermometric properties. The probability W0 depends on the spatial distance between the interacting ions. Therefore, in order to enhance the probability of the phonon assisted energy transfer, shortening ofthe Nd3+ to Yb3+ distance is desired. As already reported by many authors, an increase of the Yb3+ concentration leads to the enhancement of the quenching of the Yb3+ luminescence via the migration of energy from the excited states of Yb3+ to the quenching centers.41,42 It is especially acute in the case of the nanosized phosphors for which the distance to the particle surface is relatively low. Therefore, in order to avoid the activation of this quenching channel, the concentration of Nd3+ ions has been increased in this work. As can be seen, initially, for low Nd3+ concentrations, the probability of phonon assisted energy transfer was relatively low, which is confirmed by relatively small changes of the 2F5/2 lifetime at elevated temperatures (Fig. S3†). An increase of the Nd3+ amount up to 50% results in significant thermal quenching of the 2F5/2 state, which results from the phonon-assisted energy transfer from Yb3+ to Nd3+ ions being facilitated by the short distance between interacting ions. These results may suggest that a further increase of the Nd3+ concentration should be beneficial for the thermometric performance. However, the increase of the Nd3+ concentration leads to the shortening of the initial lifetime value (measured at 83 K) which may hinder the luminescence kinetics measurement at higher temperatures. Therefore, in order to satisfy the conditions of long luminescence lifetime and strong temperature dependence of the luminescence lifetime of the 2F5/2 state, a concentration of 50% Nd3+ seems to be optimal. It must be noted here that the luminescence lifetime values themselves determine and actually limit the temporal resolution of temperature imaging in general. Therefore, although long luminescence lifetimes simplify technical means to detect and record the signal, they may concurrently limit the capabilities to image fast and dynamic processes. The phonon assisted energy transfer between Yb3+ and Nd3+ ions leads to the significant quenching of the Yb3+ luminescence which is reflected by the lowering of the 2F5/2 → 2F7/2 emission intensity (Fig. 3a, see also Fig. S4†), which reached 50% of its initial intensity at around 0 °C. Moreover, the shape of the emission band was slightly changed which can be associated with the thermalization of the higher lying Stark components of the 2F5/2 state at elevated temperatures. As presented in Fig. 3b, the luminescence decay profile of Yb3+ ions significantly changes in this temperature range (see also Fig. S6 and S7†). Notably, an in-depth analysis of the obtained decay profiles reveals the short rise-time which is associated with the Nd3+ → Yb3+ energy transfer. Due to the fact that at higher temperatures the profiles slightly deviate from the exponential decay, the average lifetime of the excited states has been calculated as follows:
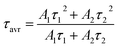 | (2) |
The analysis of the temperature dependence of τavr indicates that the RE3+ ions significantly affect the rate and the temperature of the activation of the thermal quenching of the 2F5/2 luminescence. The initial (at 110 K) τavr decreases from τavr = 0.31 ms for La3+, τavr = 0.29 ms for Y3+, τavr = 0.22 ms for Lu3+ to τavr = 0.12 ms for Gd3+. This dependence may be associated both with the interionic distance between neighboring Nd3+ and Yb3+ ions (which is dependent on the ionic radii of the RE3+ ions) and the phonon energy of the host material. It can also be noted that the value of the rise times is also affected by the host material composition. In the case of Nd0.5Y0.4Yb0.1PO4, when the temperature increases, thermal quenching of the 2F5/2 state instantly initializes. On the other hand, the quenching process started around 200 K for Nd0.5La0.4Yb0.1PO4 and Nd0.5Y0.4Yb0.1PO4. The highest thermal susceptibility reveals Nd0.5Gd0.4Yb0.1PO4 for which τavr starts to decreases above 220 K. In the case of all the host materials under investigation, the most significant τavr changes can be observed in the 200–400 K temperature range. In order to quantify the quenching process, the temperature at which τavr reached half of its initial value (T50) was considered (Fig. 3f). As can be seen, the T50 increases as follows: T50 = 256 K (Y3+), T50 = 295 K (Lu3+), T50 = 303 K (La3+) and T50 = 320 K (Gd3+). A similar trend was reported previously by Witkowski et al.43 for REPO4:Ce3+ (the stars in Fig. 3f). Although the thermal quenching process in this case was discussed in terms of electron transfer to the conduction band, a similar trend and influence of the host material was observed in the case of the Nd3+,Yb3+ co-doped systems.
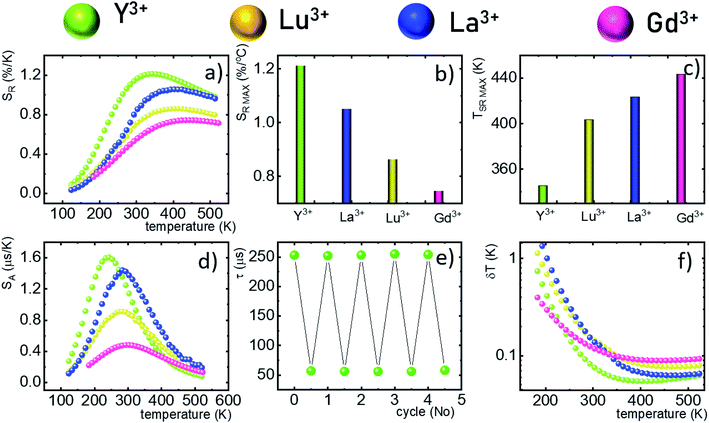
One of the most important thermographic parameters that enables to directly compare the thermometric performance of different luminescent thermometers is the relative thermal sensitivity SR which, in the case of the average luminescence lifetime used as the thermometric parameter, is defined as follows:
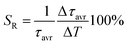 | (3) |
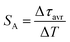 | (4) |
The maximum SA = 1.65 μs K−1 was found for Nd0.5Y0.4Yb0.1PO4. According to the expectations, the temperature at which the maximum value of SA was reached correlates well with the T50 temperature (Fig. 3f). It should be emphasized that in the case of the nanosized phosphors, their spectroscopic properties such as the shape of the emission spectra, luminescence lifetime and the ultimately thermometric properties may depend on the size of the nanoparticles. However, no such correlation could be found versus the series of passive Ln3+ dopants (Y3+, La3+, Gd3+, and Lu3+) used in our studies (Fig. S8†). Moreover, it was found that the τavr is in principle independent of the emission wavelength used, when the 950–980 nm spectral range is used (Fig. S9†). However at λem = 990 nm, a slightly longer value of the lifetime was found. This effect may also be related to the small difference in the crystallographic surrounding of some Yb3+ ions localized in the REPO4 nanocrystals (different crystallographic sites). This may modify the probabilities of the nonradiative depopulation rates of the 2F5/2 states, and since the contribution of the emission intensity of Yb3+ ions from different crystallographic sites depends on the spectral range, the lifetime may, in consequence, slightly vary with the detection wavelength used.
In order to verify the thermal stability of the synthesized nanocrystals and the repeatability of temperature readout based on the lifetime of the 2F5/2 state of the Yb3+ ions, the luminescence decay profiles were measured in several heating–cooling cycles (Fig. 4e). The obtained results confirm good thermometric performance of the Nd0.5RE0.4Yb0.1PO4 luminescent thermometers. Additionally the temperature determination uncertainty (δT) was calculated as follows:
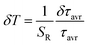 | (5) |
4. Conclusions
The thermometric performance of the Yb3+ luminescence lifetime based thermometers in Nd0.5RE0.4Yb0.1PO4 nanocrystals was investigated in a wide temperature range. Temperature dependent phonon assisted energy transfer from the 2F5/2 excited state of Yb3+ to the 4F3/2 state of Nd3+ ions was proposed as the thermal sensitivity mechanism. The influence of temperature on the τavr was investigated for different RE ions (RE = Y, Lu, La, and Gd). It was found that for the optimal concentration of 50% Nd3+ ions at elevated temperatures, the luminescence lifetime of the Yb3+:2F5/2 state was rapidly quenched. The determined temperature, at which the luminescence lifetime reached half of its initial value (T50), increases from T50 = 256 K (Y3+) through T50 = 295 K (Lu3+), T50 = 303 K (La3+) to T50 = 320 K for Gd3+ passive co-dopants. High thermal quenching of the thermometric parameter (i.e. the lifetime of the Yb3+:2F5/2 state) is reflected in the thermometric performance of the described remote temperature probe. The highest absolute and relative sensitivities were found for the Nd0.5Y0.4Yb0.1PO4 compound – i.e. SA = 1.65 μs K−1 at 225 K and SR = 1.22% K−1 at 355 K were obtained, respectively. The change of the RE ions decreases the maximum value of the SR and increases the temperature at which SRMAX is reached. High thermometric performance of the Nd0.5Y0.4Yb0.1PO4 phosphor was also confirmed by good repeatability of the temperature readout within many heating–cooling cycles and by low temperature determination uncertainty (δT = 0.05 K at 383 K). The obtained results indicate that the phonon assisted energy transfer should be considered in further studies as a promising mechanism that may boost the sensitivity of lifetime based remote temperature probes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support from the European Union's Horizon 2020 FET Open program under grant agreement no. 801305 is acknowledged.References
-
M. Dramićanin, in Woodhead Publishing Series in Electronic and Optical Materials, ed. M. B. T.-L. T. Dramićanin, Woodhead Publishing, 2018, pp. 1–12 Search PubMed
.
- J. Zhou, B. del Rosal, D. Jaque, S. Uchiyama and D. Jin, Nat. Methods, 2020, 17, 967–980 CrossRef CAS
.
- A. Bednarkiewicz, L. Marciniak, L. D. Carlos and D. Jaque, Nanoscale, 2020, 12, 14405–14421 RSC
.
- X. Wang, O. S. Wolfbeis and R. J. Meier, Chem. Soc. Rev., 2013, 42, 7834–7869 RSC
.
-
L. D. Carlos and F. Palacio, Thermometry at the Nanoscale, The Royal Society of Chemistry, 2016 Search PubMed
.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4301–4326 RSC
.
- M. Suta and A. Meijerink, Adv. Theory Simul., 2020, 2000176 CrossRef CAS
.
- C. D. S. Brites, A. Millán and L. D. Carlos, Handb. Phys. Chem. Rare Earths, 2016, 49, 339–427 CAS
.
- D. Chrétien, P. Bénit, H.-H. Ha, S. Keipert, R. El-Khoury, Y.-T. Chang, M. Jastroch, H. T. Jacobs, P. Rustin and M. Rak, PLoS Biol., 2018, 16, e2003992 CrossRef PubMed
.
- S. Arai, M. Suzuki, S.-J. Park, J. S. Yoo, L. Wang, N.-Y. Kang, H.-H. Ha and Y.-T. Chang, Chem. Commun., 2015, 51, 8044–8047 RSC
.
- S. Kiyonaka, R. Sakaguchi, I. Hamachi, T. Morii, T. Yoshizaki and Y. Mori, Nat. Methods, 2015, 12, 801–802 CrossRef CAS PubMed
.
- E. Carrasco, B. del Rosal, F. Sanz-Rodríguez, Á. J. de la Fuente, P. H. Gonzalez, U. Rocha, K. U. Kumar, C. Jacinto, J. G. Solé and D. Jaque, Adv. Funct. Mater., 2015, 25, 615–626 CrossRef CAS
.
- E. Hemmer, P. Acosta-Mora, J. Méndez-Ramos and S. Fischer, J. Mater. Chem. B, 2017, 5, 4365–4392 RSC
.
- B. del Rosal, E. Carrasco, F. Ren, A. Benayas, F. Vetrone, F. Sanz-Rodríguez, D. Ma, Á. Juarranz and D. Jaque, Adv. Funct. Mater., 2016, 26, 6060–6068 CrossRef CAS
.
-
M. Dramićanin and B. Windows, Biomedical Applications of Luminescence Thermometry, 2018 Search PubMed
.
-
M. D. Dramićanin, Luminescence Thermometry, Elsevier, 2018 Search PubMed
.
- M. Sekulić, V. Đorđević, Z. Ristić, M. Medić and M. D. Dramićanin, Adv. Opt. Mater., 2018, 6, 1–7 Search PubMed
.
- M. Suta, Ž. Antić, V. Đorđević, S. Kuzman, M. D. Dramićanin and A. Meijerink, Nanomaterials, 2020, 10, 543 CrossRef CAS PubMed
.
- L. Marciniak, A. Bednarkiewicz, D. Kowalska and W. Strek, J. Mater. Chem. C, 2016, 4, 5559–5563 RSC
.
- K. Maciejewska and L. Marciniak, Chem. Eng. J., 2020, 402, 126197 CrossRef CAS
.
- K. Kniec, M. Tikhomirov, B. Pozniak, K. Ledwa and L. Marciniak, Nanomaterials, 2020, 10, 1–12 CrossRef
.
- C. Matuszewska, K. Elzbieciak-Piecka and L. Marciniak, J. Phys. Chem. C, 2019, 123, 18646–18653 CrossRef CAS
.
- A. M. Kaczmarek, M. K. Kaczmarek and R. Van Deun, Nanoscale, 2019, 11, 833–837 RSC
.
- O. A. Savchuk, J. J. Carvajal, C. D. S. Brites, L. D. Carlos, M. Aguilo and F. Diaz, Nanoscale, 2018, 10, 6602–6610 RSC
.
- L. Labrador-Páez, M. Pedroni, A. Speghini, J. García-Solé, P. Haro-González and D. Jaque, Nanoscale, 2018, 10, 22319–22328 RSC
.
- Y. Shen, J. Lifante, N. Fernández, D. Jaque and E. Ximendes, ACS Nano, 2020, 14, 4122–4133 CrossRef CAS PubMed
.
- Y. Shen, H. D. A. Santos, E. C. Ximendes, J. Lifante, A. Sanz-Portilla, L. Monge, N. Fernández, I. Chaves-Coira, C. Jacinto, C. D. S. Brites, L. D. Carlos, A. Benayas, M. C. Iglesias-de la Cruz and D. Jaque, Adv. Funct. Mater., 2020, 2002730 CrossRef CAS
.
- K. Elzbieciak-Piecka, J. Drabik, D. Jaque and L. Marciniak, Phys. Chem. Chem. Phys., 2020, 22, 25949–25962 RSC
.
- S. Arai, S. Lee, D. Zhai, M. Suzuki and Y. T. Chang, Sci. Rep., 2014, 4, 2–7 Search PubMed
.
- L. Marciniak, K. Elzbieciak-Piecka, K. Kniec and A. Bednarkiewicz, Chem. Eng. J., 2020, 388, 124347 CrossRef CAS
.
- M. D. Chambers and D. R. Clarke, Annu. Rev. Mater. Res., 2009, 39, 325–359 CrossRef CAS
.
- M. Tan, F. Li, N. Cao, H. Li, X. Wang, C. Zhang, D. Jaque and G. Chen, Small, 2020, 16, 2004118 CrossRef CAS PubMed
.
- K. Maciejewska, B. Poźniak, M. Tikhomirov, A. Kobylińska and L. Marciniak, Nanomaterials, 2020, 10, 421 CrossRef CAS PubMed
.
- M. Runowski, A. Shyichuk, A. Tymiński, T. Grzyb, V. Lavín and S. Lis, ACS Appl. Mater. Interfaces, 2018, 10, 17269–17279 CrossRef CAS PubMed
.
- K. Riwotzki, H. Meyssamy, A. Kornowski and M. Haase, J. Phys. Chem. B, 2000, 104, 2824–2828 CrossRef CAS
.
- W. O. Milligan, D. F. Mullica, G. W. Beall and L. A. Boatner, Inorg. Chim. Acta, 1982, 60, 39–43 CrossRef CAS
.
- T. Miyakawa and D. L. Dexter, Phys. Rev. B: Solid State, 1970, 1, 2961–2969 CrossRef
.
- S. González-Pérez, I. R. Martín, F. Rivera-López and F. Lahoz, J. Non-Cryst. Solids, 2007, 353, 1951–1955 CrossRef
.
- M. O. Ramirez, D. Jaque, L. E. Bausá, I. R. Martín, F. Lahoz, E. Cavalli, A. Speghini and M. Bettinelli, J. Appl. Phys., 2005, 97, 93510 CrossRef
.
- Ł. Marciniak, A. Bednarkiewicz, M. Stefanski, R. Tomala, D. Hreniak and W. Strek, Phys. Chem. Chem. Phys., 2015, 17, 24315–24321 RSC
.
- F. T. Rabouw, P. T. Prins, P. Villanueva-Delgado, M. Castelijns, R. G. Geitenbeek and A. Meijerink, ACS Nano, 2018, 12, 4812–4823 CrossRef CAS PubMed
.
- A. Pilch, C. Würth, M. Kaiser, D. Wawrzyńczyk, M. Kurnatowska, S. Arabasz, K. Prorok, M. Samoć, W. Strek, U. Resch-Genger and A. Bednarkiewicz, Small, 2017, 13, 1701635 CrossRef
.
- D. Witkowski and D. A. Rothamer, Appl. Phys. B: Lasers Opt., 2017, 123, 226 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00285f |
| This journal is © The Royal Society of Chemistry 2021 |