Open Access Article
Open Access ArticleA quantum chemical approach for the mechanisms of redox-active metalloenzymes
Per E. M. Siegbahn *
*
Department of Organic Chemistry, Arrhenius Laboratory, Stockholm University, SE-106 91, Stockholm, Sweden. E-mail: per.siegbahn@su.se
First published on 15th January 2021
Abstract
During the past 20 years, quantum chemistry has grown to be a significant part in the investigation of mechanisms for redox-active enzymes. In our group we have developed an approach that has been applied to a large number of such systems. Hybrid density functional theory (hybrid DFT) has from the start of these investigations been the leading electronic structure tool. An understanding of how the method works in practice has significantly improved the accuracy and applicability. During the past ten years, it has been found that the results for redox enzymes mainly depend on the chosen fraction of exact exchange in the functional, and that a choice of 15% has worked best. The idea has therefore been to vary that fraction over a reasonable range and study the relative energy dependence. For modeling the enzymes, a cluster approach has been developed. In the present review the development of the method we used is described from its start in work on photosystem II, fifteen years ago. Examples from a few recent applications are described, where the metals have been iron, nickel, copper, cobalt or manganese. The results are in excellent agreement with available experiments, and a large number of new predictions have been made.
I. Introduction
Quantum chemical studies of redox-active metalloenzymes started about 20 years ago. Before that time, the methods were not regarded to be adequate for modeling redox enzymes. The high accuracy ab initio methods available were not able to handle more than about 20–30 atoms, while the density functional theory (DFT) methods, which could handle larger systems, were not considered accurate enough. Ten years earlier, in the early 1990's, an interesting new development of DFT was initiated, when a fraction of exact exchange was included in the functional.1 The methods were termed non-hybrid DFT methods. Soon afterwards, it was realized that hybrid DFT led to a much higher accuracy for the energies than the previous pure (non-hybrid) DFT methods did. However, during the first 7–8 years, the methods were almost exclusively applied on small systems, and almost never on systems including transition metal atoms. Applications of very accurate ab initio methods for small transition metal containing systems had indicated that the use of hybrid DFT would most likely not be sufficient for calculating energies. The so called multireference effects were shown to be very important, and they require a description beyond the single determinant level used in DFT. Therefore, even attempts to apply hybrid DFT on transition metal complexes were strongly criticized. The use of hybrid DFT on transition metal enzymes seemed far away. However, after applications on larger and larger systems, the confidence slowly grew on these methods, and the first application on an enzyme including a transition metal appeared in 1997.2 The early development was reviewed in 1999–2000.3,4The early applications of hybrid DFT on transition metal containing systems often gave rather accurate energies, which was surprising for many. However, there were sometimes quite large errors that obscured the picture. For example, the binding energy of small molecules to transition metal centers could be underestimated by more than 10 kcal mol−1 compared to very accurate ab initio values. During the first period of DFT applications, entropy effects were not included either, and that made the origin of the errors in the applications less obvious, since there were cancellation effects. Suggestions were made that the errors could be due to dispersion, which are not included in DFT, but dispersion effects were at that time expected to be rather small. Instead, the errors were suggested to come from missing multi-reference effects. The solution to the problem came around 2005 when dispersion effects were systematically studied and empirical methods to accurately take care of them were developed.5 It turned out that the inclusion of dispersion effectively removed the large errors of 10 kcal mol−1 also for transition metal complexes.6 At the same time, it was realized that entropy effects sometimes also needed to be included. The approach most commonly used was to only include the entropy effects in the binding or release of substrates. The approximation made was to assume that only the translational entropy of the substrate was lost upon binding.
Another line of progress concerned the modeling of the enzymes. Two different approaches were tried. In one of them, the entire enzyme was included using the QM/MM (Quantum Mechanics/Molecular Mechanics) method.7 A small QM model of the active site was generally used. In the second approach a much larger QM part was used but without the surrounding MM region of the enzyme.8 This was termed the cluster approach, and is the one that has been used in the studies reported in the present paper.
Perhaps the most important progress in modeling the energetics for redox enzymes, was the deeper understanding of how hybrid DFT works in practice. As will be described below, it was realized that for redox active enzymes, the most sensitive parameter for the relative energies is the fraction of exact exchange used in the functional. Furthermore, the empirical finding was that the optimal fraction was always in the range 10–20%, and also that the relative energies vary essentially linearly with the percentage used.9 This realization also led to a useful way of estimating the accuracy of the results.
In the present review, examples will be described on applications with the hybrid DFT method with a fraction of exact exchange as described above, using the cluster model of the enzyme. The enzymes for which the approach has been applied include the most important enzymes in biology, such as Photosystem II (PSII), nitrogenase and Cytochrome c Oxidase (CcO).10 Excellent results have been obtained in comparisons to experiments, sometimes performed years after the theoretical predictions of the mechanisms were made. A general area for the applications, where this strategy has been applied recently, concerns the enzymes that are most important in a fossil-free and environmental context, such as the ones used in H2 production and CO2 fixation.
II. Methods
The general approach used in the calculations discussed here were outlined above, and the present section will therefore be rather short. The standard B3LYP method was used throughout for the geometries, with the fraction of exact exchange equal to 20%.1 For the final energies, B3LYP was modified by using also 10% and 15%.9 In most cases 15% turned out to be optimal. The cluster models used for the active site generally contained 150–300 atoms, all described by hybrid DFT. To take account of the fact that the active site is constrained by the enzyme surrounding, some atoms in the outer part of the model were kept fixed from the X-ray structure.11 This procedure has been well tested over the years.10 One possibility was, for example, to release a constraint and observe if the effects are large for the relative energies, in which case the constraint should be removed. When large models, with more than 150 atoms are used as described here, the effects of the constraints are generally quite small. In describing polarization effects from the surrounding enzyme, standard dielectric cavity method were used. The sensitivity of the energies to the choice of the dielectric constant has been carefully tested with models ranging from small to very large.10,12 For the models of the size discussed here, the sensitivity is usually quite small and a standard choice of 4.0 has therefore generally been used. If the sensitivity is found to be large, the model should be extended rather than changing the dielectric constant.An important part of the calculations on the mechanisms of the transition metal containing enzymes discussed here was to consider also the reduction/oxidation (redox) steps. Including these steps has quite generally not been done in most applications by other groups. When the charge of a model changes, after the release or acceptance of a single electron or a proton, the electrostatic effects are very large and they reach far away from the active site. Models of the present size are therefore not appropriate for describing those cases. However, when the redox steps are proton-coupled (PCET), the charge of the active site does not change and the long-range effects are therefore minor. Fortunately, most redox steps in enzymes are of that type. If they are not proton-coupled, an empirical scheme has to be adopted, described in detail below for the case of water oxidation in PSII. Since the enzyme surrounding is essentially the same for all the four redox steps in PSII, only one experimental parameter is needed to describe the long range effects of these steps. The energies for the redox coupled electron transfer steps are then obtained from the experimental redox potential of the substrate, that gives the driving force for the reaction.
For reaching a high accuracy of the results, it is import to have a saturated basis set for describing the electronic structure. For the determination of the structures, a medium size basis set (LACVP*) has been found to be enough.13 For the optimized structures, single point calculations were done with a large basis set, with cc-pvtz(-f) for the non-metal atoms, and with LAV3P* for the metals. The programs used have been Jaguar14 and Gaussian.15
III. Results
In the present section, some examples of enzymes are described for which the methodology described above has been used. The prime example of what can be obtained is photosystem II, which together with cytochrome c oxidase, were the first enzymes where the methods were used. Focus will be on the theoretical progress, but some key experimental results will also be mentioned.Photosystem II (PSII)
This is the only enzyme in nature that is able to use sunlight to produce protons and electrons from water. O2 is a side-product. An optimized structure of the active site, termed the oxygen evolving center (OEC), is shown in Fig. 1. That structure was optimized based on the first X-ray structure obtained at a high resolution in 2011.16 It contains a metal cluster with four manganese and one calcium atom connected by oxo-bridges. There are six carboxylate ligands (aspartates, glutamates and a terminal backbone part of an alanine), and one histidine ligand (bound to Mn1). There is also one water and one hydroxide ligand bound to Mn4. Three of the Mn-atoms have an octahedral coordination, while Mn1 has an empty site (or a weakly bound water), in the lowest states. When the present calculations on PSII started around 20 years ago, no X-ray structure was available. In 2004, the first structure was obtained,17 but at a low resolution of 3.5 Å. It could be used to reasonably well define the positions of the metal atoms and which amino acid ligands that are bound to the complex. The positions and the number of oxo-atoms could only be inferred from EXAFS spectroscopy. The binding modes of the ligands were guessed. The appearance of an X-ray structure made it possible to start detailed calculations on the mechanism. Those calculations had to be unbiased concerning the uncertain parts of the structure. A small model was set up and a large number of exploratory calculations were made. It was soon realized that the optimal ligations of the amino acids were not the same as assumed for the X-ray structure from 2004. A chemically more reasonable binding was found by the calculations, more in line with the suggestions in another low resolution X-ray structure that appeared in 2005.18 In that structure, the positions of the oxo-ligands were not given, indicating that there were still large uncertainties in the structural information.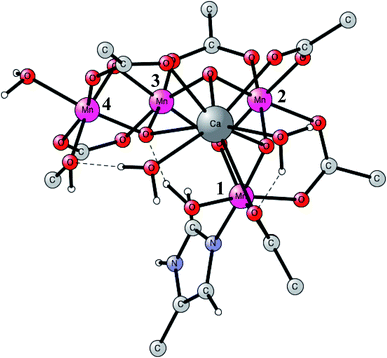 | ||
| Fig. 1 An optimized structure of the active site (OEC) of PSII. Atoms outside the active site are not shown. | ||
O2 formation was known to occur after four flashes of light. The intermediate states are termed S-states. For a rather small model of 50 atoms, the key S4 step of O–O bond formation was investigated for a structure derived from the calculations. After many attempts, a transition state was obtained in 2006, which was much lower in energy than the other possibilities tried.19 In fact, the transition state (TS) was so low, that it was immediately realized that it was most probably similar to the one actually used in PSII, even though the model was quite small. Surprisingly, the O–O bond was formed between two oxo ligands, one of them with a high spin, therefore termed an oxo–oxyl mechanism. The leading experimental suggestion at the time was instead an outside water attack on a Mn(V)-oxo ligand,20 which by the DFT calculations19 was found to have a much higher barrier. The high barrier for the water attack mechanism has been confirmed more recently in 2017 by DFT.21 Important for the low barrier of the oxo–oxyl mechanism is that the spins for the atoms involved, the two oxygens and two manganese atoms (Mn1 and Mn4) are alternating, which allowed for a smooth formation of the O–O bond. The TS structure obtained is shown in Fig. 2. For the acceptance of that mechanism, it was important to refine the structure of the active site, which was done a few years later in 2008.22,23 One major finding by the DFT calculations was the presence of an additional bridging oxo ligand, not present in the original X-ray structure. The additional oxo ligand was found to be of key importance for the mechanism.
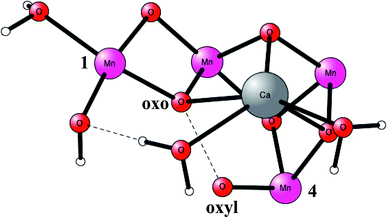 | ||
| Fig. 2 An optimized TS structure of the active site of PSII. Only the most important atoms are shown. | ||
To fully understand the mechanism of water oxidation, it was necessary to energetically follow the entire catalytic cycle, which includes also the oxidation steps.23,24 That had never been done before in any theoretical study for an enzyme. One important factor was to obtain the cost for releasing a (H+,e−)-couple from the OEC, where the electron should go to the P680+ oxidant and the proton should go to water. The approach adapted for PSII was to use the experimental redox potential of 0.8 V for the substrate reaction:
| 2H2O + 4hν → O2 + 4H+ + 4e− |
Using the measured redox potential of 1.25 V for P680, the highest one in nature, this led to a driving force for the catalytic cycle of −41.5 kcal mol−1. The actually calculated energies for releasing a single (H+,e−)-couple could then be adjusted to match that driving force. An almost equivalent way to reach a similar driving force is to use the experimental energy for a proton in water of −264.0 kcal mol−1, combined with the adjustment of the redox potential to the standard hydrogen electrode (4.281 V). That approach works since the number of electrons and protons released are the same. As noted above, the release of a neutral entity does not have any long-range effects and models with 150–300 atoms, and even smaller ones, were therefore adequate. This is not the case if a single electron or proton is released, in which case the long range effects are very large. To describe those effects would have required much larger models than the ones used, but there was an alternative. Assuming that the structure of the enzyme outside the model is reasonably similar in each transition, a single experimental result is enough for obtaining a good estimate for the effect of the surrounding of the model used. The approach for PSII was to use observations for the S1 to S2 transition, where it was known that only an electron and no proton was released, combined with the fact that there should be only a small driving force for the transition, in order not to waste energy. It is important to note that simply using the experimental value for the redox potential of the oxidant, does not work in the case of the S1 to S2 transition in PSII using limited models because of the unknown and large long-range effects from outside the model.25
There was still one problem that needed to be resolved, and that was the most important one. It was found that the computed values for the release of a (H+,e−)-couple were very sensitive to the DFT functional used. To attack that problem in a systematic way, the experience obtained from using the B3LYP functional for redox active systems was used. As mentioned in Section II, it was discovered that the results were almost exclusively dependent on the fraction of exact exchange used. Therefore, this fraction could be varied to obtain what was known from experiments. For PSII, it was found that a fraction of 15% was optimal. Varying this fraction by changing it to 10 and 20% also gave an estimate of the accuracy of the results. To identify how well the different fractions of exchange in the functionals worked, there was at the time no experimental redox potentials available for comparison, so instead a few qualitative experimental results were used. The most important experimental result was the simple fact that the states from S0 to S3 had been observed. That meant that the energies for those states have to be descending. Also, the energy difference between the S-states should not be very large since the driving force for the entire reaction is rather small. Only B3LYP with 15% was found to give a reasonable energy diagram in agreement with these qualitative experimental findings. Very large errors in the diagrams could be seen using significantly different fractions of exchange in the functionals or using other functionals.25 Since the redox potential for Mn(III) to Mn(IV) enters three times, the error in the redox potential will be multiplied by three from start to end in the energy diagram. Functionals without exact exchange, frequently used in the literature, also gave very large errors. It should be emphasized, that the large number of predictions finally made from the calculations using 15% include many previously unknown facts. For example, the structures and energies for the S0 to S4 states were predicted. For the S0 to S3 states, the predicted structures were found to be in excellent agreement with experiments from free electron laser (X-FEL) experiments performed years later in 2015–2018.26–28 However, the most important prediction was the one for the mechanism for O–O bond formation, see above.19 The actual mechanism could not be directly compared to experiments since the active S4 state is not possible to observe experimentally due to its high energy. Instead, detailed spectroscopic results for the lower S-states could be used to experimentally verify the mechanism in 2011–2012. Of largest importance here were water exchange and EPR experiments.29,30 In the context of modeling mechanisms for redox enzymes, it should finally be noted that it has very surprisingly been found that a fraction of 15% exact exchange is nearly optimal also for all other redox enzymes studied so far, see further below.
Cytochrome c oxidase (CcO)
This is another enzyme that was modeled early with the techniques mentioned above. It is the key enzyme in the respiratory chain. It uses electrons produced in the metabolism together with O2 to store energy as ATP. This is achieved by pumping protons across the membrane against the gradient. By this process around 20 times more energy can be stored from one consumed glucose molecule than would be obtained if O2 was not used. There are two different areas of main interest here. The first one is the mechanism for O2 cleavage, which is a very good example of a problem where model calculations can make an important contribution.31 The crystal structure has been solved to high precision.32 The optimized structure of the active site after the cleavage of the O–O bond is shown in Fig. 3. O2 enters the active site through a channel and becomes bound between CuB and the heme-a3 Fe in a bridging fashion. With protons supplied from two channels from the inside of the membrane and with electrons delivered from the respiratory chain, the water end product is formed. By itself, this is a very exergonic reaction which would just release a large amount of energy as heat. However, by transforming the reaction energy into proton pumping most of the energy is saved, and will eventually be stored as ATP. Together with experiments it was shown that the bond in O2 could be cleaved without additional electrons other than the ones supplied by the active site. It was found that the active site tyrosine (covalently linked to a histidine) is redox active, which was a major area of debate at the time. One big problem was to understand the role of CuB in the redox process since measurements indicated that it should have a quite low redox potential. A reinterpretation of the experiments based on a theoretical analysis, indicated that CuB actually has a quite high redox potential.33 From a methodological point of view, it is interesting to note that a fraction of 15% exact exchange led to the best agreement with experiments,9 the same fraction as for PSII.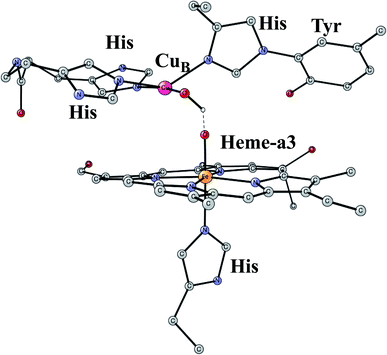 | ||
| Fig. 3 An optimized structure of the active site of CcO, obtained after the cleavage of the O–O bond of O2. | ||
The mechanism for proton pumping is the most interesting and challenging problem in CcO. The question is how the active site, situated between the inside and the outside of the membrane, is able to pump protons through a channel which is situated outside the active site. Therefore, the chemistry at the active site must be able to direct the protons from the inside to be either consumed in the active site to produce water, or to be pumped across the membrane against the chemical gradient. It has been demonstrated experimentally that for one O2, there are four protons pumped (Hp), and four protons consumed to form water.34
| O2 + 8H+ + 4e− → 2*H2O + 4*Hp + ΔE |
This means that two protons have to be transferred from the inside for every electron entering the active site, one for pumping and the other one for consumption. To understand that problem, applications of the methods described here were not enough. Another, more global, approach was also needed. The key was to construct energy diagrams for the entire pumping process, which required use of all available experimental information.35 In particular, the most useful information came from time resolved kinetic experiments.36
It was found necessary to construct very complicated energy diagrams in order to understand proton pumping. The details of the suggested pumping process can be found in the respective papers.10,35 One important realization was that the directions of the protons in the pathways can be determined by long range electrostatic effects from the active site. The charge of the active site has to change in a systematic way, which depends on the number of electrons and protons in the active site. To find the effects from the charges on the different transition states, simple electrostatic models were used, essentially depending only on the distances as given by the X-ray structure, and on the dielectric constant. The different pathways can be divided into allowed, leading to pumping, and non-allowed (leakage) pathways. The accuracy for the differences in energy for the different pathways has to be very high and was not reachable by quantum chemical models alone, but also had to include information from the kinetic experiments mentioned above.36 It was finally possible to rationalize all the experimental observations.10,35 More recently, it was also possible to suggest an explanation for how altogether four protons were pumped for each O2 and why two proton channels had to be used, as observed by experiments.37
Nitrogenase
This is the only enzyme that is able to activate the strong triple bond in N2, which constitutes about 80% of the air. Ammonia is produced, which can then be used to incorporate nitrogen into useful substances for living organisms, such as amino acids. The process is termed nitrogen fixation. The activation of N2 requires the strongest reductant in nature with a redox potential of −1.6 V. To achieve this low redox potential, a large amount of energy, provided by ATP, is needed. The catalyst for the N2 activation is an unusual complex, see Fig. 4, composed of two linked Fe4S4 cubanes for which a molybdenum has replaced an iron. Therefore, it has seven irons, nine sulfides, and one molybdenum and is termed the FeMo-cofactor. Molybdenum can be replaced by vanadium or iron, in much less common versions of nitrogenase. Also unusual, there is a rather large homocitrate ligand on molybdenum. A structure of the ground state E0 for Mo-nitrogenase was determined already in 1992.38 Structures of higher and higher resolution revealed new details. Most importantly, and very surprisingly, it was found that there is a central carbide in the structure,39,40 which is shown in the figure.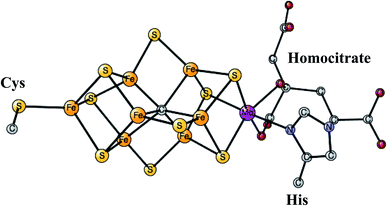 | ||
| Fig. 4 The FeMo-cofactor in Mo-nitrogenase that reduces N2 to NH3.38 | ||
Apart from the structure of E0, the kinetics of the mechanism has also been determined in detail.41 The most important conclusion was that the activation of N2 occurs after four initial reduction steps in the catalytic cycle. The intermediate states are termed E0 to E4. The overall reaction in Mo-nitrogenase is,
| N2 + 8(H+,e−) + 16ATP → 2NH3 + H2 + 16(ADP + Pi) |
A surprise in this reaction is that one H2 is produced in addition to ammonia. Even though the ground state structure has been known for decades, only pieces of the nitrogen activation mechanism has so far been determined from experiments. For example, no other structure than the one for E0 has been determined. The most important finding for the mechanism was made by EPR for the active E4 state.42 It was shown that there are two bridging hydrides, that leave as N2 becomes activated. Therefore, the experiment gives for the first time, an explanation for the release of one H2 for every N2 that is activated. The process was found to be easily reversible in E4. With two hydrides after four reduction steps, the remaining two reductions should lead to two protonations, suggested to be on the sulfides.
The model calculations for the mechanism had to start with a rather limited amount of experimental information, as described above. The ground state structure is known to high precision, and it is known both from experiments and theory to have an oxidation state of Mo3+ 3Fe2+ 5Fe3+. If this fact is combined with the conclusions from the EPR experiments, the oxidation state of the active E4 state obtained after four reductions, should be the same as the one for E0. This is very surprising since the lowest reductant in nature is used and still, the state that reduces N2 should have such a high oxidation state with five Fe3+. To reduce N2, a very low redox state was instead expected. That expectation was confirmed by the calculations, which did not lead to any activation of N2 using the suggested redox state. Furthermore, the suggested structure led to very unstable hydrides, which were found to leave the cofactor in a very exergonic step, which does not match the experimental observations of a reversible step.
The initial model calculations led to the conclusion that the cofactor needs to be reduced further. The question was where the protons, that always accompany the reductions, should go. It was found that it was not energetically possible to continue protonating the sulfides. Instead, an unexpected protonation of the carbide was possible. By protonating the carbide, it was actually possible to make four additional reductions, altogether eight from the ground state E0.43,44 The conclusion that eight reductions from E0 is needed to activate N2 may appear to be in contradiction with the kinetic experiments, which suggest that N2 should be activated after four reductions. However, the conclusion from the kinetic experiments were made under the assumption that there are no activation steps prior to catalysis. The conclusion from the model calculations was thus that there are four initial activation steps, termed A0 to A4, which lead to a formation of a terminal CH3, which should be the new E0. The oxidation state reached for E4 is then Mo3+ 7Fe2+, without any Fe3+. The optimal structure was found to have two bridging hydrides, in agreement with the suggestion by the EPR experiments. The hydrides are bound inside the cluster, in the region where the carbide was previously bound. The structure obtained for E4 is shown in Fig. 5.
It was found that the hydrides leave as H2 in a reductive elimination (re) step, in agreement with the EPR suggestion. The importance of that step is that it creates a very low redox state with Mo3+ 5Fe2+ 2Fe1+, which allows N2 to be reduced. It is also important that H2 does not form from a hydride and a proton, an hp, step, which would only lead back to E2. The calculations indeed found a barrier for the re step which is lower than the hp step, again in agreement with the analysis of the EPR experiments. After a rotation of the homocitrate, N2 binds as shown in Fig. 6.
Again, the calculations find that a fraction of exact exchange of 15% does give a reasonable energy diagram for the entire mechanism, all the way to the formation of two NH3 from one N2.43 In order to test the conclusion that activation steps are really needed, calculations have also been done for the experimentally suggested E4 state with other fractions of exact exchange,9 and with other functionals.45 It was shown that, in fact, no other DFT functional can reproduce the mechanism obtained by experiments using only four reductions before E4. All of them give a much too exergonic release of H2 to be compatible with a reversible step when N2 binds.
It should finally be emphasized, that although the calculations clearly conclude that activation steps before catalysis are needed, the suggestion that the carbide becomes protonated is less certain. Calculations are in progress investigating other possibilities, such as those where the release of H2S is involved. Structures with a missing sulfide have been found by X-ray experiments, but it is not clear that those structures are on the reaction path.
Hydrogenases
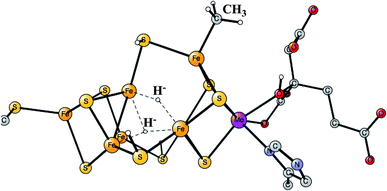
Enzymes that either make H2 from protons and electrons, or oxidize H2 to form protons and electrons are termed hydrogenases. The reduction of protons is an important process in the context of making fossil-free fuel, by using water oxidation to produce protons and electrons, and then forming H2 from these. The early theoretical work on the hydrogenases has been reviewed.46,47 The leading enzyme in nature for forming H2 is FeFe-hydrogenase, which uses a cofactor with an Fe4S4 cluster linked to an Fe2-dimer by a cysteine, together termed the H-cluster. The X-ray structure of the active site for the oxidized state (Hox) is shown in Fig. 7.48 The Fe-dimer is suggested to be the site where the H–H bond is formed. The irons are termed Fep (proximal to the Fe4S4 cluster) and Fed (distal). The dimer has some unusual features. There are two CN- and three CO ligands, where one CO is bridging the two irons. The incorporation of these unusual ligands requires a complicated set of enzymatic reactions, indicating that there must be an important reason for their presence, but which one is still not clear. Also bridging the irons is an aza-dithiolate (ADT) ligand. Another important feature is the empty site on Fed. The only possibility to have an empty site in Hox is that Fed is in a very low oxidation state, calculated to be Fed(I). Fed(II) would require an octahedral coordination. The presence of Fed(I) in turn indicates a very low charge of the H-cluster, suggested from both theory and experiments to be −3. That low charge is surprising since there is only one positive amino acid, a lysine, in the near environment of the cluster. The Fe(I) oxidation state is almost unheard of in biology, but in FeFe-hydrogenase the CN- and CO ligands are unusual and strongly bound, leading to a strong ligand field.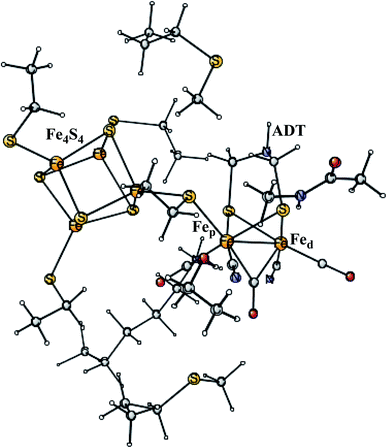 | ||
| Fig. 7 The X-ray structure of the active site of FeFe-hydrogenase.48 The structure is identified as Hox. | ||
The formation of H2 requires two reductions, involving proton coupled (H+e−) transfers.
| 2H+ + 2e− = H2 + ΔE |
There have been many suggestions for the protonation site of the of the structure obtained after the first reduction of Hox, termed Hred. The lowest energy structure, found in essentially all theoretical studies, has a bridging hydride in the Fe-dimer. It is, in fact, much more stable, by 32 kcal mol−1, than the other conformers suggested by experiments. Therefore, the hydride would easily replace the bridging CO. However, vibrational spectroscopy very clearly indicates that there is still a bridging CO in this state, showing that the protonation pathway to the bridging site must be blocked by the enzyme.49 To block such a stable site is a very unusual feature, hardly seen in any other enzyme. Instead, experiments have suggested that the protonation site in the first reduction is either on a ligand of the Fe4S4 cluster,50 or on the ADT ligand of the Fe-dimer.51
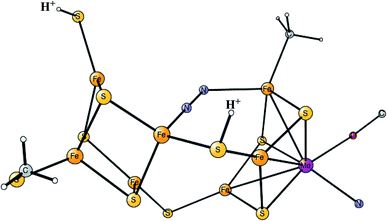
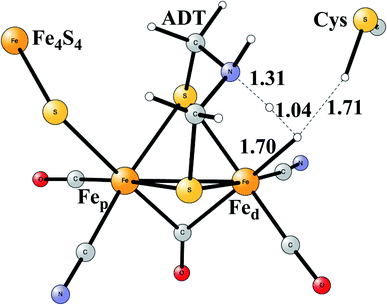
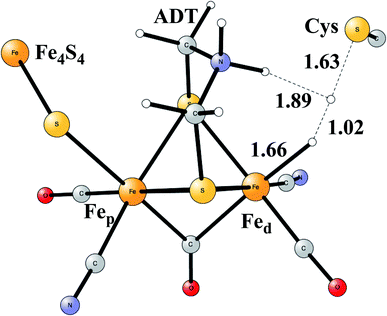
Model calculations to find the mechanism for H–H bond formation52 started by investigating the protonation sites suggested for Hred. It turned out that both sites suggested, see above, have very high energies, and they should therefore not be possible to observe, in conflict with the actual experimental observation of that state. Instead, the calculations suggested that a terminal hydride on the empty site of Fed is formed, which is 14 kcal mol−1 more stable than the other suggestions. It should be noted that the bridging hydride state is still 18 kcal mol−1 more stable that the terminal hydride, and therefore, the bridging position still has to be blocked by the enzyme. In the next reduction, forming Hhyd, the proton initially ends up on a cysteine on the Fe4S4 cluster. The observed Hred state gave an energy of −1.0 kcal mol−1 and the one for Hhyd of +3.2 kcal mol−1 compared to the starting Hox state. To form the H–H bond, the added proton in Hhyd moves to the ADT ligand in an endergonic step, which stabilizes the oxidation state of Fed(I), necessary for H–H bond formation. A TS can then be formed either between the proton on ADT and the terminal hydride on Fed, see Fig. 8, or more surprisingly, from a proton on a nearby cysteine and the terminal hydride, see Fig. 9. The latter alternative was actually found to be slightly better by −1.3 kcal mol−1. The barrier is very low, 11.4 kcal mol−1, indicating an extremely fast reaction in agreement with experiments.
As in all the other studies discussed here, the methodology was tested by varying the fraction of exact exchange. Again, the best agreement with experiments was found using 15%, but 10% also gave quite reasonable results. The sensitivity is highest for the Hred intermediate with 8 kcal mol−1 going from 10 to 20%. The sensitivity on the overall barrier height is smaller with only a difference of 1–2 kcal mol−1 going from 10 to 20%. For comparison, calculations were also done for the Hhyd state, using the PW6B95-D3 (ref. 53) and PBE0-D3,54 where the former gave an energy of +12.3 kcal mol−1 and the latter one of +8.3 kcal mol−1 counted from the Hox state. Both these functionals have a higher fraction of exact exchange, higher than the range usually investigated by the present method. Hhyd has been observed and should therefore not have an energy higher than +3 kcal mol−1, probably lower, indicating that those two functionals are not reliable in the case of FeFe hydrogenase.
The most common hydrogenases in nature are ones where the active site has a dimer between nickel and iron, therefore called NiFe hydrogenases. They are mainly used for cleavage of H2, producing protons and electrons. In some of them, the protons are transferred to the outside of the membrane against the gradient, to eventually store energy as ATP. The active site structure, shown in Fig. 10,55,56 has many features in common with the one for FeFe hydrogenase. Most strikingly, there are again ligands which are very unusual in nature, two CN- and one CO bound to the iron. There are also four cysteine ligands, two of them bridging between the metals.
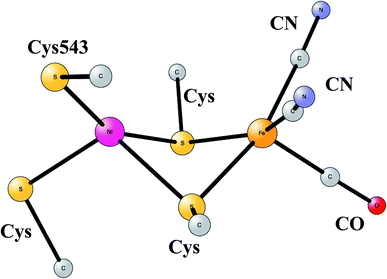 | ||
| Fig. 10 Optimized structure for the active site of NiFe hydrogenase, based on an X-ray-structure.44,45 | ||
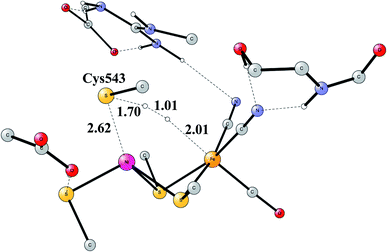
The early studies on the mechanism all converged to essentially the same type of TS for H–H cleavage. H2 enters in between the metals, and is cleaved heterolytically, leading to a bridging hydride and a proton on Cys543, as described in the review mentioned above.46 The TS obtained in the most recent study is shown in Fig. 11.57 The barrier obtained was 15.2 kcal mol−1, in good agreement with experiments. For the barrier height, it was important to include the loss of entropy, which was estimated to be 8.4 kcal mol−1, and which also led to the finding that no bound state for molecular H2 was present, as was also the case for FeFe hydrogenase, discussed above. When the proton bound to the cysteine was released to the outside, a state with Ni(III) was found, and when also the hydride was released a state with Ni(I) was reached, showing the electronic flexibility needed for nickel. Iron stays Fe(II) throughout.
The accuracy of the calculations were as usual tested by varying the exact exchange fraction. It turned out that the energy of one intermediate was quite sensitive to this variation. A fraction of 15% was again shown to be in best agreement with available experimental information, while the use of 10% gave quite erroneous results. The situation is quite different from the one for FeFe hydrogenase.
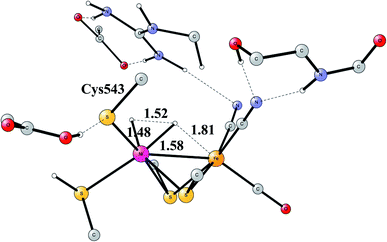
Another mechanism than the one above has been suggested from experiments for NiFe hydrogenase under certain conditions.58 It was noted that one of the intermediates that should be present in the heterolytic mechanism was sometimes missing. Model investigations were therefore initiated to find a second mechanism.57,59 The mechanism found from the model calculations was one of a homolytic, rather than a heterolytic, cleavage. The optimized TS is shown in Fig. 12. The catalytic cycle for the homolytic mechanism starts out from one intermediate in the heterolytic cycle, where there is a bridging hydride but no proton on the cysteine. The oxidation state of nickel was Ni(III). When the hydride moved to the cysteine, a state with Ni(I) was formed, which was able to cleave H2 homolytically, with a product that had two hydrides, one bridging and one terminal on nickel. The barriers for the two mechanisms were found to be about the same.
Ni,Fe CO-dehydrogenase
The increasing level of CO2 in the atmosphere is today a major climate problem. The interest of finding efficient processes to activate (fix) CO2 is therefore a growing area for scientific research. In nature, the enzyme Rubisco in plants is the one mainly responsible for fixing CO2, but does so in a very inefficient way. An interesting alternative is to use sunlight to produce protons and electrons to activate CO2. CO dehydrogenases (CODHs) are enzymes that use another strategy to activate CO2. One of them is Ni,Fe-CODH, which can activate CO2 in a reversible process.60Ni,Fe-CODH uses a cofactor with four irons and one nickel as shown in Fig. 13. It can be described as an Fe4S4-cluster in which one iron has been pushed out by a nickel. The X-ray structure has been determined with a high resolution for an intermediate with a bound CO2.61 Apart from the metal cofactor there is a hydrogen-bonded chain with His93 and Asp219 of probable high significance. There is also a positive lysine (Lys563) that can form a strong hydrogen bond to the substrate. Recently, the mechanism was investigated with the methods described in this review.62 The experimentally suggested oxidation state for the structure in the figure is Ni(II)Fe(III)3Fe(II). An important experimental result is that CO2 reduction is reversible.60 That fact can be used also for testing the accuracy of the results, as described below.
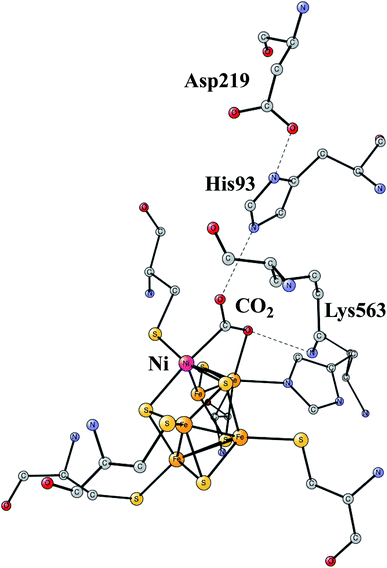 | ||
| Fig. 13 The X-ray structure of the active site for NiFe-CODH, showing the key intermediate with a bound CO2.61 | ||
Two reductions with additions of (H+,e−)-couples are needed to activate CO2. The products are CO and water.
| CO2 + 2H+ + 2e− = CO + H2O |
The structure in Fig. 13 was the starting point for the model calculations. For the mechanism of NiFeCO-DH, it was found that the His, Asp couple was protonated and that one of the sulfides on the NiFe3 cubane was protonated. The first addition of a (H+,e−)-couple led to a protonation of the bound CO2 and a cleavage of the C–O bond. The reduction by itself ws quite sensitive to the fraction of exact exchange, while the cleavage of the C–O bond was entirely insensitive. The barrier was found to vary by only a few tenths of a kcal mol−1 between 10% and 20%. The product has CO bound to nickel, while the OH− was found to be bound to the iron outside the cube. In the next reduction, a water is formed from the OH-ligand on iron. In the final step, which is not a reduction, the CO bound to nickel is replaced by a new CO2 in the preparation for the next catalytic cycle. The computed energy diagram and structures are in good agreement with experimental knowledge, using 15% exact exchange.
In designing models for CO2 fixation, it is very important to avoid formation of hydrides, which would shortcut the fixation process and instead lead to formation of H2. The pathways for hydride formation were therefore also studied. It was found that the available protons for a possible formation of the hydride were all very strongly bound and can therefore not directly lead to formation of a hydride. However, since a small amount of H2 has been found in NiFe-CODH under certain conditions,63 a process for forming hydrides needed to be explained. The explanation found was that an overreduction could take place to a small extent. With one more reduction, hydrides could form leading to H2 formation.
As mentioned above, the reductions are quite sensitive to the exchange fraction used. However, the variation is very systematic. Each reduction is about 4 kcal mol−1 easier for 10% compared to 15%, and 4 kcal mol−1 harder for 20%. This type of variation is rather common for cases where there is a change of oxidation state of the metals. In order to choose the right fraction for the reduction steps, it is very useful to compare the calculated rates for oxidation and the reverse one of reduction. It has been experimentally found that the rates for reduction and oxidation are similar, with the barrier for oxidation being a few kcal mol−1 lower. It was found that the use of 10% makes the process irreversible, and that fraction should therefore not be used. For 20% the barriers are about the same, which is tolerable, but using 15% reproduces the experimentally found difference in rates very well and is therefore again the best choice.
Mo-containing formate dehydrogenase (Mo-FDH)
This is another enzyme that can activate CO2, but in this case the product is formate, not CO as in the case of Ni,Fe-CODH,| CO2 + 2e− + H+ = HCOO− |
It can be seen on the overall reaction that there is a complication here that is not present for the other cases discussed in the review. Since the number of protons and electrons involved are not the same, this causes modeling problems. There are two reductions and one of them is therefore not proton coupled, which means that the cost for obtaining an electron has to be estimated for accepting a single electron and that is somewhat uncertain. Therefore, unlike the situation for the hydrogenases, where the only assumption made was a small, reasonable driving force, that procedure would not be enough for Mo-FDH. Instead, the second choice as described for PSII was adopted. That meant the straightforward use of the experimental redox potential, which with a small model may lead to large, somewhat unpredictable long-range effects. Since that approach did not work well for PSII, the value must be taken with caution. For Mo-FDH, it turned out that the approach actually worked very well, which must be considered as being merely a fortunate case. For the purpose of testing the accuracy, it is useful that the reaction has been found to be reversible. If the straight-forward approach had not worked, the value would have to be modified until the reaction became reversible. The work is in progress and will be presented elsewhere.
Multicopper oxidases
Enzymes that reduce O2 to water using an active site with three copper atoms are termed multicopper oxidases. An X-ray structure of the active site of one of these enzymes is shown in Fig. 14.64 For two of the copper atoms, there are three histidine ligands, while the third one has two histidines and one weakly bound water (in the figure shown with a long distance to CuT2). The oxidation state of the complex without substrate is Cu3(I,I,I). Oxidations with active sites containing copper have been regarded as prime examples where the B3LYP method does not work.65 It was therefore of high interest to investigate how the present methodology works in those cases.66 Recent electrochemical experiments was another reason for a study of these systems.67 Interestingly, it was shown that O2 reduction could actually be reversed to water oxidation for an enzyme of this type, which was the first case this had been shown for an enzyme.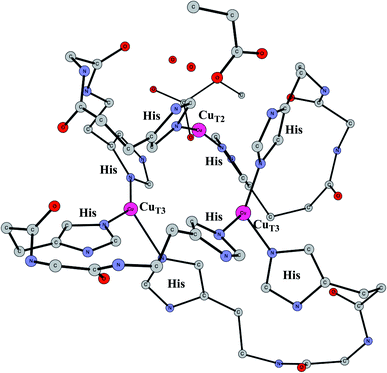 | ||
| Fig. 14 The X-ray structure of the active site for a multicopper oxidase.64 | ||
The mechanism for reduction was found66 to be the same as in the previous studies.68 O2 was found to be bound in the center of the cluster with bidentate bonding to one of the coppers and single bonds to the other ones. The full reduction of O2 requires additions of four (H+e−)-couples.
| O2 + 4(H+e−) → 2H2O + ΔE |
Since the reductions are proton coupled, the standard methodology described above can be used. The first reduction became endergonic by +5.1 kcal mol−1, where the proton goes to O2 and the electron to one of the coppers. The O–O bond in O2H was then found to be cleaved in a very exergonic step by −26.7 kcal mol−1. The barrier for that step was found to be 10.9 kcal mol−1. With the endergonicity in the previous steps the total barrier became 16.0 kcal mol−1, in reasonable agreement with experiments, which should be 12–14 kcal mol−1. Three reductions remain to go back to the ground state, two of them exergonic, the last one slightly endergonic.
The above results were obtained with a 15% fraction of exact exchange. With 20%, the total barrier became 20.6 kcal mol−1, significantly worse compared to experiments. For 10%, the barrier became 14.4 kcal mol−1, quite similar to the one for 15%, even slightly better. In conclusion, there were no signs of a breakdown of B3LYP with 15% exact exchange. The results are fully in line with the results for the other enzymes described above.
To obtain agreement with experiments for the oxidation of water was more difficult. To drive the reaction backwards, a high redox potential of 1.25 V was used, and the pH was raised to 10.5. The first three oxidations were unproblematic and became strongly exergonic. At that point a structure was obtained similar to the one for the product of the cleavage of O2H for the reduction. However, trying to go back the same pathway but in the opposite direction as for the reductive cleavage, forming the O–O bond with one oxo and one OH, led to a much too high barrier. However, with the increased redox potential and pH, it was actually possible to oxidize the system even further in an exergonic step. In that step a proton leaves from the water ligand and not from the OH ligand that should form the O–O bond. Reaching a point where two fully deprotonated oxo ligands were formed, was found to be endergonic by +6.9 kcal mol−1. From that point a TS for O–O bond formation between the two oxo ligands was found with a height of only 16.5 kcal mol−1. Adding the endergonicity of +6.9 kcal mol−1 a total barrier of 23.4 kcal mol−1 was obtained, which seems reasonable compared to the results of the electrochemical experiment, where no rate was determined but a very slow reaction was noted.
Acetyl-CoA synthase (ACS)
This enzyme is situated in the same protein as Ni-CODH, which produces CO from CO2, as described above. Remarkably, the two active sites are connected by a 140 Å long channel which transports CO from Ni-CODH to ACS.11,69 The active site complex of ACS is shown in Fig. 15.70 The complex consists of two parts. In one part, there is a cobalamin from a corrinoid/FeS protein, which binds CH3 in a Co(III) state. In the other part there is a hexa-metal cluster composed of a Fe4S4 cluster connected to a nickel dimer, which binds CO delivered from Ni-CODH. The nickel closest to Fe4S4 is termed the proximal nickel Nip, the other one Nid. The mechanism of this enzyme has recently been studied by the methods described above.71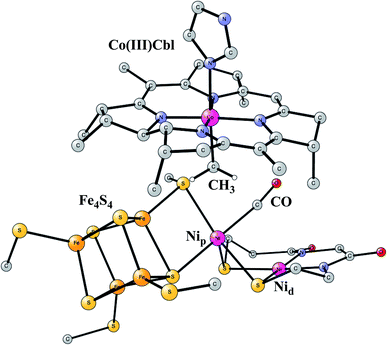 | ||
| Fig. 15 Optimized structure of the active site of Acetyl-CoA synthase (ACS) with bound CH3 and CO, based on an X-ray structure.70 | ||
The catalytic cycle occurs in a complicated sequence of steps, which cannot be described in detail here. The question of the oxidation state of Nip is one of the issues raised for the mechanism of ACS. Therefore, states with Nip(II), Nip(I) and Nip(0) were investigated. The oxidation state of Nid was found to stay Nid(II) with zero spin, in agreement with most suggestions from experiments. Another question has been the order of the binding of CO and CH3 to the complex. It turned out that the order gave very similar rate-limiting barriers. CH3 and CO both bind to Nip, and after that a C–C bond is formed between CO and CH3, with a resulting CO-CH3 ligand bound to nickel. In the next step, the substrate CoA-SH binds to Nip and becomes deprotonated. In the final part of the reaction sequence, a C–S bond is formed leading to the product CoA-S-CoCH3, which leaves the active site. There are five intermediates in that part. Both Nip(I) and Nip(II) were found to be capable of catalyzing the reaction, but not Nip(0). The overall reaction is,
| CH3-Co(III)-Cbl + CO + CoA-SH → CoA-S-CH3CO + H+ + Co(I)-Cbl |
The rate-limiting barrier was found to be the delivery of CH3 to Nip from the cobalt in Cbl. The barrier using 15% exact exchange for a triplet state was found to be 14.1 kcal mol−1 in good agreement with experiments. The barriers are very similar for both 10% and 20%. However, for the product the energies differ by about 3 kcal mol−1 between the different exchange fractions, altogether 6 kcal mol−1 between 10% and 20%, with 15% in between, with a linear variation. Since the product has Co(II) while the reactant has Co(III), it is this oxidation state change that leads to the differences. The variation is typical for redox transitions with first row transition metals. For the final part of the reaction forming the C–S bond, there are five intermediates. The use of 15% exchange gives very small energy differences between them of 1–3 kcal mol−1. For 10% and 20%, the energies are also quite similar except for one intermediate. That one occurs for a step where an electron is transferred between Nip(I) and the Fe4S4 cluster, with a corresponding change of redox states. That step is endergonic by +2.5 kcal mol−1 for 10%, exergonic by −1.4 kcal mol−1 for 15%, and exergonic by −6.1 kcal mol−1 for 20%. Since these variations are smaller than the rate-limiting barrier of 14 kcal mol−1, it cannot be definitely concluded which fraction fits experiments best. However, the use of 15% exact exchange gives the smoothest potential surface and should probably be preferred also in this case.
IV. Discussion and conclusions
This review describes a set of studies on redox active enzymes using DFT. The examples chosen are enzymes which have very different active sites. Photosystem II has an active site with a Mn4Ca cluster, cytochrome oxidase one with a heme and a copper, nitrogenase one with seven irons and a molybdenum, FeFe hydrogenase one with an Fe-dimer connected to a Fe4S4 cluster, NiFe hydrogenase one with a NiFe dimer, NiFe-CODH one with a Fe3Ni cluster connected to an outside iron, multicopper oxidase one with a Cu3 complex and finally acetyl-CoA synthase one with a nickel dimer connected to an Fe4S4 cluster, and also with a cobalamin involved. These enzymes include the ones that are regarded as the most important ones in biology. Hybrid DFT has been used in all cases and the results are all in very good agreement with experiments. The key to the success is an insight of hybrid DFT that has been reached after decades of experience. It has been found that the results almost exclusively depend on the amount of exact exchange included in the functional. In using this fraction as a parameter, which can be varied in the applications, three findings are particularly important. The first one is that a fraction between 10% and 20% is needed to get reasonable results. Furthermore, it was quite generally found that 15% gave the best agreement with experiments. It was also found that the relative energies varied essentially linearly with the choice of exact exchange in the region between 10% and 20%. With that knowledge it was also possible to get a reasonable estimate of the errors, in a much more systematic way than previously obtained using DFT.In modeling the enzymes, an approach has been developed the past decades termed the cluster approach. A quantum chemical model of the active site is used with the number of atoms usually in the range 150–300 atoms. This size of cluster should take care of charge effects from the immediate surrounding of the active cofactor. This is usually enough in cases where the charge of the model does not change during the mechanism. That is, for example, the case in the reaction steps where bonds are formed or cleaved and when proton coupled reductions or oxidations occur in the mechanism. When there is a change of charge of the model an empirical scheme is needed. A single empirical parameter is usually enough to describe the long range polarization effects. To take account of strain effects from the enzyme, points along the backbone in the periphery of the model should be fixed. That procedure has been tested by releasing constraints and observing the energetic effects. Usually there were no effect, but if there is a significant effect, a constraint may have to be released.
With the large variety of enzymes where the approach has been tested against experiments with excellent agreement, it is unlikely that many examples will be found where the approach fails. However, a failure can, of course, not be excluded in the future. A close observation of experimental results has to be kept to be aware of possible failures.
Conflicts of interest
There are no conflicts of interest.References
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. E. M. Siegbahn and R. H. Crabtree, The Mechanism of C-H Activation by Di-iron Methane Monooxygenases: Quantum Chemical Studies, J. Am. Chem. Soc., 1997, 119, 3103–3113 CrossRef CAS.
- P. E. M. Siegbahn and M. R. A. Blomberg, Density Functional Theory of Biologically Relevant Metal Centers, Annu. Rev. Phys. Chem., 1999, 50, 221–249 CrossRef CAS.
- P. E. M. Siegbahn and M. R. A. Blomberg, Transition Metal Systems in Biochemistry Studied by High Accuracy Quantum Chemical Methods, Chem. Rev., 2000, 100, 421–437 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- P. E. M. Siegbahn, M. R. A. Blomberg and S.-L. Chen, Significant van der Waals Effects in Transition Metal Complexes, J. Chem. Theory Comput., 2010, 6, 2040–2044 CrossRef CAS.
- A. Warshel and M. Levitt, Theoretical studies of enzymic reactions: dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS.
- P. E. M. Siegbahn and F. Himo, The Quantum Chemical Cluster Approach for Modeling Enzyme Reactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 323–336 CAS.
- P. E. M. Siegbahn and M. R. A. Blomberg, A systematic DFT approach for studying mechanisms of redox active enzymes, Front. Chem., 2018, 6, 644 CrossRef CAS.
- M. R. A. Blomberg, T. Borowski, F. Himo, R.-Z. Liao and P. E. M. Siegbahn, Quantum Chemical Studies of Mechanisms for Metalloenzymes, Chem. Rev., 2014, 114, 3601–3658 CrossRef CAS.
- V. Pelmenschikov, M. R. A. Blomberg and P. E. M. Siegbahn, A Theoretical Study of the Mechanism for Peptide Hydrolysis by Thermolysin, J. Biol. Inorg Chem., 2002, 7, 284–298 CrossRef CAS.
- K. H. Hopmann and F. Himo, Quantum chemical modeling of the dehalogenation reaction of haloalcohol dehalogenase, J. Chem. Theory Comput., 2008, 4, 1129–1137 CrossRef CAS.
- P. E. M. Siegbahn, Modeling Aspects of Mechanisms for Reactions Catalyzed by Metalloenzymes, J. Comput. Chem., 2001, 22, 1634–1645 CrossRef CAS.
- Jaguar, version 8.9, Schrodinger, Inc., New York, NY, 2015 CrossRef CAS; A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Jaguar: A high-performance quantum chemistry software program with strengths in life and materials sciences, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Peterssonet al., Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Crystal Structure of Oxygen-Evolving Photosystem II at a Resolution of 1.9 Å, Nature, 2011, 473, 55–60 CrossRef CAS.
- K. N. Ferreira, T. M. Iverson, K. Maghlaoui, J. Barber and S. Iwata, Architecture of the Photosynthetic Oxygen-Evolving Center, Science, 2004, 303, 1831–1838 CrossRef CAS.
- B. Loll, J. Kern, W. Saenger, A. Zouni and J. Biesiadka, Towards Complete Cofactor Arrangement in the 3.0 Å Resolution Structure of Photosystem II, Nature, 2005, 438, 1040–1044 CrossRef CAS.
- P. E. M. Siegbahn, O–O Bond Formation in the S4-State of the Oxygen Evolving Complex in Photosystem II, Chem.–Eur. J., 2006, 12, 9217–9227 CrossRef CAS.
- E. M. Sproviero, J. A. Gascon, J. P. McEvoy, G. W. Brudvig and V. S. Batista, Quantum mechanics/molecular mechanics study of the catalytic cycle of water splitting in photosystem II, J. Am. Chem. Soc., 2008, 130, 3428–3442 CrossRef CAS.
- P. E. M. Siegbahn, Nucleophilic Water Attack is not a Possible Mechanism for O-O Bond Formation in Photosystem II, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4966–4968 CrossRef CAS.
- P. E. M. Siegbahn, A Structure Consistent Mechanism for Dioxygen Formation in Photosystem II, Chem.–Eur. J., 2008, 14, 8290–8302 CrossRef CAS.
- P. E. M. Siegbahn, Structures and Energetics for O2 Formation in Photosystem II, Acc. Chem. Res., 2009, 42, 1871–1880 CrossRef CAS.
- P. E. M. Siegbahn, Water Oxidation Mechanism in Photosystem II, Including Oxidations, Proton Release Pathways, O-O Bond Formation and O2 Release, Biochim. Biophys. Acta, 2013, 1827, 1003–1019 CrossRef CAS.
- P. E. M. Siegbahn and M. R. A. Blomberg, Energy Diagrams for Water Oxidation in Photosystem II using Different Density Functionals, J. Chem. Theory Comput., 2014, 10, 268–272 CrossRef CAS.
- M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Structures of the intermediates of Kok's photosynthetic water oxidation clock, Nature, 2015, 517, 99–103 CrossRef CAS.
- M. Suga, et al., Light-induced structural changes and the site of O=O bond formation in PSII caught by XFEL, Nature, 2017, 543, 131–135 CrossRef CAS.
- Kern, et al., Structures of the intermediates of Kok's photosynthetic water oxidation clock, Nature, 2018, 563, 421–425 CrossRef CAS.
- N. Cox, L. Rapatskiy, J.-H. Su, D. A. Pantazis, M. Sugiura, L. Kulik, P. Dorlet, A. W. Rutherford, F. Neese, A. Boussac, W. Lubitz and J. Messinger, Effect of Ca2+/Sr2+ Substitution on the Electronic Structure of the Oxygen-Evolving Complex of Photosystem II: A Combined Multifrequency EPR, 55Mn-ENDOR, and DFT Study of the S2 State, J. Am. Chem. Soc., 2011, 133, 3635–3648 CrossRef CAS.
- L. Rapatskiy, N. Cox, A. Savitsky, W. M. Ames, J. Sander, M. M. Nowacyzk, M. Rögner, A. Boussac, F. Neese, J. Messinger and W. Lubitz, Detection of the Water-Binding Sites of the Oxygen-Evolving Complex of Photosystem II Using W-Band 17O Electron–Electron Double Resonance-Detected NMR Spectroscopy, J. Am. Chem. Soc., 2012, 134, 16619–16634 CrossRef CAS.
- M. R. A. Blomberg, P. E. M. Siegbahn and M. Wikström, Metal-Bridging Mechanism for O-O Bond Cleavage in Cytochrome c Oxidase, Inorg. Chem., 2003, 42, 5231–5243 CrossRef CAS.
- S. Yoshikawa, K. Shinzawa-Itoh, R. Nakashima, R. Yaono, E. Yamashita, N. Inoue, M. Yao, M. J. Fei, C. P. Libeu, T. Mizushima, H. Yamaguchi, T. Tomizaki and T. Tsukihara, Redox-coupled crystal structural changes in bovine heart cytochrome c oxidase, Science, 1998, 280, 1723–1729 CrossRef CAS.
- M. R. A. Blomberg and P. E. M. Siegbahn, Protonation of the Binuclear Active Site in Cytochrome c Oxidase Decreases the Reduction Potential of CuB, Biochim. Biophys. Acta, 2015, 1847, 1173–1180 CrossRef CAS.
- M. K. F. Wikström, Proton pump coupled to cytochrome c oxidase in mitochondria, Nature, 1977, 266, 271–273 CrossRef.
- M. R. A. Blomberg and P. E. M. Siegbahn, Proton Pumping in Cytochrome c Oxidase: Energetic Requirements and the Role of two Proton Channels, Biochim. Biophys. Acta, 2014, 1837, 1165–1177 CrossRef CAS.
- I. Belevich, D. A. Bloch, N. Belevich, M. Wikström and M. I. Verkhovsky, Exploring the proton pump mechanism of cytochrome c oxidase in real time, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2685–2690 CrossRef CAS.
- M. R. A. Blomberg and P. E. M. Siegbahn, How Cytochrome c Oxidase Can Pump Four Protons Per Oxygen Molecule at High Electrochemical Gradient, Biochim. Biophys. Acta, 2015, 1848, 364–376 CrossRef.
- J. Kim and D. C. Rees, Structural models for the metal centers in the nitrogenase molybdenum-iron protein, Science, 1992, 257, 1677–1682 CrossRef CAS.
- K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. De Beer, X-ray Emission Spectroscopy Evidences a Central Carbon in the Nitrogenase Iron-Molybdenum Cofactor, Science, 2011, 334, 974–976 CrossRef CAS.
- T. Spatzal, M. Aksoyoglu, L. M. Zhang, S. L. A. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Evidence for Interstitial Carbon in Nitrogenase FeMo Cofactor, Science, 2011, 334, 940 CrossRef CAS.
- B. K. Burgess and D. J. Lowe, Mechanism of Molybdenum Nitrogenase, Chem. Rev., 1996, 96, 2983–3012 CrossRef CAS.
- B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Mechanism of Nitrogen Fixation by Nitrogenase: The Next Stage, Chem. Rev., 2014, 114, 4041–4062 CrossRef CAS.
- P. E. M. Siegbahn, Model Calculations Suggest that the Central Carbon in the FeMo-cofactor of Nitrogenase Becomes Protonated in the Process of Nitrogen Fixation, J. Am. Chem. Soc., 2016, 138, 10485–10495 CrossRef CAS.
- P. E. M. Siegbahn, The mechanism for nitrogenase including all steps, Phys. Chem. Chem. Phys., 2019, 21, 15747–15759 RSC.
- L. Cao and U. Ryde, Extremely Large Differences in DFT Energies for Nitrogenase Models, Phys. Chem. Chem. Phys., 2019, 21, 2480–2488 RSC.
- P. E. M. Siegbahn, J. W. Tye and M. B. Hall, Computational studies of [NiFe] and [FeFe] hydrogenases, Chem. Rev., 2007, 107, 4414–4435 CrossRef CAS.
- M. Bruschi, G. Zampella, Y. Greco, L. Bertini, P. Fantucci and L. De Gioia, Hydrogenases: Theoretical Investigations Towards Bioinspired H2 Production and Activation, in Computational Inorganic and Bioinorganic Chemistry, ed. E. I. Solomon, B. King and R. Scott, John Wiley and Sons, Ltd, Chichester, England, 2013, p. 309 Search PubMed.
- J. W. Peters, W. N. Lanzilotta, B. J. Lemon and L. C. Seefedt, X-ray crystal structure of the Fe-only hydrogenase (Cpl) from Clostridium pasteurianum to 1.8 Ångstrom resolution, Science, 1998, 282, 1853 CrossRef CAS . (Errata: Science 283 (35), 2102.).
- M. W. Ratzloff, J. H. Artz, D. W. Mulder, R. T. Collins, T. E. Furtak and P. W. King, CO-bridged H-cluster Intermediates in the Catalytic Mechanism of [FeFe] Hydrogenase CaI, J. Am. Chem. Soc., 2018, 140, 623 CrossRef.
- M. Haumann and S. T. Stripp, The Molecular Proceedings of Biological Hydrogen Turnover, Acc. Chem. Rev., 2018, 51, 1755–1763 CrossRef CAS.
- J. A. Birrel, V. Pelmenschikov, N. Mishra, H. X. Wang, Y. Yoda, K. Tamasaku, T. B. Rauchfuss, S. P. Cramer, W. Lubitz and S. DeBeer, Spectroscopic and Computational Evidence that [FeFe] Hydrogenases Operate Exclusively with CO-Bridged Intermediates, J. Am. Chem. Soc., 2020, 142, 222–232 CrossRef.
- P. E. M. Siegbahn and R.-Z. Liao, The energetics for proton reduction in FeFe hydrogenase, J. Phys. Chem. A, 2020, 124, 10540–10549 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- A. Volbeda, M.-H. Charon, C. Piras, E. C. Hatchikian, M. Frey and J. C. Fontecilla-Camps, Crystal structure of the nickel-iron hydrogenase from Desulfovibrio gigas, Nature, 1995, 373, 580–587 CrossRef CAS.
- A. Volbeda, L. Martin, C. Cavazza, M. Matho, B. Faber, W. Roseboom, S. Albracht, E. Garcin, M. Rousset and J. Fontecilla-Camps, Structural differences between the ready and unready oxidized states of [NiFe] hydrogenases, J. Biol. Inorg Chem., 2005, 10, 239–249 CrossRef CAS.
- P. E. M. Siegbahn and R.-Z. Liao, The energetics of hydrogen molecule oxidation in NiFe hydrogenase, ACS Catal., 2020, 10, 5603–5613 CrossRef CAS.
- S. Kurkin, S. J. George, R. N. F. Thorneley and S. P. J. Albracht, Hydrogen-induced activation of the [NiFe]-hydrogenase from Allochromatium vinosum as studied by stopped-flow infrared spectroscopy, Biochemistry, 2004, 43, 6820–6831 CrossRef CAS.
- S. O. Nilsson-Lill and P. E. M. Siegbahn, An autocatalytic Mechanism for NiFe-Hydrogenase: Reduction to Ni(I) Followed by Oxidative Addition, Biochemistry, 2009, 48, 1056–1066 CrossRef CAS.
- M. Can, F. A. Armstrong and S. W. Ragsdale, Structure, Function, and Mechanism of the Nickel Metalloenzymes, CO Dehydrogenase, and Acetyl-CoA Synthase, Chem. Rev., 2014, 114, 4149–4174 CrossRef CAS.
- J.-H. Jeoung and H. Dobbek, Carbon Dioxide Activation at the Ni,Fe-Cluster of Anaerobic Carbon Monoxide Dehydrogenase, Science, 2007, 318, 1461–1464 CrossRef CAS.
- R.-Z. Liao and P. E. M. Siegbahn, Energetics for the mechanism of nickel-containing CO-dehydrogenase, Inorg. Chem., 2019, 58, 7931–7938 CrossRef.
- P. Amara, J.-M. Mouesca, A. Volbeda and J. C. Fontecilla-Camps, Carbon Monoxide Dehydrogenase Reaction Mechanism: A Likely Case of Abnormal CO2 Insertion to a Ni-H Bond, Inorg. Chem., 2011, 50, 1868–1878 CrossRef CAS.
- S. A. Roberts, A. Weichsel, G. Grass, K. Thakali, J. T. Hazzard, G. Tollin, C. Rensing and W. R. Montfort, Crystal structure and electron transfer kinetics of CueO, a multicopper oxidase required for copper homeostasis in Escherichia coli, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 2766–2771 CrossRef CAS.
- C. J. Cramer, M. Włoch, P. Piecuch, C. Puzzarini and L. Gagliardi, Theoretical models on the Cu2O2 torture track: Mechanistic implications for oxytyrosinase and small-molecule analogues, J. Phys. Chem. A, 2006, 110, 1991–2004 CrossRef CAS.
- P. E. M. Siegbahn, A theoretical study of O2 reduction and water oxidation in multi-copper oxidases, J. Phys. Chem. A, 2020, 124, 5849–5855 CrossRef CAS.
- R. M. Evans, B. Siritanaratkul, C. F. Megarity, K. Pandey, T. F. Esterle, S. Badiania and F. A. Armstrong, The value of enzymes in solar fuels research-efficient electrocatalysts through evolution, Chem. Soc. Rev., 2019, 48, 2039–2052 RSC.
- L. Rulisek and U. Ryde, Theoretical studies of the active-site structure, spectroscopic and thermodynamic properties, and reaction mechanism of multicopper oxidases, Coord. Chem. Rev., 2013, 257, 445–458 CrossRef CAS.
- S. W. Ragsdale and M. Kumar, Nickel-Containing Carbon Monoxide Dehydrogenase/Acetyl-CoA Synthase, Chem. Rev., 1996, 96, 2515–2540 CrossRef CAS.
- V. Svetlitchnyi, H. Dobbek, W. Meyer-Klaucke, T. Meins, B. Thiele, P. Römer, R. Huber and O. Meyer, A functional Ni-Ni-[4Fe-4S] cluster in the monomeric acetyl-CoA synthase from Carboxydothermus hydrogenoformans, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 446–451 CrossRef CAS.
- S.-L. Chen and P. E. M. Siegbahn, Insights into the Chemical Reactivity in Acetyl-CoA Synthase, Inorg. Chem., 2020, 59, 15167–15179 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |