Open Access Article
Open Access ArticleFabrication of patterned solid surfaces with highly controllable wettability
Meng Wanga,
Chuan Fei Guob,
Xiaofeng Wangc,
Bingxi Xianga,
Mingxia Qiua,
Tiefeng Hea,
Huan Yanga,
Yu Chena,
Jianjie Dong *c,
Qian Liu
*c,
Qian Liu *c and
Shuangchen Ruan*a
*c and
Shuangchen Ruan*a
aShenzhen Technology University, Shenzhen, 518118, China. E-mail: scruan@szu.edu.cn
bDepartment of Materials Science and Engineering, Southern University of Science and Technology, Shenzhen, 518055, China
cChinese Academy of Sciences (CAS) Center for Excellence in Nanoscience, CAS Key Laboratory of Nanosystem and Hierarchical Fabrication, National Center for Nanoscience and Technology, University of Chinese Academy of Sciences, Beijing, 100190, China. E-mail: dongjj@nanoctr.cn; liuq@nanoctr.cn
First published on 28th September 2021
Abstract
Precisely controlling the wettability of a solid surface is vital for a wide range of applications such as control of liquid droplet motion, water collection and the directional transport of fluids. However, fabricating a large-area solid surface with highly controllable wettability in a low-cost way is still challenging. Here we present a cost-effective method to fabricate patterned solid surfaces with highly controllable wettability by combining chemical etching technique, chemical vapor deposition technique and laser direct writing technique. We experimentally demonstrated that the contact angle of water droplets on the patterned surfaces of a porous nanofilm fabricated using the presented fabrication method can be adjusted from 94.4° to 168.2° by changing the duty ratio of the periodic pattern on the patterned surfaces. Furthermore, we experimentally demonstrated that the contact angle of water droplets on the patterned surfaces is almost independent of the shape of the unit cell of the patterns. In addition, we propose an effective surface model to accurately calculate the contact angle of water droplets on patterned solid surfaces. Using the effective surface model, the wettability of a patterned solid surface can be precisely controlled by designing the duty ratio of its periodic patterns.
1. Introduction
Since the lotus effect was investigated in depth by Barthlott and Neinhuis in 1997, superhydrophobic surfaces have received much attention.1–10 The lotus effect is a phenomenon whereby the surface of a lotus leaf repels water to form spherical droplets and the contaminating particles on it can be removed with the droplets.1,2 This effect is related to the wettability of solid surfaces. The wettability of a solid surface is mainly dependent on its chemical composition and its topography, and can be quantitatively characterized by contact angle measurements.3 A solid surface on which the contact angle of water is less than 90° is hydrophilic, and a solid surface on which the contact angle of water is greater than 90° is hydrophobic.4 A solid surface exhibiting a water contact angle greater than 150° and a sliding angle below 5° is considered a superhydrophobic surface.5,9 Owing to their potential applications such as self-cleaning, anti-icing, anti-fogging, oil-water separation and vapor generation, designing superhydrophobic surfaces has become a hot topic in recent years.9–12 Many superhydrophobic surfaces have been constructed by modifying the chemical composition and (or) changing the topography.11–27 In order to create more new functions for a solid surface, it may be necessary to specifically modify its wettability. In recent years, some solid surfaces with special wettability, which are not superhydrophobic surfaces, have been proposed to realize multiple special functions.28–32 Li et al. demonstrated that an artificial surface with gradient wettability can be used to achieve directional motion of liquid droplets,28 and Zhao et al. demonstrated that an artificial surface with gradient wettability can be used to control ice formation.29 Furthermore, an artificial surface whose multiple surface areas are selectively designed to have a special wettability distribution has been used for high-efficiency water collection.30,31 In addition, Mondal et al. demonstrated that it is possible to change the dynamic behavior of liquids in a microchannel by designing surface wettabilities.33–39 These studies indicate that precisely controlling the wettability of a solid surface is crucial for obtaining a desired function. Although the wettability of some artificial surfaces fabricated by previously reported methods has been proved to be tunable,40–42 it is still a challenge to fabricate an artificial surface whose actual wettability can be almost the same as the designed wettability.Many techniques8 including chemical etching (CE) technique,17,18 chemical vapor deposition (CVD) technique,19,20 photolithography technique43 and laser direct writing (LDW) technique44,45 have been developed to prepare solid surfaces with desired wettability (e.g., superhydrophobicity). The CE technique is a low-cost technique for fabricating large-area micro-/nanostructures, and is able to produce complex structures. However, the random fabrication error of this technique is relatively large for the fabrication of designed structures such as periodic nanoparticle arrays. For example, some experiments show that the period of silica nanoshell arrays prepared by a CE approach varies greatly at different positions on the substrate.46 The CVD technique is an effective technique for growing nanofilms and nanostructures, but it is difficult with this technique to perform precisely area-selective fabrication on the same substrate without the help of any other technique. This is because the chemical reaction does not automatically stop in many selected areas of the surface of the substrate in which one does not want to create any new films or structures during the CVD process without the help of any other technique in principle.47 The photolithography technique48 is a high-resolution technique for fabricating large-area designed structures, but it requires a mask that must be fabricated by other techniques. The LDW technique is another high-resolution technique for fabricating large-area designed structures, and it does not require any mask. In particular, the nanosecond LDW technique not only has the advantage of high resolution,49,50 but also is a cost-effective fabrication technique.22 However, the LDW technique may be time-consuming in the preparation of some large-area special nanostructures. Therefore, it is not difficult to foresee that a single fabrication technique may not be able to meet the requirements of fabricating artificial surfaces with complex functions such as liquid chips in future.
In this paper, in order to prepare artificial surfaces with highly controllable wettability, we present a cost-effective fabrication method that combines CE, CVD and nanosecond LDW techniques. In this method, the CE technique is used to fabricate nanostructures on the surface of a substrate, the CVD technique is used to deposit nanofilms of a low-surface-energy material on the nanostructures, and the nanosecond LDW technique is used to fabricate micron-scale patterns on the surface of the substrate. The presented fabrication method can effectively overcome the time-consumption shortcomings of the LDW technique in the preparation of large-area nanostructures. In addition, we propose an effective surface model to accurately calculate the contact angle of water droplets on the patterned solid surfaces. Using this effective surface model, the wettability of the patterned solid surface can be precisely controlled by designing the duty ratio of the periodic patterns created by the nanosecond LDW technique.
2. Materials and methods
2.1 Preparation of patterned solid surfaces
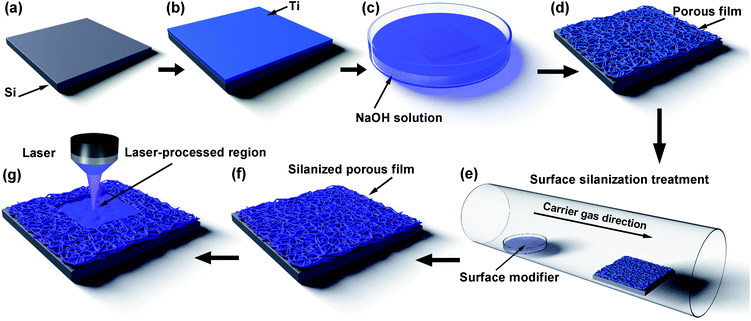
Titanium (Ti) films with a thickness of about 100 nm were deposited on silicon substrates by radio-frequency magnetron sputtering (ULVAC ACS400-C4) with a power of 50 W and a working pressure of 0.57 Pa for 3000 s (Fig. 1a and b). Then, the samples were immersed into aerated 10 M NaOH at 60 °C for 30 min to prepare porous structures on the surfaces of the samples (Fig. 1c and d). The porous films were modified with 1H,1H,2H,2H-perfluorodecyltriethoxysilane through CVD at 120 °C for 4 h (Fig. 1e and f). A LDW system (HWN LDW system-1500, laser wavelength 405 nm, laser spot size ∼300 nm, pulse width 2000 ns, and laser power 100–120 mW) was used to fabricate various patterns on the surfaces of the samples (Fig. 1g). During the fabrication process, the working parameters of the laser remained unchanged to ensure that the roughness difference of the different laser-processed surfaces is small. The patterned solid surface is composed of the surfaces in the laser-processed regions of the porous nanofilm and the surfaces in the laser-unprocessed regions of the porous nanofilm.2.2 Characterization
The morphology of the surfaces of samples was observed by a field emission scanning electron microscope (SEM, Hitachi S-4800), a laser scanning confocal microscope (LSCM, Olympus, LEXT-OLS4000) and an atomic force microscope (AFM, Park NX20). The chemical composition of the films was analyzed by energy dispersive X-ray spectrometric microanalysis (EDS). The water contact angle was measured at ambient temperature using an OCA 20 instrument (Data Physics, Germany). Deionized water (Millipore, 18 MΩ cm) was employed as the source liquid for the contact angle measurement. When each droplet naturally fell to the surface of the sample, we waited for 5 seconds and then measured the contact angle. On each surface, five locations were randomly selected for static contact angle measurement, and three water droplets of 2 μL were used to perform contact angle measurements at each location. The final value is the average of all values, and the standard deviation is used to calibrate the statistical error.3. Results and discussion
3.1 Morphology and composition studies
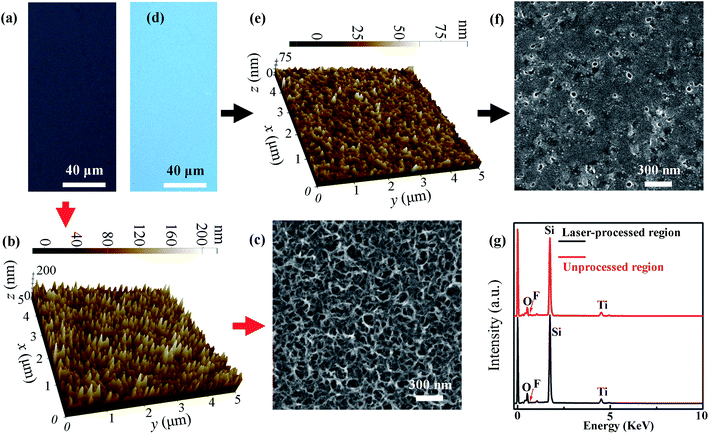
To understand the wetting behavior of water droplets on the patterned solid surface, we investigated the morphology and composition of the surfaces in the laser-processed regions and that in the laser-unprocessed regions. Fig. 2a, b and c show an optical image, AFM image and SEM image of a surface in a laser-unprocessed region, respectively. Fig. 2d–f show an optical image, AFM image and SEM image of a surface in a laser-processed region. No micron-scale surface structures were observed either in the laser-unprocessed region or in the laser-processed region. In the laser-unprocessed region, net-like nanostructures were observed (see Fig. 2c). However, in the laser-processed region, only a few nanoparticles and nanopits were observed (see Fig. 2f). The root-mean-square (RMS) roughness of the surface in the laser-unprocessed region was measured with the AFM to be 30.3 nm, and the RMS roughness of the surface in the laser-processed region was measured with the AFM to be 9.5 nm. Because 1H,1H,2H,2H-perfluorodecyltriethoxysilane is a low-surface-energy material,51 the reduction in the RMS roughness of the fabricated solid surface will result in a reduction in the water contact angle.52 The red curve and the black curve in Fig. 2g show the EDS spectra of a surface in the laser-unprocessed region and of that in the laser-processed region, respectively. The chemical composition of the surface in the laser-unprocessed region contains O, F, Si and Ti, and their relative contents are 24.84%, 3.35%, 50.62% and 9.32%, respectively. The chemical composition of the surface in the laser-processed region contains O, F, Si and Ti, and their relative contents are 27.22%, 1.09%, 55.03% and 10.43%, respectively. A big difference in the composition is that the relative content of F element is 3.35% in the laser-unprocessed region but 1.09% in the laser-processed region, which indicates that the laser processing can significantly reduce the relative content of 1H,1H,2H,2H-perfluorodecyltriethoxysilane. Therefore, the laser processing can reduce the water contact angle for the fabricated solid surface. The main mechanisms for forming the porous nanofilm, the nanoparticles and the nanopits are described as follows. During the immersion process, the hydrogen evolution reaction proceeded on the surface of the Ti nanofilm. As a result, the adsorbed hydrogen penetrated into the Ti nanofilm to form an absorbed layer. Then, the absorbed layer was dissolved into NaOH solution, resulting in the formation of the porous nanofilm that is composed of a mixture of rutile- and anatase-type TiO2.53,54 The morphology of the porous nanofilm cannot be changed significantly by the 1H,1H,2H,2H-perfluorodecyltriethoxysilane film deposited on its surface, which is due to the small thickness of the 1H,1H,2H,2H-perfluorodecyltriethoxysilane film. However, after the porous nanofilm is processed by the nanosecond laser beam of the LDW system, its surface morphology will change dramatically. When the porous nanofilm is scanned by the nanosecond laser beam with a particular intensity, it will be melted or even vaporized, which results in the formation of relatively flat local surfaces and nanopits in the laser-processed region. In addition, some nanoparticles may form when the melted materials solidify.3.2 Control over the wettability
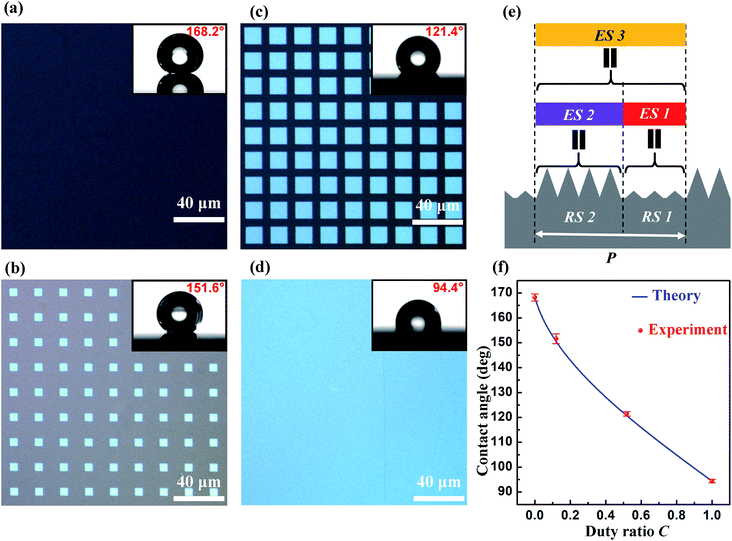
The duty ratio C of the laser-processed area is defined as the ratio of the horizontal projection area of the laser-processed surface to the horizontal projection area of the entire surface. Fig. 3a–d show optical images of fabricated surfaces with different duty ratios of the laser-processed area. The surface shown in Fig. 3a has C = 0, which has not been processed by the nanosecond laser beam, and exhibits a water contact angle of 168.2° ± 1.4°. The surface shown in Fig. 3b has a periodic array of square patterns and C = 0.120, and exhibits a water contact angle of 151.6° ± 2.0°. The surface shown in Fig. 3c also has a periodic array of square patterns, but has C = 0.519. The contact angle of water droplets on this surface is 121.4° ± 0.9°. When the entire surface is processed by the nanosecond laser beam, the duty ratio C becomes 1 and the water contact angle becomes 94.4° ± 0.7° (see Fig. 3d). It is found that the contact angle of water droplets on the fabricated surface decreases monotonically as the duty ratio C increases. Therefore, it is possible to adjust the contact angle of water droplets on the fabricated surface in the range from 94.4° to 168.2° by changing the duty ratio C.We next perform a theoretical analysis to understand in depth the tunable wettability of the fabricated surfaces. When a water droplet on an isotropic smooth surface reaches equilibrium, its contact angle can be described by Young's equation:52
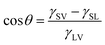 | (1) |
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA = r θA = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (2) |
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA = f θA = f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + f − 1 θ + f − 1
| (3) |
To accurately calculate the apparent contact angle of a water droplet on a patterned surface, we develop an effective surface model. In this model, rough surface 1 and rough surface 2 form a unit cell of an artificial surface with surface change period P, and are equivalent to an isotropic smooth surface with effective interfacial tensions γS1effV and γS1effL (termed effective surface 1) and an isotropic smooth surface with effective interfacial tensions γS2effV and γS2effL (termed effective surface 2), respectively, as shown in Fig. 3e. According to Young's equation, the effective contact angles of a water droplet on effective surface 1 and effective surface 2 can be expressed as cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θS1eff = (γS1effV − γS1effL)/γLV = cos
θS1eff = (γS1effV − γS1effL)/γLV = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA1 and cos
θA1 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θS2eff = (γS2effV − γS2effL)/γLV = cos
θS2eff = (γS2effV − γS2effL)/γLV = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θA2, respectively. Here θA1 and θA2 are an apparent contact angle of a water droplet on rough surface 1 with a large lateral dimension and that on rough surface 2 with a large lateral dimension, respectively. Furthermore, effective surface 1 and effective surface 2 as a whole are further equivalent to an isotropic smooth surface with effective interfacial tensions γS3effV and γS3effL (termed effective surface 3), as shown in Fig. 3e. Here γS3effV and γS3effL are expressed as γS3effV = t1γS1effV + (1 − t1)γS2effV and γS3effL = t1γS1effL + (1 − t1)γS2effL, where t1 is the ratio of the horizontal projection area of rough surface 1 to the horizontal projection area of the entire unit cell. According to Young's equation, the effective contact angle θA3eff of a water droplet on effective surface 3 can be given by
θA2, respectively. Here θA1 and θA2 are an apparent contact angle of a water droplet on rough surface 1 with a large lateral dimension and that on rough surface 2 with a large lateral dimension, respectively. Furthermore, effective surface 1 and effective surface 2 as a whole are further equivalent to an isotropic smooth surface with effective interfacial tensions γS3effV and γS3effL (termed effective surface 3), as shown in Fig. 3e. Here γS3effV and γS3effL are expressed as γS3effV = t1γS1effV + (1 − t1)γS2effV and γS3effL = t1γS1effL + (1 − t1)γS2effL, where t1 is the ratio of the horizontal projection area of rough surface 1 to the horizontal projection area of the entire unit cell. According to Young's equation, the effective contact angle θA3eff of a water droplet on effective surface 3 can be given by
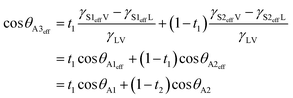 | (4) |
In this model, the effective contact angle θA3eff represents the apparent contact angle of a water droplet on the artificial surface with surface change period P, and apparent contact angles θA1 and θA2 can be calculated with eqn (2) or (3) and can also be measured directly. Because the maximum thickness of the porous nanofilms is only about 200 nm, this effective surface model is valid for the surfaces fabricated using the presented fabrication method.
For the patterned surface, the laser-processed area and the laser-unprocessed area can be viewed as rough surface 1 and rough surface 2 in the effective surface model, respectively. Therefore, θA1 and θA2 can be measured to be θA1 = 94.4° and θA2 = 168.2°. Note that t1 = C in this case. The blue solid curve in Fig. 3f shows the contact angle calculated with eqn (4) as a function of the duty ratio C. The measured values of the contact angle are presented in Fig. 3f with red circles. The theoretical results are in good agreement with the experimental results.
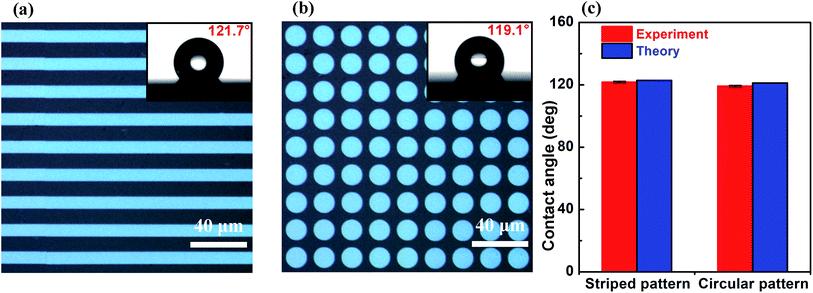
To investigate the influence of the shape of the unit cell of the pattern created with the nanosecond laser beam on the wettability of the patterned surface, a surface with a periodic array of stripes (Fig. 4a) and a surface with a periodic array of circles (Fig. 4b) were fabricated. The measured value of the contact angle of water droplets on the surface with striped pattern is 121.7° ± 0.9°, which is very close to its calculated value of 122.8° (see Fig. 4c). The measured value of the contact angle of water droplets on the surface with circular pattern is 119.1° ± 0.5°, which has a small deviation from the calculated value (see Fig. 4c). However, this deviation is smaller than 1.8% of the measured value. These results indicate that the contact angle of water droplets on the patterned surfaces is almost independent of the shape of the unit cell of the patterns. In addition, it is found that when the unit pattern is square, the difference between the theoretical value and the measured value of the contact angle is the smallest. Therefore, in order to improve the accuracy of controlling the wettability of a patterned surface, a square pattern is the best candidate for the unit cell of the patterns.
We also measured the contact angle hysteresis (i.e., the difference between the advancing and receding contact angles) of water droplets on the fabricated surfaces of samples that were placed in the laboratory for about two months. It is found that the contact angle hysteresis becomes larger as the duty ratio C of the laser-processed area increases from 0. In addition, it is also found that the contact angle hysteresis parallel to the stripe direction of the surface shown in Fig. 4a is larger than the contact angle hysteresis perpendicular to the stripe direction of the surface shown in Fig. 4a.
4. Conclusions
In conclusion, we have presented a cost-effective method to fabricate patterned surfaces with highly controllable wettability. Furthermore, we have experimentally demonstrated that the contact angle of water droplets on the surfaces fabricated using the presented fabrication method can be adjusted from 94.4° to 168.2° by changing the duty ratio of the periodic patterns created by the nanosecond LDW technique. Moreover, we have experimentally demonstrated that the contact angle of water droplets on the patterned surfaces is almost independent of the shape of the unit cell of the patterns, which can reduce the influence of fabrication errors on the accuracy of controlling the wettability of patterned surfaces. In addition, we have developed an effective surface model to accurately calculate the contact angle of water droplets on patterned solid surfaces. By using this model to design the duty ratio of periodic patterns on a patterned solid surface, its wettability can be precisely controlled. The presented fabrication method has great potential for fabricating artificial solid surfaces that can be used for liquid droplet motion control, water collection, drug delivery, and so on.Author contributions
Meng Wang: conceptualization, methodology, investigation, formal analysis, funding acquisition, validation, writing – original draft, writing – review & editing. Chuan Fei Guo: formal analysis, resources. Xiaofeng Wang: software. Bingxi Xiang: investigation. Mingxia Qiu: resources. Tiefeng He: investigation. Huan Yang: resources. Yu Chen: data curation. Jianjie Dong: conceptualization, methodology, investigation, fanalysis, validation, supervision, writing – original draft, writing – review & editing. Qian Liu: resources, funding acquisition. Shuangchen Ruan: project administration, resources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work performed at SZTU was supported by NSFC (no. 61805156) and the Shenzhen Science and Technology Planning (no. JCYJ20190813103207106). The work performed at NCNST was supported by the National Natural Science Foundation of China (no. 51971070, no. 10974037). This work was supported by the Guangdong Province University Young Innovative Talents Program (2018KQNCX404) and Post-doctoral research project of SZTU (W201960002440008, 202028555301015).References
- W. Barthlott and C. Neinhuis, Planta, 1997, 202, 1–8 CrossRef CAS.
- C. Neinhuis and W. Barthlott, Ann. Bot., 1997, 79, 667 CrossRef.
- V. Zorba, E. Stratakis, M. Barberoglou, E. Spanakis, P. Tzanetakis, S. H. Anastasiadis and C. Fotakis, Adv. Mater., 2008, 20, 4049–4054 CrossRef CAS.
- Z. Burton and B. Bhushan, Ultramicroscopy, 2006, 106, 709–719 CrossRef CAS PubMed.
- X. Feng, X. Gao, Z. Wu, L. Jiang and Q. Zheng, Langmuir, 2007, 23, 4892–4896 CrossRef CAS PubMed.
- P. Zhang and F. Y. Lv, Energy, 2015, 82, 1068 CrossRef.
- S. Xu, Q. Wang and N. Wang, Adv. Eng. Mater., 2021, 23, 2001083 CrossRef CAS.
- S. P. Dalawaia, M. A. S. Alyb, S. S. Latthea, R. Xing, R. S. Sutarc, S. Nagappand, C. Had, K. K. Sadasivunie and S. Liu, Prog. Org. Coating, 2020, 138, 105381 CrossRef.
- I. S. Bayer, Adv. Mater. Interfaces, 2020, 7, 2000095 CrossRef CAS.
- J. Jeevahan, M. Chandrasekaran, G. B. Joseph, R. Durairaj and G. Mageshwaran, J. Coat. Technol. Res., 2018, 15, 231–250 CrossRef CAS.
- K. Yin, D. Chu, X. Dong, C. Wang, J. Duan and J. He, Nanoscale, 2017, 9, 14229–14235 RSC.
- K. Yin, Z. Wu, J. Wu, Z. Zhu, F. Zhang and J. Duan, Appl. Phys. Lett., 2021, 118, 211905 CrossRef CAS.
- B. Wu, M. Zhou, J. Li, X. Ye, G. Li and L. Cai, Appl. Surf. Sci., 2009, 256, 61–66 CrossRef CAS.
- T. Nguyena, S. Park and H. Lim, Appl. Surf. Sci., 2018, 435, 585–591 CrossRef.
- J. Song, D. Wang, L. Hu, X. Huang and Y. Chen, Appl. Surf. Sci., 2018, 455, 771–779 CrossRef CAS.
- A. R. Siddiqui, W. Li, F. Wang, J. Ou and A. Amirfazli, Appl. Surf. Sci., 2021, 542, 148534 CrossRef CAS.
- M. Khodaei and S. Shadmani, Surf. Coat. Technol., 2019, 374, 1078–1090 CrossRef CAS.
- Z. Yu, C. Zhou, R. Liu, Q. Zhang, J. Gong, D. Tao and Z. Ji, Colloids Surf., A, 2020, 589, 124475 CrossRef CAS.
- A. Hozumi, D. F. Cheng and M. Yagihashi, J. Colloid Interface Sci., 2011, 353, 582–587 CrossRef CAS PubMed.
- Z. Cai, J. Lin and X. Hong, RSC Adv., 2018, 8, 491–498 RSC.
- M. R. Cardoso, V. Tribuzi, D. T. Balogh, L. Misoguti and C. R. Mendonc, Appl. Surf. Sci., 2011, 257, 3281–3284 CrossRef CAS.
- V. D. Ta, A. Dunn, T. J. Wasley, J. Li, R. W. Kay, J. Stringer, P. J. Smith, E. Esenturk, C. Connaughton and J. D. Shephard, Appl. Surf. Sci., 2016, 365, 153–159 CrossRef CAS.
- K. Sun, H. Yang, W. Xue, A. Hea, D. Zhu, W. Liu, K. Adeyemia and Y. Cao, Appl. Surf. Sci., 2018, 436, 263–267 CrossRef CAS.
- C.-V. Ngo and D.-M. Chun, Appl. Surf. Sci., 2017, 409, 232–240 CrossRef CAS.
- S. Millesa, M. Solderaa, T. Kuntzec and A. F. Lasagnia, Appl. Surf. Sci., 2020, 525, 146518 CrossRef.
- A. Žemaitis, A. Mimidisb, A. Papadopoulosb, P. Gečysa, G. Račiukaitisa, E. Stratakis and M. Gedvilas, RSC Adv., 2020, 10, 37956–37961 RSC.
- S. Kim, H. S. Kang, E. Sohn, B. Chang, I. J. Park and S. G. Lee, RSC Adv., 2021, 11, 23631–23636 RSC.
- J. Li, Y. Hou, Y. Liu, C. Hao, M. Li, M. K. Chaudhury, S. Yao and Z. Wang, Nat. Phys., 2016, 12, 606–612 Search PubMed.
- N. Zhao, M. Li, H. Gong and H. Bai, Sci. Adv., 2020, 6, eabb4712 Search PubMed.
- M. Wang, Q. Liu, H. Zhang, C. Wang, L. Wang, B. Xiang, Y. Fan, C. Guo and S. Ruan, ACS Appl. Mater. Interfaces, 2017, 9, 29248–29254 CrossRef CAS PubMed.
- Y. Hou, Y. Shang, M. Yu, C. Feng, H. Yu and S. Yao, ACS Nano, 2018, 12, 11022–11030 CrossRef CAS PubMed.
- H. Zhang, H. Zhu, X. Liang, P. Liu, Q. Zhang and S. Zhu, Appl. Surf. Sci., 2020, 513, 145810 CrossRef CAS.
- G. Kunti, P. K. Mondal, A. Bhattacharya and S. Chakraborty, Phys. Fluids, 2018, 30, 092005 CrossRef.
- P. K. Mondal, D. DasGupta, A. Bandopadhyay, U. Ghosh and S. Chakraborty, Phys. Fluids, 2015, 27, 032109 CrossRef.
- P. K. Mondal and S. Chaudhry, Phys. Fluids, 2018, 30, 042109 CrossRef.
- P. K. Mondal, U. Ghosh, A. Bandopadhyay, D. DasGupta and S. Chakraborty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023022 CrossRef PubMed.
- D. DasGupta, P. K. Mondal and S. Chakraborty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 023011 CrossRef PubMed.
- P. K. Mondal, U. Ghosh, A. Bandopadhyay, D. DasGuptaa and S. Chakraborty, Soft Matter, 2014, 10, 8512–8523 RSC.
- P. K. Mondal, D. DasGuptaa and S. Chakraborty, Soft Matter, 2015, 11, 6692–6702 RSC.
- C. Yang, X. Jing, F. Wang, K. F. Ehmann, Y. Tian and Z. Pu, Appl. Surf. Sci., 2019, 497, 143805 CrossRef CAS.
- Q. Wang, H. Wang, Z. Zhu, N. Xiang, Z. Wang and G. Sun, Surf. Interfaces, 2021, 24, 101122 CrossRef CAS.
- H. Zhang, H. Lai, Z. Cheng, D. Zhang, P. Liu, Y. Li and Y. Liu, Appl. Surf. Sci., 2020, 525, 146525 CrossRef CAS.
- J. Li, X. Zhou, J. Li, L. Che, J. Yao, G. McHale, M. K. Chaudhury and Z. Wang, Sci. Adv., 2017, 3, eaao3530 CrossRef PubMed.
- V. D. Ta, A. Dunn, T. J. Wasley, J. Li, R. W. Kay, J. Stringer, P. J. Smithc, E. Esenturk, C. Connaughtond and J. D. Shepharda, Appl. Surf. Sci., 2016, 371, 583–589 CrossRef CAS.
- M. Liu, M. Li, S. Xu, H. Yang and H. Sun, Front. Chem., 2020, 8, 835 CrossRef CAS PubMed.
- H. Zhang, Y. Zhou, Y. Li, T. J. Bandosz and D. L. Akins, J. Colloid Interface Sci., 2012, 375, 106–111 CrossRef CAS PubMed.
- M. L. Hitchman and K. F. Jensen, Chemical vapor deposition: principles and applications, Academic Press, London, 1993 Search PubMed.
- M. Totzeck, W. Ulrich, A. Göhnermeier and W. Kaiser, Nat. Photonics, 2007, 1, 629–631 CrossRef CAS.
- L. Qin, Y. Huang, F. Xia, L. Wang, J. Ning, H. Chen, X. Wang, W. Zhang, Y. Peng, Q. Liu and Z. Zhang, Nano Lett., 2020, 20, 4916–4923 CrossRef CAS PubMed.
- L. Wang, X. Wang, X. Wang and Q. Liu, Appl. Surf. Sci., 2020, 527, 146771 CrossRef CAS.
- W. Jiang, J. He, F. Xiao, S. Yuan, H. Lu and B. Liang, Ind. Eng. Chem. Res., 2015, 54, 6874–6883 CrossRef CAS.
- V. Chobaomsup, M. Metzner and Y. Boonyongmaneerat, J. Coat. Technol. Res., 2020, 17, 583–595 CrossRef CAS.
- S. Tanaka, M. Aonuma, N. Hirose and T. Tanaki, J. Electrochem. Soc., 2002, 149, D167–D171 CrossRef CAS.
- S. Tanaka, T. Iwatani, N. Hirose and T. Tanakid, J. Electrochem. Soc., 2002, 149, F186–F190 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |