Open Access Article
Open Access ArticleInsight into the Fischer–Tropsch mechanism on hcp-Fe7C3 (211) by density functional theory: the roles of surface carbon and vacancies†
Jie Renab,
Ning Ai *a and
Yingzhe Yu
*a and
Yingzhe Yu *b
*b
aCollege of Biological, Chemical Sciences and Engineering, Jiaxing University, Jiaxing 314001, P. R. China. E-mail: aining@tsinghua.org.cn
bKey Laboratory for Green Chemical Technology of Ministry of Education, R&D Center for Petrochemical Technology, Tianjin University, Tianjin 300072, P. R. China,. E-mail: yuyingzhe@tju.edu.cn
First published on 25th October 2021
Abstract
Iron carbide phases discovered in the spent iron catalysts have proved to be active in the Fischer–Tropsch process. The surface carbon of the iron carbide played a key role in the Fischer–Tropsch mechanism. Since there are two surface carbons, C1 and C2, on the hcp-Fe7C3 (211), which are close to each other, their reaction mechanisms would be significant. Hence, the DFT calculations were performed to investigate the Fischer–Tropsch mechanism involving the surface carbon. It was found that the HC1 + C2 pathway was the major C–C coupling reaction pathway with an effective energy barrier of 0.97 eV. Ethane would be the major C2 product from the HC1C2 species through the stepwise hydrogenation pathway due to the high adsorption energy of ethylene (1.67 eV). After the desorption process of ethane, the carbon vacancy would form. The carbon vacancy was found to be the CO activation site through the CO direct dissociation pathway and the carbon vacancy would recover. It was concluded that the defect-hcp-Fe7C3 (211) is the high active facet of the Fischer–Tropsch synthesis, the carbon vacancy sites are the CO activation sites and the surface carbon sites are the C–C coupling sites. The surface carbons not only act as the chain initiation sites but also act as the chain growth sites in the Fischer–Tropsch mechanism on hcp-Fe7C3 (211).
Introduction
Fischer–Tropsch synthesis (FTS) is a promising process since it can convert syngas into liquid fuels and chemicals so that other carbon-based energy such as coal and biomass can be utilized.1,2 The FTS process has been studied for a long time for the production of long-chain fuels.3,4 In a recent study, the Fischer–Tropsch synthesis was proved to produce light olefins with acceptable selectivity.5,6 Iron-based catalysts are usually selected as fundamental catalysts for the production of light olefins.7–10 The promoter addition is one of the major modifications,11–14 while the design of specific catalyst structures is another optimization method for improving the catalyst performance.15,16 However, the selectivity of light olefins in the hydrocarbon species over the iron catalysts cannot meet the economic demand in the industry.17 As a result, the performance of the iron catalysts requires urgent improvement.Nowadays, there are different kinds of iron-containing phases in the spent iron catalysts.18–23 The major iron carbide phases are ε-Fe2C, ε-Fe2.2C, Fe7C3, χ-Fe5C2, θ-Fe3C, and so on.24,25 χ-Fe5C2 and ε-Fe2C have been proved to be the active phases in the iron catalysts.26,27 θ-Fe3C is always considered as the inactive phase as it mainly appears in deactivated iron-based catalysts.28,29 Fe7C3 would be present after a long run and high-temperature Fischer–Tropsch synthesis,30,31 which has been proved to be the active phase by Brent Williams et al. and Yongwang Li et al.32,33
A comprehensive understanding of the Fischer–Tropsch mechanism on the iron catalysts would assist the researcher to improve the catalysis performance. Since the iron catalysts are composed of different iron carbide phases, the Fischer–Tropsch mechanism on the iron catalysts is also composed of the Fischer–Tropsch mechanism on different iron carbide phases. Thus, it is necessary to investigate the Fischer–Tropsch mechanism on each iron carbide phase, especially the one that was proved to be active in the Fischer–Tropsch synthesis. However, the preparation, characterization, and exploration of the single iron carbide phase under the reaction conditions are difficult. As a result, the theoretical method is used for investigating the Fischer–Tropsch mechanism on the single iron carbide phase and is applied in this research.
To date, the Fischer–Tropsch mechanism is clear for some iron carbide phases. Thanh Hai Pham et al. pointed out that the direct CO dissociation reaction and the coupling reaction of C + HC or HC + HC are the major CO activation pathway and chain-growth pathway, respectively, on the χ-Fe5C2 (510).34,35 After that, the influence of the H coverage effect on the Fischer–Tropsch mechanism was introduced by Minhua Zhang et al. Due to the existence of the H coverage effect, the CO insertion mechanism rather than the carbide mechanism is the Fischer–Tropsch mechanism on the χ-Fe5C2 (510).36 The CO activation mechanism on the χ-Fe5C2 (001), χ-Fe5C2 (221), χ-Fe5C2 (010), χ-Fe5C2 (110), χ-Fe5C2 (111) has been discussed thoroughly by Yurong He et al.37,38 On θ-Fe3C (100)39 and θ-Fe3C (010),40 the CO insertion dissociation pathway is the major CO activation mechanism and the C–C coupling mechanism. On θ-Fe3C (031), the coupling reaction of HC + HC and H2C + H2C is the major chain-growth pathway.41 However, the Fischer–Tropsch mechanism on other iron carbide phases has not yet been discussed thoroughly.
As mentioned before, the hcp-Fe7C3 phase has been proved to be active in Fischer–Tropsch synthesis by experimental research.32,33 In previous research, DFT calculations were applied to investigate the CO activation pathway on hcp-Fe7C3 (211).42 The results showed that CO would undergo the H-assisted dissociation pathway on the top site rather than the CO insertion dissociation pathway with the surface carbon. However, the C–C coupling pathway and the product formation pathway on hcp-Fe7C3 (211) are not clear. Thus, this article aims to investigate the Fischer–Tropsch mechanism on the hcp-Fe7C3 phase so that the understanding of the iron catalyst's mechanism could be improved.
According to the known mechanism on other iron carbide phases, the surface carbon that belongs to the catalyst would participate in the Fischer–Tropsch synthesis. On the Fe2C (011), Fe5C2 (010), Fe3C (001), and Fe4C (100), the surface carbon was found to be the carbon source of the product methane.43 On the χ-Fe5C2 (510), the surface carbon would undergo a stepwise hydrogenation reaction to give the HxC species. Then the HxC species can participate in the subsequent C–C coupling reaction.34–36 On θ-Fe3C (100) and θ-Fe3C (010),39,40 the surface carbon would act as the chain initiation site so that the reactant CO could be coupled with it to accomplish the CO activation pathway and chain-growth pathway. Other than theoretical work, Khodakov et al. proved that the initiation of chain growth involves the surface carbon through isotope C13 research.44 As a result, the surface carbon would always play a key role in the Fischer–Tropsch mechanism.
The previously researched model of hcp-Fe7C3 (211) showed that two surface carbons are close to each other, leading to the problem of what role they play in the Fischer–Tropsch mechanism. Hence, when the DFT calculations were performed to accomplish the full map of the Fischer–Tropsch mechanism on hcp-Fe7C3 (211), the surface carbon was considered to be the significant reactant and was thoroughly discussed in the designed reaction pathway.
In short, as the iron catalysts are combined with different kinds of iron carbide phases, including the hcp-Fe7C3 phase, the research on the Fischer–Tropsch mechanism on the hcp-Fe7C3 phase would be valuable in the iron catalysts and deserves to be researched. The experimental research on the reaction mechanism in the pure hcp-Fe7C3 phase would be difficult since the specific iron carbide would be transferred to another kind of iron carbide under the Fischer–Tropsch synthesis. Hence, DFT calculations are applied in this article to investigate the Fischer–Tropsch mechanism on the hcp-Fe7C3 (211) facet, because it possesses the largest percentage among the exposed crystal facets.
We expect that this research will provide a better comprehension of the Fischer–Tropsch mechanism on the hcp-Fe7C3 phase so that the iron-based catalysts can be understood clearly and be modified efficiently.
Computational details
Surface model
In this study, the bulk hcp-Fe7C3 was selected as the bulk catalyst according to the experimental results.33 The hcp-Fe7C3 belongs to the hexagonal system with the P63mc space group. The lattice constants of hcp-Fe7C3 are a = 6.826 Å; b = 6.826 Å; c = 4.495 Å; γ = 120°. The bulk structure of hcp-Fe7C3 was optimized with a 3 × 3 × 5 Monkhorst–Pack k-point mesh. The optimized lattice constants are a = 6.748 Å; b = 6.748 Å; c = 4.434 Å; γ = 120°, which are in agreement with the experimental values. The hcp-Fe7C3 (211) facet possesses the largest percentage among the exposed crystal facets based on the surface energy calculation36 and the XRD results (PDF #89-7273).45 The surface reactions were calculated on a p (1 × 1) hcp-Fe7C3 (211) slab with a stable terminal surface. The size of the p (1 × 1) hcp-Fe7C3 (211) slab is a = 11.14 Å; b = 8.074 Å, which could avoid the interactions between the adsorbate with itself in the neighbouring repeated images. In all calculations, the bottom two Fe layers were fixed in their bulk position, while the top two Fe layers and the adsorbents were allowed to relax. The top view and side view of the hcp-Fe7C3 (211) slab model are shown in Fig. 1.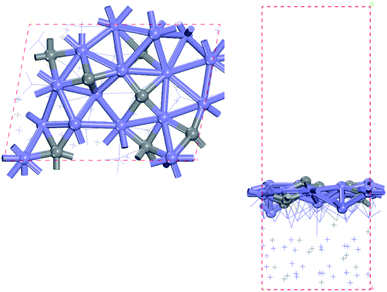 | ||
| Fig. 1 Top (left) and side (right) views of hcp-Fe7C3 (211) surface (blue: Fe atoms; gray: C atoms). | ||
First-principles calculations
The spin-polarized DFT calculations were performed via the projector augmented wave (PAW) method46–48 using the Vienna ab initio simulation package (VASP). In this article, the Perdew–Burke–Ernzerhof (PBE) functional49 with the plane wave cutoff energy of 400 eV was applied. The Brillouin zone sampling of the bulk calculation and the surface calculation were set as 3 × 3 × 5 and 2 × 2 × 1 Monkhorst–Pack grids,50 respectively. The electron smearing was employed via the Methfessel–Paxton technique with a smearing width consistent with 0.2 eV.51 The effects of van der Waals corrections were taken into account by the DFT-D3 method with Becke–Jonson (BJ) damping.52,53The convergence standard of the SCF calculation and the geometry optimization were set as 1 × 10−5 eV and 0.03 eV Å−1, respectively. The climbing-image nudged elastic band method (CI-NEB)54,55 was selected to search the transition state and to evaluate the intrinsic energy barrier. The convergence standard of the CI-NEB calculation was set as 0.05 eV Å−1. The frequency calculation was performed to confirm the TS structure after the CI-NEB calculation. Only if the TS structure of the researched elementary reaction has only one imaginary frequency can the TS structure be confirmed.
The adsorption energy of surface species is defined and calculated by Eads = E(adsorbate/slab) − [E(slab) + E(adsorbate)], in which E(adsorbate/slab) is the energy of the slab with surface adsorbate, E(slab) is the energy of the slab, and E(adsorbate) is the energy of the free adsorbate. The reaction energy and the intrinsic energy barrier are calculated by ΔEr = E(FS) − E(IS) and Ea = E(TS) − E(IS), respectively, where E(IS), E(FS), and E(TS) are the energies of the corresponding initial state (IS), final state (FS), and transition state (TS), respectively.
The reaction pathways researched in the article are combined with a series of consecutive reactions. For an elementary reaction, if the coverage of the reactant is extremely low, the reaction rate would be slow due to the mass law, even though the intrinsic energy barrier of this elementary reaction is not high. As a result, the determination of the major reaction pathway based only on the intrinsic energy barrier would be doubtful. In order to solve such a problem, the effective energy barrier56–58 was applied to evaluate the major reaction pathway. The effective energy barrier of the kth elementary reaction in the consecutive reactions is represented by Eeff,k and is calculated by 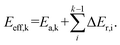 In the equation, Ea,k is the intrinsic energy barrier of the kth step elementary reaction,
In the equation, Ea,k is the intrinsic energy barrier of the kth step elementary reaction, 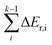 is the sum of the reaction energy from the ith step elementary reaction to the (k − 1)th step elementary reaction and the ith step elementary reaction is the elementary reaction whose initial state shows the lowest electronic energy among all the states of the studied consecutive reactions.
is the sum of the reaction energy from the ith step elementary reaction to the (k − 1)th step elementary reaction and the ith step elementary reaction is the elementary reaction whose initial state shows the lowest electronic energy among all the states of the studied consecutive reactions.
In the consecutive reactions, there are some elementary reactions, which are the transfer reaction of the surface species from one adsorption site to another, or the structure transformation reaction; these two types of reactions are named migration reactions in this article. Most of the migration reactions show relatively low intrinsic energy barrier in this article, the computational intrinsic energy barrier of each migration reaction can be found in the ESI.† To avoid the energy profile diagram being tedious and unreadable, only the reaction energies of migration reactions are taken into account in the energy profile diagram, which is named as migration energy and denoted as ΔEm.
In short, when the migration energy is applied in the energy profile diagram, the effective energy barrier of the kth elementary reaction in the consecutive reactions is calculated by 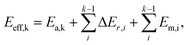 where the
where the 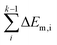 is the sum of the migration energy from the ith elementary reaction in the consecutive reactions to the (k − 1)th elementary reaction in the consecutive reactions.
is the sum of the migration energy from the ith elementary reaction in the consecutive reactions to the (k − 1)th elementary reaction in the consecutive reactions.
Results and discussion
The C–C coupling reactions of the surface carbon
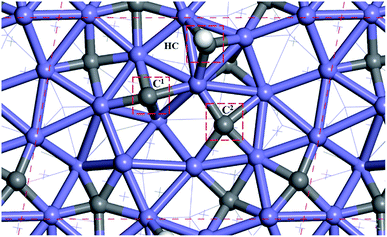
Fig. 2 shows the sites of the major carbon-containing species (in the red box) on hcp-Fe7C3 (211), which are the C1 site, C2 site, and HC site, based on the previous research.43 The C1 site and C2 site are the surface carbons that belong to the catalysts. The C1 species and C2 species are the hydrogenation products of the surface carbon. The HC site is the CO activation site of the H-assisted CO activation pathway and the HC species is the product of the known CO activation pathway.Since the H-assisted CO activation pathway is the known CO activation mechanism, the carbide mechanism seems to be the major Fischer–Tropsch mechanism on the Fe7C3 (211). The detailed possible designed reaction pathway is shown below: (1) the CO adsorption process (2) the CO activation process on the HC site. (3) The C–C coupling process of HxC species with the C1 species or C2 species to be the C2 species (4) The hydrogenation process, the product desorption process, or chain-growth process of the C2 species. (5) The recovery process of C1 or C2.
All the surface carbon-containing species are the possible reactants of the C–C coupling reaction. Before starting to calculate and research the C–C coupling process of HxC species with C1 species or C2 species, it should be noted that the distance from the C1 site to the C2 site is close to the distance from the HC site to the C1 site, and the distance from the HC site to the C2 site as shown in Fig. 2.
The distances between the C1 site, C2 site, and HC site were calculated and shown in Table 1. The results show that the distance from the C1 site to the C2 site, the distance from the HC site to the C1 site, and the distance from the HC site to C2 site are 3.212 Å, 3.205 Å, and 3.460 Å, respectively, and are close.
| Distance between C atom(Å) | C1 | C2 | HC |
|---|---|---|---|
| C1 | — | 3.212 | 3.205 |
| C2 | — | — | 3.460 |
| CH | — | — | — |
As a result, if the HxC species can be coupled with the C1 species or C2 species, the C1 species and C2 species could also possibly couple with each other.
Hence, another possible C–C coupling pathway was presented, which is denoted as the C1–C2 coupling pathway. In the C1–C2 coupling pathway, the C1 species and C2 species can be coupled with each other to be C2 species. Based on the new idea of the C1–C2 coupling pathway, the designed reaction pathway is shown in Scheme 1 and the calculated results are shown in Table 2. It was found that some of the coupling reactions showed relatively low energy barriers, which proved that the C1–C2 coupling pathway is likely to be the major C–C coupling pathway on the hcp-Fe7C3 (211).
| No | Reaction | Em | Ea | Er |
|---|---|---|---|---|
| 1 | C1 + H = HC1 | 0 | 0.73 | −0.26 |
| 2 | HC1 + H = H2C1 | 0 | 0.73 | 0.71 |
| 3 | H2C1 + H = H3C1 | 0.09 | 0.91 | 0.48 |
| 4 | H3C1 + H = H4C1 | 0 | 0.60 | 0.03 |
| 5 | C2 + H = HC2 | 0 | 0.99 | 0.23 |
| 6 | HC2 + H = H2C2 | 0 | 0.67 | 0.60 |
| 7 | H2C2 + H = H3C2 | −0.09 | 1.14 | 0.43 |
| 8 | H3C2 + H = H4C2 | 0 | 0.83 | 0.04 |
| 9 | C1 + C2 = C1C2 | 0 | 1.25 | 0.44 |
| 10 | C1+ HC2 = C1HC2 | 0 | 0.95 | 0.05 |
| 11 | C1+ H2C2 = C1H2C2 | −0.09 | 1.05 | 0.26 |
| 12 | C1+ H3C2 = C1H3C2 | −0.45 | 0.97 | 0.10 |
| 13 | HC1 + C2 = HC1C2 | 0 | 0.97 | 0.44 |
| 14 | HC1+ HC2 = HC1HC2 | 0 | 0.76 | 0.46 |
| 15 | HC1+ H2C2 = HC1H2C2 | 0.39 | 0.87 | 0.28 |
| 16 | HC1+ H3C2 = HC1H3C2 | −0.46 | 1.43 | 0.38 |
| 17 | H2C1 + C2 = H2C1C2 | 0 | 0.73 | −0.23 |
| 18 | H2C1 + HC2 = H2C1HC2 | 0 | 0.74 | 0.20 |
| 19 | H2C1 + H2C2 = H2C1H2C2 | −0.09 | 0.83 | −0.27 |
| 20 | H2C1 + H3C2 = H2C1H3C2 | −0.46 | 1.00 | 0.31 |
| 21 | H3C1 + C2 = H3C1C2 | −0.13 | 1.01 | −0.24 |
| 22 | H3C1 + HC2 = H3C1HC2 | −0.17 | 1.41 | 0.77 |
| 23 | H3C1+ H2C2 = H3C1H2C2 | −0.34 | 1.45 | 0.31 |
| 24 | H3C1+ H3C2 = H3C1H3C2 | −0.62 | 2.92 | 0.10 |
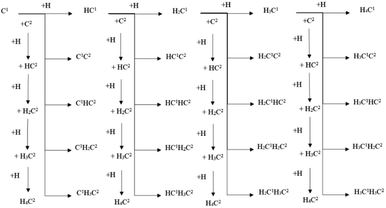
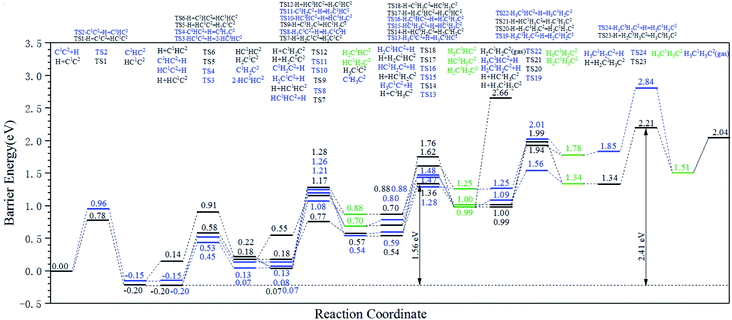
The energy profile diagrams of the C1–C2 coupling pathway are shown in Fig. 3. The C1–C2 coupling reaction pathway involving C1, HC1, H2C1, and H3C1 species are present in Fig. 3(a–d) and were denoted as the C1 coupling pathway, HC1 coupling pathway, H2C1 coupling pathway, and H3C1 coupling pathway, respectively. The black line represents the C–C coupling reaction pathway involving the C1 species and C2 species. The blue line represents the stepwise hydrogenation pathway of the C2 hydrocarbon species.
Comparing the effective energy barriers of the coupling pathways involving different C1 species and C2 species, the major C1–C2 coupling pathway would be achieved. The HC1 + C2 pathway showed the lowest effective energy barrier of 0.97 eV, while the effective energy barrier of the HC1 + HC2 pathway is close to that of the HC1 + C2 pathway (0.99 eV). The effective energy barriers of the C1 + C2 pathway and the C1 + HC2 pathway are a bit higher than that of the HC1 + C2 pathway, which are 1.25 eV and 1.18 eV, respectively. The effective energy barriers of the C1–C2 coupling reactions involving H2C species and H3C species are much higher, making them impossible.
There are two major reasons why the C–C coupling reaction involving H2C species and H3C species would show high effective energy barriers. Firstly, Table 2 shows that in the C1 coupling pathway, HC1 coupling pathway, and H2C1 coupling pathway, the intrinsic energy barrier of the C–C coupling reaction is not extremely high. However, the hydrogenation reactions of HC species are endothermic with high reaction energies, which are 0.71 eV and 0.60 eV for HC1 and HC2, respectively. The high reaction energy of the HC hydrogenation reaction represents the instability of the H2C species so that the dehydrogenation reaction of the H2C species would take place easily. Hence, the degree of coverage of the H2C species would be small on the hcp-Fe7C3 (211). The small coverage of the reactant species would result in the slow reaction rate of the specific C–C coupling reaction involving H2C species according to the mass law. Hence, the high effective energy barrier of the C1–C2 coupling pathways involving H2C could be attributed to the high instability of the H2C species. This situation was also found in other iron carbides from theoretical and experimental research.35,36
Secondly, Table 2 shows that the C–C coupling reactions involving H3C species have high intrinsic energy barriers, which could be attributed to the weak interactions between the surface and H3C species. To confirm the inference, Table 3 presents the Bader charge analysis on the C1 species. The “C”, “H1”, “H2”, and “H3” represent the number of “Bader charges” in specific atoms in the C1 species. The “charge transfer” represents the Bader charge transfer between the C1 species and hcp-Fe7C3 (211), in which “+” represents the charge obtained by the C1 species from the hcp-Fe7C3 (211).
| Species | C | H1 | H2 | H3 | Total | Charge transfer |
|---|---|---|---|---|---|---|
| C1 | 4.91 | — | — | — | 4.91 | +0.91 |
| HC1 | 4.86 | 0.87 | — | — | 5.73 | +0.73 |
| H2C1 | 4.79 | 0.87 | 0.97 | — | 6.63 | +0.63 |
| H3C1 | 4.59 | 0.83 | 0.98 | 0.90 | 7.30 | +0.30 |
| C2 | 4.92 | — | — | — | 4.92 | +0.92 |
| HC2 | 4.88 | 0.88 | — | — | 5.76 | +0.76 |
| H2C2 | 4.78 | 0.90 | 0.97 | — | 6.65 | +0.65 |
| H3C2 | 4.48 | 0.94 | 0.98 | 0.95 | 7.35 | +0.35 |
Table 3 shows that the charge obtained by the C1 species from the hcp-Fe7C3 (211) would decrease with the increase in H atoms in the C1 species. The decrease in the charge transfer indicates the decrease in the interactions between the C1 species and hcp-Fe7C3 (211). The charge transfers of the H3C1 species with the hcp-Fe7C3 (211) and the H3C2 species with the hcp-Fe7C3 (211) were +0.30 and +0.35, respectively, which are much lower as compared to the other C1 species with the hcp-Fe7C3 (211). Hence, the hcp-Fe7C3 (211) could hardly activate the C–C coupling reaction involving the H3C species so that the intrinsic energy barrier would be high as shown in Table 2. This phenomenon has also been found and reported on other iron carbides.36
The major C1–C2 coupling pathways were achieved and are shown in Scheme 2, including the C1 + C2 pathway, HC1 + C2 pathway, C1 + HC2 pathway, and HC1 + HC2 pathway. Among the major C1–C2 coupling pathways, the HC1 + C2 pathway is the preferred C1–C2 coupling pathway with an effective energy barrier of 0.97 eV.
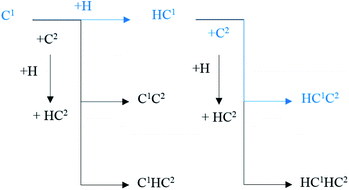 | ||
| Scheme 2 The major C1–C2 coupling pathways (black lines) and preferred C1–C2 coupling pathways (blue lines) on hcp-Fe7C3 (211). | ||
According to the results, a new possible C–C coupling pathway with a relatively low energy barrier was discovered and it could be the major C–C coupling mechanism. However, the preferred C1–C2 coupling pathway needs to be compared with other possible C–C coupling pathways to decide whether or not it could be the major C–C coupling mechanism.
The major possible C–C coupling mechanisms in the Fischer–Tropsch synthesis are the carbide mechanism and CO insertion mechanism.
On hcp-Fe7C3 (211), the C–C coupling pathway through the CO insertion mechanism has been discussed thoroughly.43 The effective energy barrier of the preferred C–C coupling pathway through the CO insertion mechanism is 1.48 eV, which is much higher than that of the preferred C1–C2 coupling pathway. Thus, the C1 species and the C2 species prefer to be coupled with each other rather than with adsorbed CO.
Another possible C–C coupling pathway is the coupling reaction between surface carbon and HxC species through the carbide mechanism, in which the HxC species are the products through the H-assisted CO activation pathway. The effective energy barrier of the HxC species formation pathway is 1.30 eV, which is also higher than that of the preferred C1–C2 coupling pathway. As a result, the effective energy barrier of the preferred C1–C2 coupling pathway is much lower than those of the other two possible C–C coupling pathways. It can be concluded that on the hcp-Fe7C3 (211), the C1–C2 coupling pathway is the major C–C coupling mechanism of the C2 species and the major coupling products are HC1C2 and HC1HC2 species.
The stepwise hydrogenation pathway of the C2 species
After the C–C coupling reaction pathway, the subsequent reaction pathways of the major C2 species are the parts of the Fischer–Tropsch mechanism on the hcp-Fe7C3 (211). The possible ensuing reaction pathways are the stepwise hydrogenation pathway and the subsequent C–C coupling pathway.The discussion of the subsequent C–C coupling pathway would be almost the same as the C–C coupling pathway discussed before, except that the chain initiation site is the C2 species rather than the C1 species. Although the influence of the carbon chain length on the C–C coupling mechanism is important, it will not be discussed here.
The stepwise hydrogenation pathway of the C2 species is another possible subsequent reaction pathway. The discussion of the stepwise hydrogenation pathway is necessary, as it could determine whether the major C2 product on the hcp-Fe7C3 (211) is acetylene, ethylene, or ethane.
The designed stepwise hydrogenation pathway is shown in Scheme 3. The idea of the designed stepwise hydrogenation pathway is the hydrogenation elementary reaction on C1 and C2 of each possible C2 species from the initial C2 species, C1C2. In each hydrogenation elementary reaction, the 3-fold H sites are thought of as the reactants. The adsorption sites and adsorption energy of possible 3-fold sites H have been discussed in the previous study.43 The calculation results of the stepwise hydrogenation pathways are shown in Table 4.
| No | Reaction | Em | Ea | Er |
|---|---|---|---|---|
| 1 | H + C1C2 = HC1C2 | 0 | 0.78 | −0.20 |
| 2 | C1C2 + H = C1HC2 | 0 | 0.96 | −0.15 |
| 3 | HC1C2 + H = HC1HC2 | 0 | 0.65 | 0.27 |
| 4 | C1HC2 + H = C1H2C2 | 0.11 | 0.68 | 0.28 |
| 5 | H + HC1C2 = H2C1C2 | 0 | 0.79 | 0.38 |
| 6 | H + C1HC2 = HC1HC2 | 0.29 | 0.73 | 0.08 |
| 7 | H + H2C1C2 = H3C1C2 | 0 | 0.59 | 0.39 |
| 8 | H2C1C2 + H = H2C1HC2 | −0.10 | 0.27 | 0.19 |
| 9 | H + C1H2C2 = HC1H2C2 | 0.42 | 0.62 | 0.15 |
| 10 | HC1HC2 + H = HC1H2C2 | 0 | 1.04 | 0.62 |
| 11 | C1H2C2 + H = C1H3C2 | 0 | 1.13 | 0.41 |
| 12 | H + HC1HC2 = H2C1HC2 | 0 | 1.21 | 0.81 |
| 13 | H3C1C2 + H = H3C1HC2 | 0.02 | 0.69 | 0.66 |
| 14 | H + HC1H2C2 = H2C1H2C2 | 0 | 0.66 | 0.33 |
| 15 | HC1H2C2 + H = HC1H3C2 | 0.10 | 0.67 | 0.20 |
| 16 | H2C1HC2 + H = H2C1H2C2 | 0 | 0.60 | 0.11 |
| 17 | H + H2C1HC2 = H3C1HC2 | 0 | 0.74 | 0.44 |
| 18 | H + C1H3C2 = HC1H3C2 | 0 | 1.22 | 1.17 |
| 19 | H2C1H2C2 + H = H2C1H3C2 | 0.10 | 0.47 | 0.25 |
| 20 | H + H2C1H2C2 = H3C1H2C2 | 0 | 0.95 | 0.89 |
| 21 | H + HC1H3C2 = H2C1H3C2 | 0 | 0.99 | 0.51 |
| 22 | H3C1HC2 + H = H3C1H2C2 | 0 | 0.76 | 0.46 |
| 23 | H + H2C1H3C2 = H3C1H3C2 | 0 | 0.87 | 0.16 |
| 24 | H3C1H2C2 + H = H3C1H3C2 | 0 | 0.99 | −0.05 |
Table 4 shows that the intrinsic energy barrier and reaction energy of the hydrogenation reaction are not high, which indicates that both the hydrogenation reaction and the dehydrogenation reaction could take place.
The energy profile diagram of the stepwise hydrogenation pathway based on the hydrogenation elementary reactions in Table 4 is shown in Fig. 4. The diagram can be divided into two parts: the hydrogenation reactions on C1 (black lines) and the hydrogenation reactions on C2 (blue lines). The green lines represent products that could be formed from both kinds of hydrogenation reactions.
According to Fig. 4, the HC1C2 species is the most stable species among the C2 species on hcp-Fe7C3 (211). Since most hydrogenation reactions of the HC1C2 species and their hydrogenation products are endothermic, the effective energy barrier of the hydrogenation reactions would increase gradually along with the increase of H atoms in the reactant.
Ethylene and ethane are two major C2 products in the Fischer–Tropsch synthesis. The effective energy barriers of the ethylene formation pathway and the ethane formation pathway are 1.56 eV and 2.41 eV, respectively. It seems that ethylene would be the major C2 product since the effective energy barrier of the ethylene formation pathway is much lower than that of the ethane formation pathway. However, the ethylene adsorption energy is 1.67 eV, which is much higher than the intrinsic energy barrier of the ethylene hydrogenation reaction (0.47 eV). As a result, the hydrogenation reaction of the ethylene adsorption would take place more easily than the ethane adsorption. The adsorption energy of ethane (0.53 eV) is lower than the intrinsic energy barrier of the ethane dehydrogenation reaction (0.70 eV). Hence, the adsorbed ethane could escape from the hcp-Fe7C3 (211) easily to form the ethane product. As a result, the ethane formation pathway is thought to be the major C2 stepwise hydrogenation pathway. The detailed ethane formation pathway is shown in Scheme 4. The effective energy barrier of the ethane formation pathway is 2.41 eV, which is much higher than that of the preferred C–C coupling pathway and the CO activation pathway. The stepwise hydrogenation pathway would be the rate-determining step.
 | ||
| Scheme 4 The preferred stepwise hydrogenation pathway of the C2 coupling product on hcp-Fe7C3 (211). | ||
The over-hydrogenation of the C2 species resulted in the ethane being be the major C2 product on hcp-Fe7C3 (211) in the Fischer–Tropsch synthesis. This could mainly be attributed to the strong interactions between the hcp-Fe7C3 (211) and the adsorbed ethylene, which is characterized by the high adsorption energy of the adsorbed ethylene. Hence, if the target product in the Fischer–Tropsch synthesis is the olefin, the over-hydrogenation phenomenon should be suppressed.
The surface recovery pathway for the defect-hcp-Fe7C3 (211)
From the previous section, C1 and C2 are the surface carbons of the hcp-Fe7C3 (211) and they could be a part of the product through the C1–C2 coupling pathway, as well as the stepwise hydrogenation pathway. Regardless of the type of hydrocarbon, once the products are desorbed from the surface, the two carbon vacancy sites would form, which are denoted as the Cv1 site and Cv2 site, and the surface is denoted as the defect-hcp-Fe7C3 (211).The structure of the defect-hcp-Fe7C3 (211) is different from that of the hcp-Fe7C3 (211). To allow the discovered Fischer–Tropsch reaction pathway to be repeatable and the discussed Fischer–Tropsch mechanism to make sense, the defect-hcp-Fe7C3 (211) should be able to recover to the hcp-Fe7C3 (211). Due to the CO being the major feedstock in the Fischer–Tropsch synthesis, the adsorption and activation pathways of CO on the Cv1 site and Cv2 site are thought to be the possible surface recovery pathway, which is denoted as the carbon vacancy recovery pathway.
The designed carbon vacancy recovery pathway contained three kinds of elementary reactions after the CO adsorption on the Cv1 site or the Cv2 site, which are the hydrogenation reactions on the carbon site, the hydrogenation reactions on the oxygen site, and the dissociation reactions of C–O bonds.
The computation results are shown in Table 5. The intrinsic energy barrier of the elementary reaction in the carbon vacancy recovery pathway is a bit high, which indicates that the carbon vacancy recovery pathway may occur with difficulty.
| No | Reaction | Em | Ea | Er |
|---|---|---|---|---|
| 1 | H + C1O = HC1O | 0 | 1.04 | 1.03 |
| 2 | C2O = C2 + O | 0 | 1.18 | −0.75 |
| 3 | H + C2O = HC2O | 0 | 1.27 | 1.13 |
| 4 | C1O = C1 + O | 0 | 1.37 | 0.17 |
| 5 | C1O + H = C1OH | 0 | 1.58 | 0.81 |
| 6 | C2O + H = C2OH | 0 | 1.66 | 1.04 |
| 7 | HC1O = HC1 + O | 0 | 0.46 | −0.90 |
| 8 | H + HC1O = H2C1O | 0 | 0.89 | 0.65 |
| 9 | HC1O + H = HC1OH | 0 | 1.64 | 1.15 |
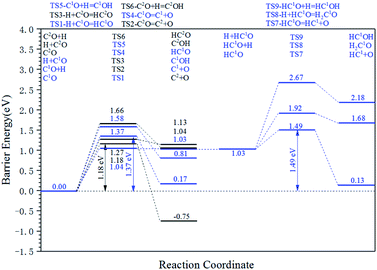
The energy profile diagram of the carbon vacancy recovery pathway is shown in Fig. 5. The blue line represents the carbon vacancy recovery pathway in the Cv1 site and the black line represents the carbon vacancy recovery pathway in the Cv2 site.
On the Cv1 site, in the first step, the HCO formation reaction showed a relatively low intrinsic energy barrier of 1.04 eV. However, in the subsequent reactions, the effective energy barrier of the HCO dissociation reaction would be high (1.49 eV) because of the high instability of HCO species. At the same time, the intrinsic energy barriers of the CO dissociation reaction and COH formation reaction were 1.37 eV and 1.58 eV, respectively. As a result, the dissociation reaction of the adsorbed CO is the preferred carbon vacancy recovery pathway in the Cv1 site.
On the Cv2 site, among the three kinds of elementary reactions in the carbon vacancy recovery pathway, the CO dissociation reaction shows the lowest intrinsic energy barrier (1.18 eV). The intrinsic energy barriers of the HCO formation pathway and COH formation pathway are 1.27 eV and 1.66 eV, respectively. Thus, the dissociation reaction of adsorbed CO is also the preferred carbon vacancy recovery pathway in the Cv2 site and the subsequent reactions of HCO species and COH species need not be taken into account.
From another perspective, the carbon vacancy recovery pathway is the CO activation pathway on carbon vacancy. Thus, the effective energy barriers of the CO activation pathway on the Cv1 site and the Cv2 site are 1.37 eV and 1.18 eV, respectively, which are close to the effective energy barrier of the H-assisted CO activation pathway on the top site (1.30 eV).
The results above indicate that the carbon vacancy is the possible CO activation site. Since the C1–C2 coupling pathway is the major C–C coupling mechanism, the surface carbon would be consumed rapidly so that the carbon vacancy would form frequently. Hence, it could be inferred that the C vacancy, especially the Cv2 site, is the major CO activation site.
After completing the carbon vacancy recovery pathway, the dissociation oxygen would be left on the hcp-Fe7C3 (211). The accumulation of surface oxygen would result in the changing of the iron carbide phase. As a result, whether the surface oxygen could be removed from the surface efficiently is the last piece of the puzzle to confirm the Fischer–Tropsch mechanism achieved in this article.
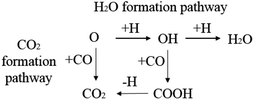
CO2 or H2O are the major products of the surface oxygen on the iron catalysts. Therefore, the H2O formation pathway and CO2 formation pathway are set as the designed oxygen removal pathways, shown in Scheme 5. The computation results are shown in Table 6.
| No | Reaction | Em | Ea | Er |
|---|---|---|---|---|
| 1 | O + H = OH | 0 | 1.30 | 0.53 |
| 2 | O + CO = CO2 | 0 | 1.40 | 0.87 |
| 3 | OH + CO = COOH | −0.01 | 1.24 | 0.89 |
| 4 | OH + H = H2O | −0.01 | 1.49 | 0.87 |
| 5 | COOH = CO2 + H | −0.02 | 0.70 | −0.30 |
The energy profile diagram of the oxygen removal pathway is shown in Fig. 6. In the first step, the intrinsic energy barriers of the O + H pathway and O + CO pathway are 1.30 eV and 1.40 eV, respectively, which are close. In the subsequent reaction, the desorption energy of CO2 is 0.53 eV, which is much lower than the intrinsic energy barrier of the OH + H pathway and OH + CO pathway. As a result, the CO2 formation pathway is the preferred oxygen removal pathway with a relatively low effective energy barrier (1.50 eV), while the H2O formation pathway is suppressed due to the high effective energy barrier of 2.01 eV.
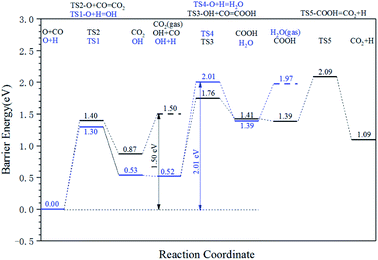 | ||
| Fig. 6 Energy profile diagram for oxygen removal pathways on hcp-Fe7C3 (211). Blue lines: the H2O formation pathways. Black lines: the CO2 formation pathways. | ||
In brief, the surface recovery pathway contains the C recovery vacancy pathway and the oxygen removal pathway is clear. The effective energy barrier of the preferred C recovery vacancy pathway in the Cv1 site, the preferred C recover vacancy pathway in the Cv2 site, and the oxygen removal pathway are 1.37 eV, 1.18 eV, and 1.50 eV, respectively. The effective energy barrier of the preferred surface recovery pathway is higher than that of the major C–C coupling mechanism but lower than the preferred C2 stepwise hydrogenation pathway. Hence, it could be proved that if the C2 product could be properly produced through the preferred C2 stepwise hydrogenation pathway, the defect-hcp-Fe7C3 (211) could also possibly recover to the hcp-Fe7C3 (211). The presence of the surface recovery pathway could confirm that the studied surface is stable under the Fischer–Tropsch synthesis reaction conditions and the Fischer–Tropsch mechanism achieved above is universal on hcp-Fe7C3 (211).
The full map of the Fischer–Tropsch mechanism and the role of the surface carbon on hcp-Fe7C3 (211)
According to the discussion in this article, the full map of the Fischer–Tropsch mechanism on hcp-Fe7C3 (211) can be achieved. The achieved Fischer–Tropsch mechanism would begin with the adsorption of CO and the dissociation H, which are from the reactant syngas, and end with the C2 product. The full map of the Fischer–Tropsch mechanism is shown in Scheme 6.On hcp-Fe7C3 (211), the Fischer–Tropsch mechanism can be divided into several parts. First, the C1 would undergo the hydrogenation reaction to form the HC species. Second, the HC1 species would be able to couple with the C2 so that the HC1C2 species would come into being. Third, the HC1C2 species would form the ethane product through a stepwise hydrogenation pathway. Fourth, two carbon vacancy sites would form after the desorption of the ethane product, resulting in the changing of the hcp-Fe7C3 (211) to the defect-hcp-Fe7C3 (211). Fifth, the CO would adsorb and dissociate directly on the C vacancy so that the C1 and C2 would recover. Sixth, the surface oxygen from the CO would be removed in the form of CO2 and the Fischer–Tropsch synthesis would restart in the first step.
In the achieved Fischer–Tropsch mechanism, the effective energy barriers of the six steps are 0.73 eV, 0.97 eV, 2.41 eV, 0.53 eV, 1.37 eV and 1.50 eV, respectively. As a result, on the hcp-Fe7C3 (211), the stepwise hydrogenation pathway is thought to be the rate-determining step of the Fischer–Tropsch mechanism. Hence, it could be inferred that the C2 species and the C vacancy would accumulate on the hcp-Fe7C3 (211) surface. Since the effective energy barrier of the C vacancy recovery pathway is not high, the Cv1 site and Cv2 site could act as the CO activation site to produce the C1 species with the co-adsorption C2 species. After that, the C–C coupling reaction could take place, possibly involving the C2 species and C1 species so that the length of the carbon chain would increase.
The adsorption energy of ethylene is high (1.67 eV). It could also be inferred that after the chain growth process, if the adsorption site of the long-chain olefins is on the same site, the adsorption energy of long-chain olefin would be close to that of ethylene, which would result in the alkane rather than the olefin being the major product on the hcp-Fe7C3 (211).
During the Fischer–Tropsch mechanism, it was found that carbon vacancy sites are the CO activation pathway sites and the surface carbon sites are the C–C coupling pathway sites; the surface carbon and its vacancy play a key role in the Fischer–Tropsch mechanism on the hcp-Fe7C3 (211).
As mentioned before, the surface carbon is always thought to be able to participate in the Fischer–Tropsch synthesis in iron carbide. On the other iron carbide, such as χ-Fe5C2 (510), θ-Fe3C (100), and θ-Fe3C (010), the surface carbon just acts as the chain initiation site, the C1 species participating in the chain growth process are the CO-activated products from the surface sites.39,40 On the hcp-Fe7C3 (211), the surface carbon not only acts as the chain initiation site but also acts as the chain growth site. Hence, it could be concluded that on the hcp-Fe7C3 (211), the total Fischer–Tropsch synthesis takes place on the vacancy site while on the other iron carbide, only a part of the Fischer–Tropsch synthesis takes place on the vacancy site. This property may result in the high reactant conversion and reaction rate of the Fischer–Tropsch synthesis.33
From another perspective, it is the defect-hcp-Fe7C3 (211) rather than the hcp-Fe7C3 (211) that is the high active facet of the Fischer–Tropsch synthesis. However, at first, the defect-hcp-Fe7C3 (211) is not thought of as the stable surface to be researched. Based on this article, it could be found that under the Fischer–Tropsch synthesis conditions, the exposed surface would change and update with the influence of CO and H2. As a result, when researching the Fischer–Tropsch mechanism on the iron carbide phase through the theoretical method, the change in the selected surface structure should be taken into account, especially the change in the surface carbon.
According to the mechanism achieved in this article, the hcp-Fe7C3 (211) shows high conversion of syngas, which is the advantage of the Fischer–Tropsch synthesis. However, the major products in the hcp-Fe7C3 (211) would be the long-chain products or the alkane products, which is the disadvantage of the Fischer–Tropsch synthesis, especially when the target products are the light olefins. As a result, promoting or suppressing the formation of the hcp-Fe7C3 phase is dependent on the purpose of the iron catalyst.
Conclusions
The Fischer–Tropsch mechanism along with the role of surface carbon and vacancies have been studied on the hcp-Fe7C3 (211). The major conclusion is shown below:First, the C1–C2 coupling pathway was presented as a possible C–C coupling pathway. In the C1–C2 coupling pathway, it was found that the HC1 + C2 pathway is the preferred C1–C2 coupling pathway with the effective energy barrier of 0.97 eV, which is much lower than that of the other possible C–C coupling pathway found before. Hence, the HC1 + C2 pathway is thought to be the major C–C coupling pathway and the HC1C2 species are the major C2 species from the C–C coupling pathway on the hcp-Fe7C3 (211).
Second, the stepwise hydrogenation pathway was discussed. Ethylene and ethane are the two major possible C2 products. Since the adsorption energy of ethylene (1.67 eV) is higher than the intrinsic energy barrier of the ethylene hydrogenation reaction (0.47 eV), the desorption process of the ethylene hardly takes place. As a result, the ethane formation pathway is the preferred stepwise hydrogenation pathway on hcp-Fe7C3 (211).
Third, the surface recovery pathway was discussed to allow the Fischer–Tropsch mechanism to make sense. The direct dissociation reaction of adsorption CO on the Cv1 site and Cv2 site is thought to be the preferred carbon vacancy recovery pathway with the effective energy barriers of 1.37 eV and 1.18 eV, respectively. The dissociated oxygen from the carbon vacancy recovery pathway would be removed from the surface in the form of CO2 with the effective energy barrier of 1.50 eV. Since the effective energy barrier of the surface recovery pathway is lower than that of the stepwise hydrogenation pathway of C2 species, the hcp-Fe7C3 (211) would likely recover from the defect-hcp-Fe7C3 (211).
Fourth, the full map of the Fischer–Tropsch mechanism on the hcp-Fe7C3 (211) was presented. In the achieved Fischer–Tropsch mechanism, the stepwise hydrogenation pathway is the rate-determining step for the high effective energy barrier (2.41 eV), which would also cause the increase in the carbon chain length. Moreover, due to the adsorption energy of ethylene, it could be inferred that the alkanes would be the major hydrocarbon products on the hcp-Fe7C3 (211).
Fifth, the roles of the surface carbon and vacancies were concluded according to the Fischer–Tropsch mechanism. It was found that the carbon vacancy sites were the CO activation pathway sites and the surface carbon sites were the C–C coupling pathway sites. The surface carbon not only acted as the chain initiation site but also acted as the chain growth site on the hcp-Fe7C3 (211). From another point of view, the circulation of the surface carbon indicated that the defect-hcp-Fe7C3 (211) was the high active facet of the Fischer–Tropsch synthesis in which the carbon vacancy was the active site.
Finally, we hope that all these findings from DFT calculations could provide a detailed and comprehensive understanding of the Fischer–Tropsch mechanism on the hcp-Fe7C3 phase and the role played by surface carbon in the Fischer–Tropsch synthesis. We hope that other researchers can utilize the information produced in this article to decide whether to promote, suppress, or modify the hcp-Fe7C3 phase in the iron catalysts. Also, we hope that the changes in the surface structure would be taken into account when researching the Fischer–Tropsch mechanism on the iron carbide phase through the theoretical method.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the College of Biological, Chemical Sciences and Engineering of Jiaxing University and the R&D Center for Petrochemical Technology of Tianjin University for providing high performance computing service.References
- M. E. Dry, Appl. Catal., A, 2004, 276, 1–3 CrossRef CAS.
- M. Stcker, Angew. Chem., Int. Ed., 2008, 47, 9200–9211 CrossRef PubMed.
- M. E. Dry, Catal. Today, 2002, 71, 227–241 CrossRef CAS.
- H. Schulz, Appl. Catal., A, 1999, 186, 3–12 CrossRef CAS.
- J. Bao, G. Yang, Y. Yoneyama and N. Tsubaki, ACS Catal., 2019, 9, 3026–3053 CrossRef CAS.
- H. M. T. Galvis and K. P. de Jong, ACS Catal., 2013, 3, 2130–2149 CrossRef.
- H. M. T. Galvis, A. C. J. Koeken, J. H. Bitter, T. Davidian, M. Ruitenbeek, A. I. Dugulan and K. P. de Jong, J. Catal., 2013, 303, 22–30 CrossRef.
- G. B. Yu, B. Sun, Y. Pei, S. H. Xie, S. R. Yan, M. H. Qiao, K. N. Fan, X. X. Zhang and B. N. Zong, J. Am. Chem. Soc., 2010, 132, 935–937 CrossRef CAS PubMed.
- B. Gu, V. V. Ordomsky, M. Bahri, O. Ersen, P. A. Chemayskii, D. Filimonov and A. Y. Khodakov, Appl. Catal., B, 2018, 234, 153–166 CrossRef CAS.
- V. V. Ordomsky, Y. Luo, B. Gu, A. Carvalho, P. A. Chernavskii, K. Cheng and A. Y. Khodakov, ACS Catal., 2017, 7, 6445–6452 CrossRef CAS.
- Z. P. Tian, C. G. Wang, J. Yue, X. H. Zhang and L. L. Ma, Catal. Sci. Technol., 2019, 9, 2728–2741 RSC.
- P. C. Psarras, J. Wilcox and D. W. Ball, Phys. Chem. Chem. Phys., 2017, 19, 5495–5503 RSC.
- Y. R. He, P. Zhao, J. J. Liu, W. P. Guo, Y. Yang, Y. W. Li, C. F. Huo and X. D. Wen, Phys. Chem. Chem. Phys., 2018, 20, 25246–25255 RSC.
- E. de Smit, F. M. F. de Groot, R. Blume, M. Havecker, A. Knop-Gericke and B. M. Weckhuysen, Phys. Chem. Chem. Phys., 2010, 12, 667–680 RSC.
- L. Oar-Arteta, M. J. Valero-Romero, T. Wezendonk, F. Kapteijn and J. Gascon, Catal. Sci. Technol., 2018, 8, 210–220 RSC.
- F. Jiang, B. Liu, W. P. Li, M. Zhang, Z. J. Li and X. H. Liu, Catal. Sci. Technol., 2017, 7, 4609–4621 RSC.
- J. Mulpuri, Ind. Eng. Chem. Res., 1990, 29, 1735–1753 CrossRef.
- T. A. Wezendonk, X. H. Sun, A. I. Dugulan, A. J. F. van Hoof, E. J. M. Hensen, F. Kapteijn and J. Gascon, J. Catal., 2018, 362, 106–117 CrossRef CAS.
- S. Janbroers, J. N. Louwen, H. W. Zandbergen and P. J. Kooyman, J. Catal., 2009, 268, 235–242 CrossRef CAS.
- O. Zhuo, L. J. Yang, F. J. Gao, B. L. Xu, Q. Wu, Y. N. Fan, Y. Zhang, Y. F. Jiang, R. S. Huang, X. Z. Wang and Z. Hu, Chem. Sci., 2019, 10, 6083–6090 RSC.
- L. W. Niu, X. W. Liu, J. J. Liu, X. Liu, X. D. Wen, Y. Yang, J. Xu and Y. W. Li, J. Catal., 2019, 371, 333–345 CrossRef CAS.
- Y. J. Li, Z. S. Li, A. Ahsen, L. Lammich, G. J. A. Mannie, J. W. H. Niemantsverdriet and J. V. Lauritsen, ACS Catal., 2019, 9, 1264–1273 CrossRef CAS.
- J. Zhang, M. Abbas and J. G. Chen, Catal. Sci. Technol., 2017, 7, 3626–3636 RSC.
- C. S. Kuivila, P. C. Stair and J. B. Butt, J. Catal., 1989, 118, 299–311 CrossRef CAS.
- C. S. Huang, L. Xu and B. H. Davis, Fuel Sci. Technol. Int., 1993, 11, 639–664 CrossRef CAS.
- R. Christoffersen and P. R. Buseck, Science, 1983, 222, 1327–1329 CrossRef CAS PubMed.
- C. Yang, H. B. Zhao, Y. L. Hou and D. Ma, J. Am. Chem. Soc., 2012, 134, 15814–15821 CrossRef CAS PubMed.
- E. de Smit, A. M. Beale, S. Nikitenko and B. M. Weckhuysen, J. Catal., 2009, 262, 244–256 CrossRef CAS.
- T. Herranz, S. Rojas, F. J. Perez-Alonso, M. Ojeda, P. Terreros and J. L. G. Fierro, J. Catal., 2006, 243, 199–211 CrossRef CAS.
- J. D. Louw, J. P. Vandenberg, L. C. Ferreira and J. J. Pienaar, J. Am. Chem. Soc., 1957, 79, 5899–5902 CrossRef CAS.
- A. K. Datye, L. Mansker and Y. M. Jin, Stud. Surf. Sci. Catal., 2000, 130, 1139–1144 CrossRef.
- B. Williams, D. Clifford, A. A. El-Gendy and E. E. Carpenter, J. Appl. Phys., 2016, 120, 6 CrossRef.
- Q. Chang, C. H. Zhang, C. W. Liu, Y. X. Wei, A. V. Cheruvathur, A. I. Dugulan, J. W. Niemantsverdriet, X. W. Liu, Y. R. He, M. Qing, L. R. Zheng, Y. F. Yun, Y. Yang and Y. W. Li, ACS Catal., 2018, 8, 3304–3316 CrossRef CAS.
- T. H. Pham, X. Z. Duan, G. Qian, X. G. Zhou and D. Chen, J. Phys. Chem. C, 2014, 118, 10170–10176 CrossRef CAS.
- T. H. Pham, Y. Y. Qi, J. Yang, X. Z. Duan, G. Qian, X. G. Zhou, D. Chen and W. K. Yuan, ACS Catal., 2015, 5, 2203–2208 CrossRef CAS.
- M. H. Zhang, J. Ren and Y. Z. Yu, ACS Catal., 2020, 10, 689–701 CrossRef CAS.
- Y. R. He, P. Zhao, J. Q. Yin, W. P. Guo, Y. Yang, Y. W. Li, C. F. Huo and X. D. Wen, J. Phys. Chem. C, 2018, 122, 20907–20917 CrossRef CAS.
- B. X. Chen, D. Wang, X. Z. Duan, W. Liu, Y. F. Li, G. Qian, W. K. Yuan, A. Holmen, X. G. Zhou and D. Chen, ACS Catal., 2018, 8, 2709–2714 CrossRef CAS.
- L. J. Deng, C. F. Huo, X. W. Liu, X. H. Zhao, Y. W. Li, J. G. Wang and H. J. Jiao, J. Phys. Chem. C, 2010, 114, 21585–21592 CrossRef CAS.
- T. Li, X. D. Wen, Y. Yang, Y. W. Li and H. J. Jiao, ACS Catal., 2020, 10, 877–890 CrossRef CAS.
- Y. F. Wang, Y. Li, S. Y. Huang, J. Wang, H. Y. Wang, J. Lv and X. B. Ma, Chem. Phys. Lett., 2017, 682, 115–121 CrossRef CAS.
- C. F. Huo, Y. W. Li, J. G. Wang and H. J. Jiao, J. Am. Chem. Soc., 2009, 131, 14713–14721 CrossRef CAS PubMed.
- M. Zhang, J. Ren and Y. Yu, Mol. Catal., 2021, 505, 111506 CrossRef CAS.
- V. V. Ordomsky, B. Legras, K. Cheng, S. Paul and A. Y. Khodakov, Catal. Sci. Technol., 2015, 5, 1433–1437 RSC.
- F. H. Herbstein and J. A. Snyman, Inorg. Chem., 1964, 3, 894–896 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- F. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Methfessel, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 19 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 10 CrossRef PubMed.
- D. Sheppard, P. H. Xiao, W. Chemelewski, D. D. Johnson and G. Henkelman, J. Chem. Phys., 2012, 136, 8 Search PubMed.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2010, 114, 1085–1093 CrossRef CAS.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2009, 113, 8858–8863 CrossRef CAS.
- J. Cheng, X. Q. Gong, P. Hu, C. M. Lok, P. Ellis and S. French, J. Catal., 2008, 254, 285–295 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra06396k |
| This journal is © The Royal Society of Chemistry 2021 |