Open Access Article
Open Access ArticleRapid and accurate estimation of protein–ligand relative binding affinities using site-identification by ligand competitive saturation†
Himanshu
Goel‡
 a,
Anthony
Hazel‡
a,
Anthony
Hazel‡
 a,
Vincent D.
Ustach
a,
Vincent D.
Ustach
 a,
Sunhwan
Jo
a,
Sunhwan
Jo
 b,
Wenbo
Yu
a and
Alexander D.
MacKerell
Jr
b,
Wenbo
Yu
a and
Alexander D.
MacKerell
Jr
 *ab
*ab
aComputer Aided Drug Design Center, Department of Pharmaceutical Sciences, University of Maryland School of Pharmacy, 20, Penn St., Baltimore, Maryland 21201, USA. E-mail: alex@outerbanks.umaryland.edu; Fax: +1-410-706-5017; Tel: +1-410-706-7442
bSilcsBio LLC, 8 Market Place, Suite 300, Baltimore, Maryland 21201, USA
First published on 25th May 2021
Abstract
Predicting relative protein–ligand binding affinities is a central pillar of lead optimization efforts in structure-based drug design. The site identification by ligand competitive saturation (SILCS) methodology is based on functional group affinity patterns in the form of free energy maps that may be used to compute protein–ligand binding poses and affinities. Presented are results obtained from the SILCS methodology for a set of eight target proteins as reported originally in Wang et al. (J. Am. Chem. Soc., 2015, 137, 2695–2703) using free energy perturbation (FEP) methods in conjunction with enhanced sampling and cycle closure corrections. These eight targets have been subsequently studied by many other authors to compare the efficacy of their method while comparing with the outcomes of Wang et al. In this work, we present results for a total of 407 ligands on the eight targets and include specific analysis on the subset of 199 ligands considered previously. Using the SILCS methodology we can achieve an average accuracy of up to 77% and 74% when considering the eight targets with their 199 and 407 ligands, respectively, for rank-ordering ligand affinities as calculated by the percent correct metric. This accuracy increases to 82% and 80%, respectively, when the SILCS atomic free energy contributions are optimized using a Bayesian Markov-chain Monte Carlo approach. We also report other metrics including Pearson's correlation coefficient, Pearlman's predictive index, mean unsigned error, and root mean square error for both sets of ligands. The results obtained for the 199 ligands are compared with the outcomes of Wang et al. and other published works. Overall, the SILCS methodology yields similar or better-quality predictions without a priori need for known ligand orientations in terms of the different metrics when compared to current FEP approaches with significant computational savings while additionally offering quantitative estimates of individual atomic contributions to binding free energies. These results further validate the SILCS methodology as an accurate, computationally efficient tool to support lead optimization and drug discovery.
1. Introduction
Computer-aided drug design (CADD) methods are used to predict various properties of drug candidates as well as to understand their structure, dynamics, and interactions with the protein and other macromolecular targets. CADD procedures have identified biologically active molecules among large collections of chemical databases and are widely used to estimate protein–ligand binding affinities to facilitate the drug development process.1–4 A large number of the computational free energy techniques, namely molecular mechanics Poisson–Boltzmann or generalized Born surface area (MM/PBSA and MM/GBSA),5–8 free energy perturbation (FEP),9 thermodynamic integration (TI),10 weighted histogram analysis method (WHAM),11,12 Bennett acceptance ratio (BAR),13 and multistate BAR (MBAR)14 are frequently used to compute absolute or relative binding free energies. Additional details about these schemes can be found in several reviews.15–27 In recent times, the FEP-based methodologies are gaining tremendous momentum with the development of mature force fields, enhanced sampling algorithms, and usage of graphics processing units (GPU) leading to provide best practices for FEP-based methods, including the lambda dynamics and envelope sampling methods that allow for multiple free energy difference to be calculated simultaneously.28–31 Most of these methods rely on sampling the system of solute and solvent configurations by molecular mechanics approaches such as Monte Carlo (MC) or molecular dynamics (MD). The accuracies of such calculations rely on adequately sampling conformational space and computing accurate energies and forces. Typically, atomistic empirical force fields for computing the intra- and inter-molecular forces are used versus quantum chemistry methods due to the high computational cost of the latter.32,33 The common force fields employed for this purpose are OPLS,34,35 AMBER/GAFF,36,37 CHARMM,38–40 and GROMOS,41,42 which can all effectively describe the key biological interactions to within a reasonable accuracy.An alternative to the above-mentioned CADD approaches is the site identification by ligand competitive saturation (SILCS) technology. The SILCS methodology is a co-solvent sampling method that is used to compute functional group binding affinity patterns through a combined grand canonical Monte Carlo (GCMC)-molecular dynamics (MD) sampling of multiple co-solvent or solute molecules representing different functional groups against a particular target protein in an aqueous solution.43 Functional group probability distributions are obtained from the simulations and converted to free energy maps (called FragMaps) that can be used to facilitate the discovery of new molecules or modifications of ligands to improve their binding affinity. The FragMaps may also be used in fragment based drug design, protein–protein interactions, pharmacophore screening, and evaluation of excipients in biologics formulation.44–53 Visualization of SILCS FragMaps also reveals the favorable and unfavorable sites for functional group interactions throughout a protein, and recently the method has been used to investigate the impact of explicit treatment of electronic polarization in a force field on functional group–protein interactions.54
In the context of lead compound optimization in a medicinal chemistry campaign it is important that a CADD method be able to predict relative binding affinities on an adequate number of compounds to lead the drug design process. The accuracy for relative binding free energy prediction should be within ∼1 kcal mol−1 to effectively guide ligand optimization.25–27 Towards achieving this level of accuracy, FEP and related methods have shown promise as exemplified by Wang et al.55 as well as subsequent studies. In the Wang et al.55 study the relative affinities of a total of 199 ligands against 8 targets were computed, with an overall mean unsigned error of 0.899 kcal mol−1 for the relative free energies, ΔΔG, reported. While FEP methods have subsequently been used to facilitate ligand design they are still limited with respect to throughput. For example, in a recent study, TI calculations for a single perturbation required a total of 144 ns of MD considering both the protein and solution environments.56 In addition, the cycle closure approach57 when applied to improve the accuracy of the estimated ΔΔG values requires additional calculations. Essentially, for each perturbation the ensemble of conformations associated with the initial and final states of the system (i.e. the parent and modified ligands) must be explicitly computed. The SILCS methodology overcomes this limitation by precomputing an ensemble of functional group conformations that are converted to free energy FragMaps that may then be reused for each ligand modification in a highly computationally efficient fashion. For example, the initial SILCS simulations encompass 20 individual 100 ns GCMC/MD simulations (10 for standard SILCS and 10 for halogen-based SILCS (SILCS-X)) that require approximately 28 hours for a system of ∼50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms to complete each of the 20 individual runs on NVIDA 2080TI GPUs on 8 core Ryzen CPUs (i.e. 560 total GPU hours for 2000 ns). This is equivalent to computing ∼15 ligand perturbations (at 144 ns per perturbation, or 40 GPU hours per perturbation). While the upfront cost of generating the FragMaps are significant, once they are calculated, the user only ever needs to run computationally inexpensive SILCS-MC docking calculations for each ligand using the generated FragMaps, with each ligand docking calculation taking approximately 8.5 minutes on a single AMD EPYC 7702P processor core. Beyond the initial cost of generating the FragMaps, the speed advantage of SILCS is directly proportional to the number of ligands, while for alchemical methods with cycle closure corrections, the speed is proportional to the number of perturbations, for which there may be multiple per ligand. Therefore, beyond ∼10–15 ligands per target, the speed of SILCS substantially outpaces that of alchemical methods with the differences becoming more significant for much larger ligand sets. The ultimate benefit of SILCS is the ability to calculate hundreds to thousands of ligand binding affinities in a single day, whereas this level of throughput is currently inaccessible to alchemical free energy methods. In addition, beyond the ΔΔG value the SILCS method yields the free energy contribution of each classified atom in the ligand to the binding affinity, information that may be used to interpret atomic contributions to changes in affinity that can be used to facilitate further ligand design, as described below.
000 atoms to complete each of the 20 individual runs on NVIDA 2080TI GPUs on 8 core Ryzen CPUs (i.e. 560 total GPU hours for 2000 ns). This is equivalent to computing ∼15 ligand perturbations (at 144 ns per perturbation, or 40 GPU hours per perturbation). While the upfront cost of generating the FragMaps are significant, once they are calculated, the user only ever needs to run computationally inexpensive SILCS-MC docking calculations for each ligand using the generated FragMaps, with each ligand docking calculation taking approximately 8.5 minutes on a single AMD EPYC 7702P processor core. Beyond the initial cost of generating the FragMaps, the speed advantage of SILCS is directly proportional to the number of ligands, while for alchemical methods with cycle closure corrections, the speed is proportional to the number of perturbations, for which there may be multiple per ligand. Therefore, beyond ∼10–15 ligands per target, the speed of SILCS substantially outpaces that of alchemical methods with the differences becoming more significant for much larger ligand sets. The ultimate benefit of SILCS is the ability to calculate hundreds to thousands of ligand binding affinities in a single day, whereas this level of throughput is currently inaccessible to alchemical free energy methods. In addition, beyond the ΔΔG value the SILCS method yields the free energy contribution of each classified atom in the ligand to the binding affinity, information that may be used to interpret atomic contributions to changes in affinity that can be used to facilitate further ligand design, as described below.
In the present manuscript, we directly compare the SILCS methodology with published results using FEP or TI methods for predicting relative ligand binding affinities. Specifically, the SILCS approach is validated against the set of eight proteins and 199 ligands considered in the work of Wang et al.55 In addition, we extend the SILCS analysis to a total of 407 ligands against the eight targets covering nearly the full set of experimentally studied ligands, of which 208 were omitted from the Wang et al.55 and subsequent studies. In this study, we did omit 14 CDK2 ligands (4, 5, 6, 11, 12, 13, 14, 16, 19, 23, 24, 27, 40, and 45) for which an experimental IC50 could not be determined. Images of the 407 ligands are included in ESI file si_ligand_images_407.pdf.† Results show the SILCS methodology to be competitive or superior to the FEP/TI methods despite requiring a fraction of the computational costs and yielding an additional level of granular information that can facilitate ligand design.
2. Computational methodology
2.1. SILCS simulations
All eight proteins (BACE,58 P38,59 CDK2,60 MCL1,61 PTP1B,62 TYK2,63,64 JNK1,65 and Thrombin66) considered by the work of Wang et al.55 were employed in this study. The ligands for all protein targets were classified into two different categories. The first category is the set of 199 ligands used by Wang et al.55 and the second is the full set of 407 ligands studied experimentally. This allows testing of the accuracy of the SILCS approach using a complete set of ligands without omitting ligands as done by Wang et al.55 without any specific justification. Some of the omitted ligands, however, do suffer from poor or incomplete experimental data, so some caution is warranted when attempting to reproduce experimental binding affinities using such data. Nevertheless, we use all the available data to perform the assessment of the SILCS technology, with only the 14 CDK2 ligands mentioned above excluded from the full set of experimentally reported ligands. The ligands were prepared by manually aligning them with crystal structure ligand orientations with the maximum common substructure in MOE (Chemical Computing Group). The experimental data of the binding affinities for all ligands were taken from their original references. It is important to mention that we have found small differences in the experimental binding affinities between our computed values and those reported by Wang et al.55 Detailed information for our computed binding affinity values from the IC50 or Ki data is provided in the ESI and files si_199.xlsx and si_407.xlsx.†A simplified flow diagram for the entire SILCS workflow yielding different qualitative and quantitative analysis is depicted in Fig. S1.† Systems for the SILCS simulations involve a protein, eight solutes, and water. All the solutes are randomly distributed in and around the protein surface at the same time followed by the addition of water molecules. Crystal waters, ligands, and cofactors were removed from each protein before system setup. The solutes include benzene, propane, methanol, formamide, dimethylether, methylammonium, imidazole and acetate in the standard version of the SILCS methodology, and fluoroethane, trifluoroethane, chloroethane, fluorobenzene, chlorobenzene, bromobenzene, dimethylether, and methanol in the halogen, “SILCS-X” version. The 2D molecular structures for all the solutes and their corresponding FragMap atom types are shown in Fig. S2.† For enhanced sampling, ten independent simulations are performed on each system. The χ1 dihedral of side chains of residues with a solvent accessible surface area (SASA)67 greater than 0.05 Å2 from GROningen MAchine for Chemical Simulation (GROMACS)68 software were set to 0 through 360° in 36° increments for the 10 simulations. The proteins were solvated by water at 55 M along with the solutes mentioned above, each at a concentration of 0.25 M, within a box size that is extended 15 Å beyond the proteins in all three dimensions. These processes were performed using the SilcsBio Software Suite (SilcsBio LLC) integrated with various GROMACS utilities. The entire system was subjected to energy minimization by using the steepest descent algorithm69 for 5000 steps followed by equilibration in the NPT ensemble for 100 ps using the velocity rescaling thermostat and Berendsen barostat.70
The SILCS simulations comprise a hybrid oscillating-μex grand-canonical Monte Carlo and molecular dynamics (GCMC-MD) approach aimed at enhancing the overall sampling of the solute or water spatial distributions including within deep or totally occluded pockets. The GCMC moves include translations, rigid-body and torsional rotations, and insertion or deletion of the solutes and water. The insertions and deletions involve exchanges between a gas phase reservoir and an active sub volume of the entire system through the excess chemical potential, which is adjusted every three GCMC-MD cycles in response to the solute concentration within the sub volume.71 The active sub volume is the volume completely encompassing the protein, with a 15 Å buffer region between the boundaries of the active sub volume and the edges of the simulation box. The GCMC moves are accepted or rejected based on the probabilities of the Metropolis72 criteria. Additional details of the GCMC simulation can be accessed in our previous work.71
The inclusion of MD allows for additional conformational sampling of the solutes and water and for conformational sampling of the protein. The MD simulations were performed in the NPT ensemble at a system temperature and pressure of 298 K and 1 atm, respectively. This temperature and pressure were controlled by the Nosé–Hoover thermostat73,74 and Parrinello–Rahman barostat.75 The timestep for the MD runs was 2 fs with periodic boundary conditions. The simulation configurations were saved every 10 ps during the entire production run. The LINCS algorithm76 was used to constrain all bonds with hydrogen atoms including water. The backbone alpha carbon atoms were restrained with a force constant of 0.12 kcal mol−1 Å−2. The non-bonded interactions were computed with a cutoff of 8 Å using the Verlet cutoff scheme. A switching function was applied for Lennard-Jones (LJ) interactions from 5 to 8 Å along with the long-range isotropic dispersion correction to the energy and pressure for LJ interaction beyond 8 Å. The long range electrostatic contribution is handled by the particle mesh Ewald (PME)77 method with a real space cutoff of 8 Å, maximum grid spacing 1.2 Å, and fourth order B-spline interpolation.
The GCMC calculations were performed using our in-house code incorporated into the SilcsBio Software Suite. For MD simulations, GROMACS version 2019.4 was used for the energy minimization, equilibration and production runs. All the GCMC-MD simulations were performed with the additive CHARMM36m78 force field. The force field parameters for the solutes and ligands were derived from the CHARMM general force field (CGenFF)79–82 program. The additive simulation also uses the CHARMM TIP3P model for water.83,84 The SILCS GCMC-MD simulations were performed in a sequential manner for a total of 126 cycles, composed of 26 GCMC-only equilibration cycles followed by 100 production cycles. Each cycle consists 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GCMC steps, with production cycles followed by a 5000-step steepest descent minimization, a 100 ps equilibration MD simulation, and a 1 ns production MD simulation. For the 26 equilibration cycles, first, all water and solute molecules were deleted in the sub-volume region, defined as the active region, and the sub-volume is then refilled using only the GCMC procedure. The initial cycle refills the (now-vacuum) sub-volume with just solute molecules to the target concentration of 0.25 M for each solute. The successive 25 cycles refilled the water molecules in the sub-volume region to the target concentration of 55 M. The data for the remaining 100 cycles were collected as the production run. The production MD simulation trajectories are used for generating FragMaps for the selected atoms by binning them into 1 Å × 1 Å × 1 Å cubic volume elements (voxels). Selected solute atom types were combined into the generic FragMaps by merging voxel occupancies of the different solutes and converting the normalized distributions into grid free energies (GFE).49 The convergence of the FragMaps is verified by computing the overlap coefficient between the first five (1 to 5) and the last five (6 to 10) independent SILCS simulations. For each FragMap, the overlap coefficient was calculated with a range between 0 to 1. The higher values of these coefficients ensure the satisfactory convergence of the FragMaps for each system. Additional details regarding the calculation of FragMaps, GFE, and overlap coefficient can be found in these ref. 45, 49 and 54.
000 GCMC steps, with production cycles followed by a 5000-step steepest descent minimization, a 100 ps equilibration MD simulation, and a 1 ns production MD simulation. For the 26 equilibration cycles, first, all water and solute molecules were deleted in the sub-volume region, defined as the active region, and the sub-volume is then refilled using only the GCMC procedure. The initial cycle refills the (now-vacuum) sub-volume with just solute molecules to the target concentration of 0.25 M for each solute. The successive 25 cycles refilled the water molecules in the sub-volume region to the target concentration of 55 M. The data for the remaining 100 cycles were collected as the production run. The production MD simulation trajectories are used for generating FragMaps for the selected atoms by binning them into 1 Å × 1 Å × 1 Å cubic volume elements (voxels). Selected solute atom types were combined into the generic FragMaps by merging voxel occupancies of the different solutes and converting the normalized distributions into grid free energies (GFE).49 The convergence of the FragMaps is verified by computing the overlap coefficient between the first five (1 to 5) and the last five (6 to 10) independent SILCS simulations. For each FragMap, the overlap coefficient was calculated with a range between 0 to 1. The higher values of these coefficients ensure the satisfactory convergence of the FragMaps for each system. Additional details regarding the calculation of FragMaps, GFE, and overlap coefficient can be found in these ref. 45, 49 and 54.
2.2. LGFE, SILCS-MC sampling and Bayesian ML FragMap optimization
The ligand grid free energy (LGFE) is defined as the summation of the atomic GFE scores based on the classification of each atom in a ligand and its overlap with the corresponding FragMap. There are four main atom classification schemes (ACS): Generic Apolar Scale (GAS21), Generic Apolar Scale with Halogens (GAX21), Specific Standard (SS21), and Specific Halogen (SX21). Details of each ACS can be found in the ESI.† In short, for the Generic ACS, several “specific” FragMaps are grouped together to produce “generic” FragMaps. For example, formamide nitrogen (FORN) and imidazole donor nitrogen (IMIH) FragMaps are combined into a generic hydrogen bond donor (GEND) FragMap, while formamide oxygen (FORO), dimethylether oxygen (DMEO), and imidazole acceptor nitrogen (IMIN) FragMaps are combined into a generic hydrogen bond acceptor (GENA) FragMap. Generic ACS also include generic non-polar (GENN), generic heterocycle carbon (GEHC), and methanol oxygen (MEOO) FragMaps. In the Specific ACS, all specific FragMaps are used, supplemented by the generic FragMaps. Additionally, both the Generic and Specific ACS can be supplemented with the halogen FragMaps obtained from SILCS-X simulations and the corresponding ACS as described in the ESI.†LGFE values are not formally correct free energies of binding but are considered to be an approximate representation of the binding free energies. For example, the LGFE does not account for contributions related to the configurational entropy associated with the connecting of atoms to make the entire ligand. Still, the LGFE score can be correlated directly with the experimental binding affinity as shown in our previous studies. Importantly, given the pre-computed nature of the FragMaps, calculation of the LGFE is instantaneous. This allows the LGFE score, along with the ligand intramolecular energy, to be used as the Metropolis criteria72 in Monte Carlo sampling of the ligand position and conformation, termed SILCS-MC. The moves employed during SILCS-MC are translations, rigid-body rotations, and rotations of dihedrals about rotatable bonds. The main objective is to sample the ligand-binding conformation in the field of the FragMaps along with the SILCS exclusion map. The exclusion map is the forbidden region of the protein in which no water or solute non-hydrogens sample during the SILCS simulations. Ligand non-hydrogen atoms overlapping with the exclusion maps are assigned a GFE energy of 1000 kcal mol−1. Thus, the energy term used in the Metropolis criteria contains intramolecular van der Waals (vdW), electrostatic, and dihedral terms based on CGenFF45 along with the LGFE and exclusion map contributions. A distance dependent dielectric (=4|r|) approach was employed to calculate the intramolecular electrostatics.85–87 In this work, we employ an exhaustive docking protocol for the SILCS-MC simulations where the ligand is randomly positioned within a radius defined by the user and given a random orientation. The center for each ligand placement sphere used in this work are listed in Table S2.† The benefit of this procedure is to explore a larger conformational space within the binding pocket. The SILCS-MC procedure begins with energy minimization of the ligand structure for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps to obtain the optimized configuration, followed by 10
000 steps to obtain the optimized configuration, followed by 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 normal MC steps and 40
000 normal MC steps and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 annealing steps. The temperature was set to 300 K for the normal MC and gradually lowered to 0 K for annealing steps. The final ligand binding conformations are selected based on the most favorable LGFE scores which alone is then used for ligand scoring. We perform five independent simulations for each ligand of a minimum of 50 MC runs each. After 50 MC runs the simulation was stopped if the three most favorable LGFE scores were within 0.5 kcal mol−1, with the simulation continued to a maximum of 250 MC runs with the simulation stopped once the three most favorable LGFE within 0.5 kcal mol−1 criteria was met or the most favorable LGFE score used from the 250 MC runs. This procedure was employed to enhance the overall sampling and find the minimum free energy binding conformation. The most favorable LGFE score and associated ligand conformation was then selected from the five independent simulations.
000 annealing steps. The temperature was set to 300 K for the normal MC and gradually lowered to 0 K for annealing steps. The final ligand binding conformations are selected based on the most favorable LGFE scores which alone is then used for ligand scoring. We perform five independent simulations for each ligand of a minimum of 50 MC runs each. After 50 MC runs the simulation was stopped if the three most favorable LGFE scores were within 0.5 kcal mol−1, with the simulation continued to a maximum of 250 MC runs with the simulation stopped once the three most favorable LGFE within 0.5 kcal mol−1 criteria was met or the most favorable LGFE score used from the 250 MC runs. This procedure was employed to enhance the overall sampling and find the minimum free energy binding conformation. The most favorable LGFE score and associated ligand conformation was then selected from the five independent simulations.
Optimization of the FragMaps was carried out by a Bayesian Markov-chain Monte Carlo simulated annealing (MCSA) approach. The purpose of the method is to train the weighting factors of each FragMap type based on experimental ligand binding affinities, which directly impacts the GFE contribution for each classified atom in the ligands and the accompanying LGFE score. It uses the Metropolis criterion where E is the difference between the new and old error function of percent correct (PC) metric. Percent correct is the number of true positives and true negatives and does not account for the magnitude of ΔΔG. It is calculated by assigning each ligand in the set as the reference ligand and then obtaining the average PC value over all the ligands. FragMap scaling factors were restrained using a flat-bottomed potential with a force constant of 500 and lower and upper limits of 0.05 and 2.00, respectively. An in-house FORTRAN code was used to achieve this objective. The Bayesian ML FragMap optimization approach was carried out for the ligands specific for each protein in the 199 and 407 ligand sets. The training of the ML model uses k-fold cross validation (k = 5) for each set of ligands which involves 80% of the ligands in a particular sets. The collection for the 80% of ligands in the different training sets can be accomplished either by random selection or identifying diverse set of ligands. For this work the ligands were categorized into different “scaffolds” according to their original experimental studies. The ligands in each scaffold were then evenly distributed among the k sets to ensure as best as possible that each training set has a representative sample of all ligand types. Scaffold classifications and ML training sets for each set of ligands can be found in the ESI file si_ligand_scaffolds.xlsx.† The training was performed using the exhaustive SILCS-MC protocol with a 5 Å radii. After training, the optimized weighting factors from each training set were used in rerunning the SILCS-MC for the entire ligand set for each protein. The final reweighting values were selected from the set that produces the best PC score from the rerun SILCS-MC simulations. Additional details about the original implementation of the LGFE, SILCS-MC sampling, and Bayesian ML can be accessed from the work of Ustach et al.49 In the previous study, the metrics RMSE and Pearson's correlation were used in addition to PC as the target data for the ML optimization.
3. Results and discussion
Eight proteins were subjected to SILCS simulations using the 2021 ACS for the standard and halogen solute sets. Analysis of overlap coefficients (OC) of the FragMaps from simulation sets 1–5 and 6–10 for each protein target showed convergence of the simulations as shown in Tables S3 and S4 of the ESI.† Most of the solutes display OC values greater than 0.8, which signifies high convergence between both sets of FragMaps. Final FragMaps used for ligand docking and analysis were computed from all ten simulations. The eight proteins and their respective ligands were subjected to SILCS-MC calculations applying the different ACS that define the functional group contributions of the ligands interacting with the protein target residues. In addition, the radii defining the extent of the binding sites were varied from 1 to 10 Å. Comparison of the SILCS-MC relative affinities with experimental data were performed based on the metrics of predictive index (PI), percent correct (PC), Pearson's correlation coefficient (R), root mean square error (RMSE), and mean unsigned error (MUE). Details of these metrics are presented in the ESI.†Computed binding affinities in the present study were calculated from the relative binding affinities of the ligands following the approach used by Wang et al.55 In that study a single ligand was chosen whose absolute binding affinity was assigned its experimental value, and the relative binding affinities from the cycle closure method were used to calculate the remaining binding affinities. Song et al.56 also applied the cycle closure correction. Since there were multiple ligands for which an experimental binding affinity was available, an average absolute binding affinity was calculated by repeating the above process with each possible ligand assigned its “true” binding affinity. This process is equivalent to globally offsetting the absolute binding affinities, ΔGcomputi = LGFEi + ΔGoffset, where ΔGoffset = 〈ΔGexper〉 − 〈LGFE〉 and 〈·〉 is the average over all ligands for which there is an experimental binding affinity, such that 〈ΔGexper〉 = 〈ΔGcomput〉. This also has the added effect of minimizing the MUE. Song et al.,56 Gapsys et al.,88 and Kuhn et al.89 similarly adjusted their reported binding affinities using the same experimental binding affinities as reported in Wang et al.55 Accordingly, we have applied the same averaging/offsetting to the LGFE values reported in this study (see ESI† for unadjusted LGFE values). In practice this allows for the results for all the proteins to be plotted on the same scale thereby facilitating visualization of the results from all the proteins (e.g.Fig. 1 below). More recently, He et al., using four of the eight protein targets showed that using a single, representative reference ligand for computing alchemical free energy-derived binding affinities, which better mimics lead optimization strategies when only one or very few experimental data are available before go/no-go decisions, can lead to reasonable absolute binding affinities.90 However, in order to provide direct comparison to previous FEP/TI studies, we only consider the correction strategy of Wang et al.55 described above. Lastly, we calculated the experimental binding affinities using the Ki or IC50 values for each ligand from their respective sources. For this study, we have used our calculated experimental binding affinities, not those reported in Wang et al.55 and used by others, for all analysis, including re-analysing results from Wang et al.,55 Song et al.,56 Gapsys et al.,88 and Kuhn et al.89 Although minimal, some results reported here differ from their source material. See ESI for more detail.†
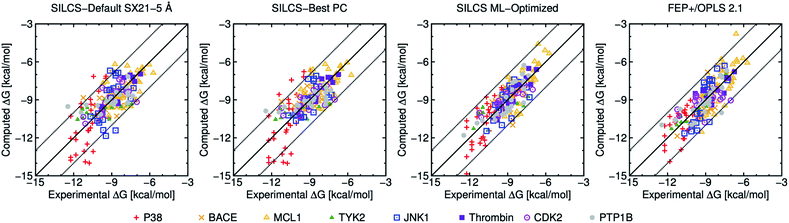 | ||
| Fig. 1 Computed versus experimental ΔG obtained from SILCS and FEP+/OPLS 2.1 with 199 ligands. “SILCS-Best PC” corresponds to results from Table 2, and “SILCS ML-Optimized” corresponds to the results from Table 3. | ||
3.1. Performance of SILCS-MC computed binding affinities for 199 ligands
Table 1 presents the average metrics for all the eight proteins including 199 ligands with different ACS and radii for the exhaustive SILCS-MC protocol. The detailed results for all sets of ACS with different ligand placement radii for all eight protein targets can be accessed in the ESI file si_199.xlsx.† The SX21 ACS with a 5 Å radii provides the highest performance in terms of R, PI, and PC metrics along with nearly the lowest MUE and RMSE values. Other ACS results with a 5 Å radius show similar performance for MUE and RMSE; however, they perform particularly worse in the R and PI metrics. The PC scores, however, range between 0.65 to 0.72 among all models with a 2, 5 or 10 Å radii. As an example, computed versus experimental binding affinities using both raw and corrected LGFE values for all models with a 5 Å radii are plotted in Fig. S4 and S5,† respectively. Another observation is that inclusion of the SILCS-X maps leads to improvements in R, PI and PC in the majority of cases, though small increases in MUE and RMSE occur in most cases. In addition, we performed a comparative study with the earlier 2018 and new 2021 ACS at 5 Å radii (Table S5†). With the exception of the standard specific models, the 2021 models provide superior performance over the 2018 models. The superior performance of SS18 over SS21 is mostly attributable to the surprisingly poor performance of the SS21 model for TYK2. In summary, the substitution of acetaldehyde with dimethylether in the standard set of SILCS solutes provides, except in certain cases, superior predictions of ligand binding affinities.| Protocol (rLP) | ACS | MUE | RMSE | R | PI | PC |
|---|---|---|---|---|---|---|
| a Ex: exhaustive, R: Pearson's correlation coefficient, PI: predictive index, PC: percent correct. | ||||||
| Ex (rLP = 1 Å) | GAS21 | 0.911 | 1.157 | 0.227 | 0.242 | 0.583 |
| Ex (rLP = 1 Å) | GAX21 | 0.943 | 1.193 | 0.266 | 0.260 | 0.587 |
| Ex (rLP = 1 Å) | SS21 | 0.892 | 1.143 | 0.362 | 0.332 | 0.631 |
| Ex (rLP = 1 Å) | SX21 | 0.951 | 1.175 | 0.456 | 0.439 | 0.649 |
| Ex (rLP = 2 Å) | GAS21 | 0.797 | 0.994 | 0.421 | 0.431 | 0.654 |
| Ex (rLP = 2 Å) | GAX21 | 0.824 | 1.034 | 0.504 | 0.517 | 0.684 |
| Ex (rLP = 2 Å) | SS21 | 0.826 | 1.020 | 0.463 | 0.457 | 0.666 |
| Ex (rLP = 2 Å) | SX21 | 0.841 | 1.032 | 0.588 | 0.578 | 0.708 |
| Ex (rLP = 5 Å) | GAS21 | 0.801 | 1.011 | 0.455 | 0.459 | 0.660 |
| Ex (rLP = 5 Å) | GAX21 | 0.828 | 1.037 | 0.533 | 0.530 | 0.683 |
| Ex (rLP = 5 Å) | SS21 | 0.817 | 1.035 | 0.473 | 0.488 | 0.677 |
| Ex (rLP = 5 Å) | SX21 | 0.800 | 1.014 | 0.614 | 0.640 | 0.719 |
| Ex (rLP = 10 Å) | GAS21 | 0.809 | 1.007 | 0.484 | 0.481 | 0.658 |
| Ex (rLP = 10 Å) | GAX21 | 0.803 | 1.019 | 0.552 | 0.563 | 0.698 |
| Ex (rLP = 10 Å) | SS21 | 0.806 | 1.001 | 0.509 | 0.508 | 0.675 |
| Ex (rLP = 10 Å) | SX21 | 0.887 | 1.088 | 0.532 | 0.510 | 0.672 |
As SILCS-MC conformational sampling is a stochastic process, unique solutions are not obtained. Therefore, to evaluate the statistical uncertainty of the reported ΔG values and the associated metric scores, we have included nine independent runs of the 199 ligands using all ACS with a 5 Å radii. Fig. S6† shows the standard deviations of the calculated ΔG values for each ligand. Most of the ligands have a standard deviation below 0.5 kcal mol−1, with CDK2 displaying the highest variability in ΔG. While there are some differences in variability between ACS for a single target, no single model is more or less variable across all eight targets. These results extend to the performance metrics as well. Fig. S7 and S8† detail the standard deviations of the MUE and PC metrics for each protein. MUE standard deviations are generally at or below 0.05 kcal mol−1, with the exception of TYK2 and CDK2, which are above ∼0.05 kcal mol−1 for all models. PC scores follow roughly the same trend as the MUE values, with standard deviations generally below 0.05, with only TYK2 values rising above 0.06 for some models. When considering all eight targets and 199 ligands, standard deviations for MUE and PC are 0.010 kcal mol−1 and 0.011, respectively.
| System | ACS | r LP | MUE | RMSE | R | PI | PC |
|---|---|---|---|---|---|---|---|
| P38 | SX21 | 1 | 1.368 | 1.675 | 0.631 | 0.653 | 0.742 |
| BACE | SS21 | 5 | 0.501 | 0.648 | 0.541 | 0.549 | 0.681 |
| MCL1 | GAX21 | 5 | 0.788 | 1.015 | 0.566 | 0.561 | 0.704 |
| TYK2 | SX21 | 5 | 0.874 | 1.050 | 0.593 | 0.721 | 0.775 |
| JNK1 | SS21 | 2 | 0.726 | 0.892 | 0.645 | 0.720 | 0.769 |
| Thrombin | GAX21 | 2 | 0.290 | 0.363 | 0.918 | 0.931 | 0.873 |
| CDK2 | SX21 | 1 | 0.670 | 0.874 | 0.668 | 0.690 | 0.767 |
| PTP1B | GAS21 | 5 | 0.642 | 0.910 | 0.781 | 0.863 | 0.828 |
| Average | 0.732 | 0.928 | 0.668 | 0.711 | 0.767 |
Customizing the protocols to specific protein targets by maximizing the performance of any one of the aforementioned metrics improves the overall performance of all metrics compared to employing a single, standard protocol for all proteins. Thus, once experimental data becomes available the computationally efficient accessibility of the SILCS-MC method to multiple scoring regimens allows for selection of the best approach for each protein target. Moreover, further improvements may be obtained via machine learning as presented below.
Presented in Table 3 are the best PC-based ML optimization results for the individual protein targets. The metrics from the PC-based ML optimization procedure for each protein target with all the ACS at 5 Å radii are presented in Table S6 and in ESI file, si_199.xlsx,† and the binding affinities are plotted in Fig. S9.† While most of the results presented in Table 3 correspond to the models with the highest PC score, targeting PC in the ML optimization can degrade the average scores of the MUE and RMSE metrics, reducing the chemical accuracy of the results. For example, the SS21* and SX21* models for CDK2 produce the highest PC scores of 0.858 and 0.850, respectively, but yielded very large MUE scores of 2.127 and 2.420 kcal mol−1, where * indicates the ML optimized values. Using either of these models for CDK2 yield an average PC score over the eight protein targets of ∼0.82; a significant improvement over the SILCS-Best PC result of 0.767. However, the average MUE increases from 0.734 to greater than 0.95 kcal mol−1. As can be seen in Fig. S9,† a large number of the CDK2 ligands have an error >2 kcal mol−1 for the SS21* and SX21* models, with few ligands within 2 kcal mol−1 of the experimental binding affinity. Since the PC metric does not account for the size of the relative binding affinities, a substantial “spreading out” of the LGFE values may occur to maximize the ordering of the affinities, as seen with the CDK2 ligands. The GAX21* model, on the other hand, produces a similar PC score of 0.825 for CDK2, but a much more reasonable MUE of 0.540 kcal mol−1, exhibiting none of the artefacts seen with the SS21* and SX21* models. Similarly, both GAX21* and SX21* models yield PC scores of 0.945 for Thrombin, but much different MUE values of 1.117 and 0.509 kcal mol−1, respectively, so the latter is chosen as the best result. Using the models from Table 3 produces average PC and MUE scores of 0.816 and 0.673 kcal mol−1, respectively. The significant changes in the CDK2 and Thrombin LGFE scores emphasize the importance of the use of restraints in the ML optimization procedure to avoid overfitting, though this still occurred with the particular system and ACS. In practice, such a problem could be identified, and the restraints used in the optimization adjusted; in the present study we used the same ML protocol for all the systems for consistency.
| System | ACS | MUE | RMSE | R | PI | PC |
|---|---|---|---|---|---|---|
| P38 | SX21*-5 Å | 0.921 | 1.103 | 0.744 | 0.755 | 0.781 |
| BACE | SS21*-5 Å | 0.536 | 0.753 | 0.563 | 0.673 | 0.733 |
| MCL1 | SS21*-5 Å | 0.776 | 0.944 | 0.782 | 0.790 | 0.792 |
| TYK2 | GAX21*-5 Å | 0.807 | 0.928 | 0.684 | 0.743 | 0.742 |
| JNK1 | GAS21*-5 Å | 0.676 | 0.821 | 0.706 | 0.730 | 0.812 |
| Thrombin | SX21*-5 Å | 0.509 | 0.555 | 0.915 | 0.963 | 0.945 |
| CDK2 | GAX21*-5 Å | 0.540 | 0.630 | 0.864 | 0.873 | 0.825 |
| PTP1B | SX21*-5 Å | 0.622 | 0.724 | 0.865 | 0.944 | 0.895 |
| Average | 0.673 | 0.807 | 0.765 | 0.809 | 0.816 |
| Method | MUE | RMSE | R | PI | PC |
|---|---|---|---|---|---|
| SILCS-Default SX21-5 Å | 0.800 | 1.014 | 0.614 | 0.640 | 0.719 |
| SILCS-Best PC | 0.732 | 0.928 | 0.668 | 0.711 | 0.767 |
| SILCS ML-Optimized | 0.673 | 0.807 | 0.765 | 0.809 | 0.816 |
| FEP+/OPLS 2.1 | 0.728 | 0.881 | 0.742 | 0.751 | 0.781 |
| AMBER/ff14SB+GAFF1.8 | 0.933 | 1.166 | 0.559 | 0.598 | 0.711 |
| Flare FEP/ff14SB+GAFF2.1 | 0.791 | 1.003 | 0.677 | 0.689 | 0.749 |
| pmx GAFF2.1 | 0.721 | 0.891 | 0.674 | 0.654 | 0.727 |
| pmx CGenFF | 0.835 | 1.088 | 0.562 | 0.591 | 0.716 |
| pmx Consensus | 0.740 | 0.900 | 0.637 | 0.659 | 0.738 |
To further compare the present results with FEP+/OPLS 2.1 we have plotted computational versus experimental binding affinities in Fig. 1. Most of the computed ΔG values for both SILCS-Best PC, SILCS ML-optimized and FEP+ are within ±2 kcal mol−1 of their experimental values as indicated by the dotted lines. In terms of individual targets, only P38 has an MUE above 1 kcal mol−1 for the SILCS-Best PC, and all protein targets yields an MUE below 1 kcal mol−1 for SILCS ML-Optimized, with pmx GAFF the only other method able to achieve this benchmark.
Fig. 2 shows the distribution of errors for SILCS-Default SX21-5 Å, SILCS-Best PC, SILCS ML-Optimized and the published FEP results. Notably, SILCS-Best PC is able to predict nearly 47% of ligands within an error of less than 0.5 kcal mol−1, while the default SILCS predicts nearly 43% within 0.5 kcal mol−1. Both the default and customized SILCS methods outperform all FEP-based methods in this metric. This is clearly an important consideration for researchers targeting a chemical accuracy of 0.5 kcal mol−1. However, for larger error ranges the unoptimized SILCS methods show mixed results, with fewer ligands with an error between 0.5–1.5 kcal mol−1, but more with an error >1.5 kcal mol−1 than other methods. ML-Optimized SILCS, on the other hand, has slightly fewer ligands with error <0.5 kcal mol−1 (40%) than SILCS-Default and SILCS-Best PC, but a greater number with error <1 kcal mol−1 (76% vs. 67% and 70%, respectively) and far fewer with error >1.5 kcal mol−1 (8% vs. 21% and 17%, respectively), outperforming all other methods in these metrics as well.
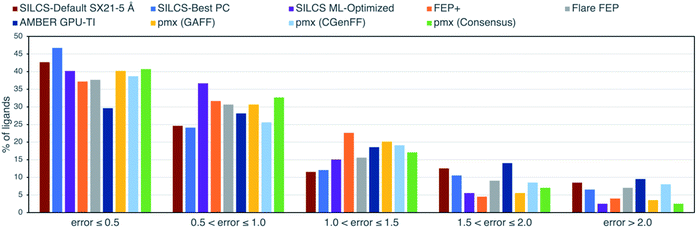 | ||
| Fig. 2 Percentage of ligands with ΔG unsigned error values (in kcal mol−1) within the specified ranges for SILCS and other published data with 199 ligands. | ||
The majority of the outliers – error >2.0 kcal mol−1 – for the SILCS-Default and Best PC methods occur for P38 with ACS SX21. Of those P38 ligands, most are associated with the substitution of a terminal benzyl group with a difluorobenzyl group. Experiments predict a free energy difference of ∼1–2 kcal mol−1 between those ligands with the benzyl group (2c, 2d, and 2h) and those with the difluorobenzyl group (2n, 2o, 2p, 2r, and 2s). For the former group of ligands, their LGFE scores are ∼3 kcal mol−1 too unfavorable, while for the latter they are ∼3 kcal mol−1 too favorable, resulting in a net 6 kcal mol−1 difference. This discrepancy is due to several factors. First, the SILCS-MC predicted pose for ligand 2d is rotated 180° from its crystal structure orientation (PDB ID: 3FLZ, Fig. S10A and B†). Ligands 2c and 2h (not shown) are also flipped. This flipping of the binding pose is most likely due to overlap between the imidazole acceptor nitrogen (IMIN) and formamide oxygen (FORO) maps in the binding pocket. The common central substructure of the P38 ligands contains an IMIN-classified nitrogen and a FORO-classified oxygen on opposite ends of the ligand. From the crystal structure, the nitrogen atom should occupy the overlap region between the two maps, but SILCS predicts that the oxygen atom occupies this region instead. The presence of non-polar (benzene and propane) carbon (GENN) and dimethylether oxygen (DMEO) maps on both ends of the binding pocket also facilitates two binding modes for the terminal benzyl and tetrahydropyran groups. The difluorobenzene substitution often corrects this misorientation due to the presence of several fluorobenzene fluorine (FLBX) binding regions on only one side of the binding pocket (Fig. S10C†), though in some cases misorientation can still occur such as in ligand 2v (Fig. S10D†). The two fluorine atoms alone contribute ∼−2.5 kcal mol−1 each to the LGFE score, accounting for most of the free energy discrepancy. From these results it is likely that the FORO maps are too favorable in the binding pocket, stabilizing an incorrect orientation of the ligand when the benzyl fluorines are not present. Consequently, the FLBX maps in this region are likely too favorable as well, exaggerating the stabilizing effect of the difluorine substitution. These results also point towards the limitation of applying full rotational and translational sampling in the SILCS-MC calculations; this may be overcome via the use of local SILCS-MC sampling based on the starting orientation of the parent compound as presented in Ustach et al.49 Consequently, PC-based ML optimization de-emphasizes the FORO and FLBX maps, reducing their respective FragMap weights to 0.41 and 0.77, while strengthening the IMIN FragMap weight to 1.15. These changes reduced the number of P38 ligands with error >2 kcal mol−1 from 10 down to just 1 and even successfully re-oriented ligand 2v, though others maintained the 180° rotation.
The use of cycle closure in the previous studies associated with the 199 ligands requires a total of 330 free energy perturbations. Table S7† lists the mean unsigned error (MUE) and root mean square error (RMSE) for the relative binding free energies (ΔΔG) between congeneric ligands for all 330 perturbations over the eight proteins. For each target, the MUE and RMSE scores from SILCS and other methods are shown in Table S8.† The individual ΔΔG values for each perturbation across eight protein targets can be accessed in the ESI file si_199.xlsx.† The SILCS-Default and SILCS-Best PC results are competitive with the Flare FEP, pmx CGenFF and AMBER GPU-TI data, with overall MUE of 1.085 and 1.065 kcal mol−1, respectively. For six of the protein targets (Thrombin, TYK2, CDK2, PTP1B, JNK1, and BACE) the MUE was less than 1 kcal mol−1 with SILCS-Best PC. SILCS ML-Optimized matches the performance of the best methods – FEP+, pmx GAFF, and pmx Consensus – with MUE and RMSE values of 0.864 and 1.079 kcal mol−1, respectively. Fig. S11† depicts the correlation plots for computed versus experimental ΔΔG obtained from SILCS and FEP+/OPLS 2.1, while Fig. S12† shows the distribution of errors for SILCS and all published results. The lower values of MUE and RMSE for all 330 perturbations further demonstrates the ability of the SILCS technique to compute ΔΔG for a range of ligands and protein targets.
Overall, the SILCS methodology is an innovative concept that provides precise and accurate ligand binding affinities across a diverse set of protein targets in a highly computationally efficient method as compared to FEP based approaches. While all the metrics utilized in this work are important for judging how accurately binding free energies are computed, in the context of a medicinal chemistry campaign PI and PC are of importance as they indicate optimal binding order predictions, information required to make go/no-go decisions with the respect to compound synthesis and experimental validation. As per these metrics, SILCS-Default performs about as well as other published methods, SILCS-Best PC is only outperformed by FEP+, and SILCS ML-Optimized surpasses the performance of FEP+ (Table 4). This demonstrates the ability of the SILCS method to successfully rank order ligand binding affinities to a similar or better degree as other well-established approaches.
3.2. Performance of SILCS computed binding affinities for 407 ligands
The results presented in the above section used a previously curated set of 199 ligands to allow direct comparison with the published studies. In this section, we repeat the same analysis for a larger set of 407 ligands, of which only 14 ligands targeting CDK2 are omitted due to the lack of reported IC50 values. Table 5 presents the average metrics from SILCS for all eight proteins with the different ACS and radii for the exhaustive SILCS-MC protocol. Detailed results for all eight protein targets can be accessed in the ESI file si_407.xlsx.† As was the case for 199 ligands, 2, 5 and 10 Å radii produce roughly similar correlation scores for most models and perform better than the 1 Å radii. The SX21 model with either a 5 or 10 Å radii again produces the overall best results when considering R, PI, and PC metric variables, while GAS21 produces the best MUE/RMSE metrics.| Protocol (rLP) | ACS | MUE | RMSE | R | PI | PC |
|---|---|---|---|---|---|---|
| a Ex: exhaustive, R: Pearson's correlation coefficient, PI: predictive index, PC: percent correct. | ||||||
| Ex (rLP = 1 Å) | GAS21 | 1.116 | 1.395 | 0.327 | 0.329 | 0.614 |
| Ex (rLP = 1 Å) | GAX21 | 1.179 | 1.460 | 0.389 | 0.372 | 0.626 |
| Ex (rLP = 1 Å) | SS21 | 1.180 | 1.458 | 0.419 | 0.409 | 0.640 |
| Ex (rLP = 1 Å) | SX21 | 1.218 | 1.494 | 0.477 | 0.478 | 0.662 |
| Ex (rLP = 2 Å) | GAS21 | 0.956 | 1.187 | 0.542 | 0.530 | 0.683 |
| Ex (rLP = 2 Å) | GAX21 | 1.039 | 1.296 | 0.556 | 0.549 | 0.690 |
| Ex (rLP = 2 Å) | SS21 | 1.080 | 1.333 | 0.501 | 0.502 | 0.679 |
| Ex (rLP = 2 Å) | SX21 | 1.106 | 1.357 | 0.586 | 0.586 | 0.704 |
| Ex (rLP = 5 Å) | GAS21 | 0.926 | 1.144 | 0.571 | 0.570 | 0.695 |
| Ex (rLP = 5 Å) | GAX21 | 0.979 | 1.209 | 0.593 | 0.588 | 0.702 |
| Ex (rLP = 5 Å) | SS21 | 0.978 | 1.220 | 0.545 | 0.527 | 0.686 |
| Ex (rLP = 5 Å) | SX21 | 1.008 | 1.251 | 0.599 | 0.612 | 0.710 |
| Ex (rLP = 10 Å) | GAS21 | 0.920 | 1.145 | 0.568 | 0.535 | 0.681 |
| Ex (rLP = 10 Å) | GAX21 | 0.963 | 1.204 | 0.597 | 0.588 | 0.703 |
| Ex (rLP = 10 Å) | SS21 | 0.960 | 1.200 | 0.565 | 0.552 | 0.691 |
| Ex (rLP = 10 Å) | SX21 | 1.039 | 1.283 | 0.588 | 0.594 | 0.706 |
| System | ACS | r LP | MUE | RMSE | R | PI | PC |
|---|---|---|---|---|---|---|---|
| P38 | SX21 | 1 | 1.368 | 1.665 | 0.621 | 0.644 | 0.733 |
| BACE | SS21 | 5 | 0.568 | 0.735 | 0.562 | 0.588 | 0.704 |
| MCL1 | GAS21 | 2 | 1.135 | 1.356 | 0.822 | 0.824 | 0.809 |
| TYK2 | GAS21 | 10 | 1.029 | 1.290 | 0.628 | 0.628 | 0.706 |
| JNK1 | GAX21 | 5 | 0.973 | 1.240 | 0.631 | 0.652 | 0.731 |
| Thrombin | GAX21 | 10 | 0.895 | 1.242 | 0.605 | 0.597 | 0.718 |
| CDK2 | SS21 | 1 | 0.800 | 1.009 | 0.638 | 0.664 | 0.727 |
| PTP1B | GAS21 | 5 | 0.936 | 1.139 | 0.790 | 0.816 | 0.804 |
| Average | 0.963 | 1.209 | 0.662 | 0.677 | 0.742 |
The average MUE for the SILCS-Best PC method has increased from 0.732 to 0.963 kcal mol−1 when expanding the set from 199 to 407 ligands. Once again, some of the P38 ligands provide larger MUE when compared to other targets. While the MUE has increased with the larger ligand set, it is still below the 1 kcal mol−1 limit. Nearly 31% of the 407 ligands have an MUE under 0.5 kcal mol−1, and 58% are under 1 kcal mol−1 as shown in Fig. S13.† Computed versus experimental binding affinities for all ACS with a 5 Å radii for 407 ligands are plotted in Fig. S14;† different ACS ranges from 0.926 to 1.008 kcal mol−1, falling roughly within the 1 kcal mol−1 limit. Overall, the SILCS performance still remains quite robust for MUE and other metric variables when considering the larger set of 407 ligands.
| System | ACS | MUE | RMSE | R | PI | PC |
|---|---|---|---|---|---|---|
| P38 | SX21*-5 Å | 1.089 | 1.340 | 0.661 | 0.687 | 0.758 |
| BACE | SS21*-5 Å | 0.559 | 0.815 | 0.658 | 0.761 | 0.773 |
| MCL1 | SX21*-5 Å | 0.913 | 1.126 | 0.886 | 0.892 | 0.859 |
| TYK2 | SX21*-5 Å | 0.886 | 1.071 | 0.762 | 0.807 | 0.777 |
| JNK1 | GAX21*-5 Å | 1.076 | 1.408 | 0.731 | 0.741 | 0.782 |
| Thrombin | GAX21*-5 Å | 0.923 | 1.133 | 0.816 | 0.854 | 0.838 |
| CDK2 | GAX21*-5 Å | 0.605 | 0.759 | 0.791 | 0.814 | 0.810 |
| PTP1B | GAS21*-5 Å | 0.903 | 1.067 | 0.815 | 0.831 | 0.810 |
| Average | 0.869 | 1.090 | 0.765 | 0.798 | 0.801 |
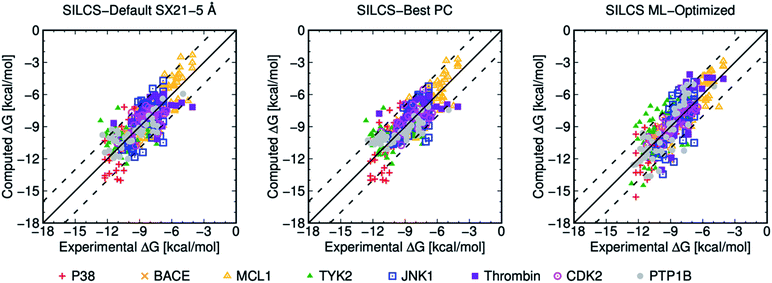 | ||
| Fig. 3 Computed versus experimental ΔG obtained from SILCS procedure for 407 ligands of eight protein targets. “SILCS-Best PC” corresponds to the results from Table 6, and “SILCS ML-Optimized” corresponds to the results from Table 7. | ||
Overall, picking a best ML-Optimized ACS for specific protein target based on their PC scores provides the average ML-Optimized PC scores of 0.816 and 0.801 for 199 and 407 ligands as shown in Tables 3 and 7. In general, ML-optimization targeting PC for the larger ligand set also produces higher MUE values for individual protein targets than for the smaller, curated ligand set, and the average MUE increases from 0.673 to 0.869 kcal mol−1 with the additional ligands. In summary, the SILCS methodology in conjunction with ML optimization can offer high quality predictions for ranking relative binding affinities with a diverse set of ligands across a diverse set of protein targets once a relatively small body of experimental data for a target is available.
3.3. Utility of SILCS atomic GFE scores beyond relative free energies of binding
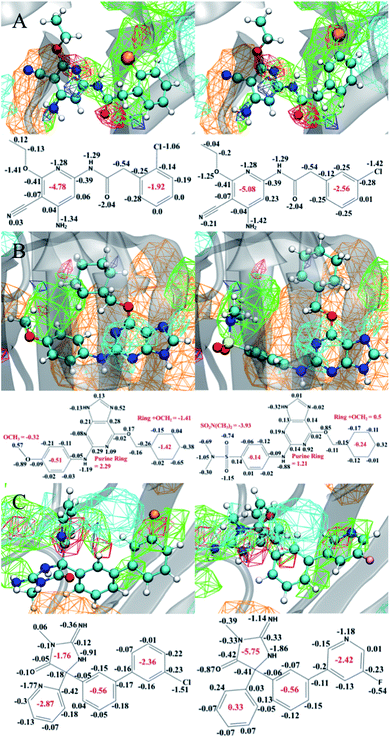
While the SILCS method is competitive with the FEP methods, as shown above, the approach has the advantage of allowing for qualitative visual analysis of the FragMaps and, quantitatively, producing the atom-based contributions to the binding affinities in the form of the GFE scores.91,92 Such information is not directly accessible in FEP and TI based approaches. In addition, even with congeneric ligand perturbations we observe both large and small changes in the bound orientation of the ligand. This is due to the random initial placement and orientation of the ligands which allows us to explore a larger range of ligand binding poses over FEP. In this context, Fig. 4 presents examples of selected congeneric ligand perturbations for JNK1, CDK2, and BACE.Fig. 4A shows congeneric JNK1 ligands that differ by an ortho to meta-chloro substitution of a phenyl ring. This results in a computed ΔΔGSILCS score of −0.87 kcal mol−1, matching well with the ΔΔGExpt value of −0.77 kcal mol−1. The overall bound orientation of the ligand in the binding site is maintained. However, there is a shift in the orientation of the chlorobenzene ring allowing the chlorine in the meta position to participate in a halogen–hydrogen bond-donor interaction, as indicated by its improved occupancy of the acceptor GENA FragMap leading to a more favorable GFE. This results in changing the summed GFE score of the full chlorophenyl ring atoms from −1.92 to −2.56 kcal mol−1. However, this accounts for only a portion of the overall ΔΔG. The remaining free energy gain is associated with more favorable interactions of the substituted pyridine ring and its constituents with the protein as indicated by the more favorable summed GFE score of −5.08 kcal mol−1versus −4.78 kcal mol−1 in the o-chloro substituted compound. Thus, the switch to m-chloro not only leads to more favorable interactions of the halogen, but also shifts the pyridine ring group on the other end of the molecule into a more favorable orientation.
In the next example, the methoxy group of a CDK2 ligand is substituted with a N,N-dimethylsulfonamide moiety as shown in Fig. 4B. This modification results in a computed ΔΔGSILCS score of −1.25 kcal mol−1, in good agreement with ΔΔGExpt of −1.45 kcal mol−1. Both hydrogen bond donor and acceptor FragMaps occupy the region occupied by the sulfonamide, such that the overall functional group makes significantly more favorable GFE contribution (−3.93 kcal mol−1) versus the methoxy group (−0.32 kcal mol−1). However, this more favorable GFE contribution leads to less favorable contributions of the phenyl ring to which it is attached and, more significantly, with the cyclohexane ring on the other end of the molecule. The bulkier sulfonamide group appears to push away the cyclohexane ring, increasing the GFE of this group and its methoxy linker by ∼2 kcal mol−1, negating about half of the increased affinity of the sulfonamide substituent. Meanwhile, the central structure adjoining these two groups – a purine ring and a phenyl ring connected via an amine nitrogen – exhibits a much smaller change of −0.4 kcal mol−1. In a design context, this type of information may indicate that altering the linker lengths in the molecule may allow for the favorable GFE contributions of both the sulfonamide and the cyclohexane ring at the other end of the molecule to be maintained.
The last example showcases two BACE ligands that differ based on the presence of modifications on both sides of the ligands as shown in Fig. 4C. On the right side, the chlorobenzyl ring is replaced with the fluoropyridine ring, while the pyridine on the left side is changed to a phenyl ring. These perturbations lead to a computed ΔΔGSILCS score of −0.85 kcal mol−1, in good agreement with the ΔΔGExpt of −0.64 kcal mol−1. Although the ΔΔG is small, analysis of the atomic GFE contributions indicates large differences in the contributions of the constituent ring systems. While the overall orientations of the ligands in the binding site is similar, the 5- and 6-membered rings on the left side of the molecule have rotated and switched locations. This leads to large changes in the contributions of the individual ring systems with the contribution of the 5-membered ring and its substituents becoming significantly more favorable while the pyridine/phenyl becoming far less favorable. The pyridine-to-phenyl transformation removes a potential hydrogen bond interaction between the pyridine nitrogen and the protein, as indicated by the generic acceptor maps in this region, allowing for the large rotation observed between these two ligands. The net effect of this rotation is ∼−0.8 kcal mol−1, accounting for nearly all of the improved binding affinity. The chlorobenzyl-to-fluoropyridine transformation, on the other hand, has almost no effect on the binding affinity. The nitrogen atom of the fluoropyridine group occupies the hydrogen bond acceptor map formerly occupied by the chlorine atom of the chlorobenzyl group, resulting in a net change of only +0.06 kcal mol−1 for this group.
The example modifications shown in Fig. 4 emphasize the value of the GFE information content in SILCS. Even in cases where the chemical modification directly contributes to the direction of the change in ΔΔG and the binding orientation of the molecule is similar, such as with the JNK1 ligands discussed above, there can be significant contributions from other parts of the ligand that might be obscured by examining only the overall ligand binding affinities. Conversely, the CDK2 ligands demonstrate how moieties distal to the chemical modification can limit its contribution to binding. In the case of multiple modifications, SILCS is able to evaluate the contributions from each modification and, in the case of the BACE ligands, it indicated that one of the modifications had no effect. Lastly, the GFE content can be used to locate sources of error, as we observed for the P38 ligands discussed in Section 3.1.3. Clearly, this atomic level of detail from the SILCS method offers significant insights into the nature of the contributions of the various regions of the ligands to ΔΔG, information that can greatly facilitate decision making in a medicinal chemistry campaign. Such information is not directly accessible to FEP-based methods.
4. Conclusions
In this work, we demonstrate the efficacy of the SILCS technology for predicting protein–ligand binding affinities for eight protein targets with both a smaller set of 199 ligands and a larger set of 407 ligands. Our primary metric for evaluating and optimizing the performance of SILCS was the rank-ordering accuracy, or percent correct (PC), of the binding affinities. The standard SILCS-MC protocol successfully achieves an average accuracy of approximately 72% and 71% in rank-ordering the ligand affinities for the sets of 199 and 407 ligands, respectively, using the default SX21 ACS with 5 Å ligand placement radii model. The average accuracy improves to 77% and 74% for the sets of 199 and 407 ligands by using the top PC scoring protocol (Best-PC). Furthermore, these accuracies improve to 82% and 80% through a Bayesian MCSA ML optimization procedure, though, for the smaller ligand set, this came at the expense of some chemical accuracy such as higher MUE and RMSE metrics. The default and optimized SILCS-MC protocols provide similar or better accuracy than other benchmarked FEP/TI methods for the 199 ligands through several metrics, including PC, MUE, RMSE, R, and PI. In addition, SILCS produces an MUE of less than 1 kcal mol−1 for both the 199 and 407 ligand sets. Thus, the SILCS method is accurate and robust and aligns with the FEP/TI approaches in producing this level of accuracy at a significantly reduced computational cost.In practice, the SILCS-MC approach offers a number of advantages over FEP/TI-based approaches. In the context of no a priori information on ligand affinities for the target protein, the SILCS-MC default method performs at levels approaching or above that of other FEP/TI methods. The overall computational cost of this effort is significantly lower with SILCS-MC as only one expensive set of SILCS simulations is required to obtain the required ensemble in the form of the FragMaps that are reused for the subsequent SILCS-MC LGFE calculations, while the ensembles must be recalculated for each modification with the FEP methods. Moreover, this problem is exacerbated by the need for additional perturbations in the context of the cycle closure method. The computational advantages of the SILCS methods are magnified as a medicinal chemistry campaign continues as only minutes on a single CPU core are required for each additional ligand. Indeed, the efficiency of the SILCS method makes it directly applicable for in silico high throughput screening. Once initial experimental data is available, the SILCS-Best method may be identified for a target leading to improved performance. Performance can be further enhanced through Bayesian ML optimization of the FragMap weights used in the SILCS-MC calculation without significant additional computational resources due to the speed and parallelizability of the SILCS-MC simulations. Use of the original SILCS FragMaps as priors for the Bayesian ML optimization allows for the approach to be applied with small training sets (11 to 42 ligands for the proteins in the 199 set and 26 to 91 ligands for the proteins in the 407 set). This allows the ML-optimization approach to be of utility early in a medicinal chemistry campaign as well as allow for further ML optimization as additional experimental data is obtained. Such an approach is not accessible to FEP and TI based methods. Another limitation of FEP/TI calculations is the need for a crystal structure of at least one ligand. This is not a requirement of SILCS, though information on the location of the binding pocket is required. It is also important to emphasize that the SILCS technology is significantly less sensitive to the ligand force field parameters as the GFE and LGFE scoring is based on the classification of the individual ligand atoms and their overlap with the respective FragMaps, though the FragMaps themselves will have dependence on the force field. For example, the difference of accuracy between the pmx CGenFF and SILCS-MC results includes contributions from potential limitations in the force field that could impact the TI ΔΔG results. Finally, the atomic GFE contributions from which the LGFE scores are obtained offer insights into the contributions of different portions of the ligands to changes in binding affinities, information that facilitates interpretation of experimental data leading to improved ligand optimization strategies. In combination, the capabilities of the SILCS approach relative to FEP/TI-based methods indicate it to be an efficient and robust computational tool to design, discover, and screen drug candidates in a fashion that can lead the drug design process.
Data availability
The SILCS FragMaps and ligands in mol2 format for each protein target along with other relevant informaton can be found in the GitHub repository (https://github.com/mackerell-lab/SILCS-MC-Chem-Sci-2021).Author contributions
H. G. and A. H. lead the research in running simulations, docking of validation sets, data analysis, and writing of the manuscript. V. D. U. prepared the ligands along with initial tests. S. J. and W. Y. helped with ΔΔG analysis, ML, and visualization. A. D. M. supervised the entire research with conceptualization, analysis and resources.Conflicts of interest
ADM Jr is co-founder and Chief Scientific Officer of SilcsBio LLC.Acknowledgements
This work was supported by NIH grant R44GM109635 and R01GM131710 and the Samuel Waxman Cancer Research Foundation. The authors acknowledge computer time and resources from the Computer-Aided Drug Design (CADD) Center at the University of Maryland, Baltimore.References
- S. J. Y. Macalino, V. Gosu, S. Hong and S. Choi, Arch. Pharmacal Res., 2015, 38, 1686–1701 CrossRef CAS PubMed.
- M. Hassan Baig, K. Ahmad, S. Roy, J. Mohammad Ashraf, M. Adil, M. Haris Siddiqui, S. Khan, M. Amjad Kamal, I. Provazník and I. Choi, Curr. Pharm. Des., 2016, 22, 572–581 CrossRef PubMed.
- M. K. Gilson and H.-X. Zhou, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 21–42 CrossRef CAS PubMed.
- R. Kim and J. Skolnick, J. Comput. Chem., 2008, 29, 1316–1331 CrossRef CAS PubMed.
- S. Genheden and U. Ryde, Expert Opin. Drug Discovery, 2015, 10, 449–461 CrossRef CAS PubMed.
- G. Rastelli, A. D. Rio, G. Degliesposti and M. Sgobba, J. Comput. Chem., 2010, 31, 797–810 CAS.
- P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan, W. Wang, O. Donini, P. Cieplak, J. Srinivasan, D. A. Case and T. E. Cheatham III, Acc. Chem. Res., 2000, 33, 889–897 CrossRef CAS PubMed.
- B. R. Miller III, T. D. McGee Jr, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, J. Chem. Theory Comput., 2012, 8, 3314–3321 CrossRef.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1995, 16, 1339–1350 CrossRef CAS.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
- D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558 CrossRef CAS PubMed.
- M. R. Reddy, M. D. Erion and A. Agarwal, Rev. Comput. Chem., 2000, 16, 217–304 CAS.
- T. Steinbrecher and A. Labahn, Curr. Med. Chem., 2010, 17, 767–785 CrossRef CAS PubMed.
- B. J. Williams-Noonan, E. Yuriev and D. K. Chalmers, J. Med. Chem., 2018, 61, 638–649 CrossRef CAS PubMed.
- R. Abel, L. Wang, D. L. Mobley and R. A. Friesner, Curr. Top. Med. Chem., 2017, 17, 2577–2585 CrossRef CAS PubMed.
- W. L. Jorgensen, Acc. Chem. Res., 2009, 42, 724–733 CrossRef CAS PubMed.
- N. Hansen and W. F. Van Gunsteren, J. Chem. Theory Comput., 2014, 10, 2632–2647 CrossRef CAS PubMed.
- M. R. Shirts, D. L. Mobley and S. P. Brown, Drug design: structure-and ligand-based approaches, 2010, pp. 61–86 Search PubMed.
- L. Wang, B. J. Berne and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1937–1942 CrossRef CAS PubMed.
- R. Abel, L. Wang, E. D. Harder, B. Berne and R. A. Friesner, Acc. Chem. Res., 2017, 50, 1625–1632 CrossRef CAS PubMed.
- Z. Cournia, B. Allen and W. Sherman, J. Chem. Inf. Model., 2017, 57, 2911–2937 CrossRef CAS PubMed.
- D. L. Mobley and P. V. Klimovich, J. Chem. Phys., 2012, 137, 230901 CrossRef PubMed.
- L. Wang, B. Berne and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1937–1942 CrossRef CAS PubMed.
- J. Z. Vilseck, N. Sohail, R. L. Hayes and C. L. Brooks III, J. Phys. Chem. Lett., 2019, 10, 4875–4880 CrossRef CAS PubMed.
- A. P. Bhati, S. Wan and P. V. Coveney, J. Chem. Theory Comput., 2018, 15, 1265–1277 CrossRef.
- H. Chen, J. D. Maia, B. K. Radak, D. J. Hardy, W. Cai, C. Chipot and E. Tajkhorshid, J. Chem. Inf. Model., 2020, 60, 5301–5307 CrossRef CAS PubMed.
- J. W. Perthold, D. e. Petrov and C. Oostenbrink, J. Chem. Inf. Model., 2020, 60, 5395–5406 CrossRef CAS PubMed.
- M. Chen, H.-Y. Ko, R. C. Remsing, M. F. C. Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein and J. P. Perdew, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10846–10851 CrossRef CAS PubMed.
- H. Goel, Z. W. Windom, A. A. Jackson and N. Rai, J. Comput. Chem., 2018, 39, 397–406 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- E. Harder, W. Damm, E. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2016, 12, 281–296 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- A. D. MacKerell Jr, B. Brooks, C. L. Brooks III, L. Nilsson, B. Roux, Y. Won and M. Karplus, in Encyclopedia of Computational Chemistry, ed. P. v. R. Schleyer, N. L. Allinger, T. Clark, J. Gasteiger, P. A. Kollman, H. F. Schaefer III and P. R. Schreiner, John Wiley & Sons, Chichester, 1998, vol. 1, pp. 271–277 Search PubMed.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- X. Zhu, P. E. Lopes and A. D. MacKerell Jr, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 167–185 CAS.
- B. A. Horta, P. T. Merz, P. F. Fuchs, J. Dolenc, S. Riniker and P. H. Hunenberger, J. Chem. Theory Comput., 2016, 12, 3825–3850 CrossRef CAS PubMed.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- O. Guvench and A. D. MacKerell Jr, PLoS Comput. Biol., 2009, 5, e1000435 CrossRef PubMed.
- E. P. Raman, W. Yu, O. Guvench and A. D. MacKerell, J. Chem. Inf. Model., 2011, 51, 877–896 CrossRef CAS PubMed.
- E. P. Raman, W. Yu, S. K. Lakkaraju and A. D. MacKerell Jr, J. Chem. Inf. Model., 2013, 53, 3384–3398 CrossRef CAS PubMed.
- S. K. Lakkaraju, W. Yu, E. P. Raman, A. V. Hershfeld, L. Fang, D. A. Deshpande and A. D. MacKerell Jr, J. Chem. Inf. Model., 2015, 55, 700–708 CrossRef CAS PubMed.
- W. Yu, S. K. Lakkaraju, E. P. Raman and A. D. MacKerell Jr, J. Comput.-Aided Mol. Des., 2014, 28, 491–507 CrossRef CAS PubMed.
- C. E. Faller, E. P. Raman, A. D. MacKerell and O. Guvench, in Fragment-Based Methods in Drug Discovery, Springer, 2015, pp. 75–87 Search PubMed.
- V. D. Ustach, S. K. Lakkaraju, S. Jo, W. Yu, W. Jiang and A. D. MacKerell Jr, J. Chem. Inf. Model., 2019, 59, 3018–3035 CrossRef CAS PubMed.
- X. He, S. K. Lakkaraju, M. Hanscom, Z. Zhao, J. Wu, B. Stoica, A. D. MacKerell Jr, A. I. Faden and F. Xue, Bioorg. Med. Chem., 2015, 23, 2211–2220 CrossRef CAS PubMed.
- W. Yu, S. Jo, S. K. Lakkaraju, D. J. Weber and A. D. MacKerell Jr, Proteins: Struct., Funct., Bioinf., 2019, 87, 289–301 CrossRef CAS PubMed.
- W. Yu, S. K. Lakkaraju, E. P. Raman, L. Fang and A. D. MacKerell Jr, J. Chem. Inf. Model., 2015, 55, 407–420 CrossRef CAS PubMed.
- S. Jo, A. Xu, J. E. Curtis, S. Somani and A. D. MacKerell, Mol. Pharm., 2020, 4323–4333 CrossRef CAS PubMed.
- H. Goel, W. Yu, V. D. Ustach, A. H. Aytenfisu, D. Sun and A. D. MacKerell, Phys. Chem. Chem. Phys., 2020, 22, 6848–6860 RSC.
- L. Wang, Y. Wu, Y. Deng, B. Kim, L. Pierce, G. Krilov, D. Lupyan, S. Robinson, M. K. Dahlgren and J. Greenwood, J. Am. Chem. Soc., 2015, 137, 2695–2703 CrossRef CAS PubMed.
- L. F. Song, T.-S. Lee, C. Zhu, D. M. York and K. M. Merz Jr, J. Chem. Inf. Model., 2019, 59, 3128–3135 CrossRef CAS PubMed.
- L. Wang, Y. Deng, J. L. Knight, Y. Wu, B. Kim, W. Sherman, J. C. Shelley, T. Lin and R. Abel, J. Chem. Theory Comput., 2013, 9, 1282–1293 CrossRef CAS PubMed.
- J. N. Cumming, E. M. Smith, L. Wang, J. Misiaszek, J. Durkin, J. Pan, U. Iserloh, Y. Wu, Z. Zhu and C. Strickland, Bioorg. Med. Chem. Lett., 2012, 22, 2444–2449 CrossRef CAS PubMed.
- D. M. Goldstein, M. Soth, T. Gabriel, N. Dewdney, A. Kuglstatter, H. Arzeno, J. Chen, W. Bingenheimer, S. A. Dalrymple, J. Dunn, R. Farrell, S. Frauchiger, J. La Fargue, M. Ghate, B. Graves, R. J. Hill, F. Li, R. Litman, B. Loe, J. McIntosh, D. McWeeney, E. Papp, J. Park, H. F. Reese, R. T. Roberts, D. Rotstein, B. San Pablo, K. Sarma, M. Stahl, M. L. Sung, R. T. Suttman, E. B. Sjogren, Y. Tan, A. Trejo, M. Welch, P. Weller, B. R. Wong and H. Zecic, J. Med. Chem., 2011, 54, 2255–2265 CrossRef CAS PubMed.
- I. R. Hardcastle, C. E. Arris, J. Bentley, F. T. Boyle, Y. Chen, N. J. Curtin, J. A. Endicott, A. E. Gibson, B. T. Golding and R. J. Griffin, J. Med. Chem., 2004, 47, 3710–3722 CrossRef CAS PubMed.
- A. Friberg, D. Vigil, B. Zhao, R. N. Daniels, J. P. Burke, P. M. Garcia-Barrantes, D. Camper, B. A. Chauder, T. Lee and E. T. Olejniczak, J. Med. Chem., 2013, 56, 15–30 CrossRef CAS PubMed.
- D. P. Wilson, Z.-K. Wan, W.-X. Xu, S. J. Kirincich, B. C. Follows, D. Joseph-McCarthy, K. Foreman, A. Moretto, J. Wu and M. Zhu, J. Med. Chem., 2007, 50, 4681–4698 CrossRef CAS PubMed.
- J. Liang, V. Tsui, A. Van Abbema, L. Bao, K. Barrett, M. Beresini, L. Berezhkovskiy, W. S. Blair, C. Chang and J. Driscoll, Eur. J. Med. Chem., 2013, 67, 175–187 CrossRef CAS PubMed.
- J. Liang, A. van Abbema, M. Balazs, K. Barrett, L. Berezhkovsky, W. Blair, C. Chang, D. Delarosa, J. DeVoss and J. Driscoll, J. Med. Chem., 2013, 56, 4521–4536 CrossRef CAS PubMed.
- H. Zhao, M. D. Serby, Z. Xin, B. G. Szczepankiewicz, M. Liu, C. Kosogof, B. Liu, L. T. Nelson, E. F. Johnson and S. Wang, J. Med. Chem., 2006, 49, 4455–4458 CrossRef CAS PubMed.
- B. Baum, M. Mohamed, M. Zayed, C. Gerlach, A. Heine, D. Hangauer and G. Klebe, J. Mol. Biol., 2009, 390, 56–69 CrossRef CAS PubMed.
- F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284 CrossRef CAS.
- D. Van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- M. Levitt and S. Lifson, J. Mol. Biol., 1969, 46, 269–279 CrossRef CAS.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- S. K. Lakkaraju, E. P. Raman, W. Yu and A. D. MacKerell Jr, J. Chem. Theory Comput., 2014, 10, 2281–2290 CrossRef CAS PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. A. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmuller and A. D. MacKerell Jr, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell Jr, J. Comput. Chem., 2010, 31, 671–690 CAS.
- K. Vanommeslaeghe and A. D. MacKerell Jr, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell Jr, J. Chem. Inf. Model., 2012, 52, 3155–3168 CrossRef CAS PubMed.
- W. Yu, X. He, K. Vanommeslaeghe and A. D. MacKerell Jr, J. Comput. Chem., 2012, 33, 2451–2468 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- W. E. Reiher, PhD thesis, Harvard University, 1985.
- R. A. Friesner, I. Prigogine and S. A. Rice, Computational methods for protein folding, WileyNew York, 2002 Search PubMed.
- A. Warshel, P. K. Sharma, M. Kato and W. W. Parson, Biochim. Biophys. Acta, Proteins Proteomics, 2006, 1764, 1647–1676 CrossRef CAS PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- V. Gapsys, L. Pérez-Benito, M. Aldeghi, D. Seeliger, H. Van Vlijmen, G. Tresadern and B. L. de Groot, Chem. Sci., 2020, 11, 1140–1152 RSC.
- M. Kuhn, S. Firth-Clark, P. Tosco, A. S. Mey, M. D. Mackey and J. Michel, J. Chem. Inf. Model., 2020, 60, 3120–3130 CrossRef CAS PubMed.
- X. He, S. Liu, T.-S. Lee, B. Ji, V. H. Man, D. M. York and J. Wang, ACS Omega, 2020, 5, 4611–4619 CrossRef CAS PubMed.
- G. A. Heinzl, W. Huang, W. Yu, B. J. Giardina, Y. Zhou, A. D. MacKerell Jr, A. Wilks and F. Xue, J. Med. Chem., 2016, 59, 6929–6942 CrossRef CAS PubMed.
- M. E. Lanning, W. Yu, J. L. Yap, J. Chauhan, L. Chen, E. Whiting, L. S. Pidugu, T. Atkinson, H. Bailey and W. Li, Eur. J. Med. Chem., 2016, 113, 273–292 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supporting information file Chem_Science_J_si.pdf provides additional description of the calculation of different metrics and comprehensive details for the atom classification schemes (ACS). The SI tables specify the weights for 2021 ACS (Table S1), ligand placement centers (Table S2), values for overlap coefficients (Tables S3 and S4), comparison of the old (2018) and new ACS (2021) for the eight targets (Table S5), metric performances based on the SILCS ML optimization for 199 (Table S6) and 407 ligands (Table S9), ΔΔG MUE and RMSE scores for the 330 perturbations (Tables S7 and S8). The SI figures include SILCS workflow (Fig. S1), SILCS solute structures and FragMap atom types (Fig. S2), experimental literature ΔG values (Fig. S3), raw versus experimental ΔG (Fig. S4), computed versus experimental ΔG for the 199 (Fig. S5) and 407 ligands (Fig. S14), standard deviations of ΔG, MUE and PC (Fig. S6–S8), computed versus experimental ΔG from ML optimization for the 199 (Fig. S9) and 407 ligands (Fig. S15), outlier ligands for P38 (Fig. S10), computed versus experimental ΔΔG for 330 perturbations (Fig. S11), percentage of ligand perturbations with ΔΔG MUE (Fig. S12), and ΔG MUE (Fig. S13†) values. 2D chemical structures of two ligands are shown with their atoms colored and labeled based on their FragMap type for all ACS (Fig. S16). The si_199.xlsx file provides all the experimental and computed values along with the literature data for ΔG and ΔΔG with 199 ligands corresponding to the eight targets. The si_407.xlsx file provides all the experimental and computed values using the SILCS methodology with 407 ligands and eight targets. The files si_ML-Opt_weights.xlsx and si_ligand_scaffolds.xlsx include the ML-Optimized weights for different FragMaps and the ligands assigned to the different scaffolds for the ML-optimization procedure, respectively. The file si_ligand_images_407.pdf presents the 2D structures of the 407 ligands considered in this study. See DOI: 10.1039/d1sc01781k |
| ‡ These authors equally contributed to this work. |
| This journal is © The Royal Society of Chemistry 2021 |