Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting chemical shifts with graph neural networks†
Ziyue
Yang
 *,
Maghesree
Chakraborty
*,
Maghesree
Chakraborty
 and
Andrew D.
White
and
Andrew D.
White
 *
*
Department of Chemical Engineering, University of Rochester, Rochester, NY, USA. E-mail: andrew.white@rochester.edu
First published on 9th July 2021
Abstract
Inferring molecular structure from Nuclear Magnetic Resonance (NMR) measurements requires an accurate forward model that can predict chemical shifts from 3D structure. Current forward models are limited to specific molecules like proteins and state-of-the-art models are not differentiable. Thus they cannot be used with gradient methods like biased molecular dynamics. Here we use graph neural networks (GNNs) for NMR chemical shift prediction. Our GNN can model chemical shifts accurately and capture important phenomena like hydrogen bonding induced downfield shift between multiple proteins, secondary structure effects, and predict shifts of organic molecules. Previous empirical NMR models of protein NMR have relied on careful feature engineering with domain expertise. These GNNs are trained from data alone with no feature engineering yet are as accurate and can work on arbitrary molecular structures. The models are also efficient, able to compute one million chemical shifts in about 5 seconds. This work enables a new category of NMR models that have multiple interacting types of macromolecules.
Introduction
NMR chemical shifts of a molecule provide detailed structural information without the sample preparation requirements of X-ray crystallography.1 This means that NMR can provide detail at room temperature and reasonable concentrations, in a physiologically relevant ensemble of conformations and even in situ.2,3 Thus there is continued interest in methods to resolve protein structure from NMR. A key step in this process is being able to predict the NMR chemical shifts from molecular structure in a forward model. A forward model is used to infer the ensemble of structures that contribute towards the experimentally observed NMR chemical shifts. In this work, we find that graph neural networks (GNNs) have good properties as a forward model and expand the types of molecular structures that can be resolved. The process of inferring the conformational ensemble with the forward model can be done via experiment directed simulation,4,5 metadynamics meta-inference,6 targeted metadynamics,7,8 Monte Carlo/optimization,9,10 biasing with restraints,11,12 Bayesian ensemble refinement,13 or other simulation-based inference methods.14–16 A direct method like a generative model that outputs structure directly would be preferred,17,18 but a forward model that can connect the chemical shift to structure would still be part of this training.An ideal NMR chemical shift predictor should be translationally and rotationally invariant, be sensitive to both chemically bonded and non-bonded interactions, be able to handle thousands of atoms, predict shifts for multiple atom types, and be differentiable which is required for most of the inference methods mentioned above. There are two broad classes of deep learning architectures that might satisfy these requirements: 3D point cloud neural networks methods that have these equivarianaces built-in,19,20 GNNs.21–23‡ The conceptual difference between these two approaches is that the 3D point cloud networks first build the local environment of each atom to compute atom features and then operate and pool the atom features without considering the molecular graph, whereas the graph neural networks compute atom features using the molecular graph at each layer. Here we use graph neural networks for two reasons. The first is their flexibility of how molecular graphs can be specified: with or without distances, with or without covalent bonds, and as a sparse graph. Secondly, our goal is to apply this model in molecular simulation, where the sparse molecular graph (i.e., a neighbor list) is available as input.
GNNs are now a common approach for deep learning with molecules due to their intuitive connection to molecular graphs and good performance.24 Early examples of graph neural networks can be found in Sperduti and Starita,25 Scarselli et al.,26 Gori et al.27 and recent surveys can be found in Bronstein et al.,21 Dwivedi et al.,22 Wu et al.,28 Battaglia et al.29 The unifying idea of a “graph” neural network is that it takes a graph as input and its output is permutation equivariant. Namely, if you swap two nodes in the input graph, the predicted node labels will swap. In most circumstances, outputs of GNNs are node labels, edge labels, or graph labels. Battaglia et al.29 proposed a unifying notation that encompasses all graph neural networks as a series of nodes, edges, and graph feature operations. Unlike convolutional layers in traditional deep learning,30 there are still numerous competing ideas about GNNs. Wu et al.28 tested about 20 GNN across seven tasks, including chemistry datasets and found no consistently best type. They did find that message-passing methods31 worked well with other deep-learning layers and building blocks.
GNNs are being widely applied in chemistry, especially in quantum machine learning.24,31–33 In this work, we have chosen message passing GNNs due to their similarity to other deep learning layers,28 simplicity, and good performance.24,28 Our models take the molecular graph as input where the features are the atom identities and the edges are feature vectors encoding the edge type (covalent bond or nearby neighbor) and distance. The output is the predicted NMR chemical shift for C, N, or H atoms. This approach is sometimes referred to as enn-s2s.23,34 Our model is trained with three datasets: the RefDB dataset of cross-referenced protein structures with NMR chemical shifts,35 the SHIFTX dataset,36 and a database of organic molecules.37
There are numerous existing NMR chemical shift prediction models. We first review those which are for protein structures. ProShift is a dense neural network with one hidden layer that uses 350 expert chosen input features like electronegativity or dihedral angle with neighbors.38 SPARTA+ uses dense neural networks with 113 expert-chosen input features.39 ShiftX+ uses an ensemble approach with boosting and uses 97 expert-chosen input features.36 ShiftX2 combines ShiftX+ with homology data with a database of known proteins with chemical shift. Note that ProShift, SPARTA+, ShiftX+ and ShiftX2 are not differentiable with respect to atom positions due to the use of input features and homology data. They are also restricted to proteins due to the use of protein-specific features that are not defined for general molecules. CamShift uses a polynomial expansion of the pair-wise distances between an atom and its neighbors to approximate the NMR chemical shift40 and thus is differentiable. This has made it a popular choice41–43 and it is implemented in the PLUMED plugin.44 However, CamShift does not treat side-chains and is insensitive to effects like hydrogen bonding. Of these select methods discussed, ShifX2 is typically viewed as most accurate and CamShift as the most useful for use in inferring protein structure in a molecular simulation. Our goal is to combine the high-accuracy approach of methods like ShiftX2 with the differentiable nature of CamShift. Furthermore, our approach does not require hand-engineered features and instead uses only the elements of the atoms and distances as input. This enables it to be used on both ligands and proteins.
Outside of protein structure, NMR prediction is a classic machine learning problem in chemistry. Paruzzo et al.45 developed a Gaussian process regression framework for prediction of NMR chemical shifts for solids. They used smooth overlap of atomic positions (SOAP) kernel to represent the molecular structural environment. Liu et al.46 used convolutional neural network (CNN) for chemical shift prediction for atoms in molecular crystals. They utilize an atom-centered Gaussian density model for the 3D data representation of a molecule. Rupp et al.47 used kernel learning methods to predict chemical shifts from a small molecule training set with DFT shifts. Jonas and Kuhn48 used graph convolutional neural network to predict 1H and 13C chemical shifts along with the uncertainties. Gerrard et al.49 used kernel ridge regression with molecular features (e.g., angles) and were able to distinguish 3D conformers. Kang et al.50 did similar work, again with a GNN and message passing. This is probably the most similar to our message passing GNN, but they considered small molecules and not 3D structure. An NMR scalar couplings prediction Kaggle competition in 201951 received 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 model entries, among which many top performing approaches utilized message passing GNNs. The data was small organic molecules and so the model tasks was less focused on macromolecules and conformational effects than this work. Examples of others' work using message passing GNNs in chemistry include Raza et al.52 who predicted partial charges of metal organic frameworks, the original message passing paper by Gilmer et al.31 which predicted energies of molecules, and St. John et al.53 who predicted bond disassociation energies. There are also first-principles methods for computing NMR chemical shifts, however we do not compare with these since their computational speed and accuracy are not comparable with empirical methods.54–56
800 model entries, among which many top performing approaches utilized message passing GNNs. The data was small organic molecules and so the model tasks was less focused on macromolecules and conformational effects than this work. Examples of others' work using message passing GNNs in chemistry include Raza et al.52 who predicted partial charges of metal organic frameworks, the original message passing paper by Gilmer et al.31 which predicted energies of molecules, and St. John et al.53 who predicted bond disassociation energies. There are also first-principles methods for computing NMR chemical shifts, however we do not compare with these since their computational speed and accuracy are not comparable with empirical methods.54–56
Model
Our GNN consists of 3 parts: (i) a dense network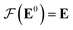 whose input is a rank 3 (omitting batch rank) edge tensor E0 with shape atom number × neighbor number × edge embedding dimension and output E is a rank 3 tensor with shape atom number × neighbor number × edge feature dimension; (ii) a message passing neural network
whose input is a rank 3 (omitting batch rank) edge tensor E0 with shape atom number × neighbor number × edge embedding dimension and output E is a rank 3 tensor with shape atom number × neighbor number × edge feature dimension; (ii) a message passing neural network 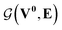 whose input is a rank 2 tensor V0 with shape atom number × node feature dimension and E. Its output is a rank 2 tensor VK with the same shape as V0; (iii) a dense network
whose input is a rank 2 tensor V0 with shape atom number × node feature dimension and E. Its output is a rank 2 tensor VK with the same shape as V0; (iii) a dense network 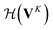 whose output is the chemical shifts. The architecture is shown in Fig. 1. Hyperparameters were optimized on a 20/80 validation/train split of the ShiftX training dataset. The hyperparameters were layer number (1–6 explored), node/edge feature dimensions (16–256, 1–32 respectively), L2 regularization,30 dropout,57 residue,58 and the use of Schütt et al.23 continuous radial basis convolutions on distance (or distance binning), choice of loss, and the use of non-linear activation in final layers. L2 regularization and dropout were found to be comparable to early-stopping on validation, so early-stop was used instead. Model training was found to diverge without residue connections, which others have seen.59 Final layer numbers are K = 4, L = 3, J = 3. The neighbor
whose output is the chemical shifts. The architecture is shown in Fig. 1. Hyperparameters were optimized on a 20/80 validation/train split of the ShiftX training dataset. The hyperparameters were layer number (1–6 explored), node/edge feature dimensions (16–256, 1–32 respectively), L2 regularization,30 dropout,57 residue,58 and the use of Schütt et al.23 continuous radial basis convolutions on distance (or distance binning), choice of loss, and the use of non-linear activation in final layers. L2 regularization and dropout were found to be comparable to early-stopping on validation, so early-stop was used instead. Model training was found to diverge without residue connections, which others have seen.59 Final layer numbers are K = 4, L = 3, J = 3. The neighbor 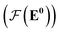 feature dimension is 4 and atom feature dimension is 256. Embeddings are used for inputs. Edges use a 1D embedding for type and distance was tiled 31 times to make a 32 size input. Binning these distances seemed to have negligible affect on performance. The atom element identities were converted to a tensor with 256 dimension embedding look-up.
feature dimension is 4 and atom feature dimension is 256. Embeddings are used for inputs. Edges use a 1D embedding for type and distance was tiled 31 times to make a 32 size input. Binning these distances seemed to have negligible affect on performance. The atom element identities were converted to a tensor with 256 dimension embedding look-up.
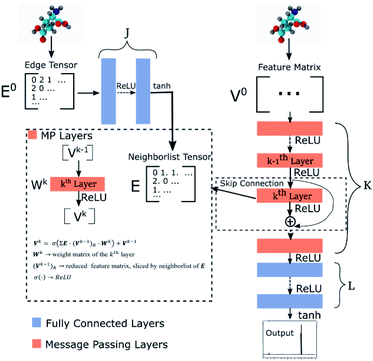 | ||
| Fig. 1 Graph neural network architecture. E0 is the input molecular graph edge features which is inverse distance and chemical bond type (covalent or non-bonded). E is the output neighbor features tensor used for MP layers. V0 is the input feature matrix, consisting only of element types. MP layers have residue connections which are defined in eqn (3). There are K MP layers and L output FC layers. Output is passed through eqn (4) to account for element NMR differences. | ||
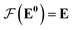 uses ReLU activation60 except in the last layer, where tanh is used. We use the general graph neural network equations from Battaglia et al.29 to define our message passing update function
uses ReLU activation60 except in the last layer, where tanh is used. We use the general graph neural network equations from Battaglia et al.29 to define our message passing update function 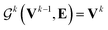 , where k indicates the kth MP layer. We first compute an intermediate edge message based on the edge feature vector and node feature vector of the sender (ϕe):
, where k indicates the kth MP layer. We first compute an intermediate edge message based on the edge feature vector and node feature vector of the sender (ϕe):
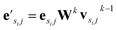 | (1) |
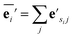 | (2) |
The node update function ϕv gives the new output feature vectors using the aggregated message from eqn (2)
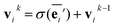 | (3) |
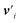 defines the new node features which are the output of the message passing layers. Our choice of message passing and lack of node update function (e.g.,. GRUs in Gilmer et al.31) makes it one of the simplest message passing variants.
defines the new node features which are the output of the message passing layers. Our choice of message passing and lack of node update function (e.g.,. GRUs in Gilmer et al.31) makes it one of the simplest message passing variants.
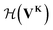 uses a tanh in the penultimate layer and the last layer used linear activation and output dimension Z. Z is the number of unique elements in the dataset. Both
uses a tanh in the penultimate layer and the last layer used linear activation and output dimension Z. Z is the number of unique elements in the dataset. Both 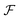 and
and 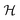 have bias.
have bias.
Output chemical shifts 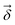 are computed as
are computed as
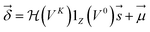
| (4) |
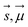 are Z pre-computed standard deviation and means of the refDB chemical shifts for each element. This chosen done to make labels be approximately from −1 to 1 for training. This also has the effect of making any chemical shift for a non-trained element (e.g., N) be 0.
are Z pre-computed standard deviation and means of the refDB chemical shifts for each element. This chosen done to make labels be approximately from −1 to 1 for training. This also has the effect of making any chemical shift for a non-trained element (e.g., N) be 0.
The loss function combined correlation and root mean squared deviation (RMSD):
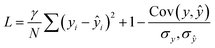 | (5) |
Methods
Data preparation
Our model was trained with three datasets. The first is a paired dataset of 2405 proteins with both X-ray resolved crystal structures and measured NMR chemical shifts created by Zhang et al.35 This was segmented into a fragment dataset of 131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015
015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 256 atom fragments with approximately 1.25 million NMR chemical shifts. To prepare the fragments, each residue in each protein was converted into a fragment. All atoms in prior and subsequent residues were included along with residues which had an atom spatially close to the center residue, but their labels (chemical shifts) were not included. Residue i is close to residue j if an atom from residue i is one of the 16 closest non-bonded atoms of an atom in residue j (i.e., they share a neighbor). We did not use distance cutoffs because neighbor lists are used in subsequent stages and if an atom is not on the neighbor list, it need not be included in the fragment. Additional preprocessing was omitting fragments with missing residues, fixing missing atoms, removing solvent/heteroatoms, ensuring the NMR chemical shifts sequenced aligned with the X-ray structures, and matching chains. This was done with PDBFixer, a part of the OpenMM framework.61 About 5% of residues were excluded due to these constraints and 0.93% were excluded because the resulting fragments could not fit into the 256 atom fragment. Some X-ray resolved crystal structures have multiple possible structures. We randomly sampled 3 of these (with replacement) so that some fragments may be duplicated. The number of fragments including these possible duplicates is 393
256 atom fragments with approximately 1.25 million NMR chemical shifts. To prepare the fragments, each residue in each protein was converted into a fragment. All atoms in prior and subsequent residues were included along with residues which had an atom spatially close to the center residue, but their labels (chemical shifts) were not included. Residue i is close to residue j if an atom from residue i is one of the 16 closest non-bonded atoms of an atom in residue j (i.e., they share a neighbor). We did not use distance cutoffs because neighbor lists are used in subsequent stages and if an atom is not on the neighbor list, it need not be included in the fragment. Additional preprocessing was omitting fragments with missing residues, fixing missing atoms, removing solvent/heteroatoms, ensuring the NMR chemical shifts sequenced aligned with the X-ray structures, and matching chains. This was done with PDBFixer, a part of the OpenMM framework.61 About 5% of residues were excluded due to these constraints and 0.93% were excluded because the resulting fragments could not fit into the 256 atom fragment. Some X-ray resolved crystal structures have multiple possible structures. We randomly sampled 3 of these (with replacement) so that some fragments may be duplicated. The number of fragments including these possible duplicates is 393![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045. This dataset will be called RefDB dataset.
045. This dataset will be called RefDB dataset.
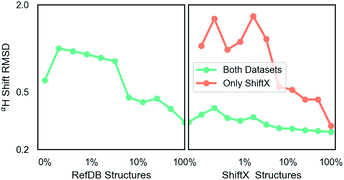
The second dataset was prepared identically and contains 197 in the training and 62 proteins in test. It is the SHIFTX dataset and contains 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878 fragments for training.36 This dataset is higher-quality (see training curves results) due to careful processing by Han et al.36 and does not have multiple possible structures. The SHIFTX test dataset of 62 proteins (7494 fragments) was used for calculation of all test data and was not included in training. These PDB IDs were also removed from the RefDB dataset so that they did not inadvertently enter training. These protein datasets contain C, N and H chemical shifts.
878 fragments for training.36 This dataset is higher-quality (see training curves results) due to careful processing by Han et al.36 and does not have multiple possible structures. The SHIFTX test dataset of 62 proteins (7494 fragments) was used for calculation of all test data and was not included in training. These PDB IDs were also removed from the RefDB dataset so that they did not inadvertently enter training. These protein datasets contain C, N and H chemical shifts.
The third dataset was 369 “metabolites” (biologically relevant organic molecules) from the human metabolome 4.0 database.37 These were converted into 3D conformers with RDKit using the method of Riniker and Landrum.62 Here, each molecule is a fragment and no segmenting of molecules was done. This is referred to as the metabolome dataset.
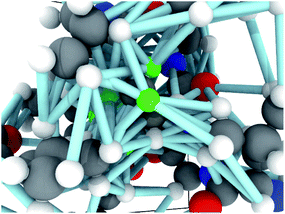
Each molecular fragment is 256 atoms represented as integers indicating element and each atom has up to 16 edges that connect it to both spatial and covalent neighbors. The edges contain two numbers: an encoding of the type of edge (covalent or spatial) and the distance. These two items encode the molecular graph. An example of a fragment from RefDB dataset is shown in Fig. 2. This approach of using covalent bonds and spatial neighbors is somewhat analogous to attention, which is an open area of research in GNNs because its effect is not always positive.63
Training
Training was done in the TensorFlow framework.64 Variables were initialized with the Glorot initializer65 and optimized with Adam optimizer66 with a learning rate schedule of [10−3, 10−3, 10−4, 10−5|10−4, 10−5, 10−5|10−5] where | indicates a switch to a new dataset, except the last which was joint training (see below). Early stopping with patience 5 was done for training. The first dataset was trained with 5 epochs, the second with 50, and the third was combined with the second for final training again with 50 epochs. The second and third dataset when combined have large class imbalance so rejection sampling was used at the residue level where metabolites were counted as a residue. Therefore, each amino acid and metabolites were seen with equal probability. Each epoch was one complete iteration through the dataset. Batch size was 16 fragments (16 × 256 atoms). Training and inference were found to take about 0.0015 seconds per fragment (5.7 μs per shift) with the full model on a single Tesla V100 GPU. Timing was averaged on the SHIFTX dataset (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878 fragments) with loading times excluded.
878 fragments) with loading times excluded.
GNN results
Unless indicated, models were trained only on H chemical shifts for assessing features and training curves. Training on all types requires the metabolome dataset and more complex joint training with rejection sampling. A log–log training curve is shown in Fig. 3 which shows Hα accuracy on the SHIFTX test dataset as a function of amount of training data. 100% here means all training data excluding validation. The SHIFTX dataset is about one tenth the size of RefDB dataset but can provide nearly the same accuracy as shown (0.29 vs. 0.26 RMSD). The RefDB dataset and SHIFTX dataset contain the same proteins, but the SHIFTX dataset are more carefully processed. This shows more careful processing of data is more important than number of structures.The final model performance with all training data is shown in Table 1. A complete breakdown per amino acid and atom name for all models is given in ESI.† Comparisons were done using the SHIFTX+ webserver§ and the latest implementation of CS2Backbone in Plumed.44 We also include the reported performance of SHIFTX+ on their website that had better performance, which could be because in our training and comparisons we did not set pH and temperatures and instead used pH = 5, temperature = 298 K (default for SHIFTX+ model). Our rationale for this decision is that we wanted a model whose input is only molecular structure, and not experimental details such as buffer, pH, temperature etc. Thus we compare to other models with the same restriction. Overall, both the models (H-shift only and all elements) have comparable performance as the state-of-the-art methods. The advantage of our GNN based approach is its efficiency and its applicability to any input molecule type. Table 1 also shows the effect of changing parameter number. There seems to be a sharp transition at the million parameters, meaning models that are much smaller can be used for intermediate accuracy. Some of the major choices of architecture design are also shown: including using dropout 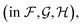 example weighting by class (amino acid), and without non-linear activation. The label variance is computed by comparing repeat measurements of the same protein structure in the RefDB dataset and should be taken as the upper-limit beyond which experimental error is more important. This non-linear scaling of accuracy with parameter number has been previously observed in GNNs.67
example weighting by class (amino acid), and without non-linear activation. The label variance is computed by comparing repeat measurements of the same protein structure in the RefDB dataset and should be taken as the upper-limit beyond which experimental error is more important. This non-linear scaling of accuracy with parameter number has been previously observed in GNNs.67
| HRMSD | Hr | HαRMSD | Hαr | # Para | |
|---|---|---|---|---|---|
| a Reported by SHIFTX+ developers, which includes temperature and pH effects. All others were computed independently in this work. | |||||
| Label variance | 0.176 | 0.965 | 0.138 | 0.967 | |
| Model (H) | 0.459 | 0.781 | 0.264 | 0.878 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 437 |
| Model (all) | 0.527 | 0.718 | 0.293 | 0.844 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 437 |
| Medium | 0.511 | 0.712 | 0.290 | 0.848 | 297![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 181 |
| Small | 0.501 | 0.726 | 0.288 | 0.849 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 123 |
| No RefDB data | 0.514 | 0.711 | 0.306 | 0.838 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 437 |
| No non-linearity | 0.594 | 0.580 | 0.338 | 0.802 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 437 |
| Weighted | 0.471 | 0.766 | 0.274 | 0.865 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 437 |
| SHIFTX+ | 0.455 | 0.787 | 0.248 | 0.890 | |
| SHIFTX+a | 0.378 | 0.836 | 0.197 | 0.932 | |
| UCBShiftX | 0.695 | 0.436 | 0.474 | 0.595 | |
| CS2Backbone | 0.716 | 0.418 | 0.417 | 0.708 | |
Fig. 4 shows the effect of input features on the model. Good model performance is observed even when the input had no distance information and only indicated if atoms are covalently bonded or are non-bonded spatial adjacent neighbors. Knowing the distance provides a small improvement in accuracy. Knowing which atoms are spatially near provides a larger improvement, as shown in the only chemical bonded model. None of the models are close to the label variance, which is the upper-bound of what is possible.
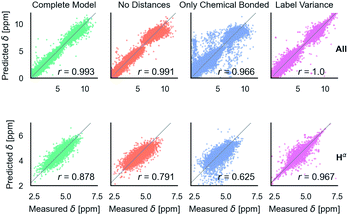 | ||
Fig. 4 Parity plots comparing edge features in the GNN. No distances means that non-bonded neighbors are included, but with no distances. Only chemical bonded means distance is included but only neighbors directly covalently bonded with an atom are included. Label variance is the variation between repeat measured NMR chemical shifts in the RefDB dataset35 and should be taken as the upper-limit beyond which experimental errors are more significant than model fit. 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 points are displayed in the top row, with most points lying on the diagonal. 5031 are shown in the bottom row. r is correlation coefficient, so for example r = 0.966 corresponds to an R2 = 0.933. 520 points are displayed in the top row, with most points lying on the diagonal. 5031 are shown in the bottom row. r is correlation coefficient, so for example r = 0.966 corresponds to an R2 = 0.933. | ||
Multitype model
After training on all element types and with metabolome dataset, model accuracy decreased slightly (Table 1). However, the model has the desired features as shown in Fig. 5. It is able to predict C, N, and H chemical shifts with good correlation and good RMSDs (N: 2.982, C: 1.652, 0.368). The correlation on the important Hα is 0.844 vs. 0.878 in the H model. Including metabolome dataset into training gives a 0.872 correlation on the withheld 20% test (74 molecules). No validation was used for this data because hyperparameters were not tuned. Training on only metabolome dataset gives 0.92 correlation on withheld data and could be taken as an approximate upper-bound because the ratio of trainable parameters (1 million) to data (369) is extreme.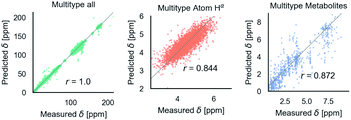 | ||
Fig. 5 Parity plots for the multitype model, which can treat C, N, H atoms and organic molecules. Multitype all is the combined plot for C, N, and H in test proteins and includes 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 163 points. Multitype atom Hα shows the performance of this model on the important Hα atom type. Metabolites is the model performance on metabolites.37 Correlation coefficients are rounded to three digits of precision. 163 points. Multitype atom Hα shows the performance of this model on the important Hα atom type. Metabolites is the model performance on metabolites.37 Correlation coefficients are rounded to three digits of precision. | ||
Fig. 6 shows phenomenological validation of the GNN model on two untrained properties: sensitivity of chemical shifts to secondary structure and hydrogen bonding. The left panel shows the average predicted chemical shifts of each amino acid and secondary structure combination. As expected based on model performance, it does well at predicting the effect of secondary structure on chemical shift. Disagreement is seen on less frequently observed combinations like cystein β-sheets and tryptophan. Most comparable models like ProShift or ShiftX36,38,39 have secondary structure (or dihedral angles) as inputs for computing chemical shifts. The end-to-end training of the GNN captures this effect. The results are consistent with previous studies68–70 which showed downfield shift of Hαδ for β-sheet and upfield shift for α-helix. The right panel shows the effect of breaking a salt bridge (ionic hydrogen bond) between an arginine and glutamic acid on the Hε chemical shift. This atom was chosen because it is observable in solution NMR. White et al.71 computed the chemical shift change to be 0.26 Δδ ppm for breaking this hydrogen bond based on single-amino acid mixture NMR. The molecular graph was fixed here to avoid effects of neighbor lists changing. The model gets a similar upfield shift and thus shows it could be used to model protein–protein interfaces where side-chain–side-chain interactions are critical. It is also consistent with previous reports72,73 where an increasing strength of hydrogen bond was associated with greater deshielding and subsequent downfield shift of Hαδ.
 | ||
| Fig. 6 The model performance on secondary structure and inter-molecular interactions. Left panel shows the effects of secondary structure on Hαδ. Each colored point is the average predicted across test data for amino acid/secondary structure combination. Vertical lines indicate uncertainty. Horizontal line indicates true average from data. Right panel shows the downfield shift of protons participating in a salt bridge (ionic hydrogen bond) between an arginine and glutamic amino acid on separate chains. Experimental data is from White et al.71 indicates relative difference in chemical shift of the NHε proton between an amidated/acetylated ARG – GLU mixed solution vs. amidated/acetylated ARG alone. | ||
Discussion
The GNN is able to compute chemical shifts for arbitrary molecules, is sensitive to both covalent and non-bonded interactions, can parse a million chemical shifts in 5 seconds, and is differentiable with respect to pairwise distances. Model accuracy is comparable to state-of-the-art performance. There is a trade-off between model accuracy and model capacity (number of elements able to predict), leaving an unanswered question of if more trainable parameters are required to diminish the gap. Training is complex since there are three datasets and they are of varying quality and sizes. Effort should be invested in better quality protein structure data. Finally, there is a large number of message passing choices and more exploration could be done.Conclusion
This work presents a new class of chemical shift predictors that requires no a priori knowledge about what features affect chemical shift. The GNN input is only the underlying molecular graph and elements and requires no details about amino acids, protein secondary structure or other features. The GNN is close to state of the art in performance and able to take arbitrary input molecules, including organic molecules. The model is highly-efficient and differentiable, making it possible to use in molecular simulation. Important physical properties also arise purely from training: β-sheets formation causes downfield shifts and breaking salt bridges causes upfield shifts. This work opens a new direction for connecting NMR experiments to molecular structure via deep learning.All code available at https://github.com/whitead/graphnmr.
Data availability
Data is available at https://github.com/ur-whitelab/nmrdata.Author contributions
Z. Y. and A. D. W. designed research; Z. Y. and A. D. W. performed research; Z. Y., M. C. and A. D. W. analyzed the data; Z. Y., M. C. and A. D. W. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant No. (1764415 and 1751471). Research reported in this work was supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R35GM137966. We thank the Center for Integrated Research Computing (CIRC) at the University of Rochester for providing computational resources and technical support.Notes and references
- J. Cavanagh, Protein NMR Spectroscopy: Principles and Practice, Elsevier, 1995 Search PubMed.
- B. Brutscher, I. C. Felli, S. Gil-Caballero, T. Hošek, R. Kümmerle, A. Piai, R. Pierattelli and Z. Sólyom, Adv. Exp. Med. Biol., 2015, 870, 49–122 CrossRef CAS PubMed.
- P. Selenko, D. P. Frueh, S. J. Elsaesser, W. Haas, S. P. Gygi and G. Wagner, Nat. Struct. Mol. Biol., 2008, 15, 321–329 CrossRef CAS PubMed.
- A. D. White and G. A. Voth, J. Chem. Theory Comput., 2014, 10, 3023–3030 CrossRef CAS PubMed.
- D. B. Amirkulova and A. D. White, Mol. Simul., 2019, 45, 1285–1294 CrossRef CAS.
- T. Löhr, A. Jussupow and C. Camilloni, J. Chem. Phys., 2017, 146, 165102 CrossRef PubMed.
- A. D. White, J. F. Dama and G. A. Voth, J. Chem. Theory Comput., 2015, 11, 2451–2460 CrossRef CAS PubMed.
- F. Marinelli and J. D. Faraldo-Gómez, Biophys. J., 2015, 108, 2779–2782 CrossRef CAS PubMed.
- O. F. Lange, P. Rossi, N. G. Sgourakis, Y. Song, H. W. Lee, J. M. Aramini, A. Ertekin, R. Xiao, T. B. Acton, G. T. Montelione and D. Baker, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10873–10878 CrossRef CAS PubMed.
- H. R. Eghbalnia, L. Wang, A. Bahrami, A. Assadi and J. L. Markley, J. Biomol. NMR, 2005, 32, 71–81 CrossRef CAS PubMed.
- K. Lindorff-Larsen, R. B. Best, M. A. DePristo, C. M. Dobson and M. Vendruscolo, Nature, 2005, 433, 128–132 CrossRef CAS PubMed.
- J. Dolenc, J. H. Missimer, M. O. Steinmetz and W. F. Van Gunsteren, J. Biomol. NMR, 2010, 47, 221–235 CrossRef CAS PubMed.
- G. Hummer and J. Köfinger, J. Chem. Phys., 2015, 143, 243150 CrossRef PubMed.
- K. Cranmer, J. Brehmer and G. Louppe, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(48), 30055–30062 CrossRef CAS PubMed.
- M. Bonomi, G. T. Heller, C. Camilloni and M. Vendruscolo, Curr. Opin. Struct. Biol., 2017, 42, 106–116 CrossRef CAS PubMed.
- W. Boomsma, J. Ferkinghoff-Borg and K. Lindorff-Larsen, PLoS Comput. Biol., 2014, 10, e1003406 CrossRef PubMed.
- W. Wang and R. Gómez-Bombarelli, npj Comput. Mater., 2019, 5, 125 CrossRef.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Science, 2019, 365(6457) CrossRef PubMed.
- N. Thomas, T. Smidt, S. Kearnes, L. Yang, L. Li, K. Kohlhoff and P. Riley, 2018, arXiv:1802.08219.
- B. Anderson, T.-S. Hy and R. Kondor, 2019, arXiv:1906.04015.
- M. M. Bronstein, J. Bruna, Y. Lecun, A. Szlam and P. Vandergheynst, IEEE Signal Process. Mag., 2017, 34, 18–42 Search PubMed.
- V. P. Dwivedi, C. K. Joshi, T. Laurent, Y. Bengio and X. Bresson, 2020, arXiv:2003.00982.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 6–13 CrossRef PubMed.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530 RSC.
- A. Sperduti and A. Starita, IEEE Trans. Neural Netw., 1997, 8, 714–735 CAS.
- F. Scarselli, A. C. Tsoi, M. Gori and M. Hagenbuchner, Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), 2004, vol. 3138, pp. 42–56 Search PubMed.
- M. Gori, G. Monfardini and F. Scarselli, Proc. Int. Jt. Conf. Neural Networks, 2005, 2, 729–734 Search PubMed.
- Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang and P. S. Yu, IEEE Trans. Neural Netw. Learn. Syst., 2020, 1–21 Search PubMed.
- P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro, R. Faulkner, C. Gulcehre, F. Song, A. Ballard, J. Gilmer, G. Dahl, A. Vaswani, K. Allen, C. Nash, V. Langston, C. Dyer, N. Heess, D. Wierstra, P. Kohli, M. Botvinick, O. Vinyals, Y. Li and R. Pascanu, arXiv Prepr. arXiv1806.01261, 2018.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, 34th Int. Conf. Mach. Learn. ICML 2017, Sydney, NSW, Australia, 2017, pp. 2053–2070 Search PubMed.
- O. A. von Lilienfeld, K. R. Müller and A. Tkatchenko, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- P. B. Jørgensen, K. W. Jacobsen and M. N. Schmidt, 32nd Conf. Neural Inf. Process. Syst., 2018 Search PubMed.
- H. Zhang, S. Neal and D. S. Wishart, J. Biomol. NMR, 2003, 25, 173–195 CrossRef CAS PubMed.
- B. Han, Y. Liu, S. W. Ginzinger and D. S. Wishart, J. Biomol. NMR, 2011, 50, 43–57 CrossRef CAS PubMed.
- D. S. Wishart, Y. D. Feunang, A. Marcu, A. C. Guo, K. Liang, R. Vázquez-Fresno, T. Sajed, D. Johnson, C. Li, N. Karu, Z. Sayeeda, E. Lo, N. Assempour, M. Berjanskii, S. Singhal, D. Arndt, Y. Liang, H. Badran, J. Grant, A. Serra-Cayuela, Y. Liu, R. Mandal, V. Neveu, A. Pon, C. Knox, M. Wilson, C. Manach and A. Scalbert, Nucleic Acids Res., 2018, 46, D608–D617 CrossRef CAS PubMed.
- J. Meiler, J. Biomol. NMR, 2003, 26, 25–37 CrossRef CAS PubMed.
- Y. Shen and A. Bax, J. Biomol. NMR, 2010, 48, 13–22 CrossRef CAS PubMed.
- K. J. Kohlhoff, P. Robustelli, A. Cavalli, X. Salvatella and M. Vendruscolo, J. Am. Chem. Soc., 2009, 131, 13894–13895 CrossRef CAS PubMed.
- D. Granata, C. Camilloni, M. Vendruscolo and A. Laio, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6817–6822 CrossRef CAS PubMed.
- P. Robustelli, K. Kohlhoff, A. Cavalli and M. Vendruscolo, Structure, 2010, 18, 923–933 CrossRef CAS PubMed.
- D. B. Amirkulova and A. D. White, J. Theor. Comput. Chem., 2018, 17, 1840007 CrossRef CAS.
- M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello, P. Banáš, A. Barducci, M. Bernetti, P. G. Bolhuis, S. Bottaro, D. Branduardi and Others, Nat. Methods, 2019, 16, 670–673 CrossRef PubMed.
- F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed.
- S. Liu, J. Li, K. C. Bennett, B. Ganoe, T. Stauch, M. Head-Gordon, A. Hexemer, D. Ushizima and T. Head-Gordon, J. Phys. Chem. Lett., 2019, 10, 4558–4565 CrossRef CAS PubMed.
- M. Rupp, R. Ramakrishnan and O. A. von Lilienfeld, J. Phys. Chem. Lett., 2015, 6, 3309–3313 CrossRef CAS.
- E. Jonas and S. Kuhn, J. Cheminf., 2019, 11, 1–7 CAS.
- W. Gerrard, L. A. Bratholm, M. J. Packer, A. J. Mulholland, D. R. Glowacki and C. P. Butts, Chem. Sci., 2020, 11, 508–515 RSC.
- S. Kang, Y. Kwon, D. Lee and Y.-S. Choi, J. Chem. Inf. Model., 2020, 60, 3765–3769 CrossRef CAS PubMed.
- L. A. Bratholm, W. Gerrard, B. Anderson, S. Bai, S. Choi, L. Dang, P. Hanchar, A. Howard, G. Huard, S. Kim, Z. Kolter, R. Kondor, M. Kornbluth, Y. Lee, Y. Lee, J. P. Mailoa, T. T. Nguyen, M. Popovic, G. Rakocevic, W. Reade, W. Song, L. Stojanovic, E. H. Thiede, N. Tijanic, A. Torrubia, D. Willmott, C. P. Butts, D. R. Glowacki and K. participants, A community-powered search of machine learning strategy space to find NMR property prediction models, 2020 Search PubMed.
- A. Raza, A. Sturluson, C. M. Simon and X. Fern, J. Phys. Chem. C, 2020 Search PubMed.
- P. C. St. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Nat. Commun., 2020, 11, 1–12 CrossRef PubMed.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 2451011–2451013 CrossRef.
- J. A. Vila, Y. A. Arnautova, O. A. Martin and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16972–16977 CrossRef CAS PubMed.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, J. Mach. Learn. Res., 2014, 15, 1929–1958 Search PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., 2016, 770–778 Search PubMed.
- G. Li, M. Muller, A. Thabet and B. Ghanem, Proc. IEEE Int. Conf. Comput. Vis., 2019, 9266–9275 Search PubMed.
- X. Glorot, A. Bordes and Y. Bengio, J. Mach. Learn. Res., 2011, 315–323 Search PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L. P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS PubMed.
- B. Knyazev, G. W. Taylor and M. R. Amer, Adv. Neural Inform. Process Syst., 2019, 4202–4212 Search PubMed.
- M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, M. Kudlur, J. Levenberg, R. Monga, S. Moore, D. G. Murray, B. Steiner, P. Tucker, V. Vasudevan, P. Warden, M. Wicke, Y. Yu and X. Zheng, Proc. 12th USENIX Symp. Oper. Syst. Des. Implementation, OSDI 2016, 2016, pp. 265–283 Search PubMed.
- X. Glorot and Y. Bengio, J. Mach. Learn. Res., 2010, 249–256 Search PubMed.
- D. P. Kingma and J. L. Ba 3rd, Int. Conf. Learn. Represent. ICLR 2015 – Conf. Track Proc., 2015 Search PubMed.
- A. Loukas, Int. Conf. Learn. Represent., 2019 Search PubMed.
- S. P. Mielke and V. V. Krishnan, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 54, 141–165 CrossRef CAS PubMed.
- F. Avbelj, D. Kocjan and R. L. Baldwin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17394–17397 CrossRef CAS PubMed.
- L. Szilágyi and O. Jardetzky, J. Magn. Reson., 1989, 83, 441–449 Search PubMed.
- A. D. White, A. J. Keefe, J. R. Ella-Menye, A. K. Nowinski, Q. Shao, J. Pfaendtner and S. Jiang, J. Phys. Chem. B, 2013, 117, 7254–7259 CrossRef CAS PubMed.
- S. P. Mielke and V. Krishnan, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 54, 141–165 CrossRef CAS PubMed.
- A. M. Da Silva, A. Ghosh and P. Chaudhuri, J. Phys. Chem. A, 2013, 117, 10274–10285 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01895g |
| ‡ We do not consider featurization like computing dihedral angles or electronegativity of atoms because they cannot generalize to arbitrary structures and derivatives do not always exist. |
| § http://shiftx2.ca/. |
| This journal is © The Royal Society of Chemistry 2021 |