Open Access Article
Open Access ArticlePolariton-assisted manipulation of energy relaxation pathways: donor–acceptor role reversal in a tuneable microcavity†
Dmitriy
Dovzhenko
 *ab,
Maksim
Lednev
a,
Konstantin
Mochalov
ac,
Ivan
Vaskan
acd,
Yury
Rakovich
ef,
Alexander
Karaulov
*ab,
Maksim
Lednev
a,
Konstantin
Mochalov
ac,
Ivan
Vaskan
acd,
Yury
Rakovich
ef,
Alexander
Karaulov
 g and
Igor
Nabiev
g and
Igor
Nabiev
 *agh
*agh
aNational Research Nuclear University MEPhI (Moscow Engineering Physics Institute), 115409 Moscow, Russia. E-mail: dovzhenkods@gmail.com
bDepartment of Physics and Astronomy, University of Southampton, Southampton, SO17 1BJ, UK
cShemyakin–Ovchinnikov Institute of Bioorganic Chemistry, Russian Academy of Sciences, 117997 Moscow, Russia
dMoscow Institute of Physics and Technology, Dolgoprudny, 141701 Moscow, Russia
eIKERBASQUE, Basque Foundation for Science, 48009 Bilbao, Spain
fDonostia International Physics Center, Polímeros y Materiales Avanzados: Física, Química y Tecnología, UPV-EHU, Centro de Física de Materiales (MPC, CSIC-UPV/EHU), 20018 Donostia – San Sebastian, Spain
gSechenov First Moscow State Medical University (Sechenov University), 119146 Moscow, Russia
hLaboratoire de Recherche en Nanosciences, LRN-EA4682, Université de Reims Champagne-Ardenne, 51100 Reims, France. E-mail: igor.nabiev@univ-reims.fr
First published on 31st August 2021
Abstract
Resonant interaction between excitonic transitions of molecules and localized electromagnetic field allows the formation of hybrid light–matter polaritonic states. This hybridization of the light and the matter states has been shown to significantly alter the intrinsic properties of molecular ensembles placed inside the optical cavity. Here, we have observed strong coupling of excitonic transition in a pair of closely located organic dye molecules demonstrating an efficient donor-to-acceptor resonance energy transfer with the mode of a tuneable open-access cavity. Analysing the dependence of the relaxation pathways between energy states in this system on the cavity detuning, we have demonstrated that predominant strong coupling of the cavity photon to the exciton transition in the donor dye molecule can lead not only to an increase in the donor–acceptor energy transfer, but also to an energy shift large enough to cause inversion between the energy states of the acceptor and the mainly donor lower polariton energy state. Furthermore, we have shown that the polariton-assisted donor–acceptor chromophores' role reversal or “carnival effect” not only changes the relative energy levels of the donor–acceptor pair, but also makes it possible to manipulate the energy flow in the systems with resonant dipole–dipole interaction and direct energy transfer from the acceptor to the mainly donor lower polariton state. Our experimental data are the first confirmation of the theoretically predicted possibility of polariton-assisted energy transfer reversal in FRET systems, thus paving the way to new avenues in FRET-imaging, remote-controlled chemistry, and all-optical switching.
Introduction
Strong light–matter coupling is a quantum electrodynamics phenomenon that takes place when the rate of resonant energy exchange (i.e., coupling strength) between the exciton transition in matter and the resonant localized electromagnetic field is higher than the competing decay and decoherence processes. Light–matter coupling then leads to the formation of two new “hybrid” light–matter (polaritonic) states with different energies, instead of the two original molecular and electromagnetic field energy states. Once the strong coupling regime is reached, the coupled system exhibits new properties possessed by neither the molecules nor the cavity.1 Hence, by controlling the coupling strength, it is possible to modulate (or even control) various properties of the system, including the eigenenergy, excited state lifetime, efficiency and efficient distances of energy transfer, conductivity, etc.2 This paves the way to a wide variety of breakthrough practical applications, such as modification of chemical reactivity,3 enhanced conductivity,4 development of low-threshold sources of coherent emission,5 and even polariton simulators and logic.6,7Recently it has been demonstrated that strong coupling can modulate both distance and efficiency of Förster resonance energy transfer (FRET).8,9 FRET is a process of non-radiative energy transfer from one fluorophore (donor) to another one (acceptor). The FRET effect only occurs when several conditions are satisfied: (i) the donor emission spectrum should overlap with the acceptor absorption spectrum; (ii) the donor and acceptor fluorophores should be in a favourable mutual orientation, and, (iii) since the FRET efficiency is inversely proportional to the sixth power of the distance between the fluorophores, the distance between the donor and the acceptor should not exceed the Förster limit (10 nm). When these conditions are satisfied, the FRET effect results in a decreased donor fluorescence emission accompanied by a simultaneously increased acceptor fluorescence emission.
Under the strong coupling regime, both donor and acceptor excitonic states could be coupled to the same microcavity optical mode, which may act as a mediator. This mediation can make it possible not only to increase the efficient distances of the energy transfer to values ten times larger than the Förster limit (to more than 100 nm),9 but also to ensure an up to sevenfold increase in the rate of energy transfer.8 This increase in the energy transfer rate leads to a significant decrease in donor fluorescence in the presence of the acceptor. As a result, the energy transfer efficiency, which is characterized by the ratio between the intensities of the donor fluorescence in the presence and absence of the acceptor, will be also significantly increased. It has been reported recently that under the strong coupling regime the energy transfer efficiency may be increased from 0.55 to 0.90.8
The possibility of increasing and controlling the FRET efficiency is promising for the development of many photonic applications, specifically for biomedical research. In this regard, one of the most powerful photonic nanotools are oligonucleotide-based molecular beacons, which are used in biosensing and specific gene identification,10–15 RNA imaging,14,16–18 revealing nucleic acid mutations,19 monitoring gene expression20 and protein–protein interactions,21 nanomedicine,14,22 cell-surface glycosylation imaging,23etc. All these applications are based on the same principle: a specifically designed molecular beacon is a circled oligonucleotide, with the donor and acceptor dye molecules conjugated to its ends and located in close vicinity to each other; hence, a strong donor-to-acceptor FRET occurs (Fig. S1 in the (ESI†)). The possibility of controlling the FRET efficiency within the molecular beacon with the use of light–matter interaction in various regimes8,24 can extend their applications. Moreover, despite the numerous published experimental studies on the use of light–matter interactions for controlling FRET, there are still some theoretical predictions to be fulfilled.
Polariton-assisted energy transfer between spatially separated molecules has been extensively studied in various configurations.8,9,25 In ref. 25, hybrid polaritonic states have been demonstrated to be an efficient energy transfer pathway between two spatially separated J-aggregates with an initially negligible direct energy transfer via dipole–dipole coupling. However, for many practical applications that we have mentioned above, it is even more intriguing to have a way to alternate the energy relaxation in a mixed media where the donor and acceptor molecules are located in close vicinity to each other, and the FRET effect is mediated by direct dipole–dipole coupling between them. In ref. 26, hybridization of the light and the matter states in a microcavity filled with a blend of two BODIPY fluorescent dyes with similar properties has been investigated. Here, the electromagnetic microcavity modes of light have been found to be coupled, at the same extent, with both donor and acceptor exciton transitions. It has been shown that, in this system, direct dipole–dipole coupling is more efficient than the energy transfer via strong coupling. Interestingly, the strong coupling to only one of the two excitonic states of the system has also been shown to be promising if the control over relaxation pathways in FRET systems has to be obtained. In ref. 27, the authors have theoretically demonstrated that, whereas exclusive strong coupling of the cavity photon to the donor states can enhance the energy transfer to the acceptors, the reverse is not true. On the other hand, it has been shown27 that, in the case of strong coupling of resonant electromagnetic modes exclusively with the acceptor, the energy of the upper polariton could be raised to values higher than the donor exciton energy. This allows energy transfer from the acceptor polariton state to the bare donor exciton with a rate of about 1 ns−1 even at a separation distance between the donor and acceptor of up to 1 μm,27,28 leading to the chromophore role reversal or “carnival effect”. It is interesting to investigate the possibility of combining these effects by means of strong coupling of exclusively the donor state to the cavity photon with a large coupling strength. This should lead to the formation of a polariton state with a relatively large fraction of the donor exciton and a small fraction of the acceptor exciton, with the energy lower than that of the original acceptor state. However, such a modification will require very strong coupling to ensure significant alteration of energy levels.
In this study, we have investigated the dependence of the photoluminescence (PL) properties of the oligonucleotide-based molecular beacons with a donor–acceptor pair of closely located FAM and TAMRA organic dyes in a tuneable microcavity in the strong coupling regime and have analysed the dependence of the polaritonic state population on the detuning of the optical microcavity mode. We have estimated the possibility of changing the relaxation pathways by varying the degree of the exciton–photon mixing in polaritonic states and analysed the specific situation when the donor is much stronger coupled with the optical mode than the acceptor is. For the best of our knowledge, we are the first to experimentally demonstrate the possibility to reverse the donor and acceptor roles (“carnival effect”) within a donor–acceptor pair of organic dyes, which has been theoretically investigated by the group of Joel Yuen-Zhou.27
Results and discussion
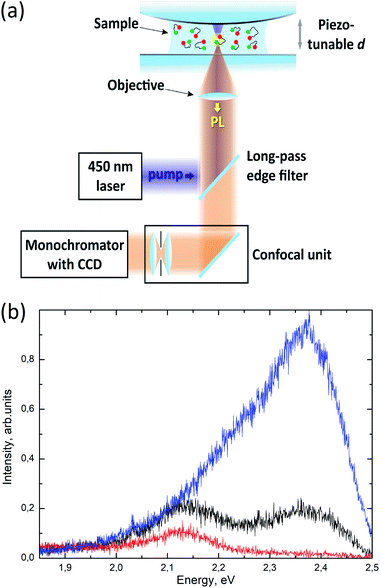
In order to investigate the feasibility of controlling the resonant energy transfer in a donor–acceptor pair of closely located organic dyes, we have employed a tuneable microcavity with a relatively small mode volume previously developed in our group.29–31 Briefly, the tuneable microcavity unit was composed of plane and convex (curvature radius, 77.3 mm) mirrors that form an unstable tuneable Fabry–Perot microcavity (Fig. 1a, see the ESI† for details). The upper mirror was made convex in order to satisfy the plane-parallelism condition at one point, thus minimizing the mode volume. The plane bottom mirror was mounted on top of a Z-piezo positioner, which provided fine tuning of the microcavity length in the range of up to 10 μm with a nanometre precision. The plane-convex design of the tuneable microcavity is characterized by rather high quality factors (up to several hundred units), whereas the mode volumes can be as low as tens of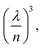 thus combining the advantages of both optical and plasmonic cavities.31 In this study, the quality factor of the microcavity mode was about 35 and the mode volume was about
thus combining the advantages of both optical and plasmonic cavities.31 In this study, the quality factor of the microcavity mode was about 35 and the mode volume was about 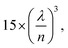 for cavity mode spectral detunings from exciton resonances, which have been used for PL anticrossing measurements and lower polariton population analysis. In order to support the claims about the mode volume in our microcavity, we made numerical calculations of the electromagnetic field distribution in it using the finite-element method (see the ESI† for details). Previously, we have demonstrated the advantages of the developed tuneable microcavity, such as a controllable distance between the mirrors with a nanometre accuracy and a small mode volume, which result in a much higher Rabi splitting energies compared to the standard optical microcavities.29 In particular, we have demonstrated a strong coupling of the ensemble of Rhodamine 6G molecules with a Rabi splitting as high as 225 meV at room temperature, which has been previously shown only for the case of surface plasmon-polaritons. A drawback of the tuneable setup developed is that we cannot observe strong coupling in the transmission spectra, which can be due to two effects. First, the area of the cavity excited with white light in transmission measurements is larger than the area of spatial localization of the coupled mode. Thus, the number of transmitted uncoupled photons from the white LED considerably exceeds the number of photons emitted from the strongly coupled states. Second, it has been shown32 that, for a low-finesse cavity, the observed values of Rabi splitting in transmission and PL measurements are significantly different. In particular, in the case of a large broadening of molecular exciton transition, high values of splitting in PL measurements can still be observed, while the splitting in transmission measurements at the same parameters tends to zero. On the other hand, strictly speaking, these calculations have been made for another type of cavity, and detailed theoretical analysis of the strong coupling of the ensembles of organic molecules in the unstable metal-mirror microcavity requires separate investigation. However, the microcavity developed here, which combines the advantages of a low energy dissipation in an optical microcavity and a small mode volume, usually characteristic of a plasmonic cavity, significantly increases the number of materials suitable for operation in a strong coupling regime, thus paving the way to plenty of new practical applications. In this study, we employed this set-up to achieve a high Rabi splitting energy of hybrid states formed by the exciton transitions in donor–acceptor pairs of organic dyes exhibiting the FRET effect and the localized resonant electromagnetic field.
for cavity mode spectral detunings from exciton resonances, which have been used for PL anticrossing measurements and lower polariton population analysis. In order to support the claims about the mode volume in our microcavity, we made numerical calculations of the electromagnetic field distribution in it using the finite-element method (see the ESI† for details). Previously, we have demonstrated the advantages of the developed tuneable microcavity, such as a controllable distance between the mirrors with a nanometre accuracy and a small mode volume, which result in a much higher Rabi splitting energies compared to the standard optical microcavities.29 In particular, we have demonstrated a strong coupling of the ensemble of Rhodamine 6G molecules with a Rabi splitting as high as 225 meV at room temperature, which has been previously shown only for the case of surface plasmon-polaritons. A drawback of the tuneable setup developed is that we cannot observe strong coupling in the transmission spectra, which can be due to two effects. First, the area of the cavity excited with white light in transmission measurements is larger than the area of spatial localization of the coupled mode. Thus, the number of transmitted uncoupled photons from the white LED considerably exceeds the number of photons emitted from the strongly coupled states. Second, it has been shown32 that, for a low-finesse cavity, the observed values of Rabi splitting in transmission and PL measurements are significantly different. In particular, in the case of a large broadening of molecular exciton transition, high values of splitting in PL measurements can still be observed, while the splitting in transmission measurements at the same parameters tends to zero. On the other hand, strictly speaking, these calculations have been made for another type of cavity, and detailed theoretical analysis of the strong coupling of the ensembles of organic molecules in the unstable metal-mirror microcavity requires separate investigation. However, the microcavity developed here, which combines the advantages of a low energy dissipation in an optical microcavity and a small mode volume, usually characteristic of a plasmonic cavity, significantly increases the number of materials suitable for operation in a strong coupling regime, thus paving the way to plenty of new practical applications. In this study, we employed this set-up to achieve a high Rabi splitting energy of hybrid states formed by the exciton transitions in donor–acceptor pairs of organic dyes exhibiting the FRET effect and the localized resonant electromagnetic field.
The donor–acceptor pairs of organic dyes employed in our experiments consisted of 6 carboxyfluorescein (FAM) used as a donor and tetramethylrhodamine (TAMRA) as an acceptor. The distance between the donor and acceptor dye molecules conjugated with the opposite termini of the oligonucleotide-based molecular beacon is determined by the diameter of the DNA double helix (about 2 nm), which is small enough to ensure efficient direct dipole–dipole coupling between them (Fig. S1†).33 The details on the chemical structures of the oligonucleotide-based molecular beacon and dye molecules, as well as on the optical properties of the dyes, are presented in the ESI.†
Fig. 1b shows the PL spectra of oligonucleotide-based molecular beacons labelled with FAM alone, TAMRA alone, or both FAM and TAMRA dyes placed onto the bottom mirror of the setup that were measured in the absence of the upper mirror; i.e., the beacons were located outside the microcavity.
FAM is a well-known organic dye with a quantum yield as high as 97%,34 with the main exciton transition characterized by a transition dipole moment ranging from 7 to 12 D (ref. 34) and the main emission peak maximum at about 2.36 eV. The TAMRA dye has a much lower quantum yield of about 22% (ref. 35) and comparable values of the transition dipole moment of about 9 D.36 The PL emission maximum of the TAMRA dye solution is about 2.13 eV. However, it is noteworthy that the transition dipole moments and PL quantum yields of the dyes may be changed upon their conjugation with the oligonucleotide due to the possible appearance of new intermolecular interactions in the conjugated samples. Fig. 1b shows that the PL spectra of the FAM–TAMRA donor–acceptor pair excited at 450 nm could be obtained by linear superposition of the PL spectra of these dyes measured separately, which indicates the absence of direct ground-state interaction between these dye molecules in the molecular beacon. Despite the low quantum yield, the PL emission from TAMRA was stronger than that from FAM in the case of the donor–acceptor pair operating in the FRET regime. The efficiency of the resonance energy transfer from FAM to TAMRA molecules was estimated to be about 80% (see the ESI† for details).
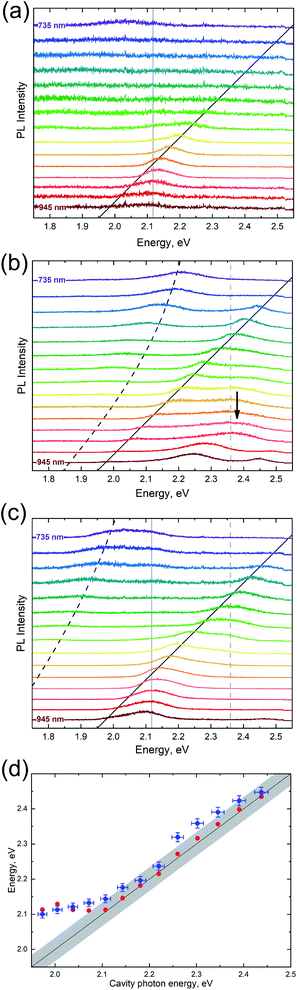
We further analysed the PL spectra of the dyes conjugated with the oligonucleotide of the molecular beacon alone and in the form of a donor–acceptor pair operating in the FRET regime and placed into the tuneable microcavity at different cavity detunings (Fig. 2). The cavity mode tuning has been performed by changing the distance between the microcavity mirrors (d) from 735 to 945 nm with 15 nm steps.
The corresponding PL emission spectra are shown in Fig. 2a–c. It is worth mentioning that the specific properties of our microcavity allowed us to detect the PL emission from molecules weakly coupled to the transverse modes of both the lowest and higher orders of the cavity (see the ESI† for details). This PL was associated with the enhanced emission peak following the cavity mode, slightly blue-shifted relative to the cavity photon spectral position corresponding to the lowest-order transverse mode of the cavity. Qualitatively, this blue shift can be understood considering the difference in signal collection efficiency between the transmission and PL measurements (see the ESI† for details). The resulting emission corresponding to this peak is satisfactorily fitted in the weak coupling approximation. Fig. 2d presents the experimentally measured dependence of the spectral position of the emission maximum associated with the weakly coupled molecules on the cavity mode detuning extracted from Fig. 2c and the corresponding model calculations. It can be seen that the calculated dependence is in good agreement with the experimental data, the difference was not exceeding the full-width-at-half-maximum (FWHM) of the cavity mode. It is also important to note that the large shift of the emission peak from the cavity mode in the region of low mode energies was due to the poor spectral overlap of the dye PL spectra with the lowest-order transverse cavity mode. Similar PL emissions from weakly coupled molecules were observed for the FAM and TAMRA dyes separately (Fig. 2a and b). It is noteworthy that, due to the non-resonant excitation through the lower mirror of the microcavity, the power of excitation inside the cavity depended on the cavity detuning. Although the intensities of the measured PL spectra presented in Fig. 2 are not calibrated against the excitation power, the necessary corrections have been made in the analysis presented below.
The molecular beacons labelled with the TAMRA dye alone and placed into the microcavity exhibited only the emission from weakly coupled molecules (Fig. 2a). We speculate that this can be caused by either the local interaction with the beacon itself or large non-radiative losses36 of excitation in the molecule leading to the loss of energy that is too fast to effectively populate the polaritonic states from the excitonic reservoir. It is noteworthy that the change in the emission intensity from the weakly coupled states of TAMRA was much bigger than that for the case of the molecular beacon labelled with the FAM dye alone. Indeed, the Purcell PL intensity enhancement for emitters with a lower quantum yield is known to be stronger than that for emitters with a higher quantum yield, because the Purcell effect changes only the radiative relaxation rate.37
The PL of molecular beacons labelled with the FAM dye alone and placed into the microcavity is shown in Fig. 2b. Considering the impact of the ensemble of weakly coupled molecules, one can clearly see the anticrossing behaviour of the PL emission peaks for cavity energies larger than 2.25 eV. The positions of the low-energy peaks in the emission spectra corresponding to the lower polaritonic branch (LPB) allow one to estimate the Rabi splitting energy to be about 457 meV, which is a rather high value for this type of a cavity. It is well known that the observation of the emission from the upper polariton branch (UPB) is difficult due to the fast relaxation (tens of femtoseconds) of the UPB to the dark states in the exciton reservoir.38 However, due to the low quality factor of the microcavity, the characteristic lifetime of a photon in the cavity is ∼10 fs, which makes it theoretically possible to observe emission from the UPB. In the PL experiments we have observed the emission peak that could be associated with the upper polariton for deeply negative detuning, which is marked in Fig. 2b. However, it is difficult to estimate the exact positions of the associated emission spectra for most other values of detuning due to the intrinsically low intensity of UPB emission, the background emission from bare donor molecules, the large spectral broadening, and the limited spectral range of detection in the setup used.
Fig. 2c shows the PL spectra recorded for different detunings of the microcavity containing molecular beacons labelled with both FAM and TAMRA dyes. As in the case of the molecular beacons labelled with the FAM or TAMRA dye alone, one can see a peak corresponding to weakly coupled molecules, whose spectral position follows the cavity photon energy with a small blue shift. The experimental and calculated dependences of the spectral position of this peak on the cavity photon energy are shown in Fig. 2d. It is worth mentioning that the relative intensity of this peak was changed relative to the emission peak of the beacons labelled with FAM alone due to the resonance energy transfer between bare donor and acceptor states. Indeed, its intensity was lower than that in the case of molecular beacons labelled with FAM alone in the donor spectral region and higher than that in the case of molecular beacons labelled with TAMRA alone in the acceptor spectral region. These effects were certainly due to the remaining highly efficient resonance energy exchange through dipole–dipole interaction upon the deposition of the molecular beacons labelled with both FAM and TAMRA dyes operating in the FRET regime inside the cavity. It is important to note that, in contrast to the case of molecular beacons labelled with the FAM dye alone, no signal from bare donor states was detected at negative detunings in the cavity photon energy range from 2.0 to 2.3 eV. The fact that the donor–acceptor dye pair outside the cavity exhibited emission from both donor and acceptor dyes with a FRET efficiency of about 80% indicated that the ratio between the donor–acceptor energy transfer rate and the donor radiative relaxation rate inside the cavity was increased. Indeed, when we consider the change of the efficiency of FRET between the donor and acceptor, we compare the emission spectra of the FRET pair outside the cavity, emission from FAM only in the cavity, and the FRET pair in the cavity. First, we estimate the FRET efficiency from the emission spectra for beacons with a pair of dyes outside the cavity using the common approach described in the ESI.† The estimated value is about 80%, which is based on the ratio between the fluorescence intensities of the donor and acceptor. Second, we compare the intensity of emission at the energy of bare donor emission maximum (about 2.3 eV) for the FAM-only beacons inside the microcavity (Fig. 2b) with the intensity of emission at the energy of the bare donor emission maximum for the beacons with the FRET pair inside the microcavity (Fig. 2c) in the cavity photon energy range from 2.0 to 2.3 eV. In this range, the cavity mode is detuned from the donor bare state and the emission at the energy corresponding to the bare states reflects the population. In the case of a cavity with FAM alone, the emission is observed from the bare states in the discussed range of negative detunings, which is a signature of a high quantum yield. Indeed, in the case of low nonradiative losses, even significant quenching of the radiative rate due to the low local density of photonic stated do not affect the intensity of the signal (see the analysis of LDOS influence on the emission in ref. 37 and 39). In contrast, for the case of beacons with the FRET pair, we did not observe any distinct emission in this region, which is in accordance with the appearance of a new channel of effective nonradiative relaxation from the donor to the acceptor due to FRET. However, the low local density of the photonic states decreases the rate of radiative relaxation, which competes with the non-radiative energy transfer. As a result of the decrease in this rate, even larger percentage of the donor excitation relaxes through the non-radiative energy transfer pathway, leading to effective increase in FRET efficiency. The zero emission in the case of the FRET pair at negative detunings at the energy corresponding to the peak emission of the bare donor molecule allows us to conclude that all the energy from the donor states was transferred to the acceptor states, because the other non-radiative mechanisms are negligible for FAM (the quantum yield of bare FAM is about 97%).
However, at positive detunings, we observed a PL peak determined by emission from the LPB, as in the case of the cavity containing molecular beacons labelled with the donor dye alone, which was red-shifted relative to the emission spectrum of the uncoupled dye molecules. Similarly to the previous cases, we were unable to detect any emission that could have been attributed to the UPB due to the typically fast energy relaxation from the upper polariton to the donor exciton reservoir. Thus, we omit the UPB from most of the discussion. Nevertheless, the presence of strong coupling was clearly evidenced by anticrossing of the LPB and uncoupled cavity mode at the cavity detunings where the cavity photon mode and donor excitons had to be degenerated. Considering the exitonic constituents as independent harmonic oscillators, we assumed that our cavity could couple together three oscillators, FAM, TAMRA, and the cavity mode. Therefore, we characterized the observed dispersion by three polariton branches. In the case of a negatively detuned cavity, we observed an emission peak that could be attributed to the middle polariton branch (MPB). However, due to the pronounced emission from weakly coupled states and large broadening of the emission spectra, this part of the emission spectrum can hardly be used to quantitatively analyse the spectral position of the MPB.
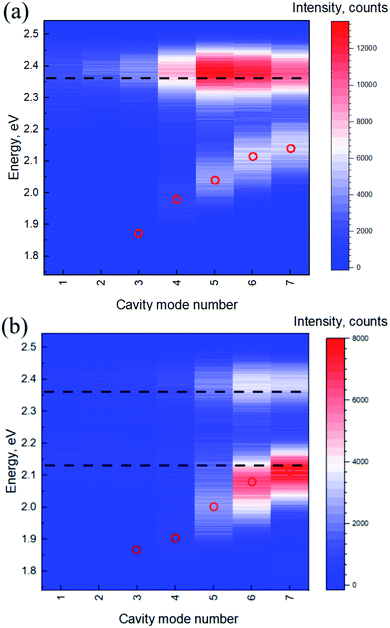
In order to unequivocally prove that the excitonic transitions in the dye molecules are in the regime of strong coupling with the optical mode of the microcavity, we made a series of measurements of the dependence of the emission spectra on the coupling strength. For this purpose, we detected the emission signal from the ensemble of beacons labelled with the FAM dye alone or with the FRET pair at zero detuning while varying the mode volume by changing the distance between the mirrors stepwise from 199 to 1393 nm. In other words, the mode number was changed from 1 to 7, which corresponded to the λ/2 and 3.5λ cavities, respectively. Fig. 3 shows the PL spectra at zero cavity detuning from the energy of the donor emission maximum at each step.
It can be seen that there is a clear dependence of the energy splitting on the separation distance between the mirrors and, hence, on the mode volume in both cases. We believe that these results unequivocally support the claim of the strong coupling in the system and, moreover, demonstrate the role of the small mode volume in obtaining large coupling strengths in systems with low-concentration solutions.
We suggest that the relatively large coupling strength for the ensemble of donor molecules at a low concentration is due to the confinement provided by the geometry of the microcavity and the mode volume several orders of magnitude lower than that of the commonly used Fabry–Perot microcavity with flat mirrors. It should be noted that, in a certain approximation, Rabi splitting scales as the square root of the ratio between the number of molecules within the mode volume and the mode volume, or equally, with the square root of molecular density. However, a smaller mode volume, first, allows a large coupling strength to be obtained with much fewer molecules,40 which significantly changes the number of states in the excitonic reservoir and governs the dynamics of relaxation in the system. Second, we would like to mention that the square root dependence of the coupling strength on the concentration arises from the Holstein–Primakoff transformation used to treat the Dicke Hamiltonian, the full solution of which is rather complicated for many-body systems.41 As a result, a giant oscillator could be used as an approximation to describe the interaction of the ensemble of molecules with the cavity mode. However, this approximation is legitimate in the particular case of low excitation, homogeneous distribution of the electromagnetic field over the ensemble, equal field intensities for different molecules, etc. If we compare the results obtained in our manuscript with the data reported for a similar system without lateral localization of the mode,42 it can be seen that, although the coupling strengths are similar in both cases, the concentration of the R6G molecules in the cited study is more than 3 orders of magnitude higher than in our case. This demonstrates the advantages of the small-mode-volume microcavity in terms of the number of molecules required for achieving the strong coupling regime.
Thus, by demonstrating the dependence of the Rabi splitting value on the mode volume we, first, have proved that a small mode volume can be used to enhance coupling even in ensembles of molecules coupled to the same optical mode and, second, have demonstrated inverse relationship of the coupling strength with the distance between mirrors and, hence, the mode volume, which is a strong signature of the strong coupling regime. We would like to emphasise that, although from the theoretical point of view, the coupling strength should be inversely proportional to the square root of the mode volume, the consideration of the real experimental system described in the manuscript should take into account two particularities which may change this dependence. First, the change in the distance between the mirrors obviously changes the lateral mode distribution in the microcavity. Second since the number of the molecules between the mirrors will be changed, the collective nature of light-matter coupling in our case also makes the dependence more complicated. As a result, the coupling strength should not necessarily be inversely proportional to the square root of the distance between the mirrors (or number of the modes used for coupling). However, the inverse sublinear relationship of coupling strength that we observed experimentally seems quite reasonable due to the reasons describes above.
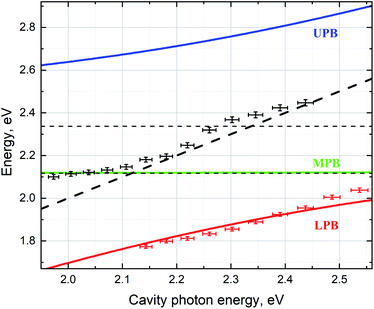
The dependence of the polariton branches on the cavity photon energy presented in Fig. 4 confirms that strong coupling occurred in this case. Experimental data were derived from the peak energies in the PL spectra for different distances between the cavity mirrors shown in Fig. 2c. In order to obtain a satisfactory fitting, we used the Jaynes–Cummings model assuming coupling between the cavity mode and the donor and the acceptor excitonic states resulting in the formation of three polaritonic branches and varied the strength of coupling between the cavity photon and both excitonic transitions (see the ESI† for details about the fitting). The best fit was achieved for the strengths of coupling with the cavity mode of 41 and 435 meV for the acceptor and donor excitons, respectively. We believe that the large values of the coupling strength are due to the three to four orders of magnitude lower mode volume of our tuneable microcavity compared to the standard plane-parallel Fabry–Perot microcavity.
In calculations, we considered the detuning to be zero at the cavity mode energy matching the emission maximum energy of the molecules instead of the absorption. Effectively, we considered the energies of the emission maxima of FAM and TAMRA molecules to be the energies of the bare excited state of the donor and acceptor, respectively. Usually, the energy of the bare state is extracted from the absorption. However, this cannot be the case for the strong coupling observed in the emission of organic molecules with large Stokes shifts. It has been shown theoretically43 that vibrational dressing appears in the strong coupling regime even for cavity states. Moreover, in the case of organic molecules with large vibrational energies, comparable to the coupling strength, the Born–Oppenheimer approximation can be violated.44 This results in a significant difference between the experimentally observed and theoretically predicted optical properties of organic molecules placed in low-mode volume cavities. In ref. 45, the tuning of the electromagnetic mode to the emission energy was required to observe the Rabi splitting of the emission for an organic molecule placed in a plasmonic nanocavity. For molecules with large Stokes shifts, it can even be impossible to observe splitting of both absorption and emission simultaneously.45
Fig. 4 also shows the energy of an uncoupled cavity photon, exciton transitions for uncoupled donor and acceptor dyes, and the energies of the emission maxima for the weakly coupled part of the molecular ensemble.
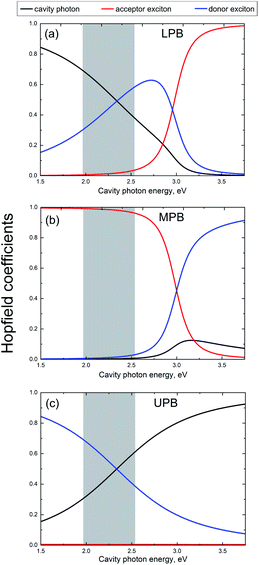
In order to determine the Hopfield coefficients, that describe the donor exciton, acceptor exciton, and photon mixing for the given coupling strengths, we further calculated the eigenfunctions of the Jaynes–Cummings Hamiltonian and represented each of them as a superposition of the initial pure photon and exciton states (see the ESI† for details). Fig. 5 shows the Hopfield coefficients for each polariton branch and their dependences on the cavity detuning. In the analysed PL spectral region, the polariton branches displayed quite different behaviours.
It can be seen from Fig. 5 that the upper and the lower polaritons mainly consist of the donor exciton and photon fractions, whose ratio is reversed for both branches upon cavity tuning. On the other hand, for the MPB, the contribution from the acceptor exciton strongly dominates the other components. However, this contribution decreases with an increase in the cavity mode energy in the same way as the relative contribution of the acceptor exciton increases significantly in the LPB. Such a redistribution of fractions in the polariton branches is in accordance with the exciton–photon coupling strengths, which differ significantly for the donor and acceptor excitons, as we have mentioned above.
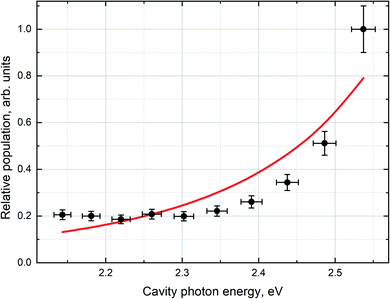
In order to quantitatively correlate the polariton population dependence on the detuning and the PL intensity measured experimentally, one need to introduce corrections arising from variations of both the photon fraction and the excitation intensity.25,26 The finite elements method was used to calculate the dependence of the excitation field intensity inside the cavity on the detuning (see the ESI† for details). In order to make the necessary corrections, we divided the measured PL intensity of the LPB by the integral intensity of non-resonant excitation at 450 nm over the volume of the microcavity in the region of cavity detuning. Finally, the relative polariton population (Fig. 6) was obtained using the following equation:25
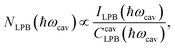 | (1) |
As can be seen from Fig. 6, the population of the LPB non-linearly increases with increasing cavity photon energy. According to the Hopfield coefficient distributions (Fig. 5a), this growth is accompanied by a linear decrease in the donor exciton fraction approximately from 0.3 to 0.6 and by a drastic increase in the acceptor exciton fraction in the LPB by almost an order of magnitude.
Now, we will analyse the population and depopulation mechanisms for the LPB using an approach described in detail in ref. 25. The simplified consideration is based on the assumptions on fast relaxation from the UPB to the donor excitonic reservoir (which typically occurs on the femtosecond timescale38) and efficient FRET of most of the energy to the acceptor reservoir. Therefore, the number of states in the acceptor excitonic reservoir can be considered constant. In principle, there are three different mechanisms determining the LPB population: scattering with vibrations from both excitonic reservoirs of the donor and acceptor and direct radiative pumping. The efficiencies of the first two mechanisms strongly depend on the corresponding exciton fraction in the LPB and should be changed with the detuning. The radiative pumping mechanism is a direct absorption of the photon emitted by the weakly coupled exciton transitions, which is accounted for by the photonic fraction in the LPB. However, it is almost negligible for cavities with a short cavity photon lifetime that contain an ensemble of molecules with a low optical density. The depopulation of the LPB occurs via radiative and non-radiative relaxations, which depend on the photon and exciton lifetimes, respectively. Thus, the mean polariton population (NLPB) in the steady state 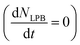 can be described by the following equation:
can be described by the following equation:
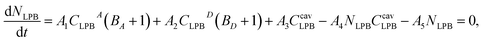 | (2) |
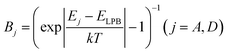 , where Ej is the bare exciton energy, ELPB is the energy of the LPB, T is the temperature in kelvins, and k is the Boltzmann constant. For the approximation of the population of the LPB in the steady state (Fig. 6), we used the following equation, which could be easily obtained from eqn (2) under some reasonable assumptions described below:
, where Ej is the bare exciton energy, ELPB is the energy of the LPB, T is the temperature in kelvins, and k is the Boltzmann constant. For the approximation of the population of the LPB in the steady state (Fig. 6), we used the following equation, which could be easily obtained from eqn (2) under some reasonable assumptions described below: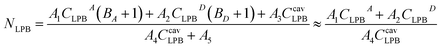 | (3) |
To derive eqn (3), we first assumed that the radiative pumping of the LPB is negligible compared to the vibrational scattering due to the low optical density of the medium inside the cavity and low cavity Q-factor. Additionally, the non-radiative relaxation of LPB to the exciton reservoirs strongly depends on the local vibrational environment and is assumed to be negligible comparing to the radiative decay mechanism,25,46 which is determined by the cavity photon lifetime (less than 10 fs). Thus, radiative decay through the photonic fraction becomes a prevailing depopulation mechanism, resulting in A4 ≫ A5. Finally, our experimental conditions (BA,B + 1) ≈ 1 should be taken into consideration. In order to obtain the best fit, we minimized the standard deviation by varying the ratio between the parameters A1,2,4. The best fit obtained with the use of this model and the experimentally observed relative population of the LPB are shown in Fig. 6.
It is important to note that the best fit was obtained with A2 tending to zero. To make it clearer, if we disregard the linear coefficient, the fitting is done by varying only one principal parameter, the ratio between the proportionality constants of vibrational scattering from the acceptor and donor reservoirs (A1 and A2). We can reformulate our finding in such a way that the best fit corresponds to the largest possible value of this ratio, with the influence of the energy transfer from the donor reservoir assumed to be negligible. This proves the energy transfer from the acceptor excitonic reservoir to be the predominant route of the lower polariton population despite the much larger donor fraction in it compared to the fraction from the acceptor, which can be called the carnival effect, the polaritonic energy state with a prevailing donor fraction being populated mainly from the acceptor exciton reservoir.
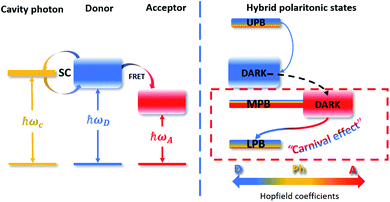
This corresponds to the low efficiency of the LPB population caused by scattering from the donor exciton reservoir, which may have been due to the relatively low rate of this process compared to the depopulation of the donor excitonic reservoir through FRET to the bare acceptor states. The latter mechanism was previously shown to be dominant over polariton-assisted energy transfer in mixed donor–acceptor ensembles.26 Thus, the energy relaxation pathways in our system can be described as follows (Fig. 7).
The non-radiatively pumped population of the UPB rapidly decays to the donor exciton reservoir.38 Then, due to the short distance between the donor and acceptor dye molecules in the molecular beacon, direct dipole–dipole FRET occurs with the efficiency close to unity. The FRET efficiency for the molecular beacon placed into the microcavity was found to be increased compared to that for the molecular beacon outside the cavity (about 80%), because we did not observe any emission from the bare donor states at negative detuning, in contrast to the donor-only case. This may have been due to the decreased rate of radiative relaxation of bare states at negative detunings, leading to the increase in FRET efficiency. The most interesting is that, once the energy had been transferred to the acceptor excitonic reservoir, it started to populate the LPB, which is mostly a mixture of the donor and cavity photon fractions due to the much higher coupling strength between the donor and the cavity photon. Thus, vibration scattering from the acceptor reservoir was shown to be the main population mechanism of the lower polariton state with the donor exciton fraction exceeding the acceptor one. It was demonstrated previously that a small absolute value of the specific exciton fraction in the polariton branch still allowed energy transfer with the corresponding excitonic reservoir.25 In our experiments, the population of the LPB depended on the relative variation of a small fraction of the acceptor exciton in the polariton state despite the considerably higher absolute value of the Hopfield coefficient, corresponding to the donor exciton. Finally, we can state that we have engineered a strongly coupled system with donor–acceptor role reversal or the “carnival effect”.27 Indeed, we have developed a system with dominant coupling between the donor and cavity photon leading to the formation of a donor-like polariton state with the lowest energy in the system. This allowed energy transfer first from the donor exciton reservoir to the acceptor exciton reservoir via standard FRET and then from the acceptor reservoir to the donor-like lower polariton state.
Conclusions
We have investigated strong coupling between the optical modes of a tuneable microcavity and the excitonic transitions of two closely located organic dye molecules.We have confirmed that in our system the resonance energy transfer between the donor and the acceptor excitonic reservoirs via direct FRET remains the dominant process of donor excitonic reservoir depopulation despite the strong coupling of the dye excitons to the cavity mode, as it has been previously demonstrated.26 However, we have shown that the energy states and relaxation pathways of the systems with strong dipole–dipole interaction can nevertheless be altered by strong coupling of their exciton transitions to the cavity photon. First, we have demonstrated a significant increase in the efficiency of energy transfer from the donor to the acceptor exciton reservoir, which tends to be unity inside the microcavity. Second, we have shown the polariton-assisted energy state inversion and energy flow alteration. Despite the efficient energy transfer between the donor and the acceptor exciton reservoir, we have observed emission from the LPB, which has been shown to have a considerably higher donor fraction compared to the acceptor one. Furthermore, we have proved that the LPB is populated mainly through vibrational scattering from the acceptor reservoir, despite the much larger absolute value of the donor exciton fraction than the acceptor fraction in the lower polariton. Thus, by obtaining strong coupling of the photonic mode with the exciton transition predominantly for the donor, we have demonstrated the so-called “carnival effect”, where the donor and acceptor reverse their roles.27,28 Consequently, energy transfer occurs first from the donor to the acceptor exciton by means of resonant dipole–dipole interaction and then from the excitonic states in the acceptor reservoir to the mainly donor LPB via vibrational scattering. This last process is particularly important for the potential use of strong coupling to harvest energy from usually “dark” states in optoelectronic devices. We speculate that our experimental findings, together with further investigations of the interplay between the polaritonic states and excitonic reservoirs, as well as control of the relaxation pathways, will pave the way to new applications of strong coupling in optically controlled FRET-imaging, remote-controlled chemistry, and all-optical switching.
Data availability
The data that support the findings of this study are available from the corresponding authors, D. D. or I. N., upon reasonable request.Author contributions
D. D., K. M. and I. V. performed the experiments and analysed the data. Y. R. and A. K. analysed the data. M. L. performed the calculations. D. D. and I. N. conceived the project and analysed experimental data. All authors contributed to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the Ministry of Education and Science of the Russian Federation (grant no. 14.Y26.31.0011). I. N. acknowledges the support from the Ministry of Higher Education, Research and Innovation of the French Republic and the University of Reims Champagne-Ardenne. The part of the work devoted to the microresonator development and adaptation was supported by the Russian Science Foundation (grant no. 21-79-30048). Y. R. acknowledges the support from the Basque Government (grant no. IT1164-19). We thank Vladimir Ushakov for the help with technical preparation of the manuscript.References
- T. W. Ebbesen, Hybrid Light–Matter States in a Molecular and Material Science Perspective, Acc. Chem. Res., 2016, 49(11), 2403–2412, DOI:10.1021/acs.accounts.6b00295.
- B. Lee, J. Park, G. H. Han, H.-S. Ee, C. H. Naylor, W. Liu, A. C. Johnson and R. Agarwal, Fano Resonance and Spectrally Modified Photoluminescence Enhancement in Monolayer MoS2 Integrated with Plasmonic Nanoantenna Array, Nano Lett., 2015, 15(5), 3646–3653, DOI:10.1021/acs.nanolett.5b01563.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Modifying Chemical Landscapes by Coupling to Vacuum Fields, Angew. Chem., Int. Ed., 2012, 51(7), 1592–1596, DOI:10.1002/anie.201107033.
- E. Orgiu, J. George, J. A. Hutchison, E. Devaux, J. F. Dayen, B. Doudin, F. Stellacci, C. Genet, J. Schachenmayer, C. Genes, G. Pupillo, P. Samorì and T. W. Ebbesen, Conductivity in Organic Semiconductors Hybridized with the Vacuum Field, Nat. Mater., 2015, 14, 1123–1129, DOI:10.1038/nmat4392.
- M. Ramezani, A. Halpin, A. I. Fernández-Domínguez, J. Feist, S. R.-K. Rodriguez, l F. J. Garcia-Vida and J. Gómez Rivas, Plasmon-Exciton-Polariton lasing, Optica, 2017, 4(1), 31–37, DOI:10.1364/OPTICA.4.000031.
- N. G. Berloff, M. Silva, K. Kalinin, A. Askitopoulos, J. D. Töpfer, P. Cilibrizzi, W. Langbein and P. G. Lagoudakis, Realizing the Classical XY Hamiltonian in Polariton Simulators, Nat. Mater., 2017, 16, 1120–1126, DOI:10.1038/nmat4971.
- A. V. Zasedatelev, A. V. Baranikov, D. Urbonas, F. Scafirimuto, U. Scherf, T. Stöferle, R. F. Mahrt and P. G. Lagoudakis, A Room-Temperature Organic Polariton Transistor, Nat. Photonics, 2019, 13, 378–383, DOI:10.1038/s41566-019-0392-8.
- X. Zhong, T. Chervy, S. Wang, J. George, A. Thomas, J. A. Hutchison, E. Devaux, C. Genet and T. W. Ebbesen, Non-Radiative Energy Transfer Mediated by Hybrid Light-Matter States, Angew. Chem., Int. Ed., 2016, 55, 6202–6206, DOI:10.1002/anie.201600428.
- X. Zhong, T. Chervy, L. Zhang, A. Thomas, J. George, C. Genet, J. A. Hutchison and T. W. Ebbesen, Energy Transfer between Spatially Separated Entangled Molecules, Angew. Chem., Int. Ed., 2017, 56, 9034–9038, DOI:10.1002/anie.201703539.
- Y. Choi, L. Kotthoff, L. Olejko, U. Resch-Genger and I. Bald, DNA Origami-Based Förster Resonance Energy-Transfer Nanoarrays and Their Application as Ratiometric Sensors, ACS Appl. Mater. Interfaces, 2018, 10(27), 23295–23302, DOI:10.1021/acsami.8b03585.
- P. Das, A. Sedighi and U. J. Krull, Cancer Biomarker Determination by Resonance Energy Transfer Using Functional Fluorescent Nanoprobes, Anal. Chim. Acta, 2018, 1041, 1–24, DOI:10.1016/j.aca.2018.07.060.
- A. Giannetti, S. Tombelli and F. Baldini, Oligonucleotide Optical Switches for Intracellular Sensing, Anal. Bioanal. Chem., 2013, 405, 6181–6196, DOI:10.1007/s00216-013-7086-8.
- T. Kuang, L. Chang, X. Peng, X. Hu and D. Gallego-Perez, Molecular Beacon Nano-Sensors for Probing Living Cancer Cells, Trends Biotechnol., 2017, 35(4), 347–359, DOI:10.1016/j.tibtech.2016.09.003.
- J. Zheng, R. Yang, M. Shi, C. Wu, X. Fang, Y. Li, J. Li and W. Tan, Rationally Designed Molecular Beacons for Bioanalytical and Biomedical Applications, Chem. Soc. Rev., 2015, 44(10), 3036–3055, 10.1039/c5cs00020c.
- M. Stobiecka, K. Ratajczak and S. Jakiela, Toward Early Cancer Detection: Focus on Biosensing Systems and Biosensors for an Anti-Apoptotic Protein Survivin and Survivin mRNA, Biosens. Bioelectron., 2019, 137, 58–71, DOI:10.1016/j.bios.2019.04.060.
- C. S. Wu, L. Peng, M. You, D. Han, T. Chen, K. R. Williams, C. J. Yang and W. Tan, Engineering Molecular Beacons for Intracellular Imaging, Int. J. Mol. Imaging, 2012, 2012, 501–579, DOI:10.1155/2012/501579.
- R. Hernandez, H. Orbay and W. Cai, Molecular Imaging Strategies for In Vivo Tracking of MicroRNAs: A Comprehensive Review, Curr. Med. Chem., 2013, 20(29), 3594–3603, DOI:10.2174/0929867311320290005.
- B. Wang, Z. You and D. Ren, Target-Assisted FRET Signal Amplification for Ultrasensitive Detection of MicroRNA, Analyst, 2019, 144, 2304–2311, 10.1039/c8an02266f.
- N. Junager, J. Kongsted and K. Astakhova, Revealing Nucleic Acid Mutations Using FörsterResonance Energy Transfer-Based Probes, Sensors, 2016, 16(8), 1173, DOI:10.3390/s16081173.
- C. Wiraja, D. C. Yeo, S. Y. Chew and C. Xu, Molecular Beacon-Loaded Polymeric Nanoparticles for Non-Invasive Imaging of mRNA Expression, J. Mater. Chem. B, 2015, 3, 6148–6156, 10.1039/c5tb00876j.
- C. El Khamlichi, F. Reverchon-Assadi, N. Hervouet-Coste, L. Blot, E. Reiter and S. Morisset-Lopez, Bioluminescence Resonance Energy Transfer as a Method to Study Protein-Protein Interactions: Application to G Protein Coupled Receptor Biology, Molecules, 2019, 24(3), 537, DOI:10.3390/molecules24030537.
- S. Tong, T. J. Cradick, Y. Ma, Z. Dai and G. Bao, Engineering Imaging Probes and Molecular Machines for Nanomedicine, Sci. China: Life Sci., 2012, 55, 843–861, DOI:10.1007/s11427-012-4380-1.
- B. Yuan, Y. Chen, Y. Sun, Q. Guo, J. Huang, J. Liu, X. Meng, X. Yang, X. Wen, Z. Li, L. Li and K. Wang, Enhanced Imaging of Specific Cell-Surface Glycosylation Based on Multi-FRET, Anal. Chem., 2018, 90(10), 6131–6137, DOI:10.1021/acs.analchem.8b00424.
- A. Konrad, M. Metzger, A. M. Kern, M. Brecht and A. J. Meixner, Controlling the Dynamics of Förster Resonance Energy Transfer Inside a Tunable Sub-wavelength Fabry–Pérot-Resonator, Nanoscale, 2015, 7, 10204–10209, 10.1039/c5nr02027a.
- D. M. Coles, N. Somaschi, P. Michetti, C. Clark, P. G. Lagoudakis, P. G. Savvidis and D. G. Lidzey, Polariton-Mediated Energy Transfer between Organic Dyes in a Strongly Coupled Optical Microcavity, Nat. Mater., 2014, 13, 712–719, DOI:10.1038/nmat3950.
- K. Georgiou, P. Michetti, L. Gai, M. Cavazzini, Z. Shen and D. G. Lidzey, Control over Energy Transfer between Fluorescent BODIPY Dyes in a Strongly Coupled Microcavity, ACS Photonics, 2018, 5(1), 258–266, DOI:10.1021/acsphotonics.7b01002.
- M. Du, L. A. Martínez-Martínez, R. F. Ribeiro, Z. Hu, V. M. Menon and J. Yuen-Zhou, Theory for Polariton-Assisted Remote Energy Transfer, Chem. Sci., 2018, 9, 6659–6669, 10.1039/c8sc00171e.
- R. F. Ribeiro, L. A. Martínez-Martínez, M. Du, J. Campos-Gonzalez-Angulo and J. Yuen-Zhou, Polariton Chemistry: Controlling Molecular Dynamics with Optical Cavities, Chem. Sci., 2018, 9, 6325–6339, 10.1039/c8sc01043a.
- D. Dovzhenko, K. Mochalov, I. Vaskan, I. Kryukova, Y. Rakovich and I. Nabiev, Polariton-Assisted Splitting of Broadband Emission Spectra of Strongly Coupled Organic Dye Excitons in Tunable Optical Microcavity, Opt. Express, 2019, 27(4), 4077–4089, DOI:10.1364/OE.27.004077.
- K. E. Mochalov, I. S. Vaskan, D. S. Dovzhenko, Y. P. Rakovich and I. Nabiev, A Versatile Tunable Microcavity for investigation of Light–Matter Interaction, Rev. Sci. Instrum., 2018, 89(5), 053105, DOI:10.1063/1.5021055.
- D. S. Dovzhenko, I. S. Vaskan, K. E. Mochalov, Y. P. Rakovich and I. R. Nabiev, Spectral and Spatial Characteristics of the Electromagnetic Modes in a Tunable Optical Microcavity Cell for Studying Hybrid Light-Matter States, JETP Lett., 2019, 109(1), 12–17, DOI:10.1134/s0370274x1901003x.
- V. Savona, L. C. Andreani, P. Schwendimann and A. Quattropani, Quantum Well Excitons in Semiconductor Microcavities: Unified Treatment of Weak and Strong Coupling Regimes, Solid State Commun., 1995, 93(9), 733–739, DOI:10.1016/0038-1098(94)00865-5.
- G. D. Scholes, Long-Range Resonance Energy Transfer in Molecular Systems, Annu. Rev. Phys. Chem., 2003, 54(1), 57–58, DOI:10.1146/annurev.physchem.54.011002.103746.
- J. J. Riesz, J. B. Gilmore, R. H. McKenzie, B. J. Powell, M. R. Pederson and P. Meredith, Transition Dipole Strength of Eumelanin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76(2), 021915, DOI:10.1103/PhysRevE.76.021915.
- U. Resch-Genger, M. Grabolle, S. Cavaliere-Jaricot, R. Nitschke and T. Nann, Quantum Dots versus Organic Dyes as Fluorescent Labels, Nat. Methods, 2008, 5(9), 763–775, DOI:10.1038/nmeth.1248.
- M. Cipolloni, B. Fresch, I. Occhiuto, P. Rukin, K. G. Komarova, A. Cecconello, I. Willner, R. D. Levine, F. Remacle and E. Collini, Coherent Electronic and Nuclear Dynamics in a Rhodamine Heterodimer–DNA Supramolecular Complex, Phys. Chem. Chem. Phys., 2017, 19(34), 23043–23051, 10.1039/c7cp01334e.
- M. Pelton, Modified Spontaneous Emission in Nanophotonic Structures, Nat. Photonics, 2015, 9, 427–435, DOI:10.1038/nphoton.2015.103.
- V. M. Agranovich, M. Litinskaia and D. G. Lidzey, Cavity Polaritons in Microcavities Containing Disordered Organic Semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(8), 085311, DOI:10.1103/PhysRevB.67.085311.
- D. Dovzhenko, I. Martynov, P. Samokhvalov, E. Osipov, M. Lednev, A. Chistyakov, A. Karaulov and I. Nabiev, Enhancement of spontaneous emission of semiconductor quantum dots inside one-dimensional porous silicon photonic crystals, Opt. Express, 2020, 28, 22705, DOI:10.1364/OE.401197.
- B. Liu, V. M. Menon and M. Y. Sfeir, The Role of Long-Lived Excitons in the Dynamics of Strongly Coupled Molecular Polaritons, ACS Photonics, 2020, 7, 2292–2301, DOI:10.1098/rsta.2010.0333.
- B. M. Garraway, The Dicke model in quantum optics: Dicke model revisited, Philos. Trans. R. Soc., A, 2011, 369, 1137–1155, DOI:10.1098/rsta.2010.0333.
- E. Hulkko, S. Pikker, V. Tiainen, R. H. Tichauer, G. Groenhof and J. J. Toppari, Effect of molecular Stokes shift on polariton dynamics, J. Chem. Phys., 2021, 154, 154303, DOI:10.1063/5.0037896.
- N. Wu, J. Feist and F. J. Garcia-Vidal, When Polarons Meet Polaritons: Exciton-Vibration Interactions in Organic Molecules Strongly Coupled to Confined Light Fields, Phys. Rev. B, 2016, 94(19), 195409, DOI:10.1103/PhysRevB.94.195409.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Cavity-Induced Modifications of Molecular Structure in the Strong-Coupling Regime, Phys. Rev. X, 2015, 5(4), 041022, DOI:10.1103/PhysRevX.5.041022.
- O. S. Ojambati, R. Chikkaraddy, W. D. Deacon, M. Horton, D. Kos, V. A. Turek, U. F. Keyser and J. J. Baumberg, Quantum Electrodynamics at Room Temperature: Coupling a Single Vibrating Molecule with Aplasmonic Nanocavity, Nat. Commun., 2019, 10, 1049, DOI:10.1038/s41467-019-08611-5.
- P. Michetti and G. C. La Rocca, Simulation of J-Aggregate Microcavity Photoluminescence, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(19), 195301, DOI:10.1103/PhysRevB.77.195301.
Footnote |
| † Electronic supplementary information (ESI) available: detailed descriptions of the properties of the molecular beacon samples, tuneable microcavity setup, PL/transmission collection system; experimental section describing sample preparation and transmission and PL measurements; calculations of the pumping intensity dependence on the cavity detuning; and description of the Jaynes–Cummings model. See DOI: 10.1039/d1sc02026a |
| This journal is © The Royal Society of Chemistry 2021 |