Open Access Article
Open Access ArticleLewis acid catalyzed heavy atom tunneling – the case of 1H-bicyclo[3.1.0]-hexa-3,5-dien-2-one†
Stefan
Henkel
 ,
Melania Prado
Merini
,
Melania Prado
Merini
 ,
Enrique
Mendez-Vega
,
Enrique
Mendez-Vega
 and
Wolfram
Sander
and
Wolfram
Sander
 *
*
Lehrstuhl für Organische Chemie II, Ruhr-Universität Bochum, 44801 Bochum, Germany. E-mail: wolfram.sander@rub.de
First published on 15th July 2021
Abstract
For many thermal reactions, the effects of catalysis or the influence of solvents on reaction rates can be rationalized by simple transition state models. This is not the case for reactions controlled by quantum tunneling, which do not proceed via transition states, and therefore lack the simple concept of transition state stabilization. 1H-Bicyclo[3.1.0]-hexa-3,5-dien-2-one is a highly strained cyclopropene that rearranges to 4-oxocyclohexa-2,5-dienylidene via heavy-atom tunneling. H2O, CF3I, or BF3 form Lewis acid–base complexes with both reactant and product, and the influence of these intermolecular complexes on the tunneling rates for this rearrangement was studied. The tunneling rate increases by a factor of 11 for the H2O complex, by 23 for the CF3I complex, and is too fast to be measured for the BF3 complex. These observations agree with quantum chemical calculations predicting a decrease in both barrier height and barrier width upon complexation with Lewis acids, resulting in the observed Lewis acid catalysis of the tunneling rearrangement.
Introduction
Quantum tunneling is a physical phenomenon allowing particles to pass through a potential barrier, even if the energy of the particle is too low to overcome the barrier classically. Quantum tunneling is present in all chemical reactions, although only observable if the tunneling probability is high enough to compete with the classical thermal reaction. Since tunneling probability decreases exponentially with the mass of the tunneling particle,1,2 many examples are reported for the hydrogen atom,3 while tunneling reactions with a dominant movement of heavy atoms are rare.4–7Examples involving tunneling of carbon atoms5 are the Cope rearrangement of semibullvalene 1,8,9 the ring-opening reactions of benzene oxide 2 to oxepine 3,10 of 3-(methylthio)-7-azabicyclo[4.1.0]hepta-2,4,6-triene 4 to ketenimine 5,11 and the related rearrangement of 1H-bicyclo[3.1.0]-hexa-3,5-dien-2-one 6 to 4-oxocyclohexa-2,5-dienylidene 7 (ref. 12 and 13) (Scheme 1). At cryogenic temperatures below 20 K, the thermal energy is not sufficient to overcome the activation barriers for these reactions, strongly indicating that tunneling is involved. Additional evidence for tunneling comes from the temperature independence of reaction rates over a large range in absolute temperature (e.g. between 3 and 20 K, where the absolute temperature raises almost sevenfold).
 | ||
| Scheme 1 Reactions involving heavy-atom tunneling investigated by matrix isolation spectroscopy.8,11–13 | ||
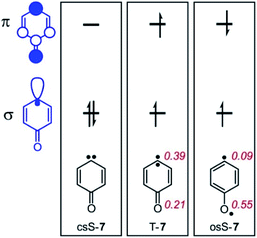
The ring opening of 6 is particularly interesting since the resulting carbene 7 has a triplet ground state, and hence intersystem crossing (ISC) has to occur at some point along the reaction coordinate.14–16 The lowest lying singlet state of carbene 7 is the open-shell (os) singlet state osS-7, which is predicted to be 8.4 kcal mol−1 above the triplet ground state T-7. The (planar) closed-shell singlet state csS-7 is with 26.1 kcal mol−1 at the CASPT2 level of theory much higher in energy.17 Thus, the ISC step in the rearrangement from 6 to 7 is likely to occur in osS-7 to give T-7.
Previously, the influence of the matrix environment on the 6 → T-7 tunneling rearrangement was investigated, and different reaction rates were observed in different inert matrices.13 In solid argon and neon the tunneling rates were similar, while noticeably accelerated rates were observed in nitrogen, krypton or xenon matrices. About 40 times faster rates were found in xenon compared to argon, which was attributed to more favorable interactions between the xenon atoms and the embedded molecules, reducing the reaction barrier.13 Similar variations of the tunneling rates depending on the matrix environment were also observed for the Cope rearrangement of semibullvalene 1 (ref. 8) and for conformational changes in carboxylic acids.18
Interactions of isolated molecules with noble gas atoms of the surrounding matrix are weak, and the observed changes of the tunneling rates probably result from cooperative interactions with the surrounding ‘solvation’ shell formed by the matrix. Interactions with Lewis acids such as H2O, CF3I, or BF3 are much stronger, and thus interactions with these molecules are expected to considerably affect tunneling rates.
Both reactant 6 and product T-7 of the tunneling reaction have carbonyl groups which can interact with Lewis acids. In addition, closed-shell singlet states of carbenes are highly basic.19 As an example, the singlet state of diphenyl carbene 8 strongly interacts with H2O by forming a hydrogen bond to the carbene center (Scheme 2).20–23 Similarly, the interaction between 8 and CF3I or BF3 results in the formation of Lewis acid–base adducts.22,24–27 In csS-7 both the carbonyl group and the carbene center can act as Lewis base, whereas in osS-7 and T-7 only the carbonyl group is expected to strongly interact with the Lewis acids. Here, we describe how the tunneling rates of the 6 → T-7 rearrangement depends on the formation of Lewis acid–base complexes with H2O, CF3I, and BF3.
 | ||
| Scheme 2 Reaction of diphenyl carbene 8 with water yielding the singlet hydrogen-bonded complex S-8⋯H2O.21 | ||
Results and discussion
Non-covalent complexes of carbene T-7 and cyclopropene 6
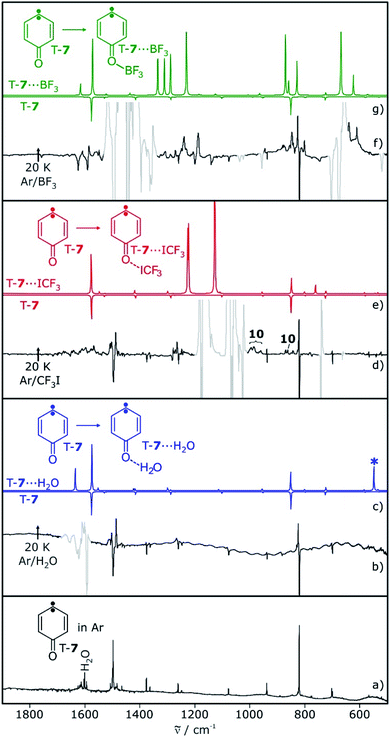
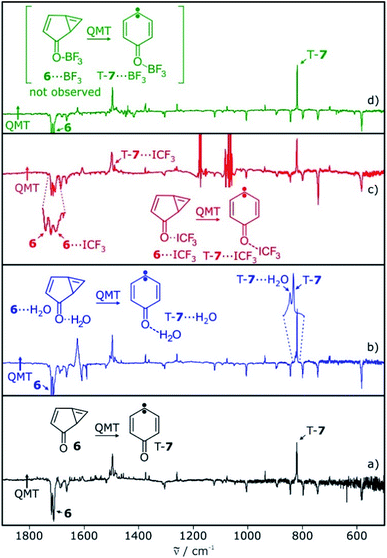
Carbene T-7 was generated by 505 nm light photolysis of matrix-isolated quinone diazide 9 as described in the literature.12,13,28 In argon matrices doped with 0.5–1% of the Lewis acids H2O, CF3I, or BF3, both the carbene and the Lewis acid were isolated, as long as the temperature is kept below 10 K to prevent diffusion of trapped species. The EPR spectrum of carbene T-7 in these matrices shows typical triplet transitions, characterized by zero-field splitting (zfs) parameters of D = 0.321 cm−1 and E = 0.006 cm−1.28,29 Annealing of these matrices for several minutes at 20 K allows for the diffusion of the small molecules and formation of complexes with T-7. The overall intensity of the EPR signals of triplet T-7 does not decrease significantly upon annealing, indicating that the triplet to singlet interconversion observed for other carbenes in similar experiments20–23 does not take place with carbene T-7. Rather, additional signals close to the original bands of T-7 are formed during annealing, suggesting slight variations of the zfs parameters in a complex between T-7 and the Lewis acids (see ESI†).The main IR bands of T-7 at 819 and 1497 cm−1 are assigned to a wagging vibration of the ring and the carbonyl stretching vibration, respectively (Fig. 1a). Differences in the IR spectra obtained after annealing of matrices containing T-7 and H2O, CF3I, or BF3 are due to shifts induced by the interaction of T-7 with the Lewis acid. These shifts agree well with computed spectra of the triplet complexes T-7⋯H2O, T-7⋯ICF3 and T-7⋯BF3 (Fig. 1).
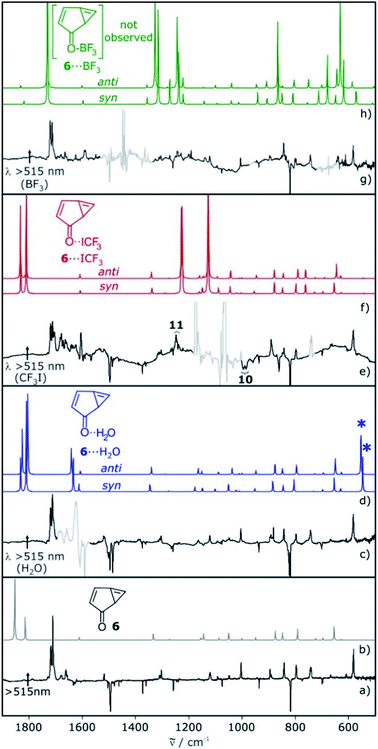
Photolysis of carbene T-7 with λ > 515 nm light generates cyclopropene 6. At the same time, 6 is tunneling back to T-7 and therefore, the conversion of carbene T-7 to cyclopropene 6 is not complete but rather reaches a stationary equilibrium after long irradiation times. Subsequent annealing of the 6/T-7 mixture in an argon matrices doped with small amounts of the Lewis acids (LA) yields the complexes 6⋯LA and T-7⋯LA (Scheme 3). The complexes of 6 are predicted to have two conformers with the Lewis acid being oriented syn or anti with respect to the cyclopropene unit.
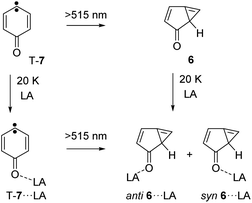 | ||
| Scheme 3 Formation of the Lewis acids complexes 6⋯LA by annealing of an argon matrix containing 6 or by photolysis of T-7⋯LA. | ||
The IR spectrum of 6 shows strong vibrations in the carbonyl stretching region at 1717 and 1721 cm−1 as well as a set of weaker signals between 700 and 900 cm−1 (Fig. 2). For the water complex 6⋯H2O a pronounced red shift of the carbonyl stretching vibration is computed at the M06-2X/def2-TZVP level of theory, while the shifts of other IR bands are rather small. Since the region of the carbonyl vibration is dominated by IR absorptions of free water, 6⋯H2O is only tentatively identified by small shifts of the signals between 700–900 cm−1, overlapping with those of 6 (Fig. 2c). 6⋯H2O is also formed by irradiation of T-7⋯H2O (Fig. 2c).
Irradiation of a mixture of T-7 and T-7⋯ICF3 gives rise to a set of signals which are assigned to 6 and 6⋯ICF3. In this case, the pronounced shifts of the bands of 6⋯ICF3 allow us to identify the complex (Fig. 2e). A new carbonyl stretching vibration is found at 1706 cm−1, red-shifted by 10 cm−1. Previously formed ylide 10 with bands at 986 and 995 cm−1 decreases under these conditions, and new bands at 1244 and 1249 cm−1 indicate the formation of the radical pair 11 (Scheme 4 and ESI†).26,27
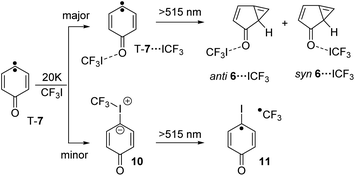 | ||
| Scheme 4 Reaction of T-7 with CF3I yielding T-7⋯ICF3 and ylide 10 and 6⋯ICF3 as well as radical pair 11 upon subsequent photolysis. | ||
Upon photolysis of a matrix containing a mixture of carbene T-7 and T-7⋯BF3, only T-7 which is not interacting with BF3 rearranges to 6 (Fig. 2g). No evidence for the formation of 6⋯BF3 is found after photolysis, and annealing of a matrix containing 6 and BF3 does also not produce 6⋯BF3. Thus, 6⋯BF3 is not stable under any of the conditions where complexes with the other Lewis acids are detected, indicating that 6⋯BF3 very rapidly rearranges back to T-7⋯BF3.
Computational analysis of T-7⋯LA and 6⋯LA
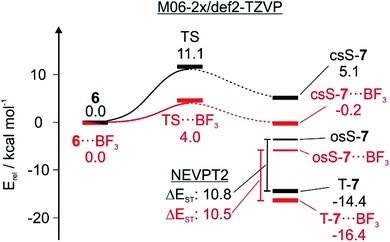
The three lowest energy electronic states of the carbene csS-7, osS-7, and T-7 show distinctively different polarities (Fig. 3). csS-7 can be described as a 1,1-zwitterion, acting as nucleophile via the filled σ orbital as well as electrophile via its empty π orbital. However, this electronic state is destabilized by the anti-aromatic character of its formal 4π ring system. Therefore, csS-7 is calculated (M06-2X/def2-TZVP) to lie 19 kcal mol−1 above T-7, and its geometry is distorted from the C2v symmetrical structure of the other electronic states to CS in order to reduce its anti-aromatic character.In contrast to csS-7, the carbene center in T-7 and osS-7 is less polarized and not expected to form strong interactions with Lewis acids or bases. Rather, in these states interactions between the Lewis acids and the carbonyl group should dominate. Previous investigations of the electronic structure of 7 have shown that while the two unpaired electrons occupy the same σ and π orbitals in T-7 and osS-7, the molecular structures of these two states are rather different.17 While the triplet is best described by a quinoidic resonance structure, additional repulsion of the unpaired electrons in osS-7 results in a larger contribution of the benzenoid resonance structure, in which the unpaired π orbital is localized more at the oxygen atom.30 This difference can be visualized by CASSCF atomic population of the π-SOMO (Fig. 3): The larger coefficient at the oxygen atom makes osS-7 more basic than T-7, and thus the excited osS state is expected to interact more strongly with Lewis acids.
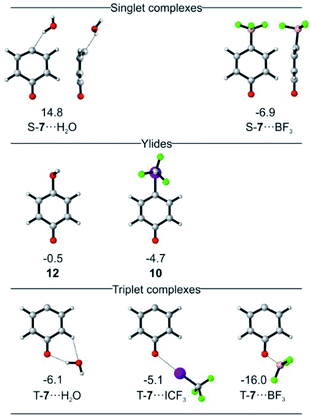
Calculations predict that the interaction of T-7 with either H2O, CF3I, or BF3 does not stabilize the singlet state enough to become ground state, in accordance with our experimental finding that the triplet complexes of T-7 are formed exclusively. Structures in which csS-7 interacts with the Lewis acid through its lone pair are only found to be relevant for csS-7⋯BF3 (Fig. 4). For H2O, a hydrogen-bonded structure is predicted to be 21 kcal mol−1 above the triplet complex, and a halogen-bonded structure with CF3I was not found in our computations. Instead, geometries are obtained in which the carbene center interacts as electrophile with the O and I atoms of H2O and CF3I, corresponding to ylides 12 or 10, respectively (Fig. 4).27 Complexes in which the carbonyl group of csS-7 interacts with the Lewis acids are also possible and the overall withdrawal of electron density from the π system results in a larger participation of the σ electrons of the carbene center and consequently a reduction of the anti-aromatic character of the csS state. Nonetheless, csS-7 remains an excited state, energetically well above T-7 and osS-7.
For T-7, the carbonyl complexes are energetically well below structures where the Lewis acids interact with the carbene center (see ESI† for multiple minima hypersurface analysis31), and hence T-7⋯H2O, T-7⋯ICF3 and T-7⋯BF3 are expected to be the dominant structures formed in the matrix (Fig. 4).
Singlet biradicals like osS-7 cannot be properly calculated by single-determinant methods such as DFT, requiring the use of multiconfigurational methods. The presence of non-covalent interactions further requires a proper treatment of the dynamic correlation and hence osS-7⋯BF3 was calculated at the NEVPT2(8,8)/6-31G* level of theory as reference. The geometry of the complex osS-7⋯BF3 is very similar to that of T-7⋯BF3 (optimized at the same level), but the interaction of the more basic osS-7 with BF3 is slightly stronger, resulting in a smaller interaction distance (see ESI†).
For 6, the main mode of interaction with Lewis acids is through the carbonyl group (Fig. 5). The binding energies for the interaction of 6 with H2O, CF3I and BF3 do not differ substantially from those calculated for T-7 at the M06-2X/def2-TZVP level of theory. An energy difference of 0.8 kcal mol−1 is calculated for the rotamers 6⋯H2O, owing to a favorable secondary interaction between the CH group of the five membered ring and the water oxygen in case of the anti isomer. In contrast, the two conformers of 6⋯ICF3 and 6⋯BF3 are calculated to be energetically degenerate.
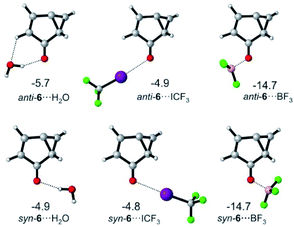 | ||
| Fig. 5 Lowest-energy complexes between 6 and H2O, CF3I and BF3. Energies relative to 6 and the non-interacting Lewis acid are given in kcal mol−1 at the M06-2X/def2-TZVP level of theory. | ||
Tunneling rearrangement
The tunneling rate constant k for the reaction of cyclopropene 6 to triplet T-7 in argon at 3 K is 1.2 × 10−6 s−1.13 The kinetic data show the dispersive behavior expected for solid state reactions. Dispersion coefficients β in the range of 0.4–0.7 are obtained by fitting the kinetic equation I = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(kt)β) + c (where I and I0 are the integrated intensities at time t and 0, respectively and c being a constant offset).8,13,32 The characteristic bands of cyclopropene 6 at 1717 cm−1 (decreasing) and carbene T-7 at 820 cm−1 (increasing) were used to determine the kinetics of the tunneling reaction of the system without Lewis acid interactions (Fig. 6a).
exp(−(kt)β) + c (where I and I0 are the integrated intensities at time t and 0, respectively and c being a constant offset).8,13,32 The characteristic bands of cyclopropene 6 at 1717 cm−1 (decreasing) and carbene T-7 at 820 cm−1 (increasing) were used to determine the kinetics of the tunneling reaction of the system without Lewis acid interactions (Fig. 6a).
In water-doped matrices, bands at 820 and 824 cm−1 are assigned to T-7 and T-7⋯H2O, respectively. These bands increase over time and allow us to monitor the kinetics of both the free and the hydrogen-bonded system (Fig. 6b). A comparison of the signal intensities of T-7 and T-7⋯H2O over time shows a steeper increase of the band assigned to T-7⋯H2O, indicating the acceleration of the tunneling reaction upon complexation (see ESI†). Tunneling rates in the range of (1.0–2.3) × 10−6 s−1 are found for the reaction of the unbound system in these experiments, in fair agreement with the reported value of 1.2 × 10−6 s−1.13 For the water complex, an average rate of 15 × 10−6 s−1 is found (Table 1). Accordingly, the hydrogen bond formed between water and the carbonyl group of 6 leads to an increase of the rate of the ring opening reaction by a factor of 11. For CF3I, it is possible to follow the carbonyl stretching vibrations of 6⋯ICF3 and T-7⋯ICF3, which are well separated from the signals of 6 and T-7 (Fig. 6c). The average reaction rate obtained for the CF3I complex is 35 × 10−6 s−1 (Table 1). Compared to the reaction of the unbound system measured in the same experiment, the halogen bond between CF3I and 6 increases the rate by a factor of 23.
| Lewis acid | k (s−1), 6 → T-7 | τ (h) | k (s−1), 6⋯LA → T-7⋯LA | τ (h) | E A (kcal mol−1) | |
|---|---|---|---|---|---|---|
| syn | anti | |||||
| — | 1.2 × 10−6 | 137 | — | — | 10.1 | |
| H2O | 2.3 × 10−6 | 66 | 14 × 10−6 | 11 | 8.2 | 9.2 |
| 1.0 × 10−6 | 165 | 16 × 10−6 | 7 | |||
| CF3I | 1.8 × 10−6 | 84 | 37 × 10−6 | 4 | 8.8 | 9.2 |
| 1.3 × 10−6 | 116 | 32 × 10−6 | 3 | |||
| BF3 | 1.5 × 10−6 | 101 | Not observed | — | 3.4 | 4.0 |
Under various experimental conditions we were not able to observe 6⋯BF3, indicating its fast rearrangement to T-7⋯BF3. All changes in the IR spectra of the tunneling rearrangement in the presence of BF3 are attributed to the rearrangement of non-interacting 6 (Fig. 6d).
The first step of the 6 → T-7 rearrangement is the formation of osS-7, which as an open-shell singlet state cannot be reliably calculated by DFT. The TS leading from closed-shell singlet 6 to osS-7, however, can be reasonably approximated by single configuration methods.13 At the M06-2X/def2-TZVP level of theory the activation barrier for the 6 → T-7 rearrangement is computed to be 10.1 kcal mol−1. Hydrogen or halogen bonding lowers the barrier by 1–2 kcal mol−1 depending on the orientation of the Lewis acid (Table 1). Interaction with BF3 leads to a drastic decrease of the barrier by 6.7 kcal mol−1. The C–C bond distance between the bridgehead atoms in the TS is reduced from 1.87 to 1.74 Å, in line with the concept of an earlier TS.
The increase of the tunneling rate is for 6⋯ICF3 larger (23×) than for 6⋯H2O (11×), despite the calculated activation barrier decreasing less for 6⋯ICF3 (1.3 kcal mol−1) than for 6⋯H2O (1.9 kcal mol−1). The barriers for the two conformers of the CF3I complexes are rather similar, while the ones for the H2O complexes differ by 1 kcal mol−1. Accordingly, a faster reaction is predicted for the syn compared to the anti6⋯H2O complex, and the observed rate presumably shows the slower anti isomer. However, the IR spectra do not allow to discriminate between these two conformers.
An approximate way to estimate barrier widths is to use intrinsic reaction coordinate (IRC) calculations. This is difficult for the 6 → T-7 rearrangement since crossings between closed-shell and open-shell and between singlet and triplet energy surfaces have to be considered. It is reasonable to assume that osS-7 is the reaction product that undergoes ISC to T-7 (Fig. 7). However, it is not clear how osS-7 is connected to csS-7 and to 6. Since both 6 and the transition state TS for the ring opening exhibit a dominant closed-shell character which can be reliably calculated using DFT methods, we only calculated the part of the IRC that connects the TS with 6 (Fig. 7). Most simple approximations of tunneling probabilities (e.g. as suggested by Bell2) assume a symmetric barrier. This assumption allows us to roughly approximate barrier widths by only using the 6 → TS part of the IRC.
On the closed-shell singlet state potential energy surface, the reaction proceeds from 6via TS to csS-7. The interactions of the Lewis acids with TS and csS-7 are stronger than with 6, resulting in a lowering of the activation barriers (Table 1). BF3 shows the largest influence on the tunneling rates, and it is therefore instructive to analyze the stabilizing effect of BF3 complexation on 6, TS, and the three electronic states of 7 (Fig. 7). The calculations (M06-2X/def2-TZVP) indicate a pronounced lowering of the TS energy from 11.1 to 4.0 kcal mol−1. The O⋯B distance is reduced from 1.65 Å in 6 to 1.57 Å in csS-7, indicating a strengthening of the Lewis acid/base interaction along the reaction coordinate. The C–C bond distance between the bridgehead atoms in the TS is also reduced by complexation, which results in a narrower tunneling barrier. Therefore, the calculations suggest that complexation results in both reducing the barrier height and narrowing the barrier width, and consequently the tunneling probability increases considerably.
We do not know at which point along the reaction coordinate the transition from the closed-shell to the open-shell state and from the singlet to the triplet state occurs, and how the tunneling affects these surface crossings. However, the final product is T-7, and osS-7 is a likely reaction intermediate. Both open-shell states interact less strongly with the Lewis acids than csS-7 making the release of the Lewis acid energetically more favorable when closing the catalytic cycle. Since under these conditions there is no decoordination, there is no catalytic turnover. H2O and CF3I are of lower Lewis acidity than BF3, and therefore the decrease of the barrier height and width is less pronounced. While the qualitative effects of complexation are the same as with BF3, the tunneling is less accelerated.
Conclusions
To expand the concept of catalysis of thermal reactions to tunneling reactions, not only the impact of the catalyst on the barrier height, but even more on the barrier width must be considered. This differentiates tunneling catalysis from conventional catalysis. While barrier widths are crucial for tunneling rates, they are difficult to predict even qualitatively. In the 6 → T-7 rearrangement the reaction is driven by the intersystem crossing and formation of T-7 as irreversible exit step. In T-7 the interaction with the Lewis acid is weaker than in TS and csS-7, which should make the decoordination step necessary to close the catalytic cycle, feasible at higher temperatures. However, under the conditions of matrix isolation with kT close to zero, vanishing entropic driving force, and the inhibition of diffusion, decoordination is not possible.In summary, the Lewis acid catalysis of the tunneling rearrangement of 6 results from the lowering of the activation barriers and narrowing of the barrier widths in the Lewis acid complexes of 6. This example demonstrates the new concept of tunneling catalysis, which might be of importance to a broad range of tunneling reactions.
Data availability
The datasets supporting this article have been uploaded as part of the ESI.Author contributions
S. H. and M. P. M. did the experiments and the DFT calculations. E. M. V. did the CAS calculations. All authors contributed to writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy-EXC-2033-Projektnummer 390677874 RESOLV.References
- R. S. Sheridan in Quantum mechanical tunneling in organic reactive intermediates, John Wiley & Sons, Inc., 2007, pp. 415–463 Search PubMed.
- R. P. Bell, The Tunnel Effect in Chemistry, Chapman and Hall, London, 1980 Search PubMed.
- D. Ley, D. Gerbig and P. R. Schreiner, Org. Biomol. Chem., 2012, 10, 3781 RSC.
- R. J. McMahon, Science, 2003, 299, 833 CrossRef CAS PubMed.
- W. T. Borden, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 20 CAS.
- C. M. Nunes, A. K. Eckhardt, I. Reva, R. Fausto and P. R. Schreiner, J. Am. Chem. Soc., 2019, 141, 14340 CrossRef CAS PubMed.
- S. Kozuch, T. Schleif and A. Karton, Phys. Chem. Chem. Phys., 2021, 23, 10888 RSC.
- T. Schleif, J. Mieres-Perez, S. Henkel, M. Ertelt, W. T. Borden and W. Sander, Angew. Chem., Int. Ed., 2017, 56, 10746 CrossRef CAS PubMed.
- T. Schleif, J. Tatchen, J. F. Rowen, F. Beyer, E. Sanchez-Garcia and W. Sander, Chem.–Eur. J., 2020, 26, 10366 CrossRef CAS PubMed.
- T. Schleif, M. Prado Merini and W. Sander, Angew. Chem., Int. Ed., 2020, 59, 20318 CrossRef CAS PubMed.
- H. Inui, K. Sawada, S. Oishi, K. Ushida and R. J. McMahon, J. Am. Chem. Soc., 2013, 135, 10246 CrossRef CAS PubMed.
- W. Sander, G. Bucher, F. Reichel and D. Cremer, J. Am. Chem. Soc., 1991, 113, 5311 CrossRef CAS.
- M. Ertelt, D. A. Hrovat, W. T. Borden and W. Sander, Chem.–Eur. J., 2014, 20, 4713 CrossRef CAS PubMed.
- C. M. Nunes, L. P. Viegas, S. A. Wood, J. P. L. Roque, R. J. McMahon and R. Fausto, Angew. Chem., Int. Ed., 2020, 59, 17622 CrossRef CAS PubMed.
- J. P. L. Roque, C. M. Nunes, L. P. Viegas, N. A. M. Pereira, T. M. V. D. Pinho e Melo, P. R. Schreiner and R. Fausto, J. Am. Chem. Soc., 2021, 143, 8266 CrossRef CAS PubMed.
- L. P. Viegas, C. M. Nunes and R. Fausto, Phys. Chem. Chem. Phys., 2021, 23, 5797 RSC.
- B. Chen, A. Y. Rogachev, D. A. Hrovat, R. Hoffmann and W. T. Borden, J. Am. Chem. Soc., 2013, 135, 13954 CrossRef CAS PubMed.
- E. M. S. Macoas, L. Khriachtchev, M. Pettersson, R. Fausto and M. Rasanen, J. Chem. Phys., 2004, 121, 1331 CrossRef CAS PubMed.
- W. Kirmse, Carbene Protonation, in Advances in Carbene Chemistry, ed. U. H. Brinker, Elsevier Science B.V., 2001, vol. 3, pp. 1–51 Search PubMed.
- P. Costa and W. Sander, Angew. Chem., Int. Ed., 2014, 53, 5122 CAS.
- P. Costa, M. Fernandez-Oliva, E. Sanchez-Garcia and W. Sander, J. Am. Chem. Soc., 2014, 136, 15625 CrossRef CAS PubMed.
- A. H. Raut, P. Costa and W. Sander, Chem.–Eur. J., 2018, 24, 18043 CrossRef CAS PubMed.
- P. Costa, I. Trosien, M. Fernandez-Oliva, E. Sanchez-Garcia and W. Sander, Angew. Chem., Int. Ed., 2015, 54, 2656 CrossRef CAS PubMed.
- P. Costa, J. Mieres-Perez, N. Özkan and W. Sander, Angew. Chem., Int. Ed., 2017, 56, 1760 CrossRef CAS PubMed.
- P. Costa, I. Trosien, J. Mieres-Perez and W. Sander, J. Am. Chem. Soc., 2017, 139, 13024 CrossRef CAS PubMed.
- S. Henkel, P. Costa, L. Klute, P. Sokkar, M. Fernandez-Oliva, W. Thiel, E. Sanchez-Garcia and W. Sander, J. Am. Chem. Soc., 2016, 138, 1689 CrossRef CAS PubMed.
- S. Henkel, I. Trosien, J. Mieres-Perez, T. Lohmiller, A. Savitsky, E. Sanchez-Garcia and W. Sander, J. Org. Chem., 2018, 83, 7586 CrossRef CAS PubMed.
- S. Henkel, M. Ertelt and W. Sander, Chem.–Eur. J., 2014, 20, 7585 CrossRef CAS PubMed.
- E. Wasserman and R. W. Murray, J. Am. Chem. Soc., 1964, 86, 4203 CrossRef CAS.
- A. Sole, S. Olivella, J. M. Bofill and J. M. Anglada, J. Phys. Chem., 1995, 99, 5934 CrossRef CAS.
- L. A. Montero, A. M. Esteva, J. Molina, A. Zapardiel, L. Hernandez, H. Marquez and A. Acosta, J. Am. Chem. Soc., 1998, 120, 12023 CrossRef CAS.
- W. Siebrand and T. A. Wildman, Acc. Chem. Res., 1986, 19, 238 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, EPR spectra, additional complex geometries and IR spectra, kinetic data, tabulated IR frequencies and optimized geometries. See DOI: 10.1039/d1sc02853g |
| This journal is © The Royal Society of Chemistry 2021 |