Extended ligand conjugation and dinuclearity as a route to efficient platinum-based near-infrared (NIR) triplet emitters and solution-processed NIR-OLEDs†
Marsel Z.
Shafikov
 *ab,
Piotr
Pander
*ab,
Piotr
Pander
 *c,
Andrey V.
Zaytsev
*c,
Andrey V.
Zaytsev
 d,
Ruth
Daniels
d,
Ruth
Daniels
 d,
Ross
Martinscroft
d,
Ross
Martinscroft
 d,
Fernando B.
Dias
d,
Fernando B.
Dias
 c,
J. A. Gareth
Williams
c,
J. A. Gareth
Williams
 *e and
Valery N.
Kozhevnikov
*e and
Valery N.
Kozhevnikov
 *d
*d
aInstitut für Physikalische und Theoretische Chemie, Universität Regensburg, Universitätsstrasse 31, Regensburg, D-93053, Germany. E-mail: shafikoff@gmail.com
bUral Federal University, Mira 19, Ekaterinburg, 620002, Russia
cDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: piotr.h.pander@durham.ac.uk
dDepartment of Applied Sciences, Faculty of Health and Life Sciences, Northumbria University, Newcastle Upon Tyne, Tyne and Wear, NE1 8ST, UK. E-mail: valery.kozhevnikov@northumbria.ac.uk
eDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK. E-mail: j.a.g.williams@durham.ac.uk
First published on 26th November 2020
Abstract
Near infrared (NIR) emission from molecular materials is typically targeted by using more extended conjugated systems compared to visible-emitting materials. But efficiencies usually fall off due to the combined effects of increasing non-radiative and lower oscillator strengths as the energy of emissive excited states decreases. Efficient NIR-emitting organic light emitting diodes (OLEDs) are rare compared to the huge progress that has been made for visible-light devices. For organometallic emitters that contain a heavy metal ion to promote phosphorescence through the effect of enhanced spin–orbit coupling (SOC), the problem is typically exacerbated by decreased metal character in the Sn and T1 excited states as the conjugation in a bound ligand increases. Here we show how the use of a dinuclear metal complex with an extended conjugated ligand allows such effects to be mitigated compared to analogous structures with just one metal centre. The complex Pt2(bis-dthpym)(dpm)2 (complex 5) is readily prepared by a double N^C cyclometallation of 4,6-bis(dithienyl)-pyrimidine (H2bis-dthpym), with the coordination sphere of each Pt centre being completed by O^O-coordinating dipivaloylmethane (dpm). This new complex displays intense NIR emission in solution, λmax = 725 nm, with essentially no “contamination” by visible light <700 nm. The photoluminescence quantum yield of 0.17 in toluene at 300 K is vastly superior to that of the analogous mononuclear complex, where reduced SOC leads primarily to ligand-based fluorescence and only very weak phosphorescence. Computational results indicate that a key reason for the superior performance of the dinuclear system is a doubling of the number of higher-lying excited singlet states with which the T1 state may couple, to promote the formally forbidden phosphorescence process. Complex 5 has been evaluated as an NIR emitter in solution-processed OLEDs. An external quantum efficiency (EQE) of 3.6% is attained using 5 doped into TBP:PBD at 5% w/w, with a turn-on voltage of 5.6 V (at 0.01 mW cm−2). The maximum radiosity of 2.7 mW cm−2 for this device is particularly high compared to most reported NIR-emitting phosphorescent OLEDs.
Introduction
Triplet-harvesting luminescent molecules incorporating heavy metals have found a profound role in OLED technology as a successful way to obtain up to 100% internal quantum efficiency (IQE).1–5 Iridium(III) and platinum(II) complexes have been intensively studied in this context6–18 and now feature as phosphorescent emitters in commercial electroluminescent displays, such as those used in smartphones.19–21 Platinum(II) phosphors have become a centre of interest for OLED engineers designing emitters that operate in the red and near infrared (NIR) regions of the spectrum. For example, the planar geometry of d8 Pt(II) complexes may allow the formation of emissive excimers or aggregates through face-to-face interactions:22–25 their red-shifted emission has been shown to afford a promising strategy for obtaining efficient deep red/NIR OLEDs.26–29 Such approaches do, however, require appropriate intermolecular interactions to be present, typically necessitating somewhat higher dopant concentrations. Unimolecular emission, yet involving two Pt(II) centres, is shown in this contribution to offer an attractive alternative.The classical strategy to tune the emission of cyclometallated complexes with phenylpyridine-based ligands is by varying the pattern of substituents in the aromatic rings, or using different carbocycles and N-heterocycles in place of benzene and pyridine respectively. The strategy relies on the fact that the HOMO and LUMO are typically localised largely on mutually different parts of the molecule, and so their energies can often be modulated essentially independently of one another. For example, the use of a more electron-rich thiophene in place of phenyl as the cyclometallating ring selectively destabilises the HOMO, typically with little influence on the LUMO, thus causing a red shift.20,21 A red-shift can also be achieved by expanding the conjugated π-system of the ligand, in line with the anticipated narrowing of the HOMO–LUMO gap that occurs for organic molecules. However, this strategy may not always translate well to organometallic emitters; for example, benzannulation has been found to be accompanied by counterintuitive blue-shifts in emission is some studies, reflecting the different structure of the T1 state.30,31 Indeed, in almost all cases, the shifting of the emission to lower energy has detrimental effects on efficiency. Firstly, the rate of non-radiative decay, knr, increases through the effects of Fermi's Golden Rule and what is commonly known as the ‘energy gap law’.32 Secondly, the reduction of metal orbital character in the excited state leads to a decrease in the triplet radiative rate constant kr, making phosphorescence less competitive with non-radiative decay and thus compromising efficiency. In OLEDs, it also facilitates undesirable triplet-quenching processes.33 Thirdly, the rate of intersystem crossing kISC from singlet to triplet may also decrease as the admixture of metal character in the pertinent excited states falls; in some instances, this can even allow notable S1 state fluorescence to appear.34–36 These trends are all evident, for example, on moving from the simple platinum(II) thienylpyridine complex Pt(thpy)(acac) to its analogue with an additional thienyl group appended, Pt(dthpy)(acac) (Fig. 1; Hthpy = 2-thienylpyridine, Hdthpy = 2-(dithienyl)pyridine‡). The former displays intense yellow/orange phosphorescence (λmax = 554 nm, ΦPL = 0.36 in CH2Cl2) whilst the latter shows only very weak red phosphorescence that is accompanied by stronger blue fluorescence.35
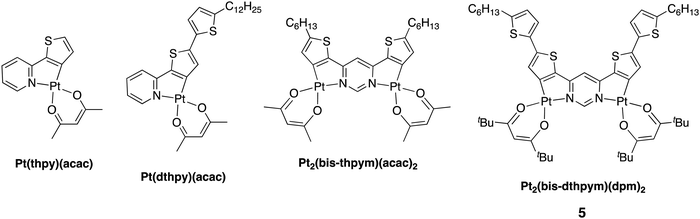 | ||
| Fig. 1 Structures of dinuclear platinum(II) complexes featuring thienylpyridine-based ligands, together with the new complex Pt2(bis-dthpym)(dpm)2 reported in this work, hereafter denoted complex 5. | ||
The use of multinuclear complexes is emerging as an effective strategy to overcome some of these problems. For example, deep red-emitting dinuclear platinum and iridium complexes bridged by cyclometallating pyrimidine type ligands have been shown to display unusually high triplet radiative decay rates and hence high phosphorescence quantum yields.37–43 Previously, in the context of thienylpyridine complexes, we showed that the dinuclear complex Pt2(bis-thpym)(acac)2 (Fig. 1; bis-thpym = 4,6-bisthienylpyrimidine) displays red emission (λmax = 612 nm in CH2Cl2) but, far from being compromised in the usual way, the quantum yield is improved (ΦPL = 0.85), thanks to a substantially higher kr than the mononuclear analogue Pt(dthpy)(acac).
In this contribution, we report a new dinuclear platinum(II) complex, Pt2(bis-dthpym)(dpm)2 [H2bis-dthpym = 4,6-bis(dithienyl)pyrimidine; Fig. 1], designed to combine the two strategies of extended π-conjugation and dinuclearity in order to red-shift the emission even further, into the NIR, without significant loss of efficiency. This novel complex – which can be regarded as the dinuclear analogue of Pt(dthpy)(acac) that gave only weak phosphorescence – shows intense luminescence in the NIR region. Its photophysical behaviour has been investigated in detail and the complex shown to function successfully as an efficient emitter in NIR-OLEDs.
Results and discussion
Synthesis
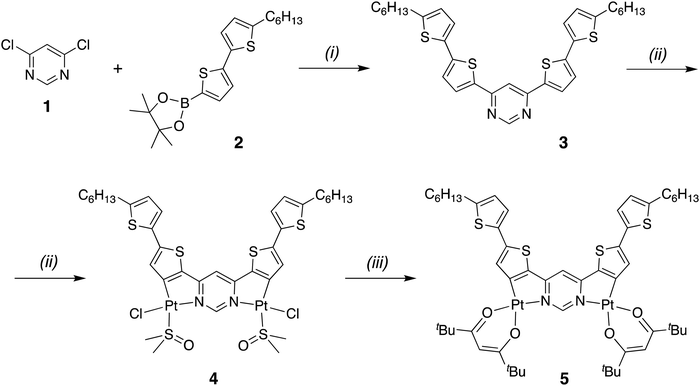
The synthesis of the requisite ditopic proligand 3 and its platination to give the desired dinuclear complex Pt2(bis-dthpym)(dpm)2, 5, is depicted in Scheme 1. The proligand was prepared by Pd-catalysed Suzuki cross-coupling of the commercially available building blocks 1 and 2. It was reacted with potassium tetrachloroplatinate in boiling acetic acid to give a highly insoluble material. By analogy with the chemistry established for related bridging cyclometalling ligands,8,43 this compound was presumed to comprise of oligomeric dichloro-bridged polynuclear species. The material was treated with DMSO at 130 °C – which has the effect of breaking up such dichloro bridges – to give complex 4, where a monodentate chloride and sulfur-bound DMSO complete the coordination sphere of each Pt(II) centre. Complex 4 is sufficiently soluble for purification by column chromatography, after which it was converted to the desired complex 5 by treatment with 2,2,6,6-tetramethyl-3,5-heptanedione (also known as dipivaloylmethane, dpmH) in the presence of sodium carbonate as a base. Complex 5 was purified by column chromatography and its identity and purity confirmed by NMR spectroscopy, high resolution mass spectrometry, elemental analysis, and X-ray diffraction (vide infra). The synthesis of the analogue with acac in place of dpm was also attempted, but poor solubility frustrated its purification.X-ray diffraction analysis
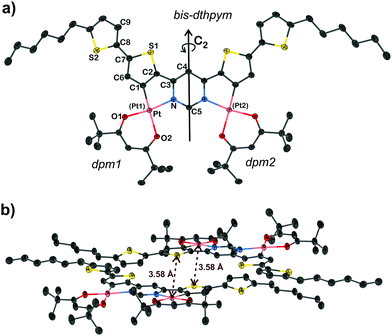
Dark red, needle-shaped crystals of 5 suitable for X-ray diffraction were obtained by slow diffusion of methanol into a solution of the complex in dichloromethane. The molecular structure in the crystal is shown in Fig. 2a. Key bond lengths and angles are listed in the caption: they are comparable to those found in C^N and O^O-coordinated mononuclear Pt(II) complexes reported previously.8,34,43,44 The molecule features a C2 principal axis through carbon atoms C4 and C5 of the central pyrimidine ring. The central, ditopic bis-thienyl-pyrimidine coordinating unit is almost planar [the C1–C2–C3–N torsion angle is 3.0(2)°] whilst the terminal thienyl rings are twisted only slightly out of that plane by 11.9(3)° (torsion angle: angle C6–C7–C8–S2). The molecules pack in head-to-tail, face-to-face pairs with an interplanar separation of 3.4–3.5 Å, suggesting strong π–π interactions between the aromatic cores, but no metallophilic Pt⋯Pt interactions are present (Fig. 2b). On the contrary, each Pt(II) centre is in a short intermolecular contact with a sulfur atom of the dithienylpyrimidine of a neighbouring molecule, with a Pt⋯S(1) interatomic distance of 3.5751(6) Å that is essentially the same as the sum of the van der Waals radii of Pt and S atoms (1.75 and 1.83 Å respectively, = 3.58 Å).45Steady-state optical spectroscopy
The absorption spectrum of 5 measured in dilute solution in toluene at room temperature (Fig. 3) displays an intense lowest-energy band centred at 562 nm, with a higher-energy shoulder at 527 nm that is probably vibrational in origin (i.e., transitions to the zeroth and first vibrational levels of the S1 state, respectively). The band is extraordinarily intense, ε = 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 M−1 cm−1 at 562 nm, an order of magnitude higher than the extinction coefficients of the lowest-energy bands in typical mononuclear Pt(II) complexes like Pt(thpy)(acac). Data for 5 and related complexes for comparison are compiled in Table 1. The strong absorption probably arises, in part, from the symmetric structure resulting in the coupling of two transition dipole moments that can give a 4-fold increase in oscillator strength (vide infra), as recently elucidated in a series mono- and dinuclear copper(I) complexes.46 There are a set of higher energy absorption bands, around 400 nm, also of quite high intensity, in addition to the anticipated ligand-based transitions further into the UV. The likely orbital parentage of the transitions is discussed further below in the context of TD-DFT calculations.
100 M−1 cm−1 at 562 nm, an order of magnitude higher than the extinction coefficients of the lowest-energy bands in typical mononuclear Pt(II) complexes like Pt(thpy)(acac). Data for 5 and related complexes for comparison are compiled in Table 1. The strong absorption probably arises, in part, from the symmetric structure resulting in the coupling of two transition dipole moments that can give a 4-fold increase in oscillator strength (vide infra), as recently elucidated in a series mono- and dinuclear copper(I) complexes.46 There are a set of higher energy absorption bands, around 400 nm, also of quite high intensity, in addition to the anticipated ligand-based transitions further into the UV. The likely orbital parentage of the transitions is discussed further below in the context of TD-DFT calculations.
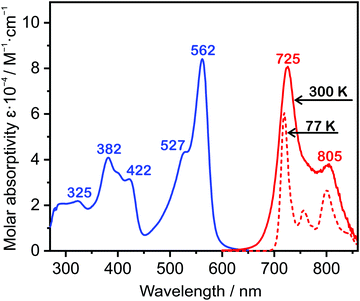 | ||
| Fig. 3 Absorption spectrum of 5 in toluene (10−5 M) at 300 K (blue line); emission spectrum under the same conditions (solid red line) and at 77 K (dashed red line), arbitrary intensity axis. | ||
| Pt(dthpy)(acac)a | Pt2(bis-thpym)(acac)2b | Pt2(bis-dthpym)(dpm)25 | ||
|---|---|---|---|---|
| a From ref. 35 data at 300 K obtained in CH2Cl2, and at 77 K in EPA. b From ref. 43 data at 300 K are for CH2Cl2 solution. c The phosphorescence of this complex is accompanied by stronger fluorescence bands at the wavelengths indicated in parenthesis labelled ‘F’. d Not determinable. e At 77 K, ΦPL = 0.23, kr = 1.9 × 104 s−1, knr = 6.4 × 104 s−1. | ||||
| Absorption at 300 K λmax/nm (ε/M−1 cm−1) | 443 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300), 350 (32 300), 350 (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600), 295 (16 600), 295 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800) 800) |
500 (53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800), 470 (22 800), 470 (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400), 400 (18 400), 400 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700), 347 (37 700), 347 (37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600), 270 (19 600), 270 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900) 900) |
562 (84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100), 421 (31 100), 421 (31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500), 382 (40 500), 382 (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900) 900) |
|
| Emission at 300 K | λ max/nm | 706, 775 [F = 495]c | 610, 660s h | 725, 805 |
| τ/μs | 2.3 | 12 | 9.0 | |
| Φ PL | <0.002 | 0.85 | 0.17 | |
| k r/104 s−1 | —d | 7.1 | 1.9 | |
| k nr/104 s−1 | —d | 1.3 | 9.3 | |
| Emission at 77 K | λ max/nm | 693, 724, 767 [F = 470, 505, 438]c | 607, 630, 660 | 720, 755, 800 |
| τ/μs | —d | 26 | 12 | |
The complex is strongly luminescent in the NIR region of the spectrum. It displays a vibrationally structured spectrum in toluene (Fig. 3), with the 0,0 component at 725 nm and a weaker vibrational shoulder at 805 nm. The measured luminescence lifetime in degassed solution is 9 μs (at 300 K), an order of magnitude that is typical of bright, triplet-emitting Pt(II) complexes. The emission quantum yield under the same conditions is 0.17, a remarkably high efficiency for solution phosphorescence in the NIR. Similar data are obtained for the complex doped at 1% by mass in a polystyrene film (λmax = 725, 815 nm; τ = 9.4 μs; ΦPL = 0.20). In a frozen glass at 77 K, the vibrational resolution is further improved, and there is a small increase in the lifetime and quantum yield by a factor of about one-third arising from a modest reduction in the rate of non-radiative decay (Table 1).
It is important to compare 5 with the related predecessors in Fig. 1 that were aimed at obtaining red-shifted emission.43 As noted in the introduction, the appendage of a thienyl ring onto the mononuclear Pt(thpy)(acac) complex to extend the ligand conjugation did indeed red-shift the luminescence, but at huge expense of efficiency: the quantum yield falls dramatically (Table 1) and intersystem crossing is slowed down such that higher-energy fluorescence competes. In 5 – the new dinuclear version of Pt(dthpy)(acac) – the emission is not only successfully red-shifted squarely into the NIR, but good efficiency is also retained that is comparable to Pt(thpy)(acac) (ΦPL = 0.36). Evidently, the dinuclear structure ensures that spin–orbit coupling and intersystem crossing remain efficient.
The emission of 5 is substantially red-shifted compared to the previously studied dinuclear complex Pt2(bis-thpym)(acac)2, for which λ0,0 = 605 nm, highlighting the influence of the extension of the π-conjugated system through appendage of thienyl groups that are roughly coplanar with the core. Despite the good efficiency of 5, there is a modest reduction in kr by a factor of just over 3-fold (Table 1). Calculations (discussed below) suggest that the relaxation of the spin-selection rule through SOC is not quite so efficient in the new complex due to reduced metal-character in the predominantly LC emissive state.5 Complex 5 is more susceptible to non-radiative decay (see knr values in Table 1), which is likewise to be expected given that its emissive state is some 2600 cm−1 lower in energy than that of Pt2(bis-thpym)(acac)2 and has a rather less rigid structure.32
Computations and theoretical considerations
DFT and TD-DFT calculations have been carried out on a model system for 5 – denoted 5′ – in which the terminal hexyl groups are replaced by methyl and acac is used in place of dpm, in order to reduce computational demands. The geometry optimisations (at the ground state S0 and lowest triplet state T1) and the time-dependent calculations were all conducted with Gaussian 09,47 using the M06 functional48 and def2-SVP49 basis sets, and with the C-PCM solvation model50 for toluene. The calculated ground state geometric parameters agree well with the experimental values from X-ray diffraction, aside from some slight deviations probably associated with crystal packing (Table S2 in the ESI†), whilst the absorption spectrum simulated by TD-DFT matches well with the experimental spectrum (Fig. S1 in the ESI†). These observations provide confidence in the suitability of the level of applied theory to give reliable insight into the electronic structure of the complex.The T1 state is the most relevant to phosphorescence and the TD-DFT calculations show it to be predominantly HOMO → LUMO (77%) in character (Table S4 in the ESI†). The HOMO is primarily localized on the aromatic (Ar) ligand with a small (10%) contribution from the Pt(II) centres (Fig. 4 and Table S3 in the ESI†), whilst the LUMO represents a π* orbital with low metal contribution (6%). Overall, the T1 state may therefore be formulated as dPt|πAr → π*Ar but with the ligand-centred 3LC (3ππ*) character dominating over the metal-to-ligand charge-transfer 3MLCT (3dπ*). The rigidity of the aromatic core (leading to minimal excited state reorganisation and favouring emission efficiency) is highlighted by the fact that even for the N–C3 bond, which is antibonding in the LUMO, the bond length increases only marginally (from 1.385 to 1.396 Å in the S0 and T1 states, respectively).
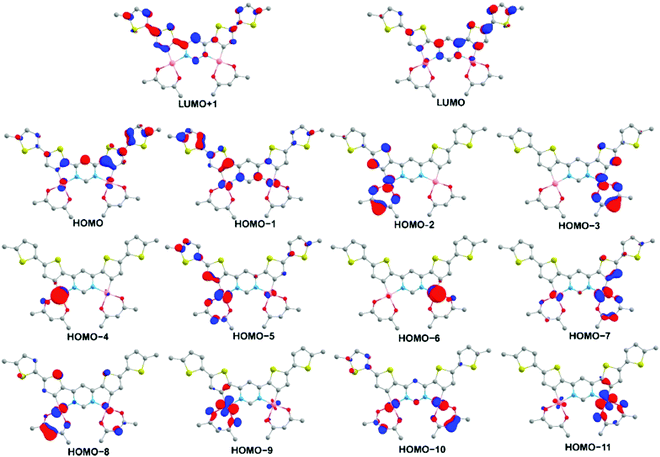 | ||
| Fig. 4 The iso-surface contour plots (iso-value = 0.05) of the orbitals of the model complex 5′ (optimized T1 state geometry) contributing to the T1 state and to excited singlet states with which T1 can undergo direct SOC. Hydrogen atoms are omitted for clarity. Contributions of the orbitals to the excited states are given in Table S4 in the ESI.† | ||
The relaxation of the formally spin-forbidden T1 → S0 phosphorescence process in transition metal complexes arises through the influence of SOC promoted by the metal ion.51 The oscillator strength f of the T1 → S0 transition is expressed by eqn (1):52
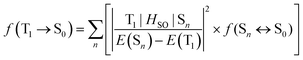 | (1) |
Here Sn refers to an excited singlet state of energy E(Sn) and HSO is the SOC operator. SOC is a short-range, one-electron interaction that scales with Z4;53 the SOC constant ζ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) of Pt is large (4481 cm−1 for atomic Pt).54,55 The T1 state of 5′ comprising an element of 3diπ* can undergo direct SOC with singlet states comprising an element of 1djπ*′ character involving the same metal centre but, by the El-Sayed rule,56 only when di ≠ dj and π* = π*′; i.e., the states in question must involve d orbitals of different angular momentum, so as to conserve the total momentum (orbital + spin) when the spin state changes. Extending the spin–orbit coupling operator as HSO = ζ
of Pt is large (4481 cm−1 for atomic Pt).54,55 The T1 state of 5′ comprising an element of 3diπ* can undergo direct SOC with singlet states comprising an element of 1djπ*′ character involving the same metal centre but, by the El-Sayed rule,56 only when di ≠ dj and π* = π*′; i.e., the states in question must involve d orbitals of different angular momentum, so as to conserve the total momentum (orbital + spin) when the spin state changes. Extending the spin–orbit coupling operator as HSO = ζ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) SL (ζ
SL (ζ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is spin–orbit coupling constant, S is spin momentum operator, L is orbital momentum operator), the SOC matrix element in formula 1 can be rewritten as follows:57–59
is spin–orbit coupling constant, S is spin momentum operator, L is orbital momentum operator), the SOC matrix element in formula 1 can be rewritten as follows:57–59
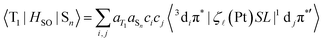 | (2) |
Here aT1 and aSn are the normalized configuration interaction coefficients of state T1 and state Sn, respectively; ci and cj are the partial contribution coefficients of the metal atomic orbitals di and dj, respectively, in the molecular orbitals involved in transitions forming states T1 and Sn. The ci and cj coefficients reduce the SOC matrix elements 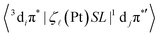 according to the dπ* character contributions to state T1 and singlets Sn. This, for example, shows the correlation between the extent of dπ* character of T1 and the phosphorescence rate T1 → S0.
according to the dπ* character contributions to state T1 and singlets Sn. This, for example, shows the correlation between the extent of dπ* character of T1 and the phosphorescence rate T1 → S0.
In the context of fulfilling the di ≠ dj and π* = π*′ requirements, when the SOC matrix element is not vanishing, analysis of the TD-DFT data (Table S4 in the ESI†) shows that the T1 state can undergo direct SOC with several higher-lying singlet states: S2 (HOMO−1 → LUMO 92%), S6 (HOMO−6 → LUMO 72%, HOMO−4 → LUMO 25%), S7 (HOMO−4 → LUMO 72%, HOMO−6 → LUMO 25%), S9 (HOMO−7 → LUMO 72%), S10 (HOMO−5 → LUMO 77%), S11 (HOMO−11 → LUMO 74%, HOMO−9 → LUMO 19%) and S13 (HOMO−11 → LUMO 74%, HOMO−9 → LUMO 19%). It is informative to note that HOMO−5 and HOMO−7 involve d-orbitals of the same angular momentum but which differ in symmetry: symmetric and anti-symmetric, respectively, with respect to C2 rotation. These molecular orbitals are a result of electronic coupling of the two sites of the symmetric dinuclear electronic structure of 5′ and they lead to two excited singlet states (S9 and S10) with which T1 can undergo direct SOC, as indicated above. Moreover, both S9 and S10 have a relatively large oscillator strength for transition to the ground state [f(S9 ↔ S0) = 0.2770, f(S10 ↔ S0) = 0.2770, Table S4 in the ESI†], which will facilitate the T1 → S0 transition rate through eqn (1). Similar reasoning applies to the orbital pairs HOMO−4 and HOMO−6, HOMO−8 and HOMO−10, and HOMO−9 and HOMO−11.
Clearly, the extent to which these higher states are implicated will also be influenced by the respective Sn–T1 energy gap in the denominator of eqn (1). But the key point here is that the symmetric dinuclear design of 5′ doubles the number of 1djπ* character-contributed singlet states that are electronically suitable for SOC with T1 (3diπ*), thereby facilitating phosphorescence and accounting for the much brighter phosphorescence of 5 over Pt(dthpy)(acac). A similar conclusion has been reached recently for iridium(III) complexes from a comparative study of mono- and dinuclear designs.42 The feature limiting the phosphorescence rate in the present case, compared to the previously studied dinuclear Pt2(bis-thpy)(acac)2, is the relatively smaller metal contribution to several higher occupied orbitals and hence weaker MLCT character not only of state T1 but also of singlets electronically suitable for SOC with T1. The metals’ contribution to the HOMO, for instance, is 10% as opposed to 26% in Pt2(bis-thpy)(acac)2.43
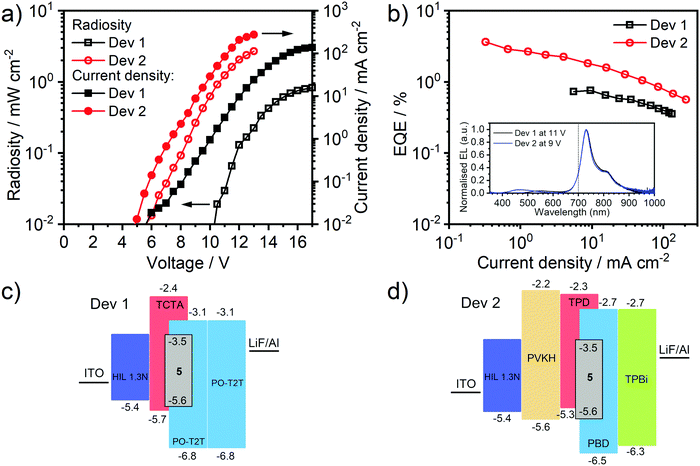
OLED Devices and photoluminescence in solid films§
With emission well into the NIR region, almost no visible light contamination, and an impressive ΦPL in solution, complex 5 clearly offers potential as an emitter to generate an efficient NIR-OLED. It has sufficient solubility for it to be incorporated into an OLED by solution-processing; notably it has good solubility in toluene, amenable to the preparation of multilayer device structures. Blend, exciplex hosts were selected as host materials, having previously been found to be very good candidates for use with metal complex phosphors.43,60–62 Two such bi-component hosts were studied: TCTA:PO-T2T,63 which is soluble in chloroform:chlorobenzene mixture, and TPD:PBD43 with good solubility in toluene. [The motivation for considering the former lies in that it has been found to exhibit thermally activated delayed fluorescence (TADF), though this property has been found not to be relevant for its performance as an OLED host for 5; detailed discussion is provided in the ESI,† Section 5.1].The photoluminescence (PL) of 5 doped in these two materials was first evaluated (5% w/w), giving ΦPL = 0.10 ± 0.01 in both hosts, and τav = 7.5 ± 0.9 and 7.4 ± 0.5 μs in TCTA:PO-T2T and TPD:PBD respectively. The somewhat lower ΦPL and τav under these conditions, compared to the values recorded in dilute solution (10−5 M) or in polystyrene (1% w/w), probably arises from the effect of intermolecular interactions between emitter molecules when at the higher concentration. OLED devices were then fabricated using the two hosts (Fig. 5). Device 1 has the structure: ITO|HIL 1.3N (45 nm)|TCTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PO-T2T (70
PO-T2T (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30) co 5% 5 (70 ± 5 nm)|PO-T2T (50 nm)|LiF (0.8 nm)|Al (100 nm). Device 2 has the structure: ITO|HIL 1.3 N (45 nm)|PVKH (10 nm)|TPD
30) co 5% 5 (70 ± 5 nm)|PO-T2T (50 nm)|LiF (0.8 nm)|Al (100 nm). Device 2 has the structure: ITO|HIL 1.3 N (45 nm)|PVKH (10 nm)|TPD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PBD (60
PBD (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) co 5% 5 (30 ± 5 nm)|TPBi (50 nm)|LiF (0.8 nm)|Al (100 nm). The PVKH is incorporated as an additional hole transport/electron blocking layer to improve charge balance.64,65 Unfortunately, neither of the approaches provides complete elimination of host emission whilst increasing the emitter loading was found to be detrimental to EQE: a compromise was achieved at 5% loading. Residual host emission suggests that 5 does not effectively trap charge carriers and that the bulk of charge recombination occurs within the host.
40) co 5% 5 (30 ± 5 nm)|TPBi (50 nm)|LiF (0.8 nm)|Al (100 nm). The PVKH is incorporated as an additional hole transport/electron blocking layer to improve charge balance.64,65 Unfortunately, neither of the approaches provides complete elimination of host emission whilst increasing the emitter loading was found to be detrimental to EQE: a compromise was achieved at 5% loading. Residual host emission suggests that 5 does not effectively trap charge carriers and that the bulk of charge recombination occurs within the host.
Both devices show strong electroluminescence (EL) with only very dim residual visible light emission. The maximum [visible] luminance¶ of only 100–200 cd m−2 – barely visible in a lit room – comprises only ≈10% of the total radiant power and <8% if the onset emission of 5 in the 680–700 nm region is excluded. The EL spectrum remains stable with increasing voltage (Fig. S10, ESI†). The NIR emission onsets and maxima are essentially the same in both devices, 680 and 731 nm respectively, and similar to the PL of 5 in solution or film. Device 2 outperforms Device 1 (max. EQE = 3.6 ± 0.5% as opposed to 0.8 ± 0.1% in Device 1) and shows a lower turn-on voltage (VON = 5.6 and 10.3 V respectively, at 0.01 mW cm−2). The difference may be attributed to the beneficial role of the PVKH layer for charge balance, reducing the hole injection barrier from HIL 1.3 N to the emissive layer and blocking electron leakage to the anode. Device 2 shows a higher current density and thus, given its generally higher EQE, is significantly more radiant (2.7 and 0.85 mW cm−2 for Devices 2 and 1 respectively). Roll-off, evaluated in terms of a J90% value33 (the current density at which the EQE drops to 90% of its initial value), is ≈10 mA cm−2 in Device 1 and ≈0.5–1 mA cm−2 in Device 2. The former is fairly typical in phosphorescent devices, while the latter is comparable to that reported in a solution-processed phosphorescent device, albeit for a visible emitter.21 The relative dearth of literature roll-off data for solution-processed NIR OLEDs does not allow the roll-off values of our devices to be set in a broader context.
In general, vacuum-deposited OLEDs using Pt(II) complexes forming bimolecular NIR-emitting excimers28 or dimers/oligomers26 outperform the maximum EQE achieved in this work but, among solution-processed devices, the EQE here of 3.6 ± 0.5% with λonset > 680 nm is perhaps the highest reported to date. Among the very few solution-processed NIR OLEDs using Pt(II) complexes, the most notable are those with porphyrin ligands that exhibit electroluminescence in the 700–850 nm region. Solution-processed OLED performance in this case does not exceed 0.5% EQE, though values up to 8% EQE have been reported in vacuum-deposited devices.66,67 In general, the best fluorescent NIR emitters show OLED efficiencies around 1–2%.68,69 Phosphorescent metal complex emitters, predominantly those based on Ir(III), have been reported that show external quantum efficiencies in the range of 0.4–2.2% for λmax > 690 nm,70–73 or even up to 5.7% for λonset ≈ 650 nm and λmax = 690 nm.74 Yet the radiosity of these devices is limited, <1 mW cm−2. The low radiosity is likely to be caused by low charge mobility in the PVK co-host used in most studies.75 The combination of PVKH layer and TPD:PBD host used in the present work, compared to usual PVK-based host, helps to increase current density, leading to more radiant devices.
Concluding remarks
The results described here have shown how the use of a dinuclear complex provides a means of side-stepping the usual problem of marked efficiency decrease that normally accompanies the shift to deep red or NIR emission associated with extended π-conjugated ligands. The phosphorescence of the new dinuclear complex 5 is promoted by its symmetric structure that doubles the number of higher-lying singlet states which are electronically suitable for SOC with the emitting triplet state T1. This effect is also manifest in the remarkably intense lowest-energy absorption band, where the symmetric structure results in the coupling of two transition dipole moments that can give a 4-fold increase in oscillator strength. The complex emits almost exclusively in the NIR region, behaviour that translates well into a solution-processed OLED. The strategy of using two Pt(II) centres in an extended conjugated system to generate low-energy unimolecular emission complements the increasingly researched approach of exploiting bimolecular aggregates or excimers. Further increases in efficiency can confidently be anticipated if future molecular design suppresses non-radiative decay pathways, for example, through enhanced rigidity.Experimental
Full details of the synthesis and characterisation of 3, 4 and 5 are provided in the ESI,† including 1H NMR spectra, mass spectral and elemental analysis data, and crystallographic details for 5 (including unit cell parameters and equipment used). The ESI,† also includes full details of optical spectroscopy; computational calculations and selected data output; electrochemistry; OLED fabrication, and further discussion of photophysical measurements and properties in the host materials.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
We thank EPSRC for support of some parts of this work (grant ref: EP/S012788/1). M. Z. S. gratefully acknowledges financial support from the German Research Foundation (DFG), Project No. 389797483.References
- M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef CAS
.
- M. A. Baldo, S. Lamansky, P. E. Burrows, M. E. Thompson and S. R. Forrest, Appl. Phys. Lett., 1999, 75, 4–6 CrossRef CAS
.
- C. Adachi, M. A. Baldo, S. R. Forrest, S. Lamansky, M. E. Thompson and R. C. Kwong, Appl. Phys. Lett., 2001, 78, 1622–1624 CrossRef CAS
.
-
Highly Efficient OLEDs with Phosphorescent Materials, ed. H. Yersin, Wiley-VCH, Weinheim, 2008 Search PubMed
.
- H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, Coord. Chem. Rev., 2011, 255, 2622–2652 CrossRef CAS
.
- J. A. G. Williams, A. Beeby, E. S. Davies, J. A. Weinstein and C. Wilson, Inorg. Chem., 2003, 42, 8609–8611 CrossRef CAS
.
- K. Li, G. S. Ming Tong, Q. Wan, G. Cheng, W. Y. Tong, W. H. Ang, W. L. Kwong and C. M. Che, Chem. Sci., 2016, 7, 1653–1673 RSC
.
- J. Brooks, Y. Babayan, S. Lamansky, P. I. Djurovich, I. Tsyba, R. Bau and M. E. Thompson, Inorg. Chem., 2002, 41, 3055–3066 CrossRef CAS
.
- K. P. Balashev, M. V. Puzyk, V. S. Kotlyar and M. V. Kulikova, Coord. Chem. Rev., 1997, 159, 109–120 CrossRef CAS
.
- J. Kalinowski, V. Fattori, M. Cocchi and J. A. G. Williams, Coord. Chem. Rev., 2011, 255, 2401–2425 CrossRef CAS
.
- J. A. G. Williams, Top. Curr. Chem., 2007, 281, 205–268 CrossRef CAS
.
- A. F. Rausch, H. H. H. Homeier and H. Yersin, Top. Organomet. Chem., 2010, 29, 193–235 CrossRef CAS
.
- W.-Y. Wong and C.-L. Ho, Coord. Chem. Rev., 2009, 253, 1709–1758 CrossRef CAS
.
- W.-Y. Wong and C.-L. Ho, J. Mater. Chem., 2009, 19, 4457–4482 RSC
.
- S. Huo, J. Carroll and D. A. K. Vezzu, Asian J. Org. Chem., 2015, 4, 1210–1245 CrossRef CAS
.
- C. Cebrián and M. Mauro, Beilstein J. Org. Chem., 2018, 14, 1459–1481 CrossRef
.
- Y. Chi and P.-T. Chou, Chem. Soc. Rev., 2010, 39, 638–655 RSC
.
- P.-T. Chou, Y. Chi, M.-W. Chung and C.-C. Lin, Coord. Chem. Rev., 2011, 255, 2653–2665 CrossRef CAS
.
- T. Tsujimura, K. Furukawa, H. Ii, H. Kashiwagi, M. Miyoshi, S. Mano, H. Araki and A. Ezaki, SID Int. Symp. Dig. Tech. Pap., 2012, 43, 605–609 CrossRef
.
- Y. Yin, M. U. Ali, W. Xie, H. Yang and H. Meng, Mater. Chem. Front., 2019, 3, 970–1031 RSC
.
- K. T. Kamtekar, A. P. Monkman and M. R. Bryce, Adv. Mater., 2010, 22, 572–582 CrossRef CAS
.
- C. N. Pettijohn, E. B. Jochnowitz, B. Chuong, J. K. Nagle and A. Vogler, Coord. Chem. Rev., 1998, 171, 85–92 CrossRef CAS
.
- S. J. Farley, D. L. Rochester, A. L. Thompson, J. A. K. Howard and J. A. G. Williams, Inorg. Chem., 2005, 44, 9690–9703 CrossRef CAS
.
- S. Develay and J. A. G. Williams, Dalton Trans., 2008, 4562–4564 RSC
.
- M. Z. Shafikov, A. F. Suleymanova, D. N. Kozhevnikov and B. König, Inorg. Chem., 2017, 56, 4885–4897 CrossRef CAS
.
- K. Tuong, Ly, R.-W. Chen-Cheng, H.-W. Lin, Y.-J. Shiau, S.-H. Liu, P.-T. Chou, C.-S. Tsao, Y.-C. Huang and Y. Chi, Nat. Photonics, 2016, 11, 63–69 CrossRef
.
- W.-C. Chen, C. Sukpattanacharoen, W.-H. Chan, C.-C. Huang, H.-F. Hsu, D. Shen, W.-Y. Hung, N. Kungwan, D. Escudero, C.-S. Lee and Y. Chi, Adv. Funct. Mater., 2020, 30, 2002494 CrossRef CAS
.
- M. Cocchi, J. Kalinowski, D. Virgili and J. A. G. Williams, Appl. Phys. Lett., 2008, 92, 113302 CrossRef
.
- M. Cocchi, J. Kalinowski, V. Fattori, J. A. G. Williams and L. Murphy, Appl. Phys. Lett., 2009, 94, 073309 CrossRef
.
- P. Mandapati, J. D. Braun, C. Killeen, R. L. Davis, J. A. G. Williams and D. E. Herbert, Inorg. Chem., 2019, 58, 14808–14817 CrossRef CAS
.
- A. Bossi, A. F. Rausch, M. J. Leitl, R. Czerwieniec, M. T. Whited, P. I. Djurovich, H. Yersin and M. E. Thompson, Inorg. Chem., 2013, 52, 12403–12415 CrossRef CAS
.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS
.
- C. Murawski, K. Leo and M. C. Gather, Adv. Mater., 2013, 25, 6801–6827 CrossRef CAS
.
- M. Z. Shafikov, D. N. Kozhevnikov, M. Bodensteiner, F. Brandl and R. Czerwieniec, Inorg. Chem., 2016, 55, 7457–7466 CrossRef CAS
.
- D. N. Kozhevnikov, V. N. Kozhevnikov, M. Z. Shafikov, A. M. Prokhorov, D. W. Bruce and J. A. G. Williams, Inorg. Chem., 2011, 50, 3804–3815 CrossRef CAS
.
- M. Z. Shafikov, A. Zaytsev, A. F. Suleymanova, F. Brandl, A. Kowalczyk, M. Gapinska, K. Kowalski, V. N. Kozhevnikov and R. Czerwieniec, J. Phys. Chem. Lett., 2020, 11, 5849–5855 CrossRef CAS
.
- V. N. Kozhevnikov, M. C. Durrant and J. A. G. Williams, Inorg. Chem., 2011, 50, 6304–6313 CrossRef CAS
.
- S. Culham, P. H. Lanoë, V. L. Whittle, M. C. Durrant, J. A. G. Williams and V. N. Kozhevnikov, Inorg. Chem., 2013, 52, 10992–11003 CrossRef CAS
.
- P.-H. Lanoë, C. M. Tong, R. W. Harrington, M. R. Probert, W. Clegg, J. A. G. Williams and V. N. Kozhevnikov, Chem. Commun., 2014, 50, 6831–6834 RSC
.
- R. E. Daniels, S. Culham, M. Hunter, M. C. Durrant, M. R. Probert, W. Clegg, J. A. G. Williams and V. N. Kozhevnikov, Dalton Trans., 2016, 45, 6949–6962 RSC
.
- G. Turnbull, J. A. G. Williams and V. N. Kozhevnikov, Chem. Commun., 2017, 53, 2729–2732 RSC
.
- M. Z. Shafikov, R. Daniels and V. N. Kozhevnikov, J. Phys. Chem. Lett., 2019, 10, 7015–7024 CrossRef CAS
.
- M. Z. Shafikov, R. Daniels, P. Pander, F. B. Dias, J. A. G. Williams and V. N. Kozhevnikov, ACS Appl. Mater. Interfaces, 2019, 11, 8182–8193 CrossRef CAS
.
- D. N. Kozhevnikov, V. N. Kozhevnikov, M. M. Ustinova, A. Santoro, D. W. Bruce, B. Koenig, R. Czerwieniec, T. Fischer, M. Zabel and H. Yersin, Inorg. Chem., 2009, 48, 4179–4189 CrossRef CAS
.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS
.
- A. Schinabeck, J. Chen, L. Kang, T. Teng, H. H. H. Homeier, A. F. Suleymanova, M. Z. Shafikov, R. Yu, C.-Z. Lu and H. Yersin, Chem. Mater., 2019, 31, 4392–4404 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS
.
- G. Baryshnikov, B. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500–6537 CrossRef CAS
.
-
N. J. Turro, V. Ramamurthy and J. C. Scaiano, Modern Molecular Photochemistry of Organic Molecules, University Science Books, Saisalito, 2010 Search PubMed
.
-
J. S. Griffith, The Theory of Transition-Metal Ions, Cambridge University Press, 1964, pp. 106–128 Search PubMed
.
-
M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, 3rd Edn, CRC Press, 2006 Search PubMed
.
- M. Blume, R. E. Watson and R. E. Peierls, Proc. R. Soc. A, 1962, 270, 127–143 CAS
.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS
.
- E. Yu-Tzu, Li, T.-Y. Jiang, Y. Chi and P.-T. Chou, Phys. Chem. Chem. Phys., 2014, 16, 26184–26192 RSC
.
-
T. Azumi and H. Miki, in Electronic and Vibronic Spectra of Transition Metal Complexes II, ed. H. Yersin, Springer Berlin Heidelberg, Berlin, Heidelberg, 1997, pp. 1–40 Search PubMed
.
- K. Nozaki, J. Chin. Chem. Soc., 2006, 53, 101–112 CrossRef CAS
.
- V. Jankus, K. Abdullah, G. C. Griffiths, H. Al-Attar, Y. Zheng, M. R. Bryce and A. P. Monkman, Org. Electron., 2015, 20, 97–102 CrossRef CAS
.
- J.-H. Lee, S.-H. Cheng, S.-J. Yoo, H. Shin, J.-H. Chang, C.-I. Wu, K.-T. Wong and J.-J. Kim, Adv. Funct. Mater., 2015, 25, 361–366 CrossRef CAS
.
- J.-H. Lee, H. Shin, J.-M. Kim, K.-H. Kim and J.-J. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 3277–3281 CrossRef CAS
.
- W.-Y. Hung, G.-C. Fang, S.-W. Lin, S.-H. Cheng, K.-T. Wong, T.-Y. Kuo and P.-T. Chou, Sci. Rep., 2014, 4, 5161 CrossRef CAS
.
- J. H. Cook, H. A. Al-Attar and A. P. Monkman, Org. Electron., 2014, 15, 245–250 CrossRef CAS
.
- R. Pashazadeh, P. Pander, A. Lazauskas, F. B. Dias and J. V. Grazulevicius, J. Phys. Chem. Lett., 2018, 9, 1172–1177 CrossRef CAS
.
- L. Huang, C. D. Park, T. Fleetham and J. Li, Appl. Phys. Lett., 2016, 109, 233302 CrossRef
.
- J. R. Sommer, R. T. Farley, K. R. Graham, Y. Yang, J. R. Reynolds, J. Xue and K. S. Schanze, ACS Appl. Mater. Interfaces, 2009, 1, 274–278 CrossRef CAS
.
- A. J. Pearson, T. Plint, S. T. E. Jones, B. H. Lessard, D. Credgington, T. P. Bender and N. C. Greenham, J. Mater. Chem. C, 2017, 5, 12688–12698 RSC
.
- A. Zampetti, A. Minotto, B. M. Squeo, V. G. Gregoriou, S. Allard, U. Scherf, C. L. Chochos and F. Cacialli, Sci. Rep., 2017, 7, 1611 CrossRef
.
- Z. Hao, M. Li, Y. Liu, Y. Wang, G. Xie and Y. Liu, Dyes Pigm., 2018, 149, 315–322 CrossRef CAS
.
- G. Fu, H. Zheng, Y. He, W. Li, X. Lü and H. He, J. Mater. Chem. C, 2018, 6, 10589–10596 RSC
.
- J. Yu, H. Tan, F. Meng, K. Lv, W. Zhu and S. Su, Dyes Pigm., 2016, 131, 231–238 CrossRef CAS
.
- Y. Liu, Z. Hao, F. Meng, P. Wang, L. Yang, Y. Wang, Y. Pei and S. Su, Chem. Phys. Lett., 2018, 699, 99–106 CrossRef CAS
.
- X. Cao, J. Miao, M. Zhu, C. Zhong, C. Yang, H. Wu, J. Qin and Y. Cao, Chem. Mater., 2015, 27, 96–104 CrossRef CAS
.
- P. Pander, S. Gogoc, M. Colella, P. Data and F. B. Dias, ACS Appl. Mater. Interfaces, 2018, 10, 28796–28802 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available: Comprehensive experimental details including synthesis and characterisation; crystallography; computational details and output; OLED fabrication; additional discussion of photophysical processes in host materials and associated data. CCDC 1954414. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0tc04881j |
| ‡ For simplicity, the naming system adopted here omits the aliphatic substituents appended onto the terminal thienyl rings: C12H25 in dthpy and C6H13 in bis-thpym and bis-dthpym. These substituents are incorporated into the proligands solely in order to enhance the solubility of the resulting complexes. |
| § Acronyms used in this section for common OLED fabrication materials are defined or explained in the ESI,† Section 7: OLED devices. |
| ¶ Note that luminance is a photopic parameter and as such gives an indication of the amount of visible light in electroluminescence. For NIR emission the luminance is thus by definition zero. |
| This journal is © The Royal Society of Chemistry 2021 |