New perspectives on the laser initiation for metal tetrazine complexes: a theoretical study†
Junqing
Yang
 *ab,
Gu-Dan
Zhang
b,
Jian-Guo
Zhang
*ab,
Gu-Dan
Zhang
b,
Jian-Guo
Zhang
 *b,
Dong
Chen
c and
Qi
Zhang
*b,
Dong
Chen
c and
Qi
Zhang
 c
c
aSchool of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China. E-mail: yjq881223@163.com
bState Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing, 100081, China. E-mail: zjgbit@bit.edu.cn
cInstitute of Chemical Materials, China Academy of Engineering Physics, Mianyang, Sichuan 621900, China
First published on 23rd November 2021
Abstract
In order to understand the relationship between laser initiation and charge transfer of metal tetrazine complexes (MTCs), several sets of MTCs with different metals and ligands were designed and their charge transfer (CT) characters were examined using a time-dependent density functional theory method (TD-DFT) in combination with UV-vis spectra, hole–electron distribution, interfragment charge transition, and transition density matrix analyses. Results show that Fe(II), Mn(II), and Cu(II) are suitable divalent transition metal cores in constructing the optical initiation tetrazine complexes. By replacing the divalent metal cores with a monovalent center, new sets of complexes are proved to possess metal-to-ligand charge transfer (MLCT) character and stronger absorption intensity in the near-infrared (NIR) region, which implies that monovalent MTCs are more in favor of low-energy laser initiation than divalent MTCs. Reasonable tuning of the structure of pyrazole substituent can expect to enhance the explosive performance while preserving the optical characteristics, which is an important design principle. This work thoroughly depicts the photoactive states for MTCs and gives a train of thought to explore new desirable laser initiation explosives.
1 Introduction
To ensure the safety of an energetic material, it is critically important to choose a suitable initiation method. Compared with traditional initiation methods, such as mechanical and electrical initiations, laser initiation is a more reliable technology and has attracted considerable attention.1–4 The advantages of laser initiation technology are (i) strong anti-interference ability, which can avoid the interference of electromagnetic waves and electrostatic signals, (ii) high safety, which can effectively isolate explosive pyrotechnic agent and power supply devices and realize insensitive ignition, and (3) easy to expand, which can realize the deflagration to blast for secondary explosives, the miniaturization of the device, and the multi-point initiation. For utilizing laser initiation technology, energetic materials are required to possess rich photophysical and photochemical properties (e.g. charge transfer). Due to the rich spectroscopic properties,5,6 together with the high thermal stability and low mechanical sensitivities,7–9 nitrogen-rich metal tetrazine complexes (MTCs) gain more and more attention in the field of energetic materials.A number of MTCs were synthesized and their properties were characterized.10–13 Research10 demonstrated that the addition of energetic groups to tetrazine ligands does not compromise the intense metal-to-ligand charge transfer (MLCT) character, i.e., the energetic groups are independent of the optical properties. Further research11 revealed that an unprecedented decrease in both the laser initiation threshold and mechanical sensitivity was achieved in Fe(II) tetrazine complexes. In spite of the accomplishments in synthetic work, theoretical insights into those photoinitiation complexes are still in shortage. There remains a mystery between photon absorption and laser initiation. Laser-initiation thresholds in the near-infrared (NIR) region are the pursuit of low-energy laser initiation. Previous research14 found that metal pyrrole–tetrazine–pyrazole complexes have the lowest energy charge transfer (CT) band peak among all MTCs, which gives better compatibility with currently available NIR lasers for the activation process.
Thus, in this work, we treat metal pyrrole–tetrazine–pyrazole complexes as the research target. Based on the diversity of the coordination modes, several sets of metal pyrrole–tetrazine–pyrazole complexes with different metals and ligands were designed and performed a detailed theoretical investigation. The laser sensitivity can be adjusted by selecting different metals and ligands. The electron excitation characterizations of all designed compounds were studied using the time-dependent density functional theory (TD-DFT) method with the help of UV-vis spectra, hole–electron distribution, interfragment charge transition (IFCT), and transition density matrix (TDM) analyses. This work gives a comprehensive description of the photoactive states of metal pyrrole–tetrazine–pyrazole complexes, which is helpful to explore new desirable laser initiation energetic materials and may offer inspiration to both experimentalists and theorists.
2 Methodology and computational details
As we know, it is necessary to adopt a proper quantum chemistry computation method for excited-state calculations to give relatively accurate descriptions. There are some commonly used methods for excited-state calculations, such as CIS (configuration interaction with single substitute),15 EOM-CCSD (equation of motion coupled cluster with single and double excitations),16 and TD-DFT (time-dependent density functional theory).17–20 CIS is a semi-empirical method that is less expensive but with a lower accuracy; EOM-CCSD can give relatively accurate results but the calculation cost is too high; the TD-DFT method is the most cost-effective among them.21 The previous TD-DFT work14 has proved that the TPSSh (TPSS hybrid)22 functions can provide results that are in excellent agreement with experimental data for the excited-state calculations of MTCs. TPSSh is a one-parameter global hybrid version of the TPSS functional,23 which matches or exceeds all prior nonempirical constructions in accuracy and consistently provides a high-quality description of diverse systems and properties. Particularly, it exhibits good performance when involves first- and second-row transition-metal complexes.24–26Based on the successful outcomes of the above previous works, the TPSSh functional and 6-311G basis set were finally chosen to optimize the structures and describe the ground and excited states of all researched complexes. A total of 70 singlet excited-state were investigated to give relatively complete UV-vis spectra. All calculations were performed using Gaussian 09 packages.27 There are two typical types of electron excitation transitions: charge-transfer excitation (CT) and local excitation (LE), classified by the space span of excitation transitions. The CT mode can be further classified as metal-to-ligand charge transfer (MLCT), ligand-to-metal charge transfer (LMCT), and ligand-to-ligand charge transfer (LLCT). The LE mode can be further classified as metal-centered transition (MC), and intraligand or ligand-centered transition (LC). To further explore the electron excitation characteristics of all constructed complexes, the analyses of hole–electron distribution, IFCT, and 2D color-filled map of TDM were performed with the help of Multiwfn28,29 and VMD30 software.
Hole–electron distribution refers to the density distribution of holes and electrons, which is a versatile way to explore the nature of transitions. The “hole” refers to the electron donor, from where the electron is excited and transferred; while the “electron” denotes the electron acceptor, i.e., the destination of the excited electron.
IFCT is a very important phenomenon in the electron excitation process. Charge transfer between any number of fragments can be obtained via quantitative IFCT analysis, an effective method to judge the nature of electron excitation. Some descriptors, i.e., Sr, D, Sr/D, and t, were employed to identify the excitation mode. Sr is to describe the overlap degree of hole and electron; D is to quantify the distance between the centroid of hole and electron; Sr/D is the quotient of parameters Sr and D; t is to evaluate the separation degree between holes and electrons. A positive or negative t suggests conspicuous or little separation, respectively. That is, a larger t together with a smaller Sr/D may give a more CT-like mode. The mathematical forms for the parameters Sr, D, and t are listed in the ESI.†
The generation of the hole–electron or the photo excitonic movement of an electron from the hole zone to the electron zone can be represented by the two-dimensional (2D) color-filled map of TDM.31,32 To intuitively observe electron donors and acceptors, TDM of electron transitions for the crucial excited states was explored.
3 All geometries of the constructed complexes
All researched transition-metal pyrrole–tetrazine–pyrazole complexes with various coordination geometries, as well as their corresponding ligands, are presented in Fig. 1. In order to explore the influence of the metal center on optical absorption, metal centers are varied: Fe(II), Mn(II), Zn(II), Co(II), Ni(II), and Cu(II), and their corresponding complexes are labeled as 1, 2, 3, 4, 5, and 6. Dimethyl and non-methyl containing pyrrole–tetrazine–pyrazole ligands are labeled as A and B, respectively. Normally, the geometries of divalent transition-metal pyrazole–tetrazine complexes are distorted octahedral with three ligands. Thus, a total of 12 kinds of complexes were designed, as shown in Fig. 1(a). From the comparison of optical absorptions of 1A–6A and 1B–6B (discussed in the following section), we found that B series is more likely to initiate with lower energy, i.e., the B ligand is more potentially available in optical initiation. Accordingly, the less bulky B ligand was utilized in other series.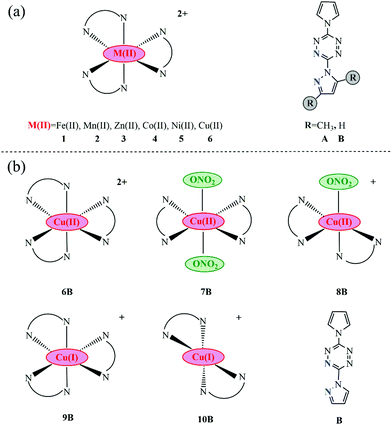 | ||
| Fig. 1 Molecular sketches of all involved complexes together with their corresponding ligands (the coordination N atoms in ligands are marked blue). | ||
In addition to forming the octahedral geometries with three ligands, Cu(II) can coordinate with two pyrazole–tetrazine ligands plus one or two counter anions and give rise to hexa- and penta-coordinated geometries, as a consequence of the Jahn–Teller distortion associated with d9 metal centers and the much flexibility of ligands.10–13,33 Thus, complexes 7B and 8B were constructed, as seen in Fig. 1b. Besides, lower-valence metal complexes are more likely to exhibit MLCT character.34 Hence, metal pyrrole–tetrazine–pyrazole complexes with Cu(I) center was also taken into account, seen 9B (hexa-coordinated) and 10B (tetra-coordinated) in Fig. 1b.
4 Results and discussion
The electron excitation characteristics of all constructed complexes were explored using UV-vis spectra, hole–electron distribution, IFCT, and TDM analyses with the help of Multiwfn28,29 and VMD.304.1 UV-vis optical absorption
UV-vis absorption spectra of 1–6 (A and B) are presented in Fig. 2a and b. Only Fe(II) and Zn(II) complexes (1A, 3A, 1B, and 3B) display several extremely strong absorption peaks around 300–600 nm with absorption magnitude varying between 0.6 to 10.0 a.u., all complexes in both A and B series have maximum absorption around the low energy region with absorption magnitude approximately varying between 0.1 to 0.2 a.u. The peak locations of low-energy CT bands are ranging from 900 to 1200 nm, which are located in the NIR region. In A series: 950 nm for 1A, 935 nm for 2A, 967 nm for 3A, 1051 nm for 4A, 979 nm for 5A, and 959 nm for 6A. In B series: 1031 nm for 1B, 839 nm for 2B, 1017 nm for 3B, 1166 nm for 4B, 1029 nm for 5B, and 1021 nm for 6B. NIR lasers are the most practical choices in optical initiation, which demonstrates that all researched complexes are potentially available in laser initiation. At the most practical and available wavelength for optical initiation of Nd:YAG lasers, i.e., at 1064 nm, the same descending absorbance trend is found in both A and B series: 1 [Fe(II)] > 2 [Mn(II)] > 6 [Cu(II)] > 5 [Ni(II)] > 3 [Zn(II)] > 4 [Co(II)]. Co(II) complexes (4A and 4B) have the weakest absorption at 1064 nm in spite of the lowest-energy CT bands. On this side, Fe(II), Mn(II), and Cu(II) are the best metal cores in constructing the optical initiation complexes. Besides, less-bulky B series are red-shifted relative to those of A in the low-energy CT bands (general trend), which suggests that the B series is more likely to initiate with lower energy. In other words, the B ligand is more photoactive than the A ligand.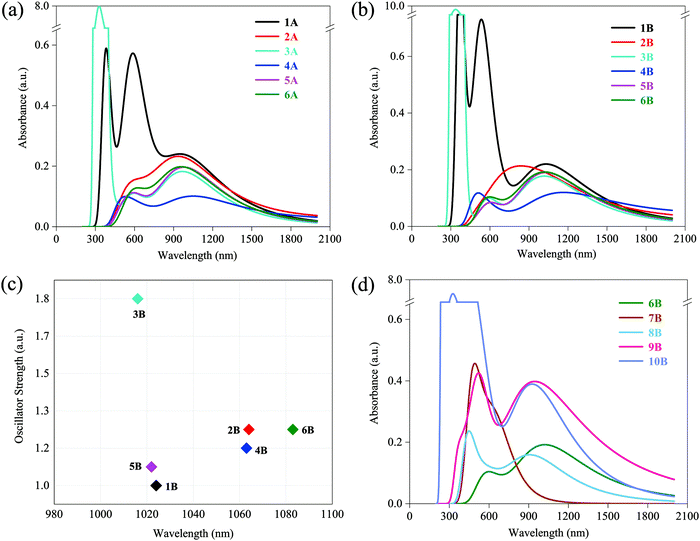 | ||
| Fig. 2 (a) UV-vis spectra of 1A–6A; (b) UV-vis spectra of 1B–6B; (c) oscillator strength vs. wavelength of the lowest energy-excited states of 1B–6B; (d) UV-vis spectra of 6B–10B. | ||
Since the broadening function is used to generate the spectra, the plotted UV-vis spectra are not representative of the actual underlying transitions. Thus, the lowest energy-excited states with larger oscillator strength that contribute to the low-energy absorption peaks were elaborated for the more photoactive B series (1B–6B), where the function of oscillator strength and wavelength is shown in Fig. 2c. Obviously, the order of descending wavelength (6B > 2B > 4B > 1B > 5B > 3B in Fig. 2c) does not follow the rank of peak locations observed in UV-vis spectra (4B > 1B > 5B > 6B > 3B > 2B in Fig. 2b). This is because the spectrum curves are obtained by function-broadening the discrete data of all excited states. That is, the lowest energy-excited state contributes to but does not predominate its corresponding absorption peak.
UV-vis absorption spectra of 7B–10B are shown in Fig. 2d. For comparison, the spectrum of 6B is also presented. As expected, low-energy CT bands of lower-valence Cu(I) complexes 9B and 10B exhibit better performance compared with that of Cu(II) complexes 6B, 7B, and 8B, with two times larger absorption magnitude of 0.4 a.u., but no sacrifice in the wavelength varying between 946 nm in 9B and 927 nm in 10B. Particularly, they show considerable absorption at 1064 nm and also have almost two times stronger absorbance than 6B. It may imply that lower-valence Cu(I) complexes have more favorable excitation characters for laser initiation and they are more promising for optical initiation than the above-mentioned divalent transition-metal complexes, which will be verified in subsequent sections. Besides, another finding is that compared with 6B, bounded NO3− makes 7B and 8B blue-shifted to some extent and 7B (two NO3− contained) blue-shifts more. Nevertheless, there still remained some absorption around 1064 nm in both 7B and 8B.
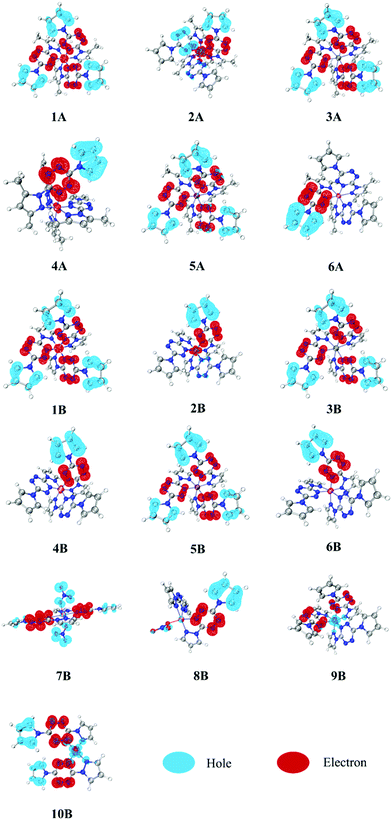
4.2 Hole–electron distributions
It is hard to depict electron excitation when it is predominated by more than one pair of molecular orbitals (MOs), or even natural transition orbitals (NTOs). Hence, we have adopted the hole–electron distribution analysis to explore the nature of transitions for all constructed complexes. The hole–electron distributions of all involved complexes are shown in Fig. 3. Blue and red colors represent holes and electrons, respectively.It can be seen from Fig. 3 that the pyrazole fragments in all complexes do not participate in the electron excitation directly. In contrast, the tetrazine and pyrrole fragments both play extremely vital roles, being electron acceptors and donors, respectively. Based on this, we decomposed each complex into several fragments and calculated the percentage of each fragment in the hole and electron zone, as shown in Table 1. In complexes 1–6, most of the hole (81–96%) and electron (77–98%) are located in pyrrole and tetrazine fragments, respectively. It suggests that the electron transfer from pyrrole fragments to tetrazine fragments, which make the complexes photoactive and thus suitable for optical initiation. This pattern is also observed in one NO3− bounded complex 8B, while in the two NO3− bounded complex 7B, the NO3− anions (76.50%) have replaced pyrrole fragments (16.27%) to become major electron donors. In complexes 2A and 2B, the metal possesses a large percentage of electrons (44.35 and 21.36%, respectively), which suggests that a lot of electrons transfer from pyrrole fragments to tetrazine fragments, and finally to metal Mn(II) fragments. As a consequence, we can observe that in 2A and 2B, one of the tetrazine fragments (right, red) acts as the electron acceptor, like in all other compounds, but one of them (left, blue) acts as an electron donor. This phenomenon can also be observed in the following IFCT analysis. It is worth noting that since the pyrazole fragments are irrelevant on the electron excitation, reasonable adjustment of the structure of pyrazole fragments can help improve the energetic performance while not affecting the optical characteristics, which provide a design principle for the new desirable laser initiation explosives.
| Complexes | Hole (%) | Electron (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Metal | Tetrazine | Pyrrole | Nitrate | Metal | Tetrazine | Pyrrole | Nitrate | |
| 1A | 0.27 | 1.46 | 98.27 | 7.07 | 91.08 | 1.85 | ||
| 2A | 8.78 | 66.23 | 24.99 | 44.35 | 54.85 | 0.80 | ||
| 3A | 0.00 | 1.97 | 98.03 | 0.15 | 97.84 | 2.01 | ||
| 4A | 0.13 | 2.34 | 97.53 | 2.36 | 95.59 | 2.05 | ||
| 5A | 1.28 | 17.26 | 81.46 | 1.36 | 96.68 | 1.96 | ||
| 6A | 0.02 | 1.70 | 98.28 | 0.81 | 97.35 | 1.84 | ||
| 1B | 0.43 | 1.58 | 97.99 | 6.66 | 91.32 | 2.02 | ||
| 2B | 1.67 | 12.29 | 86.04 | 21.36 | 76.88 | 1.76 | ||
| 3B | 0.00 | 2.10 | 97.90 | 0.16 | 97.68 | 2.16 | ||
| 4B | 0.14 | 2.66 | 97.19 | 2.45 | 95.27 | 2.28 | ||
| 5B | 0.05 | 1.98 | 97.97 | 1.17 | 96.67 | 2.16 | ||
| 6B | 0.07 | 2.52 | 97.41 | 1.88 | 95.57 | 2.55 | ||
| 7B | 1.35 | 5.88 | 16.27 | 76.50 | 0.54 | 97.02 | 0.80 | 1.63 |
| 8B | 2.25 | 2.94 | 89.74 | 5.07 | 1.39 | 96.56 | 1.95 | 0.10 |
| 9B | 58.96 | 37.51 | 3.53 | 6.55 | 92.37 | 1.08 | ||
| 10B | 31.14 | 25.37 | 43.49 | 5.40 | 93.08 | 1.52 | ||
Comparing 1–6 (A and B) with 9B and 10B, it is easy to find that divalent and monovalent metal cores play significantly different roles. The divalent metal cores in complexes 1–6 (A and B) appear to play as electron acceptors, while those monovalent ones in complexes 9B and 10B turn into electron donors. There are 58.96% and 31.14% of the hole zone located in Cu(I) in 9B and 10B, respectively, far more than their corresponding electron zone (6.55 and 5.40%, respectively). It indicates that lower-valence Cu(I) complexes are more likely to present MLCT character than divalent metal complexes. Combining the stronger absorption intensity of Cu(I) complexes in the above UV-vis spectra, we can conclude that monovalent metals may be a better choice than divalent metals for utilizing in photoinitiation. Besides, NO3−-bounded complexes 7B and 8B may have somewhat MLCT character since Cu(II) possesses a little bit larger ratio of hole zone (1.35 in 7B and 2.25% in 8B) to electron zone (0.54 in 7B and 1.39% in 8B).
4.3 Interfragment charge transition (IFCT) analysis
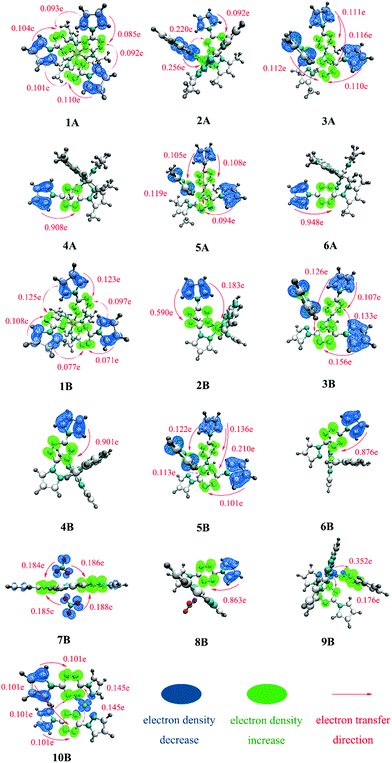
To further judge the nature of electron excitations, IFCT analysis was performed. To intuitively visualize the IFCT, the charge density difference (CDD) of all complexes was studied and plotted in Fig. 4. For clarity, only the obvious charge transfers (CT) are marked.Fig. 4 clearly shows that there is a critical difference in the excitation mode between divalent and monovalent metal cores, as the hole–electron distribution analysis. The divalent cores in complexes 1A–6A and 1B–6B may work as electron-acceptors with almost transferred electrons settling there. In comparison, monovalent Cu(I) cores in complexes 9B and 10B have obvious electron density decrease with CT of 0.528 e and 0.290 e, respectively, which further indicates that 9B and 10B possess strong MLCT character. For 7B and 8B, the above hole–electron distribution analyses show them possessing somewhat MLCT character, while the charge transfer is tiny and can be hardly observed in the CDD plot.
Table 2 lists the predicted main transition modes (CT > 0.2 e) with the descending intensity order for all researched complexes. The statistical CT data and corresponding descriptors, including Sr, D, Sr/D, and t, for all complexes, can be seen in Table S1 (ESI†). A smaller Sr/D usually corresponds to a larger t and then leads to a more conspicuous transferred electron. For example, 4 and 6 present the smallest Sr/D (4A: 0.08, 6A: 0.07; 4B: 0.08, 6B: 0.09), the largest t (4A: 2.65, 6A: 2.60; 4B: 2.60, 6B: 2.50), and thus a large number of transferred electrons (4A: 0.908 e, 6A: 0.948 e; 4B: 0.901 e, 6B: 0.876 e). There are no obvious transferred electrons found in those with larger Sr/D and smaller t.
| Complexes | Main excitation modesa | Complexes | Main excitation modesa | Complexes | Main excitation modesa |
|---|---|---|---|---|---|
| a Main transition modes are arranged in descending intensity order. | |||||
| 1A | LLCT, LC | 1B | LLCT, LC | 7B | LLCT |
| 2A | LMCT, LLCT, LC | 2B | LC, LMCT | 8B | LC |
| 3A | LLCT, LC | 3B | LLCT, LC | 9B | MLCT, LLCT |
| 4A | LC | 4B | LC | 10B | LC, LLCT, MLCT |
| 5A | LLCT, LC | 5B | LLCT, LC | ||
| 6A | LC | 6B | LC | ||
From Table 2, we can find that –CH3 groups have little influence on main excitation modes since the predicted transition modes of 1A–6A are corresponding to those of 1B–6B, with only 2A and 2B being exceptions. However, the metal valence and coordination models have a significant effect on the excitation modes. For example, the main transition mode of the Cu(II) complex 6B is LC, while those of the corresponding Cu(I) complex 9B are MLCT and LLCT; the main transition mode of the hexa-coordinated complex 7B is LLCT, while that of the penta-coordinated complex 8B is LC, which is most likely due to the different charge distributions produced by different number of NO3− groups.
4.4 Transition density matrix (TDM) analysis
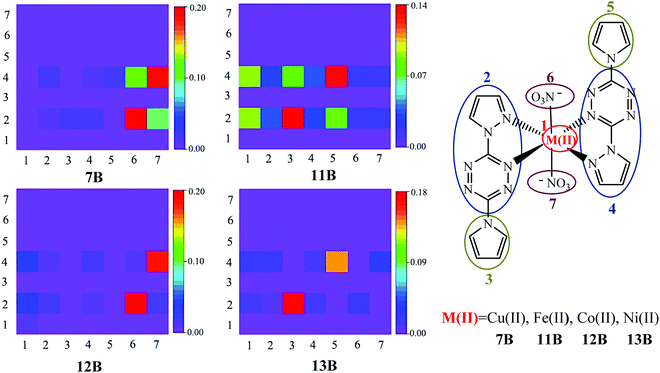
The above hole–electron distribution and IFCT analyses show that the bounded NO3− has made Cu(II) complex 7B show somewhat the MLCT character, while the charge transfer is not that obvious. To give a more comprehensive investigation of the NO3− effect on the electron transition, other three NO3− bounded complexes 11B, 12B, and 13B with Fe(II), Co(II), and Ni(II) metals, respectively, were constructed and studied. Complexes 7B and 11B–13B were divided into seven fragments and the two-dimensional (2D) color-filled maps of the TDM are depicted in Fig. 5.TDM can quantify the composition of the excited state, with each element indicating the dynamics of an exciton projected on atom or fragment pairs and thus reflecting the strength of the coherence between the donor and acceptor when the electron transits. The stronger the coherence between a pair of fragments is, the higher the value of a matrix element (brighter color in the graph) is. It is obvious from Fig. 5 that the TDM values are distributed in rows 2 and 4, suggesting that pyrazole–tetrazine fragments are crucial electron acceptors during the transition, i.e., the fact of tetrazine substituents being electron acceptors is confirmed again by TDM analysis, where pyrazole parts are irrelevant components proved by the above analyses. The elements in the diagonal direction represent the LE components, while others denote the CT ones. The hole–electron coherences of the donors NO3− (fragments 6 and 7) and pyrrole (fragments 3 and 5) to the acceptor tetrazine (fragments 2 and 4) represent the LLCT character. The coherences within the pyrrole–tetrazine–pyrazole ligand, i.e., fragments 3 and 5 to fragments 2 and 4, suggest the LC character. Observing the strongest coherence (red color) in each TDM graph, it is clear that LLCT is the strongest charge transfer of 7B and 12B; LC is the strongest charge transfer of 11B and 13B. In addition, complexes 11B–13B (especially 11B) have obvious hole–electron coherences between the donor metal cores (fragment 1) and the acceptor tetrazine substituents (fragments 2 and 4), thereby characterizing them as the MLCT mode, which further verifies that the bounded NO3− successfully turn the divalent metal complexes possessing favorable MLCT character. It should be noted that due to the slight or tiny charge transfer from Cu(II) to tetrazine in the complex 7B, almost no hole–electron coherences between the donor metal Cu(II) and acceptor tetrazine groups can be observed. More detailed analyses and comparisons on 11B–13B are given in Fig. S1 and S2 in the ESI.†
5 Conclusions
Several sets of metal pyrrole–tetrazine–pyrazole complexes were constructed and studied using the TD-DFT method. The effect of different metal cores and ligands on the electron excitation character was explored using UV-vis spectra, hole–electron distribution, IFCT, and TDM analyses. This work offers some inspiring thoughts to design and synthesize new photoactive energetic materials for laser initiation. The specific conclusions are as follows:(1) The divalent transition metal complexes 1–6 (in both A and B series) show potential availability for laser initiation due to the low-energy CT band peaks located in the NIR region. Compared with the A ligand, a less-bulky B ligand is more potentially available. Fe(II), Mn(II), and Cu(II) are more suitable divalent transition metal cores in constructing the optical initiation tetrazine complexes.
(2) Replacing the divalent metal cores with lower valence Cu(I) center, or replacing one of the ligands with one or a pair of bounded nitrate anions, can make the new set of complexes possess MLCT character. The stronger absorption intensity of monovalent complexes suggests that monovalent metals are a better choice for utilizing in photoinitiation than divalent metals.
(3) The tetrazine and pyrrole groups contribute a lot, while the pyrazole group has little to do with the electron transition process, thus, reasonable tuning of the structure of pyrazole substituent can expect to enhance the explosive performance while preserving the optical characteristics, which is a new design principle for desirable laser initiation explosives.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are thankful to the NSAF (U1830134), NSFC (21905023 and 22175025), State Key Laboratory of Explosion Science and Technology (YBKT21-02) for their generous financial support.References
- T. Nelson, J. Bjorgaard, M. Greenfield, C. Bolme, K. Brown, S. McGrane, R. J. Scharff and S. Tretiak, J. Phys. Chem. A, 2016, 120, 519–526 CrossRef CAS PubMed.
- M. T. Greenfield, S. D. McGrane, C. A. Bolme, J. A. Bjorgaard, T. R. Nelson, S. Tretiak and R. J. Scharff, J. Phys. Chem. A, 2015, 119, 4846–4855 CrossRef CAS PubMed.
- S. D. McGrane, C. A. Bolme, M. T. Greenfield, D. E. Chavez, S. K. Hanson and R. J. Scharff, J. Phys. Chem. A, 2016, 120, 895–902 CrossRef CAS.
- J. A. Bjorgaard, A. E. Sifain, T. Nelson, T. W. Myers, J. M. Veauthier, D. E. Chavez, R. J. Scharff and S. Tretiak, J. Phys. Chem. A, 2016, 120, 4455–4464 CrossRef CAS.
- G. Clavier and P. Audebert, Chem. Rev., 2010, 110, 3299–3314 CrossRef CAS.
- S. Patra, B. Sarkar, S. Ghumaan, M. P. Patil, S. M. Mobin, R. B. Sunoj, W. Kaim and G. K. Lahiri, Dalton Trans., 2005, 1188–1194, 10.1039/b500152h.
- D. E. Chavez, M. A. Hiskey and R. D. Gilardi, Angew. Chem., Int. Ed., 2000, 39, 1791–1793 CrossRef CAS PubMed.
- D. E. Chavez, M. A. Hiskey and D. L. Naud, Propellants, Explos., Pyrotech., 2004, 29, 209–215 CrossRef CAS.
- D. E. Chavez, B. C. Tappan, M. A. Hiskey, S. F. Son, H. Harry, D. Montoya and S. Hagelberg, Propellants, Explos., Pyrotech., 2005, 30, 412–417 CrossRef CAS.
- T. W. Myers, D. E. Chavez, S. K. Hanson, R. J. Scharff, B. L. Scott, J. M. Veauthier and R. Wu, Inorg. Chem., 2015, 54, 8077–8086 CrossRef CAS.
- T. W. Myers, J. A. Bjorgaard, K. E. Brown, D. E. Chavez, S. K. Hanson, R. J. Scharff, S. Tretiak and J. M. Veauthier, J. Am. Chem. Soc., 2016, 138, 4685–4692 CrossRef CAS PubMed.
- T. W. Myers, K. E. Brown, D. E. Chavez, R. J. Scharff and J. M. Veauthier, Inorg. Chem., 2017, 56, 2297–2303 CrossRef CAS.
- T. W. Myers, K. E. Brown, D. E. Chavez, R. J. Scharff and J. M. Veauthier, Eur. J. Inorg. Chem., 2016, 3178–3183 CrossRef CAS.
- A. E. Sifain, J. A. Bjorgaard, T. W. Myers, J. M. Veauthier and D. E. Chavez, J. Phys. Chem. C, 2016, 120, 28762–28773 CrossRef CAS.
- J. B. Foresman and Æ. Frisch, Exploring Chemistry with Electronic Structure Methods, PA, Pittsburgh, 2nd edn, 1996 Search PubMed.
- G. E. Scuseria and H. F. Schaefer, J. Chem. Phys., 1989, 90, 3700–3703 CrossRef CAS.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS.
- C. Van Caillie and R. D. Amos, Chem. Phys. Lett., 1999, 308, 249–255 CrossRef CAS.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef.
- Y. Y. Pan, J. Huang, Z. M. Wang, S. T. Zhang, D. W. Yu, B. Yang and Y. G. Ma, RSC Adv., 2016, 6, 108404 RSC.
- Y. Pan, J. Huang, W. Li, Y. Gao, Z. Wang, D. Yu, B. Yang and Y. Ma, RSC Adv., 2017, 7, 19576–19583 RSC.
- V. N. Staroverov, G. E. Scuseria, J. M. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 124, 224105 CrossRef PubMed.
- K. P. Jensen, Inorg. Chem., 2008, 47, 10357–10365 CrossRef CAS PubMed.
- T. Weymuth, E. P. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092–3103 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Suzerain, M. A. Robb, J. J. R. Cheeseman and J. A. Montgomery, Gaussian 09, Revision A.02, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS.
- T. Lu and F. W. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
- M. T. Sun, P. Kjellberg, W. J. D. Beenken and T. Pullerits, Chem. Phys., 2006, 327, 474–484 CrossRef CAS.
- S. Mukamel, S. Tretiak, T. Wagersreiter and V. Chernyak, Science, 1997, 277, 781–787 CrossRef CAS.
- X. J. Luan, Y. Y. Wang, D. S. Li, P. Liu, H. M. Hu, Q. Z. Shi and S. M. Peng, Angew. Chem., Int. Ed., 2005, 44, 3864–3867 CrossRef CAS PubMed.
- K. A. McNitt, K. Parimal, A. I. Share, A. C. Fahrenbach, E. H. Witlicki, M. Pink, D. K. Bediako, C. L. Plaisier, N. Le, L. P. Heeringa, D. A. V. Griend and A. H. Flood, J. Am. Chem. Soc., 2009, 131, 1305–1313 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02319e |
| This journal is © the Owner Societies 2022 |