Against the NEER principle: the third type of photochromism for GFP chromophore derivatives
Jun-Wei
Liao
,
Robert
Sung‡
and
Kuangsen
Sung
 *
*
Department of Chemistry, National Cheng Kung University, Tainan, Taiwan. E-mail: kssung@mail.ncku.edu.tw
First published on 27th November 2021
Abstract
Photochromism is the heart of photochromic fluorescent proteins. Excited-state proton transfer (ESPT) is the major cause of photochromism for the green fluorescent protein (GFP) and Z–E photoisomerization through τ-torsion is the major cause of photochromism for Dronpa (a GFP mutant). In this article, s-E-1 opens a third type of photochromism for GFP chromophore derivatives, which involves light-driven φ-torsion with no τ-torsion, followed by excited-state intramolecular proton transfer (ESIPT), and is gated by environmental polarity. Since s-E-1 does not follow Z–E photoisomerization through τ-torsion but undergoes light-driven φ-torsion, which involves equilibration of the excited-state rotamers, it is clearly against the NEER (Non-Equilibration of Excited-state Rotamers) principle.
Introduction
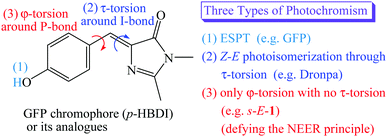
The green fluorescent protein (GFP) and its mutants have attracted interest as non-destructive fluorescent biological labels for tracking biomolecules in the last two decades.1,2 The photochromism found in the GFP or its mutants distinguishes themselves as photochromic fluorescent proteins, resulting in important applications in bioimaging, super-resolution microscopy, optogenetic control and bioelectronics.3–6 To date, two known types of photochromism have been found in the GFP or its mutants. They are excited state proton transfer (ESPT)7,8 and Z–E photoisomerization through τ-torsion,9–18 respectively (Scheme 1).In the beginning, the distinguishing photochromism found in the wild-type GFP chromophore is ESPT,1,2 in which the phenol moiety of GFP chromophore [p-hydroxybenzylidene-imidazolinone (p-HBDI)] in its first singlet excited state (S1) passes its proton on to the internal water and the surrounding peptides through the proton relay network, forming a much brighter S1 excited state of the p-HBDI anion with a fluorescence quantum yield of 0.8.7,8 (Scheme 1)
It was reported that the S1 excited states of GFP and its mutants usually relax by following Z–E isomerization through τ-torsion that will encounter a S1/S0 conical intersection (CI) for easy relaxation to the S0 ground states.9–18 Based on this relaxation mechanism, GFP mutants have been tailored by mutagenesis to distinguish themselves with the second type of photochromism involving Z–E photoisomerization through τ-torsion.10–18 (Scheme 1) This type of photochromic fluorescent proteins may stay either in the fluorescent state or in the non-fluorescent state. According to single-crystal X-ray diffraction, the fluorescent state and the non-fluorescent state were assigned to be Z- and E-isomers of p-HBDI, respectively.11–17 Because these fluorescent proteins can be reversibly switched between the two states by light or heat, they are also known as reversibly switchable fluorescent proteins (RSFPs). Among them, Dronpa is one of the most successful GFP-like RSFPs with a remarkable fluorescence quantum yield of 0.85. The major photochromism in Dronpa is Z–E photoisomerization of p-HBDI through τ-torsion, accompanied by protonation or deprotonation with the surrounding peptides and structural changes of the surrounding peptides.10–14,18
Then, a question comes up. Is the S1 excited state of GFP or its mutants relaxed through both φ-torsion and τ-torsion at the same time, or only through φ-torsion with no τ-torsion? (Scheme 1) The former is the so-called hula-twist relaxation, which is an improbable high-energy process.19 It might take place only when the Z–E photoisomerization through τ-torsion is prohibited in the restricted environment. The latter is against the NEER (Non-Equilibration of Excited-state Rotamers) principle.20–27 Who is going to believe that the S1 excited state of GFP or its mutants relax only through φ-torsion with no τ-torsion? In this article, we will prove that it does happen, and it opens the third type of photochromism for GFP chromophore derivatives (Scheme 1). However, the S1 excited state of the anion of GFP chromophore does relax through φ-torsion or τ-torsion,28 and the two relaxation pathways are not against the NEER principle because both the I-bond and the P-bond of the anion of GFP chromophore in the ground state are not single bond but have a significant π-bond character.
The NEER principle was first advanced by Havinga in 1961.20 It concludes that various conformers of the S1 excited state cannot be interconverted within the S1 lifetime through rotation around the single bonds that connect unsaturated centers in the ground state because the bond order of these single bonds in the ground state will be greatly increased in the S1 excited state. The NEER principle has been verified by the photochemistry of several compounds, such as vitamin D, 1,2-diaryl-ethenes, trienes and so on.20–27
In this article, we will show that a new GFP model chromophore 1 does not follow Z–E photoisomerization9–18 through τ-torsion, but undergoes light-driven φ-torsion, followed by excited-state intramolecular proton transfer (ESIPT). It is clearly against the NEER principle but opens the third type of photochromism for the GFP chromophore. Besides, it is also a new type of gated photochromism. The opening or closing of its gate29 depends on the environmental polarity.
Experimental
Materials
o-ABDI 30 was prepared according to the literature.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as the mobile phase to obtain 1 (0.259 g, 0.75 mmol) with a yield of 75%: 1H-NMR (CDCl3, 400 MHz) δ 1.36 (t, J = 7.12 Hz, 3H, CH3), 2.37 (s, 3H, CH3), 3.18 (s, 3H, CH3), 4.30 (q, J = 7.12 Hz, 2H, CH2), 7.18 (s, 1H, CH), 7.38–7.44 (m, 2H, PhH), 7.56–7.58 (m, 1H, PhH), 8.18 (s, 1H, NH), 8.56–8.58 (m, 1H, PhH), 11.34 (s, 1H, NH); 13C-NMR (CDCl3, 125 MHz) δ 14.37, 15.83, 26.79, 63.22, 121.71, 128.15, 128.33, 130.39, 132.64, 137.89, 140.04, 152.78, 163.84, 170.39, 180.02; HRMS (ESI, M+) m/z calc. for C16H18N4O3S, 346.1100, found: 346.1088.
1) as the mobile phase to obtain 1 (0.259 g, 0.75 mmol) with a yield of 75%: 1H-NMR (CDCl3, 400 MHz) δ 1.36 (t, J = 7.12 Hz, 3H, CH3), 2.37 (s, 3H, CH3), 3.18 (s, 3H, CH3), 4.30 (q, J = 7.12 Hz, 2H, CH2), 7.18 (s, 1H, CH), 7.38–7.44 (m, 2H, PhH), 7.56–7.58 (m, 1H, PhH), 8.18 (s, 1H, NH), 8.56–8.58 (m, 1H, PhH), 11.34 (s, 1H, NH); 13C-NMR (CDCl3, 125 MHz) δ 14.37, 15.83, 26.79, 63.22, 121.71, 128.15, 128.33, 130.39, 132.64, 137.89, 140.04, 152.78, 163.84, 170.39, 180.02; HRMS (ESI, M+) m/z calc. for C16H18N4O3S, 346.1100, found: 346.1088.
Z/E photoisomerization quantum yields
The procedure to measure Z–E photoisomerization quantum yield of 1 is like those given in the literature.31Fluorescence quantum yield measurements
The procedure to measure fluorescence quantum yield of 1 is like those in the literature.31Computational methods
All the calculations are performed using the Gaussian09 program.32 Geometry optimization of the ground states of the s-E-1 rotamer, its dimer, s-Z-1 rotamer and s-Z-1 tautomer are done at the CAM-B3LYP/6-31+G* level without any symmetry restriction in the gas phase or DMSO using the polarizable continuum model (PCM).33 Geometry optimization of the S1 excited states of the s-E-1 rotamer, s-Z-1 rotamer and s-Z-1 tautomer are done at the TD-CAM-B3LYP/6-31+G* level34,35 without any symmetry restriction in the gas phase or DMSO with the PCM model. The S1 excited-state and the S0 ground-state relaxed PESs of the s-E-1 rotamer along the dihedral angle coordinate (τ- or φ-torsion), the s-Z-1 rotamer along the dihedral angle coordinate (τ-torsion), and the s-Z-1 rotamer along the bond length coordinate of H⋯NC(S)NHC(O)OEt are calculated by constrained geometry optimization of the molecular structures at the TD-CAM-B3LYP/6-31+G* level in the gas phase or DMSO with the PCM model. For the constrained geometry optimization, the reaction coordinate is fixed but the rest are relaxed. The barrier for the φ-torsion or τ-torsion relaxation of the S1 excited state of the s-E-1 rotamer or the s-Z-1 rotamer and the barrier for the ESIPT of the s-Z-1 rotamer along the bond length coordinate of H⋯NC(S)NHC(O)OEt are calculated by minimum energy path (MEP) computation36 between the given initial and final states. The MEP computation involves constrained geometry optimization of a series of molecular structures along the reaction coordinate.36 The structures of the S1/S0 CI in the S1 excited-state and S0 ground-state PES of the s-E-1 rotamer and the s-Z-1 rotamer along τ-torsion are calculated by using the complete active space self-consistent field (CASSCF) method with the 4-31G basis set and 6 electrons in an active space of the 3 highest occupied π-orbitals and the 3 lowest virtual π-orbitals.32Results and discussion
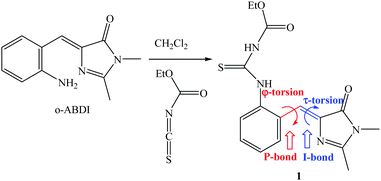
Synthesis and structure
The model compound that opens the third type of photochromism (light-driven φ-torsion, followed by ESIPT) for GFP chromophore derivatives is 1. We prepare 1 by treating o-ABDI30 with one equivalent of ethoxycarbonyl isothiocyanate in CH2Cl2 (Scheme 2).The single-crystal X-ray diffraction structure of 1 shows Z-configuration around the I-bond (i.e. C(3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(4) double bond: 1.344 Å) with τ-torsional angle [C(5)–C(4)–C(3)–N(2)] of −0.5° (Fig. 1). This Z-configuration is usually found in common GFP chromophore analogues.30,31,37–44 For the conformation around the P-bond (i.e. C(4)–C(5) single bond: 1.457 Å), 1 stays as a s-E rotamer with a φ-torsional angle [C(3)–C(4)–C(5)–C(10)] of −179.0°, and that is different from a s-Z rotamer that is usually found in common GFP chromophore analogues.30,31,37–44 The planar NHC(S)NHC(O)OEt moiety is perpendicular to the phenyl group of the s-E-1 rotamer with the torsional angle [C(5)–C(10)–N(3)–C(11)] of 105.6°. In the single crystal, the s-E-1 rotamer stays as a dimer with two intermolecular hydrogen-bonds between the imidazolinone and the NHC(S)NHC(O)OEt moieties with the O(1)–N(4) bond length of 2.865 Å, forming a rectangle cavity with a size of 3.904 Å by 5.901 Å (Fig. 1 and 2).
C(4) double bond: 1.344 Å) with τ-torsional angle [C(5)–C(4)–C(3)–N(2)] of −0.5° (Fig. 1). This Z-configuration is usually found in common GFP chromophore analogues.30,31,37–44 For the conformation around the P-bond (i.e. C(4)–C(5) single bond: 1.457 Å), 1 stays as a s-E rotamer with a φ-torsional angle [C(3)–C(4)–C(5)–C(10)] of −179.0°, and that is different from a s-Z rotamer that is usually found in common GFP chromophore analogues.30,31,37–44 The planar NHC(S)NHC(O)OEt moiety is perpendicular to the phenyl group of the s-E-1 rotamer with the torsional angle [C(5)–C(10)–N(3)–C(11)] of 105.6°. In the single crystal, the s-E-1 rotamer stays as a dimer with two intermolecular hydrogen-bonds between the imidazolinone and the NHC(S)NHC(O)OEt moieties with the O(1)–N(4) bond length of 2.865 Å, forming a rectangle cavity with a size of 3.904 Å by 5.901 Å (Fig. 1 and 2).
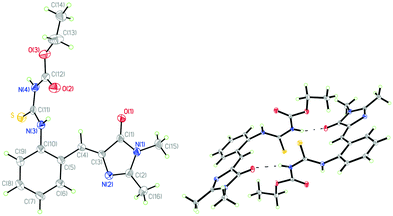 | ||
| Fig. 1 Single-crystal X-ray diffraction structures of the s-E-1 rotamer (left) and its dimer (right) with thermal ellipsoids at a 50% probability level. | ||
Equilibration among the ground-state rotamers and dimer
The optimized structures of the s-E-1 rotamer and its dimer at the level of CAM-B3LYP/6-31+G* are close to its single-crystal X-ray diffraction structure (Fig. 2). The dimer of the s-E-1 rotamer is 8.48 kcal mol−1 (13.1 kcal mol−1 in the gas phase) more stable than the two-separate s-E-1 rotamers in DMSO because of the stabilization of the two intermolecular hydrogen-bonds between the imidazolinone and the NHC(S)NHC(O)OEt moieties. Hence, the dimer dissociates very little into the two-separate s-E-1 rotamers with a dissociation constant of around 6.0 × 10−7 in DMSO.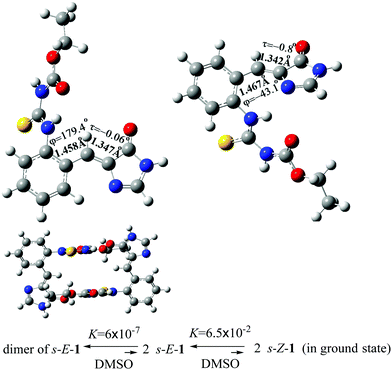 | ||
| Fig. 2 Optimized ground-state structures of the s-E-1 rotamer (top left), its dimer (bottom) and the s-Z-1 rotamer (top right), and their equilibration in DMSO at the CAM-B3LYP/6-31+G* level. | ||
Theoretically, 1 may stay as the s-E-1 and s-Z-1 rotamers, both of which are the conformational isomers around the P-bond (Fig. 2). The former is 1.62 kcal mol−1 (1.65 kcal mol−1 in the gas phase) more stable than the latter in DMSO, so the equilibrium constant for the φ-torsion from the s-E-1 rotamer to the s-Z-1 rotamer is around 6.5 × 10−2, which means that the φ-torsion equilibrium from the s-E-1 rotamer to the s-Z-1 rotamer is thermodynamically unfavourable (Fig. 2). This is consistent with its single-crystal X-ray diffraction structure, where the s-E-1 rotamer is the only conformational isomer that can be seen in the solid state. The barrier for the φ-torsion from the s-E-1 rotamer to the s-Z-1 rotamer is calculated to be 4.12 kcal mol−1 in DMSO (4.89 kcal mol−1 in the gas phase), which is much smaller than the barrier (10.8 kcal mol−1) of flipping cyclohexane.45 (Fig. 3 and 4) Hence, the φ-torsion in the ground state should be kinetically favourable but thermodynamically unfavourable at room temperature. The thing is, the s-E-1 rotamer stays as a dimer with a very small fraction of the dimer dissociating into the two-separate s-E-1 rotamers, not to mention the amount of the s-Z-1 rotamer, which is even lower than that of the s-E-1 rotamer.
Photophysics
The lowest-energy electronic absorption of s-E-1 occurs at 342 nm (ε = 8.0 × 103 M−1 cm−1) in water, 351 nm (ε = 8.8 × 103 M−1 cm−1) in methanol, 365 nm (ε = 9.0 × 103 M−1 cm−1) in DMSO, 357 nm (ε = 9.0 × 103 M−1 cm−1) in acetonitrile and 357 nm (ε = 6.7 × 103 M−1 cm−1) in cyclohexane (Table 1). They are not regularly shifted with solvent polarity, so photoexcitation of s-E-1 does not involve charge transfer. According to its high molar absorptivity (ε), the lowest-energy electronic absorption is suggested to involve π → π* electronic transition. The computational electronic absorption of 334 nm (f = 0.69) in DMSO and 329 nm (f = 0.11) in the gas phase for 1 at the TD-CAM-B3LYP/6-31+G* level is consistent with its experimental electronic absorption of 365 nm in DMSO and 357 nm in cyclohexane.| Solvent | λ abs/nm (ε) | λ f/nm (ϕf)b |
|---|---|---|
a Calcd at the TD-CAM-B3LYP/6-31+G* level with calcd results shown in the footnotes of Table 1.
b
λ
ex = 350 nm.
c Calcd λabs: 334 nm, oscillator strength (f): 0.69 in DMSO.
d Calcd λf from s-E-1: 520 nm, f: 0.01; calcd λf from s-Z-1: 473 nm, f: 0.74 in DMSO.
e Calcd λf from the s-Z-1 tautomer: 561 nm, f: 0.48 in DMSO.
f Calcd λabs: 329 nm, f: 0.11 in the gas phase.
g Calcd λf from s-E-1: 534 nm, f: 0.001; calcd λf from s-Z-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 nm, f: 0.04 in the gas phase. 484 nm, f: 0.04 in the gas phase.
|
||
| H2O | 342 (8.0 × 103) | 451 (2.4 × 10−4), 576 |
| MeOH | 351 (8.8 × 103) | 450 (3.8 × 10−4), 576 |
| DMSO | 365c (9.0 × 103) | 453d (6.9 × 10−4), 597e |
| CH3CN | 357 (9.0 × 103) | 442 (6.6 × 10−4) |
| THF | 361 (9.7 × 103) | 441 (7.7 × 10−4) |
| CH2Cl2 | 359 (9.6 × 103) | 440 (7.7 × 10−4) |
| Cyclohexane | 357f (6.7 × 103) | 434g (3.4 × 10−4) |
The S1 excited state of s-E-1 emits fluorescence at 451 and 576 nm (ϕF = 2.4 × 10−4) in water, 450 and 576 nm (ϕF = 3.8 × 10−4) in methanol, 453 and 597 nm (ϕF = 6.9 × 10−4) in DMSO, 441 nm (ϕF = 7.7 × 10−4) in THF, 440 nm (ϕF = 7.7 × 10−4) in CH2Cl2 and 434 nm (ϕF = 3.4 × 10−4) in cyclohexane (Table 1 and Fig. 5). It displays single fluorescence in a less polar solvent (cyclohexane, THF and CH2Cl2) but dual fluorescence in a more polar solvent (DMSO, methanol and water). The fluorescence with a lower wavelength is slightly red-shifted as solvent polarity increases, indicating that its S1 excited state is a little more polar than its Franck–Condon ground state. For the dual fluorescence, the one with a lower wavelength has a normal Stokes shift (7066 cm−1 in water, 6267 cm−1 in methanol and 5322 cm−1 in DMSO) while the one with a higher wavelength displays an anomalously large Stokes shift (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878 cm−1 in water, 11
878 cm−1 in water, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 cm−1 in methanol and 10
129 cm−1 in methanol and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 cm−1 in DMSO). It suggests that the fluorescence with a higher wavelength comes from the S1 excited state of the s-Z-1 tautomer that is generated by the ESIPT of the s-Z-1 rotamer. It means that a significant amount of the S1 excited state of the s-Z-1 rotamer has been generated from the S1 excited state of the s-E-1 rotamer through the φ-torsion in a polar solvent like DMSO, methanol and water. This part of the results is against the NEER principle.20–27
647 cm−1 in DMSO). It suggests that the fluorescence with a higher wavelength comes from the S1 excited state of the s-Z-1 tautomer that is generated by the ESIPT of the s-Z-1 rotamer. It means that a significant amount of the S1 excited state of the s-Z-1 rotamer has been generated from the S1 excited state of the s-E-1 rotamer through the φ-torsion in a polar solvent like DMSO, methanol and water. This part of the results is against the NEER principle.20–27
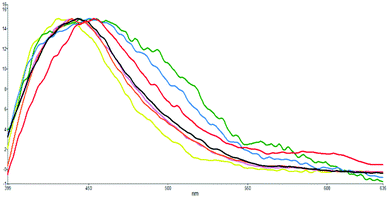 | ||
| Fig. 5 Normalized fluorescence emissions (λex: 350 nm) of s-E-1 in solvents of H2O (green), MeOH (blue), DMSO (red), CH3CN (black), CH2Cl2 (violet), THF (orange) and cyclohexane (yellow). | ||
At the TD-CAM-B3LYP/6-31+G* level, the computational fluorescence emission of 484 nm (f = 0.04) from the S1 excited-state s-Z-1 rotamer in the gas phase, instead of the computational fluorescence emission of 534 nm (f = 0.001) from the S1 excited-state s-E-1 rotamer, is close to the experimental fluorescence of 434 nm (ϕf = 3.4 × 10−4) for 1, indicating that the experimental fluorescence of 1 in cyclohexane comes from the S1 excited-state s-Z-1 rotamer, instead of the S1 excited-state s-E-1 rotamer (Table 1). The S1 excited-state s-E-1 rotamer may relax through internal conversion, fluorescence emission, φ-torsion and τ-torsion, where the τ-torsion relaxation is a high-barrier process as shown later. The oscillator strength (f = 0.001) of the fluorescence emission from the S1 excited-state s-E-1 rotamer is quite low but the oscillator strength (f = 0.04) of fluorescence emission from the S1 excited-state s-Z-1 rotamer is a little bigger, indicating that the S1 excited-state s-E-1 rotamer does not like to emit fluorescence but relaxes mostly through internal conversion and the φ-torsion relaxation to the S1 excited-state s-Z-1 rotamer works but not very well.
In DMSO, the computational fluorescence emission of 473 nm (f = 0.74) from the S1 excited-state s-Z-1 rotamer, instead of the computational fluorescence emission of 520 nm (f = 0.01) from the S1 excited-state s-E-1 rotamer, is close to the experimental low-wavelength fluorescence of 453 nm (ϕf = 6.9 × 10−4) for 1, indicating that the experimental low-wavelength fluorescence of 1 in DMSO comes from the S1 excited-state s-Z-1 rotamer, instead of the S1 excited-state s-E-1 rotamer (Table 1). The oscillator strength (f = 0.01) of fluorescence emission from the S1 excited-state s-E-1 rotamer is quite low but the oscillator strength (f = 0.74) of fluorescence emission from the S1 excited-state s-Z-1 rotamer is much bigger, indicating that the S1 excited-state s-E-1 rotamer does not like to emit fluorescence but relaxes through both internal conversion and φ-torsion relaxation to the S1 excited-state s-Z-1 rotamer, which emits fluorescence efficiently. This is consistent with the experimental result that the fluorescence quantum yield of 1 in DMSO is almost twice the fluorescence quantum yield of 1 in cyclohexane.
In DMSO, the computational fluorescence emission of 561 nm (f = 0.48) from the S1 excited-state s-Z-1 tautomer is close to the experimental high-wavelength fluorescence of 597 nm for 1, indicating that the experimental high-wavelength fluorescence of 1 in DMSO comes from the S1 excited-state s-Z-1 tautomer.
Confirmation of ESIPT by acid titration
To confirm that the higher-wavelength fluorescence of the dual fluorescence in DMSO, water and methanol is caused by ESIPT, we titrate s-E-1 in DMSO with 1, 1.3 and 2 equivalents of HCl(aq) (Fig. 6). During the acid titration, the higher-wavelength fluorescence disappears, and the dual fluorescence becomes single fluorescence. It was reported that the acidification of GFP chromophore may protonate the imidazolinone nitrogen.46 Hence, acid titration of s-E-1 may do the same thing and has its imidazolinone nitrogen (N2) being protonated. As we expected, ESIPT of the s-Z-1 rotamer involves proton transfer from the thioamide nitrogen (N3) or thioimide nitrogen (N4) to the imidazolinone nitrogen (N2) in its S1 excited state. Thus, the protonated imidazolinone nitrogen in acid titration should block the ESIPT of the s-Z-1 rotamer, causing the higher-wavelength fluorescence to disappear. Hence, this acid-titration experiment successfully confirms that the higher-wavelength fluorescence is caused by the ESIPT of the s-Z-1 rotamer.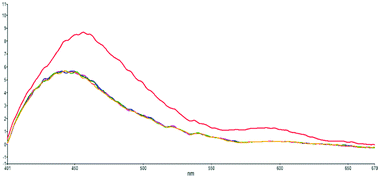 | ||
| Fig. 6 Acid-titration fluorescence emission spectra (λex: 350 nm) of s-E-1 in DMSO with 0 (red), 1 (blue), 1.3 (pink) and 2 (yellow) equivalents of HCl(aq) and each injection volume is 3 μl. | ||
The next question is which proton of the S1 excited-state s-Z-1 rotamer would be transferred to the imidazolinone nitrogen during ESIPT, the proton on the thioamide nitrogen (N3) or the proton on thioimide nitrogen (N4)? It was reported that a strong H-bond accepting solvent like DMSO may decrease the intramolecular H-bonding strength, followed by the reduction of the fluorescence quantum yield of ESIPT.47 Hence, intramolecular H-bonding strength is important for ESIPT. According to the optimized structures of the S1 excited-state and ground-state s-Z-1 rotamers (Fig. 2 and 7) only the proton on the thioamide nitrogen (N3), instead of the proton on thioimide nitrogen (N4), can form intramolecular H-bonding with the imidazolinone nitrogen. Besides, pKa of the proton on the thioamide nitrogen (N3) is calculated to be 8.11 in DMSO by using the combined methods of B3PW91/6-311++G(3df,2p)//B3LYP/6-31+G(d)//HF//CPCM/UA0,37 so it is acidic enough to undergo ESIPT. Hence, it is likely that the proton on the thioamide nitrogen (N3) is transferred to the imidazolinone nitrogen during ESIPT of the s-Z-1 rotamer.
Experimental evidence for equilibration among excited-state rotamers and tautomer
According to single-crystal X-ray diffraction structure of 1, the s-E-1 rotamer is the only conformational isomer that can be seen in the solid state, and the s-Z-1 rotamer cannot be found at all. Proton NMR spectra of 1 in both d6-DMSO and CDCl3 show that only one conformational isomer exists in the solutions (ESI‡). The conformational isomer in both d6-DMSO and CDCl3 should be the s-E-1 rotamer, instead of the s-Z-1 rotamer, based on its single-crystal X-ray diffraction structure and the computational results. It means that the φ-torsion equilibrium from the ground-state s-E-1 rotamer to the ground-state s-Z-1 rotamer is thermodynamically unfavourable. However, fluorescence emission of 1 in cyclohexane comes from the S1 excited-state s-Z-1 rotamer, instead of the S1 excited-state s-E-1 rotamer (Table 1). If there were no excited-state φ-torsion relaxation from the S1 excited state of the s-E-1 rotamer to the S1 excited state of the s-Z-1 rotamer in cyclohexane, 1 would not emit fluorescence from the S1 excited-state s-Z-1 rotamer. Besides, 1 displays dual fluorescence emissions in DMSO, MeOH or water. The one with a lower wavelength comes from the S1 excited-state s-Z-1 rotamer, instead of the S1 excited-state s-E-1 rotamer, and the one with a higher wavelength comes from the S1 excited-state s-Z-1 tautomer (Table 1). If there were no excited-state φ-torsion relaxation from the S1 excited state of the s-E-1 rotamer to the S1 excited state of the s-Z-1 rotamer, followed by ESIPT from the S1 excited state of the s-Z-1 rotamer to the S1 excited state of the s-Z-1 tautomer in DMSO, MeOH or water, 1 would not emit dual fluorescence from the S1 excited-state s-Z-1 rotamer and the S1 excited-state s-Z-1 tautomer, respectively. These pieces of experimental evidence confirm that the equilibration exists between the S1 excited-state s-E-1 rotamer, the S1 excited-state s-Z-1 rotamer and the S1 excited-state s-Z-1 tautomer.Equilibration between excited-state rotamers through φ-torsion (against the NEER principle)
The S1 excited states of the s-E-1 and s-Z-1 rotamers have been successfully optimized at the level of TD-CAM-B3LYP/6-31+G* (Fig. 7). For the S1 excited state of the s-E-1 rotamer, its I-bond [C(3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(4) double bond: 1.349 Å] still has significant double-bond character although it is a little longer in comparison with that (1.347 Å) of its ground state, and its P-bond [C(4)–C(5) single bond: 1.454 Å] still has significant single-bond character even though it is a little shorter than that (1.458 Å) of its ground state, leading to its φ-torsion relaxation much easier than its τ-torsion relaxation. This computation result is not only consistent with our experimental result that the Z–E photoisomerization quantum yield of the s-E-1 rotamer through the τ-torsion in any solvent is 0.0, but also provides an answer to the following question: “Why is this part of results against the NEER principle?”
C(4) double bond: 1.349 Å] still has significant double-bond character although it is a little longer in comparison with that (1.347 Å) of its ground state, and its P-bond [C(4)–C(5) single bond: 1.454 Å] still has significant single-bond character even though it is a little shorter than that (1.458 Å) of its ground state, leading to its φ-torsion relaxation much easier than its τ-torsion relaxation. This computation result is not only consistent with our experimental result that the Z–E photoisomerization quantum yield of the s-E-1 rotamer through the τ-torsion in any solvent is 0.0, but also provides an answer to the following question: “Why is this part of results against the NEER principle?”
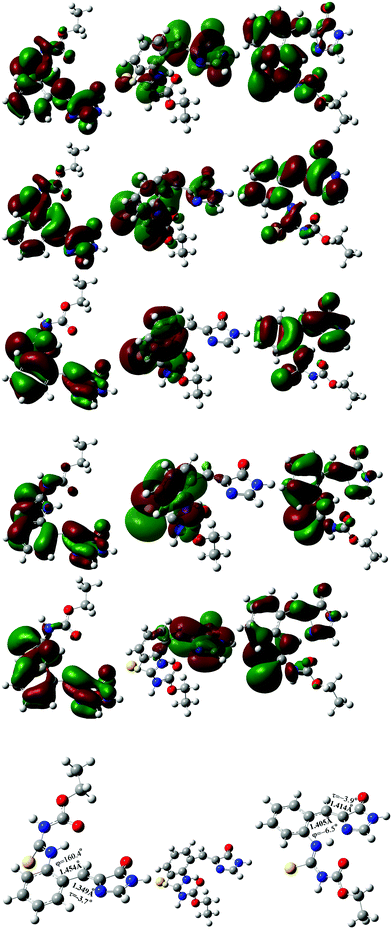
At the TD-CAM-B3LYP/6-31+G* level, the electronic configuration of the S1 excited state of the s-E-1 rotamer involves the following electronic transitions: 0.20(orbital 81 → orbital 84) + 0.16(orbital 81 → orbital 85) + 0.43(orbital 82 → orbital 84) + 0.33(orbital 82 → orbital 85) + 0.29(orbital 83 → orbital 84) + 0.20(orbital 83 → orbital 85) (Fig. 7). It has 59% of electronic transition from orbital 82 to both orbital 84 and 85, 25% of electronic transition from orbital 83 to both orbital 84 and 85, and 13% of electronic transition from orbital 81 to both orbital 84 and 85. Major electronic transition coming from orbital 82, instead of orbital 83, may explain why the S1 excited states of the s-E-1 rotamer still has the I-bond with a significant double-bond character and the P-bond with a significant single-bond character.
On the other hand, the electronic configuration of the S1 excited state of the s-Z-1 rotamer involves the electronic transition of −0.70(orbital 83 → orbital 84), indicating that it has 98% of the electronic transition from orbital 83 to orbital 84 (Fig. 7).
To explore the electron density/molecular orbital transition during φ-torsion from the S1 excited-state s-E-1 rotamer to the S1 excited-state s-Z-1 rotamer, the S1 excited-state s-E-1 rotamer with φ = 90° has been optimized at the TD-CAM-B3LYP/6-31+G* level (Fig. 7). Its electronic configuration involves the following electronic transitions: 0.45(orbital 82 → orbital 84) + 0.14(orbital 82 → orbital 85) + 0.49(orbital 83 → orbital 84) + 0.15(orbital 83 → orbital 85). It has 44% of the electronic transition from orbital 82 to both orbital 84 and 85 and 53% of the electronic transition from orbital 83 to both orbital 84 and 85. During φ-torsion from the S1 excited-state s-E-1 rotamer to the S1 excited-state s-Z-1 rotamer, electron density around the P- and I-bond of molecular orbitals 82 and 83 vanishes at φ = 90° but it reappears when the S1 excited-state s-Z-1 rotamer is formed. Molecular orbitals that are involved in the electronic configuration of the S1 excited state during the φ-torsion process get fewer and fewer.
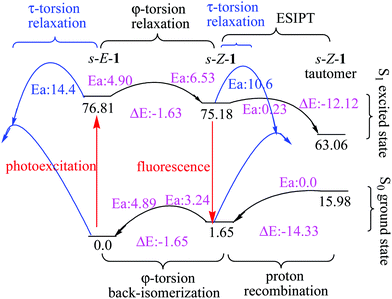
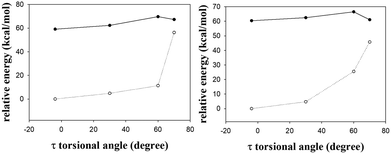
The barrier for the φ-torsion from the S1 excited state of the s-E-1 rotamer to that of the s-Z-1 rotamer in the gas phase is 4.90 kcal mol−1, which is very close to the barrier (4.89 kcal mol−1) for the ground-state φ-torsion isomerization from the s-E-1 rotamer to the s-Z-1 rotamer. It means that photoexcitation does not make the φ-torsion from the s-E-1 rotamer to the s-Z-1 rotamer kinetically more favourable in the gas phase or in less polar solvents. From the thermodynamic point of view, although the ground-state s-E-1 rotamer is 1.65 kcal mol−1 more stable than the ground-state s-Z-1 rotamer, the S1 excited-state s-E-1 rotamer is 1.63 kcal mol−1 less stable than the S1 excited-state s-Z-1 rotamer in the gas phase (Fig. 3). Hence, the φ-torsion from the s-E-1 rotamer to the s-Z-1 rotamer in the S1 potential energy surface (PES) is thermodynamically favourable. This is consistent with the experimental result that the fluorescence emission (434 nm, ϕf = 3.4 × 10−4) of 1 in cyclohexane is much closer to the calculated fluorescence emission (484 nm, f: 0.04) from the S1 excited-state s-Z-1 rotamer than the calculated fluorescence emission (534 nm, f: 0.001) from the S1 excited-state s-E-1 rotamer in the gas phase (Table 1). However, the φ-torsion from the s-E-1 rotamer to the s-Z-1 rotamer in the S1 PES in cyclohexane does not work well according to the low experimental fluorescence quantum yield and the low calculated oscillator strengths from both the S1 excited-state s-Z-1 rotamer (f: 0.04) and the S1 excited-state s-E-1 rotamer (f: 0.001). A possible explanation for that is, much faster internal conversion occurs in the S1 excited state of the s-E-1 rotamer since it has a long and flexible side chain, which easily converts electronic energies of the excited state into nuclear vibration and rotation. That might explain why the further ESIPT of s-E-1 in a less polar solvent (cyclohexane, THF and CH2Cl2) is hard to detect.
In a polar solvent like DMSO, the S1 excited-state s-Z-1 rotamer is much more stable than the S1 excited-state s-E-1 rotamer (7.4 kcal mol−1 in DMSO vs. 1.63 kcal mol−1 in the gas phase) (Fig. 3 and 4). Besides, the barrier for the φ-torsion from the S1 excited-state s-E-1 rotamer to the S1 excited-state s-Z-1 rotamer drops to 4.0 kcal mol−1, which is 0.9 kcal mol−1 less than that in the gas phase. Hence, the φ-torsion from the s-E-1 rotamer to the s-Z-1 rotamer in the S1 PES in a polar solvent like DMSO becomes both thermodynamically and kinetically much more favourable than that in the gas phase. This is consistent with the experimental result that the fluorescence emission (453 nm, ϕf = 6.9 × 10−4) of 1 in DMSO is much closer to the calculated fluorescence emission (473 nm, f: 0.74) from the S1 excited-state s-Z-1 rotamer than the calculated fluorescence emission (520 nm, f: 0.01) from the S1 excited-state s-E-1 rotamer in DMSO (Table 1). The φ-torsion from the s-E-1 rotamer to the s-Z-1 rotamer in the S1 PES in DMSO, which likely outpaces the internal conversion that happens to the S1 excited-state s-E-1 rotamer, works much better according to the higher experimental fluorescence quantum yield, the higher calculated oscillator strength (f: 0.74) from the S1 excited-state s-Z-1 rotamer and the lower calculated oscillator strength (f: 0.01) from the S1 excited-state s-E-1 rotamer. That might explain why the further ESIPT of s-E-1 is observed in a polar solvent like DMSO, methanol and water.
Calculations on ESIPT
For the S1 excited-state s-Z-1 rotamer, its I-bond [C(3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(4) double bond: 1.414 Å] is even longer and its P-bond [C(4)–C(5) single bond: 1.405 Å] is even shorter in comparison with those of the S1 excited-state s-E-1 rotamer. Both I-bond and P-bond of the S1 excited-state s-Z-1 rotamer have similar bond lengths and have a significant π-bond character, leading to difficulty in performing both φ-torsion and τ-torsion relaxation but ease to undergo ESIPT.
C(4) double bond: 1.414 Å] is even longer and its P-bond [C(4)–C(5) single bond: 1.405 Å] is even shorter in comparison with those of the S1 excited-state s-E-1 rotamer. Both I-bond and P-bond of the S1 excited-state s-Z-1 rotamer have similar bond lengths and have a significant π-bond character, leading to difficulty in performing both φ-torsion and τ-torsion relaxation but ease to undergo ESIPT.
According to the computational results in the gas phase at the TD-CAM-B3LYP/6-31+G* level, the barrier for the φ-torsion back-isomerization from the S1 excited-state s-Z-1 rotamer to the S1 excited-state s-E-1 rotamer is 6.53 kcal mol−1 and the barrier for the τ-torsion relaxation of the S1 excited-state s-Z-1 rotamer is 10.6 kcal mol−1, but the barrier for ESIPT of the s-Z-1 rotamer is as low as 0.23 kcal mol−1 (Fig. 3). Hence, the S1 excited-state s-Z-1 rotamer likely undergoes ESIPT in the gas phase or less polar solvents by transferring a proton from the thioamide nitrogen (N3) to the imidazolinone nitrogen (N2), forming the S1 excited-state s-Z-1 tautomer, which is 12.12 kcal mol−1 more stable than the S1 excited-state s-Z-1 rotamer. Then, a question comes up. Why is ESIPT of s-E-1 hard to detect in a less polar solvent (cyclohexane, THF and CH2Cl2) experimentally? A possible answer is that the problem does not appear in the ESIPT but in the φ-torsion from the S1 excited-state s-E-1 rotamer to the S1 excited-state s-Z-1 rotamer, which is thermodynamically and kinetically less favourable in comparison with the internal conversion that happens to the S1 excited-state s-E-1 rotamer in less polar solvents.
In a polar solvent like DMSO, the barrier of ESIPT is increased to 2.37 kcal mol−1 probably because DMSO (dipole moment: 3.96 Debye) stabilizes the S1 excited-state s-Z-1 rotamer (dipole moment: 7.3 Debye) better than its transition state (dipole moment: ca. 8.4 Debye) to the S1 excited-state s-Z-1 tautomer (dipole moment: 14.2 Debye) according to the “like-dissolves-like” principle, where DMSO polarity is closer to polarity of the S1 excited-state s-Z-1 rotamer than polarity of the transition state to the S1 excited-state s-Z-1 tautomer. However, our experiment shows that s-E-1 does undergo ESIPT in a polar solvent like DMSO, methanol and water (Fig. 3). Why does that happen? Even though the barrier of ESIPT is increased to 2.37 kcal mol−1 in DMSO, it is still low enough in comparison with the barrier (11.4 kcal mol−1) for the φ-torsion back-isomerization from the S1 excited-state s-Z-1 rotamer to the S1 excited-state s-E-1 rotamer and the barrier (6.1 kcal mol−1) for the τ-torsion relaxation of the S1 excited-state s-Z-1 rotamer. Hence, ESIPT is not a problem in DMSO. The key point is that, despite defying the NEER principle,20–27 the φ-torsion from the S1 excited-state s-E-1 rotamer to the S1 excited-state s-Z-1 rotamer in DMSO is much more thermodynamically and kinetically favourable than that in the gas phase, and that makes the next ESIPT become a reality (Fig. 3 and 4). Besides, the calculated fluorescence emission (561 nm) of the s-Z-1 tautomer in DMSO, which is close to the experimental fluorescence emission (597 nm) from ESIPT of 1 in DMSO, and its oscillator strength (f) of 0.48 also confirm that ESIPT from the S1 excited state of the s-Z-1 rotamer to that of the s-Z-1 tautomer in DMSO is the preferred process (Table 1).
The electronic configuration of the S1 excited state of the s-Z-1 tautomer involves the electronic transition of −0.69(orbital 83 → orbital 84), so it has 95% of electronic transition from orbital 83 to orbital 84 (Fig. 8). The molecular orbital 84 has high electron density at the antibonding π-orbital of the I-bond and the bonding π-orbital of the P-bond. That may explain why the S1 excited state of the s-Z-1 tautomer has the I-bond a little longer and the P-bond a little shorter in comparison with the ground-state s-Z-1 rotamer.
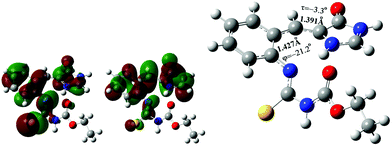 | ||
| Fig. 8 Occupied molecular orbital 83 (left), and virtual molecular orbital 84 (middle) of the optimized S1 excited state of the s-Z-1 tautomer (right) in DMSO at the TD-CAM-B3LYP/6-31+G* level. | ||
Proton recombination
After the S1 excited state of the s-Z-1 tautomer emits fluorescence, it relaxes to the ground-state s-Z-1 tautomer, which is 9.3 kcal mol−1 less stable than the ground-state s-Z-1 rotamer in DMSO (Fig. 4). Besides, the proton recombination for the ground-state s-Z-1 tautomer to turn into the ground-state s-Z-1 rotamer is almost barrierless according to the calculations at the CAM-B3LYP/6-31+G* level. Hence, the s-Z-1 tautomer is quickly relaxed to the s-Z-1 rotamer, which is not thermodynamically stable either.Re-equilibration of ground-state rotamers through φ-torsion
The barrier for the φ-torsion from the ground-state s-Z-1 rotamer to the ground-state s-E-1 rotamer in DMSO is around 2.5 kcal mol−1, (Fig. 4) which is much smaller than the barrier (10.8 kcal mol−1) to flip cyclohexane.45 Meanwhile, the former is 1.62 kcal mol−1 less stable than the latter in DMSO. Hence, the newly formed ground-state s-Z-1 rotamer from the proton recombination of the ground-state s-Z-1 tautomer won’t stay long but quickly undergoes φ-torsion back-isomerization to form the more stable s-E-1 rotamer. This computation result is consistent with our experimental result that s-E-1 is the only product we found after its photoexcitation in a polar solvent like DMSO, methanol and water.τ-Torsion relaxation of the S1 excited state (Z–E photoisomerization)
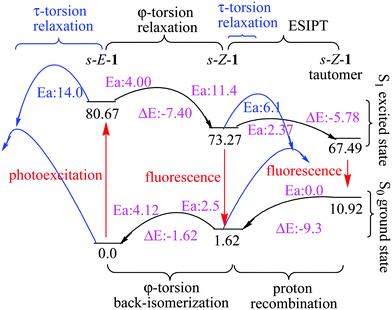
In addition to the gated photochromism involving the φ-torsion relaxation, followed by ESIPT, does the S1 excited-state s-E-1 rotamer undergo the τ-torsion relaxation that the GFP chromophore and its analogues38,39,41,42,48 usually do? According to calculations at the TD-CAM-B3LYP/6-31+G* level, the S1 excited-state and the Franck–Condon S0 ground-state PESs of the s-E-1 rotamer along the τ-torsion come close to each other and reach the S1/S0 conical intersection (CI) (Fig. 9). The optimized structure of the CI at the CASSCF(6,6)/4-31G level shows that the imidazolinone group is almost perpendicular to the benzyl group (Fig. 10). Although the CI may make the S1 excited state easily relax to the S0 ground state, the barrier for the S1 excited-state s-E-1 rotamer to reach the CI along the τ-torsion relaxation is as high as 14 kcal mol−1 in DMSO (14.4 kcal mol−1 in the gas phase), which is too high in comparison with the barrier (4.0 kcal mol−1 in DMSO and 4.9 in the gas phase) for the φ-torsion relaxation. Hence, the S1 excited-state s-E-1 rotamer unlikely relaxes to the ground state by following the τ-torsion in a polar or less polar solvent.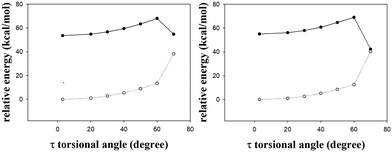 | ||
| Fig. 9 The S1 (solid line) and the Franck–Condon S0 (dashed line) relaxed PESs of the s-E-1 rotamer along τ-torsion relaxation in gas phase (left) and DMSO (right) at the TD-CAM-B3LYP/6-31+G* level. | ||
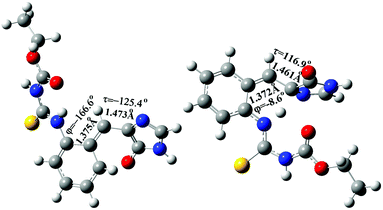 | ||
| Fig. 10 The optimized structure of the S1/S0 conical intersection (CI) of the s-E-1 rotamer (left) and the s-Z-1 rotamer (right) along τ-torsion relaxation at the CASSCF(6,6)/4-31G level. | ||
Similarly, the S1 excited-state and the Franck–Condon S0 ground-state PESs of the s-Z-1 rotamer also come close to each other along the τ-torsion and reach the S1/S0 CI, (Fig. 10 and 11) but the barrier for the S1 excited-state s-Z-1 rotamer to reach the CI along the τ-torsion relaxation is 6.1 kcal mol−1 in DMSO (10.6 kcal mol−1 in the gas phase), which is much higher than the barrier (2.37 kcal mol−1 in DMSO and 0.23 kcal mol−1 in the gas phase) for ESIPT of the s-Z-1 rotamer. Hence, the S1 excited-state s-Z-1 rotamer also unlikely relaxes to the ground state by following the τ-torsion in a polar or less polar solvent.
The above two computational results are consistent with our experimental result that the Z–E photoisomerization quantum yield of s-E-1 through τ-torsion in any solvent is 0.0 while the Z–E photoisomerization quantum yield of p-HBDI in CD3CN is 0.48.47 These results are quite unusual because the S1 excited states of GFP and its derivatives usually follow the τ-torsion relaxation (Z–E photoisomerization).38,39,41,42,48 Then, a question comes out. The fluorescence quantum yield of 1 is as low as 6.9 × 10−4 in DMSO (Table 1) and its S1 excited state does not follow τ-torsion relaxation through CI. What will be the major relaxation pathway for its S1 excited state? There are two possibilities for that. For the first possibility, just like a GFP chromophore with a strong e-donating group at the meta-position, whose S1 excited state relaxes mostly through internal conversion,49 we suggest that the major relaxation pathway for the S1 excited state of 1 is internal conversion because it has a long and flexible side chain of NC(S)NHC(O)OEt. For the second possibility, it was reported that a strong H-bond accepting solvent like DMSO may decrease the intramolecular H-bonding strength, followed by reducing the fluorescence quantum yield of ESIPT.47 It is very likely that a strong H-bond accepting solvent like DMSO may decrease the fluorescence quantum yield for ESIPT of 1.
It was reported that the barrier for the τ-torsion relaxation of the S1 excited states of GFP chromophore derivatives can be increased by adding a strong e-donating group at the meta-position, resulting in a much lower Z–E photoisomerization quantum yield (<0.1).49 Similarly, the Z–E photoisomerization quantum yield of s-E-1 is 0.0 with a high barrier for the τ-torsion relaxation, but its substituent is located at the ortho-position and is not a strong e-donating group. We also found that a GFP chromophore analogue with a strong e-donating ortho-NMe2 substituent has the Z–E photoisomerization quantum yield of 0.37 in CD3CN50 but another GFP chromophore analogue with an ortho-PhSO2NH substituent has the Z–E photoisomerization quantum yield of 0.0 in CD3CN.31 The latter selectively follows ESIPT relaxation, instead of τ-torsion relaxation. Hence, a GFP chromophore with a strong e-donating substituent at the ortho-position still has a high Z–E photoisomerization quantum yield, but a GFP chromophore with an acidic NH substituent at the ortho-position prefers ESIPT rather than τ-torsion relaxation.
The third type of photochromism
Overall, after photoexcitation, the s-E-1 rotamer does not follow τ-torsion relaxation (Z–E photoisomerization) that the GFP chromophore (p-HBDI) and its analogues38,39,41,42,48 usually follow but undergoes φ-torsion, followed by ESIPT, in a polar solvent like DMSO, methanol and water, generating dual fluorescence: one from the S1 excited state of s-Z-1 and the other from the S1 excited state of the s-Z-1 tautomer. In a less polar solvent like cyclohexane, THF and CH2Cl2, the S1 excited state of s-E-1 does not relax through φ-torsion well, not to mention relaxation through ESIPT, and single fluorescence just comes from the S1 excited state of s-Z-1. Apparently, s-E-1 opens the third type of photochromism for GFP chromophore derivatives.Conclusions
The major photochromism for the GFP is ESPT and the major photochromism for Dronpa (a GFP mutant) is Z–E photoisomerization through τ-torsion. Now, the model compound s-E-1 opens the third type of photochromism for GFP chromophore derivatives, which involves light-driven φ-torsion with no τ-torsion, followed by ESIPT. The third type of photochromism is environment sensitive. The gate is open in a polar solvent like DMSO, methanol and water, but closed in a less polar solvent like cyclohexane, THF and CH2Cl2. Hence, it is a new gated photochromism. The gated photochromism of s-E-1 may provide a blueprint to create a new type of photochromic fluorescent protein by mutagenesis.The experimental data for single-crystal X-ray diffraction structure, proton NMR spectra and fluorescence emission spectra of 1 indicate that excited-state relaxation of 1 follows the excited-state φ-torsion relaxation from the S1 excited state of the s-E-1 rotamer to the S1 excited state of the s-Z-1 rotamer in less polar solvents and follows the excited-state φ-torsion relaxation from the S1 excited state of the s-E-1 rotamer to the S1 excited state of the s-Z-1 rotamer, followed by ESIPT from the S1 excited state of the s-Z-1 rotamer to the S1 excited state of the s-Z-1 tautomer in polar solvents like DMSO, MeOH or water. Computation at the TD-CAM-B3LYP/6-31+G* level well confirms the experimental findings.
Since s-E-1 does not follow Z–E photoisomerization through τ-torsion but undergoes light-driven φ-torsion in a polar solvent like DMSO, the S1 excited-state of the s-E-1 rotamer can be converted to the S1 excited-state of the s-Z-1 rotamer within the S1 lifetime through the φ-torsion around the single bond (P-bond) that connects two unsaturated centers in the ground state. This result is clearly against the NEER principle.20–27
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Science Council of Taiwan for financial support (NSC109-2113-M-006-005) and the National Center for High-performance Computing for computer facilities and time.Notes and references
- S. R. Meech, Chem. Soc. Rev., 2009, 38, 2922–2934 RSC.
- M. Zimmer, Chem. Rev., 2002, 102, 759–781 CrossRef CAS.
- D. M. Shcherbakova, P. Sengupta, J. Lippincott-Schwartz and V. V. Verkhusha, Annu. Rev. Biophys., 2014, 43, 303–329 CrossRef CAS.
- X. X. Zhou, H. K. Chung, A. J. Lam and M. Z. Lin, Science, 2012, 338, 810–814 CrossRef CAS PubMed.
- X. X. Zhou, L. Z. Fan, P. Li, K. Shen and M. Z. Lin, Science, 2017, 355, 836–842 CrossRef PubMed.
- K. V. Korpany, et al. , J. Am. Chem. Soc., 2012, 134, 16119–16122 CrossRef CAS PubMed.
- K. Brejc, T. K. Sixma, P. A. Kitts, S. R. Kain, R. Y. Tsien, M. Ormo and S. J. Remington, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 2306–2311 CrossRef CAS.
- X. Shu, P. Leiderman, R. Gepshtein, N. R. Smith, K. Kallio, D. Huppert and S. J. Remington, Protein Sci., 2007, 16, 2703–2710 CrossRef CAS.
- R. M. Dickson, A. B. Cubitt, R. Y. Tsien and W. E. Moerner, Nature, 1997, 388, 355–358 CrossRef CAS.
- S. Habuchi, R. Ando, P. Dedecker, W. Verheijen, H. Mizuno, A. Miyawaki and J. Hofkens, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9511–9516 CrossRef CAS PubMed.
- M. Andresen, A. C. Stiel, S. Trowitzsch, G. Weber, C. Eggeling, M. C. Wahl, S. W. Hell and S. Jakobs, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 13005–13009 CrossRef CAS PubMed.
- A. C. Stiel, S. Trowitzsch, G. Weber, M. Andersen, C. Eggeling, S. W. Hell, S. Jakobs and M. C. Wahl, Biochem. J., 2007, 402, 35–42 CrossRef CAS PubMed.
- P. G. Wilmann, K. Turcic, J. M. Battad, M. C. J. Wilce, R. J. Devenish, M. Prescott and J. Rossjohn, J. Mol. Biol., 2006, 364, 213–224 CrossRef CAS.
- E. Fron, C. Flors, G. Schweitzer, S. Habuchi, H. Mizuno, R. Ando, F. C. De Schryver, A. Miyawaki and J. Hofkens, Ultrafast excited-state dynamics of the photoswitchable protein Dronpa, J. Am. Chem. Soc., 2007, 129, 4870–4871 CrossRef CAS.
- M. Andersen, M. C. Wahl, A. C. Stiel, F. Grater, L. V. Schafer, S. Trowitzsch, G. Weber, C. Eggeling, H. Grubmuller, S. W. Hell and S. Jakobs, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13070–13074 CrossRef PubMed.
- D. M. Chudakov, A. V. Feofanov, N. N. Mudrik, S. Lukyanov and K. A. Lukyanov, J. Biol. Chem., 2003, 278, 7215–7219 CrossRef CAS.
- M. L. Quillin, D. M. Anstrom, X. Shu, S. O’Leary, K. Kallio, D. M. Chudakov and S. J. Remington, Biochemistry, 2005, 44, 5774–5787 CrossRef CAS.
- S. P. Laptenok, A. A. Gil, C. R. Hall, A. Lukacs, J. N. Luliano, G. A. Jones, G. M. Greetham, P. Donaldson, A. Miyawaki, P. J. Tonge and S. R. Meech, Nat. Chem., 2018, 10, 845–852 CrossRef CAS PubMed.
- R. S. H. Liu and G. S. Hammond, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 11153–11158 CrossRef CAS PubMed.
- E. Havinga and J. L. M. A. Schlatmann, Tetrahedron, 1961, 16, 146–152 CrossRef.
- H. J. C. Jacobs and E. Havinga, Adv. Photochem., 1979, 11, 305–373 CAS.
- H. J. C. Jacobs, J. W. J. Gielen and E. Havinga, Tetrahedron Lett., 1981, 22, 4013–4016 CrossRef CAS.
- A. M. Brouwer, J. Cornelisse and H. J. C. Jacobs, Tetrahedron, 1987, 43, 435–438 CrossRef CAS.
- J. K. Whitesell, M. A. Minton and V. D. Tran, J. Am. Chem. Soc., 1989, 111, 1473–1476 CrossRef CAS.
- G. Bartocci and A. Spalletti, J. Phys. Chem. A, 2002, 106, 7068–7074 CrossRef CAS.
- T. Thompson and E. Tapavicza, J. Phys. Chem. Lett., 2018, 9, 4758–4764 CrossRef CAS.
- D. Madea, S. Mahvidi, D. Chalupa, T. Mujawar, A. Dvorak, L. Muchova, J. Janos, P. Slavicek, J. Svenda, L. Vitek and P. Klan, J. Org. Chem., 2020, 85, 13015–13028 CrossRef CAS.
- M. E. Martin, F. Negri and M. Olivucci, J. Am. Chem. Soc., 2004, 126, 5452–5464 CrossRef CAS PubMed.
- H. Bouas-Laurent and H. Durr, Pure Appl. Chem., 2001, 73, 639–665 CAS.
- Y.-H. Chen, W.-J. Lo and K. Sung, J. Org. Chem., 2013, 78, 301–310 CrossRef CAS.
- Y.-H. Chen, R. Sung and K. Sung, J. Phys. Chem. A, 2018, 122, 5931–5944 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria and M. A. Robb, J. R. Cheeseman, et al., Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS PubMed.
- P. N. Plessow, J. Chem. Theory Comput., 2018, 14, 981–990 CrossRef CAS PubMed.
- Y. H. Chen, R. Sung and K. Sung, Org. Lett., 2018, 20, 1768–1772 CrossRef CAS.
- Y. H. Chen, R. Sung and K. Sung, Chem. Commun., 2019, 55, 8991–8994 RSC.
- Y.-H. Chen, R. Sung and K. Sung, Phys. Chem. Chem. Phys., 2020, 22, 2424–2428 RSC.
- C.-Y. Chou, R. Sung, W.-L. Chang and K. Sung, Mater. Chem. Front., 2020, 4, 1714–1719 RSC.
- J.-J. Xu, R. Sung and K. Sung, J. Phys. Chem. A, 2019, 123, 4708–4716 CrossRef PubMed.
- M.-W. Fanjiang, M.-J. Li, R. Sung and K. Sung, Bioorg. Chem., 2018, 77, 300–310 CrossRef PubMed.
- R. Sung and K. Sung, J. Lumin., 2018, 202, 163–167 CrossRef.
- W.-J. Lo, Y.-H. Chen and K. Sung, J. Org. Chem., 2013, 78, 5925–5931 CrossRef.
- H. M. Pickett and H. L. Strauss, J. Am. Chem. Soc., 1970, 92, 7281–7290 CrossRef.
- X. He, A. F. Bell and P. J. Tonge, FEBS Lett., 2003, 549, 35–38 CrossRef.
- T. Chatterjee, M. Mandal and P. K. Mandal, Phys. Chem. Chem. Phys., 2016, 18, 24332–24342 RSC.
- J.-S. Yang, G.-J. Huang, Y.-H. Liu and S.-M. Peng, Chem. Commun., 2008, 1344–1346 RSC.
- T. Chatterjee, M. Mandal, V. Guide, P. P. Bag and P. K. Mandal, Phys. Chem. Chem. Phys., 2015, 17, 20515–20521 RSC.
- Y.-H. Chen, PhD Dissertation, National Cheng Kung University, 2013.
Footnotes |
| † Electronic supplementary information (ESI) available: 1H- and 13C-NMR spectra and calculation data. CCDC 2068464. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1cp03581a |
| ‡ Current address: Faculty of Family Medicine, Northern Ontario School of Medicine, Ontario, Canada. |
| This journal is © the Owner Societies 2022 |