On the nature of bonding in a new boronyl species Zn₂(BO)₂: a linear four-center two-electron σ bond

Abstract

The Zn–Zn bond as one of the metal-to-metal bonds in clusters and molecules is of fundamental interest in many areas of natural science. Neutral boronyl can be viewed as a σ radical and is found in boronyl metal complexes. However, a complex with the Zn–Zn bond stabilized by boronyl ligands has not been found so far. Herein, we report on the computational design of the simplest case of such a system: linear D_∞h OBZnZnBO. The structural and electronic properties and chemical bonding on a series of zinc complexes Zn_x(BO)_y (x = 1,2; y = 1,2) with boronyl as ligands have been studied using quantum chemical calculations at the B3LYP and PBE0 levels, respectively. For the Zn₂(BO)₂ cluster, the linear D_∞h OBZnZnBO is the global minimum, in which the calculated Zn–Zn bond length of r_Zn–Zn = 2.400 Å at the B3LYP level, which appears to be close to the latest recommended covalent radii (2.40 Å) of the proposed single bond covalent radii of the Zn–Zn bond. Chemical bonding analyses show that D_∞h OBZnZnBO possesses a linear four-center two-electron (4c–2e) σ bond. The σ bond framework has a contribution of Zn orbitals 54% and B orbitals 44%, which involve Zn 4s 20% and 4p 34%, and B 2s 28% and 2p 16%, respectively. Furthermore, the D_∞h HZnZnH and NCZnZnCN clusters also exhibit one linear 4c–2e σ bond due to the secondary contribution from the H s and C sp components, respectively. The linear 4c–2e σ bond greatly stabilizes the dizinc complexes. D_∞h OBZnZnBO is thermochemically stable with respect to the possible formation channel at room temperature, whereas the formation energy of the exergonic channel, 2ZnBO (C_∞v, ²Σ_g) → OBZnZnBO (D_∞h, ¹Σ_g), is evaluated to be −58.75 kcal mol⁻¹ at the B3LYP level. Thus, D_∞h OBZnZnBO as the first observation of the Zn–Zn covalent bond in zinc complexes with boronyl as ligands may be synthesized in laboratories in the near future.

---

1. Introduction

The chemistry of dizinc complexes began with the discovery of Zn₂X₂ in 1967, which gave evidence for the existence of the Zn–Zn bond.^1,2 The Zn–Zn bond as one of the metal-to-metal bonds in clusters and molecules is of fundamental interest in many areas of natural science. About 30 years later, the linear dizinc dihydride Zn₂H₂ was investigated both experimentally and theoretically.^3,4 Then, activities in this area have increased enormously in a few years since the determination of the structure of this molecule. Numerous theoretical studies have been devoted to investigating the electronic, structural, and spectroscopic properties of this molecule and related compounds, and new metal–metal coordination and organometallic compounds of zinc, cadmium, and mercury have been synthesized and structurally characterized. In 2004, the first stable compound decamethyl dizincocene [Cp*ZnZnCp*] that contained a Zn–Zn covalent bond was reported by Carmona and co-workers.⁵ After this finding, the Carmona group^5–9 and others^10–12 expanded the number of well-characterized complexes containing the, until then unidentified, Zn–Zn bond.¹³ Recently, some dizinc complexes with cyanides as inorganic ligands, such as NCZnZnCN and CNZnZnNC, were produced through cyanogen diluted in argon reacting with laser-ablated Zn atoms.¹⁴

Apparently, the Zn–Zn covalent bond can be stabilized not only by organic ligands, but also by inorganic ligands represented by H, Cl, and CN. The isolable relationship between the BO radical (boronyl) and H atom, which can both be considered as monovalent σ ligands, has been established by recent experimental and theoretical data.^15–20 Furthermore, boronyl (BO) possesses a strong triple bond between boron and oxygen, with BO/BO⁻ being isovalent to CN/CN⁻ and CO. Neutral boronyl can be viewed as a σ radical and has been found in boronyl metal complexes.^21,22 Novel boronyl species with metal-to-metal bonds may emerge during the pursuit in this direction. In the current contribution, we have performed a density functional theory (DFT) investigation of the structural, electronic, and bonding properties of the series of zinc complexes with boronyl as ligands. Detailed MO analyses reveal a linear 4c–2e σ bond in D_∞h OBZnZnBO. The 4c–2e σ bond is also observed in the D_∞h HZnZnH and NCZnZnCN clusters due to the secondary contribution from the H s and C sp components, respectively.

2. Computational methods

Geometries of a series of zinc complexes Zn_x(BO)_y (x = 1,2; y = 1,2) with boronyl as ligands were optimized at the B3LYP/aug-cc-pVTZ^23,24 and PBE0/aug-cc-pVTZ²⁵ levels using the Gaussian 16 software package.²⁶ The Stuttgart relativistic small core basis set and an effective core potential (Stuttgart RSC1997 ECP)²⁷ were employed for Zn. Global structural search for Zn₂(BO)₂ neutral clusters was conducted using the Molclus 1.9 program,²⁸ as well as aided by manual structural constructions according to the previous investigations of other similar clusters in references. The final confirmation of the global minimum was obtained by the single-point energies from the CCSD(T) method^29–32 at the B3LYP geometries. Born–Oppenheimer molecular dynamics (BOMD) simulations for D_∞h OBZnZnBO were performed at 300, 500, and 900 K, respectively, for 30 ps to check the dynamic behaviors using the software suite CP2K.^33,34 The NBO 5.0 program³⁵ was used to calculate the natural atomic charges. The nature of the Zn–Zn bond was analyzed using canonical molecular orbital (CMO) analyses and adaptive natural density partitioning (AdNDP).³⁶ To unveil the nature of the Zn–Zn bond in the systems studied, the atoms-in-molecules (AIM) topological analysis³⁷ and electron localization function (ELF)³⁸ analysis were carried out using the Multiwfn package³⁹ based on the wavefunctions generated at the B3LYP/aug-cc-pVTZ level.

3. Results

3.1. The chain-like structures of a series of zinc complexes with boronyl as ligands

In order to test the rationality of the method and basis set, the first stable compound decamethyldizincocene, Zn₂(5-C₅Me₅)₂ or denoted as [Cp*ZnZnCp*], the recently discovered dizinc complex NCZnZnCN with cyanides as inorganic ligands¹⁴ and the simplest known ligand dizinc molecule HZnZnH¹⁰ are optimized at different levels of theory. The geometrical parameters of these complexes using the B3LYP method with different basis sets are summarized in Table S1 (ESI†). It is indicated that for [Cp*ZnZnCp*], the calculated Zn–Zn bond distance of 2.306 Å using the Stuttgart relativistic small core basis set and an effective core potential (Stuttgart RSC1997 ECP) for Zn is in good agreement with the experimental value of 2.305(±3) Å from X-ray diffraction methods.⁵ Notably, the calculated (C₅Me₅)_center–Zn–Zn angle of 178.9° is also in excellent agreement with the average experimental value of 177.4(1)°. The B3LYP calculations (Table S2, ESI†) predict the NCZnZnCN and HZnZnH frequencies at 2275.1 and 1844.9 cm⁻¹ or 79.1 (3.6%) and 95.1 (5.4%) higher than the experimental values,^4,14 respectively, which are near the agreement between such DFT calculated and observed frequencies.^40–42 The above comparison and several research studies of boron oxide clusters^43,44 all proved the reliability of the method and the basis set chosen. In the following, we will mainly discuss the B3LYP results.

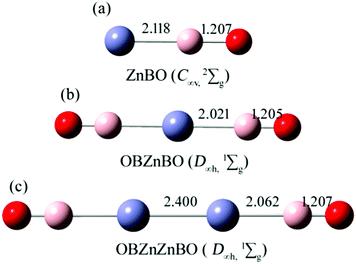
Fig. 1 shows the B3LYP computed bond lengths for the series of zinc complexes Zn_x(BO)_y (x = 1,2; y = 1,2) with boronyl as ligands. As shown in Fig. 1, the global minimum structure of the OBZnZnBO cluster is D_∞h (¹Σ_g). Alternative optimized low-lying structures are presented in the ESI,† (Fig. S1). The linear D_∞h OBZnZnBO appears well-defined on the potential energy surface, being at least 0.85 eV more stable than its rivals at single-point CCSD(T). The calculated bond length of Zn–Zn, Zn–B, and B–O in D_∞h OBZnZnBO are 2.400, 2.062, and 1.207 Å, respectively. The Zn–Zn bond distance in D_∞h OBZnZnBO (2.400 Å) is equal to the latest recommended covalent radii (2.40 Å)⁴⁵ of the proposed single bond covalent radii of the Zn–Zn. The B≡O bond distances in C_∞v ZnBO, D_∞h OBZnBO, and D_∞h OBZnZnBO are calculated to be r_B–O = 1.207, 1.205, and 1.207 Å, respectively, similar to r_B–O = 1.20 Å in a free BO radical,²¹ which indicates that the structural integrity of boronyl groups is well preserved.

Fig. 1 Optimized structures of (a) ZnBO (C_∞v, ²Σ_g), (b) OBZnBO (D_∞h, ¹Σ_g), and (c) OBZnZnBO (D_∞h, ¹Σ_g) at the B3LYP/aug-cc-pVTZ level. Bond distances are labeled in Å. Red color represents the O atoms, pink the B atoms, and purple the Zn atoms.

The minimum vibrational frequency at the B3LYP level is 38.95 cm⁻¹ due to the out-of-plane bending of terminal BO groups. This is comparable to that of 38.91 cm⁻¹ at the PBE0 level. The two levels of theory thus concertedly confirm D_∞h OBZnZnBO as a true minimum. In terms of electronic properties, the energy gap between the highest occupied and lowest unoccupied MOs is 4.53 eV (see Table 1). The NBO analysis shows that the Zn in D_∞h OBZnZnBO carries a charge of +0.385 |e|, suggesting that the Zn–Zn bond is more covalent. In line with the above natural charges, the calculated WBI for the Zn–Zn bond in D_∞h OBZnZnBO amounts to 0.425.

Table 1 Calculated Wiberg bond indices (WBIs), natural atomic charges (q, in |e|), and the HOMO–LUMO energy gap (gap, in eV) of the OBZnZnBO (D_∞h, ¹Σ_g) cluster at the B3LYP level. Also tabulated for comparison are those of isovalent D_∞h HZnZnH, and D_∞h NCZnZnCN clusters

Species	Bond	WBI	Atom	q	Gap
D ∞h OBZnZnBO	Zn–Zn	0.425	Zn	+0.385	4.53
	Zn–B	0.359	B	+0.429
	B–O	1.908	O	−0.814
D ∞h HZnZnH	Zn–Zn	0.464	Zn	+0.443	4.39
	Zn–H	0.373	H	−0.443
D ∞h NCZnZnCN	Zn–Zn	0.589	Zn	+0.606	5.51
	Zn–C	0.273	C	−0.270
	C–N	2.981	N	−0.336

---

3.2. Thermodynamic and kinetic stabilities

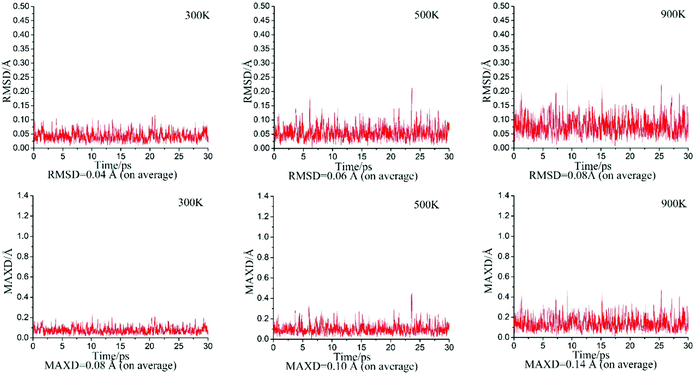
To assess the dynamic stability of D_∞h OBZnZnBO, we performed BOMD simulations⁴⁶ at the PBE0 level, for 30 ps at the selected temperatures of 300, 500, and 900 K. The calculated root-mean-square deviations (RMSDs) and maximum bond distance deviations (MAXDs) are plotted in Fig. 2. The average RMSDs are quite small (from 0.04 to 0.08 Å), indicating that the D_∞h OBZnZnBO cluster has excellent kinetic stabilities, being robust against isomerization and decomposition.

Fig. 2 Born–Oppenheimer molecular dynamics (BOMD) simulations for the OBZnZnBO (D_∞h, ¹Σ_g) cluster at selected temperatures of 300, 500, and 900 K. Root-mean-square deviations (RMSDs; in Å) and maximum bond distance deviations (MAXDs; in Å) are plotted against time (in ps).

Early studies suggested that the dizinc dihydride linear HZnZnH cluster can be obtained by ZnH dimerization.³ It is valuable to calculate the formation energy of the D_∞h OBZnZnBO cluster using linear ZnBO as reactants, according to the equation: 2ZnBO (C_∞v, ²Σ_g) → OBZnZnBO (D_∞h, ¹Σ_g), based on the H/BO analogy. The formation energy evaluated is −58.75 kcal mol⁻¹ at the B3LYP level, similar to the formation energy of −58.9 kcal mol⁻¹ for linear HZnZnH,³ suggesting that the formation of D_∞h OBZnZnBO is highly exothermic. Again, the observation is no surprise. We anticipate that D_∞h OBZnZnBO may be obtained in future laboratories.

4. Discussion

4.1. Four-center two-electron σ bond in linear D_∞h OBZnZnBO

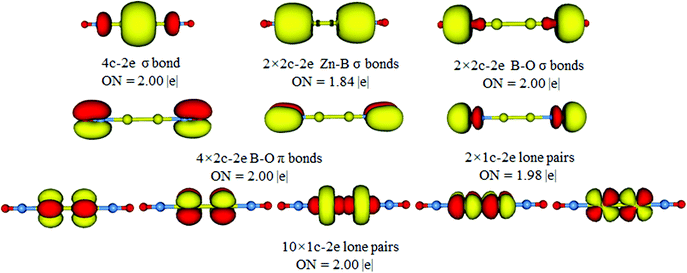
Chemical bonding dictates cluster structures and CMO analysis is of fundamental importance in understanding a molecular system. The D_∞h OBZnZnBO cluster has 42 valence electrons. All the occupied CMOs are depicted in Fig. 3 and sorted into four categories. The subset (a) has five CMOs, which are composed of Zn 4s and 4p, B 2s and 2p orbitals, and O 2p atomic orbitals (AOs). These CMOs are primarily responsible for Zn–Zn, Zn–B, and B–O σ bonding along the linear chain, respectively (Table 2). The HOMO (the highest occupied molecular orbital) is localized mainly in the B–Zn–Zn–B σ bonding region with some localized σ bonding characters. The localized σ bond framework has a contribution of Zn orbitals 54% and B orbitals 44%, which involve Zn 4s 20% and 4p 34%, and B 2s 28% and 2p 16%, respectively. It is not surprising that the localized σ bonding character also had been found to exist in the well-known [Cp*ZnZnCp*]⁵ by the Carmona group,⁶ in which, the contribution of Zn orbitals is close to 60%. HOMO−3 and HOMO−4 describe σ bonding mainly with the in-phase and out-of-phase combinations of Zn/B lobes, whereas the HOMO−5 and HOMO−6 correlate with the B–O σ bonding orbitals.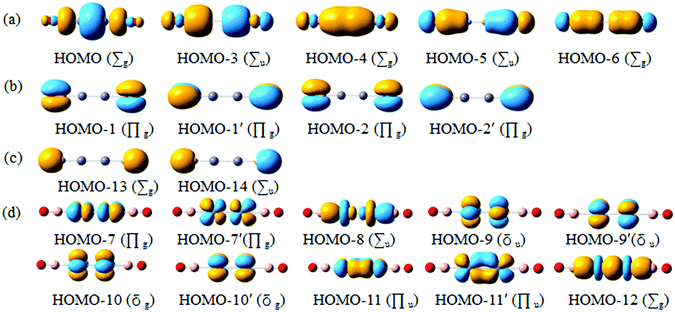

Fig. 3 Pictures of occupied canonical molecular orbitals (CMOs) for the D_∞h OBZnZnBO cluster. (a) σ bonds. (b) π bonds. (c) Two O 2s lone-pairs. (d) Two Zn 3d lone-pairs.

Subset (b) has four CMOs that are composed of B 2p and O 2p AOs. They are attributed to four B–O π bonds. For the B–O π bonds, each of them has a contribution of O orbital close to 81%, with only a small contribution from the B orbitals (about 19%). The two CMOs in subset (c) can be recombined to recover two O 2s lone-pairs, one for each O atom. The above bonding elements collectively consume 22 electrons. The remaining 20 electrons in the D_∞h OBZnZnBO cluster form π/δ frameworks. Subset (d) has ten CMOs, which are derived from Zn 3d.

The above bonding picture can be reproduced via AdNDP analysis. As presented in Fig. 4, all bonding elements are straightforward and easy to comprehend: one 4c–2e σ bond, two Zn–B σ bonds, two B–O σ bonds, four B–O π bonds, two O 2s lone-pairs, and ten Zn 3d lone-pairs. All occupation numbers (ONs) are close to ideal. Obviously, the D_∞h OBZnZnBO cluster possesses a 4c–2e σ bond as confirmed by the AdNDP data. The delocalized framework is treated as a 4c–2e B–Zn–Zn–B σ bond, which gives an ON of 2.00 |e|, probably due to the recombination of the HOMO with HOMO−3. The AdDNP analysis shows that the σ framework is truly delocalized along the B–Zn–Zn–B line and mainly on Zn–Zn. Thus, the calculated WBIs for Zn–Zn is 0.425, whereas those for Zn–B are 0.359 (Table 1).

Fig. 4 AdNDP bonding pattern for the OBZnZnBO (D_∞h, ¹Σ_g) cluster.

To further prove the rationality of the 4c–2e σ bond in D_∞h OBZnZnBO, we performed related AdNDP analysis based on the 2c–2e Zn–Zn bond. The results are given in Fig. S3 (ESI†). The ON value for the 2c–2e Zn–Zn bond is 1.40, which is much smaller than 2.00. In comparison, the ON value for the 4c–2e σ bond is 2.00 (Fig. 4). These results show that the 4c–2e σ bond may be a more reasonable interpretation.

4.2. Four-center two-electron σ bond in linear D_∞h HZnZnH and NCZn–ZnCN? Comparison of D_∞h HZnZnH and NCZn–ZnCN with D_∞h OBZnZnBO

In previous studies, linear HZn–ZnH and NCZn–ZnCN have only been characterized by the existence of Zn–Zn covalent bonds.^3,4,14 The optimized structures of HZn–ZnH (D_∞h, ¹Σ_g) and NCZn–ZnCN (D_∞h, ¹Σ_g) at the B3LYP/aug-cc-pVTZ level are shown in Fig. 5. The Zn–Zn bond distances of 2.414 Å in HZn–ZnH and 2.351 Å in NCZn–ZnCN are similar to that in linear OBZnZnBO (2.400 Å). According to the latest recommended covalent radii,⁴⁵ the Zn–Zn bonds in HZn–ZnH and NCZn–ZnCN are all close to a single bond. The calculated WBIs for Zn–Zn are 0.464 in HZn–ZnH and 0.589 in NCZn–ZnCN, respectively, in line with the bond distance (Table 1). The calculated HOMO–LUMO energy gap for HZn–ZnH is 4.39 eV, which is smaller than that for OBZnZnBO, whereas for NCZn–ZnCN, it is 5.51 eV, which is larger than that for OBZnZnBO.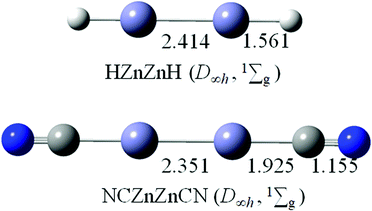

Fig. 5 Optimized structures of HZnZnH (D_∞h, ¹Σ_g) and NCZnZnCN (D_∞h, ¹Σ_g) at the B3LYP/aug-cc-pVTZ level. Bond distances are labeled in Å.

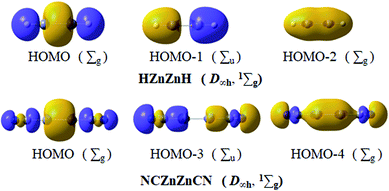
Based on the above assessment, linear HZn–ZnH and NCZn–ZnCN, as two typical inorganic dizinc complexes, should have essentially the same bonding pattern as D_∞h OBZnZnBO (¹Σ_g). Remarkably but not surprisingly, in Fig. 6, the key MOs of HZn–ZnH and NCZn–ZnCN show one-to-one correspondence to those of OBZnZnBO (Fig. 3a). For HZn–ZnH, HOMO−1 and HOMO−2 describe σ bonding mainly with the in-phase and out-of-phase combinations of Zn/H lobes. The HOMO can be formally viewed as a linear 4c–2e σ bond. The localized σ bond framework has a contribution of Zn orbitals 50%, H orbitals 50%, which involve Zn 4s 18% and 4p 32%, and H 1s 50%, respectively. The calculated Zn–Zn bond order is 0.464. Based on the similarity between CN and BO, in NCZn–ZnCN, HOMO−3 and HOMO−4 describe σ bonding mainly with the in-phase and out-of-phase combinations of Zn/C lobes. The HOMO can be treated as a 4c–2e C–Zn–Zn–C σ bond due to the Zn component (total 61%, 34% Zn 4s and 27% Zn 4p) and C component (total 24%, 11% C 2s and 13% C 2p). At the same level, the Zn–Zn calculated bond order is 0.589. So the linear 4c–2e σ bond is popular in dizinc complexes, such as the previously reported HZn–ZnH and NCZn–ZnCN and the newly presented OBZnZnBO.

Fig. 6 Key molecular orbitals (MOs) of HZnZnH (D_∞h, ¹Σ_g) and NCZnZnCN (D_∞h, ¹Σ_g).

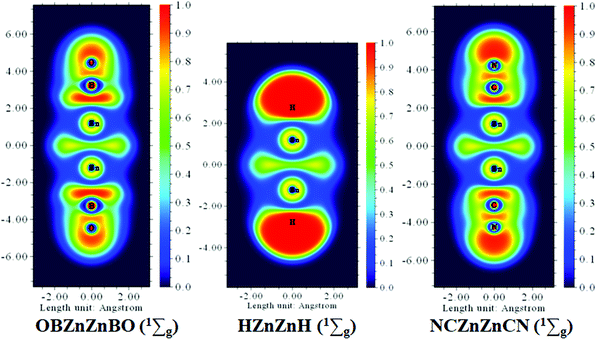
BO as a monovalent σ ligand is known to have less ability to accept electrons and hence weaker coordination than its isovalent body CN. To gain a deeper understanding of the electronic structure characteristics of the Zn–Zn bonds in Zn₂H₂, Zn₂(CN)₂, and Zn₂(BO)₂ molecules, the color-filled maps of the ELF are given in Fig. 7. It is shown that the characteristics of the ELF patterns are similar for the three systems, and the electron localization between the two zinc atoms is prominent, which clearly reveals the fact that the Zn–Zn covalent bonds exist in the present three systems.

Fig. 7 Comparison of ELF analysis for D_∞h OBZnZnBO, HZnZnH, and NCZnZnCN clusters.

Table 2 Composition analysis for selected canonical molecular orbitals (CMOs) of OBZnZnBO (D_∞h, ¹Σ_g), D_∞h HZnZnH, and D_∞h NCZnZnCN clusters

Species	CMO	Zn (%)			Total	B/H/C (%)	O/N
		4s	p	3d		s/p/total	s/p/total
a For D∞h HZnZnH and D∞h NCZnZnCN, the p orbital stands for 5p; for D∞h OBZnZnBO, the p orbital stands for 4p.
D ∞h OBZnZnBO	HOMO	9.61	16.62	—	26.51	13.88/8.07/22.00	—/1.24/1.24
	HOMO−3	14.54	1.84	0.98	17.64	10.61/11.55/22.18	0.56/9.32/9.89
	HOMO−4	25.22	0.12	1.58	27.44	3.31/5.73/8.86	1.07/12.38/13.46
	HOMO−5	2.84	0.40	0.86	4.17	6.69/0.54/7.53	4.68/32.97/37.71
	HOMO−6	6.48	0.15	1.39	8.18	7.05/0.81/8.17	4.18/28.88/33.12
	HOMO−11	—	—	49.83	49.85	—/0.13/0.13	—
	HOMO−11′	—	—	49.83	49.85	—/0.13/0.13	—
	HOMO−12	—	—	49.90	49.93	0.02/0.02/0.04	—
D ∞h HZnZnH	HOMO	8.60	16.30	0.19	25.14	24.73/—/24.73	—
	HOMO−1	16.81	1.65	1.36	20.29	29.55/—/29.55	—
	HOMO−2	32.94	0.23	2.53	36.55	13.36/—/13.36	—
	HOMO−4			47.90	47.95	2.00/—/2.00	—
	HOMO−7			50.00	50.00	—	—
	HOMO−7′			50.00	50.00	—	—
	HOMO−9	0.95		47.07	48.13	1.83/—/1.83	—
D ∞h NCZnZnCN	HOMO	17.06	13.29	0.10	30.69	5.43/6.69/12.14	1.24/5.41/6.66
	HOMO−3	3.19	0.80	0.35	4.42	0.58/5.79/6.38	10.41/27.69/38.22
	HOMO−4	12.93	0.78	0.35	14.30	1.87/0.06/1.96	9.67/23.23/33.03
	HOMO−5	7.16	0.88	10.20	18.49	11.96/10.16/22.29	4.19/4.57/8.86
	HOMO−6	9.52	0.44	9.05	19.36	11.74/10.37/22.28	3.89/4.08/8.05
	HOMO−10	—	—	49.60	49.63	—/0.33/0.33	—/0.03/0.03
	HOMO−10′	—	—	49.60	49.63	—/0.33/0.33	—/0.03/0.03
	HOMO−12	1.83	—	40.17	42.11	2.90/4.27/7.22	0.47/0.11/0.59

---

In addition, the calculated topological values for AIM are provided in Table 3. The characteristics of bond critical points (BCPs) corresponding to the Zn–Zn bond interaction were analyzed including the electron density (ρ_BCP), the Laplacian of the electron density (▽²ρ_BCP), and the electronic energy density (H_BCP). Both ▽²ρ_BCP > 0 and H_BCP <0 indicate the covalent nature of the Zn–Zn bond in these three clusters. The bond degree (BD),⁴⁷ which is defined as H_BCP/ρ_BCP, is also calculated and listed in Table 3. The values of BD suggest that the strength of the Zn–Zn covalent bond follows the order of NCZn–ZnCN > OBZnZnBO ≈ HZn–ZnH, with the Zn–Zn bond in OBZnZnBO only slightly stronger than that in HZn–ZnH.

Table 3 Calculated AIM topological parameters of Zn–Zn BCP and the intrinsic bond strength index (IBSI) for the OBZnZnBO (D_∞h, ¹Σ_g) cluster at the B3LYP/aug-cc-pVTZ level. Also tabulated for comparison are those of isovalent D_∞h HZnZnH, and D_∞h NCZnZnCN clusters

Species	ρ(BCP)	▽^2ρ(BCP)	H(BCP)	H(BCP)/ρ(BCP)	IBSI
Zn2H2	0.0641	0.0023	−0.0236	−0.3689	0.201
Zn2(CN)2	0.0701	0.0067	−0.0277	−0.3946	0.223
Zn2(BO)2	0.0657	0.0021	−0.0247	−0.3761	0.206

---

The intrinsic bond strength index (IBSI), first proposed by Klein et al.,⁴⁸ is also an efficient way to qualify the strength of chemical bonds. Here, to confirm the relative strength of the Zn–Zn bond, we have estimated their IBSI values at the B3LYP/aug-cc-pVTZ level. The calculated IBSI values of the Zn–Zn bond corresponding to HZn–ZnH, NCZn–ZnCN, and OBZnZnBO are 0.201, 0.223, and 0.206, respectively, which suggests a rough order of Zn–Zn in linear series as follows: NCZn–ZnCN > OBZnZnBO ≈ HZn–ZnH. This is also consistent with the above calculated Zn–Zn bond distance and WBIs results, as well as the calculated electron density at Zn–Zn BCPs shown in Table 3.

4.3. Predicted electronic and vibrational properties of the D_∞h OBZnZnBO cluster

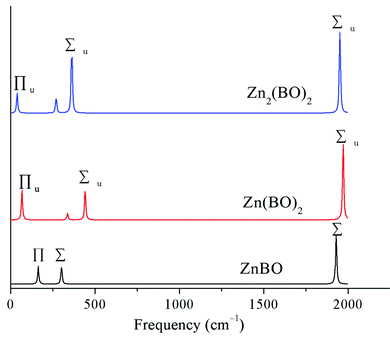
To aid the future experimental characterization studies of the D_∞h OBZnZnBO cluster, the electronic and vibrational properties were calculated. The vertical electron affinity (VEA) of the D_∞h OBZnZnBO cluster is calculated to be 1.39 and 1.24 eV at the B3LYP and single-point CCSD(T) levels, respectively. The latter value is considered more reliable, which is substantially greater than that of the D_∞h HZnZnH cluster (0.31 eV at B3LYP; 0.19 eV at single-point CCSD(T)), suggesting that D_∞h OBZnZnBO is a relatively stable species.

The infrared (IR) spectra of the series of zinc complexes Zn_x(BO)_y (x = 1,2; y = 1,2) with boronyl as ligands were simulated based on the B3LYP/aug-cc-pVTZ calculations, as shown in Fig. 8. The IR spectra are similar to each other for the three species, except for a spectral shift. Two IR-active stretching modes are observed in D_∞h OBZnZnBO at 1951 and 362 cm⁻¹, together with a weaker IR-active, out-of-plane bending mode of symmetry Π_u (38 cm⁻¹). Notably, relative to the free BO radical (1912 cm⁻¹), the vibrational frequency of OBZnZnBO (1951 cm⁻¹) is blue-shifted, making the OBZnZnBO complex a “nonclassical” boronyl species? If so, what causes the blue shift in D_∞h OBZnZnBO? Lupinetti et al. suggested that an electrostatic orbital polarization effect is responsible for the C–O blue-shift when a proton or positive charge attaches to the carbon end of CO.⁴⁶ Moreover, this view was proved to be applicable to Au⁺(CO)_n “nonclassical” carbonyl species.⁴⁷ Does this view apply to OBZnZnBO since BO⁻ is isovalent to CO? The calculated natural atomic charges (Table 1) can give us some useful information. As tabulated, the BO, B, O, and Zn in D_∞h OBZnZnBO carries −0.385, +0.429, −0.814, and +0.385 |e|, respectively. In the isolated BO, B carries +0.880 |e|. That is, in the isolated BO, the bonding orbitals in the valence shell have more electron density on the oxygen, and are thus unbalanced, which limits the effectiveness of the binding. Clearly, the attachment of Zn on the boron end of BO induces polarization that effectively balances the orbital density on both atoms, thus enhancing the binding. It is the effect that is generally attributed to causing the B–O to reach higher frequencies in D_∞h OBZnZnBO. Thus, the boronyl stretch in the series of zinc complexes Zn_x(BO)_y (x = 1,2; y = 1,2) is blue-shifted 25–60 cm⁻¹ with respect to the free BO vibration, providing evidence that these species are so-called “nonclassical” boronyl species.

Fig. 8 Simulated infrared spectra of ZnBO, Zn(BO)₂, and Zn₂(BO)₂.

5. Conclusions

In conclusion, a detailed theoretical investigation of the structural, electronic, and bonding properties of dizinc complexes with boronyl as ligands has been performed. For the linear D_∞h OBZnZnBO as the global minimum, the calculated Zn–Zn bond length of rZn–Zn = 2.400 Å at the B3LYP level, which is close to the latest recommended covalent radii (2.40 Å) of the proposed single bond covalent radii of the Zn–Zn. Chemical bonding analyses show that D_∞h OBZnZnBO possesses a linear four-center two-electron (4c–2e) σ bond. The σ bond framework has a contribution of Zn orbitals 54% and B orbitals 44%, respectively. Furthermore, the present bond concept can be applicable to D_∞h HZnZnH and NCZnZnCN, which also exhibit a linear 4c–2e σ bond due to the secondary contribution from the H s and C sp components, respectively. D_∞h OBZnZnBO is thermochemically stable with respect to possible formation channels at room temperature. Thus, D_∞h OBZnZnBO as the first observation of the Zn–Zn covalent bond in zinc complexes with boronyl as ligands may be synthesized in laboratories in the near future.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Natural Science Foundation of Shandong Province (ZR2017MB023). The authors thank Prof. Hua-Jin Zhai for the fruitful discussion and helpful suggestions.

References

1. D. H. Kerridge, J. Chem. Soc., 1963, 1178–1181,  10.1039/JR9630001178,.
2. D. H. Kerridge and S. A. Tariq, J. Chem. Soc. A, 1967, 1122–1125,  10.1039/J19670001122,.
3. T. M. Greene, W. Brown, L. Andrews, A. J. Downs, G. V. Chertihin, N. Runeberg and P. Pyykko, J. Phys. Chem., 1995, 99, 7925–7934.
4. X. F. Wang and L. Andrews, J. Phys. Chem. A, 2004, 108, 11006–11013.
5. I. Resa, E. Carmona, E. Gutierrez-Puebla and A. Monge, Science, 2004, 305, 1136–1138.
6. D. del Rio, A. Galindo, I. Resa and E. Carmona, Angew. Chem., Int. Ed., 2005, 44, 1244–1247.
7. A. Grirrane, I. Resa, A. Rodriguez, E. Carmona, E. Alvarez, E. Gutierrez-Puebla, A. Monge, A. Galindo, D. del Rio and R. A. Andersen, J. Am. Chem. Soc., 2007, 129, 693–703.
8. J. F. Van der Maelen, E. Gutierrez-Puebla, A. Monge, S. Garcia-Granda, I. Resa, E. Carmona, M. T. Fernandez-Diaz, G. J. McLntyre, P. Pattison and H. P. Weber, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2007, 63, 862–868.
9. D. del Rio, I. Resa, A. Rodriguez, L. Sanchez, R. Koppe, A. J. Downs, C. Y. Tang and E. Carmona, J. Phys. Chem. A, 2008, 112, 10516–10525.
10. Z. Zhu, R. J. Wright, M. M. Olmstead, E. Rivard, M. Brynda and P. P. Power, Angew. Chem., Int. Ed., 2006, 45, 5807–5810.
11. Z. Zhu, M. Brynda, R. J. Wright, R. C. Fischer, W. A. Merrill, E. Rivard, R. Wolf, J. C. Fettinger, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 2007, 129, 10847–10857.
12. I. L. Fedushkin, A. A. Skatova, S. Y. Ketkov, O. V. Eremenko, A. V. Piskunov and G. K. Fukin, Angew. Chem., Int. Ed., 2007, 46, 4302–4305.
13. E. Carmona and A. Galindo, Angew. Chem., Int. Ed., 2008, 47, 6526–6536.
14. L. Andrews and H. G. Cho, Angew. Chem., Int. Ed., 2020, 59, 2496–2504.
15. H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2007, 129, 9254–9255.
16. S. D. Li, H. J. Zhai and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 2573–2579.
17. H. J. Zhai, C. Q. Miao, S. D. Li and L. S. Wang, J. Phys. Chem. A, 2010, 114, 12155–12161.
18. H. J. Zhai, J. C. Guo, S. D. Li and L. S. Wang, ChemPhysChem, 2011, 12, 2549–2553.
19. H. Bai, H. J. Zhai, S. D. Li and L. S. Wang, Phys. Chem. Chem. Phys., 2013, 15, 9646–9653.
20. D. Z. Li, H. Bai, Q. Chen, H. G. Lu, H. J. Zhai and S. D. Li, J. Chem. Phys., 2013, 138, 8.
21. D. Y. Zubarev, A. I. Boldyrev, J. Li, H. J. Zhai and L. S. Wang, J. Phys. Chem. A, 2007, 111, 1648–1658.
22. T. Jian, G. V. Lopez and L. S. Wang, J. Phys. Chem. B, 2016, 120, 1635–1640.
23. R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
24. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
25. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision. A.03, Gaussian Inc., Wallingford, CT, 2016.
27. Stuttgart RSC 1997 ECP basis sets used in this work and the related references therein can be obtained at https://bse.pnl.gov/bse/portal.
28. T. Lu, Molclus program, Version 1.9.5, http://www.keinsci.com/research/molclus.html.
29. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
30. G. E. Scuseria and H. F. Schaefer III, J. Chem. Phys., 1989, 90, 3700–3703.
31. G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, J. Chem. Phys., 1988, 89, 7382–7387.
32. J. Čížek, Adv. Chem. Phys., 1969, 35–89,  DOI:10.1002/9780470143599.ch2.
33. The CP2K developers group, see http://cp2k.berlios.de/.
34. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
35. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001.
36. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
37. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
38. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
39. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
40. Y. Gong, L. Andrews, B. K. Liebov, Z. Fang, E. B. Garner III and D. A. Dixon, Chem. Commun., 2015, 51, 3899–3902.
41. X. Chen, Q. Li, Y. Gong, L. Andrews, B. K. Liebov, Z. Fang and D. A. Dixon, Inorg. Chem., 2017, 56, 5060–5068.
42. X. Chen, Q. Li, L. Andrews and Y. Gong, J. Phys. Chem. A, 2018, 122, 7099–7106.
43. W. J. Tian, L. J. Zhao, Q. Chen, T. Ou, H. G. Xu, W. J. Zheng, H. J. Zhai and S. D. Li, J. Chem. Phys., 2015, 142, 134305.
44. D. Z. Li, L. Y. Feng, L. Pei, M. Z. Song, L. J. Zhang, H. Wang and H. J. Zhai, Int. J. Quantum Chem., 2019, 119, e25907.
45. P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337.
46. J. M. Millam, V. r. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, J. Chem. Phys., 1999, 111, 3800–3805.
47. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
48. J. Klein, H. Khartabil, J.-C. Boisson, J. Contreras-García, J.-P. Piquemal and E. Hénon, J. Phys. Chem. A, 2020, 124, 1850–1860.

---

Footnote

† Electronic supplementary information (ESI) available: Typical low-lying isomers of Zn₂(BO)₂ (Fig. S1); representation of the key molecular orbitals (CMOs) of OBZnZnBO (D_∞h, ¹∑_g), D_∞h HZnZnH, and D_∞h NCZnZnCN from DFT calculations (Fig. S2); AdNDP bonding pattern for the OBZnZnBO (D_∞h, ¹∑_g) cluster based on the 2c–2e Zn–Zn bond (Fig. S3); the calculated bond length of compounds containing the Zn–Zn bond using different basis sets with the B3LYP method (Table S1); the calculated frequencies, intensities and bond lengths for zinc complexes with boronyl as ligands, and D_∞h HZnZnH and NCZnZnCN clusters (Table S2). See DOI: 10.1039/d1cp03920b

---