Ion migration mechanism in all-inorganic Ruddlesden–Popper lead halide perovskites by first-principles calculations†
Shuai
Zhao
 *ab and
Li
Xiao
*ab
*ab and
Li
Xiao
*ab
aSchool of Science, Chongqing University of Technology, Chongqing 400054, P. R. China. E-mail: zhaoshuai@cqut.edu.cn; xiaoli@cqut.edu.cn
bChongqing Key Laboratory of Green Energy Materials Technology and Systems, Chongqing 400054, P. R. China
First published on 7th December 2021
Abstract
Ion migration under light illumination or electric field could cause several complex phenomena, such as hysteresis, phase segregation, and interface passivation, in optoelectronic devices based on hybrid organic–inorganic perovskites. The high ionic conductivity of metal halide perovskites can be ascribed to the lower migration barrier of halide anions, which has been demonstrated to be inhibited by the large organic layer of two-dimensional perovskite structures. However, in all-inorganic two-dimensional perovskites, the diffusion mechanism of halide anions has not been comprehensively studied. Herein, we investigate the diffusion mechanism of halide anions in all-inorganic Ruddlesden–Popper (RP) halide perovskites by first-principles calculations. In these all-inorganic perovskites, the inorganic CsI layer can also prevent halide diffusion between the adjacent octahedral slabs via the vacancy-hopping mechanism. However, intercalation provides an additional diffusion channel for halide interstitials, which promote in-plane diffusion in RP perovskites. These results reveal the migration properties of halide vacancies and interstitials in all-inorganic RP perovskites, which would be beneficial for exploring their novel optoelectronic applications.
1. Introduction
Organic–inorganic hybrid perovskite solar cells have experienced high-speed development in the past decade.1,2 However, low stability is still an obstacle to their large-scale commercialization.3 The degradation of hybrid perovskites can occur via two mechanisms: one is the hydration and oxidization induced by moisture or oxygen, and the other is the lattice decomposition driven by ion migration.4,5 The former degradation mechanism has been ascribed to unstable organic components, which can be solved by device encapsulation or replacing organic components with inorganic monovalent cations.6 Light-enhanced ion migration is an intrinsic phenomenon and has attracted much attention for halide perovskites. For instance, anomalous current–voltage hysteresis caused by ion migration has been observed in organic–inorganic hybrid and all-inorganic halide perovskite solar cells.7 Other investigations claim that ion migration could drive self-passivation in halide perovskites and is thus beneficial for improving stability.8,9 Moreover, the resistive switching phenomenon of organic–inorganic halide perovskites has been exploited by halide migration, suggesting potential applications in resistive switching random access memory.10–12Ion migration has been proved to be mitigated in 2D perovskite structures owing to the unconnected octahedral slabs by incorporating large organic cations, such as butylammonium.13 The additional large organic layer improves the stability of 2D halide perovskite by suppressing not only the migration of intrinsic ions but also the penetration of moisture due to large hydrophobic organic cations.14 However, the quantum confinement effect resulting from the large organic layer enhances the exciton binding energy and the rate of charge recombination. To diminish the quantum confinement effect, conventional small organic cations have been developed to create organic layer in 2D halide perovskites (e.g., MA2PbI4), which have been demonstrated to possess reduced exciton binding energy and excellent conversion efficiency.15,16 Previous investigations reported the relatively low migration barrier of A-site MA cation in 3D MAPbI3 due to the protonizing effect of organic cations under illumination and electric fields.17 Inorganic cations are not facile to protonize, leading to unchanged activation energy in the dark and under illumination. Therefore, the optoelectronic properties of all-inorganic layered halide perovskites should be explored.
All-inorganic mixed-halide Ruddlesden–Popper (RP) perovskite Cs2PbI2Cl2 has been synthesized by solid-state method and exhibits markedly ambient and thermal stability.18–20 Li et al. demonstrated that this compounds shows a direct bandgap of ∼3.04 eV along the in-plane direction and the detection capacity of UV-light or α-particle.18 Pan et al. investigated the thickness dependence of the optoelectronic properties of RP Cs2PbI2Cl2 by theoretical calculations and indicated that this material would be adequate for luminescent rather than photovoltaic devices.21 Xu et al. reported the ultrahigh electron mobility (∼9.39 × 103 cm2 V−1 s−1) for 2D RP Cs2PbI2Cl2, which are higher than those of known halide perovskites.22 Guo et al. found that the photocurrents of all-inorganic 2D RP Cs2PbI2Cl2 can be significantly enhanced over three orders of magnitude when applying 2 GPa, and the lattice compression can also facilitate the dissociation of excitons by reducing the exciton binding energy.23 Given the good lattice matching degree, Yang et al. employed Cs2PbI2Cl2 nanosheets to passivate the interfaces of CsPbI2Br perovskite films and TiO2 films, achieving improved efficiency and stability.24 Moreover, the light-induced photochromism has been observed in 2D RP Cs2PbI2Cl2, which can be used in optical encryption.25 As a new type of all-inorganic perovskite, 2D RP Cs2PbI2Cl2 exhibits promising potential in optoelectronic fields. However, the behavior of ion migration in all-inorganic RP halide perovskites, to the best of our knowledge, is still not available from either experiment or theoretical calculation. Therefore, a comprehensive investigation on ion migration mechanism is significant to the enhancement of long-term stability and exploration of novel optoelectronic applications for metal halide perovskite materials.
Theoretical calculations can provide atomic scale hints for understanding the ion transport properties of perovskite materials. Eames et al. computed the activation energy of various migration of MA, Pb, and I ions in MAPbI3, revealing that the I ion is the major mobile ion with the lowest migration activation energy along the edge of the PbI6 octahedron.26 Yang et al. investigated different diffusion mechanisms of interstitialcy migration versus vacancy-mediated migration in MAPbI3; hence, MA and I ions contribute to the ion diffusion and instability of MAPbI3.27 In this work, we investigate the ion migration properties of inorganic RP Cs2PbI4 and mixed-halide Cs2PbI2Cl2 by first-principles calculations based on density functional theory (DFT). Our results reveal that although the migration of halide anions via vacancy-mediated mechanism is suppressed due to the layered structure, the interstitialcy migration exhibits quite low activation energy in the intercalation, which results in the fast diffusion of halide anions in RP halide perovskites.
2. Computation details
All DFT calculations have been implemented based on the plane-wave approach with the Quantum ESPRESSO package.28 The ultrasoft pseudopotentials with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional are employed to describe valence configurations.29 The kinetic energy cut-off of 40 Ry and the charge density cut-off of 320 Ry are adopted for wave function expansion. The 6 × 6 × 2 Monkhorst–Pack k-mesh grid is used to integrate the Brillouin zone. The lattice parameters including lattice constants and atomic positions are fully relaxed using the Broyden–Fletcher–Goldfarb–Shanno algorithm with the force convergence threshold of 10−3 Ry per Bohr and the energy convergence of 10−4 Ry. For the simulation of ion migration, the 2 × 2 × 1 supercell of the RP perovskite with 3 × 3 × 2 k-mesh grid is employed. The initial and final structures are first applied to conventional geometry optimization with the force cutoff of 10−4 Ry per Bohr and then fixed during migration. The climbing image nudged elastic band (CINEB) method is used to obtain the energy profile of migration images.30 The convergence force is set to 0.05 eV Å−1 during minimum energy pathway optimization, and spring force is employed to ensure the finding of the lowest energy path.31,323. Results and discussion
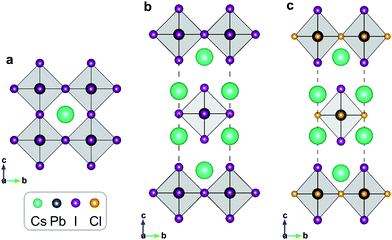
In 3D perovskite ABX3, B-site cations and X-site anions form a corner-shared octahedron skeleton, and A-site cations occupy the octahedron interstice. The 2D RP halide perovskite exhibits a sandwich structure containing octahedral slabs and spacer cations with the general chemical formula An+1BnX3n+1, where n is the layer number of octahedral slabs. The reported RP halide perovskite must employ large organic cation to separate perovskite-like slabs. Therefore, all-inorganic RP halide perovskites are rarely reported due to instability resulting from the relatively small ionic radius of inorganic monovalent cations. The mixed-halide RP perovskite is the only reported structure of all-inorganic layered perovskites that could be synthesized by solid-state method. In this structure, small chloride anions occupy the shared octahedral corner (the 4c Wyckoff site) and the large iodide anions take the out-of-plane octahedral corner (the 4e Wyckoff site). For simplification, we employ a single-layer structure (Fig. 1) to investigate the migration properties of halide anions in 2D RP perovskites.We firstly optimize the lattice parameters of all-inorganic 3D CsPbI3, 2D RP Cs2PbX4 (X = Cl, Br, I), and mixed-halide RP Cs2PbI2Cl2, which are presented in Table S1 (ESI†). The Pb–I bonds are elongated in the c-direction and simultaneously shortened in the ab-plane due to the existence of intercalation. In mixed-halide RP Cs2PbI2Cl2, the lattice constant further decreases to 5.75 Å in the ab-plane due to the smaller ionic radius of Cl, while the lattice constant and Pb–I bond in the c-direction are still close to that of RP Cs2PbI4. Given that the halide anion at the 4c site plays a role in connecting two adjacent octahedra, the hybridization of Pb with halide anion at the 4c site would be stronger than that of Pb with halide anion at the 4e site. Fig. 2 shows the calculated partial density of states for 3D CsPbI3, RP Cs2PbI4, and mixed-halide RP Cs2PbI2Cl2. In 3D CsPbI3, upper valence bands exhibit the antibonding characteristic between Pb 6s and I 5p orbitals, and all iodide anions contribute equally to the ionic interaction of PbI6 octahedron. In RP perovskites, the energy level of I4e 5p orbital is higher than that of I4c 5p orbital. Therefore, the antibonding characteristic of Pb–I4e would be stronger than that of Pb–I4c, leading to the weaker covalence bond between Pb and I4e ions. Moreover, the outer-shell electrons of A-site Cs cations do not contribute to electronic structures near the band edges. Therefore, the bond properties of the octahedron would be significant to the migration of halide anions in RP perovskites.
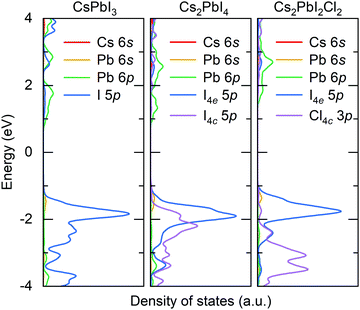 | ||
| Fig. 2 Calculated density of states for cubic CsPbI3, RP Cs2PbI4, and mixed-halide RP Cs2PbI2Cl2. The Fermi energy is set to 0. | ||
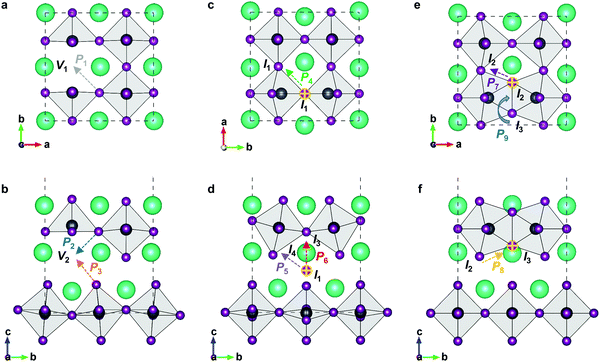
3D perovskite CsPbI3, halide anions mainly diffuse along the octahedral cage, and therefore all diffusion routes are isotropic. In RP perovskites, the removal of one halide ion could respectively create two different vacancies, i.e., V1-type vacancy at the 4c site or V2-type vacancy at the 4e site, which would show different diffusion features (Fig. 3). Moreover, the 4d Wyckoff site (0, 1/2, 1/4) in the intercalation could accommodate one halide ion to form isolated I1-type interstitial. During interstitial defect migration, the halide interstitial could temporarily form a dumbbell-like pair with one original halide ion at the 4c or 4e site. The interstitial correlated to the 4c site is respectively I2-type or I3-type defect in terms of axial direction, and the interstitial correlated to the 4e site forms I4-type defect. All defective structures are fully optimized (Fig. S1, ESI†) and employed as the initial or final states of halide migration.
In 2D RP perovskites, three paths are considered for vacancy-mediated migration: (1) P1 is the migration of the halide ion from the 4c site to the adjacent V1 site; (2) P2 denotes the migration from the 4c site to the adjacent V2 site; (3) P3 represents the migration from the 4e site to the adjacent V2 site. The migration paths are also schematically shown in Fig. 3. For the isolated I1 interstitial, three migration motions exist: (1) direct migration between two adjacent 4d sites (denoted as P4) in the intercalation; (2) the correlated interstitialcy migration between two adjacent 4d sites in the intercalation mediated by the original halide ion at the 4e site;33,34 and (3) correlated migration between two 4d sites separated by the octahedral slab mediated by the original halide ion at the 4c site. The correlated interstitialcy migration denotes that the isolated I1 interstitial migrates onto the neighboring 4e site and kicks the correlated halide ion onto the equilibrium 4d site. The I4 interstitial could serve as the intermediate state of the correlated interstitialcy migration; thus, we simply simulate the symmetrical half path (I1 → I4) of interstitialcy migration, which is denoted as P5. The symmetrical half path from the 4d site toward the 4c site is calculated as P6 migration. In addition, halide interstitials probably diffuse along the edge of octahedron via dumbbell-like motion.35 Thus, we simulated two dumbbell-like migrations between in-plane 4c sites denoted as P7 and from the 4c to the adjacent 4e site denoted as P8. Given that two species of halide interstitials are correlated to the 4c site, we also simulate the rotation mechanism P9 for the transformation between I2 and I3 interstitials.36 Halide vacancies can diffuse long-distance through any of these three migration paths but via P2 and P3 together for diffusion in the c-direction. Halide interstitials can migrate in parallel to the octahedral slab through any of P4, P5, P7, or P8. For long-range diffusion in the c-direction, halide interstitials have two transport channels. One is along the P6 individually, and the other is through the correlated interstitialcy migration P5 and dumbbell-like migration P7 sequentially.
The diffusion rate D of a defect within the bulk of a crystal material can be described by the Arrhenius equation: D ∼ exp(−ΔEa/kB·T), where kB and T are the Boltzmann constant and absolute temperature; ΔEa is the required activation energy for defect migration from one equilibrium site to the neighboring one and can be obtained by comparing the energy of the transition states optimized by the CINEB method. Fig. 4 shows the calculated energy profiles of halide migration in RP Cs2PbI4. The P1 migration in RP perovskites is similar to that of the 3D counterpart, while the energy barrier of P1 migration in Cs2PbI4 is predicted to be higher than that of the 3D analogs, e.g., 0.46 eV of the tetragonal MAPbI3.37 This finding reveals that the layered structure has a crucial effect on the migration of vacancies in halide perovskites. The P2 migration shows the lowest energy barrier of 0.33 eV among three migrations of halide vacancies. As the energy of V1-type defect structure is slightly lower than that of V2-type vacancy, the inversive direction of P2 migration has lower barrier of 0.3 eV. The P3 migration shows a high-energy barrier, suggesting that the inorganic CsI layer can suppress the migration of halide vacancies between octahedral slabs. These results indicate the intense diffusion of halide vacancies in RP Cs2PbI4 due to the low barrier of P2 migration, though this diffusion is evidently anisotropic. For halide interstitials, the migration barrier of the direct P4 is twice higher than that of the correlated P5. As mentioned above, the simulated P5 motion is the symmetrical half of correlated interstitialcy migration. The energy barrier of P5 is predicted to be equal to the difference in the energy of I1 and I4 interstitials. Therefore, the remaining half of the correlated interstitialcy migration would be a spontaneous motion. The I4 interstitial could migrate from the 4e site to the adjacent 4c site through the P8 direction. As the P8 migration has an energy barrier of 0.18 eV, the I4 interstitial probability migrates via the correlated interstitialcy motion rather than the dumbbell-like P8 migration. In addition to the combination of P5 and P8, P6 is another transport channel for halide interstitials to realize long-range diffusion in the c-direction. The energy barrier of P6 migration is predicted to be slightly higher than the sum of P5 and P8. Another in-plane mechanism of halide interstitials is P7 migration. The energy of I2 interstitial is higher than that of other interstitials, and I3 is difficult to become the I2 site via P9 rotation motion. Thus, the P7 migration is probably not a frequent motion even though it has a quite low migration barrier. Overall, we can see that the migration of isolated halide interstitial would be confined in the intercalation and shows the anisotropic diffusion feature.
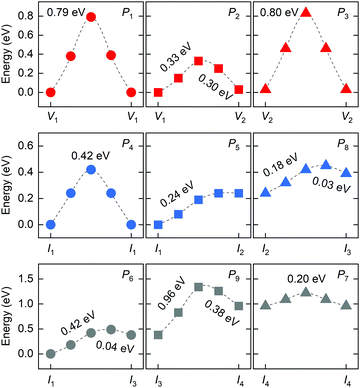 | ||
| Fig. 4 Calculated energy profiles of different migrations for halide vacancies and interstitials in RP Cs2PbI4 by using CINEB method. | ||
In the mixed-halide RP perovskite Cs2PbI2Cl2, P1 denotes the in-plane migration of Cl, and P3 represents the migration of I between two adjacent octahedral slabs. The P2 motion is not available for the long-range diffusion of halide vacancies due to different species of halide ions at the 4c and 4e sites. For Cl interstitials, the correlated interstitialcy migration P5 and the dumbbell-like migration P8 only allow the long-range axial diffusion and no longer be able to realize equatorial diffusion. For iodine interstitials, the I3-type interstitial is unstable due to the great disparity of the ionic radii of Cl and I. During the relaxation of I3-type structure, the I interstitial moves into the intercalation to form an I1-like structure (Fig. S3, ESI†). Therefore, migrations related to the I3-type interstitial are not included in this work, e.g., P6, P8, and P9. Moreover, the P7 migration is not considered for I interstitials because the I2-type interstitial cannot migrate over long distance via this dumbbell-like mechanism. Therefore, we simulate all six migrations for Cl interstitials and two migrations P4 and P5 for I interstitials in the mixed-halide RP Cs2PbI2Cl2, and their energy profiles are presented in Fig. 5. In the mixed-halide RP Cs2PbI2Cl2, the Pb–Cl bond is longer than that of RP Cs2PbCl4 and shorter than the Pb–I bond of RP Cs2PbI4. Thus, the migration bottleneck of P1 will be larger than that of Cs2PbCl4, and the bottleneck of P3 is smaller than that of Cs2PbI4, leading to lower barrier of P1 and higher barrier of P3 in the mixed-halide Cs2PbI2Cl2. In RP Cs2PbI4, the P2 migration provides the fast transport channel for halide ions vis the vacancy-hopping mechanism; while in the mixed-halide RP, this fast transport channel is not available. Therefore, the migration of halide vacancy is also suppressed in the mixed-halide RP perovskite.
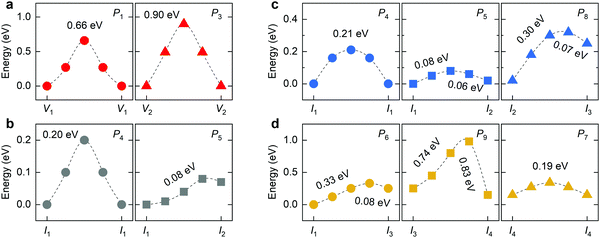 | ||
| Fig. 5 Calculated energy profiles of different migrations for (a) halide vacancies, (b) iodide interstitials, (c) and (d) chloride interstitials in mixed-halide RP Cs2PbI2Cl2 by using CINEB method. | ||
The lattice expansion of Cs2PbI2Cl2 compared with Cs2PbCl4, leading to the decrease in the energy difference between Cl interstitials related to the 4c site (e.g., I2 or I3) with the 4d site. In consideration of the low migration barrier of P7, the probability of in-plane dumbbell-like migration would be higher than that of Cs2PbI4. However, the mixed-halide RP Cs2PbI2Cl2 still has a high barrier for the rotation motion between I2 and I3. Moreover, the mixed-halide RP Cs2PbI2Cl2 shows similar properties of halide migration with RP Cs2PbI4. The migration of halide interstitials has lower barrier than that of halide vacancies along the same direction. For instance, the barrier of P7 for Cl interstitial is lower than that of P1, and the barrier of P5 for I interstitial is lower than that of P3. The correlated interstitialcy migration of isolated I1 interstitials possesses lower barrier than the direct interstitial migration. Due to the contracted lattice compared with RP Cs2PbI4, the migration distance in the ab-plane decreases as well in the mixed-halide RP Cs2PbI2Cl2. Therefore, P4 and P5 exhibit reduced barrier, suggesting the increased diffusion rate of halide interstitials in the intercalation. Only the I ion could adopt the correlated interstitialcy migration mechanism to realize long-range diffusion in the intercalation. At the end of the P5 migration, the Cl ion would migrate toward the 4c site along the P8 to form the I3-type interstitial. Consequently, the higher barrier of the P7 migration further decreases the diffusion rate of Cl interstitials along the c-direction, so the low migration barrier of P5 to some extent could not considerably facilitate the diffusion of Cl interstitials in Cs2PbI2Cl2. We should emphasize that Cl and I ions in Cs2PbI2Cl2 exhibit the lower barrier of interstitialcy migration than that of Cs2PbI4, suggesting the higher migration frequency of halide interstitials in the mixed-halide RP Cs2PbI2Cl2.
The low ion conductivity in 2D perovskites has been demonstrated by experiments and theoretical calculations, which can inhibit the J–V hysteresis of perovskite solar cells. Chen et al. reported that the migration barrier of I ions in organic–inorganic hybrid 2D RP perovskite PEA2PbI4via the vacancy-hopping mechanism is obviously higher than that of MAPbI3.38 In this hybrid RP perovskite, migration barriers are predicted to be about 0.7 eV in both P1 and P2 directions. For P1 migration, the higher barrier is derived from the smaller migration bottleneck as a result of the lattice contraction in the ab-plane; while for the P2 migration, the barrier is mainly due to the energy difference between V1 and V2 structures. In all-inorganic RP Cs2PbI4, however, this energy difference between V1 and V2 structures is quite small (about 0.03 eV). Therefore, the Cs2PbI4 shows a smaller barrier of P2 migration compared with P1 migration, which provides fast transport channel for halide ions.
The ion migration barrier is generally sensitive to the lattice parameter and the ionic interaction. In lead halide perovskites, the unique antibonding characteristic of Pb 6s with I 5p orbitals at upper valence bands weakens the Pb–I bond of the octahedron, resulting in the low barrier of halide migration.37 For RP perovskites, the edge of octahedron is also an important transport channel for halide vacancies. As mentioned previously, the peak of p orbital from the 4e site is higher than that of the 4c site. As a result, the out-of-plane I anion has weaker interaction with Pb cations than the in-plane I anions. The ion migration along the octahedral edge involves breakage and reconstruction of chemical bonds. This process is often accompanied by the charge transfer between B-site cations.39 In this study, we calculate the Bader charge of the adjacent Pb cations for the P1 migration in Cs2PbI4 (Fig. S4, ESI†). At the initial state, electrons reorganize onto PbA and PbC which are adjacent to the vacancy due to the existence of iodine vacancy, thus resulting in the lower Bader charges on PbA and PbC than that on PbB. With the movement of the I ion, the Bader charge on PbB decreases and the charge on PbC increases, indicating that electrons on PbC move to PbB. This reveals that the electronic configuration of B-site cation plays a significant role in the halide migration of perovskites. The toxicity of Pb has raised serious concerns, and much effort has been devoted to explore Pb-less or even Pb-free alternatives.40–42 It should be noted that apart from electronic properties the influence of non-Pb element on the ionic conductivity is also worthy of further considerations.
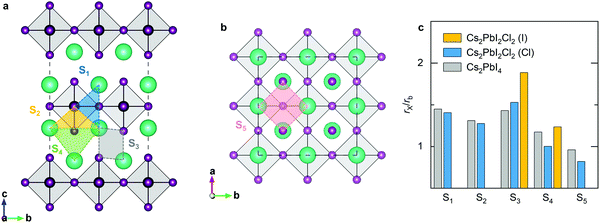
The migration bottleneck has been proposed to investigate the effect of various B-site cations on the barrier of X-site oxygen migration in ABO3-type ion-conducting perovskites.43,44 The bottleneck radius of X-site ion migration is proportional to the size of the triangle formed by the B-site cation with two adjacent A-site cations in regular perovskites, and determined by the lattice constant and the ionic radii of A-site and B-site cations. Given that the lattice constant is correlated to the ionic radius and bond properties, the ionic interaction can also influence the radius of migration bottleneck. Accordingly, the migration bottleneck is an intuitive method used to understand the tendency of migration barriers. We investigate five different bottlenecks for halide migration in RP halide perovskites (Fig. 6). The first migration bottleneck is determined by the triangle formed by the Pb cation with two adjacent Cs cations in the c-direction, which is responsible for halide migrations between two 4c sites along the octahedral edge, e.g., P1 and P7. Similarly, the second bottleneck is composed of one Pb cation with two adjacent Cs cation in the a-axis, which will affect migrations between 4c and 4e sites, e.g., P2 and P8. The third is composed of adjacent Cs cations with halide anions in the intercalation. In this case, the radius of bottleneck is determined by the diagonal length of the parallelogram. This bottleneck would influence the vacancy migration P3 and the direct interstitial migration P4. The fourth bottleneck is also a triangle composed of three adjacent Cs cations in the intercalation, which controls the P5 migration. The final one is a square formed by Cs cations with halide anions in the ab-plane, which is related to the P6 migration. In consideration of different species of halide anions in the mixed-halide RP perovskite, the ratio of the ionic radius to the bottleneck radius would be more adequate than the pure bottleneck radius to explicate the migration barrier. Consequently, we calculate the radius ratio for various migration bottlenecks based on the Shannon ionic radii and optimized lattice parameters. Apparently, the larger the bottleneck is, the lower the diffusion barrier will be; by contrast, the larger ratio implies higher barrier. For the majority of halide migrations, the radius ratio is greater than 1, which can be ascribed to the covalent bond of Pb cations with halide anions. For migrations along the octahedral edge, the second bottleneck has a smaller radius ratio than the first one, which is in accordance with the lower barriers of P2 and P7 compared with P1 and P6. The third bottleneck has the highest value of the radius ratio, which corresponds to the highest barrier of P3 migration. For the migration of isolated interstitials, the fourth bottleneck has smaller ratio than the third type, which explains the lower energy barrier of P5 than that of P4. For the P8 migration, the barrier is mainly due to the energy difference between the I1 and I3-type defects, so that the barrier is predicted to be higher than that of P5 and even the fifth bottleneck shows the smallest radius ratio.
In organic–inorganic hybrid perovskites, the organic MA cation has shown redistribution phenomenon under a small electrical field. Yuan et al. studied the MA migrations by employing the photothermal induced resonance microscopy and obtained a migration barrier of 0.36 eV for MA cations in MAPbI3.17 In these RP perovskites, the A-site cation is no longer confined by the octahedral framework, thereby the A-site cation probably participates in ion diffusion via intercalation. We simulate six different migration motions (Fig. S5, ESI†) for Cs cations in these RP perovskites, and the calculated energy profiles are presented in Fig. S6 (ESI†). In contrast to the halide migrations, the interstitial-defect migration of the Cs cation has higher barrier than the vacancy-mediated diffusion. This is also distinguished from the MA diffusion in MAPbI3 that the interstitialcy migration has a smaller barrier than the vacancy-mediated mechanism.27 The in-plane P1 migration has the lowest barrier for Cs cations among various migrations, and the barrier decreases in the order of Cl, Br, and I as a result of the expansion of the crystal lattice. In the mixed-halide Cs2PbI2Cl2, the barriers of P1 and P2 are higher than that of Cs2PbX4, probably due to the incongruous halide anions at 4c and 4e sites, leading to the smaller migration bottleneck for P1 and P2 and larger bottleneck for P3. Similarly, the migration of Cs cations in the c-direction needs P2 and P3 together. Therefore, P1 is still the most likely diffusion mechanism for Cs cations in Cs2PbI2Cl2.
4. Conclusions
We investigate the ion diffusion mechanism of halide vacancies and interstitials in the RP perovskite Cs2PbI4 and mixed-halide RP perovskite Cs2PbI2Cl2 by first-principles calculations. The interstitial migration has a lower barrier than vacancy-mediated migration along the same direction. The migration between adjacent octahedral slabs has the highest barrier among various vacancy-mediated migrations, revealing that the halide vacancy is confined within the octahedral slab in the layered RP perovskites. The halide interstitial is likely to adopt the correlated interstitialcy migration to realize long-range diffusion in the intercalation. Moreover, the migration barrier of halide interstitial penetrating the octahedral slab is about twice higher than that of the interstitialcy migration in the intercalation, indicating the anisotropic feature of interstitial diffusion. In consideration of the relatively large bandgap and high ionic conductivity, these RP halide perovskites would not be a promising visible-light absorber of solar cells, but worth exploring for other optoelectronic applications, such as resistive switching memories, artificial synapses, and photonic memory devices.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by National Natural Science Foundation of China (11947068) and Chongqing Municipal Education Commission (KJQN201801123, KJQN202001109).References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. Grätzel, The light and shade of perovskite solar cells, Nat. Mater., 2014, 13, 838–842 CrossRef PubMed.
- Y. Rong, Y. Hu, A. Mei, H. Tan, M. I. Saidaminov, S. Il Seok, M. D. McGehee, E. H. Sargent and H. Han, Challenges for commercializing perovskite solar cells, Science, 2018, 361, eaat8235 CrossRef PubMed.
- Z. Huang, A. H. Proppe, H. Tan, M. I. Saidaminov, F. Tan, A. Mei, C.-S. Tan, M. Wei, Y. Hou, H. Han, S. O. Kelley and E. H. Sargent, Suppressed Ion Migration in Reduced-Dimensional Perovskites Improves Operating Stability, ACS Energy Lett., 2019, 4, 1521–1527 CrossRef CAS.
- H. J. Snaith and P. Hacke, Enabling reliability assessments of pre-commercial perovskite photovoltaics with lessons learned from industrial standards, Nat. Energy, 2018, 3, 459–465 CrossRef.
- N.-G. Park, M. Grätzel, T. Miyasaka, K. Zhu and K. Emery, Towards stable and commercially available perovskite solar cells, Nat. Energy, 2016, 1, 16152 CrossRef CAS.
- D. H. Kang and N. G. Park, On the Current–Voltage Hysteresis in Perovskite Solar Cells: Dependence on Perovskite Composition and Methods to Remove Hysteresis, Adv. Mater., 2019, 31, 1–23 Search PubMed.
- B. Roose, A. Ummadisingu, J.-P. Correa-Baena, M. Saliba, A. Hagfeldt, M. Graetzel, U. Steiner and A. Abate, Spontaneous crystal coalescence enables highly efficient perovskite solar cells, Nano Energy, 2017, 39, 24–29 CrossRef CAS.
- B. Roose, Ion migration drives self-passivation in perovskite solar cells and is enhanced by light soaking, RSC Adv., 2021, 11, 12095–12101 RSC.
- J. A. Christians, J. S. Manser and P. V. Kamat, Best practices in perovskite solar cell efficiency measurements. Avoiding the error of Making Bad Cells Look Good, J. Phys. Chem. Lett., 2015, 6, 852–857 CrossRef CAS PubMed.
- B. Hwang and J. S. Lee, Recent Advances in Memory Devices with Hybrid Materials, Adv. Electron. Mater., 2019, 5, 1–22 CrossRef.
- J. H. Jung, S. H. Kim, Y. Park, D. Lee and J. S. Lee, Metal-Halide Perovskite Design for Next-Generation Memories: First-Principles Screening and Experimental Verification, Adv. Sci., 2020, 7, 1–8 Search PubMed.
- L. Mao, C. C. Stoumpos and M. G. Kanatzidis, Two-Dimensional Hybrid Halide Perovskites: Principles and Promises, J. Am. Chem. Soc., 2019, 141, 1171–1190 CrossRef CAS PubMed.
- Y. Chen, Y. Sun, J. Peng, J. Tang, K. Zheng and Z. Liang, 2D Ruddlesden-Popper Perovskites for Optoelectronics, Adv. Mater., 2017, 1703487, 1–15 Search PubMed.
- M. Shin, J. Kim, Y.-K. Jung, T. Ruoko, A. Priimagi, A. Walsh and B. Shin, Low-dimensional formamidinium lead perovskite architectures via controllable solvent intercalation, J. Mater. Chem. C, 2019, 7, 3945–3951 RSC.
- X. Zhu, Z. Xu, S. Zuo, J. Feng, Z. Wang, X. Zhang, K. Zhao, J. Zhang, H. Liu, S. Priya, S. F. Liu and D. Yang, Vapor-fumigation for record efficiency two-dimensional perovskite solar cells with superior stability, Energy Environ. Sci., 2018, 11, 3349–3357 RSC.
- Y. Yuan, J. Chae, Y. Shao, Q. Wang, Z. Xiao, A. Centrone and J. Huang, Photovoltaic Switching Mechanism in Lateral Structure Hybrid Perovskite Solar Cells, Adv. Energy Mater., 2015, 5, 1500615 CrossRef.
- J. Li, Q. Yu, Y. He, C. C. Stoumpos, G. Niu, G. G. Trimarchi, H. Guo, G. Dong, D. Wang, L. Wang and M. G. Kanatzidis, Cs2PbI2Cl2, All-Inorganic Two-Dimensional Ruddlesden-Popper Mixed Halide Perovskite with Optoelectronic Response, J. Am. Chem. Soc., 2018, 140, 11085–11090 CrossRef CAS PubMed.
- Q. A. Akkerman, E. Bladt, U. Petralanda, Z. Dang, E. Sartori, D. Baranov, A. L. Abdelhady, I. Infante, S. Bals and L. Manna, Fully Inorganic Ruddlesden-Popper Double Cl–I and Triple Cl–Br–I Lead Halide Perovskite Nanocrystals, Chem. Mater., 2019, 31, 2182–2190 CrossRef CAS PubMed.
- P. Acharyya, K. Maji, K. Kundu and K. Biswas, 2D Nanoplates and Scaled-Up Bulk Polycrystals of Ruddlesden–Popper Cs2PbI2Cl2 for Optoelectronic Applications, ACS Appl. Nano Mater., 2020, 3, 877–886 CrossRef CAS.
- L.-Y. Pan, Y.-F. Ding, Z.-L. Yu, Q. Wan, B. Liu and M.-Q. Cai, Layer-dependent optoelectronic property for all-inorganic two-dimensional mixed halide perovskite Cs2PbI2Cl2 with a Ruddlesden-Popper structure, J. Power Sources, 2020, 451, 227732 CrossRef CAS.
- Z. Xu, M. Chen and S. F. Liu, Layer-Dependent Ultrahigh-Mobility Transport Properties in All-Inorganic Two-Dimensional Cs2PbI2Cl2 and Cs2SnI2Cl2 Perovskites, J. Phys. Chem. C, 2019, 123, 27978–27985 CrossRef CAS.
- S. Guo, K. Bu, J. Li, Q. Hu, H. Luo, Y. He, Y. Wu, D. Zhang, Y. Zhao, W. Yang, M. G. Kanatzidis and X. Lü, Enhanced Photocurrent of All-Inorganic Two-Dimensional Perovskite Cs2PbI2Cl2via Pressure-Regulated Excitonic Features, J. Am. Chem. Soc., 2021, 143, 2545–2551 CrossRef CAS PubMed.
- S. Yang, W. Liu, Y. Han, Z. Liu, W. Zhao, C. Duan, Y. Che, H. Gu, Y. Li and S. (Frank), Liu, 2D Cs2PbI2Cl2 Nanosheets for Holistic Passivation of Inorganic CsPbI2 Br Perovskite Solar Cells for Improved Efficiency and Stability, Adv. Energy Mater., 2020, 10, 2002882 CrossRef CAS.
- X. Li, M. Chen, S. Mei, B. Wang, K. Wang, G. Xing and Z. Tang, Light-induced phase transition and photochromism in all-inorganic two-dimensional Cs2PbI2Cl2 perovskite, Sci. China Mater., 2020, 63, 1510–1517 CrossRef CAS.
- C. Eames, J. M. Frost, P. R. F. Barnes, B. C. O’Regan, A. Walsh and M. S. Islam, Ionic transport in hybrid lead iodide perovskite solar cells, Nat. Commun., 2015, 6, 2–9 Search PubMed.
- J. H. Yang, W. J. Yin, J. S. Park and S. H. Wei, Fast self-diffusion of ions in CH3NH3PbI3: the interstiticaly mechanism versus vacancy-assisted mechanism, J. Mater. Chem. A, 2016, 4, 13105–13112 RSC.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, Atomic-Scale Influence of Grain Boundaries on Li-Ion Conduction in Solid Electrolytes for All-Solid-State Batteries, J. Am. Chem. Soc., 2018, 140, 362–368 CrossRef CAS PubMed.
- C. Lan, S. Zhao, J. Luo and P. Fan, First-principles study of anion diffusion in lead-free halide double perovskites, Phys. Chem. Chem. Phys., 2018, 20, 24339–24344 RSC.
- A. Kushima, D. Parfitt, A. Chroneos, B. Yildiz, J. A. Kilner and R. W. Grimes, Interstitialcy diffusion of oxygen in tetragonal La2CoO4 + δ, Phys. Chem. Chem. Phys., 2011, 13, 2242–2249 RSC.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- A. Emly, E. Kioupakis and A. Van der Ven, Phase Stability and Transport Mechanisms in Antiperovskite Li3OCl and Li3OBr Superionic Conductors, Chem. Mater., 2013, 25, 4663–4670 CrossRef CAS.
- J. A. Dawson, J. A. Miller and I. Tanaka, First-principles insight into the hydration ability and proton conduction of the solid state proton conductor, y and Sn Co-doped BaZrO3, Chem. Mater., 2015, 27, 901–908 CrossRef CAS.
- J. Haruyama, K. Sodeyama, L. Han and Y. Tateyama, First-principles study of ion diffusion in perovskite solar cell sensitizers, J. Am. Chem. Soc., 2015, 137, 10048–10051 CrossRef CAS PubMed.
- J. Chen, D. Lee and N.-G. Park, Stabilizing the Ag Electrode and Reducing J–V Hysteresis through Suppression of Iodide Migration in Perovskite Solar Cells, ACS Appl. Mater. Interfaces, 2017, 9, 36338–36349 CrossRef CAS PubMed.
- A. M. Ritzmann, A. B. Muñoz-García, M. Pavone, J. A. Keith and E. A. Carter, Ab Initio DFT+U Analysis of Oxygen Vacancy Formation and Migration in La1−xSrxFeO3−δ (x = 0, 0.25, 0.50), Chem. Mater., 2013, 25, 3011–3019 CrossRef CAS.
- X. G. Zhao, D. Yang, J. C. Ren, Y. Sun, Z. Xiao and L. Zhang, Rational Design of Halide Double Perovskites for Optoelectronic Applications, Joule, 2018, 2, 1662–1673 CrossRef CAS.
- F. De Angelis, The Prospect of Lead-Free Perovskite Photovoltaics, ACS Energy Lett., 2021, 6, 1586–1587 CAS.
- C. N. Savory, A. Walsh and D. O. Scanlon, Can Pb-Free Halide Double Perovskites Support High-Efficiency Solar Cells?, ACS Energy Lett., 2016, 1, 949–955 CrossRef CAS PubMed.
- C. Chen, Z. M. Baiyee and F. Ciucci, Unraveling the effect of La A-site substitution on oxygen ion diffusion and oxygen catalysis in perovskite BaFeO3 by data-mining molecular dynamics and density functional theory, Phys. Chem. Chem. Phys., 2015, 17, 24011–24019 RSC.
- C. Chen and F. Ciucci, Designing Fe-based oxygen catalysts by density functional theory calculations, Chem. Mater., 2016, 28, 7058–7065 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03631a |
| This journal is © the Owner Societies 2022 |