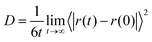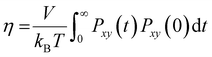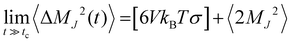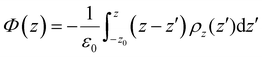Salt-in-water and water-in-salt electrolytes: the effects of the asymmetry in cation and anion valence on their properties
Andresa
Messias
 *a,
Débora A.
C. da Silva
*a,
Débora A.
C. da Silva
 b and
Eudes E.
Fileti
b and
Eudes E.
Fileti
 *c
*c
aCenter of Natural and Human Sciences, Federal University of ABC, 09210-170, Santo André, SP, Brazil. E-mail: andresamessias4@gmail.com
bCenter for Innovation on New Energies, Advanced Energy Storage Division, Carbon Sci-Tech Labs, University of Campinas, School of Electrical and Computer Engineering, Av. Albert Einstein 400, Campinas – SP, 13083-852, Brazil
cInstitute of Science and Technology of the Federal University of São Paulo, 12247-014, São José dos Campos, SP, Brazil. E-mail: fileti@gmail.com
First published on 22nd November 2021
Abstract
We investigated the structural, dynamic, energetic, and electrostatic properties of electrolytes based on the ion pairs LiCl and Li2SO4. Atomistic molecular dynamics simulations were used to simulate these aqueous electrolytic solutions at two different concentrations 2 M (normal) and 21 M (superconcentrated, WiSE). The effects of the valence asymmetry of the Li2SO4 electrolyte were also discussed for both salt concentrations. Our results differ in the physical aspect of pure electrolytes, showing the drastic effect of high concentration, in particular on the viscosity, which is dramatically increased in WiSE. This is a consequence of their reduced ionic mobility and has a direct effect on ionic conductivity. Also, our results for graphene-based supercapacitors, as indicated by some experimental work, do not indicate any better performance of WiSEs over normal electrolytes. In fact, the differences in the total capacitance, due to the concentration of ions, presented by both electrolytes are negligible. The valence asymmetry can be clearly observed in some properties but for most of them its effects could not be quantified or isolated.
Introduction
Electrochemical energy storage devices, such as batteries and supercapacitors, are considered as one of the best options for storing energy produced from renewable resources.1–3 For both batteries and supercapacitors a key factor for their functioning and effectiveness is the good performance of their electrolyte solutions.1,4,5 The search for more efficient electrolytes heavily involves aqueous electrolytes due to their cost and safety since such electrolytes are non-flammable and produced only with water and cheap salts (such as nitrates and sulfates) which reduces drastically the cost of electrolytes.5 Furthermore, aqueous electrolytes have high ionic conductivity, which typically exceeds by up to two orders of magnitude that of electrolytes based on organic solvents, which allows for a higher power capability.5 Despite these important features and desirable characteristics, aqueous electrolytes have limited energy density performance due to their low electrochemical window. This window is about 1.2 V, and when reached, it starts the process of decomposition of water into H2 and O2, ruining the entire functioning of the device.5Intense research has been carried out on improving the performance of aqueous electrolytes to mitigate the limitation related to their electrochemical window. This has been done using many different approaches, but one, in particular, has attracted a lot of attention recently. In 2015 Suo and colleagues published an important paper investigating the properties and performance of “water-in-salt” electrolytes (WiSE).6 The notable feature of this type of electrolyte is that the hydration structure of salt is very different from that found in normal aqueous (salt-in-water) electrolytes. In WiSE the salt is not only coordinated by water molecules, but also by counterions (anions) dispersed in the solution. These electrolytes have increased electrochemical stability compared to normal aqueous electrolytes. This advantage is because the electrolyte forms a passivating layer on the electrode surface, further suppressing H2 evolution. With this, the electrochemical window of the aqueous electrodes can be increased to almost 3 V.6 Following this pioneering work, several studies on the energetic and structural properties of these promising electrolytes have been reported showing remarkable results when applied as electrolytes to lithium batteries and supercapacitors.7–11
In addition to the improvement that highly concentrated electrolytes can bring, there is still an aspect that can play a significant role in the performance of electrolytes, but it has still been little investigated: the valence asymmetry of the electrolyte. This asymmetry is present when the valence of the cations and anions is not the same. For example, the aqueous LiCl electrolyte has symmetry (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), in this case, both the cation and anion have a valence of modulus 1, on the other hand, the aqueous Li2SO4 electrolyte is asymmetric (1
1), in this case, both the cation and anion have a valence of modulus 1, on the other hand, the aqueous Li2SO4 electrolyte is asymmetric (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) since the anion has a valence whose modulus is double that of the cation. Therefore, this last electrolyte is said to have valence asymmetry. In general, this asymmetry will be observed whenever the ratio between the velocity of the ions differs from (z
2) since the anion has a valence whose modulus is double that of the cation. Therefore, this last electrolyte is said to have valence asymmetry. In general, this asymmetry will be observed whenever the ratio between the velocity of the ions differs from (z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) z). This subject was recently investigated by Gupta and Stone, who studied the effect of valence asymmetry in the scope of mean field theory.12 They argue that the magnitude of the valence is what determines the mutual force exerted by the ions when cations and anions have different valences. In this case, the magnitudes of the forces experienced by the cations and anions are uneven, which leads to an asymmetry in the properties of the electrical double layer (EDL), which can have significant implications for the development of more efficient electrolytes. For example, they found that this asymmetry has an expressive effect on the diffuse charge dynamics, thus having direct consequences on the determination of the charge density and capacitance of devices for storing electrochemical energy.12
z). This subject was recently investigated by Gupta and Stone, who studied the effect of valence asymmetry in the scope of mean field theory.12 They argue that the magnitude of the valence is what determines the mutual force exerted by the ions when cations and anions have different valences. In this case, the magnitudes of the forces experienced by the cations and anions are uneven, which leads to an asymmetry in the properties of the electrical double layer (EDL), which can have significant implications for the development of more efficient electrolytes. For example, they found that this asymmetry has an expressive effect on the diffuse charge dynamics, thus having direct consequences on the determination of the charge density and capacitance of devices for storing electrochemical energy.12
This work has a dual purpose. The first is the investigation at the atomistic level of differences in the properties of LiCl and Li2SO4 aqueous electrolytes at normal (2 M) and superconcentrated (21 M, WiSE) concentrations. This will be done both by investigating the structural and dynamic properties of pure electrolytes as well as by studying the electrostatic properties of graphene electrolytic cells, for which we will determine their electrostatic potential profile and total capacitance. A second objective was to verify if our models are able to quantify the effects of the asymmetry of the valence asymmetry of the Li2SO4 electrolyte in relation to the symmetrical valence electrolyte LiCl. In this last point, any difference we can attribute to valence asymmetry will be important. Since we employ more realistic models through atomistic molecular dynamics simulations, which explicitly consider important effects such as specific interactions and hydration forces, our results can corroborate the predictions of mean field theory.12
Computational simulations
We investigated the properties of electrolytes using two different simulation series. In the first, we studied the structural, energetic, and dynamic properties of pure electrolytes. In the second series, we employed the investigated solutions in graphene electrolytic cells to evaluate their properties as electrolytes for supercapacitors. In both series, the electrolytes investigated were LiCl and Li2SO4 normal (salt-in-water, 2 M) and superconcentrated (water-in-salt, WiSE, 21 M) aqueous solutions. For all solutions 4.0 nm cubic starting boxes were generated. The molecular representations of the simulation boxes are given in Fig. 1 and the composition of each simulation is shown in Table 1. In this table, we highlight the valence asymmetry (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for the case of sulfate solutions, for which we have two cations for each anion in the solution.
1) for the case of sulfate solutions, for which we have two cations for each anion in the solution.
| Electrolytes | Ion pairs | Li cations | Cl/SO4 anions | Water molecules |
|---|---|---|---|---|
| LiCl (2 M) | 72 | 72 | 72 | 2000 |
| Li2SO4 (2 M) | 60 | 120 | 60 | 1800 |
| LiCl (21 M) | 454 | 454 | 454 | 1200 |
| Li2SO4 (21 M) | 378 | 756 | 378 | 1000 |
For the supercapacitors, the simulation cells were generated by a two-step procedure: first, the electrolyte was placed between two rigid 3.4 nm × 3.2 nm graphene electrodes, and the cells were relaxed only in the z-direction such that a new length z was obtained. Then, a new cell was generated using the relaxed distance z, but now with a 30 nm-vacuum slab inserted outside the two electrodes. With this procedure we ensured that all cells had the adequate size in order to hold the ideal number of atoms and still maintain the bulk density in the center of the electrolytic cells. The molecular representations of the supercapacitor simulation cells are provided in Fig. 2 and the details of the composition of each simulation are shown in Table 2.
| Supercapacitors | Li cations | Cl/SO4 anions | water molecules | Box (x, y, z) nm3 |
|---|---|---|---|---|
| LiCl (2 M) | 144 | 144 | 4000 | (3.4, 3.1, 11.5) |
| Li2SO4 (2 M) | 224 | 112 | 3100 | (3.4, 3.1, 11.0) |
| LiCl (21 M) | 946 | 946 | 2500 | (3.4, 3.1, 11.2) |
| Li2SO4 (21 M) | 1514 | 757 | 2000 | (3.4, 3.1, 11.5) |
For all molecular systems, we employ potential models based on the OPLS-AA force field to describe intermolecular interactions.13 The water molecule was treated using the SPC model.14 These models have been successfully applied in the description of the dynamical properties of pure ionic liquids and aqueous electrolytes and also in the modeling of the electric double layer in graphene supercapacitors.8,15,16 Atomic partial charges and Lennard-Jones parameters of the ions were taken directly from the OPLS, with the exception of the SO42− anion, which was taken from the parameterization from Jungwirth and co-workers.17 The electronic continuum correction (ECC) was applied to all ions. Standard force fields using full charges to describe divalent ions do not accurately capture ion pairing in aqueous solutions and overestimate the strength of ion–ion interactions with respect to ion–water interactions.17,18
In ECC force fields, polarization electronics is taken into account and the charges of all ions are scaled by the inverse square root of the electronics of the dielectric constant of water and reducing the radius of each ion to achieve the required ion–water distances.17 This correction has been shown to improve significantly the ion pairing properties and structure of multivalent ions in electrolytic solutions compared to standard approaches.17–20 The details of the force field parameters are summarized in Table 3.
| σ (Å) | ε (kJ mol−1) | Charge ECC | |
|---|---|---|---|
| Li+ | 1.80 | 0.07647 | +0.75 |
| Cl− | 4.417 | 0.4928 | −0.75 |
| S | 3.550 | 1.046 | +1.50 |
| O (of sulfate) | 3.150 | 0.8368 | −0.75 |
The equilibration process of the electrolyte solutions was performed in an isothermal–isobaric ensemble (NPT) with T = 300 K and p = 1 atm for 10 ns. With this run, we accumulate enough configurations to the statistics of the structural and energetic analyses. Then, from the NPT equilibrated configurations, we performed new runs using the canonical ensemble (NVT) for 100 ns under normal conditions. This NVT improved sampling was used to determine the dynamic properties of the electrolytes, such as the diffusion coefficient, viscosity, and ionic conductivity.
This is done by dynamically distributing the electrode charge using the constant potential method implemented by Laird and co-workers for the study of electrified interfaces.21,22 Both methods are equivalent to low potential differences (typically <2 V). As we are interested in smaller potentials here, we will employ the first model taking advantage of its large advantage concerning computational cost. In this way, each supercapacitor was simulated at seven different surface charge densities from σ = 0 (discharged supercapacitor) to σ = ±4.8 μC cm−2 evenly incremented by 0.8 μC cm−2. We applied the same procedure in recent work on graphene-based supercapacitors.23
For all NPT simulations, the Parrinello–Rahman barostat24 was used to maintain the constant pressure with a time constant of 2 ps and a compressibility constant of 4.5 × 10−5 bar−1. In the case of supercapacitors, the pressure control was done using semiisotropic coupling in a way in which only z length could vary. To ensure a constant temperature in the Nosé–Hoover thermostat25 a time constant of 2 ps was used. The Lennard-Jones interaction was computed by the classical shifted force technique while the long-range electrostatic correction was estimated by the Particle–Mesh–Ewald method (PME)26 which was applied beyond a cutoff radius of 0.9 nm. Periodic boundaries were employed in all directions. The integration time-step was 2.0 fs and the coordinates and thermodynamic properties were stored every 0.1 ps. All simulation cells were generated using the PACKMOL code27 and all molecular dynamics simulations were performed using the GROMACS 2020 molecular dynamics package.28
Results and discussion
To characterize the electrolytes and compare their structural properties, mainly about valence asymmetry, we determined a series of properties presented in Table 4. The characteristic differences are evident when comparing normal electrolytes and water-in-salt. WiSE have a higher mass density than the normal electrolyte, in particular for the Li2SO4 solution whose mass density is 56% higher in WiSE concentration than in normal concentration. Although no experimental results were found for Li2SO4 solutions, our results are compatible with other similar electrolytes, such as LiCl solutions for which the density at 3.5 M was 1076.3 kg m−3, while at a higher concentration, of 15.2 M, the value has been increased to 1286.2 kg m−3.29,30| Normal (2 M) | WiSE (21 M) | |||
|---|---|---|---|---|
| Property | LiCl | Li2SO4 | LiCl | Li2SO4 |
| ρ (kg m−3) | 996.8 ± 6.0 | 1119.2 ± 6.6 | 1191.2 ± 6.0 | 1751.1 ± 4.6 |
| E c (kJ mol−1 nm−3) | 1598 ± 5 | 2416 ± 6 | 4265 ± 5 | 9356 ± 38 |
| # HB's | 3388 ± 22 | 3135 ± 23 | 1456 ± 20 | 1269 ± 20 |
| D water (10−7 cm2 s−1) | 362.3 ± 1.4 | 230.6 ± 1.7 | 89.7 ± 0.6 | 25.2 ± 0.5 |
| D cation (10−7 cm2 s−1) | 164.3 ± 5.5 | 80.3 ± 1.5 | 55.5 ± 0.7 | 11.3 ± 0.3 |
| D anion (10−7 cm2 s−1) | 270.4 ± 9.1 | 63.9 ± 0.8 | 57.5 ± 0.5 | 8.4 ± 0.1 |
| η (cP) | 1.0 ± 0.2 | 1.8 ± 0.5 | 23.0 ± 0.5 | 84.2 ± 0.9 |
| σ (S m−1) | 12.1 ± 2.4 | 5.5 ± 0.6 | 8.82 ± 1.4 | 1.0 ± 0.1 |
The cohesive energy quantifies the total intermolecular interaction of a solution and is an indicator of its thermodynamics stability. This is the effect of the intense network of electrostatic interactions, and the result of a much larger number of ionic pairs present in the solution. In another view, this energy is also larger for the sulfate-based solution than for chloride one, by circa 2.0 times. This can be rationalized in terms of the formation of hydrogen bonds since the SO42− anions can form hydrogen bonds with water molecules, and besides that, this is a divalent anion, which intensifies, even more, the electrostatics among ions directly affecting the cohesive energy. Both effects lead to the increase of the internal energy of vaporization of the electrolyte and consequently its cohesive energy.8
Table 4 also presents the average number of hydrogen bonds (HB) present in each system. The hydrogen bonds are defined based on a simple geometric criterion, where two tagged molecules are considered to be bonded if the value of the donor–acceptor distance (r) is less than the rHB value and the hydrogen–donor–acceptor angle (α) is less than the αHB value. In the GROMAC software we used the gmx hbond routine to compute and analyze all the hydrogen bonds present in the systems.28 We use the default values of rHB = 0.35 nm and αHB = 30° to calculate water–water and water–sulfate hydrogen bonds,31 and their generalization to water–chloride hydrogen bonds, rHB = 0.41 nm and αHB = 30°, based on radial distribution functions.32 As can be seen, the value of this property is higher for normal electrolytes than for WiSE. This is expected since WiSE has much fewer water molecules, which are responsible for most of the hydrogen bonds in the electrolytes.7,8 The higher concentration of ions leads to an increase in electrostatic interactions, which dominates the intrinsic energy of WiSE. The reduction in the HB from the normal electrolyte to WiSE is ∼2.4 times for both salts.
The transport properties of an electrolyte are important indicators for determining its performance. The diffusion coefficient, viscosity, and ionic conductivity were calculated for all solutions and are presented in Table 4. For diffusion coefficients and viscosities, blocks of 10 ns were used, while for ionic conductivity, blocks of 30 ns were needed. A first analysis concerns the ionic mobility assessed by the diffusion coefficient, D, which was obtained by the linear adjustment of the mean quadratic displacement of ri and it was possible to calculate the D using the Einstein relation:33
Table 4 presents the ionic diffusion coefficient for all molecular species (water, Li+, Cl− and SO42−) at both concentrations. Regarding the electrolyte composition, our results indicate greater mobility of all species in Cl-based electrolyte than in SO4 one, spanning from 1.6 times for water molecules in normal electrolyte up to ∼7 times for SO42− anions in WiSE. Considering the concentrations, the mobility of the components is drastically reduced in the superconcentrated electrolytes, as expected. Note that this decrease is more accentuated in Li2SO4 electrolytes, by up to ∼9 times as we can see Dwater (from 231 to 25 × 10−7 cm−2 s−1). For LiCl electrolytes, this reduction is only 4 times (from 362 to 90 × 10−7 cm−2 s−1). We also note that in LiCl electrolytes, the anion presents higher mobility than the cation Li+ but the opposite is observed for Li2SO4 electrolytes. This is due not only to the size of SO42−, which is greater than that of Li+, but also due to its valence which is two times higher. Although in these results it is impossible to decouple the effects of these two factors (size and valence), certainly valence plays a crucial role in determining the diffusion coefficient and valence asymmetry can justifies the relative reduction of anion diffusion at high concentrations.
The reduction in the mobility of ions and water directly affects the other dynamic properties of electrolytes, such as viscosity and ionic conductivity. In this work, viscosity, η, was obtained from the Green–Kubo formula by integrating the autocorrelation function of elements outside the diagonal of the pressure tensor, Pαβ(t):34
The ionic conductivity, σ, measures the tendency of a solution to conduct ions. This involves ionic movement from one location to another through the electrolyte. The Einstein–Helfand method was employed to determine the ionic conductivity by using the linear slope of the mean displacement of the collective translational dipole moments, Mj:37
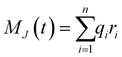 , ri being the coordinate of the center of mass of the ion i. Table 4 shows that ionic conductivity follows the inverse trend of viscosity, which decreases as the viscosity increases. For both concentrations, 2 M and 21 M, the LiCl solution proved to be a better ionic conductor than Li2SO4, and overall, the highest conductivity was found for the LiCl solution at normal concentration, 12.1 S m−1. This value is about 2.2 times higher than the corresponding SO42− anion-based solution. For the WiSE concentration, the LiCl solution is almost 9 times more conductive than Li2SO4, which has the lowest ionic conductivity among all solutions, 1.0. The comparison between the concentrations shows that in all cases, the superconcentrated electrolytes have lower ionic conductivity, up to 5.5 times, as is the case with the Li2SO4 solution, which reduces from 5.5 in 2 M to 1.0 in 21 M.
, ri being the coordinate of the center of mass of the ion i. Table 4 shows that ionic conductivity follows the inverse trend of viscosity, which decreases as the viscosity increases. For both concentrations, 2 M and 21 M, the LiCl solution proved to be a better ionic conductor than Li2SO4, and overall, the highest conductivity was found for the LiCl solution at normal concentration, 12.1 S m−1. This value is about 2.2 times higher than the corresponding SO42− anion-based solution. For the WiSE concentration, the LiCl solution is almost 9 times more conductive than Li2SO4, which has the lowest ionic conductivity among all solutions, 1.0. The comparison between the concentrations shows that in all cases, the superconcentrated electrolytes have lower ionic conductivity, up to 5.5 times, as is the case with the Li2SO4 solution, which reduces from 5.5 in 2 M to 1.0 in 21 M.
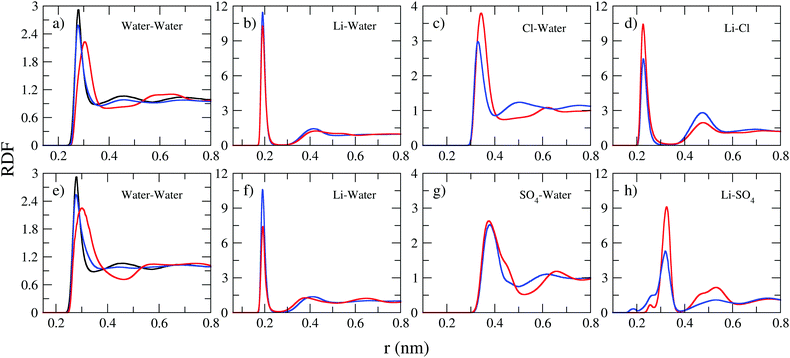
The interactions between ions and molecules are responsible for the structural properties of solutions. Such properties are investigated here in terms of radial distribution functions of the center of mass (RDF), the corresponding coordination number, calculated by the running integral of each RDF, and the spatial density functions (SDF). Fig. 3 presents selected RDFs for both normal (blue curve) and WiSE (red curve) concentrations. From Fig. 3, we can also compare the structuring of water molecules in normal and WiS electrolytes as well as in pure water (black line). As expected, water molecules are more structured in pure water than in mixtures; the black peak, corresponding to the RDF of pure water, is higher and narrower than the peaks observed for normal and WiS electrolytes. At 2 M, the RDF distribution of water is very similar to that of pure water for both salts, however with increasing LiCl or Li2SO4 concentration, the heights of the first peak in the RDFs decrease and become wider, while the weak peak at about 4.5 Å decreases with increasing salt concentration.
In pure water, each water molecule is on average solvated by ∼5.5 water molecules, this value is close to that obtained for LiCl and Li2SO4 solutions at 2 M concentration (see Table 5). Upon increasing the salt concentration to 21 M, the water–water coordination number (CN) decreases to 4.0 in the LiCl solution and to 4.3 for the Li2SO4 solution. This behavior has been previously observed in computational simulations of LiTFSI electrolytes at high concentrations.7
| Pair | Normal (2 M) | WiSE (21 M) | ||
|---|---|---|---|---|
| LiCl | Li2SO4 | LiCl | Li2SO4 | |
| Water–water | 5.4 | 5.9 | 4.0 | 4.3 |
| Cation–water | 3.9 | 3.5 | 2.4 | 1.4 |
| Anion–water | 6.9 | 14.4 | 5.7 | 12.2 |
| Cation–anion | 0.1 | 0.5 | 1.5 | 2.6 |
For all solutions, the pair correlation functions of Li–water present their first peak at 0.25 nm with a narrow shape, indicating a well-defined orientation of the water molecules in the first hydration shell (see Fig. 3b and f). Lithium ions are highly coordinated with about 3.5–4.0 in 2 M aqueous water solutions of LiCl. This result is consistent with the observation that the lithium ion is solvated by four water molecules.38,39 However, it is important to emphasize the reduction in the height of the first peaks of the RDF (Li–water) with the increase in concentration. In fact, lithium solvation is severely reduced in WiSE by up to 2.5 times (from 3.5 water molecules in 2 M Li2SO4 solution to 1.4 in 21 Li2SO4 solution), which is a direct consequence of the reduction of water amount in superconcentrated electrolytes.
The asymmetry in cation and anion valence clearly manifests itself in the analysis of the RDF of anion–water pairs. The corresponding first peaks (see the middle panels in Fig. 3) of the anion–water RDFs are farther away (0.4–0.5 nm), lower but broader than the corresponding Li–water pairs. As the valence of the SO42− anion is twice the valence of the Cl− anion, we observed a strong impact on the structuring of the electrolytes and, as we can see in Table 5, the number of water molecules coordinated with the SO42− anion is twice as high as that coordinates the anion Cl−. This valence asymmetry is also manifested in RDF's cation–anion, whose first coordination sphere ends at an intermediate distance of ∼0.30 nm and have narrow and intense peaks. For these distributions, we see from Table 5 that the SO42− anion coordinates a much larger number of cations than the Cl− anion.
Several aspects of aqueous electrolyte solutions are directly related to ions modifying the local structure of water. Highly charged ions cause strong electrostatic ordering of nearby water molecules and reduce their H bonds. For example, in a recent study, Mukherjee and Saha showed that the presence of divalent ions, such as SO42−, has a much greater impact on the local structure of the aqueous solution than a monovalent ion such as Cl−.40 Both reduce the translational and rotational entropy of the surrounding water molecules, but SO42− does it to a much greater extent. Effects of this nature justify the detailed investigation of the effects of valence asymmetry for the properties of electrolytes, those that affect their performance as electrolytes for batteries and supercapacitors.
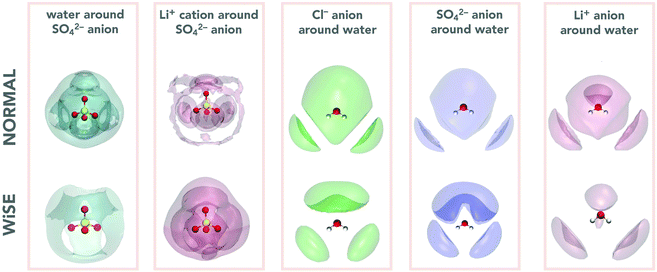
The analysis of the structure of electrolytes through the analysis of RDFs can be complemented by determining the spatial distribution functions, SDFs.41 The SDF is a three-dimensional distribution of probabilities of finding the molecules/ions of the system in a particular configuration and provide us with additional insights into the local structure and its relationship with the properties of these systems. In this work our interest is in determining the distribution of a given ion around a water molecule, as well as the distribution of water molecules around SO42− anion. It is worth mentioning that the distributions around the anion Cl− and the cation Li+ were not calculated since for these systems, which have only symmetrical spherical interactions, the pair distribution function will not contain angular dependence, and the SDF will simply be a spherical shell.
Two first blocks of Fig. 4 present the SDF around SO42− anions; the first being the water distribution (in dark green) and the second the Li+ distribution (in red) around the anion. These SDFs make clear the structural impact of concentration on the coordination of the SO42− anion, showing that the distributions of water molecules and Li+ cations show opposite trends. This is because in 2 M there are more water molecules and fewer Li+ cations, so SDF is more intense for water than for Li+. The situation is reversed for the 21 M concentration, where the amount of Li+ cation is much greater, reflecting a greater intensity of its SDF. It is interesting to note that the water and Li+ distributions overlap out of phase, i.e., where the water SDF has the maximum intensity the cation one has minimum intensity and vice versa. The last three blocks of Fig. 4 show the ion SDFs around the water molecule. Here we can see that in all three cases the SDF is more spatially distributed for the 2 M concentration and more compact for 21 M. We also see that the anion and cation distributions tend to overlap, which indicates a strong cation–anion correlation in the water coordination structure.
To investigate the performance of electrolytes we created graphene electrolytic cells from which we determined the structural properties of the electrical double layer formed at the electrode–electrolyte interface as well as its electrostatic properties. The formation of an EDL is an important physical process of purely electrostatic origin and, in principle, reversible, being the main electrochemical energy storage pathway of a supercapacitor.
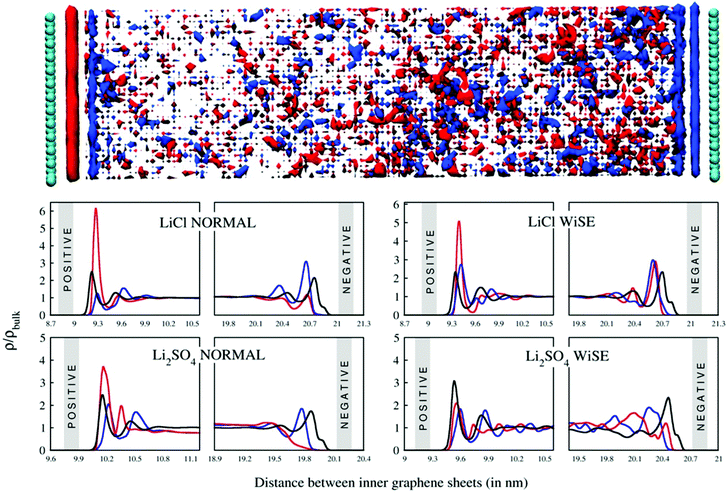
Analysis of the structure and composition of the EDL can be done in terms of the mass density profile of water and ions in the vicinity of the device's electrodes. In Fig. 5, the mass density profiles are presented, both normalized in relation to the bulk density. This normalization is convenient because, in addition to standardizing the graphs, it facilitates the analysis of the relative heights between the profile peaks. The analysis is performed for the supercapacitor charged with a 4.8 μC cm−2 charge, but it does not change qualitatively for the other charges used. We see that for all profiles the layering arrangement of the electrolyte extends over an ∼1 nm range from the electrode surface (as can be seen by the ion SDF, top of Fig. 5), except for WiSE Li2SO4, for which density fluctuations can be observed beyond this distance. This behavior is characteristic for aqueous electrolytes in contact with graphene electrodes.42,43 We also see the high density of lithium ions in the EDL (blue curve) close to the negative electrode, with very intense peaks in all cases, except again from WiSE Li2SO4, for which the SO42− anion strongly interacts with the negative electrode. These peaks for cations are always accompanied by smaller peaks corresponding to anions and water, which are also adsorbed, in smaller numbers, from the surface of the negative electrode. On the other hand, the EDL on the positive electrode surface is composed of a higher density of anions and water, especially at normal concentrations. In all cases the anions project into direct contact with the positive electrode, which can be seen by the black curved tail, closest to its surface. The behavior of the EDL and its composition in the results we present here are consistent with the EDL structures for aqueous electrodes that have been found previously.42,43
The effects of valence asymmetry could not be observed in the mass density profiles. As the peaks related to Cl− and SO42− anions depend on their shape and size, it is not possible to isolate this effect, since the geometry of the anions is very different. Even so, although the peaks related to anions are very similar, it is possible that the asymmetry effect is being masked by some other simultaneous effect. This could only be observed in a model system, where all anions had equal parameters, differing only in their valence.
The electrostatic potential profile was determined in this work by integrating the one-dimensional Poisson equation along the length z of the box, according to the expression:
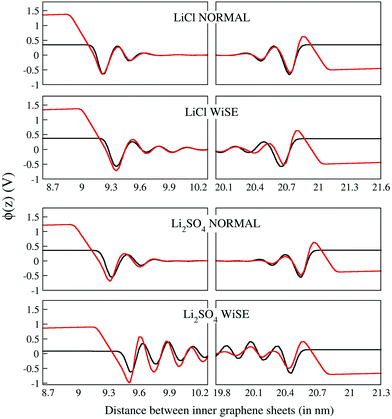
The electrostatic potential profiles obtained for all electrolytes are shown in Fig. 6 for the discharged (black curve) and charged (with a density of 4.8 mC cm−2, red curve) supercapacitors. As is typical for aqueous electrolytes, these profiles show fluctuations on the surface of the electrodes that attenuate to within ∼1.0 nm for electrolytes at normal concentration and go beyond 1.5 nm for WiSEs.
There is no evidence that charge asymmetry had any influence on liquids at normal concentrations; note that the corresponding curves for LiCl and Li2SO4 electrolytes are very similar. On the other hand, the same comparison for the WiSE liquid shows a fluctuation that persists for a much longer distance, for the Li2SO4 electrolyte. Here, it is possible that the effect of charge asymmetry has some relevant role since there is a much larger number of divalent anions in the electrolyte and, consequently, a greater influence of these on the electrostatic potential profiles. In any case, there is no observable effect on the absolute value of the downside potential.
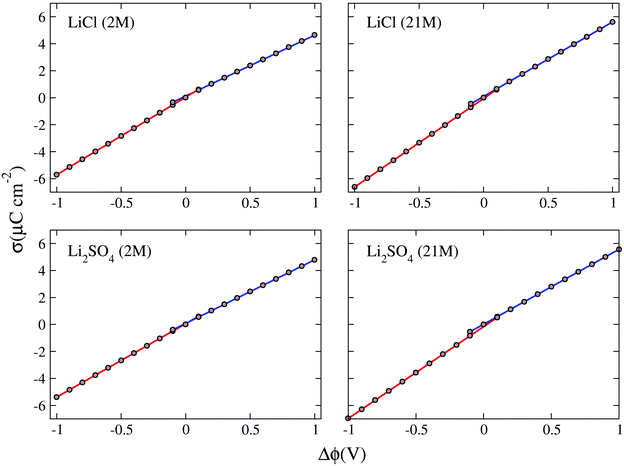
The potential drop along the supercapacitors shows a direct relationship with the charge density: the higher the charge, the greater the potential. The values found for the potential drops were associated with the two respective charge densities to obtain the σ × Δϕ curves presented in Fig. 7. In these plots all values for drop potential were corrected with potential zero charge.44 The linear adjustments in the positive and negative potential portions allowed us to obtain the capacitances of negative (C−) and positive (C+) electrodes. These capacitances taken in a series combination resulted in the total EDL capacitance (Ctotal) of the supercapacitor, as shown in Table 6.
| Supercapacitors | C − | C + | C total |
|---|---|---|---|
| LiCl (2 M) | 5.75 | 4.53 | 2.53 |
| LiCl (21 M) | 5.44 | 4.71 | 2.52 |
| Li2SO4 (2 M) | 6.55 | 5.51 | 3.00 |
| Li2SO4 (21 M) | 6.01 | 5.86 | 2.97 |
The negative and positive electrode capacitances showed asymmetry related to the composition of the double layer, indicated by the difference between the values C− and C+, which ranged from 2.5% for the WiSE Li2SO4 supercapacitor to 21% for the LiCl supercapacitor at normal concentration. This asymmetry in electrode capacitances, which has already been observed in previous work, originates from the asymmetry in the ions and their different interaction with the electrodes.15 The results for the double-layer total capacitance suggest that Li2SO4 supercapacitors (∼3.0 μF cm−2) can have up to 20% more yield than LiCl supercapacitors (∼2.5 μF cm−2), regardless of the concentration. For the capacitances the valence asymmetry, if any, was masked by other concurrent effects. More detailed and specific work will be needed to reveal the contribution of these effects.
Conclusions
Atomistic molecular dynamics simulations were employed to investigate the properties of electrolytes based on LiCl and Li2SO4 ion pairs at two different concentrations 2 M (normal) and 21 M (superconcentrated, WiSE). For this, a series of simulations was carried out in order to determine the structural, dynamic, and energetic properties of the pure electrolytes. The second series of simulations was conducted to investigate the performance of the solutions as electrolytes in supercapacitors. In this case, we determine their electrostatic properties, such as the electrostatic potential profile and the electrical double layer capacitance. The effects of valence asymmetry of the Li2SO4 electrolyte were discussed for all analyses performed.The structural, dynamic, and energetic properties characterized the physical aspect of pure electrolytes, showing the drastic effect of high concentration. For example, the viscosity of LiCl and Li2SO4 aqueous electrolytes is about ∼23 and ∼47 times higher for water-in-salt electrolytes than for normal concentrations. This is a consequence of their reduced ionic mobility and has a direct effect on ionic conductivity. In this work we made reasonable inferences about the valence asymmetry effect but, a definitive conclusion can be obtained only from results using standardized models (where all other parameters are equal), with identical LJ particles. This protocol is the only way to reveal the quantitative aspect of the valence effects. This work is being prepared and we would submit it for review shortly.
Our results do not reveal the advantages of WiSEs compared to normal electrolytes, as indicated by some experimental work.45–47 In fact, the differences in the total capacitance, due to the concentration of ions, presented by both electrolytes are negligible. Similar discrepancies between simulated and experimental results have been observed before in other computational work involving normal electrolytes and superconcentrated electrolytes.8,48 and is probably due to some effect that occurs at the electrode/electrolyte interface and is not being captured by classical simulations. As is well known, classical simulations do not take into account any important effects such as oxidation reactions that occur in pseudocapacitive systems and that drastically influence the final value of capacitance.
Finally, the valence asymmetry can be unmistakably observed in some properties. However, in most of them, when present, the effects of this asymmetry could not be quantified or isolated, indicating that specific calculations, in model systems, will need to be performed so that it is possible to unequivocally assess the real magnitude of these effects.
Conflicts of interest
There are no conflicts to declare.Author contributions
A. M., D. A. C. S.: investigation, formal analysis and visualization of data, writing – original and review draft. E. E. F.: investigation, conceptualisation, methodology, supervision, writing – original and review draft.Acknowledgements
The authors gratefully acknowledge support from FAPESP (São Paulo Research Foundation) and Shell, Grant Number 2017/11631-2, the strategic importance of the support given by ANP (Brazil's National Oil, Natural Gas and Biofuels Agency) through the R&D levy regulation and CNPq (National Council for Scientific and Technological Development).References
- C. Zhan, C. Lian, Y. Zhang, M. W. Thompson, Y. Xie, J. Wu, P. R. C. Kent, P. T. Cummings, D. E. Jiang and D. J. Wesolowski, Computational Insights into Materials and Interfaces for Capacitive Energy Storage, Adv. Sci., 2017, 4(7), 1700059 CrossRef.
- T. Brousse, D. Bélanger, K. Chiba, M. Egashira, F. Favier, J. Long, J. R. Miller, M. Morita, K. Naoi, P. Simon and W. Sugimoto, Materials for electrochemical capacitors, Springer Handbooks, 2017, pp. 495–561 Search PubMed.
- W. Raza, F. Ali, N. Raza, Y. Luo, K. H. Kim, J. Yang, S. Kumar, A. Mehmood and E. E. Kwon, Recent advancements in supercapacitor technology, Nano Energy, 2018, 52, 441–473 CrossRef CAS.
- H. Zhang, X. Liu, H. Li, I. Hasa and S. Passerini, Challenges and Strategies for High-Energy Aqueous Electrolyte Rechargeable Batteries, Angew. Chem., Int. Ed., 2021, 60, 598–616 CrossRef CAS.
- L. Xia, L. Yu, D. Hu and G. Z. Chen, Electrolytes for electrochemical energy storage, Mater. Chem. Front., 2017, 1, 584–618 RSC.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, ‘Water-in-salt’ electrolyte enables high-voltage aqueous lithium-ion chemistries, Science, 2015, 350, 938–943 CrossRef CAS.
- Y. Zhang, N. H. C. Lewis, J. Mars, G. Wan, N. J. Weadock, C. J. Takacs, M. R. Lukatskaya, H. G. Steinrück, M. F. Toney, A. Tokmakoff and E. J. Maginn, Water-in-Salt LiTFSI Aqueous Electrolytes. 1. Liquid Structure from Combined Molecular Dynamics Simulation and Experimental Studies, J. Phys. Chem. B, 2021, 125, 4501–4513 CrossRef CAS.
- P. Inoue, E. Fileti and T. Malaspina, Computational Study of the Properties of Acetonitrile/Water-in-Salt Hybrid Electrolytes as Electrolytes for Supercapacitors, J. Phys. Chem. B, 2020, 124, 5685–5695 CrossRef CAS PubMed.
- M. McEldrew, Z. A. H. Goodwin, A. A. Kornyshev and M. Z. Bazant, Theory of the Double Layer in Water-in-Salt Electrolytes, J. Phys. Chem. Lett., 2018, 9, 5840–5846 CrossRef CAS PubMed.
- Z. Li, R. Bouchal, T. Mendez-Morales, A. L. Rollet, C. Rizzi, S. Le Vot, F. Favier, B. Rotenberg, O. Borodin, O. Fontaine and M. Salanne, Transport Properties of Li-TFSI Water-in-Salt Electrolytes, J. Phys. Chem. B, 2019, 123, 10514–10521 CrossRef CAS PubMed.
- D. A. Corrêa da Silva, M. J. Pinzón, A. Messias, E. E. Fileti, A. Pascon, D. Franco, L. M. Silva and H. Zanin, Effect of conductivity, viscosity, and density of water-in-salt electrolytes on the electrochemical behavior of supercapacitors: molecular dynamics simulations and in-situ characterization studies, Mater. Adv., 2021, 1, 945–966 Search PubMed.
- A. Gupta and H. A. Stone, Electrical Double Layers: Effects of Asymmetry in Electrolyte Valence on Steric Effects, Dielectric Decrement, and Ion–Ion Correlations, Langmuir, 2018, 34, 11971–11985 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, Intermolecular Forces, D. Reidel, Dordrecht, 1981 Search PubMed.
- A. Neto and E. Fileti, An atomistic physico-chemical description of acetonitrile/tricyanomethanide based electrolytes, J. Mol. Liq., 2019, 292, 111439 CrossRef CAS.
- Z. Yu, H. Wu and R. Qiao, Electrical Double Layers near Charged Nanorods in Mixture Electrolytes, J. Phys. Chem. C, 2017, 121, 9454–9461 CrossRef CAS.
- E. Pluhařová, P. E. Mason and P. Jungwirth, Ion pairing in aqueous lithium salt solutions with monovalent and divalent counter-anions, J. Phys. Chem. A, 2013, 117, 11766–11773 CrossRef.
- E. Pluhařová, H. E. Fischer, P. E. Mason and P. Jungwirth, Hydration of the chloride ion in concentrated aqueous solutions using neutron scattering and molecular dynamics, Mol. Phys., 2014, 112, 1230–1240 CrossRef.
- E. Duboué-Dijon, P. E. Mason, H. E. Fischer and P. Jungwirth, Hydration and Ion Pairing in Aqueous Mg2+ and Zn2+ Solutions: Force-Field Description Aided by Neutron Scattering Experiments and Ab Initio Molecular Dynamics Simulations, J. Phys. Chem. B, 2018, 122, 3296–3306 CrossRef.
- M. Kohagen, P. E. Mason and P. Jungwirth, Accounting for Electronic Polarization Effects in Aqueous Sodium Chloride via Molecular Dynamics Aided by Neutron Scattering, J. Phys. Chem. B, 2016, 120, 1454–1460 CrossRef CAS.
- Z. Wang, Y. Yang, D. L. Olmsted, M. Asta and B. B. Laird, Evaluation of the constant potential method in simulating electric double-layer capacitors, J. Chem. Phys., 2014, 141(18), 184102 CrossRef.
- Z. Wang, D. L. Olmsted, M. Asta and B. B. Laird, Electric potential calculation in molecular simulation of electric double layer capacitors, J. Phys.: Condens. Matter, 2016, 28, 464006 CrossRef.
- E. E. Fileti, Electric double layer formation and storing energy processes on graphene-based supercapacitors from electrical and thermodynamic perspectives, J. Mol. Model., 2020, 26(6), 159 CrossRef CAS.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé-Hoover chains: The canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- I. Pethes, The structure of aqueous lithium chloride solutions at high concentrations as revealed by a comparison of classical interatomic potential models, J. Mol. Liq., 2018, 264, 179–197 CrossRef CAS.
- I. Harsányi, L. Temleitner, B. Beuneu and L. Pusztai, Neutron and X-ray diffraction measurements on highly concentrated aqueous LiCl solutions, J. Mol. Liq., 2012, 165, 94–100 CrossRef.
- A. Luzar and D. Chandler, Hydrogen-bond kinetics in liquid water, Nature, 1996, 379, 55–57 CrossRef CAS.
- D. Laage and J. T. Hynes, Reorientional dynamics of water molecules in anionic hydration shells, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11167–11172 CrossRef CAS.
- P. F. F. Almeida and W. L. C. Vaz, in Structure and dynamics of membranes: From cells to vesicules, ed. R. Lipowsky and E. Sackmann, Elsevi., Amsterdam, 1995, pp. 305–357 Search PubMed.
- B. Hess, Determining the shear viscosity of model liquids from molecular dynamics simulations, J. Chem. Phys., 2002, 116, 209 CrossRef CAS.
- G.-J. Guo, Y.-G. Zhang, K. Refson and Y.-J. Zhao, Viscosity and stress autocorrelation function in supercooled water: a molecular dynamics study, Mol. Phys., 2002, 100, 2617–2627 CrossRef CAS.
- K. Tanaka, A Physico-chemical Study of Concentrated Aqueous Solutions of Lithium Chloride, Z. Naturforsch., A: Phys. Sci., 1991, 46(1–2), 141–147 CrossRef CAS.
- C. Schröder, M. Haberler and O. Steinhauser, On the computation and contribution of conductivity in molecular ionic liquids, J. Chem. Phys., 2008, 128(13), 134501 CrossRef.
- S. Pratihar and A. Chandra, A first principles molecular dynamics study of lithium atom solvation in binary liquid mixture of water and ammonia: Structural, electronic, and dynamical properties, J. Chem. Phys., 2011, 134, 1–9 Search PubMed.
- X. Li and Z. Z. Yang, Hydration of Li +-ion in atom-bond electronegativity equalization method-7P water: A molecular dynamics simulation study, J. Chem. Phys., 2005, 122(8), 084514 CrossRef.
- D. Saha and A. Mukherjee, Impact of Ions on Individual Water Entropy, J. Phys. Chem. B, 2016, 120, 7471–7479 CrossRef CAS PubMed.
- P. G. Kusalik and I. M. Svishchev, The spatial structure in liquid water, Science, 1994, 265, 1219–1221 CrossRef CAS PubMed.
- E. E. Fileti and G. Colherinhas, Investigating the asymmetry in the EDL response of C60/graphene supercapacitors, Phys. Chem. Chem. Phys., 2019, 21, 15362–15371 RSC.
- D. A. C. Da Silva, A. J. Paulista Neto, A. M. Pascon, E. E. Fileti, L. R. C. Fonseca and H. G. Zanin, Exploring doped or vacancy-modified graphene-based electrodes for applications in asymmetric supercapacitors, Phys. Chem. Chem. Phys., 2020, 22, 3906–3913 RSC.
- E. Paek, A. J. Pak and G. S. Hwang, A Computational Study of the Interfacial Structure and Capacitance of Graphene in [BMIM][PF6] Ionic Liquid, J. Electrochem. Soc., 2013, 160, A1–A10 CrossRef CAS.
- F. Malchik, N. Shpigel, M. D. Levi, T. S. Mathis, A. Mor, Y. Gogotsi and D. Aurbach, Superfast high-energy storage hybrid device composed of MXene and Chevrel-phase electrodes operated in saturated LiCl electrolyte solution, J. Mater. Chem. A, 2019, 7, 19761–19773 RSC.
- Q. Liu, J. Zhou, C. Song, X. Li, Z. Wang, J. Yang, J. Cheng, H. Li and B. Wang, 2.2 V high performance symmetrical fiber-shaped aqueous supercapacitors enabled by “water-in-salt” gel electrolyte and N-Doped graphene fiber, Energy Storage Mater., 2020, 24, 495–503 CrossRef.
- X. Bu, L. Su, Q. Dou, S. Lei and X. Yan, A low-cost “water-in-salt” electrolyte for a 2.3 V high-rate carbon-based supercapacitor, J. Mater. Chem. A, 2019, 7, 7541–7547 RSC.
- Z. Li, G. Jeanmairet, T. Méndez-Morales, B. Rotenberg and M. Salanne, Capacitive Performance of Water-in-Salt Electrolytes in Supercapacitors: A Simulation Study, J. Phys. Chem. C, 2018, 122, 23917–23924 CrossRef CAS.
| This journal is © the Owner Societies 2022 |