Stable copernicium hexafluoride (CnF6) with an oxidation state of VI+†
Shu-Xian
Hu
 a and
Wenli
Zou
a and
Wenli
Zou
 *b
*b
aDepartment of Physics, University of Science and Technology Beijing, Beijing 100083, P. R. China
bInstitute of Modern Physics, Northwest University, and Shaanxi Key Laboratory for Theoretical Physics Frontiers, Xi'an, Shaanxi 710127, P. R. China. E-mail: zouwl@nwu.edu.cn
First published on 30th November 2021
Abstract
As the heaviest group 12 element known currently, copernicium (Cn) often presents the oxidation states of I+, II+, and rarely IV+ as in its homologue mercury. In this work we systematically studied the stability of some oxides, fluorides, and oxyfluorides of Cn by two-component relativistic calculations and found that the CnF6 molecule with an oxidation state of VI+ has an extraordinary stability. CnF6 may decompose into CnF4 by conquering an energy barrier of about 34 kcal mol−1 without markedly releasing heat. Our results indicate that CnF6 may exist under some special conditions.
1 Introduction
The elements of group 12 with the electronic configuration (n − 1)d10ns2 usually contribute only the two ns valence electrons for bonding, and consequently their highest oxidation state (OS) is II+. Due to the stability of fully occupied (n − 1) d orbitals, they are commonly not considered to be transition metal elements by chemists. This perspective has been partly changed since the HgF4 molecule with an OS of IV+ was experimentally verified,1 which is distinguished from Zn and Cd where their outer d-orbitals are too inert to form a chemical bond; very recently, the kinetically stable HgF6 molecule was also predicted in theory, where the mercury atom presents an OS of VI+.2Moving to the heavier element copernicium (Cn with Z = 112) in group 12, the half-life of its longest-lived known isotope 285Cn being as long as 34 seconds,3 it was experimentally confirmed that Cn has more metallic character than early expected noble-gas-like behavior via the interaction with a gold surface,4 whereas modern first-principle simulations showed that Cn is a solid semiconductor5 or a volatile liquid.6,7 Because of the large relativistic 7s contraction associated with the 6d expansion, the electronic configuration of Cn at its ground state is 6d3/247s26d5/26 at the full relativistic level8 and becomes 6d3/247s26d5/25 for Cn+ and 6d3/247s26d5/24 for Cn2+.9 Therefore, the extended 6d5/2 spinors may be involved in chemical bonding which makes Cn adopt some high oxidation states in suitable conditions.8 Previous theoretical calculations have shown that CnF4 (IV+) is more stable than CnF2 (II+) in the decomposition CnF4 → CnF2 + F2,8,10,11 but this is contrary to CnCl4.10,11 Inspired by HgF6 previously studied by us,2 it raises an interesting question of whether Cn can form a compound with a high OS of VI+. In this study, we have examined the stability of a series of Cn oxides, fluorides, and oxyfluorides and explored the roles of Cn 6d and 7s orbitals in the stabilization.
2 Computational details
For super-heavy elements the total spin S is not a good quantum number anymore due to a very strong spin–orbit coupling, and therefore two-component relativistic methods are performed throughout this study, except some analyses of properties.In the two-component relativistic density functional theory (DFT) calculations, the PBE0 functional12,13 is combined with either the spin–orbit relativistic effective core potentials (SOECP) to replace 92 (for Cn) and 2 (O and F) core electrons14,15 or the all-electron exact two-component (X2C) relativistic Hamiltonian16,17 with the atomic mean-field (AMF) approach for two-electron SO integrals18 and the atomic block approximation for unitary transformation (AU).19 AU replaces the molecular unitary transformation in the full X2C by a series of atomic ones, which is nearly a lossless approximation to X2C for light atom–light atom and heavy atom–light atom types of bonds, and may speed up analytic derivative calculations.19 The corresponding basis sets are ECP92MDFQ-TZVP (Cn)15 and Pitzer's cc-pVTZ-PP (O and F)20 for SOECP/PBE0, whereas re-contracted Dyall-VTZP21 (Cn; see the ESI†) and x2c-TZVPall-2c22 (F) are adopted for X2C-AU/PBE0. All the atomic and molecular systems in this study are closed-shell ones,‡ except O, F, O2, and CnF. For these open-shell systems, their closed-shell monoanions (or dianions) are calculated instead using two-component DFT and then corrected using the first (or second) ionization energies by the two-component Fock-space CCSD (coupled cluster with single and double excitation) method.23
In order to capture electronic correlations more accurately, the two-component CCSD(T) method (CCSD with perturbative triple excitations) combined with SOECP is also used to optimize the geometries of Cn fluorides analytically,24 where all the electrons, except the core ones replaced by SOECP,14,15 are correlated. The adopted valence basis sets are ECP92MDFQ-TZVP for Cn15 and the re-contracted cc-pVTZ-PP for F.25 At the optimized geometries, a two-point extrapolation scheme26 with triple- and quadruple-ζ basis sets15,25 is carried out to estimate the complete basis set (CBS) limit (see the ESI† for details).
The DIRAC 1827 and CFOUR 2.0β28 program packages are used for SOECP/PBE0 and SOECP/CCSD(T) calculations, respectively, whereas the X2C-AU/PBE0 calculations are performed using the BDF program29 to utilize the analytic derivative algorithm for geometry optimization and vibrational frequency calculations.19 The oxidation states are estimated using the LOBA (localized orbital bonding analysis) procedure30 implemented in the Multiwfn31 program.
3 Results
3.1 Stability of Cn oxides, fluorides, and oxyfluorides
Table 1 collects the decomposition energies (ΔE) of oxides, fluorides, and oxyfluorides of Cn calculated using the two-component relativistic DFT with the PBE0 hybrid functional12,13 and SOECP, which are compared with literature data.10,11,32 The zero-point energies (ZPEs) are not included in these results. In the Cn fluorides (decomposition reactions 1–5), CnF4 is more stable than CnF2, being consistent with early studies.8,11 More interestingly, the energy change in reaction 5 is quite small, indicating that CnF6 is more likely to exist than the lighter homologue HgF6 by comparing their reaction energies.2 The decomposition of CnF6 will be comprehensively studied later by more accurate methods. In the decomposition of Cn oxides (reactions 6–10), the dissociation energy of CnO is only 5.7 kcal mol−1, being close to the one of 4.6 kcal mol−1 reported by Titov et al.32 and comparable to the value of 4.7 kcal mol−1 for the homologue HgO.33 CnO2 has a considerable vertical excitation energy of 1.44 eV by SOECP/TDDFT for the first excited spinor state (I)0u−, and it is 2 and 73 kcal mol−1 more stable in energy than CnO and CnO3, respectively, according to reactions 7 and 9. However, the exothermic reaction 8 indicates that CnO2 is not thermodynamically stable even if it exists. As for the Cn oxyfluorides CnOF2 and CnO2F2 (reactions 11–14), they are thermodynamically unstable and could decompose spontaneously into CnF2 and O2, so there is no possibility of their existence.| No. | Reactant | Symmetry | Product | ΔE (kcal mol−1) | |
|---|---|---|---|---|---|
| TWa | Reference | ||||
| a This work. b 4c-Dirac–Fock MP2 results from ref. 10. c 2c-ZORA/B3LYP/STO-QZ4P results from ref. 11. d Kramers-unrestricted SOECP/PBE0 results from ref. 32. | |||||
| 1 | CnF | C ∞v | Cn + F | 18.0 | 13.4b |
| 2 | CnF2 | D ∞h |
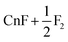
|
63.3 | |
| 3 | Cn + F2 | 62.3 | 60.3b, 63.7c | ||
| 4 | CnF4 | D 4h | CnF2 + F2 | 28.2 | 23.1,b 27.4c |
| 5 | CnF6 | O h | CnF4 + F2 | −1.4 | |
| 6 | CnO | C ∞v | Cn + O | 5.7 | 4.6d |
| 7 | CnO2 | D ∞h |
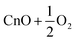
|
2.2 | |
| 8 | Cn + O2 | −50.7 | |||
| 9 | CnO3 | D 3h |
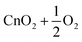
|
−73.0 | |
| 10 | CnO + O2 | −70.8 | |||
| 11 | CnOF2 | C 2v | CnO + F2 | 35.2 | |
| 12 |
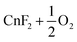
|
−79.9 | |||
| 13 | CnO2F2 | C 2v | CnO2 + F2 | 4.6 | |
| 14 | CnF2 + O2 | −108.3 | |||
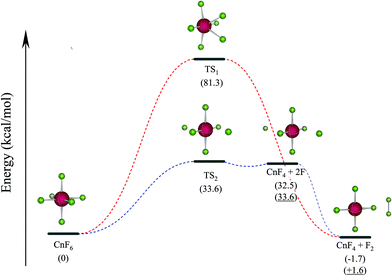
To further confirm the stability of CnF6, the decomposition reaction (I) CnF6 → CnF4 + F2 (i.e. reaction 5 in Table 1) is studied by X2C-AU/PBE0. Furthermore, reaction (II) CnF6 → CnF4 + 2F not included in Table 1 is also computed at the same level since our early study of HgF6 showed that the homologue reaction HgF6 → HgF4 + 2F is the rate-determining step.2 The two reactions are demonstrated in Fig. 1, whereas the barrier heights at transition states (TS) and reaction energies are collected in Table 2 and are compared with the results by SOECP/PBE0 as well as the more accurate SOECP/CCSD(T)/CBS method.
| Reaction | Methoda | ΔE | ΔEZPE | ΔH298.15 | ΔG298.15 | |
|---|---|---|---|---|---|---|
| a (A) X2C-AU/PBE0, (B) SOECP/PBE0 and (C) SOECP/CCSD(T)/CBS. b ZPE and thermochemical quantities are computed by X2C-AU/PBE0. | ||||||
| (I) | (A) | −0.1 | −1.7 | −1.1 | −13.0 | |
| (B)b | −1.4 | −3.0 | −2.4 | −14.3 | ||
| (C)b | 3.2 | 1.6 | 2.2 | −9.7 | ||
| TS1 | (A) | 82.9 | 81.3 | 81.6 | 78.6 | |
| (II) | (A) | 35.7 | 32.5 | 34.0 | 15.7 | |
| (B)b | 35.7 | 32.5 | 34.0 | 15.7 | ||
| (C)b | 36.8 | 33.6 | 35.1 | 16.8 | ||
| TS2 | (A) | 36.4 | 33.6 | 34.7 | 28.3 | |
Reaction (I) is slightly exothermic by X2C-AU/PBE0 and SOECP/PBE0 but endothermic by SOECP/CCSD(T)/CBS in enthalpies at 298.15 K (ΔH298.15); nevertheless, after including the entropic contributions (mainly due to the translational entropy), the negative Gibbs free energy changes at 298.15 K (ΔG298.15) at the three levels of theory imply that this reaction is exothermic at high temperatures. Because of a very high energy barrier at TS1 of about 81 kcal mol−1 to be conquered, reaction (I) seems very difficult to take place. Reaction (II) is intensely endothermic with a lower barrier of about 34 kcal mol−1 at TS2. From the spin-free (sf) perspective, TS2 is mainly caused by the avoided crossing between the closed-shell ground state and the repulsive first triplet state (F˙⋯CnF4⋯F˙). It should be noted that the two isolated fluorine atoms in the products may be severely exothermic by forming a fluorine molecule, leading to the same products as in reaction (I), and moreover this process may be accelerated if there are other isolated fluorine atoms detached from adjacent CnF6 molecules. Consequently, the final products of CnF6 decomposition are CnF4 and F2, which is protected by a barrier of about 34 kcal mol−1 at TS2. Utilizing the transition state theory with ΔG298.15 = 28.3 kcal mol−1 given in Table 2, the estimated rate constant of CnF6 decomposition is 1.1 × 10−8 s−1, leading to a half-life of 2.0 years. It can be expected accordingly that CnF6 is both thermodynamically and dynamically stable at least at low temperatures under gas phase or rare-gas matrix isolation conditions. This result corrects also Malli's early study of CnF6 (probably the first and the only study of CnF6 published before this work) where CnF6, as well as HgF4 and CnF4, was considered “unbound” by Dirac–Hartree–Fock calculations.34 This contradiction is mainly due to the lack of important electronic correlations in the latter: a comparison between the SOECP/HF and SOECP/CCSD(T) energies shows that the contributions of electronic correlations are about +25 (HgF4), +17 (CnF4), and +31 kcal mol−1 (CnF6) to ΔE.
3.2 Properties of Cn fluorides
Some structural and electronic properties of Cn fluorides 285CnFn (n = 1, 2, 4, and 6) are summarized in Table 3, including point group symmetry, Cn–F bond length (RCn–F), energy gap (εHOMS–LUMS) between the highest occupied molecular spinor (HOMS) and the lowest unoccupied molecular spinor (LUMS), vertical excitation energy of the first excited spinor state (T1v), generalized Mayer's bond order (BO) of the Cn–F bond, natural electron configuration and NPA atomic charge (Q) of Cn by natural bond orbital (NBO) analysis35 implemented in the NBO 6.0 program,36 Cremer's adiabatic force constant37,38 of local Cn–F bond stretching (kaCn–F), and harmonic vibrational frequencies (ω) with the corresponding irreducible representation. Mulliken population analyses on spin-free and spin-dependent wavefunctions are consistent within 10%, and the deviation of spin-free NBO analysis may be expected to be within this range.| CnF | CnF2 | CnF4 | CnF6 | |
|---|---|---|---|---|
| a By SOECP/PBE0. b By SOECP/CCSD(T). c Spin-free calculations. | ||||
| Symmetry | C ∞v | D ∞h | D 4h | O h |
| R Cn–F (Å) | 2.069 | 1.920 | 1.927 | 1.933 |
| 2.108a | 1.926a | 1.929a | 1.932a | |
| — | 1.958b | 1.948b | 1.951b | |
| OSCn | I+ | II+ | IV+ | VI+ |
| ε HOMS–LUMS (eV) | 4.06 | 7.19 | 6.22 | 5.68 |
| T 1v (eV) |
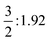
|
2g: 4.69 | A 1g: 3.23 | E g: 2.92 |
| BOCn–F | 0.51 | 0.81 | 0.82 | 0.81 |
| Configurationc | 6d9.77s1.8 | 6d9.47s1.4 | 6d8.97s1.0 | 6d8.57s0.8 |
| Q Cn (|e|)c | +0.44 | +1.11 | +1.97 | +2.57 |
| k a Cn–F (mDyn Å−1) | 1.92 | 4.77 | 4.63 | 4.50 |
| ω (cm−1) | σ +: 427 | πu: 227 | b 2g: 167 | t 2g: 163 |
| σ g +: 673 | b 2u: 212 | t 2u: 230 | ||
| σ u +: 676 | a 2u: 243 | t 1u: 259 | ||
| e u: 248 | e g: 621 | |||
| b 1g: 639 | a 1g: 644 | |||
| a 1g: 659 | t 1u: 690 | |||
| e u: 684 | ||||
The closed-shell ground states of the polyatomic CnFn molecules may be confirmed by the large HOMS–LUMS gaps and the considerable first excitation energies, and the 3(n + 1)-6 real frequencies without an imaginary one guarantee these high-symmetric minima. The BO values of Cn–F show that it is basically a single bond in CnF2, CnF4, and CnF6 but a half bond in CnF, which are in qualitative agreement with the trends of Cn–F bond lengths and force constants. The half bond in CnF may be well explained by the three-electron in two-orbital model:39 the covalent interactions between the Cn 6dσ + 7s hybrid orbital and F 2pσ shift the former remarkably to form a singly occupied antibonding orbital, leading to a simplified electronic configuration of (σ)2(σ*)1 as in the case of the lighter homologue HgF, and therefore the empirical bond order is (2 − 1)/2 = 0.5. This means that the Nalewajski–Mrozek bond order of 1.0 for HgF in ref. 2 might be too rough.
With the help of natural localized molecular orbital analysis, the atomic composition of each Cn–F natural bond orbital in CnFn may be estimated, as provided in Table 4. It can be seen that the bond orbitals are mainly due to the Cn 6d–F 2pσ covalent interactions, accompanied by some secondary Cn 7s–F 2pσ ones, being contrary to the cases of HgFn2 due to the exchanging order of (n)s and (n − 1)d. The (n)p hybridizations also play important roles in lighter homologues HgF2, HgF4, and HgF62 but are negligible in CnF2, CnF4, and CnF6, indicating that Cn 6d is much easier to bond than Hg 5d without the involvement of Cn 7p.
| Species | Composition of each natural bond orbital |
|---|---|
| CnF | 54% Cn (40% 7s + 60% 6d), 46% F (1% 2s + 99% 2pσ) |
| CnF2 | 27% Cn (49% 7s + 50% 6d), 73% F (8% 2s + 92% 2pσ) |
| CnF4 | 33% Cn (34% 7s + 65% 6d), 67% F (5% 2s + 95% 2pσ) |
| CnF6 | 38% Cn (24% 7s + 76% 6d), 61% F (4% 2s + 96% 2pσ) |
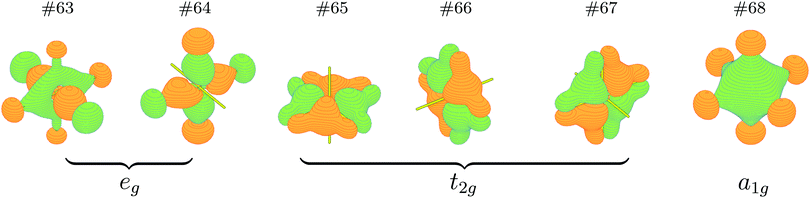
It is just very apparent that the NPA atomic charges of Cn are almost equal to those of the lost electrons on the 6d7s valence orbitals, which significantly increase from +0.44 |e| for CnF (I+) to +1.11 |e| for CnF2 (II+), +1.97 |e| for CnF4 (IV+), and +2.57 |e| for CnF6, so the oxidation state of Cn in CnF6 should be the highest one in these species. On the other hand, six bonding orbitals for the six Cn–F single bonds of CnF6 have been formed, as plotted in Fig. 2. These two proofs suggest that the oxidation state of Cn in CnF6 can be as large as VI+, which is broadly in line with the ratio of NPA atomic charges of Cn in CnF4 and CnF6, i.e. QIV+Cn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QVI+Cn = 0.76
QVI+Cn = 0.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ≈ OSIV+Cn
1 ≈ OSIV+Cn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OSVI+Cn = 0.67
OSVI+Cn = 0.67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. As a result of validation, the formal oxidation states of Cn in the four fluorides are estimated by LOBA, being respectively I+, II+, IV+, and VI+ as we expect.
1. As a result of validation, the formal oxidation states of Cn in the four fluorides are estimated by LOBA, being respectively I+, II+, IV+, and VI+ as we expect.
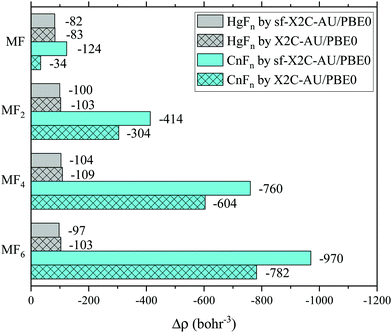
In experiments, the oxidation states of target atoms may be probed by the Mössbauer isomer shifts, which are closely related to the contact densities or effective contact densities, i.e. the total electron densities of occupied s and p1/2 spinors around the nucleus.40,41 We have computed the effective contact densities of Cn in the fluorides by X2C-AU/PBE0 as well as the spin-free variant (see also the sf-X2C-AU/CCSD(T) results in the ESI†). The density changes (Δρ) relative to the reference density of the isolated Cn atom are shown in Fig. 3 and are compared with the results of mercury fluorides. Contrary to the non-monotonic decrease of density in mercury fluorides,40,41 Δρ in copernicium fluorides decreases monotonically in a greater ratio, being proportional to the oxidation state of Cn. The two different trends of Δρ are not surprising since the screening effect of Cn 6d5/2 (or 6d in the spin-free case) is relatively weaker than the one of Hg 5d5/2 (or 5d) considering E(6d3/2) < E(7s) < E(6d5/2) (or E(7s) < E(6d)).
4 Conclusions
In this study we reported a stable compound of copernicium, CnF6. Comprehensive calculations show that the CnF6 molecule is protected by a considerable energy barrier of about 34 kcal mol−1 in the decomposition CnF6 → CnF4 + F2, being almost as stable as CnF4, and therefore CnF6 may exist under cryogenic conditions in rare-gas matrices as the experimental ones of HgF4.1 Various analyses of properties indicate that the Cn atom in CnF6 possesses a rarely high oxidation state of VI+, which may be attributed to the relativistic contraction of 7s and expansion of 6d. In the oxides and oxyfluorides of Cn, however, the oxidation states of both IV+ and VI+ are not stable due to the weaker electronegativity of oxygen relative to fluorine, and thus CnF4 and CnF6 are probably the only two species of Cn with higher oxidation states than II+. We hope that our results will deepen the understanding of group 12 chemistry.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 21976014 and 22073072) and was also supported by The Double First-class University Construction Project of Northwest University.Notes and references
- X. Wang, L. Andrews, S. Riedel and M. Kaupp, Angew. Chem., Int. Ed., 2007, 46, 8371–8375 CrossRef CAS.
- C. Gao, S.-X. Hu, H. Han, G. Guo, B. Suo and W. Zou, Comput. Theor. Chem., 2019, 1160, 14–18 CrossRef CAS.
- Y. T. Oganessian, V. K. Utyonkov, Y. V. Lobanov, F. S. Abdullin, A. N. Polyakov, I. V. Shirokovsky, Y. S. Tsyganov, G. G. Gulbekian, S. L. Bogomolov, B. N. Gikal, A. N. Mezentsev, S. Iliev, V. G. Subbotin, A. M. Sukhov, A. A. Voinov, G. V. Buklanov, K. Subotic, V. I. Zagrebaev, M. G. Itkis, J. B. Patin, K. J. Moody, J. F. Wild, M. A. Stoyer, N. J. Stoyer, D. A. Shaughnessy, J. M. Kenneally, P. A. Wilk, R. W. Lougheed, R. I. Il'kaev and S. P. Vesnovskii, Phys. Rev. C, 2004, 70, 064609 CrossRef.
- R. Eichler, N. V. Aksenov, A. V. Belozerov, G. A. Bozhikov, V. I. Chepigin, S. N. Dmitriev, R. Dressler, H. W. Gäggeler, A. V. Gorshkov, M. G. Itkis, F. Haenssler, A. Laube, V. Y. Lebedev, O. N. Malyshev, Y. T. Oganessian, O. V. Petrushkin, D. Piguet, A. G. Popeko, P. Rasmussen, S. V. Shishkin, A. A. Serov, A. V. Shutov, A. I. Svirikhin, E. E. Tereshatov, G. K. Vostokin, M. Wegrzecki and A. V. Yeremin, Angew. Chem., Int. Ed., 2008, 47, 3262–3266 CrossRef CAS PubMed.
- N. Gaston, I. Opahle, H. W. Gäggeler and P. Schwerdtfeger, Angew. Chem., Int. Ed., 2007, 46, 1663–1666 CrossRef CAS.
- J.-M. Mewes, O. R. Smits, G. Kresse and P. Schwerdtfeger, Angew. Chem., Int. Ed., 2019, 58, 17964–17968 CrossRef CAS.
- J.-M. Mewes and P. Schwerdtfeger, Angew. Chem., Int. Ed., 2021, 60, 7703–7709 CrossRef CAS.
- M. Seth, P. Schwerdtfeger and M. Dolg, J. Chem. Phys., 1997, 106, 3623 CrossRef CAS.
- D. C. Hoffman, D. M. Lee and V. Pershina, in The Chemistry of the Actinide and Transactinide Elements, 4th edn, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer, Dordrecht, 2010, p. 1672 Search PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2011, 129, 603–613 Search PubMed.
- A. Ghosh and J. Conradie, Eur. J. Inorg. Chem., 2016, 2989–2992 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1998, 110, 6158–6170 CrossRef.
- L. F. Pacios and P. A. Christiansen, J. Chem. Phys., 1985, 82, 2664–2671 CrossRef.
- T. Hangele and M. Dolg, J. Chem. Phys., 2013, 138, 044104 CrossRef PubMed.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104 CrossRef PubMed.
- J. Liu and L. Cheng, J. Chem. Phys., 2018, 148, 144108 CrossRef.
- W. Zou, G. Guo, B. Suo and W. Liu, J. Chem. Theory Comput., 2020, 16, 1541–1554 CrossRef CAS.
- J.-P. Blaudeau, S. R. Brozell, S. Matsika, Z. Zhang and R. M. Pitzer, Int. J. Quant. Chem., 2000, 77, 516–520 CrossRef CAS.
- K. G. Dyall, Theor. Chem. Acc., 2011, 129, 603–613 Search PubMed.
- P. Pollak and F. Weigend, J. Chem. Theory Comput., 2017, 13, 3696–3705 CrossRef CAS PubMed.
- L. Visscher, E. Eliav and U. Kaldor, J. Chem. Phys., 2001, 115, 9720–9726 CrossRef CAS.
- F. Wang and J. Gauss, J. Chem. Phys., 2008, 129, 174110 CrossRef.
- D. Deng, Y. Lian and W. Zou, Chem. Phys. Lett., 2017, 685, 251–258 CrossRef.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- T. Saue, R. Bast, A. S. P. Gomes, H. J. A. Jensen, L. Visscher, I. A. Aucar, R. Di Remigio, K. G. Dyall, E. Eliav, E. Fasshauer, T. Fleig, L. Halbert, E. D. Hedegård, B. Helmich-Paris, M. Iliaš, C. R. Jacob, S. Knecht, J. K. Laerdahl, M. L. Vidal, M. K. Nayak, M. Olejniczak, J. M. H. Olsen, M. Pernpointner, B. Senjean, A. Shee, A. Sunaga and J. N. P. van Stralen, J. Chem. Phys., 2020, 152, 204104 CrossRef CAS PubMed.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS.
- Y. Zhang, B. Suo, Z. Wang, N. Zhang, Z. Li, Y. Lei, W. Zou, J. Gao, D. Peng, Z. Pu, Y. Xiao, Q. Sun, F. Wang, Y. Ma, X. Wang, Y. Guo and W. Liu, J. Chem. Phys., 2020, 152, 064113 CrossRef PubMed.
- A. J. W. Thom, E. J. Sundstrom and M. Head-Gordon, Phys. Chem. Chem. Phys., 2009, 11, 11297–11304 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS.
- A. Oleynichenko, A. Zaitsevskii, S. Romanov, L. V. Skripnikov and A. V. Titov, Chem. Phys. Lett., 2018, 695, 63–68 CrossRef CAS.
- B. C. Shepler and K. A. Peterson, J. Phys. Chem. A, 2003, 107, 1783–1787 CrossRef CAS.
- G. L. Malli, in Fundamental World of Quantum Chemistry: A Tribute to the Memory of Per-Olov Löwdin, ed. E. J. Brändas and E. S. Kryachko, Springer, Dordrecht, 2004, vol. III, pp. 334–348 Search PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO version 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2013 Search PubMed.
- Z. Konkoli and D. Cremer, Int. J. Quant. Chem., 1998, 67, 1–9 CrossRef CAS.
- E. Kraka, W. Zou and Y. Tao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, 1480 Search PubMed.
- D. Cremer, E. Kraka and M. Filatov, ChemPhysChem, 2008, 9, 2510–2521 CrossRef CAS PubMed.
- S. Knecht, S. Fux, R. Van Meer, L. Visscher, M. Reiher and T. Saue, Theor. Chem. Acc., 2011, 129, 631–650 Search PubMed.
- H. Zhu, C. Gao, M. Filatov and W. Zou, Phys. Chem. Chem. Phys., 2020, 22, 26776–26786 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Computational details, optimized structures by SOECP/PBE0, X2C-AU/PBE0, and SOECP/CCSD(T), and harmonic vibrational frequencies by X2C-AU/PBE0. See DOI: 10.1039/d1cp04360a |
| ‡ Although CnO2 is an open-shell system in the spin-free case with a configuration of πg2, it becomes a closed-shell one in the two-component case where the configuration is π1/2g2π3/2g0 with a spin–orbit splitting of about 3.0 eV. |
| This journal is © the Owner Societies 2022 |