A combined DFT-predictive and experimental exploration of the sensitivity towards nucleofuge variation in zwitterionic intermediates relating to mechanistic models for unimolecular chemical generation and trapping of free C₂ and alternative bimolecular pathways involving no free C₂

Abstract

Following the recent report of the chemical generation and trapping at room temperatures of C₂, generated from an alkynyl phenyl iodonium salt, a computational analysis had indicated that both unimolecular fragmentation and bimolecular substitution mechanisms for the process could be envisaged. Here a combined theoretical and experimental analysis explores how the energetics of these mechanisms and resulting experimental products respond to variation in the nucleofuge. When the phenyl iodonium nucleofuge is replaced by pyridinium, trapping products are again obtained, which we conclude favours a bimolecular mechanism involving no free C₂. Trapped products in greater yield were also observed using dibenzothiophenium as the nucleofuge in both condensed solution phase and most significantly in a two-flask room temperature experiment in which a volatile species, presumed to be C₂, is transferred and trapped in a second flask. The energetics of the unimolecular fragmentation process producing C₂ are predicted to be too high to correspond to a facile thermal reaction, which means that an experimental/theoretical dichotomy remains to be explained.

---

Introduction

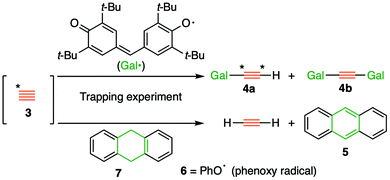
The long history¹ of the diatomic species C₂, of recent interest because of the intense debates about its bond order (2,3 or 4)² took a new turn recently regarding its reactivity, with the report of room temperature generation and trapping of this species by chemical means.^3,4 The reaction was thought to proceed at ambient or low temperatures from the transient zwitterionic intermediate 2 (X = IPh), itself formed by treating precursor 1 with a source of fluoride anion. The proposed mechanism involved unimolecular fragmentation of 2 to produce X = iodobenzene and 3 (free singlet state C₂, Fig. 1), followed by its trapping in solution using either 9,10-dihydroanthracene 7 or galvinoxyl radical and resulting in isolation of products 5/4 and from which participation of free C₂ was inferred (Fig. 2).^3,4 Scrambling of ¹³C label in product 4a (Fig. 2, C_α : C_β = ca. 8 : 2–1 : 1) also supported this conclusion.³

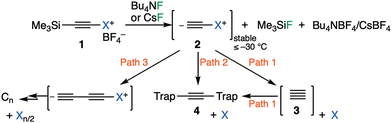Fig. 1 Reaction scheme for proposed^3,4 chemical synthesis of singlet free C₂3 with alternatives. Path 1: unimolecular fragmentation followed by bimolecular trapping. Path 2: bimolecular trapping by 1,1- or 1,2-substitution. Path 3: bimolecular dimerisation via 1,1- or 1,2-substitution.

Fig. 2 Trapping experiments used for inferring the existence of singlet free C₂.

A commentary on this report^5,6 observed that the computed thermodynamics of this reaction using three different estimates indicated that the production of free C₂ and X = iodobenzene (path 1, Fig. 1) was likely to be highly endoenergic, in the range of +(43–53) kcal mol⁻¹ and therefore that room temperature production of C₂ seemed unlikely. A follow up analysis⁷ explored the possibility that bimolecular reactions between 2 and the traps (path 2, Fig. 1), or between 2 and itself to give ultimately polymeric carbon (path 3, Fig. 1), might provide alternative mechanistic routes to the observed products and which would also rationalise the ¹³C scrambling, whilst avoiding liberation of free C₂. Here this study is extended to computing the bimolecular transition states and unimolecular fragmentation energies using a variety of different leaving groups X, in order to establish how the energetics of the mechanistic paths shown in Fig. 1 respond to the nature of the nucleofuge group X (Fig. 1). As a result of these studies we felt in appropriate to then suggest that the original experiments be repeated with a new selection of leaving groups X. Accordingly, the experimental response of the putative C₂ precursors 1a–d with different nucleofuges (1a: X = iodo, 1b: λ³-iodanyl, 1c: pyridinio, and 1d: dibenzosulfonio groups) to trapping experiments was undertaken to establish the scope of this method for generating putative 3.

Computational details

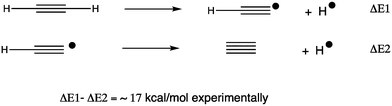
The CHAMP portal⁸ was used as an electronic notebook for managing the project, enabled with one-click FAIR data publishing to the Imperial College data repository.⁹ To study the energetics and mechanism of these reactions, a calibrated procedure was selected as used previously;⁶ ωB97XD¹⁰/Def2-TZVPPD¹¹/SCRF¹² = dichloromethane solvent.¹³ The calibration involved comparison of computed energies for C₂¹⁴ against the reaction sequence shown in Scheme 1, the energies of which are directly derived from experimental measurements.¹⁵ The CCSD(T) couple-cluster method¹⁶ emerged as closely matching the experimental results for the thermochemistry of formation of C₂. A variety of DFT-based methods were tested and all predicted the energy of the highly correlated C₂ species to be significantly too high; if corrected by 28 kcal mol⁻¹, the ωB97XD DFT method can be brought into congruence with both experiment and the CCSD(T) method. This correction is applied only to reactions involving C₂. For the substitution reactions described below, which do not involve this species, the uncorrected ωB97XD and the CCSD(T) methods agreed^7,14 to within 1.5 kcal mol⁻¹ for a model system X = MeI (larger groups are not computationally viable using the CCSD(T) method, where computation times of >10 years were estimated for the groups X described below). Further cancellation of error might be expected for a range of reactions differing only in the nature of group X (Fig. 1). All located transition states have one negative force constant with the correct vectors, which can be inspected as 3D animated models using a FAIR-enabled version of Table 1.¹⁷

Scheme 1 Calibration reactions for thermochemistry.

Table 1 Calculated ωB97XD/Def2-TZVPPD/SCRF = DCM Free energies for reactions of 2^a

2, X=	ΔΔG(3+X)−2^b	ΔΔG^‡TS1,1^c	ΔΔG^‡TS1,2^c	ΔΔG, unimolecular vs. bimolecular^d
a Calculations at the ωB97XD/Def2-TZVPPD/SCRF = dichloromethane level, data repository collection DOI: 10.14469/hpc/8168 for full details of calculation. b ΔΔG for the reaction 2 →(3 + X) in kcal mol^−1, corrected by −28.0 kcal mol^−1 for estimated error in the calculated ΔG for C2 at this level. c ΔΔG298 transition state activation energies in Hartree for TS1,1 or TS1,2 the substitution step; for a standard state of 0.044M (1 atm). d ΔΔG (kcal mol^−1) for unimolecular fragmentation of ΔG(3+X)−2) – the lower of ΔGTS1,1 or ΔGTS1,2.
2Pyridinium	83.7	30.1	27.9	55.8
Pyridinium + 6^e	83.7	23.8	24.8	59.9
Pyridinium + 7^f	83.7	47.8	27.9	55.8
2Me3P	117.6	45.7	34.5	83.1
2Me2O	42.3	23.7	24.6	18.6
2Me2S	79.6	34.3	27.2	52.4
Me2S + 6	79.6	27.4	24.4	55.2
Me2S + 7	79.6	45.6	28.0	51.6
2Dibenzothiophenium	64.0	32.8	26.9	37.1
Dibenzothiophenium + 6	64.0	27.4	25.0	39.0
2Me2Se	77.1	33.2	28.1	49.1
2Me2Te	82.7	35.4	26.5	56.2
2MeF	−2.4	12.9	14.9	−15.3
2MeCl	32.1	22.7	21.0	11.1
2MeBr	35.6	22.0	19.4	16.2
2MeI	46.0	24.5	21.4	24.6
2PhI	43.6	23.1	19.6	24.0
PhI + 6	43.6	19.6	19.6	24.0
2MeF2I	36.3	20.3	12.5	23.8
MeF2I + 6	36.3	26.3	23.2	13.1

---

Experimental details

Substrates

Iodoalkyne 1a, alkynyl(aryl)-λ³-iodane 1b, N-alkynylpyridinium salt 1c, and S-alkynylsulfonium salt 1d were prepared according to the reported procedures (S1–S4, ESI†). All of these starting materials used were greater than 99% purity, which was confirmed by ¹H NMR. ¹H NMR spectra of 1a–d are shown in the ESI† (Section 4, copies of ¹H NMR spectra and GCMS chart). Tetrabutylammonium fluoride trihydrate (≥98%), 9,10-dihydroanthracene (>98.0%(GC)), galvinoxyl free radical, iodobenzene (>99.0%(GC)), 4-phenylpyridine (>98.0%(GC)), and dibenzothiophene (>98.0%(GC)) were purchased from Tokyo Kasei Co. The purity of these reagents (except for galvinoxyl free radical) was also confirmed by ¹H NMR (NMR spectra are shown in Section 4, copies of ¹H NMR spectra and GCMS chart) prior to use. The purity of galvinoxyl free radical was confirmed by GC/GCMS and was determined to be >99%. Dichloromethane (>99.5% by gas chromatography) was purchased from Kanto Chemical Co., Inc., degassed by purging with argon, and dried with a solvent purification system containing a one-meter column of activated alumina. All trapping reactions were carried out either in a two-necked flask or connected flasks under an argon atmosphere.

General procedure

To a stirred solution of C₂-precursor 1 (0.065 mmol) and trapping agent (50 equivalent for 9,10-dihydroanthracene and 1.2 equivalent for galvinoxyl radical) in dichloromethane (1.3 mL), tetrabutylammonium fluoride trihydrate (1.2 equivalent) was added in one portion at −78 °C and the solution was gradually warmed to room temperature for 3–72 h (disappearance of starting material was monitored by ¹H NMR, except for 1a). After concentration of the reaction mixture under a reduced pressure, the resulting residue was then analyzed by ¹H NMR (ethyl acetate as an internal standard) and atmospheric pressure chemical ionization mass spectrometry (APCIMS). For the trapping reaction with galvinoxyl radical, excess 1,4-cyclohexadiene was added (in order to quench any remaining galvinoxyl radical) prior to ¹H NMR measurement. The formation of acetylene was confirmed by GCMS with a PLOT column (Rt-U-Bond, 0.25 mm × 30 m, 30 °C) or silver nitrate testing.

Solvent-free connected flask experiment

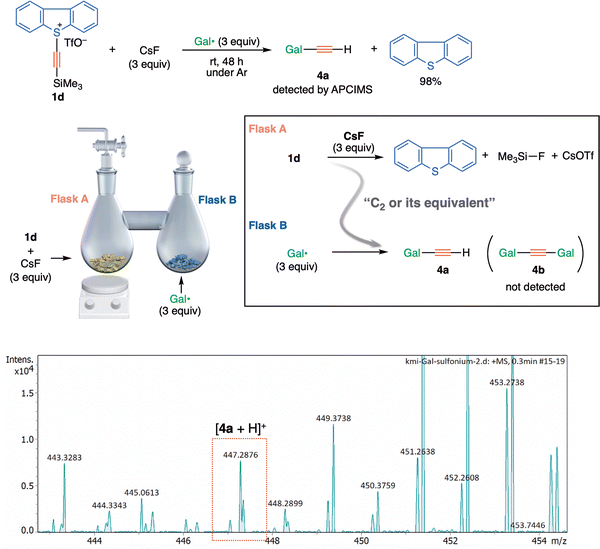
S-(Trimethylsilylethynyl)dibenzothiophenium salt 1d (33 mg, 0.077 mmol) and cesium fluoride (35.0 mg, 0.231 mmol) was placed in one of a pair of connected flasks (Flask A), and galvinoxyl radical (97 mg, 0.231 mmol) was placed in the other flask (Flask B). The reaction mixture in Flask A was vigorously stirred at room temperature for 48 hours under argon. The contents of Flask B were directly analyzed by APCIMS. The contents of Flask A were analyzed by ¹H NMR (ethyl acetate was an internal standard).

Results and discussion

There are two basic mechanisms for the reaction of the zwitterionic species 2, namely unimolecular fragmentation to give 3 (free C₂) followed by bimolecular trapping of this species (Fig. 1, path 1) or immediate bimolecular reactions involving no free C₂ (paths 2 and 3). The presence of the species 2 (X = IPh) has been confirmed during the fluorolysis of alkynyl(aryl)-λ³-iodane with Bu₄NF in dichloromethane and was stable below −30 °C.³ One potential strategy for differentiating between these mechanistic pathways would be to vary the nature of the group X. The leaving group ability of X would be expected to impact directly upon the unimolecular fragmentation path 1, whereas its effect might be attenuated for the bimolecular trapping paths 2 or 3 (Fig. 1). To explore if this hypothesis is correct, the energetics for a variety of new leaving groups X were obtained computationally using density functional theory, with the results collected in Table 1.¹⁷ This shows the energetics of bimolecular dimerization of species 2 (path 3) as well as reaction of 2 with either dihydroanthracene or a phenoxy radical model as trapping agents (path 2). The calculated ωB97XD DFT free energy of the two-stage unimolecular dissociation path 1 needs correction for the exceptional error in the calculated energy of 3 itself, as described previously.^6,14,15 The difference in free energy between the dissociation path 1 and the transition states leading to bimolecular reaction via either 1,1 or 1,2 substitution⁷ (paths 2 or 3) is shown in the last column of the table. The effect the nature of the leaving group X has on this difference will now be discussed.

We start by noting that for the substituents X = Me₃P through to MeF, the calculated free energy of unimolecular dissociation of 2 to give X and 3 (C₂) spans ΔΔG = 117.6 to −2.4 kcal mol⁻¹. Of these, only values <∼35 kcal mol⁻¹ would be considered as thermally accessible below ∼313 K. In contrast, the activation barriers for direct bimolecular reactions of 2 over this span of substituents range from ΔΔG^‡ 34.5 to 12.5 kcal mol⁻¹, a very much smaller span for which the entire range is potentially thermally accessible. The last column in Table 1 indicates the difference in free energy between the unimolecular dissociation path 1 resulting in the formation of 3 from 2 and the lowest energy of the two bimolecular paths 2 and 3 for reaction of 2 involving either 1,1- or 1,2-substitution.⁷ We note that the relative free energy of path 1 in this column should be increased by a further ∼10 kcal mol⁻¹ to reflect the entropic penalty for the bimolecular reaction between 3 and trap, with the thermal barrier for this reaction expected to be very small or even zero.⁷ For leaving groups such as X = pyridinium, the difference between the paths is so large that one might confidently state that only bimolecular paths 2 and 3 are viable. There is only one substituent for which unimolecular dissociation is actually predicted to be more favourable than the bimolecular mode, and that is for X = MeF, which is not a realistic group for synthetic testing. The activation free energy of the bimolecular route for e.g. X = dibenzothiophenium is ∼25 kcal mol⁻¹, which can be considered as falling into a thermally accessible range. This example and X = pyridinium are the ones that were selected for experimental testing, by virtue of their synthetic accessibility.

Following this theoretical evaluation, we turned to an experimental protocol for evaluating the ability of the C₂ precursors 2, as potentially generated from the starting materials 1a–d representing different nucleofuges (X = iodo, λ³-iodanyl, pyridinio, and sulfonio groups respectively), to be trapped using our previous radical trapping protocol.³ Firstly, the attempted reaction of (trimethylsilyl)iodoacetylene (1a, X = iodo) with a fluoride ion source (Bu₄NF) in the presence of galvinoxyl radical or 9,10-dihydroanthracene was investigated (Fig. 3A), but no distinct evidence was obtained for the formation of radical-trapped products (ethynylated galvinoxyl 4a, anthracene 5), nor was acetylene detected and alkyne 1a was recovered exclusively. In sharp contrast, as expected, alkynyl-λ³-iodane 1b (X = λ³-iodanyl), which has ca. 10¹² times greater nucleofuge capability (-I(Ph)X) than an iodo group,¹⁸ led to good yields of trapped products 4a or 5 under similar reaction conditions. This confirms the importance of the nucleofuge in this transformation (Fig. 3B).

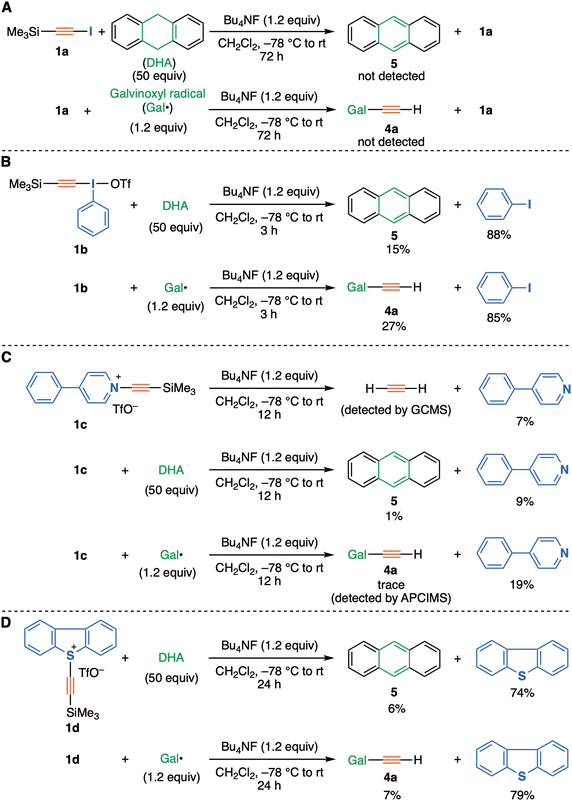Fig. 3 Trapping experiments with (A) iodoacetylene 1a, (B) alkynyl-λ³-iodanes 1b, (C) 4-phenyl-pyridinium salt 1c, (D) dibenzosulfonium salt 1d.

Significantly, the theoretically evaluated pyridinium-type precursor 1c (X = 4-phenylpyridinium triflate) was also found to serve as a precursor. Thus, in the presence/absence of trapping agents, not only acetylene gas but also radical-trapped products 4a or 5 were detected/obtained in low yields, being accompanied by the formation of 4-phenylpyridine (Fig. 3C). Similar to our previous report, the formation of di(galvinoxy)acetylene 4b was not observed in solution, probably due to the rapid hydrogen abstraction of transient ethynyl radical from the solvent, dichloromethane.^3,19 All of these experimental results suggest that the in situ generation of the zwitterionic species 2 could act as a C₂ synthon, even with much a much weaker leaving group such as 4-phenylpyridine. However this result does not distinguish between unimolecular and bimolecular trapping mechanisms (path 1 vs. path 2). The activation free energy for path 2 bimolecular trapping is predicted to be within a thermally accessible range, whereas the energy for path 1 is computed to be 60 + ∼10 = ∼70 kcal mol⁻¹ higher than that for path 2 (Table 1).

Use of the dibenzothiophenium precursor 1d, which bears a more potent nucleofuge than pyridine, has provided further evidence in the form of higher yields of trapped products 4a and 5 as obtained under similar conditions (Fig. 3D). The computed path 2 bimolecular free energy barriers for this substituent and the pyridinium-type substrate were similar (Table 1). Based on these two trapping experiments, we consider that the rate of desilylation yielding intermediate 2 as well as the following processes has a relatively modest dependency on both the electron withdrawing- and the leaving group ability of X in the precursors 1. This is more congruent with the predicted behaviour of path 2 rather than of path 1, for which a much higher dependency on X is predicted.

Significantly however, the solid-state solvent-free connected flask experiment using sulfonium 1d also afforded a trapped product 4a, although to a small extent (Fig. 4). The presence of 4a in a separated flask (Flask B) suggests that the evolution of a volatile species, presumed to be 3, would occur in Flask A, which is consistent with the previous results obtained with alkynyl-λ³-iodane 1b and 1b-¹³C (counter ion: BF₄⁻).^3,19 The absence of di(galvinoxyl)acetylene 4b in Flask B might reflect the poorer ability of 1d (X= dibenzothiophenium) to act as a precursor of 3, compared with 1b (X = λ³-iodanyl) under the reaction conditions.

Fig. 4 Solvent-free connected flask experiment using sulfonium salt 1d-CsF and galvinoxyl radical. (A) Reaction conditions. (B) Details of reaction equipment. (C) Atmospheric-pressure chemical ionisation (APCIMS) spectrum of the contents in a flask B.

At this stage therefore, we cannot explain the discrepancy between the (solid-state solvent-free connected flask) experimental results and theoretical estimations of the energy required to liberate a free C₂ species. An alternative mechanism might be necessary to solve the conundrum.

Conclusions

The single-flask solution phase experiments indicating trapping using two different precursors 2 (X = pyridinium and dibenzothiophenium) are consistent with a bimolecular mechanism (path 2) involving no liberation of free 3. The theoretical free energies of the unimolecular path 1 for X = dibenzothiophenium and particularly for pyridinium are so much higher than it seems less likely that this mechanism could be followed. A mystery remains however for the connected flask trapping experiment, which suggest that the precursor with the good nucleofuge 1d can produce an argon-borne intermediate that results in transfer to flask B and then apparent trapping of C₂ (3). This seemingly indicates that path 1 is followed under these conditions, despite the contra-indications from the theoretical evaluation. More experiments to further confirm the identity of this gas-borne intermediate and perchance provide insight into the experimental/theoretical dichotomy are needed.

Data availability

All relevant FAIR (Findable, Accessible, Interoperable, Reusable) datasets are available from a data repository via the master collection DOI: 10.14469/hpc/8168 and datasets cited therein.

Author contributions

H. S. Rzepa performed the calculations, M. Arita, K. Miyamoto and M. Uchiyama performed the experiments and all authors contributed to writing the text.

Conflicts of interest

The authors declare no conflicts of interest.

Notes and references

1. T. W. Schmidt, Acc. Chem. Res., 2021, 54, 481–489,  DOI:10.1021/acs.accounts.0c00703.
2. S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., 2013, 52, 3020–3033.
3. K. Miyamoto, S. Narita, Y. Masumoto, T. Hashishin, M. Kimura, M. Ochiai and M. Uchiyama, ChemRxiv, 2019, preprint,  DOI:10.26434/chemrxiv.8009633.
4. K. Miyamoto, S. Narita, Y. Masumoto, T. Hashishin, T. Osawa, M. Kimura, M. Ochiai and M. Uchiyama, Nat. Commun, 2020, 11, 2134,  DOI:10.1038/s41467-020-16025-x.
5. H. S. Rzepa, ChemRxiv, 2020, preprint DOI:10.26434/chemrxiv.12237980.
6. H. S. Rzepa, Nat. Commun., 2021, 12, 1241,  DOI:10.1038/s41467-021-21433-8.
7. H. S. Rzepa, Phys. Chem. Chem. Phys., 2021, 23, 12630–12636,  10.1039/D1CP02056K.
8. M. J. Harvey, N. J. Mason and H. S. Rzepa, J. Chem. Inf. Model., 2014, 54, 2627–2635,  DOI:10.1021/ci500302p; C. Cave-Ayland, M. J. Bearpark, C. Romain and H. S. Rzepa, J. Open Source Soft., 2022, 7, 3824,  DOI:10.21105/joss.03824.
9. M. J. Harvey, A. McLean and H. S. Rzepa, J. Cheminform., 2017, 9, 4,  DOI:10.1186/s13321-017-0190-6.
10. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620,  10.1039/B810189B.
11. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820,  DOI:10.1021/acs.jcim.9b00725.
12. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comp. Chem., 2003, 24, 669–681,  DOI:10.1002/jcc.10189.
13. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
14. H. S. Rzepa, Imperial College Research Data Repository, 2021 DOI:10.14469/hpc/7721.
15. D. Danovich, P. C. Hiberty, W. Wu, H. S. Rzepa and S. Shaik, Chem. Euro. J., 2014, 20, 6220–6232,  DOI:10.1002/chem.201400356 , and Table 2 therein.
16. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918,  DOI:10.1063/1.443164.
17. H. S. Rzepa, Imperial College Research Data Repository, 2021 DOI:10.14469/hpc/8280 and the master collection at DOI:10.14469/hpc/8168.
18. T. Okuyama, T. Takino, T. Sueda and M. Ochiai, J. Am. Chem. Soc., 1995, 117, 3360–3367,  DOI:10.1021/ja00117a006.
19. K. Miyamoto, S. Narita, Y. Masumoto, T. Hashishin, T. Osawa, M. Kimura, M. Ochiai and M. Uchiyama, Nat. Commun., 2021, 12, 1245,  DOI:10.1038/s41467-021-21439-2.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01214f

---