Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning enabling high-throughput and remote operations at large-scale user facilities†
Tatiana
Konstantinova‡
 a,
Phillip M.
Maffettone‡
a,
Phillip M.
Maffettone‡
 a,
Bruce
Ravel
a,
Bruce
Ravel
 b,
Stuart I.
Campbell
b,
Stuart I.
Campbell
 a,
Andi M.
Barbour
a,
Andi M.
Barbour
 a and
Daniel
Olds
a and
Daniel
Olds
 *a
*a
aBrookhaven National Laboratory, Upton, New York 11973, USA. E-mail: dolds@bnl.gov
bNational Institute of Standards and Technology, Gaithersburg, MD 20899, USA
First published on 20th May 2022
Abstract
Imaging, scattering, and spectroscopy are fundamental in understanding and discovering new functional materials. Contemporary innovations in automation and experimental techniques have led to these measurements being performed much faster and with higher resolution, thus producing vast amounts of data for analysis. These innovations are particularly pronounced at user facilities and synchrotron light sources. Machine learning (ML) methods are regularly developed to process and interpret large datasets in real-time with measurements. However, there remain conceptual barriers to entry for the facility general user community, whom often lack expertise in ML, and technical barriers for deploying ML models. Herein, we demonstrate a variety of archetypal ML models for on-the-fly analysis at multiple beamlines at the National Synchrotron Light Source II (NSLS-II). We describe these examples instructively, with a focus on integrating the models into existing experimental workflows, such that the reader can easily include their own ML techniques into experiments at NSLS-II or facilities with a common infrastructure. The framework presented here shows how with little effort, diverse ML models operate in conjunction with feedback loops via integration into the existing Bluesky Suite for experimental orchestration and data management.
1 Introduction
The past decade has seen a surge in the use of artificial intelligence (AI) and machine learning (ML) across the sciences. These tools have become essential for interpreting increasingly large datasets, which are simply too massive to be effectively analyzed manually. Not only has AI enabled interpretation of these datasets, it has increased the pace at which decisions are made,1 and in some cases outperformed human expertise.2 Applications of AI have enabled significant strides in physics,3 chemistry,4,5 materials science,6 and biology.7 It is thus unsurprising that light sources and central facilities have begun to look toward these technologies for active decision making, experimental monitoring, and guided physics simulations.8–10 In the following, we outline the challenges that are necessitating the adoption of AI, describe how to navigate the barrier to entry as a scientist, demonstrate some archetypal uses of AI, and exemplify their facile deployment at a variety of experiments across a central facility using the Bluesky software suite.11The pressing need to create new tools to optimize human effort at synchrotron light sources stems from the rate of data production from high-throughput and automated experiments in concert with traditionally slow, post hoc analysis techniques. In 2021, it is estimated that the National Synchrotron Lightsource II (NSLS-II) will create many petabytes of data, with all US Department of Energy light sources producing data in the exabyte (1 billion gigabytes) range over the next decade.12 The developments of new tools are underscored by the increasing transition to partially or fully autonomous operation for safe and effective experiments. Regardless of operating mode, beamline use remains a supply-limited resource for researchers. As such, there has been a surge of interest in optimal use of experimental resources,1,13 especially with beamline science.14 As key emerging technologies, AI and ML enable experiments at the light source to be performed more efficiently, intelligently, and safely.8 Unfortunately, the need for these tools comes with a mismatch of expertise: the predominant users of beamlines are experts in the materials of interest or analytical techniques, and not necessarily in AI or computer science.
Another substantive barrier to utility is real-time integration of AI with experimental workflows. Even with accessible and interpretable AI, the high-volume data acquisition from automated and remote experiments is creating a necessity for on-the-fly monitoring and model predictions. As experiments are commonly programmed to run ahead of time, measurements will continue indefinitely or on a fixed schedule, unless interrupted by the experimenter. These naively automated experiments suffer from several common pitfalls, including: allocating excessive measurement time to uninteresting samples, neglecting pivotal changes in the experiment and continuing measurements during operational failures. Real-time monitoring would solve these challenges by enabling researchers (or algorithms) to re-allocate measurement time to promising samples or parameters on-the-fly, as well as to stop or revisit an experiment that is not producing a fruitful measurement. The initial steps toward this monitoring have been implemented as data reduction techniques that operate on raw data streams using analytical or empirical computation. These techniques take a high dimensional data stream (2-d, 3-d, time series, etc.) and reduce it to a lower dimensional and interpretable signal.15,16 Given the surge of new techniques and accessible software frameworks for developing AI models,17–19 more general interfaces are necessary to enable the growing suite of AI tools to be accessible at beamlines.
It is worth defining what exactly is the relationship between AI, ML, deep learning, and other learning methods. Artificial intelligence is an overarching term for any technique used to have machines imitate or approximate human intelligence and behavior.3 A subset of these techniques falls under the definition of machine learning, which is essentially applied statistics for making accurate predictions. To this end, a simple and common form of ML is linear regression: fitting a line to a set of points, to subsequently use that line as a prediction for new points. The line of best fit serves as a ML model for the function of those points, to be validated when applied to new data. A particularly strong model will be predictive for new data beyond the domain of the initial training data (i.e. extrapolative). More complex statistical models exist, and these make up the toolkit of ML. A subset of these models are considered ‘deep’ models, which are capable of learning new mappings between ordinate spaces by using multiple layers that progressively extract higher-level features from the raw data.3 Critical to scientist are the kinds of data the model consumes, and the nature and uncertainty of outputs, inference, visualizations, or directives it produces.
While these contemporary methods are fit to solve the immense data challenges presented during routine beamline scientific operations, there continues to exist conceptual and technical barriers the hinder beamline users and staff from readily integrating these methods. The technical barriers to entry occur with model building and model deployment. The former challenge is addressed with the many accessible resources and platforms for designing AI solutions, of which we favor the Python ecosystem.3,17,20 It is a common case that a domain-specific AI model is developed prior to an experiment or through collaboration with technical experts external to an experiment. In this circumstance, facile integration at the beamline is necessary for utilizing the model during the experiment. Through three distinct relevant challenges, we will explore the different paradigms of what can be learned, with a limited focus on model details, and various operating modes of deployment. Our principal objective is to enable the reader to understand when and how to consider AI—or alternatively when it serves a limited purpose for their experiment—and to demonstrate recent technological innovations that facilitate the use of AI at modern beamlines.
One challenge can be ensuring researchers applying these methods are accessing the best tool for their job. Thematically, we will focus on three domains of ML: (i) unsupervised learning as a mechanism for analyzing and visualizing unlabeled data; (ii) anomaly detection for identifying rare events or points in a data stream; (iii) and supervised learning for predicting functional labels or values associated with a data stream. Unsupervised learning algorithms identify and react to commonalities in data without knowledge of the class, category, label for each datum. These approaches have been effective in reducing the dimensionality of a large dataset, and segregating physical response functions such as diffraction data21 and other spectra.22,23 Anomaly, or outlier, detection, is a reframing of unsupervised learning for identifying rare events that differ significantly from the majority of the data. The detected outliers can be scientifically intriguing as in the case of gravitational waves,24 or experimentally detrimental, as in the case of system failure.25 Supervised learning predicts output labels that can be discrete (classification), such as identifying phases of matter in a dataset,26 or a continuous response signal (regression) like temperature or energy.6
Herein, we demonstrate the utility of diverse machine learning methods for real-time monitoring of streaming data from three distinct experimental challenges at the National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory (BNL). We describe these use cases pedagogically, so that they may be instructive to operators and users of the facility, opening with general instructions to overcome conceptual hurdles with developing an AI solution. In Section 3, we demonstrate on-the-fly data segregation during a total scattering measurement, splitting a 1-d dataset into relevant components using unsupervised dimensionality reduction. This is a common challenge when conducting a diffraction experiment across phase transitions (e.g. over a composition or temperature gradient), and allows a researcher to focus on regions near the transition. Then, in Section 4 we explore the challenge of flagging a measurement when something is different from the norm established based on historical data. This unusual behavior can be caused by experimental artifacts during data collection, e.g. change of beam brightness, beam-induced sample damage, or by novel observations, e.g. a phase transition or a resonant excitation. This is particularly relevant in measurements with very sparse data points24 or for quality control.27 Finally, in Section 5 we solve the operational challenge of identifying failed measurements as they occur using supervised learning. In the case of X-ray absorption spectroscopy (XAS), there is a well defined feature in a measurement that when not present, indicates a failed measurement. By labeling a small set of experimental data, a supervised classification approach is shown to correctly classify new measurements. We close with a discussion on how each of these approaches is technically implemented and comment on the infrastructure of the Bluesky project11 for enabling everyday use of AI at central research facilities.
2 Pipeline for developing an AI solution
While we employed a variety of different modelling techniques and data sources in the following, the general approach (Fig. 1) to developing an AI-based solution is similar throughout. The first step is defining the problem. By understanding which of the archetypal domains the problem falls into and the key performance metrics, one may define the approach to take with the data as well as the suite of models available to explore. Secondly, the process of data ingestion needs to be well defined. Bluesky's data model and Databroker are an example11 of a community supported framework that are suitable for solving the engineering challenge8 of interaction with data for AI-enhanced experiments.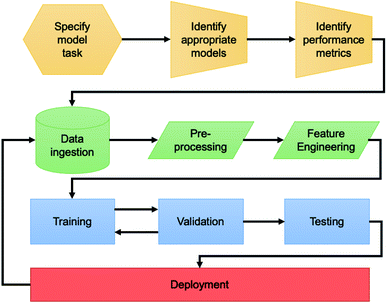 | ||
| Fig. 1 Flowchart describing the pipeline for developing an AI solution for a beamline science problem. | ||
The next steps in the flowchart are related to data collection and handling. The size of the dataset for a model development depends on the problem, the intended model and data availability. It is important that the training data captures the diversity and relative frequency of the intended use cases. Many models benefit from having large amount training data, which are available at synchrotron user facilities. However, labeled data remain a limited resource. The cost of labeling additional data should be weighted against the expected performance increase in each particular case. Having too large dataset can also pose a problem for model development. Some algorithms, like anomaly detection, do not perform well for very large data sets. More generally, ability of a model to learn new information saturates at certain amount of data, while demand for computational resources keep growing. Datasets used in this work are less than 1000 points.
Once access to the historical or active data stream is established, it can be prepared as input for the AI algorithms. In some cases, this requires only reformatting or rescaling the data so that it is tailored for specific AI algorithms, where in others this can require domain-specific data processing, such as reducing measured detector patterns into integrated spectra. It can be valuable to perform an additional data preparation step of feature engineering: a procedure of generating a new set of calculated variables (or features) from the original data. New features aim to simplify the functional form of a suitable model (e.g. power transformations of a variable to fit a linear model in case of a polynomial dependence), reduce the variable range (e.g. ‘day’/‘night’ instead of a timestamp), or extract physically meaningful information from raw data (e.g. frequency, phase and amplitude from a wave signal of an arbitrary duration). Properly designed features can significantly improve the accuracy of the model and reduce the need for computational resources. We demonstrate feature engineering in the examples of anomaly detection (Section 4) and supervised learning (Section 5) by using learning from a set of summary statistics of the data instead of the raw data.
Once processed, data can then be split into training, validation, and/or test subsets to allow for effective model selection. Best practices for constructing these datasets can be found in ref. 28. The training dataset is used to condition (or fit) the models that are being considered, i.e. to obtain the value of parameters that are directly used during model application, such as variables' coefficients in a regression model. This dataset is used to minimize the models' loss functions by adjusting their respective parameters. The validation dataset is not used to train directly, but it is the basis to provide an unbiased evaluation of a given model's performance when comparing it to other models. The validity of each trained model is evaluated by comparing the predicted response function of the validation dataset (i.e., “model output”) against the true response, which is established by scientists curating the data. A series of metrics suitable to the problem are used to quantify the performance of a model on the training and validation datasets. The data for the training and validation sets should come from similar distributions to make the comparison of model performance for them meaningful. However, the data generation process needs to be taken into account when splitting the data. For example, measurements repeated at similar conditions during the same experiment should be attributed to the same set. There is no standard rule for the splitting ratio as long as all sets are representative of the data distribution. 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 split for training, validation and test sets, respectively, is common. If a test (holdout) set is not available during the model training, a 80
20 split for training, validation and test sets, respectively, is common. If a test (holdout) set is not available during the model training, a 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 split between the sets is typical. However, for larger amount of data, validation set can be smaller.
20 split between the sets is typical. However, for larger amount of data, validation set can be smaller.
Caution here is taken around the bias–variance trade-off. High bias is a common source of underfitting, i.e., when the validation metrics equal or outperform the training metrics due to a model or feature set that lack the ability to express the complexity in the data. High variance occurs during overfitting, i.e., when the validation metrics significantly underperform the training metrics due to an overparameterized model that interprets noise in the training data as significant for generalization. Finally, occasionally a test dataset (or holdout set) is employed to evaluate the set of final models. Care must be taken not to expose the model to the test dataset during training so as not to bias the selection. This paradigm of splitting the data into sets is especially well suited for supervised learning tasks where labels are available.
Finally, the suite of selected models found appropriate for the task are tuned and trained. Each model type has a set of adjustable hyperparameters that impact its training and performance (the description of hyperparameters is left to the resources on specific models and their implementation documentation).17 These hyperparameters are tuned while each model is evaluated using the training and validation datasets. The pairings of models and hyperparameters are compared using their validation metrics. A few common metrics are employed in this work to evaluate models that can be expressed in terms of binary correctness: true positives, TP, true negatives, TN, false positives, FP, and false negatives, FN. The fraction of correct model predictions is called the accuracy,
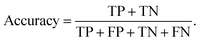 | (1) |
The precision describes the proportion of positive identifications that were actually correct,
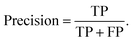 | (2) |
In anomaly detection, precision is commonly re-framed to the false discovery rate,
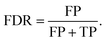 | (3) |
And the recall describes the proportion of actual positives was identified correctly,
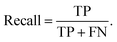 | (4) |
Lastly, a balanced metric of the precision and recall, F1 score is calculated from the harmonic mean of precision and recall,
 | (5) |
Having a validation set helps to recognize model's over-fitting, which can be controlled by various approaches. Among them are having large enough dataset to meet the model capacity (i.e. the number of coefficient in regression model), regularization,29 building an ensemble of models30 and sub-sampling.31
Once a suitable model has been trained, validated, and tested, it needs to be deployed. The deployment strategies vary from incorporating a fully pre-trained model into online or offline data analysis, to fitting the model actively during an experiment using newly acquired data. Each step of the model development pipeline from problem definition to model deployment can be revisited in an iterative cycle as new data arrives or the core challenges change.
3 Unsupervised learning
When a dataset has no labels to predict, or has no labels available for each datum, we turn to unsupervised learning for finding hidden patterns in the data. These methods require limited human supervision, often taking only input hyperparameters, and are commonly used for visualization of a dataset.20 Unsupervised methods can be categorically split between clustering and dimensionality reduction. When confronted with unlabeled data that requires visualization or segregation, the choice of which of these approaches to use depends on the dimensionality of the data and framing of the problem: some algorithms will provide only groupings, while others can potentially provide meaningful information about the groups themselves.Clustering methods are concerned with dividing data into related groups based on similar properties and/or features. These include algorithms such as Gaussian mixture model,32k-means clustering,33 and hierarchical clustering.34 Commonly used during exploratory data analysis or to produce preliminary groupings, these methods are difficult to evaluate in their true unlabeled setting and are often ranked using a similar labeled dataset or a fully labeled portion of the original data.20 The choice of model is often dependent on the shape of the data distribution. Strong examples of failure modes in two dimensions is offered in the scikit-learn documentation.17
In relation, dimensionality reduction attempts to reduce or project the data into a lower dimensional subspace that captures the underlying core information of the data. These include principal component analysis (PCA),35 singular value decomposition (SVD),36 non-negative matrix factorization (NMF),37 and deep methods such as variational autoencoders.38 These methods are often used to cast a problem with many input variables down to a more manageable number of features and have found utility across the natural sciences. One attribute underpinning their utility is the production of a series of basis vectors during the dimensionality reduction. In the case of spectral decomposition, the non-negative basis vectors can have physical significance as end members of the dataset.37,39 We use this property here in the live exploration of total scattering data via NMF, which constructs a components matrix, H, and a weights matrix, W, such that their product approximates the true dataset, V, by minimizing the Frobenius norm of the difference, ‖V − WH‖F.
| V ≈ WH | (6) |
The shape of V is m × n, the shape of W is m × p and the shape of H is p × n, where m is the number of spectra, n is the length of each spectra, and p is the number of components or end-members.
Commonly, analytical measurements are conducted across a series of state variables, for example temperature, pressure, or composition. The combined hardware and software innovations at central facilities enable ex situ and in situ characterization8 with predetermined measurement plans. In these circumstances, large amounts of data are collected across distinct phases or other state regions of interest, with no prior knowledge of labels or transitions. It is often not until after the experiment is complete that the researcher has the opportunity to separate these regions, at which point they may be unable to experimentally explore interesting regions in more depth. We demonstrate this challenge using total scattering studies from the Pair Distribution Function (PDF) beamline at NSLS-II of the molten salt NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CrCl3 (molar ratio 78
CrCl3 (molar ratio 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22), wherein the coordination changes of particular ions across phases impact corrosion characteristics.40 Knowledge of these materials and their corrosion characteristics is essential for their utility in molten-salt nuclear reactor designs.
22), wherein the coordination changes of particular ions across phases impact corrosion characteristics.40 Knowledge of these materials and their corrosion characteristics is essential for their utility in molten-salt nuclear reactor designs.
During a temperature scan in a single sample, various crystalline and amorphous phases and their mixtures will emerge. An unsupervised method is required that can separate sets of patterns (i.e. regions of temperature) that are distinct, thus turning a vast dataset into actionable knowledge. Various unsupervised methods can be used to segregate diffraction data using different metrics.41 Recent developments in NMF show promise for spectral functions that are positive linear combinations within mixtures.21,42 NMF reduces the dataset such that each data point is described by a strictly additive mixture of relatively few non-negative end members (e.g., unique phases or components). The number of end members can be decided automatically based on other algorithmic approaches.39 However, given the ease of calculation and knowledge of the researcher about the materials system and potentially relevant phases, it is more effective to grant the user control over this number. Furthermore, a researcher can focus the decomposition algorithm on a spectral range of interest. This enables the researcher to conduct rapid analysis during a variable scan and makes effective use of remaining measurement time for scientific output.
We deployed NMF using the Bluesky framework43 in the study of molten NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
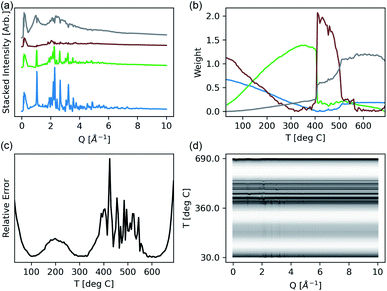
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CrCl3 across a temperature range of 27–690 °C. Each raw 1-d spectrum in this experiment consisted of 2072 reciprocal space points. We here used the scikit-learn implementation17 of NMF to calculate the decomposition in eqn (6) each time a new measurement is completed and combined the computation with a dynamic plotting using matplotlib.44 This implementation allows for on-the-fly monitoring and analysis of an experiment, whereas previous approaches—even those depending on ML—are focused solely on post hoc analysis. The resulting display that this implementation produces is compared against a stacked plot of all of the data colored by temperature in Fig. 2. Overall, 133 spectra were collected during the experiment.
CrCl3 across a temperature range of 27–690 °C. Each raw 1-d spectrum in this experiment consisted of 2072 reciprocal space points. We here used the scikit-learn implementation17 of NMF to calculate the decomposition in eqn (6) each time a new measurement is completed and combined the computation with a dynamic plotting using matplotlib.44 This implementation allows for on-the-fly monitoring and analysis of an experiment, whereas previous approaches—even those depending on ML—are focused solely on post hoc analysis. The resulting display that this implementation produces is compared against a stacked plot of all of the data colored by temperature in Fig. 2. Overall, 133 spectra were collected during the experiment.
In this instance, a maximum of four end-members, and thus phases of interest, were included. The weights of each component, W, are shown across the temperature range, showing a smoothly varying mixture of three plausible phases in the low temperature regime, and an abrupt transition around 400 °C. These correspond to solid mixtures and a second order phase transition to the liquid region. Also shown is the presence of the third (green) end member in liquid regime, suggesting kinetically stabilized crystallites during melting. As evidenced by the increased relative error, the model is failing to fit the data in the region from 400–500 °C. This can be attributed to the existence of spurious anomalous features in the diffraction data during the co-existence of the amorphous and crystalline phases40 that would require far more than 4 components to fit well. However, as the application of NMF here is being used to highlight and cluster regions of interest in the data, and not necessarily extract physically real components, the limited 4-component model is effective. Since NMF is only considering linear combinations of components, any substantial peak shifting (from changing lattice parameters or coordination) may appear as a distinct component. While some innovative models have attempted to handle peak shifting,21 they were not considered in this study as we constrained our focus to integrating NMF into an on-the-fly data acquisition process. As opposed to declaring distinct phases—a task more suited for full pattern refinement45—NMF highlights unique regions of interest in the temperature scan for interpretation. This summary is refreshed in real time with each sequential measurement, granting the user immediate insight.
Unsupervised ML methods are very impactful beyond this particular total scattering example, and easily adapted to any spectral measurement. As presented, NMF enabled researchers to make effective use of limited beam time, by identifying potential experimental regions of interest and conditions for focused measurement on the fly. This method trivially expands to locate any second order phase transitions and conduct a subsequent more detailed scan in that temperature regime. Since advanced detectors now measure in the MHz range, data sorting is not manually feasible, and unsupervised approaches could also be used to automate such tasks. These concepts are directly amendable to increasing automation and adaptive learning6,46 efforts in materials research. As implemented (see Code availability), the decomposition and clustering algorithms can be readily deployed onto other beamlines or types of measurement that produce relatively low dimensional data (1-d or small 2-d). For higher dimensional data, deep learning algorithms could be used in tandem to reduce the data or identify latent features.38
4 Anomaly detection
Anomaly detection algorithms aim to identify unexpected observations that are significantly different from the remaining majority of observations. Such algorithms are used for many different tasks, including credit card fraud detection,47 discovering unusual power consumption,27 and identifying cyber security threats.48 Isolating anomalous instances can be accomplished using supervised or unsupervised learning. Further detailed in Section 5, supervised algorithms require the training data to be labeled and have a proper distribution of the different types of abnormal cases that can be encountered. However, the knowledge of potential types of anomalous data is often not available before the data are taken. Unsupervised algorithms, on the other hand, do not assume the knowledge of types of possible irregularities. They are based on the presumption that majority of the data is normal with anomalies being rare and divergent from the ordinary data. Such algorithms tend to learn the distribution of the normal data according to specific hyperparameters. Sample points that are unlikely to come from this distribution are labeled as outliers. In the circumstance when all data outside the expected norm cannot be predicted and labeled, but still need to be identified, unsupervised anomaly detection is an incredibly useful tool.Here, we focus on three unsupervised algorithms: local outlier detection49 (LOD), elliptical envelope50 (EE) and isolation forest51 (IFT). The LOD algorithm identifies the regions with similar local density of points based on several nearest neighbors (Fig. 3a). The points with local density smaller than their neighbors are identified as outliers. The degree of certainty with which a point is attributed to outliers depends on the number of nearest neighbors considered—an additional hyperparameter of the model. The EE algorithm assumes that the normal data are centered around a single point and fits a multidimensional ellipsoid around the center (Fig. 3b). Whether or not each point is considered an outlier is based on the Mahalanobis distance between the point and this elliptical distribution. Exploratory analysis of the principle components shows that the normal data in our case constitute a single cluster, though its shape is not close to elliptical in some planes. The IFT algorithm isolates outlier points in a series of data splits. It has an isolation tree as its basic structure. Such tree is built by randomly selecting a variable and a split point until each leaf of the tree contains only samples with the same values. A path to the leaf is equal to the number of partitioning necessary to isolate the sample. The length of a path to a point, averaged over the collection of the trees (the forest), is the metric used to determine if it is an outlier (Fig. 3c). The algorithm is known to outperform other methods for variety of cases, though is can be computationally expensive for high-dimensional data.
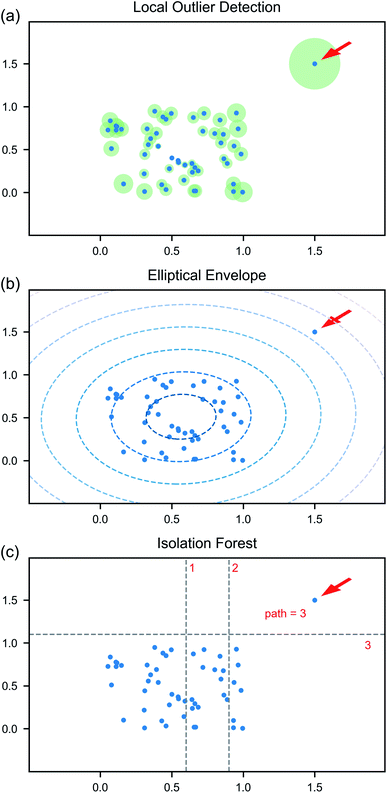 | ||
| Fig. 3 Graphical description of anomaly detection algorithms: (a) local outlier detection, (b) elliptical envelope, and (c) isolation forest. | ||
Synchrotron user facilities can benefit from integrating anomaly detection tools into their operations. Often in a measurement setting, it is necessary to highlight when a result is different from what is expected. In some cases, this amounts to recognizing an equipment failure early, thus allowing the researcher to react promptly. In other instances, this would take the form of finding new or interesting data points within a larger dataset. Both tasks would normally require constant monitoring of collected signals by the researcher. Anomaly detection algorithms can be integrated in the online data analysis for prompt evaluating of the measurements, reducing the need for human efforts.
We built an anomaly detection toolkit for the time series collected for the X-ray Photon Coherent Scattering (XPCS) experiments.52,53 During the measurements, series of scattering images (frames) are recorded by the 2-d area detector (e.g. CCD). As part of the analysis, the photon intensity for a group of pixels is autocorrelated over time since the decorrelation of the speckles' intensity is reflective of the inherent sample's dynamics. Consequently, the events like a sample motion, the X-ray beam drift, or changes in the beam intensity can lead to artifacts in the correlation functions.8 In some occasions, changes of the scattering peak's position or intensity can be due to intrinsic properties of the samples. As the anomalous events encountered during the data collection, they should be investigated by a researcher, who can dynamically adjust the experimental plan or conditions. Since experiments last extended periods of time (on the order of days) and are controlled by pre-assembled plans, it is critical to have an automated tool that alarms the researcher about anomalous observations, so they may target the most critical experimental conditions first and then make appropriate decisions regarding subsequent measurements and analysis.
The data for this work were collected by processing results of previous measurements at the CSX beamline at NSLS-II. For multiple regions of interest at the 2-d detector for each frame we calculate 6 time series: the total intensity, the standard deviation of binned pixels' intensity counts, the center of mass coordinates and its standard deviations for both directions. These variables are chosen because they can be directly calculated and reported by the detector's control software during an experiment and circumvent the need for more time consuming post-processing of scattering images. The number of points in each time series ranges from 20 to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400, with mean number being 2792.
400, with mean number being 2792.
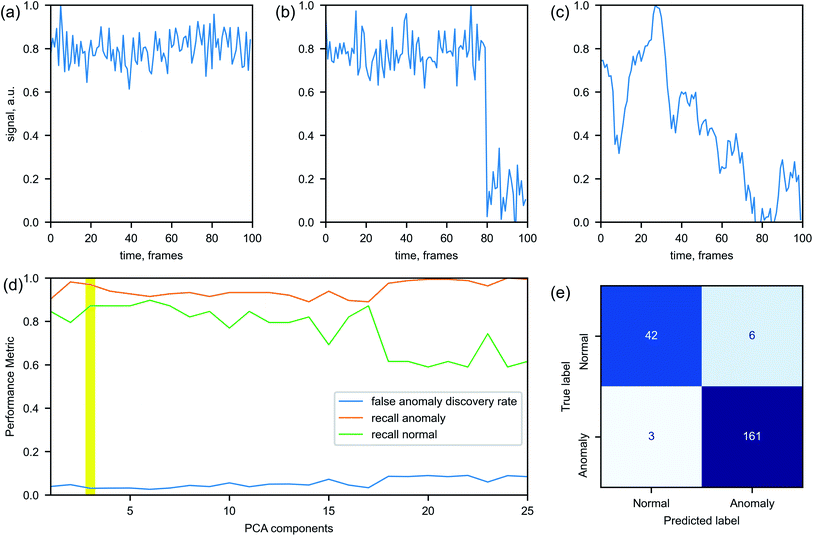
While such algorithms do not require the labeled data for the training, we annotate a dataset for the purpose of evaluating the models' performance. Each example is labeled as ‘normal’ or ‘anomalous’ based on the expert knowledge. Fig. 4 illustrates how an intensity time series can look in a normal Fig. 4(a) and anomalous Fig. 4(b) and (c) cases. In a normal case, all considered experimental parameters are (almost) stationary, while anomalous cases may contain sudden jumps or significant drifts of the parameters' values. The duration of each time series ranges from tens to thousands of frames. To be processed by the anomaly detection algorithms, the series need to be converted to a set of variables of a fixed length.
We engineered a set of 93 features to capture the statistical diversity of the variable length data. The derived features include (i) standard deviation to mean ratio within the series, (ii) autocorrelation coefficients up to 4th order, (iii) ratio of a parameter's standard deviation to the standard deviation of its first time derivative, (iv) difference of parameter values at the beginning and the end of the scan. The feature engineering aims to highlight the lack (presence) of trends and discontinuities in normal (anomalous) cases and can be helpful in other ML tasks involving sequential data. The features were calculated from the time series following two preprocessing steps: centering the series around their mean values and normalizing by the mean values. The second step was not included for the series related to the intensity peak positions as their absolute displacement can be indicative of outliers and thus should be preserved.
As EE and LOD use Euclidean distance measure in the base of their algorithms, it is likely that the models do not perform well in a high-dimensional space. Moreover, the number of variables is comparable to the number of examples in our train set, increasing the potential risk of over-fitting. To address these concerns we control the dimensionality of the data. We employ an unsupervised dimensionality reduction technique, principle component analysis (PCA),35 similar to that presented in Section 3 to reduce the size of our engineered feature vectors. PCA is a linear approximation of the data in a new orthogonal coordinate system, such that the greatest variance by some scalar projection of the data comes to lie on the new coordinates. These scalar projections are used as our reduced dimensions.
Overall, 727 time series are processed. The data are divided into exclusive sets for training, validation and testing. Only the ‘normal’ data are used for training the models and the training set contains 80% of all normal examples – the rest is evenly divided between the validation and the test set. In doing so, we ensure that the assumption of the models about majority of the data being ‘normal’ is satisfied during training. Since the considered models do not rely on the data labels for training process, a significant presence of anomalous examples in the training set could deteriorate a model performance. The validation dataset is used for identifying optimal hyperparameters of the models. In addition to the 10% of the normal examples, it contains 50% of the anomalous examples. The rest of the data belong to the test set, which is used for the final models' assessment. The model performance can be evaluated through various parameters calculated from the confusion matrix (Fig. 4). Recall R reflects the rate of correctly identified normal (anomalous) labels among all normal (anomalous) examples and false anomaly discovery rate FDR reflects the ratio of incorrectly identified labels among all examples labeled as anomaly.
The key hyperparameters we tune across all models are the dimensionality of the input signals (the number of principle components) and the contamination level. The contamination level is the percentage of anomalous examples in the train set. Despite only normal data being in the training set, we let a small portion of them to be identified as anomalous, i.e. having false anomalous labels, in expectation that an actual outlier will be even further away from the main cloud of normal data and thus correctly identified by the model. This approach prioritizes having false positives (alarms being raised prematurely) over false negatives (alarms which should have been raised being missed). The hyperparameters of the models are optimized by maximizing the products R × FDR for the normal and anomalous data in the validation set. An example of selection of the optimal number of the principle components is shown in Fig. 4(d).
The results of our performance comparison across three anomaly detection models are shown in Table 1. LOD has the least percentage of incorrectly labeled normal data, but it slightly under-performs in identifying anomalies comparing to other algorithms. Comparing to the LOD, the IFT algorithm demonstrates better results in correctly identifying the anomalous test data, but it mislabels more of the normal examples than other algorithms do. In our case, the EE algorithm has the best performance when considering both recall and false discovery rate. Depending on the application priorities, the threshold value of the model's metric can be adjusted to reduce either false positive or false negative outcomes (see ESI† for precision-recall curves).
| Models | LOD | EE | IFT |
|---|---|---|---|
| Recall anomaly | 0.92 | 0.98 | 0.98 |
| False anomaly discovery rate | 0.026 | 0.036 | 0.042 |
This example with XPCS clearly demonstrates that anomaly detection algorithms can be an effective tool for identifying unusual signals, such as in the presented time series data, in X-ray light source measurements. Automatic flagging of such observations helps optimize the workload of XPCS researchers, freeing them from the necessity of manually evaluating every dataset. The innovations here including feature engineering, dimensionality reduction, and online unsupervised anomaly detection are not limited to applications in XPCS or even to time series. The sequence of these methods could be applied directly to any one-dimensional equally spaced data arrays, where the order of observations is important, e.g., spectra, line cuts of two-dimensional images, temperature series. More generally, the model is applicable for filtering out artefacts in a set of repetitive measurements performed54,55 to obtain appropriate statistics in case of a weak signal, which can include higher order dimensions when suitable feature engineering is employed.
5 Supervised classification
Supervised learning is a very common task in science and engineering and based on the same principles as standard fitting procedures or regression. Its core objective is to find an unknown function that maps input data to output labels. When those labels are discrete, this is considered a classification task, and when those labels are continuous, it is considered a regression task. A particularly desirable outcome of supervised learning is transferability: a model trained on a one dataset should be predictive on another, and not simply interpolative. As such, it is advantageous to perform feature engineering—which biases the generalization of the approach to the engineer's discretion—or utilize deep approaches that ‘learn’ the proper featurization. In general, a problem can be cast as a supervised learning problem if there is labeled data available, and that data format can be mapped as an input for the available algorithms.The broad impact of supervised learning is undeniable, impacting technologies in our daily lives through image classification,56 speech recognition,57 and web-searches.58 However, in the domains of applied materials science and crystallography, these contemporary approaches have accelerated physical simulations,3 property prediction,6 and analytical techniques such as diffraction59 and microscopy.60 Each of these advances is underpinned by a variety of models, some of which require deep learning to accomplish. Model selection for supervised learning is dependent on both the size of the labeled dataset, and the dimensionality or shape of the data.6 In general, with small datasets (˂10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points), it is advisable to consider statistical ML algorithms over deep learning for transferable predictive performance that does not over fit. We will here demonstrate an application of supervised learning employed on a beamline to classify data quality in a binary fashion, as simply ‘good’ or ‘bad’ data.
000 points), it is advisable to consider statistical ML algorithms over deep learning for transferable predictive performance that does not over fit. We will here demonstrate an application of supervised learning employed on a beamline to classify data quality in a binary fashion, as simply ‘good’ or ‘bad’ data.
In many circumstances there is a stark and identifiable contrast between ‘good’ and ‘bad’ data during a materials analysis measurement. Where we use the term ‘good’ to describe data that is ready for immediate interpretation, and ‘bad’ to describe data that may be uninterpretable or which merits human intervention prior to being ready for interpretation. Bad data stems from a variety of sources, including but not limited to weak signal-to-noise ratio, improper sample alignment, or instrumentation failure. Contrary to the experimental situations we presented for anomaly detection (Section 4), these bad data are well defined and can readily be labeled. However, there is a pressing need for on-the-fly analysis to identify when ‘bad’ data arises during an automated experiment, so as to enable rapid intervention. In this case, the supervised learning approaches that were not well suited for anomaly detection are useful.
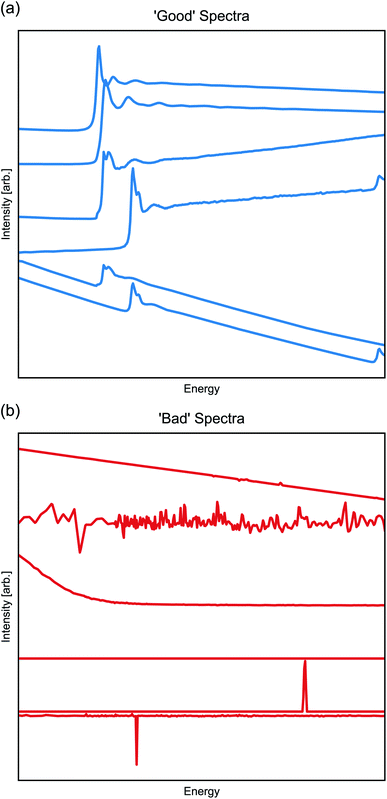
At the Beamline for Materials Measurement (BMM) at NSLS-II, X-ray absorption fine structure (XAFS) is routinely measured via X-ray absorption spectroscopy (XAS) in a high-throughput automated experiment. The XAFS measurement varies the incident photon energy to measure the energy-dependent, X-ray-absorption cross section, which provides a direct assessment of valence and other chemical information and which may be analyzed to recover details of local partial pair distribution functions.61 XAFS is regularly measured in two modes at a hard X-ray beamline like BMM. In transmission, the optical opacity of the sample is measured by the attenuation of the incident beam intensity as it passes through the sample. Here, the absorption cross section changes dramatically as the energy of the incident beam is scanned through the binding energy of a deep-core electron, resulting in the emission of a photo-electron and the creation of a short-lived core-hole. In fluorescence, the absorption cross section is determined by measuring the emission of the secondary photon produced when the core-hole created by the photo-excitation of the deep-core electron is refilled by the decay of a higher-lying electron. The energy range of this scan depends on the chemistry and composition of the sample and on other experimental considerations. To make the measurements accessible to non-sequential ML algorithms, every spectra is down-sampled to contain 400 members; however, the energy bounds of the spectra are not adjusted. The results of these experiments and processing are thus a set of 1-d vectors with 400 members, with typical ‘good’ spectra shown in Fig. 5a.
The spectra are easily labeled as good or bad data, as the good data will undergo a sharp and significant change in intensity (called an ‘absorption edge’ in XAFS), while the bad data (Fig. 5b)—regardless of root cause—will lack an absorption edge and take the appearance of random noise or featureless background signal. Regardless of the ease of this pattern recognition task, the current approach for good/bad classification requires human intervention and judgement, which is not ideal for remote, high-throughput, and/or overnight data collection. A ML-based classification will make for more efficient use of the beamtime. From a set of previously collected and labeled spectra, we applied a suite of classification models with some achieving 100% accuracy on an unseen test-set. We considered Random Forrest (RF),62 Support Vector Machine (SVM),63 Multi-layer perceptron (MLP),64k-Neighbors,65 and Gaussian Process (GP) classifiers.66 In all cases, we used the default hyperparameters in the scikit-learn implementation, except for MLP models where we reduced the default hidden nodes to 10.
We compared the performance of these models across different splits of the labeled dataset (Table 2). In the first approach, a set of 711 data from transmission and fluorescence data of variable quality was randomly split into training and validation sets (80% training and 20% validation). We refer to these approach as uniform validation. In the second approach (unique validation), data from a set of ‘very good’ measurements were retained for the validation set with 10% of the remaining data sampled for validation (156 total). This unique validation approach allows for testing of the extensibility of models, that is, how well they will behave on data outside of the scope of training. In both approaches, we explored each model's performance on the raw spectra (Fig. 5) after normalization onto the range [0,1], and on a set of statistical features that were calculated from the spectra and their first derivatives: (i) autocorrelation coefficients for lag 1–4, (ii) mean of the first 5 values, (iii) mean of the last 5 values, (iv) mean of the intensity, (v) standard deviation of the intensity, (vi) sum of the intensity, and (vii) location of the intensity maximum. These features were normalized by the maximum for the training data of each feature.
| Models | Raw spectra | Engineered features | ||
|---|---|---|---|---|
| Uniform validation F1-score | Unique validation F1-score | Uniform validation F1-score | Unique validation F1-score | |
| RF | 0.986 | 0.829 | 0.990 | 0.874 |
| SVM | 0.995 | 0.807 | 0.990 | 0.982 |
| MLP | 1.00 | 1.00 | 0.986 | 0.957 |
| k-Neighbors | 0.995 | 0.807 | 0.990 | 0.947 |
| GP | 0.990 | 0.803 | 0.986 | 0.988 |
Based on the results in Table 2, the challenge of effective representation becomes apparent. In the case of using the raw spectra, only the MLP models are able to make accurately predictions on data from new experiments. However, when the ML algorithms are fed derived features that capture the most important information, the models can be more effectively generalized to new data. The models trained on raw spectra fail to classify spectra with rising edges of new shapes or in different positions. This lack of generalization is unsurprising because these models do not create their own abstractions, whereas when abstractions are provided by feature engineering, the models become more useful beyond the training data. Other approaches to creating abstractions without biased feature engineering exist in the field of deep learning. Convolutional neural networks trained on the raw spectra dataset, similar to the multi-layer perceptrons, approach 100% validation accuracy where shallow models fail. These approaches are beyond the scope of this paper, being less accessible to the average scientist; however, their success underscore the value of feature engineering with expert knowledge since those features can be ‘learned’ by deep algorithms.
6 Deployment interfaces
The final component of the AI pipeline referenced in Fig. 1 is deployment. The complexity of steps involved in model deployment can vary considerably depending on the application. The simplest deployment strategy is to provide a pre-trained model to a user. While this approach has its advantages, such as ease of testing and flexibility of workflow modification, it also requires a lot of user intervention to utilize the model via managing file transfer, data inputs and outputs, as well as the interpretation of the model output. As such, to produce superior experimental research, the most user friendly interfaces would produce no additional “work” for the user, by allowing for AI tools that are seamlessly integrated into existing workflows. Such an interface enables both human-in-the-loop operation,67 and completely autonomous experiments.13,68 While many of the beamlines at NSLS-II use similar interfaces, it is common for particular experiments or beamlines to have bespoke software solutions built on or interfacing with common frameworks, such as Bluesky43 or Ophyd.69 Here we outline how each of the proceeding sections was implemented, to demonstrate the diverse integration modes across the facility. Each of these deployment techniques and training strategies can be found in the accompanying code repository.Firstly, it is useful to have a generic interface to expect with AI models, so that similar models can be deployed in different experimental processes regardless of other design decisions. This separates the design of the agent from the management of data streaming, in-line callbacks, or application specific techniques. Following recent work in adaptive experiments at NSLS-II and the developments of Bluesky Adaptive70,71 we implemented all presented models with a tell–report–ask interface. That is, each model had a tell method to tell the model about new data, a report method to generate a report or visualization, and an ask method to ask the model what to do next. While the latter method is required with adaptive learning in mind, it enables simple adaptations such as a model detecting an anomaly and wishing to pause the experiment. This generic interface suits most needs for AI at the beamline, and allows users to ‘plug-and-play’ the models they have developed without considering how the data is being streamed or other communication protocols. A complete tutorial using the tell–ask components to deploy multiple AI models can be found at ref. 71, and all the models presented here have been made available (see Code availability statement).
The example deployment of NMF demonstrates how the tell–report–ask interface can be used with an established collection of data, and not requiring explicit streaming. At the PDF beamline at NSLS-II, raw diffraction images from a 2-d area detector are streamed as documents to data reduction software, that produces data for scientific interpretation as a 1-d pattern stored in a file system locally or on a distributed server. Here, we employ the tell–report–ask interface inside a file system watcher. The model is told about new data each time new files appear, and subsequently generates a new report, i.e. the visualization shown in Fig. 2. Due to the inexpensive nature of updating the NMF model, this gives the researcher a developing model and visualization over time. This example also shows how to include both model training and evaluation in-line with an experimental data stream.
It is possible to train and use a model completely offline using the corpus of data generated over an extended period of time without the need to constantly update the model after a new measurement. For the anomaly detection model, we used data from multiple experimental measurements, separated by an expert into normal and anomalous groups. The training of the model and selection of the best performer is done in a Jupyter Notebook environment because simple pipelines are all that is required for development and testing. The model can be deployed for both online data streaming application and for offline analysis. Its self-contained simplicity allows a user to insert the model to work best in their preferred workflow. In the examples accompanying this work, we demonstrate tell–report–ask interface for the file system. Alternatively, this can be implemented using the following pseudo code with a databroker catalog for the most recent measurement.
Here, the AnomalyAgent() is designed in a way that it only ingests the experiment identification number and the dictionary of the time series, without being tied to the way that the dictionary is created. The data can be processed from the catalog or from hdf5 files in folder. With either interface, the model can access the data and return a prediction of whether the measurement is considered an anomaly. The output of the model can be utilized by subsequent AI-guided analysis and results extraction.72 The model does not have to be updated after each new measurement is added to the folder and routine model updates can be scheduled when sufficient amount of new data are acquired and labeled. The process of model update and application can easily be automated using Papermill.73
In our deployment of supervised learning for identifying failed measurements at BMM, we constructed a part of Bluesky plan—a callback—to publish the report from the model onto Slack,74 a common business communication platform, in the form of emojis. This enables remote monitoring of an experiment for potential failures, as well as a timeline of those failures. We use a class with the tell–report interface, separate from the callback designed by the beamline scientist, so that the models and report styles can be easily interchanged. The ML models can either be loaded from disk or retrained from a standard dataset at the start of a each experiment. Each time a measurement is taken, a report is generated based on the model classification and passed to the callback that processes the report for Slack. This deployment shows how the same interface used for monitoring directories in a file system, can be quickly linked to streaming data, and publish results to the internet or a chat service.
7 Conclusions
AI opens opportunities for making many beamline experiments more efficient in various aspects from data collection and analysis to planning next steps. As the rate of data production continues to increase with new high-throughput technologies, and remote operations requirements grow, new analytical tools need to be developed to accommodate this increased flux of data in a distributed manner. Herein we tackled three unique experimental challenges at NSLS-II that fall under individual archetypes of machine learning: unsupervised segregation, anomaly detection, and supervised classification. We integrate non-negative matrix factorization to separate key components of total scattering spectra across a temperature driven phase transition. Secondly, we deploy anomaly detection to warn a user of substantial changes in the time evolution of XPCS data. And lastly, we train a supervised binary classifier to separate good data that is ready for immediate analysis and bad data that requires experimental intervention during an XAFS experiment. Use of these AI methods is aimed to increase scientific outcome of the experiments and does not rely on large-scale computational resources or extended software development skills. Each of the models could be trained on a personal computer in a matter of minutes or even seconds. Open-source Python libraries, such as scikit-learn,17 make encapsulated implementation of elaborate algorithms available for researchers from wide range of disciplines.Beyond the scope of this work, yet still relevant to beamline science are adaptive learning and reinforcement learning.75 Adaptive learning is an extension of supervised learning where the algorithm can ask for more data to improve its model, and has been used in experimental optimization and search.13,68,76,77 Reinforcement learning approaches a related task of learning an optimal policy given a reward and penalty structure. This has recently been demonstrated for optimizing beamline operations and resource allotment.14,75 Deploying these techniques at a beamline are significant enough to warrant their own study,14,77 albeit the tools we develop here are designed with adaptive protocols in mind.
The integration of each considered model into the Bluesky Suite for experimental orchestration and data management underpins their accessibility to beamline users and staff that are unfamiliar with ML, and extensibility to new applications. These extensions include similar thematic data challenges at different experiments and algorithmic development to incorporate adaptive experiments which depend on the feedback from ML.78 Given this framework and the scientific python ecosystem, there are boundless opportunities for further applications of these and different ML approaches in high-throughput and distributed experimental feedback loops.
Data availability
The source code and data to reproduce the examples in this work is available at https://www.github.com/bnl/pub-ML_examples/. https://doi.org/10.11578/dc.20220118.1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research used the PDF, CSX, and BMM beamlines of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory (BNL) under Contract No. DE-SC0012704 and resources of a BNL Laboratory Directed Research and Development (LDRD) projects 20-032 “Accelerating materials discovery with total scattering via machine learning” and 20-038 “Machine Learning for Real-Time Data Fidelity, Healing, and Analysis for Coherent X-ray Synchrotron Data”. We would like to acknowledge Anthony DeGennaro who is a co-PI for LDRD 20-038 from BNL Computer Science Initiative (CSI) and Thomas Caswell who is a co-PI for LDRD 20-032 from BNL NSLS-II.Notes and references
- Z. Zhou, X. Li and R. N. Zare, ACS Cent. Sci., 2017, 3, 1337–1344 CrossRef CAS PubMed.
- N. Brown and T. Sandholm, Science, 2019, 365(6456), 885–890 CrossRef CAS PubMed.
- P. Mehta, M. Bukov, C.-H. Wang, A. G. Day, C. Richardson, C. K. Fisher and D. J. Schwab, Phys. Rep., 2019, 810, 1–124 CrossRef PubMed.
- P. S. Gromski, A. B. Henson, J. M. Granda and L. Cronin, Nat. Rev. Chem, 2019, 3(2), 119–128 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- R. Batra, L. Song and R. Ramprasad, Nat. Rev. Mater., 2020, 6(8), 655–678 CrossRef.
- A. W. Senior, R. Evans, J. Jumper, J. Kirkpatrick, L. Sifre, T. Green, C. Qin, A. Žídek, A. W. R. Nelson, A. Bridgland, H. Penedones, S. Petersen, K. Simonyan, S. Crossan, P. Kohli, D. T. Jones, D. Silver, K. Kavukcuoglu and D. Hassabis, Nature, 2020, 577, 706–710 CrossRef CAS PubMed.
- S. Campbell, D. B. Allan, A. Barbour, D. Olds, M. Rakitin, R. Smith and S. B. Wilkins, Machine Learning: Science and Technology, 2020 Search PubMed.
- J. Duris, D. Kennedy, A. Hanuka, J. Shtalenkova, A. Edelen, P. Baxevanis, A. Egger, T. Cope, M. McIntire, S. Ermon and D. Ratner, Phys. Rev. Lett., 2020, 124, 124801 CrossRef CAS PubMed.
- F. Ren, L. Ward, T. Williams, K. J. Laws, C. Wolverton, J. Hattrick-Simpers and A. Mehta, Sci. Adv., 2018, 4, eaaq1566 CrossRef PubMed.
- D. Allan, T. Caswell, S. Campbell and M. Rakitin, Synchrotron Radiat. News, 2019, 32, 19–22 CrossRef.
- N. Schwarz, S. Campbell, A. Hexemer, A. Mehta and J. Thayer, Driving Scientific and Engineering Discoveries Through the Convergence of HPC, Big Data and AI, 2020, pp. 145–156 Search PubMed.
- L. M. Roch, F. Häse, C. Kreisbeck, T. Tamayo-Mendoza, L. P. E. Yunker, J. E. Hein and A. Aspuru-Guzik, Sci. Robot., 2018, 3, 5559 CrossRef PubMed.
- P. M. Maffettone, J. K. Lynch, T. A. Caswell, C. E. Cook, S. I. Campbell and D. Olds, Machine Learning: Science and Technology, 2021 Search PubMed.
- xpdAcq library, https://xpdacq.github.io Search PubMed.
- S. K. Abeykoon, Y. Zhang, E. D. Dill, T. A. Caswell, D. B. Allan, A. Akilic, L. Wiegart, S. Wilkins, A. Heroux, K. K. van Dam, M. Sutton and A. Fluerasu, 2016 New York Scientific Data Summit (NYSDS), 2016, pp. 1–10 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/, Software available from https://www.tensorflow.org Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, in Advances in Neural Information Processing Systems 32, Curran Associates, Inc., 2019, pp. 8024–8035 Search PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning (Information Science and Statistics), Springer-Verlag, Berlin, Heidelberg, 2006 Search PubMed.
- V. Stanev, V. V. Vesselinov, A. G. Kusne, G. Antoszewski, I. Takeuchi and B. S. Alexandrov, Npj Comput. Mater., 2018, 4, 43 CrossRef.
- F. Bonnier and H. Byrne, Analyst, 2012, 137, 322–332 RSC.
- S. Wasserman, J. phys., IV, 1997, 7, C2-203 Search PubMed.
- B. P. e. Abbott, Phys. Rev. Lett., 2016, 116, 061102 CrossRef CAS PubMed.
- A. Borghesi, A. Bartolini, M. Lombardi, M. Milano and L. Benini, Proceedings of the AAAI Conference on Artificial Intelligence, 2019, pp. 9428–9433 Search PubMed.
- M. R. Carbone, M. Topsakal, D. Lu and S. Yoo, Phys. Rev. Lett., 2020, 124, 156401 CrossRef CAS PubMed.
- J.-S. Chou and A. S. Telaga, Renew. Sustain. Energy Rev., 2014, 33, 400–411 CrossRef.
- A. Y.-T. Wang, R. J. Murdock, S. K. Kauwe, A. O. Oliynyk, A. Gurlo, J. Brgoch, K. A. Persson and T. D. Sparks, Chem. Mater., 2020, 32, 4954–4965 CrossRef CAS.
- P. J. Bickel, B. Li, A. B. Tsybakov, S. A. van de Geer, B. Yu, T. Valdés, C. Rivero, J. Fan and A. van der Vaart, Test, 2006, 15, 271–344 CrossRef.
- O. Sagi and L. Rokach, Wiley Interdiscip. Rev.: Data Min. Knowl. Discov., 2018, 8, e1249 Search PubMed.
- Y. Yao and H. Wang, J. Data Sci., 2021, 19, 151–172 CrossRef.
- A. W. Moore, Adv. Neural Inf. Process. Syst., 1999, 543–549 Search PubMed.
- S. Lloyd, IEEE Trans. Inf. Theor., 1982, 28, 129–137 CrossRef.
- J. H. W. Jr, J. Am. Stat. Assoc., 1963, 58(301), 236–244 CrossRef.
- M. Ringnér, Nat. Biotechnol., 2008, 26, 303–304 CrossRef PubMed.
- A. A. Coelho, J. Appl. Crystallogr., 2003, 36, 86–95 CrossRef CAS.
- H. S. Geddes, H. Blade, J. F. McCabe, L. P. Hughes and A. L. Goodwin, Chem. Commun., 2019, 55, 13346–13349 RSC.
- C. Doersch, arXiv e-prints, 2016, arXiv:1606.05908.
- P. J. Rousseeuw, J. Comput. Appl. Math., 1987, 20, 53–65 CrossRef.
- Q.-J. Li, D. Sprouster, G. Zheng, J. C. Neuefeind, A. D. Braatz, J. Mcfarlane, D. Olds, S. Lam, J. Li and B. Khaykovich, ACS Appl. Energy Mater., 2021, 4, 3044–3056 CrossRef CAS.
- Y. Iwasaki, A. G. Kusne and I. Takeuchi, Npj Comput. Mater., 2017, 3, 1–9 CrossRef CAS.
- P. M. Maffettone, A. C. Daly and D. Olds, Appl. Phys. Rev., 2021, 8, 041410 CAS.
- Bluesky website, https://blueskyproject.io Search PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS.
- S. Langner, F. Häse, J. D. Perea, T. Stubhan, J. Hauch, L. M. Roch, T. Heumueller, A. Aspuru-Guzik and C. J. Brabec, Adv. Mater., 2020, 32, 1907801 CrossRef CAS PubMed.
- P. H. Tran, K. P. Tran, T. T. Huong, C. Heuchenne, P. HienTran and T. M. H. Le, Proceedings of the 2018 international conference on e-business and applications, 2018, pp. 6–9 Search PubMed.
- M. H. Bhuyan, D. K. Bhattacharyya and J. K. Kalita, IEEE Commun. Surv. Tutor., 2013, 16, 303–336 Search PubMed.
- M. M. Breunig, H.-P. Kriegel, R. T. Ng and J. Sander, Proceedings of the 2000 ACM SIGMOD international conference on Management of data, 2000, pp. 93–104 Search PubMed.
- P. J. Rousseeuw and K. V. Driessen, Technometrics, 1999, 41, 212–223 CrossRef.
- F. T. Liu, K. M. Ting and Z. Zhou, 2008 Eighth IEEE International Conference on Data Mining, 2008, pp. 413–422 Search PubMed.
- O. G. Shpyrko, J. Synchrotron Radiat., 2014, 21, 1057–1064 CrossRef CAS PubMed.
- S. K. Sinha, Z. Jiang and L. B. Lurio, Adv. Mater., 2014, 26, 7764–7785 CrossRef CAS PubMed.
- D. Cookson, N. Kirby, R. Knott, M. Lee and D. Schultz, J. Synchrotron Radiat., 2006, 13, 440–444 CrossRef CAS PubMed.
- C. Gati, G. Bourenkov, M. Klinge, D. Rehders, F. Stellato, D. Oberthür, O. Yefanov, B. P. Sommer, S. Mogk and M. Duszenko, et al., IUCrJ, 2014, 1, 87–94 CrossRef CAS PubMed.
- D. Lu and Q. Weng, Int. J. Rem. Sens., 2007, 28, 823–870 CrossRef.
- D. R. Reddy, in Readings in Speech Recognition, ed. A. Waibel and K.-F. Lee, Morgan Kaufmann, San Francisco, 1990, pp. 8–38 Search PubMed.
- M. Pazzani and D. Billsus, Mach. Learn., 1997, 27, 313–331 CrossRef.
- J.-W. Lee, W. B. Park, J. H. Lee, S. P. Singh and K.-S. Sohn, Nat. Commun., 2020, 11, 86 CrossRef CAS PubMed.
- K. Kaufmann, C. Zhu, A. S. Rosengarten, D. Maryanovsky, T. J. Harrington, E. Marin and K. S. Vecchio, Science, 2020, 367, 564–568 CrossRef CAS PubMed.
- X-Ray Absorption and X-Ray Emission Spectroscopy: Theory and Applications, ed. C. L. Jeroen and A. van Bokhoven, Wiley, 2016 Search PubMed.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297 Search PubMed.
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, Learning internal representations by error propagation, California univ san diego la jolla inst for cognitive science technical report, 1985 Search PubMed.
- E. Fix and J. L. Hodges, Int. Stat. Rev., 1989, 57, 238–247 CrossRef.
- M. N. Gibbs and D. J. MacKay, IEEE Trans. Neural Network., 2000, 11, 1458–1464 CrossRef CAS PubMed.
- E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi, I. Foster, C. P. Gomes, J. M. Gregoire, A. Mehta, J. Montoya, E. Olivetti, C. Park, E. Rotenberg, S. K. Saikin, S. Smullin, V. Stanev and B. Maruyama, Matter, 2021, 4, 2702–2726 CrossRef.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- Ophyd library, https://nsls-ii.github.io/ophyd Search PubMed.
- Bluesky Adaptive source code, https://github.com/bluesky/bluesky-adaptive Search PubMed.
- Bluesky Adaptive tutorial, https://blueskyproject.io/tutorials/Adaptive%20RL%20Sampling/Adaptive%20Sampling.html Search PubMed.
- T. Konstantinova, L. Wiegart, M. Rakitin, A. M. DeGennaro and A. M. Barbour, Sci. Rep., 2021, 11, 14756 CrossRef CAS PubMed.
- Papermill project, https://papermill.readthedocs.io/ Search PubMed.
- Slack software, https://slack.com/ Search PubMed.
- N. Bruchon, G. Fenu, G. Gaio, M. Lonza, F. H. O'Shea, F. A. Pellegrino and E. Salvato, Electronics, 2020, 9, 781 CrossRef CAS.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Chem. Sci., 2018, 9(39), 7642–7655 RSC.
- M. M. Noack, K. G. Yager, M. Fukuto, G. S. Doerk, R. Li and J. A. Sethian, Sci. Rep., 2019, 9, 11809 CrossRef PubMed.
- Z. Li, M. A. Najeeb, L. Alves, A. Z. Sherman, V. Shekar, P. Cruz Parrilla, I. M. Pendleton, W. Wang, P. W. Nega, M. Zeller, J. Schrier, A. J. Norquist and E. M. Chan, Chem. Mater., 2020, 32, 5650–5663 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2dd00014h |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |