Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High-throughput computational screening of nanoporous materials in targeted applications
Emmanuel
Ren
 ab,
Philippe
Guilbaud
ab,
Philippe
Guilbaud
 b and
François-Xavier
Coudert
b and
François-Xavier
Coudert
 *a
*a
aChimie ParisTech, PSL University, CNRS, Institut de Recherche de Chimie Paris, 75005 Paris, France. E-mail: fx.coudert@chimieparistech.psl.eu
bCEA, DES, ISEC, DMRC, Univ. Montpellier, Marcoule, France
First published on 15th June 2022
Abstract
Due to their chemical and structural diversity, nanoporous materials can be used in a wide variety of applications, including fluid separation, gas storage, heterogeneous catalysis, drug delivery, etc. Given the large and rapidly increasing number of known nanoporous materials, and the even bigger number of hypothetical structures, computational screening is an efficient method to find the current best-performing materials and to guide the design of future materials. This review highlights the potential of high-throughput computational screenings in various applications. The achievements and the challenges associated to the screening of several material properties are discussed to give a broader perspective on the future of the field.
1 Introduction
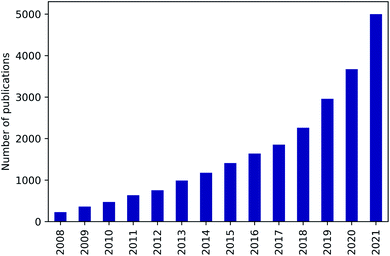
Nanoporous materials are characterised by a high internal surface area on which a large number of molecules can physically or chemically adsorb on. They can thus be used in various key sectors of the industry, such as gas separation and capture,1 storage,2 heterogeneous catalysis3,4 or drug delivery.5,6 Among notable examples we can cite H2 and CH4 purification and storage, CO2 capture, CO removal for fuel cell technology, desulfurisation of transportation fuels, and other technologies for meeting increasingly higher environmental standards. Moreover, nanoporous materials can have different chemical natures (inorganic, organic, or hybrid) and porosity (macroporous, mesoporous, or microporous). This opens up a large space of possible properties to explore and to find the most suitable structure for each specific application.Nanoporous materials can be used in a very wide range of applications, but systematically identifying the best material may seem like searching for a needle in a haystack. In fact, hundreds of thousands structures have been synthesised and possibly millions of materials are yet to be studied. A purely experimental approach, in addition to be expensive and time-consuming, would never be exhaustive to screen all these structurally and chemically diverse materials. Beyond this experimental limitation, large-scale computational screening studies can enable a more in-depth exploration of the existing materials, as well as generate novel hypothetical structures with potentially better performance. Even if the idea of this thorough exploration and the required databases of computationally-generated or experimentally-sourced structures were known for a very long time,7–9 research interest on computational screening applied to nanoporous materials has just experienced a rapid growth in the last decade (see Fig. 1). Several factors can explain this recent expansion: (1) the emergence of open databases of material structures and properties has opened the access for a growing number of scientists;10–14 (2) the advances in the in silico construction of hypothetical nanoporous materials have created new datasets to explore;15–17 (3) efficiently implemented open-source software have granted access to simulation tools for a much larger research community;18,19 (4) increasingly efficient supercomputers are now more and more available;20 (5) text and data mining have generated new databases of unreported properties from existing literature;21,22 (6) and the size of screenable databases have been increased by several orders of magnitude thanks to artificial intelligence techniques.23–26
Given the aforementioned scientific advances, computational screening, that was commonly used on small series of materials, began to be used on larger databases to identify top performing candidates, to better understand the main explanatory factors at the origin of the performance and to objectively set theoretical performance limits for a given application. Borrowing some techniques from the new field of data science, screening techniques are now applied to predict key performance indicators. These figures of merit are related to a variety of material properties such as electronic structure,27–29 chemical and catalytic activity,30–32 thermal properties,33–35 mechanical properties,36,37 transport and thermodynamic properties for adsorption.38–41
The present work is by no mean an exhaustive review of all the works on the subject, but it aims at giving nonspecialist readers a high-level overview of the potential of computational screening in a large variety of applications, and of the diversity of the different approaches used in this field of research. First, a brief survey of the development of materials databases and screening methodologies is given along with some examples illustrating the major milestones. Then, the thermodynamic properties linked to the adsorption processes are thoroughly reviewed; before moving to kinetic effects, looking at the prediction of transport properties. Finally, other aspects that differ from the adsorption process such as the computational screening of mechanical, thermal and catalytic properties are described at the end. We conclude by outlining some of the perspectives of the field.
2 Screening methodologies
2.1 Nanoporous material databases
Before building any screening strategy or performing any computational screening, one needs to generate a set of files describing the atomic structure of the materials. Nanoporous materials can have different degrees of crystallinity from perfectly crystalline to completely amorphous. Most of the computational work is focused on crystalline structures, since the atoms are well-described within a periodic framework, which enables faster simulations. The presence of defects are also usually neglected, which could explain some of the discrepancies between simulations and experiments. And amorphous materials are described by thousands of atomic positions in order to grasp their intrinsic non-periodicity.44 One can distinguish roughly four main classes of crystalline nanoporous materials: the inorganic zeolites (e.g. aluminosilicates, aluminophosphates), the porous polymer networks, the covalent organic frameworks (COFs) and the metal–organic frameworks (containing the zeolitic imidazolate frameworks i.e. ZIFs and others). This diversity of nanoporous materials offer a wide range of potential candidates for any targeted applications.The International Zeolite Association (IZA) gave a standardised set of 244 zeolites (in their idealized all-silica form) that can be used for screening purposes. To generate a dataset of structures, existing experimental database like the Cambridge Structural Database can be exploited. However, the raw structures determined experimentally by X-ray cannot be used directly as is. To obtain a computation-ready dataset, Chung et al. used algorithmic cleaning procedures to build the publicly available Computation-Ready Experimental MOF (CoRE MOF) database.45,46 CoRE MOF 2019 contains about 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOF structures, which is the biggest experimental database. Similar approach applied to organic frameworks led to the construction of a set of 187 COFs with disorder-free and solvent-free structures.47,48
000 MOF structures, which is the biggest experimental database. Similar approach applied to organic frameworks led to the construction of a set of 187 COFs with disorder-free and solvent-free structures.47,48
These experiment-based databases can already be used in computational screenings to retrieve valuable information, but unknown structures that are yet to be discovered are not represented. To overcome the limits and biases of experimental synthesis, artificial ways of generating nanoporous material datasets can be used, which proved to be extremely efficient. The first in silico generated database of about 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs used a recursion-based assembly (or tinkertoy-like) algorithm to combine 102 building blocks.41 Martin and Haranczyk then proposed a topology-specific structure assembly algorithm that leverage the topological information of the structures.49 Inspired by this algorithm, topology-based databases emerged a few years later with the set of 13
000 MOFs used a recursion-based assembly (or tinkertoy-like) algorithm to combine 102 building blocks.41 Martin and Haranczyk then proposed a topology-specific structure assembly algorithm that leverage the topological information of the structures.49 Inspired by this algorithm, topology-based databases emerged a few years later with the set of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOF structures generated using the Topologically Based Crystal Constructor (ToBaCCo) algorithm developed by Colon, Gómez-Gualdrón and Snurr.50 Later, Boyd and Woo proposed another topology-based algorithm using a graph theoretical approach and generated a 300
000 MOF structures generated using the Topologically Based Crystal Constructor (ToBaCCo) algorithm developed by Colon, Gómez-Gualdrón and Snurr.50 Later, Boyd and Woo proposed another topology-based algorithm using a graph theoretical approach and generated a 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures database (BW-DB) based on 46 different network topologies.51 Similar approaches are used for other classes of materials, Deem and coworkers proposed a dataset of nearly 2.6 million hypothetical zeolite structures.52–54 However, one could wonder if these hypothetical structures are synthesisable and can remain stable under operational conditions (e.g. thermal, mechanical, radioactive constraints). To discuss their synthetic likelihood, Anderson and Gómez-Gualdrón computed the free energies of 8500 hypothetical structures and compared them to experimentally observed MOF structures.55 This type of prediction can be very useful as it enables to gauge the relative stability of each materials and to only consider the stable structures. Later, Nandy et al. performed a meta-analysis of thousands of articles associated to the CoRE MOF 2019 database to extract their experimental solvent-removal stability and thermal decomposition temperature.150 These data were then leveraged in the training of multiple ML models to predict stability; such predictions can be very useful to gauge the relative stability of each material and to restrict screening to only structures considered experimentally stable. Other types of materials have been explored, Turcani et al. published 60
000 structures database (BW-DB) based on 46 different network topologies.51 Similar approaches are used for other classes of materials, Deem and coworkers proposed a dataset of nearly 2.6 million hypothetical zeolite structures.52–54 However, one could wonder if these hypothetical structures are synthesisable and can remain stable under operational conditions (e.g. thermal, mechanical, radioactive constraints). To discuss their synthetic likelihood, Anderson and Gómez-Gualdrón computed the free energies of 8500 hypothetical structures and compared them to experimentally observed MOF structures.55 This type of prediction can be very useful as it enables to gauge the relative stability of each materials and to only consider the stable structures. Later, Nandy et al. performed a meta-analysis of thousands of articles associated to the CoRE MOF 2019 database to extract their experimental solvent-removal stability and thermal decomposition temperature.150 These data were then leveraged in the training of multiple ML models to predict stability; such predictions can be very useful to gauge the relative stability of each material and to restrict screening to only structures considered experimentally stable. Other types of materials have been explored, Turcani et al. published 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 organic cage structures and used machine learning to predict their stability based on the shape persistence metric.56
000 organic cage structures and used machine learning to predict their stability based on the shape persistence metric.56
The Materials Genome Initiative, a 100 million dollar effort from the White House that aims to “discover, develop, and deploy new materials twice as fast”, led to the creation of the “Materials Project”, a centralised database containing all the above mentioned structures.57–59 The fast development of this nanoporous materials genome motivated Boyd et al. to write a comprehensive review on all the initiatives on generating new data for computational analysis.60
Yet, the sole increase in size of the databases is not enough. One needs to add diversity to have more general knowledge on the maximum performance and the explanatory features of such performance. Moreover, the diversity of structures ensure the quality of the predicted best materials for a given application. To qualitatively or quantitatively assess the diversity of a database, inventive methodologies have been developed. For instance, Martin, Smit and Haranczyk proposed a Voronoi hologram representation as a way of measuring similarities between structures to generate geometrically diverse subsets of a database.61 Moosavi et al. made a comparative study of the diversity of three well-known databases CoRE MOF 2019,46 BW-DB51 and ToBaCCo50,62 using geometrical and chemical descriptors to design a theoretical strategy for generating the most diverse set of materials.63 Another approach consists in searching for similarities instead of differences in the materials by studying topological patterns in the data.64 These investigations on the data structures give a solid ground to develop novel materials by objectively defining similarity, diversity and novelty. From the analysis gathered so far, one would need to radically change the approach by proposing materials with new chemistry, topology or mechanism (e.g. flexibility) in order to significantly improve the diversity of the current databases.
2.2 Evolution of screening methods
In its early stage, computational screening has been used on small series of nanoporous materials to generate specific knowledge on some sub-classes of materials. These small-scale screenings combined with experiments helped faster identification of good performing candidates, but they failed to establish general rules of design or to explore the unknown. Larger-scale screenings overcame these limitations by trying to exhaustively cover the whole spectrum of nanoporous materials.With the development of a nanoporous materials genome, several articles proposed methods to screen thousands of structures. Other challenges arose, such as the design of more efficient methods than the brute force screening or the analysis of big data. Two research groups led by R. Snurr and J. Hupp began to address those questions, they used a “funnel-like” approach to efficiently screen about 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hypothetical MOF structures.41 To do so, they performed a first screening involving less steps of simulation on the whole dataset, then they extracted a subset of top performing structures to perform a second round with more simulation steps. This procedure is repeated until a few materials are selected by a final round of simulations with reasonable accuracy. Similar “funnel-like” procedures have then been used in other field of applications as described in the Fig. 2. This type of screening saves precious computation time by balancing the complexity of the calculation with the amount of data to be screened. The most demanding simulations or experiments are only applied to the few most promising structures. This method can rather efficiently identify top candidates, but it can't draw quantitative structure–property relationships (QSPR), beside facing scalability issues above a critical dataset size.
000 hypothetical MOF structures.41 To do so, they performed a first screening involving less steps of simulation on the whole dataset, then they extracted a subset of top performing structures to perform a second round with more simulation steps. This procedure is repeated until a few materials are selected by a final round of simulations with reasonable accuracy. Similar “funnel-like” procedures have then been used in other field of applications as described in the Fig. 2. This type of screening saves precious computation time by balancing the complexity of the calculation with the amount of data to be screened. The most demanding simulations or experiments are only applied to the few most promising structures. This method can rather efficiently identify top candidates, but it can't draw quantitative structure–property relationships (QSPR), beside facing scalability issues above a critical dataset size.
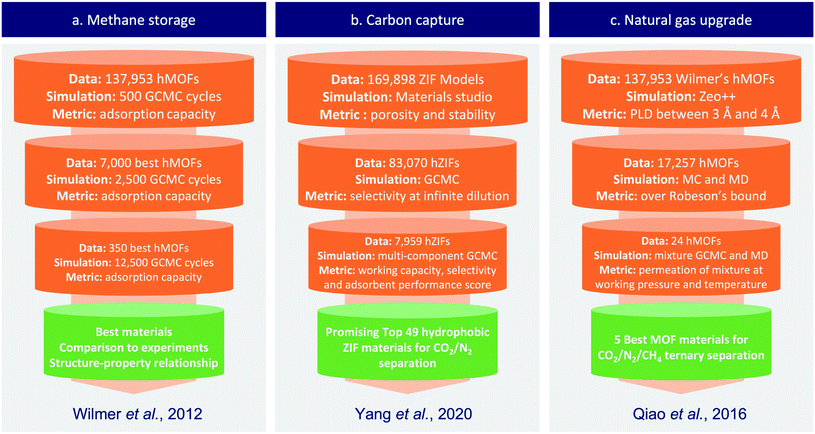 | ||
| Fig. 2 Simplified representation of typical funnel-type screening procedures, exemplified on three different applications from the published literature. (a) Wilmer et al.41 used a series of bi-component Grand Canonical Monte Carlo (GCMC) calculations at different levels of complexity to screen a large dataset of hypothetical MOFs for methane storage application. (b) Yang et al.42 used simulations at infinite dilution to pre-screen the dataset before using computationally demanding simulations and multiple metrics to find the most promising ZIFs for carbon capture. (c) In Qiao et al.,43 transport properties were screened along standard adsorption properties to find the best materials for the targeted CO2/N2/CH4 ternary separation; similarly, cheaper calculations at infinite dilution were carried out in a first step, before using more expensive calculations at working pressure and temperature. | ||
To overcome these new challenges, people are looking increasingly towards transferable models trained by a machine learning (ML) algorithm on a diverse and size-limited sub-sample. Ideally, such a model is transferable to potentially millions of structures and can provide valuable QSPR. For instance, Fernandez et al.65 used multiple linear regression analysis, decision tree regression, and nonlinear support-vector machine models to extract QSPR and establish rules of designing well-performing MOFs for methane storage, while identifying promising structures. In this first work they only used geometrical descriptors to describe methane storage,65 but realising the importance of chemical descriptors, they proposed the atomic property weighted radial distribution function as a powerful descriptor to predict CO2 uptakes.66 More importantly, they proved that ML can be used as a pre-screening tool to avoid running time-costly simulations by correctly identifying around 95% of the top 1000 best performing materials. Recently, the same group used similar techniques to predict CO2 working capacity as well as CO2/H2 selectivity in MOFs for precombustion carbon capture.67
2.3 ML-assisted high-throughput screening
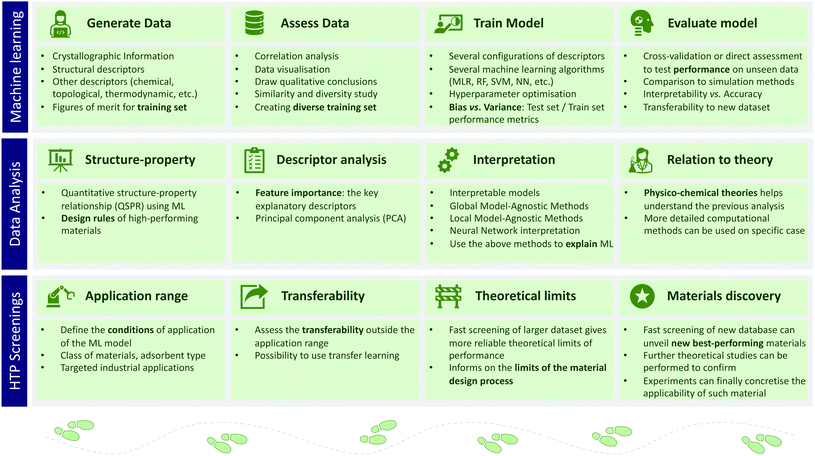
We saw the use of ML in the comprehension of the structure–property relationships, but it can also assist high-throughput screenings as illustrated in the Fig. 3. In an ML-assisted screening, one needs to consider first the type of algorithm and the features or descriptors. The descriptors exhaustively describe the physicochemical properties, while the ML algorithms set rules for learning patterns in the data. At the end, the ML model needs to be predictive while maintaining a high level of interpretability68 and reproducibility.69 To illustrate this approach, a few studies of such ML-assisted high-throughput screenings and their particular contributions to the field are presented below.Regarding energy descriptors, different ones can be used alongside the most basic geometrical ones. For instance, Simon et al. introduced the Voronoi energy, combined with structural descriptors they used them to predict Xe/Kr selectivity of over 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures using a random forest model.70 Bucior et al. also used an energy-based descriptor, the energy histogram, to predict the cryogenic storage capacity of hydrogen three times faster than traditional simulations.71
000 structures using a random forest model.70 Bucior et al. also used an energy-based descriptor, the energy histogram, to predict the cryogenic storage capacity of hydrogen three times faster than traditional simulations.71
Descriptors based on the analysis of data have also been studied and enable to find similarly performing materials. Based on advanced knowledge on mathematics and topology, Lee et al. used a topological data analysis-based descriptor, called persistent homology and resembling barcodes, to screen a zeolite database for methane storage and carbon capture applications.72 Later, Yongjin Lee led his group to propose an ML prediction method using the same pore geometry barcodes.29 More recently, Moosavi et al. built geometric landscapes, a representation for energy-structure–function maps based on geometric similarity, quantified by persistent homology.73
To model the chemical behaviour of materials, one developed several chemical descriptors. In particular, Borboudakis et al. introduced the chemical building block as a feature or descriptor of their ML models. In their study, they integrated all the models into a unified algorithm called “Just Add Data” and concluded that random forest and support vector machine were outperforming the other algorithms they tested.74 Recently, the same group continued on providing a universal (transferable on different materials) ML algorithm by using the type of atom instead of the previous building block description, which led to an increased performance on the prediction of methane and carbon dioxide adsorption capacities.75 Anderson et al. used the chemical building blocks of the MOF and the Lennard–Jones parameters of existing or “alchemical” adsorbates to train a neural network model for adsorption isotherms prediction.76
Through the scope of different types of descriptors, we introduced some ML-assisted approach to computational screenings. Fig. 3 gives a higher-level view on how machine learning is practically applied. One can find a more comprehensive review on big-data science applied to porous materials written by Jablonka et al.77 The authors go through the selection of diverse data, the design of meaningful descriptors, ML algorithms, the best practices in the training process of an ML model, the measurement of its performance and the interpretation of the model to avoid the “black box” effect.
Beyond the reluctance to apply data science to fundamental sciences, one should not associate machine learning with the “end of theory”; physicochemical theories can guide the development of the descriptors at the base of any ML models and the interpretation of these models is impossible without scientific insights. The laws of physics are not explicitly included in an ML model, interpretability and exploitability methods can help cover these flaws by identifying potential nonphysical behaviours, or confirming its consistency in describing known physical behaviours, or unveiling unexpected scientific insights.68 If the model fails to meet some standards, further developments are needed for the descriptors to contain all relevant information, or to draw a more consistent relationship between the descriptors and the desired metric. Without a well-designed (containing all physical information) set of descriptors, an ML approach cannot make reliable predictions. The recent developments presented here are confirming this close interplay between data science and theory.
3 Thermodynamic properties of adsorption
In its early development, computational screening was mainly used to predict thermodynamic properties in adsorption processes. Three main applications have been identified in the associated literature: gas storage (for energy or medical applications), gas separation (noble gas, hydrocarbons, carbon dioxide, etc.) and post-combustion CO2 capture. These applications are closely linked to urgent environmental and energy issues that are yet to be solved. Screening can guide the development of better performing materials by shedding light upon unknown structure–property relationship, probes possible theoretical limitations (unreachable targets) and identifies potential candidates that need to be experimentally tested.3.1 Gas storage
One can leverage the high surface density of the nanoporous materials, especially the MOFs, to stock in very low-density gas. In the field of energy storage or transportation, natural gas (mainly methane) or hydrogen are considered plausible alternative fuels to replace conventional ones for transport. The US Department of Energy (US DOE) recently financed research programs and set target for methane and hydrogen storage. Nanoporous materials could reduce energy, infrastructure and security cost due to the required compression and cooling. In this section, we are focusing on high-throughput screening for methane storage in nanoporous materials, before broadening the scope hydrogen and other perspectives.One of the pioneering works in computational screening was published in 2011 by Wilmer et al.41 They performed a large-scale screening of 137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 hypothetical MOF structures to estimate the methane storage capacity of each MOF at 35 bar and 298 K based on the US DOE standards. Back then, the US DOE set a target methane capacity value of 180 volSTP−1 (which has since been achieved by several materials reported in the literature). In their large-scale analysis, Wilmer et al. found over 300 hypothetical MOFs that meet the targeted requirements and the best one can store up to 267 volSTP−1, surpassing the state-of-the-art of the time. From their large dataset, a preliminary structure–property relationship analysis revealed that void fraction values of approximately 0.8 and gravimetric surface areas in a range 2500–3000 m2 g−1 resulted in the highest methane capacities. Optimal pore size are also shown to be around the size of one or two methane molecule(s). Maximisation of gravimetric surface area was a common strategy in the MOF design for storage applications, but this study showed the existence of an optimal range of surface area values. Computational screenings can draw clear relationships between structural descriptors and performance. Later, a more quantitative relationship was drawn by Fernandez et al. using ML models as illustrated on Fig. 4. Beware not to over-interpret the relation given by the response surface, since the identified maxima do not always have a physical reality, especially where there is no training data in the area pointed by the red arrows. However, it highlights promising unexplored feature space and shows potential research directions.
953 hypothetical MOF structures to estimate the methane storage capacity of each MOF at 35 bar and 298 K based on the US DOE standards. Back then, the US DOE set a target methane capacity value of 180 volSTP−1 (which has since been achieved by several materials reported in the literature). In their large-scale analysis, Wilmer et al. found over 300 hypothetical MOFs that meet the targeted requirements and the best one can store up to 267 volSTP−1, surpassing the state-of-the-art of the time. From their large dataset, a preliminary structure–property relationship analysis revealed that void fraction values of approximately 0.8 and gravimetric surface areas in a range 2500–3000 m2 g−1 resulted in the highest methane capacities. Optimal pore size are also shown to be around the size of one or two methane molecule(s). Maximisation of gravimetric surface area was a common strategy in the MOF design for storage applications, but this study showed the existence of an optimal range of surface area values. Computational screenings can draw clear relationships between structural descriptors and performance. Later, a more quantitative relationship was drawn by Fernandez et al. using ML models as illustrated on Fig. 4. Beware not to over-interpret the relation given by the response surface, since the identified maxima do not always have a physical reality, especially where there is no training data in the area pointed by the red arrows. However, it highlights promising unexplored feature space and shows potential research directions.
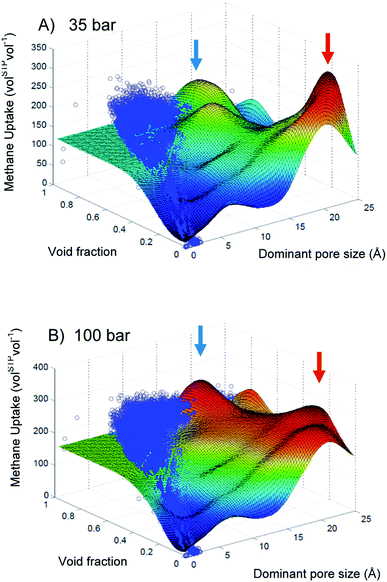 | ||
| Fig. 4 Two-dimensional response surfaces of the support vector machine (SVM) models trained by Fernandez et al. for methane storage at (A) 35 bar and (B) 100 bar using void fraction and dominant pore size. The blue dots represent the GCMC simulated uptake values. The color of the surface represents the methane storage value, from blue (lowest values) to red (highest values). Blue and red arrows indicate maxima on the response surface. Reprinted with permission from ref. 65. Copyright 2013 American Chemical Society. | ||
Since then new materials above the target have been found and the US DOE decided to set a higher target of 315 volSTP−1. Until now, this new target is not yet reached. This is why the recent developments have focused on assessing the feasibility of such a target by accelerating the screening methods so that more data can be screened, and by interpreting the QSPR models to extract important knowledge for the design of novel materials. For instance, Gómez-Gualdrón et al. showed that even by artificially quadrupling the Lennard–Jones interaction factor ε and by increasing the delivery temperature by 100 K, the newly set target is only reached by a handful of MOFs.78 This study suggests the impossibility to reach the DOE target using a preconceived (experimentally or theoretically) material to store methane. However, this theoretical limitation can be overcome by increasing the surface density of sites with high affinity with methane and by increasing the delivery temperature.
Later, a larger-scale screening on methane storage was carried out by Simon et al. on 650![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 experimental and hypothetical structures of zeolites, MOFs, and PPNs. This study confirmed that the classes of materials currently being investigated were unlikely to meet the new target. The authors suggested that it wasn't surprising since the target was based on economical arguments, while the screening is based on thermodynamic arguments.79 This example illustrates the power of large scale screening to settle questions of physical feasibility (if simulations are accurate) and hence avoiding experimental efforts spent on impossible tasks.
000 experimental and hypothetical structures of zeolites, MOFs, and PPNs. This study confirmed that the classes of materials currently being investigated were unlikely to meet the new target. The authors suggested that it wasn't surprising since the target was based on economical arguments, while the screening is based on thermodynamic arguments.79 This example illustrates the power of large scale screening to settle questions of physical feasibility (if simulations are accurate) and hence avoiding experimental efforts spent on impossible tasks.
More recently, a dataset containing trillions of hypothetical MOFs have been screened for methane storage.80 Lee et al. developed a methodology using machine learning combined with genetic algorithm to perform the largest screening until now. In addition to confirming most of the results (theoretical limits and QSPR) found by previous screenings, 96 MOFs were found to outperform the current world record. This study shows the scaling potential of ML-assisted screenings in handling “Big data”.
Similarly computational high-throughput screenings have been applied to other storage applications such as hydrogen storage. Computational screenings showed that cryogenic storage of hydrogen can meet the DOE target of 50 g L−1.62,81,82 Anderson et al. performed a large scale screening based on neural networks to test out multiple pressure/temperature swing conditions to find that the maximal deliverable capacity cannot exceed 62 g L−1.83 Compared to the density of liquid hydrogen (72 g L−1), this upper limit seems reasonable since the adsorbent material takes at least 10–20% of the tank. Here, we only showed some flagship results of the field. For a more detailed meta-analysis, Bobbitt and Snurr wrote a very complete review on computational high-throughput screening of MOFs for hydrogen storage.84
3.2 Gas separation
As a representative example of what could be done in the field of gas separation, we are going to focus on Xe/Kr separation. These noble gases have multiple applications in the medical (e.g. anaesthesia, painkiller),85,86 aeronautical87,88 or lighting sectors,89,90 just to cite a few. The industry more commonly uses cryogenic distillation to separate xenon and krypton from the ambient air, which requires a compression and cooling of the gas mixture. But this technology can laboriously be deployed in very security-sensitive cases such as the treatment of radioactive off-gases from nuclear plants. Nanoporous materials can be used as a safer, cheaper and less energy-intensive alternative. Computational screenings is an ideal tool to kick-start the development of this new technology by identifying rapidly the best candidates.The first large-scale computational screening on Xe/Kr adsorption-based was performed by Sikora et al. based on the same approach previously developed for methane storage by their group at the Northwestern University.91 This study was based on the same 137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures of hypothetical MOFs.41 They calculated the Xe/Kr selectivity using Monte Carlo molecular simulations on the whole database by iteratively increasing the number of steps and selecting the best materials similar to the approach on Fig. 2. By analysing the relationships between pore sizes and selectivity, they confirmed a hypothesis from a smaller scale study that the pores should be between the size of 1 to 2 xenon molecules.92 Tube-like channel were also found to favour better selectivity. Moreover, they found that top performing materials could have selectivities around 500; but we can only conclude on the order of magnitude of the theoretical limitation of the Xe/Kr selectivity, considering the statistical uncertainty of the simulation.
000 structures of hypothetical MOFs.41 They calculated the Xe/Kr selectivity using Monte Carlo molecular simulations on the whole database by iteratively increasing the number of steps and selecting the best materials similar to the approach on Fig. 2. By analysing the relationships between pore sizes and selectivity, they confirmed a hypothesis from a smaller scale study that the pores should be between the size of 1 to 2 xenon molecules.92 Tube-like channel were also found to favour better selectivity. Moreover, they found that top performing materials could have selectivities around 500; but we can only conclude on the order of magnitude of the theoretical limitation of the Xe/Kr selectivity, considering the statistical uncertainty of the simulation.
Seizing the opportunity of a formidable expansion of the nanoporous materials database triggered by the Materials Genome Initiative, Simon et al. screened 670![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 experimental and hypothetical nanoporous material structures for Xe/Kr separation.70 It is one of the largest-scale screening performed in this area. Inspired by the work of Fernandez and co-workers,65 they used ML algorithms to train a model on a diverse subset of 15
000 experimental and hypothetical nanoporous material structures for Xe/Kr separation.70 It is one of the largest-scale screening performed in this area. Inspired by the work of Fernandez and co-workers,65 they used ML algorithms to train a model on a diverse subset of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures. This method allowed them to run time-consuming molecular simulations only on this training set, before applying the ML model to predict the selectivity values on the larger set of structures. On top of analysing the links between pore descriptors and selectivity, they rationalised it using theoretical pore models of spherical and cylindrical geometries to confirm the findings of Snurr and co-workers.91,92 By comparing the structural descriptors of good-performing and bad-performing structures, they concluded that geometrical descriptors wasn't enough to explain the performance (see Fig. 5). The analysis of a few top candidates suggests that different chemical insights could explain their good performance. For SBMOF-1 or KAXQIL,93 an experimental MOF, its higher performance was explained by the tube-like 1D channel with a very favourable binding site formed by carbon aromatic rings. This nanoporous material was later tested using breakthrough experiments and proved to be one of the most promising candidates.94 This close collaboration between computation and experimentation is a testimony of the potential of computational screenings to find nanoporous materials for any targeted application.
000 structures. This method allowed them to run time-consuming molecular simulations only on this training set, before applying the ML model to predict the selectivity values on the larger set of structures. On top of analysing the links between pore descriptors and selectivity, they rationalised it using theoretical pore models of spherical and cylindrical geometries to confirm the findings of Snurr and co-workers.91,92 By comparing the structural descriptors of good-performing and bad-performing structures, they concluded that geometrical descriptors wasn't enough to explain the performance (see Fig. 5). The analysis of a few top candidates suggests that different chemical insights could explain their good performance. For SBMOF-1 or KAXQIL,93 an experimental MOF, its higher performance was explained by the tube-like 1D channel with a very favourable binding site formed by carbon aromatic rings. This nanoporous material was later tested using breakthrough experiments and proved to be one of the most promising candidates.94 This close collaboration between computation and experimentation is a testimony of the potential of computational screenings to find nanoporous materials for any targeted application.
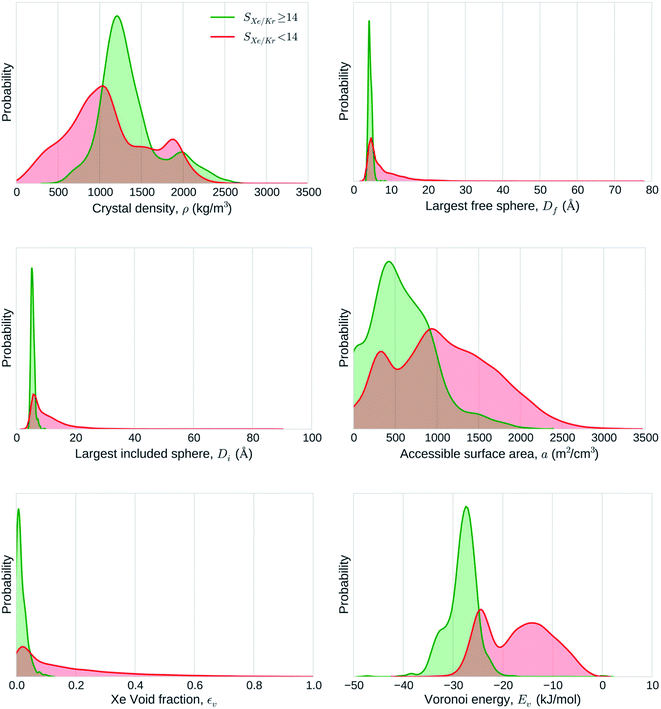 | ||
| Fig. 5 Statistical analysis of the adsorptive separation of xenon/krypton mixtures by nanoporous materials. The graphs represent the distributions of structural descriptors explored by highly selective (green) and poorly selective (red) materials separately. Reprinted with permission from ref. 70. Copyright 2015 American Chemical Society. | ||
The experimental work on Xe/Kr separation on SBMOF-1 revealed discrepancies between the selectivity values obtained experimentally and computationally.94 The assumption of rigid crystal structures in the molecular simulations could partially explain the difference observed. Witman et al. proposed that the flexibility of the materials, that weren't considered in the screening of Simon et al., could explain the lower selectivity observed experimentally.95 In this study, they screened the Henry regime separation of about 4000 MOF structures of the CoRE MOF 2014 database,45 and found that intrinsic flexibility, i.e. the thermal vibration of the material, can make the pore size derive from the ideal value for the separation and hence lower the selectivity. This study further confirms the importance of the pore size by highlighting the effect of its evolution over time.
In 2019, Chung et al. screened the most extensive simulation-ready and experimentally synthesised MOF structures for Xe/Kr separation.46 This study pointed out the potential of coordinated solvent molecules to fine-tune the selectivity for any separation application, since their presence can enhance selectivity in some cases. The results of their screening confirms the potential of structures such as SBMOF-1 found by Simon et al., but they also described a few structures with similar selectivity but with better xenon uptake. The authors emphasise the importance of considering other figures of merit such as the adsorption capacity. Other factors should be taken into account to find the best trade-off between all the relevant figures of merit; we could think of the kinetics of such a separation, the effect of flexibility on the performance, the stability of the materials (especially in radioactive environment), the financial aspects, and more. Some of these aspects will be tackled in the following sections of this review.
Beside noble gas separation, carbon capture could benefit greatly from the use of nanoporous materials and we can find extensive literature on computational screening targeting this application.42,96–100 Findley and Sholl performed a screening of CoRE MOF 2014 to find the best structures for CO2 capture in humid conditions.101 After finding candidates, they performed quantum calculations but found that the classical methods with generic force fields overestimated the performance, highlighting the limits of the methodology. For a more in depth review on separation, Daglar and Kaskin described the recent development of high-throughput screening focusing mainly on CO2 separation from methane of diazote.102
4 Transport properties
In the previous section, the thermodynamic properties only described the state of equilibrium of the adsorption process. But sometimes the transient state can last long before reaching the equilibrium, which makes the process more time-consuming. Thus, the transport properties complete the thermodynamic description of the adsorption process inside a nanoporous material. For example, a low diffusion rate would mean for storage applications more time and energy needed to fill-up the tanks, or for separation applications a less selective process than expected. In more extreme cases of molecular sieves for fluid separation, the transport properties become predominant to assess the performance. One can leverage the difference of the molecules diffusion coefficients to selectively filter gas mixtures through a nanoporous membrane.103 Here, the main subject becomes the transient state and not the equilibrium. This section is thus dedicated to the kinetics of the adsorption process to better model the time required to reach the equilibrium or to study out-of-equilibrium processes such as molecular sieving by nanoporous membranes.4.1 Diffusion calculation to model the kinetics of adsorption
In most computational screenings, the diffusion coefficient considered is the self-diffusion coefficient that describes an infinite-dilution case. Other multi-component diffusion coefficients could be considered, but for simplicity and clarity they won't be mentioned in this review. The calculation of the self-diffusion coefficient gives a first estimation of the kinetics in a storage or a separation process in the limit of low adsorption loading.There are two approaches to estimate the diffusion inside a porous material: the first one relies on molecular dynamics (MD) and the second one on transition state theories. In the first approach, one analyses the mean squared displacement of the adsorbed molecule moving in the material. In the second, one identifies minimum energy path along the material to identify transition states (TS) to calculate diffusion energy barriers. The MD-based method requires fewer assumptions and is therefore more reliable than the TS-based method, but the latter is computationally more efficient in the case of low diffusion rate (diffusivity lower than 10−11 m2 s−1).
State-of-the-art MD simulations could calculate rather accurate diffusion coefficients, but the computational cost scales quickly with the number of structures. To use this method on a large dataset without spending to much computation time, Watanabe and Sholl pre-screened the pore sizes of 1163 MOFs to select only the structures within a certain range of PLD (pore limiting diameters).38 A restricted list of 359 MOFs was then used to carry out MD simulations to calculate diffusion coefficients. The results of this final screening are then used to extract the most promising structures for further experimental or computational investigation. Similarly, Qiao et al. used a multi-stage screening to find the best membrane-material within about 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hypothetical MOFs for a CO2/N2/CH4 separation.43 They started to select materials based on pore geometry analysis; then they calculated Henry's coefficient and diffusion coefficients at infinite dilution; finally they compared the binary permselectivitys to extract 24 promising MOFs for ternary adsorption and diffusion calculation at the desired pressure and temperature conditions.
000 hypothetical MOFs for a CO2/N2/CH4 separation.43 They started to select materials based on pore geometry analysis; then they calculated Henry's coefficient and diffusion coefficients at infinite dilution; finally they compared the binary permselectivitys to extract 24 promising MOFs for ternary adsorption and diffusion calculation at the desired pressure and temperature conditions.
Another approach replaces MD simulations with more computationally efficient TS-based methods to determine diffusion coefficients. Haldoupis et al. developed an algorithm to identify diffusion paths by exploiting an energy grid with a clustering algorithm. The diffusion paths are then analysed to identify the pores and the channels, and to calculate key geometric (PLD, largest cavity diameter) and energetic (Henry's constant, diffusion activation energy) features.104 As represented in see Fig. 6, they found a clear dependence of the diffusion energy barrier to the PLD. As one of the first TS-based screenings, it is still subject to many development perspectives. For instance, the approach is limited to spherical adsorbates and rigid frameworks. Moreover, the diffusion coefficients are approximated using a simplistic hopping model for a qualitative analysis. This method is highly efficient, but the accumulation of approximations makes a quantitative systematic analysis of diffusion coefficients out of reach.
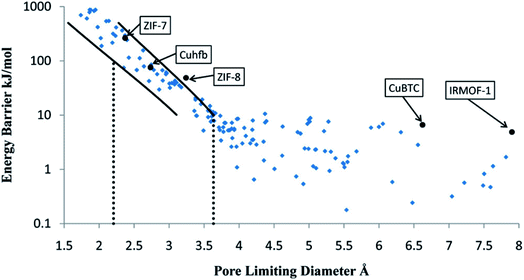 | ||
| Fig. 6 Calculated energy barrier for the diffusion of CH4 in 216 metal–organic frameworks (MOFs), shown as a function of the pore-limiting diameter. The solid lines represents statistical upper and lower bounds on the energy barrier, in a transition state theory approach. Reprinted with permission from ref. 104. Copyright 2010 American Chemical Society. | ||
Later, Kim et al. introduced a flood fill algorithm to obtain all the points within a given energy.105 These points are then identified as channels or blocked regions. Along the channels, local minimums of energy are defined as lattice sites and transition states are defined perpendicular to the diffusion direction. A random walk is then computed along the lattice sites with hop-rates defined according to the activation energy. A diffusion coefficient is then calculated in each three directions of the space and an average diffusion coefficients is finally determined. A comparison with the MD method on the IZA zeolite structures shows good agreement, but there are still some discrepancies explained by correlated hops in the case of rapid diffusion or by the presence of complicated channel profiles. Inspired by this work, Mace et al. developed a similar method that progressively fill the energy grid to detect transition states, hence removing the previous restriction to orthogonal cells only.106 The diffusion coefficient is now computed using a kinetic Monte Carlo simulation allowing the adsorbate to jump freely in all directions instead of restricting it in a single dimension. This new method, called TuTraSt, handles very complex diffusion paths (like in the AEI zeolite). This new approach seems to be promising as it is in good agreement with MD simulations, while being 2–3 orders of magnitude faster. However, the time performance could improve tremendously by translating it from Matlab to C++ and by implementing parallelisation procedures.
Very recently a massively parallel GPU-accelerated string method has been implemented and shared publicly to compute very efficiently diffusion coefficients based on the transition state theory.107 The recent developments in the prediction of diffusion coefficients in nanoporous materials point towards a promising future for the screening of transport properties applied to even larger databases. Going further, Bukowski et al. reviewed thoroughly diffusion in nanoporous solids as an attempt to connect theory to experiments.108
4.2 Membrane materials for gas separation
In separation application, the study of the transport properties can evaluate the feasibility of the thermodynamic equilibrium, crucial for any bed separation process. If this separation is not feasible, kinetic separation or partial molecular sieving are to be considered. Some notable examples are: air separation in zeolites using pressure swing adsorption,109 N2/O2 separation in carbon molecular sieves,110 or N2 removal from natural gas.111 In kinetic separation, the valuable metric is not the selectivity anymore, but the permselectivity, i.e. the product of the selectivity and the permeability (ratio of diffusion coefficients). Therefore, the screening of diffusion coefficients gives complementary information to the thermodynamic selectivity screenings. Here, we give some examples of such screening and the main descriptors that partially explains the computed figures of merit.To give an overview on the potential of computational screenings to predict transport properties, we are now going to focus on the membrane separation applied to natural gas upgrading. The separation of CH4 from N2 and CO2 is a crucial step of this upgrading process. In 2016, a large scale high-throughput screening (see Fig. 2 for the approach) of hypothetical MOF membranes for upgrading natural gas has been performed using MD simulations.43 In that work, Qiao et al. confirmed the existence of MOF materials with performances beyond the upper bound for N2/CH4 and CO2/CH4 separations previously determined by Robeson on a large set of polymeric membranes.112 This Robeson's upper bound is systematically crossed by MOF materials in computational screenings, see as an example the Fig. 7. This can be explained by the fact that MOFs perform better that polymeric frameworks and the simulations at this level of theory. They also identified 24 MOFs suitable for the ternary CO2/N2/CH4 separation using a multi-stage screening described in the previous section.
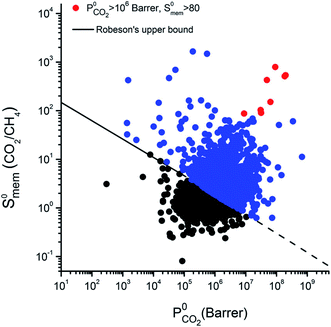 | ||
| Fig. 7 Selectivity and permeability of metal–organic framework (MOF) membranes for CO2/CH4 separation, computed at infinite dilution by combining Grand Canonical Monte Carlo and molecular dynamics simulations.114 The black solid line represents the Robeson's upper bound.112,117 MOFs that can exceed the bound are shown in blue, and the 8 top-performing MOF membranes are shown with red symbols. Reprinted with permission from ref. 114. Copyright 2018 American Chemical Society. | ||
Two years later, Qiao et al. used the same approach to study this ternary separation on a database of synthesised structures.113 Applying machine learning techniques to their data, they performed a QSPR analysis. Using a principal component analysis, they notably found that the permeability is higher when materials have high PLD and void fraction coupled with low density and percentage of pores within a characteristic range. The opposite was found to be true for high membrane selectivity for the CO2/CH4 separation. Using decision tree algorithms, they gave objective procedures of selecting the best separation membranes based on some key descriptors. Finally, they studied in detail some of the best performing materials found by a support vector machine algorithm.
Altintas and Keskin later performed a screening on the same database for CO2/CH4 membrane separation to identify the best performing materials and perform more computationally demanding simulations.114 The simulations in rigid structures at infinite dilution show a large number of structures above the Robeson's upper bound as shown in Fig. 7, this crossing of the upper bound can be explained by either a better performance of MOF membranes compared to the polymeric membranes used by Robeson, or an overestimation due to oversimplified assumptions (infinite dilution, rigidity). But when higher pressures and flexibility are considered, the selectivity values are dropping down closer to the upper boundary, hence confirming the overestimation of the performance in screenings based on rigid approximations at infinite dilution. Budhathoki et al. developed a screening methodology for MOFs in mixed matrix membranes for carbon capture applications by estimating permeation values in these composite materials using a Maxwell model.115 The authors even proposed a pricing for each material compared to their relative performance. Similar studies have been carried out on different materials, Yan et al. showed the influence of decorating COFs with different chemical compounds on the membrane selectivity.116
The transport properties screening is based on the calculation of diffusion coefficients at infinite dilution and in rigid molecules. There are different methods to calculate them (mainly MD and TS-based methods). Flexibility and pressure dependence are very hard to incorporate directly in the screening procedures. Researchers usually consider these factors at the end of the screening on the most promising structures because of the computational complexity of the corresponding simulations. To take account of pressure dependence, we need an MD simulation of several adsorbates that takes much more time than running single component simulations,118,119 which makes it harder to include in a high-throughput screening. Flexibility could be taken account by calculating snapshots and running multiple MD simulations, or by using flexible force fields, which means in both cases an increase in computational run-time. Some faster methods of quantitatively predicting the impact of flexibility on diffusion are being investigated in ZIFs and could give an interesting alternative to these expensive methodologies.120
5 Non-adsorptive properties
Due to their high internal surface area, adsorption applications were a natural outlet for nanoporous materials. However, these materials can be used in many other applications. This section is dedicated to the physical and chemical properties not directly related to the adsorption process inside nanoporous materials such as catalytic activity,30–32 mechanical properties,36,37 or thermal properties.33–35 These properties require a more refined description of the atomic interactions within the material. DFT simulations are usually performed to accurately retrieve these properties. However, the computational cost required is multiplied by several orders of magnitude compared to classical simulations. The size of the datasets screened are therefore much smaller (a few hundreds maximum), and the use of ML can potentially speed up the whole process. ML is based on lower cost descriptors,121,122 or it can be used in ML potentials for molecular simulations.123,1245.1 Catalytic activity
Beyond adsorption properties, screening procedures have been applied to chemical properties such as catalytic activities. Heterogeneous catalysis is generally performed using metallic nonporous structures, the use of nanoporous materials can increase dramatically the active surface area and the catalytic activity. Consequently, MOFs have been demonstrated to show catalytic properties for several chemical reactions. Just to cite a few, one can think of hydrogenation, hydrolysis, oxidation, among others explicitly covered by McCarver et al. in their review.125 Considering the sheer amount of possible materials, computational studies are potentially more effective than experimental ones. Therefore, computational screenings evolved in the last decade aiming at studying larger datasets.Although the vast majority of computational screenings have been done on small series, there are a few systematic screenings of larger datasets. The scarcity of the latter can be explained by the high level of computational cost required. Here, we show some examples of such attempts by focusing on the example of C–H bond activation for the conversion of alkanes into alcohols in the presence of nitrous oxide.
Inspired by enzymatic catalysis of the reaction of small alkanes with N2O into alcohols, Vogiatzis et al. identified 7 iron containing MOF structures out of 5000 structures from the CoRE MOF database.126 They found two descriptors that govern the catalytic activity: (1) the N–O dissociation energy of N2O on the adsorption site and (2) the energy difference between two spin states of the intermediate. Using a screening on these descriptors, three structures were identified as promising for further experimental studies. The best one has been computationally demonstrated to catalytically and selectively oxidise ethane to ethanol in presence of N2O. Moreover, the authors found that defects played a major role in the observed catalytic activity.
Later, Rosen et al. enlarged the scope of materials screened to other metals.127 From an 838 DFT-optimised MOFs subset of CoRE MOF 2014, the authors selected 168 MOFs that were likely to have open metal sites and pore-limiting diameters that allows the diffusion of the reactants. They then used a fully automated workflow to place the reactants in the adsorption site and relaxed the system using periodic DFT calculations. As shown in Fig. 8, using the bond activation energy Ea,C–H and the metal–oxo formation energy ΔEO as key parameters, they classified the materials according to their relative stability and reactivity to find the best materials for the application. These energies were then analysed using physicochemical descriptors such as the spin density on the oxygen and the metal–oxygen distance.
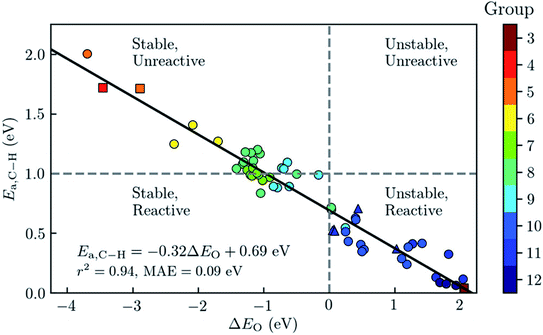 | ||
| Fig. 8 Analysis of a diverse set of experimentally derived metal–organic frameworks (MOFs) with accessible metal sites for the oxidative activation of methane. The graph shows the predicted barrier for the C–H bond activation of methane, Ea, as a function of the metal–oxo formation energy, ΔEO. For each material, the symbol colour refers to the group number of the metal in the periodic table. The best-fit line has is plotted in black, and has a mean absolute error (MAE) of 0.09 eV. MOFs with Ea < 1 eV are classified as being reactive toward C–H bond activation and MOFs with ΔEO < 0 as having thermodynamically favoured active sites when using O2 as the reference state. Reprinted with permission from ref. 127. Copyright 2019 American Chemical Society. | ||
This type of brute force screening can be quickly cumbersome, as a result many researchers in the field are trying to find key structure–activity relationships to accelerate future computational screenings. Several descriptors have been developed for high-throughput screenings: Butler et al. used electron removal energies to explain photocatalytic behaviours of MOFs;128 Rosen et al. showed that the energy required to form the metal–oxide intermediate was a key descriptor of the thermal catalysis of alkane oxidation by N2O;129 and Fumanal et al. show a screening protocol based on two energy-based descriptors to predict photocatalytic properties of MOFs.130 Lately, Rosen et al. screened thousands of MOF structures to compare different DFT functionals and leveraged the data calculated to train machine learning models that can rapidly predict MOF band gaps.131
The development of ML methods are also critical in the field,132 but the lack of centralised database with high precision descriptors is a challenge for the future of these methods. The influence of defects, the different ways of modelling MOFs as periodic structures or clusters, the diversity of structures and the stability of such structures remain open problems. Yet, it does not threaten the major role of high-throughput screenings in the early design process of any nanoporous materials for catalysis. To conclude this brief overview, we point the readers to a more exhaustive presentation of the matter.133
5.2 Mechanical properties
In the past decade, there has been a growing interest in the systematic study of physical properties of various classes of materials, including inorganic materials and framework materials. Among these physical properties, mechanical properties have been a topic of particular interest, as they are crucial for many applications, and at the same time can be computed by relatively standard methodologies. In particular, is it possible to calculate linear elastic constants (the second-order elastic tensor) in the zero-Kelvin limit by strain/stress or strain/energy approaches, performing a series of DFT calculations of strained structures and calculating the elastic constants. From these constants, all other mechanical properties can be evaluated by tensorial analysis,134 including the bulk modulus, Young's modulus, shear modulus, Poisson's ratio, etc. This type of calculation can be coupled with any available quantum chemistry code,135 and is even integrated in some packages, like CRYSTAL17.136One of the first studies that investigated systematically the elastic properties of a family of materials was a 2013 study of all-silica zeolites,137i.e., crystalline and porous SiO2 polymorphs. While this dealt with only 121 zeolitic frameworks out of 244 known structures, it showed that systematic studies at the DFT level were computationally tractable, and that they provided physical insight into the link between microscopic structure and macroscopic physical properties. This study demonstrated, among other things, that a small number of zeolites presented large negative linear compressibility (NLC), which could be linked to the wine-rack motif of their frameworks.
Looking outside of the specific case of zeolites, other groups have applied DFT calculations of elastic constants in a high-throughput manner. de Jong et al. leveraged the structures of the Materials Project,58,59 trying to chart the diversity of elastic properties across the whole space of inorganic crystalline compounds.138 As shown in the Fig. 9, they provided a database containing the full elastic information of 1181 inorganic compounds initially, and has grown steadily since then, containing more almost 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 records to date.139 This dataset has been used in two different ways by researchers in the field.
000 records to date.139 This dataset has been used in two different ways by researchers in the field.
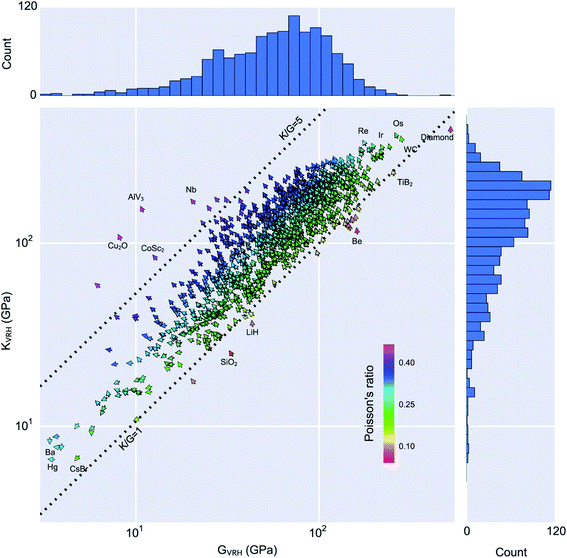 | ||
| Fig. 9 Statistical analysis of the calculated volume per atom, Poisson's ratio, bulk modulus KVRH and shear modulus GVRH of 1181 compounds in the Materials Project database. In the vector field-plot, arrows pointing at 12 o'clock correspond to minimum volume-per-atom and move anti-clockwise in the direction of maximum volume-per-atom, which is located at 6 o'clock. Reprinted from ref. 138 under CC-BY license. Copyright 2015 de Jong et al. | ||
Firstly, the exploration of the database of elastic properties by tensorial analysis has allowed to study quantitatively the occurrence of certain “anomalous” or rare mechanical behaviour, including negative linear compressibility, very high anisotropy, or negative Poisson's ratio (also called auxeticity). Indeed, such properties are considered rare and usually sought after—the materials exhibiting these anomalous behaviours are mechanical metamaterials.140 In addition to their fundamental interest, such materials have applications in materials engineering: for example in energy dissipation (as shock absorbers and for bulletproofing), energy storage, as well as acoustics.141 However, it was not possible until now to quantify exactly “how rare” they are. Chibani et al. showed through a systematic exploration of available mechanical properties of crystalline materials that general mechanical trends, which hold for isotropic (noncrystalline) materials at the macroscopic scale, also apply on average for crystals. Moreover, they could quantify the presence of materials with rare anomalous mechanical properties: 3% of the crystals were found to feature negative linear compressibility, and only 0.3% to exhibit complete auxeticity (negative Poisson's ratio in all directions of space).
Secondly, the datasets of mechanical properties were used as a basis to accelerate the discovery of novel materials with targeted behaviour. Dagdelen et al. used search algorithms to identify 38 candidate materials exhibiting features correlating with auxetic behaviour, from more than 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials in the Materials Project database.142 Performing DFT calculations on these 38 structures, they could identify 7 new auxetic compounds. In a more complex setup, Gaillac et al.37 have used a multi-scale modelling strategy for the fast exploration and identification of novel auxetic materials. They combined classical force fields MD simulations with DFT calculations on candidate materials, and then used this reference DFT data to train an ML algorithm. They found that the accuracy of this multi-scale method exceeds the current low-computational-cost approaches for screening. In a similar work, Moghadam et al. used molecular simulation to train an artificial neural network (ANN) for the prediction of the bulk modulus of metal–organic frameworks.143 This shows the potential of such methodologies to treat very different (chemically as well as structurally) classes of materials.
000 materials in the Materials Project database.142 Performing DFT calculations on these 38 structures, they could identify 7 new auxetic compounds. In a more complex setup, Gaillac et al.37 have used a multi-scale modelling strategy for the fast exploration and identification of novel auxetic materials. They combined classical force fields MD simulations with DFT calculations on candidate materials, and then used this reference DFT data to train an ML algorithm. They found that the accuracy of this multi-scale method exceeds the current low-computational-cost approaches for screening. In a similar work, Moghadam et al. used molecular simulation to train an artificial neural network (ANN) for the prediction of the bulk modulus of metal–organic frameworks.143 This shows the potential of such methodologies to treat very different (chemically as well as structurally) classes of materials.
5.3 Thermal properties
While mechanical properties (in the elastic regime) have been by far the most studied physical property in nanoporous materials, others have also been occasionally screened. We can cite, in particular, the systematic study of piezoelectric tensors by de Jong et al., on almost a thousand crystalline compounds, by first-principles calculations based on density functional perturbation theory.144 We can also cite efforts to calculate thermal properties in a high-throughput setup, using the quasi-harmonic approximation (QHA).145 This method requires the calculation of each structure's phonon modes at various volumes, and can be coupled to any electronic structure program.146 It is, however, quite computationally intensive, and sensitive to the parameters of the QHA methodology (range of volume, range of temperature, precision of the frequency calculation, etc.). Therefore, it has been limited so far to modest numbers of structures: a dataset of 75 inorganic structures by Toher et al.,33 and more recently a dataset of 134 pure SiO2 zeolites by Ducamp et al.35 Very recent work in our group on the prediction of thermal properties through machine learning based on structural features alone indicates that thermal behaviour is more difficult than mechanical behaviour to predict, and might require the use of a wider set of structural descriptors, or more advanced ML models.1226 Outlook
In this review, we highlighted the advances in computational screening of nanoporous materials for some archetypal cases through the scope of their physical and chemical properties. Although each type of property requires a specific simulation methodology and has distinct challenges, the essence and general workflow of high-throughput screening does not fundamentally change. The goal is to generate quickly and accurately increasing amounts of valuable data in order to analyse it. With the increase of high-performance computing (HPC) resources and the help of statistical tools such as machine learning, screening techniques have seen a rapid acceleration in recent years. Researchers can more efficiently analyse larger and larger databases and help theoreticians better understand the origins of the performance, hence guiding the design process of nanoporous materials.Despite the progress made, important drawbacks of the current methodologies remain. High-throughput screenings rely too much on oversimplified assumptions such as the rigidity of the framework, the absence of defects, the use of Lennard–Jones potentials and inaccurate charges. For instance, the rigidity of the framework only takes into account one conformation of the framework. Yet, thermal agitation induces a “breathing” movement of the framework with an amplitude dependent on its intrinsic flexibility. The pores of the framework can change depending on the number of adsorbates to interact more optimally with them, which can be induced by a change in pressure. The issue of flexibility is rarely tackled, and when considered, it is only on the few most selective structures given by an inaccurate screening based on the rigid crystal approximation. One can wonder about the results obtained if it is applied to larger sets of structures. Witman et al. found that flexibility applied to top performing materials can decrease the selectivity, because the pore does not have an optimal size anymore.95 In some cases, the selectivity of a well performing material can even increase to become a top performing one. Computational screenings can be closer to predict experimental values of selectivity, diffusivity, and other key performance metrics.
Many open problems remain for the design of efficient high-throughput computational screenings. The connection between different properties for a given application is not systematically integrated in the screening procedures. For example, in methane storage, the working capacity of the material is the main property to optimise, but the kinetics of the adsorption/desorption or the mechanical resistance to compaction amongst others also need to be considered. Designing a nanoporous material is in fact a multivariate optimisation problem with tacit constraints, for example the synthesisability. Moreover, the transferability of the methodology to a broad range of materials is often achieved at the expense of accuracy in specific cases. And one can rightly question the universality of depending on faster but less elaborated models, which boils down to a trade-off problem between prediction accuracy and computational cost (or complexity). For instance, classical force-fields are broadly used in rigid materials for adsorption properties, but the switch to more costly ab initio methods or the addition of flexibility can result in a more accurate description at the expense of computational resources. The use of ML algorithms can be a way out of this apparent deadlock. They can learn sufficient information on as small a subset as possible to accurately predict the performance of other materials on a large dataset. It could in the future reduce the size of the dataset that needs to be accurately screened by computationally expensive simulations, while maintaining the quality of the predictions.
The development of such ML-assisted screenings is paired with the advances in data science techniques and algorithms, but more importantly to the construction of descriptors tailored to the many possible application. This construction work cannot be dissociated to the physical and chemical intuition of the scientists. Topological, chemical, electronic and other descriptors have been developed on top of the more common geometrical and thermodynamic descriptors, which displays the importance of strong physical chemistry knowledge. The discovery of novel relevant descriptors remains the main lever for increased performance of the ML models and is closely related to a rigorous theoretical work.
The development of databases is another key aspect in the promotion of data science in the field of materials science in general, and nanoporous materials chemistry in particular. The diversity of materials, the inclusion of experimental data (successful or failed), the addition of under studied classes of materials (e.g. amorphous) are all key aspects to upgrade the existing database. Even if existing attempts to create a centralised database have been initiated by the materials project,139 this database does not contain all the existing information on each material.
In the future, computational high-throughput screening could be integrated more tightly into the design process of nanoporous materials, hence further improving its efficiency. The computational pre-screening can be coupled with automated screenings of the most promising materials to finally identify candidates for further studies. This automated design process is described by Lyu et al. in their paper on “Digital Reticular Chemistry” and set out promising perspectives for computational screenings in the field.147 Some studies are already pioneering this new research area by combining high-throughput characterisations, active learning algorithms and robotic synthesis.148,149 Another step towards faster industrialisation would integrate process modelling to enrich the purely atomistic approach.
Funding
This work was financially supported by Orano.Author contributions
All authors: conceptualisation, writing – original draft, review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Isabelle Hablot for discussions on the topic of adsorption-based separation. This work was posted as a preprint at https://arxiv.org/abs/2202.09886.References
- J. R. Li, R. J. Kuppler and H. C. Zhou, Selective gas adsorption and separation in metal–organic frameworks, Chem. Soc. Rev., 2009, 38(5), 1477, 10.1039/b802426j.
- R. Morris and P. Wheatley, Gas storage in nanoporous materials, Angew. Chem., Int. Ed., 2008, 47(27), 4966–4981, DOI:10.1002/anie.200703934.
- A. T. Bell, The impact of nanoscience on heterogeneous catalysis, Science, 2003, 299(5613), 1688–1691, DOI:10.1126/science.1083671.
- B. K. Singh, S. Lee and K. Na, An overview on metal-related catalysts: metal oxides, nanoporous metals and supported metal nanoparticles on metal organic frameworks and zeolites, Rare Met., 2019, 39(7), 751–766, DOI:10.1007/s12598-019-01205-6.
- J. D. Rocca, D. Liu and W. Lin, Nanoscale metal–organic frameworks for biomedical imaging and drug delivery, Acc. Chem. Res., 2011, 44(10), 957–968, DOI:10.1021/ar200028a.
- M. C. Bernini, D. Fairen-Jimenez and M. Pasinetti, et al., Screening of bio-compatible metal–organic frameworks as potential drug carriers using monte carlo simulations, J. Mater. Chem. B, 2014, 2(7), 766–774, 10.1039/c3tb21328e.
- Crystallography: protein data bank, Nature, 1971, 233, 223, DOI:10.1038/newbio233223b0.
- S. Gražulis, D. Chateigner and R. T. Downs, et al., Crystallography open database – an open-access collection of crystal structures, J. Appl. Crystallogr., 2009, 42, 726–729, DOI:10.1107/S0021889809016690.
- C. R. Groom, I. J. Bruno and M. P. Lightfoot, et al., The cambridge structural database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179, DOI:10.1107/S2052520616003954.
- F.-X. Coudert, Materials databases: the need for open, interoperable databases with standardized data and rich metadata, Adv. Theory Simul., 2019, 2, 1900131, DOI:10.1002/adts.201900131.
- J. J. de Pablo, B. Jones and C. L. Kovacs, et al., The Materials Genome Initiative, the interplay of experiment, theory and computation, Curr. Opin. Solid State Mater. Sci., 2014, 18, 99–117, DOI:10.1016/j.cossms.2014.02.003.
- J. J. de Pablo, N. E. Jackson and M. A. Webb, et al., New frontiers for the Materials Genome Initiative, npj Comput. Mater., 2019, 5, 99, DOI:10.1038/s41524-019-0173-4.
- A. Jain, S. P. Ong and G. Hautier, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002, DOI:10.1063/1.4812323.
- A. Jain, K. A. Persson and G. Ceder, Research update: the Materials Genome Initiative: data sharing and the impact of collaborative ab initio databases, APL Mater., 2016, 4, 053102, DOI:10.1063/1.4944683.
- M. D. Foster, O. Delgado Friedrichs and R. G. Bell, et al., Chemical evaluation of hypothetical uninodal zeolites, J. Am. Chem. Soc., 2004, 126, 9769–9775, DOI:10.1021/ja037334j.
- C. E. Wilmer and R. Q. Snurr, Large-scale generation and screening of hypothetical metal–organic frameworks for applications in gas storage and separations, in, Topics in current chemistry, Springer International Publishing, 2013, p. 257–289, DOI:10.1007/128_2013_490.
- P. G. Boyd and T. K. Woo, A generalized method for constructing hypothetical nanoporous materials of any net topology from graph theory, CrystEngComm, 2016, 18, 3777–3792, 10.1039/C6CE00407E.
- T. F. Willems, C. H. Rycroft and M. Kazi, et al., Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials, Microporous Mesoporous Mater., 2012, 149(1), 134–141, DOI:10.1016/j.micromeso.2011.08.020.
- D. Dubbeldam, S. Calero and D. E. Ellis, et al., Raspa: molecular simulation software for adsorption and diffusion in flexible nanoporous materials, Mol. Simul., 2016, 42(2), 81–101 CrossRef CAS.
- D. J. Lim, T. R. Anderson and T. Shott, Technological forecasting of supercomputer development: the march to exascale computing, Omega, 2015, 51, 128–135, DOI:10.1016/j.omega.2014.09.009.
- V. Tshitoyan, J. Dagdelen and L. Weston, et al., Unsupervised word embeddings capture latent knowledge from materials science literature, Nature, 2019, 571, 95–98, DOI:10.1038/s41586-019-1335-8.
- C. J. Court and J. M. Cole, Magnetic and superconducting phase diagrams and transition temperatures predicted using text mining and machine learning, npj Comput. Mater., 2020, 6, 38, DOI:10.1038/s41524-020-0287-8.
- K. T. Butler, D. W. Davies and H. Cartwright, et al., Machine learning for molecular and materials science, Nature, 2018, 559, 547–555, DOI:10.1038/s41586-018-0337-2.
- E. Kim, K. Huang and S. Jegelka, et al., Virtual screening of inorganic materials synthesis parameters with deep learning, npj Comput. Mater., 2017, 3, 1120, DOI:10.1038/s41524-017-0055-6.
- G. Borboudakis, T. Stergiannakos and M. Frysali, et al., Author correction: chemically intuited, large-scale screening of mofs by machine learning techniques, npj Comput. Mater., 2017, 3, 1–7, DOI:10.1038/s41524-017-0051-x.
- S. Chibani and F.-X. Coudert, Machine learning approaches for the prediction of materials properties, APL Mater., 2020, 8, 080701, DOI:10.1063/5.0018384.
- J. Hachmann, R. Olivares-Amaya and S. Atahan-Evrenk, et al., The Harvard Clean Energy Project: large-scale computational screening and design of organic photovoltaics on the world community grid, J. Phys. Chem. Lett., 2011, 2, 2241–2251, DOI:10.1021/jz200866s.
- D. W. Davies, K. T. Butler and A. J. Jackson, et al., Computational screening of all stoichiometric inorganic materials, Chem, 2016, 1, 617–627, DOI:10.1016/j.chempr.2016.09.010.
- X. Zhang, A. Chen and Z. Zhou, High-throughput computational screening of layered and two-dimensional materials, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2019, 9, e1385, DOI:10.1002/wcms.1385.
- A. K. Singh, K. Mathew and H. L. Zhuang, et al., Computational screening of 2D materials for photocatalysis, J. Phys. Chem. Lett., 2015, 6, 1087–1098, DOI:10.1021/jz502646d.
- J. Greeley, T. F. Jaramillo and J. Bonde, et al., Computational high-throughput screening of electrocatalytic materials for hydrogen evolution, Nat. Mater., 2006, 5, 909–913, DOI:10.1038/nmat1752.
- S. Back, K. Tran and Z. W. Ulissi, Discovery of acid-stable oxygen evolution catalysts: high-throughput computational screening of equimolar bimetallic oxides, ACS Appl. Mater. Interfaces, 2020, 12, 38256–38265, DOI:10.1021/acsami.0c11821.
- C. Toher, J. J. Plata and O. Levy, et al., High-throughput computational screening of thermal conductivity, Debye temperature, and Grüneisen parameter using a quasiharmonic Debye model, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 174107, DOI:10.1103/PhysRevB.90.174107.
- S. Sarikurt, T. Kocabaş and C. Sevik, High-throughput computational screening of 2D materials for thermoelectrics, J. Mater. Chem. A, 2020, 8, 19674–19683, 10.1039/D0TA04945J.
- M. Ducamp and F.-X. Coudert, Systematic study of the thermal properties of zeolitic frameworks, J. Phys. Chem. C, 2021, 125(28), 15647–15658, DOI:10.1021/acs.jpcc.1c03975.
- S. Chibani and F. X. Coudert, Systematic exploration of the mechanical properties of 13621 inorganic compounds, Chem. Sci., 2019, 10, 8589–8599, 10.1039/C9SC01682A.
- R. Gaillac, S. Chibani and F.-X. Coudert, Speeding up discovery of auxetic zeolite frameworks by machine learning, Chem. Mater., 2020, 32, 2653–2663, DOI:10.1021/acs.chemmater.0c00434.
- T. Watanabe and D. S. Sholl, Accelerating applications of metal–organic frameworks for gas adsorption and separation by computational screening of materials, Langmuir, 2012, 28(40), 14114–14128, DOI:10.1021/la301915s.
- J. Kim, L. C. Lin and R. L. Martin, et al., Large-scale computational screening of zeolites for ethane/ethene separation, Langmuir, 2012, 28, 11914–11919, DOI:10.1021/la302230z.
- S. Han, Y. Huang and T. Watanabe, et al., High-Throughput Screening of Metal–Organic Frameworks for CO2 Separation, ACS Comb. Sci., 2012, 14, 263–267, DOI:10.1021/co3000192.
- C. E. Wilmer, M. Leaf and C. Y. Lee, et al., Large-scale screening of hypothetical metal–organic frameworks, Nat. Chem., 2011, 4(2), 83–89, DOI:10.1038/nchem.1192.
- L. Yang, C. Shi and L. Li, et al., High-throughput model-building and screening of zeolitic imidazolate frameworks for CO2 capture from flue gas, Chin. Chem. Lett., 2020, 31(1), 227–230, DOI:10.1016/j.cclet.2019.04.025.
- Z. Qiao, C. Peng and J. Zhou, et al., High-throughput computational screening of 137953 metal–organic frameworks for membrane separation of a CO2/N2/CH4 mixture, J. Mater. Chem. A, 2016, 4(41), 15904–15912, 10.1039/c6ta06262h.
- R. Thyagarajan and D. S. Sholl, A database of porous rigid amorphous materials, Chem. Mater., 2020, 32(18), 8020–8033, DOI:10.1021/acs.chemmater.0c03057.
- Y. G. Chung, J. Camp and M. Haranczyk, et al., Computation-ready, experimental metal–organic frameworks: a tool to enable high-throughput screening of nanoporous crystals, Chem. Mater., 2014 oct, 26(21), 6185–6192, DOI:10.1021/cm502594j.
- Y. G. Chung, E. Haldoupis and B. J. Bucior, et al., Advances, updates, and analytics for the computation-ready, experimental metal–organic framework database: CoRE MOF 2019, J. Chem. Eng. Data, 2019, 64(12), 5985–5998, DOI:10.1021/acs.jced.9b00835.
- M. Tong, Y. Lan and Q. Yang, et al., Exploring the structure-property relationships of covalent organic frameworks for noble gas separations, Chem. Eng. Sci., 2017, 168, 456–464, DOI:10.1016/j.ces.2017.05.004.
- D. Ongari, A. V. Yakutovich and L. Talirz, et al., Building a consistent and reproducible database for adsorption evaluation in covalent–organic frameworks, ACS Cent. Sci., 2019, 5(10), 1663–1675 CrossRef CAS PubMed.
- R. L. Martin and M. Haranczyk, Construction and characterization of structure models of crystalline porous polymers, Cryst. Growth Des., 2014, 14(5), 2431–2440, DOI:10.1021/cg500158c.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Topologically guided, automated construction of metal–organic frameworks and their evaluation for energy-related applications, Cryst. Growth Des., 2017, 17, 5801–5810, DOI:10.1021/acs.cgd.7b00848.
- P. G. Boyd and T. K. Woo, A generalized method for constructing hypothetical nanoporous materials of any net topology from graph theory, CrystEngComm, 2016, 18(21), 3777–3792, 10.1039/c6ce00407e.
- D. J. Earl and M. W. Deem, Toward a database of hypothetical zeolite structures, Ind. Eng. Chem. Res., 2006, 45(16), 5449–5454, DOI:10.1021/ie0510728.
- M. W. Deem, R. Pophale and P. A. Cheeseman, et al., Computational discovery of new zeolite-like materials, J. Phys. Chem. C, 2009, 113(51), 21353–21360, DOI:10.1021/jp906984z.
- R. Pophale, P. A. Cheeseman and M. W. Deem, A database of new zeolite-like materials, Phys. Chem. Chem. Phys., 2011, 13(27), 12407, 10.1039/c0cp02255a.
- R. Anderson and D. A. Gómez-Gualdrón, Large-scale free energy calculations on a computational metal–organic frameworks database: toward synthetic likelihood predictions, Chem. Mater., 2020, 32(19), 8106–8119, DOI:10.1021/acs.chemmater.0c00744.
- L. Turcani, R. L. Greenaway and K. E. Jelfs, Machine learning for organic cage property prediction, Chem. Mater., 2018, 31(3), 714–727, DOI:10.1021/acs.chemmater.8b03572.
- T. Kalil and C. Wadia, Materials Genome Initiative: A Renaissance of American Manufacturing, The National Science And Technology Council, 2011 Search PubMed.
- The materials genome initiative, 2022, https://www.mgi.gov/ Search PubMed.
- A. Jain, S. P. Ong and G. Hautier, et al., Commentary: The Materials Project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002, DOI:10.1063/1.4812323.
- P. G. Boyd, Y. Lee and B. Smit, Computational development of the nanoporous materials genome, Nat. Rev. Mater., 2017, 2(8), 17037, DOI:10.1038/natrevmats.2017.37.
- R. L. Martin, B. Smit and M. Haranczyk, Addressing challenges of identifying geometrically diverse sets of crystalline porous materials, J. Chem. Inf. Model., 2011, 52(2), 308–318, DOI:10.1021/ci200386x.
- D. A. Gómez-Gualdrón, Y. J. Colón and X. Zhang, et al., Evaluating topologically diverse metal–organic frameworks for cryo-adsorbed hydrogen storage, Energy Environ. Sci., 2016, 9(10), 3279–3289, 10.1039/c6ee02104b.
- S. M. Moosavi, A. Nandy and K. M. Jablonka, et al., Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11, 4068, DOI:10.1038/s41467-020-17755-8.
- Y. Lee, S. D. Barthel and P. Dłotko, et al., Quantifying similarity of pore-geometry in nanoporous materials, Nat. Commun., 2017, 8, 15396, DOI:10.1038/ncomms15396.
- M. Fernandez, T. K. Woo and C. E. Wilmer, et al., Large-scale quantitative structure–property relationship (QSPR) analysis of methane storage in metal–organic frameworks, J. Phys. Chem. C, 2013, 117(15), 7681–7689, DOI:10.1021/jp4006422.
- M. Fernandez, N. R. Trefiak and T. K. Woo, Atomic property weighted radial distribution functions descriptors of metal–organic frameworks for the prediction of gas uptake capacity, J. Phys. Chem. C, 2013, 117(27), 14095–14105, DOI:10.1021/jp404287t.
- H. Dureckova, M. Krykunov and M. Z. Aghaji, et al., Robust machine learning models for predicting high CO2 working capacity and CO2/H2 selectivity of gas adsorption in metal organic frameworks for precombustion carbon capture, J. Phys. Chem. C, 2019, 123(7), 4133–4139, DOI:10.1021/acs.jpcc.8b10644.
- F. Oviedo, J. L. Ferres and T. Buonassisi, et al., Interpretable and explainable machine learning for materials science and chemistry, 2021, https://arxiv.org/abs/2111.01037 Search PubMed.
- F. X. Coudert, Reproducible research in computational chemistry of materials, Chem. Mater., 2017, 29(7), 2615–2617, DOI:10.1021/acs.chemmater.7b00799.
- C. M. Simon, R. Mercado and S. K. Schnell, et al., What are the best materials to separate a xenon/krypton mixture?, Chem. Mater., 2015, 27, 4459–4475, DOI:10.1021/acs.chemmater.5b01475.
- B. J. Bucior, N. S. Bobbitt and T. Islamoglu, et al., Energy-based descriptors to rapidly predict hydrogen storage in metal–organic frameworks, Mol. Syst. Des. Eng., 2019, 4(1), 162–174, 10.1039/c8me00050f.
- Y. Lee, S. D. Barthel and P. Dłotko, et al., High-throughput screening approach for nanoporous materials genome using topological data analysis: application to zeolites, J. Chem. Theory Comput., 2018, 14(8), 4427–4437, DOI:10.1021/acs.jctc.8b00253.
- S. M. Moosavi, H. Xu and L. Chen, et al., Geometric landscapes for material discovery within energy–structure–function maps, Chem. Sci., 2020, 11(21), 5423–5433, 10.1039/d0sc00049c.
- G. Borboudakis, T. Stergiannakos and M. Frysali, et al., Author correction: chemically intuited, large-scale screening of MOFs by machine learning techniques, npj Comput. Mater., 2017, 3, 47, DOI:10.1038/s41524-017-0051-x.
- G. S. Fanourgakis, K. Gkagkas and E. Tylianakis, et al., A universal machine learning algorithm for large-scale screening of materials, J. Am. Chem. Soc., 2020, 142(8), 3814–3822, DOI:10.1021/jacs.9b11084.
- R. Anderson, A. Biong and D. A. Gómez-Gualdrón, Adsorption isotherm predictions for multiple molecules in MOFs using the same deep learning model, J. Chem. Theory Comput., 2020, 16(2), 1271–1283, DOI:10.1021/acs.jctc.9b00940.
- K. M. Jablonka, D. Ongari and S. M. Moosavi, et al., Big-data science in porous materials: materials genomics and machine learning, Chem. Rev., 2020, 120(16), 8066–8129 CrossRef CAS PubMed . Available from: 10.1021/acs.chemrev.0c00004.
- D. A. Gómez-Gualdrón, C. E. Wilmer and O. K. Farha, et al., Exploring the limits of methane storage and delivery in nanoporous materials, J. Phys. Chem. C, 2014, 118(13), 6941–6951, DOI:10.1021/jp502359q.
- C. M. Simon, J. Kim and D. A. Gomez-Gualdron, et al., The materials genome in action: identifying the performance limits for methane storage, Energy Environ. Sci., 2015, 8, 1190–1199, 10.1039/C4EE03515A.
- S. Lee, B. Kim and H. Cho, et al., Computational screening of trillions of metal–organic frameworks for high-performance methane storage, ACS Appl. Mater. Interfaces, 2021, 13(20), 23647–23654, DOI:10.1021/acsami.1c02471.
- N. S. Bobbitt, J. Chen and R. Q. Snurr, High-throughput screening of metal–organic frameworks for hydrogen storage at cryogenic temperature, J. Phys. Chem. C, 2016, 120(48), 27328–27341, DOI:10.1021/acs.jpcc.6b08729.
- A. W. Thornton, C. M. Simon and J. Kim, et al., Materials genome in action: Identifying the performance limits of physical hydrogen storage, Chem. Mater., 2017, 29(7), 2844–2854, DOI:10.1021/acs.chemmater.6b04933.
- G. Anderson, B. Schweitzer and R. Anderson, et al., Attainable volumetric targets for adsorption-based hydrogen storage in porous crystals: molecular simulation and machine learning, J. Phys. Chem. C, 2018, 123(1), 120–130, DOI:10.1021/acs.jpcc.8b09420.
- N. S. Bobbitt and R. Q. Snurr, Molecular modelling and machine learning for high-throughput screening of metal-organic frameworks for hydrogen storage, Mol. Simul., 2019, 45(14–15), 1069–1081, DOI:10.1080/08927022.2019.1597271.
- S. C. Cullen and E. G. Gross, The anesthetic properties of xenon in animals and human beings, with additional observations on krypton, Science, 1951, 113(2942), 580–582, DOI:10.1126/science.113.2942.580.
- T. F. Holsträter, M. Georgieff and K. J. Föhr, et al., Intranasal application of xenon reduces opioid requirement and postoperative pain in patients undergoing major abdominal surgery: a randomized controlled trial, J. Am. Soc. Anesth., 2011, 115(2), 398–407, DOI:10.1097/aln.0b013e318225cee5.
- M. Patterson, J. Foster, T. Haag, et al., NEXT: NASA's evolutionary xenon thruster, in 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, American Institute of Aeronautics and Astronautics, 2002, DOI:10.2514/2002-3832.
- I. Coxhill and D. Gibbon, A xenon resistojet propulsion system for microsatellites, in 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, American Institute of Aeronautics and Astronautics, 2005, DOI:10.2514/2005-4260.
- G. D. Jarman, E. W. R. Barlow and L. Boersma, Application of long-arc xenon lighting for plant growth experiments, Agron. J., 1974, 66(5), 703–706, DOI:10.2134/agronj1974.00021962006600050029x.
- T. Tanaka, T. Hayashi and T. Nagayama, et al., Proposal of novel degradation diagnosis method for photovoltaic module employing xenon flash lighting system and detector capacitor, Energy Convers. Manage., 2019, 186, 450–461, DOI:10.1016/j.enconman.2019.02.059.
- B. J. Sikora, C. E. Wilmer and M. L. Greenfield, et al., Thermodynamic analysis of Xe/Kr selectivity in over 137000 hypothetical metal–organic frameworks, Chem. Sci., 2012, 3, 2217, 10.1039/c2sc01097f.
- P. Ryan, O. K. Farha and L. J. Broadbelt, et al., Computational screening of metal-organic frameworks for xenon/krypton separation, AIChE J., 2010, 57(7), 1759–1766, DOI:10.1002/aic.12397.
- D. Banerjee, Z. Zhang and A. M. Plonka, et al., A calcium coordination framework having permanent porosity and high CO2/N2 selectivity, Cryst. Growth Des., 2012, 12, 2162–2165, DOI:10.1021/cg300274n.
- D. Banerjee, C. M. Simon and A. M. Plonka, et al., Metal–organic framework with optimally selective xenon adsorption and separation, Nat. Commun., 2016, 7, 11831, DOI:10.1038/ncomms11831.
- M. Witman, S. Ling and S. Jawahery, et al., The influence of intrinsic framework flexibility on adsorption in nanoporous materials, J. Am. Chem. Soc., 2017, 139(15), 5547–5557, DOI:10.1021/jacs.7b01688.
- E. Haldoupis, S. Nair and D. S. Sholl, Finding MOFs for highly selective CO2/N2 adsorption using materials screening based on efficient assignment of atomic point charges, J. Am. Chem. Soc., 2012, 134(9), 4313–4323, DOI:10.1021/ja2108239.
- J. M. Huck, L. C. Lin and A. H. Berger, et al., Evaluating different classes of porous materials for carbon capture, Energy Environ. Sci., 2014, 7(12), 4132–4146, 10.1039/c4ee02636e.
- S. Li, Y. G. Chung and R. Q. Snurr, High-throughput screening of metal–organic frameworks for CO2 capture in the presence of water, Langmuir, 2016, 32(40), 10368–10376, DOI:10.1021/acs.langmuir.6b02803.
- L. A. Darunte, A. D. Oetomo and K. S. Walton, et al., Direct air capture of CO2 using amine functionalized MIL-101(Cr), ACS Sustainable Chem. Eng., 2016, 4(10), 5761–5768, DOI:10.1021/acssuschemeng.6b01692.
- J. Park, R. P. Lively and D. S. Sholl, Establishing upper bounds on CO2 swing capacity in sub-ambient pressure swing adsorption via molecular simulation of metal–organic frameworks, J. Mater. Chem. A, 2017, 5(24), 12258–12265, 10.1039/c7ta02916k.
- J. M. Findley and D. S. Sholl, Computational screening of MOFs and zeolites for direct air capture of carbon dioxide under humid conditions, J. Phys. Chem. C, 2021, 125(44), 24630–24639, DOI:10.1021/acs.jpcc.1c06924.
- H. Daglar and S. Keskin, Recent advances, opportunities, and challenges in high-throughput computational screening of MOFs for gas separations, Coord. Chem. Rev., 2020, 422, 213470, DOI:10.1016/j.ccr.2020.213470.
- E. S. Miandoab, S. H. Mousavi and S. E. Kentish, et al., Xenon and krypton separation by membranes at sub-ambient temperatures and its comparison with cryogenic distillation, Sep. Purif. Technol., 2021, 262, 118349, DOI:10.1016/j.seppur.2021.118349.
- E. Haldoupis, S. Nair and D. S. Sholl, Efficient calculation of diffusion limitations in metal organic framework materials: a tool for identifying materials for kinetic separations, J. Am. Chem. Soc., 2010, 132(21), 7528–7539, DOI:10.1021/ja1023699.
- J. Kim, M. Abouelnasr and L. C. Lin, et al., Large-scale screening of zeolite structures for CO2 membrane separations, J. Am. Chem. Soc., 2013, 135(20), 7545–7552, DOI:10.1021/ja400267g.
- A. Mace, S. Barthel and B. Smit, Automated multiscale approach to predict self-diffusion from a potential energy field, J. Chem. Theory Comput., 2019, 15(4), 2127–2141, DOI:10.1021/acs.jctc.8b01255.
- M. Zhou and J. Wu, Massively parallel GPU-accelerated string method for fast and accurate prediction of molecular diffusivity in nanoporous materials, ACS Appl. Nano Mater., 2021, 4(5), 5394–5403, DOI:10.1021/acsanm.1c00727.
- B. C. Bukowski, F. J. Keil and P. I. Ravikovitch, et al., Connecting theory and simulation with experiment for the study of diffusion in nanoporous solids, Adsorption, 2021, 27(5), 683–760, DOI:10.1007/s10450-021-00314-y.
- D. M. Ruthven and S. Farooq, Air separation by pressure swing adsorption, Gas Sep. Purif., 1990, 4(3), 141–148, DOI:10.1016/0950-4214(90)80016-E.
- C. R. Reid and K. M. Thomas, Adsorption of gases on a carbon molecular sieve used for air separation: linear adsorptives as probes for kinetic selectivity, Langmuir, 1999, 15(9), 3206–3218, DOI:10.1021/la981289p.
- Y. Wang and R. T. Yang, Chemical liquid deposition modified 4a zeolite as a size-selective adsorbent for methane upgrading, CO2 capture and air separation, ACS Sustainable Chem. Eng., 2019, 7(3), 3301–3308, DOI:10.1021/acssuschemeng.8b05339.
- L. M. Robeson, Correlation of separation factor versus permeability for polymeric membranes, J. Membr. Sci., 1991, 62(2), 165–185, DOI:10.1016/0376-7388(91)80060-J.
- Z. Qiao, Q. Xu and J. Jiang, High-throughput computational screening of metal-organic framework membranes for upgrading of natural gas, J. Membr. Sci., 2018, 551, 47–54, DOI:10.1016/j.memsci.2018.01.020.
- C. Altintas and S. Keskin, Molecular simulations of MOF membranes and performance predictions of MOF/polymer mixed matrix membranes for CO2/CH4 separations, ACS Sustainable Chem. Eng., 2018, 7(2), 2739–2750, DOI:10.1021/acssuschemeng.8b05832.
- S. Budhathoki, O. Ajayi and J. A. Steckel, et al., High-throughput computational prediction of the cost of carbon capture using mixed matrix membranes, Energy Environ. Sci., 2019, 12(4), 1255–1264, 10.1039/c8ee02582g.
- T. Yan, Y. Lan and M. Tong, et al., Screening and design of covalent organic framework membranes for CO2/CH4 separation, ACS Sustainable Chem. Eng., 2018, 7(1), 1220–1227, DOI:10.1021/acssuschemeng.8b04858.
- L. M. Robeson, The upper bound revisited, J. Membr. Sci., 2008, 320, 390–400, DOI:10.1016/j.memsci.2008.04.030.
- S. Keskin and D. S. Sholl, Screening metal-organic framework materials for membrane-based methane/carbon dioxide separations, J. Phys. Chem. C, 2007, 111(38), 14055–14059, DOI:10.1021/jp075290l.
- S. Keskin and D. S. Sholl, Efficient methods for screening of metal organic framework membranes for gas separations using atomically detailed models, Langmuir, 2009, 25(19), 11786–11795, DOI:10.1021/la901438x.
- C. Han, Y. Yang and D. S. Sholl, Quantitatively predicting impact of structural flexibility on molecular diffusion in small pore metal–organic frameworks—a molecular dynamics study of hypothetical ZIF-8 polymorphs, J. Phys. Chem. C, 2020, 124(37), 20203–20212, DOI:10.1021/acs.jpcc.0c05942.
- J. D. Evans and F. X. Coudert, Predicting the mechanical properties of zeolite frameworks by machine learning, Chem. Mater., 2017, 29(18), 7833–7839, DOI:10.1021/acs.chemmater.7b02532.
- M. Ducamp and F. X. Coudert, Prediction of thermal properties of zeolites through machine learning, J. Phys. Chem. C, 2022, 126, 1651–1660, DOI:10.1021/acs.jpcc.1c09737.
- M. Eckhoff and J. Behler, From molecular fragments to the bulk: development of a neural network potential for MOF-5, J. Chem. Theory Comput., 2019, 15(6), 3793–3809, DOI:10.1021/acs.jctc.8b01288.
- P. Friederich, F. Häse and J. Proppe, et al., Machine-learned potentials for next-generation matter simulations, Nat. Mater., 2021, 20(6), 750–761, DOI:10.1038/s41563-020-0777-6.
- G. A. McCarver, T. Rajeshkumar and K. D. Vogiatzis, Computational catalysis for metal-organic frameworks: an overview, Coord. Chem. Rev., 2021, 436, 213777, DOI:10.1016/j.ccr.2021.213777.
- K. D. Vogiatzis, E. Haldoupis and D. J. Xiao, et al., Accelerated computational analysis of metal–organic frameworks for oxidation catalysis, J. Phys. Chem. C, 2016, 120(33), 18707–18712, DOI:10.1021/acs.jpcc.6b07115.
- A. S. Rosen, J. M. Notestein and R. Q. Snurr, Structure–activity relationships that identify metal–organic framework catalysts for methane activation, ACS Catal., 2019, 9(4), 3576–3587, DOI:10.1021/acscatal.8b05178.
- K. T. Butler, C. H. Hendon and A. Walsh, Electronic chemical potentials of porous metal–organic frameworks, J. Am. Chem. Soc., 2014, 136(7), 2703–2706, DOI:10.1021/ja4110073.
- A. S. Rosen, J. M. Notestein and R. Q. Snurr, Identifying promising metal–organic frameworks for heterogeneous catalysis via high-throughput periodic density functional theory, J. Comput. Chem., 2019, 40(12), 1305–1318, DOI:10.1002/jcc.25787.
- M. Fumanal, G. Capano and S. Barthel, et al., Energy-based descriptors for photo-catalytically active metal–organic framework discovery, J. Mater. Chem. A, 2020, 8(8), 4473–4482, 10.1039/c9ta13506e.
- A. S. Rosen, V. Fung and P. Huck, et al., High-throughput predictions of metal–organic framework electronic properties: theoretical challenges, graph neural networks, and data exploration, npj Comput. Mater., 2022, 8, 112, DOI:10.1038/s41524-022-00796-6.
- A. S. Rosen, S. M. Iyer and D. Ray, et al., Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery, Matter, 2021, 4(5), 1578–1597, DOI:10.1016/j.matt.2021.02.015.
- A. S. Rosen, J. M. Notestein and R. Q. Snurr, Realizing the data-driven, computational discovery of metal-organic framework catalysts, Curr. Opin. Chem. Eng., 2022, 35, 100760, DOI:10.1016/j.coche.2021.100760.
- A. Marmier, Z. A. Lethbridge and R. I. Walton, et al., ElAM: a computer program for the analysis and representation of anisotropic elastic properties, Comput. Phys. Commun., 2010, 181, 2102–2115, DOI:10.1016/j.cpc.2010.08.033.
- R. Golesorkhtabar, P. Pavone and J. Spitaler, et al., ElaStic: a tool for calculating second-order elastic constants from first principles, Comput. Phys. Commun., 2013, 184, 1861–1873, DOI:10.1016/j.cpc.2013.03.010.
- R. Dovesi, A. Erba and R. Orlando, et al., Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, 171, DOI:10.1002/wcms.1360.
- F. X. Coudert, Systematic investigation of the mechanical properties of pure silica zeolites: stiffness, anisotropy, and negative linear compressibility, Phys. Chem. Chem. Phys., 2013, 15, 16012, 10.1039/c3cp51817e.
- M. de Jong, W. Chen and T. Angsten, et al., Charting the complete elastic properties of inorganic crystalline compounds, Sci. Data, 2015, 2, 345, DOI:10.1038/sdata.2015.9.
- The Materials Project, 2022, available online at https://materialsproject.org/.
- F. X. Coudert and J. D. Evans, Nanoscale metamaterials: meta-MOFs and framework materials with anomalous behavior, Coord. Chem. Rev., 2019, 388, 48–62, DOI:10.1016/j.ccr.2019.02.023.
- J. U. Surjadi, L. Gao and H. Du, et al., Mechanical metamaterials and their engineering applications, Adv. Eng. Mater., 2018, 21, 1800864, DOI:10.1002/adem.201800864.
- J. Dagdelen, J. Montoya and M. de Jong, et al., Computational prediction of new auxetic materials, Nat. Commun., 2017, 8, 124, DOI:10.1038/s41467-017-00399-6.
- P. Z. Moghadam, S. M. Rogge and A. Li, et al., Structure-mechanical stability relations of metal-organic frameworks via machine learning, Matter., 2019, 1(1), 219–234, DOI:10.1016/j.matt.2019.03.002.
- M. de Jong, W. Chen and H. Geerlings, et al., A database to enable discovery and design of piezoelectric materials, Sci. Data, 2015, 2, 746, DOI:10.1038/sdata.2015.53.
- A. Togo, L. Chaput and I. Tanaka, et al., First-principles phonon calculations of thermal expansion in Ti3SiC2, Ti3AlC2, and Ti3GeC2, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174301, DOI:10.1103/PhysRevB.81.174301.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- H. Lyu, Z. Ji and S. Wuttke, et al., Digital reticular chemistry, Chem, 2020, 6(9), 2219–2241, DOI:10.1016/j.chempr.2020.08.008.
- R. L. Greenaway, V. Santolini and M. J. Bennison, et al., High-throughput discovery of organic cages and catenanes using computational screening fused with robotic synthesis, Nat. Commun., 2018, 9, 2849, DOI:10.1038/s41467-018-05271-9.
- S. M. Moosavi, A. Chidambaram and L. Talirz, et al., Capturing chemical intuition in synthesis of metal-organic frameworks, Nat. Commun., 2019, 10, 539, DOI:10.1038/s41467-019-08483-9.
- A. Nandy, C. Duan and H. J. Kulik, Using machine learning and data mining to leverage community knowledge for the engineering of stable metal–organic frameworks, J. Am. Chem. Soc., 2021, 143(42), 17535–17547, DOI:10.1021/jacs.1c07217.
| This journal is © The Royal Society of Chemistry 2022 |