Emergent hydrogen bonding in dense LiOD

Abstract

We report the first full-structural analysis of two ambient temperature phases (II, III) of LiOD as a function of pressure, and present a direct-structural confirmation of a hydrogen-bonded network in the high-pressure phase-III. LiOD has been measured using neutron powder diffraction up to a maximum pressure of 4.1 GPa. The sample is observed to transform from tetragonal phase-II (P4/nmm) to phase-III at a pressure of 1.16(3) GPa. The previously suggested monoclinic structure of phase-III, isostructural with NaOD, is shown to strongly misfit the measured data, while a new tetragonal structure (I4₁/acd), suggested in the literature from a first-principles calculation, is found to fit the pattern extremely well. Neutron diffraction data from this new tetragonal structure agree with earlier spectroscopic evidence for a hydrogen-bonded network within the system. This tetragonal structure has not been observed in any other alkali-metal hydroxide before now. Details of the hydrogen bond lengths, lattice strains through the transition, and the compressibility of each phase are presented. This revised structure may have implications as to how LiOD is used for high-pressure/high-temperature materials synthesis.

---

Introduction

LiOH is commercially extremely important, as it is used as a primary precursor in the synthesis of a number of Li-ion battery related materials.¹ It is growing in use to become the main source of Li for the production of cathode materials in Li-ion batteries (e.g. LiCoO₂), overtaking the use of the more easily obtained Li₂CO₃, due to its greater solubility in water and other solvents enabling more precise synthesis, and lower synthesis temperatures which affect the operation and life-cycle of the battery.² It is also an essential material used for CO₂ removal or ‘scrubbing’ for sub-nautical,³ and space vessels, and an important additive used in lithium soaps as a grease or lubricant. The electrochemical behaviour of cathode materials can be altered through substituting e.g. Co with alternative elements. Pressure has been used to stabilise the substitution of Co with much larger elements, such as Ga, from a LiOH synthesis route to LiCoO₂ at 3 GPa.⁴ This pressure is accessible for mass industrial production and could lead to important future advances in battery design. However, as the vast majority of cathode materials are synthesised at ambient pressure, there is surprisingly little known about the properties of LiOH under non-ambient conditions. A primary motivation for doing this is to understand the nature of the bonding within such a material, where it is expected that there may be a fundamental balance between hydrogen, and lithium bonding,⁵ which will strongly affect the chemistry during high-pressure synthesis routes.

LiOH is unusual as an alkali-hydroxide, in that the structure of phase-II doesn’t support, or perhaps more accurately, only has an extremely weakly formed hydrogen-bonded network, as the hydroxyl group arrangement leads to a large H⋯O separation (approximately 3.5 Å), with nearest neighbour hydroxyl groups being antialigned.⁶ In contrast, the heavier-alkali hydroxides (K, Rb, Cs) are more extensively hydrogen bonded,⁷ while NaOH is anomalous; the hydrogenous form of which shows no hydrogen bonding, while the deuterated form has a low-temperature phase with a hydrogen-bonded network. While all alkali-metal hydroxides have long O⋯O separations, NaOH is at the limit where the effects of hydrogen bonding on the structure are negligible, while the deuterated counterpart has a low-temperature phase transition to an extensively hydrogen-bonded state. When the structure is substituted with D, there is sufficient contraction in the hydrogen bond length to form a stronger hydrogen-bonded network at low temperatures, which is one contributing factor to the favourability of a new structure.⁸ This effect can similarly be induced in the hydrogenous form with a small amount of applied pressure at low temperatures.⁹ Unlike heavier alkali-hydroxides, which show low-temperature phases with zig-zag hydrogen-bonded chains,¹⁰ LiOH-II is the stable phase down to 10 K.¹¹ Above 648 K at ambient pressure, a first-order transition to an unknown structure, phase-I, is observed close to the melting temperature, where the formation of Li₂O is suppressed.^11,12

Structurally, LiOH is unique among the other alkali-metal hydroxides. Under ambient conditions, it crystallises with tetragonal symmetry (P4/nmm),¹³ designated as phase-II. In this phase, each –OH group forms the cap of a square pyramid formed of Li atoms, which are each coordinated to four O atoms. Neighbouring –OH groups are anti-aligned in the ab-plane, and are aligned along the c-axis, analogous to the α-PbO structure¹⁴ (see Fig. 1). The closest related alkali-metal hydroxide, NaOH, instead crystallises with orthorhombic (Cmcm) symmetry with a similar pyramidal motif, but with the Na coordinated to five O atoms.¹⁵ KOH and RbOH both crystallise with monoclinic (P2₁/m) symmetry, but the –OH libration is such that exact H positions are difficult to determine, though the pyramidal motif is assumed in the average structure, with the metal ion being essentially coordinated to six O atoms, forming a distorted octahedral NaCl-type structure.¹⁶

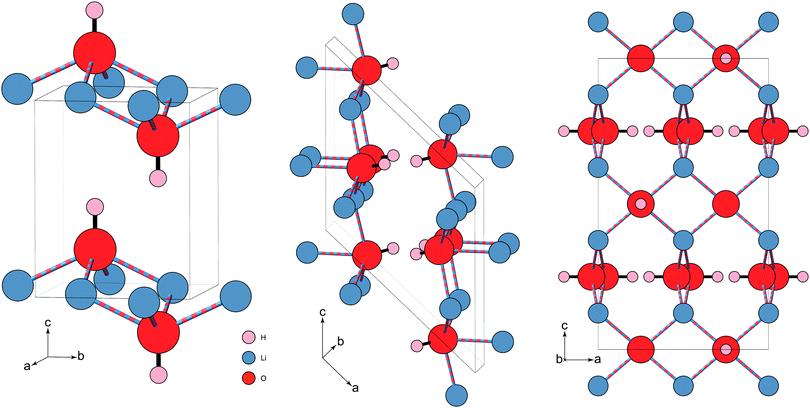Fig. 1 Three proposed structures of LiOH. (left) The known ambient pressure/temperature tetragonal phase-II (P4/nmm). The square pyramidal units are stacked anti-aligned in the ab-plane, and aligned along the c-axis. (middle) The proposed monoclinic structure (P2₁/c) of phase-III (Adams et al.¹⁸). The motif is changed, forming a more distorted Li substructure. Zig-zag hydrogen bonding chains (not shown) are formed along the b-axis. (right) proposed high-pressure phase-III tetragonal structure (I4₁/acd) (Hermann et al.²¹). For simplicity, the structure is shown only in the ac-plane, though the –OH capped, square pyramidal units from the ambient structure still feature, albeit flattened, and in a more complex arrangement. The hydrogen bonding in this tetragonal structure (not shown) forms linear chains along the a- and b-axes, in alternating stacked layers along c. Both high-pressure structures have considerably shorter O⋯H distances. The two structures proposed for phase-III are listed in Table 1. Note: the Li⋯O ‘bonds’ are illustrated differently to indicate that the Li⁺ is coordinated to four OH⁻ through ‘lithium-bonding’.²²

At ambient temperature, LiOH has been shown via IR and Raman spectroscopy to undergo a pressure-induced phase transition above approximately 0.7 GPa.¹⁷ Neutron diffraction was used to measure LiOD, and confirmed the phase transition to phase-III at 1.7 GPa, showing a large isotope effect. This was indexed with a monoclinic (P2₁/c) cell,¹⁸ assuming a structure similar to that of the low-temperature phase of NaOD where the Li remains coordinated to four O atoms (see Fig. 1, and Table 1), but the motif changes to an irregular form.¹⁹ This was inferred from relative peak intensities, as the data were of insufficient quality for a Rietveld refinement.¹⁸ Importantly, both the –OH and –OD Raman stretching bands were observed to broaden and soften slightly with pressure, indicating a slight weakening of the O–H bond, and the formation of hydrogen bonding in phase-III. Ab initio molecular dynamics confirm the monoclinic symmetry,²⁰ and reproduce the observations from Raman and IR of the –OH mode, while first-principles density function theory calculations have suggested an alternative, energetically more favourable structure for phase-III.²¹ In this case the symmetry remains tetragonal (I4₁/acd), which instead suggests a rearrangement of the hydroxide ions, where the local environment remains very similar to that of phase-II, but with a more complex rotated arrangement of the pyramidal units. The pyramidal units themselves are also flattened, with the Li and O atoms essentially planar to each other.

Table 1 Summary of the two contending structures for phase-III, as supported by previous diffraction data, and calculations. Note: the settings of each space group have been transformed from those originally reported, to the standard setting. The coordinates for the monoclinic structure are based on the low-temperature structure of NaOD,^21,23 as they were not refined directly by Adams et al.¹⁸

	Adams et al.^18	Hermann et al.^21
Space group	P21/c	I41/acd
a-axis (Å)	6.5628	5.975
b-axis (Å)	3.0970	—
c-axis (Å)	6.2660	10.228
β (°)	135.68	90
	H 4e (0.41, 0.78, 0.68)	H 16e (0.799, 0, ¼)
	Li 4e (0.84, 0.58, 0.73)	Li 8a (0, ¼, ⅜)
		Li 8b (0, ¼, ⅛)
	O 4e (0.24, 0.55, 0.03)	O 16e (0.463, 0, ¼)

---

The only previous structural study of this material was limited in scope due to the low data quality, and resolution, and therefore did not report any information on the structural evolution of LiOD-II with pressure, or the structure of the new phase-III.¹⁸ The present study has collected neutron powder-diffraction data at high pressure with improved quality and reports the refined structure of LiOD-III, and the evolution of LiOD-II leading up to it. This is therefore the first direct-structural evidence of the tetragonal phase-III, and the formation of a hydrogen-bonded network in LiOD. This may have important implications for the chemistry of Li-ion cathode materials synthesised from LiOH under high pressure.

Experimental details

Polycrystalline LiOH·H₂O with 99.9 at% ⁷Li was supplied by Sigma Aldrich, this included a small Li₂CO₃ impurity. Isotopic ⁷Li enrichment of the sample reduces the level of neutron absorption, improving the measured signal, and simplifying the attenuation corrections. LiOH was extracted from the LiOH monohydrate through vacuum annealing the sample at approximately 380 K for 24 hours. Deuteration reduces incoherent scatter from H, and has a good coherent scattering length, providing better information on the D-atom positions in the cell. The sample was deuterated through dissolution in degassed D₂O at 310 K for 2 hours, cooling to room temperature before freeze-drying with liquid nitrogen. Ambient pressure characterisation with neutron diffraction confirmed full deuteration.

High-pressure time-of-flight neutron powder diffraction was performed on the PEARL instrument at the ISIS Neutron and Muon Source.²⁴ For the high-pressure data, the sample was loaded into a null-scattering encapsulated TiZr gasket, with a mixture (1 : 1 by volume) of perdeuterated iso-/n-pentanes added as a pressure transmitting medium. A V3 Paris-Edinburgh press was used to apply load to the sample, using single toroidal ZrO₂/Al₂O₃ anvils. The sample pressure was determined from the equation of state of Li₂CO₃.²⁵ All data were reduced and corrected for attenuation using Mantid,²⁶ and Rietveld refinements were performed using Fullprof.²⁷

Results

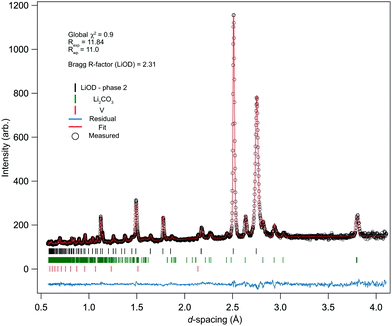
The ambient pressure/temperature diffraction pattern was measured to confirm the levels of deuteration and purity of the bulk sample. The data and calculated profile from the refined phase-II structure are shown in Fig. 2, and the refined structural parameters are summarised in Table 2. The quality of the fit is good, and the refined parameters are in reasonable agreement with known literature values for phase-II of LiOD. It is well known that the thermal motion of the hydrogen atoms is a source of uncertainty;²⁸ in the present study the atomic displacement parameters were refined isotropically. Note that while previous studies have reported bond lengths ‘corrected’ for uncertainties due to displacement parameters,¹³ the values reported in Table 2 are the uncorrected values. In the previous studies, H was used rather than D, so it is reasonable to expect a slightly reduced O–D bond length. The pattern showed noticeable anisotropic strain broadening in the sample, most noticeably in the (110) reflection (see ca. 2.75 Å in Fig. 2). This is an effect of the vacuum dehydration of the sample, as X-ray analysis of the monohydrate showed no broadening, though the data are still adequately fitted, and the model refines stably.

Fig. 2 Refinement of the phase-II structure of LiOD against neutron powder-diffraction data collected at ambient conditions. The black circles are the measured data, the red line is the calculated profile, and the blue line shows the residual from the fit. The black (upper) tick marks are from phase-II of LiOD, the green (middle) tick marks are for Li₂CO₃, and the red (lower) tick marks are for the V canister. The neutron absorption cross-section for ⁷Li is still large, contributing to larger uncertainties on the measured data, leading to a large expected R-factor.

Table 2 Refined crystallographic structural parameters, and key bond lengths of LiOD phase-II (P4/nmm) at ambient conditions. With the origin set at the centre of the 2-fold rotation axis, Li sits on the 2a Wyckoff position (¾, ¼, 0), O and D sit on the 2c Wyckoff position (¼, ¼, z). Uncertainties on the refined values are shown where available from literature data. The measurement technique is also indicated; neutron powder diffraction (NPD), or neutron single-crystal diffraction (NSXD). In the present study, the displacement parameters (B) were refined isotropically, where it is implied that B₁₁ ≡ B₃₃

	Present study	Mair^29	Dachs^13
	NPD	NPD	NSXD
a-axis (Å)	3.5458(2)	3.549	3.55
c-axis (Å)	4.3458(4)	4.334	4.33
Volume (Å^3)	54.640(6)	54.588	54.57
Oz	0.1933(8)	0.1938(4)	0.1951(5)
Dz	0.3928(9)	0.410(1)	0.4069(14)
B ^Li11 (Å^2)	0.49(6)	0.38(2)	0.85(12)
B ^Li33 (Å^2)	—	0.93(5)	2.4(3)
B ^O11 (Å^2)	0.49(3)	0.34(3)	1.28(4)
B ^O33 (Å^2)	—	0.68(2)	2.01(11)
B ^D11 (Å^2)	5.14(10)	1.28(4)	5.7(2)
B ^D33 (Å^2)	—	0.85(4)	2.8(2)
Li–O (Å)	1.959(2)	1.963	1.96
O–D (Å)	0.867(9)	0.937(7)	0.917(8)

---

Structural evolution at high pressure

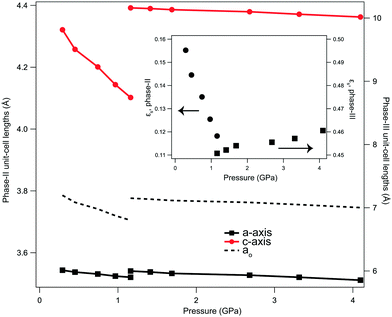
The reduction in unit-cell volume for phase-II was fitted to a second-order Birch–Murnaghan equation of state (EOS), with values of V₀ = 55.5(2) ų (Z = 2), K₀ = 11.4(7) GPa (see ESI†). The pyramidal Li–O motif (see left panel of Fig. 1) is found to be relatively rigid, resulting in an order-of-magnitude disparity in the compression between the a- and c-axes. Over the 0.9 GPa pressure range where phase-II is present, the a/b-axes were found to compress by only 0.643(11)%, compared with 5.07(2)% along the c-axis. The disparity in compressibilities in phase-II may partly explain why the (110) reflection is initially broadened post dehydration from the monohydrate. The reduction in volume caused by the removal of H₂O is preferentially accommodated by c-axis reduction, which may leave the a/b-axes partially strained. The axis reduction with pressure was found to be approximately linear, with compressibilities (K):

K_a,II = −2.62(12) × 10⁻² Å GPa⁻¹

K_c,II = −2.52(12) × 10⁻¹ Å GPa⁻¹

The D⋯O separation was determined to reduce from 3.431(11) to 3.298(12) Å, and the O–D bond reduced from approximately 0.891(11) to 0.835(12) Å over this pressure range. Full structural parameters and the EOS fit are provided in the ESI.†

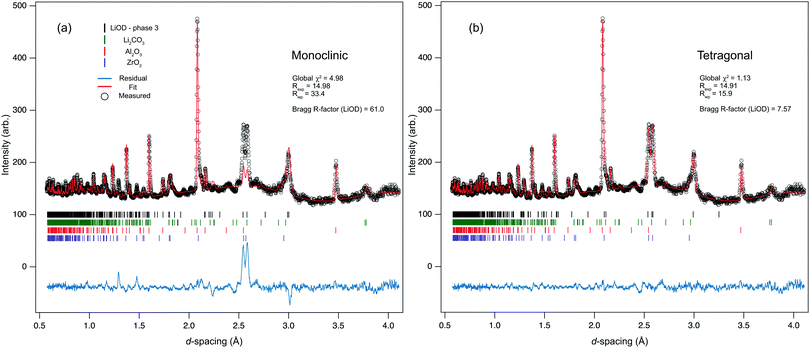
The sample was observed to begin transforming from phase-II to -III at 1.16(3) GPa, where phase coexistence between the two indicated a first-order transition. By 1.25 GPa the sample was pure phase-III. The data at this pressure were fitted against both proposed models in Table 1. From a LeBail fit, the lattice parameters for the monoclinic structure were refined to be similar to those reported by Adams et al.¹⁸ However, when the NaOD-type structure was fitted to the data, there were clear intensity mismatches around principal reflections. Fully relaxing the structure led to little improvement in the overall fit and an unphysical model. In contrast, the tetragonal model of phase-III fitted much better, providing a closer intensity match to the peaks at approximately 2.6 Å. To verify the robustness of the model, the deuterium atom was moved away from the special position, and placed onto a general (x, y, z)-coordinate with reduced occupancy, and allowed to refine. Within error, it returned to the original position, fully occupying a 16e site, supporting the antiferroelectric-type arrangement of the –OH groups.

Fig. 3 shows a comparison of the fits against the two models and also reports the goodness-of-fit parameters. The value of the global χ² drops from 4.98 for the monoclinic structure, to 1.13 when the tetragonal structure is fitted to the data, metrically demonstrating a significant improvement in fit. The phase transition results in a large volume discontinuity (approximately 10%), and significant reduction in compressibility of the sample, with V₀ = 376.3(4) ų (Z = 16), K₀ = 39.1(8) GPa. In phase-III the a/b-axes and c-axis compress at a comparable rate:

K_a,III = −4.91 (11) × 10⁻² Å GPa⁻¹

K_c,III = −4.93 (12) × 10⁻² Å GPa⁻¹

Fig. 3 Comparison of the two candidate models for phase-III of LiOD, following Rietveld refinement against the data collected at 1.41(5) GPa. Black circles are the measured data, the red line is the calculated profile, and the blue line is the residual to the fit. The tick marks (from top to bottom) index LiOD (black), Li₂CO₃ (green), Al₂O₃ (red), and ZrO₂ (blue). Al₂O₃ and ZrO₂ are contributions from the anvil material. In (a) the sample is indexed as monoclinic (P2₁/c), with structural parameters similar to the low-temperature phase of NaOD as discussed in the text, whereas in (b) the sample is indexed as tetragonal (I4₁/acd). The goodness of fit parameters are shown for each candidate structure.

At 1.41(5) GPa the O–D bond length in phase-III is 1.122(12) Å which stays essentially unchanged with pressure, and the D⋯O separation is 1.869(12) Å, reducing only slightly to 1.807(11) Å by 4.1 GPa. This is significantly reduced from that in phase-II, and clearly indicative of hydrogen bonding in the system (this value is approximately 1.9 Å for ice VIII). The lengthening of the O–D bond, and shortening of the D⋯O separation, is clear evidence for the emergence of more extensive hydrogen bonding in this material in phase-III, consistent with spectroscopic observations of the O–H stretching frequency.¹⁷ No additional features were observed in the diffraction spectra up to the maximum pressure of 4.1 GPa. The refined atomic coordinates for this phase are listed in the ESI.†

Discussion

Hydrogen bonded systems at ambient pressure show an inverse correlation between the O–D and D⋯O separations;³⁰ the covalent bond is stronger, but the hydrogen bond causes it to lengthen. Similarly, under pressure, the covalent O–D bond can be seen to lengthen with reducing D⋯O;^31,32 though it is commonly found in the literature for the O–D bond to instead remain invariant over the pressure range considered,³³ as for NaOD-V,^7,34 or sometimes decrease as with Mg(OH)₂,³⁵ and Ca(OD)₂.³⁶ In the present study, phase-II of LiOD shows a clear decrease in the O–D bond distance with applied pressure at a rate of approximately −0.09(3) Å GPa⁻¹. For phase-III, there is a greater degree of scatter on the O–D bond distances, which overall implies that they are pressure invariant within the error of the measurements, while the D⋯O separation reduces.

The bulk modulus of phase-II, K₀ = 11.4(7) GPa, is very low compared to a number of other group-I and group-II hydroxides, being typically 50% and 70% lower.³⁷ with NaOH phase-III (also known as α-NaOH) being the one exception. NaOH phase-III has a reported K₀ = 25.0(4) GPa, though with a negative pressure derivative K′ = −16.0(7).³⁸ If the negative curvature in the low-pressure region is ignored, and the data from Beck and Lederer³⁸ are refitted with a second-order Birch–Murnaghan EOS, then K₀ ≈ 12 GPa, closer to the value determined for LiOD in the present study, though this completely fails to fit the data below 0.2 GPa for NaOH phase-III. As the ambient forms of KOH, RbOH, and CsOH have similar compressibilities with a hydrogen-bonded network, suggesting that electrostatics don't dominate this property, the same might be expected for LiOD and NaOH without a hydrogen-bonded network. Their high-pressure forms contrast this, with LiOD phase-III being significantly less compressible (K₀ = 39.1(8) GPa) than NaOH phase-V (K₀ = 29.7(4) GPa,³⁷), despite having similar transition pressures, and LiOD phase-III having approximately 20% lower density at ∼ 1 GPa. While one might expect the high-density form of LiOD-III to be more compressible than NaOH-V based purely on electrostatics, this is not found to be the case, indicating that the hydrogen- and ionic-bonding play a much more balanced role in the behaviour of this material.

Relating the difference in compressibilities to the hydrogen bonding in LiOD is non-trivial. Both NaOH/D phase-V have been shown to demonstrate no softening of the O–H stretching mode with pressure, thought to be due to bent hydrogen bonds.⁹ This was later demonstrated to be the case in NaOD by Loveday et al.,³⁴ who also posited that if both nearest and next-nearest O atoms are part of the hydrogen-bonded network, then the latter is weakened in favour of the former with further applied pressure. In LiOD phase-III, the hydrogen bonding is purely linear, and this seemingly contributes to a lower overall compressibility compared with the canted structure of NaOH phase-V.

The length of the hydrogen bond in phase-III is shorter than that found in ice VIII, and so might conventionally be called a ‘strong’ hydrogen bond, however, this fails to consider the effect of strain on the system caused by the repulsion between the terminal O²⁻ ions.³⁹ The symmetry of the phase-III structure constrains the hydrogen bond to be linear (∠O–D⋯O ≡ 180^o), such that each O atom has a nearest neighbour parallel and perpendicular to it. The O⋯O separation in LiOD phase-III was determined to be 2.992(14) Å parallel-to, and 2.9933(6) Å perpendicular-to the hydrogen bonds, this results in a slightly more symmetric bond than would be energetically optimal, and is subsequently less ‘strong’ than in ice.³⁹ This reasoning lies in good agreement with the measured O–H stretching frequency from Raman and infrared,¹⁷ and the calculated weighted bond valence sum at 1.41(5) GPa is 0.864 v.u., consistent with the trend observed by Lutz et al.²⁵

The transition between phase-II and -III of LiOD is reconstructive, whereby the system restructures through a rotation of the tetrahedral units with the O–H bond moving into the ab-plane, and a change in translational symmetry. As such, there is no direct group-subgroup relation between the two phases. It is therefore expected that the transition is driven by homogeneous strain on the lattice. As detailed by Carpenter et al.,⁴⁰ the variation of lattice parameters at a phase transition can be interpreted in terms of macroscopic strain, separate from the expected changes due to thermal expansion or length contraction due to applied stress, caused by the microscopic rearrangement of the structure. While the strains in LiOD cannot be directly allocated to an active symmetry mode, due to the reconstructive nature of the transition, the determined strains are still informative, as it is assumed that the progression between phase-II and -III occurs through an intermediate subgroup common to both. As both phases are tetragonal, it can be assumed that the unstrained sample would have cubic-symmetry, allowing the calculation of lattice strains relative to a pseudo-cubic cell (axis length, a_o, see ESI†) in each phase. The calculated strain (see ESI†) is analogous to the ‘tetragonal strain’ of the system, though is corrected for the expected lattice contraction due to pressure. The absolute values between the two phases cannot be directly compared, as the rearrangement of the system does not allow for any meaningful correction for different values of Z. The volumetric strain can be corrected for Z, and shows an overall reduction in strain at the transition, and qualitatively ε_s reduces with applied pressure in phase-II, changes discontinuously at the point of transition, and then increases approximately linearly with further applied pressure in phase-III (Fig. 4). This shows that decreasing the c-axis length in phase-II, and therefore D⋯O separation, reduces the strain in the system. When reduced sufficiently the system then rearranges into a more complex hydrogen-bonded network where the cell is more constrained, resulting in an increase in strain with further applied pressure. This positive slope of ε_s for phase-III suggests that the system tends towards a lower symmetry form at higher pressure still; this would be consistent with a transition to LiOH phase-IV at higher pressures, though we have insufficient data to expand on this further.²¹

Fig. 4 Unit-cell lengths for phase-II and phase-III of LiOD as a function of pressure. The dashed lines show the calculated pseudo-cubic lattice parameter, a_o, used to subtract the effects of isothermal compression, as explained in the main text. (inset) Spontaneous strains, ε_s for phase-II (circles) and phase-III (squares) as a function of pressure. Both y-axes are on a common scale but are offset to show the change in gradient. Error bars are present but are smaller than the data markers.

The onset of phase-III is found to occur at approximately 0.6 GPa lower pressure than previously reported for LiOD.¹⁸ The reason for this discrepancy is not clear but may be related to differences in the pressure medium used between the two studies. Fluorinert is known to be non-hydrostatic at much lower pressures than a mixture of pentanes. Alternatively, it may be related to the rate of compression differing between the experiments.

Conclusion

This study is the first full-structural characterisation of phases-II and -III as a function of pressure. The high-pressure phase-III of LiOD has been shown to have tetragonal symmetry, contrary to previous suggestions of orthorhombic or monoclinic structures analogous to those of NaOH/D.¹⁸ The transition is first-order, as shown by phase-coexistence, and is reconstructive in nature via rotation of the hydroxide groups and reformation of the Li⋯O tetrahedral coordination. This new structure is unique amongst all the alkali-metal hydroxide systems to date while maintaining the basic structural motifs of phase-II. The D⋯O separation is 1.869(12) Å at 1.16(3) GPa, strongly supporting the presence of a hydrogen-bonded network, in agreement with spectroscopic observations. This shows that while hydrogen bonding becomes more prominent, the motif is dominated by the Li⋯O coordination. Pressure is found to reduce the lattice strain in phase-II (consistent with the observed transition to a higher symmetry) though this subsequently increases the lattice distortion in phase-III, potentially leading to an additional transition to a lower symmetry, at higher pressures still. The nature of phase-III is expected to have an impact in applications where LiOH is used in the high-pressure synthesis of substituted cathode materials for Li-ion batteries, exactly whether this structural alteration is beneficial to the process or not remains to be determined, and requires further study.

Author contributions

The conceptualisation and formal analysis were performed by C. J. R. The investigation was performed by C. J. R, C. L. B. and N. P. F. The original draft was prepared by C. J. R. and was reviewed and edited by C. L. B. and N. P. F.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Science and Technology Facilities Council for providing neutron beamtime on the PEARL instrument at the ISIS Neutron and Muon Source,⁴¹ and are grateful to James Tellam (Deuteration Facility, ISIS Neutron and Muon Source) for their assistance in the deuteration of the sample.

Notes and references

1. S. G. Booth, A. J. Nedoma, N. N. Anthonisamy, P. J. Baker, R. Boston, H. Bronstein, S. J. Clarke, E. J. Cussen, V. Daramalla, M. De Volder, S. E. Dutton, V. Falkowski, N. A. Fleck, H. S. Geddes, N. Gollapally, A. L. Goodwin, J. M. Griffin, A. R. Haworth, M. A. Hayward, S. Hull, B. J. Inkson, B. J. Johnston, Z. Lu, J. L. MacManus-Driscoll, X. Martínez De Irujo Labalde, I. McClelland, K. McCombie, B. Murdock, D. Nayak, S. Park, G. E. Pérez, C. J. Pickard, L. F. J. Piper, H. Y. Playford, S. Price, D. O. Scanlon, J. C. Stallard, N. Tapia-Ruiz, A. R. West, L. Wheatcroft, M. Wilson, L. Zhang, X. Zhi, B. Zhu and S. A. Cussen, APL Mater., 2021, 9, 109201.
2. B. Fitch, M. Yakovleva and S. Meiere, Lithium Hydroxide Based Performance Improvements for Nickel Rich Ncm Layered Cathode Material, ECS Meeting Abstracts, 2016, p. 469.
3. D. D. Williams and R. R. Miller, Ind. Eng. Chem. Fundam., 1970, 9, 454–457.
4. R. Stoyanova, E. Zhecheva, G. Bromiley, T. B. Ballaran, R. Alcántara, J.-I. Corredor and J.-L. Tirado, J. Mater. Chem., 2002, 12, 2501–2506.
5. X. Chen, Y.-K. Bai, C.-Z. Zhao, X. Shen and Q. Zhang, Angew. Chem., 2020, 132, 11288–11291.
6. H. D. Lutz, K. Beckenkamp and H. Möller, J. Mol. Struct., 1994, 322, 263–266.
7. W. G. Marshall, R. J. Nelmes, J. M. Besson, S. Klotz and G. Hamel, Rev. High Pressure Sci. Technol., 1998, 7, 376–378.
8. P. W. R. Bessonette and M. A. White, J. Chem. Phys., 1999, 110, 3919–3925.
9. M. P. Krobok, P. G. Johannsen and W. B. Holzapfel, J. Phys.: Condens. Matter, 1992, 4, 8141.
10. B. Mach, H. Jacobs and W. Schäfer, Z. Anorg. Allg. Chem., 1987, 553, 187–195.
11. J. M. Kiat, G. Boemare, B. Rieu and D. Aymes, Solid State Commun., 1998, 108, 241–245.
12. V. A. Khitrov, N. N. Khitrova and V. F. Khmelkov, Zh. Obshch. Khim., 1953, 23, 1630–1632.
13. H. Dachs, Z. Kristallogr. – Cryst. Mater., 1959, 112, 60–67.
14. J. Leciejewicz, Acta Crystallogr., 1961, 14, 1304.
15. H. Stehr, Z. Kristallogr. – Cryst. Mater., 1967, 125, 332–359.
16. H. Jacobs, J. Kockelkorn and T. Tacke, Z. Anorg. Allg. Chem., 1985, 531, 119–124.
17. D. M. Adams and J. Haines, J. Phys. Chem., 1991, 95, 7064–7067.
18. D. M. Adams, A. G. Christy and J. Haines, J. Phys. Chem., 1992, 96, 8173–8176.
19. H.-J. Bleif and H. Dachs, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1982, 38, 470–476.
20. M. Pagliai, M. Iannuzzi, G. Cardini, M. Parrinello and V. Schettino, ChemPhysChem, 2006, 7, 141–147.
21. A. Hermann, N. W. Ashcroft and R. Hoffmann, J. Chem. Phys., 2014, 141, 024505.
22. A. B. Sannigrahi, T. Kar, B. G. Niyogi, P. Hobza and P. Schleyer, Chem. Rev., 1990, 90, 1061–1076.
23. T. J. Bastow, M. M. Elcombe and C. J. Howard, Solid State Commun., 1986, 57, 339–341.
24. C. L. Bull, N. P. Funnell, M. G. Tucker, S. Hull, D. J. Francis and W. G. Marshall, High Press. Res., 2016, 36, 493–511.
25. C. J. Ridley, 2021, In preparation.
26. O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.
27. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
28. H. D. Lutz, C. Jung, M. Trömel and J. Lösel, J. Mol. Struct., 1995, 351, 205–209.
29. S. L. Mair, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 542–547.
30. T. Steiner and W. Saenger, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 348–357.
31. S. K. Sikka and S. M. Sharma, Phase Transitions, 2008, 81, 907–934.
32. J. B. Parise, K. Leinenweber, D. J. Weidnner, K. Tan and R. B. Von Dreele, Am. Mineral., 1994, 79, 193–196.
33. S. K. Sikka, Curr. Sci., 1997, 73, 195–197.
34. J. S. Loveday, W. G. Marshall, R. J. Nelmes, S. Klotz, G. Hamel and J. M. Besson, J. Phys.: Condens. Matter, 1996, 8, L597.
35. M. Catti, G. Ferraris, S. Hull and A. Pavese, Phys. Chem. Miner., 1995, 22, 200–206.
36. H. Xu, Y. Zhao, J. Zhang, D. D. Hickmott and L. L. Daemen, Phys. Chem. Miner., 2007, 34, 223–232.
37. J. W. Otto and W. B. Holzapfel, J. Phys.: Condens. Matter, 1995, 7, 5461–5476.
38. H. P. Beck and G. Lederer, J. Chem. Phys., 1993, 98, 7289–7294.
39. I. D. Brown, Chem. Rev., 2009, 109, 6858–6919.
40. M. A. Carpenter, E. K. H. Salje and A. Graeme-Barber, Eur. J. Mineral., 1998, 10, 621–691.
41. C. J. Ridley, C. L. Bull and N. P. Funnell, Structural study of LiOD, 2020.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma01024g

---