Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The consistent behavior of negative Poisson's ratio with interlayer interactions†
Yancong
Wang
 a,
Linfeng
Yu
a,
Fa
Zhang
ab,
Qiang
Chen
a,
Yuqi
Zhan
a,
Lingwei
Meng
a,
Xiong
Zheng
*a,
Huimin
Wang
a,
Linfeng
Yu
a,
Fa
Zhang
ab,
Qiang
Chen
a,
Yuqi
Zhan
a,
Lingwei
Meng
a,
Xiong
Zheng
*a,
Huimin
Wang
 *c,
Zhenzhen
Qin
*c,
Zhenzhen
Qin
 *d and
Guangzhao
Qin
*d and
Guangzhao
Qin
 *a
*a
aState Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, P. R. China. E-mail: xzheng@hnu.edu.cn; gzqin@hnu.edu.cn
bState Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, P. R. China
cHunan Key Laboratory for Micro-Nano Energy Materials & Device and School of Physics and Optoelectronics, Xiangtan University, Xiangtan 411105, Hunan, China. E-mail: wanghmin@xtu.edu.cn
dSchool of Physics and Microelectronics, Zhengzhou University, Zhengzhou 450001, China. E-mail: qzz@zzu.edu.cn
First published on 6th April 2022
Abstract
A negative Poisson's ratio (NPR) is of great interest due to having novel applications in lots of fields. Films are the most commonly used form in practical applications, which involve multiple layers. However, the effect of interlayer interactions on the NPR is still unclear. In this study, based on first principles calculations, we systematically investigate the effect of interlayer interactions on the NPR by comparably studying single-layer graphene, few-layer graphene, single-layer h-BN, bilayer h-BN, and a graphene-BN heterostructure. It is found that they almost have the same geometry-strain response. Consequently, the NPRs in bilayer graphene, triple-layer graphene, bilayer h-BN, and the graphene-BN heterostructure are consistent with those in single-layer graphene and h-BN. The fundamental mechanism lies in the responses to strain of the orbital coupling being consistent under the effect of interlayer interactions. The deep understanding of the NPR with the effect of interlayer interactions as achieved in this study is beneficial for the future design and development of micro-/nanoscale electromechanical devices with novel functions based on nanostructures.
1. Introduction
The Poisson's ratio, which varies from −1 to 0.5 on the basis of the classical elasticity theory,1 is one of the significant parameters to describe mechanical and physical properties. The existence of a negative Poisson's ratio (NPR) is also rational in theory. In recent years, a NPR has been found in lots of materials, which are well known as auxetic materials. The NPR, which may enable many novel applications, attracts great interest because of the typically enhanced toughness, shear resistance, and sound and vibration absorption.2 In the literature, there are extensive studies of NPR in bulk auxetic structures,3,4 metals,5,6etc. Besides, several models have been proposed for an explanation.7–10 Recently, the discovery of NPRs in metal nanowires and carbon nanotubes has been reported.11,12 In the study of two dimensional (2D) materials, like the representative graphene, a NPR was discovered in 2D materials with specific engineering, such as introducing vacancy defects,13 creating periodic pores,14 cutting into nanoribbons,15etc. In addition, an intrinsic in-plane NPR has been found in 2D materials when applying strain along a special direction without any external modification of the structure, shape or composition. For instance, a NPR has been recently discovered by prediction in 2D honeycomb structures of graphene, silicene, h-BN, h-GaN, h-SiC, and h-BAs.7 Moreover, there are also some studies focusing on out-of-plane NPR, such as in TiN,16 phosphorene,17,18 arsenic,19,20 GeS,21 SnSe,22 and graphene+.23However, the studies in the literature focus on the NPR in single-layer 2D materials, while limited studies have been done on the in-plane NPR of multi-layer 2D materials. In addition, the Poisson's ratio of bulk graphite is positive, which is quite different from the NPR of single-layer graphene, despite the fact that the structure of bulk graphite can be viewed as a stack of many layers of single-layer graphene. As a result, the effects of interlayer interaction on the in-plane NPR are still not clear. In fact, there are lots of further research studies to be conducted in this area. For instance, graphene film is usually used in reality instead of graphene, which involves multiple layers. Here, bilayer graphene is a model for the study of the layer effect. Moreover, heterojunction structures with stacking of different materials are also an interesting topic. Besides, most of the previous explanations of NPR materials are based on the analysis of the evolution of geometric parameters, and only a few studies have explored the mechanism at the electronic level.9,19 Thus, it is necessary to study the effect of interactions between layers on the NPR of few-layer 2D materials and achieve a more fundamental understanding.
In this study, we systematically investigate the response of strain and key geometric parameters for bilayer graphene, triple-layer graphene, and a graphene-BN heterostructure (gra-BN) with strain applied. It is found that the in-plane NPR is consistent among these structures while the NPR in bilayer graphene and gra-BN is weakened to different degrees. The mechanism is uncovered by analyzing the response of orbital coupling to strain. The results deepen the understanding of NPR, which would shed light on future design of micro-/nanoscale electromechanical devices.
2. Materials and methods
All the calculations are performed using the Vienna ab initio simulation package (VASP),24 which is based on density functional theory (DFT). The Perdew–Burke–Ernzerhof25 (PBE) generalized gradient approximation (GGA) is chosen as the exchange–correlation functional. Long-range van der Waals interactions were taken into account using the optB88 vdW functional.26,27 We use the classical single-layer graphene and two kinds of representative bilayer graphene with the same crystal orientation but different stacking (AA and AB stacking, as shown in Fig. 1). AA stacking corresponds to the stacking pattern of two single-layers paired with each other, while AB stacking corresponds to the stacking pattern moving one of the layers in the opposite direction for one-third of the [1,1] crystallographic vector.28 The kinetic energy cutoff of the wave functions is set as 1000 eV for all the calculations. The Monkhorst–Pack29k-mesh of 19 × 11 × 1 is used to sample the Brillouin zone (BZ), and the energy convergence threshold is set as 10−6 eV. Uniaxial strains along the typical zigzag and armchair directions are applied. The strain is defined as (I − I0)/I0, where I is the lattice constant with stretching and I0 is the original lattice constant without stretching. The stress is scaled by replacing the thickness including the vacuum space with the effective layer thickness for more accurate simulation results. Specifically, for flat materials like graphene and h-BN, the effective layer thickness is the sum of the actual distance between the two layers and the van der Waals diameter of the C atoms.30–34 In all cases, the geometric parameters are fully optimized with the Herman-Feynman force on all atoms less than 10−4 V Å−1. The stability of the structures is verified by calculating the phonon dispersion (see Fig. S3 in the ESI† for more details). The optimized interlayer distances in AA and AB bilayer graphene and gra-BN are 3.55, 3.37 and 3.47 Å, respectively. While without considering the vdW interlayer interaction, the optimized interlayer distances of the AA and AB bilayer graphene are 4.6 and 4.4 Å, respectively. This is much larger than the vdW diameter and can be viewed as a structural optimization of two separate single-layer graphenes.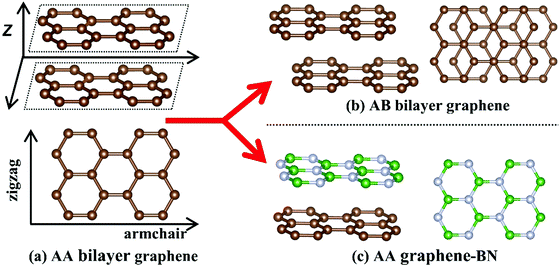 | ||
| Fig. 1 Schematics of the structures of bilayer graphene in (a) AA and (b) AB stacking, and graphene-BN in (c) AA stacking. | ||
3. Results
With strain applied, the mechanical response of single-layer graphene and bilayer graphene with AA and AB stacking are studied. Previous studies show that graphene can sustain a large strain (≥25%) and has a large breaking strength.35,36 The breaking strength is found to be 42 N m−1 of graphene.35 Considering that the effective thickness of graphene is about 0.35 nm, the fracture strength of 42 N m−1 graphene is 125.4 GPa, which is greater than the maximum stress achieved along the two stretch directions in Fig. 2, 108 and 98 GPa. Generally speaking, from an experimental point of view, experimental results can be influenced by defects, temperature effects, or other elements that may react with the graphene layer. Because of the above reality, the theoretical value of the prediction is often higher than the experimental value. However, this does not affect the prediction of the NPR of graphene materials and the exploration of its potential mechanism.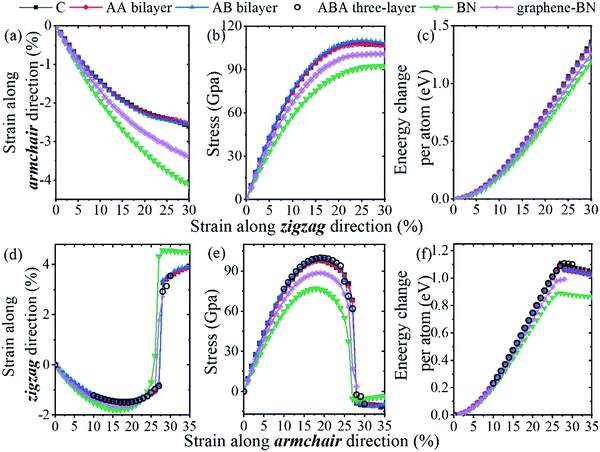 | ||
| Fig. 2 The anisotropic response of the (a and d) driven strain, (b and e) stress, and (c and f) energy change per atom with strain applied along the (a–c) zigzag and (d–f) armchair directions. | ||
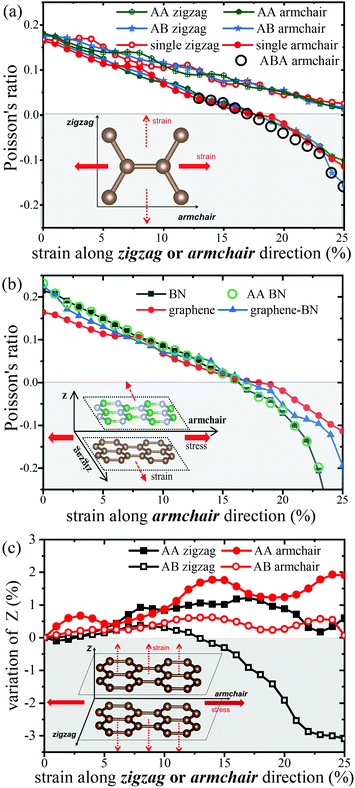
Fig. 2 shows the response of strain, stress and energy per atom for the single-layer graphene, AA/AB bilayer, ABA triple-layer graphene, BN and graphene-BN heterostructures. Generally, three physical parameter responses to the strain along the zigzag direction are continuous. However, with a significantly large strain applied, a mutant (28%) is found for the response to the strain along the armchair direction, which means that the structure failed when the strain along the armchair direction is larger than 28%. It can be found that the response to the strain along the zigzag direction in this study is a common phenomenon, and the lattice constant along the armchair direction decreases with increasing strain along the zigzag direction. While Fig. 2(d) shows that the lattice constant decreases when the strain along the armchair direction is between 0% and around 15%, the lattice constant increases abnormally when the strain is larger than 15%, which indicates the appearance of NPR phenomena. The stress along the stretch direction increases except for the situations where NPR exists. The highest stress is found at the condition where the NPR starts to appear, and then the stress decreases with the increase of stretch. As for the energy per atom, it keeps growing regardless of the existence of the negative Poisson effect. Because the strain in the stretching direction is positive, and so is the stress, there is no stress in the other direction. Then positive work is being done and the energy is being put into the system. Moreover, the responses to strain of the AA/AB bilayer graphene and single-layer graphene are almost the same, which demonstrates the consistency in the responses of strain, stress and energy of the three materials. Besides, the curve of the single-layer graphene is found to be slightly higher than that of bilayer graphene, as shown in Fig. 2(d), which is similar to the results reported in previous work on the study of multilayer graphene via molecular dynamics simulations.37
To get a more precise and intuitive view of the NPR, the Poisson's ratio is calculated and the results are shown in Fig. 3. It is well known that the Poisson's ratio is defined as8
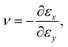 | (1) |
With the results of single-layer and bilayer graphene, it is interesting to further investigate what happens in three-layer graphene. The black pentagons in Fig. 3(a) show that the A–B–A stacking triple graphene basically possesses the same NPR as bilayer graphene. This is possibly because the third and first layers are far apart from each other. Thus, the interaction on in-plane NPR is weak and the NPR is consistent. Note that there is a sharp drop of the NPR in the ABA and AB stacking conditions as the stretch strain reaches 24%, which is probably because the structure has become less stable when the stretch strain reaches 25%.
It's worth mentioning that we also studied the NPR of heterostructures in Fig. 3(b). In terms of the large variation trend, the NPR of gra-BN is consistent with that of multilayer graphene. There is also little difference between single-layer and bilayer BN stacked in AA stacking. However, there are still some interesting differences. It is shown that the graphene-BN heterostructure significantly enhances the NPR of single-layer graphene after the NPR occurs in the stretching process along the armchair direction. In this process, the NPR effect of heterojunctions is still smaller than that of single-layer BN. However, before the NPR occurs, the situation is just the opposite: BN has the smallest NPR, single-layer graphene has the strongest NPR, and the heterostructure is in the middle position.
Moreover, the variation of the distance between layers (Z) is calculated when strain is applied. The results in Fig. 3(c) indicate interesting NPR phenomena along the out-of-plane direction, which will be useful for vertical vibration isolation applications of graphene-layered devices. Further study to explore mechanisms of this out-of-plane NPR phenomenon needs to be conducted in future.
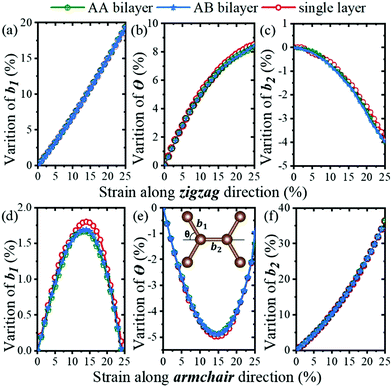
To get insight into the variation process of the inner geometric structure, we calculate the length of bond (b1, b2) and angle (θ). As shown in Fig. 4, there is nearly no difference for single-layer graphene and AA/AB bilayer graphene. This indicates that the three materials have almost the same inner geometric variation during stretching, which gives rise to the same results regarding the strain in Fig. 2 and the NPR in Fig. 3. With further consideration, the interaction force between layers has nearly no influence on the in-plane variation. However, it is noticeable that single-layer graphene has a slightly larger geometric structure change than that of bilayer graphene when the strain is applied in the armchair direction, especially with respect to b1 and θ in Fig. 4(d and e). In addition, Fig. 4 shows the reason why the NPR phenomena appear and the different response to strain applied along different vertical directions at the geometric level. Fig. 4(a–c) show that it is monotonic that b1 and θ increase, and b2 decreases, resulting in the positive Poisson's ratio. While Fig. 4(d and e) show that b1 and θ increase first and then decrease, which is an abnormal variation response to the lattice stretching. These abnormal variations result in the NPR. It is understandable that the increasing of b1 and θ has opposite effects on the NPR. The increasing of θ causes the length of the zigzag to increase while the increasing of b1 leads to decreasing length of the zigzag. Because the strain along the stretch direction is increasing statically, we can take only the lattice constant of another direction (Izigzag and Iarmchair) into consideration. Izigzag and Iarmchair correspond to the lattice constants in two different stretch directions, respectively, which can be written as
Izigzag = 2 × b1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (2) |
Iarmchair = 2 × b2 + 2 × b1 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (3) |
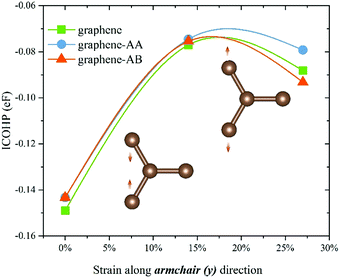
To further explore the mechanism of abnormally increasing θ, the Crystal Orbital Hamilton Population (COHP) was introduced to evaluate the interactions of C atoms. And the integrated values of COHP (ICOHP) were used to quantitatively analyze the strength of the interaction between two atoms at each end of θ, where the smaller value of ICOHP means a stronger interatomic interaction. As shown in Fig. 5, before the occurrence of NPR (<14% strain applied along armchair direction), the value of ICOHP keeps increasing and the constraint of in-plane interaction becomes weaker. As the interaction strength reaches the weakest, graphene can no longer maintain shrinkage along the zigzag direction, resulting in geometric inverse angular (θ) expansion. By comparing the AA bilayer, AB bilayer and single-layer graphene, we found a slight difference in their ICOHP value variation, which also led to a slight difference in geometric variation [Fig. 4(d and e)].
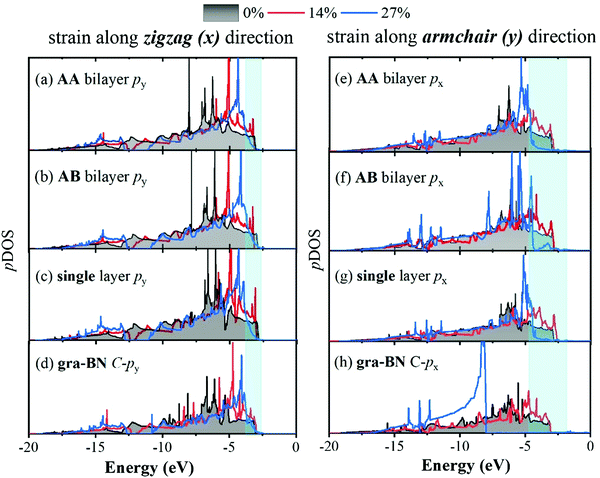
To understand the internal mechanism of the NPR, we investigated the projected density of states (pDOS) to study the electronic function of three representative strength conditions (0%, 14%, and 27% corresponding to the cases with no strain, before NPR, and after NPR, respectively). With comparison of the hybridized C-px/py orbitals and the solo C-pz orbital closing to the valence band maximum (VBM) of the three different materials with two-direction stretch (Fig. S1 in the ESI†), we find the recognized difference between the response to the px orbital (along zigzag direction) of the stretch along the armchair direction and the response to the py orbital (along armchair direction) of the stretch along the zigzag direction, causing the different response to the armchair and zigzag direction stretching. As shown in Fig. 6(e–h), the four material's px-DOSs closing to the VBM increase slightly first and then decrease significantly, which means the interaction force along the zigzag direction (x) decreases largely, causing θ to increase abnormally in Fig. 4(e). This is the essential variation causing the NPR. While in Fig. 6(a–d), the four materials’ py-DOSs closing to the VBM have a small variation and almost monotonic decline, which may cause the monotonic variation of the geometric parameter in Fig. 4(a–c) and the response to positive Poisson's ratio.
Furthermore, we find that the px-DOS has almost the same trend in AA/AB bilayer graphene and single-layer graphene because most electrons are constrained to move in a 2D plane (see Fig. S2 in the ESI† for more information).38 However, compared with single and bilayer graphene, it's worth pointing out that whether the stretching is in the direction of armchair or zigzag, the pDOS of single-layer graphene changes the most, which is probably because the interlayer interaction in the two-layer structure weakens the coupling in the in-plane direction slightly (px or py). In particular, the degree of decline for the single-layer graphene has the largest reduction between 14% and 27% stretching along the armchair direction in Fig. 6(e–g), causing the obviously larger geometry changes (b1 and θ in Fig. 4(d and e)) than AA and AB bilayer graphene. In addition, Fig. 6(h) illustrates that the C-px of the gra-BN heterostructure has a huge decrease after the occurrence of NPR, which is much larger than that of single and bilayer graphene, and this is also the reason why the degree of NPR of gra-BN is larger than that of single-layer and bilayer graphene.
4. Discussion and conclusions
In summary, by studying the strain, stress, energy per atoms and geometric responses to axial stretching with single-layer graphene, few-layer graphene, h-BN, and a graphene-BN heterostructure, we found that the responses and NPR among them have almost the same behavior, indicating the weak effect of interlayer interactions on the in-plane NPR. This suggests that the difference between single-layer graphene and bulk graphite is a novel phenomenon of NPR in graphene caused by dimensional changes, which cannot be simply explained as the effect of interlayer interactions. In addition to the consistent behavior of the NPR, it is found that the variation of θ and b1 in the single-layer graphene is larger than that in the bilayer graphene. Moreover, by studying the pDOS, it is indicated that px slightly increases first and then decreases significantly during stretching along the armchair direction (y), which means that the interaction along the zigzag direction (x) decreases and then causes θ to increase abnormally, leading to in-plane NPR. In contrast, py changes slightly and mononously during stretching along the zigzag direction (x), and there is no NPR phenomenon. Moreover, the px of single-layer graphene decreases slightly more than that of bilayer graphene and the px of the gra-BN heterostructure decreases more significantly than that of single and bilayer graphene, which also leads to the greatest variation of geometric parameters (θ and b1) in single-layer graphene and the greatest degree of NPR in gra-BN. This may be because the interlayer interactions weaken the coupling of the in-plane px orbital. Thus, the consistency of NPR in few-layer and single-layer graphene, and further BN and the graphene-BN heterostructure is explained. The interlayer interactions may affect the in-plane coupling of p-orbitals slightly, leading to differences in the in-plane geometric changes. Our study provides a deep understanding on the effect of interlayer interaction and reveals the internal mechanism of NPR in bilayer and single-layer graphene at the level of electron interaction. It is expected to shed light on future design and development of micro-/nanoscale electromechanical devices with novel functions based on nanostructures.It should be noted that although the interlayer interaction is weak in multilayer graphene, the effect of interlayer interaction on the in-plane thermal conductivity of graphene is significant, which is also governed by the lattice dynamics and electronic structures. For instance, the in-plane thermal conductivity of bilayer graphene is much lower than that of single-layer graphene.39Thus, the consistent behavior of NPR with interlayer interactions is anomalous considering the remarkable effect of interlayer interaction on the lattice dynamics and thermal transport behavior. In future studies, more investigations could be conducted on multilayer systems with stronger interlayer interactions, such as MoS2,40 where the effect of interlayer interactions on NPR could be significant.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Author contributions
G. Q. supervised the project. Y. W. and L. Y. performed all the calculations and analysis. All the authors contributed to interpreting the results. The paper was written by Y. W. with contributions from all the authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Changsha Municipal Natural Science Foundation (Grant No. kq2014034). The numerical calculations in this paper have been done on the supercomputing system of the National Supercomputing Center in Changsha. X. Z. is supported by the Fundamental Research Funds for the Central Universities (Grant No. 531118010490) and the National Natural Science Foundation of China (Grant No. 52006059). H. W. is supported by the National Natural Science Foundation of China (Grant No. 51906097). Z. Q. is supported by the National Natural Science Foundation of China (Grant No. 11847158 and 11904324) and the China Postdoctoral Science Foundation (2018M642776). G. Q. is supported by the National Natural Science Foundation of China (Grant No. 52006057), the Fundamental Research Funds for the Central Universities (Grant No. 531119200237 and 541109010001), the Changsha Municipal Natural Science Foundation (Grant No. kq2014034), and the State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body at Hunan University (Grant No. 52175013). The authors declare that there are no competing interests.References
- J.-W. Jiang, S. Y. Kim and H. S. Park, Auxetic nanomaterials: Recent progress and future development, Appl. Phys. Rev., 2016, 3, 041101 Search PubMed.
- A. W. Lipsett and A. I. Beltzer, Reexamination of dynamic problems of elasticity for negative Poisson's ratio, J. Acoust. Soc. Am., 1988, 84, 2179–2186 CrossRef.
- W. Yang, Z.-M. Li, W. Shi, B.-H. Xie and M.-B. Yang, Review on auxetic materials, J. Mater. Sci., 2004, 39, 3269–3279 CrossRef CAS.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Poisson's ratio and modern materials, Nat. Mater., 2011, 10, 823–837 CrossRef CAS PubMed.
- R. H. Baughman, J. M. Shacklette, A. A. Zakhidov and S. Stafström, Negative Poisson's ratios as a common feature of cubic metals, Nature, 1998, 392, 362–365 CrossRef CAS.
- F. Milstein and K. Huang, Existence of a negative Poisson ratio in fcc crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 2030–2033 CrossRef CAS.
- G. Qin and Z. Qin, Negative Poisson's ratio in two-dimensional honeycomb structures, npj Comput. Mater., 2020, 6, 51 CrossRef CAS.
- J.-W. Jiang, T. Chang, X. Guo and H. S. Park, Intrinsic Negative Poisson's Ratio for Single-Layer Graphene, Nano Lett., 2016, 16, 5286–5290 CrossRef CAS PubMed.
- Z. Qin, G. Qin and M. Hu, Origin of anisotropic negative Poisson's ratio in graphene, Nanoscale, 2018, 10, 10365–10370 RSC.
- L. Rothenburg, A. A. Berlin and R. J. Bathurst, Microstructure of isotropic materials with negative Poisson's ratio, Nature, 1991, 354, 470–472 CrossRef.
- S. I. Kundalwal and V. Choyal, Transversely isotropic elastic properties of carbon nanotubes containing vacancy defects using MD, Acta Mech., 2018, 229, 2571–2584 CrossRef.
- D. T. Ho, S.-Y. Kwon and S. Y. Kim, Metal [100] Nanowires with Negative Poisson’s Ratio, Sci. Rep., 2016, 6, 27560 CrossRef CAS PubMed.
- J. Grima, S. Winczewski, L. Mizzi, M. Grech, R. Cauchi, R. Gatt, D. Attard, K. Wojciechowski and J. Rybicki, Tailoring Graphene to Achieve Negative Poisson’s Ratio Properties, Adv. Mater., 2015, 27, 1455–1459 CrossRef CAS PubMed.
- K. W. Wojciechowski, A. Alderson, J. N. Grima and F. Scarpa, Auxetics and Other Systems with “Negative” Characteristics, Phys. Status Solidi B, 2020, 257, 2000496 CrossRef CAS.
- J.-W. Jiang and H. S. Park, Negative Poisson's Ratio in Single-Layer Graphene Ribbons, Nano Lett., 2016, 16, 2657–2662 CrossRef CAS PubMed.
- L. Zhou, Z. Zhuo, L. Kou, A. Du and S. Tretiak, Computational Dissection of Two-Dimensional Rectangular Titanium Mononitride TiN: Auxetics and Promises for Photocatalysis, Nano Lett., 2017, 17, 4466–4472 CrossRef CAS PubMed.
- J.-W. Jiang and H. S. Park, Negative Poisson's ratio in single-layer black phosphorus, Nat. Commun., 2014, 5, 4727 CrossRef CAS PubMed.
- Y. Du, J. Maassen, W. Wu, Z. Luo, X. Xu and P. D. Ye, Auxetic Black Phosphorus: A 2D Material with Negative Poisson's Ratio, Nano Lett., 2016, 16, 6701–6708 CrossRef CAS PubMed.
- K. Chinnathambi and M. Ezawa, Arsenene: Two-dimensional buckled and puckered honeycomb arsenic systems, Phys. Rev. B, 2015, 91, 085423 CrossRef.
- J. Han, J. Xie, Z. Zhang, D. Yang, M. Si and D. Xue, Negative Poisson’s ratios in few-layer orthorhombic arsenic: First-principles calculations, Appl. Phys. Express, 2015, 8, 041801 CrossRef.
- L. C. Gomes, Enhanced piezoelectricity and modified dielectric screening of two-dimensional group-IV monochalcogenides, Phys. Rev. B, 2015, 92, 214103 CrossRef.
- L.-C. Zhang, G. Qin, W.-Z. Fang, H.-J. Cui, Q.-R. Zheng, Q.-B. Yan and G. Su, Tinselenidene: a Two-dimensional Auxetic Material with Ultralow Lattice Thermal Conductivity and Ultrahigh Hole Mobility, Sci. Rep., 2016, 6, 19830 CrossRef CAS PubMed.
- L. Yu, Z. Qin, H. Wang, X. Zheng and G. Qin, Half-negative Poisson's ratio in graphene+ with intrinsic Dirac nodal loop, Cell Rep. Phys. Sci., 2022, 3, 100790 CrossRef.
- G. Kresse, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- J. Lin, W. Fang, W. Zhou, A. R. Lupini, J. C. Idrobo, J. Kong, S. J. Pennycook and S. T. Pantelides, AC/AB Stacking Boundaries in Bilayer Graphene, Nano Lett., 2013, 13, 3262–3268 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- A. Mj, T. Vc and K. Rb, Honeycomb carbon, https://pubmed.ncbi.nlm.nih.gov/19610631/, (accessed February 17, 2021).
- D. L. Nika and A. A. Balandin, Two-dimensional phonon transport in graphene, J. Phys.: Condens. Matter, 2012, 24, 233203 CrossRef PubMed.
- H. Li, H. Ying, X. Chen, D. L. Nika, A. I. Cocemasov, W. Cai, A. A. Balandin and S. Chen, Thermal conductivity of twisted bilayer graphene, Nanoscale, 2014, 6, 13402–13408 RSC.
- Z. Qin, G. Qin, X. Zuo, Z. Xiong and M. Hu, Orbitally driven low thermal conductivity of monolayer gallium nitride (GaN) with planar honeycomb structure: a comparative study, Nanoscale, 2017, 9, 4295–4309 RSC.
- G. Qin, Anomalously temperature-dependent thermal conductivity of monolayer GaN with large deviations from the traditional <span class, Phys. Rev. B, 2017, 95, 195416 CrossRef.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Large-scale pattern growth of graphene films for stretchable transparent electrodes, Nature, 2009, 457, 706–710 CrossRef CAS PubMed.
- B. Deng, J. Hou, H. Zhu, S. Liu, E. Liu, Y. Shi and Q. Peng, The normal-auxeticity mechanical phase transition in graphene, 2D Mater., 2017, 4, 021020 CrossRef.
- T. Ohta, A. Bostwick, T. Seyller, K. Horn and E. Rotenberg, Controlling the Electronic Structure of Bilayer Graphene, Science, 2006, 313, 951–954 CrossRef CAS PubMed.
- F. Duan, C. Shen, H. Zhang and G. Qin, Hydrodynamically enhanced thermal transport due to strong interlayer interactions: A case study of strained bilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 105, 125406 CrossRef CAS.
- L. Yu, Q. Yan and A. Ruzsinszky, Negative Poisson's ratio in 1T-type crystalline two-dimensional transition metal dichalcogenides, Nat. Commun., 2017, 8, 15224 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00118g |
| This journal is © The Royal Society of Chemistry 2022 |