Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mixing of acoustic and optical excitations in Ru/Co based multilayers
P.
Ntetsika
a,
G.
Mitrikas
 b,
G.
Litsardakis
b,
G.
Litsardakis
 c and
I.
Panagiotopoulos
c and
I.
Panagiotopoulos
 *ad
*ad
aDepartment of Materials Science and Engineering, University of Ioannina, Ioannina 45110, Greece. E-mail: ipanagio@uoi.gr
bInstitute of Nanoscience and Nanotechnology, National Centre for Scientific Research-Demokritos, Athens, Greece
cLaboratory of Materials for Electrotechnics, Department of Electrical and Computer Engineering, Aristotle University of Thessaloniki, Thessaloniki, Greece
dInstitute of Materials Science and Computing, University Research Center of Ioannina (URCI), 45110 Ioannina, Greece
First published on 30th May 2022
Abstract
Two series of [Ru10/Cox)]12 and [Ru6/Cr3/Cox)]12x = 16–60 easy-plane anisotropy multilayers (all thicknesses in Å), prepared by sputter deposition, are studied by cavity FMR. The resonance fields of the modes excited by setting the rf field perpendicular to the saturating (in-plane) field are in good agreement with the values predicted for pure acoustic modes by a simple two-macrospin model. In contrast, the resonance fields of the modes excited by setting the rf field parallel to the saturating field, are lower than those expected for pure optical modes. This is attributed to the existence of hybridized mixed modes. Micromagnetic simulations show that (a) the inhomogeneous magnetization profile along the multilayer thickness is sufficient to give rise to mode mixing and (b) that mode mixing is not limited to the region where the frequencies of the acoustic and optical modes coincide.
Introduction
Synthetic antiferromagnets (SAFs) are based on the oscillatory interlayer exchange coupling of thin magnetic layers through metal, typically mediated by the Ruderman–Kittel–Kasuya–Yosida (RKKY) mechanism via the conduction electrons.1 The low field tunability of the magnetic state in SAFs opened the route to the discovery of giant magnetoresistance phenomena and their implementation in spin-valves and magnetic tunnel junctions.2 It is the same tunability that makes them attractive for other applications such as tunable magnonics3–5 and terahertz nano-oscillators.6–8 In early studies, the focus was on the optimization of the SAFs for spin valves while the study of dynamic properties was used mainly to derive anisotropies and interfacial coupling strengths.9 Today there is a renewed interest in SAF systems for their dynamic properties and for their possible incorporation in synthetic antiferromagnetic spintronic structures.10The antiferromagnetic interlayer exchange coupling in SAFs gives rise to two distinct modes (acoustic/optical) distinguished according to the correlation of the magnetic moment precession between adjacent magnetic layers. As the names indicate, for acoustic modes the resonances approach zero at zero field, while the optical modes possess useful high frequencies at zero-applied field.11 Several works have focused on these aspects of SAF systems in FeCoB/Cr/FeCoB,12 FeCoB/Al2O3/FeCoB,13 Pt/Co/Ir/Co/Pt,14 and CoFeB/Ru/CoFeB.15,16 A study based on an all-optical pump-probe technique showed that the dynamic exchange coupling increased the damping of the optical mode owing to the spin-pumping effect at the CoFeB/Ru interfaces.17 The frequencies of the modes, as a function of the applied field, depend on the magnetic state and therefore on the uniaxial magnetic anisotropy (HK) and antiferromagnetic interlayer exchange coupling (Hex), which provide control of the dynamic properties. Thus, the frequencies of the modes can be used to extract the coupling and anisotropy parameters as has been used in early18 and recent studies.6 As the frequencies of the optical and acoustic modes depend on the applied field, there is a point where they tend to coincide. It has been shown that the optical and acoustic spin-wave modes get hybridized at these degeneracy points.4,5,19 The mode coupling is reported to be mediated by the dipolar fields generated by the magnetization motion of spin waves and the out-of-plane tilt angle.4 It therefore increases with the wave number of excited spin waves and the angle between the external magnetic field and spin-wave propagation directions5 and can be enhanced by applying an out of-plane bias field20 or constructing a structurally asymmetrical SAF.19 Here, we expand these studies to multilayer systems, where other mode mixing mechanisms may come into play. We present a Ferromagnetic Resonance (FMR) study of two series of [Ru10/Cox)]12 and [Ru6/Cr3/Cox)]12x = 16–60 multilayers (all indices inside the brackets denote thickness in Å, the index 12 refers to the repetitions of the period of the stack). The films have been prepared by sputter deposition and have easy-plane anisotropy but no anisotropy within the plane. The use of chromium gives an extra degree of freedom in tailoring the exchange coupling and anisotropy independently as both have interfacial contributions that scale inversely with the layer thickness. Co/Cr heterostructures have received much less attention than Fe/Cr since there is a crystal structure mismatch between Cr and Co.21 It is found that the [Ru10/Cox)]12 can give higher zero-field optical modes and therefore has more interesting dynamical properties. We propose that mode coupling is linked to the inhomogeneous magnetization profile along the multilayer thickness. Thus, the mode mixing is not limited to the region where the frequencies of the optical and acoustic modes coincide.
Experimental details
The multilayered [Ru10/Cox)]12 and [Ru6/Cr3/Cox)]12 (with x = 14–60, all thicknesses in Å) films have been deposited on rotating substrates, at room temperature by magnetron sputtering, using a multi-source deposition system. The values of the Ru and Ru/Cr layer thickness were chosen to maximize the RKKY exchange interactions in each case. The Co, Cr (7.62 cm diameter) and Ru (5.08 cm diameter) sources are in confocal geometry: i.e., pointing at an angle of 45 deg to the (horizontal) substrate plane, which is rotated during the deposition. The target to substrate distance is 15 cm. Prior to the deposition, the chamber was evacuated to a base pressure better than 7 × 10−5 Pa and the process gas (Ar) pressure during deposition was 0.47 Pa. Co has been deposited at a rate of 0.75 Å s−1 by applying a DC power of 100 W, chromium at 1.15 Å s−1 with 130 W DC, and Ru at 0.40 Å s−1 using 120 W RF. The samples were sputtered on thermally oxidized Si(100) wafers. The magnetic measurements were done using a vibrating sample magnetometer (VSM) of Lakeshore Cryotronics Inc. (model 7312) with eight sensing coils (four per component) and a 20 kOe electromagnet and a QD Versalab VSM with 30 kOe field. The ferromagnetic resonance (FMR) measurements were performed at room temperature using a Bruker ESP 380E spectrometer equipped with a rectangular ER 4102ST or a dual-mode ER 4116DM cavity. The dc-field was always in the film plane. When the exciting rf field is parallel to the dc-field the excitation of optical modes for which the motion of the spins is symmetric with respect to the dc-field direction are favored. On the other hand, setting the rf field perpendicular to the dc favors the excitation of acoustic modes. The microwave frequency was measured with a HP 5350B microwave frequency counter. Spectra were obtained using a microwave power of 20.9 mW, modulation frequency of 100 kHz, modulation amplitude of 1 mT, a field-sweep range of 450 mT and an acquisition time of 167 s. The cavity frequencies were 9.76 GHz for the rf(⊥) and 9.34 for the rf(‖) measurements.Magnetic properties and FMR
Since the films are deposited on rotating substrates there is no anisotropy within the film plane. VSM measurements have been used to characterize the anisotropy and the coupling strength between the layers. The shape anisotropy is the dominant term: for all the films the saturation field within the plane H‖ is lower than the saturation field along the film normal H⊥. In short, the anisotropy is easy plane, but without any preferential orientation within the film plane. Due to the lack of anisotropy within the plane, the scissor-like magnetization state between successive Co layers (due to the competition between the interlayer AF coupling and dc magnetic field) is attained gradually, without any spin-flop transition.22 The RKKY exchange field n be estimated from the in-the plane saturation field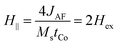 . The factor 2 enters because each Co layer is coupled to two neighbouring layers. This holds strictly only for an infinite layer stack, without outer layers. However, for our case with N = 12 Co layers, the micromagnetic simulations (Section 4) show that the effect of the two outer layers (which are coupled to only one layer) is negligible. For the measurements along the film normal apart from the shape anisotropy, the magnetocrystalline (Kmc) and interfacial anisotropy (KS) contributions must also be considered. The total uniaxial anisotropy would be
. The factor 2 enters because each Co layer is coupled to two neighbouring layers. This holds strictly only for an infinite layer stack, without outer layers. However, for our case with N = 12 Co layers, the micromagnetic simulations (Section 4) show that the effect of the two outer layers (which are coupled to only one layer) is negligible. For the measurements along the film normal apart from the shape anisotropy, the magnetocrystalline (Kmc) and interfacial anisotropy (KS) contributions must also be considered. The total uniaxial anisotropy would be 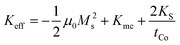 and the field HK required for perpendicular saturation in opposition to the anisotropy is
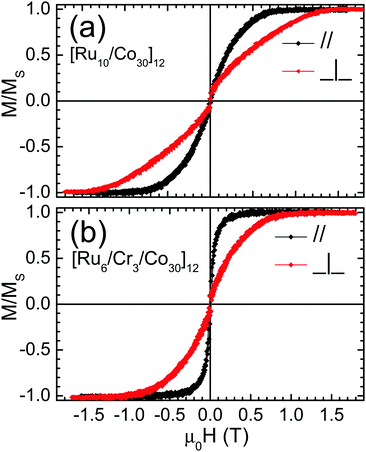
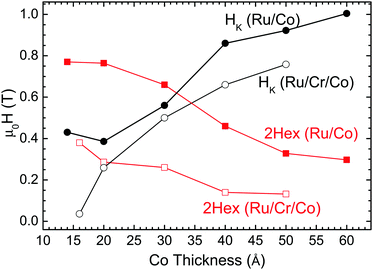
and the field HK required for perpendicular saturation in opposition to the anisotropy is 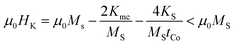 . The values of Hex and HK are estimated by the saturation field parallel and perpendicular to the film plane H‖, H⊥ respectively using H‖ = 2Hex, H⊥ = HK + 2Hex. Typical curves for [Ru10/Co30)]12 and [Ru6/Cr3/Co30)]12 samples are shown in Fig. 1. The obtained values are summarized in Table 1 along with the FMR resonance fields. The dependence of Hex and HK on the Co layer thickness is presented in Fig. 2. The thickness dependences can be explained by the decreasing interfacial contributions as the thickness increases: the main contribution to HK is the shape anisotropy. Thus, the total anisotropy is in-plane. The interfacial contribution tends to drive the anisotropy to the perpendicular and reduces the absolute value of HK. Therefore, HK increases with Co thickness. On the other hand, for in-plane measurements, the exchange field is mainly of interfacial origin, so it is expected to decrease with thickness. Some deviations may arise from magnetostatic coupling.
. The values of Hex and HK are estimated by the saturation field parallel and perpendicular to the film plane H‖, H⊥ respectively using H‖ = 2Hex, H⊥ = HK + 2Hex. Typical curves for [Ru10/Co30)]12 and [Ru6/Cr3/Co30)]12 samples are shown in Fig. 1. The obtained values are summarized in Table 1 along with the FMR resonance fields. The dependence of Hex and HK on the Co layer thickness is presented in Fig. 2. The thickness dependences can be explained by the decreasing interfacial contributions as the thickness increases: the main contribution to HK is the shape anisotropy. Thus, the total anisotropy is in-plane. The interfacial contribution tends to drive the anisotropy to the perpendicular and reduces the absolute value of HK. Therefore, HK increases with Co thickness. On the other hand, for in-plane measurements, the exchange field is mainly of interfacial origin, so it is expected to decrease with thickness. Some deviations may arise from magnetostatic coupling.
| Layering | VSM | Macrospin model | FMR (rf⊥dc and rf‖dc) | |||
|---|---|---|---|---|---|---|
| μ 0 H ‖ | μ 0 H ⊥ | μ 0 H ac | μ 0 H opt | μ 0 H res (⊥) | μ 0 H res (‖) | |
| [Ru(10)/Co(14)]12 | 0.77 | 1.20 | 0.24 | 0.66 | — | — |
| [Ru(10)/Co(20)]12 | 0.76 | 1.15 | 0.25 | 0.64 | 0.25 | — |
| [Ru(10)/Co(30)]12 | 0.66 | 1.22 | 0.22 | 0.58 | 0.22 | 0.39 |
| [Ru(10)/Co(40)]12 | 0.46 | 1.32 | 0.18 | 0.41 | 0.19, 0.12 | 0.34, 0.21, 0.09, 0.03 |
| [Ru(10)/Co(50)]12 | 0.33 | 1.25 | 0.16 | 0.28 | 0.14 | 0.12 |
| [Ru(10)/Co(60)]12 | 0.30 | 1.30 | 0.15 | 0.25 | 0.12 | 0.07 |
| [Ru(6)/Cr(3)/Co(16)]12 | 0.38 | 0.42 | 0.24 | — | 0.25 | — |
| [Ru(6)/Cr(3)/Co(20)]12 | 0.29 | 0.55 | 0.29 | — | 0.21 | — |
| [Ru(6)/Cr(3)/Co(30)]12 | 0.26 | 0.76 | 0.18 | 0.14 | 0.16 | — |
| [Ru(6)/Cr(3)/Co(40)]12 | 0.14 | 0.80 | 0.13 | — | 0.15 | — |
| [Ru(6)/Cr(3)/Co(50)]12 | 0.13 | 0.89 | 0.12 | 0.34 | 0.12 | — |
For fields lower than 2Hex, the sample is unsaturated and the acoustic and optical resonances are expected at:4
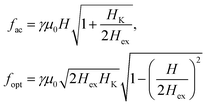 | (1) |
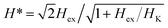 for which the frequencies of the optical and acoustic branches coincide. For fields H‖ > 2Hex the sample is saturated, and the acoustic resonance coincides with that of a single ferromagnetic layer
for which the frequencies of the optical and acoustic branches coincide. For fields H‖ > 2Hex the sample is saturated, and the acoustic resonance coincides with that of a single ferromagnetic layer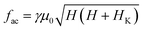 | (2) |
The FMR spectra are presented in Fig. 3. Using the H‖, H⊥ obtained from the VSM data we derive the parameters Hex and HK. Then using eqn (1) (with the frequencies set to the cavity frequency fc), the expected field values of the acoustic and optical FMR resonances (Hac, Hopt) can be calculated as:
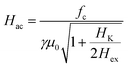 | (3a) |
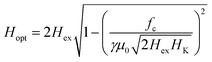 | (3b) |
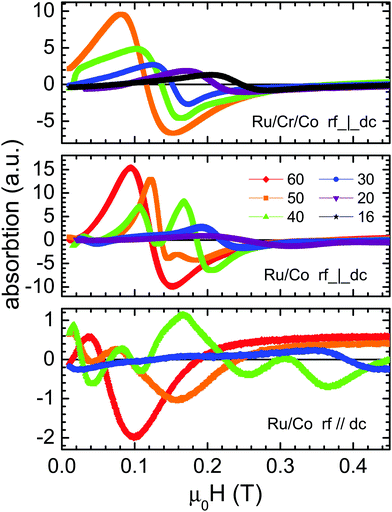 | ||
| Fig. 3 FMR spectra for different multilayers measured with the rf perpendicular/parallel to in-plane dc field. The numbers indicate the Cobalt layer thickness in Å. | ||
The application of an rf field perpendicular/parallel to the in-plane dc field favours the excitation of acoustic/optical modes respectively.4,23 Thus the Hac and Hopt should be compared to the experimentally observed FMR resonance fields Hres(⊥) and Hres(‖) obtained when rf⊥dc and rf‖dc respectively. For the acoustic resonances there is a fair agreement between the calculated values and those observed by FMR for γ = 32 GHz/T, a value which is close to that obtained for Pt/Co/W multilayers prepared under the same conditions.24 The [Ru(10)/Co(14)]12 sample did not give a measurable signal in the FMR. The expected frequency of the zero-field optical mode 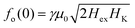 , which is interesting for applications, is between 17.4 and 20.1 GHz for the [Ru10/Cox)]12 series. For the [Ru6/Cr3/Cox)]12 series it takes lower values, ranging between 4 and 11.5 GHz. The FMR measurements with rf‖dc did not give resonances for any of the [Ru(6)/Cr(3)/Co(x)]12 samples. This can be partially attributed to the fact that for most of these samples fo(0) is below the rf frequency of the cavity and according to eqn (3b) cannot be observed:
, which is interesting for applications, is between 17.4 and 20.1 GHz for the [Ru10/Cox)]12 series. For the [Ru6/Cr3/Cox)]12 series it takes lower values, ranging between 4 and 11.5 GHz. The FMR measurements with rf‖dc did not give resonances for any of the [Ru(6)/Cr(3)/Co(x)]12 samples. This can be partially attributed to the fact that for most of these samples fo(0) is below the rf frequency of the cavity and according to eqn (3b) cannot be observed:
The [Ru(10)/Co(20)]12 samples gave resonances with rf‖dc but at frequencies which are lower than those of the expected pure optical modes. For [Ru(10)/Co(40)]12 the higher resonance is at a value 0.34 T, between the calculated Hac, Hopt whereas the second is very close to the Hac. Similarly, the [Ru(10)/Co(30)]12 sample resonance field value of 0.39 T lies between Hac and Hopt. For rf‖dc resonances below Hac appear. These findings can be qualitatively explained by hybridization of optical and acoustic modes, in accordance with the discussion of micromagnetic simulations’ results in the next section.
Micromagnetic simulations
The micromagnetic simulations have been done using the mumax3 package25 for a model system of 12 Co layers of thickness tCo = 25 Å, with antiferromagnetic interlayer coupling. Based on the magnetic measurements the saturation magnetization was set to MS = 1160 kA m−1 and the uniaxial anisotropy to Kmc = 460 kJ m−3 which represents a typical value for our samples. It is larger than the 290 kJ m−3 of the single Co layer due to the interfacial contributions. Note that these values are lower than the μ0M2S = 1690 kJ m−3 required for perpendicular anisotropy. Thus, the magnetization is easy-plane. The bulk intralayer exchange stiffness was set to Aex = 17 pJ m−1.26 The interfacial RKKY exchange was set to JAF = −0.5 mJ m−2 The cell size was set to 2.5 nm which is smaller than the characteristic exchange length scale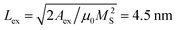 . The lateral simulation cell size was set to 320 nm × 320 nm. An array of 10 × 10 extra in-plane images was set, as pseudo-periodic boundary conditions, to better account for the demagnetizing field of thin film geometry.
. The lateral simulation cell size was set to 320 nm × 320 nm. An array of 10 × 10 extra in-plane images was set, as pseudo-periodic boundary conditions, to better account for the demagnetizing field of thin film geometry.
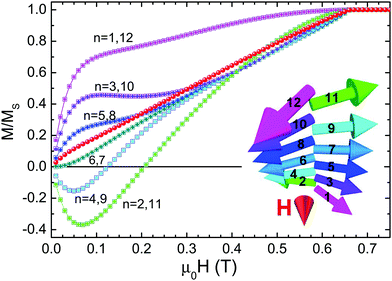
In Fig. 4 the total magnetization as a function of the applied field is shown for the multilayer and is compared with the curves for each of the constituent Co layers. The total magnetization increases linearly and reaches saturation at a value of 0.67 Tesla. This is exactly what is predicted by a two-macrospin model for which the saturation field should be μ0H‖ = μ02Hex = 4JAF/(MstCo). The factor 2 accounts for the fact that each layer is coupled on both sides. The fact that the two outer layers are not coupled on both sides does not seem to affect the response of the multilayer as a whole: It does not even lead to a reduction of (N − 1)/N = 11/12 (where N is the number of layers) as a simple linear scaling would suggest. To check this fact, we have also simulated N = 2,4 and 8. For N = 2 we get the expected value μ0H‖ = μ0Hex = 2JAF/(MstCo). For N = 4 we get 87% instead of 75% of 2Hex, and for N = 8 we already get 98.5% instead of 87.5% of the 2Hex. However, the lack of coupling of the outer layers (n = 1, 12 at Fig. 4) has a significant impact on their saturation which proceeds much faster that the average linear dependence. This forces their adjacent layers (n = 2, 11) to the opposite direction and so on, yielding the layer dependent approach to saturation sketched in Fig. 4. In short, at a specific applied external field the symmetry axis of the scissor state varies along the film thickness. Due to the symmetry the dependence of the n-th layer coincides with that of the (13-n)th.
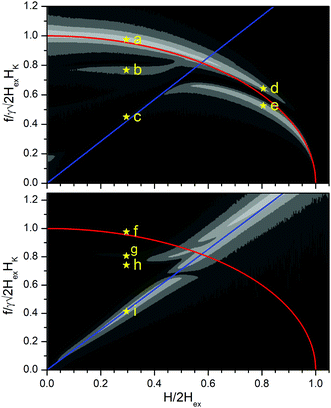 | ||
Fig. 5 Amplitude of FFT transform of the magnetization component along the exciting rf field as a function of frequency and dc field for a [Ru/Co)]12 SAF multilayer. The plotted quantity is 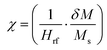 . The upper/lower panels are derived by setting the exciting rf field parallel/perpendicular to the magnetizing dc field respectively. The color map (between black and white) is not linear but corresponds to the values 03 × 10−3, 0.6 × 10−3, 1.2 × 10−3, 2.4 × 10−3, 4.8 × 10−3, 9.6 × 10−3 and 19.2 × 10−3. The frequencies predicted by the macrospin model (eqn (1) and (2)) are superimposed. A red curve is used for the optical mode and blue for the acoustic. The mode profiles at the points marked by the star symbols (a–i) are given in Fig. 6. . The upper/lower panels are derived by setting the exciting rf field parallel/perpendicular to the magnetizing dc field respectively. The color map (between black and white) is not linear but corresponds to the values 03 × 10−3, 0.6 × 10−3, 1.2 × 10−3, 2.4 × 10−3, 4.8 × 10−3, 9.6 × 10−3 and 19.2 × 10−3. The frequencies predicted by the macrospin model (eqn (1) and (2)) are superimposed. A red curve is used for the optical mode and blue for the acoustic. The mode profiles at the points marked by the star symbols (a–i) are given in Fig. 6. | ||
The resonance frequencies are extracted following the methods and considerations described in ref. 27 for each magnetic state (different dc field value H) along the saturation curve, an exciting external field having a time dependence following a sinc function, is applied and the resulting magnetic response is Fourier analysed. The sampling time step was set to 5 ps (frequencies up to 100 GHz) and the exciting field amplitude was μ0Hrf = 1 mT. The peaks of the Fourier transform correspond to the resonance modes. Setting the sinc pulse perpendicular/parallel to the dc field H (always in-plane) favours the excitation of acoustic/optical modes respectively.4 A 2D-contour map of the Fourier transform amplitude as a function of frequency and applied field is shown in Fig. 5. The plotted quantity is the amplitude of the variation of the magnetization component δM along the direction of Hrf divided by the Hrf amplitude 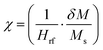 . The frequency is normalized to the value
. The frequency is normalized to the value 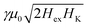 of the zero-field optical mode. The applied field is normalized to the saturation field against the AF exchange interlayer coupling which is equal to 2Hex. On the contour maps the frequencies predicted by eqn (1) and (2) are superimposed. The H* is the field at the point where the acoustic (blue) and optical (red) curves meet. Fig. 5 shows that at even low applied fields several modes of mixed character with frequencies between those of the acoustic and optical branches are exited. All modes can be characterized by the phase difference of the precession between the consecutive cobalt layers. In an ideal acoustic mode, the phase difference should be zero while for an ideal optical mode, it is expected to be 180 deg. Plots giving the phase difference between consecutive cobalt layers are shown in Fig. 6.
of the zero-field optical mode. The applied field is normalized to the saturation field against the AF exchange interlayer coupling which is equal to 2Hex. On the contour maps the frequencies predicted by eqn (1) and (2) are superimposed. The H* is the field at the point where the acoustic (blue) and optical (red) curves meet. Fig. 5 shows that at even low applied fields several modes of mixed character with frequencies between those of the acoustic and optical branches are exited. All modes can be characterized by the phase difference of the precession between the consecutive cobalt layers. In an ideal acoustic mode, the phase difference should be zero while for an ideal optical mode, it is expected to be 180 deg. Plots giving the phase difference between consecutive cobalt layers are shown in Fig. 6.
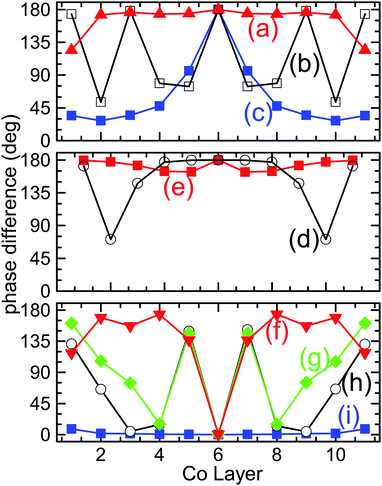 | ||
| Fig. 6 Mode profiles: The phase difference of the precessional motion between consecutive cobalt layers for the points marked by the star symbols (a–i) in Fig. 5. The X-axis denotes the number n of the layer and the y axis the phase difference between the n-th and the (n + 1)-th layer. The profile (a) is closer to a pure optical mode whereas the profile (i) is closer to a pure acoustic mode. The rest of the profiles indicate a mixed character. | ||
The modes with frequencies close to those predicted by the macrospin model (blue and red lines in Fig. 5) have profiles closer to what is expected for pure modes of either acoustic or optic character. Mode “(a)” has phase differences δφ close to 180 deg, except for the outer layers, for which δφ = 125 deg. Therefore, it is close to what is expected for an optical mode. Mode “(i)” has phase differences δφ close to zero, except for the outer layers for which δφ = 8 deg. Thus, it is close to what is expected for an acoustic mode. The rest of the modes have mixed character. The existence of these mixed resonances can explain the extra FMR peaks observed in some samples as well as the fact that their frequencies are lower than those expected by the simple macrospin model.
The micromagnetic simulation of Fig. 5 can serve as a basis to qualitatively understand the deviations of the optical modes from the expected values of the macrospin modes. For the [Ru10/Cox)]12 samples the values of 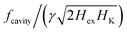 range between 0.48 to 0.56. In this region, there is a strong deviation between the predictions of the macrospin model and the exact micromagnetic model which gives a splitting of the optical mode. For a specific frequency (i.e. a specific horizontal line in Fig. 5) there will be two resonance fields: one below and one above the one predicted by the macrospin model (red curve). Of course, as each sample has its own parameters Hex, HK a different simulation should be done in each case using the sample specific parameters. For the [Ru10/Co40)]12 sample for instance the FMR rf‖dc the macrospin model predicts a peak at 0.41 Tesla, but the optical mode at 0.41 is split into two modes (0.35 Tesla and 0.43 Tesla), the lower of which coincides with the observed peak. The rf‖dc peak at 0.21 Tesla is close to the acoustic mode predicted at 0.19 Tesla. The peaks at fields lower than 0.1 Tesla are not predicted and could be attributed to domain effects which go beyond our micromagnetic model. In short, we claim that since the preferential excitation of either acoustic or optical modes depends on the orientation of the exciting field with respect to the magnetization direction, the variation of the magnetization profile along the multilayer thickness favours the emergence of mixed modes that can qualitatively explain the data. In contrast, if we simulate a simple SAF bilayer, which does not allow for any variation of the magnetization along its thickness, this mechanism of mixed mode creation ceases to work (Fig. 7).
range between 0.48 to 0.56. In this region, there is a strong deviation between the predictions of the macrospin model and the exact micromagnetic model which gives a splitting of the optical mode. For a specific frequency (i.e. a specific horizontal line in Fig. 5) there will be two resonance fields: one below and one above the one predicted by the macrospin model (red curve). Of course, as each sample has its own parameters Hex, HK a different simulation should be done in each case using the sample specific parameters. For the [Ru10/Co40)]12 sample for instance the FMR rf‖dc the macrospin model predicts a peak at 0.41 Tesla, but the optical mode at 0.41 is split into two modes (0.35 Tesla and 0.43 Tesla), the lower of which coincides with the observed peak. The rf‖dc peak at 0.21 Tesla is close to the acoustic mode predicted at 0.19 Tesla. The peaks at fields lower than 0.1 Tesla are not predicted and could be attributed to domain effects which go beyond our micromagnetic model. In short, we claim that since the preferential excitation of either acoustic or optical modes depends on the orientation of the exciting field with respect to the magnetization direction, the variation of the magnetization profile along the multilayer thickness favours the emergence of mixed modes that can qualitatively explain the data. In contrast, if we simulate a simple SAF bilayer, which does not allow for any variation of the magnetization along its thickness, this mechanism of mixed mode creation ceases to work (Fig. 7).
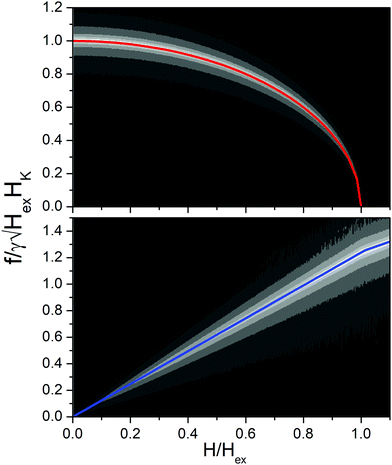 | ||
Fig. 7 Amplitude FFT transform of the magnetization component along the exiting rf field as a function of frequency and dc field for a [Ru/Co)]2 SAF bilayer. The plotted quantity is 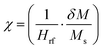 . The upper/lower panels are derived by setting the exciting rf field parallel/perpendicular to the magnetizing dc field respectively. The color map (between black and white) is not linear but corresponds to the values 1 × 10−3, 2 × 10−3, 4 × 10−3, 8 × 10−3, 12 × 10−3, and 16 × 10−3. The frequencies predicted by the macrospin model (eqn (1) and (2), but with 2Hex → Hex) are superimposed. A red curve is used for the optical mode and blue for the acoustic. . The upper/lower panels are derived by setting the exciting rf field parallel/perpendicular to the magnetizing dc field respectively. The color map (between black and white) is not linear but corresponds to the values 1 × 10−3, 2 × 10−3, 4 × 10−3, 8 × 10−3, 12 × 10−3, and 16 × 10−3. The frequencies predicted by the macrospin model (eqn (1) and (2), but with 2Hex → Hex) are superimposed. A red curve is used for the optical mode and blue for the acoustic. | ||
Conclusions
We have studied Ferromagnetic Resonance (FMR) in two series of [Ru10/Cox]12 and [Ru6/Cr3/Cox)]12, x = 16–60 Å, SAF-multilayers prepared by sputter deposition having easy-plane anisotropy and zero anisotropy within the plane.The resonance fields of the acoustic modes are in good agreement with the values predicted by macrospin models when using the interlayer exchange and anisotropy fields independently derived by the quasistatic (VSM) magnetic measurements. The optical modes are more interesting as they can give high frequencies at zero-applied field. However, to observe optical modes by cavity FMR, 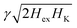 must exceed the resonance frequency of the cavity. For the [Ru6/Cr3/Cox)]12 series the values of anisotropy and exchange fields were low and the optical modes were not accessible. For the [Ru10/Cox]12 series the resonance fields of the optical modes are lower than expected. We attribute this to the existence of hybridized mixed modes as the resonances for these samples appear within the region where the optical modes are split. Although the micromagnetic simulations in Fig. 5 indicate that the hybridized modes can be observed for both rf⊥dc and rf‖dc we have experimentally observed only the latter. This may be attributed to the FMR signals for the acoustic modes being one order of magnitude greater. The existence of inhomogeneous modes that can be described as coupled acoustic and optical modes has been previously reported20,23 and gained renewed interest lately.4,5,19 The coupling mechanism is related to asymmetry due to obliquely applied external magnetic fields or of the sample itself. Since the preferential excitation of either acoustic or optical modes depends on the orientation of the exciting field with respect to the magnetization direction, the variation of the magnetization profile along the multilayer thickness, revealed by our micromagnetic simulations, implies the emergence of such hybridized modes. Thus, mode mixing is not limited to near the region where the frequencies of the optical and acoustic modes coincide.
must exceed the resonance frequency of the cavity. For the [Ru6/Cr3/Cox)]12 series the values of anisotropy and exchange fields were low and the optical modes were not accessible. For the [Ru10/Cox]12 series the resonance fields of the optical modes are lower than expected. We attribute this to the existence of hybridized mixed modes as the resonances for these samples appear within the region where the optical modes are split. Although the micromagnetic simulations in Fig. 5 indicate that the hybridized modes can be observed for both rf⊥dc and rf‖dc we have experimentally observed only the latter. This may be attributed to the FMR signals for the acoustic modes being one order of magnitude greater. The existence of inhomogeneous modes that can be described as coupled acoustic and optical modes has been previously reported20,23 and gained renewed interest lately.4,5,19 The coupling mechanism is related to asymmetry due to obliquely applied external magnetic fields or of the sample itself. Since the preferential excitation of either acoustic or optical modes depends on the orientation of the exciting field with respect to the magnetization direction, the variation of the magnetization profile along the multilayer thickness, revealed by our micromagnetic simulations, implies the emergence of such hybridized modes. Thus, mode mixing is not limited to near the region where the frequencies of the optical and acoustic modes coincide.
Conflicts of interest
There are no conficts to declare.Acknowledgements
The research work was supported by the Hellenic Foundation for Research and Innovation (HFRI) under the 3rd Call for HFRI PhD Fellowships (Fellowship Number: 5383).References
- D. E. Bürgler, in: Handbook of Magnetic Materials, ed., K. H. J. Buschow, 2001, 13 Search PubMed.
- A. Fert, Rev. Mod. Phys., 2008, 80, 1517–1530 CrossRef CAS.
- M. Ishibashi, Y. Shiota, T. Li, S. Funada, T. Moriyama and T. Ono, Sci. Adv., 2020, 6, eaaz6931 CrossRef CAS PubMed.
- A. Sud, C. W. Zollitsch, A. Kamimaki, T. Dion, S. Khan, S. Iihama, S. Mizukami and H. Kurebayashi, Phys. Rev. B, 2020, 102, 100403 CrossRef CAS.
- Y. Shiota, T. Taniguchi, M. Ishibashi, T. Moriyama and T. Ono, Phys. Rev. Lett., 2020, 125, 17203 CrossRef CAS PubMed.
- T. Seki, H. Tomita, A. A. Tulapurkar, M. Shiraishi and T. Shinjo, Appl. Phys. Lett., 2009, 94, 212505 CrossRef.
- B. Jianga, W. Zhanga, H. Zhonga, Y. Zhanga, S. Yua, G. Hana, S. Xiaoa, G. Liua, S. Yana, J. Lib and S. Kang, J. Magn. Magn. Mater., 2019, 490, 165470 CrossRef.
- R. Cheng, D. Xiao and A. Brataas, Phys. Rev. Lett., 2016, 116, 207603 CrossRef PubMed.
- P. Grünberg, R. Schreiber, Y. Pang, U. Walz, M. B. Brodsky and H. Sowers, J. Appl. Phys., 1987, 61, 3750–3752 CrossRef.
- R. A. Duine, K. J. Lee, S. S.-P. Parkin and M. D. Stiles, Nat. Phys., 2018, 14, 217–219 Search PubMed.
- H. J. Waring, N. A.-B. Johansson, I. J. Vera-Marun and T. Thomson, Phys. Rev. Appl., 2020, 13, 034035 Search PubMed.
- Y. Gong, Z. Cevher, M. Ebrahim, J. Lou, C. Pettiford, N. X. Sun and Y. H. Ren, J. Appl. Phys., 2009, 106, 063916 CrossRef.
- X. Xing, M. Liu, S. Li, O. Obi, J. Lou, Z. Zhou, B. Chen and N. X. Sun, IEEE Trans. Magn., 2011, 47, 3104–3107 CAS.
- R. B. Morgunov, A. V. Yurov, V. A. Yurov, A. D. Talantsev, A. I. Bezverhnii and O. V. Koplak, Phys. Rev. B, 2019, 100, 144407 CrossRef CAS.
- S. Li, Q. Li, J. Xu, S. Yan, G. X. Miao, S. Kang, Y. Dai, J. Jiao and Y. Lü, Adv. Funct. Mater., 2016, 26, 3738–3744 CrossRef CAS.
- S. Li, C. Wang, X. M. Chu, G. X. Miao, Q. Xue, W. Zou, M. Liu, J. Xu, Q. Li, Y. Dai, S. Yan, S. Kang, Y. Long and Y. Lü, Sci. Rep., 2016, 6, 33349 CrossRef CAS PubMed.
- A. Kamimaki, S. Iihama, T. Taniguchi and S. Mizukami, Appl. Phys. Lett., 2019, 115, 132402 CrossRef.
- P. Grünberg, R. Schreiber, Y. Pang, M. B. Brodsky and H. Sowers, Phys. Rev. Lett., 1986, 57, 2442 CrossRef PubMed.
- C. Dai and F. Ma, Appl. Phys. Lett., 2021, 118, 112405 CrossRef.
- Z. Zhang, L. Zhou, P. E. Wigen and K. Ounadjela, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6094 CrossRef CAS PubMed.
- H. Zabel, Philos. Mag. B, 2000, 80, 293–306 CrossRef CAS.
- See for instance §3.1 in D. E. Bürgler, P. Grünberg, S. O. Demokritov and M. T. Johnson, Handb. Magn. Mater., 2001, 13, 1–85 Search PubMed.
- N. M. Kreines, D. I. Kholin, V. F. Meshcheryakov, M. A. Milyaev, L. N. Romanshev and V. V. Ustinov, JETP Lett., 1998, 67(9), 727–732 CrossRef.
- I. Benguettat-El Mokhtari, A. Mourkas, P. Ntetsika, I. Panagiotopoulos, Y. Roussigné, S. M. Cherif, A. Stashkevich, F. Kail, L. Chahed and M. Belmeguenai, J. Appl. Phys., 2019, 126, 133902 CrossRef.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. V. Waeyenberge, AIP Adv., 2014, 4, 107133 CrossRef.
- X. Liu, M. M. Steiner, R. Sooryakumar, G. A. Prinz, R. F.-C. Farrow and G. Harp, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 12166 CrossRef CAS PubMed.
- D. Kumar and A. O. Adeyeye, J. Appl. Phys., 2017, 50, 343001 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |