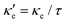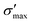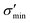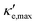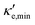Open Access Article
Open Access Article2D GeP3 and blue P: promising thermoelectric materials for room- and high-temperature applications†
Lucas Prett
Campagna
a,
Marcos
Veríssimo-Alves
a,
Debora C. M.
Rodrigues
 b,
Marcelo F. C.
Albuquerque Filho
b,
Pedro
Venezuela
b,
Wanderlã L.
Scopel
c and
Rodrigo G.
Amorim
b,
Marcelo F. C.
Albuquerque Filho
b,
Pedro
Venezuela
b,
Wanderlã L.
Scopel
c and
Rodrigo G.
Amorim
 *a
*a
aDepartamento de Física, ICEx, Universidade Federal Fluminense – UFF, Volta Redonda/RJ, Brazil. E-mail: rgamorim@id.uff.br
bInstituto de Física, Universidade Federal Fluminense – UFF, Niterói/RJ, Brazil
cDepartamento de Física, Universidade Federal do Espírito Santo – UFES, Vitória/ES, Brazil
First published on 23rd April 2022
Abstract
Thermoelectric materials have attracted great attention from the research community due to their capability to convert heat into electricity. Among these materials, two-dimensional (2D) systems are potential candidates for thermoelectric applications due to their unique electronic, mechanical and optical properties. In this work, we combine Density Functional Theory and Boltzmann Transport Equation (BTE) calculations to investigate the performance of 2D hexagonal Germanene (Ge), blue Phosphorene (blue P) and GeP3 as thermoelectric materials. The Seebeck (S), electric conductivity (σ) and thermal electronic conductivity (κe) are obtained with the SIESTA and BoltzTraP codes by means of a module especially developed for this aim in combination with the Spglib library, while the lattice thermal conductivity (κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) is obtained with the phono3py code. The studied materials have charge carrier concentrations close to 1018 cm−2, and blue P displays the largest electric figure of merit (ZTe ∼ 1.0), followed by GeP3 and Ge. Regarding the maximum ZTe for each of the investigated materials, we find that blue P has a central peak with ZT(blueP)e = 1.0 at T = 800 K, Germanene has a pronounced peak with ZT(Ge)e = 0.45 at T = 340 K and GeP3 has two such peaks, with
) is obtained with the phono3py code. The studied materials have charge carrier concentrations close to 1018 cm−2, and blue P displays the largest electric figure of merit (ZTe ∼ 1.0), followed by GeP3 and Ge. Regarding the maximum ZTe for each of the investigated materials, we find that blue P has a central peak with ZT(blueP)e = 1.0 at T = 800 K, Germanene has a pronounced peak with ZT(Ge)e = 0.45 at T = 340 K and GeP3 has two such peaks, with 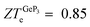 and 0.98 at T = 300 K and T = 10 K, respectively. For all three compounds, κ
and 0.98 at T = 300 K and T = 10 K, respectively. For all three compounds, κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (T) in the range T = 200–700 K decreases monotonically with increasing T, with ratios
(T) in the range T = 200–700 K decreases monotonically with increasing T, with ratios 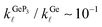 and
and 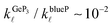 , indicating that the electronic contributions to ZTGeP3 establish its upper bound. Our findings suggest that GeP3 can be a promising room-temperature thermoelectric material if further tailoring of its electronic properties allow for an increase in ZTe.
, indicating that the electronic contributions to ZTGeP3 establish its upper bound. Our findings suggest that GeP3 can be a promising room-temperature thermoelectric material if further tailoring of its electronic properties allow for an increase in ZTe.
1 Introduction
A large amount of the energy generated globally is wasted due to thermal dissipation, in a scenario where the world's demand increases yearly. One alternative for reducing energy waste is to convert thermal energy into electricity. Thermoelectric materials are thus promising candidates for energy waste reduction due to their capability to convert heat into electricity. This type of material can be also be applied to convert electricity into heat. A measure of the conversion efficiency is the so-called figure of merit, ZT: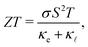 | (1) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) are the electronic and lattice contributions, respectively, to the total thermal conductivity, κ = κe + κ
are the electronic and lattice contributions, respectively, to the total thermal conductivity, κ = κe + κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . An initial indication of whether a candidate thermoelectric material merits further investigation as such is the electronic contribution to the figure of merit, ZTe:
. An initial indication of whether a candidate thermoelectric material merits further investigation as such is the electronic contribution to the figure of merit, ZTe: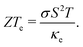 | (2) |
For applications, thermoelectric materials must have ZT > 1 and while few naturally exhibit such large ZT, it is possible to engineer the electronic and structural properties of materials to specifically increase it. In particular, the groundbreaking proposal that dimensionality reduction would increase ZT due to quantum confinement effects,1 contributed to a renewed interest in the field, which was further intensified with the synthesis of different 2D materials. A recent review by Ouyang et al2 shows new possibilities for improving thermoelectric performance. Some of the mechanisms listed by the authors to tune the thermoelectric properties of 2D materials are: (i) carrier doping, for semiconducting materials; (ii) an increase in the number of layers, which in some cases, such as GeP3, can lead to an insulator-metal transition, (iii) bandgap tuning by application of strain and (iv) suppression of phonon modes by defects. Other exciting possibilities are the exploitation of phonon coherence and of the effects of topological properties of materials on electrons and phonons.
Snyder et al.3 discussed the way to maximize ZT in semiconductors, where for viable applications the carrier concentrations should be in the range of 1018–1021 cm−3. However, as highlighted by Wu et al.,4 for wide bandgap semiconductors such carrier densities are hard to attain, since it is very difficult to dope them. However, for heavily doped narrow bandgap semiconductors, the parameters involved in the expression for ZT – the Seebeck coefficient S, the electric conductivity σ and the thermal conductivity κ – are strongly interdependent.
Since experimental graphene exfoliation,5 different 2D materials have been explored and successfully synthesized such as Phosphorene,6,7 Silicene,8–10 h-BN,11–13 Germanene,14–16 Borophene,17,18 GeP3,19 and also 2D hybrid materials Graphene/h-BN20–22 and MoS2.23,24 Monolayers of chalcogenide materials such as GaS, GaSe, and GaTe, semiconductors with indirect bandgap,25 have already been successfully synthesized on different substrates and their thermoelectric properties have been thoroughly studied. They presented high values of ZT for temperatures below room temperature.
Applications of thermoelectric materials can be devised for many temperature conditions, but a significant impact will be attained for those with high ZT at room temperature, which will allow for energy conversion by many sources of ordinary, daily usage. Moreover, its constituent elements should be environmentally friendly and preferably lightweight. Germanene (Ge), and GeP3, materials with similar hexagonal lattices, are potentially promising 2D materials for thermoelectric applications at room temperature. Phosphorene (P), another promising 2D thermoelectric material, has three allotropes, the most stable of which is hexagonal blue P, with a lattice similar to those of Ge and GeP3. All three materials are made of reasonably lightweight chemical elements of low toxicity.
The large 2 eV bandgap and structural stability of blue P make it particularly suitable for high-voltage and high-temperature applications, which led to several studies focusing on its thermoelectric properties. Jain and Alan predicted the thermal conductivity of blue P to be 78 W m−1 K−1 at 300 K and isotropic, decreasing under bi-axial stress.26 Liao et al.27 explored the effect of electron–phonon coupling on blue P's thermoelectric properties, showing that the power factor is maximum at 200 K, with half of the value of black P. They ascribed it to the larger bandgap of blue P and stronger electron–phonon scattering rates compared to black P. Hu et al.28 studied the thermoelectric properties of black/blue P vertical heterostructures, showing that the reduction of the thermal conductivity associated to van der Waals interaction results in enhanced thermoelectric performance when compared to their monolayer counterparts.
Germanene (Ge), proposed theoretically by Ciraci et al.29 in 2009, has both a high-buckled (HB) and low-buckling (LB) structure, c. van der Waals multilayer germanene was synthesized by Bianco et al.,30 where they claim that single- or few-layer Ge may be obtained by mechanical exfoliation. They also synthesized hydrogen-terminated germanium (GeH), where it was demonstrated that this material is stable up to 348 K and presents slow oxidation under air exposure. Regarding the thermoelectric properties of Ge, Yang et al.31 estimated the upper limit of the figure of merit as ZTe = 0.41, at room temperature. Peng et al.32 obtained a thermal conductivity κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 2.4 W m−1 K−1 for Ge at 300 K, decreasing monotonically with increasing temperature.
= 2.4 W m−1 K−1 for Ge at 300 K, decreasing monotonically with increasing temperature.
The bulk phase of GeP333 is known since 1970, but only recently its 2D monolayer structure was proposed.19 The monolayer phase is semiconducting due to the strong quantum electronic confinement, with a predicted 0.55 eV bandgap. The lower bandgap, in comparison to that of blue P, suggests that it would be more suitable for milder conditions of voltage and temperature, closer to room temperature. Besides GeP3, the existence of other 2D mono-layered triphosphide materials has been theoretically predicted, such as InP334 and SnP3.35 Very recently, Sun et al.36 have investigated the thermoelectric properties of InP3, GaP3, SbP3 and SnP3 monolayers, predicting high Seebeck coefficients and low thermal conductivities.
In this work, we perform Density Functional Theory (DFT) and Boltzmann Transport Equation (BTE) calculations to explore the thermoelectric properties of 2D hexagonal Ge, GeP3 and blue P. For each of these materials, the Seebeck coefficient S, the electronic conductivity σ and electronic and lattice thermal conductivities, κe and κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , respectively, are obtained as a function of the temperature T. With these quantities for each studied system, the figure of merit ZT is explored for different operation temperatures, investigating the role of κ
, respectively, are obtained as a function of the temperature T. With these quantities for each studied system, the figure of merit ZT is explored for different operation temperatures, investigating the role of κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) in the values of ZT particularly.
in the values of ZT particularly.
2 Methodology
We used an ab initio total energy method based on DFT,37,38 as deployed in the SIESTA39 and Quantum Espresso40 codes, for the electronic structure calculations. Thermoelectric properties are calculated using the BTE as implemented in the BoltzTraP code.41 Since the two codes (DFT and BTE) are independent, we developed a SIESTA module to link them. Details on how to incorporate the module to SIESTA, compilation flags and code validation are discussed in the ESI.† The DFT calculations were performed with the Generalized Gradients Approximation of Perdew, Burke and Ernzerhof (GGA-PBE),42 norm-conserving Troullier–Martins pseudopotentials,43 a double-ζ basis set including polarization orbitals (DZP), and the Brillouin Zone (BZ) is sampled according to the Monkhorst–Pack (MP) method.44 The optimal values for the mesh cutoff and MP sampling grid are 300 Ry and (8 × 8 × 1), respectively. For structural relaxations, the residual force components for each atom are lower than 0.001 eV Å−1.The lattice thermal conductivity (κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) was calculated using a full solution of the linearized phonon Boltzman equation (LBTE), as implemented in PHONO3PY code.45,46 A supercell of 6 × 6 × 1(2 × 2 × 1) was employed for Germanene and Phosphorene (GeP3) with 19 × 19 × 1 q-point sampling meshes. For the supercell approach, the second- and third-order force constant models were calculated with finite displacements of 0.03 Å.
) was calculated using a full solution of the linearized phonon Boltzman equation (LBTE), as implemented in PHONO3PY code.45,46 A supercell of 6 × 6 × 1(2 × 2 × 1) was employed for Germanene and Phosphorene (GeP3) with 19 × 19 × 1 q-point sampling meshes. For the supercell approach, the second- and third-order force constant models were calculated with finite displacements of 0.03 Å.
3 Results
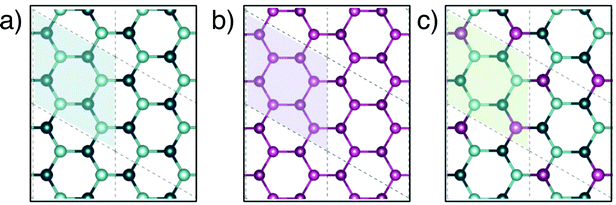
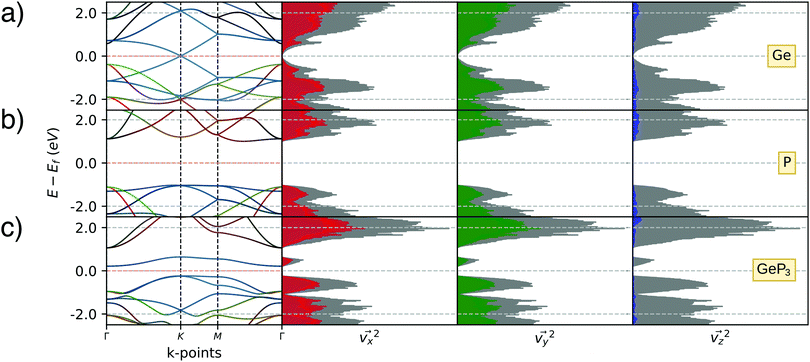
Fig. 1a–c present top views of the fully relaxed 2D geometries for Ge, blue P and GeP3, respectively. Since the unit cell for GeP3 contains 8 atoms, we use 2 × 2 supercells for Ge and blue P, to have the same number of the atoms for each material. Structural parameters for Ge, GeP3 and blue P are shown in Table 1. Our results are in good agreement with previously published results, with a maximum deviation of in-plane lattice parameter of 1.75% for Ge. All structures are buckled with overall good agreement for the buckling parameter δ, but a sizeable 5% deviation for bond lengths can be seen in GeP3.Fig. 2 shows the band structures projected over p-orbitals and their respective distributions of squared electronic group velocity for monolayer Ge, GeP3 and blue P. Monolayer Ge (Fig. 2a) has semi-metallic character with a Dirac cone at the K point of the Brillouin zone, which is associated with pz orbitals as reported in the literature.47 Blue P (Fig. 2c) is a semiconductor character with an indirect bandgap of 2.00 eV, in agreement with the results of Zhu et al.49 The valence band maximum (VBM) and conduction band minimum (CBM) have predominant σ (px and py) and π (pz) orbitals, respectively. Monolayer GeP3 (Fig. 2b) is a semiconductor with a 0.45 eV indirect bandgap and the VBM and CBM are ascribed to pz orbitals of the Ge atoms, in agreement with results from Jing et al.19 Regarding thermoelectric properties, Fig. 2a–c (right panels) shows that the greatest contribution to v2(k) is given by the x and y components in essentially similar amounts, while the z contribution is negligible. This is consistent with the fact that electrons are confined to the basal plane of the material, where electronic and thermal conduction will take place.
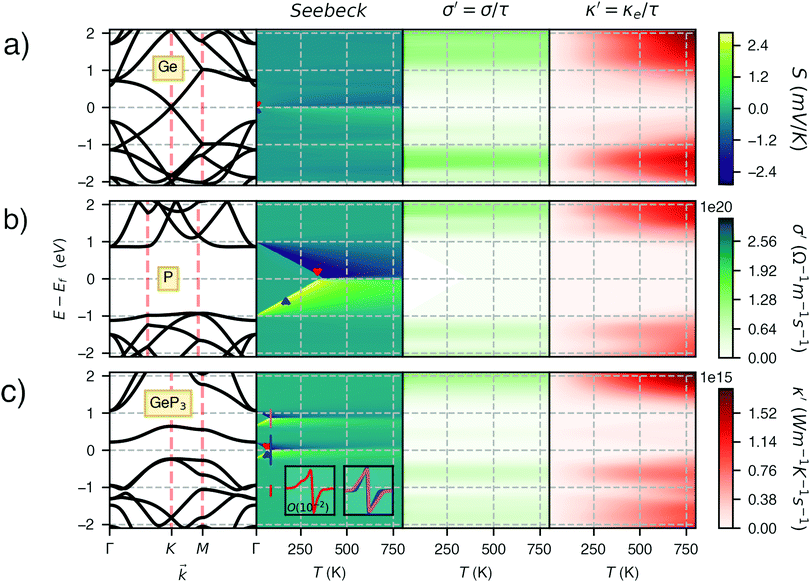
Fig. 3 shows heat maps for the Seebeck coefficient (S), for the scaled electric conductivity σ′ = σ/τ and for the electronic thermal conductivity 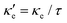 , where τ is the electronic scattering time, for each investigated material in the range −2.0< E–Ef < +2.0. For Ge (Fig. 3a), the values of S are very small throughout the whole temperature range, and at 10 K the maximum and minimum values are +0.852 and −0.685 mV K−1, respectively. The positive sign of S in the region E–Ef < 0.0 eV indicates electrical transport by holes, while the negative sign in the region E–Ef > 0.0 eV indicates that carriers are electrons. At 300 K, our calculations yield S = ±0.14 mV K−1 around EF, which is consistent with previously published works.31 In the energy range −1.0< E–Ef < + 1.0 eV, σ′(T) and
, where τ is the electronic scattering time, for each investigated material in the range −2.0< E–Ef < +2.0. For Ge (Fig. 3a), the values of S are very small throughout the whole temperature range, and at 10 K the maximum and minimum values are +0.852 and −0.685 mV K−1, respectively. The positive sign of S in the region E–Ef < 0.0 eV indicates electrical transport by holes, while the negative sign in the region E–Ef > 0.0 eV indicates that carriers are electrons. At 300 K, our calculations yield S = ±0.14 mV K−1 around EF, which is consistent with previously published works.31 In the energy range −1.0< E–Ef < + 1.0 eV, σ′(T) and 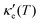 have smaller values in comparison to the rest of the energy range considered. From the graph it can also be inferred that
have smaller values in comparison to the rest of the energy range considered. From the graph it can also be inferred that 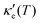 increases with T, consistent with the results of Chegel et al.51
increases with T, consistent with the results of Chegel et al.51
At 10 K, blue P has negligible S(E–Ef) values over the energy range −2.0 < E–Ef < 2.0 eV except at E–Ef = ±1.0 eV, as seen in Fig. 3b. Interestingly, these energy values coincide with the CBM and VBM energies, and with the small spread of S(E–Ef) at 10 K, we can infer that S(E–Ef) is a sharp peak. For 10 ≤ T ≤ 340 K, the peaks in S(E–Ef) broaden, displaying a sharp edge followed by a slower decay (in absolute value) as one moves towards higher or lower energies, and negligible values between the peak edges. With increasing T, the distance between these edges decreases in an approximate linear fashion up to T ∼ 340 K and the broadening of the S(E–Ef) peaks increases; on the other hand, S(E–Ef) varies differently for positive and negative E–Ef. In the E–Ef range between the sharp edges, both σ′ and 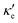 have negligible values, in agreement with the results of ref. 27, and increase outside this energy range.
have negligible values, in agreement with the results of ref. 27, and increase outside this energy range.
GeP3, whose properties are displayed in Fig. 3c, displays a richer behavior, similar in some aspects to that of blue P, but with important differences. At T = 10 K, as in the case of blue P, very narrow peaks in S(E–Ef) appear at the energies corresponding to band energy extrema, in the energy range −0.25 < E–Ef < 1.00 eV. However, the presence of an isolated conduction band with relatively low dispersion gives rise to two pairs of peaks in S(E–Ef), all of them with a much narrower broadening than those of blue P. The positive peaks are located at the VBM and the maximum of the first CB, while the negative ones are located at the minima of the first and second CB. For increasing T up to 70 K, the distance between adjacent peaks in GeP3 decreases in an approximately linear fashion, in a similar way to blue P, and remains essentially constant for higher temperatures. For completeness, we mention that there is actually a third pair of peaks in S(E–Ef); however, they occur at E ≤ −1.0 eV, and are approximately two orders of magnitude less intense than the other peaks. Table 2 summarizes the maximum and minimum values of S, σ′ and 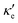 , along with the values at which they occur.
, along with the values at which they occur.
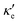 (W m−1 K−1 s−1). Numbers in parenthesis are the temperature T (K) at which they occur
(W m−1 K−1 s−1). Numbers in parenthesis are the temperature T (K) at which they occur
For good thermoelectric performance, the material's power factor, PF = σS2, should be maximized and the electrical thermal conductivity, κe, minimized. This is a difficult task, however, since high values of σ, in general, imply large κe. Fig. 4 shows ZTe as a function of charge carrier density n for 200 ≤ T ≤ 700 K for Germanene, blue P and GeP3. For Ge (Fig. 4a), two main peaks around n = 0 and three smaller ones are observed for higher n. The main peaks broaden and slightly displace towards higher energies with increasing T. The value of ZTe at 300 K is in agreement with previously published work.31
 | ||
| Fig. 4 The electronic figure of merit at different temperatures for: (a) germanene, (b) blue P and (c) GeP3. | ||
For blue P (Fig. 4b), the curves for ZTe (T) are very different from those for Ge. Near room temperatures (200–300 K), ZTe displays a peak with value 1 at n = 0, indicating that maximization of ZTe in this temperature range would not require any doping. At T ≥ 300 K, however, ZTe drops to zero, rising sharply for minimal values of electron (n < 0) or hole (n > 0) doping, broadening with rising T. Thus, our results suggest that blue P would still be a good thermoelectric material in a broad range of T with a minimal amount of electron doping.
In turn, the ZTe curves of GeP3 (Fig. 4c) display a behaviour intermediate to those of Ge and blue P. First, we note that ZTe now displays two intense pairs of peaks, reflecting that S(E–Ef) is large for two different energy ranges. Remarkably, while ZTe shows sharp drops to zero at all values of T, it would not require any doping for its maximization, since the first drop occur at values slightly below n = 0. As T rises, the peaks broaden as for blue P, with a small decrease in their maximum values.
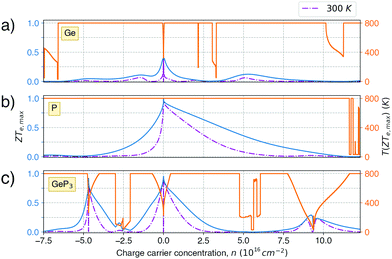
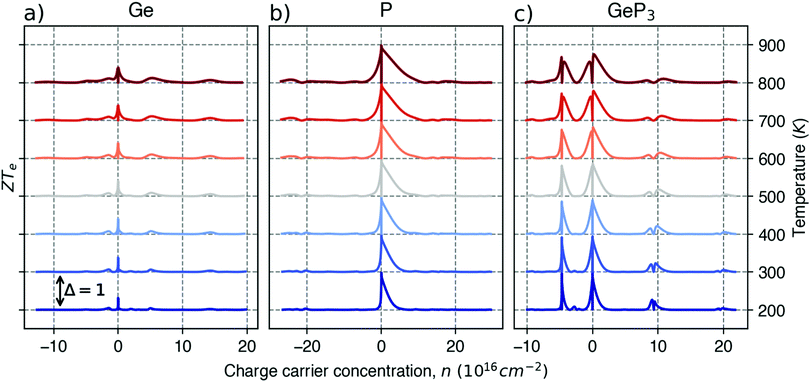
Fig. 5 shows the maximum value of ZTe, ZTe,max (left y-axis, blue) and the temperature T at which it occurs (right y-axis, orange) as a function of the excess carrier concentration n, for the three materials studied. It also shows ZTe,max for a fixed temperature of 300 K (purple dash-dotted line), for considerations on room-temperature performance. From this figure, we can infer the temperatures at which the material presents a maximum in ZTe,max and the amount of n- or p-doping required to achieve it, thus serving as an aid in tailoring the material for obtaining maximum thermoelectric performance. In the analysis that follows, we shall refer to the temperatures at which the maxima of ZTe,max occur as working temperatures (Tw) of the three materials studied. The amount of doping, n, will be given in units of 1018 carriers cm−2 and Tw will be given in K. Table 3 lists the above mentioned values.
| ZT e,max | n (1016 cm−2) | T (K) | T w (K) | ZT (T=300K)e | n (1016 cm−2) | |
|---|---|---|---|---|---|---|
| Ge | 0.05 | −4.7 | 800 | 325 | 0.01 | −4.9 |
| 0.11 | −1.4 | 800 | 0.07 | −1.5 | ||
| 0.40 | 0.0 | 325 | 0.38 | 0.0 | ||
| — | — | — | 0.02 | 1.8 | ||
| 0.12 | 5.3 | 800 | 0.06 | 5.1 | ||
| P | 0.03 | −7.2 | 800 | 800 | 0.01 | −6.7 |
| 1.00 | 0.0 | 800 | 0.92 | 0.0 | ||
| — | — | — | 0.02 | 9.3 | ||
| GeP3 | 0.90 | −4.7 | 270 | 300 | 0.74 | −4.7 |
| 0.16 | −2.8 | 94 | 0.28 | −4.7 | ||
| 0.95 | 0.0 | 229 | 0.84 | 0.1 | ||
| 0.29 | 9.2 | 112 | 0.20 | 9.0 | ||
| 0.23 | 9.6 | 265 | 0.23 | 9.6 | ||
ZT (Ge)e,max(n,T) displays four broad peaks. Despite having Tw at room temperature ranges, it indicates that Ge will perform poorly as a thermoelectric material at all temperatures, even if spurious doping happens, for range 200–800 K since ZT(Ge)e,max at Tw is well below 1. In contrast, peaks in ZT(P)e,max (Fig. 5b) occur mostly at T = 800 K for all carrier concentrations, except at n ≥ 11.5, and the ZT(P)e(n,T) curve displays a broad cusp shape and two others where ZT(P)e(n,T) is close to zero. Although blue P has a high Tw, which could affect n significantly, the cusp is very broad, suggesting it could have acceptable thermoelectric performance even if spurious doping should happen. While T(P)w = 800 K, the data in Table 3 show an acceptable value for ZTe at T = 300 K, and from Fig. 5b it can be inferred that blue P could also perform almost equally well in thermoelectric devices at this temperature.
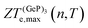 , in turn, displays a complex behaviour, with two broad cusp-shaped peaks of potential interest for thermoelectric applications, and a second pair of broader, but lower, pair of peaks occurring at high values of n. Table 3 shows that GeP3 will not be able to operate optimally at room temperature, since these two values of
, in turn, displays a complex behaviour, with two broad cusp-shaped peaks of potential interest for thermoelectric applications, and a second pair of broader, but lower, pair of peaks occurring at high values of n. Table 3 shows that GeP3 will not be able to operate optimally at room temperature, since these two values of 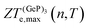 occur well below it. However, the values of ZTe (n = 0, T = 300 K) are comparable to those for blue P. In particular,
occur well below it. However, the values of ZTe (n = 0, T = 300 K) are comparable to those for blue P. In particular, 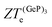 (n = 0, T = 300 K) is only 9% lower than that of blue P at the same temperature. As remarked earlier, ZTe is at best a first indicator of thermoelectric performance. In actual applications, lattice vibrations are likely to have a non-negligible contribution, and it must be explicitly considered. Using eqn (2), eqn (1) can be rewritten as
(n = 0, T = 300 K) is only 9% lower than that of blue P at the same temperature. As remarked earlier, ZTe is at best a first indicator of thermoelectric performance. In actual applications, lattice vibrations are likely to have a non-negligible contribution, and it must be explicitly considered. Using eqn (2), eqn (1) can be rewritten as
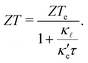 | (3) |
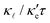 , the better the thermoelectric performance.
, the better the thermoelectric performance.
To estimate the contribution of the lattice thermal conductivity, we have calculated κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (T) in the range 200–800 K, shown in Fig. 6. Table 4 summarizes our calculated values of
(T) in the range 200–800 K, shown in Fig. 6. Table 4 summarizes our calculated values of 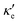 and κ
and κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , along with relaxation times τ, averaged for the zigzag and armchair directions,52–54 and the calculated total ZT at T = 300 K, for electron and hole transport. In ref. 52–54, the authors determine the scattering times in the deformation potential approximation, and therefore they do not consider the polar optical phonon contribution to the conductivities. Within this approximation, Table 4 clearly shows that GeP3 has superior thermal lattice properties, when compared to blue P; the latter, however, has lower scattering times. Therefore, both GeP3 and blue P have comparable ZT(el,h) values, with a slightly higher value for hole transport in blue P. Since T(P)w is 800 K, it will display peak performance at high-temperature applications, although it would also have comparable (but slightly lower) performance for room-temperature applications. In turn, GeP3 would perform better in room-temperature applications, given its Tw = 300 K.
, along with relaxation times τ, averaged for the zigzag and armchair directions,52–54 and the calculated total ZT at T = 300 K, for electron and hole transport. In ref. 52–54, the authors determine the scattering times in the deformation potential approximation, and therefore they do not consider the polar optical phonon contribution to the conductivities. Within this approximation, Table 4 clearly shows that GeP3 has superior thermal lattice properties, when compared to blue P; the latter, however, has lower scattering times. Therefore, both GeP3 and blue P have comparable ZT(el,h) values, with a slightly higher value for hole transport in blue P. Since T(P)w is 800 K, it will display peak performance at high-temperature applications, although it would also have comparable (but slightly lower) performance for room-temperature applications. In turn, GeP3 would perform better in room-temperature applications, given its Tw = 300 K.
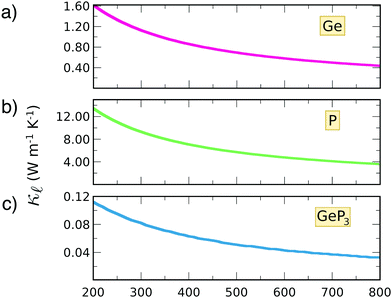 | ||
| Fig. 6 Thermal conductivity as a function of temperature for (a) germanene; (b) blue P and (c) GeP3. | ||
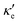 and κ
and κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , relaxation times for electron and hole transport averaged for zigzag and armchair directions (taken from ref. 52 for Ge, ref. 53 for P and ref. 54 for GeP3), for all three materials studied at T = 300 K. Thermal lattice conductivities are given in W m−1 K−1, thermal electronic conductivities are in units of 1013 and relaxation times are given in ps
, relaxation times for electron and hole transport averaged for zigzag and armchair directions (taken from ref. 52 for Ge, ref. 53 for P and ref. 54 for GeP3), for all three materials studied at T = 300 K. Thermal lattice conductivities are given in W m−1 K−1, thermal electronic conductivities are in units of 1013 and relaxation times are given in ps
4 Conclusions
We have combined DFT and Boltzmann Transport Equation calculations to explore the thermal properties of 2D Ge, blue P and GeP3. This combination was possible by the development of a module for the SIESTA code using the Spglib library to output the calculation results in a format suitable for post-processing with BoltzTraP. A GitHub link for downloading the module code, along with instructions and compilation flags for incorporation in SIESTA, are provided in the ESI.†Our electronic structure results suggest that 2D Ge is metallic, while blue P and GeP3 are semiconductors, with a literature good agreement. Optimal charge carrier concentrations for thermoelectric operation are in the range 1016 cm−2 for all three materials. Our calculations also show that GeP3 has the lowest κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) in the temperature range T = 200–800 K, and Ge and blue P have κ
in the temperature range T = 200–800 K, and Ge and blue P have κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) one and two orders of magnitude higher, respectively, in the same temperature range.
one and two orders of magnitude higher, respectively, in the same temperature range.
ZT
(Ge)e,max displays many broad peaks for a wide range of excess charge carrier concentrations n. However, as expected for a metallic material, all peaks are much lower than 1, which implies that Ge is unsuitable for thermoelectric applications. ZT(P)e,max displays one broad but pronounced peak at n ≈ 0 and T = 800 K, being only slightly below 1 at T = 300 K. 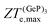 , on the other hand, presents two broad peaks at n = 0 and n = −4.7 × 1016 carriers cm−2 for T = 229 and 270 K, respectively, being also slightly under 1 for these values of n and T. Nevertheless, at T = 300 K and n = 0.1 × 1016 carriers cm−2,
, on the other hand, presents two broad peaks at n = 0 and n = −4.7 × 1016 carriers cm−2 for T = 229 and 270 K, respectively, being also slightly under 1 for these values of n and T. Nevertheless, at T = 300 K and n = 0.1 × 1016 carriers cm−2, 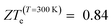 .
.
An interesting feature suggested by our calculations is that the dominant part of ZT for GeP3 and blue P is electronic: despite having κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) differing by three orders of magnitude, κe ≪ κ
differing by three orders of magnitude, κe ≪ κ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) for both materials and, as suggested by eqn (3), ZT is reduced essentially to ZTe. Therefore, there could be room for further improvement of ZTe for both GeP3 and blue P through strain and defect engineering. The effects of strain on
for both materials and, as suggested by eqn (3), ZT is reduced essentially to ZTe. Therefore, there could be room for further improvement of ZTe for both GeP3 and blue P through strain and defect engineering. The effects of strain on 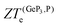 will be the subject of a future publication.
will be the subject of a future publication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Brazilian agencies CAPES, CNPq, FAPES and the LNCC (SCAFMat2), CENAPAD-SP for computer time. WLS and RGA thank for financial support from CNPq (301648/2017-4 and 421227/2018-4) and (2535/2017-1, 437182/2018-5 and 313076/2020-0), respectively. RGA also acknowledge financial support from FAPERJ grant numbers E-26/010.101126/2018, E-26/210.077/2022 and E-26/202.699/2019. DCMR also thank FAPERJ grant numbers E-26/202.085/2020 and E-26/202.086/2020. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001.Notes and references
- L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 12727–12731 CrossRef CAS PubMed.
- Y. Ouyang, Z. Zhang, D. Li, J. Chen and G. Zhang, Ann. Phys., 2019, 531, 1800437 CrossRef CAS.
- G. J. Snyder and E. S. Toberer, Materials for sustainable energy: a collection of peer-reviewed research and review articles from Nature Publishing Group, 2011, pp. 101–110 Search PubMed.
- J. Wu, Y. Chen, J. Wu and K. Hippalgaonkar, Adv. Electron. Mater., 2018, 4, 1800248 CrossRef.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-E. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- R. N. Pedrosa, R. G. Amorim and W. L. Scopel, Nanotechnology, 2020, 31, 275201 CrossRef CAS PubMed.
- S. Cahangirov, M. Topsakal, E. Aktürk, H. S. Ahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804 CrossRef CAS PubMed.
- P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501 CrossRef PubMed.
- R. G. Amorim and R. H. Scheicher, Nanotechnology, 2015, 26, 154002 CrossRef PubMed.
- K. K. Kim, A. Hsu, X. Jia, S. M. Kim, Y. Shi, M. Hofmann, D. Nezich, J. F. Rodriguez-Nieva, M. Dresselhaus, T. Palacios and J. Kong, Nano Lett., 2012, 12, 161–166 CrossRef PubMed.
- M. S. Bresnehan, G. R. Bhimanapati, K. Wang, D. W. Snyder and J. A. Robinson, ACS Appl. Mater. Interfaces, 2014, 6, 16755–16762 CrossRef CAS PubMed.
- X. Chen, J. F. Dobson and C. L. Raston, Chem. Commun., 2012, 48, 3703–3705 RSC.
- S. Jiang, S. Butler, E. Bianco, O. D. Restrepo, W. Windl and J. E. Goldberger, Nat. Commun., 2014, 5, 3389 CrossRef PubMed.
- E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 4414–4421 CrossRef CAS PubMed.
- M. E. Dávila and G. Le Lay, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- G. Silvestre, W. L. Scopel and R. Miwa, Nanoscale, 2019, 11, 17894–17903 RSC.
- T. L. G. Cabral, L. T. S. De Miranda, D. C. de Melo Rodrigues, F. A. de Souza, W. L. Scopel and R. G. Amorim, J. Phys.: Condens. Matter, 2021, 34, 095502 CrossRef PubMed.
- Y. Jing, Y. Ma, Y. Li and T. Heine, Nano Lett., 2017, 17, 1833–1838 CrossRef CAS PubMed.
- G. Lu, T. Wu, P. Yang, Y. Yang, Z. Jin, W. Chen, S. Jia, H. Wang, G. Zhang and J. Sun, et al. , Adv. Sci., 2017, 4, 1700076 CrossRef PubMed.
- F. A. De Souza, R. G. Amorim, W. L. Scopel and R. H. Scheicher, Nanotechnology, 2016, 27, 365503 CrossRef PubMed.
- F. A. L. de Souza, G. Sivaraman, J. Hertkorn, R. G. Amorim, M. Fyta and W. L. Scopel, J. Mater. Chem. A, 2019, 7, 8905–8911 RSC.
- G. Sivaraman, F. A. de Souza, R. G. Amorim, W. L. Scopel, M. Fyta and R. H. Scheicher, J. Phys. Chem. C, 2016, 120, 23389–23396 CrossRef CAS.
- A. Perez, R. G. Amorim, C. E. P. Villegas and A. R. Rocha, Phys. Chem. Chem. Phys., 2020, 22, 27053–27059 RSC.
- B. P. Bahuguna, L. Saini, R. O. Sharma and B. Tiwari, Phys. Chem. Chem. Phys., 2018, 20, 28575–28582 RSC.
- A. Jain and A. J. McGaughey, Sci. Rep., 2015, 5, 1–5 Search PubMed.
- Z. Liu, J. Morales-Ferreiro and T. Luo, Appl. Phys. Lett., 2018, 113, 063903 CrossRef.
- R. Hu, Z. Zhou, C. Sheng, L. Wang, J. Liu, S. Han and H. Liu, Phys. Chem. Chem. Phys., 2020, 22, 22390–22398 RSC.
- S. Cahangirov, M. Topsakal, E. Aktürk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804 CrossRef CAS PubMed.
- E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 4414–4421 CrossRef CAS PubMed.
- K. Yang, S. Cahangirov, A. Cantarero, A. Rubio and R. D'Agosta, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 125403 CrossRef.
- B. Peng, H. Zhang, H. Shao, Y. Xu, G. Ni, R. Zhang and H. Zhu, Phys. Rev. B, 2016, 94, 245420 CrossRef.
- P. Donohue and H. Young, J. Solid State Chem., 1970, 1, 143–149 CrossRef CAS.
- N. Miao, B. Xu, N. C. Bristowe, J. Zhou and Z. Sun, J. Am. Chem. Soc., 2017, 139, 11125–11131 CrossRef CAS PubMed.
- S. Sun, F. Meng, H. Wang, H. Wang and Y. Ni, J. Mater. Chem. A, 2018, 6, 11890–11897 RSC.
- Z. Sun, K. Yuan, Z. Chang, S. Bi, X. Zhang and D. Tang, Nanoscale, 2020, 12, 3330–3342 RSC.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- K. Mizokami, A. Togo and I. Tanaka, Phys. Rev. B, 2018, 97, 224306 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- S. J. Zaveh, M. Roknabadi, T. Morshedloo and M. Modarresi, Superlattices Microstruct., 2016, 91, 383–390 CrossRef.
- M. Derivaz, D. Dentel, R. Stephan, M.-C. Hanf, A. Mehdaoui, P. Sonnet and C. Pirri, Nano Lett., 2015, 15, 2510–2516 CrossRef CAS PubMed.
- Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802 CrossRef PubMed.
- W. Zhang, H. Enriquez, Y. Tong, A. Bendounan, A. Kara, A. P. Seitsonen, A. J. Mayne, G. Dujardin and H. Oughaddou, Small, 2018, 14, 1804066 CrossRef PubMed.
- R. Chegel and S. Behzad, Sci. Rep., 2020, 10, 1–12 CrossRef PubMed.
- X.-S. Ye, Z.-G. Shao, H. Zhao, L. Yang and C.-L. Wang, RSC Adv., 2014, 4, 21216–21220 RSC.
- J. Xiao, M. Long, X. Zhang, J. Ouyang, H. Xu and Y. Gao, Sci. Rep., 2015, 5, 9961 CrossRef CAS PubMed.
- B. Zeng, M. Long, X. Zhang, Y. Dong, M. Li, Y. Yi and H. Duan, J. Phys. D: Appl. Phys., 2018, 51, 235302 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00265e |
| This journal is © The Royal Society of Chemistry 2022 |