Open Access Article
Open Access ArticleExciton–phonon coupling in alanine-based hybrid lead bromide†
Nailson
Vasconcelos
 ab,
Bruno S.
Araújo
ab,
Bruno S.
Araújo
 ac,
Dieric S.
Abreu
ac,
Dieric S.
Abreu
 d,
Mayra A.
P. Gómez
d,
Mayra A.
P. Gómez
 a,
Alejandro P.
Ayala
a,
Alejandro P.
Ayala
 a and
Carlos William A.
Paschoal
a and
Carlos William A.
Paschoal
 *a
*a
aDepartamento de Física, Universidade Federal do Ceará, Campus do Pici, 60440-900, Fortaleza, CE, Brazil. E-mail: paschoal.william@fisica.ufc.br
bInstituto Federal de Educação, Ciência e Tecnologia do Maranhão, Campus Barreirinhas, Rodovia MA-225 - Km 04, 65590-000, Barreirinhas, MA, Brazil
cInstitut Lumière Matière, UMR5306 Université Lyon 1-CNRS, Université de Lyon, F-69622, Villeurbanne, Cedex, France
dLaboratório de Espectroscopia Molecular (LEM), Departamento de Química Fundamental, Instituto de Química, Universidade de São Paulo, Av. Prof. Lineu Prestes 748, São Paulo 05508-000, Brazil
First published on 16th September 2022
Abstract
Recently, hybrid metal–halide perovskite-like compounds have emerged as promising materials for optoelectronic applications. Such materials show optical properties that are usually tunable by the so-called perovskite dimensionality as well as octahedral distortion and connectivity. In this study, we have investigated the optical properties of an alanine-based 2D hybrid lead bromide with simultaneous edge- and corner-sharing [PbBr6]4− octahedra. This compound has a large bandgap of 3.62 eV and broad photoluminescence, which are correlated through structural properties. Also, we showed that this emission exhibits a CCT of 3385 K corresponding to the “warm” white light emission characteristic of self-trapped exciton formation. Finally, we showed that the strong exciton–phonon interaction is the main mechanism of photoluminescence broadening.
Introduction
Over the past two decades, hybrid semiconductor solid-state materials were projected to be promising materials for optoelectronic applications ranging from active materials in photovoltaic solar cells, light-emitting diodes (LEDs), and photodetectors to photocatalysts.1–6 Such promising applications arise from their unique optoelectronic properties (e.g., high wide-optical absorption and accessible small bandgaps) due to the rich chemical constitution and spatial arrangement of their hybrid organic–inorganic constituents.7–10 As the most prominent example of hybrid semiconductors, prototypical cubic three-dimensional (3D) hybrid organic–inorganic lead halide perovskites with the general chemical formula ABX3 (A = small organic monocation; B = Pb2+, and X = Cl−, Br−, and I−) and the 3D corner-sharing framework of anionic octahedra [PbX6]4− with organic A-site monocations occupying the cuboctahedral voids exhibit all the aforesaid remarkable characteristics, but suffer from structural instability under environmental conditions (e.g., exposure to radiation, heat, and humidity).11–13 This instability is associated with their intrinsic soft lattices and inherent brittle crystal structures with small bulk moduli, which are due to the ionicity of the metal–halide bond and the weakly bonded organic cations within the voids of the inorganic framework.14–17 The nature of these interactions has motivated a series of investigations related to the origins and effects of usual thermal fluctuations in halide perovskites.18–20 Based on a comparative study between the hybrid (CH3NH3PbBr3) and inorganic (CsPbBr3) structures, Yaffe et al.21 showed that local polar fluctuations are intrinsic to the general lead-halide perovskite structure, and the presence of dipolar organic cations is not the only condition driving local polar fluctuations. In addition to the intrinsic contribution of inorganic components in these fluctuations, the elongation of metal–halide bonds due to the presence of a large organic cation in the structure can make the lattice softer, intensifying the effects of octahedral anharmonicity.22Another underlying factor that drives the lattice instability and optoelectronic properties of perovskites is the presence of stereochemically active 6s2(5s2) electron lone pairs. According to Fabini et al.,23 the interaction of lone pairs with anions regulates and expands the energy bands, contributes to tolerance factors, increases the electronic mobility, and makes the bandgap sensitive to pressure and temperature variations. Furthermore, the energy imbalance due to its presence induces an anharmonicity scenario that contributes to octahedral distortions. For example, Gao et al.24 analyzed the interaction between the geometric (ionic size) and lone pair (covalence) effects of different metallic cations (M = Pb, Sn, and Ge) in the structure of CsMBr3 halide perovskites. They showed that the lone pair stereochemical activity contributes to strong octahedral tilt instabilities that induce liquid-like behavior in all examined crystals.
Designing and building new perovskite-like structures based on suitable organocations occupying A-sites and/or alloying halides and metals occupying the X and B sites, respectively, have been the most adopted strategies to circumvent instability in hybrid perovskites and also achieve and modulate the desired properties. The success of such approaches inherently depends on the steric effects that could be easily estimated by the so-called Goldschmidt tolerance factor (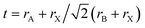 ; r – the ionic radii of A, B, and X ions).8,25,26 For instance, stable hybrid lead halide perovskite-like structures show a narrow range of t values (0.8–1.0), limiting the organic cation to those with a small apparent ionic radius.26–29 Using cations in the A-site out of the aforementioned optimum tolerance factor range destabilizes the perovskite lattice, resulting in structural distortions that seriously affect their remarkable properties (e.g., the octahedral tilt impacts the Jahn–Teller distortion of inorganic octahedra, thus affecting the bandgap, carrier transport, and exciton–phonon coupling).30,31
; r – the ionic radii of A, B, and X ions).8,25,26 For instance, stable hybrid lead halide perovskite-like structures show a narrow range of t values (0.8–1.0), limiting the organic cation to those with a small apparent ionic radius.26–29 Using cations in the A-site out of the aforementioned optimum tolerance factor range destabilizes the perovskite lattice, resulting in structural distortions that seriously affect their remarkable properties (e.g., the octahedral tilt impacts the Jahn–Teller distortion of inorganic octahedra, thus affecting the bandgap, carrier transport, and exciton–phonon coupling).30,31
In fact, only methylammonium cations (CH3NH3+, MA, r = 217 pm) have been reported as a suitable A-site occupant in a thermodynamically stable cubic phase (perovskite structure), yielding prototypical MAPbI3 (t = 0.91).32,33 Cations with different sizes, charges, shapes, and functional chemical groups can provoke severe distortions in the [PbX6]4− octahedra and, ultimately, a disruption that determines the connectivity and dimensionality of the metal–halide inorganic framework. For instance, when organic bulky A-site cations exceed t > 1.0, two scenarios are more likely: (i) the formation of new phases where the fundamental building blocks consist of corner- and face- or edge-sharing octahedra (usually called a “perovskitoid”) that fit large cations into empty cavities of its 3D inorganic network and (ii) dimensionality reduction of the inorganic lattice, resulting in low-dimensional perovskites (0- to quasi-2D), which commonly crystalize in Ruddlesden–Popper (An+1BX3n+1, A = organic monocation) and Dion–Jacobson (A′An-1BX3n+1, A′ = organic dication) structure types with corner-sharing octahedral connectivity (called “perovskite-like”)7,34,35 or less common low-dimensional phases with face- and edge-sharing octahedral connectivities.36–38 For example, Kour and co-workers39 recently reported a highly luminescent low-dimensional perovskitoid with a large Stokes shift related to their puckered PbI6− framework comprising both the corner- and face-sharing octahedra.
Despite such a diversity of structural connectivity, in all the low-dimensional phases of hybrid perovskites, the dielectric constant of organic and inorganic layers, which resembles a natural quantum well structure, dictates most of their (di-)electrical and spectroscopy properties. For instance, the strong electron–phonon coupling observed in low-dimensional hybrid perovskite-like compounds promotes a strong quantum/dielectric confinement leading to a larger exciton binding energy and a wider optical bandgap, which drives the nature of exciton radiative recombination (i.e., fluorescence).10,40–42
Also, molecular cation spacers with a small dielectric constant (ε) lead to a reduction in the exciton Bohr radius, resulting in a significant exciton binding energy (Eb) enhancement, leading to the dielectric confinement, whereas the increase of the exciton Bohr radius, due to the high dielectric constant of the organic layer spacers, implies a decrease of the exciton binding energy.43–45 In the case of 3D perovskites, the low binding energy between electrons and holes and the frequency-dependent dielectric response facilitate the charge carrier screening process, which has made these materials applicable in the development of low-cost absorbers in solar cells.1,46,47 On the other hand, the strong binding energy generated by the dielectric constant between the organic and inorganic layers makes exciton trapping a recurrent phenomenon in low-dimensional perovskites, whose quantum confinements can be gradually reduced as the number of metal–halide sheets in each inorganic layer is reduced (n value), and the optical absorption onset and exciton binding energies are red-shifted.48–50 Additionally, this high confining power can also be tuned by organic cations that make up the potential barriers, which, unlike 3D perovskites, play a complex role in high-frequency dielectric screening.49 For example, Smith et al.51 showed that the intercalation of highly polarizable molecules in the layered structures can reduce the electronic confinement in perovskites from layers with a high confinement power (n = 1).
Along these lines, the deliberated choice of organic molecules to compose hybrid low-dimensional perovskites as dielectric spacers must play a fundamental role in the optoelectronic applications that, beyond stability,52 require tunable exciton-binding energies,42,53,54 high photoluminescence quantum efficiencies,43 and strong exciton–phonon couplings.55,56 In addition to the aforementioned intended characteristics, the choice of organic spacers must consider a set of well-defined7 features that determine their suitability as a spacer in hybrid 2D perovskites.57,58 Noticeably, the presence of functional chemical groups, with a polar proton-rich donors,58,59 is important because they are capable of forming multiple hydrogen bonds,60 as well as they establish a strong Coulombic interaction with inorganic moieties making all the hybrid structures stable.61
For example, Xie et al.62 reported a study regarding the stability and optical properties of single crystals of new 2D perovskite-like compounds with the chemical formula (A′)mPbIm+2 (A′ = COOH(CH2)nNH3, n = 1, 3, 5, 7, and 9). They demonstrate the ability of bifunctional organic cations of amino acids to influence the structures of low dimensional perovskites, finding diversity in the connectivity modes of the [PbI6]4− octahedra, with edge-, face-, and corner-sharing structures. In addition, they observed tunable optical properties resulting from different octahedral distortion modes. The reported band gaps calculated for the series agree with the established tendency based on the connectivity of lead perovskite-like compounds, where corner-sharing < edge-sharing < face-sharing.36,37
Recently, Sirenko et al.63 showed an approach to obtain 2D chiral hybrid layered lead-halide perovskite-like structures based on α-alanine, where they report a set of four new compounds consisting of an enantiomeric pair (D- and L-alanine based) of bromide perovskites, and another one of iodide. They present a set of experiments to characterize the structure and describe some electronic properties, but with scarce discussion about their underlying properties. This fact highlights the necessity of investigating pure amino acid-based perovskites to help elucidate some aspects concerning the rich structure that presents a hydrogen-bond network that seems to drive the connectivity in the corner-sharing inorganic moiety.
Thus, in this paper, we discuss the role and influence of octahedral distortions and connectivity on the electronic properties of 2D chiral perovskite L-alaninePbBr3·H2O (AlaPbBr3·H2O), an enantiomer similar to that previously reported by Sirenko et al.,63 which was investigated by electronic absorption spectroscopy and temperature-dependence photoluminescence performed in addition to Raman spectroscopy measurements to prove that the exciton–phonon interaction is one of the primary mechanisms in emission spectra broadening. These findings may improve our understanding of the role of connectivity in the resulting optoelectronic effects.
Materials and methods
Chemicals
PbBr2 (beads, 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 999%), HBr (puriss, p.a., ≥67%), and L-alanine (BioUltra, ≥99.5%) were purchased from Sigma-Aldrich and used without further purification. Ethanol (EtOH, anhydrous, 99,8%, Sigma-Aldrich) was dried over 4 Å molecular sieves (beads, 8–12 mesh, Sigma-Aldrich) for 72 h prior to use. All other chemicals were of chromatographic grade and used as received.
999%), HBr (puriss, p.a., ≥67%), and L-alanine (BioUltra, ≥99.5%) were purchased from Sigma-Aldrich and used without further purification. Ethanol (EtOH, anhydrous, 99,8%, Sigma-Aldrich) was dried over 4 Å molecular sieves (beads, 8–12 mesh, Sigma-Aldrich) for 72 h prior to use. All other chemicals were of chromatographic grade and used as received.
Synthesis of AlaBr
AlaBr was first synthesized by standard acid–base neutralization, where HBr was slowly added into a cold ethanolic solution of base-free L-alanine under continuous stirring in an ice bath for 1 h. The ethanol and residual water were removed by low-vacuum rotary evaporation. Then, a white polycrystalline powder (DMAI powder) was copiously washed with diethyl ether and finally dried in a vacuum oven overnight.Synthesis of [CH3–CH(NH3)–COOH]PbBr3·H2O (AlaPbBr3·H2O)
Single crystals were prepared from a mixture of 2 mol of excess of AlaBr and 1 mol of PbBr2 dissolved in a mixture of HBr/EtOH (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 v/v) with continuous stirring in a glycerin bath and heated at 100 °C for 1 h. The solution was slowly cooled down to 70 °C, and the yellow single crystal prismatic parallelepipeds precipitated was immediately filtered and washed with diethyl ether several times and finally dried in a vacuum oven overnight.
2 v/v) with continuous stirring in a glycerin bath and heated at 100 °C for 1 h. The solution was slowly cooled down to 70 °C, and the yellow single crystal prismatic parallelepipeds precipitated was immediately filtered and washed with diethyl ether several times and finally dried in a vacuum oven overnight.
X-Ray diffraction measurements
The X-ray diffraction data of the pale yellow single crystal of AlaPbI3·H2O were collected using a Bruker D8 VENTURE Kappa geometry diffractometer, equipped with a PHOTON II CPAD detector, a CuKα INCOATEC IμS 3.0 microfocus source (λ = 1.54178 Å) and an APEX 3 control software.64 The data reduction was performed using SAINT.65 The intensities were corrected for absorption using SADABS.66 Using Olex2,67 the structures were solved by intrinsic phasing through SHELXT68 and refined by full-matrix least-squares using SHELXL.69 All non-hydrogen atoms were refined anisotropically. Hydrogen atom positions were calculated geometrically and refined using the riding model. Crystallographic data of AlaPbBr3·H2O have been deposited at The Cambridge Crystallographic Data Center under the code CCDC 2164940.Differential scanning calorimetry (DSC)
Differential scanning calorimetry (DSC) measurements were carried out using a Maia 200 F3 (Netzsch) calorimeter at heating and cooling rates of 5 K min−1 and 10 K min−1 under a constant nitrogen flow of 50 mL min−1.Photoluminescence spectroscopy
Photoluminescence (PL) spectra were recorded in a backscattering configuration using a T64000 JobinVon spectrometer in a single grating (1800 grooves mm−1) configuration equipped with the liquid N2-cooled charge-coupled device (CCD) detector and a 365 nm UV led as excitation source through a confocal Olympus microscope (50 ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) objective, N.A. 0.90). The experimental resolution was 0.10 nm
objective, N.A. 0.90). The experimental resolution was 0.10 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) for 20 accumulations of 10
for 20 accumulations of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s. The temperature-dependent PL measurement was performed using a helium-based refrigeration system, CSA-202, coupled with a Lakeshore temperature controller model 11330. The cooling system is supported using an EXT70H/NW40 Edwards turbo molecular vacuum pump. The PL spectra were deconvoluted with split-pseudovoigt functions using the Fityk software (version 0.9.8). The chromaticity coordinates (x, y), the calculated color temperature (CCT), and the color rendering index (CRI) were calculated using the Collor Calculator by OSRAM Sylvania, Inc.
s. The temperature-dependent PL measurement was performed using a helium-based refrigeration system, CSA-202, coupled with a Lakeshore temperature controller model 11330. The cooling system is supported using an EXT70H/NW40 Edwards turbo molecular vacuum pump. The PL spectra were deconvoluted with split-pseudovoigt functions using the Fityk software (version 0.9.8). The chromaticity coordinates (x, y), the calculated color temperature (CCT), and the color rendering index (CRI) were calculated using the Collor Calculator by OSRAM Sylvania, Inc.
UV-Vis diffuse reflectance spectroscopy
The room temperature spectrum was recorded using a Shimadzu UV-2600 spectrophotometer with an ISR-2600 Plus integrating sphere within a 200–800 nm range. The reflectance spectrum was transformed into an absorption spectrum by the Kubelka–Munk function.70Raman and IR spectroscopy
The Raman spectrum was recorded over the range of 50–3800 cm−1 with a 632.8 nm HeNe laser as the excitation source using a LabRAM Jobin–Yvon (Horiba) spectrometer, equipped with a charge-coupled device (CCD) cooled with liquid nitrogen. The peaks were deconvoluted with Lorentzian functions using the Fityk software (version 0.9.8).The ATR-FTIR spectrum was recorded in the range of 200–4000 cm−1 with a resolution of 4 cm−1 using a Bruker Vertex 70 V FT-IR spectrometer, excited by a Globar source. OPUS software was used for the baseline corrections.
Results and discussion
Crystalline structure
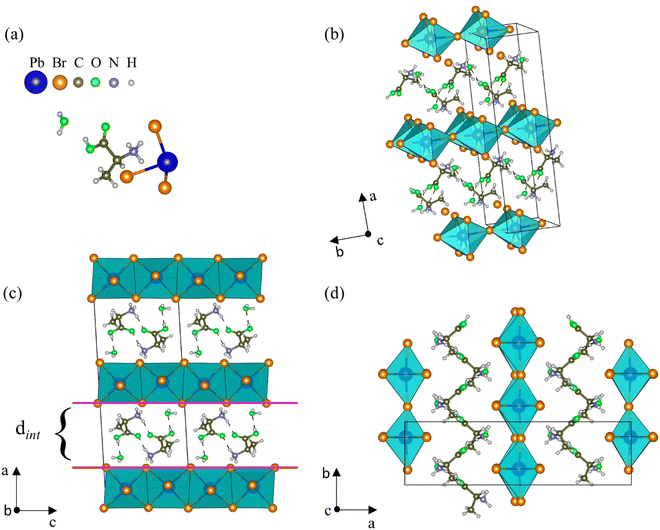
At room temperature, AlaPbBr3·H2O single crystals crystallize in a monoclinic structure with space group C2, whose lattice parameters are a = 21.8573(12) Å, b = 6.0851(4) Å, c = 8.7665(5) Å, and β = 93.367(2)°. Except for the fact that the crystals synthesized here have a completely ordered structure, the solved structural parameters of our samples are close to the similar structure of the L-alanine-based bromide perovskite previously reported by Sirenko et al.,63 except that the H and O sites of the carboxyl group, which in their work are disordered. The full information about the unit cell and data refinement is presented in Table S1 (ESI†).As shown in Fig. 1(a), the asymmetric unit is constituted by one [NH3–CH(NH2)–COOH]+ cation (from now called Ala), one [PbBr3]− anion, and one water molecule. In the AlaPbBr3·H2O structure, each Pb2+ ion is surrounded by six Br− ions, forming a [PbBr6]4− octahedral coordination geometry. Such octahedra are connected along the bc plane, forming inorganic layers between organic binders stacked along the a axis (Fig. 1(b)).
Regarding the structural configuration of AlaPbBr3·H2O, an intercalated configuration between the organic and inorganic layers can be noted. The distance among the layers is characterized by an interlayer spacing (dint) of 6.74 Å (Fig. 1(c)) that slices the planes of the family (110) of the perovskite-like structure. This interlayer spacing is controlled by the size of the organic cations that, through the protonated amine NH3+ and a water molecule, establish Br–H, Br–N, and Br–O bonds with the inorganic sublattices. The lengths of such bonds and other connections between the organic molecules are shown in Table S2 (ESI†). These interactions promote significant changes in the length and angle of the Pb–Br and Pb–Br–Pb bonds, forming irregular octahedra with simultaneous corner- and edge-sharing along the axial and equatorial axes (Fig. 1(c and d)), respectively. Additionally, the presence of the water molecule makes local hydrogen bonding contribute to tuning the connectivity of the lead octahedra, leading to hybrid lead-based halide compounds to present outstanding optical and dimensional properties.37,60 Besides, changes in the inorganic sublattice influence the dynamics of charge carriers, exciton–phonon interactions, and the gap energy.33,62
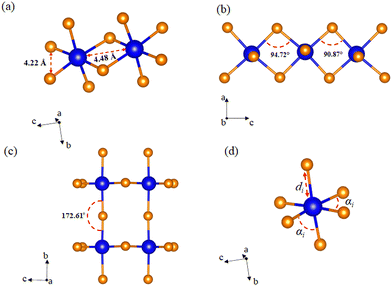
Unlike the usual corner-sharing octahedral connectivity observed in standard 2D perovskite-like compounds, AlaPbBr3·H2O also presents side-sharing connections. Gautier et al.71 pointed out that such a feature plays an essential role in the photoluminescence quantum yield (PLQY) of self-trapped excitons. This side sharing implies new Pb–Br–Pb connections in the equatorial plane of the octahedra (bc plane) (Fig. 2(a)). One of the reasons for the improvement in luminescence is the significant shortening of the Pb–Pb distances (4.48 Å) that reduce the angle of the Pb–Br–Pb connections to a minimum value of 90.87 Å (Fig. 2(b)). This reduction becomes more significant than the angle formed in the corner sharing connections of the octahedron, whose value is 172.6° (Fig. 2(c)). These values correlate with the different lengths in the Pb–Br connections along the equatorial axis, which presented maximum and minimum values of 3.07 Å and 2.98 Å, respectively. These lengths also lightly differ on the axial axis, with values of 3.12 Å and 2.97 Å.
Optical properties
Regarding the optical properties, UV-Vis diffuse reflectance spectroscopy under room conditions and temperature-dependent photoluminescence measurements were performed on AlaPbBr3·H2O single crystals. Fig. 3 presents the absorption spectrum at room temperature obtained for AlaPbBr3·H2O crystals and its estimated bandgap obtained through the Tauc approach.72 Such an absorption spectrum shows an intense peak with an onset at around 282 nm followed by a secondary peak, whose onset is around 364 nm. According to the Tauc plot, AlaPbBr3·H2O presents a direct bandgap of Eg = 3.62 eV and a secondary one at a lower energy edge of Eex = 3.07 eV. Such excitonic behavior is similar in nature with room temperature stable self-trapped excitons (STE) observed for other 2D perovskitelike compounds.36,73,74 In contrast, Sirenko et al.63 observed only a single peak, whose bandgap was Eg = 3.12 eV for the enantiomeric pair of bromide perovskites. However, they obtained the spectrum from powder, while we obtained it from several microcrystals. It is important to clarify this point because, usually, the optical properties of hybrid halide perovskite-like compounds are very sensitive to size processing.75–78 Additionally, a step followed by a tail around 480 nm, which presents a lower intensity concerning the other peaks, could be attributed to another lower energy substrate. However, when we applied the Tauc Plot method, it did not present enough intensity to estimate the bandgap, therefore being disregarded in our discussions.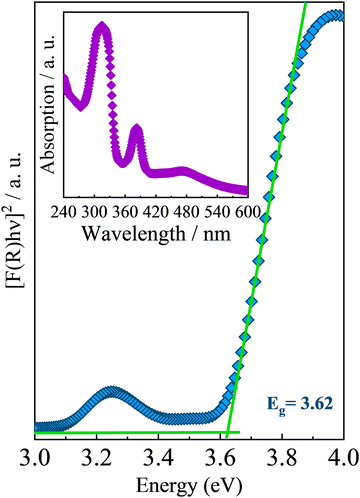 | ||
| Fig. 3 UV-Vis optical absorption spectrum of AlaPbBr3·H2O at room temperature. The inset shows the estimated bandgap obtained by using the Tauc approach.72 | ||
The large Stokes shift between the fundamental edge Eg and the excitonic peak Eex is also evidence of a STE interaction, whose exciton binding energy (EBE), according to Cortecchia et al.,74 can be obtained by taking the difference between the energy of excitonic transition and the onset of the high-energy absorption (see Fig. S1 in the ESI†). In the case of AlaPbBr3·H2O, we observed a difference of around 370 meV. This large EBE is close to that reported by Dammak et al., 200979 for lead iodide hybrid 2D perovskite-like compounds, and it is related to the 2D confinement and the large dielectric disparity between the organic and inorganic layers in quantum well structures.80,81 Additionally, with the small thickness of the inorganic layer (n = 1 octahedron), the electron and hole wavefunctions are more overlapped in the wells, leading to a larger exciton binding energy.82,83
The optical transitions in perovskite materials are mainly related to the s and p orbitals of Pb and the s orbital of Br, with the valence band corresponding to the 4p states of Br− and the 6s states of Pb2+, while the bottom of the conduction band primarily consists of Pb 6p states.74,80,84 Being closely related to structural characteristics, changes in Pb–Br–Pb bond angles formed by [PbBr6]−4 adjacent octahedra can modify the antibonding orbital interactions. Such modifications can set the distance between the valence and conduction bands, tuning the bandgap.85 In the case of AlaPbBr3·H2O, the loss in the antibonding interaction due to the octahedral edge-sharing, which implies in Pb–Br–Pb angles around 90° (see Fig. 2b), induces a reduction of lone pair electrons in energy, resulting in a relatively flat electronic energy band and, consequently, a wider bandgap.86
The relationship between the bandgap width and octahedral connectivity in halide perovskites was reported in previous works based on bromides and iodides.36,37,62,86 Such studies present a direct proportionality between the octahedral connectivity and the bandgap as a trend, in the following order: corner-sharing < edge-sharing < face-sharing. Our calculated bandgap of 3.62 eV is close to those reported by L. Mao et al.36 for a series of white-light-emitting hybrid lead bromide perovskites, such as 1D (C6H16N2)3Pb2Br10 (2,6-dmpz), three-layered 2D (C5H14N2)2Pb3Br10 (mpz) and 3D (C5H14N2)PbBr4 (hmp), which has a similar octahedral connectivity (corner- and edge-sharing octahedra) to AlaPbBr3·H2O.
The Fig. 4(a) shows the photoluminescence (PL) spectrum of AlaPbBr3·H2O single crystals measured at room temperature with a 365 nm excitation source, which shows a broad emission profile centered at 600 nm. In general, it is expected that a higher level of local octahedral distortion provides the formation of self-trapped states, resulting in a broad-band emission spectrum with a significant Stokes shift from the exciton absorption peak.36,87
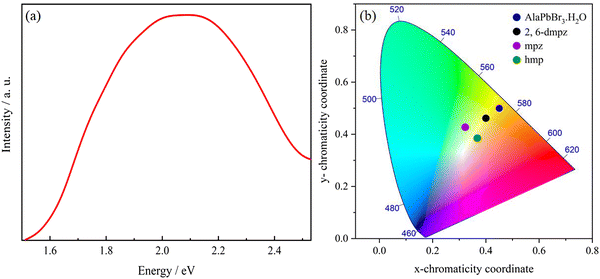 | ||
| Fig. 4 (a) Steady-state PL spectrum (excited at 365 nm) at room temperature of AlaPbBr3·H2O single crystals. (b) Chromaticity coordinates of AlaPbBr3·H2O in the 1931 color space chromaticity diagram, compared with the results observed for the edge- and corner-sharing octahedral compounds 2,6-dmpz, mpz and hmp.36 The chromaticity coordinates (x and y), CCT, and CRI are calculated using the software Color Calculator by OSRAM Sylvania, Inc. | ||
Since octahedral distortions play a fundamental role in the optical properties of this kind of compound, it is important to evaluate the degrees of the individual octahedral distortion in AlaPbBr3·H2O. Thus, we calculated the bond length quadratic elongation (λ) and the bond angle variance (σ2),62,84,88,89 which are given by eqn (1) and (2)
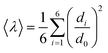 | (1) |
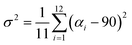 | (2) |
The main optical characteristic of self-trapped excitons is a broadband that leads to white light emission.2 The color rendering index (CRI) value is a quantitative measure that represents the ability of the light source to accurately reflect the true color of an illuminated sample.96 The CRI analysis provides a 60 CRI index for AlaPbBr3·H2O, which is slightly lower when compared to most commercially available LEDs presenting a CRI index of around 80.97 From Fig. 4(b), the emission of AlaPbBr3·H2O has the CIE (International Commission on Illumination) chromaticity coordinates of (0.45, 0.50) with a contribution from the yellow region of the spectrum compared to pure white light, which has the chromaticity coordinates of (0.33, 0.33). This gives the emission with a correlated color temperature (CCT) of 3385 K, corresponding to “warm” white light. L. Mao et al.97 also report this “warm” light emission for 2,6-dmpz, mpz, and hmp (Fig. 4(b)). In such a study, they observed that a broad emission was also given by possible internal distortions and octahedral connectivity and reported by Zhao et al.93 in face-sharing perovskites with large bandgaps and yellowish-green emissions.
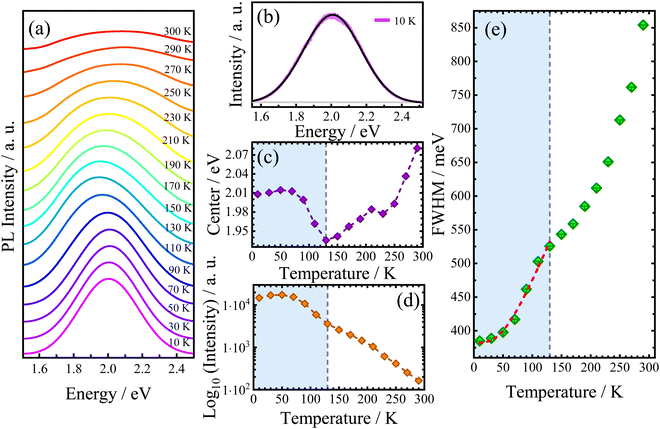
Since the electronic properties of AlaPbBr3·H2O are intrinsically related to the structural organization, its optical properties also could be sensitive to temperature variations. Thus, we measured the temperature-dependent photoluminescence (PL) emission behavior of AlaPbBr3H2O single crystals in the temperature range between 10 K and 300 K (Fig. 5(a)). Due to the asymmetric shape of PL bands, the best-fitting curves have been obtained by deconvolution with the split pseudo–Voigt function (see the ESI†), as shown in Fig. 5(b).
As shown in Fig. 5(c), the redshift in the peak position (center) is interrupted by an abrupt change in the slope at 130 K. After this, it starts increasing up to room temperature. Such anomalous behaviors already have been studied in previous works and may be related to structural phase transitions, which induce abrupt changes in all PL band parameters.54,98 In fact, all curves exhibit a discontinuity at 130 K. From our DSC analysis (see Fig. S2 in the ESI†), it is found that no events occurred in this temperature range. However, a more detailed structural analysis is still needed.
In 2D hybrid quantum wells, the intrinsic pathways of exciton recombinations are related to exciton–phonon interactions,99 and it has been reported that hybrid perovskites based on lead halides exhibit very strong exciton–phonon interactions.100,101 In this scenario, the temperature dependent emission broadening (Γ(T)) has been a key feature for the investigation of this phenomenon.93,99 Nevertheless, different mechanisms of scattering involving charge carriers and phonons or even impurities are associated with different correlations on the temperature dependent PL linewidth. Such mechanisms can be expressed as follows:56
| Γ(T) = Γ0 + Γac + ΓLO + Γimp = Γ0 + γacT + γLOn(T) + γimpe−Eb/kBT | (3) |
To provide further information about the PL broadening mechanism, the obtained Γ(T) was fitted by using eqn (3). Our best fittings were reached considering the contributions Γ0 + Γac + ΓLO. To preserve our fittings and discussions about the exciton–phonon coupling, we consider only the region that precedes the discontinuity point selecting just the temperature range between 10 and 130 K. According to the best fits, considering the extrapolated inhomogeneous broadening term Γ0 = 383 meV, we obtain the following coupling constants: γac = 46 μeV K−1 and γLO = 355 meV. Such values confirm the higher contribution of large electron–phonon coupling to the broadening of PL emission via the Fröhlich interaction. Such large LO coupling strengths are found in other 2D hybrid lead bromide perovskites and is related to the stronger exciton confinement in the thinner quantum well structure (n = 1).83,102 Indeed, when LO phonons are thermally activated, the strong electron–phonon interaction switches the curve tending from a linear regime (involving lower energy acoustic phonon contribution) to a super-linear regime.83 From our FWHM temperature dependence analysis, this behavior can be observed in the range of 70 K to 130 K, as shown in Fig. 5(e). Surprisingly, this change in linearity via the LO Fröhlich interaction occurs in the same range as redshifts simultaneously observed in the emission and intensity parameters, as seen in Fig. 5(c and d), respectively. This suggests that an enhancement in the electron–phonon interaction via thermal activation can induce a shift of PL emission to lower energies and also reduce the intensity of its emission. Additionally, a stability interval (up to 70 K) is observed in the integrated PL intensity, which could be associated with the large EBE with respect to kBT, where kB is the Boltzmann constant, which has been extensively investigated in 2D hybrid perovskite-like compounds.79
In addition to the evidence of exciton–phonon coupling in our sample, eqn (3) also provides further information about the Fröhlich interaction, suggesting that phonons would mediate these interactions.56,93,103 In this case, the obtained ELO value of 14.2 meV corresponds to a phonon of frequency at 115 cm−1. To assign this phonon we performed Raman spectroscopy in this sample at room temperature. Fig. 6 shows the room-temperature unpolarized Raman-active spectrum. According to the group theory analysis, based on the site occupation of the C2 monoclinic space group of AlaPbBr3·H2O, we expect 126 vibrational polar modes at the Γ point of the Brillouin zone. Such phonons can be decomposed on to the irreducible representation of the factor group 2 as 62A ⊕ 61B.104 We observed 77 modes of those 126 predicted by group theory analysis. As already observed in other hybrid perovskite compounds, the spectrum can be analyzed in two different regions. First, the low wavenumber range (50–300 cm−1) corresponds to [PbBr6]−4 octahedral modes mixed with the organic cation [(NH3)–(CH2)2–COOH] lattice modes (Fig. 6(a));77,92,105 and, a second range, beyond 300 cm−1, in which we observe the organic molecule internal modes (Fig. 6(b and c)). The bands at 103 cm−1 and 136 cm−1 are assigned to the symmetric stretching modes of Br–Pb–Br, νs (Br–Pb–Br), and Br–Pb, νs (Br–Pb), respectively. While the mode at 123![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1 to the Br–Pb asymmetric stretching, νas (Br–Pb).77,106–108 The same active vibrational modes were observed in our ATR-FTIR analysis (see Fig. S3 in the ESI†) and are in good agreement with the previously reported study by Sirenko et al.63 Thus, the corresponding phonon at 115 cm−1 that couples with excitons is close in energy to the Pb–Br phonon observed in our Raman spectrum in the range of 80–140 cm−1, as shown in Fig. 6. This suggests that the LO phonon modes of Pb–Br ions play the dominant role in the electron–phonon excitonic interaction.
cm−1 to the Br–Pb asymmetric stretching, νas (Br–Pb).77,106–108 The same active vibrational modes were observed in our ATR-FTIR analysis (see Fig. S3 in the ESI†) and are in good agreement with the previously reported study by Sirenko et al.63 Thus, the corresponding phonon at 115 cm−1 that couples with excitons is close in energy to the Pb–Br phonon observed in our Raman spectrum in the range of 80–140 cm−1, as shown in Fig. 6. This suggests that the LO phonon modes of Pb–Br ions play the dominant role in the electron–phonon excitonic interaction.
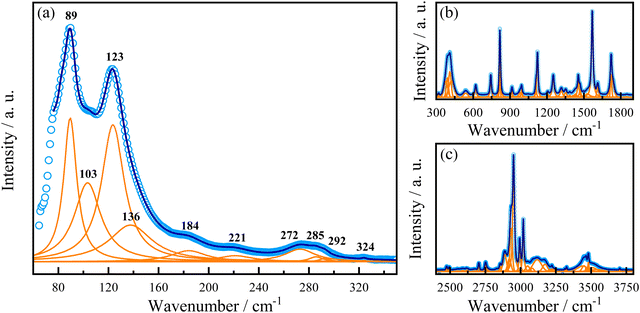 | ||
| Fig. 6 Raman spectrum of AlaPbBr3·H2O at 300 K. (a) Low-, (b) middle- and (c) high-wavenumber range. For the high-wavenumber spectrum, please see Fig. S4 and S5 in the ESI.† | ||
Conclusions
In conclusion, we investigated AlaPbBr3·H2O, a 2D hybrid lead bromide perovskite-like compound. This compound exhibits simultaneous edge- and corner-sharing [PbBr6]4− octahedral connectivities. We observed a bandgap–structure and PL–structure correlation, in which a large bandgap of 3.62 eV is due to the formation of a near 90° degree Pb–Br–Pb bond angle, and the broad PL emission comes from a considerable octahedral distortion level in the crystal structure. At room temperature, this emission exhibits a CCT of 3385 K corresponding to the “warm” white light emission, characteristic of self-trapped exciton formation. In addition, the temperature-dependent PL emission suggests a strong exciton–phonon interaction as the main mechanism of PL broadening. Hence, our work provides advances in the study and understanding of the structure–property relationships of 2D hybrid perovskites with octahedral connectivity modes that can be extended to non-conventional ones. Such investigations are fundamentals in the development of white-light solid-state lighting and other optoelectronic applications.Conflicts of interest
There are no conflicts to be declared.Acknowledgements
We are thankful to the FUNCAP (PRONEX PR2-0101-00006.01.00/15), the FAPESP (Grant 2019/21939-0), the CNPq (Grants 303711/2019-1 and 424842/2018-1), and the CAPES (Grant 88882.349938/2019-01) for financial support.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- E. R. Dohner, A. Jaffe, L. R. Bradshaw and H. I. Karunadasa, J. Am. Chem. Soc., 2014, 136, 13154–13157 CrossRef CAS PubMed.
- S. S. Bhosale, A. K. Kharade, E. Jokar, A. Fathi, S. M. Chang and E. W. G. Diau, J. Am. Chem. Soc., 2019, 141, 20434–20442 CrossRef CAS PubMed.
- M. Min, R. F. Hossain, N. Adhikari and A. B. Kaul, ACS Appl. Mater. Interfaces, 2020, 12, 10809–10819 CrossRef CAS PubMed.
- T. Liu, W. Shi, W. Tang, Z. Liu, B. C. Schroeder, O. Fenwick and M. J. Fuchter, ACS Nano, 2022, 16, 2682–2689 CrossRef CAS PubMed.
- Y.-H. Kim, H. Cho and T.-W. Lee, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11694–11702 CrossRef CAS PubMed.
- L. Mao, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 1171–1190 CrossRef CAS PubMed.
- J. Huang, M. Lai, J. Lin and P. Yang, Adv. Mater., 2018, 30, 1802856 CrossRef PubMed.
- V. Adinolfi, W. Peng, G. Walters, O. M. Bakr and E. H. Sargent, Adv. Mater., 2018, 30, 1700764 CrossRef PubMed.
- Y. Chen, Y. Sun, J. Peng, J. Tang, K. Zheng and Z. Liang, Adv. Mater., 2018, 30, 1703487 CrossRef PubMed.
- S. Paek, C. Roldán-Carmona, K. T. Cho, M. Franckevičius, H. Kim, H. Kanda, N. Drigo, K. Lin, M. Pei, R. Gegevičius, H. J. Yun, H. Yang, P. A. Schouwink, C. Corminboeuf, A. M. Asiri and M. K. Nazeeruddin, Adv. Sci., 2020, 7, 2001014 CrossRef CAS PubMed.
- L. Mao, H. Tsai, W. Nie, L. Ma, J. Im, C. C. Stoumpos, C. D. Malliakas, F. Hao, M. R. Wasielewski, A. D. Mohite and M. G. Kanatzidis, Chem. Mater., 2016, 28, 7781–7792 CrossRef CAS.
- H. Huang, M. I. Bodnarchuk, S. V. Kershaw, M. V. Kovalenko and A. L. Rogach, ACS Energy Lett., 2017, 2, 2071–2083 CrossRef CAS PubMed.
- Z. Deng, G. Kieslich, P. D. Bristowe, A. K. Cheetham and S. Sun, APL Mater., 2018, 6, 114202 CrossRef.
- W. Chu, W. A. Saidi, J. Zhao and O. V. Prezhdo, Angew. Chem., Int. Ed., 2020, 59, 6435–6441 CrossRef CAS PubMed.
- C. Zheng and O. Rubel, J. Phys. Chem. C, 2019, 123, 19385–19394 CrossRef CAS.
- R. Matheu, J. A. Vigil, E. J. Crace and H. I. Karunadasa, Trends Chem., 2022, 4, 206–219 CrossRef CAS.
- D. A. Egger, A. Bera, D. Cahen, G. Hodes, T. Kirchartz, L. Kronik, R. Lovrincic, A. M. Rappe, D. R. Reichman and O. Yaffe, Adv. Mater., 2018, 30, 1800691 CrossRef PubMed.
- M. Menahem, Z. Dai, S. Aharon, R. Sharma, M. Asher, Y. Diskin-Posner, R. Korobko, A. M. Rappe and O. Yaffe, ACS Nano, 2021, 15, 10153–10162 CrossRef PubMed.
- C. Gehrmann and D. A. Egger, Nat. Commun., 2019, 10, 3141 CrossRef PubMed.
- O. Yaffe, Y. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik, M. G. Kanatzidis, J. S. Owen, A. M. Rappe, M. A. Pimenta and L. E. Brus, Phys. Rev. Lett., 2017, 118, 136001 CrossRef PubMed.
- X. Li, S. A. Cuthriell, A. Bergonzoni, H. Dong, B. Traoré, C. C. Stoumpos, P. Guo, J. Even, C. Katan, R. D. Schaller and M. G. Kanatzidis, Chem. Mater., 2022, 34, 1132–1142 CrossRef CAS.
- D. H. Fabini, R. Seshadri and M. G. Kanatzidis, MRS Bull., 2020, 45, 467–477 CrossRef.
- L. Gao, L. Yadgarov, R. Sharma, R. Korobko, K. M. McCall, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis, A. M. Rappe and O. Yaffe, Mater. Adv., 2021, 2, 4610–4616 RSC.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC.
- Y. Wei, Z. Cheng and J. Lin, Chem. Soc. Rev., 2019, 48, 310–350 RSC.
- A. Mancini, P. Quadrelli, G. Amoroso, C. Milanese, M. Boiocchi, A. Sironi, M. Patrini, G. Guizzetti and L. Malavasi, J. Solid State Chem., 2016, 240, 55–60 CrossRef CAS.
- B. Park and S. Il Seok, Adv. Mater., 2019, 31, 1805337 CrossRef PubMed.
- S. Burger, M. G. Ehrenreich and G. Kieslich, J. Mater. Chem. A, 2018, 6, 21785–21793 RSC.
- T. Umebayashi, K. Asai, T. Kondo and A. Nakao, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155405 CrossRef.
- D. Gui, L. Ji, A. Muhammad, W. Li, W. Cai, Y. Li, X. Li, X. Wu and P. Lu, J. Phys. Chem. Lett., 2018, 9, 751–755 CrossRef CAS PubMed.
- Z. Li, M. Yang, J.-S. Park, S.-H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292 CrossRef CAS.
- Y. Fu, M. P. Hautzinger, Z. Luo, F. Wang, D. Pan, M. M. Aristov, I. A. Guzei, A. Pan, X. Zhu and S. Jin, ACS Cent. Sci., 2019, 5, 1377–1386 CrossRef CAS PubMed.
- C. J. Dahlman, N. R. Venkatesan, P. T. Corona, R. M. Kennard, L. Mao, N. C. Smith, J. Zhang, R. Seshadri, M. E. Helgeson and M. L. Chabinyc, ACS Nano, 2020, 14, 11294–11308 CrossRef CAS PubMed.
- X. Li, W. Ke, B. Traoré, P. Guo, I. Hadar, M. Kepenekian, J. Even, C. Katan, C. C. Stoumpos, R. D. Schaller and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 12880–12890 CrossRef CAS PubMed.
- L. Mao, P. Guo, M. Kepenekian, I. Hadar, C. Katan, J. Even, R. D. Schaller, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 13078–13088 CrossRef CAS PubMed.
- M. E. Kamminga, G. A. de Wijs, R. W. A. Havenith, G. R. Blake and T. T. M. M. Palstra, Inorg. Chem., 2017, 56, 8408–8414 CrossRef CAS PubMed.
- X. Li, Y. He, M. Kepenekian, P. Guo, W. Ke, J. Even, C. Katan, C. C. Stoumpos, R. D. Schaller and M. G. Kanatzidis, J. Am. Chem. Soc., 2020, 142, 6625–6637 CrossRef CAS PubMed.
- P. Kour, M. Chenna Reddy, S. Pal, S. Sidhik, T. Das, P. Pandey, S. P. Mukherjee, S. Chakraborty, A. D. Mohite and S. Ogale, Angew. Chem., Int. Ed., 2021, 60, 18750–18760 CrossRef CAS PubMed.
- K. M. McCall, C. C. Stoumpos, S. S. Kostina, M. G. Kanatzidis and B. W. Wessels, Chem. Mater., 2017, 29, 4129–4145 CrossRef CAS.
- G. Antonius and S. G. Louie, Phys. Rev. B, 2022, 105, 085111 CrossRef CAS.
- S. Neutzner, F. Thouin, D. Cortecchia, A. Petrozza, C. Silva and A. R. Srimath Kandada, Phys. Rev. Mater., 2018, 2, 064605 CrossRef CAS.
- C. Katan, N. Mercier and J. Even, Chem. Rev., 2019, 119, 3140–3192 CrossRef CAS PubMed.
- M. Kumagai and T. Takagahara, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 12359–12381 CrossRef CAS PubMed.
- T. Ishihara, J. Takahashi and T. Goto, Solid State Commun., 1989, 69, 933–936 CrossRef CAS.
- I. Anusca, S. Balčiūnas, P. Gemeiner, Š. Svirskas, M. Sanlialp, G. Lackner, C. Fettkenhauer, J. Belovickis, V. Samulionis, M. Ivanov, B. Dkhil, J. Banys, V. V. Shvartsman and D. C. Lupascu, Adv. Energy Mater., 2017, 7, 1700600 CrossRef.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- J. Even, L. Pedesseau and C. Katan, ChemPhysChem, 2014, 15, 3733–3741 CrossRef CAS PubMed.
- M. R. Filip, D. Y. Qiu, M. Del Ben and J. B. Neaton, Nano Lett., 2022, 22, 4870–4878 CrossRef CAS PubMed.
- B. Traore, L. Pedesseau, L. Assam, X. Che, J.-C. Blancon, H. Tsai, W. Nie, C. C. Stoumpos, M. G. Kanatzidis, S. Tretiak, A. D. Mohite, J. Even, M. Kepenekian and C. Katan, ACS Nano, 2018, 12, 3321–3332 CrossRef CAS PubMed.
- M. D. Smith, L. Pedesseau, M. Kepenekian, I. C. Smith, C. Katan, J. Even and H. I. Karunadasa, Chem. Sci., 2017, 8, 1960–1968 RSC.
- E. S. Vasileiadou, B. Wang, I. Spanopoulos, I. Hadar, A. Navrotsky and M. G. Kanatzidis, J. Am. Chem. Soc., 2021, 143, 2523–2536 CrossRef CAS PubMed.
- X. Hong, T. Ishihara and A. V. Nurmikko, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 6961–6964 CrossRef CAS PubMed.
- F. Li, L. Yang, Z. Cai, K. Wei, F. Lin, J. You, T. Jiang, Y. Wang and X. Chen, Nanoscale, 2018, 10, 20611–20617 RSC.
- K. M. Mccall, C. C. Stoumpos, S. S. Kostina, M. G. Kanatzidis and B. W. Wessels, Chem. Mater., 2017, 29, 4129–4145 CrossRef CAS.
- H. J. Snaith, A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pe, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 11755 CrossRef PubMed.
- X. Li, J. M. Hoffman and M. G. Kanatzidis, Chem. Rev., 2021, 121, 2230–2291 CrossRef CAS PubMed.
- D. B. Mitzi, in Progress in Inorganic Chemistry, ed., K. D. Karlin, John Wiley & Sons, Inc., Hoboken, NJ, USA, 1999, vol. 48 BT-P, pp. 1–121 Search PubMed.
- B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558–4596 CrossRef CAS PubMed.
- B.-B. Bin Cui, Y. Han, B. Huang, Y. Zhao, X. Wu, L. Liu, G. Cao, Q. Du, N. Liu, W. Zou, M. Sun, L. Wang, X. Liu, J. Wang, H. Zhou and Q. Chen, Nat. Commun., 2019, 10, 5190 CrossRef PubMed.
- J. H. J.-H. H. Lee, J. H. J.-H. H. Lee, E.-H. H. Kong and H. M. Jang, Sci. Rep., 2016, 6, 21687 CrossRef CAS PubMed.
- G. Xie, L. Wang, P. Li, S. Song, C. Yao, S. Wang, Y. Liu, Z. Wang, X. Wang and X. Tao, ACS Appl. Mater. Interfaces, 2021, 13, 3325–3335 CrossRef CAS PubMed.
- V. Y. Sirenko, O. I. Kucheriv, D. D. Naumova, I. Fesich, R. Linnik, A. Dascalu, S. Shova, I. O. Fritsky and I. A. Gural’skiy, New J. Chem., 2021, 45, 12606–12612 RSC.
- Version 2018.9, Bruker AXS Inc., Madison, Wisconsin, USA Search PubMed.
- Version 8.36, B. A. Inc., Madison, Wisconsin, USA Search PubMed.
- L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, J. Appl. Crystallogr., 2015, 48, 3–10 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12, 593–601 Search PubMed.
- R. Gautier, F. Massuyeau, G. Galnon and M. Paris, Adv. Mater., 2019, 31, 1807383 CrossRef PubMed.
- J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi, 1966, 15, 627–637 CrossRef CAS.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Chem. Mater., 2016, 28, 2852–2867 CrossRef CAS.
- D. Cortecchia, J. Yin, A. Bruno, S.-Z. A. Lo, G. G. Gurzadyan, S. Mhaisalkar, J.-L. Brédas and C. Soci, J. Mater. Chem. C, 2017, 5, 2771–2780 RSC.
- Z. Chen, Q. Dong, Y. Liu, C. Bao, Y. Fang, Y. Lin, S. Tang, Q. Wang, X. Xiao, Y. Bai, Y. Deng and J. Huang, Nat. Commun., 2017, 8, 1890 CrossRef PubMed.
- Y. Dang, G. Liu, J. Song, L. Meng, Y. Sun, W. Hu and X. Tao, ACS Appl. Mater. Interfaces, 2020, 12, 37713–37721 CrossRef CAS PubMed.
- W. Castro Ferreira, B. S. Araújo, M. A. P. Gómez, F. E. O. Medeiros, C. W. de Araujo Paschoal, C. B. da Silva, P. T. C. Freire, U. F. Kaneko, F. M. Ardito, N. M. Souza-Neto and A. P. Ayala, J. Phys. Chem. C, 2022, 126, 541–550 CrossRef CAS.
- Q. Shang, Y. Wang, Y. Zhong, Y. Mi, L. Qin, Y. Zhao, X. Qiu, X. Liu and Q. Zhang, J. Phys. Chem. Lett., 2017, 8, 4431–4438 CrossRef CAS PubMed.
- T. Dammak, M. Koubaa, K. Boukheddaden, H. Bougzhala, A. Mlayah and Y. Abid, J. Phys. Chem. C, 2009, 113, 19305–19309 CrossRef CAS.
- E. Hanamura, N. Nagaosa, M. Kumagai and T. Takagahara, Mater. Sci. Eng., B, 1988, 1, 255–258 CrossRef.
- M. Kumagai and T. Takagahara, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 12359–12381 CrossRef CAS PubMed.
- Q. Shang, Y. Wang, Y. Zhong, Y. Mi, L. Qin, Y. Zhao, X. Qiu, X. Liu and Q. Zhang, J. Phys. Chem. Lett., 2017, 8, 4431–4438 CrossRef CAS PubMed.
- H. Long, X. Peng, J. Lu, K. Lin, L. Xie, B. Zhang, L. Ying and Z. Wei, Nanoscale, 2019, 11, 21867–21871 RSC.
- Y. Fu, X. Jiang, X. Li, B. Traore, I. Spanopoulos, C. Katan, J. Even, M. G. Kanatzidis and E. Harel, J. Am. Chem. Soc., 2020, 142, 4008–4021 CrossRef CAS PubMed.
- J. L. Knutson, J. D. Martin and D. B. Mitzi, Inorg. Chem., 2005, 44, 4699–4705 CrossRef CAS PubMed.
- C. C. Stoumpos, L. Mao, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2017, 56, 56–73 CrossRef CAS PubMed.
- Y. Toyozawa, S. Elsheikhi and S. Elsheikhi, Reference Module in Materials Science and Materials Engineering, Elsevier, 2016 Search PubMed.
- K. Z. Du, Q. Tu, X. Zhang, Q. Han, J. Liu, S. Zauscher and D. B. Mitzi, Inorg. Chem., 2017, 56, 9291–9302 CrossRef CAS PubMed.
- K. Z. Du, Q. Tu, X. Zhang, Q. Han, J. Liu, S. Zauscher and D. B. Mitzi, Inorg. Chem., 2017, 56, 9291–9302 CrossRef CAS PubMed.
- R. Zhang, X. Xu, X. Mao, Z. Wang, P. Wang, Y. Yang, J. Chen, R. Lu, W. Deng and K. Han, Laser Photonics Rev., 2022, 16, 2100689 CrossRef CAS.
- S. Wu, B. Zhou and D. Yan, ACS Appl. Mater. Interfaces, 2021, 13, 26451–26460 CrossRef CAS PubMed.
- B. Dhanabalan, Y.-C. Leng, G. Biffi, M.-L. Lin, P.-H. Tan, I. Infante, L. Manna, M. P. Arciniegas and R. Krahne, ACS Nano, 2020, 14, 4689–4697 CrossRef CAS PubMed.
- J.-Q. Zhao, C.-Q. Jing, J.-H. Wu, W.-F. Zhang, L.-J. Feng, C.-Y. Yue and X.-W. Lei, J. Phys. Chem. C, 2021, 125, 10850–10859 CrossRef CAS.
- C. Li, Z. Luo, Y. Liu, Y. Wei, X. He, Z. Chen, L. Zhang, Y. Chen, W. Wang, Y. Liu, X. Chang and Z. Quan, Adv. Opt. Mater., 2022, 10, 2102746 CrossRef CAS.
- K. Wu, A. Bera, C. Ma, Y. Du, Y. Yang, L. Li and T. Wu, Phys. Chem. Chem. Phys., 2014, 16, 22476–22481 RSC.
- M. D. Smith and H. I. Karunadasa, Acc. Chem. Res., 2018, 51, 619–627 CrossRef CAS PubMed.
- L. Mao, Y. Wu, C. C. Stoumpos, M. R. Wasielewski and M. G. Kanatzidis, J. Am. Chem. Soc., 2017, 139, 5210–5215 CrossRef CAS PubMed.
- A. Yangui, S. Pillet, A. Mlayah, A. Lusson, G. Bouchez, S. Triki, Y. Abid and K. Boukheddaden, J. Chem. Phys., 2015, 143, 224201 CrossRef CAS PubMed.
- Y. Lekina and Z. X. Shen, J. Sci.: Adv. Mater. Devices, 2019, 4, 189–200 Search PubMed.
- M. D. Smith, A. Jaffe, E. R. Dohner, A. M. Lindenberg and H. I. Karunadasa, Chem. Sci., 2017, 8, 4497–4504 RSC.
- K. Gauthron, J.-S. Lauret, L. Doyennette, G. Lanty, A. Al Choueiry, S. J. Zhang, A. Brehier, L. Largeau, O. Mauguin, J. Bloch and E. Deleporte, Opt. Express, 2010, 18, 5912 CrossRef CAS PubMed.
- M. Liang, W. Lin, Q. Zhao, X. Zou, Z. Lan, J. Meng, Q. Shi, I. E. Castelli, S. E. Canton, T. Pullerits and K. Zheng, J. Phys. Chem. Lett., 2021, 12, 4965–4971 CrossRef CAS PubMed.
- K. Thirumal, W. K. Chong, W. Xie, R. Ganguly, S. K. Muduli, M. Sherburne, M. Asta, S. Mhaisalkar, T. C. Sum, H. Sen Soo and N. Mathews, Chem. Mater., 2017, 29, 3947–3953 CrossRef CAS.
- D. L. Rousseau, R. P. Bauman and S. P. S. Porto, J. Raman Spectrosc., 1981, 10, 253–290 CrossRef CAS.
- K. Machida, A. Kagayama and Y. Saito, J. Raman Spectrosc., 1978, 7, 188–193 CrossRef CAS.
- N. S. Dahod, A. France-Lanord, W. Paritmongkol, J. C. Grossman and W. A. Tisdale, J. Chem. Phys., 2020, 153, 044710 CrossRef CAS PubMed.
- G. Batignani, G. Fumero, A. R. Srimath Kandada, G. Cerullo, M. Gandini, C. Ferrante, A. Petrozza and T. Scopigno, Nat. Commun., 2018, 9, 1971 CrossRef PubMed.
- R. G. Niemann, A. G. Kontos, D. Palles, E. I. Kamitsos, A. Kaltzoglou, F. Brivio, P. Falaras and P. J. Cameron, J. Phys. Chem. C, 2016, 120, 2509–2519 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2164940. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ma00752e |
| This journal is © The Royal Society of Chemistry 2022 |