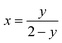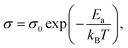Unusual electronic transport in (1 − x)Cu₂Se–(x)CuInSe₂ hierarchical composites

Abstract

The ability to control the relative density of electronic point defects as well as their energy distribution in semiconductors could afford a systematic modulation of their electronic, optical, and optoelectronic properties. Using a model binary hybrid system Cu₂Se–CuInSe₂, we have investigated the correlation between phase composition, microstructure, and electronic transport behavior in the synthesized composites. We found that both Cu₂Se and CuInSe₂ phases coexist at multiple length scales, ranging from sub-ten nanometer to several micrometers, leading to the formation of a hybrid hierarchical microstructure. Astonishingly, the electronic phase diagram of the (1 − x)Cu₂Se–(x)CuInSe₂ (15% ≤ x ≤ 100%) hierarchical composites remarkably deviates from the trend normally expected for composites between a heavily doped semiconductor (Cu₂Se) and a poorly conducting phase (CuInSe₂). A sudden 3-fold increase in the electrical conductivity and carrier concentration along with a marginal increase in the carrier mobility is observed for composites at the vicinity of equimolar composition (48% ≤ x ≤ 52%). The carrier concentration increases from ∼1.5 × 10²⁰ cm⁻³ for the composites with x ≤ 45% to 5.0 × 10²⁰ cm⁻³ for x = 50%, and remains constant at 4.5 × 10²⁰ cm⁻³ with x value in the range of 52% < x ≤ 90%, then quickly drops to 8 × 10¹⁸ cm⁻³ for pristine CuInSe₂ phase (x = 100%). The atypical electronic behavior was rationalized in the light of the formation of an inter-band (IB) within the band gap, which arises from the hybridization of native electronic point defects from both Cu₂Se and CuInSe₂ phases in the resulting hierarchical composites. The result points to a new strategy to modulate the electronic structure of semiconductor composites to maximize interaction and coupling between two fundamentally contrasting properties enabling access to electronic hybrid systems with potential applications as interactive and stimuli-responsive multifunctional materials.

---

1. Introduction

Semiconductor materials and devices have been powering the information technologies since the invention of transistor in 1947,¹ and continue to bring about technological innovations, which deeply revolutionize our lives today. An important step in designing a semiconductor with a unique functionality, such as electrical conductivity, light absorption and emittance, magnetism, etc.^2–5 relies on the understanding and manipulation of the type, density, as well as the energy distribution of electronic point defects within the crystal structures. Point defects are crucial in dictating the electronic performance of semiconductors as they afford the opportunity to control more fundamental parameters, namely the carrier concentration and mobility, that significantly influence macroscopic properties, such as the magnetism,⁶ piezoelectricity,⁷ superconductivity,⁸ thermoelectricity,^9,10etc.

Point defects engineering via doping the host material using heterovalent atoms or/and through deliberate off-stoichiometry,¹¹ remains the most popular approach to tune the concentration of free carriers in semiconductors. The change generated by doping is usually monotonic, especially when the dopant only generates one type of electronic defect. For example, the number of free electrons (holes) would increase with increasing donor (acceptor) dopant concentration until a bottleneck is reached.^12,13 This feature has given researchers an intuitive approach to improve the functionalities of semiconductors, however, it can usually only optimize the intrinsic single functionality.

Unfortunately, this traditional method of tuning dopant concentration may be insufficient for the development of more intelligent semiconductors for next generation high-performance electronic devices, such as stimuli responsive multifunctional semiconductors, which can adapt to varying environments or allow remote control over one functionality by another. In pursuit of such advanced semiconductors, efforts have been made to incorporate dopants that can add new functionalities to the host material. For example, Ni²⁺ was integrated into ZnSe, CdZnS and CuInS₂ nanocrystals to enable above room-temperature ferromagnetism which coexisted with the tunable optical emission originating from the nanocrystals.¹⁴ Currently, many efforts to design multifunctional semiconductors have been focused on doping transition metals in quantum dots hosts,¹⁵ taking advantage of their quantum confinement effects. Despite many advantages of quantum dots (chemical and physical tunability, high quantum efficiency), there still exist numerous challenges for this nanoscale semiconductor, particularly its metastability and synthesis difficulties.¹⁶ In addition, the coupling between the coexisting functionalities in traditional multifunctional materials remains weak. Therefore, exploring new ways to create strongly interacting multifunctionalities in semiconductors is of paramount importance if one wants to develop high-performance stimuli-responsive semiconductors for next generation electronic devices.

Here, we introduce an elegant approach to multifunctional semiconducting materials featuring a strong interaction between two fundamentally contrasting functionalities. Our strategy consists of the structural integration, at multiple length scales (from nano- to micron-scale), of two phases with dissimilar but related structures and chemistries, each of which possesses a single functionality, into a hybrid composite hierarchical structure. We anticipate that the unique intimate connectivity between structural fragments from both phases at multiscale can give rise to strong interaction between the coexisting functionalities, which could lead to new physical phenomena and stimuli-responsive behaviors.

To explore this concept, we have synthesized a series of hybrid (1 − x)Cu₂Se/(x)CuInSe₂ (15% ≤ x ≤ 100%) composites within which Cu₂Se-rich and CuInSe₂-rich domains with various size and shapes are intimately integrated at the micron as well as nanometer scale. The Cu₂Se–CuInSe₂ hybrid system provides a model platform for the investigation of how the hierarchical structure integration of two semiconductors with different band gaps and electrical conductivities modifies electronic transport in the resulting composites. Beyond the similarity in their chemical constituents, both Cu₂Se and CuInSe₂ are well studied technologically important materials. β-Cu₂Se is a narrow band gap semiconductor that has attracted increasing attention for use as a promising thermoelectric material,^17–23 whereas CuInSe₂ is a wider band gap semiconductor with high absorption coefficient used as a solar absorber layer in solar cell devices.^24,25 Moreover, a recent study on Cu₂Se reported the electroresistance effect, induced by electric-field-driven crystalline orientation change.²⁶ Therefore it is reasonable to expect that (1 − x)Cu₂Se/(x)CuInSe₂ composites would exhibit interactions with several external stimuli, such as light, temperature gradient and electric potential. In addition, the coexistence of native donor and acceptor point defects in both pristine Cu₂Se and CuInSe₂ phases makes this system particularly attractive for investigations of the change in the interaction between these defects upon varying the phase ratio between Cu₂Se and CuInSe₂. The systems provide the opportunity to probe the electronic band structure of various (1 − x)Cu₂Se/(x)CuInSe₂ composites. For instance, elucidating how the density and distribution of donor and acceptor point defects are altered in various composites could pave the way to a better understanding of the dynamics of electronic transport under various external stimuli such as temperature and illumination.

(1 − x)Cu₂Se/(x)CuInSe₂ composites with the desired hierarchical integration between Cu₂Se-rich and CuInSe₂-rich domains were fabricated through a single step solid-state transformation of a CuSe₂ template following a reaction concept described by Olvera et al.¹⁷ The similarity in the lattice parameters (within the ab plane) of the cubic β-Cu₂Se and the tetragonal CuInSe₂ phases at the reaction temperature facilitates the formation of stable semi-coherent interfaces, which enables the creation of Cu₂Se nano-domains within the CuInSe₂ micron size domain ([Cu₂Se]_nano@[CuInSe₂]_micron) simultaneously with the formation of CuInSe₂ nano domains within the Cu₂Se micron size particle ([CuInSe₂]_nano@[Cu₂Se]_micron). With the unique microstructure, unexpected trend in electrical conductivity was revealed, with a sudden large increase near the equimolar compositions (48% ≤ x ≤ 52%). Investigation of carrier concentration and mobility on selected compositions not only explains the observed large increase in the electrical conductivity for equimolar compositions, but also indicates a significant alteration of the density and energy distribution of point defects in various composites and suggests a unique interaction between point defects for nearly equimolar compositions. The observed peculiar electronic behavior for equimolar (1 − x)Cu₂Se/(x)CuInSe₂ composites is rationalized within the context of an interband (IB) formation arising from the hybridization of shallow and deep acceptor states from both the Cu₂Se and CuInSe₂ phases. This work demonstrates that several unexpected stimuli-responsive semiconducting behaviors with potentially significant technological applications may emerge from hierarchical hybrid structures constructed between different semiconductors.

2. Experimental section

2.1. Sample preparation

High-purity Cu (99.5%, Alfa Aesar), Se (≥99.5%, Sigma-Aldrich) and In (99.99%, Alfa Aesar) powders were used for the material synthesis. The (1 − x)Cu₂Se/(x)CuInSe₂ composites were synthesized via a one-step solid-state reaction, following the chemical equation below:

CuSe₂ + (y)In + 3(1 − y)Cu → (y)CuInSe₂ + 2(1 − y)Cu₂Se

The mole fraction (x) of CuInSe₂ reported for various (1 − x)Cu₂Se/(x)CuInSe₂ composites is calculated as:

The CuSe₂ precursor was synthesized through a solid-state reaction of stoichiometrically mixed elemental Cu and Se powders. The mixed powder was flame-sealed into a quartz tube under dynamic vacuum (10⁻³ torr). The sealed tube was heated at 210 °C for 24 hours, followed by another heating at 320 °C for 36 hours. A second annealing of the resulting product at 270 °C for an additional 72 hours was necessary to obtain a single phase CuSe₂ sample. To prepare (1 − x)Cu₂Se/(x)CuInSe₂ composites, the desired amount of In and Cu powders were thoroughly mixed with the CuSe₂ precursor and sealed in a quartz tube under a residual pressure of 10⁻³ torr. The mixtures were reacted following a stepwise heating profile: 150 °C for 24 hours, 320 °C for 48 hours and 600 °C for 48 hours. This process enables the simultaneous conversion of CuSe₂ into CuInSe₂ and Cu₂Se. The final product was pulverized into fine powder by hand-grinding. Then the powder was loaded into a graphite die and densified at 500 °C under vacuum using a uniaxial hot press with a pressure of 100 MPa. Two rectangular bar-shape specimens were cut out from the obtained high-density cylindrical bulk sample, one of which was used for electrical conductivity measurement, and another was used for the Hall measurement.

2.2. Characterization

Powder X-ray diffraction (PXRD) was conducted to determine the phase composition and crystal structure of both the as-synthesized powder and the densified samples. The Rigaku Smartlab X-ray diffractometer was operated at 40 kV and 44 mA with Cu Kα incident radiation (λ = 1.54059 Å), and a D/tex ultra 250 high-speed detector on the receiving side. Differential scanning calorimetry (DSC) was carried out on a Netzsch DSC 404 F1 Pegasus to investigate the evolution of the thermal behavior of Cu₂Se and CuInSe₂ phases in (1 − x)Cu₂Se/(x)CuInSe₂ composites upon varying the CuInSe₂ phase fraction (x value). DSC data also helped to assess the thermal stability of the samples. The microstructure and phase distribution of the densified samples were evaluated by a JEOL JSM-7800FLV scanning electron microscope, which was operated under backscatter electron (BSE) detection mode. Chemical composition was also analyzed by the energy dispersive spectrum (EDS) mapping with the attached Oxford XMaxN 80 mm² silicon-drift energy-dispersive X-ray spectrometer. Nano-scale phase integration was examined by a JEOL 3100R05 transmission electron microscope (TEM) with double Cs correction, operated at 300 kV. The electrical conductivity was measured with a ULVAC-RIKO ZEM-3 system by four-probe method from room temperature up to 773 K with low-pressure helium gas. Hall coefficient was obtained on a home-built instrument under ±0.5 T magnetic field.

3. Results and discussion

3.1. Synthesis and microstructure

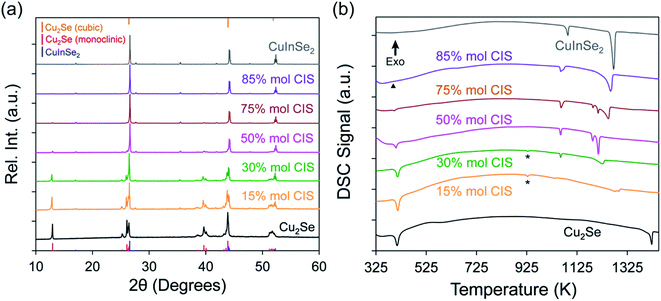
The approach utilized to synthesize the array of (1 − x)Cu₂Se/(x)CuInSe₂ composites is adapted from the versatile topochemical method previously developed in our group.^17,27 This synthesis concept relies on the reductive solid-state transformation of a sacrificial template CuSe₂, where Cu²⁺ and (Se₂)²⁻ are reduced to Cu⁺ and Se²⁻ upon introduction of metallic copper and indium powders. Due to the compositional and structural similarities between CuSe₂ and the targeted phases (Cu₂Se and CuInSe₂), a direct and simultaneous conversion from the CuSe₂ precursor to the final products in a single step is expected, which minimizes the formation of undesirable impurities. To probe the comprehensive changes in the electronic transport properties, as well as the microstructure evolution, within various portions of the Cu₂Se–CuInSe₂ pseudo-binary system, a total number of 23 compositions were selected and prepared. They can be divided into four groups: (i) 15% ≤ x ≤ 30% (4 samples); (ii) 40% ≤ x ≤ 60% (7 samples); (iii) 65% ≤ x ≤ 90% (7 samples), and (iv) 92% ≤ x ≤ 100% (4 samples). In addition, pure Cu₂Se (x = 0%) was also synthesized for use as a comparison.

To investigate the effectiveness of the facile synthesis method, the as-synthesized powders were evaluated by X-ray diffraction (XRD). As shown in the Fig. 1a, all diffraction peaks of various (1 − x)Cu₂Se/(x)CuInSe₂ composites can be indexed with monoclinic α-Cu₂Se (C2/c) and tetragonal CuInSe₂ (I4̄2d). The change in the phase fraction can be qualitatively characterized by the variation in the relative peak intensity between α-Cu₂Se (∼13° and ∼40°) and CuInSe₂ (∼26° and ∼44°). The intensity of the diffraction peaks for α-Cu₂Se gradually decreases upon increasing the CuInSe₂ concentration (x value), while those associated with the CuInSe₂ phase increase. Based on the phase diagram (Fig. S1a†), Cu₂Se and CuInSe₂ have very limited solubility in each other at room temperature (<3 mol% CuInSe₂ in Cu₂Se matrix, and <2 mol% Cu₂Se in CuInSe₂ matrix). Therefore, it is anticipated that both phases would be clearly distinguished within most of our synthesized compositions (15% ≤ x ≤ 98%). However, the diffraction peaks from the Cu₂Se phase surprisingly almost vanish starting from x ≥ 50% and completely disappear at x = 85%, while the diffraction peaks from the CuInSe₂ phase dominate (Fig. S2†). Although this observation can be partially explained by the stronger diffraction power of the CuInSe₂ phase compared to the Cu₂Se phase, owing to its larger average atomic number (Z_av(CuInSe₂) = 36.5; Z_av(Cu₂Se) = 30.7), it also suggests that a significant portion of the Cu₂Se phase is present at the subnanometer scale, which may lead to diffuse scattering. The XRD patterns of various composites after hot-pressing (Fig. S3†) are similar to those of the as-synthesized powder samples. No peaks associated with the decomposition were detected after compaction at 500 °C and 100 MPa, showing their good thermal stability. The change in the peak ratios after densification can be attributed to preferential orientation after uniaxial pressing.

Fig. 1 Representative powder X-ray diffraction (PXRD) patterns and differential scanning calorimetry (DSC) curves of as-prepared (1 − x)Cu₂Se/(x)CuInSe₂ composites. (a) All XRD diffraction peaks can be indexed with Cu₂Se (monoclinic) and CuInSe₂ (tetragonal) showing high purity of the synthesized composites. With increasing x value, the peak intensities of Cu₂Se are reduced while those of CuInSe₂ continuously grow. Cu₂Se (cubic) might also exist with high concentration of CuInSe₂. (b) Most (1 − x)Cu₂Se/(x)CuInSe₂ composites show two characteristic phase transitions resulted from the microscale Cu₂Se and CuInSe₂ phases. An endothermic peak at ∼929 K is denoted by *, which suggests the existence of nano-scale CuInSe₂ phase. The absence of an endothermic peak at ∼410 K is denoted by ^▲, which indicates the formation of nano-scale Cu₂Se phase.

The coexistence of both Cu₂Se and CuInSe₂ phases within various (1 − x)Cu₂Se/(x)CuInSe₂ composites was further confirmed by differential scanning calorimetry (DSC) measurements on the power samples(Fig. 1b). In the pure Cu₂Se phase, the endothermic peaks at ∼410 K and ∼1420 K correspond to the phase transition from α-Cu₂Se to β-Cu₂Se and the melting temperature. Likewise, thermal events in pure CuInSe₂ associated with the phase transition from tetragonal to cubic CuInSe₂ and its melting can be observed at ∼1087 K and ∼1270 K, respectively. Those two characteristic phase transition temperatures are also noted on the DSC heating curves for various (1 − x)Cu₂Se/(x)CuInSe₂ composites. The high-temperature peaks of all composites agree with the complex incongruent melting behavior in the Cu₂Se–CuInSe₂ pseudo-binary phase diagram (Fig. S1b†). The DSC curves further prove the successful synthesis of the composites.

There are also two interesting features, which are not shown in the phase diagram, but observed in our measurements. For samples with 15% ≤ x ≤ 45%, a small endothermic peak is shown at ∼929 K (Fig. 1b and S4†), which is about 150 K below the tetragonal-to-cubic phase transition temperature of bulk CuInSe₂. The appearance of this peak cannot be indexed on the phase diagram and is possibly due to the presence of detectable amount of nanoscale CuInSe₂ crystals that result in the depressed phase transition temperature compared to bulk CuInSe₂. Similar behavior has been observed in nanocrystalline Cu₂S^28,29 and Ag₂Se,³⁰ where the large surface-to-volume ratio of nanoscale phases significantly decreases the solid-to-solid phase transition temperature. The magnitude of the peak at ∼929 K gradually decreases until x = 48% where it is no longer detectable. In the meantime, another endothermic peak at ∼1060 K continues to grow. This peak at ∼1060 K should also correspond to the tetragonal-to-cubic phase transition of CuInSe₂ since it becomes gradually closer to the phase transition peak of the pure CuInSe₂ with the increasing x value. But this CuInSe₂ phase would be on a much larger scale. Because the phase transition temperature is usually linearly dependent on the reciprocal crystallite size³¹ and this temperature is only ∼30 K lower than the bulk phase transition temperature (∼1087 K), the size of this CuInSe₂ phase is probably on microscale. The relative variation of these two distinguishable phase transition peaks indicates that, CuInSe₂ mostly crystalizes in nanoscale at lower concentration (x < 48%). With the increasing content of CuInSe₂, its microscale phase starts to emerge and is coexisting with the CuInSe₂ nanoscale phase. Starting from x = 48%, the microscale CuInSe₂ phase dominates. Another unusual characteristic is that starting from samples with x = 40%, the endothermic peak associated with the α-Cu₂Se to β-Cu₂Se phase transition (∼410 K) quickly diminishes and completely vanishes for samples with x ≥ 85%. This is different from the prediction of the phase diagram (Fig. S1b†). Similarly, when crystallite size of Cu₂Se is reduced to nanoscale, its phase transition is shifted to a much lower temperature. Given the moderate phase transition temperature of bulk Cu₂Se (∼410 K), it is likely that nanoscale Cu₂Se can adopt the cubic structure at room temperature, which will no longer experience phase transition when temperature increases. This also explains why the monoclinic α-Cu₂Se phase is not being observed on the XRD patterns of samples with x ≥ 85% (Fig. S2†). Since all peaks of β-Cu₂Se cubic phase almost overlap with those of tetragonal CuInSe₂ (Fig. 1a) and the latter has stronger diffraction power, it was hard to differentiate the cubic β-Cu₂Se phase in the XRD patterns. The cooling curves of all composites (Fig. S4e–h†) match well with the heating curves without any impurity peaks, showing good thermal stability and reversibility of phase formation in all samples. The characteristic variation in the thermal behavior of Cu₂Se and CuInSe₂ phases within various (1 − x)Cu₂Se/(x)CuInSe₂ composites strongly points to a significant alteration in the multiscale integration of the coexisting phases with the increasing CuInSe₂ phase fraction.

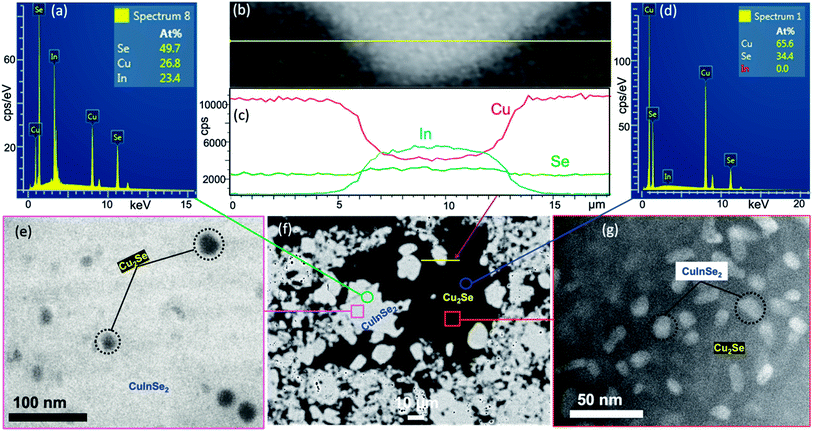
To assess the evolution of the microstructure in (1 − x)Cu₂Se/(x)CuInSe₂ composites with the phase fraction (x values), SEM and TEM studies were performed on selected compositions after hot pressing. As shown in Fig. 2, back scattered electron (BSE) images of samples with x = 15%, 45%, 50% and 90% revealed the formation of a two-phase mixture, as indicated by the light-grey and the black domains. The energy dispersive spectrum (EDS) composition mapping of both domains showed a higher concentration of copper (Cu) element within the black domains, whereas the indium (In) element was exclusively observed within the light-grey areas (Fig. S5†). Selenium (Se) was distributed in both domains, with higher concentration of Se overlapping with the areas of In, which is consistent with the larger stoichiometric ratio of Se in CuInSe₂ compared to Cu₂Se. This result strongly suggests that the black domain is predominantly the Cu₂Se-rich phase, whereas the light-grey domain is the CuInSe₂-rich phase. The composition of each domain was further confirmed by EDS point analysis. It was found that the light-grey domain contains ∼27 at% Cu, ∼23 at% In and ∼50 at% Se (Fig. 3a), which is close to the stoichiometry of CuInSe₂. Likewise, the black domain was found to contain ∼66 at% Cu and ∼34 at% Se (Fig. 3d), which is consistent with Cu₂Se stoichiometry. Line-scan analysis across the microscale boundaries between the Cu₂Se and CuInSe₂ domains shows a rapid drop of the Cu content and a rapid increase of the In concentration upon crossing the boundary from the black to light-grey domain (Fig. 2b and c), which suggests a limited degree of solid-solution within the relatively thin, ∼2 μm, boundary between the two phases.

Fig. 2 BSE images of selected (1 − x)Cu₂Se/(x)CuInSe₂ composites. (a) and (d) x = 15%; (b) x = 45%; (c) and (f) x = 50%; (e) x = 90%. The formation of submicron particles of the Cu₂Se phase within large particles of the CuInSe₂ phase are readily seen. Inversely, small particles of the CuInSe₂ phase are also observed within the microscale Cu₂Se particles. This highlights the integration of coexisting phases at sub-micron and micron levels. (d) and (f) show that the level of intermixing between small particles of both Cu₂Se and CuInSe₂ phase increases with increasing x value, suggesting the simultaneous co-nucleation of both phases during the local solid-state transformation of the CuSe₂ matrix by reacting with elemental Cu and In.

Fig. 3 Illustration of the all-scale (nano to micron) hierarchical integration of Cu₂Se and CuInSe₂ phases within the Cu₂Se(50%)–CuInSe₂(50%) composite. EDS point analysis of CuInSe₂-rich domain (a) and Cu₂Se-rich domain (d); (b) line scan across CuInSe₂/Cu₂Se interfaces and (c) composition mapping revealing the sharp variation in the In and Cu contents. This suggests a poor solubility between the coexisting phases. (e) High magnification TEM image of the CuInSe₂-rich domain revealing the presence of nanometer scale Cu₂Se particles ([Cu₂Se]_nano@[CuInSe₂]_micron). (g) High magnification TEM image of the Cu₂Se-rich domain revealing the presence of nanometer scale CuInSe₂ particles ([CuInSe₂]_nano@[Cu₂Se]_micron). (f) BSE image showing the micrometer scale integration of CuInSe₂ and Cu₂Se domains.

Interestingly, both domains appear in various sizes ranging from submicron (∼0.1 μm) to several tens of microns. A careful examination of the SEM images from selected samples also revealed the presence of many small particles of the black domain within micron-size particles of the light-grey phase. This indicates the micron-scale integration of the Cu₂Se phase within the CuInSe₂ domain (Fig. 2). Inversely, some small particles of the light-grey phase can also be seen within the black domain, which also points to micron-scale integration of CuInSe₂ phase within the Cu₂Se domain. The level of intermixing between the coexisting Cu₂Se-rich and CuInSe₂-rich domains increases with the increasing CuInSe₂ content, which is manifested by the formation of a higher density of dark and light-grey domains with increasingly smaller size (Fig. 2c and f). The formation of such a mixture of intertwined small particles of both domains, instead of the agglomeration of Cu₂Se and CuInSe₂ particles into larger domains, suggests a simultaneous nucleation and growth of both phases through a local competing reduction and solid-state transformation of the CuSe₂ template by elemental Cu and In during the reaction. This mutual integration of Cu₂Se and CuInSe₂ domains at microscale also suggests the formation of a relatively stable Cu₂Se/CuInSe₂ interfaces. Therefore, one can anticipate further mutual integration of the Cu₂Se and CuInSe₂ domains at nanometer and even atomic scale. To probe this hypothesis, high magnification TEM images of the sample with x = 50% were obtained by focusing the analysis on small areas of micron size particles: the (i) CuInSe₂-rich (light-grey domain) and (ii) Cu₂Se-rich (dark domain) phases. Indeed, our result revealed the presence of (i) nanometer scale particles of the Cu₂Se phase within the CuInSe₂ domain ([Cu₂Se]_nano@[CuInSe₂]_micron) as shown in Fig. 3e, and (ii) nanometer scale particles of CuInSe₂ phase within the Cu₂Se domain ([CuInSe₂]_nano@[Cu₂Se]_micron) as shown in Fig. 3g. This multiscale mutual integration between Cu₂Se and CuInSe₂ phases signifies the formation of a hierarchical structure within the composites. Given the unique distributions of these two phases at nano and micron scales, it is anticipated that the electronic behaviors of the composites would be significantly different from those of the microscale composites obtained through simple mixing of Cu₂Se and CuInSe₂.

3.2. Electronic properties

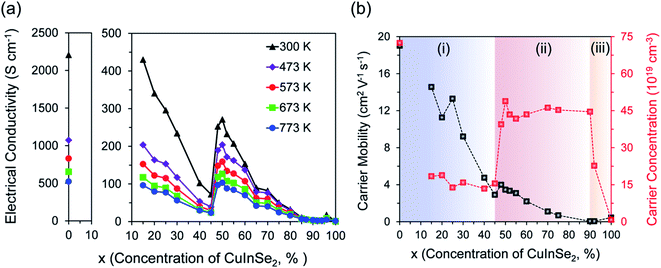
To explore the effect of the variation in the fraction of Cu₂Se and CuInSe₂ phases and the correlated change in the hierarchical microstructure, on the electronic properties of (1 − x)Cu₂Se/(x)CuInSe₂ composites, temperature-dependent electrical conductivity measurement was performed on the entire series of samples. As shown in Fig. 4a, the phase-dependent electrical conductivity of (1 − x)Cu₂Se/(x)CuInSe₂ hierarchical composites at selected temperatures exhibits interesting peculiar features that could not be anticipated for a simple mixture between a heavily doped semiconductor, Cu₂Se, and an intrinsic semiconductor, such as CuInSe₂ (Fig. S6†). At 300 K, the electrical conductivity of pristine Cu₂Se is 2207 S cm⁻¹ whereas the pure CuInSe₂ phase displays a much lower electrical conductivity of ∼0.55 S cm⁻¹. The electrical conductivity of (1 − x)Cu₂Se/(x)CuInSe₂ composites initially decreases drastically upon incorporating various fractions of CuInSe₂. For instance, the electrical conductivity at 300 K drops 5 folds to ∼430 S cm⁻¹ for x = 15% and continues to decrease linearly with increasing x value reaching a minimum of ∼70 S cm⁻¹ for x = 45%. Astonishingly, the electrical conductivity abruptly increases by 3.5 folds to ∼250 S cm⁻¹ upon further increasing the CuInSe₂ content to 48% and reaches the maximum value of ∼275 S cm⁻¹ for the composition with x = 50%. Further increasing the CuInSe₂ phase fraction beyond the equimolar composition resulted in a gradual drop in the electrical conductivity to values as low as 0.5 S cm⁻¹ for compositions with x > 85%. Interestingly, the minimal electrical conductivity value observed at the onset of the discontinuity (x = 45%) is not matched until the composition with x = 70% is reached. This trend is valid at all temperatures between 300 and 773 K, suggesting the thermal stability of the microstructure of (1 − x)Cu₂Se/(x)CuInSe₂ composites within this temperature window.

Fig. 4 (a) Dependence of electrical conductivity on concentration of CuInSe₂ phase at different temperatures. (b) Hole concentration and mobility of (1 − x) Cu₂Se/(x) CuInSe₂ composites. The results are categorized into three regions based on the trend of the hole concentration.

While the initial drop in the electrical conductivity of samples with x ≤ 45% can be anticipated from the incorporation of a poorly conductive secondary phase within a highly conductive matrix,^24,32–36 the observed sudden large increase for the 48 mol% and 50 mol% CuInSe₂, suggests either the formation of a new phase, such as Cu₃InSe₃, with a different molecular structure and thus different electronic band structure, or a sharp alteration of the electronic band structures of both Cu₂Se and CuInSe₂ phases, owing to their multiscale hierarchical integration within the (1 − x)Cu₂Se/(x)CuInSe₂ composites. The former hypothesis can be ruled out, because the XRD, SEM and TEM only show the coexistence of Cu₂Se and CuInSe₂ phases in the sample with x = 50% and the Cu₃InSe₃ phase is absent below 1180 K from the Cu₂Se–CuInSe₂ pseudo binary phase diagram (Fig. S1a†).

Therefore, the unusual phase-dependent behavior of the electrical conductivity of (1 − x)Cu₂Se/(x)CuInSe₂ composites must be rationalized by assuming the alteration of the original electronic band structure of the constituent phases to form a hybrid electronic structure as discussed below. However, we must first elucidate the underlying physics governing the observed change in the electrical conductivity of various samples. Since the electrical conductivity is directly related to carrier concentration (P_H) and mobility (μ_H), σ = eP_Hμ_H, it is necessary to investigate how P_H and μ_H change with the compositions. Therefore, Hall effect measurement at 300 K on selected samples was conducted to extract the Hall coefficient (R_H). The carrier concentration and mobility were then obtained using P_H = 1/(eR_H) and μ_H = σR_H, where σ and e are the electrical conductivity and the elementary charge, respectively. All samples show positive R_H values at 300 K indicating holes as majority charge carriers (Fig. S8†). At 300 K, pristine Cu₂Se displays a hole concentration of 7.2 × 10²⁰ cm⁻³ and hole mobility of 19 cm² V⁻¹ s⁻¹(Fig. 4b), both of which are comparable to the values in the literature.^20,37 On the other hand, pure CuInSe₂ exhibits a significantly lower hole concentration (∼8 × 10¹⁸ cm⁻³) and hole mobility (∼0.5 cm² V⁻¹ s⁻¹) compared to pristine Cu₂Se, which explains its inferior electrical conductivity value. Similar to the phase-dependent electrical conductivity (Fig. 4a), the variation of the carrier concentration and carrier mobility of (1 − x)Cu₂Se/(x)CuInSe₂ composites with increasing CuInSe₂ content (x values) can be divided into three regions. For compositions with x ≤ 45%, the carrier concentration of various composites remains nearly constant at ∼1.5 × 10²⁰ cm⁻³, whereas the carrier mobility drastically decreases from 14 cm² V⁻¹ s⁻¹ for the sample with x = 15% to 3 cm² V⁻¹ s⁻¹ for the sample with x = 45%. The large drop in the carrier mobility suggests that the initial drop in the electrical conductivity of (1 − x)Cu₂Se/(x)CuInSe₂ composites with x ≤ 45% likely originates from the increased scattering of free carriers at the Cu₂Se/CuInSe₂ interfaces between α-Cu₂Se matrix and CuInSe₂ inclusions rather than by a drop in the carrier density within the Cu₂Se matrix. Within this composition range, the Cu₂Se-matrix is largely dominated by the α-Cu₂Se phase, which is doped through partial dissolution of elemental In within its crystal lattice, giving rise to incoherent α-Cu₂Se/CuInSe₂ interfaces. This explains the drop in the carrier mobility of (1 − x)Cu₂Se/(x)CuInSe₂ composites with x ≤ 45% as well as their lower carrier density compared to pristine Cu₂Se.

For compositions with 45% < x ≤ 90%, a sudden increase in the carrier concentration from ∼1.5 × 10²⁰ cm⁻³ for x = 45% to ∼4.0 × 10²⁰ cm⁻³ (x = 48%) and then to ∼5.0 × 10²⁰ cm⁻³ (x = 50%) is observed. The carrier concentration then remains constant at ∼4.5 × 10²⁰ cm⁻³ with further increase in the CuInSe₂ content up to x = 90% (Fig. 4b). Within the composition range of 90% ≤ x < 100%, the matrix is dominated by the CuInSe₂ phase with Cu₂Se acting as inclusions. A sharp drop in the carrier density from ∼4.5 × 10²⁰ cm⁻³ to ∼2.3 × 10²⁰ cm⁻³ is observed upon increasing the CuInSe₂ content from x = 90% to x = 92%. Note that the carrier density for the composition with x = 92% remains ∼29 times larger than that of pristine CuInSe₂. One can therefore understand the carrier density trend within region (III) as doping of the insulating CuInSe₂ phase by electronic defects from the Cu₂Se phase.

The carrier density and mobility phase diagram at 300 K, illustrated in Fig. 4b, sheds light on the unusual dependence of the electrical conductivity of (1 − x)Cu₂Se/(x)CuInSe₂ composites on the CuInSe₂ phase fraction. For instance, it is now evident from this data that the enhancement in the electrical conductivity observed for samples with x = 48% and 50% originates from the large increase in the carrier concentration. One explanation of the observed increase in the carrier density of samples with 48% ≤ x ≤ 90%, compared to the sample with x = 45% could be the increase in the fractions of β-Cu₂Se within these samples, owing to its highly disordered and mobile Cu⁺ ions. However, the strength of such explanation is diminished by the observed marginal increase in the carrier mobility for samples with x = 48% and x = 50% compared to the sample with x = 45%. This is because the large increase in carriers scattering (carrier–carrier scattering as well as carrier scattering by mobile Cu⁺ ions) that would normally result from the increase in hole density, and Cu disorder should lead to a drastic reduction in the carrier mobility rather than the observed marginal increase in carrier mobility. Therefore, a more complex doping mechanism, which considers the electronic interaction between the coexisting Cu₂Se and CuInSe₂ phases, must be explored to rationalize the observed surprising increase in both the carrier density and carrier mobility for the samples with x = 48% and 50%, as discussed below.

3.3. Band picture for hierarchical composites

To explore the interactions of electronic defects in composites consisting of Cu₂Se and CuInSe₂, it is imperative to first understand the impurity defects in individual components. CuInSe₂ initially behaves like a weakly degenerate semiconductor from 300–500 K (Fig. S6 and S7a†). This indicates the existence of a shallow acceptor level, which is already ionized at comparatively low temperatures. Since the lowest acceptor level in CuInSe₂ (CIS) is copper vacancy, [V_Cu]_CIS⁻ with the activation energy of only 0.03 eV,³⁸ it is reasonable to deduce that Cu vacancies in the CuInSe₂ phase are ionized at 300 K. Increasing the temperature enhances carrier scattering, leading to the observed decreasing trend in the electrical conductivity. Once the temperature rises above 500 K, the electrical conductivity shows an interesting increasing trend in CuInSe₂, which is similar to the reports on other chalcopyrites, such as (Cu,Ag)(In,Ga)Te₂,^39–41 and it is believed to be related to in-gap deeper acceptor levels. To understand the essence of the thermally activated conduction, the electrical conductivity of CuInSe₂ at high temperature was assessed using the Arrhenius equation:
where σ₀ is the conductivity at infinite temperature, E_a is the activation energy, and k_B is the Boltzmann constant.^32,34 The activation energy is found to be ∼0.2 eV, which is much smaller than the well-known band gap of CuInSe₂ (1.04 eV ^42,43), corroborating the assumption that another defect acceptor state is present in between the valence and conduction bands. Therefore, when the temperature increases, electrons are excited to the acceptor state leaving behind free holes in the valence band, which leads to an increase of the electrical conductivity. Once the acceptor state is fully occupied at 740 K, the conductivity enters the saturation range (Fig. S6†). By comparing our result with the theoretically predicted values of the defect energy level in CuInSe₂, we conclude that this acceptor state is likely from [V_In]_CIS⁻, which was calculated to be at around 0.17 eV above the E_v.³⁸

Similar analyses can be conducted on composites with x = 90% and 94% and the results are presented in Fig. S7b.† It shows that the carrier activation energy continues to decrease linearly from 0.2 eV for 100% CuInSe₂ to 0.06 eV for 90% CuInSe₂. This rapid decline in the activation energy again points to the significant influence of Cu₂Se on the electronic structure of CuInSe₂. Since CuInSe₂ does not have additional acceptor states between the aforementioned [V_Cu]_CIS⁻ and [V_In]_CIS⁻ states, the origin for this significant decrease in activation energy with just 10% Cu₂Se addition must be the incorporation of extrinsic [V_Cu]_CS⁻ acceptor states by the Cu₂Se (CS) phase. This analysis is reasonable, because it is well-known that Cu vacancies are generated easily in Cu₂Se due to its negative formation energy.^37,44 The low activation energy of Cu vacancies and its high density also explain why Cu₂Se shows a heavily doped semiconducting behavior (Fig. S6†), despite its moderate band gap of 1–1.2 eV reported for α-Cu₂Se.^45,46

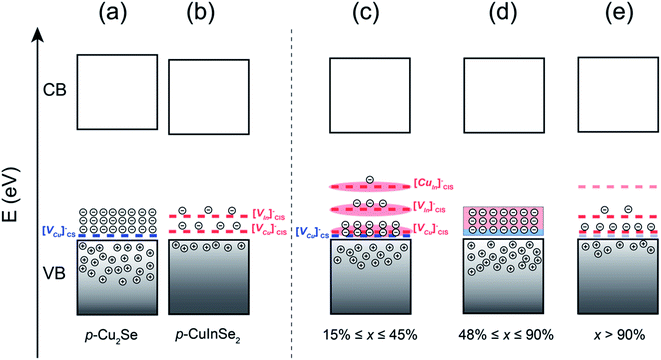
Strengthened by this knowledge of the distribution of various acceptor states in Cu₂Se and CuInSe₂, the band structures for the pristine phases are schematically illustrated in Fig. 5a and b. It is also worthwhile to note that, besides the defect levels mentioned above, new defects can form upon integrating Cu₂Se and CuInSe₂ phases together. Indeed, a careful evaluation of the elemental concentrations in Cu₂Se and CuInSe₂ phases (Table S1†) reveals that Cu₂Se is always Cu-poor, while CuInSe₂ is Cu-rich, suggesting diffusion of Cu from Cu₂Se to CuInSe₂. These off-stoichiometries can also result in the formation of antisite defects [Cu_In]_CIS⁻ in CuInSe₂, which is a much deeper acceptor state with the activation energy of 0.29 eV above E_v.³⁸

Fig. 5 Schematic band structures for (a) pure Cu₂Se, (b) CuInSe₂, and (1 − x)Cu₂Se/(x)CuInSe₂ composites with (c) 15% ≤ x ≤ 45%, (d) 48% ≤ x ≤ 90% and (e) x > 90%. The blue and red dashed lines are acceptor states in Cu₂Se and CuInSe₂, respectively. The acceptor state in Cu₂Se is [V_Cu]_CS⁻. The lower-level acceptor state in CuInSe₂ is [V_Cu]_CIS⁻, while the higher ones are [V_In]_CIS⁻ and [Cu_In]_CIS⁻. The pink shaded areas demonstrate the band broadening effect with the increasing amount of CuInSe₂. The connected strips in (d) represents the formation of an interband by the shallow and deep acceptor states through hybridization. The semitransparent dashed lines in (e) means a gradual disappearance of [V_Cu]_CS⁻ and [Cu_In]_CIS⁻ states.

To rationalize the unexpected change in the electronic properties observed for (1 − x)Cu₂Se/(x)CuInSe₂ composites, we propose a band picture illustrated in Fig. 5c–e, which takes into account the distribution of electronic defects from both Cu₂Se and CuInSe₂ phases. This assumes that the multiscale hierarchical integration of Cu₂Se and CuInSe₂ phases at both nanometer and micrometer scales in various samples facilitates the interaction of their electronic structures leading to the integration and merging of their work functions. This results in the incorporation of both the shallow acceptor state from the Cu₂Se phase ([V_Cu]_CS⁻) and the shallow and deep acceptor states from the CuInSe₂ phase ([V_Cu]_CIS⁻, [V_In]_CIS⁻, [Cu_In]_CIS⁻) within the narrow band gap of the (1 − x)Cu₂Se/(x)CuInSe₂ hierarchical nanocomposites.

For composites with low CuInSe₂ content (15% ≤ x ≤ 45%), the three acceptor states from CuInSe₂ coexist with the acceptor state in Cu₂Se as discrete states. However, only [V_Cu]_CS⁻ and [V_Cu]_CIS⁻ acceptor states are ionized at 300 K given their low activation energies. The deeper acceptor states, [V_In]_CIS⁻ and [Cu_In]_CIS⁻, are not much accessible to thermally excited electrons from the VB at 300 K. Because the density of [V_Cu]_CS⁻ defects is greater in Cu₂Se than the [V_Cu]_CIS⁻ in the CuInSe₂ phase and the former is not fully compensated by the latter, the overall hole density in (1 − x)Cu₂Se/(x)CuInSe₂ hierarchical nanocomposites initially decreases rapidly upon incorporation of a small fraction of CuInSe₂ (x < 15%). As the fraction of CuInSe₂ phase reaches the percolation limit, x ≥ 15%, the higher density of point defects leads to band broadening^47–50 of the defect levels, which effectively decreases their activation energies (Fig. 5c). Therefore, an increase in the fraction of the CuInSe₂ phase within the range 15% ≤ x ≤ 45% does not significantly change the concentration of point defects that are accessible to thermally excited carrier at 300 K, since the extrinsic [V_Cu]_CIS⁻, [V_In]_CIS⁻, [Cu_In]_CIS⁻ defects incorporated from the CuInSe₂ phase balanced the reduction in the fraction of [V_Cu]_CS⁻ resulting from the decrease in the fraction of the Cu₂Se phase. This explains the relatively constant value of the hole density at 300 K for composites within the range 15% ≤ x ≤ 45%. However, all the point defects contribute to carriers scattering along with the high density of α-Cu₂Se/CuInSe₂ interfaces. This explains the observed drastic decrease in the carrier mobility and the electrical conductivity (Fig. 4) upon increasing the content of CuInSe₂ from x = 15% to x = 45%.

For samples approaching the equimolar compositions (48% ≤ x ≤ 52%), the observed unique electronic behavior when compared to samples with x ≤ 45%, such as the 3-fold increase in both the electrical conductivity and the carrier density, suggests a significant change in the electronic band structure. For instance, the sharp increase in the carrier density implies that deep acceptor states in those samples are now accessible by thermally excited carriers from the VB of the Cu₂Se matrix, and therefore contribute to the electronic conduction. One possible change in the electronic band structure that would lead to such an increase in the density of accessible acceptor states is the formation of an inter-band (IB) with impurity states distributed within a narrower energy range as illustrated in Fig. 5d. As mentioned above, the acceptor states from CuInSe₂ would experience band broadening, and their resultant bandwidth would increase with the increasing x value (increasing density of point defects). Specifically, the deeper acceptor defect, [Cu_In]_CIS⁻, whose concentration depends on both the fraction of Cu₂Se and CuInSe₂ phases, will likely reach the maximum concentration near the equimolar composition. Therefore, it is possible that within this composition range, a critical point for impurity bands variation is reached, where orbitals of deep acceptor states can partially overlap with those of the shallow acceptor states, leading to some degree of hybridization. This mechanism explains well the concurrent increase in the carrier density and carrier mobility. Since the hybridization of impurity states, arising from the integration and merging of electronic band structures of both phases, increases the density of available acceptor states while eliminating the energy barrier at the interfaces, it minimizes carrier scattering. The formation of such an inter-band of hybridized impurity states is presumably a consequence of the high degree of intermixing that results from the hierarchical integration of both Cu₂Se and CuInSe₂ phases with nearly equimolar ratio. The intimate contact between both phases at the atomic, nanometer and micron scales in the hierarchical structure effectively facilitates the merging of their band structures. Therefore, one can conclude from this analysis that the deviation from the anticipated monotonic change of hole concentration with increasing CuInSe₂ content is a manifestation of a more complex interactions between Cu₂Se and CuInSe₂ owing to their unique hierarchical micro-structure, rather than merely a consequence of the elemental doping effect reported in other composites consisting of Cu₂Se and copper metal chalcogenides^18,19,51

For compositions in the range 52% ≤ x ≤ 90%, the band hybridization progresses, while the concentration of [V_Cu]_CS⁻ from Cu₂Se continues to decrease. These two trends counteract each other and help maintain an almost constant carrier concentration. Meanwhile, the carrier mobility decreases with the increasing CuInSe₂ content, which explains the observed drop in the electrical conductivity within this composition range (Fig. 4a). The drop in the carrier mobility with increasing x value within this composition range, where the CuInSe₂ phase dominates, can be attributed to the intensified carrier scattering due to the increase in the density of ionized deep acceptor defects from CuInSe₂ phase within the band gap. This is in contrast to the scattering of carriers at α-Cu₂Se/CuInSe₂ interfaces, as proposed above for compositions with low CuInSe₂ content (x ≤ 45%). Cubic β-Cu₂Se and tetragonal CuInSe₂ have similar lattice parameters at the ab plane with <1% difference (a = 5.833 Å for β-Cu₂Se; a = b = 5.796 Å for CuInSe₂). This leads to a high degree of coherency between CuInSe₂ and β-Cu₂Se in those samples which mitigates carrier scattering. However, the increased phase fraction of CuInSe₂ contributes to a higher density of electronic defects, such as [V_Cu]_CIS⁻, [V_In]_CIS⁻, and [Cu_In]_CIS⁻, leading to increased carrier–impurity scattering.

For compositions with x > 90%, the decreasing presence of the Cu₂Se phase eventually leads to the disappearance of [V_Cu]_CS⁻ defects from Cu₂Se and a rapid drop in the fraction of [Cu_In]_CIS⁻ acceptor states from CuInSe₂, as illustrated by the semitransparent dashed lines in Fig. 5e. This explains the observed rapid drop in the hole density. In the meantime, a slight enhancement in carrier mobility is observed, which is due to the elimination of the β-Cu₂Se as the secondary phase in the CuInSe₂ matrix. Owing to the semi-coherent interfaces between those two phases, the increase in the carrier mobility is minimal.

Overall, the hierarchical structural integration of Cu₂Se and CuInSe₂ phases together with the hybridization between their native acceptor states explains the intriguing behavior in the carrier concentration and electrical conductivity observed in various composites in the range of 48% ≤ x ≤ 90%.

4. Conclusions

We have demonstrated an elegant approach to construct a bulk hierarchical structure in the (1 − x)Cu₂Se/(x)CuInSe₂ composites, where domains from Cu₂Se and CuInSe₂ phases are mutually integrated from nano to micron scale. Using temperature dependent electrical conductivity data on 23 samples and carrier concentration data on selected samples in the composition range 15% ≤ x ≤ 100%, we established the electronic transport phase diagram for the (1 − x)Cu₂Se/(x)CuInSe₂ composites. We found that the CuInSe₂ content has a great influence on the microstructure as well as on the electronic properties of various composites. For instance, the degree of intermixing between Cu₂Se-rich and CuInSe₂-rich domains can be tuned from Cu₂Se-rich matrix/CuInSe₂-inclusions for compositions with x ≤ 45% (region I) to CuInSe₂-matrix/Cu₂Se-inclusions for compositions with x > 90% (region III) through systematic variation of the phase ratio (Cu₂Se : CuInSe₂). The maximum level of intermixing was observed for near equimolar compositions where both Cu₂Se and CuInSe₂ phases can simultaneously be regarded as the inclusions and as the matrices. Variations in the electrical conductivity with changes in the phase concentration detected over a broad range of temperatures (300–773 K) featured an unusual trend. An initial rapid decrease in the electrical conductivity with the increasing CuInSe₂ content was observed for compositions with x ≤ 45% (region I), then a sudden large increase in the conductivity was observed in phases having near equimolar compositions, followed by a weaker drop thereafter. Carrier concentration and mobility phase diagrams revealed that while the rapid decrease in the electrical conductivity for compositions with x ≤ 45% is largely due to a fast drop in the carrier mobility, the sudden increase in the electrical conductivity for near equimolar compositions and the subsequent weaker drop are consequences of the unexpected large increase in the carrier density of samples with 48% ≤ x ≤ 90% (region II). Such an unusual increase in the carrier density is interpreted as a manifestation of the formation of an inter-band of hybridized impurity states due to the complex interactions between intrinsic acceptor states from Cu₂Se and CuInSe₂ phases, which is presumably facilitated by their unique hierarchical integration. Our work not only provides electronic phase diagrams for the (1 − x)Cu₂Se/(x)CuInSe₂ system as a potential multifunctional composite, but it also introduces hierarchically integrated phases as a new design approach to couple multifunctionalities in bulk composite materials, which may pave the way to uncover new and exciting physical properties.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the Department of Energy, Office of Basic Energy Sciences under Award # DE-SC-00018941. This work made use of the TEM from the Michigan Materials Characterization Center, (MC)², purchased with funds from the National Science Foundation Awards (DMR-0723032).

References

1. I. M. Ross, Proc. IEEE, 1998, 86, 7–28.
2. H. J. Queisser and E. E. Haller, Science, 1998, 281, 945–950.
3. E. R. Weber, Phys. B, 2003, 340, 1–14.
4. E. G. Seebauer and K. W. Noh, Mater. Sci. Eng., R, 2010, 70, 151–168.
5. J. B. Yi, C. C. Lim, G. Z. Xing, H. M. Fan, L. H. Van, S. L. Huang, K. S. Yang, X. L. Huang, X. B. Qin, B. Y. Wang, T. Wu, L. Wang, H. T. Zhang, X. Y. Gao, T. Liu, A. T. S. Wee, Y. P. Feng and J. Ding, Phys. Rev. Lett., 2010, 104, 137201.
6. P. Wachter and E. Kaldis, Solid State Commun., 1980, 34, 241–244.
7. C. H. Wang, W. S. Liao, Z. H. Lin, N. J. Ku, Y. C. Li, Y. C. Chen, Z. L. Wang and C. P. Liu, Adv. Energy Mater., 2014, 4, 1400392.
8. Z. Z. Wang, J. Clayhold, N. P. Ong, J. M. Tarascon, L. H. Greene, W. R. McKinnon and G. W. Hull, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 7222.
9. Y. Zhao, J. S. Dyck, B. M. Hernandez and C. Burda, J. Am. Chem. Soc., 2010, 132, 4982–4983.
10. H. Anno, K. Matsubara, Y. Notohara, T. Sakakibara and H. Tashiro, J. Appl. Phys., 1999, 86, 3780–3786.
11. M. Balkanski and R. F. Wallis, Semiconductor physics and applications, Oxford University Press, 2000.
12. C. G. Van De Walle, D. B. Laks, G. F. Neumark and S. T. Pantelides, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 9425.
13. T. J. Smart, V. U. Baltazar, M. Chen, B. Yao, K. Mayford, F. Bridges, Y. Li and Y. Ping, Chem. Mater., 2021, 33, 4390–4398.
14. S. Jana, B. B. Srivastava, S. Jana, R. Bose and N. Pradhan, J. Phys. Chem. Lett., 2012, 3, 2535–2540.
15. N. Pradhan, S. Das Adhikari, A. Nag and D. D. Sarma, Angew. Chem., Int. Ed., 2017, 56, 7038–7054.
16. F. P. García de Arquer, D. V. Talapin, V. I. Klimov, Y. Arakawa, M. Bayer and E. H. Sargent, Science, 2021, 373, eaaz8541.
17. A. A. Olvera, N. A. Moroz, P. Sahoo, P. Ren, T. P. Bailey, A. A. Page, C. Uher and P. F. P. Poudeu, Energy Environ. Sci., 2017, 10, 1668–1676.
18. R. Lu, A. Olvera, T. P. Bailey, C. Uher and P. F. P. Poudeu, ACS Appl. Mater. Interfaces, 2020, 12, 58018–58027.
19. R. Lu, T. P. Bailey, C. Uher and P. F. P. Poudeu, ACS Appl. Energy Mater., 2020, 3, 9133–9142.
20. H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and J. Snyder, Nat. Mater., 2012, 11, 422–425.
21. L. Yang, Z. G. Chen, G. Han, M. Hong, Y. Zou and J. Zou, Nano Energy, 2015, 16, 367–374.
22. L. L. Zhao, X. L. Wang, J. Y. Wang, Z. X. Cheng, S. X. Dou, J. Wang and L. Q. Liu, Sci. Rep., 2015, 5, 1–6.
23. D. Byeon, R. Sobota, K. Delime-Codrin, S. Choi, K. Hirata, M. Adachi, M. Kiyama, T. Matsuura, Y. Yamamoto, M. Matsunami and T. Takeuchi, Nat. Commun., 2019, 10, 1–7.
24. F. O. Adurodija, M. J. Carter and R. Hill, Sol. Energy Mater. Sol. Cells, 1996, 40, 359–369.
25. A. Rockett and R. W. Birkmire, J. Appl. Phys., 1991, 70, R81–R97.
26. H. Bai, J. Wu, X. Su, H. Peng, Z. Li, D. Yang, Q. Zhang, C. Uher and X. Tang, Nat. Commun., 2021, 12, 1–6.
27. A. Olvera, P. Sahoo, S. Tarczynski and P. F. P. Poudeu, Chem. Mater., 2015, 27, 7179–7186.
28. J. B. Rivest, L. Fong, P. K. Jain, M. F. Toney and A. P. Alivisatos, J. Phys. Chem. Lett., 2011, 2, 2402–2406.
29. Y. Li, W. Qi, Y. Li, E. Janssens and B. Huang, J. Phys. Chem. C, 2012, 116, 9800–9804.
30. A. Sahu, D. Braga, O. Waser, M. S. Kang, D. Deng and D. J. Norris, Nano Lett., 2014, 14, 115–121.
31. R. C. Garvie and M. F. Goss, J. Mater. Sci., 1986, 21, 1253–1257.
32. M. Varela, J. L. Morenza, J. Esteve and J. M. Codina, J. Phys. D: Appl. Phys., 1984, 17, 2423–2427.
33. S. C. Park, S. H. Kwon, J. S. Song and B. T. Ahn, Sol. Energy Mater. Sol. Cells, 1998, 50, 43–49.
34. T. Datta, R. Noufi and S. K. Deb, Appl. Phys. Lett., 1985, 47, 1102–1104.
35. R. R. Philip, B. Pradeep, G. S. Okram and Y. Ganesan, Semicond. Sci. Technol., 2004, 19, 798–806.
36. M. A. Abdullaev, D. K. Magomedova, R. M. Gadzhieva, E. I. Terukov, Y. A. Nikolaev, Y. V. Rud’ and P. P. Khokhlachev, Semiconductors, 2001, 35, 870–872.
37. J. Y. Tak, W. H. Nam, C. Lee, S. Kim, Y. S. Lim, K. Ko, S. Lee, W. S. Seo, H. K. Cho, J. H. Shim and C. H. Park, Chem. Mater., 2018, 30, 3276–3284.
38. S. B. Zhang, S. H. Wei, A. Zunger and H. Katayama-Yoshida, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 9642.
39. Y. Cao, X. Su, F. Meng, T. P. Bailey, J. Zhao, H. Xie, J. He, C. Uher and X. Tang, Adv. Funct. Mater., 2020, 30, 2005861.
40. H. Xie, S. Hao, S. Cai, T. P. Bailey, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2020, 13, 3693–3705.
41. H. Xie, S. Hao, T. P. Bailey, S. Cai, Y. Zhang, T. J. Slade, G. J. Snyder, V. P. Dravid, C. Uher, C. Wolverton and M. G. Kanatzidis, J. Am. Chem. Soc., 2021, 143, 5978–5989.
42. H. T. Shaban, M. Mobarak and M. M. Nassary, Phys. B, 2007, 389, 351–354.
43. A. J. Nelson, A. B. Swartzlander, J. R. Tuttle, R. Noufi, R. Patel and H. Höchst, J. Appl. Phys., 1993, 74, 5757–5760.
44. X. Zhao, S. Ning, N. Qi, Y. Li, Y. Dong, H. Zhang, J. Liu, B. Ye and Z. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 58936–58948.
45. G. K. Padam, Thin Solid Films, 1987, 150, 89–92.
46. H. Chi, H. Kim, J. C. Thomas, G. Shi, K. Sun, M. Abeykoon, E. S. Bozin, X. Shi, Q. Li, X. Shi, E. Kioupakis, A. Van Der Ven, M. Kaviany and C. Uher, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1–5.
47. T. F. Lee and T. C. McGill, J. Appl. Phys., 1975, 46, 373–380.
48. S. R. Dhariwal, V. N. Ojha and G. P. Srivastava, IEEE Trans. Electron Devices, 1985, 32, 44–48.
49. E. Arushanov, J. H. Schön, H. Matsushita and T. Takizawa, Phys. Status Solidi, 1999, 176, 1009–1016.
50. L. Essaleh, S. M. Wasim and J. Galibert, J. Appl. Phys., 2001, 90, 3993–3997.
51. F. S. Liu, Z. N. Gong, M. J. Huang, W. Q. Ao, Y. Li and J. Q. Li, J. Alloys Compd., 2016, 688, 521–526.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1 to S8 and Table S1. See https://doi.org/10.1039/d2na00230b

---