Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion-specific nanoscale compaction of cysteine-modified poly(acrylic acid) brushes revealed by 3D scanning force microscopy with frequency modulation detection†
Akihisa
Yamamoto
 *a,
Takahiko
Ikarashi
*a,
Takahiko
Ikarashi
 b,
Takeshi
Fukuma
b,
Takeshi
Fukuma
 bc,
Ryo
Suzuki
bc,
Ryo
Suzuki
 a,
Masaki
Nakahata
de,
Kazuki
Miyata
a,
Masaki
Nakahata
de,
Kazuki
Miyata
 *bc and
Motomu
Tanaka
*bc and
Motomu
Tanaka
 *af
*af
aCenter for Integrative Medicine and Physics, Institute for Advanced Study, Kyoto University, Kyoto 606-8501, Japan. E-mail: yamamoto.akihisa.6w@kyoto-u.ac.jp
bDivision of Nano Life Science, Kanazawa University, Kanazawa 920-1192, Japan. E-mail: k-miyata@staff.kanazawa-u.ac.jp
cNano Life Science Institute (WPI-NanoLSI), Kanazawa University, Kanazawa 920-1192, Japan
dDepartment of Materials Engineering Science, Graduate School of Engineering Science, Osaka University, Osaka 560-8531, Japan
eDepartment of Macromolecular Science, Graduate School of Science, Osaka University, Osaka 560-0043, Japan
fPhysical Chemistry of Biosystems, Institute of Physical Chemistry, Heidelberg University, 69120 Heidelberg, Germany. E-mail: tanaka@uni-heidelberg.de
First published on 15th September 2022
Abstract
Stimuli-responsive polyelectrolyte brushes adapt their physico-chemical properties according to pH and ion concentrations of the solution in contact. We synthesized a poly(acrylic acid) bearing cysteine residues at side chains and a lipid head group at the terminal, and incorporated them into a phospholipid monolayer deposited on a hydrophobic silane monolayer. The ion-specific, nanoscale response of polyelectrolyte brushes was detected by using three-dimensional scanning force microscopy (3D-SFM) combined with frequency modulation detection. The obtained topographic and mechanical landscapes indicated that the brushes were uniformly stretched, undergoing a gradual transition from the brush to the bulk electrolyte in the absence of divalent cations. When 1 mM calcium ions were added, the brushes were uniformly compacted, exhibiting a sharper brush-to-bulk transition. Remarkably, the addition of 1 mM cadmium ions made the brush surface significantly rough and the mechanical landscape highly heterogeneous. Currently, cadmium-specific nanoscale compaction of the brushes is attributed to the coordination of thiol and carboxyl side chains with cadmium ions, as suggested for naturally occurring, heavy metal binding proteins.
Introduction
Stimuli-responsive polymers have attracted interest for use in various drug delivery and microencapsulation applications because these substances can protect and/or release materials in response to the surrounding environment.1 In particular, polyelectrolyte brushes have been grafted on surfaces to give the materials adaptable functionalities. In these cases, the physical properties of the surface can be modulated based on the electrostatic properties of the external media (e.g., pH and salt concentrations).2–4 The structures and mechanical properties of polymer brushes have been measured experimentally using X-ray/neutron reflectivity,5,6 quartz crystal microbalance with dissipation (QCM-D),7,8 tribology,9,10 and microinterferometry.11,12Among the various techniques, atomic force microscopy (AFM) is commonly used to investigate the mechanical properties of polymer brushes via nanoindentation.13,14 Recently, Fukuma et al., developed three-dimensional scanning force microscopy (3D-SFM) based on frequency modulation AFM (FM-AFM),15 which has been utilized to construct force maps of material surfaces. During the measurement process, a cantilever tip scans in the vicinity of the interface both parallel and perpendicular to the surface, and the frequency shift of the oscillating cantilever is recorded in 3D space. This technique has been successful in visualizing the 3D force maps of the surfaces of various materials in water, e.g., minerals,16,17 graphene,18 graphite,19 and supported phospholipid bilayers.20 A key advantage of this technique is that it can be used to investigate the density distribution of water at the solid/water interface. By exploiting this unique functionality, 3D-SFM has been applied to observe the ammonia-mediated hydration of poly(vinyl alcohol) coated surfaces.21 However, to our knowledge, no experimental studies have demonstrated the potential of 3D-SFM to detect dynamic modulations of hydrated polymer brushes driven by external chemical stimuli.
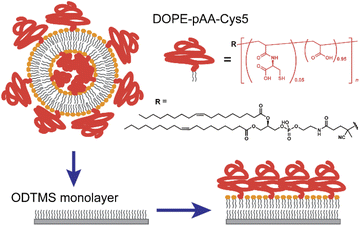
In this study, we functionalized the surface of planar lipid membranes (i.e., supported membranes)22,23 with poly(acrylic acid) brushes bearing cysteine side chain functional groups (pAA-Cys) by incorporating the lipids covalently coupled with pAA-Cys (i.e., DOPE-pAA-Cys5) into the matrix lipids (Fig. 1). In these materials, pAA-Cys5 moieties interact with divalent Cd2+ ions similar to naturally occurring proteins24 because pAA-Cys has both –SH and –COOH groups. We investigated how pAA-Cys brushes adapt their structure and mechanical landscape near the interface following the addition of Cd2+ ions. We used lipids and lipopolymers with identical hydrocarbon chains to prevent phase separation.25 The lateral average distance between lipopolymer molecules 〈d〉 can be precisely controlled by taking advantage of the self-assembling nature of lipids and lipopolymers and tuning the molar fraction of lipopolymers χlipo, such that
| 〈d〉 = (Alipid/χlipo)0.5, | (1) |
Materials and methods
Chemicals and reagents
Sodium chloride (NaCl), cadmium chloride (CdCl2), toluene, and n-butylamine were purchased from Nacalai Tesque (Kyoto, Japan). Calcium chloride (CaCl2) was purchased from Wako Pure Chemical Industries, Ltd. (Osaka, Japan). Tris(hydroxymethyl)aminomethane, S-trityl-L-cysteine and 2-(dodecylthiocarbonothioylthio)-2-methylpropionic acid (DDMAT) were purchased from Sigma-Aldrich (St. Louis, MO, USA). 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE) were purchased from Avanti Polar Lipids (Alabaster, AL, USA). Texas Red™ 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine triethylammonium salt (Texas Red™ DHPE) was purchased from Invitrogen (Carlsbad, CA, USA). N-Octadecyltrimethoxysilane (ODTMS) was purchased from Fluorochem Ltd. (Derbyshire, UK). Potassium hydroxide (KOH), sodium hydroxide (NaOH), acryloyl chloride, acrylic acid (AA), dimethyl sulfoxide (DMSO), acetone, hexane, trifluoroacetic acid (TFA), diethyl ether, 4,4′-azobis(4-cyanovaleric acid) (ACVA), N-hydroxysuccinimide (NHS), N,N-dimethylformamide (DMF), 4 Å molecular sieves, dichloromethane (DCM), and triethylamine (Et3N) were obtained from FUJIFILM Wako Pure Chemical Co. (Osaka, Japan). Ethanol was purchased from Japan Alcohol Trading Co., Ltd. (Tokyo, Japan), and Si wafers were obtained from SUMCO (Tokyo, Japan). Water from a Millipore Integral system (Merck, Darmstadt, Germany) was used throughout this study.Synthetic methods
1H-NMR spectra were recorded at 400 MHz with a JNM-ECS400 NMR spectrometer (JEOL, Tokyo, Japan). For all NMR measurements, chemical shifts were referenced to the solvent values (δ = 2.49 or 7.26 ppm for DMSO-d6 or CDCl3, respectively). Silica gel column chromatography was performed using a Biotage Isolera One instrument (Biotage AB, Uppsala, Sweden) equipped with a SNAP Ultra Column cartridge. Gel permeation chromatography (GPC) measurements of DOPE-pAA-Cys5 was carried out using a high performance liquid chromatography (HPLC) system (CBM-20A/LC-20AD/SIL-10AXL/DGU-20 A3R/CTO-20AC, Shimadzu, Kyoto, Japan) equipped with an SB-804 HQ column (Shodex, Tokyo, Japan) and a refractive index (RI) detector (RID-20A, Shimadzu, Kyoto, Japan), using Tris–HCl buffer (10 mM) containing 100 mM NaCl as an eluent at a flow rate of 0.7 mL min−1 at 25 °C. ReadyCal-Kit polyethylene glycol (PEG) (PSS GmbH, Mainz, Germany) was used as the calibration standard. S-Trityl-L-cysteine acrylamide (S-Tri-Cys-AAm) was prepared according to a previous report.28Synthesis of ACVA-DOPE
ACVA-DOPE (Fig. S1†) was prepared according to a previous report.29 ACVA-NHS (250 mg, 0.53 mmol), DOPE (939 mg, 1.3 mmol), and Et3N (175 μL, 1.3 mmol) were dissolved in 50 mL of DCM dried with 4 Å molecular sieves. Volatile chemicals were evaporated after stirring the solution for 3 d at room temperature. Hexane (10 mL) was added to the residue, and the mixture was allowed to stir for 2 d, followed by filtration with a 0.45 μm poly(tetrafluoroethylene) (PTFE) filter. After evaporation of the solvent, ACVA-DOPE was obtained as a colorless oil.Synthesis of the DOPE-pAA-Cys5 lipopolymer
DOPE-pAA-Cys5 was synthesized via copolymerization of S-Tri-Cys-AAm and AA, using ACVA-DOPE as an initiator and DDMAT as a chain transfer agent, followed by deprotection of the trityl group with TFA. Briefly, S-tri-Cys-AAm (0.05 mmol), AA (0.95 mmol), ACVA-DOPE (0.01 mmol), and DDMAT (0.01 mmol) were dissolved in 1 mL of ethanol dried with 4 Å molecular sieves. The solution was purged with nitrogen gas for 1 h, sealed, and heated in an oil bath at 70 °C overnight. After cooling to room temperature, the solution was poured into diethyl ether (10 mL) with stirring. The resulting precipitate was collected by centrifugation (3500 rpm, 5 min). After decanting the supernatant, TFA (1 mL) was added, and the mixture was stirred for 1 h at room temperature. The solution was poured into diethyl ether (10 mL). The resulting precipitate was washed with diethyl ether (2 × 10 mL) and dried under vacuum at room temperature. Successful polymerization and deprotection were confirmed by 1H-NMR.Functionalization of solid substrates with the ODTMS monolayer
Silicon wafers were cut into 10 × 10 mm squares and immersed in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of H2SO4/H2O2 for 15 min to obtain a hydrophilic surface. After thorough rinsing with water, the samples were dried under N2 gas and stored in a vacuum chamber at 70 °C. Then, the wafers were immersed in a mixture containing 80 mL toluene, 4.2 mL ODTMS, and 0.4 mL n-butylamine, sonicated for 60 min at 10 °C, and let stand for another 30 min. To remove residual chemicals, the samples were rinsed, then sonicated for 2 min in toluene and stored in a vacuum chamber at 70 °C. The quality of the ODTMS coating was confirmed after each preparation based on the water contact angle, θ > 90°.30
1 mixture of H2SO4/H2O2 for 15 min to obtain a hydrophilic surface. After thorough rinsing with water, the samples were dried under N2 gas and stored in a vacuum chamber at 70 °C. Then, the wafers were immersed in a mixture containing 80 mL toluene, 4.2 mL ODTMS, and 0.4 mL n-butylamine, sonicated for 60 min at 10 °C, and let stand for another 30 min. To remove residual chemicals, the samples were rinsed, then sonicated for 2 min in toluene and stored in a vacuum chamber at 70 °C. The quality of the ODTMS coating was confirmed after each preparation based on the water contact angle, θ > 90°.30
Preparation of the supported membrane
Mixtures of DOPC/DOPE-pAA-Cys5 = 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 mol% or DOPC/DOPE-pAA-Cys5/Texas-Red-DHPE = 94
5 mol% or DOPC/DOPE-pAA-Cys5/Texas-Red-DHPE = 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol% were suspended in isopropanol. Lipid dry films were prepared following the gentle evaporation of isopropanol by a flow of N2 gas in a glass vial and storage in a vacuum chamber at room temperature overnight. The films were resuspended at a final concentration of 1 mg mL−1 in 100 mM NaCl buffered with 10 mM Tris–HCl (pH = 7.4). The products were then sonicated for 30 min at ∼1 W using a tip sonicator (XL2000-600, Misonix, Newtown, CT, USA) and centrifuged (Sorvall Legend Micro 21R, Thermo Scientific, Waltham, MA, USA) to obtain a suspension of small unilamellar vesicles (SUV). The SUV suspensions were then incubated onto the ODTMS-functionalized solid substrates overnight (Fig. 1). After thorough pipetting to remove excessive SUVs, the solution was replaced with fresh 10 mM Tris–HCl buffer solutions (pH = 7.4) containing designated metal ions (e.g., 100 mM NaCl, 100 mM NaCl + 1 mM CaCl2, or 100 mM NaCl + 1 mM CdCl2) by exchanging the solutions at least 10 times of the initial volume using a pipette. The lateral average distance between the lipopolymer molecules, 〈d〉 = 3.6 nm, was calculated from eqn (1), using the cross-sectional area of the single phospholipid membrane Alipid ≈ 0.6 nm2 and the molar fraction of lipopolymers χlipo = 0.05.
1 mol% were suspended in isopropanol. Lipid dry films were prepared following the gentle evaporation of isopropanol by a flow of N2 gas in a glass vial and storage in a vacuum chamber at room temperature overnight. The films were resuspended at a final concentration of 1 mg mL−1 in 100 mM NaCl buffered with 10 mM Tris–HCl (pH = 7.4). The products were then sonicated for 30 min at ∼1 W using a tip sonicator (XL2000-600, Misonix, Newtown, CT, USA) and centrifuged (Sorvall Legend Micro 21R, Thermo Scientific, Waltham, MA, USA) to obtain a suspension of small unilamellar vesicles (SUV). The SUV suspensions were then incubated onto the ODTMS-functionalized solid substrates overnight (Fig. 1). After thorough pipetting to remove excessive SUVs, the solution was replaced with fresh 10 mM Tris–HCl buffer solutions (pH = 7.4) containing designated metal ions (e.g., 100 mM NaCl, 100 mM NaCl + 1 mM CaCl2, or 100 mM NaCl + 1 mM CdCl2) by exchanging the solutions at least 10 times of the initial volume using a pipette. The lateral average distance between the lipopolymer molecules, 〈d〉 = 3.6 nm, was calculated from eqn (1), using the cross-sectional area of the single phospholipid membrane Alipid ≈ 0.6 nm2 and the molar fraction of lipopolymers χlipo = 0.05.
Optical microscopy
Fluorescence microscopy images were captured with a Zeiss Axiovert microscope (Carl Zeiss, Oberkochen Germany) equipped with a digital CMOS camera (ORCA-Flash4.0, Hamamatsu Photonics, Shizuoka, Japan) and an LED illumination system (X-Cite 120LED, Excelitas technologies, Waltham, MA, USA).AFM measurements
AFM measurements were performed using a custom-built AFM instrument with an ultralow-noise cantilever deflection sensor and a highly stable photothermal cantilever excitation system.31–33 The AFM was controlled with a commercially available controller (ARC2, Oxford Instruments, Oxfordshire, UK) using a modified software. A commercially available phase-locked loop circuit (Nanonis OC4, SPECS, Berlin, Germany) was used to oscillate the cantilever at its resonance frequency in liquid f0 with a constant amplitude and to detect the frequency shift Δf induced by the force variation. The cantilevers (160AC, OPUS, Sofia, Bulgaria) with a nominal spring constant k = 26 N m−1 were used. The f0 and the quality factor Q were determined for each measurement; f0 = 120.2 kHz and Q = 7.8 in 100 mM NaCl, f0 = 137.9 kHz and Q = 8.0 in 100 mM NaCl + 1 mM CaCl2, and f0 = 139.0 kHz and Q = 8.9 in 100 mM NaCl + 1 mM CdCl2. The cantilever tips were coated with an Si thin film using a sputter coater (KST-CSPS-KF1, K's Tech, Ibaraki, Japan) to obtain an apex diameter of approximately 20 nm.34For the 2D-FM-AFM measurements, a square 500 × 500 nm area was scanned at a scan rate of 1 Hz (512 × 512 pixels), with the setpoint Δfsp = 488 Hz.
For the 3D-SFM measurements, the cantilever tip scanned vertically following a rapid sinusoidal curve, while slowly scanning in the lateral direction. During this tip scan, the Δf induced by the force variation was recorded to produce a 3D Δf image; the tip-sample distance was regulated continuously such that the average Δf was equal to a setpoint value Δfsp. This allowed us to simultaneously obtain a 3D Δf image and a 2D height image. Sections of 100 × 100 nm in area with a height of 6 nm (for NaCl and NaCl + CaCl2 solutions) or 8 nm (for NaCl + CdCl2 solutions) were scanned (128 × 128 × 256 pixels) with a constant setpoint to compare the forces measured in all the buffer solutions. In this study, we carefully optimized the setpoint at 3.9 kHz, at which we could gain the highest contrast.
Data analysis
AFM data were processed with the open-source software, Gwyddion,35 to analyze the topography images and a self-written program in LabVIEW (National Instruments, Austin, TX, USA) to analyze the 3D-SFM images.The autocorrelation analysis of the topography images was conducted using a self-written algorithm in MATLAB 2021b (Natick, MA, USA). For a given image Δh(x,y) consisting of (m × n) pixels, the autocorrelation G can be calculated as follows:
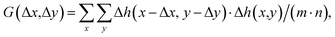 | (2) |
| G = F−1{|F(Δh(x,y))|2}/(m·n) | (3) |
The vertical Δf curves plotted as a function of the height were converted to force curves according to Sader's model,36 where the interaction force between the tip and sample F is expressed as shown in eqn (4),
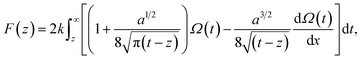 | (4) |
Results and discussion
Synthesis and characterization of DOPE-pAA-Cys5
First, DOPE-pAA-Cys5 was synthesized via reversible addition–fragmentation chain transfer (RAFT) copolymerization using ACVA-DOPE as a radical initiator with a DOPE moiety. Fig. S1† shows the 1H-NMR spectra of ACVA-DOPE and DOPE-pAA-Cys5. Peaks corresponding to ACVA-DOPE were also observed in the NMR spectrum of DOPE-pAA-Cys5. Fig. S2† shows the GPC trace of DOPE-pAA-Cys5, which gave a unimodal peak with Mw = 7.1 × 103 (PEG standard) and Mw/Mn = 1.9. These results indicate that the polymer was successfully synthesized with DOPE at the end.Formation of supported lipid membranes doped with the lipopolymer
The formation of a DOPC monolayer incorporating 5 mol% DOPE-pAA-Cys5 was monitored by doping 1 mol% Texas Red-DHPE (refer to the Materials and methods section). The acquired image (Fig. 2) shows a uniform fluorescence signal, indicating that the lipids and lipopolymers formed a homogeneous monolayer on the hydrophobic ODTMS surface with no sign of phase separation. It is noted that the circular bright spots in the image could be SUVs remaining on the supported membrane after rinsing.Cd2+ ions induce roughening of the pAA-Cys5 polymer brush
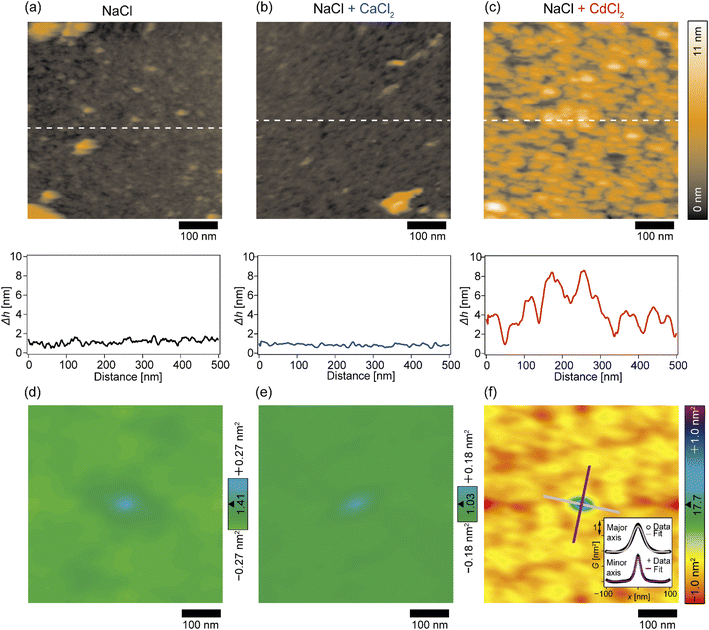
The topographic profiles of the DOPC/DOPE-pAA-Cys5 monolayer surface in the absence or presence of divalent cations were characterized using 2D-FM-AFM. The minimum positional height Δh in the field of view is defined as Δh = 0 nm. In the absence of divalent cations, the surface of the pAA-Cys5 brush had a smooth topographic profile (Fig. 3a, top). The line profile corresponding to the dashed line indicates that the height fluctuation was well below ±1 nm (Fig. 3a, bottom). The root mean square (RMS) roughness calculated from the 100 × 100 nm area at the center was RMS0 = 0.23 nm. When 1 mM CaCl2 was added to the solution, the brush surface remained smooth, with a RMSCa = 0.15 nm (Fig. 3b). Remarkably, the topographic profile of the brush surface was distinct in the presence of 1 mM CdCl2, exhibiting dense hemi-ellipsoidal protrusions (Fig. 3c, top). The calculated RMSCd = 1.47 nm was significantly larger than those obtained under the other studied conditions.To examine whether pAA-Cys5 brushes adopt specific structural features in the absence or presence of divalent cations, we calculated the autocorrelations of the topographical images (Fig. 3d–f) via fast Fourier transformation within the framework of the Wiener–Khinchin theorem (refer to the Materials and methods section). As presented in Fig. 3d, the autocorrelation map reveals no characteristic features in the absence of divalent cations. Similarly, the autocorrelation function remained featureless when 1 mM CaCl2 was added to the solution (Fig. 3e). The featureless autocorrelation maps in Fig. 3d and e are consistent with the uniform topographic profiles in Fig. 3a and b. In contrast, when 1 mM CdCl2 was added to the solution, the autocorrelation map (Fig. 3f) showed a distinct pattern. First, we found an intense peak in the center of the autocorrelation map corresponding to the characteristic sizes of protrusions. From the full width at half maximum (FWHM) of the intensity profile along the major and minor axes (Fig. 3f, inset), the characteristic lengths were determined to be 41 nm and 22 nm, respectively. It should be noted that these values are much larger than the lateral average distance between lipopolymer molecules 〈d〉 = 3.6 nm. Even though the object size might be overestimated due to technical artifacts such as the finite size effect of the cantilever tip37,38 and a thermal drift during scanning, each protrusion might consist of multiple polymer chains. Secondly, similarly intense local maxima were observed around the central peak in the autocorrelation map, which indicates that these protrusions were densely packed. However, there is no clear pattern in the autocorrelation map, suggesting that these protrusions do not take any distinct pattern in the presence of Cd2+. To confirm this point, we performed the fast Fourier transform (FFT) of the topographic profile (Fig. S3†) and found no distinct patterns, suggesting that these protrusions do not form a 2D lattice. This finding seems reasonable as both lipids and lipopolymers are in a fluid Lα phase, in which hydrocarbon chains are disordered and uniformly mixed. It is also notable that the central ellipse showed a slight tilt with respect to the horizontal scanning direction, which might be caused by a thermal drift. However, we were not able to correct the topographic profiles, because there was no reference pattern with clear order.39,40 Thus, although the topographic profiles might be distorted due to drift, the autocorrelation analysis suggested that pAA-Cys5 brushes formed uniformly sized protrusions and assembled randomly only in the presence of Cd2+ ions.
Cd2+ ions induce an inhomogeneous Δf field near the interface
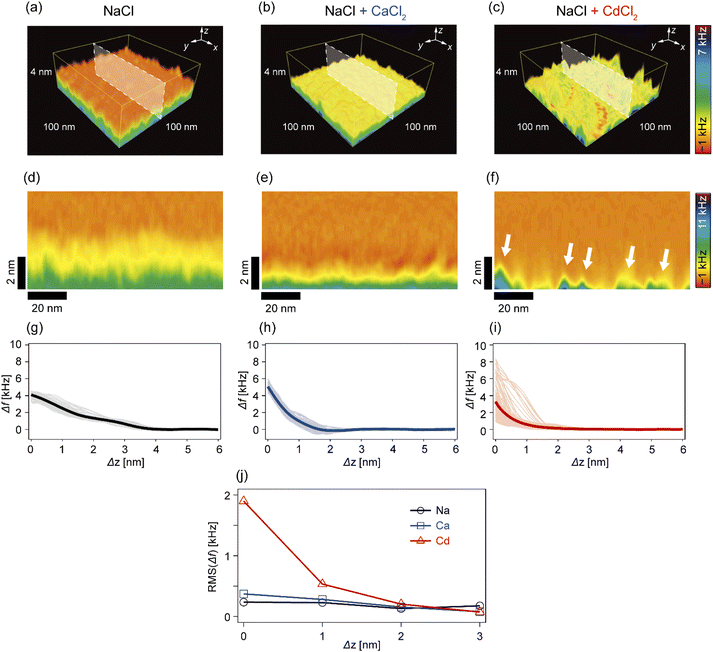
In the next step, we investigated how Cd2+ and Ca2+ ions modulated the nanoscopic mechanical landscape in the vicinity of pAA-Cys5 brush surfaces. Fig. 4a–c show the 3D Δf maps over a 100 × 100 nm × 4 nm area. The bottom planes of each 3D map (where Δz = 0 nm) coincide with the topographical surfaces determined with a setpoint value of Δfsp (refer to the Materials and methods section), which can vary at each xy position. A transparency filter was applied to the color map to visualize the high Δf regions (Fig. S4†). The pAA-Cys5 brushes in NaCl solution showed uniformly low Δf values near the surface (Fig. 4a). Notably, Δf gradually converged to the level in the bulk. The 3D Δf map in the presence of an additional 1 mM CaCl2 (Fig. 4b) also shows a uniform profile near the surface. However, in this case, the transition to the bulk occurred more sharply at a shorter distance, which suggested uniform compaction of pAA-Cys5 brushes. In the presence of an additional 1 mM CdCl2 (Fig. 4c), the 3D Δf map is distinct. The 3D maps reveal heterogeneous domains, similar to those observed in the 2D topographical map (Fig. 3c).To gain further insight into the transition from the brush to the bulk electrolyte, we extracted the xz cross-sections from the 3D Δf maps. As shown in Fig. 4d, the Δf value of pAA-Cys5 in NaCl decayed to that of the bulk level over a depth of 4 nm. This relatively broad transition from the polymer to the bulk electrolyte can be attributed to weak forces originating from the conformational fluctuations of hydrated pAA-Cys5 brushes. In the electrolyte containing additional Ca2+ (Fig. 4e), the width of the transition zone was approximately 2 nm, which was narrower than in the NaCl buffer. This result suggests that pAA-Cys5 brushes became compact in the presence of Ca2+, similar to other negatively charged polymers.41–43 Remarkably, the xz cross-section of pAA-Cys5 in the presence of Cd2+ (Fig. 4f) was generally heterogeneous in the x-direction, which is different from the other conditions. Some regions had Δf values comparable to those of the bulk phase and were attributed to gaps/defects. In fact, the lateral size of “triangular” features with high Δf values near Δz = 0 nm (indicated by white arrows) was similar to that of the hemi-ellipsoidal protrusions observed in the 2D topography map (Fig. 3c). Fig. 4g–i present the frequency shift curves (Δf–Δz), which highlight the differences in the shapes and widths of the “polymer-to-electrolyte transitions”. The thick solid lines represent the mean of 128 curves collected from the xz cross-sections shown in Fig. 4d–f. In the buffer containing only NaCl (Fig. 4g), the onset of Δf increase was observed at Δz ≈ 4 nm. The individual Δf–Δz profiles overlap with one another, indicating that the mechanical properties near the brush/electrolyte interface are uniform over the surface. In the buffer containing additional Ca2+ ions (Fig. 4h), Δf begins increasing at Δz ≈ 2 nm. When 1 mM CdCl2 was added to the buffer (Fig. 4i), the Δf–Δz profiles become significantly more heterogeneous. Most Δf–Δz profiles show an onset of increase at Δz ≈ 2 nm, while others show an increase starting at Δz ≤ 1 nm. The RMS “roughness” of Δf was plotted as a function of Δz to obtain another measure of the heterogeneity of mechanical properties near the brush/electrolyte interface (Fig. 4j). The presence of Cd2+ ions led to an inhomogeneous Δf profile in the vicinity of Δz = 0 nm, although this heterogeneous Δf distribution converges to that of the other conditions already at Δz ≥ 2 nm.
Ion-specific modulation of the mechanical properties of pAA-Cys5 brushes
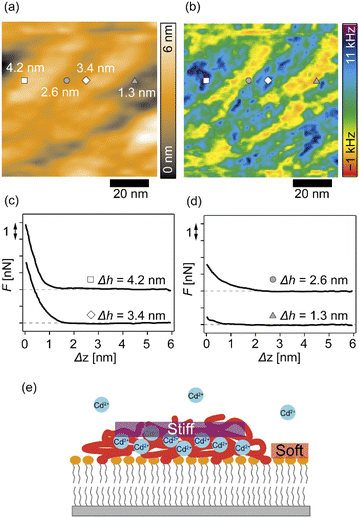
We further analyzed the 3D-SFM data to examine whether the topographical heterogeneity characterized by hemi-ellipsoidal protrusions was correlated with the mechanical heterogeneity of pAA-Cys5 brushes in the presence of Cd2+ ions. Fig. 5a shows the Δh profile of the pAA-Cys5 brush surface in the presence of 1 mM CdCl2 scanned over an area of 100 × 100 nm. The corresponding Δf profile at Δz = 0 nm measured by 3D-SFM is presented in Fig. 5b. We selected four representative points: two near the top of the protrusions (Δh = 4.2 and 3.4 nm, indicated by a white square and a white diamond, respectively) and two in the lower, smoother regions (Δh = 2.6 and 1.3 nm, indicated by a grey circle and a grey triangle, respectively). Using eqn (4), the Δf obtained from 3D-SFM can be converted into a force F to obtain force curves. Fig. 5c and d show the force curves from the protrusions and smooth regions, respectively. The increase in F during the approach is notably sharper in the protrusions (Fig. 5c) relative to that in the smooth regions (Fig. 5d), which suggests that the protrusions are stiffer than the smooth regions. In general, such a force–distance relationship can be used to calculate Young's modulus E of the films using a modified Hertz model44,45 as expressed in eqn (5),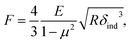 | (5) |
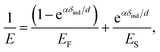 | (6) |
Additionally, the lateral shift between the Δh map (Fig. 5a) and the Δf map at Δz = 0 nm (Fig. 5b) appeared because during the 3D-SFM measurements, the feedback gain was optimized for the vertical sinusoidal oscillation of the cantilever. This enabled the sensitive detection of Δf without scratching the surface; however, it also caused a slight delay in the adjustment of the average vertical position of the cantilever. Although a quantitative E map could not be obtained, a direct comparison of Δh and Δf maps enables us to connect the surface topography and mechanical properties on the nanoscale. Currently we interpret that the “stiffer protrusions” correspond to collapsed pAA-Cys5 brushes and the “softer, smoother regions” to the underlying phospholipid monolayer (Fig. 5e).
Fig. S5† shows the overlayed force curves extracted from Fig. 4g–i. Similar to the corresponding Δf curves (Fig. 4g), the force curves in NaCl buffer overlap with one another, showing a slow increase to F = 3.5 nN at the interface with the onset of F increase at Δh = 4 nm (Fig. S5a†). This is reasonable because the interface between hydrated polyelectrolyte brushes and the electrolyte is diffusive.52,53 In the presence of an additional 1 mM CaCl2, the onset of F increase was observed at a shallower position (Δh = 2 nm), and F increased to F = 2 nN at the interface (Fig. S5b†). A minor deviation in the force curves indicated that the pAA-Cys5 brushes were uniformly compacted and therefore stiffened following the binding of Ca2+ ions. Interestingly, the force curves in the presence of Cd2+ ions showed a much more pronounced deviation (Fig. S5c†). Both the onset of F increase and the F value at Δh = 0 nm exhibited wide distributions, implying that pAA-Cys5 brushes formed stiff domains on the surface of the phospholipid monolayer. The formation of collapsed domains in the presence of Cd2+ ions suggested that the compaction-induced dehydration of pAA-Cys5 brushes altered the affinity of the solvent (water) to monomers. Further investigations, including in situ observations of changes in the viscoelasticity of pAA-Cys5 using 3D-SFM or other techniques (e.g., QCM-D) would provide further insights into the ion-specific, dynamic modulation of polyelectrolyte brushes.
Conclusions
In this study, we investigated the modulation of topography and mechanical properties of supported lipid monolayers incorporating lipids functionalized with linear poly(acrylic acid) chains with cysteine side chains (DOPE-pAA-Cys5) induced by different metal ions. We found that the topographical profile of pAA-Cys5 brushes obtained by 2D-FM-AFM in the electrolyte containing no divalent cation (100 mM NaCl, 10 mM Tris–HCl, pH = 7.4) was very homogeneous, whose RMS0 = 0.23 nm (Fig. 3a). In fact, autocorrelation analysis of Δh showed no clear feature (Fig. 3d). The mechanical landscape, characterized by the 3D Δf map (Fig. 4a) and its xz cross-section (Fig. 4d), was also highly uniform, suggesting that the hydrated pAA-Cys5 brushes are stretched into the bulk electrolyte. The slow increase in the Δf–Δz curves (Fig. 4g) and a very low RMS(Δf) = 0.24 kHz at Δz = 0 nm (Fig. 4j) implied a smooth transition from the polymer to the bulk electrolyte.The addition of 1 mM CaCl2 caused a distinct change in both topographical and mechanical properties of the brush/electrolyte interface. In the presence of Ca2+ ions, pAA-Cys5 brushes became smoother, which could be characterized by the very small roughness, RMSCa = 0.15 nm (Fig. 3b) with no characteristic feature (Fig. 3e). The 3D Δf map and its xz cross-section (Fig. 4b and e) were smoother, and the increase in Δf was much sharper (Fig. 4h) than the corresponding values obtained in the absence of Ca2+ ions, RMS(Δf) = 0.37 kHz at Δz = 0 nm (Fig. 4j), indicating that pAA-Cys5 brushes are uniformly compacted by the presence of Ca2+ ions. The most remarkable difference was observed when 1 mM CdCl2 was added to the electrolyte. The surface topography became very rough (RMSCd = 1.47 nm, Fig. 3c), displaying hemi-ellipsoidal features. The autocorrelation analysis suggested that these protrusions had a similar size and assembled randomly (Fig. 3f). Accordingly, the 3D Δf map became highly heterogeneous (Fig. 4c), and the xz cross-section (Fig. 4f) clearly indicates the coexistence of stiff protrusions and defects. The heterogeneity of the mechanical landscape was clearly visible from a broad distribution of the Δf–Δz curves, resulting in RMS(Δf) = 1.90 kHz at Δz = 0 nm (Fig. 4j). These data suggest that pAA-Cys5 brushes “collapsed” in the presence of Cd2+ ions, where water might not be a good solvent for pAA-Cys5.
3D-SFM also provides with a unique possibility to correlate nanoscale heterogeneities in the surface topography (Fig. 5a) and the mechanical landscape (Fig. 5b) observed in the presence of Cd2+ ions. The force curves extracted from 2 × “higher” positions (Fig. 5c) and 2 × “lower” positions (Fig. 5d) showed distinctly different increases. Although the quantification of mechanical parameters, such as Young's modulus, from the force curves was not possible with our multilayered lipid/polymer systems, a sharper increase in Δf shown in Fig. 5c suggests that the higher regions (protrusions) are stiffer than the lower region showing a markedly slower increase, as schematically shown in Fig. 5e.
It should be noted that the change in chain conformation and mechanical properties of the polymer brush induced by Cd2+ ions are reversible, as we recently demonstrated by using quartz-crystal microbalance with dissipation (QCMD).54 The compaction and stiffening of the polymer brush due to Cd2+ ions observed in the current study coincide well with the decrease in the frequency and the increase in the energy dissipation measured by QCMD. We currently interpret that the Cd2+-specific compaction of pAA-Cys5 brushes originates from the coexistence of both –SH and –COOH moieties, which share common features with the naturally occurring proteins that form coordination complexes with heavy metal ions, because the polymers lacking either –SH or –COOH moieties showed no remarkable response to Cd2+ ions.54 More detailed structural studies on the coordination complex analysis with NMR or the change in vibrational bands using infrared spectroscopy will allow for the molecular-level mechanism understanding of the observed ion-specific response and the rational design of adaptable polymer brushes that are modulated by specific ions.
Author contributions
M. T. and K. M. designed and directed the research. M. N. synthesized and characterized the lipopolymers. A. Y., T. I., K. M., and R. S. performed the experiments and analysed the data. A. Y., K. M., T. F., M. N., and M. T. wrote the manuscript, and all the authors were involved in the discussion throughout the manuscript preparation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the JSPS KAKENHI (JP19H05719 to M. N. and M. T.; JP20H05212 to K. M.) and the German Science Foundation (SPP2171 Ta253/14-2 and Germany's Excellence Strategy -2082/1-390761711 to M. T.). A. Y., M. N., and M. T. thank German-Japanese University Alliance (HeKKSaGOn Alliance) for support. A. Y. thanks the Program for the Development of Next-generation Leading Scientists with Global Insight (L-INSIGHT), sponsored by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. K. M. and T. F. thank the World Premier International Research Center Initiative (WPI), MEXT, Japan. M. T. thanks the Nakatani Foundation for support. We thank Edanz (https://jp.edanz.com/ac) for editing a draft of this manuscript.Notes and references
- M. A. Stuart, W. T. Huck, J. Genzer, M. Muller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef PubMed.
- J. Rühe, M. Ballauff, M. Biesalski, P. Dziezok, F. Gröhn, D. Johannsmann, N. Houbenov, N. Hugenberg, R. Konradi, S. Minko, M. Motornov, R. R. Netz, M. Schmidt, C. Seidel, M. Stamm, T. Stephan, D. Usov and H. Zhang, Adv. Polym. Sci., 2004, 165, 79–150 CrossRef.
- F. Zhou and W. T. Huck, Phys. Chem. Chem. Phys., 2006, 8, 3815–3823 RSC.
- M. Ballauff and O. Borisov, Curr. Opin. Colloid Interface Sci., 2006, 11, 316–323 CrossRef CAS.
- T. P. Russell, Phys. B, 1996, 221, 267–283 CrossRef CAS.
- A. Takahara, Y. Higaki, T. Hirai and R. Ishige, Polymers, 2020, 12, 1624 CrossRef CAS.
- S. Moya, O. Azzaroni, T. Farhan, V. L. Osborne and W. T. Huck, Angew. Chem., Int. Ed. Engl., 2005, 44, 4578–4581 CrossRef CAS.
- N. R. Hollingsworth, S. I. Wilkanowicz and R. G. Larson, Soft Matter, 2019, 15, 7838–7851 RSC.
- N. D. Spencer and W. T. Tysoe, The Cutting Edge of Tribology, World Scientific Publishing, 2015 Search PubMed.
- S. K. Sinha and B. J. Briscoe, Polymer Tribology, Imperial College Press, Distributed by World Scientific, London, Singapore, Hackensack, NJ, 2009 Search PubMed.
- Y. Higaki, B. Frohlich, A. Yamamoto, R. Murakami, M. Kaneko, A. Takahara and M. Tanaka, J. Phys. Chem. B, 2017, 121, 1396–1404 CrossRef CAS.
- C. Monzel, M. Veschgini, J. Madsen, A. L. Lewis, S. P. Armes and M. Tanaka, Langmuir, 2015, 31, 8689–8696 CrossRef CAS PubMed.
- J. L. Cuellar, I. Llarena, S. E. Moya and E. Donath, Macromolecules, 2013, 46, 2323–2330 CrossRef CAS.
- T. Farhan, O. Azzaroni and W. T. S. Huck, Soft Matter, 2005, 1, 66–68 RSC.
- T. Fukuma, Sci. Technol. Adv. Mater., 2010, 11, 033003 CrossRef PubMed.
- H. Songen, B. Reischl, K. Miyata, R. Bechstein, P. Raiteri, A. L. Rohl, J. D. Gale, T. Fukuma and A. Kuhnle, Phys. Rev. Lett., 2018, 120, 116101 CrossRef PubMed.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101 CrossRef PubMed.
- C. W. Yang, K. Miyazawa, T. Fukuma, K. Miyata and I. S. Hwang, Phys. Chem. Chem. Phys., 2018, 20, 23522–23527 RSC.
- W. Foster, K. Miyazawa, T. Fukuma, H. Kusumaatmaja and K. Voiotatchovsky, Nanoscale, 2020, 12, 5452–5463 RSC.
- H. Asakawa, S. Yoshioka, K.-i. Nishimura and T. Fukuma, ACS Nano, 2012, 6, 9013–9020 CrossRef CAS PubMed.
- T. Ikarashi, T. Yoshino, N. Nakajima, K. Miyata, K. Miyazawa, Y. Morais Jaques, A. S. Foster, M. Uno, C. Takatoh and T. Fukuma, ACS Appl. Nano Mater., 2020, 4, 71–83 CrossRef.
- E. Sackmann, Science, 1996, 271, 43–48 CrossRef CAS PubMed.
- M. Tanaka and E. Sackmann, Nature, 2005, 437, 656–663 CrossRef CAS.
- D. H. Hamer, Annu. Rev. Biochem., 1986, 55, 913–951 CrossRef CAS.
- O. Purrucker, A. Fortig, R. Jordan and M. Tanaka, ChemPhysChem, 2004, 5, 327–335 CrossRef CAS PubMed.
- T. Kaindl, H. Rieger, L. M. Kaschel, U. Engel, A. Schmaus, J. Sleeman and M. Tanaka, PLoS One, 2012, 7, e42991 CrossRef CAS.
- H. Rieger, H. Y. Yoshikawa, K. Quadt, M. A. Nielsen, C. P. Sanchez, A. Salanti, M. Tanaka and M. Lanzer, Blood, 2015, 125, 383–391 CrossRef CAS.
- V. E. Podasca, T. Buruiana, C. D. Varganici and E. C. Buruiana, J. Polym. Res., 2017, 24, 103 CrossRef.
- H. Wang, Z. Chen, L. Xin, J. Cui, S. Zhao and Y. Yan, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 2175–2185 CrossRef CAS.
- H. Hillebrandt and M. Tanaka, J. Phys. Chem. B, 2001, 105, 4270–4276 CrossRef CAS.
- T. Fukuma and S. P. Jarvis, Rev. Sci. Instrum., 2006, 77, 043701 CrossRef.
- T. Fukuma, Rev. Sci. Instrum., 2009, 80, 023707 CrossRef PubMed.
- T. Fukuma, M. Kimura, K. Kobayashi, K. Matsushige and H. Yamada, Rev. Sci. Instrum., 2005, 76, 053704 CrossRef.
- S. M. R. Akrami, H. Nakayachi, T. Watanabe-Nakayama, H. Asakawa and T. Fukuma, Nanotechnology, 2014, 25, 455701 CrossRef CAS PubMed.
- D. Nečas and P. Klapetek, Open Phys., 2012, 10, 181–188 Search PubMed.
- J. E. Sader and S. P. Jarvis, Appl. Phys. Lett., 2004, 84, 1801–1803 CrossRef CAS.
- A. Engel, C.-A. Schoenenberger and D. J. Müller, Curr. Opin. Struct. Biol., 1997, 7, 279–284 CrossRef CAS.
- M. Tutus, F. F. Rossetti, E. Schneck, G. Fragneto, F. Forster, R. Richter, T. Nawroth and M. Tanaka, Macromol. Biosci., 2008, 8, 1034–1043 CrossRef CAS PubMed.
- L. Jones and P. D. Nellist, Microsc. Microanal., 2013, 19, 1050–1060 CrossRef CAS.
- Y. Wu, Z. Fan, Y. Fang and C. Liu, IEEE Trans. Instrum. Meas., 2021, 70, 1–12 Search PubMed.
- X. Xu, D. Mastropietro, M. Ruths, M. Tirrell and J. Yu, Langmuir, 2019, 35, 15564–15572 CrossRef CAS.
- A. Kundagrami and M. Muthukumar, J. Chem. Phys., 2008, 128, 244901 CrossRef PubMed.
- E. Schneck, E. Papp-Szabo, B. E. Quinn, O. V. Konovalov, T. J. Beveridge, D. A. Pink and M. Tanaka, J. R. Soc., Interface, 2009, 6(Suppl 5), S671–S678 CAS.
- H. Hertz, für die Reine und , Angew. Math. , 1882, 92, 156–171 CrossRef.
- H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- S. Suresh, Science, 2001, 292, 2447–2451 CrossRef CAS.
- J. Domke and M. Radmacher, Langmuir, 1998, 14, 3320–3325 CrossRef CAS.
- H. Shulha, X. Zhai and V. V. Tsukruk, Macromolecules, 2003, 36, 2825–2831 CrossRef CAS.
- M. F. Doerner and W. D. Nix, J. Mater. Res., 1986, 1, 601–609 CrossRef.
- J. Czajor, W. Abuillan, D. V. Nguyen, C. Heidebrecht, E. A. Mondarte, O. V. Konovalov, T. Hayashi, D. Felder-Flesch, S. Kaufmann and M. Tanaka, RSC Adv., 2021, 11, 17727–17733 RSC.
- A. Cartagena and A. Raman, Biophys. J., 2014, 106, 1033–1043 CrossRef CAS.
- E. Schneck, E. Papp-Szabo, B. E. Quinn, O. V. Konovalov, T. J. Beveridge, D. A. Pink and M. Tanaka, J. R. Soc., Interface, 2009, 6, S671–S678 CrossRef CAS.
- H. Ahrens, S. Förster and C. A. Helm, Phys. Rev. Lett., 1998, 81, 4172–4175 CrossRef CAS.
- A. Yamamoto, K. Hayashi, A. Sumiya, F. Weissenfeld, S. Hinatsu, W. Abuillan, M. Nakahata and M. Tanaka, Front. Soft Matter, 2022, 2, 959542 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00350c |
| This journal is © The Royal Society of Chemistry 2022 |