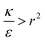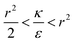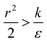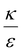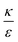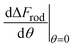Open Access Article
Open Access ArticleThe aspect ratio effect on the cytotoxicity of inert nano-particles flips depending on particle thickness, and is one of the reasons for the literature inconsistency†
Yifat
Brill-Karniely‡
 *ab,
Ouri
Schwob‡
a and
Ofra
Benny
*ab,
Ouri
Schwob‡
a and
Ofra
Benny
 *a
*a
aInstitute for Drug Research, The School of Pharmacy, Faculty of Medicine, The Hebrew University of Jerusalem, Jerusalem, 9112001, Israel. E-mail: yifat.brill@mail.huji.ac.il; ofra.benny@mail.huji.ac.il
bInstitute of Animal Science, Agricultural Research Organization (ARO), The Volcani Center, Bet-Dagan, Israel
First published on 29th September 2022
Abstract
The interaction of inert nano-particles with cells has significant effect on the potential cytotoxicity of the particles. The role of particle aspect ratio in the interaction with cells was largely studied in the literature; however non consistent conclusions were obtained. In the present study a detailed physical model is presented as well as a set of experimental work and a scan of literature data. The aim was to investigate the role of particle size and aspect ratio in cell uptake, and to examine possible sources of the literature inconsistency. Cells which provide the first line of contact with particles in the human body were incubated with seven types of particles. These included spherical and rod gold nanoparticles, as well as larger spherical polystyrene particles in various sizes. We stress that in order to achieve comparative insight careful attention needs to be given to the experimental conditions and to the data analysis. Furthermore, our physical model shows that conclusions regarding the role of aspect ratio in NP uptake largely depend on the radius of the particles. The aspect ratio cannot be regarded as a sole geometrical parameter which determines the interaction of inert nano-particles with cells. When discussing particles larger than 10 nm (for which passive diffusion is irrelevant), the effect of the aspect ratio flips depending on the particle thickness. For particles thicker than ∼35 nm, the longer they are the more toxic they would be, however this trend opposes for thinner NPs, where larger aspect ratio results in reduced uptake and toxicity. Therefore, rod non-functionalized particles whose thickness is between 15 and 30 nm, and are relatively long, are expected to be the safest, with minimal cytotoxicity.
Introduction
The increasing use of nanoparticles (NPs) in various technological applications can in general be divided into two groups. One is the use of particles as drug carriers whose specific interaction with target cells is desired. Another group includes very wide usage in various fields such as cosmetics, agriculture, electronics and more in which the particles are not aimed to make physical interactions with cells. However, such interaction may occur as a side effect – raising concerns related to toxicity to the body upon exposure, thus there is unmet need in assessing the safety of NPs. A major aspect of NP toxicity results from physical interaction of the particles with cells. Insights related to the non-specific interaction of inert particles with cells, which result from physical rather than biological mediators, is essential for collective knowledge. Such information is crucial for the design of particles whose cell uptake is minimal, and are potentially expected to be safer. Specifically, tuning the size and shape of particles can control the levels of their toxicity by affecting the mechanical interaction between the cells and the particles.While the effect of the size and shape of gold NPs on the interaction with cells was largely studied, the conclusions in the scientific literature were non-consistent, especially regarding the role of the aspect ratio (AR). Fig. 1A shows a collection of uptake experiments preformed in previous published studies (and includes also results from the present work).1–5 In all of these experiments the role of gold NP aspect ratio was tested, however the trends observed were non-consistent. For comparing the different sets of data, in Fig. 1A the highest uptake value of each experiment was fixed to a value of 1 and other results from the same experiment were scaled accordingly. While the conclusion from some of the experiments was that elevated aspect ratio increases particle uptake by cells, other studies claimed the opposite, and in several experiments clear relations were not observed.
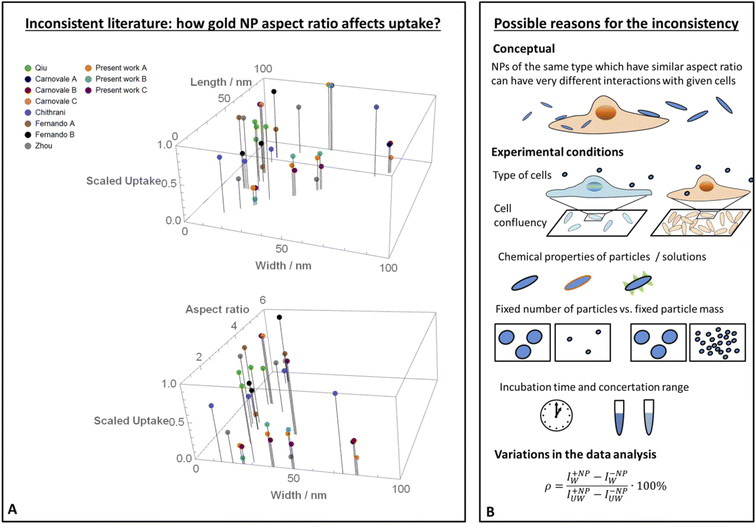 | ||
| Fig. 1 Literature inconsistency. (A) A comparison between results published in different studies (including the present work), which examined how the uptake of gold NPs by cells was affected by the particles aspect ratio.1–5 In each experiment, the highest uptake was scaled to 1 and other data points from the same experiment were normalized accordingly. The scaled data is shown as a function of the width and length of the particles (top), or as a function of the width and aspect ratio (bottom). In both of these presentations, it is clear that the trends were non-consistent. (B) Proposed reasons for the literature inconsistency. A conceptual point is that the aspect ratio cannot be regarded as the sole geometrical parameter; in the present work we show that AR effect flips depending on the NP radius. Other explanations include different behavior of cell types, variations in experimental conditions such as cell confluency, chemical properties of the particles, different definitions of fixed NP amount, variations in incubation time, concentration range and also differences in the data analysis. | ||
In the present study we combine physical theories with uptake experiments in order to investigate the role of particle size and AR in the interaction with cells, and to examine causes of the literature inconsistency. Our theoretical model, which nicely agrees with the experimental data, explains that the effect of AR largely depends on the diameter of the particles. Importantly, the aspect ratio effect on the uptake flips depending on NP diameter, and this can explain opposing conclusion in the literature. Existing studies often examine how the AR affects the interaction with cells, regardless of the absolute size of the nanoparticles. However, we claim here that the absolute particle diameter needs to be regarded for comparative knowledge about the role of the AR in cell uptake and cytotoxicity. Fig. 1B illustrates possible reasons for the literature inconsistency, which apart from this conceptual issue regard also the experimental conditions or the data analysis.
In our experimental work three human cell types were tested, which provide the first line of contact with particles in the human body: skin keratinocytes (HaCat cells), colorectal adenocarcinoma cells (Caco-2) and primary umbilical vein endothelial cells (HUVEC). While particle coating and functionalization largely affect the toxicity and interaction with cells,1,6,7 here we focused on inert particles without functional groups, in order to isolate the mechanical effects. In repeating experiments the three cell types were incubated with spherical and rod gold nanoparticles. HaCat and Caco-2 cells were also incubated with spherical polystyrene particles from nano to sub-micron scale.
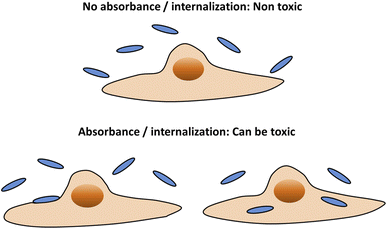
Any interaction of particles with cells can potentially lead to damage in cell function. While non functionalized particles such as gold NPs, are sometimes considered non-toxic, they can reduce biological functionality.8,9 Cell damage can be caused not only due to the insertion of particles into cells; it may also arise from interactions of adsorbed particles at the cell membrane.8,10 Damage in cell functionality does not necessarily correlate with cell death. Thus, when human safety is concerned, it should be desirable to minimize any type of physical contact between particles and cells. Therefore, our aim here was to point on particle parameters that would prevent either stable membrane adhesion or cell internalization – as both processes can potentially damage the cells (Fig. 2). The terminology of “uptake” here does not distinguish between particle internalization and adsorption, as both would be un-desirable in the context of human safety. We discuss here NPs larger than 10 nm, for which passive diffusion is not relevant.11 Below 10 nm passive diffusion mechanisms of cell entrance can occur, leading to massive uptake, and then the NPs may be very toxic.12,13
Experimental
Cell culture
Human keratinocyte cell line, HaCaT cells (ThermoFisher), were maintained in Dulbecco's modified Eagle's medium (DMEM, ThermoFisher) supplemented with 10% (V/V) fetal bovine serum and 1% antibiotics (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg per ml streptomycin and 10
000 μg per ml streptomycin and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 units per ml penicillin) at 37 °C with 5% CO2. Colon colorectal adenocarcinoma, Caco-2 cells (ATCC), were grown in Dulbecco's modified Eagle's medium (DMEM, ThermoFisher) supplemented with 10% (V/V) fetal bovine serum, 1% antibiotics (10
000 units per ml penicillin) at 37 °C with 5% CO2. Colon colorectal adenocarcinoma, Caco-2 cells (ATCC), were grown in Dulbecco's modified Eagle's medium (DMEM, ThermoFisher) supplemented with 10% (V/V) fetal bovine serum, 1% antibiotics (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg per ml streptomycin and 10
000 μg per ml streptomycin and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 units per ml penicillin) and 1% non-essential amino acids solution (MEM-Eagle) at 37 °C with 5% CO2. Human Umbilical Vein Endothelial Cells, HUVEC (Lanza), were grown in PeproGrow MacroV kit (Peprotech) at 37 °C with 5% CO2. All cell-lines were Mycoplasma-free (EZ-PCR Mycoplasma Test Kit Biological Industries, catalog number 2070020).
000 units per ml penicillin) and 1% non-essential amino acids solution (MEM-Eagle) at 37 °C with 5% CO2. Human Umbilical Vein Endothelial Cells, HUVEC (Lanza), were grown in PeproGrow MacroV kit (Peprotech) at 37 °C with 5% CO2. All cell-lines were Mycoplasma-free (EZ-PCR Mycoplasma Test Kit Biological Industries, catalog number 2070020).
Uptake experiments with polystyrene particles
Fluorescently labelled purple polystyrene spherical particles were purchased from Spherotech Inc. (USA), Ex. 488 nm, Em. 545/60 nm. Particle diameters were 50, 300 and 800 nm. HaCat and Caco-2 cells were seeded in 96 well clear bottom plates (Corning, Sigma) and cultured until cells reached 90% confluency. The cells were incubated with particles for 24 hours. The fluorescence was then detected with a Microplate Reader (SYNERGY-HT, Biotek, USA), in excitation: 530 emission: 590. Then the plates were washed thoroughly with PBS and the fluorescence was measured again. Cells without beads were used to obtain a baseline signal. Each value represents an average of five repeats and each experiment was performed in two independent duplicates.Uptake experiments with gold nanoparticles
Fluorescently labelled gold nanoparticles were purchased from Creative Diagnostics. The spherical NPs were of 25, 40 or 50 nm, and the rods were of 40 × 100 nm. HUVEC, HaCaT and Caco-2 cells were seeded at 5500, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 45
000 and 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per well respectively in black 96 wells per plate with clear bottom (Greiner). To obtain uniform distribution of the cells on the surface and avoid non-specific adherence of the gold nanoparticles, cells were seeded in small media volume. The volume was completed to 200 μL after cell adherence. Cells were cultured until 90% confluency and gold nanoparticles were then added in different concentrations. Cells were incubated for additional 24 hours. The fluorescence was then detected with a Microplate Reader (SYNERGY-HT, Biotek, USA), using a screening mode with 25 measurements per well, in excitation: 635, emission: 665. The plates were then washed thoroughly with PBS and the fluorescence was measured again. Cells without beads were used to obtain a baseline signal. Each value represents an average of five repeats and each experiment was performed in two independent duplicates.
000 cells per well respectively in black 96 wells per plate with clear bottom (Greiner). To obtain uniform distribution of the cells on the surface and avoid non-specific adherence of the gold nanoparticles, cells were seeded in small media volume. The volume was completed to 200 μL after cell adherence. Cells were cultured until 90% confluency and gold nanoparticles were then added in different concentrations. Cells were incubated for additional 24 hours. The fluorescence was then detected with a Microplate Reader (SYNERGY-HT, Biotek, USA), using a screening mode with 25 measurements per well, in excitation: 635, emission: 665. The plates were then washed thoroughly with PBS and the fluorescence was measured again. Cells without beads were used to obtain a baseline signal. Each value represents an average of five repeats and each experiment was performed in two independent duplicates.
Uptake calculation
The percentage of uptake was defined as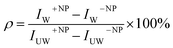 . In this expression IW+NP and IW−NP stand for the fluorescence intensities in the washed plates in the presence or absence of particles, respectively. IUW+NP and IUW−NP are the same values for the non-washed plates. In this expression the numerator is proportional to the number of NPS which physically interacted with the cells, whereas the denominator is proportional to the total number of particles. Thus this calculation provides the fraction of particles which interacted with the cells, relative to the total amount of particles.
. In this expression IW+NP and IW−NP stand for the fluorescence intensities in the washed plates in the presence or absence of particles, respectively. IUW+NP and IUW−NP are the same values for the non-washed plates. In this expression the numerator is proportional to the number of NPS which physically interacted with the cells, whereas the denominator is proportional to the total number of particles. Thus this calculation provides the fraction of particles which interacted with the cells, relative to the total amount of particles.
Confocal imaging of cells after incubation with gold particles
HaCat cells were seeded at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per well in 8 wells Ibidi Slide. After a day NPs were added to the cells and incubated with them for 1.5 hour. Cells were then fixed using glutaraldehyde 4% for 10 min. Cytoplasms (actin) and nucleus were stained using Phalloidin (555) and Dapi for 20 min. Cells were washed three time. Images were then collected using a Leica SP8 confocal microscope, ×63 water objective (N.A 1.2), EX/EM sets: 405/430–460 (nucleus), 638/644–703 (actin), 552/560–580 (NP) or using Nikon Yokogawa W1 Spinning Disk or inverted Nikon fluorescence microscopy.
000 cells per well in 8 wells Ibidi Slide. After a day NPs were added to the cells and incubated with them for 1.5 hour. Cells were then fixed using glutaraldehyde 4% for 10 min. Cytoplasms (actin) and nucleus were stained using Phalloidin (555) and Dapi for 20 min. Cells were washed three time. Images were then collected using a Leica SP8 confocal microscope, ×63 water objective (N.A 1.2), EX/EM sets: 405/430–460 (nucleus), 638/644–703 (actin), 552/560–580 (NP) or using Nikon Yokogawa W1 Spinning Disk or inverted Nikon fluorescence microscopy.
Cryo TEM in gold nanoparticles
Gold nanoparticles solutions (3 μL) were applied onto a glow-discharged TEM grid (300-mesh Cu grid) coated with a holey carbon film (Lacey substrate, Ted Pella, Ltd., Redding, CA, USA). The excess liquid was blotted, and the specimens were vitrified by a rapid plunging into liquid ethane pre-cooled with liquid nitrogen using Vitrobot Mark IV (FEI). The vitrified samples were examined at −177 °C using FEI Tecnai 12 G2 TWIN TEM (FEI, USA) operated at 120 kV and equipped with a Gatan model 626 cold stage. The images were recorded by a 4k × 4k FEI Eagle CCD camera in low dose mode. TIA software (Tecnai Imaging and Analysis) was used to record the images.Statistics
Statistical data was analyzed on GraphPad Prism 8 (http://www.graphpad.com, San Diego, CA). Studies containing two groups were assessed using the unpaired two-tailed Student's t-test. Studies containing more than three groups were compared and analyzed using a one-way analysis of variance (ANOVA). Differences were considered statistically significant for p < 0.05.Results & discussion
Literature inconsistency
Fig. 1A shows a comparison between different studies which examined how gold NP uptake by cells was affected by the particles aspect ratio.1–5 For a comparative presentation, data from each experiment was scaled relative to the highest uptake observed in this experiment. For each experiment the highest uptake was normalized to a value of 1 and other data points were scaled relative to this value. Such definition allows comparing the trends observed in different studies. Fig. 1A shows the scaled data either as a function of the width and length of the particles, or as a function of the width and aspect ratio. In both of these presentations, it is clear that the trends were non-consistent. While the conclusion from some of the experiments was that elevated aspect ratio increases particle uptake by cells (we note this effect here by AR+), other studies claimed the opposite (AR−), and in several experiments clear relations were not observed.Possible reasons for this inconsistency are illustrated in Fig. 1B. A main point stressed here is that while often uptake measurements are shown as a function of the AR alone, the aspect ratio should not be a sole geometrical parameter to be regarded. For example, the same types of NPs, one with dimensions of 30 × 60 nm and the other of 50 × 100 nm, can have very different interaction with the same cell types, even though both have AR of 2. Therefore, the common case at which the x axis in uptake plots represents the AR but the different NPs tested did not share the same thickness or length – can be misleading. This can be a major reason for the variations of trends observed in the literature. This concept is thoroughly discussed below and is highlighted by our conclusions from the theoretical model, showing that the AR effect flips from AR+ to AR− depending on the NP radius.
Apart from this conceptual notion, variations in the experimental conditions can also result in the literature inconsistency. A trivial point is that different cell types can behave in different manner and provide varying uptake trends – even for inert non-functionalized particles. For example, we show below that the elastic modulus of cell membranes, which vary between cell types, affects the critical radius at which the system flips from AR+ to AR−. Other reasons are related to cell confluency, which affects both biological and physical properties of the cells, and thus can alter uptake trends. Moreover, chemical properties of both the particles and the solutions, even in the case of non-functionalized particles can have a major effect on the types of the interactions between the particles and the cells. In addition, in the presence of biological solutions, proteins can be adsorbed on the surface of gold NPs and form a shell of protein corona which can affect the interaction of the particles with cells.9,14
Determining how the fixed amount of particles in a given experiment is defined can also make large differences between studies. That is, while some researchers use fixed number of particles per volume, others use fixed mass. Other factors are related to experimental conditions such as the incubation time and the range of the concentration used. Moreover, the data analysis can differ between experiments. For example, it would be important to pay attention whether the results are normalized relative to the total amount of particles or to the total amount of cells.
The non-uniformity of the conclusions in the literature raises the need for reliable comparative knowledge. Below we present both uptake experiments and a physical model, for capturing in a consistent manner the role of NP geometry in the uptake process. The effect of spherical NP size was tested, as well as the AR role in cell uptake. The physical model provided a ‘zoom out’ look for a wide range of geometrical parameters.
Size effect in polystyrene sub-micron beads: smaller are safer
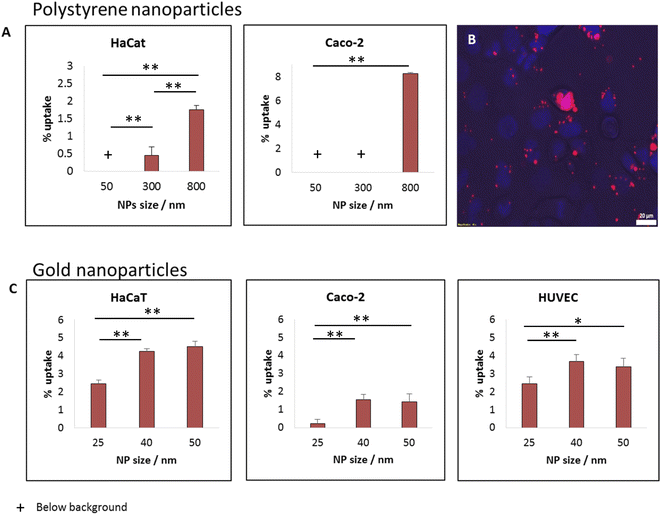
For studying how the size of spherical particles affected their uptake by cells and their cytotoxicity, we recorded the uptake of fluorescently labelled polystyrene beads of different size by CaCo-2 and HaCat cells. A wide range of particle size was tested: 50, 300 and 800 nm. After 24 hours of incubation, we saw clear monotonic dependence on particle size, whereas the largest particles, of 0.8 μm had the highest uptake levels, as shown in Fig. 3A for concentration of 25 μg ml−1. Varying the concentration to 5 μg ml−1 did not change this trend, as shown in Fig. S1.† In previous work we suggested that the increased uptake with bead size results from an intuitive energetic interplay. When the particles are larger, the membrane – particle contact area is wider, thus the gain in adhesion energy in the adsorption process would be large.15 The adhesion energy can then be sufficient to overcome the energetic penalty of membrane bending, which is essential for the adsorption process. This results in fewer uptake events in the case of smaller beads.15While both HaCat and Caco-2 cells demonstrated increase in uptake with particle size, the pattern of this increase was different between the cell types. In the HaCat cells there was a more gradual raise, while for Caco-2 cells the uptake of both 50 and 300 nm particles was vanishing, with a sharp increase reaching ∼8% uptake of the 800 nm beads. The fluorescence microscopy image in Fig. 3B demonstrates the uptake of 800 nm beads by Caco-2 cells. The differences between the responses of the cells results from internal dissimilarities between cell types. This emphasizes the importance of examining a wide span of cells when aiming to preform cytotoxicity assessments.
Size effect in gold nano-beads: smaller are safer
The increase in particle uptake with the size of the particles indicates that whenever possible, smaller particles (above the passive penetration scale) should be preferable to be used for industrial purposes, to increase their safety for humans. To further examine options to reduce particle toxicity within smaller particle scale, we preformed uptake measurements with fluorescently labelled gold beads of varying diameters: 25, 40 or 50 nm. Fig. 3C shows uptake experiments with 12.5 μg ml−1 of the gold NPs with three cell types: Caco-2, HaCat and HUVEC. Also within this small nano-scale of particles, the smaller NPs were found to be potentially the safest. While the uptake of the 25 nm NPs was the lowest (for the three cell types), the uptake levels of 40 and 50 nm beads was similar to each other. This may result from several causes. First, the difference between 40 and 50 nm may not be significant enough for varying the uptake patterns of the cells. Another option is related to energetic arguments leading to non-monotonic dependence on particle size.3,15Shape effect in gold NPs: 40 nm spheres are safer than rods with the same width
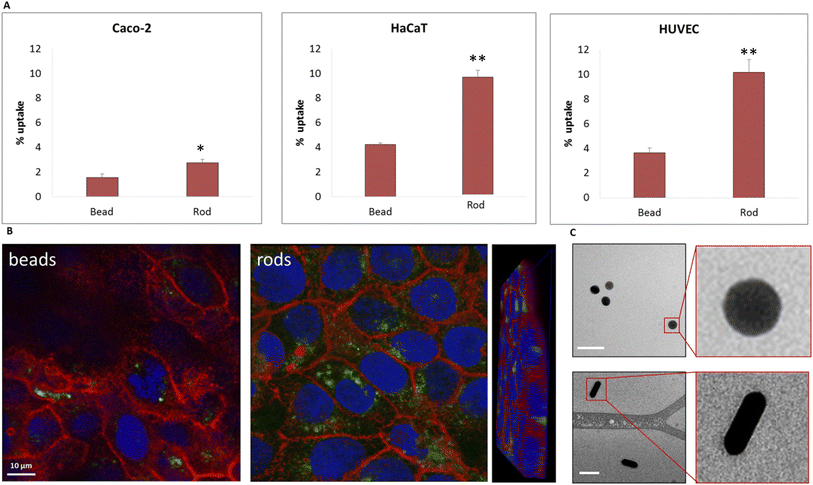
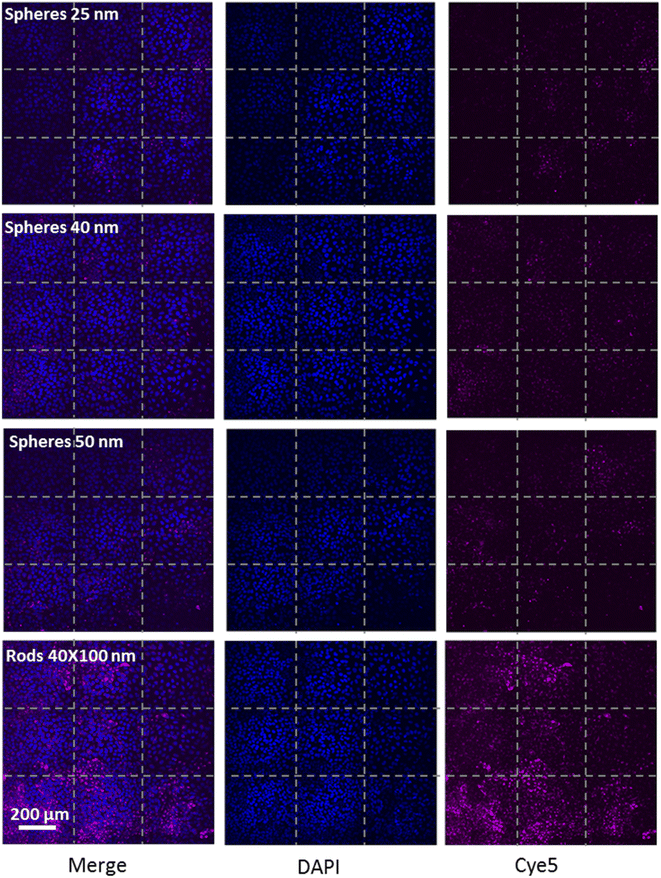
We further examined the role of particle aspect ratio (AR) in controlling the physical interaction with cells. For that, we compared the uptake of spherical and rods NPs, both comprising a diameter of 40 nm, while the rods were of length 100 nm; thus the particles were of AR of 1 and 2.5, respectively. Fig. 4A shows that the uptake of rods was clearly higher than that of the spheres in all cell types tested. Confocal images (Fig. 4B, Movie S1†) demonstrated the high uptake of the rods relative to the spheres in HaCat cells. In order to exclude particle aggregation, we preformed Cryo TEM imaging (Fig. 4C and S2†). No aggregates were observed, and the ratio between the number of particles observed in the imaging and the NP concentration was the same for the two concentrations tested (25 and 50 μg ml−1). This verified that there were no aggregates adsorbed by the cleaning filter during the freezing procedure, indicating that the lack of aggregates observed in the images can reliably indicate on the absence of NP aggregation.Fig. 5 demonstrates the effect of particles size and shape in their uptake by HaCat cells. Confocal images are shown after 24 h of incubation with gold nano-beads of 25, 40 and 50 nm diameter, and nano rods of diameter 40 nm and length 100 nm. It is well shown that increasing the bead size raised the uptake by the cells, and that the uptake of rod particles by was dramatically higher than that of spheres.
Physical model: the effect of the aspect ratio flips depending on NP radius
The aim of the physical model below is to provide comparative knowledge about the uptake of non-functionalized spheres or rods nanoparticles, for understanding the dependence of the uptake on particle size and AR. Such knowledge will assist in the design of nanoparticles that would be of minimal toxicity. For isolating physical effects, we discuss here the interaction of cells with particles with no surface functionalization, similar to the particles used in our experiments. In this case the interaction would be non-selective, and membrane adsorption would result from non-specific adhesion.11,15 For particles larger than 10 nm, for which passive diffusion is not relevant, different endocytosis mechanisms involve the engulfment of NPs by the cell plasma membrane.11 An established assumption is that stable adhesion of the particle to the outer cell membrane is a pre-condition to full engulfment and uptake.15–17 Full uptake requires dynamical processes, such as cytoskeleton re-arrangement. It would be reasonable that the pathways which initiate such dynamics are fully operated only after some time of stable contact. Thus identifying the conditions at which stable adhesion is inhibited would be relevant in order to prevent also cell insertion. This definition would be relevant to different pathways of endocytosis, which usually differ from one another in the active involvement of proteins that accelerate and stabilize full particle engulfment as well as the formation of vesicles encapsulating the particles.11 Due to the above, an initial stable envelope of the particle by the cell membrane is hypothesized in our model to be a necessary step for full engulfment and internalization into the cell.The interaction of a single particle with a cell is considered here, neglecting particle–particle interactions (in accordance with our findings regarding the absence of particle aggregation). As noted, for purposes of human safety we are interested in preventing uptake processes which include both cell adsorption and penetration. Since stable adhesion is assumed to be a pre-condition for full particle internalization, knowledge about particle adsorption would be relevant for preventing both of the uptake processes. For this aim it is useful to use a thermodynamic model which describes the change in free energy upon the formation of contact between the NP and the cell membrane.
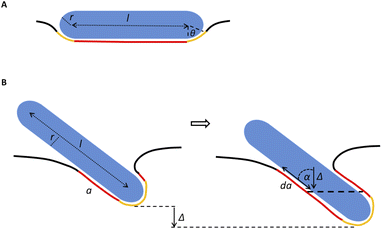
Our model assumes that the particles are large enough (>10 nm) so that their passive diffusive penetration into cells would not be relevant. On the other hand, the particles are in the nano-rather than micro-scale, so that the involvement of the cytoskeleton would be negligible, and the main deformed compartment of the cell during particle uptake would be the membrane.15,18 The rod particles are assumed to have spherocylinder geometry with radius r and length l. l is defined as the cylinder length excluding the spherical edges, therefore the case of l = 0 represents a spherical particle of radius r (Fig. 6A). We primarily regard here the case of parallel contact between the particle and the cell, as illustrated in Fig. 6A (the tilted scenario shown in Fig. 6B will be discussed below). This is in accordance with previous work suggesting that particles rotate into parallel configuration for increasing the contact area with the cell membrane.19 Then, assuming azimuthal symmetry in the wrapping of the particle by the cell membrane, we can define the reaction coordinate as the wrapping angle θ shown in Fig. 6A. The leading terms in the free energy change result from the membrane deformation on the one hand, and from the non-specific adhesion on the other hand. Since the indentation of the particle is in the nanometer scale, in plane tension of the membrane would be negligible. Thus the main energetic factor of membrane distortion results from membrane bending due to the particle wrapping. The particle and cell surfaces are assumed to be smooth and tightly adhering along their contact surface. Long range interactions that are of weaker order are neglected here. Moreover, the membrane is assumed to be homogeneous with zero spontaneous curvature.
Based on the above, we can write the change in the free energy upon the contact of a rod nanoparticle with the outer membrane of a cell:
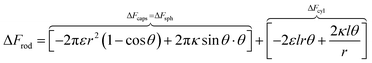 | (1) |
The first two terms describe the contribution arising from the contact at the hemispheres at the edges of the rod (marked in yellow in Fig. 6A), including the membrane bending in the vicinity of the caps (black in Fig. 6A). These terms are identical to the case of a single round bead partly wrapped by a cell membrane. The first term describes the nonspecific adhesion within the spherical cap contact 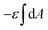 , assuming that it is uniform, whereas ε is the contact energy per unit area and dA a surface element; the second term reflects the membrane bending with the bending modulus κ, as previously derived based on Helfrisch's theory of membrane elasticity.15,20 This term includes both the contact surface at the partly wrapped hemispheres, and the bent membrane in the vicinity of the caps, which is bounded by the plane of hemisphere – cylinder contact (yellow and black, respectively, in Fig. 6A).15 The two terms on the right regard the contribution of the cylindrical body of the rod (red mark in Fig. 6A). The third term is the adhesion energy along the cylindrical contact. The last energetic term here describes membrane bending due to the cylindrical contact. The mean curvature is then
, assuming that it is uniform, whereas ε is the contact energy per unit area and dA a surface element; the second term reflects the membrane bending with the bending modulus κ, as previously derived based on Helfrisch's theory of membrane elasticity.15,20 This term includes both the contact surface at the partly wrapped hemispheres, and the bent membrane in the vicinity of the caps, which is bounded by the plane of hemisphere – cylinder contact (yellow and black, respectively, in Fig. 6A).15 The two terms on the right regard the contribution of the cylindrical body of the rod (red mark in Fig. 6A). The third term is the adhesion energy along the cylindrical contact. The last energetic term here describes membrane bending due to the cylindrical contact. The mean curvature is then 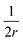 so that the Helfrisch based bending term provides
so that the Helfrisch based bending term provides 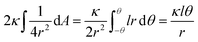 , where dA is the area element. The factor of 2 in the fourth term results from the contribution of membrane bending in the vicinity of the physical contact along the cylinder. This unbound surface, whose boundaries are defined by the planes of the cylinder – hemisphere contacts, is assumed to be identical to the cylindrical bound regime. Such geometry provides smooth connection of this surface with the unbound membrane near the hemispheres, whose contribution is inserted in the second term.15
, where dA is the area element. The factor of 2 in the fourth term results from the contribution of membrane bending in the vicinity of the physical contact along the cylinder. This unbound surface, whose boundaries are defined by the planes of the cylinder – hemisphere contacts, is assumed to be identical to the cylindrical bound regime. Such geometry provides smooth connection of this surface with the unbound membrane near the hemispheres, whose contribution is inserted in the second term.15
In order to understand the effect of particle AR on the cytotoxicity of NPs, we can investigate whether the cylindrical terms increase or decrease the adsorption probability, relative to beads with l = 0. For that we examine only the contribution arising from the cylindrical regime and look on the following derivative
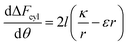 | (2) |
The sign of this derivative indicates on the contribution of the cylindrical term to the uptake probability. We can distinguish between two scenarios. When 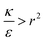 the expression in eqn (2) will be positive, namely the uptake of rods would be less probable than the uptake of spheres. Moreover, from the linear dependence of eqn (2) in l we see that the longer are the rods the less probable their uptake would be. On the other hand, for
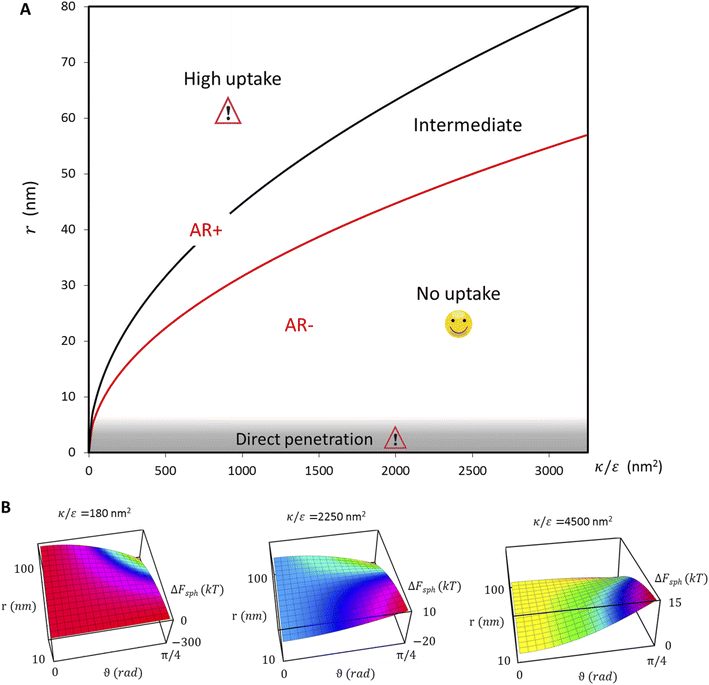
the expression in eqn (2) will be positive, namely the uptake of rods would be less probable than the uptake of spheres. Moreover, from the linear dependence of eqn (2) in l we see that the longer are the rods the less probable their uptake would be. On the other hand, for 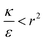 , ΔFcyl is a monotonically decreasing function thus rods would be more probable to be taken by cells than spheres, with increasing probability the longer the rods are. Fig. 7A shows a phase diagram in which these two regimes are separated by a red curve.
, ΔFcyl is a monotonically decreasing function thus rods would be more probable to be taken by cells than spheres, with increasing probability the longer the rods are. Fig. 7A shows a phase diagram in which these two regimes are separated by a red curve.
This conclusion is significant, as it means that (in the case of parallel contact for now), the radius of the particle determines what would be the effect of the AR on the uptake probability. This can be a major cause for the inconsistency of the results in the literature: increasing AR can either raise or suppress the uptake probability, and the exact effect depends on the rod thickness. Based on that we can define a critical radius r*, for which the effect of the AR flips:
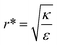 | (3) |
For rods with radius below r*, increasing the particle AR would reduce the uptake probability and consequently also the cytotoxicity (AR−). The reason for this behavior is very intuitive. For thinner rods, increasing their length would provide only small contribution to the contact area, however it will largely increase the membrane bending penalty due to their large curvature. However, for thicker rods whose radius is larger than r*, the effect of AR would be the opposite: the uptake of longer rods would be higher (AR+). In this case, the curvature would be smaller and the increase in the contact area more significant, therefore the uptake probability will raise with the increase of particle AR.
In the phase diagram shown in Fig. 7A the y-axis represents NP radius and the x-axis is the ratio 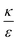 . This ratio may vary between cells, and also depends on the type of particles. κ, the bending modulus of the membrane, is typically in the order of a few kBT (ref. 21) in thermal energy units, where kB is the Boltzmann constant and T the absolute temperature. The larger is this constant, the higher is the energetic membrane penalty required for NP uptake. ε reflects the adhesive energy per unit area, and depends on the nature of the non-specific interaction between the given particles and cells. Previous work suggest values of ε in the range of 10−3kBT/nm2 for inert particles.15 The larger is ε the higher is the energetic gain upon NP-cell contact. Thus the ratio
. This ratio may vary between cells, and also depends on the type of particles. κ, the bending modulus of the membrane, is typically in the order of a few kBT (ref. 21) in thermal energy units, where kB is the Boltzmann constant and T the absolute temperature. The larger is this constant, the higher is the energetic membrane penalty required for NP uptake. ε reflects the adhesive energy per unit area, and depends on the nature of the non-specific interaction between the given particles and cells. Previous work suggest values of ε in the range of 10−3kBT/nm2 for inert particles.15 The larger is ε the higher is the energetic gain upon NP-cell contact. Thus the ratio 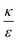 reflects the energetic interplay between membrane bending penalty and the gain in adhesion energy, in the passive process of NP adsorption. Typical values of r* would be in the scale of few tens of nm. For example, for κ = 1kBT and ε = 0.003kBT/nm2, r* is ∼18 nm. In our experimental results, AR+ effect was observed for NP radius of 20 nm. The higher is the ratio
reflects the energetic interplay between membrane bending penalty and the gain in adhesion energy, in the passive process of NP adsorption. Typical values of r* would be in the scale of few tens of nm. For example, for κ = 1kBT and ε = 0.003kBT/nm2, r* is ∼18 nm. In our experimental results, AR+ effect was observed for NP radius of 20 nm. The higher is the ratio 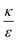 the more “difficult” it would be for cells to uptake particles, due to the large bending required relative to the gain in adhesion energy. Then r* would be larger, meaning that the system will flip from AR− to AR+ in larger rod thickness, since then the increase in contact area will be large enough to compensate the membrane bending (red curve in Fig. 7A).
the more “difficult” it would be for cells to uptake particles, due to the large bending required relative to the gain in adhesion energy. Then r* would be larger, meaning that the system will flip from AR− to AR+ in larger rod thickness, since then the increase in contact area will be large enough to compensate the membrane bending (red curve in Fig. 7A).
In the above discussion parallel contact was assumed. We would like now to gain insight about the general case in which the particle can contact the membrane in a tilted position (Fig. 6B). The rotation is not relevant for symmetrical spheres. As for rods, the rotational degrees of freedom affect the interaction with the cell through several aspects as has been previously studied.19 When investigating the passive adhesion of a rod to the membrane, the orientation affects the energetic interaction with the cell. Moreover, the distribution of the polar contact angle is not uniform as it depends on the spatial angle probability. For the present discussion, we wish to understand whether tilted orientation would affect the role of AR in the uptake process. In other words, we need to examine how the polar angle between the rod and the membrane plane affects the role of NP length in the sign of the free energy derivative. For intuitive knowledge, we look at an infinitesimal indentation Δ with fixed polar angle α, which leads to a differential increase in the cylindrical length of the contact area, da = Δ/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α (see Fig. 6B). Then we can write:
α (see Fig. 6B). Then we can write:
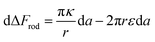 | (4) |
The first term here is the change in the membrane bending energy in the cylindrical regime marked in red in Fig. 6B, due to a Δ indentation. The adhered area is assumed to be azimuthally uniform relative to the axis perpendicular to the unperturbed membrane. This term is again derived from the Helfrisch free energy 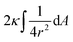 with
with 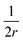 being the mean curvature of the membrane and dA a surface element. The second term is the adhesion energy
being the mean curvature of the membrane and dA a surface element. The second term is the adhesion energy 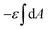 , assuming that it is uniform along the contact area. This model implies that the area of the tilted cylinder which reflects the change in the contact area due to a Δ indentation (red lines in Fig. 6B) equals the surface area of a straight cylinder of radius r and length da. For this process, the changes in the membrane bending energy within the cap margin, or outside the contact area (yellow and black, respectively, in Fig. 6B), are expected to be negligible. The dependence on l comes from integration of dΔFrod over some fraction of the NP coverage. From eqn (4) we learn that the leading terms in such integration would be linear in l and will not depend on α. The contribution of the leading cylindrical terms in the case of a tilted rod would be similar to the case of parallel contact. Since rotational degrees of freedom do not affect the energetic interaction of spherical beads with the cell, we can learn that when aiming to gain comparative knowledge about the role of the aspect ratio, the conclusions from the case of parallel contact will be relevant also for a tilted case. It should be noted however that for absolute uptake probabilities a full derivation needs to be done.
, assuming that it is uniform along the contact area. This model implies that the area of the tilted cylinder which reflects the change in the contact area due to a Δ indentation (red lines in Fig. 6B) equals the surface area of a straight cylinder of radius r and length da. For this process, the changes in the membrane bending energy within the cap margin, or outside the contact area (yellow and black, respectively, in Fig. 6B), are expected to be negligible. The dependence on l comes from integration of dΔFrod over some fraction of the NP coverage. From eqn (4) we learn that the leading terms in such integration would be linear in l and will not depend on α. The contribution of the leading cylindrical terms in the case of a tilted rod would be similar to the case of parallel contact. Since rotational degrees of freedom do not affect the energetic interaction of spherical beads with the cell, we can learn that when aiming to gain comparative knowledge about the role of the aspect ratio, the conclusions from the case of parallel contact will be relevant also for a tilted case. It should be noted however that for absolute uptake probabilities a full derivation needs to be done.
From the above discussion we learned about the AR+ or AR− trends, namely about the effect of the aspect ratio in the uptake of rods, with the comparison to spheres as a reference. This information cannot be full without investigating the reference case of spheres and understanding when spheres are likely to be taken by cells. Our experimental results indicated that smaller spheres will be taken less and therefore safer for use. In order to test this via our model, we can search for extremum of ΔFsph by comparing the derivative to zero: 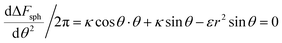 . Since the passive engulfment of spherical beads involves minor membrane wrapping we can use small angle approximation and get
. Since the passive engulfment of spherical beads involves minor membrane wrapping we can use small angle approximation and get 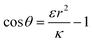 . Thus the condition for extremum would be
. Thus the condition for extremum would be 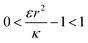 or
or 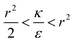 . The second derivative under small angle approximation is
. The second derivative under small angle approximation is 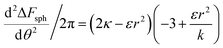 . When there is extremum the left multiplier is positive since
. When there is extremum the left multiplier is positive since 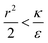 due to the condition for extremum. The right multiplier would be negative since
due to the condition for extremum. The right multiplier would be negative since 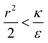 and therefore also
and therefore also 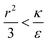 . Thus in the extremum the second derivative would be negative, namely there would be a barrier in the free energy change ΔFsph. The conclusion would be that for
. Thus in the extremum the second derivative would be negative, namely there would be a barrier in the free energy change ΔFsph. The conclusion would be that for 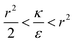 , passive bead adhesion by cell membrane would not be a spontaneous process, and the uptake probability would depend on factors such as temperature, as well as on κ of the given cell and on the adhesion strength ε. In addition, since this is an AR+ regime, the uptake of rods would be higher than that of spheres. This regime is termed “intermediate” in the phase diagram shown in Fig. 7A.
, passive bead adhesion by cell membrane would not be a spontaneous process, and the uptake probability would depend on factors such as temperature, as well as on κ of the given cell and on the adhesion strength ε. In addition, since this is an AR+ regime, the uptake of rods would be higher than that of spheres. This regime is termed “intermediate” in the phase diagram shown in Fig. 7A.
We now examine the parameter regime 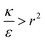 . Then, there is no extremum namely ΔFsph would be a monotonic function. The first term of the derivative
. Then, there is no extremum namely ΔFsph would be a monotonic function. The first term of the derivative 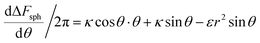 is positive by definition. The sum of the second and third terms would also be positive in this range since κ > εr2. Thus the function ΔFsph would be monotonically increasing, and stable NP adhesion is not expected occur. Importantly, this means that non-functionalized NPS whose radius is smaller than r* (eqn (3)) are expected to be of very low cytotoxicity – this is noted by the “No Uptake” zone in Fig. 7A. Since this is also an AR− regime, the uptake of rods would be even lower, meaning that inert thin nano-rods are expected to be very safe for use. It is important to recall here that this discussion is relevant only for diameters larger than 10 nm, otherwise direct diffusion mechanisms may be relevant.
is positive by definition. The sum of the second and third terms would also be positive in this range since κ > εr2. Thus the function ΔFsph would be monotonically increasing, and stable NP adhesion is not expected occur. Importantly, this means that non-functionalized NPS whose radius is smaller than r* (eqn (3)) are expected to be of very low cytotoxicity – this is noted by the “No Uptake” zone in Fig. 7A. Since this is also an AR− regime, the uptake of rods would be even lower, meaning that inert thin nano-rods are expected to be very safe for use. It is important to recall here that this discussion is relevant only for diameters larger than 10 nm, otherwise direct diffusion mechanisms may be relevant.
The last parameter regime to discuss would be 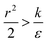 , in which there is no extremum as well. Again, the first term of the derivative is positive. The sum of the second and third terms is negative since
, in which there is no extremum as well. Again, the first term of the derivative is positive. The sum of the second and third terms is negative since 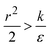 and therefore
and therefore 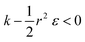 thus of course that k − r2ε < 0. Using small angle approximation we can compare the absolute values of the positive vs. the negative terms. Then, since
thus of course that k − r2ε < 0. Using small angle approximation we can compare the absolute values of the positive vs. the negative terms. Then, since 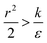 we have also
we have also 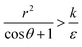 , thus the whole expression would be negative. Thus for
, thus the whole expression would be negative. Thus for 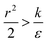 we see that ΔFsphere is decreasing monotonically. In addition, since this is an AR+ regime ΔFrod would be decreasing with larger gradient. The important conclusion would be that both spheres and rods are expected to massively be taken by cells then, which can result in large cytotoxicity (“High uptake” in Fig. 7A).
we see that ΔFsphere is decreasing monotonically. In addition, since this is an AR+ regime ΔFrod would be decreasing with larger gradient. The important conclusion would be that both spheres and rods are expected to massively be taken by cells then, which can result in large cytotoxicity (“High uptake” in Fig. 7A).
Fig. 7B shown three representative surface plots of ΔFsph as a function of θ and r. The ratio 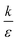 increases from the left plot to the right one. The lower is this ratio, the “easier” it is for the cells to engulf the particles, and indeed we see the decrease in ΔFsph into negative values for
increases from the left plot to the right one. The lower is this ratio, the “easier” it is for the cells to engulf the particles, and indeed we see the decrease in ΔFsph into negative values for 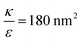 . Increasing
. Increasing 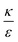 (middle and right plots) shift ΔFsph to be an increasing function, and this effect is mostly pronounced the smaller are the beads, where the adhesion energy is not enough for compensating the membrane bending penalty. This reflects again the higher expected cytotoxicity of the larger spheres, and its dependence on
(middle and right plots) shift ΔFsph to be an increasing function, and this effect is mostly pronounced the smaller are the beads, where the adhesion energy is not enough for compensating the membrane bending penalty. This reflects again the higher expected cytotoxicity of the larger spheres, and its dependence on 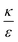 .
.
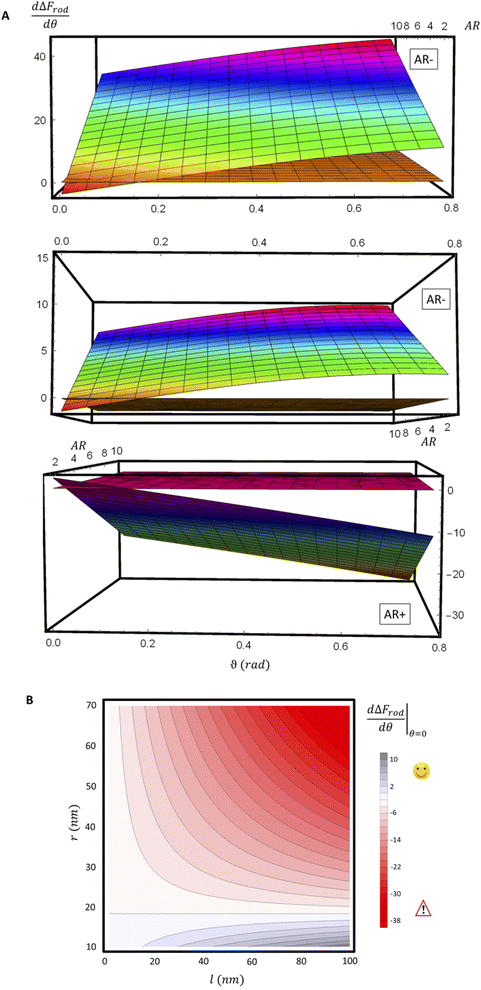
For a further investigation of the role of AR, we can also look at the derivative of ΔFrod with respect to θ, which combines both effects of the cylinder and the hemispheres of the particles. Fig. 8A shows this derivative as a function of θ and of the aspect ratio AR, where we used the relation 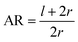 (since as noted l is defined as the cylinder length, excluding the hemispheres). The plots in Fig. 8A correspond to three values of r: 20, 40 or 60 nm; typical values of 0.002kBT/nm2 and 2.3kBT, respectively, were used for ε and κ. For a clearer view the zero plane was added to the surface plots as a reference. In both of the upper curves, the radii are smaller than r* and we can see that increasing the uptake ratio results in positive values of the derivative and reduces the uptake probability. However, in the case of r = 60 nm (bottom of Fig. 8A), the AR effect flips from AR− to AR+, whereas the derivative at the onset of sphere (AR = 1) uptake is positive, and becomes negative only for larger values of the AR. An intuitive presentation is given in Fig. 8B, where
(since as noted l is defined as the cylinder length, excluding the hemispheres). The plots in Fig. 8A correspond to three values of r: 20, 40 or 60 nm; typical values of 0.002kBT/nm2 and 2.3kBT, respectively, were used for ε and κ. For a clearer view the zero plane was added to the surface plots as a reference. In both of the upper curves, the radii are smaller than r* and we can see that increasing the uptake ratio results in positive values of the derivative and reduces the uptake probability. However, in the case of r = 60 nm (bottom of Fig. 8A), the AR effect flips from AR− to AR+, whereas the derivative at the onset of sphere (AR = 1) uptake is positive, and becomes negative only for larger values of the AR. An intuitive presentation is given in Fig. 8B, where 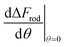 is shown. In the color code blue represent positive values, which indicate on vanishing uptake and higher safety of the rods, and the red represent negative values and increased probability for cytotoxicity. A threshold in r* ∼ 18 nm, at which the system switches from AR− to AR+ is observed.
is shown. In the color code blue represent positive values, which indicate on vanishing uptake and higher safety of the rods, and the red represent negative values and increased probability for cytotoxicity. A threshold in r* ∼ 18 nm, at which the system switches from AR− to AR+ is observed.
Conclusions
Non-functionalized nanoparticles such as gold NPs are often considered harmless to cells as they typically do not affect the viability of the cells. However, negative outcomes that can affect human health can result also from damage in cell functionality, and not only from cell death. Previous work found that prolonged exposure to gold NPs can be harmful.8,13,22 It was also suggested that cytotoxicity post interaction with gold NPs can arise not only from endocytosis of the particles, but also from interactions at cell membrane.8,10 To maximize the potential safety of nanoparticles, it would be desirable that the particles would not cause either cell death or reduction in functionality. A main step towards this goal would be to prevent physical interaction between the particles and the cells. Thus uptake resulting both from NP adsorption to the cell membrane, or from NP internalization into the cells would be non-desirable.It is thus clear that minimizing the uptake of non-functional particles by cells is a crucial factor in the design of particles for various usages that could be safer for humans. Specifically, the effect of NP size and aspect ratio is of increasing interest. While this topic has been previously studied, there was no consensus in the scientific committee regarding the role of particle aspect ratio in controlling the cytotoxicity potential of the particles. The source of this inconsistency was a major topic of the present study.
We stress here that in order to achieve comparative insight careful attention needs to be given to the experimental conditions and to the data analysis (Fig. 1B). A major conceptual issue is that rod like particles cannot be described only by their AR, while ignoring their absolute width or length. In previous studies, the effect of AR was examined by comparing particles with different ARs, however often neither NP thickness nor NP width was kept constant. We showed here that the absolute size of particles, and not only the ratio between their length and thickness, has a major role in the interaction with cells. Based on our physical model, the effect of AR on the uptake opposes when examining thin or thick particles. Fig. 7 and 8 summarize conclusions regarding the role of aspect ratio in NP uptake, which largely depends on the radius of the particles. For thicker particles (typically more than ∼35 nm) the longer they are the more toxic they would be (AR+), however this trend opposes for thinner NPs, where larger aspect ratio results in reduced toxicity (AR−). The width at which this transition occurs depends on the local bending rigidity of the cell membrane and on the strength of the non-specific interactions: 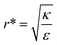 .
.
The main conclusions of the present work are thus as follows. First, for obtaining consistency in the messages regarding the role of NP AR in cell uptake and the cytotoxicity, there should be uniformity in the experimental conditions. These include cell types, cell confluency, chemical properties of the particles and the solutions, definitions of fixed NP amount, incubation time, concentration range and also the data analysis. Moreover, a main message of our work is that the radius of NPs is critical in determining the role of the aspect ratio. The AR effect flips depending on the radius of the particle: for common cell parameters, particles thicker than ∼35 nm would be more toxic when they are longer. However, for thinner particles the longer they are the less toxic they would be. Based on our physical model, non-functionalized particles whose thickness is between 15 and 30 nm, and are relatively long, are expected to be the safest, with minimal uptake. In a future study it can be desirable to make experimental measurements with a large library of non-functionalized particles of the same type, with varying dimensions and AR, keeping uniform experimental conditions. Moreover, it would be desirable to study numerous types of cells.
Author contributions
YBK: conception, experimental design, physical model, literature analysis, paper writing. OS: experimental design, uptake experiments, sample preparation for microscopy, results analysis. OB: conception, experimental design, result analysis, gaining funding, and project supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Natalie Orehov for the spinning disc microscopy images and Talya Millo for a fluorescence microscopy image. We would like to thank Dr Einat Zelinger, director of the CSI microscopy core facility at HUJI agriculture campus, for the confocal imaging of HaCat cells. We would like to thank Dr Yael Levi-Kalisman from the HUJI Center for Nanoscience and Nanotechnology for the Cryo TEM images of the gold nanoparticles. This project was funded by the Israeli Ministry of Science and Technology, grant #3-13574, European Research Council (ERC)-PoC 101061967, ERC-starter grant 756762, Israel Science Foundation grant no. ISF 877/19 and the Teacher-Scholars program of The Hebrew University of Jerusalem supported by the Jerusalem Municipality, JDA and the Trump Foundation.References
- Y. Qiu, et al., Surface chemistry and aspect ratio mediated cellular uptake of Au nanorods, Biomaterials, 2010, 31(30), 7606–7619 CrossRef CAS PubMed.
- C. Carnovale, G. Bryant, R. Shukla and V. Bansal, Identifying Trends in Gold Nanoparticle Toxicity and Uptake: Size, Shape, Capping Ligand, and Biological Corona, ACS Omega, 2019, 4, 242–256 CrossRef CAS.
- B. Chithrani, A. A. Ghazani and W. C. W. Chan, Determining the Size and Shape Dependence of Gold Nanoparticle Uptake into Mammalian Cells, Nano Lett., 2006, 6(4), 662–668 CrossRef CAS PubMed.
- D. Fernando, S. Sulthana and Y. Vasquez, Cellular Uptake and Cytotoxicity of Varying Aspect Ratios of Gold Nanorods in HeLa Cells, ACS Appl. Bio Mater., 2020, 3(3), 1374–1384 CrossRef CAS PubMed.
- H. Zhou, et al., Gold nanoparticles impair autophagy flux through shape-dependent endocytosis and lysosomal dysfunction, J. Mater. Chem. B, 2018, 6(48), 8127–8136 RSC.
- A. Sani, C. Cao and C. Cui, Toxicity of gold nanoparticles (AuNPs): A review, Biochem. Biophys. Rep., 2021, 26, 100991 CAS.
- K. Govindaraju, R. Selvaraj, D. Sivaraman, R. Selvaraj, R. Manikandan and V. Ganesh Kumar, Nanotoxicity Assessment of Functionalized Gold Nanoparticles in Sprague–Dawley Rats, J. Cluster Sci., 2017, 28, 2933–2951 CrossRef.
- P. Chandran and R. T. Thomas, Gold Nanoparticles in Cancer Drug Delivery, Nanotechnology Applications for Tissue Engineering, ScienceDirect, 2015, pp. 221–237 Search PubMed.
- P. Wang, et al., Interaction of gold nanoparticles with proteins and cells, Sci. Technol. Adv. Mater., 2015, 16(3), 034610 CrossRef PubMed.
- C. Lasagna-Reeves, et al., Bioaccumulation and toxicity of gold nanoparticles after repeated administration in mice, Biochem. Biophys. Res. Commun., 2010, 393(4), 649–655 CrossRef CAS.
- M. Sousa de Almeida, et al., Understanding nanoparticle endocytosis to improve targeting strategies in nanomedicine, Chem. Soc. Rev., 2021, 50(9), 5397–5434 RSC.
- R. Coradeghini, et al., Size-dependent toxicity and cell interaction mechanisms of gold nanoparticles on mouse fibroblasts, Toxicol. Lett., 2013, 217(3), 205–216 CrossRef CAS PubMed.
- Y. Pan, et al., Size-dependent cytotoxicity of gold nanoparticles, Small, 2007, 3(11), 1941–1949 CrossRef CAS PubMed.
- C. Corbo, et al., The impact of nanoparticle protein corona on cytotoxicity, immunotoxicity and target drug delivery, Nanomedicine, 2016, 11(1), 81–100 CrossRef CAS PubMed.
- Y. Brill-Karniely, et al., Triangular correlation (TrC) between cancer aggressiveness, cell uptake capability, and cell deformability, Sci. Adv., 2020, 6(3), eaax2861 CrossRef CAS PubMed.
- D. M. Richards and R. G. Endres, The mechanism of phagocytosis: two stages of engulfment, Biophys. J., 2014, 107(7), 1542–1553 CrossRef CAS PubMed.
- A. Zak, et al., Distinct timing of neutrophil spreading and stiffening during phagocytosis, Biophys. J., 2022, 121(8), 1381–1394 CrossRef CAS PubMed.
- Y. Brill-Karniely, Mechanical Measurements of Cells Using AFM: 3D or 2D Physics?, Front. Bioeng. Biotechnol., 2020, 8, 605153 CrossRef PubMed.
- R. Vacha, F. J. Martinez-Veracoechea and D. Frenkel, Receptor-mediated endocytosis of nanoparticles of various shapes, Nano Lett., 2011, 11(12), 5391–5395 CrossRef CAS.
- W. Helfrich, Elastic properties of lipid bilayers: theory and possible experiments, Z. Naturforsch., C, 1973, 28(11), 693–703 CrossRef CAS PubMed.
- C. Händel, et al., Cell membrane softening in human breast and cervical cancer cells, New J. Phys., 2015, 17, 083008 CrossRef.
- T. Mironava, et al., Gold nanoparticles cellular toxicity and recovery: effect of size, concentration and exposure time, Nanotoxicology, 2010, 4(1), 120–137 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00453d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |