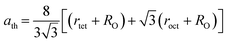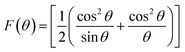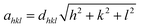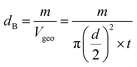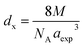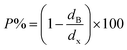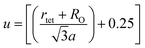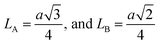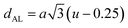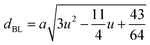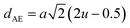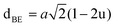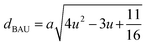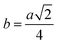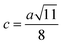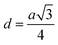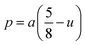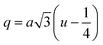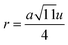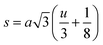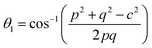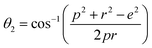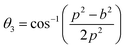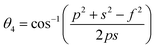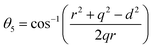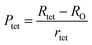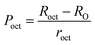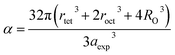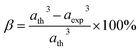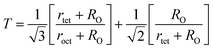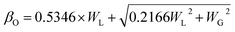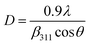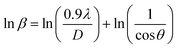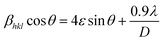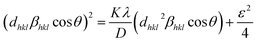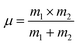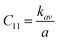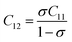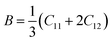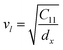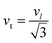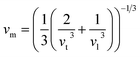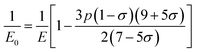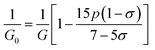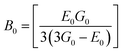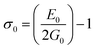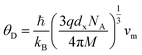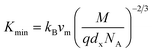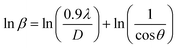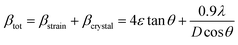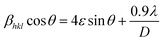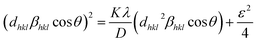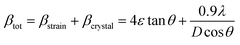DOI:
10.1039/D1RA09090A
(Paper)
RSC Adv., 2022,
12, 8502-8519
Structural characteristics, cation distribution, and elastic properties of Cr3+ substituted stoichiometric and non-stoichiometric cobalt ferrites†
Received
15th December 2021
, Accepted 17th January 2022
First published on 17th March 2022
Abstract
Structural, elastic and cation distribution properties have been investigated on stoichiometric and non-stoichiometric cobalt ferrites. Crystal structure, formation of spinel type ferrite, chemical bonding, cation distribution, and thermal properties of two series of Cr3+ substituted stoichiometric and non-stoichiometric various cobalt ferrites with general formula Co1−xCrxFe2O4 (S1), and Co1+xCrxFe2−xO4 (S2) were reported. Samples are synthesized by the solid-state reaction technique via planetary ball milling. X-ray diffraction (XRD) analysis confirms the formation of a single phase cubic spinel structure with the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Rietveld refinement results show that Cr occupies both the tetrahedral (A-site) and octahedral sites (B-site). The experimental lattice parameters show increasing trends for both the series with increase of Cr content. The cation–anion vacancies, chemical bonding, and the displacement of oxygen have been evaluated to understand the effect of Cr substitution and how the non-stoichiometry affects the physical and chemical properties of the material. The crystallite size is found to be the decreasing value with an increase of Cr concentration for both series of samples. Specific vibrational modes from the FTIR spectra suggest a gradual change of inversion of the ferrite lattice with the increase of Cr concentration which is also evident from Rietveld refinement data. The elastic properties analysis reveals that the synthesized samples for both series are ductile in nature. The non-stoichiometric structure with excess Co2+ may pave a new way to realize the lowering of Curie temperature of ferrite that is expected to improve the magnetocaloric properties.
m. Rietveld refinement results show that Cr occupies both the tetrahedral (A-site) and octahedral sites (B-site). The experimental lattice parameters show increasing trends for both the series with increase of Cr content. The cation–anion vacancies, chemical bonding, and the displacement of oxygen have been evaluated to understand the effect of Cr substitution and how the non-stoichiometry affects the physical and chemical properties of the material. The crystallite size is found to be the decreasing value with an increase of Cr concentration for both series of samples. Specific vibrational modes from the FTIR spectra suggest a gradual change of inversion of the ferrite lattice with the increase of Cr concentration which is also evident from Rietveld refinement data. The elastic properties analysis reveals that the synthesized samples for both series are ductile in nature. The non-stoichiometric structure with excess Co2+ may pave a new way to realize the lowering of Curie temperature of ferrite that is expected to improve the magnetocaloric properties.
1. Introduction
Ferrites are ferrimagnetic materials usually used in high density recording media and satellite communication as well as microwave devices in electronic industries due to their ease of fabrication, low cost, moderate saturation magnetization, mechanical strength, and chemical stability.1 In the last decade, the synthesis of spinel ferrites emerged extensively due to their diversified use in technological applications.2,3 In particular, cobalt ferrite (COF) has got enormous importance both in technological as well as biomedical applications.3–13 Intensive studies on COF have been carried out with varying doping and/or substituting the divalent or trivalent cations and synthesizing them by different methods.3,14,15 In order to confirm the crystallinity and the phase of the synthesized materials, Rietveld refinement has been significantly used on the X-ray diffraction (XRD) data of the samples.1,9–11,16 Amri et al.1 have calculated the theoretical lattice parameters along with hopping lengths, oxygen positional parameters, cation–cation and cation–anion bond lengths of Ni–Zn–Al ferrite. Kumar et al.14 have reported on the estimation of the lattice parameters by using Nelson–Riley (N–R) function, intrinsic strain and crystallite size by using Williamson–Hall (W–H) method. It has also been studied that the crystallite size and intrinsic strain can be determined from the XRD peak broadening analysis by using several ways such as W–H method, size strain plot (SSP), Scherer method, and the modified Scherer method (MS).14,17,18 However, it is reported that SSP and MS methods are found more significant compared to that of W–H and Scherer methods, because both SSP and MS can be observed at a lower angle where the accuracy is found to be very high.18 On the other hand, the formation of ferrite and identification of the chemical bonds can be analyzed from the Fourier transform infrared (FTIR) spectra.1,19–21 Several techniques for the measurement mechanical properties have been used to calculate the elastic and mechanical properties. FTIR is one of the suitable techniques found to calculate the elastic and thermal properties. The elastic moduli, Debye temperature, and minimum thermal conductivity can be calculated by using stiffness, lattice parameters, and X-ray density which have been reported in various literatures1,19,20,22 Chandekar, et al.22 reported the corrected zero porosity elastic moduli estimated from the calculated elastic moduli and porosity.
The synthesis and characterization of ferrites have attracted increasing attention in recent years. Many efforts have been attempted to expand potential applications by improving their properties. Research on inorganic compounds with a non-stoichiometric ratio is a great challenge. Andersen et al.23 reported the local and long-range magnetic structure of non-stoichiometric nanocrystalline spinel type iron oxide. They have found the vacancy ordering in the structure which reveals the shorter coherence length on the non-stoichiometric spinel type iron oxide. In addition various literature on non-stoichiometric compounds have been found,24–28 where remarkable effects of non-stoichiometry on structural, and magnetic properties have been presented.
This study focuses on how Cr3+ affect the structure of stoichiometric COF with the formula Co1−xCrxFe2O4 (S1) and non-stoichiometric COF having the formula Co1+xCrxFe2−xO4 (S2), where x = 0.125, 0.25, 0.375, and 0.50. The cation distribution has been calculated using site occupancy data extracted from the Rietveld refined XRD data. Besides, the theoretical and experimental lattice parameters, oxygen positional parameter, tolerance factor, ionic packing coefficient, vacancy parameter, bond lengths, bond angles, density, and porosity of the above-mentioned samples of both the series have been determined. Crystallite size estimation by various methods such as W–H, SSP, Scherer, MS, and Rietveld methods has also been explained in this study. FTIR spectra have been illustrated to confirm the ferrite formation for the samples of both the investigated series. In addition, elastic and thermal properties have also been explained from the FTIR and structural data. A correlation between the elastic properties and structural properties has been established for exploiting their advanced applications. The main focus of this work is to find the structural defects of COF with Cr3+ substitution at the Co2+ site. In addition, effects of non-stoichiometry on the structure of COF are also explored.
2. Experimental procedure
2.1 Synthesis technique
The selected two series of stoichiometric and non-stoichiometric COF denoted as S1 and S2 have been synthesized by the standard solid-state reaction method. The required amount of Co2O3 (98.0%), Cr2O3 (99.9%), and Fe2O3 (96.0%) are weighed in an analytical balance and hand mixed in a mortar pestle for 2 h. The mixed powders are milled in a planetary ball mill (MSK-SFM-1) for 12 h. The milled powders are calcined at 800 °C for 6 h for a complete solid-state reaction through diffusion of particles. Then the powders of each composition are pressed into pellets by applying a hydraulic pressure of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi. Finally, the pellets are sintered at 1200 °C for 6 h in a furnace and rcrushed in to fine powders.
000 psi. Finally, the pellets are sintered at 1200 °C for 6 h in a furnace and rcrushed in to fine powders.
2.2 Characterizations
The X-ray diffraction (XRD) data of the synthesized samples are taken using a Rigaku Smart Lab X-ray diffractometer with Cu-Kα radiation (λ = 1.5406 Å) with the scanning angle 2θ within the range of 10 to 80°. The Rietveld refinement was carried out using the Full-Prof software integrated in Match-3 software. Room temperature Fourier transform infrared (FTIR) spectroscopy (Spectrometer model-IR Prestige-21) in the region 350–4000 cm−1 was used to find out the functional groups and vibrational structure of the synthesized samples. The parameters related to structural, elastic, and thermal properties are calculated using the XRD data and FTIR spectra.
3. Results
3.1 XRD analysis
The X-ray diffraction patterns along with Rietveld refined data have been shown in Fig. 1, 2, and 3 for the parent COF, other samples of the series S1, and S2, respectively. XRD pattern of the parent COF satisfy the Bragg's condition at 2θ values of 30.37°, 35.76°, 43.4°, 53.84°, 57.4°, and 62.92° with corresponding crystal planes are indexed with (220), (311), (400), (511), and (440), respectively. These sharp peaks, corresponding to the aforesaid (hkl) planes indicate a single phased inverse spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m of parent COF that has been confirmed by the crystallography open database (COD No. 5910063) as reported in the literature.29 No impurity phase has been observed in the pattern for the parent COF which signifies the phase purity of COF. The XRD patterns for the samples of the stoichiometric series S1 and non-stoichiometric series S2 shown in Fig. 2 and 3, reveal the formation of spinel structure (COD No. 910063). The peak positions of (311) plane for both the series S1 and S2 have been shifted towards the lower 2θ angle with an increase of Cr content as shown in Fig. 2(b) and 3(b), which imply an increase of the lattice parameters as a result of Cr substitution.
m of parent COF that has been confirmed by the crystallography open database (COD No. 5910063) as reported in the literature.29 No impurity phase has been observed in the pattern for the parent COF which signifies the phase purity of COF. The XRD patterns for the samples of the stoichiometric series S1 and non-stoichiometric series S2 shown in Fig. 2 and 3, reveal the formation of spinel structure (COD No. 910063). The peak positions of (311) plane for both the series S1 and S2 have been shifted towards the lower 2θ angle with an increase of Cr content as shown in Fig. 2(b) and 3(b), which imply an increase of the lattice parameters as a result of Cr substitution.
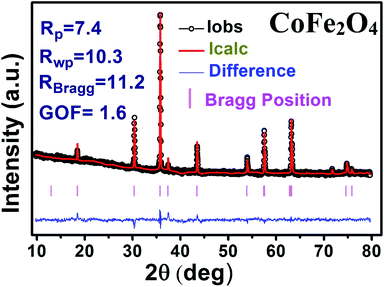 |
| | Fig. 1 Rietveld analysis of XRD pattern of CoFe2O4. | |
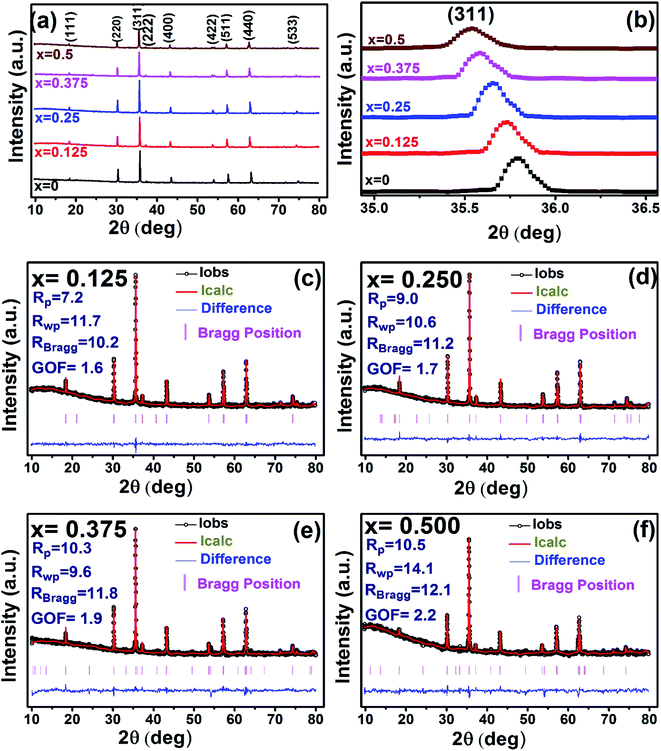 |
| | Fig. 2 Rietveld analysis of XRD patterns for all samples of S1 (Co1−xCrxFe2O4) series. | |
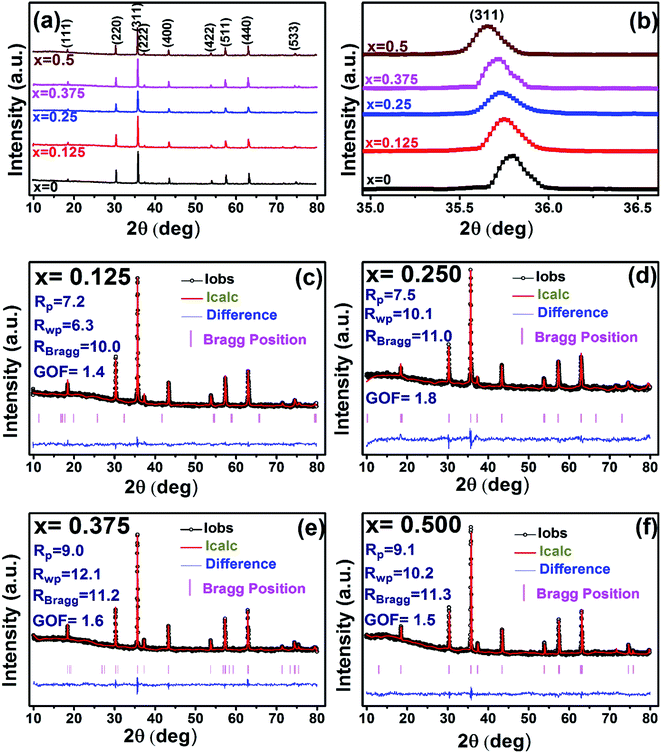 |
| | Fig. 3 Rietveld analysis of XRD patterns for all samples of S2 (Co1+xCrxFe2−xO4). series. | |
3.1.1 Estimation of cation distribution. The cation distribution of the samples at the tetrahedral and octahedral sites of spinel structure has been determined by comparing the observed X-ray intensities from the specific planes of (220), (440), (400), and (422). The ratios of observed and calculated intensities viz. I220/I400, I220/I440, I422/I440, and I400/I440 are considered to evaluate the cation distribution. From the calculation of structure factor, it is reported that (220) and (440) are sensitive to cation distribution at the tetrahedral site, while (400) and (422) are sensitive to cation distribution at the octahedral site.30 The general formulae for cation distribution at the tetrahedral site and octahedral site for samples of the series S1, and S2, are as follows:
| Possible cation distribution of S1 series is [CoαCrβFeγ]tet[Co1−x−αCrx−βFe2−γ]octO4 |
| Possible cation distribution of S2 series is [CoαCrβFeγ]tet[Co1+x−αCrx−βFe2−x−γ]octO4 |
where α,β, and![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ are the cationic parameters for the tetrahedral site and α + β + γ = 1. For COF x = β = 0. The cation distribution has been calculated by the above formulae and tabulated in Table 1. The value of the inversion parameter as determined by calculating the ratio between Fe3+ at the tetrahedral site and Fe3+ at octahedral site Fetetra/Feocta has also been tabulated in Table 1. Using the exact cation distribution the ionic radius for the tetrahedral site (rtet), and octahedral site (roct), have been calculated by the following relations:16
γ are the cationic parameters for the tetrahedral site and α + β + γ = 1. For COF x = β = 0. The cation distribution has been calculated by the above formulae and tabulated in Table 1. The value of the inversion parameter as determined by calculating the ratio between Fe3+ at the tetrahedral site and Fe3+ at octahedral site Fetetra/Feocta has also been tabulated in Table 1. Using the exact cation distribution the ionic radius for the tetrahedral site (rtet), and octahedral site (roct), have been calculated by the following relations:16
| rtet = αrCo + βrCr + γrFe for both the series, |
| roct = 0.5 × {(1 − x − α)rCo + (x − β)rCr + (2 − γ)rFe} for S1, |
| roct = 0.5 × {(1 + x − α)rCo + (x − β)rCr + (2 − x − γ)rFe} for S2, |
where rCo, rCr, and rFe are the ionic radii of Co2+, Cr3+, and Fe3+, respectively. The calculated ionic radii for the tetrahedral site and octahedral site are tabulated in Table 1.
Table 1 Possible cation distribution for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4)
| Series |
S1 |
S2 |
| x |
0.000 |
0.125 |
0.250 |
0.375 |
0.500 |
0.125 |
0.250 |
0.375 |
0.500 |
| Tetrahedral site(±2%) |
Co |
0.132 |
0.100 |
0.090 |
0.070 |
0.050 |
0.179 |
0.121 |
0.042 |
0.012 |
| Cr |
0 |
0.057 |
0.110 |
0.166 |
0.232 |
0.011 |
0.012 |
0.018 |
0.008 |
| Fe |
0.868 |
0.843 |
0.800 |
0.764 |
0.718 |
0.810 |
0.867 |
0.940 |
0.980 |
| Octahedral site (±2%) |
Co |
0.868 |
0.775 |
0.660 |
0.555 |
0.450 |
0.946 |
1.129 |
1.333 |
1.488 |
| Cr |
0 |
0.068 |
0.140 |
0.209 |
0.268 |
0.114 |
0.238 |
0.357 |
0.492 |
| Fe |
1.132 |
1.157 |
1.200 |
1.236 |
1.282 |
1.065 |
0.883 |
0.685 |
0.520 |
| Calculated |
I400/I440 |
0.77 |
0.76 |
0.81 |
0.81 |
0.83 |
0.83 |
0.85 |
0.80 |
0.80 |
| I220/I440 |
0.98 |
0.82 |
1.11 |
1.05 |
1.06 |
1.14 |
1.08 |
1.05 |
0.80 |
| Observed |
I400/I440 |
0.74 |
0.75 |
0.72 |
0.76 |
0.78 |
0.84 |
0.90 |
0.78 |
0.77 |
| I220/I440 |
1.03 |
1.03 |
1.10 |
1.02 |
1.01 |
1.25 |
1.24 |
1.00 |
1.04 |
| Inversion parameter (y) |
0.76 |
0.72 |
0.66 |
0.62 |
0.56 |
0.76 |
0.98 |
1.37 |
1.88 |
|
| Ionic radius (Å) |
rtet |
0.63 |
0.64 |
0.65 |
0.66 |
0.68 |
0.64 |
0.63 |
0.62 |
0.61 |
| roct |
0.69 |
0.68 |
0.68 |
0.67 |
0.66 |
0.73 |
0.78 |
0.83 |
0.87 |
Fig. 4 represents the Energy Dispersive (EDS) spectra for all samples. The elemental analysis are performed from these spectra. From the data of EDS spectra, it is confirmed that chemical composition of the synthesized samples are close to the respective nominal composition.
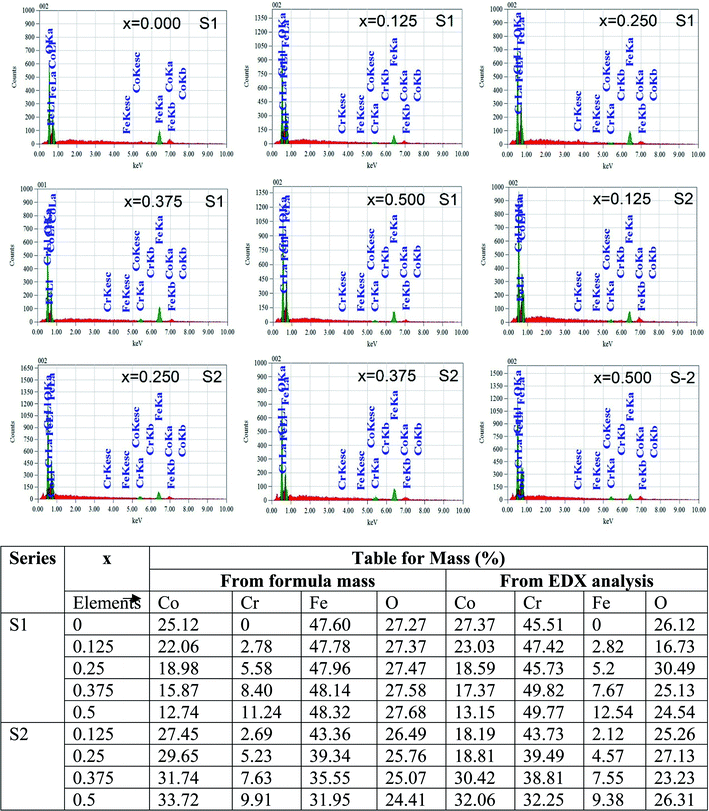 |
| | Fig. 4 EDX spectra of all samples of S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). series with mapping of compositions. | |
3.1.2 Lattice parameter estimation. To determine true value of lattice parameter (atrue) from XRD data, Nelson–Riley (N–R) extrapolating function (eqn (A2)) has been used.17 The lattice parameter for each Bragg position has been calculated using eqn (A3). The N–R function vs. ahkl graph has been plotted for each sample which is shown in Fig. 5 for both the series S1 and S2, respectively. From Fig. 5 the true value of lattice parameters for each sample have been determined by extrapolating θ = 0°. The extracted value of atrue for each sample have been illustrated in Fig. 6. The lattice parameters calculated from the XRD data by using Match-3 software are denoted by aexp, and these values for the both series of samples have been illustrated in Fig. 6. The lattice parameters calculated using the eqn (A1) are denoted by ath, and these values also have been illustrated in Fig. 6. It is observed that aexp for the sample of both series follows the similar increasing trend of the ath and atrue with the Cr content which implies that aexp is reliable. This increase in lattice parameter for S1 series may be caused due to the larger ratio of Cr2+/Co2+ at tetrahedral site than the Cr3+/Co2+ ratio at octahedral site. The increasing trends of lattice parameter for S2 are due to the excess Co2+ with an ionic radius of 0.75 Å which is larger than that of Cr3+ (0.63 Å).31 Since unit cell volume is directly proportional to the lattice constant, hence it follows a similar trend of the lattice constant.
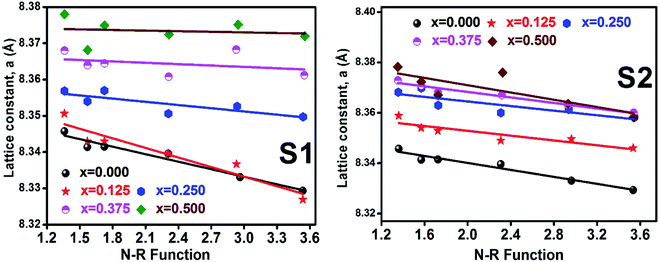 |
| | Fig. 5 Nelson–Riley plot for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
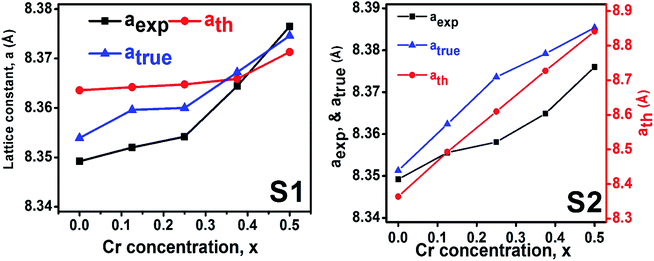 |
| | Fig. 6 Lattice constants as function of Cr content for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
3.1.3 Density and porosity estimation. The bulk density dB, crystal density dx, and porosity (P) for both series of samples have been calculated using eqn (A4), (A5), and (A6), respectively and have been illustrated as a function of Cr concentration in Fig. 7. The density extracted from the Rietveld refined data is denoted as dreit is also presented in Fig. 7. These parameters have been listed in Table 2. It is seen that the dx, and dB show a similar decreasing trend with the increase in Cr content which agrees with the Rietveld refined density dreit. The decreasing trend of the density is due to the molecular weight loss of the investigated samples. Furthermore, it is seen that the dx and dB follow the increasing trend with the Cr content that is also agrees with the dreit for the samples of the series S2. This increasing nature of density may have been caused by the molecular weight gain due to the non-stoichiometry of samples of the series S2. The porosity is found to increase with the addition of Cr content for the samples of both series.
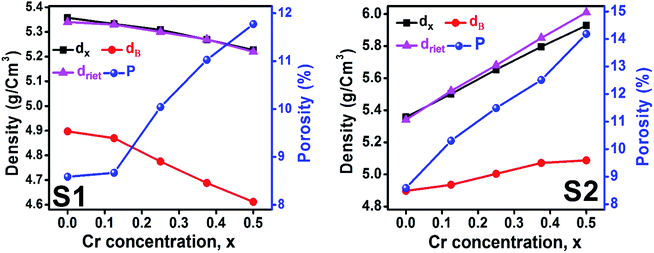 |
| | Fig. 7 Density and porosity as function of Cr content for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
Table 2 Lattice parameter, density, and porosity for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4)
| Series |
x |
aexp (Å) |
Vexp (Å3) |
atrue (Å) |
Vtrue (Å3) |
ath (Å) |
Vth (Å3) |
dx (g cm−3) |
dB (g cm−3) |
dreit (g cm−3) |
P (%) |
| S1 |
0 |
8.3492 |
582.01 |
8.3539 |
582.45 |
8.3635 |
585 |
5.36 |
4.90 |
5.34 |
9 |
| 0.125 |
8.3520 |
582.6 |
8.3596 |
579.51 |
8.3642 |
585 |
5.33 |
4.87 |
5.33 |
9 |
| 0.250 |
8.3542 |
583.06 |
8.3600 |
578.15 |
8.3647 |
585 |
5.31 |
4.78 |
5.29 |
10 |
| 0.375 |
8.3644 |
585.2 |
8.3672 |
577.47 |
8.3658 |
586 |
5.27 |
4.69 |
5.27 |
11 |
| 0.500 |
8.3765 |
587.74 |
8.3746 |
576.55 |
8.3713 |
587 |
5.31 |
4.61 |
5.22 |
13 |
| S2 |
0.125 |
8.3556 |
582.39 |
8.3705 |
586.48 |
8.4927 |
613 |
5.52 |
4.94 |
5.52 |
11 |
| 0.250 |
8.3581 |
589.32 |
8.3896 |
590.50 |
8.6096 |
638 |
5.67 |
5.00 |
5.68 |
12 |
| 0.375 |
8.3649 |
595.80 |
8.3958 |
591.81 |
8.7272 |
665 |
5.82 |
5.07 |
5.85 |
13 |
| 0.500 |
8.376 |
604.68 |
8.4061 |
593.99 |
8.8414 |
691 |
5.95 |
5.09 |
6.01 |
15 |
3.1.4 Oxygen positional parameter, interionic distance and bond angle estimation. When tetrahedral interstices are occupied by divalent ion then the expansion in tetrahedral site is relatively larger than octahedral site due to the difference of ionic radii of cations. This expansion can be explained by oxygen positional parameter, u, which gives quantitative measure of the displacement of oxygen ions. This displacement takes place whenever there is a difference in the radii of substituted and replaced ions. The value of u can be calculated from the ath using the eqn (A7).The calculated u values for both series are listed in Table 4. As seen in that table, u value is almost invariant with Cr content for both series found to be almost equal to that of the parent COF. In a cubic spinel structure the ideal value of u is equal to 3/8 = 0.375. The calculated value of u is slightly larger than that of ideal value, which may be due to the anion displacement from its ideal position. From the analysis of u and δ (= u − 0.375), it is confirmed that lattice is slightly distorted for all the samples of both series.33
The inter-ionic distance between magnetic ions is named as hopping length in tetrahedral site (LA) and octahedral site (LB) which gives information about the strength of spin interaction of ions. The hopping lengths have been calculated by using Stanley's equations (eqn (A8)).1 The calculated values of LA and LB have been tabulated in Table 3 for both the series. Hopping lengths decrease for S1 series, and increase for S2 series with the increasing Cr content.
Table 3 Values of hopping lengths (LA, LB), tetrahedral bond length (dAL), octahedral bond lengths (dBL), tetrahedral edge length (dAE), shared and unshared octahedral edge (dBE, dBEU), interatomic bond lengths and angles for all samples of series S1(Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4)
| Series |
S1 |
S2 |
| x |
0.000 |
0.125 |
0.250 |
0.375 |
0.500 |
0.125 |
0.250 |
0.375 |
0.500 |
| LA (Å) |
3.623 |
3.622 |
3.617 |
3.616 |
3.614 |
3.667 |
3.717 |
3.768 |
3.809 |
| LB (Å) |
2.958 |
2.957 |
2.953 |
2.952 |
2.951 |
2.994 |
3.035 |
3.077 |
3.11 |
| dAL (Å) |
1.945 |
1.956 |
1.968 |
1.982 |
1.998 |
1.926 |
1.893 |
1.86 |
1.832 |
| dBL (Å) |
2.011 |
2.006 |
2.000 |
1.996 |
1.993 |
2.023 |
2.042 |
2.063 |
2.083 |
| dAE (Å) |
3.176 |
3.194 |
3.215 |
3.237 |
3.263 |
3.145 |
3.091 |
3.037 |
2.991 |
| dBE (Å) |
2.727 |
2.711 |
2.692 |
2.677 |
2.659 |
2.762 |
2.818 |
2.877 |
2.931 |
| dBEU (Å) |
2.956 |
2.958 |
2.959 |
2.964 |
2.969 |
2.957 |
2.956 |
2.958 |
2.961 |
| Me–Me distances (Å) |
b |
2.9569 |
2.9572 |
2.9574 |
2.9577 |
2.9597 |
3.0026 |
3.0439 |
3.0855 |
3.1259 |
| c |
3.4673 |
3.4676 |
3.4678 |
3.4683 |
3.4705 |
3.5209 |
3.5693 |
3.6181 |
3.6654 |
| d |
3.6215 |
3.6218 |
3.6220 |
3.6225 |
3.6248 |
3.6774 |
3.7280 |
3.7789 |
3.8284 |
| e |
5.4322 |
5.4327 |
5.4330 |
5.4337 |
5.4373 |
5.5162 |
5.5921 |
5.6684 |
5.7426 |
| f |
5.1216 |
5.1220 |
5.1223 |
5.1230 |
5.1263 |
5.2007 |
5.2723 |
5.3442 |
5.4142 |
| Me–O distances (Å) |
p |
2.0113 |
2.0056 |
1.9987 |
1.9923 |
1.9861 |
2.0543 |
2.1027 |
2.1523 |
2.1990 |
| q |
1.9484 |
1.9588 |
1.9712 |
1.9829 |
1.9973 |
1.9579 |
1.9500 |
1.9405 |
1.9337 |
| r |
3.7310 |
3.7508 |
3.7745 |
3.7970 |
3.8245 |
3.7491 |
3.7340 |
3.7158 |
3.7028 |
| s |
3.6674 |
3.6711 |
3.6754 |
3.6797 |
3.6865 |
3.7171 |
3.7567 |
3.7959 |
3.8349 |
| Bond angles (degree) |
θ1 |
122.23 |
122.00 |
121.74 |
121.49 |
121.21 |
122.67 |
123.41 |
124.17 |
124.85 |
| θ2 |
140.27 |
139.39 |
138.35 |
137.40 |
136.35 |
142.08 |
145.27 |
148.86 |
152.38 |
| θ3 |
94.62 |
94.98 |
95.43 |
95.85 |
96.33 |
93.90 |
92.73 |
91.58 |
90.58 |
| θ4 |
126.30 |
126.38 |
126.47 |
126.56 |
126.66 |
126.14 |
125.89 |
125.63 |
125.40 |
| θ5 |
71.54 |
70.98 |
70.31 |
69.68 |
68.99 |
72.70 |
74.68 |
76.80 |
78.75 |
The tetrahedral and octahedral bond lengths (dAL) and (dBL), tetrahedral edge length (dAE), and shared octahedral edge lengths (dBE) and un-shared lengths (dBEU) have been calculated using eqn (A9)–(A13). The calculated dAL, dBL, dAE, dBE, and dBEU values for both the series have been listed in Table 3. From this Table, it is seen that the values of dAL, dAE have increased while the values of dBL, dBE, and dBEU have reduced with an increase in Cr content for both the series S1, and S2.
Magnetic interaction strength for cubic spinel and spinel-like ferrite depends on the cation–cation (Me–Me) bond length and cation–anion (Me–O) bond length and bond angle that have been calculated using the eqn (A14)–(A27). All the calculated bond lengths and bond angles have been presented in Table 3. As seen in Table 3, there is decreasing and increasing trend in Me–Me for the S1 and S2 series, respectively. The Me–O distance shows an increasing trend for both the series. The bond angles show a decreasing trend with the increasing Cr content for both series. The decreasing trend of Me–Me and the bond angles may be due to the smaller ionic radius of Cr3+ than that of the Co2+ for the samples of the series S1. But in the case of the samples of series S2, this decreasing in Me–Me and bond angles is most likely due to the combined effects of smaller ionic radius of Cr3+ and excess of Co2+ ions therein. This behavior of bond length and bond angles for the samples of the series S1, and S2 imply the lattice expansion with the increase in Cr content, which is found to be in agreement with the lattice volume.
To confirm the presence of cation or anion vacancies, estimation of ionic packing coefficient is required. The ionic packing coefficient of tetrahedral site Ptet and octahedral site Poct have been calculated by the eqn (A28) and (A29), respectively. The values for Ptet and Poct have been presented in Table 4 for both the series. From Table 4, it is observed that the values of Ptet and Poct are less than one, which suggests the existence of cation and anion vacancies in the parent COF.34 For series S1, the values of Ptet and Poct increase for increasing Cr content and the values are close to 1, which indicates the reduction of ion (cation and anion) vacancies. On the other hand, Ptet and Poct have been found to be decrease with increasing Cr3+ content which indicates enhancement of ion (cation and anion) vacancies.
Table 4 Oxygen positional parameter, ionic packing coefficient, fulfillment coefficient, vacancy parameter, and tolerance factor for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4)
| Series |
x |
Oxygen positional parameter, u and deviation, δ |
Ionic packing coefficient |
Fulfillment coefficient α |
Vacancy parameter β |
Tolerance factor T |
| u |
δ |
Pa |
Pb |
| S1 |
0 |
0.3845 |
0.0095 |
0.9867 |
0.9967 |
0.5819 |
0.5145 |
1.038 |
| 0.125 |
0.3852 |
0.0102 |
0.9877 |
0.9982 |
0.5811 |
0.4370 |
1.040 |
| 0.250 |
0.3860 |
0.0110 |
0.9884 |
0.9988 |
0.5804 |
0.3783 |
1.043 |
| 0.375 |
0.3868 |
0.0118 |
0.9919 |
0.9991 |
0.5782 |
0.0526 |
1.045 |
| 0.500 |
0.3877 |
0.0127 |
0.9944 |
1.0008 |
0.5758 |
−0.1860 |
1.048 |
| S2 |
0.125 |
0.3831 |
0.0081 |
0.9426 |
0.9589 |
0.5887 |
4.7671 |
1.027 |
| 0.250 |
0.3807 |
0.0057 |
0.9016 |
0.9239 |
0.5972 |
8.5123 |
1.014 |
| 0.375 |
0.3784 |
0.0033 |
0.8621 |
0.8940 |
0.6062 |
11.9433 |
1.000 |
| 0.500 |
0.3763 |
0.0013 |
0.8259 |
0.8692 |
0.6150 |
14.9758 |
0.990 |
The degree of ionic packing coefficient can be evaluated by calculating the fulfillment coefficient (α) of the unit cell using eqn (A30). The vacancy parameter β is defined as normalized values of ions at the nodal point of the spinel structure which is calculated using eqn (A31). The values of α (tabulated in Table 4) show close to 0.58 for all the samples which confirm that our synthesized samples exhibit inverse spinel structure as explained in the earlier literature.34 The values of β listed in Table 4 show a low vacancy parameter which implies that the missing ions are lesser for parent COF. For series S1 the values of β shows the decreasing trend up to x = 0.375 that implies reducing the missing ions due to Cr substitution. But at higher Cr content, it shows the negative value, which are most likely due to the excess of ions. The excess of ions dominates due to higher Cr content in series S1. But in series S2, β values increase strongly with an increase of Cr content that dominates the enhancement of metallic behavior from semiconducting behavior due to the higher values of Co2+ ions.35
The tolerance factor (T) is another property to get an idea about the impurities of these type of materials. Hence the T have been calculated using eqn (A32) that have been tabulated in Table 4 for both the series. It is observed that T is slightly higher than one which indicates that the synthesized sample is slightly distorted from the inverse spinel structure. In both the series, the values of T are found to decrease with the increase of Cr content indicating the reduction of distortion from the central atom resulting the improvement of inverse spinel structure.
3.1.5 Crystallite size estimation. To evaluate crystallite size, analysis of X-ray profiles is the most effective and easiest way. To calculate crystallite size and strain of the powdered samples various methods have been used such as: Scherrer, Modified Scherrer, Size strain plot, and Williamson–Hall plot. In every case, XRD data have generally been used because of X-ray line broadening comes out mainly from three factors: (i) instrumental effect, (ii) crystallite size, and (iii) local lattice strain. To exclude the instrumental broadening, a standard silicon X-ray powder diffraction data is recorded under the same condition and eliminated from the observed peak width. The full width at half maximum (FWHM) of all peak positions from the XRD has been estimated using a nonlinear combined curve fitting function that includes Gaussian and Lorentzian functions. The FWHM data has been calculated by using the eqn (A33). In addition, the instrumental broadening (βi) is removed by using the eqn (A34). The values for βi are 0.092°, 0.099°, 0.117°, 0.186°, 0.21°, and 0.208° for the (220), (311), (400), (511), and (440) peaks, respectively. The average crystallite size (D) have been calculated by using observed FWHM of the most intense peak (311) with the help of Scherrer equation (eqn (A35)). The calculated values of D using this method are listed in Table 5.
Table 5 Crystallite size (D) and strain (ε) estimated by different methods for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4)
| Series |
x |
Scherrer method |
Modified Scherrer method |
Rietveld refined method |
Williamson–Hall Method |
Size Strain Method |
| D (nm) |
D (nm) |
D (nm) |
ε |
D (nm) |
ε |
D (nm) |
ε |
| S1 |
0 |
46 |
53 |
61 |
0.00092 |
71 |
0.000725 |
60 |
1.41 × 10−5 |
| 0.125 |
46 |
51 |
57 |
0.00085 |
70 |
0.000746 |
52 |
5.91 × 10−6 |
| 0.250 |
45 |
49 |
52 |
0.00071 |
64 |
0.000775 |
51 |
9.35 × 10−6 |
| 0.375 |
39 |
45 |
51 |
0.00058 |
60 |
0.000909 |
50 |
1.33 × 10−5 |
| 0.500 |
39 |
43 |
46 |
0.00046 |
56 |
0.000905 |
47 |
1.40 × 10−5 |
| S2 |
0.125 |
47 |
50 |
59 |
0.00075 |
67 |
0.000786 |
58 |
1.14 × 10−5 |
| 0.250 |
40 |
43 |
49 |
0.00068 |
52 |
0.000624 |
45 |
5.94 × 10−5 |
| 0.375 |
37 |
40 |
41 |
0.00051 |
43 |
0.000374 |
42 |
5.55 × 10−6 |
| 0.500 |
39 |
39 |
38 |
0.00046 |
43 |
0.000353 |
40 |
2.21 × 10−6 |
Scherrer equation is used to determine D for most intense peak, but since the constant value of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is not maintained with the increase in 2θ and resulting errors in the D values. To avoid the above-mentioned errors, Monshi et al. in 2012 employed some modifications in the use of the Scherrer equation and introduced the following formula:18
θ is not maintained with the increase in 2θ and resulting errors in the D values. To avoid the above-mentioned errors, Monshi et al. in 2012 employed some modifications in the use of the Scherrer equation and introduced the following formula:18
To evaluate the more accurate values of D, 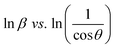 the graph has been plotted for all the selected peaks. Then y-intercepts,
the graph has been plotted for all the selected peaks. Then y-intercepts, 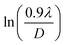 , have been determined by the linear fitting on this graph using the origin software for the sample of series S1, and S2, as shown in Fig. 8. The calculated D values taking
, have been determined by the linear fitting on this graph using the origin software for the sample of series S1, and S2, as shown in Fig. 8. The calculated D values taking 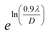 for all the samples have been tabulated Table.
for all the samples have been tabulated Table.
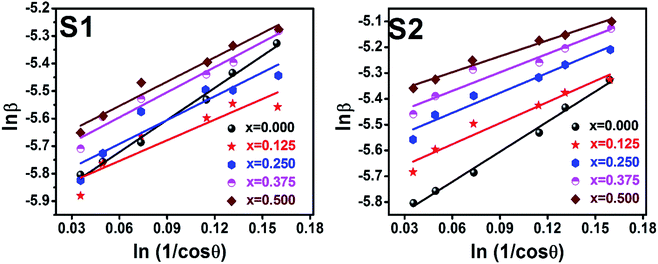 |
| | Fig. 8 Modified Scherer plots for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
Scherrer and modified Scherrer methods can provide the only information about the crystallite size but not the information about the intrinsic strain of the lattice. As such, Williamson–Hall method has been utilized to calculate both D and the strain, ε of the materials. According to this method, a total physical broadening, βtot, have been calculated by the following relation:14,17
or,
Here,
βhkl is the total broadening due to strain and size in a particular peak having the (
hkl) value which is written exchange of
βtot.
Fig. 9 show the
βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ vs.
θ vs. 4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ graph corresponding to each diffraction peak for the samples of series S1, and S2, respectively. In every case for all the samples, the slope and
y-intercept have been noted from the linear fitted curve, which gives the
ε and
D of the investigated samples. The
ε and
D for all the samples have been listed in
Table 5 in Appendix B.
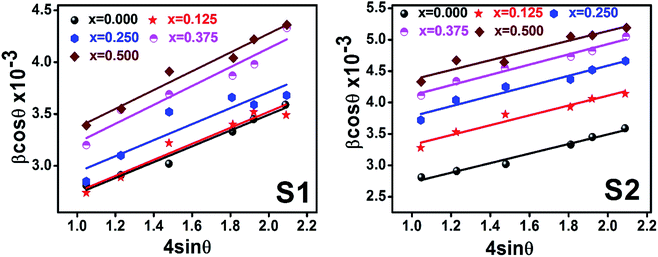 |
| | Fig. 9 Williamson–Hall Plot for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
Williamson–Hall method describes isotropic peak broadening due to the combination of size and strain-induced effect as a function of a 2θ.To better evaluation of ε and D another model known as “size–strain plot (SSP)” has been used. In this method, higher angle reflections are less important than lower angle reflections. In the SSP method, the following relation has been considered:17
Here,
dhkl is lattice spacing for different (
hkl) planes. The (
dhklβhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ)
2 are plotted as a function of
dhkl2βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ and their linear fitted curve have been drawn using the origin software as shown in
Fig. 10. The slope and
y-intercept have been extracted for all the samples that provides the values of
D and
ε of both series and presented in
Table 5. In addition, the
D and
ε values extracted by the Match-3 software from the Rietveld refined XRD data have also been listed in
Table 5. The
D values calculated by using all the methods is found to be decreasing trend with the increasing Cr content for both series as shown in
Fig. 11. This decreasing trend is most likely due to the peak broadening.
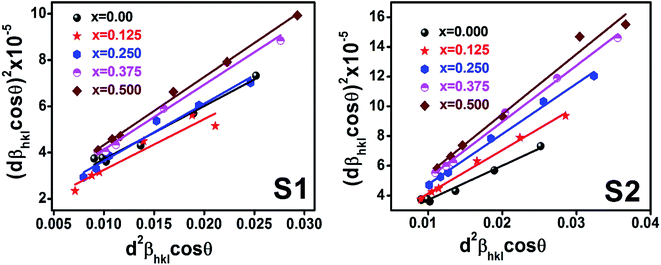 |
| | Fig. 10 Size strain plot for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
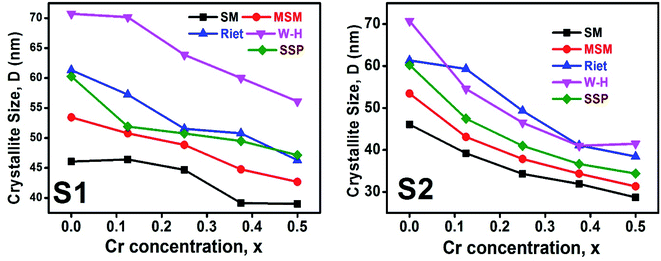 |
| | Fig. 11 The D values calculated using Scherer method (SM), modified Scherer method (MSM), Rietveld method (riet), Williamson–Hall (W–H), and size strain plot (SSP) for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
3.2 FTIR analysis
Fig. 12 illustrate the FTIR spectrum in the wavenumber range of 350–3000 cm−1 for the samples of both series at room temperature. From the FTIR spectra, two distinct absorption bands at 554 cm−1 (ν1) and 372 cm−1 (ν2) are observed for the parent COF. The symmetrical stretching vibrations of metal–oxygen at tetrahedral and octahedral sites have been observed at the higher band ν1, and lower band ν2, respectively. For all samples, it is seen that both ν1, and ν2 are increased with the increase of Cr content as shown in the inset of Fig. 12. The values ν1, and ν2 have been listed in Table 6. A clear absorption band has been noticed at around 3000 cm−1 (ν3). This may be attributed to the H–O–H stretching vibrations due to the effect of moisture during fabrication of the studied samples.
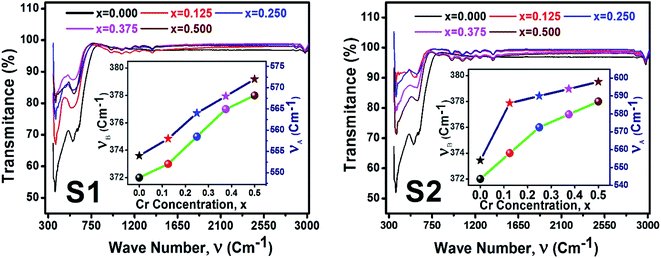 |
| | Fig. 12 FTIR spectrum for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
Table 6 Absorbtion wave number (ν1, ν2), force constant, stiffness constant, wave velocity, elastic constant, Pugh ratio, Poisson ratio Debye temperature, and minimum thermal constant for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4)
| Series |
S1 |
S2 |
| x |
0 |
0.125 |
0.250 |
0.375 |
0.500 |
0.125 |
0.250 |
0.375 |
0.500 |
| ν1 (cm−1) |
371 |
373 |
375 |
377 |
378 |
374 |
376 |
377 |
378 |
| ν2 (cm−1) |
554 |
558 |
564 |
568 |
572 |
586 |
590 |
594 |
598 |
| Force constant |
kt (N m−1) |
290 |
294 |
300 |
305 |
309 |
324 |
329 |
333 |
338 |
| ko (N m−1) |
130 |
131 |
133 |
134 |
135 |
132 |
133 |
134 |
135 |
| kab (N m−1) |
210 |
213 |
217 |
219 |
222 |
228 |
231 |
234 |
236 |
| Stiffness costant |
C11 (GPa) |
251 |
255 |
260 |
264 |
268 |
273 |
277 |
280 |
284 |
| C12 (GPa) |
105 |
106 |
106 |
106 |
106 |
110 |
110 |
109 |
108 |
| Wave velocity |
vl (ms−2) |
6843 |
6911 |
6999 |
7080 |
7158 |
7035 |
6986 |
6940 |
6912 |
| vt (ms−2) |
3950 |
3990 |
4041 |
4087 |
4133 |
4062 |
4033 |
4007 |
3991 |
| vm (ms−2) |
4156 |
4197 |
4250 |
4299 |
4348 |
4272 |
4243 |
4215 |
4198 |
| Elastic constant |
B (GPa) |
153 |
156 |
157 |
158 |
160 |
164 |
165 |
166 |
167 |
| G (Gpa) |
84 |
84 |
87 |
88 |
89 |
91 |
92 |
93 |
95 |
| E (GPa) |
216 |
220 |
223 |
226 |
229 |
234 |
237 |
239 |
241 |
| Pugh ratio (B/G) |
1.84 |
1.83 |
1.82 |
1.80 |
1.79 |
1.81 |
1.79 |
1.78 |
1.76 |
| Σ |
0.29 |
0.29 |
0.29 |
0.29 |
0.28 |
0.29 |
0.28 |
0.28 |
0.28 |
| Zero porosity elastic constant |
E0 (GPa) |
261 |
266 |
280 |
291 |
300 |
298 |
310 |
322 |
340 |
| G0 (Gpa) |
100 |
102 |
107 |
111 |
115 |
114 |
119 |
124 |
131 |
| B0 (GPa) |
226 |
230 |
238 |
244 |
250 |
252 |
259 |
265 |
275 |
| σ0 |
0.31 |
0.31 |
0.30 |
0.30 |
0.30 |
0.30 |
0.30 |
0.29 |
0.29 |
| B0/G0 |
2.26 |
2.25 |
2.22 |
2.19 |
2.16 |
2.20 |
2.16 |
2.14 |
2.09 |
| θD (K) |
593 |
599 |
606 |
612 |
618 |
610 |
605 |
601 |
598 |
| Kmin |
1.31 |
1.33 |
1.34 |
1.36 |
1.37 |
1.35 |
1.34 |
1.33 |
1.32 |
3.2.1. Calculation of force constant. The wavenumbers ν1 and ν2 of the infrared active phonon mode is directly connected to the force constant. The force constant kt and ko at the tetrahedral and octahedral site of cubic spinel structure has been calculated by the Waldron relation (eqn (A39)–(A41)). The average force constant kav = (kt + ko)/2 have shown in Fig. 13 for the all samples of both series. From the Fig. 13, it is seen that the average force constant kav increases for the samples of both series which is as usually related to the Me–Me bond distances and bond angles.
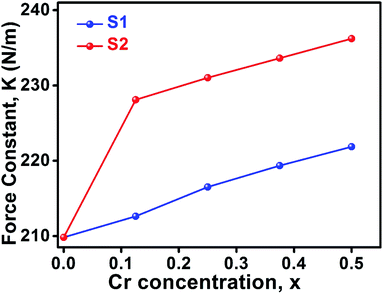 |
| | Fig. 13 Force constant as a function of Cr content all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
3.2.2 Elastic properties analysis. Ferrites demonstrate important elastic properties and thermal behavior due to their interatomic and interionic forces. Although the elastic properties of such materials are determined by applying external stress, according to the analysis of various research, a technique based on the structural and FTIR data parameter related to elastic properties along with thermal properties has been calculated for exploring the correlations with the other properties.1,20–22 According to Hook's law, the stress ηi, strain εijand stiffness Cij are correlated on the basis of the stress–strain approach.40 The stiffness Cij are used to calculate the elastic constants. For cubic symmetry, only three stiffness C11, C12, and C44 are considered to be dominant, where C11 represents the elasticity in length and C12 and C44 represents the elasticity in shape. The stiffness constant C11 and C12 are calculated using eqn (A43) and (A44), and the values are tabulated in Table 6.The bulk modulus, B, rigidity modulus, G, Young's modulus, E, Poisson's ratio, σ, longitudinal wave velocity, vl, transverse wave velocity, vt, and the mean velocity, vm, have also been calculated for all samples of both series using the eqn (A46)–(A51). The calculated values of all these elastic constants with Cr content for both the series have been graphically presented in Fig. 14. The values of E, B, and G are found to increase with increasing Cr content. The measured elastic moduli however do not provide enough information on the mechanical properties of the investigated samples due to the presence of porosity. Hence, to improve the elastic nature of the materials, the corrected zero porosity elastic moduli have been calculated by using Hasselman and Fularth's formula (eqn (A51)–(A54)). The corrected zero porosity elastic moduli (E0, B0, and G0) have been listed in Table 6 which shows the larger value than the measured E, B, and G. From Table 6, it is seen that the values of E0, B0, and G0 show the similar trend with the values of E, B, and G as a function of Cr concentration for the samples of both series.
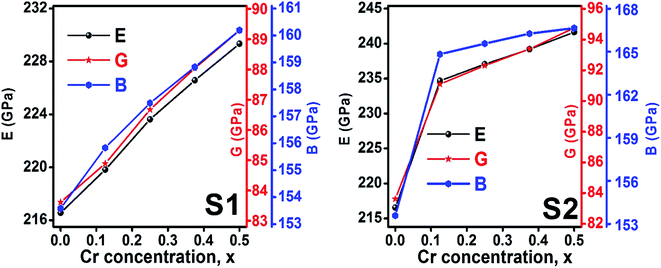 |
| | Fig. 14 Elastic modulus as a function of Cr content for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
Ductility and brittleness behavior of a material can be estimated by the Pugh's ratio.42 The Pugh's ratios (B/G) are illustrated in Fig. 15 for the samples of both series. According to Frabtsevich et al.43 the brittleness and ductility nature can be confirmed from the value of σ. The calculated values of σ are also illustrated in Fig. 15. It is observed that both the Pugh's ratio and σ are higher than that of their respective critical values 1.75 and 0.26, respectively. This reveals the ductile nature of the synthesized samples.42,43 The ductility decrease with the increase of Cr content for both the series which may be due to the substitution of brittle Cr with ductile Co and Fe for the sample of both series. In addition, σ for all the samples are in the range of 0.27–0.30 which lies in between −1 to 0.5 which implies that the investigated samples are of isotropic elastic in nature.
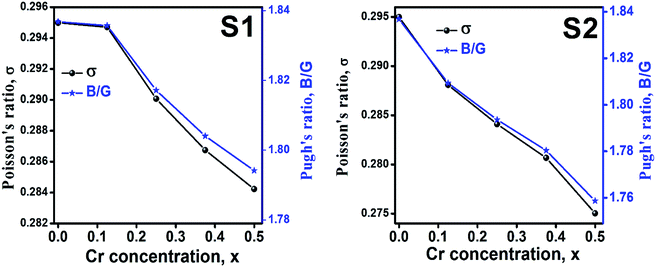 |
| | Fig. 15 Poison's ratio and Pugh's ratio as a function of Cr content for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
3.2.3 Thermodynamic properties. The Debye temperature, θD, is a significant parameter to know about the thermodynamic properties of a solid that originates from the maximum lattice vibration of the atoms. According to Anderson's formula the θD can be calculated using the eqn (A55). Thermal conductivity is one of the thermodynamic properties of a material that indicates the ability to conduct heat. The minimum value of thermal conductivity, Kmin, have been calculated by the eqn (A56). The calculated θD and Kmin have been presented in Fig. 16 as a function of Cr content for all samples of both series. It is observed that θD and Kmin increases with the increase of Cr content for S1 series. However, for S2 series both θD and Kmin shows the maximum value for x = 0.125, and beyond this value of Cr content they decrease.
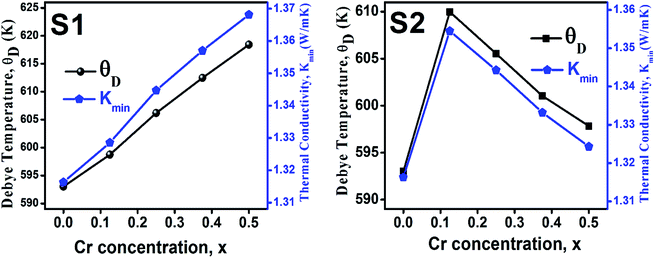 |
| | Fig. 16 Debye temperature and thermal conductivity as a function of Cr content for all samples of series S1 (Co1−xCrxFe2O4) and S2 (Co1+xCrxFe2−xO4). | |
4. Discussion
The analysis of structural, mechanical, and thermal properties of the samples of two series S1, and S2, show almost similar behavior in most of their properties. For the stoichiometric series S1, the XRD pattern shows a single phase cubic structure for all Cr contents. For a lower value of Cr3+ substitution with Co2+, cation–anion vacancies dominated. However, for higher values of Cr3+, negative values of vacancy parameter have been found. This negative vacancy parameter dominates the excess Cr3+ replaced with the Co2+ and these excess ions are not too high, so no impurity peaks have been observed in the XRD patterns. A slight distortion of inverse spinel structure has been confirmed from the tolerance factor for all samples of both series. The dominance of Cr3+ with extra Co2+ ions due to lowering the packing fraction demonstrates strongly increasing trend of vacancy parameter with increase of Cr3+ and leading to transform semiconducting to metallic behavior in S2 series. However, a single phase cubic structure is observed for the samples of S2 series without any impurity peak in the XRD patterns. The observed anion displacement for the samples of two series are dominated by the deviation of oxygen positional parameters from their standard value of 0.375. Expansion of lattice volume for the series S1 has been observed due to the larger ratio of Cr2+/Co2+ at tetrahedral site than the Cr3+/Co2+ ratio at octahedral site. In S2 series, Fe3+ has been replaced by Cr3+ with a simultaneous addition of Co2+, resulting an increase in lattice volume. In series S1, both the dx and dB show a decreasing trend, which may be attributed to the increase of Cr3+ with a lower density of 7.14 g cm−3 than that of Co2+ (8.9 g cm−3).45 Although pelletization pressure and sintering temperature for all samples were the same, there is an increasing trend of ductility with an increase of Cr content. At higher sintering temperature (>1100 °C) the ductility of Cr/Cr-based alloys and composite is reported to improve.46
In series S2, Cr metal having lower density replaced the Fe (7.87 g cm−3) with slightly higher density.45 However, addition of same amount of Co metal with high density, resulted in the increasing trend of dB, and dx with a increase in porosity. However, the ductility is found to decrease possibly due to excess Co2+. In addition, an increase of excess Co with lower shear modulus presumably plays a prominent role in lowering the ductile nature for the sample series S2. The decreasing trend of ductility as a function of Cr content are observed due to the increase of the Cr3+/Fe2+ ratio. In series S1, the θD shows an increasing trend due to the greater θD of Cr than that of Co.47 In series S2, the θD increases at lower Cr content (=0.125) but at a higher Cr content (>0.125), θD decreases due to the increase of Co/Cr ratio, and decrease of Fe/Cr ratio.
5. Conclusions
Two series of Cr3+ substituted cobalt ferrite with stoichiometric (S1 series) and non-stoichiometric (S2 series) ratios have been synthesized by the standard solid-state reaction technique. XRD patterns for all samples of both series indicate a single phase cubic spinel structure with a space group of Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. FTIR spectra of the synthesized samples also confirm the spinel structure. The cation distribution calculated from the extracted Rietveld refined data confirms the mixed spinel structure of all samples of both series. In both the stoichiometric and non-stoichiometric series, an enhancement of lattice parameter have been found. From the analysis of elastic properties, it is found that all the samples for both series are ductile in nature. For the stoichiometric series Cr3+ together with Co2+ is assumed to have influenced the structural and mechanical properties. In addition, non-stoichiometric compositions provide an opportunity to tailor Co2+/Cr3+ and Fe3+/Cr3+ in the inverse spinel ferrite which causes the defect in structure, and modification of mechanical behavior.
m. FTIR spectra of the synthesized samples also confirm the spinel structure. The cation distribution calculated from the extracted Rietveld refined data confirms the mixed spinel structure of all samples of both series. In both the stoichiometric and non-stoichiometric series, an enhancement of lattice parameter have been found. From the analysis of elastic properties, it is found that all the samples for both series are ductile in nature. For the stoichiometric series Cr3+ together with Co2+ is assumed to have influenced the structural and mechanical properties. In addition, non-stoichiometric compositions provide an opportunity to tailor Co2+/Cr3+ and Fe3+/Cr3+ in the inverse spinel ferrite which causes the defect in structure, and modification of mechanical behavior.
6 Appendix-A
Equations belonging to Section 3:
Equation for theoretical lattice parameter:1
| |
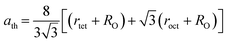 | (A1) |
where
RO (=1.32 Å) is the ionic radius of oxygen.
The N–R function is as follows:17
| |
 | (A2) |
The lattice parameter for each Bragg position:30
| |
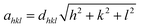 | (A3) |
Here,
ahkl,
dhkl are the lattice constant and interplanar spacing respectively.
Equations for bulk density dBand X-ray density dx32
| |
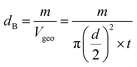 | (A4) |
| |
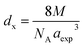 | (A5) |
Equation for porosity:8
| |
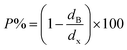 | (A6) |
where
M is the molecular mass calculated from molecular formulae,
aexp is the experimental lattice constant and
NA (=6.02 × 10
23) is Avogadro's number.
Equation for oxygen positional parameter u:1
| |
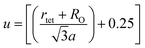 | (A7) |
Stanley's equations:1
| |
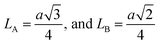 | (A8) |
The equations for tetrahedral and octahedral bond lengths (dAL) and (dBL), tetrahedral edge length (dAE), and shared (dBE) and un-shared octahedral edge lengths (dBEU) are as follows:1
| |
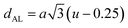 | (A9) |
| |
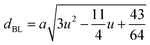 | (A10) |
| |
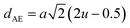 | (A11) |
| |
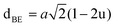 | (A12) |
| |
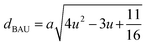 | (A13) |
Equations for various bond length and bond angles:1
Me–Me distances
| |
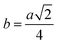 | (A14) |
| |
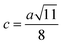 | (A15) |
| |
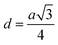 | (A16) |
| |
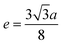 | (A17) |
| |
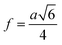 | (A18) |
Me–O distances
| |
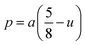 | (A19) |
| |
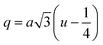 | (A20) |
| |
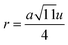 | (A21) |
| |
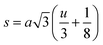 | (A22) |
Bond angles
| |
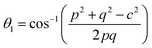 | (A23) |
| |
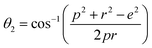 | (A24) |
| |
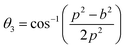 | (A25) |
| |
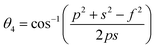 | (A26) |
| |
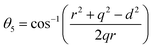 | (A27) |
Equations for the ionic packing coefficient Ptet and Poct at the tetrahedral and octahedral sites:34
| |
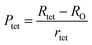 | (A28) |
| |
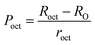 | (A29) |
Here,
Rtet (=
dAL) and
Rtet (=
dBL)are the average bond length at tetrahedral and octahedral sites respectively.
Equation for the fulfillment coefficient (α) of the unit cell using the following relation:34
| |
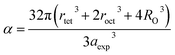 | (A30) |
Equation of vacancy parameter β:34
| |
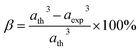 | (A31) |
Equation for tolerance factor calculation:36
| |
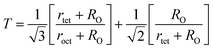 | (A32) |
The FWHM data has been calculated by using the following relation:37
| |
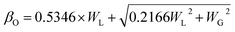 | (A33) |
Here,
βO is observed FWHM,
WL, and
WG is the Lorentzian and Gaussian width respectively. The instrumental broadening (
βi) removal equation:
34| | |
βhkl = [(βO − βi)(βO2 − βO2)0.5]0.5
| (A34) |
The Scherrer equation:17
| |
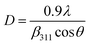 | (A35) |
Here,
β311 is the FWHM at (311) plane (most intense peak),
λ (=1.5406 Å) represents the wavelength of incident X-rays.
Modified Scherrer equation:22
| |
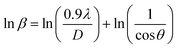 | (A36) |
Williamson–Hall relation:14,21
or,
| |
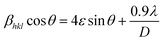 | (A37) |
Here,
βhkl is the total broadening due to strain and size in a particular peak having the (
hkl) value which is written exchange of
βtot.
Equation for the size strain plot:21
| |
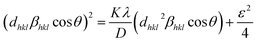 | (A38) |
Here,
dhkl is lattice spacing for different (
hkl) planes.
Force constant according to Waldron relation:21
Here,
c is the velocity of light,
μ is the reduced mass which we have calculated by the following relation:
38,39| |
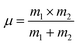 | (A42) |
where
m1 is the weighted average of atomic weights of the cations residing at the A-site or B-site while
m2 is the atomic weight of oxygen anion.
Equation for the stiffness constant C11, C12:21
| |
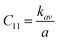 | (A43) |
| |
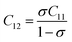 | (A44) |
Here,
σ is the Poisson's ratio as a function of pore fraction
P. The corresponding relation for
σ is as follows:
21| | |
σ = 0.324(1 − 1.043P)
| (A45) |
Some elastic properties related equations:40,41
Bulk modulus:
| |
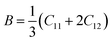 | (A46) |
Longitudinal wave velocity,
| |
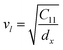 | (A47) |
Here,
dx is the X-ray density.
Transverse wave velocity,
| |
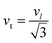 | (A48) |
Rigidity modulus,
Young's modulus,
Mean velocity,
| |
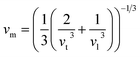 | (A51) |
Hasselman and Fularth's formulae for the corrected zero porosity elastic moduli:21,41
| |
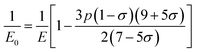 | (A52) |
| |
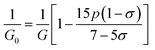 | (A53) |
| |
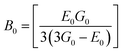 | (A54) |
| |
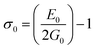 | (A55) |
Anderson's formula for the Debye temperature, θD:44
| |
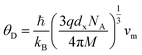 | (A56) |
where ℏ is Planck's constant,
kB is Boltzmann's constant,
NA is Avogadro's number,
dx is the density,
M is the molecular mass, and
q is the number of atoms per unit formula.
Equations for thermal conductivity:38
| |
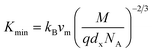 | (A57) |
7 Appendix B
Conflicts of interest
There is no conflicts to declare.
Acknowledgements
The authors are thankful to the Committee for Advanced Studies & Research (CASR), Grant No. 343(15), Bangladesh University of Engineering and Technology for the financial support of this research.
References
- N. Amri, J. Massoudi, K. Nouri, M. Triki, E. Dhahri and L. Bessais, Influence of neodymium substitution on structural, magnetic and spectroscopic properties of Ni–Zn–Al nano-ferrites, RSC Adv., 2021, 11, 13256–13268 RSC.
- S. Akhtar, Q. Khan, S. Anwar, G. Ali, M. Maqbool, M. Khan, S. Karim and L. Gao, A Comparative Study of the Toxicity of Polyethylene Glycol-Coated Cobalt Ferrite Nanospheres and Nanoparticles, Nanoscale Res. Lett., 2019, 14(1), 386 CrossRef CAS PubMed.
- S. Jauhar, J. Kaur, A. Goyal and S. Singhal, Tuning the properties of cobalt ferrite: a road towards diverse applications, RSC Adv., 2016, 6(100), 97694–97719 RSC.
- S. K. Gore, S. S. Jadhav, V. V. Jadhav, S. M. Patange, M. Naushad, R. S. Mane and K. H. Kim, The structural and magnetic properties of dual phase cobalt ferrite, Sci. Rep., 2017, 7(1), 2524 CrossRef PubMed.
- S. Y. Srinivasan, K. M. Paknikar, D. Bodas and V. Gajbhiye, Applications of cobalt ferrite nanoparticles in biomedical nanotechnology, Nanomedicine, 2018, 13(10), 1221–1238 CrossRef CAS PubMed.
- A. Hai, B. Alqassem, G. Bharath, K. Rambabu, I. Othman, M. A. Haija and F. Banat, Cobalt and nickel ferrites based capacitive deionization electrode materials for water desalination applications, Electrochim. Acta, 2020, 363, 137083 CrossRef CAS.
- M. S. Shakil, M. A. Hasan, M. F. Uddin, A. Islam, A. Nahar, H. Das, M. N. I. Khan, B. P. Dey, B. Rokeya and S. M. Hoque, In Vivo Toxicity Studies of Chitosan-Coated Cobalt Ferrite Nanocomplex for Its Application as MRI Contrast Dye, ACS Appl. Bio Mater., 2020, 3(11), 7952–7964 CrossRef CAS PubMed.
- M. Z. Ahsan, M. A. Islam and F. A. Khan, Tunability of ac Conductivity in Manganese doped Cobalt ferrite Nanoparticles, Results Phys., 2021, 21, 103782 CrossRef.
- M. Z. Ahsan, M. A. Islam, A. A. Bally and F. A. Khan, Spectroscopic analysis for electric and magnetic properties of manganese doped cobalt nanoferrite, Results Phys., 2020, 17, 103172 CrossRef.
- M. Z. Ahsan, M. A. Islam and F. A. Khan, Effects of sintering temperature on ac conductivity, permittivity, and permeability of manganese doped cobalt ferrite nanoparticles, Results Phys., 2020, 19, 103402 CrossRef.
- M. Z. Ahsan, F. A. Khan and M. A. Islam, Frequency and temperature dependent intrinsic electric properties of manganese doped cobalt ferrite nanoparticles, Results Phys., 2019, 14, 102484 CrossRef.
- M. Z. Ahsan, F. A. Khan and M. A. Islam, Frequency and Temperature Dependent Dielectric and Magnetic Properties of Manganese Doped Cobalt Ferrite Nanoparticles, J. Electron. Mater., 2019, 48(12), 7721–7729 CrossRef CAS.
- M. Z. Ahsan and M. A. Islam, A Theoretical Approach: Effects of Mn Substitution in Cobalt Ferrite, Am. J. Appl. Sci., 2019, 5(3), 56–61 Search PubMed.
- G. Kumar, R. K. Kotnala, J. Shah, V. Kumar, A. Kumar, P. Dhiman and M. Singh, Cation distribution: a key to ascertain the magnetic interactions in a cobalt substituted Mg–Mn nanoferrite matrix, Phys. Chem. Chem. Phys., 2017, 19(25), 16669–16680 RSC.
- P. Bera, R. V. Lakshmi, B. H. Prakash, K. Tiwari, A. Shukla, A. K. Kundu and H. Barshilia, Solution combustion synthesis, characterization, magnetic, and dielectric properties of CoFe2O4 and Co0.5M0.5Fe2O4 (M = Mn, Ni, and Zn), Phys. Chem. Chem. Phys., 2020, 22, 20087–20106 RSC.
- R. Saravanan, Ferrite Materials for Memory Applications, Material research foundation, 2017, vol. 18, p. 29 Search PubMed.
- S. Debnath and R. Das, Cobalt doping on
nickel ferrite nanocrystals enhances the micro-structural and magnetic properties: Shows a correlation between them, J. Alloys Compd., 2020, 156884 Search PubMed.
- A. Monshi, M. R. Foroughi and M. R. Monshi, Modified Scherrer Equation to Estimate More Accurately Nano-Crystallite Size Using XRD, World J. Nano Sci. Eng., 2012, 02(03), 154–160 CrossRef.
- D. Nath, F. Singh and R. Das, X-Ray Diffraction Analysis by Williamson-Hall, Halder-Wagner and Size-Strain Plot Methods of CdSe Nanoparticles- A comparative study, Mater. Chem. Phys., 2019, 122021 Search PubMed.
- D. Bouokkeze, J. Massoudi, W. Hzez, M. Smari, A. Bougoffa, K. Khirouni and L. Bessais, Investigation of the structural, optical, elastic and electrical properties of spinel LiZn2Fe3O8 nanoparticles annealed at two distinct temperatures, RSC Adv., 2019, 9(70), 40940–40955 RSC.
- K. V. Chandekar and K. M. Kant, Size-strain analysis and elastic properties of CoFe2O4nanoplatelets by hydrothermal method, J. Mol. Struct., 2018, 1154, 418–427 CrossRef CAS.
- K. V. Chandekar, M. Shakir and S. AlFaify, A structural, elastic, mechanical, spectroscopic, thermodynamic, and magnetic properties of polymer coated CoFe2O4 nanostructures for various applications, J. Mol. Struct., 2020, 127681 CrossRef CAS.
- H. L. Andersen, B. A. Frandsen, H. P. Gunnlaugsson, M. R. V. Jørgensen, S. J. L. Billinge, K. M. Ø. Jensen and M. Christensen, Local and long-range atomic/magnetic structure of non-stoichiometric spinel iron oxide nanocrystallites, IUCrJ, 2021, 8(1), 33–35 CrossRef CAS PubMed.
- N. Kumar, R. K. Singh and H. K. Satyapal, Structural, optical, and magnetic properties of non-stoichiometric lithium substituted magnesium ferrite nanoparticles for multifunctional applications, J. Mater. Sci.: Mater. Electron., 2020, 31, 9231–9241 CrossRef CAS.
- E. E. Ateia, S. K. Abdel-Aal, K. Seham and A. Abd Allah, Synthesis and characterization of nonstoichiometric potassium/magnesium nanoferrites for multifunctional applications, J. Mater. Sci.: Mater. Electron., 2017, 29(2), 1–8 Search PubMed.
- Y. Xu, D. Sun, H. Hao, D. Gao and Y. Sun, Non-stoichiometric Co (ii), Ni (ii), Zn (ii)-ferrite nanospheres: size controllable synthesis, excellent gas-sensing and magnetic properties, RSC Adv., 2016, 6(101), 98994–99002 RSC.
- I. C. Nlebedim, A. J. Moses and D. C. Jiles, Non-stoichiometric cobalt ferrite, CoxFe3−xO4 (x=1.0 to 2.0): Structural, magnetic and magnetoelastic properties, J. Magn. Magn. Mater., 2013, 343, 49–54 CrossRef CAS.
- C. Dun, G. Xi, Y. Zhang, X. Heng, Y. Liu, X. Xing and R. Liang, Magnetic and magnetostrictive properties of non-stoichiometric cobalt ferrite synthesized from spent Li-ion batteries, J. Magn. Magn. Mater., 2020, 167185 CrossRef CAS.
- R. W. G. Wyckoff Structure of Crystals The Chemical Catalog Company, INC, New York, 2nd edn, 1931, p. 290 Search PubMed.
- S. M. Patange, S. E. Shirsath, S. S. Jadhav and K. M. Jadhav, Cation distribution study of nanocrystalline NiFe2−xCrxO4 ferrite by XRD, magnetization and Mössbauer spectroscopy, Phys. Status Solidi A, 2011, 209(2), 347–352 CrossRef.
- M. J. Iqbal and M. R. Siddiquah, Electrical and magnetic properties of chromium-substituted cobalt ferrite nanomaterials, J. Alloys Compd., 2008, 453(1–2), 513–518 CrossRef CAS.
- M. A. Rahman, M. T. Islam, M. S. J. Singh, M. Samsuzzaman and M. E. H. Chowdhury, Synthesis and characterization of Mg–Zn ferrite based flexible microwave composites and its application as SNG metamaterial, Sci. Rep., 2021, 11, 7654 CrossRef CAS.
- B. B. V. S. V. Prasad, Cation distribution, structural and electric studies on cadmium substituted nickel–zinc ferrite, Mod. Phys. Lett. B, 2014, 28(19), 1450155 CrossRef.
- K. A. M. Khalaf, A. D. Al-Rawas, H. M. Widatallah, K. S. Al-Rashdi, A. Sellai, A. M. Gismelseed and A. H. Al-Rajhi, Influence of Zn 2+ ions on the structural and electrical properties of Mg1−xZnxFeCrO4spinels, J. Alloys Compd., 2016, 657, 733–747 CrossRef CAS.
- T. Groń, Influence of vacancies and mixed valence on the transport processes in solid solutions with the spinel structure, Philos. Mag. Lett., 1994, 70(1), 121–132 Search PubMed.
- M. I. Arshad, S. Arshad, K. Mahmood, A. Ali, N. Amin, R. Umaid-ur and M. Ajaz-un Nabi, Impact of Mg doping on structural, spectral and dielectric properties of Cd–Cu nano ferrites prepared via sol-gel auto combustion method, Phys. B, 2020, 412496 CrossRef CAS.
- P. M. Shafi and A. Chandra Bose, Impact of crystalline defects and size on X-ray line broadening: A phenomenological approach for tetragonal SnO2 nanocrystals, AIP Adv., 2015, 5, 057137 CrossRef.
- K. B. Modi, S. J. Shah, N. B. Pujara, T. K. Pathak, N. H. Vasoya and I. G. Jhala, Infrared spectral evolution, elastic, optical and thermodynamic properties study on mechanically milled Ni0.5Zn0.5Fe2O4 spinel ferrite, J. Mol. Struct., 2013, 1049, 250–262 CrossRef CAS.
- N. Bouhadouza, A. Rais, S. Kaoua, M. Moreau, K. Taibi and A. &Addou, Structural and vibrational studies of NiAlxFe2−xO4 ferrites (0≤x≤1), Ceram. Int., 2015, 41(9), 11687–11692 CrossRef CAS.
- M.-M. Wu, L. Wen, B.-Y. Tang, L.-M. Peng and W.-J. Ding, First-principles study of elastic and electronic properties of MgZn2 and ScZn2 phases in Mg–Sc–Zn alloy, J. Alloys Compd., 2010, 506(1), 412–417 CrossRef CAS.
- D. P. H. Hasselman and R. M. Fulrath, Effect of Small Fraction of Spherical Porosity on Elastic Moduli of Glass, J. Am. Ceram. Soc., 1964, 47(1), 52–53 CrossRef CAS.
- Y. Pan and W. M. Guan, Probing the balance between ductility and strength: transition metal silicides, Phys. Chem. Chem. Phys., 2017, 19(29), 19427–19433 RSC.
- S. A. B. I. N. Frantsevich and F. F. Voronov, Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, I. N. Frant, Naukova Dumka, Kiev, 1983 Search PubMed.
- Physics Acoustics, ed. O. L. Anderson and W. P. Mason, Academic Press, New York, 1965, vol. 3B, pp. 43–95 Search PubMed.
- https://sciencenotes.org/density-elements-periodic-table/.
- Y. F. Gu, H. Harada and Y. Ro, Chromium and chromium-based alloys: Problems and possibilities for high-temperature service, JOM, 2004, 56(9), 28–33 CrossRef CAS.
- http://www.knowledgedoor.com/2/elements_handbook/debye_temperature.html.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra09090a |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
A. K. M. Akther Hossain
*a,
A. K. M. Akther Hossain a,
M. Z. Ahsan
a,
M. Z. Ahsan b,
M. A. A. Ballya,
M. Samir Ullaha,
S. M. Hoque
b,
M. A. A. Ballya,
M. Samir Ullaha,
S. M. Hoque c and
F. A. Khana
c and
F. A. Khana
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Rietveld refinement results show that Cr occupies both the tetrahedral (A-site) and octahedral sites (B-site). The experimental lattice parameters show increasing trends for both the series with increase of Cr content. The cation–anion vacancies, chemical bonding, and the displacement of oxygen have been evaluated to understand the effect of Cr substitution and how the non-stoichiometry affects the physical and chemical properties of the material. The crystallite size is found to be the decreasing value with an increase of Cr concentration for both series of samples. Specific vibrational modes from the FTIR spectra suggest a gradual change of inversion of the ferrite lattice with the increase of Cr concentration which is also evident from Rietveld refinement data. The elastic properties analysis reveals that the synthesized samples for both series are ductile in nature. The non-stoichiometric structure with excess Co2+ may pave a new way to realize the lowering of Curie temperature of ferrite that is expected to improve the magnetocaloric properties.
m. Rietveld refinement results show that Cr occupies both the tetrahedral (A-site) and octahedral sites (B-site). The experimental lattice parameters show increasing trends for both the series with increase of Cr content. The cation–anion vacancies, chemical bonding, and the displacement of oxygen have been evaluated to understand the effect of Cr substitution and how the non-stoichiometry affects the physical and chemical properties of the material. The crystallite size is found to be the decreasing value with an increase of Cr concentration for both series of samples. Specific vibrational modes from the FTIR spectra suggest a gradual change of inversion of the ferrite lattice with the increase of Cr concentration which is also evident from Rietveld refinement data. The elastic properties analysis reveals that the synthesized samples for both series are ductile in nature. The non-stoichiometric structure with excess Co2+ may pave a new way to realize the lowering of Curie temperature of ferrite that is expected to improve the magnetocaloric properties.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi. Finally, the pellets are sintered at 1200 °C for 6 h in a furnace and rcrushed in to fine powders.
000 psi. Finally, the pellets are sintered at 1200 °C for 6 h in a furnace and rcrushed in to fine powders.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m of parent COF that has been confirmed by the crystallography open database (COD No. 5910063) as reported in the literature.29 No impurity phase has been observed in the pattern for the parent COF which signifies the phase purity of COF. The XRD patterns for the samples of the stoichiometric series S1 and non-stoichiometric series S2 shown in Fig. 2 and 3, reveal the formation of spinel structure (COD No. 910063). The peak positions of (311) plane for both the series S1 and S2 have been shifted towards the lower 2θ angle with an increase of Cr content as shown in Fig. 2(b) and 3(b), which imply an increase of the lattice parameters as a result of Cr substitution.
m of parent COF that has been confirmed by the crystallography open database (COD No. 5910063) as reported in the literature.29 No impurity phase has been observed in the pattern for the parent COF which signifies the phase purity of COF. The XRD patterns for the samples of the stoichiometric series S1 and non-stoichiometric series S2 shown in Fig. 2 and 3, reveal the formation of spinel structure (COD No. 910063). The peak positions of (311) plane for both the series S1 and S2 have been shifted towards the lower 2θ angle with an increase of Cr content as shown in Fig. 2(b) and 3(b), which imply an increase of the lattice parameters as a result of Cr substitution.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ are the cationic parameters for the tetrahedral site and α + β + γ = 1. For COF x = β = 0. The cation distribution has been calculated by the above formulae and tabulated in Table 1. The value of the inversion parameter as determined by calculating the ratio between Fe3+ at the tetrahedral site and Fe3+ at octahedral site Fetetra/Feocta has also been tabulated in Table 1. Using the exact cation distribution the ionic radius for the tetrahedral site (rtet), and octahedral site (roct), have been calculated by the following relations:16
γ are the cationic parameters for the tetrahedral site and α + β + γ = 1. For COF x = β = 0. The cation distribution has been calculated by the above formulae and tabulated in Table 1. The value of the inversion parameter as determined by calculating the ratio between Fe3+ at the tetrahedral site and Fe3+ at octahedral site Fetetra/Feocta has also been tabulated in Table 1. Using the exact cation distribution the ionic radius for the tetrahedral site (rtet), and octahedral site (roct), have been calculated by the following relations:16
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is not maintained with the increase in 2θ and resulting errors in the D values. To avoid the above-mentioned errors, Monshi et al. in 2012 employed some modifications in the use of the Scherrer equation and introduced the following formula:18
θ is not maintained with the increase in 2θ and resulting errors in the D values. To avoid the above-mentioned errors, Monshi et al. in 2012 employed some modifications in the use of the Scherrer equation and introduced the following formula:18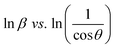 the graph has been plotted for all the selected peaks. Then y-intercepts,
the graph has been plotted for all the selected peaks. Then y-intercepts, 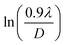 , have been determined by the linear fitting on this graph using the origin software for the sample of series S1, and S2, as shown in Fig. 8. The calculated D values taking
, have been determined by the linear fitting on this graph using the origin software for the sample of series S1, and S2, as shown in Fig. 8. The calculated D values taking 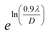 for all the samples have been tabulated Table.
for all the samples have been tabulated Table.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ vs. 4
θ vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ graph corresponding to each diffraction peak for the samples of series S1, and S2, respectively. In every case for all the samples, the slope and y-intercept have been noted from the linear fitted curve, which gives the ε and D of the investigated samples. The ε and D for all the samples have been listed in Table 5 in Appendix B.
θ graph corresponding to each diffraction peak for the samples of series S1, and S2, respectively. In every case for all the samples, the slope and y-intercept have been noted from the linear fitted curve, which gives the ε and D of the investigated samples. The ε and D for all the samples have been listed in Table 5 in Appendix B.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 are plotted as a function of dhkl2βhkl
θ)2 are plotted as a function of dhkl2βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and their linear fitted curve have been drawn using the origin software as shown in Fig. 10. The slope and y-intercept have been extracted for all the samples that provides the values of D and ε of both series and presented in Table 5. In addition, the D and ε values extracted by the Match-3 software from the Rietveld refined XRD data have also been listed in Table 5. The D values calculated by using all the methods is found to be decreasing trend with the increasing Cr content for both series as shown in Fig. 11. This decreasing trend is most likely due to the peak broadening.
θ and their linear fitted curve have been drawn using the origin software as shown in Fig. 10. The slope and y-intercept have been extracted for all the samples that provides the values of D and ε of both series and presented in Table 5. In addition, the D and ε values extracted by the Match-3 software from the Rietveld refined XRD data have also been listed in Table 5. The D values calculated by using all the methods is found to be decreasing trend with the increasing Cr content for both series as shown in Fig. 11. This decreasing trend is most likely due to the peak broadening.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. FTIR spectra of the synthesized samples also confirm the spinel structure. The cation distribution calculated from the extracted Rietveld refined data confirms the mixed spinel structure of all samples of both series. In both the stoichiometric and non-stoichiometric series, an enhancement of lattice parameter have been found. From the analysis of elastic properties, it is found that all the samples for both series are ductile in nature. For the stoichiometric series Cr3+ together with Co2+ is assumed to have influenced the structural and mechanical properties. In addition, non-stoichiometric compositions provide an opportunity to tailor Co2+/Cr3+ and Fe3+/Cr3+ in the inverse spinel ferrite which causes the defect in structure, and modification of mechanical behavior.
m. FTIR spectra of the synthesized samples also confirm the spinel structure. The cation distribution calculated from the extracted Rietveld refined data confirms the mixed spinel structure of all samples of both series. In both the stoichiometric and non-stoichiometric series, an enhancement of lattice parameter have been found. From the analysis of elastic properties, it is found that all the samples for both series are ductile in nature. For the stoichiometric series Cr3+ together with Co2+ is assumed to have influenced the structural and mechanical properties. In addition, non-stoichiometric compositions provide an opportunity to tailor Co2+/Cr3+ and Fe3+/Cr3+ in the inverse spinel ferrite which causes the defect in structure, and modification of mechanical behavior.