Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A benchmark study of aromaticity indexes for benzene, pyridine and the diazines – I. Ground state aromaticity†
Jacob Pedersen and
Kurt V. Mikkelsen
and
Kurt V. Mikkelsen *
*
Department of Chemistry, University of Copenhagen, Copenhagen, DK-2100, Denmark. E-mail: kmi@chem.ku.dk
First published on 19th January 2022
Abstract
Five different aromaticity indexes are benchmarked for benzene, pyridine and the diazines in their ground states. A basis set study was performed using the Pople style, Karlsruhe and Dunning's correlation consistent basis sets. Ten different DFT functionals, including LSDA, PBE, PBE0, B3LYP, CAM-B3LYP, wB97XD, M06-2X, SOGGA11X, M11 and MN15 were benchmarked by comparison with CCSD, CASSCF and MP2. Large out-of-plane imaginary frequencies were observed for some of the optimized structures at the correlated wavefunction level of theory. It was found that the DFT functionals in general predict the para-delocalization index, multicenter index and aromatic fluctuation index to be approximately 70%, 50% and 45% larger, respectively, compared to the CCSD method. Comparisons of the DFT functionals showed that the wB97XD, CAM-B3LYP and M06-2X functionals performed the best. Furthermore, the basis set dependence of the DFT functionals was found to be large for the electron sharing indexes. Based on these findings, it is recommended to perform ground state calculations of aromaticity indexes at the wB97XD, CAM-B3LYP or M06-2X level of theory utilizing a simple basis set of triple-ζ quality.
1 Introduction
The concept of aromaticity is cumbersome, because no general accepted definition of it exists. However, the concept is widely used and provides various application options in chemical engineering.1,2 The latest one being in MOlecular Solar Thermal (MOST) energy storage systems,3–5 in which aromaticity reversal between different electronic states potentially can extend the storage lifetime and enhance the switching properties of the organic photoswitches.6,7Aromaticity is usually associated with a set of rather characteristic physicochemical properties, including cyclic electron delocalization, energetic stabilization, bond length equalization, exalted magnetic susceptibility, etc.8 As a consequence, aromaticity cannot be uniquely quantified nor measured directly. Instead, various indexes are designed to scale aromaticity by means of some of the characteristic physicochemical properties, and these are used as a measure for the amount of aromaticity in a given molecule. Hence, in order to get a reliable measure of the aromaticity in a molecule, multiple aromaticity indexes are required, since the properties are not necessarily are present simultaneously or related to each other.9–11
Molecular electronic structure calculations were performed in this study in order to calculate the aromaticity indexes (further description in the computational approach section). The accuracy of the aromaticity indexes is then directly related to the accuracy of the electronic structure theory used in the calculations. Highly correlated wavefunction methods are believed to yield very accurate results in general, but at a high cost.12 The molecules examined in this study is rather small, however, these molecules represent the set of the most common unit-structures, that constitutes many polycyclic arenes and heteroarenes. Thus, the behavior of the aromaticity indexes is believed to be encapsulated by this set of molecules.
Kohn–Sham Density Functional Theory (KS–DFT) is a different approach, in which the KS Fock operator is approximated. The challenge with KS–DFT is, that the exchange-correlation (XC) potential is unknown and cannot be approximated systematically, meaning that no lower or upper bound for the system exists.13 The variational principle provides a lower bound for the wavefunction methods, which can be approached systematically by including more Slater determinants, thereby recovering more electron correlation.14 Consequently, the DFT functionals must be benchmarked by comparison with either experimental data or results obtained from highly correlated wavefunction methods, in order to check the accuracy of the calculated properties. However, the DFT functionals may perform differently for different properties, thereby requiring a separate benchmark study for each property. This benchmark study is for the aromaticity indexes; HOMA,15,16 PDI,17 MCI,18 AV1245![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 and FLU19 (see Section 2).†
19 and FLU19 (see Section 2).†
1.1 Quantum theory of atoms in molecules
If the molecular volume is divided into vector subspaces, each containing one atom of the molecule, one can define the molecular properties in terms of atomic contributions. In Quantum Theory of Atoms In Molecules (QTAIM), the molecular wavefunction is partitioned in either Hilbert space or in real space, hence allowing for a topological analysis of the electron density in each vector subspace. The wavefunction partition is preferable performed in real space, since the choice of basis set dictates the accuracy of the partition in Hilbert space.20,21The electron density is uniquely defined and exists in all space, guaranteed by the principles of quantum mechanics.22,23 The uniqueness of the wavefunction partition is then ensured by taking the electron density as central variable. The one electron density γ(1) is defined in terms of the Reduced Density Matrix (RDM) method.19 For convenience, the electron pair density γ(2) is similarly stated here:
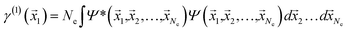 | (1) |
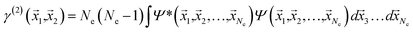 | (2) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) denotes the combined spatial and spin coordinate of the electron. Information about the dynamics of the electron density is then obtained by examination of the vector fields in each vector subspace. Each subspace satisfy the ‘quantum condition’, which states that the subspace must be bounded by a surface S, defined such that the inner product of the electron density gradient ∇γ(1) and any vector n(
denotes the combined spatial and spin coordinate of the electron. Information about the dynamics of the electron density is then obtained by examination of the vector fields in each vector subspace. Each subspace satisfy the ‘quantum condition’, which states that the subspace must be bounded by a surface S, defined such that the inner product of the electron density gradient ∇γ(1) and any vector n(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ), perpendicular to the surface S, is zero at all points on the surface:
), perpendicular to the surface S, is zero at all points on the surface:
∇γ(1)(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) · n( ) · n(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) = 0, ∀ ) = 0, ∀![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ∈ S( ∈ S(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) )
| (3) |
Any such surfaces are in the framework of QTAIM called zero-flux surfaces.21,24 Evaluation of the electron density gradient at different initial points in the vector fields allows one to trace out gradient paths and construct contour maps or phase portraits, depending on which space is used for the partitioning. Assuming real space, the critical points (ω, σ) are characterized by the rank of the Hessian (ω) and the signature of its eigenvalues (σ = λ1 + λ2 + λ3).24
A Nuclear Critical Point (NCP) is defined as a local maximum (3,−3) of the electron density and indicates presence of a nucleus. Bond Critical Points (BCP)s are saddle points (3,−1), and they are located between two NCPs. It is noted, that the unstable manifolds (defined as the set of initial points; ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (t) →
(t) → ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) * as − t → ∞, with t being the time) connect two NCPs, whereas the stable manifolds separate the basins assigned to each of the NCPs. A basin is defined as the region, in which all of the initial points move towards the attracting NCP. Hence, unstable manifolds indicate movement of electrons between two basins, i.e. electron sharing, and they are in the framework of QTAIM called atomic interaction lines or bond paths. A molecular graph is a collection of multiple bond paths. The stable manifolds satisfy the quantum condition and are the zero-flux surfaces. A Ring Critical Point (RCP) is defined as (3,1) and is found in the interior of ring structures (Fig. 1).21,24
* as − t → ∞, with t being the time) connect two NCPs, whereas the stable manifolds separate the basins assigned to each of the NCPs. A basin is defined as the region, in which all of the initial points move towards the attracting NCP. Hence, unstable manifolds indicate movement of electrons between two basins, i.e. electron sharing, and they are in the framework of QTAIM called atomic interaction lines or bond paths. A molecular graph is a collection of multiple bond paths. The stable manifolds satisfy the quantum condition and are the zero-flux surfaces. A Ring Critical Point (RCP) is defined as (3,1) and is found in the interior of ring structures (Fig. 1).21,24
2 Aromaticity indexes
The Harmonic Oscillator Model of Aromaticity (HOMA), defined by J. Kruszewski and T. M. Krygowski, is a geometrical aromaticity index.15,16
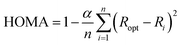 | (4) |
The empirical constant α is chosen, such that the HOMA index is equal to one for an aromatic molecule with equalized bond lengths and zero for the molecule in its Kekulé structure, i.e. with alternating bond lengths. The number of bonds with π-electrons is denoted n, and Ri is the bond length of the i-th bond. The bond-specific optimal bond length Ropt is calculated by minimization of the energy caused by forced steric strain in the molecule, also called deformation energy.16
Aromaticity indexes based on π-electron delocalization are commonly called Electron Sharing Indexes (ESI)s, and they are defined in terms of quantities from the QTAIM formalism.19 The difference between two independent one electron densities and the corresponding electron pair density is the exchange-correlation density (XCD) γxc(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 1,
1,![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 2).
2).
γxc(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 1, 1, ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 2) = γ(1)( 2) = γ(1)(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 1)γ(1)( 1)γ(1)(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 2) − γ(2)( 2) − γ(2)(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 1, 1, ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 2) 2)
| (5) |
Integration of the XCD with respect to two different basins of attraction gives the delocalization index (DI):19
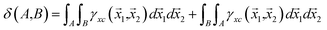 | (6) |
The atoms in a ring are ordered by the string 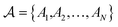 , where N is the number of atoms and by definition; A1 = AN+1. The Para–Delocalization Index (PDI), defined for six-membered rings only by J. Poater et al., is the average value of the DI for all para-related atoms.17
, where N is the number of atoms and by definition; A1 = AN+1. The Para–Delocalization Index (PDI), defined for six-membered rings only by J. Poater et al., is the average value of the DI for all para-related atoms.17
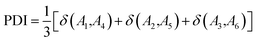 | (7) |
P. Butlinck et al. defined the Multicenter Index18 (MCI) in terms of the Iring index, which was developed by M. Giambiagi et al.25 six years earlier.
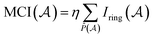 | (8) |
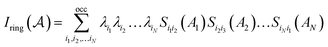 | (9) |
The normalization constant has been identified as η = 1/(2N).19 The permutation operator 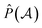 works on the string
works on the string 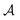 , thereby producing N! permutations. The atomic overlap matrix is the overlap between the two natural orbitals ϕNOi and ϕNOj on atom A.
, thereby producing N! permutations. The atomic overlap matrix is the overlap between the two natural orbitals ϕNOi and ϕNOj on atom A.
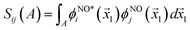 | (10) |
The natural orbitals and occupation numbers are the eigenvectors and the corresponding eigenvalues of the diagonal electron density matrix:
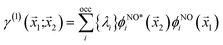 | (11) |
Delocalization of π-electrons between para-related carbon atoms has been observed to be larger than between the corresponding meta-related.17 Based on these findings, E. Matito et al. introduced the AV1245 index, which measures the delocalization between atoms of the positional relationship 1, 2, 4 and 5. The AV1245 index is defined as the mean of the MCI values of these atoms.19
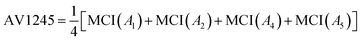 | (12) |
The aromatic fluctuation (FLU) index, also defined by E. Matito et al.,26 quantifies the delocalization–fluctuation over all adjacent atoms.
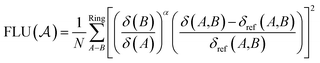 | (13) |
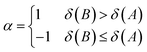 | (14) |
The atomic valence δ(A) can be shown to equal the difference between the electron population in a basin and half of the XCD integrated over the same basin twice. δref(A,B) is the reference DI of atom A and B from a chosen reference molecule.19
3 Computational approach
The aromaticity indexes were calculated for the molecules (Fig. 2) in their ground states according to the procedure in Scheme S1 (located in the ESI).† The molecules were geometrical optimized in vacuum prior to the wavefunction calculations, and the frequencies were calculated to validate, that the optimized structures were local minima. Each step in the wavefunction preparation has been calculated at the same level of theory. All wavefunction calculations were performed in the Gaussian 16 (Rev A.03) program.27 (See ESI† for route section and z-matrices).Single (or multiple) large out-of-plane imaginary frequencies were observed in some of the correlated wavefunction optimization and frequency calculations performed in Gaussian 16. Previous studies have shown similar results; optimized planar arenes turned out to be transitions states.28,29 In this study, the predicted transition structures were re-optimized in the Dalton (2016.1) program.30 The frequencies were similarly re-calculated in Dalton (when possible, or else in Gaussian 16), and for one of the calculations (pyridine at CASSCF(8,8)/6-31+G(d)), the frequencies confirmed, that the re-optimized structure now was a local minimum. The wavefunction for the re-optimized structure was then re-calculated in Gaussian 16. In a previous study, D. Asturiol et al. were able to turn all encountered transition structures into local minima by introducing a counterpoise correction.29 However, since only a few of the optimized structures were transition structures, no further corrections were performed. Further discussion of the imaginary frequencies and its consequences is given in the results and discussion section.
3.1 Electronic structure calculation
Second-order Møller-Plesset perturbation theory31–36 (MP2), Complete Active Space Self-Consistent Field37–39 (CASSCF) and Coupled Cluster including singles and doubles40–43 (CCSD) have been used to benchmark the ten DFT functionals; LSDA,44 PBE,45 PBE0,46 B3LYP,47 CAM-B3LYP,48 wB97XD,49 M06-2X,50 SOGGA11X,51 M11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 and MN15.53 (Table 1). The results calculated at the CCSD level of theory are used as reference. Concerning the CASSCF calculations, the number of orbitals in the active space was six for benzene and eight for the rest of the molecules. The number of electrons was chosen to match the number of orbitals used in the active space. However, it was not possible to calculate the frequencies of pyridine at the CASSCF(8,8)/6-311+G(d) and -/Def2SVP level of theory in Gaussian 16. This problem was solved by reducing the active space to (6,6).
52 and MN15.53 (Table 1). The results calculated at the CCSD level of theory are used as reference. Concerning the CASSCF calculations, the number of orbitals in the active space was six for benzene and eight for the rest of the molecules. The number of electrons was chosen to match the number of orbitals used in the active space. However, it was not possible to calculate the frequencies of pyridine at the CASSCF(8,8)/6-311+G(d) and -/Def2SVP level of theory in Gaussian 16. This problem was solved by reducing the active space to (6,6).
| Electronic structure methods | ||
|---|---|---|
| Wavefunction based | Reference | |
| CCSD | 40–43 | |
| CASSCF | 37–39 | |
| MP2 | 31–36 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| KS-DFT | Description/note66 | |
| LSDA | Local spin density approximation | 44 |
| PBE | Generalized gradient approximation | 45 |
| PBE0 | Correlation corrected PBE | 46 |
| B3LYP | Correlation from LYP + VWN III | 47 |
| CAM-B3LYP | Long-range corrected | 48 |
| wB97XD | Long-range corrected + dispersion | 49 |
| M06-2X | Minnesota functional | 50 |
| SOGGA11X | Minnesota functional | 51 |
| M11 | Minnesota functional | 52 |
| MN15 | Minnesota functional | 53 |
Pople style,54–58 Karlsruhe59 and Dunning's correlation consistent60,61 (cc) basis sets in both double-ζ and triple-ζ quality have been utilized for each of the electronic structure methods. Previous studies have shown, that the Pople style basis sets work very well with one set of diffuse and polarized functions added to the heavy atoms.62,63 Hence, in this study, the double-ζ and triple-ζ Pople style basis sets refer to the 6-31+G(d) and 6-311+G(d) basis sets. The Karlsruhe and Dunning's cc basis sets have furthermore been augmented with diffuse functions, and one additional set of diffuse and polarized functions have been added to the hydrogen atoms in the Pople style basis sets (Table 1). It was not possible to perform the CASSCF calculations with the augmented basis sets due to linear dependence, thus they have been neglected.
The electronic structure theory has been specified in the wavefunction files for CCSD, MP2, CASSCF, LSDA, PBE, PBE0, B3LYP and M06-2X.64
3.2 Wavefunction analysis
The wavefunction partition and topological analysis were performed in the AIMAll software package.65 The AIMExt program were used to localize and characterize the critical points, and the AIMInt program were used for the numerical integration of the atomic basins.65 All AIMAll-calculations were performed with the same settings.The output of the numerical integrations were then used in the ESI-3D program68 to obtain the aromaticity indexes (see ESI† for method-specification in the AIMAll calculations and for generic input-file in the ESI-3D calculations).
4 Results and discussion
In this section, the imaginary frequencies and its consequences are initially discussed, followed by an assessment of the basis set performance. The DFT functionals are then benchmarked by comparison with the results obtained by the correlated wavefunction methods, and the aromaticity in the molecules from this study is finally assessed.The electronic energy, zero point energy (ZPE) and sum of electronic and zero point energy are obtained in the process of calculating the aromaticity indexes. For future reference, these energetics are reported together with the aromaticity indexes in the ESI,† but they will not be further discussed.
4.1 Transition structures
Concerning the predicted transition structures, the observed imaginary frequencies and the associated level of theory used in the calculations are listed in Table 2.| Transition structures | ||
|---|---|---|
| Molecule | Level of theory | Frequency |
| Benzene | CCSD/6-31++G(d,p) | 741.75i |
| -/6-311+G(d) | 137.53i | |
| -/6-311++G(d,p) | 949.02i | |
| -/Def2SVPD | 1245.53i | |
| MP2/6-31++G(d,p) | 956.42i | |
| -/6-311+G(d,p) | 466.57i | |
| -/6-311++G(d,p) | 1190.70i | |
| -/Def2SVPD | 1377.96i | |
| Pyridine | CASSCF(8,8)/6-31+G(d) | 1528.84i, 1387.88i, 1052.72i, 645.89i |
| -/6-311+G(d,p) | 2045.66i, 1462.91i, 1254.60i, 882.73i | |
| -/Def2TZVP | 2009.55i, 966.02i, 589.62i, 374.49i | |
| -/cc-pVTZ | 952.56i, 470.91i, 465.01i | |
| Pyridazine | MP2/6-311++G(d,p) | 223.22i |
| Pyrimidine | CASSCF(8,8)/cc-pVTZ | 890.18i, 561.23i |
It is noted, that transition states only were predicted at the correlated wavefunction level of theory and not for the single-determinant based DFT functionals. All the imaginary frequencies are rather large, and simulations in GaussView 6.0.16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 revealed, that the associated vibrations are out-of-plane. The majority of these surprising results occurred at the MP2 level of theory using the Pople style basis sets. These findings are in agreement with previous studies.28,29
69 revealed, that the associated vibrations are out-of-plane. The majority of these surprising results occurred at the MP2 level of theory using the Pople style basis sets. These findings are in agreement with previous studies.28,29
Most of the transition structures were predicted for benzene, and it is observed, that those from CCSD and MP2 calculations have in common, that the used basis sets contain diffuse functions. Moreover, all of the transition structures at the CASSCF level of theory were calculated with basis sets of triple-ζ quality, expect for the double-ζ Pople style basis set. In contrast, a mix of both double-ζ and triple-ζ basis sets resulted in transition states for the CCSD and MP2 calculations.
Properties calculated utilizing truncated basis sets might be different from the complete basis sets limit. This difference is known as the Basis Set Incompleteness Error (BSIE).70 Basis Set Superposition Error (BSSE) effects are introduced, when atom-centered basis functions overlap the function space of another atom, thereby increasing the number of basis functions used for the description of the other atom. This artificial improvement of the basis set counteracts the BSIE and helps compensate for the basis set deficiencies.71 BSSE effects are frequently encountered, when two or more molecules are studied. The analog of BSSE effects in single molecules (intramolecular BSSE effects) have similarly been reported.72 Both BSIE and the BSSE effects affect the potential energy surface, which introduces artificial effects into energy-based properties, such as frequencies.29
The BSIE and BSSE effects are highly entangled, however, it has been proposed that the intramolecular BSSE effects are the cause of the imaginary frequencies in aromatic planar arenes.29,70 Treating the imaginary frequencies as caused by intramolecular BSSE effects, the problem can be fixed by introducing a counterpoise correction.71 As mentioned in the computational approach section, D. Asturiol et al. presented an effective way to partition systems, thereby enabling for counterpoise corrections.29
The calculated aromaticity indexes are expected to be of comparable size. If the results obtained at one level of theory are notably different from the general tendencies, it might be an attribute of the intramolecular BSSE effects or an error. However, no such distinct results are observed (see the next two subsections). Hence, it is concluded, that the intramolecular BSSE effects have no or at least small enough effect not to noted in the aromaticity indexes.
4.2 Basis set analysis
Only the basis set dependence of the aromaticity indexes are examined in this section. The performance of the basis sets is discussed for each aromaticity index, starting with benzene and then extended to include pyridine and the diazines. | ||
| Fig. 3 Basis set dependence of the HOMA index for benzene. The basis sets are listed on the horizontal axis, and the HOMA index is given along the vertical axis. | ||
Augmentation with diffuse functions for the Karlsruhe and Dunning's cc-basis sets is seen to make no notable difference compared to the values obtained by the ‘bare’ basis sets. The double-ζ Karlsruhe and Dunning's cc basis sets at the CCSD and MP2 level of theory are exceptions. In these cases, the index is lowered (−∼0.02), when diffuse functions are included in the basis sets. Addition of diffuse and polarized functions to the hydrogens for the Pople style basis sets is noted to have a negligible effect on the index.
The basis set dependence of the HOMA index is similarly plotted for pyridine and the diazines. The figures are available in the ESI.† Overall, the performance of the basis sets is consistent with the observations done for benzene.
 | ||
| Fig. 4 Basis set dependence of the PDI (top) and MCI (bottom) for benzene. The basis sets are listed on the horizontal axis, and the associated property is given along the vertical axis. | ||
 | ||
| Fig. 5 Basis set dependence of the AV1245 index for benzene. The basis sets are listed on the horizontal axis, and the AV1245 index is given along the vertical axis. | ||
The basis set dependence of the PDI, MCI and AV1245 index for pyridine and the diazines are available in the ESI.† Comparison of the basis set dependencies reveals similar tendencies as described for benzene. Furthermore, it is observed that the PDI tends to converge towards larger values, as each type of basis sets become larger. In contrast, the indexes goes towards smaller values for the MCI and AV1245 index, as each type of basis sets are enlarged.
 | ||
| Fig. 6 Basis set dependence of the FLU index for benzene. The basis sets are listed on the horizontal axis, and the FLU index is given along the vertical axis. | ||
The basis set dependence of the FLU index is available for pyridine and the diazines in the ESI.† It is noted, that the DFT-calculated FLU index is much more basis set dependent for the other molecules than for benzene. In general, the basis set performance for the wavefunction methods are in agreement with the observations for benzene, expect for the increasement in the index when utilizing the Pople style triple-ζ basis sets. The index is generally slightly lowered, similarly as for the Karlsruhe and Dunning's cc basis sets. However, concerning the DFT functionals, the index is increased by ∼0.003, when the larger triple-ζ Pople style and Karlsruhe basis sets are used. The increasement observed for the Dunning's cc basis sets is negligible. Addition of diffuse and polarized functions to the hydrogens for the Pople style basis sets is seen to increase the index for the wavefunction methods but not for the DFT functionals. A slight increasement is, however, observed for all methods for the double-ζ Karlsruhe and Dunning's cc basis sets, when diffuse functions are added.
4.3 Benchmarking of DFT functionals
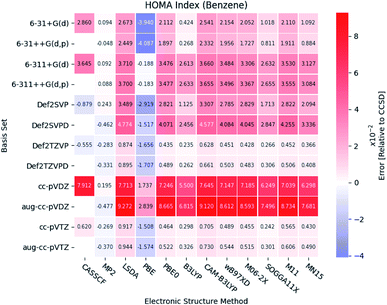
Under the assumption that the aromaticity indexes calculated at the CCSD level of theory are the most accurate, these results can be used as reference. Thus, the results from the DFT functionals are benchmarked by comparison with those from the correlated wavefunction methods.Large errors are similarly observed for all the DFT functionals, when Dunning's double-ζ cc basis sets are used. It is noted, that the pure DFT functional, PBE, significantly underestimates the HOMA index, except in combination with the triple-ζ Pople style basis sets.
In general, small errors are observed for the hybrid functionals, when the triple-ζ Karlsruhe and Dunning's cc basis sets are used. Comparison of the different DFT functionals reveals, that the results from B3LYP are in best agreement with the reference. Next follows the two Minnesota functionals SOGGA11X and MN15. Relative differences between the HOMA indexes for pyridine and the diazines are available in the ESI.† The tendencies found for the other molecules are in agreement with the ones observed for benzene.
A statistical summary of the aromaticity indexes are given in the Tables 41–45 (located in the ESI†). From the tables, it is seen that the DFT functionals in general overestimates the HOMA index, expect for PBE. This is in agreement with the relative placement of the electronic structure methods in Fig. 3. The overestimation stems from the fact, that the DFT functionals in general predict smaller bond lengths than CCSD, which translate into larger HOMA indexes.
The standard deviation observed within CCSD and MP2 is high compared to the DFT functionals, meaning that the choice of basis set is crucial for the accuracy of the HOMA index. However, the standard deviation of the DFT functionals is in general small. This leads to a favoring of the computationally less demanding double-ζ basis sets, since the effect of using the more elaborate basis sets is negligible, whereas the computational saving is significant.
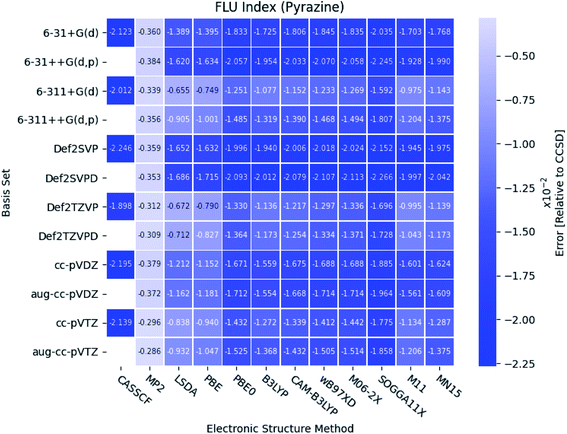
As seen in Fig. 8, the FLU indexes calculated with the triple-ζ basis sets are in better agreement with the references than the corresponding double-ζ basis sets. This trend is only prominent for the diazines, especially in pyrazine. Furthermore, for pyridine and the diazines, the relative errors for the two pure DFT functionals, LSDA and PBE, are observed to be small compared to the other more elaborate DFT functionals. In addition, comparable results are obtained with the B3LYP, M11, MN15 and the two long-range corrected CAM-B3LYP and wB97XD functionals.
With respect to the rest of the ESIs, it is seen that the SOGGA11X functional provides results slightly closer to those from CCSD than the other DFT functionals, closely followed by the M06-2X functional for the MCI and AV1245 index. Since the standard deviation for the MCI, AV1245 index and FLU index is large for the DFT functionals, and because the triple-ζ basis sets were found to predict the better results (see also next subsection), it is recommended to use basis sets of triple-ζ quality for the calculations of the ESIs.
4.4 Assessment of aromaticity
In the following assessment of aromaticity, the aromaticity indexes are interpreted in terms of Scheme 1.10,75 According to Hückel's rule,76 all five molecules are aromatic in their ground states.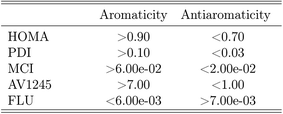 | ||
| Scheme 1 Interpretation scheme used to assign the values of the aromaticity indexes as either aromatic or antiaromatic. | ||
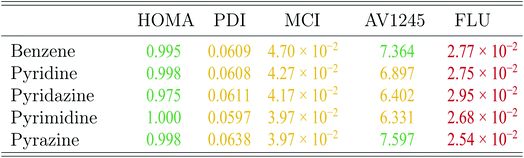
The aromaticity indexes for the five molecules obtained at the CCSD/aug-cc-pVTZ level of theory are listed and interpreted in Table 3. From the table, it is seen, that the HOMA indexes imply, that all five molecules are aromatic, in agreement with Hückel's rule. In contrast, the FLU indexes indicate, that the molecules are antiaromatic. Concerning the PDI, MCI and AV1245 index, only the latter clearly indicates that benzene and pyrazine are aromatic. However, it is noted, that these values are only just large enough to indicate aromaticity. The rest of the indexes can be assigned slightly to both properties.
These findings are quite surprising and unexpected. Unfortunately, examination of all calculated aromaticity indexes reveals, that similarly sized index values are obtained in all correlated wavefunction calculations, except in CASSCF calculations due to reasons discussed earlier. The PDI and FLU index of benzene, pyridine and pyrimidine have been calculated at the CISD/6-31G(d) level of theory in a previous study. Comparison of these values with the ones obtained in this study by CCSD and MP2 shows, that the PDI values, in this study, in general is 20% smaller than those previously obtained. Similarly, the FLU indexes, calculated by wavefunction methods in this study, are one order of magnitude larger than those calculated in the previous study.19
However, if the attention is directed towards the results obtained by the DFT functionals, then almost all of the calculated aromaticity indexes indicate aromaticity. Only a few of the calculated PDI, MCI and FLU index values are dissimilar in their interpretation, and it is noted, that the majority of them are only just below the threshold of predicting aromaticity. Exceptions are observed for the FLU indexes of the diazines, in which some of the values indicate antiaromaticity. For both the PDI and FLU index, it is seen, that the two pure DFT functionals in combination with the double-ζ Pople style and Karlsruhe basis sets in particular predict antiaromatic character. The SOGGA11X functional is similarly observed to predict dissimilar MCI and FLU index values, however, this is expected, since the benchmark study showed, that the results obtained at the SOGGA11X level of theory were in best agreement with the results from CCSD calculations.
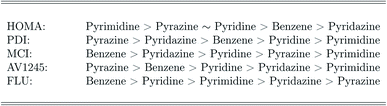
The ranking of the relative amount of aromaticity in the molecules is based on the averaged aromaticity indexes from Tables 41–45,† and it follows from Scheme 2. It is clear from Scheme 2, that the amount of aromaticity relative to each other differ depending on which aromaticity index is used to measure the amount of aromaticity. This is in perfect agreement with previous studies; it is extremely difficult to find a consensus among the aromaticity indexes.77 The ability to undergo electrophilic aromatic substitution reactions has previously been used to rank the relative amount of aromaticity between molecules, and a similar ranking, as proposed by the FLU index, has been reported.78
It is problematic, that the correlated wavefunction calculations only agree with the DFT functionals in the case of the HOMA index, and that their interpretation of the FLU index is completely different compared to the one based on the DFT calculations. Benzene, pyridine and the diazines are aromatic molecules,79–85 meaning that this benchmark study unequivocally demonstrates, that the correlated wavefunction methods in combination with the ESIs fail to describe the aromaticity of the studied molecules. This is very surprising, since CCSD is known to be an extremely accurate and well-balanced method that usually never fails.74
The recommend DFT functionals are therefore not the ones in best agreement with the correlated wavefunction methods, but the DFT functionals; wB97XD, CAM-B3LYP and M06-2X, which have been observed to perform very consistently and to predict an appropriate amount of aromaticity throughout this study. In addition, based on these DFT functionals, the relative amount of aromaticity (based on each individual aromaticity index) is in agreement with the averaged ordering observed for the FLU index and the previously reported ranking.78
5 Conclusion
The amount of aromaticity in the molecules; benzene, pyridine and the diazines in their ground states have been assessed by five different aromaticity indexes, including the HOMA index, PDI, MCI, AV1245 index and FLU index. The performance of the Pople style, Karlsruhe and Dunning's cc basis sets in both double-ζ and triple-ζ quality, with and without diffuse functions added, have been investigated for their performance with respect to calculation of aromaticity indexes. Furthermore, correlated wavefunction methods, including CCSD, CASSCF and MP2 have been used to benchmark the ten DFT functionals; LSDA, PBE, PBE0, B3LYP, CAM-B3LYP, wB97XD, M06-2X, SOGGA11X, M11 and MN15.A couple of the optimized structures from correlated wavefunction calculations turned out to be transition structures, as large out-of-plane imaginary frequencies were obtained from frequency calculations. These findings will join the group of surprising results observed for several planar arenes at the correlated wavefunction level of theory, as reported in previous studies.28,29
The basis set study showed, that the larger amount of aromaticity were predicted for the HOMA index and the PDI, when the larger triple-ζ basis sets were used compared to the corresponding double-ζ basis sets. The opposite were observed for the MCI, AV1245 index and FLU index. Addition of diffuse functions to the Karlsruhe and Dunning's cc basis sets were in general observed to lower the amount of aromaticity in the molecules. Similar effects were noted for the inclusion of diffuse and polarized functions to the hydrogens for the Pople style basis sets. However, the effects were often negligible, though mostly appearing for the double-ζ Pople style and Karlsruhe basis sets. Based on these findings, it is recommend to save the extra computational time and not include additional diffuse functions in the basis sets.
Comparison of the aromaticity indexes obtained by the different electronic structure methods revealed, that the CASSCF method with only one correlated orbital per electron in the active space performed poorly. In addition, the DFT functionals were found to predict the PDI, MCI and AV1245 index to be ∼70%, ∼50% and ∼45% larger, respectively, compared to CCSD. The DFT-calculated FLU indexes were observed to be three orders of magnitude smaller than the corresponding indexes obtained at correlated wavefunction level of theory. The correlated wavefunction methods and DFT functionals only predicted results of comparable size in their calculations of the HOMA index. Overall, wB97XD, CAM-B3LYP and M06-2X were found to perform the best for the calculations of aromaticity indexes. The pure DFT functionals, LSDA and PBE were conversely found to perform the worst, except for calculation of the FLU index. Examination of the DFT functionals showed a large basis set dependence for the ESIs. It is recommended to use the wB97XD, CAM-B3LYP or M06-2X functional in combination with a simple basis set of triple-ζ quality, where ‘simple’ means no inclusion of additional diffuse functions, since their effect was found to be negligible.
Assessment of the aromaticity indexes showed, that the DFT functionals in general predicted all five molecules to be aromatic regardless of which aromaticity index used. Concerning the correlated wavefunction methods, aromaticity was only clearly indicated by the HOMA indexes. Hence, the correlated wavefunction methods in combination with the ESIs failed to describe the aromaticity of the studied molecules, which was highly unexpected.
In order to proceed with the computational studies concerning the importance and effects of build-in aromaticity in photoisomerization reactions,6,7 this benchmark study clearly needs to be extended to include excited states. The next papers in this series will be a benchmark study of the aromaticity indexes for the first excited singlet and triplet states and investigations of the effects of solvents on the aromaticity indexes using electronic structure methods including the coupling to the surrounding solvent.86–89 When an accurate (and preferable cheap) description of ground state and excited state aromaticity is determined, the amount of aromaticity must be determined for a variety of molecules, allowing for hierarchical ranking of aromatic molecules.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge the Danish Council for Independent Research, DFF-0136-00081 B, and the European Union's Horizon 2020 Framework Programme under grant agreement number 951801 for financial support. The authors would like to thank Prof. PhD Stephan P. A. Sauer and Assoc. Prof. PhD Thorsten Hansen from University of Copenhagen for valuable discussions on Dalton and QTAIM respectively. A special thanks goes to Peter Søndergaard and PS-DATA for providing computer resources to speed up the wavefunction analyses.References
- T. M. Krygowski and H. Szatylowicz, Aromaticity: what does it mean?, ChemTexts, 2015, 1, 12 CrossRef CAS PubMed.
- P. W. Fowler, M. Lillington and L. P. Olson, Aromaticity, π-electron delocalization, and ring currents, Pure Appl. Chem., 2007, 79, 969–979 CAS.
- A. Lennartson, A. Roffey and K. Moth-Poulsen, Designing photoswitches for molecular solar thermal energy storage, Tetrahedron Lett., 2015, 56, 1457–1465 CrossRef CAS.
- M. B. Nielsen, N. Ree, K. V. Mikkelsen and M. Cacciarini, Tuning the dihydroazulene–vinylheptafulvene couple for storage of solar energy, Russ. Chem. Rev., 2020, 89, 573 CrossRef CAS.
- M. D. Kilde, M. Mansø, N. Ree, A. U. Petersen, K. Moth-Poulsen, K. V. Mikkelsen and M. B. Nielsen, Norbornadiene–dihydroazulene conjugates, Org. Biomol. Chem., 2019, 17, 7735–7746 RSC.
- A. B. Skov, N. Ree, A. S. Gertsen, P. Chabera, J. Uhlig, J. S. Lissau, L. Nucci, T. Pullerits, K. V. Mikkelsen, M. B. Nielsen, T. I. Sølling and T. Hansen, Excited-State Topology Modifications of the Dihydroazulene Photoswitch Through Aromaticity, ChemPhotoChem, 2019, 3, 577 Search PubMed.
- B. Durbeej, J. Wang and B. Oruganti, Molecular photoswitching aided by excited-state aromaticity, ChemPlusChem, 2018, 83, 958–967 CrossRef CAS PubMed.
- P. R. Schleyer and H. Jiao, What is aromaticity?, Pure Appl. Chem., 1996, 68, 209–218 CAS.
- A. R. Katritzky, P. Barczynski, G. Musumarra, D. Pisano and M. Szafran, Aromaticity as a quantitative concept. 1. A statistical demonstration of the orthogonality of classical and magnetic aromaticity in five-and six-membered heterocycles, J. Am. Chem. Soc., 1989, 111, 7–15 CrossRef CAS.
- E. Matito, An electronic aromaticity index for large rings, Phys. Chem. Chem. Phys., 2016, 18, 11839–11846 RSC.
- J. Cioslowski, E. Matito and M. Sola, Properties of aromaticity indices based on the one-electron density matrix, J. Phys. Chem. A, 2007, 111, 6521–6525 CrossRef CAS PubMed.
- R. J. Bartlett and M. Musiał, Coupled-cluster theory in quantum chemistry, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Insights into current limitations of density functional theory, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- E. K. U. Gross, L. N. Oliveira and W. Kohn, Rayleigh-Ritz variational principle for ensembles of fractionally occupied states, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 37, 2805 CrossRef PubMed.
- J. Kruszewski and T. M. Krygowski, Definition of aromaticity basing on the harmonic oscillator model, Tetrahedron Lett., 1972, 13, 3839–3842 CrossRef.
- T. M. Krygowski, Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of π-electron systems, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78 CrossRef CAS.
- J. Poater, X. Fradera, M. Duran and M. Solá, The delocalization index as an electronic aromaticity criterion: application to a series of planar polycyclic aromatic hydrocarbons, Chem.–Eur. J., 2003, 9, 400–406 CrossRef CAS PubMed.
- P. Bultinck, M. Rafat, R. Ponec, B. V. Van Gheluwe, R. Carbo-Dorca and P. Popelier, Electron delocalization and aromaticity in linear polyacenes: atoms in molecules multicenter delocalization index, J. Phys. Chem. A, 2006, 110, 7642–7648 CrossRef CAS PubMed.
- E. Matito, M. Solá, P. Salvador and M. Duran, Electron sharing indexes at the correlated level. Application to aromaticity calculations, Faraday Discuss., 2007, 135, 325–345 RSC.
- R. F. W. Bader, Molecular fragments or chemical bonds, Acc. Chem. Res., 1975, 8, 34–40 CrossRef CAS.
- R. F. W. Bader, Atoms in molecules, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- M. Born, Quantenmechanik der stoßvorgänge, Z. Phys., 1926, 38, 803–827 CrossRef CAS.
- M. Born, Quantum mechanics of collision processes (Translation of ref. 22), Z. Phys., 1926, 38, 803 CrossRef CAS.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- M. Giambiagi, M. S. Giambiagi, C. D. S. Silva and A. P. Figueiredo, Multicenter bond indices as a measure of aromaticity, Phys. Chem. Chem. Phys., 2000, 2, 3381–3392 RSC.
- E. Matito, M. Duran and M. Solá, The aromatic fluctuation index (FLU): a new aromaticity index based on electron delocalization, J. Chem. Phys., 2005, 122, 014109 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- D. Moran, A. C. Simmonett, F. E. Leach, W. D. Allen, P. v. R. Schleyer and H. F. Schaefer, Popular theoretical methods predict benzene and arenes to be nonplanar, J. Am. Chem. Soc., 2006, 128, 9342–9343 CrossRef CAS PubMed.
- D. Asturiol, M. Duran and P. Salvador, Intramolecular basis set superposition error effects on the planarity of benzene and other aromatic molecules: a solution to the problem, J. Chem. Phys., 2008, 128, 144108 CrossRef PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekstroem, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernandez, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Haettig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenaes, S. Hoest, I.-M. Hoeyvik, M. F. Iozzi, B. Jansik, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjaergaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnaes, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. Rybkin, P. Salek, C. C. M. Samson, A. Sanchez de Meras, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thoegersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Agren, The Dalton quantum chemistry program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284, DOI:10.1002/wcms.1172.
- C. Møller and M. S. Plesset, Note on an approximation treatment for many-electron systems, Phys. Rev., 1934, 46, 618 CrossRef.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, A direct MP2 gradient method, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Semi-direct algorithms for the MP2 energy and gradient, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, MP2 energy evaluation by direct methods, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- M. Head-Gordon and T. Head-Gordon, Analytic MP2 frequencies without fifth-order storage. Theory and application to bifurcated hydrogen bonds in the water hexamer, Chem. Phys. Lett., 1994, 220, 122–128 CrossRef CAS.
- S. Sæbø and J. Almlöf, Avoiding the integral storage bottleneck in LCAO calculations of electron correlation, Chem. Phys. Lett., 1989, 154, 83–89 CrossRef.
- E. Dalgaard and P. Jørgensen, Optimization of orbitals for multiconfigurational reference states, J. Chem. Phys., 1978, 69, 3833–3844 CrossRef CAS.
- D. Hegarty and M. A. Robb, Application of unitary group methods to configuration interaction calculations, Mol. Phys., 1979, 38, 1795–1812 CrossRef CAS.
- R. H. A. Eade and M. A. Robb, Direct minimization in MC SCF theory. The quasi-newton method, Chem. Phys. Lett., 1981, 83, 362–368 CrossRef CAS.
- E. Dalgaard and H. J. Monkhorst, Some aspects of the time-dependent coupled-cluster approach to dynamic response functions, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 1217 CrossRef CAS.
- G. D. Purvis III and R. J. Bartlett, A full coupled-cluster singles and doubles model: the inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations, J. Chem. Phys., 1988, 89, 7382–7387 CrossRef CAS.
- G. E. Scuseria and H. F. Schaefer III, Is coupled cluster singles and doubles (CCSD) more computationally intensive than quadratic configuration interaction (qcisd)?, J. Chem. Phys., 1989, 90, 3700–3703 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the pbe0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 96, 5648–5652 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- R. Peverati and D. G. Truhlar, Communication: a global hybrid generalized gradient approximation to the exchange-correlation functional that satisfies the second-order density-gradient constraint and has broad applicability in chemistry, J. Chem. Phys., 2011, 135, 191102 CrossRef PubMed.
- R. Peverati and D. G. Truhlar, Improving the accuracy of hybrid meta-GGA density functionals by range separation, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- S. Y. Haoyu, X. He, S. L. Li and D. G. Truhlar, MN15: a Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7, 5032–5051 RSC.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self—consistent molecular orbital methods. XII. Further extensions of Gaussian—type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- R. B. J. S. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. R. Schleyer, Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, New basis set exchange: an open, up-to-date resource for the molecular sciences community, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- S. T. Olsen, J. Elm, F. E. Storm, A. N. Gejl, A. S. Hansen, M. H. Hansen, J. R. Nikolajsen, M. B. Nielsen, H. G. Kjærgaard and K. V. Mikkelsen, Computational methodology study of the optical and thermochemical properties of a molecular photoswitch, J. Phys. Chem. A, 2015, 119, 896–904 CrossRef CAS PubMed.
- M. Koerstz, J. Elm and K. V. Mikkelsen, Benchmark Study of the Structural and Thermochemical Properties of a Dihydroazulene/Vinylheptafulvene Photoswitch, J. Phys. Chem. A, 2017, 121, 3148–3154 CrossRef CAS PubMed.
- Format specification for AIM Extended Wavefunction Files (.wfx files). Version 1.0.4c, accessed 12/31-20, http://aim.tkgristmill.com/wfxformat.html Search PubMed.
- A. K. Todd, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019, http://aim.tkgristmill.com Search PubMed.
- Density Functional (DFT) Methods. Section: ”Keywords: Hybrid Functionals”, Accessed 1/1-21, https://gaussian.com/dft/ Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- E. Matito, ESI-3D: Electron Sharing Indexes Program for 3D Molecular Space Partitioning, Institute of Computational Chemistry and Catalysis (IQCC), University of Girona, Catalonia, Spain, 2006, http://iqc.udg.es/%7Eeduard/ESI Search PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView 6.0.16, Semichem, Inc., 2000–2016 Search PubMed.
- R. M. Balabin, Communications: intramolecular basis set superposition error as a measure of basis set incompleteness: can one reach the basis set limit without extrapolation?, J. Chem. Phys., 2010, 132, 211103 CrossRef PubMed.
- F. B. Van Duijneveldt, J. G. C. M. Van Duijneveldt-van de Rijdt and J. H. Van Lenthe, State of the art in counterpoise theory, Chem. Rev., 1994, 94, 1873–1885 CrossRef CAS.
- L. F. Holroyd and T. van Mourik, Insufficient description of dispersion in B3LYP and large basis set superposition errors in MP2 calculations can hide peptide conformers, Chem. Phys. Lett., 2007, 442, 42–46 CrossRef CAS.
- P. B. Karadakov, Ground-and excited-state aromaticity and antiaromaticity in benzene and cyclobutadiene, J. Phys. Chem. A, 2008, 112, 7303–7309 CrossRef CAS PubMed.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, Chichester, England, 2000 Search PubMed.
- R. Papadakis and H. Ottosson, The excited state antiaromatic benzene ring: a molecular Mr Hyde?, Chem. Soc. Rev., 2015, 44, 6472–6493 RSC.
- G. Portella, J. Poater and M. Sola, Assessment of Clar's aromatic π-sextet rule by means of PDI, NICS and HOMA indicators of local aromaticity, J. Phys. Org. Chem., 2005, 18, 785–791 CrossRef CAS.
- J. A. N. F. Gomes and R. B. Mallion, Aromaticity and ring currents, Chem. Rev., 2001, 101, 1349–1384 CrossRef CAS PubMed.
- M. G. Bures, B. L. Roos-Kozel and W. L. Jorgensen, Computer-assisted mechanistic evaluation of organic reactions. 11. Electrophilic aromatic substitution, J. Org. Chem., 1985, 50, 4490–4498 CrossRef CAS.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- K. Jug and A. M. Köster, Aromaticity as a multi-dimensional phenomenon, J. Phys. Org. Chem., 1991, 4, 163–169 CrossRef CAS.
- R. S. Hosmane and J. F. Liebman, Aromaticity of heterocycles: experimental realization of dewar-breslow definition of aromaticity, Tetrahedron Lett., 1991, 32, 3949–3952 CrossRef CAS.
- A. T. Balaban, D. C. Oniciu and A. R. Katritzky, Aromaticity as a cornerstone of heterocyclic chemistry, Chem. Rev., 2004, 104, 2777–2812 CrossRef CAS PubMed.
- C. W. Bird, The application of a new aromaticity index to six-membered ring heterocycles, Tetrahedron Lett., 1986, 42, 89–92 CrossRef CAS.
- F. Feixas, E. Matito, J. Poater and M. Sola, Aromaticity of distorted benzene rings: exploring the validity of different indicators of aromaticity, J. Phys. Chem. A, 2007, 111, 4513–4521 CrossRef CAS PubMed.
- S. M. Bachrach, Aromaticity of annulated benzene, pyridine and phosphabenzene, J. Organomet. Chem., 2002, 643, 39–46 CrossRef.
- T. D. Poulsen, P. R. Ogilby and K. V. Mikkelsen, Solvent effects on the O2(a1Δg)−O2(X3Σg−) radiative transition: comments regarding charge-transfer interactions, J. Phys. Chem. A, 1998, 102, 9829–9832 CrossRef CAS.
- K. O. Sylvester-Hvid, K. V. Mikkelsen, D. Jonsson, P. Norman and H. Agren, Nonlinear optical response of molecules in a nonequilibrium solvation model, J. Chem. Phys., 1998, 109, 5576–5584 CrossRef CAS.
- K. V. Mikkelsen, P. Jorgensen, K. Ruud and T. Helgaker, A multipole reaction-field model for gauge-origin independent magnetic properties of solvated molecules, J. Chem. Phys., 1997, 106, 1170–1180 CrossRef CAS.
- K. V. Mikkelsen, K. Ruud and T. Helgaker, Magnetizability and nuclear shielding constants of solvated water, Chem. Phys. Lett., 1996, 253, 443–447 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2ra00093h |
| This journal is © The Royal Society of Chemistry 2022 |