Open Access Article
Open Access ArticleElectronic effects on the mechanism of the NAD+ coenzyme reduction catalysed by a non-organometallic ruthenium(II) polypyridyl amine complex in the presence of formate †
Marta Chrzanowska a,
Anna Katafias
a,
Anna Katafias a,
Rudi van Eldik
a,
Rudi van Eldik *ab and
Jeanet Conradie
*ab and
Jeanet Conradie *cd
*cd
aFaculty of Chemistry, Nicolaus Copernicus University in Toruń, Gagarina 7, 87-100 Toruń, Poland. E-mail: rudi.vaneldik@fau.de
bDepartment of Chemistry and Pharmacy, University of Erlangen-Nuremberg, Egerlandstr. 1, 91058 Erlangen, Germany
cFaculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein 9300, Republic of South Africa. E-mail: ConradJ@ufs.ac.za
dDepartment of Chemistry, UiT – The Arctic University of Norway, N-9037 Tromsø, Norway
First published on 1st August 2022
Abstract
In the present study, electronic effects on the mechanism of the NAD+ coenzyme reduction in the presence of formate, catalysed by a non-organometallic ruthenium(II) polypyridyl amine complex, were investigated. The [RuII(terpy)(ampy)Cl]Cl (terpy = 2,2′:6′,2′′-terpyridine, ampy = 2-(aminomethyl)pyridine) complex was employed as the catalyst. The reactions were studied in a water/ethanol mixture as a function of formate, catalyst, and NAD+ concentrations at 37 °C. The overall process was found to be 11 to 18 times slower than for the corresponding ethylenediamine (en) complex as the result of π-back bonding effects of the ampy ligand. The mechanistic studies revealed a complete set of reactions that accounted for the overall catalytic cycle based on a formate-induced hydride transfer reaction to form the reduced coenzyme, NADH. The geometries of the ruthenium(II)-ampy complexes involved in the catalytic cycle and free energy changes for the main steps were predicted by DFT calculations. Similar calculations were also performed for the analogues ruthenium(II)-en and ruthenium(II)-bipy complexes (bipy = 2,2′-bipyridine). The DFT calculated energies show that both the solvent-formato exchange and the formato-hydrido conversion reactions have negative (favourable) energies to proceed spontaneously. The reactions involving the en complex have the more negative (favourable) reaction energies, followed by the ampy complex, in agreement with faster reactions for en complexes and slower reactions for bipy complexes than for ampy complexes.
Introduction
It is well known that reducing pyridinium salts to dihydropyridine compounds is one of the metabolism-sustaining processes.1,2 Eqn (1) presents one of such processes in all living cells.| NAD+ + 2e− + Haq+ ⇌ NADH | (1) |
NAD+ and NADH are the oxidised and reduced forms of nicotinamide adenine dinucleotide (NAD) coenzyme, respectively. The reaction outlined in eqn (1) involves the transfer of two electrons and one proton (PCET), which equals the transfer of a hydride ion, H−. The process is fully reversible, and the NAD+/NADH couple is a crucial biological electron/hydride transporter.2,3 Therefore, NAD is fundamental for maintaining the optimal redox state of cells for their life and proper functioning. Loss of the redox balance (called redox stress) in favour of the reducing equivalents (reductive stress) or the reactive oxygen species (oxidative stress) results in cell damage or death, leading to various disorders of living organisms.4 On the other hand, redox stress could be beneficial in treating many diseases, especially cancer.5–8 The relationship between the redox (oxidative/reductive) stress and the pathogenic state of cells and modification of cellular redox balance as a novel approach to targeted therapeutic strategies are the subjects of many publications.9–16
An essential contribution to the development of redox-based therapy was made recently by Sadler and co-workers, who applied organometallic complexes to regulate the cellular redox state. It turned out that Ru(II) complexes with metal–carbon bonds alter the [NAD+]/[NADH] ratio using formate as a hydride source. Under such conditions, the balance between NAD+ and NADH tilts towards the reduced form of the NAD coenzyme and leads to reductive stress.17–23 Being intrigued by the results of Sadler and co-workers, we successfully applied a non-organometallic [RuII(terpy)(en)(H2O/EtOH)]2+ complex (terpy = 2,2′:6′,2′′-terpyridine, en = ethylenediamine) as a potential catalyst for the reduction of NAD+ to NADH in the presence of formate.24 Thus, the ability to catalyse the region-selective transfer of a hydride ion to NAD+ is not a unique property of organometallic ruthenium(II) species, and similar effects can be reached in the presence of non-organometallic ruthenium(II) polypyridyl complexes. Based on kinetic and spectroscopic studies, we proposed the mechanism of the catalytic cycle for the reduction of NAD+ to NADH in the presence of [RuII(terpy)(en)(H2O/EtOH)]2+ and formate in water/ethanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v) solution.24
9, v/v) solution.24
Recently, we reported results of our studies on tuning the reactivity of a series of analogues of the en complex mentioned above, of general formula [RuII(terpy)(N^N)X]+/2+ (N^N = bidentate ligand, X = Cl− or H2O). We concluded that the rate of displacing a monodentate ligand, the first step of the proposed mechanism of the catalytic NAD+–NADH conversion, depends on the electronic and steric effects provided by bidentate ligands.25–28 Based on these studies, we expect that the catalytic efficiency will depend markedly on the nature of the coordinated bidentate ligand. The same effect was also observed for organometallic complexes studied by Sadler et al.17,18,21 Therefore, we extended our work to the [RuII(terpy)(ampy)Cl]Cl (ampy = 2-(aminomethyl)pyridine) and [RuII(terpy)(bipy)Cl]Cl·2H2O (bipy = 2,2′-bipyridine) complexes. These complexes are by one or two orders of magnitude less labile than the en analogue, for the aquation and water substitution reactions by chloride and thiourea at 25 °C, respectively.28
Experimental
Chemicals
All chemicals were of analytical reagent grade and used without further purification. RuCl3·xH2O was purchased from Abcam. 2-(Aminomethyl)pyridine, 2,2′:6′,2′′-terpyridine, 2,2′-bipyridine, lithium chloride, methanol-d4, deuterium oxide, sodium formate-d, β-nicotinamide adenine dinucleotide sodium salt, and MES sodium salt, were obtained from Merck. Sodium formate, sodium tetrahydroborate, and solvents were purchased from Avantor Performance Materials Poland SA. Deionized water was obtained from a Millipore Milli-Q water reagent system (Millipore, Bedford, MA, USA).Synthesis of the complex
The [Ru(terpy)(ampy)Cl]Cl and [Ru(terpy)(bipy)Cl]Cl·2H2O were synthesised according to procedures described earlier.25,26 The complexes were fully characterised both in the solid-state and in solution, as reported before.25,26 Solutions of [Ru(terpy)(ampy)(H2O)]2+ and [Ru(terpy)(bipy)(H2O)]2+ were prepared by spontaneous aquation of the parent chlorido complexes (ca. 2 h and 11 h, respectively) at room temperature. Solutions were prepared at least a day before the measurements.Instrumentation
UV-Vis spectral analyses and kinetic studies were carried out using a conventional spectrophotometer Shimadzu UV-1601 PC and Shimadzu UV2600i with Peltier Temperature Controllers. Single wavelength kinetic data were processed with the EnzFiter software. 1H NMR spectra were recorded on a Bruker Avance-700 NMR spectrometer in D2O/CD3OD (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v) solution; chemical shifts were referenced to TMS.
9, v/v) solution; chemical shifts were referenced to TMS.
Kinetic measurements
All Ru(II) aqua complex reactions were followed spectrophotometrically using a conventional method. The experiments were carried out in water/ethanol solutions (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
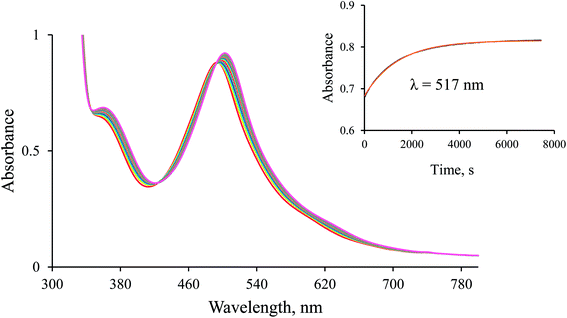
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v, unless otherwise stated) in the presence of air. The temperature was kept constant at 36.8 ± 0.1 °C and controlled before and after each experiment. All measurements were repeated at least twice. The anation reaction, initiated by adding small aliquots of an aqueous solution of the aqua complex to the thermostated formate solution, was monitored as an absorbance increase at 517 nm.
9, v/v, unless otherwise stated) in the presence of air. The temperature was kept constant at 36.8 ± 0.1 °C and controlled before and after each experiment. All measurements were repeated at least twice. The anation reaction, initiated by adding small aliquots of an aqueous solution of the aqua complex to the thermostated formate solution, was monitored as an absorbance increase at 517 nm.
Overall spectral changes accompanying the examined catalytic process were recorded within the 300–800 nm wavelength range. Reactions were initiated by adding small aliquots of a thermostated aqueous sodium formate solution to a thermostated water/ethanol solution of NAD+ and the Ru(II) complex. Several experiments in solutions of varying water to ethanol volume ratios, namely 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, 1
7, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, were conducted to investigate the effect of alcohol concentration on the rate of the catalytic process. Additional kinetic tests were performed in MES buffer solutions of pH 7.1.
3, were conducted to investigate the effect of alcohol concentration on the rate of the catalytic process. Additional kinetic tests were performed in MES buffer solutions of pH 7.1.
NMR and UV-Vis studies
A large excess of solid NaBH4 was added to a deaerated hot solution of [Ru(terpy)(ampy)(H2O)]2+ in D2O/CD3OD (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v) to synthesise the [Ru(terpy)(ampy)H]+ complex. The final concentrations of the reagents were as follows: 6.4 × 10−3 M Ru(II), 0.26 M NaBH4. The mixture was refluxed and a 1H-NMR spectrum was recorded approximately 10 min after the reaction was initiated. To register an electronic absorption spectrum, the solution prepared as described above was diluted by introducing a few drops of it into an argon purged water/ethanol solution (1
9, v/v) to synthesise the [Ru(terpy)(ampy)H]+ complex. The final concentrations of the reagents were as follows: 6.4 × 10−3 M Ru(II), 0.26 M NaBH4. The mixture was refluxed and a 1H-NMR spectrum was recorded approximately 10 min after the reaction was initiated. To register an electronic absorption spectrum, the solution prepared as described above was diluted by introducing a few drops of it into an argon purged water/ethanol solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v) in a gas-tight spectrophotometric cell.
9, v/v) in a gas-tight spectrophotometric cell.
DFT method
The density functional theory study on the compounds was done on the molecules in the gas phase, with the Scalar relativistic ZORA (Zeroth Order Regular Approximation to the Dirac equation)29–31 Hamiltonian, the OLYP GGA (Generalized Gradient Approximation)32,33 functional using Grimme's D3 dispersion correction34 and ZORA TZ2P all-electron relativistic basis sets, all as implemented in the ADF program system.35,36 Frequency analyses were done on all complexes to verify minima.Results and discussion
Preliminary observations
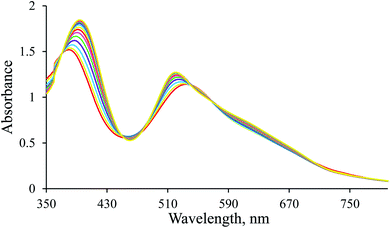
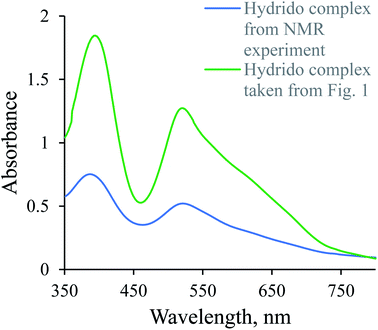
1H-NMR spectra were recorded to confirm the in situ formation of the hydrido complex using a much higher concentration of the complex and a larger excess of borohydride (selected conditions for the NMR experiment). A signal characteristic of the hydrido complex was observed at −27.59 ppm. Additional confirmation for the formation of the hydrido complex was obtained from a comparison of the UV-Vis spectrum of a diluted sample used in the NMR experiment with the last spectrum shown in Fig. 1 (see Fig. 2).
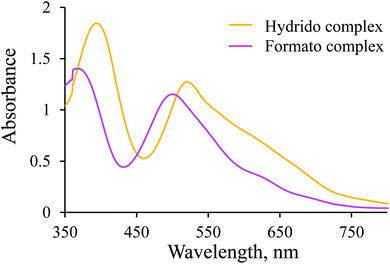
Since the [Ru(terpy)(ampy)H]+ complex is stable under the conditions described above, CO2(g) was passed through its solution to convert it into the corresponding formato complex. The observed shift of the absorption maxima towards shorter wavelengths (hypsochromic effect) is characteristic of the substitution of a hydride ion by formate, and proves the formation of the [Ru(terpy)(ampy)(HCOO)]+ complex (Fig. 3). This experiment shows that it is possible to obtain the formato complex as described before for the corresponding en and bipy complexes.24,37
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v solution). The spectral changes accompanying the reaction are reported in Fig. 5. Kinetic traces recorded under pseudo-first-order conditions appeared to be single exponential, as demonstrated in the given inset.
9, v/v solution). The spectral changes accompanying the reaction are reported in Fig. 5. Kinetic traces recorded under pseudo-first-order conditions appeared to be single exponential, as demonstrated in the given inset.
The non-linear dependence of the pseudo-first-order rate constant (kobs) on the formate concentration presented in Fig. 6 reveals the reversibility of the examined process, indicated by the significant intercept of the plot.
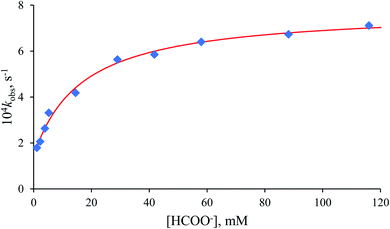 | ||
Fig. 6 Dependence of kobs on [HCOO−] for the anation of [RuII(terpy)(ampy)(H2O/EtOH)]2+ by HCOO−. Experimental conditions: [Ru(II)] = 0.106 mM, T = 36.8 °C, in water/ethanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v) solution. 9, v/v) solution. | ||
The kinetics of the formation of the formato complex can be accounted for in terms of a rate-determining ligand exchange process (k1 and k−1), preceded by a rapid ion-pair formation step (Q1) as outlined in eqn (2).
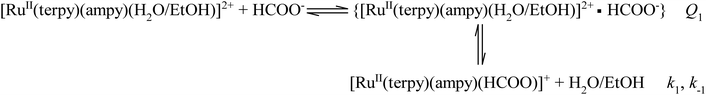 | (2) |
The rate expression derived for reactions (2) is given in eqn (3),
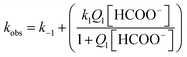 | (3) |
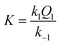 | (4) |
The obtained results demonstrate that the substitution reaction of [RuII(terpy)(ampy)(H2O/EtOH)]2+ with formate takes 6.5 h and 1.5 h at the lowest and highest formate concentration, respectively. It shows that the examined ampy complex reacts 11–18 times slower than its analogue [RuII(terpy)(en)(H2O/EtOH)]2+. This is in good agreement with detailed studies on the substitution behaviour of both complexes in an aqueous solution and is essential for revealing the mechanism of the catalytic process.25,26,28
The k1/k−1 ratio found for the ampy complex is higher than that of the en analogue, favouring the formation of the formato complex. Values of the ion-pair formation constant Q1 are similar for both complexes. In this way, the value of the overall equilibrium constant K for the ampy complex is much higher than for the en complex (Table 1). As a consequence, 24% of the Ru(II)-ampy complex and only 5% of the Ru(II)-en complex exist in the formato form in solution of the lowest formate concentration (ca. 1 mM), whereas in the case of the highest formate concentration (ca. 120 mM), 97% of [RuII(terpy)(ampy)(H2O/EtOH)]2+ and 87% of [RuII(terpy)(en)(H2O/EtOH)]2+ are converted into the formato complexes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, v/v) solution. Experimental conditions: [Ru(II)] = 10.6 × 10−2 mM, T = 36.8 °C
9, v/v) solution. Experimental conditions: [Ru(II)] = 10.6 × 10−2 mM, T = 36.8 °C
| Parameter | Value | |
|---|---|---|
| [RuII(terpy)(ampy)(H2O/EtOH)]2+ | [RuII(terpy)(en)(H2O/EtOH)]2+ | |
| k1, s−1 | (6.3 ± 0.2) × 10−4 | (4.8 ± 0.2) × 10−3 |
| Q1, M−1 | 61 ± 10 | 41 ± 7 |
| k1Q1, M−1 s−1 | 0.039 ± 0.006 | 0.20 ± 0.04 |
| k−1, s−1 | (1.4 ± 0.2) × 10−4 | (3.4 ± 0.1) × 10−3 |
| K = k1Q1/k−1, M−1 | 286 ± 1 | 59 ± 13 |
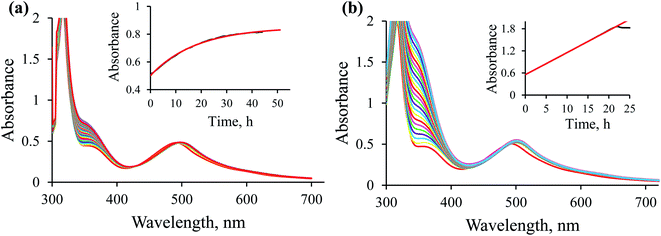
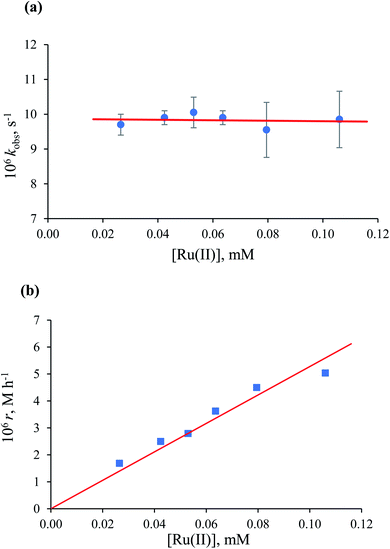
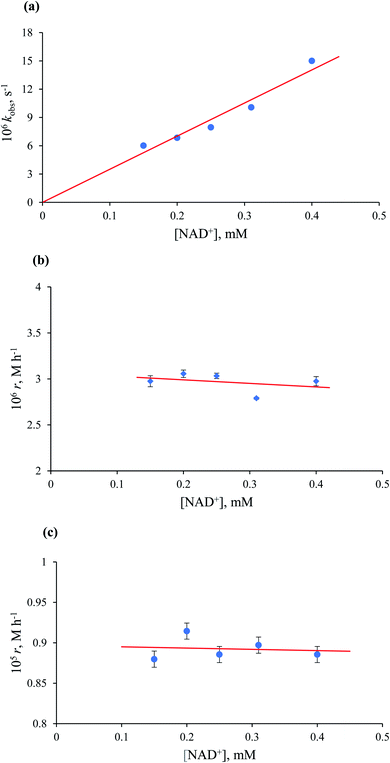
In general, all kinetic data obtained at [HCOO−] ≤ 1.35 mM showed first-order behaviour (see Fig. 7a), and the observed rate constant was independent of the formate concentration, with an average value of (9.7 ± 0.1) × 10−6 s−1 at [Ru(II)] = 5.3 × 10−2 mM and 36.8 °C. Mixed zero- and first-order behaviour was observed in the range of [HCOO−] = 1.65–2.20 mM. At [HCOO−] ≥ 7.20 mM, typical zero-order kinetic profiles with characteristic ‘dead-ends’ were recorded (see Fig. 7b).
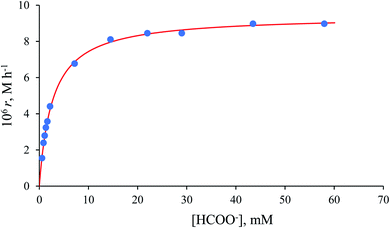
The collected kinetic data as a function of formate concentration are summarised in Table S1.† Values of the initial rate and zero-order rate constants calculated at low and high excess of formate, respectively, show a non-linear dependence on the formate concentration and pass through the origin within the error limits (Fig. 8).
This kind of dependence can be accounted for by the general reaction mechanism outlined in eqn (5) and (6):
 | (5) |
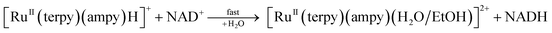 | (6) |
A rapid and reversible formation (Q2) of the ion-pair precursor {[RuII(terpy)(ampy)(HCOO)]+·HCOO−} (eqn (5)) is followed by a rate-limiting generation (k2) of the hydrido complex (eqn (5)), from which the hydride ion is transferred to NAD+ in a fast subsequent reaction step (eqn (6)). Concomitantly, the starting [RuII(terpy)(ampy)(H2O/EtOH)]2+ complex is reformed. The experimental data in Fig. 8 were fitted to eqn (7):
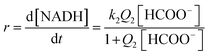 | (7) |
At low formate concentration, the rate law (7) simplifies to:
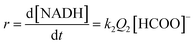 | (8) |
At high formate concentration, the rate law (7) simplifies to:
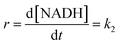 | (9) |
The maximum rate of the overall process k2 = (9.4 ± 0.1) × 10−6 M h−1 and precursor ion-pair formation constant Q2 = 373 ± 16 M−1 at 36.8 °C. The initial slope of the plot in Fig. 8 is given by k2Q2 = (3.5 ± 0.2) × 10−3 h−1, which is the first-order rate constant.
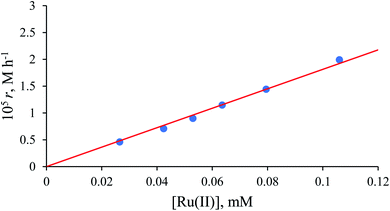
Values of the zero-order rate constant (r) obtained at high formate concentration show a linear dependence on the Ru(II) concentration (Fig. 10). All kinetic data are summarised in Table S2.†
| H2O/EtOH, v/v | 105 r, M h−1 | 102 kobs, h−1 | 105 ra, M h−1 |
|---|---|---|---|
| a Initial rate. Experimental conditions: [Ru(II)] = 5.3 × 10−2 mM, [NAD+] = 0.31 mM.b [HCOO−] = 58 mM.c [HCOO−] = 43.5 mM, T = 36.8 °C. | |||
| Ru-ampyb | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9 |
0.897 ± 0.001 | — | — |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 7 |
0.883 ± 0.001 | — | — |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.619 ± 0.001 | — | — |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | 0.79 ± 0.02 | 0.194 ± 0.001 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Ru-enc | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9 |
1.97 ± 0.01 | — | — |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 7 |
1.10 ± 0.01 | — | — |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | 2.2 ± 0.1 | 0.49 ± 0.06 |
| [RuII(terpy)(N^N)(solvent)]2+ + HCOO− ⇌ [RuII(terpy)(N^N)(HCOO−)]+ + solvent | (10) |
| [RuII(terpy)(N^N)(HCOO−)]+ + HCOO− ⇌ [RuII(terpy)(N^N)H+] + HCOO− + CO2 | (11) |
| DFT reaction | N^N | Solvent | Reactants | Products | ΔE (eV) | ΔG (eV) |
|---|---|---|---|---|---|---|
| (10) | Bipy | EtOH | [RuII(terpy)(N^N)(solvent)]2+ + HCOO− | [RuII(terpy)(N^N)(HCOO)]+ + solvent | −6.54 | −6.58 |
| Ampy | −6.62 | −6.67 | ||||
| en | −6.69 | −6.70 | ||||
| Bipy | H2O | −6.91 | −6.89 | |||
| Ampy | −7.00 | −6.98 | ||||
| en | −7.06 | −7.01 | ||||
| (11) | Bipy | [RuII(terpy)(N^N)(HCOO)]+ + HCOO− | [RuII(terpy)(N^N)H]+ + HCOO− + CO2 | 0.02 | −0.46 | |
| Ampy | −0.08 | −0.62 | ||||
| en | −0.13 | −0.71 |
The geometries of the [RuII(terpy)(N^N)(solvent)]2+ reactant molecules of the DFT reaction (10) (reaction (2) for N^N = ampy) are distorted octahedral with the solvent molecules trans to the nitrogen of the N^N ligand. The N–Ru–N and N–Ru–O angles are lower than 90° as expected for a real octahedral molecule due to the strain of the tridentate terpy and bidentate N^N ligands. For the molecules containing the unsymmetrical ampy ligand, the solvent is coordinated trans to the amine nitrogen. The isomers of [RuII(terpy)(ampy)(solvent)]2+ with the amine nitrogen cis to the solvent molecule are more than 0.1 eV higher (both electronic and free energy), for both solvents EtOH and H2O and thus less likely. The obtained trans orientation also agrees with the fact that the [RuII(terpy)(ampy)(solvent)]2+ molecules were obtained from [Ru(terpy)(ampy)Cl]Cl, where the Cl was experimentally shown to be trans to the amine nitrogen.26 The DFT calculated geometries of [RuII(terpy)(bipy)(H2O)]2+ molecules and [RuII(terpy)(en)(H2O)]2+ molecules agree with the reported experimental solid-state structures (see ref. 25, 39 and 40 (bipy) and [ref. 25 and 41] (en)). Although experimental solid-state structures of [RuII(terpy)(N^N)(EtOH)]2+ molecules could not be found in the literature, the DFT calculations indicate these molecules as stable, though the DFT reaction (10) for the molecules containing water, is slightly favoured compared to the reaction of the molecules with EtOH (lower electronic and free energy changes, Table 3).
When formate (HCOO−) is added to [RuII(terpy)(N^N)(solvent)]2+, hydrogen bonding between formate and the O atom of the solvent molecule occurs to produce a stable ion-pair reaction intermediate {[RuII(terpy)(N^N)(solvent)]2+·HCOO−}. It is followed by the substitution of the coordinated solvent by formate to form a stable formate complex [RuII(terpy)(N^N)(HCOO)]+, see the geometries in Fig. 12. The DFT calculated [RuII(terpy)(N^N)(HCOO)]+ geometries agree with that of a reported experimental solid-state structure of [RuII(terpy)(bipy)(HCOO)]+.42
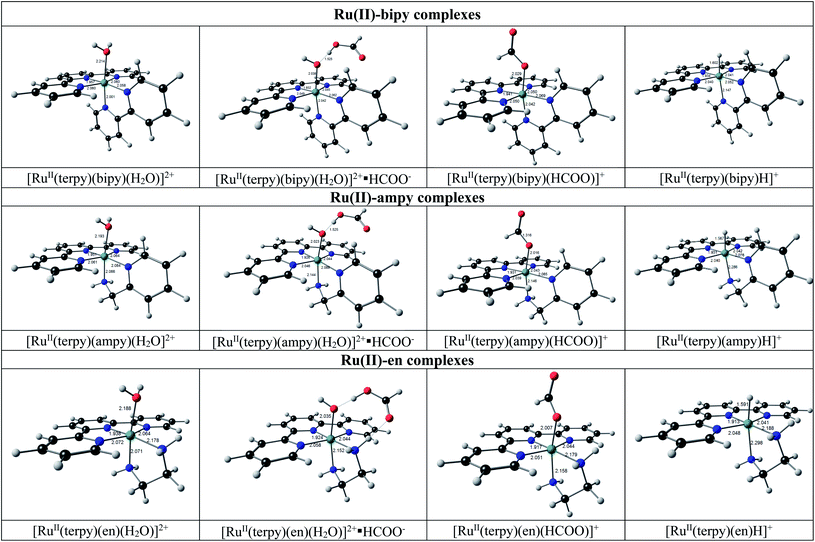 | ||
| Fig. 12 Structures of complexes predicted for the conversion of [RuII(terpy)(N^N)(H2O)]2+ into [RuII(terpy)(N^N)H]+ by DFT calculations. See Fig. S2† for the related [RuII(terpy)(N^N)(EtOH)]2+ and {[RuII(terpy)(N^N)(EtOH)]2+·HCOO−} complexes. Colour scheme used for atoms (online version): Ru (green), O (red), C (black), N (blue), and H (white). | ||
The ion-pair formation step (reaction (2)) is much faster, with a more favourable free energy change of ca. −7 eV (e.g., −6.91 eV for N^N = ampy and solvent = H2O) than the slower substitution step (reaction (2)) with a much smaller free energy change of ca. −0.1 eV (e.g., −0.07 eV for N^N = ampy and solvent = H2O). The DFT calculated electronic and free energy changes of DFT reaction (10), corresponding to the net reaction of (2) for N^N = ampy, slowly decrease when considering the bipy, ampy, and en complexes, respectively, in agreement with a faster reaction for the en complexes, see energies in Table 3.
For DFT reaction (11), the conversion of formato into hydrido complexes (corresponding to the net reaction of (5) for N^N = ampy), the calculated energy changes also slowly decrease when considering the bipy, ampy, and en complexes in agreement with a faster reaction for the en complexes, see energies in Table 3.
The structures of the hydrido complexes [RuII(terpy)(N^N)H]+ are shown in Fig. 12. No experimental solid-state structure of a ruthenium(II)-terpy-hydrido complex containing a bidentate N^N ligand could be found in the literature; only ruthenium(II)-terpy-hydrido complexes containing two triphenylphosphine groups.42,43 The [RuII(terpy)(ampy)H]+ complex has the amine nitrogen trans to H, with the [RuII(terpy)(ampy)H]+ complex with the amine nitrogen cis to the H more than 0.2 eV higher in both electronic and free energies. Some possible reaction intermediates were also identified for reaction (5) of the Ru-ampy complex (Fig. 13). The geometry of the intermediates differs by (i) the relative positions of H and CO2 to the singly coordinated ampy, (ii) the coordination N of singly coordinated ampy (through N amine or N pyridyl), and (iii) the orientation of the uncoordinated pyridyl ring. The molecule with H and the amine nitrogen trans to H in the axial positions, CO2 and the terpy N's in the equatorial positions, with one uncoordinated pyridyl ring, has the lowest energy. The aromatic pyridyl ring is not bonded to ruthenium, orientated near parallel to the terpy rings, and stabilized by π–π interactions between the aromatic rings. A similar uncoordinated pyridyl ring, also orientated near parallel to terpy rings, is observed for the solid-state structure of a ruthenium(II) polypyridyl complex [Ru(terpy)(proline)(PPh3)],44 though the distance between the rings was much larger in the latter.
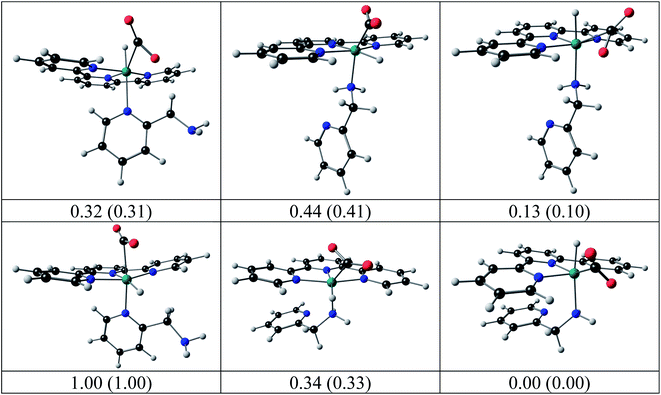 | ||
| Fig. 13 Possible intermediates for reaction (5) calculated by DFT, relative electronic energy, with free energy in brackets (eV), indicated. Colour scheme used for atoms (online version): Ru (green), O (red), C (black), N (blue), and H (white). | ||
DFT calculations identified the geometries and energies of the ruthenium reactants, products, and possible reaction intermediates involved in the kinetic reactions measured in this study. The DFT calculated energies show that the solvent-formato exchange and the formato-hydrido conversion reactions have negative (favourable) energies to proceed spontaneously and that the reactions involving en-containing molecules, have the more negative (favourable) energies, followed by ampy-containing molecules, in agreement with a faster reaction for en-containing molecules and slower reactions for bipy-containing molecules.
Overall discussion
The newly studied ampy complex reacts 11–18 times slower than the en complex under the selected conditions. This results from displacing the ethylenediamine ligand by 2-(aminomethyl)pyridine and the π-back bonding effect of the pyridine ring. A similar effect was observed for the corresponding complex with 2,2′-bipyridine (bipy) as a N^N bidentate spectator ligand. The stronger π-back bonding effect of bipy decreased the reactivity of the Ru(II) complex by many orders of magnitude, such that the hydride transfer reaction to the NAD+ coenzyme was extremely slow (see Fig. S1†). By way of comparison, the NAD+ reduction reaction catalysed by [RuII(terpy)(ampy)(H2O/EtOH)]2+ completes within 21 h and is accompanied by an absorbance increase of ca. 1.3 at 340 nm (due to formation of NADH, Fig. 7b), whereas ΔA340 during the reaction catalysed by [RuII(terpy)(bipy)(H2O/EtOH)]2+ reaches a value of only 0.2 after ca. 42 h under the same experimental conditions (Fig. S1†).The studied conversion of NAD+ to NADH in the presence of formate starts with the anation of the [RuII(terpy)(ampy)(H2O/EtOH)]2+ complex (see Scheme 1), which leads to the generation of the [RuII(terpy)(ampy)(HCOO)]+ complex (step 1). In the second step, the excess of HCOO− enables the formation of the outer-sphere ion-pair complex {[RuII(terpy)(ampy)(HCOO)]+·HCOO−}. Subsequently (step 3), the slow, formate-induced rearrangement of the formato complex (from an end-on to an O,H bonding mode of formate) occurs. The O,H-bonded format complex releases the formate-CO2 adduct and forms the hydrido complex [RuII(terpy)(ampy)H]+ in step 4. The latter complex donates the hydride anion to NAD+ to form NADH in a non-rate determining step, and regenerates the [RuII(terpy)(ampy)(H2O/EtOH)]2+ complex (step 5). In this way, the catalyst is reformed, as shown in the overall reaction Scheme 1. Since the reduction of NAD+ to NADH by NaBH4 occurs on a much shorter time scale24 than the decarboxylation reaction of the precursor {[RuII(terpy)(ampy)(HCOO)]+·HCOO−}, the release of a formate-CO2 adduct is suggested to be the rate-determining step of the overall redox process, catalysed by the Ru(II)-ampy complex (see Scheme 1).
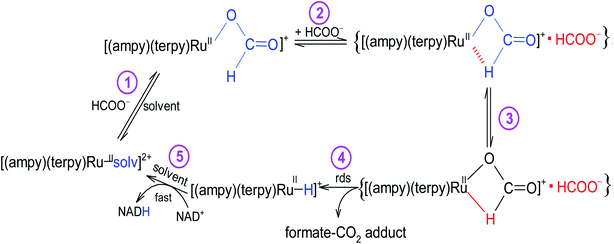 | ||
| Scheme 1 The mechanism proposed for the NAD+ coenzyme reduction in the presence of formate catalysed by a non-organometallic ruthenium(II) polypyridyl amine complex. | ||
Author contributions
MCh performed the synthetic work and kinetic measurements. JC performed DFT calculations. AK and RvE developed the manuscript concept and accepted responsibility for the reported work. All authors contributed equally to writing the manuscript.Conflicts of interest
There is no conflict of interest among the authors.Acknowledgements
This project was supported financially by the National Science Center, Poland, Grant No. 2019/33/N/ST4/00700. J. Conradie has received support from the South African National Research Foundation (grant numbers 129270 and 132504). The High-Performance Computing facility of the UFS, the CHPC of South Africa (Grant No. CHEM0947), and the Norwegian Supercomputing Program (UNINETT Sigma2, Grant No. NN9684K) are acknowledged for computer time.References
- I. Pérez-Torres, V. Guarner-Lans and M. E. Rubio-Ruiz, Int. J. Mol. Sci., 2017, 18, 2098 CrossRef.
- R. L. Reyes and K. Tanaka, Kimika, 2017, 28, 32 CrossRef.
- W. Xiao, R. S. Wang, D. E. Handy and J. Loscalzo, Antioxid. Redox Signaling, 2018, 28, 251 CrossRef CAS PubMed.
- L. Chaiswing, W. H. St. Clair and D. K. St. Clair, Antioxid. Redox Signaling, 2018, 29, 1237 CrossRef CAS PubMed.
- M. D. Forrest, bioRxiv, 2015, 019307 Search PubMed.
- B. Poljsak, J. Clin. Exp. Oncol., 2016, 5, 4 CrossRef.
- S. M. Hong, S. W. Hwang, T. Wang, C. W. Park, Y. M. Ryu, J. H. Jung, J. H. Shin, S. Y. Kim, J. L. Lee, C. W. Kim, J. L. Lee, C. W. Kim, G. Yoon, K. H. Kim, S. J. Myung and K. Y. Choi, Cancer Sci., 2019, 110, 629 CrossRef CAS PubMed.
- A. F. Santidrian, A. Matsuno-Yagi, M. Ritland, B. B. Seo, S. E. LeBoeuf, L. J. Gay, T. Yagi and B. Felding-Habermann, J. Clin. Invest., 2013, 123, 1068 CrossRef CAS PubMed.
- I. Batinic-Haberle, A. Tovmasyan and I. Spasojevic, Redox Biol., 2015, 5, 43 CrossRef CAS PubMed.
- Redox-active therapeutics. Oxidative stress in applied basic research and clinical practice, ed. I. Batinic-Haberle, J. Reboucas and I. Spasojevic, Springer International Publishing, Switzerland, 2016 Search PubMed.
- L. Chaiswing, L. W. H. St. Clair and D. K. St. Clair, Antioxid. Redox Signaling, 2018, 29, 1237 CrossRef CAS PubMed.
- C. Hegedűs, K. Kovács, Z. Polgár, Z. Regdon, É. Szabó, A. Robaszkiewicz, H. J. Forman, A. Martner and L. Virág, Redox Biol., 2018, 16, 59 CrossRef PubMed.
- K. Wang, J. Jiang, Y. Lei, S. Zhou, Y. Wie and C. Huang, Trends Biochem. Sci., 2019, 44, 401 CrossRef CAS PubMed.
- A. Privat-Maldonado, A. Schmidt, A. Lin, K. D. Weltmann, K. Wende, A. Bogaerts and S. Bekeschus, Oxid. Med. Cell. Longevity, 2019, 9062098 CAS.
- J. L. Quiles, C. Sánchez-González, L. Vera-Ramírez, F. Giampieri, M. D. Navarro-Hortal, J. Xiao, J. Llopis, M. Battino and A. Varela-López, Antioxid. Redox Signaling, 2020, 33, 860 CrossRef CAS PubMed.
- A. M. Barbosa, J. F. Sarmento-Neto, J. E. R. Menezes Filho, I. C. G. Jesus, D. S. Souza, V. M. N. Vasconcelos, F. D. l. Gomes, A. Lara, J. S. S. Araújo, S. S. Mattos, C. M. L. Vasconcelos, S. Guatimosim, J. S. Cruz, I. Batinic-Haberle, D. A. M. Araújo, J. S. Rebouças and E. R. Gomes, Oxid. Med. Cell. Longevity, 2020, 4850697 CAS.
- S. Betanzos-Lara, A. Habtemariam and P. J. Sadler, J. Mex. Chem. Soc., 2013, 57, 160 CAS.
- J. J. Soldevilla-Barreda, I. Romero-Canelon, A. Habtemariam and P. J. Sadler, Nat. Commun., 2015, 6, 6582 CrossRef PubMed.
- C. Imberti and P. J. Sadler, Adv. Inorg. Chem., 2020, 75, 3 CrossRef CAS.
- P. Zhang and P. J. Sadler, J. Organomet. Chem., 2017, 839, 5 CrossRef CAS.
- J. P. C. Coverdale, J. Song, G. J. Clarkson, J. Kasparkova, A. Habtemariam, V. Brabec, J. A. Wolny, V. Schüneman and P. J. Sadler, Dalton Trans., 2018, 47, 7178 RSC.
- J. J. Soldevila-Barreda, P. C. A. Bruijnincx, A. Habtemariam, G. J. Clarkson, R. J. Deeth and P. J. Sadler, Organometallics, 2012, 31, 5958 CrossRef CAS.
- M. J. Chow and W. H. Ang, in Inorganic and Organometallic Transition Metal Complexes with Biological Molecules and Living Cells, ed. K. K.-W. Lo, Academic Press, 2017, ch. 4, pp. 119–146 Search PubMed.
- M. Chrzanowska, A. Katafias and R. van Eldik, Inorg. Chem., 2020, 59, 14944 CrossRef CAS PubMed.
- M. Chrzanowska, A. Katafias, O. Impert, A. Kozakiewicz, A. Surdykowski, P. Brzozowska, A. Franke, A. Zahl, R. Puchta and R. van Eldik, Dalton Trans., 2017, 46, 10264 RSC.
- M. Chrzanowska, A. Katafias, A. Kozakiewicz, R. Puchta and R. van Eldik, J. Coord. Chem., 2018, 71, 1761 CrossRef CAS.
- M. Chrzanowska, A. Katafias, A. Kozakiewicz and R. van Eldik, Inorg. Chim. Acta, 2020, 504, 119449 CrossRef CAS.
- C. D. Hubbard, D. Chatterjee, M. Oszajca, J. Polaczek, O. Impert, M. Chrzanowska, A. Katafias, R. Puchta and R. van Eldik, Dalton Trans., 2020, 49, 4599 RSC.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943 CrossRef CAS.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. F. Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 Search PubMed.
- S. Kern and R. van Eldik, Inorg. Chem., 2012, 51, 7340 CrossRef CAS PubMed.
- W.-H. Wang, S. Xu, Y. Manaka, Y. Suna, H. Kambayashi, J. T. Muckerman, E. Fujita and Y. Himeda, ChemSusChem, 2014, 7, 1976 CrossRef CAS PubMed.
- X.-J. Yang, F. Drepper, B. Wu, W.-H. Sun, W. Haehnel and C. Janiak, Dalton Trans., 2005, 256 RSC.
- K. Qvortrup, C. J. McKenzie and A. D. Bond, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, m1400 CrossRef CAS.
- N. Grover, N. Gupta, P. Singh and H. H. Thorp, Inorg. Chem., 1992, 31, 2014 CrossRef CAS.
- H. Konno, A. Kobayashi, K. Sakamoto, F. Fagalde, N. E. Katz, H. Saitoh and O. Ishitani, Inorg. Chim. Acta, 2000, 299, 155 CrossRef CAS.
- A. Pramanik, N. Bag and A. Chakravorty, J. Chem. Soc., Dalton Trans., 1992, 97 RSC.
- P. Kumar, A. K. Singh, J. K. Saxena and D. S. Pandey, J. Organomet. Chem., 2009, 694, 3570 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra01890j |
| This journal is © The Royal Society of Chemistry 2022 |